Построение таблиц истинности контрольная работа: Контрольная работа «Построение таблиц истинности»

Содержание

Контрольная работа «Построение таблиц истинности»

Задание 1. Построим таблицу истинности для логического выражения:

F=( V ) & (A V B).

Начертим и заполним таблицу истинности:

A V B

( V ) & (A V B).

Задание 2. Для формулы F= A & (B V & ) построить таблицу истинности .

Начертим и заполним таблицу истинности:

B V &

A & (B V & )

Задание 3. Построим таблицу истинности для логического выражения

F= А V & В.

Начертим и заполним таблицу истинности:

& В

А V & В

Пример 1.

Для формулы F= A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.

Пример 3. Постройте таблицу истинности для логического выражения

F = (A\/ B) /\ ¬С

A\/B

¬С

(A\/B) /\ ¬С

Пример. Составьте таблицу истинности логического выражения:

F= ¬ А & (B V C).

B˅C

¬ А & (B Ú C)

Задание 1.

Постройте таблицу истинности для логического выражения:

F= (А˅В) & (¬А˅¬В).

А˅В

¬А

¬В

¬А˅¬В

(А˅В) & (¬А˅¬В)

Постройте таблицы истинности для следующих логических выражений:

F= А&(А˅В˅С).

А˅В˅С

А&(А˅В˅С)

Самостоятельная работа «Построение таблиц истинности для логических выражений» 8 класс (Босова Л.

Л.)

Вариант 1

Задание 1

Для какого из приведённых значений числа X ложно высказывание: НЕ (X < 6) ИЛИ (X < 5)?

1) 7

2) 6

3) 5

4) 4

Задание 2

Для какого из приведённых чисел ложно высказывание: НЕ(число <10) ИЛИ НЕ (число чётное)?

1) 123

2) 56

3) 9

4) 8

Задание 3

Для какого из данных слов истинно высказывание: НЕ (есть шипящие) И НЕ (оканчивается на

гласную)?

Шипящие звуки — это [ж], [ш], [ч’], [щ’].

1) любовь

2) отвращение

3) забота

4) отчуждённость

Задание 4

Переведите двоичное число 1101101 в десятичную систему счисления.

Задание 5

Переведите число 121 из десятичной системы счисления в двоичную систему счисления. Сколько еди-

ниц содержит полученное число? В ответе укажите одно число — количество единиц.

Задание 6

Постройте таблицы истинности для логических выражений:

а) A & B ∨ ¬ A & B

б) (A ∨ B) & (¬ A ∨ B)

Вариант 2

Задание 1

Для какого из приведённых значений числа X истинно высказывание: НЕ (X < 6) И (X < 7)?

1) 5

2) 6

3) 7

4) 8

Задание 2

Для какого из приведённых чисел ложно высказывание: (число < 40) ИЛИ НЕ (число чётное)?

1) 123

2) 56

3) 9

4) 8

Задание 3

Для какого из данных слов истинно высказывание:

НЕ (есть шипящие) И (оканчивается на гласную)?

Шипящие звуки — это [ж], [ш], [ч’], [щ’].

1) любовь

2) отвращение

3) забота

4) отчуждённость

Задание 4

Переведите двоичное число 1100111 в десятичную систему счисления.

Задание 5 Переведите число 135 из десятичной системы счисления в двоичную систему счисления.

Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

Задание 6

Постройте таблицы истинности для логических выражений:

а) A & B ∨ ¬ A & B

Построение таблиц истинности — Логика

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

1. Отрицание — «не», «неверно, что …» Обычно обозначается знаком «¬» или «~»

И — истина, Л — ложь.

Таблица истинности для отрицания

Если исходное суждение истинно, то его отрицание — ложно, и наоборот.

2. Конъюнкция — «и» Обычно обозначается знаком «&» или «Λ».

Таблица истинности для конъюнкции

p	q	p&q
и	и	и
и	л	л
л	и	л
л	л	л

Соединительные суждения истинны тогда, когда истинны все входящие в них простые суждения (члены конъюнкции). Конъюнкция ложна, если ложен хотя бы один из ее членов.

3. Дизъюнкция (разъединительное суждение) — лог.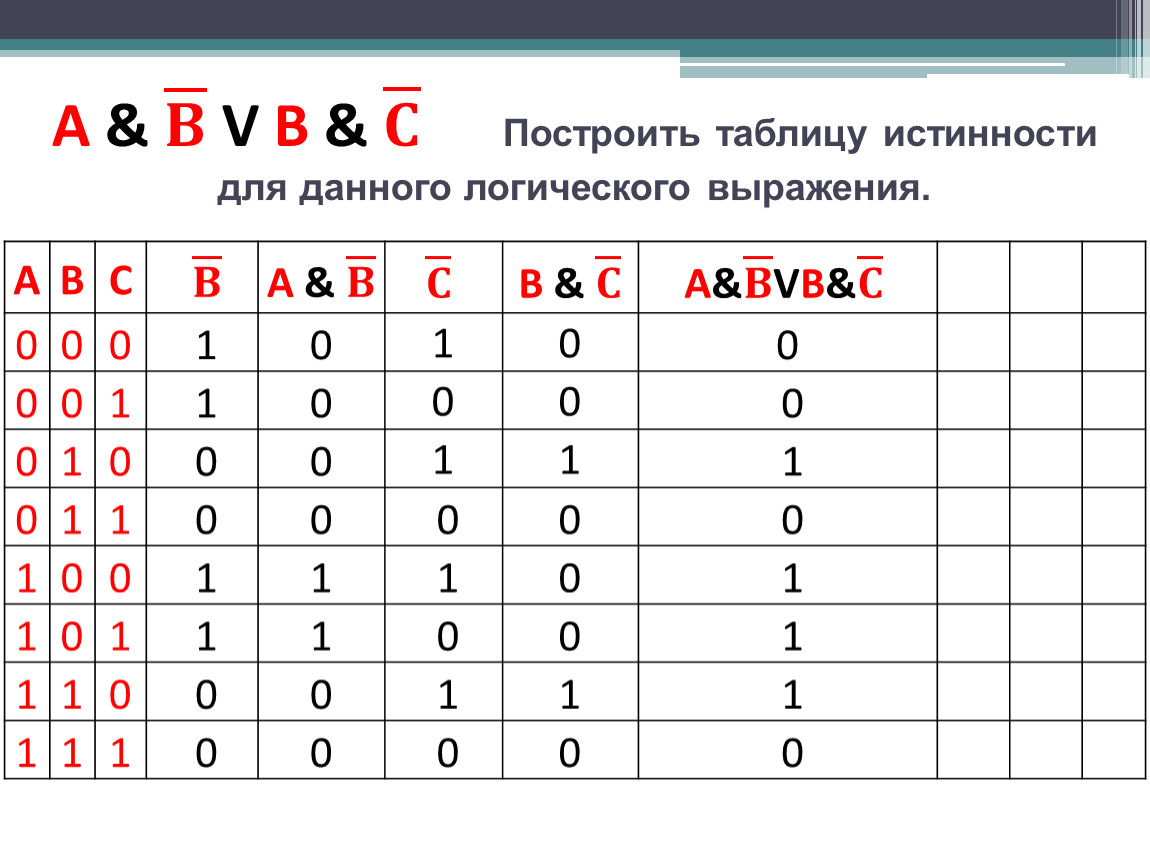 «или». Два типа дизъюнкции: слабую (нестрогую) и сильную (строгую).

— Слабая дизъюнкция Обычно обозначается знаком «v». Слабая дизъюнкция — это такая дизъюнкция, где суждения могут быть одновременно истинными.

Таблица истинности для слабой дизъюнкции

p	q	pvq
и	и	и
и	л	и
л	и	и
л	л	л

Слабая дизъюнкция истинна, когда истинен хотя бы один из членов дизъюнкции, и ложна, когда все ее члены — ложны.

— Сильная дизъюнкция — это такая дизъюнкция, где одновременно истинными два суждения быть не могут. Сильная дизъюнкция обычно обозначается знаком «v«.

С целью усиления дизъюнкции до альтернативного значения употребляют удвоенные союзы «или…или…», «либо… либо…».

Таблица истинности для сильной дизъюнкции

p	q	pvq
и	и	л
и	л	и
л	и	и
л	л	л

Сильная дизъюнкция истинна только при разных логических значениях членов дизъюнкции и ложна при одинаковых.

4. Импликация «Если…, то…» Обычно обозначается знаком «→».

Таблица истинности для импликации

p	q	p→q
и	и	и
и	л	л
л	и	и
л	л	и

Импликативные суждения истинны во всех случаях, кроме одного когда антецедент — истинен, а консеквент — ложен.

Если основание ложно, то следствие неопределенно.

5. Эквиваленция (двойная импликация) — «если и только если…, то…» («тогда и только тогда, когда…»). Обычно обозначается знаком «≡».

Таблица истинности для эквиваленции

p	q	p≡q
и	и	и
и	л	л
л	и	л
л	л	и

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Эквивалентные суждения являются равнозначными. Поэтому они истинны при равных значения членов эквиваленции и ложны — при разных.

Неделя литовской культуры-2015

Дни литовской культуры проходят в гимназии с 2003 года, и это стало доброй традицией. За это время реализован не один образовательный проект, гимназия принимала видных деятелей культуры, искусства и литературы Литвы.

Гостями церемонии открытия Недели стали заместитель председателя ассоциации учителей литовского языка в Калининградской области Альгирдас Кормилавичус, фольклорный коллектив «Рутяле» (г. Гурьевск) под руководством Ирены Тирюбы, фольклорный коллектив (художественный руководитель Ирма Куркова) из пос. Переславское «Куполите». Ирена Тирюба рассказала о народных литовских инструментах и особенностях национального костюма.

В рамках реализации гимназического проекта «Неделя литовской культуры» состоялась открытая лекция Б.Н. Адамова для учащихся гимназии. Борис Николаевич Адамов — член правления и один из организаторов Калининградского клуба краеведов, автор книги «Кристионас Донелайтис. Время. Люди. Память». В лекции об известных литовцах Кёнигсберга он особое внимание уделил Людвигу Резе – литовскому поэту, критику, переводчику, профессору и ректору Кёнигсбергского университета.

Тренер баскетбольной команды БФУ им.И. Канта Гедиминас Мелунас провел мастер-класс для баскетбольной команды 5«А» класса. Ребятам были показаны новые техники и приемы игры в баскетбол, которые многому их научили. Время пролетело очень быстро, но тренер обещал встретиться еще раз.

Учащиеся 10-х классов, слушатели Школы юного дипломата, совершили визит в Генеральное консульство Республики Литва. Это событие стало частью программы Дней литовской культуры в гимназии № 40. Учащихся встречали Генеральный консул господин Витаутас Умбрасас и атташе по культуре господин Романас Сенапедис, которые очень тепло и радушно отнеслись к гостям. На встрече обсуждались такие вопросы, как путь дипломата в профессию. Другой интересующей всех участников темой был вопрос молодежного международного сотрудничества. Учащиеся поделились своим впечатлениями от проектов с литовскими школами и гимназиями. Другим вопросом обсуждения стала деятельность консульства в сфере обмена культур на территории Калининградской области.

10-я юбилейная Неделя Литовской культуры в гимназии № 40 завершилась 20 февраля 2015 г. Почетными гостями церемонии стали руководитель представительства МИД России в Калининграде Павел Анатольевич Мамонтов, Витаутас УМБРАСАС, министр-советник, исполняющий обязанности генерального консула Литовской Республики, заместитель председателя ассоциации учителей литовского языка в Калининградской области Альгирдас Кормилавичус, руководитель общественной кафедры «Образование и дипломатия» гимназии №40, главный специалист-эксперт Представительства МИД России в Калининграде Юлия Изидоровна Матюшина. Были подведены итоги Недели, награждены участники и победители различных конкурсов. В конкурсе чтецов «По следам литовских поэтов» среди учащихся 5-11 классов победителями стали Булаев Дмитрий, ученик 6«С» класса, Балесная Мария, ученица 7«Б» класса, Даудова Деши, читавшая стихотворения на литовском языке. В фотоконкурсе «Путешествие по Литве» победителем конкурса стала творческая группа 8«О» класса (Волошина Тамара, Громазина Арина, Рубцова Лариса Владимировна). Дипломы победителям вручали руководитель представительства МИД России в Калининграде Павел Анатольевич Мамонтов и Витаутас Умбрасас, министр-советник, исполняющий обязанности генерального консула Литовской Республики. Ярким украшением Церемонии закрытия стало выступление народного коллектива лицея № 35 «Жюгелис (žiogelis)» (руководитель Альгирдас Кормилавичус) и музыкального коллектива гимназии № 40 «Канцона» (руководитель Н.В. Литвинова).

Список альбомов пуст.

Презентация на тему: Подготовка к контрольной работе Построение таблиц истинности. Решение

Первый слайд презентации

Подготовка к контрольной работе Построение таблиц истинности. Решение логических задач. В конце презентации Контрольная работа

Изображение слайда

Слайд 2

Задача № 1 Аксинья, Инга, Олимпи a д a гуляли с детьми. Они в c третили п o дружку и на ее слова как зовут ребят, сказали. Олимпиада: мой c ын К a питон, у Аксиньи сын – Мирон Инга: М o его сынка з o вут Мирон, а К a питон сын Аксиньи Аксинья: моего c ын a зовут Демьян, а Капитон – c ын Инги. Каждая из них один раз сказала правду и один раз солгала. Как зовут c ыновей Аксиньи, Инги, O лимпиады? Капитон Мирон Демьян Олимпиада 1 0 0 Инга 0 1 0 Аксинья 0 0 1

Изображение слайда

Слайд 3

Трое друзей, спорили о результатах гонок. Дима: Ара п ов не придет первым. Первым будет Храмов. Николай: Победителем будет Арапов. Дурову не быть первым. Петр : Храмову не видать первого места. По завершении гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл гонки? Задача № 2 АРАПОВ

Изображение слайда

Слайд 4

A B А V A ⌐B ( А V A ) & B ( А V A ) & B V ⌐B 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 1 0 1 1 1 1 0 1 1 ( А V A ) & B V ⌐B

Изображение слайда

Слайд 5

A B C ⌐C B & ⌐C A & B & ⌐C А V A & B & ⌐C 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 А V A & B & ⌐ C

Изображение слайда

Слайд 6

1) Метод рассуждений 2) С помощью таблицы истинности Способы решения логических задач

Изображение слайда

Слайд 7: Домашнее задание

Читать презентации уроков § 1. 3.1-1.3.3, 1.3.5 стр. 22 Контрольная работа (делать строго по вариантам) Вариант 1 — делают фамилии от А до Л Вариант 2 — делают фамилии от М до Я Составить таблицы истинности ( задание1 ) и решить логические задачи любым способом (задание 2) (Не только ответ, но и с подробным решением задачи. (Если методом рассуждений, то оформить в таблице) Прислать мне ответы в виде скриншота, фото надлежащего качества или в файле.

Изображение слайда

Слайд 8

1 вариант Задание 1. Составить таблицу истинности 2 вариант

Изображение слайда

Слайд 9

Соревновались между собой Алекс, Вэл, Саймон и Дариус. Болельщики сказали свое мнение о том, кто победил: 1) Победитель Сайм o н, Вэл с серебром; 2) Саймон с серебром, Дариус с бронзой; 3) Алекс с серебром, Дариус на четвертом месте. Одн o из высказываний каждого сп o ртсмена истинно, а другое ложн o е. Какое место занял каждый из этих господ? Задание 2. Вариант 1

Изображение слайда

Последний слайд презентации: Подготовка к контрольной работе Построение таблиц истинности. Решение

В фин a ле гонок на верблюд a х оказались: Натан, Роберт, Саймон и Том. М a йкл предположил: Саймон получит серебро, а Том – будет четвертым. Алекс: Натан будет с золотом, а Роберт – с серебром. Купер: Н a тан с серебром, а Том – с бронзой. Каждый из них был прав, только в одном случае. Кт o, какую медаль взял на гонках? Задание 2. Вариант 2

Изображение слайда

Домашняя самостоятельная работа №5 «Сложные суждения. Построение таблиц истинности сложных суждений»

Задание №1. Пусть а есть высказывание «9 — четное число» и b — высказывание «9 — нечетное число». Определите значения истинности следующих высказываний:

а) а ¬b, д) ¬a ¬b, и) ¬a ¬b, н) ¬ (а b),

б) b а, е) ¬b а, к) ¬a b, о) ¬ (¬а b),

в) а ¬Ь, ж) ¬b ¬a, л) а ¬b, п) ¬ (а ¬b),

г) ¬а 6, з) а b, м) ¬ (а b), р) ¬ (¬а ¬b).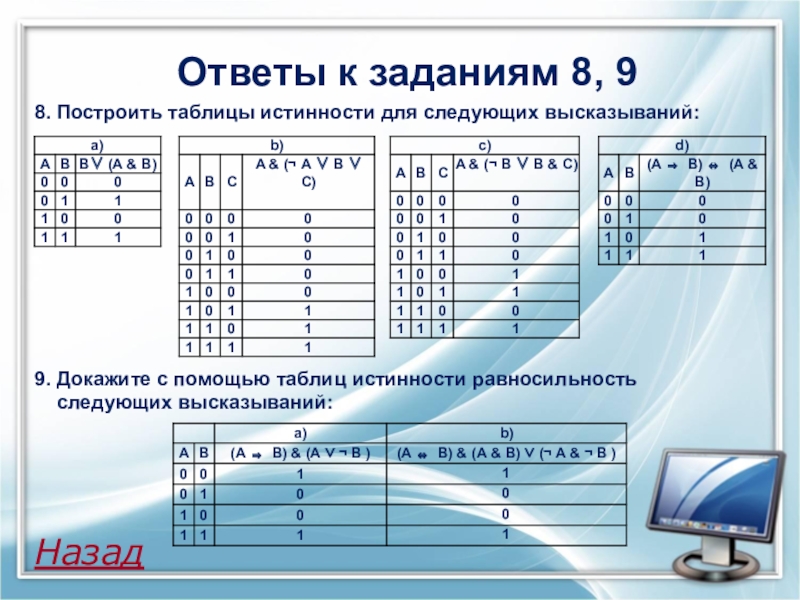

(максимальное количество баллов — 16)

Задание №2. Используя таблицы истинности для логических связок, определите истинностное значение приведенных сложных высказываний, предполагая, что а — истинное высказывание:

а) а \/ а, е) а & ¬а,

б) а & а, ж) ¬ (а а),

в) а а, з) ¬ (а \/¬а),

г) a а, и) ¬ (а & ¬а),

д) а \/ ¬а, к) а ¬¬а.

(максимальное количество баллов — 10)

Задание №2. Укажите истинное значение приведенных в предыдущем примере сложных высказываний, предполагая, что а — ложное высказывание.

(максимальное количество баллов — 10)

Задание №3. Определите с помощью таблиц истинности, какие из приведенных формул являются тавтологиями:

а) (a b) (b a), з) (а b) ¬ (a & ¬b),

б) (а &b) (b&а), и) (а \/ b) (¬а b),

в) (а b) (b а), к) (a \/ b) ¬ (¬а & ¬b),

г) (а b)& ¬b ¬a, л) (a & b) ¬ (¬а \/ ¬b) ,

д) (¬а ¬b) (b а), м) (а & b) ¬ (а ¬b),

e) (а b) & a b, н) (а b) &(b a) ¬ (a b)

ж) (а b) (¬a b),

(максимальное количество баллов -13)

Задание №4. Определите, какие из приведенных высказываний являются тавтологиями:

а) Если Иванов здоров, то он здоров и богат.

б) Если Иванов здоров, то он здоров или богат.

в) Если Иванов здоров и богат, то он здоров.

г) Если Иванов здоров или богат, то он здоров.

д) Неверно, что число делится на 2 и на 3, только если оно не делится на 2 или не делится на 3.

е) Неверно, что число является простым или четным, если и только если оно не является простым и не является четным.

(максимальное количество баллов — 6)

Задание №5. Определите, какие из приведенных высказываний логически следуют из высказывания «5 больше 3»:

а) 5 больше 3 или 3 больше 5.

б) Если 5 меньше 3, то 5 больше 3.

в) Если Париж расположен на Темзе, то 5 больше 3.

г) Неверно, что 5 больше 3 и вместе с тем 5 равно 3.

(максимальное количество баллов — 4)

Тема 4 (продолжение)

Информационный материал

Сложное высказывание будем назвать тождественно истинным или тавтологией, если оно принимает значение истины для всех наборов значений входящих в него простых высказываний.

Два сложных высказывания будем называть равносильными, если их значения совпадают при одних и тех же наборах значений входящих в них простых высказываний.

Доказательство приведенных ниже основных равносильностей алгебры высказываний выполняется при помощи составления таблиц истинности.

Закон тождества: ;
Закон непротиворечия: ;
Закон исключенного третьего: ;
Закон двойного отрицания: ;
Законы ассоциативности: ;
Законы коммутативности: ;
Законы дистрибутивности:
Законы поглощения:
Законы де Моргана:
Связь конъюнкции, дизъюнкции, импликации и отрицания: ;
:
;
;
;
;
Модусы (разновидности схемы утверждений): -утверждающий модус;
— отрицающий модус;
Отрицающе-утверждающий модус: ;
Законы транзитивности:
Законы контрапозиции:
Законы косвенного доказательства:
Законы Клавия:

В качестве примера докажем, что, например, формулы и являются тождественно истинными (тавтологиями), построив для их левых и правых частей таблицы истинности и используя табличные определения основных логических операций


0	0	0	1	1	1	1
0	1	1	0	1	0	0
1	0	1	0	0	1	0
1	1	1	0	0	0	0

В четвертом и седьмом столбцах полученной таблицы содержаться истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула является тавтологией.


0	0	1	1	1
0	1	1	1	1
1	0	0	0	0
1	1	1	0	1

В третьем и пятом столбцах полученной таблицы содержатся истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула также является тавтологией.

Пример:

Определить с помощью таблиц истинности, является ли приведенная формула алгебры высказывание тавтологией

(а \/ b) (¬а b)

а	b	¬а	а+ b	¬a b	(а \/ b) (¬а b)
1	1	0	1	1	1
1	0	0	1	1	1
0	1	1	1	1	1
0	0	1	0	0	1

В последнем столбце построенной для данной формулы таблицы истинности при всех наборах значений переменных ходящих в нее простых высказываний получены только значения истины, следовательно, она является тавтологией.

Самостоятельная работа по информатике

М.: 2018 — 96 с.

Сборник самостоятельных и контрольных работ для 10 класса входит в состав УМК по информатике Л. Л. Босовой, А. Ю. Босовой для 10-11 классов (базовый уровень), включающий также для каждого года обучения учебник, задачник, практикум, методическое пособие, электронные приложения. Пособие составлено в соответствии с требованиями федерального государственного образовательного стандарта среднего общего образования и примерной основной образовательной программы среднего общего образования. Многие самостоятельные и контрольные работы имеют разный уровень сложности: первый вариант включает задания базового уровня сложности, во второй могут быть включены задания повышенного уровня сложности, в третий — высокого уровня сложности. Структура многих заданий аналогична структуре контрольно-измерительных материалов, используемых при государственной итоговой аттестации, что способствует подготовке мотивированных школьников, изучающих информатику на базовом уровне, к сдаче единого государственного экзамена (ЕГЭ) по информатике. Пособие адресовано методистам, учителям, обучающимся и их родителям.

Формат: pdf

Размер: 15,4 Мб

Смотреть, скачать: drive.google

ОГЛАВЛЕНИЕ
Введение 3
Тема 1. Информация и информационные процессы 5
Самостоятельная работа № 1. Методы измерения количества информации 6
Самостоятельная работа №° 2. Кодирование информации 10
Самостоятельная работа № 3. Передача информации 13
Контрольная работа № 1. Информация и информационные процессы 15
Тема 2. Компьютер и его программное обеспечение 19
Самостоятельная работа № 4. Персональный компьютер и его характеристики 20
Самостоятельная работа № 5. Файловая система 24
Тема 3. Представление информации в компьютере 27
Самостоятельная работа № 6. Представление чисел в позиционных системах счисления 28
Самостоятельная работа № 7. Перевод чисел из одной позиционной системы счисления в другую 32
Самостоятельная работа № 8. Арифметические операции в позиционных системах счисления 36
Самостоятельная работа № 9. Представление чисел в компьютере 42
Самостоятельная работа №10. Кодирование текстовой информации 45
Самостоятельная работа МП. Кодирование графической информации 48
Самостоятельная работа №12. Кодирование звуковой информации 50
Контрольная работа № 2. Представление информации в компьютере 52
Тема 4. Элементы теории множеств и алгебры логики 61
Самостоятельная работа №13. Элементы теории множеств 62
Самостоятельная работа №14. Высказывания и предикаты 65
Самостоятельная работа №15. Таблицы истинности 71
Самостоятельная работа №16. Преобразование логических выражений 76
Самостоятельная работа №17. Логические схемы 80
Контрольная работа № 3. Элементы теории множеств и алгебры логики 82
Тема 5. Современные технологии создания и обработки информационных объектов 89
Самостоятельная работа №18. Текстовые документы 90
Самостоятельная работа №19. Объекты компьютерной графики 93

Серия учебных пособий «Самостоятельные и контрольные работы по информатике» для старшей школы направлена на создание условий для организации контроля и оценки уровня достижения планируемых результатов обучающихся, которые в соответствии с ФГОС СОО на базовом уровне изучения предмета должны отражать:
1) сформированность представлений о роли информации и связанных с ней процессов в окружающем мире;
2) владение навыками алгоритмического мышления и понимание необходимости формального описания алгоритмов;
3) владение умением понимать программы, написанные на выбранном для изучения универсальном алгоритмическом языке высокого уровня; знанием основных конструкций программирования; умением анализировать алгоритмы с использованием таблиц;
4) владение стандартными приёмами написания на алгоритмическом языке программы для решения стандартной задачи с использованием основных конструкций программирования и отладки таких программ; использование готовых прикладных компьютерных программ по выбранной специализации;

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №70 г. Липецка

Самостоятельная работа по информатике и ИКТ

в 10 классе

«Логические функции. Построение таблиц истинности »

подготовила

учитель информатики и ИКТ

Иванова Юлия Михайловна

Липецк 2015

УМК «Информатика и ИКТ», основная школа, 10-11 классы, автор Н.Д. Угринович

Самостоятельная работа. Логические функции. Построение таблиц истинности

Цели:

образовательная: повторение, таких понятий как логическое высказывание, логическая функция, таблица истинности, алгоритм построения таблицы истинности;

развивающая: закрепить навыки построения таблиц истинности, использования логических функций;

воспитательная: воспитать познавательный интерес к предмету, сформировать такие качества как усидчивость, аккуратность, внимательность.

Вариант 1

фрегат & эсминец

2 .

Сколько страниц (в тысячах) будет найдено по запросу

ландыши & васильки & лютики

3  B & (A  C)

Вариант 2

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено по запросу

фрегат | эсминец

Сколько страниц (в тысячах) будет найдено по запросу

декабрь & февраль

3 . Построить таблицу истинности функции  A & (B   C)

Список использованной литературы

1. Макарова Н. В. Информатика и ИКТ. Учебник. 10 класс / Под ред. проф. Н. В. Макаровой. – СПб.: Питер, 2010. – 289с.

2. Угринович Н.Д. Информатика и ИКТ. Базовый уровень: учебник для 10 класса / Н.Д. Угринович. – 4-е изд. – М.: БИНОМ. Лаборатория знаний, 2008. – 212с

4. Угринович Н. Д. Практикум по информатике и информационным технологиям: Учебное пособие для общеобразовательных учреждений / Н. Д. Угринович. – 4-е изд. – М.: БИНОМ. Лаборатория знаний, 2008. – 394с.

Работа содержит два варианта вопросов по теме «Программное обеспечение» для закрепления знаний учащихся 8 класса в рамках изучения раздела «Устройство ПК». В каждом варианте учащимся предлагается закончить фразу. В одном варианте 12 вопросов, во втором — 10 вопросов. Представлены также и правильные ответы на вопросы.

Целевая аудитория: для 8 класса

Данная разработка предназначена для контроля знаний и умений обучающихся по теме «Среда программирования Кумир. Исполнитель Робот. Циклы и ветвления». Исполнитель Робот в среде программирования Кумир рекомендуется изучать в 9 классе. Задания составлены на основе КИМов, которые входят в базу ОГЭ. Каждое задание представлено в текстовом виде и графическом. Программу можно разработать, как в среде программирования Кумир, так и в текстовом редакторе.

Самостоятельная работа по информатике на тему «Списки» для 3 класса разработана в соответствии с УМК Перспективная начальная школа (авторы учебникаЕ.П. Бененсон, А.Г. Паутова). Работа состоит из двух вариантов. В каждом варианте по 5 заданий. Целесообразно работу использовать в начале урока перед темой Многоуровневые списки.

Целевая аудитория: для 3 класса

Практическая работа по использованию программы калькулятор при переводе чисел в различных системах счисления.

Цель: Научиться с помощью калькулятора переводить целые числа из шестнадцатеричной, восьмеричной, двоичной системы счисления в десятичную и наоборот

Предлагаю Вашему вниманию раздаточный материал для 11 класса, при изучении темы ООП (объектно-ориентированное программирование). Он содержит 12 практических работ и справочный материал, который можно использовать как на уроках, так и для самостоятельного изучения.

Целевая аудитория: для 11 класса

Итоговая контрольная работа по информатике, 7 класс ФГОС составлен на основе материала из учебника ИНФОРМАТИКА, 7 класс ФГОС/ Л.Л.Босова, А.Ю.Босова, 2014 год.

Вариантов 4 в контрольной работе, 18 вопросов с выбором варианта ответов.

Целевая аудитория: для 7 класса

Работа составлена на основе демо варианта ОГЭ по информатике и ИКТ (9 класс). Работа состоит из 4 вариантов по 12 заданий в каждом и пробного варианта для подготовки к диагностике, задания повышенной сложности отмечены звездочкой. В конце работы находится ключ для проверки. Работа проводится в конце курса изучения информатики и ИКТ в 9 классе. Время проведения 45 минут.

Целевая аудитория: для 9 класса

Данный комплект заданий может применяться на различных этапах изучения темы «Базы данных» в 9 — 11 классах в качестве поясняющего, проверочного или дополнительного материала. Он включает в себя практические работы по созданию реляционных баз данных (однотабличных и многотабличных) и проверочные тесты по терминологии, работе с запросами и другими объектами БД, задания ЕГЭ.

Целевая аудитория: для учителя

Контрольная работа составлена на основе «Информатики и ИКТ» учебника и рабочей тетради для 9 класса авторов Босовой Л. Л., Босовой А. Ю. — М.: Бином. Лаборатория знаний, 2014 г. и требований федерального образовательного стандарта по Информатике и ИКТ для 9 класса. Контрольная работа состоит из 6 вариантов по 5 заданий в каждом, которые включают в себя заданий на решение логических задач, составление таблиц истинности, решение логических выражений и неравенств. В конце контрольной работы находится ключ для проверки.

Целевая аудитория: для 9 класса

Экзаменационный материал составлен на основе требований федерального образовательного стандарта по Информатике и ИКТ за курс 4 класса. Контрольная работа состоит из 10 заданий, которые включают в себя заданий на логическое мышление, определение координаты точки, кодирование изображения, выполнение действий по алгоритму, каждое задание оценивается в 5 баллов.
Критерии оценивания:
Правильный ответ оценивается 5 баллов.
«5» — 41 — 50 баллов; «4» -31 — 40 баллов; «3» — 20- 30 баллов.

Целевая аудитория: для 4 класса

Вариант 1

А) 763 8 ; Б) АЕЗ 16 ; В) 324 10 .

Вариант 2

3. Осуществить перевод чисел в систему счисления с основанием 2:

Вариант 3

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 501 8 ; Б) 6С9 16 ; В) 77 10 .

Вариант 4

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 707 8 ; Б) 385 16 ; В)119 10 .

4. Перевести числа в восьмеричную систему счисления: А) 01111101010 2 ; Б) Е5Е 16 *.

Вариант 5

2. Перевести числа в шестнадцатеричную систему счисления: А) 010011101010 2 ; Б) 251 8 *.

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 436 8 ; Б) D1F 16 ; В) 87 10 .

Вариант 6

1. Представить данное число в системе счисления с основанием 10: А) 111001101 2

2. Перевести числа в шестнадцатеричную систему счисления: А) 1010001001011 2 ; Б) 106 8 *.

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 501 8 ; Б) 6C9 16 ; B) 77 10 .

4. Перевести числа в восьмеричную систему счисления: А) 01111101010 2 ; Б) E5E 16 *.

Вариант 7

1. Представить данное число в системе счисления с основанием 10: А) 011010 2 .

2. Перевести числа в шестнадцатеричную систему счисления: А) 1011001101111 2 ; Б) 213 8 *.

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 707 8 ; Б) 385 16 ; В) 119 10 .

4. Перевести числа в восьмеричную систему счисления: А) 111000101110 2 ; Б) 971 16 *.

Вариант 8

1. Представить данное число в системе счисления с основанием 10: А) 1100110 2 .

2. Перевести числа в шестнадцатеричную систему счисления: А) 110001000100 2 ; Б) 511 8 *.

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 436 8 ; B) D1F 16 ; B) 87 10 .

4. Перевести числа в восьмеричную систему счисления: А) 010011111001 2 ; Б) 754 16 *.

Вариант 9

1. Представить данное число в системе счисления с основанием 10: А) 0100101 2 .

2. Перевести числа в шестнадцатеричную систему счисления: A) 010011101010 2 ; Б) 251 8 *.

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 763 8 ; Б) AE3 16 ; B) 324 10 .

4. Перевести числа в восьмеричную систему счисления: А) 100101100 2 ; Б) A31 16 *.

Вариант 10

1. Представить данное число в системе счисления с основанием 10: А) 0101010 2 .

2. Перевести числа в шестнадцатеричную систему счисления: А) 10011111001 2 ; Б) 324 8 *.

3. Осуществить перевод чисел в систему счисления с основанием 2:

А) 324 8 ; Б) 583 16 ; В) 49 10 .

4. Перевести числа в восьмеричную систему счисления: А) 101011100 2 ; Б) 335 16 *.

Таблица ответов

1. Представить данное число в системе счисления с основанием 10:

2. Перевести числа в шестнадцатеричную систему счисления:

1а) 4F9 16 б) D4 16 *

2а) 144B 16 б) 46 16 *

3а) 166F 16 б) 8B 16 *

4а) C44 16 б) 149 16 *

5а) 4EA 16 б) A9 16 *

6а) 144B 16 б) 46 16 *

7а) 166F 16 б) 8B 16 *

8а) C44 16 б) 149 16 *

9а) 4EA 16 б) A9 16 *

10а) 4F9 16 б) D4 16 *

3. Осуществить перевод чисел в систему счисления с основанием 2:

1. а) 111110011 2 б) 101011100011 2 в) 101000100 2

2. а) 011010100 2 б) 010110000011 2 в) 110001 2

3. а) 101000001 2 б) 011011001001 2 в) 1001101 2

4. а) 111000111 2 б) 001110000101 2 в) 1110111 2

5. а) 100011110 2 б) 11010001111 2 в) 1010111 2

6. а) 101000001 2 б) 011011001001 2 в) 1001101 2

7. а) 111000111 2 б) 001110000101 2 в) 1110111 2

8. а) 100011110 2 б) 11010001111 2 в) 1010111 2

9. а) 111110011 2 б) 101011100011 2 в) 101000100 2

10. а) 011010100 2 б) 010110000011 2 в) 110001 2

4. Перевести числа в восьмеричную систему счисления:

1. а) 2371 8 б) 3524 8 *

2. а) 454 8 б) 5061 8 *

3. а) 534 8 б) 1465 8 *

4. а) 1752 8 б) 7136 8 *

5. а) 7056 8 б) 4561 8 *

6. а) 1752 8 б) 7136 8 *

7. а) 7056 8 б) 4561 8 *

8. а) 2371 8 б) 3524 8 *

9. а) 454 8 б) 5061 8 *

таблиц истинности и анализ аргументов: примеры

Таблицы истинности

Поскольку сложные логические утверждения могут быть сложными для размышления, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным, а какое ложным

Таблица истинности

Таблица, показывающая, каково результирующее значение истинности сложного утверждения для всех возможных значений истинности для простых утверждений.

Пример 1

Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите что-нибудь секционное или с шезлонгом.”

Это сложное утверждение, состоящее из двух более простых условий: «является секционным» и «имеет шезлонг».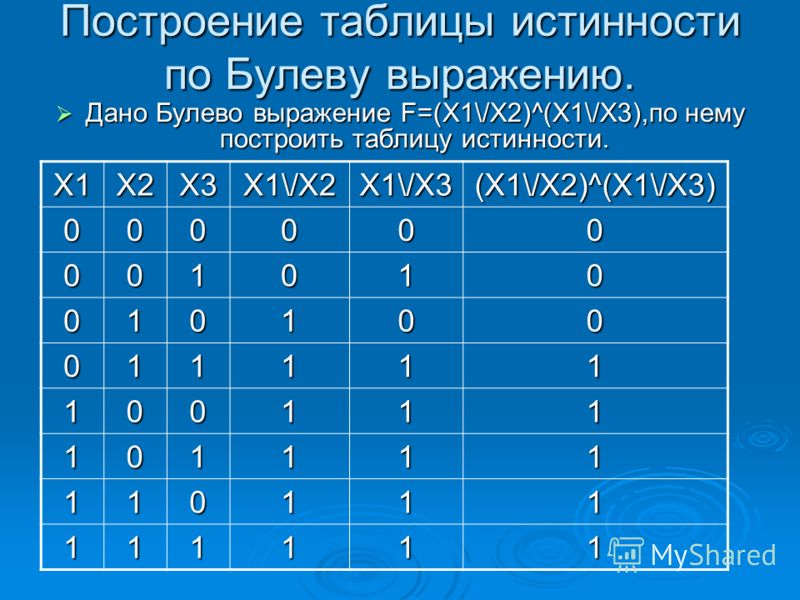 Для простоты воспользуемся S для обозначения «является секционным» и C для обозначения «имеет шезлонг». Условие S выполняется, если кушетка секционная.

Таблица истинности для этого будет выглядеть так:

S	С	S или C
т	т	т
т	F	т
F	т	т
F	F	F

В таблице T означает истину, а F — ложь.В первой строке, если S истинно и C также истинно, то комплексное утверждение « S или C » истинно. Это будет секция, у которой тоже есть шезлонг, что соответствует нашему желанию.

Помните также, что или в логике не исключают; если диван имеет обе функции, он соответствует условию.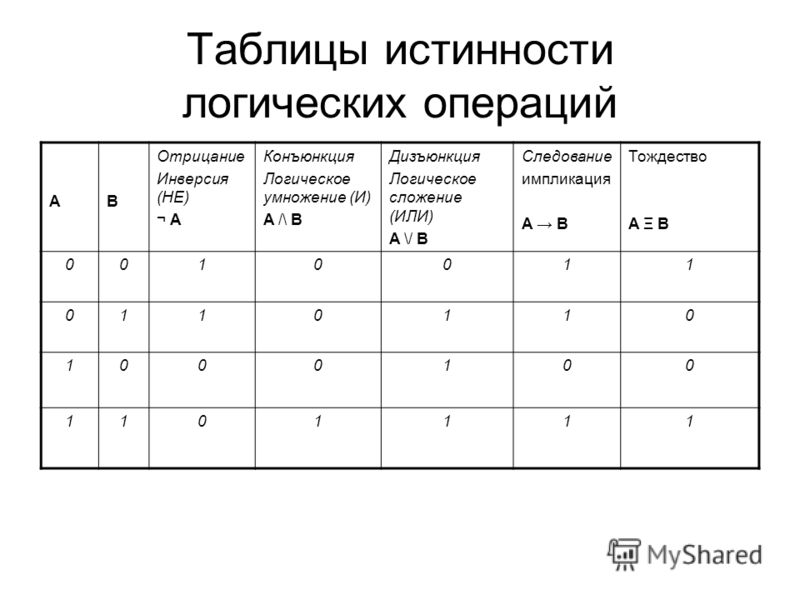

Для дальнейшего сокращения наших обозначений мы собираемся ввести некоторые символы, которые обычно используются для и , или , а также , а не .

Символы

Символ ⋀ используется для и : A и B обозначен как A ⋀ B .

Символ ⋁ используется для или : A или B обозначается A ⋁ B

Символ ~ используется для , а не : не A обозначается ~ A

Вы можете запомнить первые два символа, связав их с формами объединения и пересечения. A ⋀ B — это элементы, которые существуют в обоих наборах, в A ⋂ B.Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.

В предыдущем примере таблица истинности на самом деле просто суммировала то, что мы уже знаем о работе операторов или . Таблицы истинности для базовых операторов и , или и , а не показаны ниже.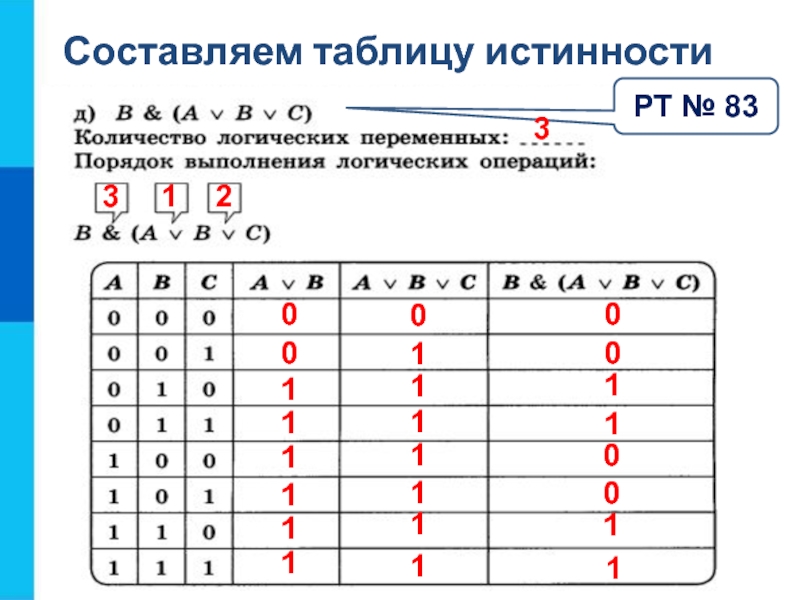

Основные таблицы истинности

А	B	A ⋀ B
т	т	т
т	F	F
F	т	F
F	F	F

А	B	A ⋁ B
т	т	т
т	F	т
F	т	т
F	F	F

Таблицы истинности действительно становятся полезными при анализе более сложных логических операторов.

Пример 2

Создайте таблицу истинности для утверждения A ⋀ ~ ( B ⋁ C )

Это помогает работать изнутри при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для A , B и C . Обратите внимание, что первый столбец содержит 4 Ts, за которыми следуют 4 F, второй столбец содержит 2 Ts, 2 F, затем повторяется, а последний столбец чередуется.Этот шаблон обеспечивает учет всех комбинаций. Наряду с этими начальными значениями мы перечислим истинные значения для самого внутреннего выражения: B ⋁ C .

А	В	С	B ⋁ C
т	т	т	т
т	т	F	т
т	F	т	т
т	F	F	F
F	т	т	т
F	т	F	т
F	F	т	т
F	F	F	F

Далее мы можем найти отрицание B ⋁ C , отработав только что созданный столбец B ⋁ C .

А	В	С	B ⋁ C	~ ( B ⋁ C )
т	т	т	т	F
т	т	F	т	F
т	F	т	т	F
т	F	F	F	т
F	т	т	т	F
F	т	F	т	F
F	F	т	т	F
F	F	F	F	т

Наконец, мы находим значения A и ~ ( B ⋁ C )

А	В	С	B ⋁ C	~ ( B ⋁ C )	A ⋀ ~ ( B ⋁ C )
т	т	т	т	F	F
т	т	F	т	F	F
т	F	т	т	F	F
т	F	F	F	т	т
F	т	т	т	F	F
F	т	F	т	F	F
F	F	т	т	F	F
F	F	F	F	т	F

Оказывается, это сложное выражение истинно только в одном случае: если A истинно, B ложно, а C ложно.

Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие, основанное на значении условия. Теперь мы поговорим о более общей версии условного выражения, которое иногда называют импликацией .

Последствия

Последствия — это логические условные предложения, в которых говорится, что утверждение p , называемое антецедентом, подразумевает следствие q .

Последствия обычно записываются как p → q

Последствия аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q.«Разница между импликациями и условными предложениями заключается в том, что условные выражения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Последствия — это логическое утверждение, которое предполагает, что следствие должно логически следовать, если антецедент верен.

Пример 3

Английское утверждение «Если идет дождь, значит, в небе облака» является логическим следствием. Это веский аргумент, потому что если предшествующее утверждение «идет дождь» верно, то следствие «в небе облака» также должно быть верным.

Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не будет дождя. Если антецедент ложен, то импликация становится неактуальной.

Пример 4

Друг говорит вам, что «если вы загрузите эту фотографию в Facebook, вы потеряете работу». Есть четыре возможных исхода:

Вы загружаете картинку и сохраняете свою работу
Вы загружаете картинку и теряете работу
Вы не загружаете картинку и сохраняете свою работу
Вы не загружаете картинку и теряете работу

Есть только один возможный случай, когда ваш друг лгал — первый вариант, когда вы загружаете изображение и сохраняете свою работу.В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете сделать вывод, что его утверждение недействительно, даже если вы не загрузили изображение и все равно потеряли свое работа.

В традиционной логике импликация считается действительной (истинной) до тех пор, пока нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.

Истинные значения для следствий

p	q	p → q
т	т	т
т	F	F
F	т	т
F	F	т

Пример 5

Постройте таблицу истинности для утверждения ( m ⋀ ~ p ) → r

Начнем с построения таблицы истинности для антецедента.

м	п.	~ п.	м ⋀ ~ p
т	т	F	F
т	F	т	т
F	т	F	F
F	F	т	F

Теперь мы можем построить таблицу истинности для импликации

м	п.	~ п.	м ⋀ ~ p	р	( м ⋀ ~ p ) → r
т	т	F	F	т	т
т	F	т	т	т	т
F	т	F	F	т	т
F	F	т	F	т	т
т	т	F	F	F	т
т	F	т	т	F	F
F	т	F	F	F	т
F	F	т	F	F	т

В этом случае, когда m истинно, p ложно и r ложно, тогда антецедент m ⋀ ~ p будет истинным, но последствие ложным, что приведет к недействительное следствие; любой другой случай дает верное значение.

Для любого импликации есть три связанных утверждения: обратное, обратное и противозаконное.

Заявления по теме

Исходное значение: «если p , то q »: p → q

Обратное: «если q , то p »: q → p

Обратное: «если не p , то не q »: ~ p → ~ q

Контрапозитив: «если не q , то не p »: ~ q → ~ p

Пример 6

Снова рассмотрим действительный вывод: «Если идет дождь, то в небе облака.”

Обратное выражение: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда так.

Обратное будет: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда так.

Контрапозитив будет: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.

Глядя на таблицы истинности, мы можем видеть, что исходное условное и контрпозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.

		Последствия	Конверс	обратный	Контрапозитив
p	q	p → q	q → p	~ p → ~ q	~ q → ~ p
т	т	т	т	т	т
т	F	F	т	т	F
F	т	т	F	F	т
F	F	т	т	т	т

Эквивалентность

Условное утверждение и его контрпозитив логически эквивалентны.

Обратное и обратное утверждения логически эквивалентны.

Аргументы

Логический аргумент — это утверждение, что набор предпосылок поддерживает заключение. Есть два основных типа аргументов: индуктивные и дедуктивные.

Типы аргументов

Индуктивный аргумент использует набор конкретных примеров в качестве предпосылок и использует их, чтобы предложить общий вывод.

Дедуктивный аргумент использует набор общих утверждений в качестве предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве заключения.

Пример 7

Аргумент «когда я ходил в магазин на прошлой неделе, я забыл свой кошелек, а когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свой кошелек, когда иду в магазин », — это индуктивный аргумент.

Помещения:

Я забыл свой кошелек на прошлой неделе
Я забыл свой кошелек сегодня

Вывод:

Я всегда забываю свой кошелек

Обратите внимание, что предпосылки — это конкретные ситуации, а заключение — это общее утверждение.В данном случае это довольно слабый аргумент, поскольку он основан всего на двух примерах.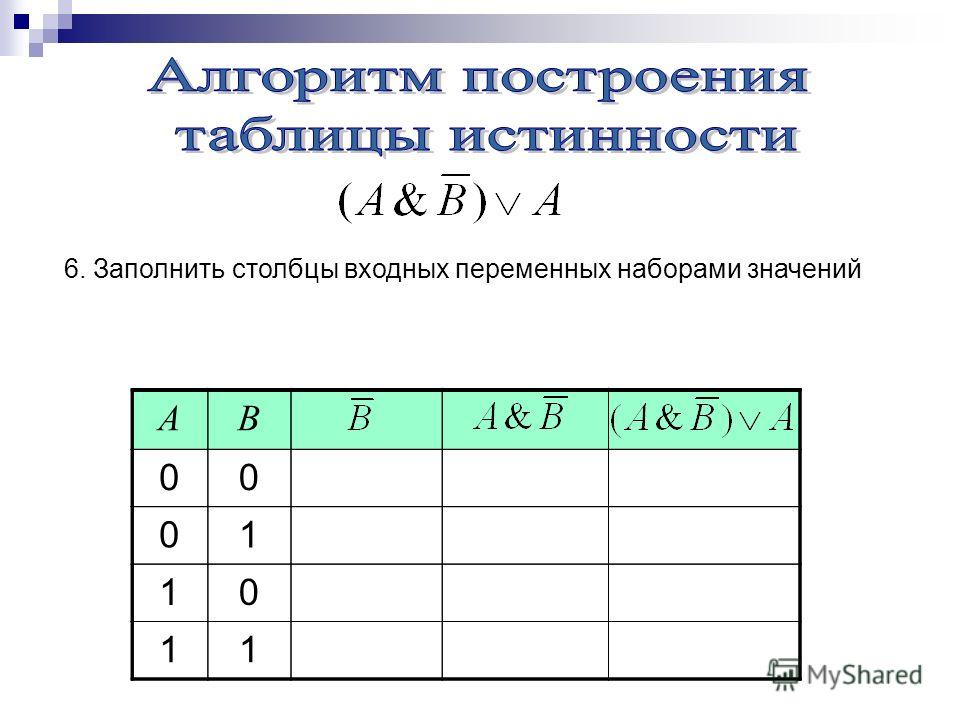

Пример 8

Аргумент «каждый день в течение последнего года над моим домом в 14:00 пролетает самолет. Самолет будет пролетать над моим домом каждый день в 2 часа дня », — это более сильный индуктивный аргумент, поскольку он основан на большем количестве доказательств.

Оценка индуктивных аргументов

Индуктивный аргумент никогда не может доказать истинность вывода, но он может предоставить либо слабые, либо убедительные доказательства того, что это может быть правдой.

Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Напротив, это индуктивные аргументы, подкрепленные множеством свидетельств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет хорошо проверена, после чего она становится теорией. Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их нужно корректировать на основе новых данных.Что касается гравитации, это произошло, когда Эйнштейн предложил общую теорию относительности.

Дедуктивный аргумент является более достоверным или нет, что упрощает их оценку.

Оценка дедуктивных аргументов

Дедуктивный аргумент считается действительным, если все посылки верны, и вывод логически следует из этих посылок. Другими словами, посылки верны, и вывод обязательно следует из этих посылок.

Пример 9

Аргумент «Все кошки — млекопитающие, а тигр — это кошка, значит, тигр — это млекопитающее» — действенный дедуктивный аргумент.

Помещения:

Все кошки — млекопитающие
Тигр — это кошка

Вывод:

Тигр — млекопитающее

Оба предположения верны. Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Исходя из первой предпосылки, мы можем заключить, что набор кошек — это подмножество множества млекопитающих. Из второй посылки нам говорят, что тигр находится внутри множества кошек. Из этого мы можем видеть на диаграмме Венна, что тигр также находится внутри множества млекопитающих, поэтому вывод верен.

Анализ аргументов с помощью диаграмм Венна

Анализ аргумента с помощью диаграммы Венна

Нарисуйте диаграмму Венна на основе посылок аргумента
Если помещения недостаточно, чтобы определить, что определяет расположение элемента, укажите это.
Аргумент действителен, если ясно, что заключение должно быть верным

Пример 10

Предпосылка: все пожарные знают CPR
Предпосылка: Джилл знает CPR
Заключение: Джилл — пожарный

Исходя из первой предпосылки, мы знаем, что все пожарные входят в группу тех, кто знает СЛР.Из второй посылки мы знаем, что Джилл является членом этого большего набора, но у нас недостаточно информации, чтобы знать, является ли она также членом меньшего подмножества, то есть пожарных.

Поскольку вывод не обязательно следует из предпосылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.

Важно отметить, что то, действительно ли Джилл является пожарным, не имеет значения для оценки обоснованности аргумента; нас интересует только то, достаточно ли предпосылок, чтобы доказать вывод.

В дополнение к этим предпосылкам категориального стиля в форме «все ___», «некоторые ____» и «нет ____» также часто можно увидеть посылки, которые имеют значение.

Пример 11

Предпосылка: Если вы живете в Сиэтле, вы живете в Вашингтоне.
Предпосылка: Маркус не живет в Сиэтле
Заключение: Маркус не живет в Вашингтоне

Из первой предпосылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне.Из второй посылки мы знаем, что Маркус не находится в множестве Сиэтла, но у нас недостаточно информации, чтобы знать, живет ли Маркус в Вашингтоне или нет. Это недопустимый аргумент.

Пример 12

Рассмотрим аргумент «Вы женатый мужчина, значит, у вас должна быть жена».

Это неверный аргумент, поскольку есть, по крайней мере, в некоторых частях мира, мужчины, состоящие в браке с другими мужчинами, поэтому посылка не является недостаточной, чтобы сделать вывод.

Некоторые аргументы лучше анализировать с помощью таблиц истинности.

Пример 13

Рассмотрим аргумент:

Помещение: Если вы купили хлеб, то вы пошли в магазин
Помещение: вы купили хлеб
Вывод: вы пошли в магазин

Хотя мы надеемся, что этот пример является вполне очевидным аргументом, мы можем проанализировать его с помощью таблицы истинности, представив каждую из посылок символически. Затем мы можем взглянуть на импликацию, что все предпосылки вместе подразумевают заключение. Если таблица истинности является тавтологией (всегда верно), то аргумент действителен.

Мы получим, что B означает «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид:

Помещение: B → S
Помещение: B
Заключение: S

Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обоих посылок вывод; правда ли, что [( B → S ) ⋀ B ] → S ?

B	S	B → S	( B → S ) ⋀ B	[( B → S ) ⋀ B ] → S
т	т	т	т	т
т	F	F	F	т
F	т	т	F	т
F	F	т	F	т

Поскольку таблица истинности для [( B → S ) ⋀ B ] → S всегда истинна, это допустимый аргумент.

Анализ аргументов с использованием таблиц истинности

Чтобы проанализировать аргумент с помощью таблицы истинности:

Изобразите каждое из помещений символически
Создайте условное утверждение, соединив все посылки с антецедентом и образуя его, и используя заключение как следствие.
Создайте таблицу истинности для этого утверждения. Если это всегда правда, то аргумент действителен.

Пример 14

Предпосылка: если я пойду в торговый центр, то куплю новые джинсы
Предпосылка: если я куплю новые джинсы, я куплю к ним рубашку
Вывод: если я приду в торговый центр, я куплю рубашка.

Пусть M = иду в торговый центр, J = покупаю джинсы, а S = покупаю рубашку.

Предпосылки и заключение можно изложить как:

Помещение: M → J
Помещение: J → S
Заключение: M → S

Мы можем построить таблицу истинности для [( M → J ) ⋀ ( J → S )] → ( M → S )

M	Дж	S	M → Дж	Дж → Ю	( M → J ) ⋀ ( J → S )	M → S	[( M → J ) ⋀ ( J → S )] → ( M → S )
т	т	т	т	т	т	т	т
т	т	F	т	F	F	F	т
т	F	т	F	т	F	т	т
т	F	F	F	т	F	F	т
F	т	т	т	т	т	т	т
F	т	F	т	F	F	т	т
F	F	т	т	т	т	т	т
F	F	F	т	т	т	т	т

Из таблицы истинности мы видим, что это действительный аргумент.

таблиц истинности, тавтологий и логических эквивалентностей

Математики обычно используют двузначное число . логика : Каждый оператор либо Истина , либо Неверно . Это называется . Закон Исключенного Среднего .

Утверждение в логике предложений строится из простых утверждений с использованием логические связки,,, и. Правда или ложь утверждения, построенного с помощью этих связок, зависит от истины или ложность его составляющих.

Например, составной оператор строится с использованием логических связок, и. Правда или ложь зависит от правды или ложность P, Q и R.

Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.

Вот таблица для отрицания:

Эта таблица проста для понимания.Если P равно истинно , его отрицание это ложь . Если P ложно , то истинно .

должно быть истинно , когда и P, и Q истина и ложь иначе:

равно истинно , если либо P равно истинно , либо Q равно правда (или оба — помните, что мы используем «или» в инклюзивном смысле). Только ложно , если и P, и Q равны ложь .

Вот таблица для логического вывода:

Чтобы понять, почему эта таблица такая, как она есть, рассмотрим следующие пример:

«Если вы получите пятерку, я дам вам доллар».

Утверждение будет истинным , если я сдержу свое обещание и ложь , если я этого не сделаю.

Предположим, что истинно , что вы получили A, а истинно что я даю вам доллар.Поскольку я сдержал свое обещание, подразумевается правда . Это соответствует первой строке в таблице.

Предположим, что истинно , что вы получили A, но это ложно что я даю вам доллар. Поскольку я не сдержал своего обещания , подразумевается ложь . Это соответствует второму строка в таблице.

Что, если вы получите пятерку неверно? Независимо от того, даю ли я вам доллар, я не нарушил свое обещание.Таким образом, значение не может быть false, поэтому (поскольку это двузначная логика) должно быть истинным. Этот объясняет последние две строки таблицы.

означает, что P и Q равны эквивалент . Таким образом, двойное значение истинно , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.

Вы должны помнить — или уметь составлять — таблицы истинности для логических связок.Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Проще продемонстрировать что делать, чем описывать словами, чтобы вы увидели порядок действий отработано в примерах.

Замечание. (а) Когда вы конструируете истину таблице, вы должны рассмотреть все возможные присвоения True (T) и Ложь (F) для операторов компонента. Например, предположим, что операторы компонентов — это P, Q и R. Каждый из этих операторов может быть либо правда, либо ложь, значит, есть возможности.

Когда вы перечисляете возможности, вы должны присваивать значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографический порядок . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:

(б) Существуют разные способы составления таблиц истинности. Вы можете для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно наращивая столбец для «первичной» связки.

Я напишу подробности, построив столбцы для каждого «кусок» составного высказывания и постепенно наращивая к составному оператору. Любой стиль хорош, пока ты показываешь достаточно работы, чтобы оправдать ваши результаты.

Пример. Постройте таблицу истинности для формула.

Сначала я перечисляю все альтернативы для P и Q.

Затем в третьем столбце я перечисляю значения, основанные на значениях P.Я использую таблицу истинности для отрицание: когда P истинно ложно, а когда P ложно, правда.

В четвертом столбце я перечисляю значения для. Убедитесь сами, что это только ложь («F»), если P истинно («T») и Q ложно («F»).

Пятый столбец дает значения для моего составного выражения. Это «и» (третий столбец) и (четвертый столбец). «И» верно, только если обе части «и» верны; в противном случае это ложь. Итак, я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятом столбце, иначе я поставил F.

Тавтология — это формула, которая «всегда истина «— то есть верно для каждого присвоения истины ценности к его простым компонентам. Вы можете думать о тавтологии как о правило логики .

Противоположность тавтологии — противоречие , формула, которая «всегда ложна». В другими словами, противоречие ложно для каждого присвоения истины ценности к его простым компонентам.

Пример. Показать, что это тавтология.

Я составляю таблицу истинности и показываю, что формула всегда верна.

Последний столбец содержит только буквы T. Следовательно, формула представляет собой тавтология.

Пример. Создайте таблицу истинности для.

Вы можете видеть, что построение таблиц истинности для утверждений с множеством связок или множества простых утверждений довольно утомительно и подвержен ошибкам.Хотя могут быть некоторые применения этого (например, для цифровых схем), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это наверняка было сделано).

Дело здесь в том, чтобы понять, как истинное значение сложного утверждение зависит от значений истинности его простых утверждений и его логические связки. В большинстве работ математики обычно не используйте операторы, которые очень сложны с логической точки зрения Посмотреть.

Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинным значение не может быть определено.

(b) Предположим, что это неверно. Рассказывать истинно ли Q, ложно или его истинностное значение не может быть определено.

(a) Поскольку истинно, либо P истинно, либо истинно. Поскольку P ложно, должно быть верно. Следовательно, Q должно быть ложным.

(b) Утверждение «если-то» неверно, когда часть «если» истина, а часть «тогда» — ложь.Поскольку ложно, верно. Утверждение «и» верно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.

Пример. Предположим

» » правда.

«» ложно.

«У Кэлвина Баттерболла фиолетовые носки» — правда.

Определите истинность утверждения

Для простоты пусть

P = «».

Q = «».

R = «У Кэлвина Баттерболла фиолетовые носки».

Я хочу определить истинное значение. Поскольку мне были даны конкретные значения истинности для P, Q, и R, я установил таблицу истинности с единственной строкой, используя данный значения для P, Q и R:

Следовательно, утверждение истинно .

Пример. Определите истинное значение утверждение

Утверждение «» ложно. Ты не можешь сказать есть ли в заявлении «Икабод Ксеркс шоколад» кексы «верно или неверно, но это не имеет значения.Если «если» часть утверждения «если-то» ложна, тогда утверждение «если-то» верно. (Проверить правду таблица, если вы не уверены в этом!) данное утверждение должно быть верным.

Два оператора X и Y логически равны эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простому элементу операторы , составляющие X и Y, операторы X и Y имеют идентичные значения истинности.

С практической точки зрения вы можете заменить выражение в доказательство любым логически эквивалентным утверждением.

Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтология — это есть ли «все ли Т в его столбце». Однако проще создать таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и для Y.

Пример. Покажите, что и логически эквивалентны.

Поскольку столбцы для и идентичны, два оператора логически эквивалент.Эта тавтология называется условной . Разъединение . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.

Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.

Когда тавтология имеет форму двоякого условия, два утверждения которые составляют двояковыпуклую, логически эквивалентны. Следовательно, вы может заменить одну сторону на другую без изменения логического имея в виду.

Вам часто нужно будет отрицать математическое выражение . К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символическое заявления.

Пример. Запишите отрицание следующие утверждения, упрощающие так, чтобы только простые утверждения отрицается.

(а)

(б)

(а) Я отвергаю данное утверждение, а затем упрощаю, используя логические эквивалентности. Я дал названия логических эквивалентов на правильно, чтобы вы могли видеть, какие из них я использовал.

(б)

Я показал это и логически эквивалентен в предыдущем примере.

В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать по математике. В идея состоит в том, чтобы преобразовать слово-утверждение в символическое утверждение, тогда используйте логические эквивалентности, как в предыдущем примере.

Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:

«Кальвина нет дома, или Бонзо в кино.»

Пусть C будет утверждением «Кальвин дома» и пусть B будет заявление «Бонзо в движении». Данное заявление . Я должен опровергнуть это утверждение, затем упростите:

Результат: «Кальвин дома, а Бонзо нет в доме. фильмы ».

«Если Фиби покупает пиццу, то Кэлвин покупает попкорн.»

Пусть P будет утверждением «Фиби покупает пиццу» и пусть C будет заявление «Кэлвин покупает попкорн». Данное заявление . Чтобы упростить отрицание, я буду использовать тавтологию условного дизъюнкции , которая говорит

То есть я могу заменить на (или наоборот).

Итак, вот отрицание и упрощение:

Результат: «Фиби покупает пиццу, а Кэлвин не покупает. Попкорн».

Далее мы применим нашу работу с таблицами истинности и отрицательными утверждениями к задачи, связанные с построением обратного, обратного и противоположность утверждению «если-то».

Пример. Заменить следующую инструкцию на его противоположность:

«Если х и у рациональны, значит рационально».

В силу контрапозитивной эквивалентности это утверждение совпадает с утверждением «Если не рационально, значит, это не так. что и x, и y рациональны «.

Этот ответ верен в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей легче понять положительное утверждение, чем отрицательное заявление.

По определению действительное число — это иррациональное , если это не рационально. Так что я мог бы заменить часть «если» в противоположно выражению «иррационально».

«Тогда» часть контрапозитива — это отрицание «и» заявление.Вы могли бы повторить это так: «Это не случай, когда и x рационально, и y рационально «. (Слово «оба» гарантирует, что отрицание применимо ко всему «И», а не только «х рационально».)

По закону ДеМоргана это эквивалентно: «x нерационально или y не рационально «. В качестве альтернативы я мог бы сказать:» x есть иррационально или y иррационально ».

Объединив все вместе, я мог бы выразить контрапозитив как: «Если иррационально, то либо x иррационально или y иррационально «.

(Как обычно, я добавил слово «либо», чтобы было ясно, что часть «затем» — это целое выражение «или».)

Пример. Покажите, что обратное и обратное обратное условному выражению логически эквивалентны.

Позвольте быть условным. Обратное. Обратное.

Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для. Вместо этого я воспользуюсь некоторыми известными тавтологиями.

Начнем с:

Помните, что я могу заменить выражение логическим эквивалент.Например, на последнем шаге я заменил Q, потому что два оператора эквивалентны Двойное отрицание.

Пример. Предположим, что x — действительное число. Рассмотреть возможность заявление

«Если, то.»

Постройте обратное, обратное и противоположное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и противоположное — используя свои знания алгебры.

Обратное — «Если, то».

Контрапозитив — «Если, то».

Исходное утверждение неверно:, но. Поскольку исходное утверждение эквивалентно контрапозитивный, контрапозитивный тоже должен быть ложным.

Верно и обратное. Обратное логически эквивалентно обратное, значит, верно и обратное.

\новая страница

\ centerline {\ bigssbold Список тавтологий}

Контактная информация

Домашняя страница Брюса Икенаги

Авторские права 2019 Брюс Икенага

[SL07] Срок действия

§1.Метод полной таблицы истинности

В этом руководстве мы изучаем, как использовать метод полной таблицы истинности для проверки достоверности секвенции в SL. Рассмотрим эту действительную последовательность:

P, (P → Q) и модели; Q

Чтобы доказать, что это справедливо, мы рисуем таблицу, в верхней строке которой содержатся все различные буквы предложения в аргументе, за которыми следуют предпосылки, а затем заключение. Затем, используя тот же метод, что и при составлении сложных таблиц истинности, мы перечисляем все возможные присвоения значений истинности буквам предложения слева.В нашем конкретном примере, поскольку в предложении всего две буквы, должно быть 4 присваивания:

Следующим шагом будет составление таблицы истинности для всех посылок, а также заключения:

В заполненной таблице истинности первые две ячейки в каждой строке дают нам назначение значений истинности, а следующие три ячейки сообщают нам значения истинности посылок и заключения по каждому назначению. Если аргумент действителен, то каждое присваивание, в котором все предпосылки истинны, также является присваиванием, при котором заключение истинно.Бывает, что есть только одно присвоение (первая строка), в котором верны обе посылки. Из последней ячейки строки видно, что вывод верен и при таком назначении. Итак, этот аргумент оказался верным.

В общем, чтобы определить достоверность, просматривайте каждую строку таблицы истинности, чтобы найти строку, в которой ВСЕ предпосылки истинны, И заключение ложно. Сможете найти такой ряд? В противном случае аргумент верен. Если есть одна или несколько строк, то аргумент недействителен.

Обратите внимание, что в приведенной выше таблице вывод неверен во второй и четвертой строке. Почему они не показывают, что аргумент неверен? ответ

§2. Еще примеры

Помните, что «(P → Q), ~ P, следовательно, ~ Q» недопустимо. Посмотрите на таблицу истинности и определите, какая линия должна это показать? ответ

Чтобы показать, что секвенция недействительна, мы находим одно или несколько назначений, в которых все предпосылки истинны, а вывод ложен. Такое присвоение известно как , аннулирующее присвоение (контрпример) для секвенции.

Давайте посмотрим на несколько более сложную последовательность и нарисуем таблицу истинности:

(~ P∨Q), ~ (Q → P) и модели; (Q↔ ~ P)

Снова мы рисуем таблицу истинности для посылок и заключения:

Чтобы помочь нам вычислить истинностные значения WFF при каждом назначении, мы используем метод полной таблицы истинности, чтобы сначала записать истинностные значения букв предложения, а затем шаг за шагом вычислить истинностные значения всех WFF. шаг. Истинные значения полных WFF для каждого назначения записываются под основным оператором WFF.Как видите, самое важное — это третье задание. Поскольку нет присваивания, в котором посылки истинны, а заключение ложно, секвенция действительна.

Изучите эту таблицу и ответьте на вопросы:

Какая последовательность проверяется на достоверность в этой таблице? ответ
Действительна ли последовательность в соответствии с этой таблицей? ответ

Верно или неверно?

Для любых трех формул φ, ψ и γ, если φ & models; ψ и ψ & модели; γ, затем φ & models; γ.ответ
Для любых двух формул φ и ψ, если φ & модели; ψ, затем ψ & models; φ? ответ
Для любых двух формул φ и ψ, если φ не влечет ψ, то ψ влечет φ ответ

Используйте метод полной таблицы истинности для определения достоверности этих последовательностей:

((P → Q) & R), (~ Q∨R) и модели; (P↔ (Q↔R))
(((P&Q) & ~ S) & (~ Q↔R)), ~ (~ R → S) & модели; ((P → Q) → (S → R))

Смотрите эту страницу для ответов.

Убедитесь сами, что WFF в каждой паре WFF, представленных ниже, логически эквивалентны друг другу:

(P → Q), (~ Q → ~ P)
(P↔Q), (~ P↔ ~ Q)
~ (PvQ), (~ P & ~ Q)
~ (P&Q), (~ Pv ~ Q)

§3.Некоторые неофициальные комментарии о разрешимости

Одна вещь, которую вы могли заметить в методе полной таблицы истинности, заключается в том, что он может помочь мы определяем действительность любой секвенции в SL. Можно написать программу, которая, учитывая любая конечная секвенция в SL в качестве входных данных после конечного числа шагов обработки, производит вывод «Да», если последовательность действительна, или вывод «Нет», если это не так. Конечно, компьютеру потребуется много памяти, если последовательность длинная, но в принципе это можно сделать.Это примерно то, что имеют в виду логики, когда говорят, что валидность в SL разрешима . Интуитивно все зависит от того, существует ли алгоритм или компьютерная программа, которая может предоставить доказательство действительности или недействительности последовательности.

Что интересно и, возможно, удивительно, так это то, что разрешимость больше не достигается, когда мы имеем дело с некоторыми более мощными системами логики. Одно из важнейших открытий современной логики состоит в том, что математика неразрешима.В частности, первая теорема Гёделя о неполноте говорит, что любые непротиворечивые математические системы должны включать утверждения, которые нельзя ни доказать, ни опровергнуть. Другими словами, невозможно, чтобы компьютерная программа могла определить, верны ли эти утверждения.

Раздел 1.1

Раздел 1.1 Логические формы и эквиваленты

Логическая форма и логика Эквивалентность | Определения | Сложный Заявления | Таблицы истинности

Логическая эквивалентность | Законы ДеМоргана | Таблица логических эквивалентов

Логический Форма и логическая эквивалентность

Содержание утверждения не совпадает с его логической формой.Например, рассмотрите 2 следующих утверждения:

Если Салли просыпается поздно или опаздывает на автобус, она опоздает на работу. Поэтому, если Салли приходит на работу вовремя, она не просыпалась поздно и не опаздывала на автобус.

Если x — действительное число такое, что x <-2 или x> 2, то x ²> 4. Следовательно, если x ² < 4, то x > -2 и x < 2.

Логический анализ не помогает определить достоинства аргумента.Вместо это помогает проанализировать форму аргумента, чтобы определить, является ли Вывод следует из истинности предыдущих утверждений. В то время как содержание двух приведенных выше утверждений различно, их логическая форма похожий.

Пусть p заменяет утверждения «Салли поздно просыпается». и «x — действительное число такое, что x <-2».
Пусть q означает утверждения «Салли опаздывает на автобус». и «x — действительное число такое, что x> -2».
Пусть r означает утверждения «Салли опаздывает на работу». и «x ²> 4».

Тогда общая форма для обоих приведенных выше аргументов:

Если p или q, то r.
Следовательно, если не r, то не p и не q.

Практические упражнения

Д Е Ф И Н И Т И О Н С
Аргумент:	последовательность утверждений, направленных на доказательство истины утверждения или утверждения.
Заявление:	предложение, которое истинно или ложно, но не то и другое одновременно. Это также называется предложением.
Отрицание:	, если p — переменная оператора, отрицание p — это «не p », обозначается ~ p . Если п верно, то ~ p ложно.
Соединение:	, если p и q — переменные инструкции, то соединение p и q составляет « p и q «, обозначено pq . Конъюнкция истинна только тогда, когда истинны обе переменные. Если 1 или обе переменные ложны, pq ложно.
Дизъюнкция:	, если p и q — переменные инструкции, то дизъюнкция p и q составляет « p или q «, обозначено pq . Дизъюнкция истинна, если истинны одна или обе переменные. шт. ложно, только если обе переменные ложны.
Тавтология:	Форма утверждения, которая всегда верна. Правда делает не полагаться на значения отдельных утверждений, замененных на переменные оператора, но от логической структуры самого оператора. (т.е. вы получите пятерку в этом классе или нет).
Противоречие:	Форма заявления, которая всегда ложна. Как тавтология, ложность заключается не в отдельных переменных утверждения, а в логическая структура самого высказывания.(т.е. я всегда вру.)

Составные отчеты

используйте символы (логические И), (логическое ИЛИ), и ~ (НЕ) для построения сложных логических операторов из более простых.

Пусть p = «жарко» и пусть q = «солнечно». Тогда заявление «Не жарко, но солнечно». можно написать символически:

~ стр в

Практические упражнения

Однако утверждения должны иметь четко определенные истинностные значения — они должны быть либо истинными, либо ложными.Истинность утверждения может быть выражена по таблице истинности . А таблица истинности для данного утверждения отображает результирующие значения истинности для различных комбинации значений истинности для переменных. Правда соединения утверждение может быть логически выведено с использованием известных значений истинности для различных части заявления.

Таблица истинности для ~ стр.		Таблица истинности для pq			Таблица истинности для pq
п	*~ стр.*	п.	кв	*шт.*	п.	кв	*шт.*
т	Ф.	т	т	т	т	т	т
Ф.	т	т	Ф.	Ф.	т	Ф.	т
		Ф.	т	Ф.	Ф.	т	т
		Ф	Ф	Ф	Ф.	Ф	Ф

Практические упражнения

Логическая эквивалентность:

Два оператора логически эквивалентны тогда и только тогда, когда их результирующие формы логически эквивалентны, когда идентичны переменные оператора используются для представления операторов компонентов.

Две формы операторов логически эквивалентны тогда и только тогда, когда их результирующие таблицы истинности идентичны для каждого варианта переменных утверждения.

***шт.*** и qp имеют одинаковые значения истинности, поэтому они логически эквивалентны .
p	кв	*шт.*	qp
т	т	т	т
т	Ф.	Ф.	Ф.
Ф.	т	Ф.	Ф.
Ф.	Ф	Ф	Ф

Другие логически эквивалентные утверждения включают:

Чтобы проверить логическую эквивалентность 2 утверждений, постройте таблица истинности, которая включает в себя каждую переменную, которая должна быть оценена, а затем проверить чтобы увидеть, эквивалентны ли результирующие значения истинности двух утверждений.

Законы ДеМоргана

Отрицание конъюнкции (логическое И) двух операторов. логически эквивалентен дизъюнкции (логическое ИЛИ) каждого оператора отрицание.Это звучит не так, но это означает, что «не (A и B) « логически эквивалентно », а не А или нет Б ».

Аналогично отрицание дизъюнкции 2 утверждений логически эквивалентен соединению отрицания каждого утверждения. Положил просто «не (A или B)» логически эквивалент «не A и не B» . Символически это можно записать как

Эти два утверждения логически эквивалентны (щелкните здесь для определения), и это можно проверить используя таблицу истинности.

Таблица логики Эквиваленты:

Следующая таблица может быть использована для сокращения составных операторов до более простые формы. Данные переменные инструкции p, q, и r , тавтология t и противоречие c, следующее правила логического удержания:

Логические эквиваленты могут использоваться для упрощения форм выписок и подтверждения или опровергнуть эквивалентность, чтобы создать эффективный и логически правильный компьютер программ или для помощи в проектировании цифровых логических схем.

Чтобы упростить эквивалентность, начните с одной стороны уравнения и попытайтесь чтобы заменить его части эквивалентными выражениями. Продолжайте делать это до тех пор, пока вы достигли желаемой формы выписки.

Практические упражнения

2. Схемы и таблицы истинности — Sireum Logika

В этой главе мы рассматриваем основные понятия о воротах и изучаем взаимосвязь между схемами и компьютерными программами на основе назначений.Это готовит почву для анализа современных программ.

2.1. Гейтс и таблицы истинности

Вот четыре основных входа:

P AND Q	P OR Q	НЕ P	P IMPLY Q

На приведенных выше чертежах входные провода обозначены именами P и К .Вычисляемый выходной сигнал исходит от крайнего правого провода, выходящего из ворота. Для этих простых вентилей можно полностью проверить каждую перестановку потенциальных входов и суммируйте результаты в таблице, называемой таблицей истинности.

Давайте исследуем логический элемент AND. Логический элемент И излучает высокое напряжение ( 1 ) точно при обнаружении высокого напряжения на входных проводах P и Q ; иначе излучается низкое напряжение ( 0 ). Физическое поведение ворот можно описать следующим образом: в следующей таблице.:

 И: P Q |
------------
     1 1 | 1
     1 0 | 0
     0 1 | 0
     0 0 | 0

В оставшейся части этого курса мы будем использовать T (читать «верно») для 1 и F (читается как «ложь») для 0 . Это потому, что мы будем изучать приложения, которые выходят далеко за рамки теории схем. и арифметика с основанием два. Вот таблицы истинности для вентилей AND, OR, NOT и IMPLY:

Примечание

Заглавные буквы P и Q предназначены для заполнения, а не переменные строго названы P и Q.Их использование позволяет избежать многословного: «Правая рука. Боковой операнд »и« Левый операнд ».

OR иногда называют «включающим или», поскольку пока одно из его входы — истина, тогда его выход — истина. Это отличается от обычного United Утверждает использование английского языка. Как правило, в устном и письменном английском языке «или» несет эксклюзивный оттенок. Если предлагается выбор «кофе или чай», это понимается что вы можете выбрать одно, но не оба. Логическое «или» допускает возможность обоих. Это более точно переводится на английский язык как «и / или».

Значение ворот IMPLY будет рассмотрено позже в этой главе. это включены сюда, чтобы объединить всю информацию о воротах.

Стандартно записывать каждый вентиль в линейной записи, то есть вместо рисунок, пишем P ∧ Q . (Традиция писать линейные обозначения для представления двумерных Структуры уходят в прошлое на века в физике и математике.) Обозначения следующие (традиционные математические обозначения предусмотрены для Ваш справочник.)

Выход	ASCII	Математика	UNICODE
И	∧	∧	`∧`
ИЛИ	в	∨	`∨`
НЕ	~	¬	`¬`
ПОДРАЗУМЕВАЕТСЯ	->	⇒	`→`

В этих примечаниях обычно используются нотации UNICODE.

Мы также можем составить ворота для определения новых операций.

Например, эта схема, записанная ¬ (P ∧ Q) , определяет это расчет выходов:

 P Q | ¬ (P ∧ Q)
--------------
Т Т | F
T F | Т
F T | Т
F F | Т

, который мы можем проработать поэтапно, например:

Начнем с записи значения каждого набора входов слева под их соответствующий символ справа. Затем мы применяем оператор (гейт) с наивысший приоритет (рассматривается в разделе «Приоритет логических операторов» ниже).В нашем случае «()» делает символ И ( ∧ ) наивысшим.

Назначение истинности — это уникальная перестановка возможных входов для системы. Для-гейта это последовательность с двумя переменными. Рассматривая первую строку, мы видим у нас есть «T ∧ T» — глядя на это в таблице истинности ∧-ворот, мы видим, что результат также «T», и мы записываем это под символом «∧». Мы делаем одно и то же все другие задания правды.

После первоначальной расшифровки значений истинности под их соответствующие переменные, мы ищем истинностные значения в таблицах ворот, а не переменные.Также обратите внимание, что хотя ∧ является симметричным, то есть «T F» == «F T» == «F» ПОДРАЗУМЕВАЕМЫЙ ворот нет.

Теперь мы ищем значение под символом «∧» в таблице ¬ gate. Во-первых строке мы видим, что присвоение истинности для первой строки, «T», равно «F», и запись его под символом «¬». Сделайте это для каждого ряда, и все готово.

2.1.1. Таблицы с характеристиками истинности

В нашем исследовании логики будет удобно характеризовать логические формулы с помощью описание их таблиц истинности.Если все присвоения истинности для логической формулы Верно, формула называется тавтологией. Формула p ∨ ¬ p является тавтология. В следующем примере * обозначает верхний уровень или последний оценивается оператор.

 1 *
2 ------------
3p | п ∨ ¬ п
4 ------------
5T | Т Т Ф Т
6F | F T T F
7 ------------
8Тавтология

Формула, для которой каждое присвоение истинности ложно, называется противоречивой. В Формула p ∧ ¬ p противоречива (или противоречит).

 1 *
2 ------------
3p | п ∧ ¬ п
4 ------------
5T | T F F T
6F | F F T F
7 ------------
8 Противоречие

Формула, для которой одни присвоения истинности ложны, а другие истинны, называется контингент. Уравнение p q | ¬ (q ∧ q) , сверху условно. 2 истинности заданий), конечно, возможно (хотя и раздражает) вычислить эти столы своими руками.32 записи. Это займет немного (предназначено каламбур) более 1100 лет, чтобы написать вручную, если вы можете в среднем одно задание истины в секунду.

Учитывая, что вас, вероятно, никогда не попросят написать реальное приложение так же просто, как сложение целых чисел, легко сделать вывод, что это невозможно доказать правильность программ по таблицам истинности. Неспособность протестировать программу исчерпывающая проверка каждого входа или состояния известна как комбинаторный взрыв проблема.

Хорошо … тогда почему мы заставляем вас учить таблицы истинности? Ну даже когда более продвинутый методы применяются для доказательства логических утверждений, подчеркивая их надежность это примитивные правила, которые легко выразить и усвоить с помощью таблиц истинности.

2.2. Таблицы истинности Logika

С этого момента в курсе предполагается, что вы будете использовать отформатированный в Logika формат. таблицы истинности. Таблица истинности Logika для формулы ¬ (P ∧ Q) :

 1 *
2 ------------
3p | п ∨ ¬ п
4 ------------
5T | Т Т Ф Т
6F | F T T F
7 ------------
8Тавтология

Таблицы истинности Logika имеют стандартный формат (синтаксис) и семантическое значение. Все элементы таблицы истинности должны быть включены, чтобы считаться правильными.

Первая строка всегда будет содержать одну звездочку ( * ) над последним вычисленным оператором. в формуле.Это также может называться «высший уровень» или «низший прецедент». оператор. Почему он называется оператором «верхнего уровня», будет рассмотрено конец этой главы.

Далее идет строка из - (знак минус) символов, длина этих строк должна быть не меньше в качестве третьей строки, чтобы избежать ошибок.

Третья строка содержит «переменные | формула ». Поскольку Logika использует заглавные буквы в качестве зарезервированные слова, в качестве имен переменных используются строчные буквы. Кроме того, переменные должны быть перечислены в алфавитном порядке.

Четвертая строка — это еще одна строка - .

Далее идут задания истины. Соглашение должно начинаться со всего Истины и прогресса линейно ко всем False. Должны использоваться заглавные T и F . В задании правды каждой переменной сопоставляется истина или ложь.

После назначений Истины идет еще один ряд - .

Наконец идет стол. Когда все присвоение истины заставляет формулу быть истинной, слово Тавтология используется без сопроводительной таблицы.Аналогично, когда все присвоения истинности ложны, используется Противоречие . Все остальные результаты Условные , см. пример на рисунке выше.

Порядок приоритета логических операторов от высшего к низшему:

Круглые скобки изменяют порядок операций, как в нормальной алгебре. Выражения в круглых скобках оцениваются от наиболее глубоко вложенных к наименее глубоко вложенные (внутри наружу).

2.3. Странная история с неуместными воротами

Проницательный читатель заметит, что таблицы истинности → очень отличаются от ∧ и ∨ .Начнем с того, что присвоения истинности ∧ и ∨ симметричны; если [T F] == F, то [F T] == F. Это неверно в отношении импликации, потому что p → q является составным утверждение, которое утверждает, что p обладает знаниями, достаточными для вывода q.

Давайте использовать конкретный пример из K-State. Если я знаю, что ты по специальности в информатике (факт p), то я знаю, что вы специализируетесь на инженерии (факт q).

 по специальности информатика → по специальности инженер
           p → q

Однако, наоборот, специальность "Инженерное дело" → специальность "Информатика" не обязательно верно.

Некоторые студенты склонны объединять «p обладает знаниями, достаточными для вывода q», чтобы означать «P == q», и удивлены и возмущены тем, что назначение истины [F T] в ПОДРАЗУМЕВАЕМЫЙ гейт — ИСТИНА. p → q не означает p == q или q == p

В таблице истинности для p → q результат отражает существование серийного номера. связь между p и q . Сначала должно быть p , затем q также должно быть быть правдой, чтобы утверждение было правдой.

Если оба верны, ссылка верно, и импликация (связь) между p и q верна.

Если p истинно, а q ложно, очевидно, что p не обладает достаточными знаниями чтобы вывести q, поэтому связь не верна (ложь).

Наконец, если p не истинно, нет никакого способа узнать, сохраняются ли отношения. В этом случае импликация считается истинной или бессмысленно истинной. Конечно нет доказательства того, что это ложь.

Последствия в логике были формализованы Уильямом Оккамом в его книге Summa Logicae в 14 веке. Эти несколько запутанные правила добавляют огромную выразительную силу логике и вычислениям. Без них в программах не было бы ветвлений (без IF, без FOR, без WHILE).

2.4. Общая логическая формула (схема) Эквивалентность

2.4.1. Равенство

Два (или более) логических оператора считаются равными IFF (тогда и только тогда, когда ↔ ), они имеют одинаковое значение истинности для каждого присвоения истинности; я.е. их таблицы истинности оценивать точно так же. Примером равных являются q ∧ p и p ∧ (q ∧ p)

 1 *
 2 --------------
 3p q | (p ∧ q)
 4 --------------
 5T T | Т Т Т
 6T F | T F F
 7F T | F F T
 8F F | F F F
 9 ---------------
10Контингент
11- T: [T T]
12- F: [F F] [F T] [T F]

 1 *
 2 -------------------
 3p q | p ∧ (q ∧ p)
 4 -------------------
 5T T | Т Т Т Т Т
 6T F | Т F F F T
 7F T | F F T F F
 8F F | F F F F F
 9 --------------------
10Контингент
11- T: [T T]
12- F: [F F] [F T] [T F]

Поиск эквивалентных логических выражений меньшего числа вентилей (состояний) важен для несколько полей.В компьютере наука, меньшее количество состояний может привести к меньшему количеству памяти, меньшему количеству операций и меньшему количеству программ. В компьютерная инженерия, меньшее количество ворот означает меньшее количество цепей, меньшее количество энергии и меньше тепла.

С технической точки зрения, двусмысленность — это еще один способ выразить качество. Однако мы еще не ввели оператор «равно».

p = q ↔ (p → q) ∧ (q → p)

2.4.2. Двойное отрицание

В Logika и во многих других логических приложениях двойное отрицание эффективно компенсируют друг друга.Это не единственно возможное толкование из ¬п , но именно он реализован в Логике. Мы можем обсудить другие интерпретации в разделе логики высказываний.

2.4.3. Исключающее ИЛИ (XOR)

Как обсуждалось ранее, «или» широко используется в английском языке в исключительном смысле. (p XOR q) можно выразить несколькими способами:

 (п ∧ ¬ q) ∨ (¬p ∧ q)
(p ∨ q) ∧ ¬ (p ∧ q)

В классе мы не принимаем использование оператора XOR, вы должны выразить все формулы в терминах AND, OR, NOT и IMPLY.

2.4.4. Закон Де Моргана

Закон Де Моргана — это утверждение о взаимосвязи между AND и НЕ-ИЛИ (ИЛИ) ( ¬ (p ∨ q) ). В частности:

p ∧ q ↔ ¬ (¬ p ∨ ¬ q)
p ∨ q ↔ ¬ (¬ p ∧ ¬ q)

Это имеет важное значение для компьютерной инженерии, позволяя все логические конструкции должны быть выражены только двумя типами основных ворота, И-НЕ и НЕ; значительная экономия интегрированного производства микросхем.

Огастес Де Морган также ввел термин «математическая индукция» и предоставил строгие правила. подход для его доказательства.Математическая индукция — основа многих доказательства информатики в области алгоритмов, языков и вычислительная сложность.

2.4.5. Эквивалентность последствий

Наконец, импликация может быть выражена как отрицание и ИЛИ; или как его контрположительное заявление.

(p → q) ↔ ¬ p ∨ q
(p → q) ↔ (¬ q → ¬ p) контрпозитивное утверждение

Обратное предположение может быть правдой, а может и не быть

(p → q) ??? (q → p) обратное (НЕ ОБЯЗАТЕЛЬНО ЭКВИВАЛЕНТНОСТЬ)

Примечание

Хотя большинство формул, представленных в этом разделе, верны эквивалентности, ЕСЛИ вас попросят доказать, что они равны по таблице истинности, ожидается, что вы составите таблицу истинности для каждой стороны ↔ и показать, что их ценности совпадают для каждого задания истинности.

2,5. Почему его называют оператором «верхнего уровня»

Вернемся к 2-битному сумматору и рассмотрим только схему Q1. В цепи, можно сказать, что знания текут по проводам, где они трансформируются воротами, и новое знание переходит к следующей точке.

В схеме, аннотированной выше, ясно, какие знания (факты и выведенные факты) в каждом сегменте провода. Обычная математика, отсюда и информатика методика состоит в том, чтобы представить этот тип потока знаний в специализированном виде Граф называется деревом.Дерево представлено набором узлов и ребер, один узел выбирается в качестве «корня», и все узлы имеют уникальный путь (набор ребер), ведущие к корневому узлу. Условно дерево рисуют перевернутым, с корнем наверху и листьями, свисающими снизу.

В информатике в качестве корня выбирается узел, обеспечивающий «Окончательный ответ» на проблему. Как видите, ребра несут факты и узлы. операторы, которые выводят новые факты.

Древовидное представление компьютерной программы является фундаментальной абстракцией для специалист в области информатики.Современные компиляторы и интерпретаторы берут написанную программу на языке программирования высокого уровня и преобразовать его в абстрактное синтаксическое дерево (AST), который тогда преобразован в машинный код. Для языков в функциональной парадигме (C # и Java находятся в императивной и / или объектной парадигмах), существует сильная корреляция между структурой программы высокого уровня и структурой AST.

Когда мы сравниваем дерево с логическим утверждением, мы видим самый низкий приоритет оператор — корень дерева; отсюда и термин «оператор верхнего уровня».

 *
(¬ (A1 ∧ B1)) ∧ (A1 ∧ B1)

2.6. Знания путешествуют по проводам цепи

До сих пор мы делали вид, что уровни низкого и высокого напряжения проходят по проводке. схемы. Но на самом деле по кругу движутся знания. Это можно понять по некоторым картинкам. Вот схема:

, а вот его кодировка в уравнениях:

 R = P ∧ Q
S = R ∨ Q
Т = ¬ S

Перерисуем схему по вертикали и положим рядом с заданием. уравнения:

Каждому проводу в цепи присвоено имя.Это всего лишь имен переменных . Действительно, первых (электронных) компьютерных программ в 1940-х годах были Описание электрических схем как это. Современный компьютер с хранимой программой, разработанный Джоном фон Нейманом в 1950-х годах, использовали регистры хранения для хранения значений имен переменных и использовали процессор для вычисления значений уравнений. Таким образом, процессор плюс регистры может моделировать схему, и все компьютерные программы — это просто описания цепей, в которых протекает по проводам (переменным) .

Это источник компьютерного программирования на основе переменных и присваиваний. Теперь в каждой из программных точек , отмеченных звездочками на приведенной выше диаграмме, что информация путешествует по проводам? Мы могли бы использовать схему с некоторыми входами, чтобы увидеть, «что происходит». Скажем, мы предоставляем true для P и false для Q :

На схеме показаны значения на проводах с маркировкой P , Q , R и S когда они путешествуют по цепи.Но это просто отслеживание значений переменных в программе присваивания. мы написали! «Выходная переменная» / запись с именем T имеет значение true .

Не менее интересно то, что мы можем анализировать программу / схему до , это полностью протестирован. Например, предположим, что схема будет вставлена в плату, где ее P wire всегда будет получать на входе t, но мы не знаем, что получит Q . Что мы можем предсказать о поведении схемы, когда она встроена в плату? Это:

На диаграмме мы видим, что R = Q указано после логического элемента AND.Откуда нам это знать? Во-первых, мы знаем, что R = P ∧ Q . Но P = истинное . Мы заменяем true на P и получаем R = true ∧ Q . Затем мы проводим анализ случаев и рассматриваем варианты возможного значения Q : Если Q равно true , тогда true ∧ Q равно true ∧ true , что упрощает до true , то есть к значению Q . Точно так же, когда Q является ложным , тогда t ∧ Q также является ложным .Следовательно, в обоих случаях истинных ∧ Q равно Q .

Приведенное выше рассуждение является вычетом — мы вывели из фактов P = истинное и R = P ∧ Q , что R = Q . Весь смысл этого курса — научиться делать такие выводы.

Другие вычеты в примере рассчитываются с аналогичным использованием подстановка, упрощение и анализ случаев.

Смысл предыдущего примера в том, что мы можем вывести (предсказать) свойства схему перед ее использованием.Эти вычеты дополняют тестирование.

Затем предположим, что мы ничего не знаем о P и Q в качестве входных данных. Что можно сказать о выходе схемы? Ну а вот это:

констатирует очевидное! Но внимательно изучив таблицы истинности, мы можем также заявить, что Т = ¬Q . Позже в курсе мы узнаем правила вычета , которые вычисляют этот результат, а не полагаясь на таблицы истинности.

Наконец, мы можем создавать схемы с тремя или более входами, например.грамм., (¬ (P ∧ Q)) ∨ рэндов вычисляет:

Здесь столбец под OR определяет вывод. Мы видим, что эта схема излучает ложь только тогда, когда P и Q истинны и R ложно. Это намек на то, что схема ¬ (P ∧ Q ∧ ~ R) ведет себя так же. (имеет ту же таблицу истинности), что и приведенная выше. Еще одна эквивалентная схема — (¬P) ∨ (¬Q) ∨ R. (Почему?)

В схемотехнике поиск эквивалентных схем с меньшим числом вентилей и переменных экономит электроэнергию, время и материал.

Это примечание было адаптировано из CIS 301 Дэвида Шмидта, 2008 г., Глава 0 примечание курса.

Он был обновлен в 2018 году доктором Джоном Хэтклиффом и Джорджем Лавецци
, чтобы соответствовать синтаксису Logika и более точно соответствовать курсу
KSU CIS 301, который преподавался весной 2018 года.

«Непротиворечивые» и «непоследовательные»

Здесь мы рассмотрим согласованность и непоследовательность и то, как мы можем проверить их с помощью таблиц истинности.

Набор утверждений соответствует тогда и только тогда, когда все утверждения в наборе могут быть истинными вместе. Набор утверждений несовместим с тогда и только тогда, когда невозможно, чтобы все утверждения в наборе были истинными вместе. Очевидно, что для определения того, во что верить, важно определить, когда наборы утверждений последовательны, а когда нет. Если мы обнаруживаем, что некоторые из утверждений, которые, по нашему мнению, противоречат друг другу, то мы должны что-то сказать.Нет смысла продолжать верить им всем, потому что они никак не могут быть правдой. Мы, по крайней мере, хотим, чтобы то, что мы верим, было последовательным. Мы можем проверить на непротиворечивость и непоследовательность на основе логической формы высказываний (непротиворечивость / непротиворечивость PL), используя таблицы истинности. Мы строим таблицу истинности для предложений в наборе, а затем проверяем, существует ли хотя бы одна строка , в которой все предложения истинны. Если есть, то набор является PL согласованным; если нет, это несовместимо с PL.Посмотрите на таблицу истинности предложений «(P ⋁ ~ Q)» и «(~ P ⋁ Q)» (рис. 1).

Рисунок 1. Пример таблицы истинности, демонстрирующей непротиворечивость

Предложения PL соответствуют . Есть по крайней мере одна строка, в которой оба они верны. На самом деле, их два: они оба истинны, когда ‘P’ и ‘Q’ оба истинны (первая строка), и они также оба истинны, когда ‘P’ и ‘Q’ оба ложны (последняя строка) . Теперь посмотрите на таблицу истинности для предложений «~ (P ⋁ Q)», «~ P», «Q» (рис. 2).

Рисунок 2.Пример таблицы истинности, показывающей несогласованность

Из этого видно, что эти три предложения (PL) несовместимы с . Нет строки, в которой (нет возможной ситуации из , в которой) все три предложения верны.

3 ключевых приема для создания таблиц истинности

Таблицы истинности датируются 1902 годом логиком Чарльзом Сандерсом Пирсом, который использовал их как метод отображения алгебраической логики.Таблицы истинности эволюционировали с годами. Поскольку все больше людей полагаются на них для представления логических результатов, они стали более полезными в других областях и теперь играют важную роль в бизнес-процессах и автоматизации.

Что такое таблица истинности?

Таблица истинности — это, по сути, правило, представленное в виде таблицы. Однако эти таблицы — это нечто большее, чем просто базовое определение. Они представляют собой способ представления информации и логической последовательности действий входных данных.

Таблицы истинности встроены в Excel как таблицы со строками и столбцами.В верхней части таблицы, в заголовках столбцов, находятся условия, на которых основано правило, выраженные в структуре существительного / глагола.

Например, если вы должны создать таблицу истинности, которая извлекает тип автомобиля из списка производителей автомобилей, у вас может быть столбец с заголовком «CarType In List». CarType будет существительным, а Contains — глаголом. Строки ниже будут отображать различные типы автомобилей. Важно отметить, что таблица истинности позволяет сравнивать все возможные комбинации из нескольких входных данных; он не ограничивается вводом из одного столбца.

Это помогает предприятиям, позволяя таблице истинности замкнуть цикл с выводом. Последний столбец в таблице истинности выражает результат после сбора данных из входа или входов. Выходные данные могут быть другим фрагментом данных или могут быть инструкциями о том, какое действие следует предпринять, вызывая поток. Так же, как они могут обрабатывать несколько входных данных, таблицы истинности могут возвращать более одного результата.

Ключевые приемы построения таблиц истинности

Использование математических методов в традиционных таблицах истинности может немного затруднить их использование с точки зрения бизнеса.Однако если посмотреть на таблицы истинности как на способ определения логических результатов, легче увидеть, как они применяются к автоматизации бизнеса и процессов. Такое мышление поможет вам понять некоторые ключевые приемы, которые упростят создание и использование таблиц истинности, чтобы вы могли использовать их для облегчения потоков и автоматизации бизнес-процессов.

1. Понимание различных типов вывода
Первый трюк при построении таблиц истинности — понять различные типы вывода:

Правило возврата данных (одиночное) возвращает в поток единственную переменную.
Правило возврата данных (множественное) возвращает несколько переменных в поток.
Составной тип для случаев, когда у вас есть несколько выходных данных в таблице истинности, если вы хотите получить доступ к каждому выходу индивидуально, а не как к объекту.
Правило действия передает значение и выполняет поток.

Понимание различных типов правил позволяет вам лучше понять концепцию того, что вы можете делать с таблицами истинности и правила, которые вы создаете с ними.

2. Понять, как таблицы истинности автоматизируют потоки

Это чрезвычайно полезно, когда вам нужно проанализировать данные из различных входов и принять решение на основе оценки этих данных.На основе оценки входных данных таблица истинности может выводить решение «да» или «нет», предоставлять оценочную стоимость или запрашивать дополнительную информацию. Это может быть полезно, если вы пытаетесь автоматизировать процесс самообслуживания для конечных пользователей. Таблицы истинности также дают вам возможность направлять информацию на утверждение или автоматизировать ввод данных на основе оценки входных данных. Например, если ввод красный, данные могут быть отправлены одному отделу или человеку для утверждения. Если поле ввода синее, данные будут перемещены в другой отдел или другого человека.

3. Можно использовать внешние таблицы истинности

Не все таблицы истинности требуют ручного ввода данных. Фактически, данные внешней таблицы истинности — это распространенный метод заполнения столбцов таблицы истинности. Электронные таблицы Excel, файлы CSV, базы данных и даже данные из веб-службы или очереди сообщений могут заполнять входные данные таблиц истинности, что позволяет таблице истинности собирать информацию из внешних источников, чтобы избежать дублирования ввода данных. Это не только экономит время, но и сохраняет единый источник истины, поскольку данные из внешней таблицы истинности должны редактироваться в источнике, а не в самой таблице истинности.Зарегистрируйтесь, чтобы посмотреть наш недавний веб-семинар по внешним таблицам истинности здесь.

Как программное обеспечение Decisions помогает вам с таблицами истинности

Когда дело доходит до таблиц истинности, вам нужно решение, которое максимально упрощает не только их построение, но и превращение вывода в автоматизированные потоки.

Построение таблиц истинности контрольная работа: Контрольная работа «Построение таблиц истинности»

Контрольная работа «Построение таблиц истинности»

Самостоятельная работа «Построение таблиц истинности для логических выражений» 8 класс (Босова Л.

Построение таблиц истинности — Логика

Неделя литовской культуры-2015

Презентация на тему: Подготовка к контрольной работе Построение таблиц истинности. Решение

Первый слайд презентации

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7: Домашнее задание

Слайд 8

Слайд 9

Последний слайд презентации: Подготовка к контрольной работе Построение таблиц истинности. Решение

Домашняя самостоятельная работа №5 «Сложные суждения. Построение таблиц истинности сложных суждений»

Тема 4 (продолжение)

Самостоятельная работа по информатике

таблиц истинности и анализ аргументов: примеры

Таблицы истинности

Таблица истинности

Пример 1

Символы

Основные таблицы истинности

Пример 2

Последствия

Пример 3

Пример 4

Истинные значения для следствий

Пример 5

Заявления по теме

Пример 6

Эквивалентность

Аргументы

Типы аргументов

Пример 7

Пример 8

Оценка индуктивных аргументов

Оценка дедуктивных аргументов

Пример 9

Анализ аргументов с помощью диаграмм Венна

Пример 10

Пример 11

Пример 12

Пример 13

Анализ аргументов с использованием таблиц истинности

Пример 14

таблиц истинности, тавтологий и логических эквивалентностей

[SL07] Срок действия

§1.Метод полной таблицы истинности

§2. Еще примеры

§3.Некоторые неофициальные комментарии о разрешимости

Раздел 1.1

2. Схемы и таблицы истинности — Sireum Logika

2.1. Гейтс и таблицы истинности

2.1.1. Таблицы с характеристиками истинности

2.2. Таблицы истинности Logika

2.3. Странная история с неуместными воротами

2.4. Общая логическая формула (схема) Эквивалентность

2.4.1. Равенство

2.4.2. Двойное отрицание

2.4.3. Исключающее ИЛИ (XOR)

2.4.4. Закон Де Моргана

2.4.5. Эквивалентность последствий

2,5. Почему его называют оператором «верхнего уровня»

2.6. Знания путешествуют по проводам цепи

«Непротиворечивые» и «непоследовательные»

Рисунок 1. Пример таблицы истинности, демонстрирующей непротиворечивость

Рисунок 2.Пример таблицы истинности, показывающей несогласованность

3 ключевых приема для создания таблиц истинности

Что такое таблица истинности?

Ключевые приемы построения таблиц истинности

Как программное обеспечение Decisions помогает вам с таблицами истинности

Добавить комментарий Отменить ответ