Контрольная работа по геометрии «Подобие треугольников»
Контрольная работа №3 8 класс
Подобие треугольников
1 вариант
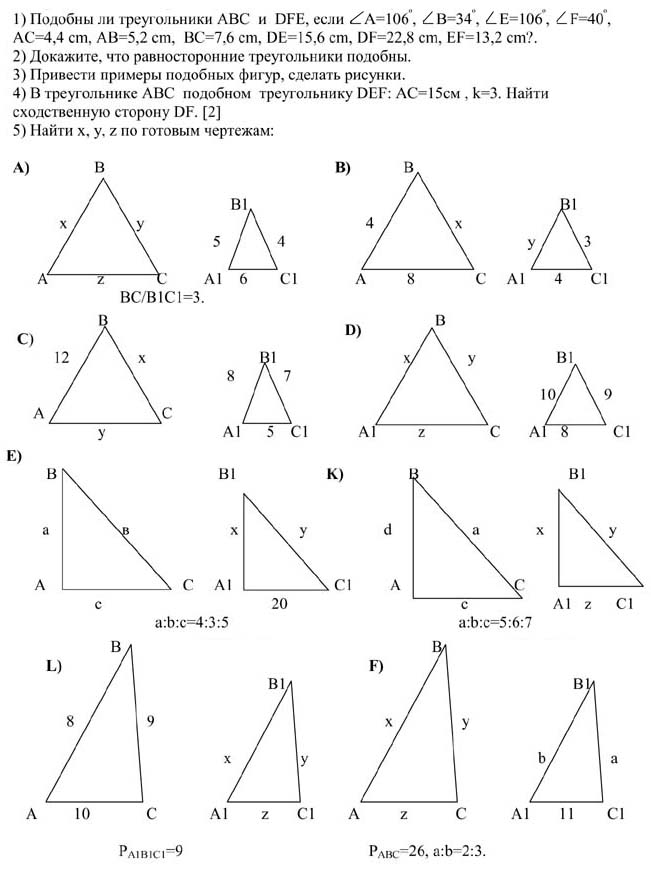
1.Найти на рисунке 1 подобные треугольники и доказать их подобие.
2.В треугольнике АВС проведена прямая МК параллельная стороне АС. Точки М и К принадлежат сторонам АВ и ВС соответственно; АВ=24 см, АМ= 9 см, ВС=16 см. Найти ВК.
3.В прямоугольном треугольнике АВС с прямым углом С проведена высота СН из прямого угла. Катет ВС=10 см, а его проекция на гипотенузу – 8 см. Найти высоту треугольника АВС и его площадь.
4.В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О, АД=12 см, ВС=4см. Найти площадь треугольника ВОС, если площадь треугольника АОД равна
45 см2.
5. В равнобедренном треугольнике АВС с основанием АС равным10 см проведена средняя линия ТК равная 4 см , параллельно боковой стороне треугольника. Найти периметр треугольника АТК.
2 вариант
1.Найти на рисунке 2 подобные треугольники и доказать их подобие.
2.В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О.
АО=15 см, АС=27 см, ВС=8 см. Найти АД.
3.В прямоугольном треугольнике АВС с прямым углом С проведена высота СН из прямого угла. Проекции катетов на гипотенузу равны 5 см и 4 см соответственно. Найти высоту треугольника АВС и его площадь.
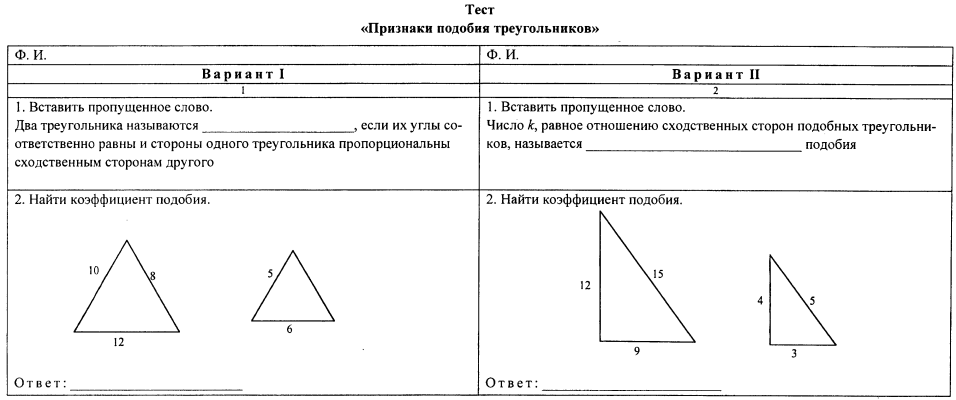
4. В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О, площадь треугольника АОД равна 32 см2, площадь треугольника ВОС равна 8 см2. Найти меньшее основание трапеции, если большее из них равно 10 см.
5.В равнобедренном треугольнике АВС с боковой стороной 10 см проведена средняя линия ТК равная 6 см, параллельно основанию. Найти периметр треугольника ВТК.
рис .1 рис.2
|
Контрольная работа по геометрии 8 класс 1 вариант
а) Докажите, что AO : OC = BO : OD. б) Найдите AB, если OD=15 см, OB=9 см, CD=25 см.
2. Найдите отношение площадей треугольников ABC и KMN, если AB=8 см, BC=12 см, AC=16 см, KM=10 см, MN=15 см, NK=20 см. 3. Стороны треугольника равны 10 см, 17 см и 21 см. Периметр подобного ему треугольника равен 72 см. Найдите стороны второго треугольника.
|
Контрольная работа по геометрии 8 класс 2 вариант
а) Докажите, что AB : BM = CB : BN. б) Найдите MN, если AM=6 см, BM=8 см, AC=21 см. 3. Стороны треугольника относятся как 3:2:4. Периметр подобного треугольника равен 108 см. Найдите стороны второго треугольника.
|
Контрольная работа по геометрии № 1 «Признаки подобия треугольников»
Контрольная работа по геометрии № 1 «Признаки подобия треугольников»
Цель: выявление знаний учащихся и степени усвоения ими приёмов решения задач на
применение признаков подобия треугольников.
План урока
I. Домашнее задание: п.103 – 106 повторить; принести циркуль.
II. Организация учащихся на проведение работы.
III.
Докажите
подобие
треугольников
ABC
Найдите KM.
и
KBM.
1. Докажите
подобие
треугольников
ABC
Найдите KM.
и
KBM.
2. Через точку K стороны AB
прямоугольного
треугольника
проведена прямая, перпендикулярная
гипотенузе ВС и пересекающая её в
точке М. Найдите BC, если AC = 20 см,
2. Через точку М стороны KP
треугольника FPK проведена прямая,
параллельная
и
пересекающая сторону FP в точке Т.
Найдите TM, если
стороне
FK
3 KM = 8 см, KB = 10 см.
3. Стороны параллелограмма
KMPT равны 9 см и 13,5 см. Сумма его
высот MA и MB, проведённых из
вершины тупого угла M, равна 15 см.
Найдите высоты параллелограмма.
FK = 52 см, FT = 12 см, TP = 36 см.
3. Диагонали трапеции ABCD
пересекаются в т.O. Основания AD и BC
равны соответственно 7,5 см и 2,5 см,
BD = 12 см. Найдите BO и OD.
4А.В. Погорелов. Геометрия. 9 класс. §11. Контрольные вопросы, ответы
- Подробности
- Родительская категория: Математика
- Категория: Геометрия, 9 класс, контрольные вопросы, ответы
Страница 1 из 2
Вопрос 1.
Что такое преобразование подобия?
Ответ. Преобразование фигуры \(F\) в фигуру \(F’\) называется преобразованием подобия, если при этом проеобразовании расстояния между точками изменяются в одно и то же число раз (рис. 233). Это значит, что если произвольные точки \(X\), \(Y\) фигуры \(F\) при преобразовании подобия переходят в точки \(X’\), \(Y’\) фигуры \(F’\), то \(X’Y’ = k\cdot XY\), причем число \(k\) — одно и то же для всех точек \(X\), \(Y\). Число \(k\) называется коэффициентом подобия. При \(k = 1\) преобразование подобия, очевидно, является движением.
Вопрос 2. Что такое гомотетия (центр гомотетии, коэффициент гомотетии)?
Ответ. Пусть \(F\) — данная фигура и \(O\) — фиксированная точка (рис. 234). Проведем через произвольную точку \(X\) фигуры \(F\) луч \(OX\) и отложим на нем отрезок \(OX’\), равный \(k\cdot OX\), где \(k\) — положительное число. Преобразование фигуры \(F\), при котором каждая ее точка \(X\) переходит в точку \(X’\), построенную указанным способом, называется гомотетией относительно центра \(O\).
Число \(k\) называется коэффициентом гомотетии, фигуры \(F\) и \(F’\) называется гомотетичными.
Вопрос 3. Докажите, что гомотетия есть преобразование подобия.
Ответ. Теорема 11.1. Гомотетия есть преобразование подобия.
Доказательство. Пусть \(O\) — центр гомотетии, \(k\) — коэффициент гомотетии, \(X\) и \(Y\) — две произвольные точки фигуры (рис. 235).
При гомотетии точки \(X\) и \(Y\) переходят в точки \(X’\) и \(Y’\) на лучах \(OX\) и \(OY\) соответственно, причем \(OX’ = k\cdot OX\), \(OY’ = k\cdot OY\). Отсюда следуют векторные равенства
\(\overline{OX’} = k\overline{OX},\, \overline{OY’} = k\overline{OY}\).
Вычитая эти равенства почленно, получим:
\(\overline{OY’} — \overline{OX’} = k(\overline{OY} — \overline{OX})\).
Так как \(\overline{OY’} — \overline{OX’} = \overline{X’Y’}\), \(\overline{OY} — \overline{OX} = \overline{XY}\), то \(\overline{X’Y’} = k\overline{XY}\).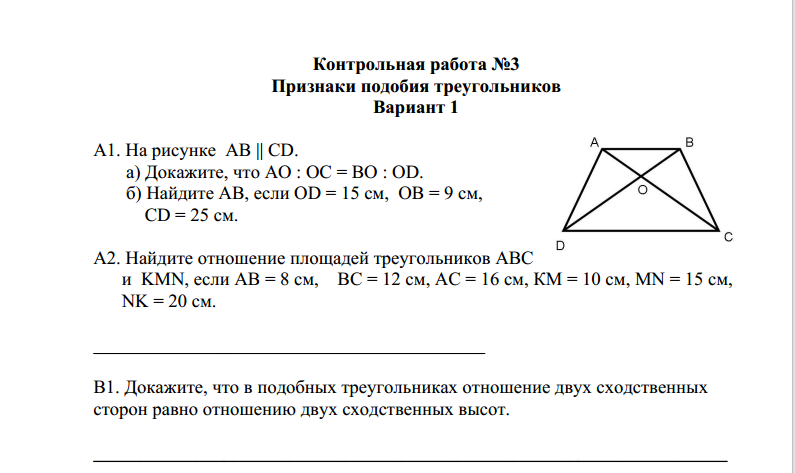
Значит, \(|\overline{X’Y’}| = k|\overline{XY}|\), т.е. \(X’Y’ = kXY\). Следовательно, гомотетия есть преобразование п
Геометрия 9 Контрольная 1 (Мерзляк) . 4 варианта
Геометрия 9 Контрольная 1 (Мерзляк). Контрольная работа по геометрии в 9 классе «Решение треугольников» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Ответов нет.
Геометрия 9 класс (УМК Мерзляк)
Контрольная работа № 1
Решение треугольников
Вариант 1
- Две стороны треугольника равны 6 см и 8 см, а угол между ними – 60°. Найдите третью сторону треугольника и его площадь.
- В треугольнике ABC известно, что AB = 3√2 см, ∠C = 45°, ∠A = 120°. Найдите сторону BC треугольника.
- Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 7 см, 10 см и 13 см.
- Одна сторона треугольника на 8 см больше другой, а угол между ними равен 120°. Найдите периметр треугольника, если его третья сторона равна 28 см.
- Найдите радиус окружности, описанной около треугольника со сторонами 13 см, 20 см и 21 см.
- Две стороны треугольника равны 6 см и 8 см, а медиана, проведённая к третьей стороне, – √14 см. Найдите неизвестную сторону треугольника.
Вариант 2
- Две стороны треугольника равны 10 см и 12 см, а угол между ними – 120°. Найдите третью сторону треугольника и его площадь.
- В треугольнике ABC известно, что AC = 5√2 см, ∠B = 45°, ∠C = 30°. Найдите сторону AB треугольника.
- Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 6 см, 8 см и 11 см.
- Одна сторона треугольника на 3 см меньше другой, а угол между ними равен 60°. Найдите периметр треугольника, если его третья сторона равна 7 см.
- Найдите радиус окружности, вписанной в треугольник со сторонами 4 см, 1 3 см и 1 5 см.
- Стороны треугольника равны 4 см, 5 см и 7 см. Найдите медиану треугольника, проведённую к его меньшей стороне.
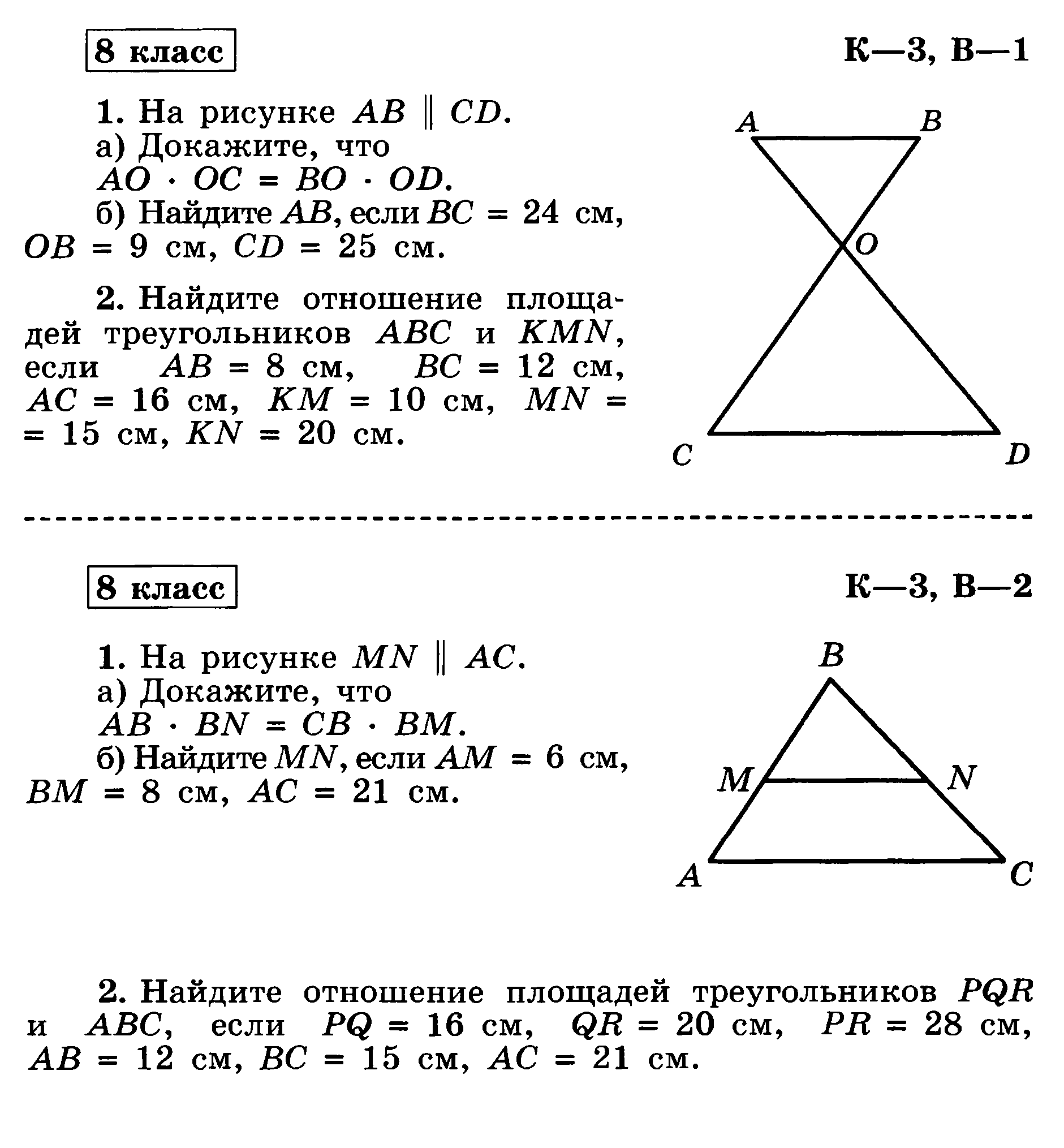
Вариант 3
- Две стороны треугольника равны 8 см и 4√3 см, а угол между ними – 30°. Найдите третью сторону треугольника и его площадь.
- В треугольнике ABC известно, что BC = 7√2 см, ∠A = 135°, ∠B = 30°. Найдите сторону AC треугольника.
- Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 5 см, 9 см и 12 см.
- Одна сторона треугольника на 6 см больше другой, а угол между ними равен 120°. Найдите периметр треугольника, если его третья сторона равна 21 см.
- Найдите радиус окружности, описанной около треугольника со сторонами 18 см, 20 см и 34 см.
- Две стороны треугольника равны 7 см и 9 см, а медиана, проведённая к третьей стороне, – √29 см. Найдите неизвестную сторону треугольника.
Вариант 4
- Две стороны треугольника равны 6 см и 4√2 см, а угол между ними – 135°. Найдите третью сторону треугольника и его площадь.
- В треугольнике ABC известно, что AC = 9√3 см, ∠B = 60°, ∠C = 45°. Найдите сторону AB треугольника.
- Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 9 см, 10 см и 14 см.
- Одна сторона треугольника на 10 см меньше другой, а угол между ними равен 60°. Найдите периметр треугольника, если его третья сторона равна 14 см.
- Найдите радиус окружности, вписанной в треугольник со сторонами 5 см, 12 см и 15 см.
- Стороны треугольника равны 5 см, 7 см и 10 см. Найдите медиану треугольника, проведённую к его большей стороне.
Найдите сторону AB треугольника.
Вернуться к Списку контрольных работ по геометрии 9 класс (Мерзляк)
Вы смотрели: Геометрия 9 Контрольная 1 (Мерзляк). Контрольная работа по геометрии в 9 классе «Решение треугольников» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Цитаты из пособия «Геометрия 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
| |||||||||||||||||||||||||||||||||||||||||||||||||||
ФГОС
Ф. Бутузова для 9 класса.похожих треугольников
Два треугольника похожи, если разница только в размере (и, возможно, в необходимости перевернуть или перевернуть один).
Все эти треугольники похожи:
(равные углы отмечены таким же количеством дуг)
Некоторые из них имеют разные размеры, а некоторые перевернуты или перевернуты.
Для одинаковых треугольников:
Все соответствующие углы равны
и
Все соответствующие стороны имеют одинаковое соотношение
Также обратите внимание, что соответствующие стороны обращены к соответствующим углам.Например, стороны, обращенные к углам с двумя дугами, соответствуют друг другу.
Соответствующие стороны
В подобных треугольниках соответствующие стороны всегда находятся в одинаковом соотношении.
Например:
Треугольники R и S похожи. Равные углы помечены одинаковым количеством дуг.
Какова соответствующая длина?
- Длины 7 и a соответствуют (они обращены к углу, отмеченному одной дугой)
- Длины 8 и 6. 4 соответствуют (обращены к углу, отмеченному двумя дугами)
- Длины 6 и b соответствуют (обращены к углу, отмеченному тремя дугами)
4 соответствуют (обращены к углу, отмеченному двумя дугами)Расчет длин соответствующих сторон
Иногда мы можем вычислить длины, которых еще не знаем.
- Шаг 1: Найдите отношение соответствующих сторон
- Шаг 2: Используйте это соотношение, чтобы найти неизвестную длину
Пример: найти длины a и b треугольника S
Шаг 1. Найдите отношение
Мы знаем все стороны треугольника R и
Мы знаем сторону 6.4 Треугольник S
6.4 обращен к углу, отмеченному двумя дугами, как и сторона длиной 8 в треугольнике R .
Таким образом, мы можем сопоставить 6.4 с 8 , и поэтому отношение сторон в треугольнике S к треугольнику R будет:
от 6,4 до 8
Теперь мы знаем, что длины сторон в треугольнике S равны 6,4 / 8, умноженным на длин сторон в треугольнике R .
Шаг 2: Используйте соотношение
a обращен к углу с одной дугой, как и сторона длиной 7 в треугольнике R .
a = (6,4 / 8) × 7 = 5,6
b обращен к углу с тремя дугами, как и сторона длиной 6 в треугольнике R .
b = (6,4 / 8) × 6 = 4,8
Готово!
Треугольников (сходство и соответствие) Рабочие листы
В чем разница между подобием и конгруэнтностью треугольников?
В математике формы, углы и пропорции помогают объяснить разницу между сходством и соответствием.Конгруэнтные фигуры совпадают друг с другом и показывают одинаковые размеры при наложении. Две конгруэнтные формы имеют одинаковый размер и форму, но их ориентация может различаться.
Сходство означает быть похожим друг на друга, но не быть идентичным. По форме похожие объекты могут быть одинаковыми, но иметь разные размеры. СОГЛАСОВАННЫЕ ТРЕУГОЛЬНИКИ — Конгруэнтные треугольники идентичны по форме и размеру.
Углы и стороны одного треугольника будут идентичны соответствующим углам и сторонам другого треугольника.Это означает, что если один треугольник накладывается на другой, они идеально совпадают друг с другом. СВОЙСТВА СООТВЕТСТВУЮЩИХ ТРЕУГОЛЬНИКОВ — Соответствие SSS: SSS означает «сторона, сторона, сторона». Два треугольника конгруэнтны, если все три стороны одного треугольника равны соответствующим трем сторонам другого треугольника.
Соответствие SAS: SAS означает «сторона, угол, сторона». Два треугольника считаются конгруэнтными по Сэди, если две стороны и включенный угол одного треугольника совпадают с соответствующими двумя сторонами и включенным углом.Соответствие ASA: ASA означает «угол, сторона, угол». Два треугольника называются конгруэнтными, если два угла и любая сторона одного треугольника совпадают с соответствующими двумя сторонами и любым углом другого треугольника. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ — Два треугольника подобны, если все их углы равны и соответствующие стороны имеют одинаковое отношение.
Есть три способа доказать подобие треугольников: AA, SAS, SSS. СВОЙСТВА ПОДОБНЫХ ТРЕУГОЛЬНИКОВ — AA Сходство: AA означает «угол, угол».Это означает, что если два треугольника называются подобными, то два угла одного треугольника равны двум углам другого треугольника.
Сходство SAS: SAS означает «сторона, угол, сторона». Это означает, что два треугольника считаются подобными, если:
— соотношение сторон равно отношению двух других сторон, т.е. две пары сторон находятся в равном соотношении.
— Включенные углы равны.
Сходство SSS: SSS означает «сторона, сторона, сторона». Два треугольника подобны, если все три пары сторон у них одинаковы.Этот набор рабочих листов и уроков показывает учащимся, как определять и использовать похожие и / или совпадающие треугольники.
похожих треугольников | Помощь с математикой
Подобные треугольники имеют одинаковую общую форму и отличаются только размером. Это верно и для всех других групп подобных фигур. Все приведенные ниже рисунки одного цвета похожи.
Примечание: все круги любого диаметра представляют собой похожие фигуры. То же самое можно сказать обо всех квадратах и всех равносторонних треугольниках.
Учащиеся обычно изучают похожие треугольники и другие похожие фигуры в 8-м классе.
Сходство фигур часто обсуждается с концепцией конгруэнтности. Конгруэнтные фигуры бывают не только одинаковой формы (как у похожих фигур), но и одинакового размера. Здесь вы найдете больше о конгруэнтных фигурах, а также руководство по различным типам преобразований, которые можно применить для создания конгруэнтных или похожих фигур.
Разница между сходством и соответствием заключается в том, что аналогичные фигуры подвергались расширению (или, говоря более общим языком, они были изменены в размере, масштабированы, увеличены или уменьшены).Здесь вы найдете больше информации о расширениях и подобных фигурах.
Как определить, похожи ли треугольники
Два треугольника ниже выглядят так, как будто они могут быть похожими, но мы не можем сказать наверняка, если не знаем больше о длине сторон и / или углах внутри треугольника.
Чтобы определить, похожи ли треугольники, мы должны сравнить соответствующие стороны и / или соответствующие углы. В двух приведенных ниже примерах показаны соответствующие стороны и соответствующие углы.
AB и DE — соответствующие стороны
BC и EF — соответствующие стороны
CA и FD — соответствующие стороны
∠BAC и ∠EDF — соответствующие углы
∠ACB и ∠DFE — соответствующие углы
∠CBA и ∠ FED — соответствующие углы
AB и XY — соответствующие стороны
BC и YZ — соответствующие стороны
CA и ZX — соответствующие стороны
∠BAC и ∠YXZ — соответствующие углы
∠ACB и ∠XZY — соответствующие углы
∠CBA и ∠ZYX — соответствующие углы
Есть несколько комбинаций условий, которые показывают, должны ли два треугольника быть подобными.
| Если все три пары соответствующих сторон имеют одинаковое отношение, то треугольники подобны. | Если два из соответствующих углов равны, то треугольники подобны. |
Два момента, на которые следует обратить внимание:
1) Если две пары соответствующих углов равны, тогда третья пара также всегда будет равна (так как сумма трех углов в треугольнике всегда равна 180 °).
2) Если один набор условий (например, соответствующие стороны в одинаковом соотношении) верен, то другой набор (например,грамм. соответствующие углы равны).
Другой набор условий, которые объединяются, чтобы показать сходство в треугольниках, — это когда две пары соответствующих сторон находятся в соотношении и пары соответствующих углов, включенных между этими сторонами, равны. Два прямоугольных треугольника ниже показывают пример этого.
Проблемы с похожими треугольниками
Сходны ли два треугольника ниже?
Задача ниже — это пример того, как свойства подобных треугольников могут быть использованы для решения реальных проблем, которые могут возникнуть.
Джо устал беспокоиться о том, могут ли соседи видеть его гостиную из своего дома.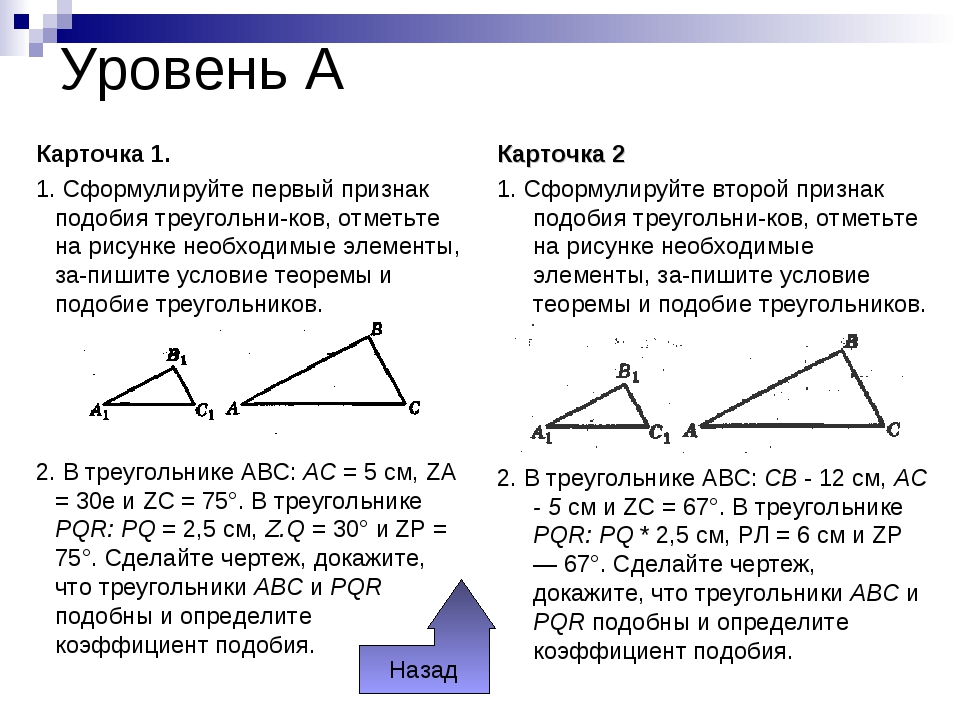
Он решил построить достаточно высокий забор, чтобы закрывать вид из окна верхнего этажа. Ему нужно решить, на какой высоте можно построить забор. Джо сделал некоторые измерения и набросал их, как показано ниже. Мы можем использовать то, что мы знаем о подобных треугольниках, чтобы найти высоту, на которой Джо должен сделать свой новый забор.
Джо сделал несколько измерений и набросал их, как показано ниже.
Мы можем использовать то, что мы знаем о подобных треугольниках, чтобы найти высоту, на которой Джо должен сделать свой новый забор.
| Мы можем создать рисунок на основе эскиза Джо. Мы назовем недостающее измерение , которое нам нужно найти «x». | |
| У нас есть два похожих треугольника | |
| Мы можем вычислить значение x. 1,8 / x = 8/3 | 8x = 3 x 1,8 8x = 5,4 x = 0,675 м |
| Оглядываясь на наш чертеж , мы видим, что нам нужно добавить значение, которое мы вычислили для x, на 2. 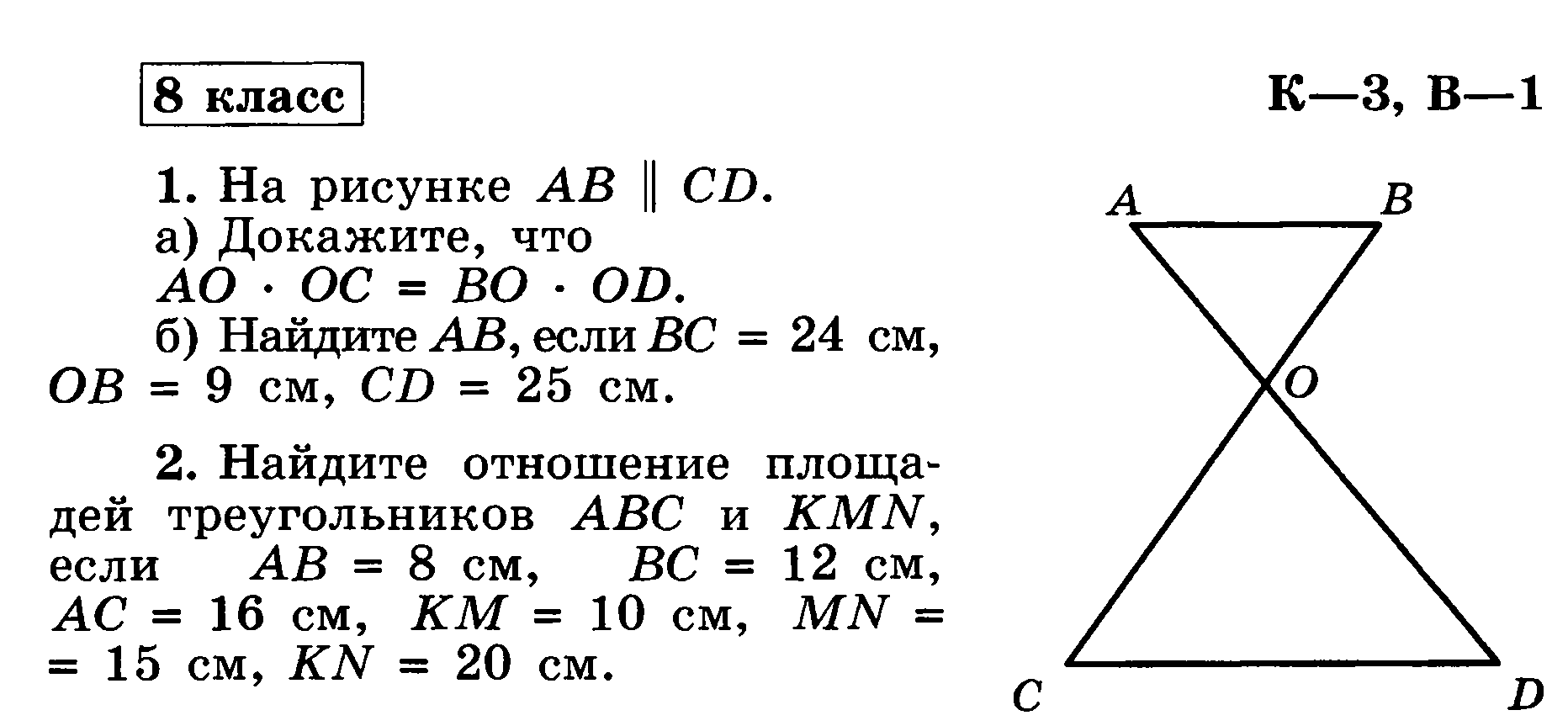 0 м, чтобы найти минимальную высоту забора. | 0,675 м + 2,0 м = 2,675 м Забор Джо должен быть не менее 2,675 м, чтобы закрыть обзор для соседей. Это довольно высокий забор. Может, ему нужны шторы! |
Рабочие листы схожести
Щелкните по приведенным ниже ссылкам и попросите вашего ребенка опробовать рабочие листы на сходство в треугольниках и других подобных фигурах.
похожих треугольников — математическая открытая ссылка
похожих треугольников — математическая открытая ссылка Определение: треугольники похожи, если имеют одинаковую форму, но могут быть разных размеров.
(Они все еще похожи, даже если один повернут, или один является зеркальным отображением другого).
Попробуй Перетащите любую оранжевую точку в вершину любого треугольника. Оба треугольника изменят форму и останутся похожими друг на друга.
Треугольники похожи, если они имеют одинаковую форму, но не обязательно одинакового размера.
Вы можете думать об этом как о «увеличении» или «уменьшении», увеличивая или уменьшая треугольник, но сохраняя его основную форму.
На рисунке выше, когда вы перетаскиваете любую вершину на треугольнике PQR, другой треугольник принимает ту же форму, но в два раза меньше.В формальных обозначениях мы можем написать
который читается как « Треугольник PQR похож на треугольник P’Q’R ‘». Буква с небольшой вертикальной чертой после нее, например P ‘, читается как « P prime ».
Свойства подобных треугольников
Соответствующие углы совпадают (одна и та же величина)
Итак, на рисунке выше, угол P = P ‘, Q = Q’ и R = R ‘.Соответствующие стороны имеют одинаковую пропорцию.
Выше PQ вдвое больше длины P’Q ‘.Следовательно, остальные пары сторон также находятся в той же пропорции. PR вдвое больше P’R ‘, а RQ вдвое больше R’Q’. Формально в двух одинаковых треугольниках PQR и P’Q’R ‘:
Вращение
Один треугольник можно вращать, но пока они одинаковой формы, треугольники остаются похожими.
На рисунке ниже треугольник PQR похож на P’Q’R ‘, хотя последний повернут.
по часовой стрелке 90 °.
В этом конкретном примере треугольники одинакового размера, поэтому они также конгруэнтный.
Отражение
Один треугольник может быть зеркальным отражением другого, но до тех пор, пока они имеют одинаковую форму, треугольники остаются похожими. Он может отражаться в любом направлении: вверх, вниз, влево, вправо. На рисунке ниже треугольник PQR является зеркальным отображением P’Q’R ‘, но по-прежнему считается похожим на него.Как определить, похожи ли треугольники
Любой треугольник определяется шестью мерками (три стороны, три угла). Но вам не нужно знать их все, чтобы показать, что два треугольника похожи.Подойдут разные группы по три человека. Треугольники подобны, если:- AAA (угол угла)
Все три пары соответствующих углов одинаковы.
См. Похожие треугольники AAA. - SSS в одинаковой пропорции (боковая сторона)
Все три пары соответствующих сторон имеют одинаковую пропорцию
См. Подобные треугольники SSS. - SAS (сторона бокового угла)
Две пары сторон в одинаковой пропорции и равный прилегающий угол.
См. Подобные треугольники SAS.
Подобные треугольники SSS.Подобные треугольники могут иметь общие части
Два треугольника могут быть похожими, даже если у них есть общие элементы. На рисунке ниже больший треугольник PQR подобен меньшему STR. S и T — середины PR и QR соответственно. Они разделяют вершину R и часть сторон PR и QR. Они похожи на основе AAA, поскольку соответствующие углы в каждом треугольнике одинаковы.Другие похожие темы
Подобные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Теоремы подобия треугольника
Прежде чем пытаться понять подобие треугольников, очень важно понять концепцию пропорций и соотношений, потому что подобие полностью основано на этих принципах.
Сходство треугольников — это еще одна связь, которую могут иметь два треугольника.
Мы уже узнали о конгруэнтности, где все стороны должны быть одинаковой длины. Точно так же углы должны быть равны, а все стороны пропорциональны.Сходство — это отношение эквивалентности.
Два треугольника $ ABC $ и $ DEF $ похожи, поэтому мы пишем: $ \ bigtriangleup ABC \ sim \ bigtriangleup DEF $.
Есть четыре теоремы, которые мы можем использовать, чтобы определить, похожи ли два треугольника.
Теорема AA
Два треугольника подобны, если их два соответствующих угла конгруэнтны.
Пусть $ ABC $ — заданный треугольник. Итак, как мы можем построить подобный треугольник?
Мы расширим отрезки $ \ overline {AB} $ и $ \ overline {AC} $ на вершины $ B $ и $ C $ соответственно.На прямой $ AC $ мы выбираем точку $ D $ и строим прямую, параллельную прямой $ BC $ и проходящую через точку $ D $. Пересечение ранее построенной прямой и прямой $ AB $ составляет точку $ E $.
Полученный треугольник $ AFD $ подобен данному треугольнику $ ABC $, как показано ниже.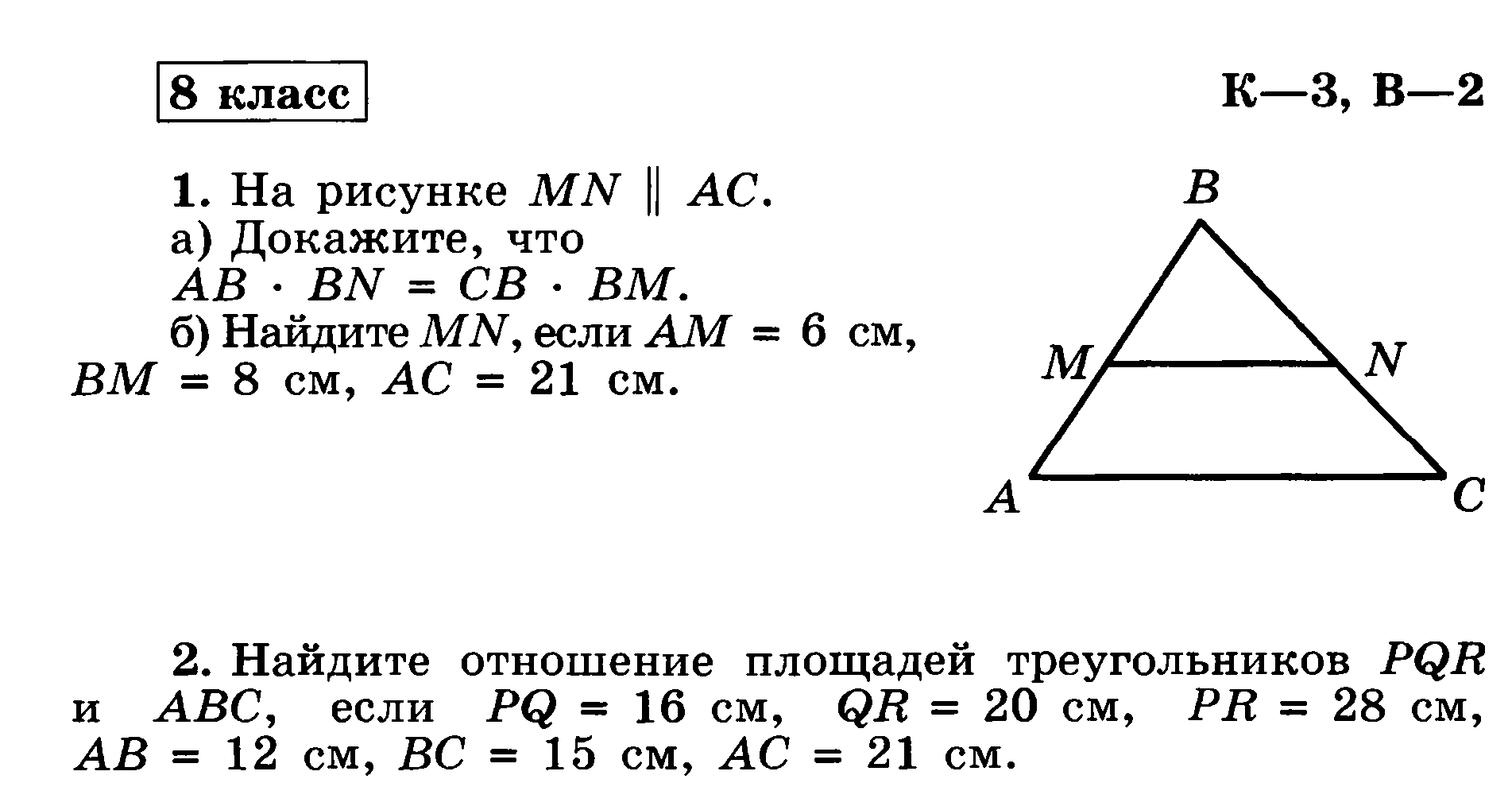
$ \ beta = \ beta ’, \ gamma = \ gamma’ \ Rightarrow \ alpha = \ alpha ’$ (если два соответствующих угла имеют равную меру, то третий также равен и соответствует).
Также верны следующие пропорции:
$ \ frac {\ mid AB \ mid} {\ mid AF \ mid} = \ frac {\ mid AC \ mid} {\ mid AD \ mid} = \ frac {\ mid CB \ mid} {\ mid DF \ mid} $.
Теорема SSS
Два треугольника подобны, если длины всех соответствующих сторон пропорциональны.
Треугольники $ ABC $ и $ DEF $ являются аналогичными треугольниками, если:
Пример 1 .
Это следующие треугольники
$$ \ треугольник {ABC}: \ quad a = 2, \ quad b = 4, \ quad c = 5, $$
$$ \ треугольник {DEF}: \ quad d = 4, \ quad e = 8, \ quad f = 10 $$
похоже?
Решение :
У нас:
$$ \ frac {a} {d} = \ frac {b} {e} = \ frac {c} {f} \ Rightarrow \ frac {2} {4} = \ frac {4} {8} = \ frac {5} {10} \ Rightarrow \ frac {1} {2} = \ frac {1} {2} = \ frac {1} {2}.
$$
Отсюда следует, что треугольники $ ABC $ и $ DEF $ подобны по теореме SSS.
Если мы нашли другое значение в какой-либо части, треугольники не похожи.
Теорема SAS
Два треугольника подобны, если соответствующие длины двух сторон пропорциональны, а включенные углы совпадают.
Треугольники $ ABC $ и $ DEF $ похожи, если $ \ alpha = \ alpha ‘$ и $ \ frac {\ mid DE \ mid} {\ mid AB \ mid} = \ frac {\ mid AC \ mid} {\ mid DF \ mid} $. Отсюда следует, что все соответствующие углы равны, а длины всех сторон пропорциональны.{\ circ} $$
похоже?
Решение :
Это должно быть: $ \ frac {a} {w} = \ frac {b} {e} $.
У нас:
$$ \ frac {20} {10} = \ frac {5} {2.5} \ Rightarrow 2 = 2. $$
Эти две соответствующие стороны пропорциональны, и включенные углы равны. Следовательно, треугольники $ ABC $ и $ WER $ являются подобными треугольниками согласно теореме SAS.
Теорема SSA
Два треугольника подобны, если длины двух соответствующих сторон пропорциональны и их соответствующие углы на большем из этих двух совпадают.{\ circ} $$
похоже?
Решение :
Надо сравнить все стороны по длине.
В данном случае
$$ \ frac {a} {b ‘} = \ frac {b} {a’} \ Rightarrow \ frac {6} {12} = \ frac {3} {6} \ Rightarrow \ frac {1} {2 } = \ frac {1} {2}, $$
, что верно. Угол, противоположный стороне самой длинной стороны в треугольнике $ ABC $, равен $ \ alpha $, а угол, противоположный самой длинной стороне треугольника $ GHJ $, равен $ \ beta $.
Отсюда следует, что $ \ alpha = \ beta $, что означает, что треугольники $ ABC $ и $ GHJ $ подобны по теореме SSA.
Листы схожести треугольников
Подобные треугольники (740,4 КБ, 1 976 обращений)
Подобные прямоугольные треугольники (179,2 КБ, 1148 обращений)
похожих треугольников: периметры и области
Подобные треугольники: периметры и области
Когда два треугольника похожи, уменьшенное отношение любых двух соответствующих сторон называется масштабным коэффициентом подобных треугольников.На рисунке 1 Δ ABC ∼ Δ DEF .
Рисунок 1 Подобные треугольники с масштабным коэффициентом 2: 1.
Соотношения соответствующих сторон 6/3, 8/4, 10/5. Все они уменьшаются до 2/1. Затем говорят, что масштабный коэффициент этих двух одинаковых треугольников равен 2: 1.
Периметр Δ ABC составляет 24 дюйма, а периметр Δ DEF составляет 12 дюймов. Когда вы сравниваете соотношение периметров этих похожих треугольников, вы также получаете 2: 1.Это приводит к следующей теореме.
Теорема 60: Если два одинаковых треугольника имеют масштабный коэффициент a : b, , то отношение их периметров будет a : b.
Пример 1: На рисунке 2 Δ ABC ∼ Δ DEF . Найти периметр Δ DEF
Рисунок 2 Периметр подобных треугольников.
На рис. 3 показаны два похожих прямоугольных треугольника с масштабным коэффициентом 2: 3.Поскольку GH ⊥ GI и JK ⊥ JL , их можно рассматривать как основание и высоту для каждого треугольника. Теперь вы можете найти площадь каждого треугольника.
Рисунок 3 Нахождение площадей одинаковых прямоугольных треугольников с масштабным коэффициентом 2: 3.
Теперь вы можете сравнить соотношение площадей этих одинаковых треугольников.
Это приводит к следующей теореме:
Теорема 61: Если два одинаковых треугольника имеют масштабный коэффициент a : b , то отношение их площадей будет a 2 : b 2 .
Пример 2: На рисунке 4 Δ PQR ∼ Δ STU . Найдите площадь Δ STU .
Рисунок 4 Использование масштабного коэффициента для определения соотношения между площадями одинаковых треугольников.
Масштабный коэффициент подобных треугольников составляет 5: 8.
Пример 3: Периметры двух одинаковых треугольников находятся в соотношении 3: 4. Сумма их площадей составляет 75 см 2 .Найдите площадь каждого треугольника.
Если называть треугольники Δ 1 и Δ 2 , то
Согласно теореме 60, это также означает, что масштабный коэффициент этих двух похожих треугольников равен 3: 4.
.