ОЦЕНИВАНИЕ КОНТРОЛЬНЫХ РАБОТ ПО МАТЕМАТИКЕ В НАЧАЛЬНОЙ ШКОЛЕ
Формы контроля уровня достижений и критерии оценки по математике.
В контрольной работе:
задания должны быть одного уровня для всего класса;
задания повышенной трудности выносятся в «задания повышенной сложности (повышенный уровень)», которое предлагается для выполнения всем ученикам и их невыполнение не влияет на общую оценку работы; обязательно разобрать их решение при выполнении работы над ошибками;
оценка не снижается, если есть грамматические ошибки и аккуратные исправления;
за неряшливо оформленную работу, несоблюдение правил каллиграфии оценка по математике снижается на 1 балл, но не ниже «3».
Контрольная работа.
Работа, состоящая из выражений:
«5» — без ошибок.
«4» -1-2 грубая и 1-2 негрубые ошибки.
«3» — 2-3 грубые и 1-2 негрубые ошибки или 3 и более негрубых ошибки.
«2» — 4 и более грубых ошибки.
Работа, состоящая из задач:
«5» — без ошибок.
«4» — 1-2 негрубых ошибки.
«3» — 1 грубая и 3-4 негрубые ошибки.
«2» — 2 и более грубых ошибки.
Комбинированная работа:
«5» – нет ошибок;
«4» – 1 – 2 ошибки, но не в задаче;
«3» – 2 – 3 ошибки, 3 – 4 негрубые ошибки, но ход решения задачи верен;
«2» – не решена задача или более 4 грубых ошибок.
Грубые ошибки:
Вычислительные ошибки в выражениях и задачах.
Ошибки на незнание порядка выполнения арифметических действий.
Неправильное решение задачи (пропуск действия, неправильный выбор действий, лишние действия).
Не решенная до конца задача или выражение.
Невыполненное задание.
Нерациональный прием вычислений.
Неправильная постановка вопроса к действию при решении задачи.
Неверно сформулированный ответ задачи.
Неправильное списывание данных (чисел, знаков).
Недоведение до конца преобразований.
Тест
Оценка «5» ставится за 90-100% правильно выполненных заданий
Оценка «4» ставится за 66 — 89% правильно выполненных заданий
Оценка «3» ставится за 50-65% правильно выполненных заданий
Оценка «2» ставится, если правильно выполнено менее 50% заданий
Критерии оценивания по математике | Статья по математике (3 класс):
Инструментарий для оценивания результатов
Система оценки достижения планируемых результатов освоения предмета
Критерии оценивания
В соответствии с требованиями Стандарта, при оценке итоговых результатов освоение программы по математике должны учитываться психологические возможности младшего школьника, нервно-психические проблемы, возникающие в процессе контроля, ситуативность эмоциональных реакций ребенка.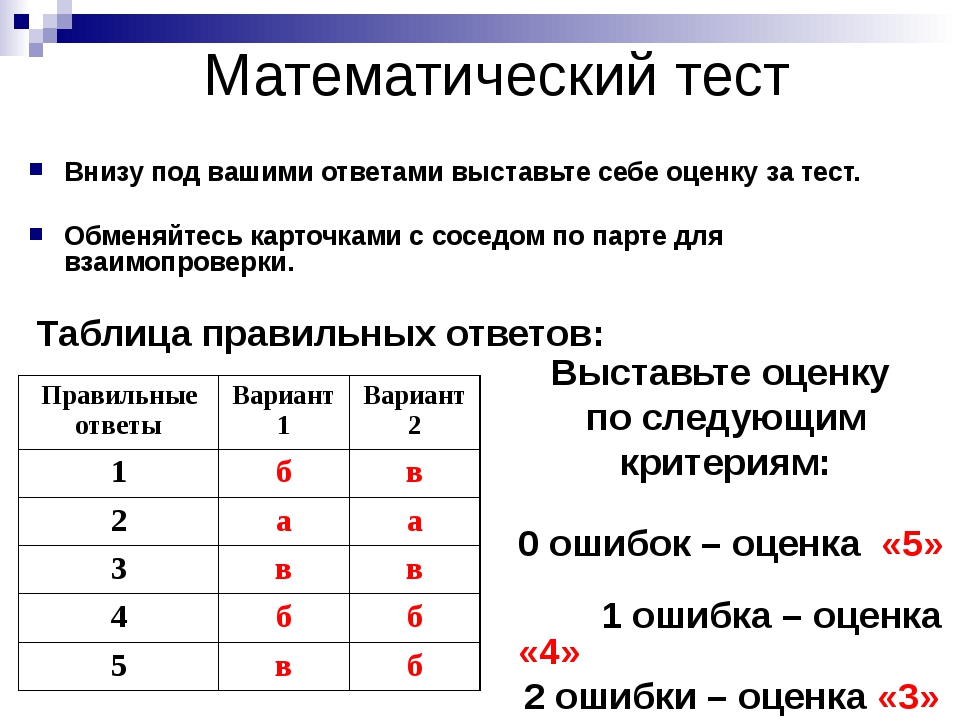
Система оценки достижения планируемых результатов изучения математики предполагает комплексный уровневый подход к оценке результатов обучения. Объектом предметных результатов служит способность третьеклассников решать учебно — поз-тельные и учебно-практические задачи. Оценка индивидуальных образовательных достижений ведётся «методом сложения», при котором фиксируется достижение опорного уровня его превышение.
В соответствии с требованиями Стандарта, составляющей комплекса оценки достижений являются материалы стартовой диагностики, промежуточных и итоговых стандартизированных работ по математике. Остальные работы подобраны так, чтобы их совокупность демонстрировала нарастающие успешность, объём и глубину знаний, достижение более высоких уровней формируемых учебных действий.
Текущий контроль по математике осуществляется в письменной и устной форме. Письменные работы для текущего контроля проводятся не реже одного раза в неделю в форме самостоятельной работы или арифметического диктанта.
Работы для текущего контроля состоят из нескольких однотипных заданий, с помощью которых осуществляется всесторонняя проверка только одного определенного умения.
Тематический контроль по математике проводится в письменной форме. Для тематических проверок выбираются узловые вопросы программы: приемы устных вычислений, измерение величин и др. Проверочные работы позволяют проверить, например, знание табличных случаев сложения, вычитания, умножения и деления. В этом случае для обеспечения самостоятельности учащихся подбирается несколько вариантов работы, каждый из которых содержит около тридцати примеров на сложение и вычитание или умножение и деление. На выполнение такой работы отводится 5-6 минут урока.
Основанием для выставления итоговой оценки знаний служат результаты наблюдений учителя за повседневной работой учеников, устного опроса, текущих, диагностических и итоговых стандартизированных контрольных работ. Однако последним придается наибольшее значение.
В конце года проводится итоговая комплексная проверочная работа на межпредметной основе.
Одной из ее целей является оценка предметных и метапредметных результатов освоения программы по математике в третьем классе: способность решать учебно-практические и учебно-познавательные задачи, сформированность обобщённых способов деятельности, коммуникативных и информационных умений.
Нормы оценок по математике | |||
Работа, состоящая из примеров: | Работа, состоящая из задач. | Комбинированная работа | Контрольный устный счет. |
«5» — без ошибок. | «5» — без ошибок. | «5» — без ошибок. | «5» — без ошибок. |
«4» -1 грубая и 1 -2 негрубые ошибки. | «4» — 1-2 негрубых ошибки. | «4» — 1 грубая и 1-2 негрубые ошибки, при этом грубых ошибок не должно быть в задаче. | «4»- 1-2 ошибки. |
«3»-2-3 грубые и 1-2 негрубые ошибки или 3 и более негрубых ошибки | «3» — 1 грубая и 3-4 негрубые ошибки. | «3» — 2-3 грубые и 3-4 негрубые ошибки, при этом ход решения задачи должен быть верным. | «3» — 3-4 ошибки. |
«2» — 4 и более грубых ошибки. | «2» — 2 и более грубых ошибки. | «2» — 4 грубые ошибки. | |
Оценивание контрольной работы — Шкала оценки знаний — Требования — Каталог статей
Контрольная работа состоит из 5 заданий разного уровня сложности.
Первое задание самое легкое и заключается в выборе правильного варианта ответов из предложенных.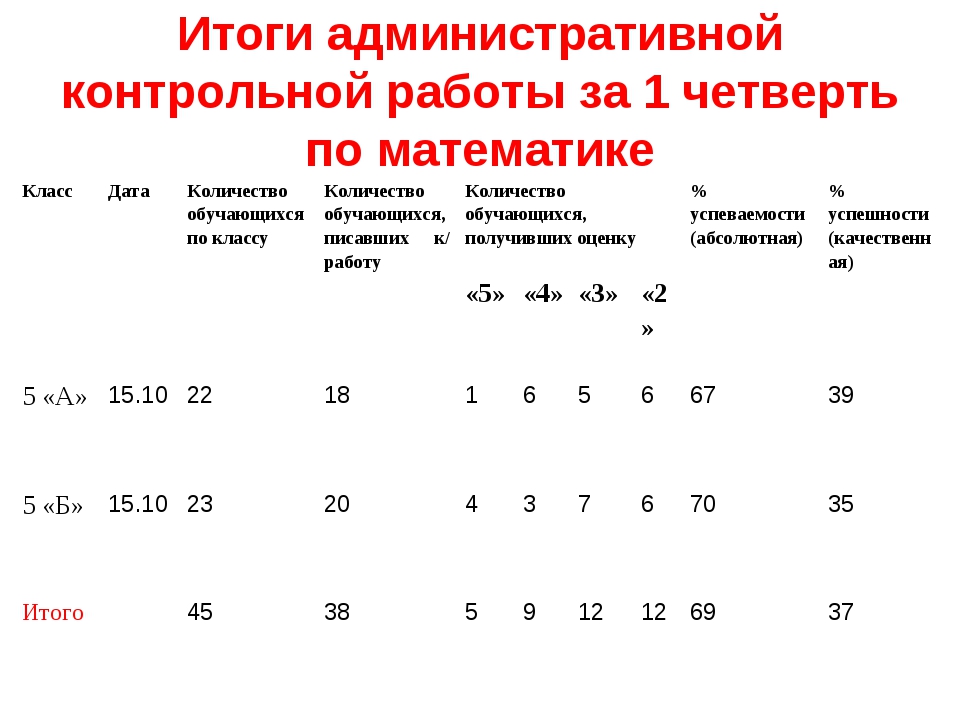
Нужно указать только номер или букву правильного варианта. За такое задание дается 2 балла из 30 возможных. Если ученик выполнит в контрольной работе правильно только первое задание, то отметка будет соответственно 2 (двойка) по десятибалльной шкале.
Если ученик не выполнит правильно ни одного задания, то его отметка за контр. работу будет
Второе задание предполагает решение простейшей задачи в одно действие с подстановкой уже имеющихся данных. Нужно оформлять такую задачу по правилам оформления задачи: записать краткое условие через «дано:», перевести единицы измерения величин в СИ, записать расчетную формулу и только после этого подставлять в формулу величины и производить расчеты, записать ответ. За выполнение такого задания дается 4 балла из 30 возможных. Если до этого было правильно сделано первое задание, то в сумме (2+4) получается 6 баллов из 30, что соответствует отметке 4 (четверка) по десятибалльной шкале.
Последующие задания — третье, четвертое, пятое — предполагают решение задач более высокого уровня с применением двух и более формул. Эти задачи также нужно оформлять по всем требованиям оформления задач по физике.
Задания не обязательно решать по-порядку. Можно решить правильно первое и пятое задание и получить в сумме (2+10) 12 баллов из 30, что соответствует отметке 6 (шесть), а можно решить первое, второе и третье задание и получить в сумме (2+4+6) те же 12 баллов и отметку 6 (шесть).
Отметка за выполнение контрольных работ
выставляется с применением следующих шкал:
Количество баллов за выполнение задания снижается:
- не менее чем на 50 процентов, если в нём допущена существенная ошибка,
- не менее чем на 20 процентов, если в нём допущена несущественная ошибка.
Количество баллов за выполнение задания, в котором допущена погрешность, снижается не более чем на 10 процентов.
К категории существенных относятся ошибки, свидетельствующие о том, что учащийся не знает формул, не усвоил правила, законы, принципы, не умеет оперировать ими и применять к решению задач и оценке полученного результата, не умеет проводить прямые измерения физических величин.
К категории несущественных относятся ошибки, связанные с незнанием единиц физических величин, неумением преобразовать их в единицы СИ, неумением оценивать точность отсчёта при проведении измерений физической величины, ошибки вычислительного характера.
К категории погрешностей относятся погрешности, связанные с нерациональными способами решения задач и математических преобразований и вычислений, небрежным выполнением записей, рисунков, графиков, схем, допущением грамматических ошибок в физических терминах.
|
|
Нормы оценок
Отметка «5» – без ошибок.
Отметка «4» – 1 грубая и 1-2 негрубые ошибки.
Отметка «3» – 2-3 грубые и 1-2 негрубые ошибки или 3 и более негрубых ошибки.
Отметка «2» – 4 и более грубых ошибки.
Работа, состоящая из задач
Отметка «5» – без ошибок.
Отметка «4» –1-2 негрубые ошибки.
Отметка «3» –1 грубая и 3-4 и более негрубых ошибки.
Отметка «2» – 2 и более грубых ошибки.
Комбинированная работа:
Отметка «5» – без ошибок.
Отметка «4» – 1 грубая и 1-2 негрубые ошибки, при этом грубых ошибок не должно быть в задаче.
Отметка «3» – 2-3 грубые и 3-4 негрубые ошибки, при этом ход решения должен быть верным.
Отметка «2» – 4 и более грубых ошибки.
Контрольный устный счет:
Отметка «5» – без ошибок.
Отметка «4» – 1-2 ошибки.
Отметка «3» – 3-4 ошибки.
Отметка «2» – 5 и более ошибок.
Грубые ошибки:
1.Вычислительные ошибки в примерах и задачах.
2.Ошибки на незнание порядка выполнения арифметических действий.
3. Неправильное решение задачи (пропуск действия, неправильный выбор действий, лишние действия).
4. Не решена до конца задача или пример.
5. Невыполненное задание.
Негрубые ошибки:
1. Нерациональный прием вычислений.
2. Неправильная постановка вопроса к действию при решении задачи.
3. Неверно сформулированный ответ задачи.
4. Неправильное списывание данных (чисел, знаков).
5. Не доведение до конца преобразований.
За грамматические ошибки, допущенные в работе, оценка по математике не снижается.
За неряшливо оформленную работу, несоблюдение правил каллиграфии оценка по математике снижается на 1 балл, но не ниже «3».
2. ОЦЕНКА ПИСЬМЕННЫХ РАБОТ ПО РУССКОМУ ЯЗЫКУ.
2.1. ДИКТАНТ.
Объем диктанта:
1-й класс – 15-17 слов.
2-й класс – 1-2 четверть – 25-35 слов.
3-4 четверть – 35-52 слова.
3-й класс – 1-2 четверть – 45-53 слова.
3-4 четверть – 53-73 слова.
4-й класс – 1-2 четверть – 58-77 слов.
3-4 четверть – 76-93 слова.
Отметка «5» – за работу, в которой нет ошибок.
Отметка «4» – за работу, в которой допущено 1-2 ошибки.
Отметка «3» – за работу, в которой допущено 3-5 ошибок.
Отметка «2» – за работу, в которой допущено более 5 ошибок.
Учет ошибок в диктанте:
1. Повторная ошибка в одном и том же слове считается за 1 ошибку (например, ученик дважды в слове «песок» написал вместо «е» букву «и»).
2. Ошибки на одно и то же правило, допущенные в разных словах, считаются как две ошибки (например, ученик написал букву «т» вместо «д» в слове «лошадка» и букву «с» вместо «з» в слове «повозка»).
Ошибкой считается:
1. Нарушение орфографических правил при написании слов, включая ошибки на пропуск, перестановку, замену и вставку лишних букв в словах.
2. Неправильное написание слов, не регулируемых правилами, круг которых очерчен программой каждого класса (слова с непроверяемыми написаниями).
3. Отсутствие знаков препинания, изученных в данный момент в соответствии с программой; отсутствие точки в конце предложения не считается за ошибку, если следующее предложение написано с большой буквы.
Примечание:
2 исправления считаются за 1 ошибку.
Примечание.
При оценке контрольной работы учитывается в первую очередь правильность ее выполнения.
При оценивании работы учитель принимает во внимание каллиграфический навык.
При оценивании работы принимается во внимание не только количество, но и характер ошибок. Например, ошибка на невнимание в меньшей мере влияет на оценку, чем ошибки на изученное правило, в особенности на давно изученные орфограммы.
2.2. ГРАММАТИЧЕСКОЕ ЗАДАНИЕ.
Отметка «5» – без ошибок.
Отметка «4» – правильно выполнено не менее 3/4 заданий.
Отметка «3» – правильно выполнено не менее 1/2 заданий
Отметка «2» – правильно выполнено менее 1/2 заданий.
2.3. КОНТРОЛЬНОЕ СПИСЫВАНИЕ
Отметка «5» – за безукоризненно выполненную работу, в которой нет исправлений.
Отметка «4» – за работу, в которой допущена 1 ошибка и 1-2 исправления.
Отметка «3» – за работу, в которой допущены 2-3 ошибки и 1-2 исправления.
Отметка «2» – за работу, в которой допущены 4 и более ошибок.
2.4. СЛОВАРНЫЙ ДИКТАНТ
|
Объем: 2-й класс – 8-10 слов. 3-й класс – 10-12 слов. 4-й класс – 12-15 слов. |
Отметка «5» – без ошибок. Отметка «4» – 1 ошибка и 1 исправление. Отметка «3» – 2 ошибки и 1 исправление. Отметка «2» – 3-5 ошибок. |
3.
СОЧИНЕНИЕ И ИЗЛОЖЕНИЕ.
Любое сочинение и изложение оценивается двумя отметками: первая ставится за содержание и речевое оформление (соблюдение языковых норм и правил выбора стилистических средств), вторая—за соблюдение орфографических и пунктуационных норм.
Обе оценки считаются оценками по русскому языку, за исключением случаев, когда проводится работа, проверяющая знания учащихся по литературе. В этом случае первая оценка (за содержание и речь) считается оценкой по литературе.
3.1. ИЗЛОЖЕНИЕ.
Отметка за содержание и речевое оформление:
Отметка «5» – правильно и последовательно воспроизведен авторский текст.
Отметка «4» – незначительно нарушена последовательность изложения мыслей, имеются единичные (1-2) фактические и речевые неточности.
Отметка «3» – имеются некоторые отступления от авторского текста, допущены отдельные нарушения в последовательности изложения мыслей, в построении 2-3 предложений, беден словарь.
Отметка «2» – имеются значительные отступления от авторского текста, пропуск важных эпизодов, главной части, основной мысли и др., нарушена последовательность изложения мыслей, отсутствует связь между частями, отдельными предложениями, крайне однообразен словарь.
Отметка за соблюдение орфографических и пунктуационных норм:
Отметка «5» – нет речевых и орфографических ошибок, допущено 1 исправление.
Отметка «4» – имеются 1-2 орфографические ошибки и допущено 1 исправление.
Отметка «3» – имеются 3-6 орфографические ошибки и 1-2 исправления.
Отметка «2» – имеются более 6 орфографических ошибок.
3.2. СОЧИНЕНИЕ.
Отметка за содержание и речевое оформление:
Отметка «5» – логически последовательно раскрыта тема.
Отметка «4» – незначительно нарушена последовательность изложения мыслей, имеются единичные (1-2) фактические и речевые неточности.
Отметка «3» – имеются некоторые отступления от темы, допущены отдельные нарушения в последовательности изложения мыслей, в построении 2-3 предложений, беден словарь.
Отметка «2» – имеются значительные отступления от темы, пропуск важных эпизодов, главной части, основной мысли и др., нарушена последовательность изложения мыслей, отсутствует связь между частями, отдельными предложениями, крайне однообразен словарь.
Отметка за соблюдение орфографических и пунктуационных норм:
Отметка «5» – нет речевых и орфографических ошибок, допущено 1 исправление.
Отметка «4» – имеются 1-2 орфографические ошибки и допущено 1 исправление.
Отметка «3» – имеются 3-6 орфографических ошибки и 1-2 исправления.
Отметка «2» – имеются более 6 орфографических ошибок.
Критерии Оценки Контрольной Работы По Математике – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Критерии Оценки Контрольной Работы По Математике
В Интернете Я ндекс нашёл 13 млн ответов
Структура и механизм оценивания самостоятельных работ , которые проводятся в рамках поурочного контроля, определяются педагогом в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с использованием.
..
Контрольная работа , самостоятельная работа , которые проводятся в рамках тематического контроля, должны включать по одному или по два задания в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с…
Структура и механизм оценивания самостоятельных работ , которые проводятся в рамках поурочного контроля, определяются педагогом в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с использованием…
Наряду с контрольными работами по определенным разделам темы следует проводить итоговые контрольные работы по всей
При оценке письменных работ по математике различают грубые ошибки, ошибки и недочеты. Грубыми в 5-6 классах считаются ошибки…
Оценивание контрольной работы . Контрольная работа состоит из 5 заданий разного уровня сложности. Первое задание самое легкое и заключается в выборе правильного варианта ответов из предложенных. Нужно указать только номер или букву правильного варианта.
Шкалы оценки контрольных и самостоятельных работ . Шкала 1. Номер задания.
При оценивании письменных работ следует учитывать орфографические (ошибки в написании слов) и пунктуационные (ошибки в постановке знаков препинания).
К письменным ответам относятся: домашние, проверочные , практические, контрольные , творческие работы , письменные ответы на вопросы теста
Единые нормы являются основой при оценке как контрольных , так и всех других письменных работ по математике.
Оформление, проверка и оценивание самостоятельных, контрольных и. экзаменационных работ учащихся. При проведении текущей
По учебному предмету «Математика » у учащихся 5-11 классов проверяются наиболее важные учебные работы ( на выбор учителя) не менее…
Контрольная работа , самостоятельная работа , которые проводятся в рамках тематического контроля, должны включать по одному или по два задания в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с.
..
Нормы Оценок письменных работ (контрольная работа , самостоятельная работа , текущая письменная работа ) по математике в v—vi классах.
Критерии оценивания по признакам трех уровней успешности.
Критерии оценки поведения учащихся общеобразовательных учреждений.
Письменные контрольные работы . Контрольными письменными работами являются
На выполнение контрольной работы по теме (тематический контроль) отводится 15 — 20 минут урока.
оценки знаний умений и навыков учащихся. при проверке письменных контрольных и. самостоятельных работ.
1. оценка письменных работ по математике . Работа, состоящая из примеров: Отметка «5» – без ошибок. Отметка «4» – 1 грубая и 1-2 негрубые ошибки.
Оценка Результатов Учебной Деятельности Учащихся ПО Учебному Предмету «Искусство (Отечественная И Мировая Художественная Культура)» Приказ от 29.09.2010 г. № 635 Оценка результатов учебной деятельности учащихся по иностранному…
Математика . 1. Оценка письменных контрольных работ обучающихся по математике.
Критерии . оценивания знаний учащихся с 5-9 класс. Русский язык. «Нормы оценки…» призваны обеспечить одинаковые требования к знаниям, умениям и навыкам учащихся по русскому языку.
Рекомендации по оценке учебной деятельности учащихся по математике. Опираясь на эти рекомендации, учитель оценивает знания, умения и
2. Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
Размещение рекламы
+ 375 (17) 336-91-01
Хостинг: HOSTER.BY
Поиск реализован на основе Яндекс.XML
Шкала оценивания контрольных работ по математике
Оценивание контрольной работы — Шкала оценки знаний…
Нормы оценки результатов учебной деятельности — Гимназия №19…
Критерии и нормы оценок по математике
Критерии оценки учебной деятельности по математике
Северный Кавказ Реферат Скачать
Курсовой Офицер Организатор И Руководитель Воспитания Курсантов
Инвестиционная Привлекательность Предприятия Курсовая
Зарубежные Рефераты
Контрольная Работа По Английскому За Первую Четверть
«Сферы» Критерии оценивания проверочных работ по математике в 5 классе
«Сферы» Критерии оценивания проверочных работ по математике в 5 классеГлава 1.
Линии| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 3 задания | 3 задания | 4 задания |
| Дополнительная часть | 1 задание | 2 задания |
Глава 2. Натуральные числа
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 5 заданий | 8 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 5 заданий | 6 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 3.
Действия с натуральными числами| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 7 заданий | 7 заданий | 8 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 4 задания | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 4. Использование свойств действий при вычислениях
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 6 заданий | 6 заданий | 7 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 4 задания | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 5.
Углы и многоугольники| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 5 заданий | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 6. Делимость чисел
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 7 заданий | 8 заданий | 9 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 5 заданий | 6 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 7.
Треугольники и четырехугольники| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 5 заданий | 6 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 8. Дроби
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 7 заданий | 7 заданий | 8 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 6 заданий | 6 заданий | 7 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 9.
Действия с дробями. Сложение и вычитание дробей| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 6 заданий | 6 заданий | 7 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 4 задания | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 9. Действия с дробями.
Умножение и деление дробей| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 5 заданий | 6 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 4 задания | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 10. Многогранники
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 5 заданий | 6 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Глава 11.
Таблицы и диаграммы| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 5 заданий | 6 заданий | 6 заданий |
| Дополнительная часть | 1 задание |
Итоговая проверочная работа за первое полугодие
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 7 заданий | 7 заданий | 8 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 4 задания | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
Итоговая проверочная работа за второе полугодие
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 6 заданий | 6 заданий | 7 заданий |
| Дополнительная часть | 1 задание | 2 задания |
| Отметка | «зачет»(«3») | «4» | «5» |
|---|---|---|---|
| Обязательная часть | 4 задания | 4 задания | 5 заданий |
| Дополнительная часть | 1 задание | 2 задания |
6 Оценка аттестата по математике | Измерение того, что имеет значение: концептуальное руководство для оценки по математике
П OSTSCRIPT Три предложенных здесь принципа — содержание, обучение и справедливость — функционируют как гироскоп для реформы математического оценивания, который поможет продолжить реформу математики и привести к новым оценкам, которые отражают важную математику, поддерживают хорошее обучение и способствуют развитию возможностей каждого учащегося.
учить.
Система наведения этого гироскопа является мощным инструментом на пути к реформе системы оценивания. Однако это всего лишь инструмент, сам по себе недостаточный для решения поставленной задачи. Не менее важны пригодность судна для рейса, экипаж, способный внести необходимые корректировки в середине курса, а также подробная навигационная карта, показывающая желаемый порт.
Сосудом реформы является общенациональный акцент на системных изменениях: скоординированный ответ всех основных компонентов образовательной системы (учебная программа, преподавание, оценка, управление, педагогическое образование, школьная организация и т. Д.)). По математике судно особенно крепкое и хорошо спущено на воду. Уже доступны описания задачи (Все на счету), цели того, что студенты должны изучать (Учебный план и стандарты оценки), и методы обучения, необходимые для поддержки этого обучения (Профессиональные стандарты преподавания математики). NCTM сейчас разрабатывает третий из серии томов стандартов, на этот раз по оценке.
В этом томе, который планируется выпустить весной 1995 года, будут изложены стандарты оценивания, которые служат целому ряду целей — от обучения в классе до политики, оценки программ, планирования и распределения студентов.Три компонента стандартов — учебная программа, педагогика и оценивание — обеспечивают основу для обновления педагогического образования, переосмысления школьной организации, усиления реализации реформ и содействия диалогу о системных изменениях между многими заинтересованными сторонами в математическом образовании.
Резервы на рейс обеспечиваются материальными ресурсами, что стимулирует широкое участие в реформе оценивания. Эти ресурсы предоставляют богатый набор примеров высококачественного оценивания, созвучного видению математики и математического образования, выраженному в Стандартах .Некоторые предоставляют конкретные примеры, иллюстрирующие всеобъемлющие идеи (например, Mathematics Assess —
4 Оценивание для поддержки изучения математики | Измерение того, что имеет значение: концептуальное руководство для оценки по математике
, как правило, путем подсчета количества вопросов, на которые даны правильные ответы, и сравнения баллов одного человека с баллами другого на основании их относительного процентильного ранга.
Так называемые оценки с привязкой к норме уже много лет беспокоят педагогов.Несмотря на то, что высказывались различные критические замечания по поводу ссылки на нормы, основная проблема образования заключается в том, что такая информация недостаточно полезна для улучшения обучения и обучения и может, фактически, иметь контрпродуктивные образовательные последствия. В классе учителя и ученики должны знать, что ученики понимают хорошо, что они понимают хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных студентов могут быть использованы вне контекста класса, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.
Программы оценивания должны информировать учителей и учеников о том, что ученики узнали, как они учатся и как они думают о математике. |
Например, чтобы спланировать свое обучение, учителя должны знать о текущем понимании каждым учеником того, чему будут учить.
Таким образом, программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и как они думают о математике.Чтобы эта информация была полезной для учителей, она должна включать анализ конкретных сильных и слабых сторон понимания учащимся, а не только оценок вне контекста.
Чтобы обучение было эффективным, результаты оценки должны быть своевременными. 35 Учебе учащихся не способствуют компьютерные распечатки, отправляемые учителям после того, как классы закончились в течение года и ученики ушли, ни учителя, которые уделяют слишком много времени оценке оценок.В частности, необходимо найти новые способы дать учителям и ученикам более непосредственные знания об успеваемости учеников по оценкам, предписанным внешними властями, чтобы эти оценки, а также собственные оценки учителя могли использоваться для улучшения обучения. Даже если основной целью оценки является определение достижений школы, штата или страны, оценка должна предоставлять учащимся и учителям отчеты об их успеваемости.
Школьное время дорого.Когда учащимся не сообщают об их ошибках и заблуждениях, не говоря уже о том, чтобы помочь их исправить, оценка может как усилить недопонимание, так и потратить драгоценное учебное время впустую.
Когда форма оценивания незнакома, учителя несут особую ответственность перед своими учениками, чтобы сообщить им заранее
Аутентичные методы оценки по математике
В основе аутентичного оценивания лежит оценка способности учащегося применять полученные знания по математике в контексте «реального мира».
Получайте релевантные учебные материалы и обновления, доставляемые прямо в ваш почтовый ящик. Подпишитесь сегодня! Присоединиться Вместо заучивания наизусть и пассивного тестирования, аутентичные оценочные тесты по математике фокусируются на аналитических навыках учащегося и его способности объединить то, что они узнали, наряду с творчеством с письменными и устными навыками.
Также оцениваются результаты совместной работы групповых проектов. Важно знать не только изучение процесса вычислений, но и то, как взять готовый продукт и применить его в другой ситуации.
Была разработана потребность в улучшенном тесте для точной оценки роста учащегося. Он называется аутентичным оценочным тестом по математике. Тесты с множественным выбором не всегда точно отражают понимание материала отдельным учащимся. Он показывает, успешно ли ученик запоминает. Вместо тестов, нацеленных на вспоминание конкретных фактов, тест по аутентичной математике предлагает учащимся продемонстрировать различные навыки и концепции, которые они усвоили, и объяснить, когда было бы целесообразно использовать эти факты и навыки решения проблем в своей жизни.
Шесть способов использовать аутентичную математику для оценивания в классе
Оценка эффективности
Студенты могут продемонстрировать, чему они научились, и как решать проблемы с помощью совместных усилий при совместном решении сложной проблемы.
Они не только учатся работать в команде, но и учатся проводить мозговой штурм и использовать свои отдельные крупицы знаний на благо всего.
Краткие справки
Как правило, небольшое исследование начинается с основной математической задачи (или может быть адаптирована к любому другому школьному предмету), в которой учащийся может продемонстрировать, как он или она усвоили основные концепции и навыки.В качестве учителя попросите учеников интерпретировать, вычислять, объяснять, описывать или предсказывать то, что они анализируют. Как правило, это задания продолжительностью от 60 до 90 минут для отдельного человека (или групповых проектов), над которыми он может работать самостоятельно, писать ответы на вопросы, а затем опрашивать отдельно.
Вопросы с открытым ответом
Учитель может оценить, насколько ученик понимает реальный мир и как связаны аналитические процессы, запрашивая в ходе викторины открытые ответы, например:
- краткий письменный или устный ответ
- математическое решение
- чертеж
- диаграмма, диаграмма или график
Эти открытые вопросы могут быть примерно 15-минутными оценками и могут быть преобразованы в крупномасштабный проект.
Портфели
По мере того, как учащиеся изучают концепции в течение учебного года, они могут быть задокументированы, и они покажут прогресс и улучшения, а также позволят проводить самооценку, редактировать и исправлять. Их можно записать разными способами, в том числе:
- ведение журнала
- обзор коллег
- иллюстрации и схемы
- групповые отчеты
- студенческих заметок и конспектов
- черновиков до готовой работы
Самооценка
После того, как учитель четко объяснил и представил ожидания до проекта, а затем, когда проекты будут завершены, попросите учеников оценить свои собственные проекты и участие.Ответы на следующие вопросы помогут студентам научиться объективно оценивать себя и свою работу:
- Что было для вас самым сложным в этом проекте?
- Как вы думаете, что вам следует делать дальше?
- Если бы вы могли выполнить это задание снова, вы бы поступили иначе? Если да, то что?
- Что вы узнали из этого проекта?
Вопросы с несколькими вариантами ответов
Обычно вопросы с несколькими вариантами ответов не отражают подлинного математического контекста оценивания.
Разрабатываются вопросы с несколькими вариантами ответов, которые раскрывают понимание необходимых математических идей, а также объединяют более одной концепции. Эти вопросы рассчитаны на 2–3 минуты каждый.
Черты характера, полученные в ходе аутентичных оценочных тестов по математике
Этот ситуативный тип обучения, при котором учащиеся изучают уроки решения реальных задач, может быть использован в математике. Эти идеи представлены следующим образом:
- Мышление и рассуждение: Побуждение учащихся к взаимодействию в таких действиях, которые включают сбор данных, исследование, исследование, интерпретацию, рассуждение, моделирование, проектирование, анализ, формирование гипотез, использование метода проб и ошибок, обобщение и проверку решений.
- Настройки: Позволяет студентам работать индивидуально или в небольших группах.
- Математические инструменты: Студенты учатся использовать символы, таблицы, графики, рисунки, калькуляторы и компьютеры.
- Отношение и предрасположенность: Студенты в этой учебной среде учатся настойчивости, саморегулирующемуся поведению и рефлексии, участию и особому энтузиазму в изучении различных ситуаций.
Изучите образовательные методы для улучшения успеваемости учащихся по математике.Степень магистра математического образования поможет вам узнать о передовых методах успешного обучения на уроках математики.
Присоединяйтесь к Resilient EducatorПодпишитесь на нашу рассылку, чтобы получать контент, доставляемый в ваш почтовый ящик. Щелкните или коснитесь кнопки ниже. |
Возможно, вы также прочитаете
Теги: Инструменты оценки, Математика и естественные наукиДобро пожаловать в оценочный проект по математике
Добро пожаловать в оценочный проект по математикеОЦЕНКА 21
ST CENTURY MATHДобро пожаловать в проект оценки математики
Главное меню
Проект MathNIC выпустил бесплатные инструменты, чтобы помочь школам и школьным округам быть более эффективными в организации, улучшении, поддержке преподавания и обучения, а также в общении с родителями и сообществом.
Посетите mathnic.org для получения подробной информации.
Хью Буркхардт и Малкольм Свон получили престижную награду от ICMI за работу команды в области математического образования.
Подробнее…
Классные задачи занимает центральное место в отчете Research for Action о влиянии MDC на преподавание и обучение.
Все наши материалы можно скачать бесплатно и воспроизводить как есть для некоммерческое использование.Точные условия варьируются в зависимости от материала. Запросы на: [email protected].
Проект оценки по математике является частью сотрудничества по математическому дизайну, инициированного Фондом Билла и Мелинды Гейтс. Целью проекта было спроектировать и разработать хорошо спроектированные
инструменты для формирующего и итогового оценивания, которые раскрывают математические знания и рассуждения учащихся, помогая учителям направлять их к совершенствованию и контролировать успеваемость.
Инструменты актуальны для любой учебной программы, которая направлена на углубление понимания учащимися математических концепций и развитие их способности применять эти знания для решения нестандартных задач.
Подробнее о проекте по оценке математических навыков
100 уроков для формирующего оценивания, некоторые сосредоточены на развитии математических понятий, другие на решении нестандартных задач. Перед первым использованием этих уроков рекомендуется прочитать Краткое руководство для учителей и администраторов (PDF).
Набор из 94 образцовых итоговых оценочных заданий на проиллюстрировать диапазон целей производительности, требуемых CCSSM. Задания сопровождаются оценочными рубриками и примерами оцениваемых студенческих работ.
Заполните формы итогового теста и рубрики, призванные помочь
Учителя и ученики следят за своими успехами, используя ряд типов задач, подобных разделу «Задачи».
5 модулей-прототипов, которые поощряют группы учителей к изучению практические и педагогические концепции, лежащие в основе материалов, такие как как формирующая оценка, совместное обучение и использование неструктурированные проблемы.
Пакет «Обучение для устойчивого понимания математики» (TRU Math) — это набор инструментов с приложениями для профессионального развития и исследований, основанный на структуре для характеристики мощной учебной среды.
творческих способов оценить понимание математики
Учителя математики творчески переосмысливают оценки учеников, что позволяет им получить более широкую картину концептуального понимания математики детьми, пишет Мэдлин Уилл для Education Week . И хотя этот творческий подход к оценке знаний учащихся, по крайней мере частично, обусловлен дистанционным обучением, эти стратегии эффективны и имеют смысл в течение обычного учебного года.
«Я думаю, что это хорошо для многих из нас, учителей математики, потому что это заставляет нас переосмыслить то, что должны выполнять экзамены», — сказал Уиллу учитель математики Мэтью Ректор.«В прошлом большинство из нас рассматривало оценивание как инструмент ранжирования: поставьте ребенку оценку и двигайтесь дальше. Оценки должны быть направлены на продвижение математических знаний ».
В то время как учителя в течение некоторого времени переосмысливали систему оценивания, переход к дистанционному обучению «помог сохранить импульс», — сказала Уиллу Трена Вилкерсон, президент Национального совета учителей математики. «Учителя творчески и нестандартно думают о том, как оценить понимание и мышление учеников, а затем как использовать это для поддержки решений в отношении обучения.”
Используйте знакомые технические инструменты, чтобы понять математическое мышление
Вместо того, чтобы постоянно просить учеников решить ряд уравнений, Уилл поговорил с учителями, которые теперь просят учеников объяснить математическую концепцию или «разбить проблему и объяснить, как они достигают ее решения».
Учащиеся могут выбрать способ записи своей работы: в документ Google, через видео или сделав снимок своей работы на бумаге. «Это позволяет им лучше выражать свои мысли, — сказал Уиллу учитель математики в старшей школе Бобсон Вонг, — и очень сложно заниматься плагиатом.«
Учитель математики средней школы Эмма Чиаппетта любит просить своих продвинутых учеников по линейной алгебре создавать видео, обучающие их одноклассникам приложениям и концепциям. Чтобы проверить, насколько эффективно ее ученики объясняют алгебраические понятия, каждый из них пытается решить несколько задач, связанных с видеоуроком сверстника.
Тереза Уильямс, учитель математики в средней школе Лабораторной школы Университета Вайоминга в Ларами, штат Вайоминг, проводит пятиминутные собеседования, чтобы оценить успеваемость своих учеников и информировать ее о преподавании.«Полезно составить контрольный список того, что вы ожидаете от опытного ученика, — отмечает Уильямс. «Это отлично подходит для детей, которые знают намного больше, чем они показали при [традиционном] оценивании», и дает учащимся «множество возможностей показать, что они хороши».
Попробуйте математические журналы или рефлексивное ведение журнала
Письмо может быть мощным способом обучения, «потому что оно задействует оба полушария мозга», — пишет координатор математики средней школы Алессандра Кинг.«Эффективное письмо также проясняет и упорядочивает мысли студента». Некоторые учителя просят учащихся вести «рефлексивный дневник о математических концепциях», чтобы оценить, насколько учащиеся усвоили материал, пишет Уилл, предоставляя богатую картину того, на каком этапе находятся дети на математическом блоке.
Кинг любит заставлять своих учеников-математиков размышлять и писать о математике, прося их создать математический журнал, в котором они сосредоточатся на том, как математические концепции применяются в реальном мире. «Это был один из моих самых популярных проектов — студенты с удивлением открывают для себя бесчисленное множество приложений математики.”
Она начинает с составления списка статей по математике из газет, журналов, подкастов и видео для студентов на выбор, а затем обобщает их для онлайн-журнала.
«Для оценки я создал простую рубрику, которая учитывает понимание содержания, ясность общения, редактирование, критическое мышление, инициативу и творчество», — говорит Кинг. Специально для студентов, которым нравится читать и писать больше, чем «вычислительная сторона математики», этот проект дает им возможность продемонстрировать свое понимание математических концепций, одновременно получая «более сильное понимание полезности и эффективности математики.”
Назначьте проекты, связанные с реальным миром
С помощью переписи населения Массачусетса учащиеся по алгебре 1 учителя средней математики Джои Грабовски выбирают категориальные группы, такие как пол или раса, и количественные переменные, такие как доход или возраст, а затем «сравнивают распределения двух или более групп людей». Затем они пишут отчет о своем статистическом анализе. Использование проектов вместо модульных тестов для оценки своих учеников дает Грабовски уникальный взгляд на их мышление, пишет Уилл.
«[Со статистическим отчетом] они анализируют и критикуют вещи», — говорит он. «Компьютеры могут делать за нас многие из этих вычислений, но не могут интерпретировать данные».
Когда разразилась пандемия, школьная учительница математики Чиаппетта разместила в Интернете предложения своих учеников-статистиков по проектам. Она обменяла прогулки по галерее на виртуальные на Flipgrid и попросила студентов оставлять там отзывы о проектах одноклассников. «После определенного момента для меня не имеет смысла опрашивать моих учеников об их расчетах», — сказал Чиаппетта.«Проекты, которые выполняют мои студенты, позволяют мне оценить их способность применять эти расчеты в контексте».
Активно признавать ошибки
Создание класса, в котором нет места ошибкам, важно для всех учащихся по академическим предметам, но особенно в классе математики, который может вызывать беспокойство у студентов. Кэрол Двек, профессор психологии Стэнфордского университета и автор книги Mindset: The New Psychology of Success , сказала: «Каждый раз, когда студент совершает ошибку… у них растет синапс.”
Уилл отмечает, что учителя используют эту идею и в оценках, нормализуют ошибки и просят учащихся решать проблемы, которые намеренно решаются неправильно, требуя от учащихся выявлять ошибки, а затем выяснять, как их решать.
Учитель алгебры 1 Роберт Макосланд сказал Уиллу, что ему нравится давать студентам возможность повторить, давая студентам время для работы над проблемами, с которыми они боролись в предыдущих оценках. Когда студенты учились дома, он обнаружил, что «первоначальные оценки были неестественно высокими, возможно, потому, что студенты искали ответы дома.Но по мере того, как его ученики становились более уверенными в своих способностях решать сложные задачи, «результаты нормализуются», и он смог объяснить ученикам, что «научиться понимать математику — это не о том, что правильно или неправильно. … Нет серьезных ошибок ».
Распределительные тесты Math Mammoth для 1-7 классов (бесплатная оценка по математике)
Эти бесплатных диагностических тестов помогут вам определить уровень вашего ребенка или ученика в математике и ТОЧНО выяснить, где у них есть пробелы (если таковые имеются).Это тесты на конец года (EOY) — другими словами, их нужно сдавать ПОСЛЕ изучения определенного класса.
Несмотря на то, что тесты ЯВЛЯЮТСЯ тестами для размещения по программе Math Mammoth, завершенной учебной программой , они работают одинаково хорошо с оценочными тестами GENERIC по математике.
Использование тестов позволит вам адаптировать инструкцию, чтобы помочь ребенку / ученику именно там, где они больше всего нуждаются в помощи. Вы можете ЛЕГКО узнать, не изучил ли ваш ученик определенные темы, потому что в тестах вопросы сгруппированы по темам .Достаточно взглянуть на результаты тестов по «разделам» похожих задач (сложение, умножение, измерение, геометрия, разметка, решение задач).
Если есть сомнения, вы всегда можете прислать мне результаты анализов вашего ребенка. (Просто пришлите мне количество баллов за каждый тестовый элемент.)
Для начала просмотрите тесты и попытайтесь найти самый высокий уровень, который, как вы ДУМАЕТЕ, пройдет ваш ученик или ребенок. Тогда вы, естественно, проведете этот тест.
Видео ниже объясняет основы того, КАК использовать эти тесты:
В этой таблице показаны возможные диапазоны баллов и способы интерпретации результата:
| Оценка | Значение |
|---|---|
| 90% или более | Провести тест следующего более высокого уровня. |
| от 80% до 89% | Учащийся может перейти на следующий уровень по математике Мамонт. |
| от 70% до 79% | Учащийся, вероятно, сможет перейти на следующий уровень по математике Мамонт, но ему может потребоваться помощь в заполнении пробелов. Используйте свое суждение. |
| от 50% до 69% | Учащийся может быть переведен в класс экзамена. Или вы можете провести следующий тест более низкого уровня, чтобы получить более полное представление о том, что студент знает и чего не знает. |
| менее 50% | Провести следующий тест более низкого уровня. |
Однако вполне возможно, что только один тест не даст вам хорошего обзора того, что студент усвоил. Так что не бойтесь проводить два или даже три теста — или частей, тестов. Например, предположим, что ученик набрал 70% по тесту, и, в частности, он получил низкий балл в разделе теста по геометрии. В этом случае полезно также управлять разделами ГЕОМЕТРИЯ тестов следующего более низкого уровня, чтобы выяснить, насколько «велик» разрыв в геометрии.
Иногда ученик, который серьезно отстает, может получить низкий балл даже по ТРЕМЯ следующим тестам. По сути, их навыки и знания, так сказать, «повсюду». Таким учащимся может быть полезен индивидуальный подход, при котором материалы, которые они будут изучать, будут точно соответствовать имеющимся у них пробелам.
Еще одна важная вещь. Чтобы снизить стресс от сдачи теста, не устанавливайте строгих ограничений по времени для завершения теста. Мы не хотим, чтобы у студентов возникло какое-либо беспокойство из-за этого промежуточного теста или тестов.Некоторые дети уже испытывают тревогу по поводу сдачи тестов и / или математики в целом. В таких случаях было бы лучше избегать даже этих тестов или, по крайней мере, отложить их до тех пор, пока тревога несколько не утихнет.
- Тест на конец года по математике Мамонт, 1 класс
Ответы на экзамен на конец года по математике Мамонт, 1 класс - Тест на конец года по математике на мамонта, 2 класс
Ответы на экзамен на конец года по математике на мамонта, 2 класс - Тест на конец года по математике на мамонта, 3 класс
Ответы на экзамен на конец года по математике на мамонта, 3 класс - Тест на конец года по математике на мамонта, 4 класс
Ответы на экзамен на конец года по математике на мамонта, 4 класс - Экзамен на конец года по математике «Мамонт», 5 класс
Ответы на экзамен на конец года по математике «Мамонт», 5 класс - Тест на конец года по математике на мамонта, 6 класс
Ответы на экзамен на конец года по математике на мамонта, 6 класс - Тест на конец года по математике на мамонта, 7 класс (предварительная алгебра)
Ответы на экзамен на конец года по математике на мамонта, 7 класс
Совет: Если вы заметили, что у вашего ребенка проблемы с одной или двумя концептуальными областями в конкретном тесте, но в остальном все хорошо, вы можете использовать книги серии Math Mammoth Blue, чтобы «заполнить эти пробелы».Вы также можете отправить мне электронное письмо с результатами теста, если не можете решить, какую книгу Blue Series вам следует использовать для такой коррекционной работы.
Рабочие тетрадиMath Mammoth для проверки на уровне класса также можно использовать для выявления слабых мест или для проверки тем на уровне всего класса.
Пример
Вот пример результатов теста одного ученика и совета по размещению, который я дал родителю этого ученика.
Предыстория : ученик начал домашнее обучение в том же году, когда были сданы тесты, и технически учится в 7-м классе.Она начала делать учебники по алгебре 1. Однако родитель заметила, что она не знает основную информацию о дробях, решила поискать приложение и наткнулась на Math Mammoth.
Ученица сдала три экзамена в конце года: для 6, 5 и 4 класса. Она не очень хорошо сдала тест для 6 класса, но вы можете увидеть ее работу для 4 и 5 классов по ссылкам. ниже. Если вы решите отправить мне результатов теста вашего ребенка , нет необходимости отправлять мне полный тест, как это сделал этот человек, но это хороший пример.Большинство людей присылают мне только количество баллов за различные тестовые задания.
А вот и моя оценка и рекомендации:
Привет,Я думаю, что будет хорошей идеей начать ее с 5 класса по математике Мамонт.
Кроме того, я считаю, что ей следует изучить эти книги из серии Blue.
- Ранняя геометрия, потому что она, кажется, не понимает концепций площади и периметра, которые имеют первостепенное значение. Эта книга предназначена для 1–3 классов, поэтому некоторые темы в ней слишком простые, и она может их пропустить.
- Геометрия 1 — предназначена для 4-5 классов. Ей нужно будет сначала изучить уроки 4-го класса (углы, четырехугольники, треугольники и т. Д.). Обратите внимание, что часть содержания здесь совпадает с 5-м классом ММ. Она может изучать совпадающие уроки из любого источника.
- Измерение 1 — это для классов 1-3, но ей, возможно, придется с самого начала пересмотреть все, что касается единиц измерения. Некоторые уроки могут быть слишком простыми и их можно пропустить — судите сами.
- Измерение 2 — для 4-6 классов. Обратите внимание, что часть содержания здесь частично совпадает с 5-м и 6-м классами ММ. Она может изучать совпадающие уроки из любого источника.
- Десятичные 1
Она не поняла основ того, как дробь и десятичная дробь связаны вместе — что, опять же, является очень фундаментальной концепцией. Она должна изучить книгу «Десятичные дроби 1», прежде чем начинать главу «Десятичные дроби» в 5 классе.
Помимо этих нескольких областей (геометрия, измерения, десятичные дроби), ее можно поместить в MM 5.
Кстати, не перекладывайте все задачи, связанные с расчетами (большие наборы упражнений) ни на один из материалов. Достаточно сначала назначить 1/3 из них. Если у нее возникнут трудности, то используйте остальное (и это может быть так, если речь идет, скажем, о периметре и площади).
И она очень хорошо справилась с первыми двумя разделами итогового теста 5-го класса, что означает, что она, возможно, могла бы пропустить первые две главы MM5. Вы можете позволить ей изучить обзоры глав и / или тесты из этих 2 глав.Проверьте и посмотрите, как она справляется с ними, а затем используйте свое суждение, если ей нужно будет изучить какие-либо уроки из этих глав.
К счастью, она также разбирается в дробной арифметике, что ускоряет выполнение части 5-B.
Я очень рад, что ее «пробелы» в общем-то не решают проблемы! Намного легче разобраться с такими темами, как единицы измерения, площадь и периметр, чем исправить общую неспособность решать текстовые задачи (что характерно для многих детей).
С уважением,
Мария Миллер
Вопросы по размещению
- Мой K-ученик хочет усложнить задачу и заняться математикой в первом классе. Как я могу узнать, подходит ли моему ребенку вариант Light Blue 1?
«Голубой» класс 1 начинается с того же материала, что и книги из серии «Голубой»: добавление 1 и вычитание 1. Просмотрите их, просмотрите их образцы и содержание, и это, вероятно, скажет вам, готовы ли ваши дети к 1 классу. .
- Я думал, что мой ребенок раньше хорошо успевал по математике (получал пятерки и пятерки), но он / она все равно не сдал тест на определение уровня своего класса.
Это обычное явление для детей, которые учатся в государственной школе или по другой математической программе. Как правило, это связано с тем, что (i) Math Mammoth широко использует многоступенчатые задачи со словами, начиная со 2-го класса; и (ii) ребенок, возможно, не изучил все темы другой учебной программы, чем те, которые рассматриваются в MM.Геометрия и измерения часто оказываются такими областями.
Чтобы наверстать упущенное, см. Совет выше по использованию книг Blue Series. Еще одна вещь, которую вы можете сделать, — это ускорить прохождение более ранних уровней Math Mammoth, например, изучив обзоры глав и остановившись, чтобы изучить любую концепцию, которую ребенок не понял.
Такой процесс обычно можно выполнить всего за несколько месяцев, так что не беспокойтесь! Гораздо важнее получить прочную основу в математике, чем смотреть на уровни обучения и просто продолжать.В математике очень важно понимать предыдущие концепции, потому что в противном случае ученик в конечном итоге потерпит неудачу, и большинство из них также начнут ненавидеть математику.
См. Также эту ветку на дискуссионном форуме домашнего обучения: Неожиданный опыт прохождения экзамена по математике на мамонта в конце года.
- Студент пропускает (или даже не пытается) большинство задач со словами в тесте, но справляется с задачами с расчетами.
Это ОБЫЧНАЯ ситуация для многих студентов. Обычно это происходит из-за отсутствия заданий на правильное слово в математической программе, по которой студент учился.Прочтите, что я написал о проблеме со словами, чтобы лучше понять ее происхождение.
На этой странице вы также найдете список РЕСУРСОВ, которые могут вам помочь. Дополнительно или в качестве альтернативы, ваш ученик может просмотреть определенные книги из Синей серии, делаю только задачи со словами и уроки, относящиеся к задачам со словами. Используйте это как ориентир:
Учащийся попытался сдать итоговый тест 2-го класса:
Сложить и вычесть 2-A, Сложить и вычесть 2-B и половину сложить и вычесть 3.Учащийся попытался сдать экзамен в конце учебного года в 3-м классе:
(возможно, сложить и вычесть 2-A) Сложить и вычесть 2-B, сложить и вычесть 3, умножить 1 и разделить 1.Учащийся сдал итоговый тест 4-го класса:
Сложение и вычитание 3, умножение 1, деление 1, умножение 2 и раздел 2. - Мой ребенок хорошо сдал тест , за исключением такой-то области или темы. Можете ли вы помочь мне выбрать лечебные материалы?
См. Следующую таблицу.
- Я использую Math-U-See, и мой ребенок не изучал некоторые материалы, которые вы освещаете, раньше, чем MUS. Как мне перейти на Math Mammoth?
Я бы просто порекомендовал вам сначала пройти тест на определение уровня знаний, чтобы точно узнать, что она знает, а что нет в тех темах, которые MUS не так широко освещает, например, измерения, деньги, часы, геометрия и решение проблем. .
Затем, после того как ребенок сдал тест, вы можете выбрать книги из серии Blue, посвященные конкретным темам (см. Таблицу выше).
Помните также, я готов помочь вам с этими решениями. Просто дайте мне знать результаты тестирования ребенка по разделам.
Мария Миллер
Практический тест по математике (примеры вопросов)
Если вы собираетесь поступать в колледж или университет, возможно, в ближайшем будущем вам предстоит сдать тест по математике. Школы используют эти тесты как инструмент для определения подходящего уровня математических классов для поступающих учеников. Эти экзамены сдаются после того, как студент уже принят в зачисление; они не участвуют в процессе подачи заявления в колледж.Кроме того, в этих тестах нет положительных или отрицательных результатов.
Есть несколько причин, по которым колледжи сдают эти экзамены. Во-первых, в стране тысячи средних школ, и нет двух абсолютно одинаковых. Некоторые школы отлично справляются с подготовкой своих учеников к математике на уровне колледжа, некоторые достаточно компетентны в этой задаче, а другие плохо справляются с этой задачей. Поэтому тот факт, что у ученика есть аттестат о среднем образовании, не очень помогает, когда колледжи стремятся подобрать учеников с правильной курсовой работой.
Вторая причина заключается в том, что некоторые ученики от природы хороши в математике, в то время как другие с трудом успевают за ними. Если ученика, не обладающего сильными математическими способностями, поместят на неправильный курс колледжа, результаты могут быть плачевными. В лучшем случае студент не проходит курс и в следующем семестре вынужден начинать с более легкого класса. В худшем случае студент разочаровывается из-за того, насколько тяжелой кажется работа на уровне колледжа, сдается и бросает учебу.
Меньше всего колледжи хотят, чтобы их поступающие студенты разочаровывались и бросали учебу из-за того, что они не справляются со своей задачей.Они используют контрольные экзамены по математике, чтобы убедиться, что каждый ученик начинает с того уровня математики, к которому он должным образом подготовлен. Затем студенты могут использовать свои успехи на менее сложных курсах как основу для занятий на продвинутых курсах.
Каждый колледж разрабатывает свой собственный экзамен по математике, поэтому точное содержание и количество вопросов в тесте будут варьироваться от школы к школе. Однако они, как правило, очень похожи. Если вас просят сдать экзамен по математике, вы должны ожидать, что увидите вопросы, охватывающие широкий спектр математических тем.Будут рассмотрены основы арифметики — сложение, вычитание, умножение, деление, десятичные дроби и дроби. Вы также увидите вопросы о более сложной математике, такой как предалгебра, алгебра, построение графиков, тригонометрия и т. Д. Вопросы обычно охватывают алгебраические дроби, корни и показатели, расширяющиеся полиномы, уравнения и неравенства, комплексные числа, факториалы, определители, линии, параболы, логарифмы и т. д.
Практически во всех колледжах вы будете сдавать установочный экзамен по математике на компьютере, и все вопросы будут с несколькими вариантами ответов.В некоторых школах вам не разрешат использовать калькуляторы любого типа, но некоторые школы разрешат вам принести базовый калькулятор с четырьмя функциями, или он будет предоставлен на компьютере. Правила повторного тестирования также различаются от школы к школе — некоторые колледжи не разрешают повторное тестирование, но другие разрешают вам повторить попытку, если вы не удовлетворены своей оценкой.
Не каждая школа требует, чтобы все учащиеся сдали вступительные экзамены на курсы математики. Во многих школах, если абитуриент набирает достаточно высокий балл по ACT или SAT, он может пропустить вступительные экзамены и сразу же приступить к занятиям по математике с углубленным изучением.Если вас просят пройти контрольный тест, очень важно подготовиться к нему. Если ваш результат достаточно высок, вы можете сэкономить много времени, денег и скуки, пропустив коррекционные и базовые уроки математики в колледже. Вам больше понравится учиться в колледже, и вы, вероятно, быстрее получите диплом.