Логарифмические уравнения логарифмические неравенства контрольная работа: Контрольная работа по математике «Логарифмические уравнения и неравенства»

Контрольная работа по математике (логарифмические уравнения и неравенства) для 10-го класса от Сообщества математиков в 2016 году

Ответы

Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Статистика и загрузка

Скачать

Если загрузка не началась автоматически, повторите попытку или нажмите сюда!

Просмотров	516	181	Загрузок
Добавил	Гость	27.08.2018	Дата
День	Понедельник	15:51	Время

Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.

Все материалы сайта представлены исключительно в ознакомительных целях.

---

Источник/автор материала: Учительская для математиков

---

Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием.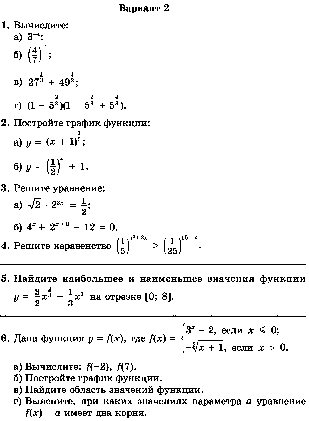

Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.

Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.

---

Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]

Справочные материалы

Загрузка формул…

Загрузка тестирования…

Обсуждения

Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Контрольная работа по математике (Логарифмы. Логарифмические и показательные уравнения и неравенства) для 10-го класса от педсовета в 2018 году

Ответы

Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Статистика и загрузка

Скачать

Если загрузка не началась автоматически, повторите попытку или нажмите сюда!

Просмотров	202	60	Загрузок
Добавил	Гость	26. 02.2020	Дата
День	Среда	21:47	Время

Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.

Все материалы сайта представлены исключительно в ознакомительных целях.

---

Источник/автор материала: педсовет — персональный помощник педагога

---

Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.

Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.

---

Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]

Справочные материалы

Загрузка формул…

Загрузка тестирования…

Обсуждения

Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Контрольная работа. Логарифмические уравнения и неравенства. (базовый + профильный уровень)

Кр. №5. (Соц. эк.) Вар. 1.
Вычислите:
а) ;
б) .
Решите уравнение:
а) ;
б)
в)
Решите неравенство:
а) ;
б) ;
в) .
Исследуйте функцию на монотонность и экстремумы.
Кр. №5. (Соц. эк.) Вар. 2.
Вычислите:
а) ;б) .
Решите уравнение:
а) ;
б)
в)
Решите неравенство:
а) ;
б) ;
в) .
Исследуйте функцию на монотонность и экстремумы.
Кр. №5. (Соц. эк.) Вар. 1.
Вычислите:

а) ;
б) .
Решите уравнение:
а) ;
б)
в)
Решите неравенство:
а) ;
б) ;
в) .
Исследуйте функцию на монотонность и экстремумы.
Кр. №5. (Соц. эк.) Вар. 2.
Вычислите:
а) ;б) .
Решите уравнение:
а) ;
б)
в)
Решите неравенство:
а) ;
б) ;
в) .
Исследуйте функцию на монотонность и экстремумы.
Кр. №5. (Гум.) Вар. 1.
1. Вычислите:
1) ;
2) ;

2. Решите уравнения:

3. Решите неравенства:
Кр. №5. (Гум.) Вар. 2.
1. Вычислите:
1) ;
2) ;
2. Решите уравнения:

3. Решите неравенства:

Кр. №5. (Гум.) Вар. 1.
1. Вычислите:
1) ;
2) ;

2. Решите уравнения:

3. Решите неравенства:
Кр. №5. (Гум.) Вар. 2.
1. Вычислите:
1) ;
2) ;
2. Решите уравнения:

3. Решите неравенства:

Кр. №5. (Гум.) Вар. 1.
1. Вычислите:
1) ;
2) ;

2. Решите уравнения:

3. Решите неравенства:
Кр. №5. (Гум.) Вар. 2.
1. Вычислите:
1) ;
2) ;
2. Решите уравнения:

3. Решите неравенства:

Контрольная работа №3. Логарифмические уравнения и неравенства Вариант 1 Вычислите:. Решите уравнение:. Решите неравенство: Найдите область определения функции



Контрольная работа №3. Логарифмические уравнения и неравенства Вариант 1 Вычислите:. Решите уравнение:. Решите неравенство: Найдите область определения функции

---

Похожие:

	Контрольная работа №3. Показательные уравнения и неравенства Вариант решите неравенство: 1) (;-2) 2) (-2;+) 3) (2;+) 4) (-;4) найдите множество значений функции у=3+3		Контрольная работа №4. Вариан 1 Решите уравнение: Решите неравенство: Решите уравнение и найдите корни, принадлежащие промежутку
	Контрольная работа №2. Корень п-ой степени Вариант Вычислите : 10. 0,3 Вычислите > Решите уравнение = 3 х. Решите систему Вариант 2 Вычислите		Контрольная работа №8 (Итоговая) 2 урока Вариант 1 1 Найдите область определения функции: 2 Решите уравнение: 3 Исследуйте функцию на возрастание, убывание и экстремум Площадь прямоугольника равна 36 д Какую длину должны иметь его стороны, чтобы периметр прямоугольника был наименьшим?
	Контрольная работа №3 «Решение уравнений» вариант 1 Решите уравнение: а 21 + Х = 56; б у 89 = 90. Найдите значение выражения: а а + т, если а = 20, т = 70 Решите с помощью уравнения задачу: «В автобусе было 78 пассажиров. На остановке несколько человек вышло и осталось 59 пассажиров….		Контрольная работа №6 Вариант 1 1 Решите неравенство: 2 к графику функции проведена касательная через точку с абсциссой Прямолинейное движение точки описывается законом Найдите её скорость и ускорение в момент времени t = (Время измеряется в секундах,…
	Решение неравенств вариант 1 Решите неравенство: а) 6 Х  18; в) 0,5( Х 2) + 1,5 Х х + б) 4 Х > 36; Решите систему неравенств Решите неравенство и укажите наибольшее целое число, удовлетворяющее этому неравенству		Найдите корень уравнения. Найдите корень уравнения Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите больший из корней
	Контрольная работа Решите уравнение, укажите корень уравнения (или сумма корней, если их несколько)		Найдите корень уравнения Решите уравнение. Если уравнение имеет более одного корня, в ответе укажите меньший из них

Разместите кнопку на своём сайте:
Документы Документы

---

База данных защищена авторским правом ©lib2.podelise.ru 2000-2013
При копировании материала обязательно указание активной ссылки открытой для индексации.
обратиться к администрации

Логарифмические неравенства

1.Решить неравенство:

   

ОДЗ:

   

   

Решение:

   

Так как основание логарифма больше 1, то знак неравенства сохраняем:

   

   

   

Ответ:

 

2.Решить неравенство:

   

ОДЗ:

   

   

Решение:

   

Так как основание логарифма меньше 1, то знак неравенства меняем:

   

   

   

Пересекаем решение и ОДЗ, имеем:

 

3.Решить неравенство:

   

ОДЗ:

   

Решим методом интервалов.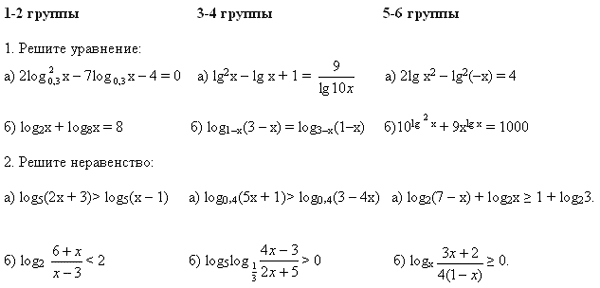 Корень числителя – , корень знаменателя – эта точка выколота всегда, корень числителя – тоже выколотая точка, так как знак строгий. Таким образом, .

Решение:

   

   

Переходим к сравнению подлогарифмических выражений, знак сохраняем: основание больше 1:

   

   

   

   

Корень числителя – , корень знаменателя – эта точка выколота всегда, корень числителя – точка закрашенная, она войдет в решение, так как знак неравенства не строгий. Таким образом, .

При наложении решения на ОДЗ получим:

Ответ: .

 

4.Решить неравенство:

   

ОДЗ:

   

   

Решение этой системы –

Решение:

   

   

   

   

   

   

Корни:

   

   

Поскольку знак неравенства нестрогий, то точки входят в решение: на рисунке их нужно изобразить закрашенными. Решение неравенства: .

Накладывая решение на область допустимых значений, получаем:

Ответ:

 

5.Решить неравенство:

   

ОДЗ:

   

Решение этой системы –

Решение:

   

   

   

   

   

Точка 1 является выколотой – это корень знаменателя, точка 2 – корень четной кратности, а мы помним, что в таких точках знак интервала не изменяется! Поэтому решение будет выглядеть так:

Решение неравенства

Решение неравенства:

   

Это полностью укладывается в ОДЗ, поэтому ответ таким и будет:

Ответ:

 

6.Решить неравенство:

   

ОДЗ:

   

Допустимые значения :

Решение неравенства проведем методом рационализации:

   

   

   

Упрощаем:

   

   

Раскладываем на множители:

   

Отмечаем полученные точки на координатной прямой:

Решение неравенства

Наложив это решение на ОДЗ, имеем:

Ответ:

 

55. Логарифмические неравенства | Контрольные работы по математике и д

Логарифмическим неравенством называется такое неравенство, в котором неизвестная величина содержится или под знаком логарифма, или в его основании.

Особенностью решения логарифмических неравенств является учет ОДЗ входящих в него логарифмов. В отличие от логарифмических уравнений, условия, определяющие ОДЗ, целесообразно записывать вместе с решением в одной системе, так как в ходе решения некоторые условия на ОДЗ учитываются сразу. Необходимо внимательно следить за величиной основания логарифма, так как при положительном основании логарифма, которое меньше единицы, знак неравенства меняется на противоположный.

Типы неравенств и способы их решения

Всюду далее F(X), G(X), H(X) – некоторые выражения с переменной.

I тип: неравенство вида

(6.16)

Где A > 0.

1. Если 0 < A < 1, то неравенство (6.16) равносильно системе

(6.17)

2. Если A > 1, то неравенство (6.16) равносильно системе

Заметим, что в этом случае первое неравенство системы (6.17) можно не решать, так как во втором неравенстве

(6.18)

Решение неравенства (6.18) сводится к решению совокупности двух систем:

Неравенство F(X) > 0 во второй системе можно не решать, так как оно справедливо при выполнении двух других неравенств этой системы.

II тип: неравенство вида

(6.19)

1. Если 0 < A < 1, то неравенство (6.19) равносильно системе

(6.20)

Неравенство G(X) > 0 в системе (6.20) можно не решать, так как оно выполняется при условии выполнения двух других неравенств этой системы.

2. Если то неравенство (6.19) равносильно системе

(6.21)

Неравенство в системе (6.21) можно не решать.

(6.22)

Поскольку в основании содержится переменная величина, то в общем случае решение неравенства (6.22) зависит от величины основания по сравнению с числом 1. Поэтому решаем совокупность двух систем:

III тип: неравенство вида

(6.23)

Где F – некоторое выражение относительно

Необходимо заменить и решить неравенство F(Y) > 0. Полученные в качестве решения последнего неравенства промежутки записывают в виде неравенств относительно Y, а затем возвращаются к старой переменной.

Аналогично решают неравенства I – III типов, в которых вместо знака > использованы знаки ³, <, £.

Пример 1. Решить неравенство

Решение. Имеем неравенство I типа. Так как основание логарифма меньше числа 1, то решение неравенства сводится к решению системы

Используем далее метод интервалов (рис. 6.13).

Рис. 6.13

Получаем ответ:

Пример 2. Решить неравенство

Решение. Данное неравенство относится к I типу. Поэтому решаем совокупность двух систем

Первая система решений не имеет. Решаем вторую систему

Второе неравенство этой системы не решаем, так как оно справедливо, если выполняется последнее неравенство. Получаем:

Используем метод интервалов (рис. 6.14).

Рис. 6.14

Получаем ответ:

Пример 3. Решить неравенство

Решение. Это неравенство II типа, причем основание логарифма больше числа 1. Поэтому решаем систему

Получаем

Подводя итог, приходим к ответу:

Пример 4. Решить неравенство

Решение. Имеем неравенство III типа.

Заменяем и решаем кубическое неравенство

Разлагаем левую часть неравенства на множители:

Используем далее метод интервалов (рис. 6.15).

Рис. 6.15

Получили решение Записываем его в виде:

Возвращаемся к неизвестной X и с учетом ОДЗ заданного неравенства имеем:

Получаем ответ:

< Предыдущая		Следующая >

Как решать логарифмические уравнения

В этом уроке обсуждаются два способа решения логарифмических уравнений. Используемый метод зависит от типа логарифмического уравнения, которое вы пытаетесь решить. Продолжайте читать, и вы узнаете, как быстро решить задачу ниже!

Первый тип , который вы научитесь решать, имеет следующий формат:

log _b X = Y

Чтобы решить его, вам просто нужно записать его в экспоненциальной форме как X = b ^Y

Пример # 1

log (2x + 1) = 3

log ₁₀ (2x + 1) = 3

Записав его в экспоненциальной форме, мы получаем

2x + 1 = 10 ³

2x + 1 = 1000

2x = 999

x = 499.5

Проверка x = 499,5

log ₁₀ (2 x 499,5 + 1) = log ₁₀ (1000) = 3, поскольку 10 ³ = 1000

Иногда, когда вы решаете логарифмические уравнения, вам нужно чтобы поместить все логарифмы в одну сторону уравнения. Пример № 2 показывает, как это сделать.

Пример № 2

log ₅ (30x — 10) — 2 = log ₅ (x + 6)

Вы можете решить это так же, как и в примере №1.

Начните с того, что поместите все логарифмы в одну сторону уравнения.

журнал ₅ (30x — 10) — журнал ₅ (x + 6) — 2 = журнал ₅ (x + 6) — журнал ₅ (x + 6)

журнал ₅ (30x — 10) — журнал ₅ (x + 6) -2 = 0

журнал ₅ (30x — 10) — журнал ₅ (x + 6) -2 + 2 = 0 + 2

журнал ₅ (30x — 10) — журнал ₅ (x + 6) = 2

журнал ₅ [(30x — 10) / (x + 6)] = 2

Теперь, когда он имеет формат, который мы хотим, мы можем просто записать в экспоненциальной форме.

30x — 10 / x + 6 = 5 ²

30x — 10 / x + 6 = 25 (после умножения обеих сторон на x + 6)

30x — 10 = 25 (x + 6)

30x — 10 = 25x + 150

30x — 25x = 150 + 10

5x = 160

x = 32

Проверить x = 32

журнал ₅ (30x — 10) — 2 = журнал ₅ (x + 6)

журнал ₅ (30 x 32-10) — 2 = журнал ₅ (32 + 6)

журнал ₅ (960-10) — 2 = журнал ₅ (32 + 6)

журнал ₅ (950) — 2 = журнал ₅ (38)

4.26-2 = 2,26

2,26 = 2,26

x = 32 — хороший ответ.

Теперь вы узнаете, как решать логарифмические уравнения , которые имеют следующий формат

log _b X = log _b Y

Чтобы решить эту проблему, вам просто нужно увидеть этот журнал _b X = log _b Y тогда и только тогда, когда X = Y

Дополнительные примеры, показывающие, как решать логарифмические уравнения с использованием логарифмических свойств.

Пример № 3

журнал ₆ (2x — 4) + журнал ₆ (4) = журнал ₆ 40

журнал ₆ 4 (2x — 4) = журнал ₆ 40

журнал ₆ 8x — 16 = журнал ₆ 40

8x — 16 = 40

8x = 40 + 16

8x = 56

x = 7

Проверить x = 7

журнал ₆ (2 x 7-4) + журнал ₆ (4) = журнал ₆ 40

журнал ₆ (14-4) + журнал ₆ (4) = журнал ₆ 40

журнал ₆ (10) + журнал ₆ (4) = журнал ₆ 40

6 журнал _{10 x 4) = журнал 6 40}

9 0006 журнал ₆ (40) = журнал ₆ 40

хорошо

Пример # 4

журнал ₃ x + журнал ₃ (x + 3) = журнал ₃ (2x + 6)

журнал ₃ x (x + 3) = журнал ₃ (2x + 6)

журнал ₃ (x ² + 3x) = журнал ₃ (2x + 6)

x ² + 3x = 2x + 6

x ² + 3x — 2x — 6 = 0

x ² + x — 6 = 0

(x — 2) (x + 3) = 0

x = 2 и x = -3

Проверка x = 2

журнал ₃ 2 + журнал ₃ (2 + 3) = журнал ₃ (2 x 2 + 6)

журнал ₃ 2 + журнал ₃ (5) = журнал ₃ (4 + 6)

журнал ₃ 2 (5) = журнал ₃ (4 + 6)

журнал ₃ (10) = журнал ₃ (10)

x = 2 — хороший ответ. {x} $, используйте метод логарифмического дифференцирования.n) = n \ cdot \ log_a (x)

долл. США

$ \ ln \ left (y \ right) = x \ ln \ left (x \ right) $

5

Выведите обе части равенства относительно $ x $

.

$ \ frac {d} {dx} \ left (\ ln \ left (y \ right) \ right) = \ frac {d} {dx} \ left (x \ ln \ left (x \ right) \ right) $

6

Примените правило произведения для дифференцирования: $ (f \ cdot g) ‘= f’ \ cdot g + f \ cdot g ‘$, где $ f = x $ и $ g = \ ln \ left (x \ right) $

$ \ frac {d} {dx} \ left (\ ln \ left (y \ right) \ right) = \ frac {d} {dx} \ left (x \ right) \ ln \ left (x \ right) + x \ frac {d} {dx} \ left (\ ln \ left (x \ right) \ right) $

Промежуточные ступени

$ \ frac {d} {dx} \ left (\ ln \ left (y \ right) \ right) = 1 \ ln \ left (x \ right) + x \ frac {d} {dx} \ left (\ ln \ left (x \ right) \ right) $

Любое выражение, умноженное на $ 1 $, равно самому себе

$ \ frac {d} {dx} \ left (\ ln \ left (y \ right) \ right) = \ ln \ left (x \ right) + x \ frac {d} {dx} \ left (\ ln \ влево (х \ вправо) \ вправо) $

7

Производная линейной функции равна $ 1 $

$ \ frac {d} {dx} \ left (\ ln \ left (y \ right) \ right) = \ ln \ left (x \ right) + x \ frac {d} {dx} \ left (\ ln \ влево (х \ вправо) \ вправо) $

Объясните больше 8

Производная натурального логарифма функции равна производной функции, деленной на эту функцию. х \ влево (\ лн \ влево (х \ вправо) +1 \ вправо) $

Почему шкала pH логарифмическая?

Шкала pH логарифмическая, что означает, что разница в 1 единице pH составляет разницу в 10 раз! На прошлой неделе мы представили именно то, что мы измеряем при измерении pH — активность ионов водорода.

pH — невероятно важный параметр, который измеряется практически во всех областях, связанных с качеством воды. Он играет роль во вкусе (кислый = свежий, нейтральный = мягкий, щелочной = несъедобный) и в сохранности пищи. При отборе проб и мониторинге окружающей среды высокие или низкие значения pH могут указывать на загрязнение. При очистке сточных вод pH регулируется как часть разрешения NPDES, и многие процессы зависят от pH. Это лишь некоторые из областей применения, в которых pH играет решающую роль.

Термин «pH» происходит от латинского слова и является аббревиатурой от «Potentia Hydrogenii» — мощность водорода. Шкала pH обычно используется для представления активности ионов водорода.

На шкале pH значения pH ниже 7 представляют собой кислые растворы (активность ионов водорода выше активности ионов гидроксида), а значения выше 7 представляют собой щелочные растворы. При pH = 7 активность иона водорода и гидроксид-иона равны (таблица 1).

Как видно из таблицы 1, возможный диапазон активности ионов водорода (H +) и гидроксида (OH-) может охватывать многие порядки величины.Чтобы легко управлять и отображать широкий диапазон активности ионов, используется логарифмическая шкала pH. Другие параметры, которые имеют невероятно широкий диапазон возможных значений, также используют логарифмическую шкалу, например, измерение звука в децибелах (дБ) или измерение энергии, выделяемой при землетрясении, с использованием шкалы Рихтера.

Таблица 1: Активность иона водорода и гидроксид-иона по шкале pH

Изменение шкалы pH на 1.0 единица pH означает, что активность ионов водорода отличается на порядок (т. Е. В 10 раз). Например, активность водородных ионов при pH 4 в 10 раз больше, чем при pH 5.

Из-за логарифмической природы шкалы pH некорректно просто усреднять значения pH и сообщать их. Вместо этого более уместно указать среднее значение pH или диапазон наблюдаемых значений pH.

Уравнение [1] представляет собой определение pH по отрицательному логарифмическому основанию 10 активности ионов водорода.

[1] pH = -lg aH +

---

Из-за разницы между концентрацией и активностью измерение pH не может быть напрямую основано на концентрации ионов водорода в растворах. Кроме того, невозможно добиться абсолютной калибровки шкалы pH по концентрации ионов водорода. Такая калибровка всегда будет только приближением.

Следовательно, на практике измерение pH основано на обычной шкале pH.Обычные значения pH измеряются по сравнению со значениями pH стандартных буферных растворов. При условии тщательного выполнения калибровки и измерения все значения pH становятся сопоставимыми, независимо от датчика или измерительного оборудования, использованного для их регистрации.

Мы сталкиваемся с предметами с различным уровнем pH каждый день, как показано на Рисунке 1 ниже.

Рисунок 1: Значения pH повседневных предметов

Следите за обновлениями … в следующую pH-пятницу мы обсудим наиболее часто используемый датчик pH — стеклянный электрод.

YSI предлагает множество платформ для измерения pH. Будь то для лаборатории (MultiLab, TruLab), отбора проб окружающей среды (Pro Plus, ProDSS, Pro10) или для долгосрочного мониторинга (EXO1, EXO2), у YSI есть то, что вам нужно!

Является ли pH измерением концентрации или активности ионов водорода?

Методы измерения pH — преимущества и недостатки

Увеличьте срок службы pH-электрода за 3 практических шага

Проблемы с калибровкой pH-метра

? Ознакомьтесь с этими 12 советами!

Решение более сложных логарифмических уравнений

Иногда логарифмические уравнения более сложные.Давайте рассмотрим несколько из этих случаев:

1. Если у вас одинаковый логарифм с обеих сторон, их аргументы будут равны
друг другу.

Пример:

Поскольку основание натурального логарифма — е, возведем обе части в степени е.

С обеих сторон e и ln отменяют, оставляя нас с этим:

5x = 4x + 2

Как видите, аргументы (значение в скобках) равны друг другу. Вы можете запомнить этот ярлык или просто следовать обычной процедуре, как мы только что сделали.

Теперь мы можем перейти к решению уравнения:

x = 2

2) Иногда кажущееся решение неверно.

Помните, что для логарифма с положительным основанием аргумент (значение в скобках) должен быть положительным. Таким образом, если решение для x дает отрицательный аргумент, решение недействительно.

Пример:

В этом случае оба аргумента должны быть больше или равны 0. Когда мы найдем наше решение, мы проверим их, чтобы убедиться, что это правда.

Решим уравнение. Так как у нас есть общий журнал с обеих сторон, аргументы равны друг другу:

4x = x — 12

3x = -12

x = -4

Давайте вернем -4 в аргументы. Получаем бревно (-16) с обеих сторон. Но это невозможно, поскольку 10 нельзя возвести в степень и получить отрицательное число. Это неверный ответ.

Таким образом, это уравнение не имеет решения.

3) Иногда необходимо использовать правила журнала.

Пример:

Поскольку журналы добавляются, мы должны умножить их аргументы:

И решить:

Мы должны решить это с помощью формулы корней квадратного уравнения.

Это точный ответ. Или мы можем оценить с помощью нашего калькулятора:

Поскольку результат отрицательный, это не решение

Ответ: или

Практика: Решите каждое логарифмическое уравнение. Убедитесь, что каждое решение действительно. При необходимости округлите ответ до ближайшей тысячной.

No related posts.