Контрольная работа №1 по алгебре (8 класс) ПО УМК Ю.М. Колягина
Просмотр содержимого документа
«Контрольная работа №1 по алгебре (8 класс) ПО УМК Ю.М. Колягина»
Контрольная работа № 1(8 класс)
Вариант 1
1. Решить уравнение:
а) (4х – 3) ∙ (х + 1) = 0;
б) 3х2 – х = 0;
в) х2 – 81 = 0.
2. Записать неравенство, которое получится, если из обеих частей неравенства
c + 3d c – 4d вычесть число: 2c; -5d.
3. Умножить обе части данного неравенства на число m:
а) 3,1 2,1 m = 51; б) m = — 2.
4. Доказать, что: (х – 5) ∙ (х + 1) (х – 1) ∙ (
Доказать, что если а 3 и b 8, то:
а) а + 6b 51; б) а + b 6.
Контрольная работа № 1(8 класс)
Вариант 2
1. Решить уравнение:
а) (5х – 1) ∙ (х + 3) = 0;
б) 2х – х2 = 0;
в) х2 – 64 = 0.
2. Записать неравенство, которое получится, если из обеих частей неравенства
5а – 3b а + 2b вычесть число: 3а; -2а.
3. Умножить обе части данного неравенства на число
а) 2,5 m = 2; б) m = — 4.
4. Доказать, что: (а + 3) ∙ (а – 5) а – 4) ∙ (а + 3), то а — 3.
Доказать, что если а 3 и b 8, то:
а) 4а + b 20; б) а + b 3.
Колягин. Алгебра 8 класс. Дидактические материалы (Просвещение)
| Переплет | мягкий |
| ISBN | 978-5-09-072779-2 |
| Формат | 60×90/16 (145×215мм) |
| Год издания | 2020 |
| Соответствие ФГОС | ФГОС |
| Количество томов | 1 |
| Серия | Математика и информатика |
| Издательство | Просвещение |
| Автор | Ткачева М. В., Фёдорова Н.Е., Шабунин М.И. В., Фёдорова Н.Е., Шабунин М.И. |
| Возрастная категория | |
| Раздел | Алгебра |
| Тип издания | Дидактический материал |
| Язык | русский |
Описание к товару: «Ткачева.
 Алгебра 8 класс. Дидактические материалы. УМК Колягин Ю.М.»
Алгебра 8 класс. Дидактические материалы. УМК Колягин Ю.М.»Данная книга предназначена для учителей, работающих по учебнику «Алгебра. 8 класс» авторов Ю.М.Колягина и др. Она содержит задания, дополняющие систему упражнений учебника, и позволяет организовать дифферецированную и индивидуальную работу учащихся на всех этапах урока. В главах пособия содержатся материалы к каждому параграфу учебника, а также контрольная или самостоятельная работа по теме. Все задания имеют балловую оценку уровня их сложности и ответы. др.
Издательство: ПРОСВЕЩЕНИЕ
Серия: Математика и информатика
Вы можете получить более полную информацию о товаре «Колягин. Алгебра 8 класс. Дидактические материалы (Просвещение)«, относящуюся к серии: Математика и информатика, издательства Просвещение, ISBN: 978-5-09-072779-2, автора/авторов: Ткачева М.В., Фёдорова Н.Е., Шабунин М.И., если напишите нам в форме обратной связи.
ГДЗ по Алгебре 8 класс дидактические материалы Ткачева
Авторы: Ткачева М. В., Федорова Н.Е., Шабунин М.И..
В., Федорова Н.Е., Шабунин М.И..
Курс алгебры в восьмом классе готовит учащимся новые серьезные испытания. Преодолеть их будет несложно, если иметь под рукой надежного помощника в виде ГДЗ по алгебре 8 класс дидактические материалы Ткачева.
В течение этого года школьникам предстоит изучить много важных и сложных тем:
- арифметические действия с дробями;
- решение квадратных уравнений;
- графики квадратичной и корневой функций;
- решение дробных рациональных уравнений и др.
Эти знания будут использоваться не только при дальнейшем изучении алгебры и геометрии, но и для решения уравнений и задач по физике и химии. Любой пробел в знаниях в восьмом классе может привести к серьезным последствиям в будущем. К тому же, уже через год всем учащимся предстоит сдать государственный экзамен. А для этого нужна серьезная практическая подготовка. Даже во время пропуска занятий ученикам не составляет большого труда изучить по учебнику теорию, но на практике они сразу оказываются в тупике. Именно эти проблемы позволит решить сборник ГДЗ.
Даже во время пропуска занятий ученикам не составляет большого труда изучить по учебнику теорию, но на практике они сразу оказываются в тупике. Именно эти проблемы позволит решить сборник ГДЗ.
Практика с ГДЗ по алгебре к дидактическим материалам для 8 класса Ткачевой
Сборник разработан в соответствии с оригинальным УМК и содержит в себе подробно описанные алгоритмы решения уравнений, неравенств, задач и построения графиков с готовыми правильными ответами. Кроме того, имеется шесть полностью разобранных контрольных работ.
Все материалы выполнены в соответствии с действующими федеральными образовательными стандартами и могут использоваться, в том числе для подготовки к ОГЭ по математике.
Что даст ученикам пособие, кроме возможности переписать правильные ответы в тетрадь с домашним заданием? На самом деле, вдумчивая работа с материалами ГДЗ позволит:
- оперативно проверить собственное решение;
- найти и исправить допущенные ошибки;
- понять свои слабые места и повторить теорию и алгоритмы;
- научиться грамотно оформлять решение и правильный ответ согласно требованиям экзаменационной комиссии;
- улучшить навыки самостоятельной и ответственной работы;
- повысить промежуточную и итоговую успеваемость.

Кроме того, решебник по алгебре для дидактических материалов за 8 класс (авторы: Ткачева М. В., Федорова Н. Е., Шабунин М. И.) позволяет существенно сэкономить восьмиклассникам время на подготовку домашнего задания, которое можно будет уделить другим важным дисциплинам или внешкольным занятиям и хобби.
Описание УМК Алгебра. Колягин Ю.М. (7-9) — Группа компаний «Просвещение»
Авторы: Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин
Линия предназначена для работы в 7-9 классах общеобразовательных организаций и является переработанной линией УМК Ш.А. Алимова и др. по алгебре.
В состав УМК входят:
- учебники
- Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин. Алгебра. 7 класс
- Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин. Алгебра. 8 класс
- Ю.М. Колягин, М.В. Ткачёва, Н.
 Е. Фёдорова, М.И. Шабунин. Алгебра. 9 класс
Е. Фёдорова, М.И. Шабунин. Алгебра. 9 класс
- сборник рабочих программ
- рабочая тетрадь
- дидактические материалы
- тематические тесты
- методические рекомендации
Учебники соответствуют Федеральному государственному образовательному стандарту основного общего образования. Материал учебников концентрируется на пяти основных содержательных линиях: числовой, алгебраических преобразований, уравнений и неравенств, функциональной, стохастической. Деятельностный подход в обучении реализуется в учебниках с помощью развивающих материалов в рубриках: «Диалог об истории», «Это интересно», «Шаг вперёд», «Разговор о важном», «Это полезно», «Практические и прикладные задачи». Материал каждого параграфа дополнен перечнем основных понятий и системой устных вопросов и заданий. Система вводных упражнений ориентирована на организацию тематического повторения учебного материала. В конце каждой главы приводится перечень изученных новых понятий, формул, алгоритмов и способов действий. Предложен список тем исследовательских работ. В конце каждого учебника курса приводится список дополнительной научно-популярной и исторической литературы, которую учащиеся смогут использовать в ходе учебного процесса и при написании творческих работ.
Предложен список тем исследовательских работ. В конце каждого учебника курса приводится список дополнительной научно-популярной и исторической литературы, которую учащиеся смогут использовать в ходе учебного процесса и при написании творческих работ.
Рабочие тетради состоят из трёх разделов: первый — упражнения для подготовки учащихся к изучению нового материала, второй – упражнения, дополняющие упражнения учебника, третий – упражнения для проверки уровня усвоения материала.
Дидактические материалы содержат задания, дополняющие систему упражнений учебника, материалы контрольных и самостоятельных работ по темам. Все задания имеют балловую оценку.
Тематические тесты содержат тесты ко всем главам учебника, составленные в четырёх вариантах.
Особенности линии УМК:
- в основе курса лежит числовая линия
- дидактический принцип построения курса — индуктивный подход к введению новых понятий: от частного к общему
- структура и содержание учебников составлены таким образом, чтобы помочь учащимся смоделировать учебный процесс в целом и отдельные уроки в частности
- трёхуровневая система упражнений позволяет выбрать индивидуальную траекторию обучения
- дополнительным развивающим потенциалом обладают занимательные тексты к каждому параграфу, построенные в форме бесед
Авторы: Ю. М.Колягин, М.В.Ткачёва, Н.Е.Фёдорова и др.
М.Колягин, М.В.Ткачёва, Н.Е.Фёдорова и др.
Комплект обладает свойством преемственности со всеми действующими учебниками алгебры основной школы, особенно тесные с УМК алгебры для 7—9 классов авторов Ю. М. Колягина, М. В. Ткачёвой, Н. Е. Фёдоровой, М. И. Шабунина.
В состав УМК входят:
- учебники:
- Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни). 10 класс
- Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни). 11 класс
- дидактические материалы
- тематические тесты
- методические рекомендации
Учебники соответствуют Федеральному государственному образовательному стандарту среднего (полного) общего образования. В учебниках содержится избыточная разноуровневая система задач и упражнений (многие задачи приведены с решениями и указаниями), позволяющая успешно подготовиться к ЕГЭ. Практическая, прикладная и мировоззренческая направленность курса обеспечивает понимание роли математики во всех сферах деятельности человека.
В учебниках содержится избыточная разноуровневая система задач и упражнений (многие задачи приведены с решениями и указаниями), позволяющая успешно подготовиться к ЕГЭ. Практическая, прикладная и мировоззренческая направленность курса обеспечивает понимание роли математики во всех сферах деятельности человека.
Дидактические материалы содержат задания, дополняющие систему упражнений учебника, и позволяют организовать дифференцированную работу учащихся. В пособии содержатся примеры и задачи с подробными решениями, задания для самостоятельной работы. Задания имеют балловую оценку уровня их сложности и ответы.
Тематические тесты. В пособии предложены задания на двух уровнях сложности с указанием времени их выполнения. Учитель может использовать их перед контрольными работами для определения уровня сформированности знаний и умений учащихся по теме.
Методические рекомендации. Пособие написано в соответствии с концепцией обучения алгебре и началам математического анализа учебников. Дан обзор основных теоретических идей каждой главы, а также сформулированы предметные, метапредметные и личностные цели изучения этой главы. Методические рекомендации даются по изучению каждого параграфа, приводится планирование уроков с указанием заданий для работы в классе и дома с учётом применения УМК, приведены решения сложных упражнений. В конце каждой главы даны рекомендации по проведению урока обобщения и тематическая контрольная работа.
Дан обзор основных теоретических идей каждой главы, а также сформулированы предметные, метапредметные и личностные цели изучения этой главы. Методические рекомендации даются по изучению каждого параграфа, приводится планирование уроков с указанием заданий для работы в классе и дома с учётом применения УМК, приведены решения сложных упражнений. В конце каждой главы даны рекомендации по проведению урока обобщения и тематическая контрольная работа.
Особенности линии УМК:
- теоретический материал изложен дифференцированно;
- наличие во всех пособиях УМК условий и решений задач разной степени трудности;
- система упражнений во всех пособиях УМК даёт возможность проверить уровень подготовленности учащихся как обычных, так и математических классов.
Тематическое планирование по алгебре (8 класс)
2
НЕРАВЕНСТВА
Положительные и отрицательные числа
Числовые неравенства
Основные свойства числовых неравенств
Сложение и умножение неравенств
Строгие и нестрогие неравенства
Контрольная работа №1
Неравенства с одним неизвестным
Решение неравенств
Система неравенств с одним неизвестным
Решение систем неравенств
Модуль числа
Контрольная работа №2
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
Приближенные значения величин
Оценка погрешности
Округление чисел
Относительная погрешность
Контрольная работа №3
КВАДРАТНЫЕ КОРНИ
Арифметический квадратный корень
Действительные числа
Квадратный корень из степени
Квадратный корень из произведения
Квадратный корень из дроби
Контрольная работа № 4
КВАДРАТНЫЕ УРАВНЕНИЯ
Квадратное уравнение и его корни
Неполные квадратные уравнения
Метод выделения полного квадрата
Решение квадратных уравнений
Приведенное квадратное уравнение. Теорема Виета
Теорема Виета
Уравнения, сводящиеся к квадратным
Контрольная работа № 5
Решение задач
Решение систем
Контрольная работа № 6
КВАДРАТИЧНАЯ ФУНКЦИЯ
Определение квадратичной функции
Функция y=
Функция y= a
Функция y= a+c
Построение графика
Контрольная работа № 7
КВАДРАТНЫЕ НЕРАВЕНСТВА
Квадратное неравенство и его решение
Решение неравенства с помощью графика
Метод интервалов
Контрольная работа № 8
ИТОГОВОЕ ПОВТОРЕНИЕ
ГДЗ по Алгебре за 8 класс Ш.А. Алимов, Ю.М. Колягин
авторы: Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров.
Издательство: Просвещение 2015 год.
Обучение может быть не только продуктивным, но и приятным, без страхов и паники. Все, что для этого нужно – вооружиться достойными источниками знаний. Одним из них является Алгебра для 8 класса автора Ш.А. Алимов. ГДЗ идет к рабочей тетради по алгебре за 8 класс Колягин Ю.М. Это грамотно структурированный помощник, который сумеет облегчить жизнь не только самим школьникам, но также тем, кто следит за их развитием.
Что представляет собой Алгебра 8 класс
В решебнике представлена удобная подача сложной информации, предусматривающая деятельный подход к каждому уроку. Это доступный для понимания, как учениками, так и взрослым, уровень, позволяющий без проблем осваивать новые горизонты и обеспечивающий правильное решение заданий в будущем.
Структура издания:
— 6 тематических глав, соответствующих ФГОС;
— упражнения для повторения пройденного курса;
— задания для домашнего выполнения;
— краткое содержание предмета за 7 и 8 класс;
— верные (правильные) ответы на предложенные задания в ГДЗ;
Основные направления, раскрываемые авторами:
— уравнения;
— неравенства;
— алгебраические преобразования;
— логические высказывания;
— числовые, функциональные и стохастические тематики;
Получение уверенных знаний будет еще более простым, если придерживаться рекомендаций авторов: подробное изучение текста глав, поиск ответов на каждый номер вопроса к ней, изучение определений понятий, повторение ранее изученного, добросовестное выполнение и упражнений и тестов по теме.
Чем полезна книга для учителей, детей и родителей
Работа с учебником позволит:
— рационально составлять рабочие программы на основе госстандартов;
— детальнее разобраться в тонкостях темы для полноценного усвоения материала;
— самостоятельно проводить проверочные работы по школьной программе;
— родителям контролировать правильность выполнения задач;
— с отличным результатом выполнять контрольные работы в классе;
Дополнительным преимуществом этого учебника является уникальная система его составления, которая предполагает развитие у учащегося не только метапредметных способностей, но и личностных качеств. Доступ к простым знаниям можно получить, читая книгу онлайн или приобретя ее в личное пользование.
Решебник по Алгебре за 8 класс Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров на Гитем ми
Обучение не обязательно должно быть скучным и неприятным. Если вооружиться стоящими инструментами, можно легко заинтересовать учащегося как гуманитарными, так и точными науками. Один из таких инструментов – Алгебра для 8 класса автора Ш.А. Алимов. Это простой для восприятия, грамотно структурированный учебник с ГДЗ, подход к освоению которого основан на последовательном решении простых задач.
Если вооружиться стоящими инструментами, можно легко заинтересовать учащегося как гуманитарными, так и точными науками. Один из таких инструментов – Алгебра для 8 класса автора Ш.А. Алимов. Это простой для восприятия, грамотно структурированный учебник с ГДЗ, подход к освоению которого основан на последовательном решении простых задач.
Как оставлена Алгебра Ш.А. Алимова
Авторы руководствовались необходимостью упрощения подачи информации с точным сохранением ее смысла. Грамотное чередование теории и практики, а также наличие подсказок позволяют ученику не чувствовать себя беспомощным и придавленным гранитом науки.
Содержание представляют следующие разделы:
— темы, распределенные по шести последовательным главам;
— решение заданий на повтор пройденного;
— упражнения для самостоятельного контроля;
— тезисное изложение азов 7 и 8 классов;
— верные (правильные) ответы на все вопросы в учебнике;
— предметный указатель.
Изучение любой главы должно заканчиваться поиском ответов на каждый номер вопроса, работой с тестами и уравнениями, а также кратким обзором по изложенным в данном разделе методам и определениям. Это позволит лучше закрепить приобретенные навыки и в будущем без проблем писать даже самые сложные контрольные работы.
Какую помощь в образовательном процессе оказывает решебник
Такой проводник в постижении тонкостей данного предмета позволяет легче вздохнуть не только самим школьникам, но также их родителям и даже преподавателям. Благодаря представленному материалу:
— преподаватель сможет более рационально составлять рабочую программу с соблюдением требований ФГОС;
— школьник получит возможность детально разобраться в непростом предмете и спокойно чувствовать себя на уроке;
— родитель сможет должным образом контролировать знания ребенка.
Данное пособие – это надежный помощник для лучше структуризации и упрощения образовательного процесса с возможностью выполнения проверочных работ. Благодаря использованию книги онлайн или в печатном виде, можно меньше времени уделять битве с цифрами и символами и больше — разностороннему развитию.
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.

- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или уточнить у системного администратора.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файлах cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Прямой синтез цеолитов MFI ядро-оболочка с пространственно суженными тримодальными мезопорами посредством контролируемой ортогональной самосборки
rsc.org/schema/rscart38″> Управление иерархией пор в пористых материалах — привлекательная, но трудная задача для кристаллических цеолитов. Здесь мы сообщаем о цеолитах MFI ядро-оболочка, имеющих тримодальные мезопоры с размером, постепенно уменьшающимся от поверхности к ядру, синтезированные с помощью подхода с одним горшком посредством контролируемой ортогональной самосборки .Новые пространственно разрешенные структуры мезопор приписываются наноразмерному разделению фаз между взаимно связанными взаимодействиями органосилановой супрамолекулярной сборки и упорядочением каркаса цеолита. Высокоиерархическая архитектура цеолита с сужающимся распределением мезопор позволила обеспечить пространственно разрешенную адсорбцию флуоресцентных молекул, улучшить каталитические характеристики в реакциях конденсации и усовершенствовать нанореактор для реакций сочетания из-за ослабленных диффузионных ограничений.Успешный синтез тонко настроенных цеолитов с более крупными мезопорами, постепенно разделенными на более мелкие мезопоры (иерархический тип I), может открыть возможности для возникающих новых пористых структур, демонстрирующих более высокую степень иерархии, которые в настоящее время недоступны для многих кристаллических оксидов или связанных материалов.
У вас есть доступ к этой статье
Подождите, пока мы загрузим ваш контент… Что-то пошло не так. Попробуйте еще раз?Локальный хроматиновый контекст определяет генетические детерминанты реакции распространения гетерохроматина
% PDF-1.4
%
1 0 obj
>>>
endobj
35308 0 объект
> поток
PDF :: API2 2. 031 [linux] application / pdf
031 [linux] application / pdf
 ‘jUU 궎 Ix2a ݡ 5 кВб%
* + 9ID
. & ({) t ~ & XRty
‘jUU 궎 Ix2a ݡ 5 кВб%
* + 9ID
. & ({) t ~ & XRtyПубликации | Лаборатория Герценберга
В 1978 году Раевский и др. использовали мощную разрешающую способность сортировщика клеток с активацией флуоресценции (FACS) для выделения изотипа «переключаемых вариантов» миеломных клеток из большой культуры миеломных клеток. Используя флуоресцентно-конъюгированные антитела, специфичные к изотипу иммуноглобулина, не экспрессируемому исходной линией миеломных клеток, они успешно окрашивали и впоследствии сортировали клетки с редкими вариантами переключения.Эти вариантные клетки секретировали миеломный белок другого изотипа иммуноглобулина, но идентичный идиотипу (-ам) вариабельной (V) области, что и антитело, продуцируемое родительской линией миеломы. Таким образом, эти клетки, очевидно, переключились с экспрессии гена, кодирующего константную часть одной тяжелой цепи, на экспрессию другой, при этом экспрессируя тот же ген вариабельной области тяжелой цепи, который кодирует сайт объединения антигена антитела. Хотя другие исследователи наблюдали аналогичные варианты переключения изотипа после мутагенеза ilne миеломных клеток MPC 11 с использованием техники клонирования в мягкий агар, эти исследователи продемонстрировали, что редкие варианты спонтанного переключения можно выборочно окрашивать на вариант иммуноглобулина, экспрессируемый на их поверхностной мембране, и впоследствии отсортировывать используя FACS.Совсем недавно авторы и другие использовали FACS для выделения гибридом вариантов с переключением изотипа, продуцирующих моноклональные антитела с выбранной специфичностью и желаемой функциональной активностью. Эксперименты показали, что спонтанное переключение гена иммуноглобулина происходит в гибридомах с частотами, аналогичными частотам, отмеченным для культивированных клеток миеломы. Более того, специфичность связывания переключенного моноклонального антитела идентична специфичности связывания исходной родительской молекулы иммуноглобулина.Таким образом, путем определения методологии, необходимой для выбора варианта переключения, клон гибридомы, продуцирующий моноклональное антитело с желаемой специфичностью, может быть модифицирован для секреции антиген-специфического иммуноглобулина с изотипом желаемой биологической активности.
Хотя другие исследователи наблюдали аналогичные варианты переключения изотипа после мутагенеза ilne миеломных клеток MPC 11 с использованием техники клонирования в мягкий агар, эти исследователи продемонстрировали, что редкие варианты спонтанного переключения можно выборочно окрашивать на вариант иммуноглобулина, экспрессируемый на их поверхностной мембране, и впоследствии отсортировывать используя FACS.Совсем недавно авторы и другие использовали FACS для выделения гибридом вариантов с переключением изотипа, продуцирующих моноклональные антитела с выбранной специфичностью и желаемой функциональной активностью. Эксперименты показали, что спонтанное переключение гена иммуноглобулина происходит в гибридомах с частотами, аналогичными частотам, отмеченным для культивированных клеток миеломы. Более того, специфичность связывания переключенного моноклонального антитела идентична специфичности связывания исходной родительской молекулы иммуноглобулина.Таким образом, путем определения методологии, необходимой для выбора варианта переключения, клон гибридомы, продуцирующий моноклональное антитело с желаемой специфичностью, может быть модифицирован для секреции антиген-специфического иммуноглобулина с изотипом желаемой биологической активности. Возможность выбора гибридом с переключением вариантов, продуцирующих моноклональные антитела с конкретным изотипом иммуноглобулинов, может значительно улучшить применение технологии моноклональных антител. Даже среди подклассов мышиного IgG, а именно IgG1, IgG2a и IgG3, существуют серьезные различия.Сравнение сегментарной гибкости с использованием наносекундной флуоресцентной спектроскопии показало, что IgG2b является наиболее гибким, IgG2a — немного менее гибким, а IgG1 — относительно жестким. Кроме того, каждый подкласс иммуноглобулинов обладает дискретной биологической активностью. IgG2a и IgG2b фиксируют комплемент морских свинок и кроликов обычным путем, тогда как IgG1 и IgG3 — нет. Молекулы IgG1, но не IgG2a, IgG2b или IgG3, способны опосредовать пассивные кожные анафилактические (PCA) реакции у мышей.Подклассы IgG2a и IgG2b, но не IgG1, опосредуют ту же реакцию у морских свинок. Совсем недавно авторы обнаружили различия между этими тремя классами мышиного иммуноглобулина в их способности участвовать в антителозависимой клеточной цитотоксичности человека (ADCC).
Возможность выбора гибридом с переключением вариантов, продуцирующих моноклональные антитела с конкретным изотипом иммуноглобулинов, может значительно улучшить применение технологии моноклональных антител. Даже среди подклассов мышиного IgG, а именно IgG1, IgG2a и IgG3, существуют серьезные различия.Сравнение сегментарной гибкости с использованием наносекундной флуоресцентной спектроскопии показало, что IgG2b является наиболее гибким, IgG2a — немного менее гибким, а IgG1 — относительно жестким. Кроме того, каждый подкласс иммуноглобулинов обладает дискретной биологической активностью. IgG2a и IgG2b фиксируют комплемент морских свинок и кроликов обычным путем, тогда как IgG1 и IgG3 — нет. Молекулы IgG1, но не IgG2a, IgG2b или IgG3, способны опосредовать пассивные кожные анафилактические (PCA) реакции у мышей.Подклассы IgG2a и IgG2b, но не IgG1, опосредуют ту же реакцию у морских свинок. Совсем недавно авторы обнаружили различия между этими тремя классами мышиного иммуноглобулина в их способности участвовать в антителозависимой клеточной цитотоксичности человека (ADCC). IgG2a функционирует лучше, чем IgG2b при ADCC человека, тогда как IgG1 неактивен. Кроме того, изотипы мышиного иммуноглобулина противоопухолевых антител, по-видимому, различаются по своей способности влиять на рост опухоли в экспериментальных модельных системах на животных.Таким образом, изотип данного моноклонального антитела может играть решающую роль в его биологической эффекторной функции. Возможность отбора клеток с переключаемым вариантом из гибридомы, первоначально отобранной по специфичности связывания секретируемого ею моноклонального антитела, может позволить продуцировать специфические моноклональные клетки с изотипами желаемой биологической активности.
С 1978 года авторы упростили и улучшили процесс выбора варианта переключения с помощью FACS. Первые варианты переключения были выделены только после повторных циклов отбора вариантов FACS, включающих месяцы культивирования ткани.В настоящее время возможно обнаруживать и, в большинстве случаев, напрямую клонировать клетки с вариантами переключения только за один раунд выбора FACS.
IgG2a функционирует лучше, чем IgG2b при ADCC человека, тогда как IgG1 неактивен. Кроме того, изотипы мышиного иммуноглобулина противоопухолевых антител, по-видимому, различаются по своей способности влиять на рост опухоли в экспериментальных модельных системах на животных.Таким образом, изотип данного моноклонального антитела может играть решающую роль в его биологической эффекторной функции. Возможность отбора клеток с переключаемым вариантом из гибридомы, первоначально отобранной по специфичности связывания секретируемого ею моноклонального антитела, может позволить продуцировать специфические моноклональные клетки с изотипами желаемой биологической активности.
С 1978 года авторы упростили и улучшили процесс выбора варианта переключения с помощью FACS. Первые варианты переключения были выделены только после повторных циклов отбора вариантов FACS, включающих месяцы культивирования ткани.В настоящее время возможно обнаруживать и, в большинстве случаев, напрямую клонировать клетки с вариантами переключения только за один раунд выбора FACS. Здесь авторы описывают эти достижения, которые значительно облегчают процесс выбора варианта переключения.
Здесь авторы описывают эти достижения, которые значительно облегчают процесс выбора варианта переключения.
АЛГЕБРАУроки для 9 класса УРОК № 5 Тема. Цель занятия: добиться усвоения учащимися понятий «складывать неравенства построчно» и «умножать неравенства построчно», а также содержания свойств числовых неравенств, выражаемых теоремами о членное сложение и почленное умножение числовых неравенств и их последствий. Развивать умение воспроизводить названные свойства числовых неравенств и использовать эти свойства для оценки значений выражений, а также продолжить работу над навыками доказательства неравенств, сравнения выражений с использованием определения и свойств числовых неравенств Тип урока: усвоение знаний, развитие первичных навыков. Видимость и оборудование: подтверждающая записка № 5. На уроках I. Организационный этап Учитель проверяет готовность учеников к уроку, настраивает их на работу. II. Проверка домашнего задания Студенты выполняют тестовые задания с последующей проверкой. III. Формулировка цели и задач урока. Для осознанного участия учащихся в постановке цели урока можно предложить им практические задания геометрического содержания (например, оценить периметр и площадь прямоугольника, длина соседних сторон которого составляет оценивается в виде двойных неравенств).В ходе беседы преподаватель должен направить мысль учеников на то, что хотя задачи аналогичны тем, которые решались на предыдущем уроке (см. Урок №4, оценивайте значение выражений), однако, в отличие от названных, они не могут быть решены теми же средствами, потому что необходимо оценивать значения выражений, содержащих две (а в перспективе и более) буквы. Таким образом, студенты осознают наличие противоречия между знаниями, которые они получили до этого момента, и необходимостью решения конкретной проблемы. Результатом выполненной работы является постановка цели урока: изучить вопрос о таких свойствах неравенств, которые могут применяться в случаях, аналогичных описанным в предлагаемом задании для учащихся; для чего необходимо четко сформулировать математическим языком и в устной форме, а затем вывести соответствующие свойства числовых неравенств и научиться использовать их в сочетании с ранее изученными свойствами числовых неравенств для решения типовых задач. IV. Обновление базовых знаний и умений учащихся Устные упражнения 1. Сравните числа a и b, если: 1) а — б = -0,2; 2) а — b = 0,002; 3) а = б — 3; 4) а — б = м 2; 5) а = б — м 2. 3. Сравните значения выражений a + b и ab, если a = 3, b = 2. Обоснуйте свой ответ. Полученное соотношение будет выполнено, если: 1) а = -3, б = -2; 2) а = -3, б = 2? В.Формирование знаний План освоения нового материала 1. Свойство о члене путем добавления числовых неравенств (с уточнением). 2. Свойство почленного умножения числовых неравенств (с уточнением). 3. Последствия. Свойство почленного умножения числовых неравенств (с уточнением). 4. Примеры применения проверенных свойств. Сопроводительная записка № 5
Методический комментарий Для осознанного восприятия нового материала преподаватель может на этапе обновления базовых знаний и умений учащихся предложить решения устных упражнений с воспроизведением, соответственно определяя сравнение чисел и свойства изучаемых числовых неравенств. Обычно студенты хорошо усваивают содержание теорем сложения слагаемых и умножения числовых неравенств, но опыт работы указывает на склонность студентов к определенным ложным обобщениям. Поэтому, чтобы не допустить ошибок в формировании знаний учащихся по данному вопросу путем демонстрации примеров и контрпримеров, преподаватель должен акцентировать внимание на следующих моментах: · Сознательное применение свойств числовых неравенств невозможно без умения записать эти свойства как математическим языком, так и в устной форме; · Почтовые теоремы сложения и умножения числовых неравенств выполняются только для неоднородностей одного знака; · Свойство почленного сложения числовых неравенств выполняется при определенном условии (см. Выше) для любых чисел и теореме почленного умножения (в форме, указанной в справочном примечании No.5) только для положительных чисел; Теоремы о почленном вычитании и почленном делении числовых неравенств не изучаются, поэтому в случаях, когда необходимо оценить разность или дробь выражений, эти выражения представляют в виде суммы или произведения соответственно, а затем при определенных условиях используют свойства членного сложения и умножения числовых неравенств . Vi. Формирование навыков Устные упражнения 1.Добавить посроченные неравенства: 1) а> 2, б> 3; 2) с -2, д 4. Или можно одно и то же неравенство умножать постепенно? Обоснуйте ответ. 2. Умножьте почтовые неравенства: 1) а> 2, б> 0,3; 2) c> 2, d> 4. Или можно такие же неровности? Обоснуйте ответ. 3. Определите и подтвердите правильность утверждения, что если 2 a 3, 1 b 2, то: 1) 3 а + б 5; 2) 2 ab 6; 3) 2 — 1 а — б 3 — 2; Письменные упражнения Для реализации дидактической цели урока необходимо выполнить упражнения следующего содержания: 1) складывать и умножать эти числовые неравенства посменно; 2) оценивает значение суммы, разницы, произведения и частного двух выражений согласно этим оценкам каждого из этих чисел; 3) оценивает значение выражений, содержащих эти буквы, согласно этим оценкам каждой из этих букв; 4) доказать неравенство с помощью теорем о сложении и умножении слагаемых числовых неравенств и с помощью классических неравенств; 5), чтобы повторить свойства числовых неравенств, изученные на предыдущих уроках. Методический комментарий Письменные упражнения, которые предлагаются для решения на этом этапе урока, должны способствовать развитию устойчивых навыков поэлементного сложения и умножения неравенств в простых случаях. (При этом прорабатывается очень важный момент: проверка соответствия записи неравенств условию теоремы и правильности записи суммы и произведения левой и правой частей неравенств.Подготовительная работа проводится во время выполнения устных упражнений.) Для лучшего усвоения материала от студентов следует потребовать воспроизвести изученные теоремы при комментировании действия. После того, как студенты успешно разработали теоремы в простых случаях, они могут постепенно переходить к более сложным случаям (чтобы оценить разницу и частное двух выражений и более сложных выражений). На этом этапе работы учитель должен следить за тем, чтобы ученики не совершали типичных ошибок, пытаясь изменить ситуацию и оценить долю своих собственных ложных правил. Также на уроке (конечно, если позволяет время и уровень усвоения учащимися содержания материала) следует уделить внимание упражнениям по использованию изученных теорем для доказательства более сложных неравенств. Vii. Итоги урока Известно, что 4 на 5; 6 b 8. Найдите неправильные неравенства и исправьте ошибки. Обоснуйте ответ. 1) 10 а + б 13; 2) -4 а — б -1; 3) 24 ab 13; 4); 5); 7) 100 a2 + b 2169? VIII.Домашнее задание 1. Изучите теоремы о сложении и умножении слагаемых числовых неравенств (с уточнением). 2. Выполняйте репродуктивные упражнения, аналогичные классным упражнениям. 3. На повторение: упражнения по применению определения сравнения чисел (для выявления неточностей и для сравнения выражений). | резюме других презентаций||||||
Русские театры — В поисках баланса
Театр за последние 20 лет идет в ногу с изменениями в гражданском обществе в России. Общество сильно изменилось, а общее количество театров с 1990-х годов существенно выросло. Причина возрождения театра — рост экономики и, как следствие, увеличение среднего дохода.После того, как жажда осязаемого статуса удовлетворена, люди жаждут опыта: театр сейчас в моде, и, кроме того, поход в театр считается изощренным.
Театр в целом — и особенно в России — это гораздо больше, чем просто развлекательный объект. Это хранитель национального культурного и языкового наследия, источник вдохновения и творчества, носитель социальных ценностей. Одна из основных задач правительства — предоставить всем гражданам России доступ к этим произведениям искусства.Выдающиеся представители культурного сообщества, такие как Александр Колягин, председатель Союза театральных деятелей России и директор театра Et cetera, объявили театр общественным благом, которое организует социальную среду, и что это не услуга, измеряемая рентабельностью. Вклад театра в социальный капитал неоценим, поэтому государственную поддержку театра следует рассматривать как инвестиции, а не расходы.
Одна из основных задач правительства — предоставить всем гражданам России доступ к этим произведениям искусства.Выдающиеся представители культурного сообщества, такие как Александр Колягин, председатель Союза театральных деятелей России и директор театра Et cetera, объявили театр общественным благом, которое организует социальную среду, и что это не услуга, измеряемая рентабельностью. Вклад театра в социальный капитал неоценим, поэтому государственную поддержку театра следует рассматривать как инвестиции, а не расходы.
Некоторые факты и цифры
По данным национальной статистики, в 2016 году количество государственных и муниципальных театров достигло 651.В том же году 87 553 человека были наняты актерами, театральной труппой и административным персоналом. Театральные труппы использовали 1394 здания, 20% из которых были внесены в список культурного наследия. Однако почти 25% зданий находились в неудовлетворительном состоянии и остро нуждались в серьезной реконструкции. Эта проблема актуальна для региональных театров, которые не могут позволить себе реконструкцию и обновление своих помещений, или некоторые театры действительно опасаются, что здания и помещения, в которых они базируются, могут быть отобраны у них инвесторами.Общая вместимость залов составила 234 028 мест. Только 2% сидений были пригодны для использования людьми с ограниченными физическими возможностями.
Эта проблема актуальна для региональных театров, которые не могут позволить себе реконструкцию и обновление своих помещений, или некоторые театры действительно опасаются, что здания и помещения, в которых они базируются, могут быть отобраны у них инвесторами.Общая вместимость залов составила 234 028 мест. Только 2% сидений были пригодны для использования людьми с ограниченными физическими возможностями.
В 2016 году в государственных театрах России было сыграно почти 3000 спектаклей. Всего было 175 452 выступления, в том числе гастрольные (17%) и гастрольные в России и за рубежом (3%). Большинство постановок были поставлены по пьесам классиков зарубежных авторов 19 и 20, -х годов веков и авторов советской эпохи. Пьесы современных российских авторов составляют лишь 17% новых драматических постановок.1,7 миллиарда рублей (25,8 миллиона долларов) было потрачено на новые производства.
В сезоне 2015/2016 общая посещаемость театров составила 31,5 миллиона человек. Если учесть численность населения России, это удручающе малая цифра — всего 250 человек из 1000. Одна из причин низкой посещаемости — нехватка региональных театров. На миллион жителей приходится всего 3,2 театра, и только в 18,8% городов России есть хотя бы один театр. Более того, почти половина населения живет в местах, куда они вообще не могут попасть ни в один театр.Опросы показывают, что 47% респондентов редко посещают театры, а 29% респондентов никогда в жизни не посещали театр.
Если учесть численность населения России, это удручающе малая цифра — всего 250 человек из 1000. Одна из причин низкой посещаемости — нехватка региональных театров. На миллион жителей приходится всего 3,2 театра, и только в 18,8% городов России есть хотя бы один театр. Более того, почти половина населения живет в местах, куда они вообще не могут попасть ни в один театр.Опросы показывают, что 47% респондентов редко посещают театры, а 29% респондентов никогда в жизни не посещали театр.
Правовой статус и государственное финансирование
По своему правовому статусу российские театры можно разделить на две категории: государственные и муниципальные театры и частные театры. Государственные и муниципальные театры снова делятся на некоммерческие организации, бюджетные организации и государственные или автономные организации; последний является относительно новым.С 2007 года некоторые некоммерческие и бюджетные театры в регионах по всей России были преобразованы в автономные организации. Государственные театры также можно классифицировать в зависимости от их полномочий: федеральные театры, местные театры, театры Министерства культуры и театры других ведомств. Частные театры могут быть как коммерческими, так и некоммерческими организациями различных организационно-правовых форм. В России роль личности в истории имеет решающее значение. В результате не только экономическое, но и культурное благополучие региона во многом зависит от доброй воли и ресурсов губернатора.
Государственные театры также можно классифицировать в зависимости от их полномочий: федеральные театры, местные театры, театры Министерства культуры и театры других ведомств. Частные театры могут быть как коммерческими, так и некоммерческими организациями различных организационно-правовых форм. В России роль личности в истории имеет решающее значение. В результате не только экономическое, но и культурное благополучие региона во многом зависит от доброй воли и ресурсов губернатора.
Государственное финансирование является основным источником доходов большинства государственных и муниципальных театров. Согласно отчетам Министерства культуры, их общий бюджет на 2016 год составил 81 миллиард рублей (1,3 миллиарда долларов). Только 29% приходилось на собственные доходы театров, в то время как основная часть годового дохода поступала из федерального (66%) и региональных или муниципальных бюджетов (3%). Для некоторых театров доля государственного финансирования превышала 75% годового бюджета. Пожертвования спонсоров составили чуть более 2% годового бюджета театров.
Пожертвования спонсоров составили чуть более 2% годового бюджета театров.
К сожалению, реальность такова, что все государственные театры коммерчески нерентабельны, и из этого правила нет исключения. Даже известные репертуарные театры, показывающие значительное количество спектаклей за сезон, не могут добиться нулевой прибыли на покрытие расходов. Если ранжировать государственные театры по совокупному доходу, который они получают от всех источников, то в чартах попадут высококлассные театры Москвы и Санкт-Петербурга: Большой театр (Москва), Мариинский театр (Санкт-Петербург), Михайловский театр, Вахтанговский театр (Москва), МХАТ (Москва), Театр эстрады (Москва) и др.Некоторые эксперты видят корень проблемы в отсутствии конкуренции между государственными театрами. Усердные попытки привлечь потребителей побудят их улучшать продукт, как и на любом другом рынке.
Автономный театр получает финансирование по контракту на государственные закупки, так называемое муниципальное задание на определенный финансовый период (три года). Любопытно, что такая форма поддержки ставит театр на один уровень с другими социальными услугами для жителей. Перечень услуг и стандарты их качества определяются федеральным агентством в конкретной сфере.В нашем случае это Министерство культуры и муниципальное управление культуры. Театр обязан провести в целом определенное количество спектаклей, поставить определенное количество новых постановок, привлечь не менее определенного количества посетителей и продать не менее определенного количества билетов. В список также входит количество туров и гастрольных выступлений, участие в фестивалях и оказание услуг инвалидам. Качество услуг также измеряется процентным соотношением заполненных помещений, темпами роста посещаемости аудитории по сравнению с прошлым годом, процентной долей аудитории, удовлетворенной предоставляемыми услугами, и другими показателями.Агентство заранее рассчитывает затраты на запланированные работы и выделяет фиксированную сумму финансирования для выполнения работ. К концу года театр сообщает цифры, заполнив специальную форму, в которой указаны все параметры.
Любопытно, что такая форма поддержки ставит театр на один уровень с другими социальными услугами для жителей. Перечень услуг и стандарты их качества определяются федеральным агентством в конкретной сфере.В нашем случае это Министерство культуры и муниципальное управление культуры. Театр обязан провести в целом определенное количество спектаклей, поставить определенное количество новых постановок, привлечь не менее определенного количества посетителей и продать не менее определенного количества билетов. В список также входит количество туров и гастрольных выступлений, участие в фестивалях и оказание услуг инвалидам. Качество услуг также измеряется процентным соотношением заполненных помещений, темпами роста посещаемости аудитории по сравнению с прошлым годом, процентной долей аудитории, удовлетворенной предоставляемыми услугами, и другими показателями.Агентство заранее рассчитывает затраты на запланированные работы и выделяет фиксированную сумму финансирования для выполнения работ. К концу года театр сообщает цифры, заполнив специальную форму, в которой указаны все параметры. Отчет размещен в открытом доступе на сайте театра. Если задача не выполнена на 100%, финансирование может быть пересмотрено на следующий период.
Отчет размещен в открытом доступе на сайте театра. Если задача не выполнена на 100%, финансирование может быть пересмотрено на следующий период.
Другие методы финансирования включают субсидии и стипендии, которые ежегодно выделяются театрам во всех регионах Российской Федерации.Ежегодно 600 государственным театрам выделяются регулярные субвенции. Ведущие театры получают гранты Президента России, которые в основном расходуются на заработную плату актеров и сотрудников. Выдающиеся артисты получают личные гранты на открытие мастерских и постановку новых пьес. Союз театральных деятелей Российской Федерации ведет профессиональные лаборатории и школы для внедрения инноваций и повышения творческих и управленческих навыков сотрудников. Молодые люди, занятые в сфере искусства, получают ежемесячное повышение от правительства России в размере 20 000 рублей (~ 283 евро).147 муниципальным театрам будет выделено 670 миллионов рублей (9 477 000 евро) на период 2017–2020 годов на обновление инфраструктуры и другие расходы.
Время от времени тот или иной правительственный чиновник будет указывать на то, что подходы к финансированию государственных и муниципальных театров следует изменить с фиксированной системы на систему стипендий, чтобы более эффективные театры получали больше денег. Это нетривиальная задача, так как критерии эффективности театров были предметом горячих споров.Все разговоры об оптимизации могут быть попыткой еще больше сократить постепенно уменьшающийся объем поддержки культуры (который едва достигает 0,5% ВВП).
Некоторые кинотеатры уже знают, что их будущее финансирование будет сокращено, и испытывают трудности с обеспечением безопасности для себя. Мариинский театр, например, использует свою главную сцену круглый год, а летом закрывает ее на реконструкцию только на десять дней. Когда театр в отпуске или на гастролях, сцену используют приглашенные труппы.Драматический театр имени Федора Волкова (Ярославль) готов пересмотреть штатное расписание и сделать приоритетными ремонтные работы. Впрочем, количество выступлений и проводимых международных фестивалей в любом случае останется на том же уровне. Пермскому Молодежному театру и Хабаровскому Молодежному театру придется отказаться от гастролей и отложить запланированное повышение зарплат. Однако они настроены оптимистично и готовы участвовать в конкурсах на внешние гранты и проекты и более эффективно использовать внутренние ресурсы при создании новых пьес.
Впрочем, количество выступлений и проводимых международных фестивалей в любом случае останется на том же уровне. Пермскому Молодежному театру и Хабаровскому Молодежному театру придется отказаться от гастролей и отложить запланированное повышение зарплат. Однако они настроены оптимистично и готовы участвовать в конкурсах на внешние гранты и проекты и более эффективно использовать внутренние ресурсы при создании новых пьес.
Фестивали и туры
Театральные фестивали — яркая и отличительная черта российской культурной сцены. По данным Союза театральных деятелей России, ежегодно почти в 100 городах проводится 256 фестивалей различных видов искусства. Наиболее известны «Золотая маска», Театр Чехова, а также другие фестивали, которые проходят в Москве. В региональных русских театрах регулярно проходят разноплановые фестивали из Европы.
Театры из центральных городов и регионов летом часто дают гастроли в других регионах.Гастроли значительно расширяют местный репертуар, увеличивая и разнообразя его, предоставляя более широкий выбор публике, поскольку обычный репертуар регионального театра составляет 10–15 представлений ежегодно. Транспортные расходы на туры за границу компенсируются Министерством культуры РФ или принимающей страной. В 2014 году была запущена программа «Большие туры» (Большие гастроли). Он продвигает гастроли федеральных театров и театров Министерства культуры в регионах. Особенно приветствуются спектакли для молодой публики, поскольку коммерческие туры считают их убыточными и обычно не включают в свою программу.Цель программы — сделать спектакли доступными в регионах, где нет средств, чтобы приглашать театры самостоятельно. В 2017 году туры охватят 45 регионов Российской Федерации, всего 70 городов. Федеральное правительство компенсирует театру и покрывает его дорожные расходы, в то время как регионы несут ответственность за проживание и технического райдера. Политика ценообразования на билеты также оставлена на усмотрение регионов.
Транспортные расходы на туры за границу компенсируются Министерством культуры РФ или принимающей страной. В 2014 году была запущена программа «Большие туры» (Большие гастроли). Он продвигает гастроли федеральных театров и театров Министерства культуры в регионах. Особенно приветствуются спектакли для молодой публики, поскольку коммерческие туры считают их убыточными и обычно не включают в свою программу.Цель программы — сделать спектакли доступными в регионах, где нет средств, чтобы приглашать театры самостоятельно. В 2017 году туры охватят 45 регионов Российской Федерации, всего 70 городов. Федеральное правительство компенсирует театру и покрывает его дорожные расходы, в то время как регионы несут ответственность за проживание и технического райдера. Политика ценообразования на билеты также оставлена на усмотрение регионов.
Молодежный театр
Молодежный театр для детей и подростков — высоко ценимый вид искусства в России.Театр — один из важнейших каналов социализации и воспитания художественного и творческого вкуса. Неоценимо влияние первых положительных впечатлений на формирование будущего увлечения искусством. Молодежному театру важно говорить на такие важные темы, как толерантность, одиночество и самоубийство. В 2016 году 11% государственных и муниципальных театров были молодежными, в то время как почти 70% гастрольных спектаклей в других регионах составили спектакли из репертуара молодежных театров.57% спектаклей государственных и муниципальных театров ориентированы на юную публику. По 39 фестивалям общее количество молодежных фестивалей в России достаточно велико. В 2017 году и позже молодежные театры получат ок. 4,2 миллиона евро ежегодно от государства. Примерно 3 миллиона поделят между областными и городскими молодежными театрами. Финансирование будет в первую очередь направлено на новые постановки для разнообразия репертуара.
Неоценимо влияние первых положительных впечатлений на формирование будущего увлечения искусством. Молодежному театру важно говорить на такие важные темы, как толерантность, одиночество и самоубийство. В 2016 году 11% государственных и муниципальных театров были молодежными, в то время как почти 70% гастрольных спектаклей в других регионах составили спектакли из репертуара молодежных театров.57% спектаклей государственных и муниципальных театров ориентированы на юную публику. По 39 фестивалям общее количество молодежных фестивалей в России достаточно велико. В 2017 году и позже молодежные театры получат ок. 4,2 миллиона евро ежегодно от государства. Примерно 3 миллиона поделят между областными и городскими молодежными театрами. Финансирование будет в первую очередь направлено на новые постановки для разнообразия репертуара.
Есть много театров для детей младшего возраста, в том числе кукольные; В то же время по-прежнему не хватает театров для подростков и зрителей от 12 лет.Несмотря на то, что многие репертуарные театры ставят спектакли на основе литературы из школьной программы по литературе, все же остаются проблемы, которые важны для подростков, но не освещаются в спектаклях. Подростки однозначно выросли из сказок с сладострастными героями, вылепленными в советской дидактической манере «Туйз» (Театр юного зрителя). Однако взрослые проблемы в драмах могут показаться слишком сложными. Ни при каких обстоятельствах следует избегать многословия и покровительственного отношения.
Подростки однозначно выросли из сказок с сладострастными героями, вылепленными в советской дидактической манере «Туйз» (Театр юного зрителя). Однако взрослые проблемы в драмах могут показаться слишком сложными. Ни при каких обстоятельствах следует избегать многословия и покровительственного отношения.
В последнее время молодежный театр наполнился новой кровью — на поле появились молодые режиссеры, не стесняющиеся экспериментировать. В 2016 году на знаменитом фестивале «Золотая маска» была создана отдельная секция для молодежных театров Kids ’Weekend, в которой представлены постановки для всех возрастов: от малышей до подростков. Включенные в программу шестнадцать шоу из разных регионов России показали высокую посещаемость.
Частные молодежные театры обычно небольшие и мобильные.Они часто играют в школах, детских садах и других образовательных центрах, потому что не могут позволить себе арендовать подходящее место со сценой, а их декорации обычно легко транспортировать. Некоторые из них регулярно гастролируют по Европе. Когда маленький молодежный театр и большой драматический театр работают вместе, это может быть очень плодотворным и сочетать свежие идеи с деньгами. Театры открыли лабораторию молодежного театра, где молодые режиссеры могут ставить новые пьесы современных драматургов. В центре Мейерхольда создана программа «Детский центр им. Мейерхольда», где актеры приобщают юных зрителей к искусству пересказа художественных текстов.
Некоторые из них регулярно гастролируют по Европе. Когда маленький молодежный театр и большой драматический театр работают вместе, это может быть очень плодотворным и сочетать свежие идеи с деньгами. Театры открыли лабораторию молодежного театра, где молодые режиссеры могут ставить новые пьесы современных драматургов. В центре Мейерхольда создана программа «Детский центр им. Мейерхольда», где актеры приобщают юных зрителей к искусству пересказа художественных текстов.
Частные театры: спектакль или лаборатория
Частные театры получают поддержку через проектное финансирование, а также могут претендовать на государственное финансирование. В 2016 году 43 частных театра из Санкт-Петербурга получили финансирование в размере 496 000 евро от городского управления культуры. Нефинансовая поддержка, такая как предоставление дополнительных площадок, также является большим подспорьем, поскольку арендная плата составляет львиную долю постоянных затрат. Она также включает льготные ссуды, страхование, социальные льготы и т. Д. Однако такая поддержка создает сложную взаимозависимость между театром и государством.Некоторые правительственные чиновники используют угрозу, чтобы сократить поддержку или потребовать более подробный отчет об использованных средствах, как рычаг и как средство контроля репертуара независимого театра. Это случай Театра.doc и театральной студии под руководством Кирилла Серебренникова.
Д. Однако такая поддержка создает сложную взаимозависимость между театром и государством.Некоторые правительственные чиновники используют угрозу, чтобы сократить поддержку или потребовать более подробный отчет об использованных средствах, как рычаг и как средство контроля репертуара независимого театра. Это случай Театра.doc и театральной студии под руководством Кирилла Серебренникова.
Помимо сценической деятельности, театры получают деньги от организации мероприятий, производства фильмов, участия в концертах и т. Д. Некоторые театры привлекают спонсоров, которые дают деньги на новые театральные постановки в обмен на рекламу или запрашивают скидки у энергетических компаний в обмен на билеты.Другие театры получают регулярные пожертвования от предпринимателей, например, Театр Сергея Женовача.
Маленькие театры изобилуют новаторскими и противоречивыми постановками и творческими идеями, но им не хватает капитала. Напротив, нерепертуарные труппы прибыльны и успешно конкурируют с репертуарным театром. Некоторые нерепертуарные труппы, такие как Театр Антона Чехова, Независимый театральный проект, Арт-Партнер XXI, Квартет «Я» и другие, присутствуют на театральном рынке более десяти лет.Причины их успеха очевидны. Театры угождают вкусам массовой публики. В сезоне обычно бывает один-два хита, комедии, мелодрамы и детективы со звездными актерами в главных ролях. Половина спектаклей проходит в другом регионе. Театры экономят на количестве нанятых актеров (не более семи / восьми на спектакль), на периоде репетиций, на декорациях (без сложного ключевого элемента), на расходах на аренду (переход от одного места аренды к другому) и максимизируют доход от боксов (сценический зал не менее 700–1000 кресел).Процесс привлечения намного проще, поскольку действующие лица работают по контракту.
Некоторые нерепертуарные труппы, такие как Театр Антона Чехова, Независимый театральный проект, Арт-Партнер XXI, Квартет «Я» и другие, присутствуют на театральном рынке более десяти лет.Причины их успеха очевидны. Театры угождают вкусам массовой публики. В сезоне обычно бывает один-два хита, комедии, мелодрамы и детективы со звездными актерами в главных ролях. Половина спектаклей проходит в другом регионе. Театры экономят на количестве нанятых актеров (не более семи / восьми на спектакль), на периоде репетиций, на декорациях (без сложного ключевого элемента), на расходах на аренду (переход от одного места аренды к другому) и максимизируют доход от боксов (сценический зал не менее 700–1000 кресел).Процесс привлечения намного проще, поскольку действующие лица работают по контракту.
Любительские театры
Любительские театры финансируются участниками, волонтерами и за счет краудфандинга. Они могут показаться незначительными и вряд ли заслуживающими упоминания, когда мы говорим о профессиональных театрах, но эти крохотные арт-коллективы составляют основу любой театральной деятельности. Любительские театры иногда выдумывают новые инициативы и практики и, подобно гусеницам, превращающимся в бабочек, превращаются в профессиональные, пусть и небольшие, единицы и создают свои собственные культурные ниши.Сам Станиславский и его труппа начали ставить художественную самодеятельность на домашней сцене своего особняка.
Любительские театры иногда выдумывают новые инициативы и практики и, подобно гусеницам, превращающимся в бабочек, превращаются в профессиональные, пусть и небольшие, единицы и создают свои собственные культурные ниши.Сам Станиславский и его труппа начали ставить художественную самодеятельность на домашней сцене своего особняка.
Любительские театры часто привлекают полупрофессиональных актеров, например студентов театральных школ, которые будут участвовать только для развлечения и практики. Иногда они получают бесплатное место для репетиций и выступлений в обмен на обучение детей и участие в городских культурных мероприятиях. В некоторых аспектах любительские театры вполне могут превосходить ожидания и с энтузиазмом придерживаться профессиональной этики и передового опыта.Например, Fellowship Art Group в Москве успешно приобрела официальные лицензии на постановку немецких и американских мюзиклов ( Rebecca; Tick, Tick,… Boom !; I Love You, You’re Perfect, Now Change ) . Как полупрофессиональный театр, они получили скидку на права, объявив ограниченное количество спектаклей. Но в художественном отношении скидок не было: сценарии были переведены на русский язык; В спектаклях участвовали актеры с неплохим вокалом и артистизмом, которые прошли прослушивание на спектакль, была живая музыка и скромная, но стильная декорация.
Как полупрофессиональный театр, они получили скидку на права, объявив ограниченное количество спектаклей. Но в художественном отношении скидок не было: сценарии были переведены на русский язык; В спектаклях участвовали актеры с неплохим вокалом и артистизмом, которые прошли прослушивание на спектакль, была живая музыка и скромная, но стильная декорация.
Заключение
Традиционный или репертуарный театр известен в России уже два столетия. Постоянный ансамбль является колыбелью новаторского искусства и совершенствует традиционное искусство. Знаменитые артисты передают свои навыки молодым актерам в процессе интенсивного рабочего взаимодействия. Скоро театр станет меньше зависеть от государственного финансирования. Без поддержки традиционный театр играл бы только развлекательную роль и имел бы ограниченный репертуар.Жители небольших городов были бы еще дальше от гастрольных театров поблизости, поскольку у них нет достаточно просторных зданий, чтобы служить площадками для выступлений коммерческой компании.
Живое искусство находится в вечном движении и в постоянном поиске баланса. Формалистические и прозаичные практики — не то, что нужно театру. Про канатоходца пел Владимир Высоцкий, культовый русский бард и, кстати, актер театра на Таганке:
«Смотрите! Ему грозит падение — он снова на веревке! Совершенно не защищен, он вменяемый или ненормальный? Даже малейший поворот — и его толкнет.Но должна быть причина, по которой ему нужно пройти все четыре четверти пути! »
Театр идет долгой и извилистой дорогой в будущее. Нам посчастливилось стать свидетелями его превращения во что-то, даже более впечатляющее.
Оксана Бондаренко — опытный исследователь в области прикладной экономики. Она получила глубокое понимание в таких областях, как торговая и регуляторная политика, коррупция, сельское хозяйство, бюджетная реформа, культурная политика. Бондаренко проанализировал влияние фильмов на доверие и альтруизм, изучил ценовые стратегии театров и спрос на билеты в театр для Министерства культуры России, проанализировал статьи по экономике театра для двух академических журналов.Академические интересы Бондаренко лежат в области экономической психологии. Она является докторантом Высшей школы экономики и проводит лабораторные эксперименты по изучению экономических моделей рациональности человеческого поведения. Также она выступает в любительском музыкальном театре.
Эмилия Деменцова — театральный критик, преподаватель, главный редактор сценария кинокомпании «Спутник». Она является докторантом Московского государственного университета имени М.В. Ломоносова, а также является членом Международной ассоциации театральных критиков и Союза журналистов России.Деменцова вела культурный обозреватель на каналах Critical Stages , European Stages , The Hollywood Reporter , Комсомольская правда , Theatron , Theater World и других. Она является стипендиатом Оксфордского фонда России. Награждена премией Международного пресс-клуба «Вызов — XXI век» за авторскую серию театральных рецензий и Всероссийскую литературную премию «Золотое перо».

 Умножение дробей 16
Умножение дробей 16 Сравнение номеров (повтор) 59
Сравнение номеров (повтор) 59 Решение квадратных неравенств 102
Решение квадратных неравенств 102 Функция y = \\ / x «130
Функция y = \\ / x «130 Свойства числовых неравенств 160
Свойства числовых неравенств 160 Определение квадратичной функции 197
Определение квадратичной функции 197 Попробуем разобраться сами, исходя из тех кусочков информации по этой теме, которые до сих пор содержатся в учебниках и в сборниках заданий для подготовки к ЕГЭ и поступления в вузы.
Попробуем разобраться сами, исходя из тех кусочков информации по этой теме, которые до сих пор содержатся в учебниках и в сборниках заданий для подготовки к ЕГЭ и поступления в вузы.
 Д. В связи с этим стоит добавить к записанным определениям уточнение относительно указанного числового набора, который является оценочным: оценка не должна быть в любом случае, он должен соответствовать целям, для которых он был найден.Например, для решения уравнения подходит оценка … Но эта оценка уже не подходит для решения уравнения, здесь значения выражения нужно оценивать по-другому, например так:.
Д. В связи с этим стоит добавить к записанным определениям уточнение относительно указанного числового набора, который является оценочным: оценка не должна быть в любом случае, он должен соответствовать целям, для которых он был найден.Например, для решения уравнения подходит оценка … Но эта оценка уже не подходит для решения уравнения, здесь значения выражения нужно оценивать по-другому, например так:. Более того, процесс получения оценок часто удобно описывать в терминах оценки значений функции. В частности, в некоторых случаях оценка выражения получается путем нахождения наибольшего и наименьшего значений соответствующей функции.
Более того, процесс получения оценок часто удобно описывать в терминах оценки значений функции. В частности, в некоторых случаях оценка выражения получается путем нахождения наибольшего и наименьшего значений соответствующей функции. .. Понятно, что в этом случае мы ограничились бы поиском первой очевидной оценки, и, естественно, мы не стали бы напрягаться в поиске второй оценки. Но в других случаях может оказаться, что одна из оценок не подходит для решения поставленной задачи. Например, наша первая оценка не позволяет решить уравнение, а оценка позволяет это сделать.То есть в этом случае первой очевидной оценки нам будет недостаточно, и нам придется найти вторую оценку.
.. Понятно, что в этом случае мы ограничились бы поиском первой очевидной оценки, и, естественно, мы не стали бы напрягаться в поиске второй оценки. Но в других случаях может оказаться, что одна из оценок не подходит для решения поставленной задачи. Например, наша первая оценка не позволяет решить уравнение, а оценка позволяет это сделать.То есть в этом случае первой очевидной оценки нам будет недостаточно, и нам придется найти вторую оценку. .. Понятно, что оценка более точная оценки … Другими словами, оценка более грубая.
.. Понятно, что оценка более точная оценки … Другими словами, оценка более грубая. Шабунин]; изд. Жижченко А.Б. — 3-е изд. — М .: Просвещение, 2010. — 368 с .: ил. — ISBN 978-5-09-022771-1.
Шабунин]; изд. Жижченко А.Б. — 3-е изд. — М .: Просвещение, 2010. — 368 с .: ил. — ISBN 978-5-09-022771-1.
 Все акции с дробями 18
Все акции с дробями 18  Оценка ошибки аппроксимации 66
Оценка ошибки аппроксимации 66  Главное свойство фракции.
Главное свойство фракции.  Преобразование выражений,
Преобразование выражений,  Устранение неравенств 172
Устранение неравенств 172  Термин сложение и умножение неравенств. Применение числовых свойств неравенства для оценки значений выражений
Термин сложение и умножение неравенств. Применение числовых свойств неравенства для оценки значений выражений


 Докажем неравенство (m + n) (mn + 1)> 4mn, если m> 0, n> 0.
Докажем неравенство (m + n) (mn + 1)> 4mn, если m> 0, n> 0.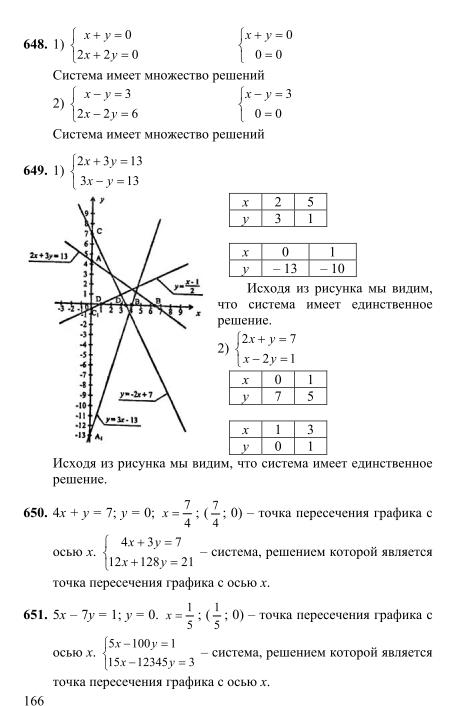 предыдущие уроки (см. выше), а также рассмотрение вопроса о соответствующих свойствах числовых неравенств.
предыдущие уроки (см. выше), а также рассмотрение вопроса о соответствующих свойствах числовых неравенств. ..
..

 Задержка введения степени с целым отрицательным показателем … Знайте определение степени с целым отрицательным показателем. 2.
Задержка введения степени с целым отрицательным показателем … Знайте определение степени с целым отрицательным показателем. 2. МОУ «Кисловская общеобразовательная школа». Руководитель: учитель математики Баранникова Е.А. Кисловка — 2008 (Презентация к уроку алгебры в 8 классе). Найдите x2 и k.Работу выполнил: ученик 8-го класса В. Слинько Решение квадратных уравнений по теореме Виета.
МОУ «Кисловская общеобразовательная школа». Руководитель: учитель математики Баранникова Е.А. Кисловка — 2008 (Презентация к уроку алгебры в 8 классе). Найдите x2 и k.Работу выполнил: ученик 8-го класса В. Слинько Решение квадратных уравнений по теореме Виета.