Карты контроля качества. Контрольные карты

Контрольные карты

Контроль качества по атрибутивному признаку

Резюме

Проблема текущего мониторинга качества продукции в процессе ее производства всегда остро стояла перед производителями. Если под мониторингом качества понимать не только непосредственную проверку пригодности выпускаемого изделия, но и наблюдение за тенденциями изменения качества, то поставленная задача представляется достаточно трудоемкой.

Для решения подобных вопросов в условиях современного производства менеджеры по контролю качества используют методики и процедуры, основанные на статистическом анализе характеристик изделий.

Одним из таких инструментов являются незаменимые при поточном мониторинге качества контрольные карты (или контрольные карты Шухарта), визуализирующие статистические характеристики исследуемого производственного процесса.

В данном материале рассматриваются модельные примеры контрольных карт и на их основе демонстрируются способы выявления нарушений качества.

Общий подход к текущему контролю качества достаточно прост. В процессе производства проводятся выборочные измерения изделий. После этого на графике (карте) строятся диаграммы изменчивости выборочных значений плановых спецификаций в выборках, и рассматривается степень их близости к заданным значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или оказывается, что выборочные значения находятся вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки.

Критерии серий служит для выделения систематических тенденций в расположении точек контрольной карты, которые могут указать на разладку контролируемого процесса.

Далее мы рассмотрим основные виды контрольных карт.

Контроль по непрерывному признаку

Для контроля качества по непрерывному признаку (анализа изменчивости параметров) обычно применяются X-bar, R или S карты.

На X-bar карту наносятся значения выборочных средних для того, чтобы контролировать отклонение непрерывной переменной от среднего значения.

На контрольную R-карту наносятся значения размахов выборок для контроля за степенью изменчивости непрерывного параметра, на S и S2 картах строятся соответственно графики выборочных стандартных отклонений и дисперсий.

Далее приводится несколько примеров контроля качества на основе X-bar и R-карт.

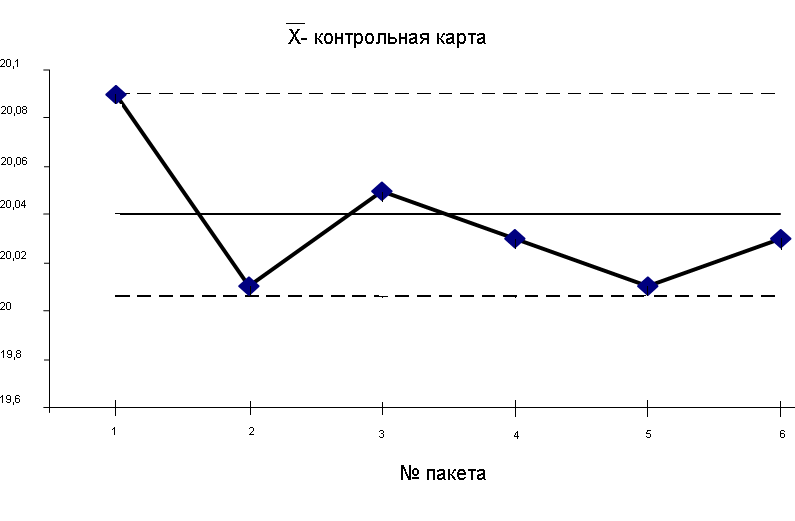
Рисунок 1

Данный пример (см. Рисунок 1) демонстрирует контрольные карты «хорошего» процесса. Точки на обеих контрольных картах находятся внутри контрольных пределов. При этом не наблюдается ни систематических смещений (трендов), ни каких-либо других признаков выхода процесса из-под контроля: точки обеих карт равномерно (во всяком случае, на основе визуального анализа) колеблются относительно соответствующих средних линий.

Среднее значение шестой выборки находится достаточно близко к нижнему контрольному пределу, однако на фоне общей положительной картины, это не является тревожным событием. Управляемость процесса также подтверждается хорошей подгонкой гистограмм наблюдаемых выборочных средних и размахов теоретическим нормальным распределением (гистограммы в левой части рисунка).

Рисунок 2

В следующем примере, на рисунке выше приводятся «плохие» контрольные карты. Явно видно, что процесс плохо управляем: выборочные средние 1-й и 4-й выборок находится вне контрольных пределов. Также настораживает то, что шесть из семи выборочных средних находятся по одну сторону средней линии.

Дополнительно на разладку производственного процесса указывает гистограмма распределения выборочных средних (левый верхний график), показывающая явное отличие распределения средних от нормального.

Стоит также отметить, что при явных выбросах на X-bar карте, значения выборочных размахов (R-карта) лежат в рамках контрольных пределов.

Рисунок 3

В данном примере контрольных карт (см. Рисунок 3) демонстрируется обратная ситуация. Средние значения по выборкам (точки на X-bar карте) находятся в контрольных пределах, при этом на R-карте размахов имеется выброс (размах второй выборки выше верхнего контрольного предела). Большие значения в выборке с критическим размахом сокращаются с малыми значениями, в результате чего, выборочное среднее значение находится в пределах нормы. Также стоит отметить небольшое систематическое смещение на карте средних, но его при малом количестве выборок и критическом размахе значений такое смещение можно считать не существенным на данном этапе исследования.

В итоге в такой ситуации требуется проведение мероприятий по снижению разброса значений исследуемого параметра, после чего перейти к более глубокому анализу выборочных средних.

Рисунок 4

В следующем примере (см. Рисунок 4) снова можно наблюдать наличие выбросов на X-bar карте и их отсутствие на карте размахов. Однако наиболее показательным результатом в данном примере является наличие заметного тренда на обеих картах: положительного на карте средних и отрицательного на карте размахов. Систематическое снижение значений выборочных размахов означает сходимость процесса (уменьшение разброса значений). Казалось бы, это – положительное явление. Но, при положительном тренде значений средних, процесс, скорее всего, сходится к значению, лежащему вне контрольных пределов. В итоге, в скором времени, все измерения исследуемого параметра могут оказаться вне значений спецификаций.

Контроль качества по атрибуту

Другим типом контрольных карт являются карты по атрибутивному признаку (атрибуту) – например, по числу дефектных деталей в партии, по числу отклонений характеристик изделия от стандарта в расчете на выборку.

Преимущество контрольных карт по атрибутивному признаку состоит в возможности быстро получить общее представление о различных аспектах качества анализируемого изделия; то есть, на основании различных критериев качества инженер может сразу принять или забраковать продукцию.

Контрольные карты по атрибутивному признаку иногда позволяют обойтись без применения дорогих точных приборов и требующих значительных затрат времени для измерительных процедур. Кроме того, этот тип контрольных карт более понятен менеджерам, которые не разбираются в тонкостях методов контроля качества. Таким образом, с помощью этих карт можно более убедительно продемонстрировать руководству наличие проблем с качеством изделий.

Однако, по сравнению с контрольными картами по атрибутивному признаку, карты для непрерывных переменных обладают большей чувствительностью. Благодаря этому, контрольные карты для непрерывных переменных могут указать на существование проблемы ухудшения качества, прежде чем в потоке продукции появятся настоящие бракованные изделия, выделяемые с помощью контрольной карты по атрибутивному признаку.

Контрольные карты для непрерывных переменных можно считать предвестниками проблем ухудшения качества, которые предупреждают об их наличии задолго до того, как в процессе производства резко возрастет доля бракованных изделий.

Для контроля качества продукции по атрибутивному признаку обычно используются следующие типы карт:

• С-карта
• U-карта
• Np-карта
• P-карта

При использовании С- и U-карт принимается предположение о том, что дефекты контролируемой характеристики продукции встречаются сравнительно редко и контрольные пределы для данных типов карт рассчитываются на основе свойств распределения Пуассона (распределения редких событий).

В свою очередь контрольные пределы для Np- и P-карт рассчитываются на основе биномиального распределения, а не распределения редких событий. Поэтому данный тип карт должен использоваться в том случае, когда обнаружение дефекта не является редким событием (например, происходит более чем у 5% проверенных единиц продукции).

При этом на С- и Np-картах отображается число дефектов (в партии, в день, на один станок), а на U- и P-картах отображается относительная частота дефектов, то есть отношение числа обнаруженных дефектов к числу проверенных единиц продукции.

Рисунок 5

На рисунке выше представлен пример P-карты по атрибуту. На основе визуального анализа графика можно заключить, что данный процесс является управляемым: не наблюдается значений вне контрольных пределов (выбросов), нет заметного тренда, а также не наблюдаются систематические тенденции в расположении точек на карте.

Рисунок 6

В противовес предыдущему графику на данной P-карте (см. Рисунок 6) демонстрируется «плохой» процесс. В шестой и седьмой выборках встречается более 80% бракованных изделий, что выше предопределенных контрольных пределов. Естественно такой высокий процент отбраковки продукции свидетельствует о наличии серьезных проблем качества данного производственного процесса.

Рисунок 7

На следующей P-карте (см. Рисунок 7) также представлен пример «плохого» процесса. Причем, помимо выброса в последней выборке (80% брака), можно наблюдать систематическое увеличение процента бракованных изделий.

Аналогично продемонстрированным методам проводится визуальный анализ качества на основе других карт по атрибуту. Далее приводятся некоторые примеры текущего контроля качества на основе C-карты.

Рисунок 8

На этой С-карте показан хорошо управляемый технологический процесс: количество бракованной продукции в каждой выборке находится в рамках контрольных пределов.

Рисунок 9

А в этом примере (см. Рисунок 9) на C-карте наблюдается выброс (первая выборка). Однако соответствующие статистики по остальным выборкам находятся в рамках контрольных пределов. Таким образом, на основании этой карты, исключив первую выборку, можно считать процесс управляемым. Если проблемная выборка отражает начало реального технологического процесса, то, скорее всего, ее неудовлетворительное качество связано с первоначальной настройкой процесса. В этом случае рекомендуется провести дополнительный анализ качества продукции, выпущенной на начальном этапе и, исключив имеющийся выброс, признать процесс управляемым.

Резюме

В заключение еще раз хочется подчеркнуть высокую эффективность применения контрольных карт в управлении качеством. Используя подходящие средства графического отображения, человеческий глаз способен отлавливать признаки ухудшения качества и тревожные тенденции в режиме поточного конвейерного производства.

При этом мощный аналитический пакет, такой как STATISTICA, способен взять на себе практически всю работу по обнаружению признаков разладки технологического процесса в online режиме, оставив оператору лишь анализ наиболее изощренных критериев визуальной проверки качества (малых трендов).

В начало

Содержание портала

statistica.ru

Лекция № 10 (2 ч) основы контрольных карт шухарта. Типы контрольных карт

План:

10.1 Основы контрольных карт Шухарта

10.2 Типы контрольных карт Шухарта

10.1 Основы контрольных карт Шухарта

Задача статистического управления процессами — обеспечение и поддержание процессов на приемлемом и стабильном уровне, гарантируя соответствие продукции и услуг установленным требо­ваниям. Главный статистический инструмент, используемый для этого, — контрольная карта. Метод контрольных карт помогает определить, действительно ли процесс достиг статистически управляемого состояния на правильно заданном уровне или остается в этом состоянии, а затем поддерживать управление и высокую степень однородности важнейших харак­теристик продукции или услуги посредством непрерывной записи информации о качестве продукции в процессе производства. Использование контрольных карт и их тщательный анализ ведут к лучшему пониманию и совершенствованию процессов.

Контрольные карты Шухарта (ККШ) являются основным инструментом статистического управления качеством. ККШ применяют для сравнения получаемой по выборкам информации о текущем состоянии процесса с контрольными границами, представляющими пределы собственной изменчивости (разброса) процесса. ККШ используют для оценки того, находятся или не находятся производственный процесс, процесс обслуживания или административного управления в статистически управляемом состоянии. Первоначально ККШ были разработаны для применения в промышленном производстве. В настоящее время их широко используют в сфере обслуживания и других областях.

Контрольная карта – это графический способ представления и сопоставления информации, основанный на последовательности выборок, отражающих текущее состояние процесса, с границами, установленными на основе внутренне присущей процессу изменчивости.

Теория контрольных карт различает два вида изменчивости. Первый вид – изменчивость из-за «случайных (обычных величин), обусловленная бесчисленным набором разнообразных причин, присутствующих постоянно, которые нелегко или невозможно выявить. Каждая из таких причин составляет очень малую долю общей изменчивости, и не одна из них не значима сама по себе. Тем не менее, сумма всех этих причин измерима и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управ­ленческих решений и выделения ресурсов на улучшение процесса и системы. Второй вид — реальные перемены в процессе. Они могут быть следствием некоторых определяе­мых причин, не присущих процессу внутренне, и могут быть устранены. Эти выявляемые причины рассматриваются как «неслучайные» или «особые» причины изменения. К ним могут быть отнесены поломка инструмента, недостаточная однородность материала, производ­ственного или контрольного оборудования, квалификация персонала, невыполнение процедур и т. д.

Цель контрольных карт — обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости. Процесс нахо­дится в статистически управляемом состоянии, если изменчивость вызвана только случайными причи­нами. При определении этого приемлемого уровня изменчивости любое отклонение от него считают результатом действия особых причин, которые следует выявить, исключить или ослабить.

Карта Шухарта требует данных, получаемых выборочно из процесса через примерно равные интервалы. Интервалы могут быть заданы либо по времени (например ежечасно), либо по количеству продукции (каждая партия). Обычно каждая подгруппа состоит из однотипных единиц продукции или услуг с одними и теми же контролируемыми показателями, и все подгруппы имеют равные объемы. Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое подгруппы и размах подгруппы R или выборочное стандартное отклонение S. Карта Шухарта — это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответ­ствующую эталонному значению характеристики. При оценке того, находится ли процесс в статисти­чески управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, ус­тановленное в технических условиях, или ее номинальное значение, основанное на предыдущей ин­формации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Щухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (рисунок 9 ).

1 2 3 4 5 6

Порядковый номер выборки

USL

CL

LCL

Рисунок 9 - Вид контрольной карты

Контрольные границы на карте Шухарта находятся на расстоянии Зот центральной линии,где — генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствующий коэффициент. Эта мера не вклю­чает межгрупповых вариаций, а оценивает только изменчивость внутри подгрупп.

Границы ±3указывают, что около 99,7 % значений характеристики подгрупп попадут в этипределы при условии, что процесс находится в статистически управляемом состоянии. Другими слова­ми, есть риск, равный 0,3 % (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. Употребляется слово «приблизительно», поскольку отклонения от исходных предположений, таких как вид распределения данных, будут влиять на значения вероятности.

Некоторые консультанты предпочитают вместо множителя, равного 3, значение 3,09, чтобы обеспечить номинальное значение вероятности 0,2 % (в среднем два вводящих в заблуждение наблюде­ния на тысячу), но Шухарт выбрал число 3, чтобы не давать поводов к рассмотрению точных вероят­ностей. Аналогично некоторые консультанты применяют фактические значения вероятностей для карт, основанных на ненормальных распределениях, таких как карты размахов и долей несоответствий, и в этом случае в карте Шухарта также используют границы на расстоянии ± 3вместо вероятностных пределов, упрощая эмпирическую интерпретацию.

Вероятность того, что нарушение границ в самом деле случайное событие, а не реальный сигнал, считается столь малой, что при появлении точки вне границ следует предпринять определенные дей­ствия. Так как действие предпринимается именно в этой точке, то Зконтрольные границы иногданазываются «границами действий».

Часто на контрольной карте границы проводят еще и на расстоянии 2.Тогда любое выборочное значение, попадающее за границы 2а, может служить предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Поэтому границы ±2иногда называют «пре­дупреждающими» .

При применении контрольных карт возможны два вида ошибок: первого и второго рода.

Ошибка первого рода возникает, когда процесс находится в статистически управляемом состоя­нии, а точка выскакивает за контрольные границы случайно. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку найти и устранить причину несуществующей проблемы.

Ошибка второго рода возникает, когда рассматриваемый процесс не управляем, а точки случай­но оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статисти­чески управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода - функция трех факторов: ширины контрольных границ, степени неуправ­ляемости и объема выборки. Их природа такова, что можно сделать лишь общее утверждение о величи­не ошибки.

Система карт Шухарта учитывает только ошибки первого рода, равные 0,3 % в пределах границ 3. Поскольку в общем случае непрактично делать полную оценку потерь от ошибки второго рода в конкретной ситуации, а удобно произвольно брать малый объем подгруппы (4 или 5 единиц), целесо­образно использовать границы на расстоянии ± Зи сосредоточивать внимание в основном на управле­нии и улучшении качества самого процесса.

Если процесс статистически управляем, контрольные карты реализуют метод непрерывной ста­тистической проверки нулевой гипотезы о том, что процесс не изменился и остается стабильным. Но поскольку значение конкретного отклонения характеристики процесса от цели, которое могло бы привлечь внимание, обычно нельзя определить заранее, как и риск ошибки второго рода, и объем выборки не рассчитывается для удовлетворения соответствующего уровня риска, то карту Шухарта не стоит рассматривать с точки зрения проверки гипотез. Шухарт подчеркивал именно эмпиричес­кую полезность контрольных карт для установления отклонений от состоянии статистической управ­ляемости, а не их вероятностную интерпретацию. Некоторые пользователи применяют кривые опера­тивных характеристик как средства для интерпретации проверок гипотез.

Когда наносимое значение выходит за любую из контрольных границ или серия значений прояв­ляет необычные структуры, состояние статистической управляемости подвергается сомне­нию. В этом случае надо исследовать и обнаружить неслучайные (особые) причины, а процесс можно остановить или скорректировать. Как только особые причины найдены и исключены, процесс снова готов к продолжению работы. При возникновении ошибки первого рода можно не найти никакой особой причины. Тогда считают, что выход точки за границы представляет собой достаточно редкое случайное явление при нахождении процесса в статистически управляемом состоянии.

Если контрольную карту процесса строят впервые, то часто оказывается, что процесс статисти­чески неуправляем. Контрольные границы, рассчитанные на основе данных такого процесса, будут иногда приводить к ошибочным заключениям, поскольку они могут оказаться слишком широкими. Следовательно, прежде чем устанавливать постоянные параметры контрольных карт, надо привести процесс в статистически управляемое состояние.

studfiles.net

Контрольные карты

При организации любого производственного процесса возникает задача установки пределов характеристик изделия, в рамках которых произведенная продукция удовлетворяет своему предназначению. Вообще говоря, существует два "врага" качества продукции: (1) отклонения от плановых спецификаций и (2) слишком большой разброс реальных характеристик изделий (относительно плановых спецификаций). На ранних стадиях отладки производственного процесса для оптимизации этих двух показателей качества часто используются методы планирования.

Общий подход к текущему контролю качества достаточно прост. В процессе производства проводятся выборки изделий заданного объема. После этого на специально разлинованной бумаге строятся диаграммы изменчивости выборочных значений плановых спецификаций в этих выборках и рассматривается степень их близости к заданным значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или оказывается, что выборочные значения находятся вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки. Иногда такие специально разлинованные бумаги называют контрольными картами Шухарта (в честь W. A. Shewhart, который общепризнанно считается первым, применившим на практике описываемые здесь методы анализа в 1924 г).

Виды контрольный карт

по шкале измерения

§     качественные

§     количественные

По выборочному параметру

§     среднего

§     среднеквадратического отклонения

§     медиана

§     размах

Контрольные карты по количественным признакам

Контрольные карты используются для статистического контроля и регулирования технологического процесса. На контрольную карту наносят значения некоторой статистической характеристики (точки), рассчитываемые по данным выборок в порядке их получения, верхнюю и нижнюю контрольные границы Кв (или UCL) и Кн (или LCL), верхнюю и нижнюю границы технических допусков Тв и Тн (при их наличии), а также среднюю линию (CL). Иногда используют также предупредительные границы Кп. Для расчёта границ и построения контрольной карты используют обычно 20...30 точек. Пример контрольной карты представлен на рисунке 6.1.

Рис. 6.1. Пример контрольной карты.

По положению точек относительно границ судят о налаженности или разлаженности технологического процесса. Обычно процесс считают разлаженным в следующих случаях:

1 Некоторые точки выходят за контрольные пределы.

2 Серия из семи точек оказывается по одну сторону от средней линии. Кроме того, если по одну сторону от средней линии находятся:

а) десять из серии в одиннадцать точек

б) двенадцать из четырнадцати точек

в) шестнадцать из двадцати точек

3  Имеется тренд (дрейф), т.е. точки образуют непрерывно повышающуюся или непрерывно понижающуюся кривую.

4 Две – три точки оказываются за предупредительными двухсигмовыми границами

5 Приближение к центральной линии. Если большинство точек находится внутри полуторасигмовых линий, это значит, что в подгруппах смешиваются данные из различных распределений

6 Имеет место периодичность, т.е. то подъём, то спад с примерно одинаковыми интервалами времени

7 Контрольные границы шире поля допуска. В идеальном случае достаточно, чтобы контрольные границы составляли ¾ величины поля допуска.

Если процесс налажен (достигнута необходимая точность и стабильность), на контрольную карту продолжают наносить точки, но через 20...30 точек пересчитывают контрольные границы. Они должны совпадать с исходными границами. Если контрольная карта показывает, что процесс разлажен, находят причины разладки и производят наладку.

Бывают контрольные карты по количественным признакам (для непрерывных значений) и по качественным признакам (для дискретных значений). По количественным признакам используют в основном следующие контрольные карты:

-карта средних арифметических значений (-карта)

-карта медиан (-карта)

-карта средних квадратичных отклонений (s-карта)

-карта размахов (R-карта)

-карта индивидуальных значений (x-карта)

Карта средних значений используется для контроля отклонения параметра от нормы и настройки на норму. Точки на контрольной карте – это средние значения небольших выборок, обычно одинакового объёма, из 3...10 элементов:

 , где n – объём выборки (подгруппы).

Для получения выборок можно также использовать результаты измерений, проводившихся через одинаковые промежутки времени, путём разбиения их на группы.

Средние значения выборок находят с одним лишним знаком по сравнению с исходными данными. Среднюю линию рассчитывают как среднее из средних значений выборок:

 , где k – число подгрупп (число точек). Обычно k = 20...30.

Контрольные границы рассчитывают по формуле

 , где  - среднее квадратичное отклонение всей совокупности данных. В этом выражении (как и при расчёте контрольных границ для других видов контрольных  карт) коэффициент 3 используется, исходя из правила трёх сигм.

Карта медиан используется вместо карты средних значений, когда хотят упростить расчёты. Точки на карте – это медианы выборок одинакового объёма из 3...10 элементов. Медиана – это при нечётном объёме выборки середина вариационного ряда, при чётном объёме выборки – среднее из двух значений середины вариационного ряда.

Средняя линия - это среднее из медиан выборок. Контрольные границы находят по формуле

Карта медиан менее точна, чем карта средних значений. При использовании для расчётов компьютера применение карты медиан вместо карты средних значений вряд ли оправдано.

Карта средних квадратичных отклонений используется для контроля рассеяния показателя. Точки на карте – средние квадратичные отклонения выборок одинакового объёма из 3...10 элементов. Средняя линия  - это среднее из СКО выборок. Контрольные границы:

         , где c2 – критерий Пирсона, n – объём выборки, a - уровень значимости. Обычно принимают a = 0,0027, что соответствует доверительной вероятности 0,9973. Часто на s-карте используют только верхнюю границу.

Карта размахов используется вместо карты средних квадратичных отклонений, когда хотят упростить расчёты. При этом карта размахов менее точна.

При построении R-карты берут 20...30 выборок одинакового объёма из 2...10 элементов. Точки ан карте – размахи выборок. Размах выборки R – это разность между максимальным xmax и минимальным xmin значениями выборки. Средняя линия  - это среднее размахов выборок. Контрольные границы рассчитывают по формулам:

При уровне значимости 0,0027 коэффициенты D3 и D4 можно найти из табл. 6.1. При n<7 нижняя контрольная граница не используется.

Таблица 6.1.

Часто при статистическом регулировании технологических процессов используют двойные карты, отражающие как отклонение параметра от нормы, так и его рассеяние. Это могут быть, например, -карты или другие.

Контрольные карты по качественным признакам

По качественным признакам (или по альтернативному признаку) различают следующие контрольные карты:

-        карта доли дефектной продукции (p-карта)

-        карта числа дефектных единиц продукции (pn-карта)

-        карта числа дефектов (c-карта)

-        карта числа дефектов на единицу продукции (u-карта)

Карта доли дефектной продукции. Применяется для контроля и регулирования технологического процесса по доле дефектных изделий в выборке. Точки на контрольной карте ставят по значениям доли дефектной продукции в выборках:

, где ni – объём i-й выборки, x – количество бракованных изделий в выборке. Выборка берётся за смену, сутки или более.

Среднюю линию рассчитывают по уравнению

, где k – число выборок. Обычно k = 20...30.

Контрольные границы находят по уравнению

Объём выборки подбирают так, чтобы в ней было в основном от 1 до 5 дефектных изделий. Если объём выборки неодинаков при каждом отборе, то контрольные границы вычисляют при каждом отборе (для каждой точки), т.е. границы в этом случае непостоянны.

Карта числа дефектных единиц продукции. Используется для контроля и регулирования технологического процесса по числу дефектных изделий в выборке. Используют выборки постоянного объёма. Объём выборки подбирают так, чтобы в ней было в основном от 1 до 5 дефектных изделий. Точки наносят на карту по количеству дефектных изделий в выборке pin. Среднюю линию рассчитывают как значение

Контрольные границы находят по уравнению , где . Если Кн<0, его не рассматривают.

Карта числа дефектов. В этих картах регистрируется число дефектов c, выявленных в установленной единице контролируемой продукции, например, в рулоне ткани или бумаги, на определённой площади пластика, стекла и т.п. Предусматривают такую единицу контролируемой продукции, чтобы она содержала в основном 1...5 дефектов.

Среднюю линию находят по уравнению

Контрольные границы 

Карта числа дефектов на единицу продукции. Используется вместо с-карты, когда параметр единицы продукции (например, площадь, длина) не является постоянной величиной, т.е объём выборки непостоянен. Точки на u-карте – это значения ui=ci/ni, где ci – число дефектов в i-й выборке. Средняя линия

Контрольные границы: . Поскольку объём выборки непостоянен, границы тоже непостоянны, и их вычисляют для каждой точки.

Разладка процесса: критерии серий

Когда точка на контрольной карте, соответствующая выборочному значению контролируемой характеристики (например, среднему значению в X-карте) оказывается вне ограниченной контрольными переделами области, это дает основания предполагать, что производственный процесс разладился. Далее, при этом необходимо отслеживать появление систематической тенденции в расположении точек (например, выборочных средних) на контрольной карте, так как наличие такой тенденции может служить свидетельством тренда среднего значения контролируемого процесса.  Эти критерии иногда называют критериями серий типа AT&T или критериями против альтернатив специального вид. Термин специальные альтернативы, как альтернатива случайным или общим причинам, был использован в работе Шухарта (Shewhart) для того, чтобы сделать разграничение между нормальным производственным процессом, вариации в котором появляются только в силу действия случайных причин, и вышедшим из-под контроля процессом , в котором вариации характеристик обусловлены некоторыми неслучайными, то есть специальными факторами (см. Montgomery, 1991, стр. 102).

Как и обсуждавшиеся ранее контрольные пределы, выраженные в единицах сигмы, критерии серий имеют в своей основе "статистическое" обоснование. Так, например, вероятность того, что любое выборочное среднее значение для X-карты окажется выше центральной линии, равна 0.5 при следующих условиях: (1) производственный процесс находится в нормальном состоянии (т.е. центральная линия проведена через значение, равное среднему контролируемой характеристики генеральной совокупности изделий), (2) средние значения следующих друг за другом выборок независимы (т.е. отсутствует автокорреляция) и (3) выборочные средние значения контролируемой характеристики распределены по нормальному закону. Проще говоря, при таких условиях для выборочного среднего значения шансы попасть выше или ниже центральной линии составляют 50 на 50. Поэтому вероятность того, что два следующих друг за другом выборочных средних окажутся выше центральной линии, будет равна 0.5, умноженному на 0.5 , т.е. 0.25.

Соответственно, вероятность того, что выборочные средние девяти последующих выборок (или серия из 9 точек контрольной карты) окажется с одной стороны от центральной линии, составит 0.59 = .00195. Заметим, что это значение приблизительно равно вероятности того, что отдельное выборочное среднее значение не попадет в интервал, ограниченный контрольными пределами в 3 сигма (при условии нормального распределения выборочных средних и нормальности производственного процесса). Поэтому, в качестве еще одного индикатора разладки производственного процесса можно рассматривать ситуацию, когда девять последовательных выборочных средних находятся с одной стороны от центральной линии.

Зоны A, B, C. Обычно для задания критериев поиска серий область контрольной карты над центральной линией и под ней делится на три "зоны".

По умолчанию, зона А определяется как область, расположенная на расстоянии от 2 до 3 сигма по обе стороны от центральной линии. Зона В определяется как область, отстоящая от центральной линии на расстояние от 1 до 2 сигма, а зона С - как область, расположенная между центральной линией по обе ее стороны и ограниченная прямой, проведенной на расстоянии одной сигма от центральной линии.

9 точек в зоне С или за ее пределами (с одной стороны от центральной линии). Если этот критерий выполняется (т.е. если на контрольной карте обнаружено такое расположение точек), то делается вывод о возможном изменении среднего значения процесса в целом. Заметим, что здесь делается предположение о симметричности распределения исследуемых характеристик качества вокруг среднего значения процесса на графике. Но это условие не выполняется, например, для R-карт, S-карт и большинства карт по альтернативному признаку. Тем не менее, данный критерий полезен для того, чтобы указать занимающемуся контролем качества инженеру на присутствие потенциальных трендов процесса. Например, здесь стоит обратить внимание на последовательные выборочные значения с изменчивостью ниже среднего, так как с их помощью можно догадаться, каким образом снизить вариацию процесса.

6 точек монотонного роста или снижения, расположенные подряд. Выполнение этого критерия сигнализирует о сдвиге среднего значения процесса. Часто такой сдвиг обусловлен изнашиванием инструмента, ухудшением технического обслуживания оборудования, повышением квалификации рабочего и т.п.

14 точек подряд в "шахматном" порядке (через одну над и под центральной линией). Если этот критерий выполняется, то это указывает на действие двух систематически изменяющихся причин, которое приводит к получению различных результатов. Например, в данном случае может иметь место использование двух альтернативных поставщиков продукции или отслеживание двух различных альтернативных воздействий.

2 из 3-х расположенных подряд точек попадают в зону A или выходят за ее пределы. Этот критерий служит "ранним предупреждением" о начинающейся разладке процесса. Заметим, что для данного критерия вероятность получения ошибочного решения (критерий выполняется, однако процесс находится в нормальном режиме) в случае Х-карт составляет приблизительно 2 %.

4 из 5-ти расположенных подряд точек попадают в зону B или за ее пределы. Как и предыдущий, этот критерий может рассматриваться в качестве индикатора - "раннего предупреждения" о возможной разладке процесса. Процент принятия ошибочного решения о наличии разладки процесса для этого критерия также находится на уровне около 2%.

15 точек подряд попадают в зону C (по обе стороны от центральной линии). Выполнение этого критерия указывает на более низкую изменчивость по сравнению с ожидаемой (на основании выбранных контрольных пределов).

8 точек подряд попадают в зоны B, A или выходят за контрольные пределы, по обе стороны от центральной линии (без попадания в зону C). Выполнение этого критерия служит свидетельством того, что различные выборки подвержены влиянию различных факторов, в результате чего выборочные средние значения оказываются распределенными по бимодальному закону. Такая ситуация может сложиться, например, когда отмечаемые на Х-карте выборки изделий были произведены двумя различными станками, один из которых производит изделия со значением контролируемой характеристики выше среднего, а другой - ниже.

yuschikev.narod.ru

Карты контроля качества



Карты контроля качества

Основные задачи

При организации любого производственного процесса возникает задача установки пределов характеристик изделия, в рамках которых произведенная продукция удовлетворяет своему предназначению. Вообще говоря, существует два "врага" качества продукции: (1) отклонения от плановых спецификаций и (2) слишком большой разброс реальных характеристик изделий (относительно плановых спецификаций). На ранних стадиях отладки производственного процесса для оптимизации этих двух показателей качества часто используются методы планирования эксперимента (см. Планирование эксперимента). Методы, содержащиеся в модуле "Контроль качества", предназначены для построения процедур контроля качества продукции в процессе ее производства, т.е. текущего контроля качества. За детальным описанием принципов построения контрольных карт и примерам обратитесь к работам Buffa (1972), Duncan (1974), Grant and Leavenworth (1980), Juran (1962), Juran and Gryna (1970), Montgomery (1985, 1991), Shirland (1993) или Vaughn (1974). В качестве превосходных вводных курсов, построенных на основе подхода "как - чтобы", можно указать монографии Hart and Hart (1989) и Pyzdek (1989), а также изданные на немецком языке курсы Rinne and Mittag (1995) и Mittag (1993). 

Общий подход

Общий подход к текущему контролю качества достаточно прост. В процессе производства проводятся выборки изделий заданного объема. После этого на специально разлинованной бумаге строятся диаграммы изменчивости выборочных значений плановых спецификаций в этих выборках и рассматривается степень их близости к заданным значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или оказывается, что выборочные значения находятся вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки. Иногда такие специально разлинованные бумаги называют контрольными картами Шуэрта (в честь W. A. Shewhart, который общепризнанно считается первым, применившим на практике описываемые здесь методы анализа; см. Shewhart, 1931).

Интерпретация контрольных карт. В компьютерном варианте контрольных карт наиболее часто встречается ситуация, когда на экране находятся две карты (и две гистограммы), одна из них называется Х-картой, а другая - R-картой.

В обеих контрольных картах по горизонтальной оси откладываются номера соответствующих выборок; по вертикальной оси в случае X -карты отложены выборочные средние исследуемых характеристик, а в случае R-карты - размахи соответствующих выборок. Пусть, например, производятся контрольные измерения диаметра поршневых колец, изготавливаемых на вашем предприятии. Тогда центральная линия на X -карте будет соответствовать размеру, используемому в качестве стандарта (например, установленному диаметру кольца в миллиметрах), в то время как центральная линия R-карты будет соответствовать приемлемому (т.е. находящемуся в пределах плановой спецификации) размаху диаметра поршневого кольца в выборках; таким образом, последняя контрольная карта представляет собой карту изменчивости процесса (чем больше изменчивость, тем больше диапазон отклонения от стандарта). Кроме центральной линии, на карте обычно присутствуют две дополнительные горизонтальные прямые, обозначающие верхний и нижний контрольные пределы (ВКП и НКП соответственно). Принципы определения этих линий обсуждаются ниже. Обычно нанесенные на карты отдельные точки соответствуют выборочным значениям и соединяются прямыми линиями. Если результирующая кривая на графике выходит за верхний или нижний контрольный предел или ее конфигурация выражает определенную тенденцию поведения для следующих друг за другом выборок (см. Критерий серий), то это рассматривается как указание на существование проблем с качеством.

Установка контрольных пределов

Несмотря на то, что можно достаточно произвольно определить момент разладки производственного процесса (например, при выходе соответствующих значений за границы верхних и нижних контрольных пределов), обычной практикой является применение статистических методов для определения этого момента. В разделе Элементарные понятия статистики обсуждаются свойства выборочного распределения, а также дается сводка характеристик нормального распределения. Метод установления верхнего и нижнего контрольных пределов представляет собой прямое следствие применения  описанных в этом разделе принципов.

Пример. Предположим, вы контролируете среднее значение некоторой величины - например, диаметра поршневых колец. Пусть среднее значение диаметров и дисперсия в процессе производства не меняются. Тогда выборочные средние, полученные для последовательных выборок, будут распределены нормально относительно истинного среднего. Более того, не вдаваясь в тонкости, связанные с выводом формул, можно заключить (согласно центральной предельной теореме и сделанному предположению о нормальности выборочных средних размеров колец; см, например, работу Hoyer and Ellis, 1996), что стандартное отклонение распределения выборочных средних будет равно сигме (стандартному отклонению отдельных наблюдений или измерений диаметра отдельных колец), деленному на квадратный корень из n (n - размер выборки). Следовательно, примерно 95% значений выборочных средних попадут в интервал   ±1.96 *сигма/квадратный корень из n (обсуждение соответствующих свойств нормального распределения проводится в разделе Элементарные понятия статистики). На практике обычно заменяют 1.96 на 3 (при этом в интервал попадают приблизительно 99% выборочных средних) и определяют верхний и нижний контрольные пределы как плюс-минус 3 сигма соответственно. 

Общий случай. Описанный выше частный принцип установления контрольных пределов применяется во всех типах контрольных карт. После выбора контролируемой характеристики (например, стандартного отклонения) оценивается ее ожидаемая изменчивость в выборках того размера, который будет использоваться в контролируемой процедуре. Затем с помощью полученных оценок изменчивости устанавливают контрольные пределы карты.

Наиболее часто используемые типы контрольных карт

Классификация типов контрольных карт часто осуществляется согласно типам величин, которые выбраны для отслеживания характеристик качества. Так, различают контрольные карты для непрерывных переменных и контрольные карты по альтернативному признаку. В частности, для контроля по непрерывному признаку обычно строятся следующие контрольные карты:

• X-карта. На эту контрольную карту наносятся значения выборочных средних для того, чтобы контролировать отклонение от среднего значения непрерывной переменной (например, диаметров поршневых колец, прочности материала и т.д.).
• R-карта. Для контроля за степенью изменчивости непрерывной величины в контрольной карте этого типа строятся значения размахов выборок.
• S-карта. Для контроля за степенью изменчивости непрерывной переменной в контрольной карте данного типа рассматриваются значения выборочных стандартных отклонений.
• S**2-карта. В контрольной карте данного типа для контроля изменчивости строится график выборочных дисперсий.

Для контроля качества продукции по альтернативному признаку обычно применяются следующие типы контрольных карт:

• C-карта. В таких контрольных картах строится график числа дефектов (в партии, в день, на один станок, в расчете на 100 футов трубы и т.п.). При использовании карты этого типа делается предположение, что дефекты контролируемой характеристики продукции встречаются сравнительно редко, при этом контрольные пределы для данного типа карт рассчитываются на основе свойств  распределения Пуассона (распределения редких событий).

  

• U-карта. В карте данного типа строится график относительной частоты дефектов, то есть отношения числа обнаруженных дефектов к n - числу проверенных единиц продукции (здесь n обозначает, например, число футов длины трубы, объем партии изделий). В отличие от C-карты, для построения карты данного типа не требуется постоянство числа единиц проверяемых изделий, поэтому ее можно использовать при анализе партий различного объема.
• Np-карта. В контрольных картах этого типа строится график для числа дефектов (в партии, в день, на станок), как и в случае С-карты. Однако, контрольные пределы этой карты рассчитываются на основе биномиального распределения, а не распределения редких событий Пуассона. Поэтому данный тип карт должен использоваться в том случае, когда обнаружение дефекта не является редким событием (например, когда обнаружение дефекта происходит более чем у 5% проверенных единиц продукции). Этой картой можно воспользоваться, например, при контроле числа единиц продукции, имеющих небольшой брак.
• P-карта. В картах данного типа строится график процента обнаруженных дефектных изделий (в расчете на партию, в день, на станок и т.д.). График строится так же, как и в случае U-карты. Однако контрольные пределы для данной карты находятся на основе биномиального распределения (для долей), а не распределения редких событий. Поэтому P-карта наиболее часто используется, когда появление дефекта нельзя считать редким событием (если, например, ожидается, что дефекты будут присутствовать в более чем 5% общего числа произведенных единиц продукции).

Все перечисленные выше типы карт допускают возможность построения кратких карт для производственных серий (краткие контрольные карты) и контрольных карт для нескольких процессов (многопоточные групповые карты).

Краткие контрольные карты

Краткая контрольная карта (контрольная карта для кратких производственных серий) представляет собой график наблюдаемых значений характеристик качества (значений непрерывной переменной или альтернативного признака) для нескольких частей процесса, причем все значения контролируемой характеристики наносятся на одну и ту же карту. Разработка кратких контрольных карт стала следствием необходимости адаптации контрольных карт к тем ситуациям, когда требуется выполнить несколько десятков измерений контролируемой характеристики процесса, прежде чем вычислить контрольные пределы. Часто данное требование выполняется с трудом на тех стадиях производственного процесса, в ходе которых изготавливается ограниченное (малое) число деталей, которые необходимо подвергнуть измерениям.

Так, например, на целлюлозно-бумажном комбинате процесс может быть организован следующим образом: выпускается только три-четыре больших рулона бумаги определенного сорта (часть процесса), а затем переходят к выпуску бумаги другого сорта. Однако, если измерения переменных (таких, например, как толщина бумаги или альтернативных признаков, таких, как наличие/отсутствие пятен) производятся для нескольких десятков рулонов, скажем, десяти различных сортов, то контрольные пределы для переменной "толщина бумаги" и признака "наличие/отсутствие пятен" могут быть вычислены на основе преобразованных значений (в рамках краткой производственной серии). Более точно, эти преобразования заключаются в таком изменении масштаба контролируемых переменных, при котором амплитуды их изменения в различных производственных сериях (различных частях процесса) будут сравнимыми. Контрольные пределы, рассчитанные по этим преобразованным значениям, могут применяться в дальнейшем при контроле толщины бумаги и наличия/отсутствия пятен, вне зависимости от сорта выпускаемой бумаги. Для того чтобы определить, произошла разладка процесса или нет, могут быть использованы статистические процедуры контроля процесса. Этими процедурами можно воспользоваться также для постоянного контроля производства и разработки способов постоянного улучшения качества.

Более подробное описание кратких карт контроля качества можно найти в работах Bothe (1988), Johnson (1987) или Montgomery (1991).

Краткие карты для переменных

Номинальная карта, карта плановых спецификаций. Существует несколько типов кратких контрольных карт. Наиболее часто используются следующие карты: номинальная карта и карта плановых спецификаций. При построении данных карт преобразование наблюдаемых значений контролируемой характеристики в различных частях процесса производится путем вычитания определенной постоянной из измерений (для наблюдений каждой части используется своя постоянная). В качестве таких постоянных могут выступать как значения номинала для соответствующих частей процесса (результатом такого подхода будет номинальная краткая карта), так и плановые спецификации, рассчитанные по "историческим" средним контролируемой характеристики для каждой части (краткая X-карта плановых спецификаций и краткая R-карта плановых спецификаций). Так, например, сравнение внутренних диаметров поршневых колец для различных блоков мотора, находящихся в производстве, только тогда может быть обоснованно, когда до проведения сравнения из измерений диаметров будут вычтены средние разности между внутренними диаметрами поршневых колец для моторов различного размера (для определения непротиворечивости значений диаметров). Такое сравнение становится возможным при построении краткой номинальной карты или краткой карты плановых спецификаций. Заметим, что при построении номинальной карты и карты плановых спецификаций делается предположение о равенстве дисперсий различных частей процесса, чтобы применение рассчитанных по общей оценке сигма процесса контрольных пределов можно было считать корректным.

Стандартизованная краткая карта. Если изменчивость различных частей процесса нельзя считать одинаковой, то прежде чем нанести на одну карту данные, относящиеся к разным частям процесса,  необходимо провести еще одно преобразование. При построении карты данного типа это преобразование заключается в следующем: вычисляются отклонения выборочных средних контролируемой характеристики от средних для соответствующих частей процесса (т.е. от номинальных значений или плановых спецификаций для частей), далее для каждой части процесса эти отклонения делятся на постоянные, пропорциональные изменчивости соответствующих частей. Так, в случае кратких X-карты и R-карты, для построения точек графика X-карты вначале из каждого выборочного среднего вычитается определенная постоянная, соответствующая рассматриваемой части процесса (т.е. среднее этой части процесса или значение номинала для данной части), затем эта разность делится на другую постоянную - например на средний размах соответствующей части процесса. В результате таких преобразований масштабы выборочных средних различных частей процесса станут сравнимыми.

Краткие карты по альтернативному признаку

В случае контрольных карт по альтернативному признаку (C-, U-, Np- или P-карт) оценка изменчивости процесса (доля, частота и т.д.) зависит от среднего значения процесса (средней доли, средней относительной частоты и т.д.) - так, например, стандартное отклонение доли p равно квадратному корню из p*(1-p)/n). Следовательно, для альтернативных признаков могут быть построены только стандартизованные краткие карты. К примеру, точки краткой P-карты находятся вычитанием из соответствующих выборочных значений долей p средних p для части процесса, с последующим делением результата на стандартное отклонение средних p.

Многопоточные групповые карты

Групповая контрольная карта дает возможность нанести данные для нескольких потоков наблюдаемых значений непрерывной переменной или альтернативного признака (характеристик качества) на одну и ту же карту. Это упрощает интерпретацию карты при одновременном управлении большим числом процессов или их характеристик. Здесь термином "потоки процесса" могут обозначаться данные, полученные для различных станков, сборочных линий, операторов и так далее. Все эти данные могут быть нанесены на одну контрольную карту.

При построении групповой X-карты для каждой из выборок с измерениями контролируемой характеристики на карту наносится две точки, в результате чего на графике образуются две линии. Верхняя из них представляет собой график наиболее высоких средних значений каждой выборки для всех нанесенных на карту потоков переменных или альтернативных признаков, а нижняя - подобный график наименьших средних значений каждой выборки. Для каждой выборки верхняя и нижняя точка представляют собой максимальное и минимальное средние всех нанесенных на карту потоков переменных или альтернативных признаков. Если эти экстремальные значения не выходят за рамки заданных контрольных пределов, очевидно, что все остальные средние также будут находиться в области, ограниченной контрольными пределами. Следовательно, с помощью групповой X-карты, можно быстро определить, не началась ли разладка процесса в одном или нескольких потоках процесса или контролируемых характеристиках, не переходя к проверке всех измерений подряд.

В групповых R-, S- или S**2-картах для переменных, как и в групповых C-, U-, Np- или P-картах  для альтернативных признаков, две точки, наносимые на карту для каждой выборки, соответствуют минимальному и максимальному размаху, стандартному отклонению и т.п. от средних переменных или альтернативных признаков, измеряемых для каждой выборки в нескольких потоках. Как и в случае групповой X-карты, сравнение этих экстремальных значений с заданными контрольными пределами   дает возможность быстро определить, не началась ли разладка потока процесса или его контролируемой характеристики.

Групповая карта для одной части процесса называется стандартной групповой картой или, обычно, просто групповой картой. Групповые карты для нескольких частей процесса называются групповыми краткими картами. Для построения групповых кратких карт используется та же процедура, что и для стандартных групповых карт; единственное их отличие от стандартных состоит в том, что точки на график наносятся только после того, как будут выполнены все преобразования данных в пределах отдельных частей процесса.

Неравные объемы выборок

При построении на контрольной карте графика для выборок неодинакового объема контрольные пределы, находящиеся по обе стороны от центральной линии (плановой спецификации), не могут быть изображены прямыми линиями. Так, например, вернувшись к формуле сигма/квадратный корень из n, которая была введена для вычисления контрольных пределов X-карты, можно видеть, что неравные значения n приведут к получению различных контрольных пределов для разных объемов выборки. Существует три способа, позволяющих справиться с такой ситуацией.

Средние объемы выборок. В том случае, когда желательно оставить контрольные пределы в виде прямых линий (например, чтобы облегчить чтение карты и ее использование в презентациях), можно найти среднее значение объема выборки n по всем рассматриваемым выборкам и установить контрольные пределы на основе полученного среднего объема выборки. Эту процедуру нельзя назвать "точной". И все же, пока объемы выборок несильно отличаются друг от друга, применение данного метода можно считать вполне адекватным.

Переменные контрольные пределы. С другой стороны, для каждой выборки можно отдельно определить контрольные пределы на основе ее объема. При таком подходе будут получены переменные контрольные пределы. На графике такие пределы будут изображены ступенчатой линией. Этот метод позволяет получить точные контрольные пределы для каждой из использующихся выборок. Однако при этом теряется простота и наглядность контрольных пределов, отмечаемых на карте прямой линией.

Стабилизированная (нормализованная) карта. Наилучший вариант - изображающиеся прямыми линиями контрольные пределы, которые при этом точны - может быть получен путем стандартизации контролируемой численной характеристики (среднего значения, доли и т.д.) согласно единицам сигмы. При этом контрольные пределы изображаются прямыми линиями, но расположение точек выборочных значений на графике определяется не только значениями контролируемой характеристики, но и объемом n соответствующих выборок. Недостаток данного метода заключается в следующем: по вертикальной оси контрольной карты (оси Y) величины выражаются в единицах сигма, а не в первоначальных единицах измерения контролируемой характеристики, поэтому их нельзя считывать по выводимому на графике значению. Так, например, выборочная величина со значением 3 отстоит на 3 сигма от плановой спецификации. Для перевода данного значения в первоначальные единицы измерения придется выполнить некоторый объем вычислений.

Контрольные карты для непрерывных переменных и контрольные карты по альтернативному признаку

Иногда инженеру, занимающемуся контролем качества, приходится выбирать между применением контрольной карты для непрерывных переменных и контрольной карты по альтернативному признаку.

Преимущества контрольных карт по альтернативному признаку. Преимущество контрольных карт по альтернативному признаку состоит в возможности быстро получить общее представление о различных аспектах качества анализируемого изделия; то есть, на основании различных критериев качества инженер может сразу принять или забраковать продукцию. Далее, контрольные карты по альтернативному признаку иногда позволяют обойтись без применения дорогих точных приборов и требующих значительных затрат времени измерительных процедур. Кроме того, этот тип контрольных карт более понятен менеджерам, которые не разбираются в тонкостях методов контроля качества. Таким образом, с помощью таких карт можно более убедительно продемонстрировать руководству наличие проблем с качеством изделий.

Преимущества контрольных карт для непрерывных переменных. Контрольные карты для непрерывных переменных обладают большей чувствительностью, чем контрольные карты по альтернативному признаку (см. Montgomery, 1985, стр. 203). Благодаря этому, контрольные карты для непрерывных переменных могут указать на существование проблемы ухудшения качества, прежде чем в потоке продукции появятся настоящие бракованные изделия, выделяемые с помощью контрольной карты по альтернативному признаку. В работе Montgomery (1985) автор называет контрольные карты для непрерывных переменных основными индикаторами  ухудшения качества, которые предупреждают об этих проблемах задолго до того, как в процессе производства резко возрастет доля бракованных изделий.

Контрольные карты для отдельных наблюдений

Кроме выборок, состоящих из нескольких наблюдений, контрольные карты для переменных могут быть построены также для отдельных наблюдений, полученных в ходе производственного процесса. Иногда такой подход необходим в силу дороговизны, неудобства или невозможности анализа выборок, состоящих из ряда наблюдений. Примером может служить ситуация, когда число претензий потребителей или случаев возврата изделий может быть получено только по итогам месяца, тем не менее, существует необходимость в проведении текущего анализа этих данных для выявления ухудшения качества продукции. Другим широко встречающимся примером применения карт данного типа является проверка автоматическим тестирующим прибором каждой единицы произведенной продукции. В этом случае обычно стремятся обнаружить небольшие отклонения качества выпускаемой продукции (например, постепенное ухудшение качества, обусловленное износом  оборудования). При этом наилучшее применения находят контрольные карты типа CUSUM, MA, и EWMA (контрольные карты для накопленных сумм и взвешенных средних).

Разладка процесса: критерии серий

Как уже было отмечено ранее в вводной части, когда точка на контрольной карте, соответствующая выборочному значению контролируемой характеристики (например, среднему значению в X-карте) оказывается вне ограниченной контрольными переделами области, это дает основания предполагать, что производственный процесс разладился. Далее, при этом необходимо отслеживать появление систематической тенденции в расположении точек (например, выборочных средних) на контрольной карте, так как наличие такой тенденции может служить свидетельством тренда среднего значения контролируемого процесса.  Эти критерии иногда называют критериями серий типа AT&T (см. AT&T, 1959) или критериями против альтернатив специального вида (см. Nelson, 1984, 1985; Grant and Leavenworth, 1980; Shirland, 1993). Термин специальные альтернативы, как альтернатива случайным или общим причинам, был использован в работе Шуэрта (Shewhart) для того, чтобы сделать разграничение между нормальным производственным процессом, вариации в котором появляются только в силу действия случайных причин, и вышедшим из-под контроля процессом , в котором вариации характеристик обусловлены некоторыми неслучайными, то есть специальными факторами (см. Montgomery, 1991, стр. 102).

Как и обсуждавшиеся ранее контрольные пределы, выраженные в единицах сигмы, критерии серий имеют в своей основе "статистическое" обоснование. Так, например, вероятность того, что любое выборочное среднее значение для X-карты окажется выше центральной линии, равна 0.5 при следующих условиях: (1) производственный процесс находится в нормальном состоянии (т.е. центральная линия проведена через значение, равное среднему контролируемой характеристики генеральной совокупности изделий), (2) средние значения следующих друг за другом выборок независимы (т.е. отсутствует автокорреляция) и (3) выборочные средние значения контролируемой характеристики распределены по нормальному закону. Проще говоря, при таких условиях для выборочного среднего значения шансы попасть выше или ниже центральной линии составляют 50 на 50. Поэтому вероятность того, что два следующих друг за другом выборочных средних окажутся выше центральной линии, будет равна 0.5, умноженному на 0.5 , т.е. 0.25.

Соответственно, вероятность того, что выборочные средние девяти последующих выборок (или серия из 9 точек контрольной карты) окажется с одной стороны от центральной линии, составит 0.59 = .00195. Заметим, что это значение приблизительно равно вероятности того, что отдельное выборочное среднее значение не попадет в интервал, ограниченный контрольными пределами в 3 сигма (при условии нормального распределения выборочных средних и нормальности производственного процесса). Поэтому, в качестве еще одного индикатора разладки производственного процесса можно рассматривать ситуацию, когда девять последовательных выборочных средних находятся с одной стороны от центральной линии. Со статистической интерпретацией других, более сложных критериев можно ознакомиться в работе Duncan (1974).

Зоны A, B, C. Обычно для задания критериев поиска серий область контрольной карты над центральной линией и под ней делится на три "зоны".

По умолчанию, зона А определяется как область, расположенная на расстоянии от 2 до 3 сигма по обе стороны от центральной линии. Зона В определяется как область, отстоящая от центральной линии на расстояние от 1 до 2 сигма, а зона С - как область, расположенная между центральной линией по обе ее стороны и ограниченная прямой, проведенной на расстоянии одной сигма от центральной линии.

9 точек в зоне С или за ее пределами (с одной стороны от центральной линии). Если этот критерий выполняется (т.е. если на контрольной карте обнаружено такое расположение точек), то делается вывод о возможном изменении среднего значения процесса в целом. Заметим, что здесь делается предположение о симметричности распределения исследуемых характеристик качества вокруг среднего значения процесса на графике. Но это условие не выполняется, например, для R-карт, S-карт и большинства карт по альтернативному признаку. Тем не менее, данный критерий полезен для того, чтобы указать занимающемуся контролем качества инженеру на присутствие потенциальных трендов процесса. Например, здесь стоит обратить внимание на последовательные выборочные значения с изменчивостью ниже среднего, так как с их помощью можно догадаться, каким образом снизить вариацию процесса.

6 точек монотонного роста или снижения, расположенные подряд. Выполнение этого критерия сигнализирует о сдвиге среднего значения процесса. Часто такой сдвиг обусловлен изнашиванием инструмента, ухудшением технического обслуживания оборудования, повышением квалификации рабочего и т.п. (Nelson, 1985).

14 точек подряд в "шахматном" порядке (через одну над и под центральной линией). Если этот критерий выполняется, то это указывает на действие двух систематически изменяющихся причин, которое приводит к получению различных результатов. Например, в данном случае может иметь место использование двух альтернативных поставщиков продукции или отслеживание двух различных альтернативных воздействий.

2 из 3-х расположенных подряд точек попадают в зону A или выходят за ее пределы. Этот критерий служит "ранним предупреждением" о начинающейся разладке процесса. Заметим, что для данного критерия вероятность получения ошибочного решения (критерий выполняется, однако процесс находится в нормальном режиме) в случае Х-карт составляет приблизительно 2 %.

4 из 5-ти расположенных подряд точек попадают в зону B или за ее пределы. Как и предыдущий, этот критерий может рассматриваться в качестве индикатора - "раннего предупреждения" о возможной разладке процесса. Процент принятия ошибочного решения о наличии разладки процесса для этого критерия также находится на уровне около 2%.

15 точек подряд попадают в зону C (по обе стороны от центральной линии). Выполнение этого критерия указывает на более низкую изменчивость по сравнению с ожидаемой (на основании выбранных контрольных пределов).

8 точек подряд попадают в зоны B, A или выходят за контрольные пределы, по обе стороны от центральной линии (без попадания в зону C). Выполнение этого критерия служит свидетельством того, что различные выборки подвержены влиянию различных факторов, в результате чего выборочные средние значения оказываются распределенными по бимодальному закону. Такая ситуация может сложиться, например, когда отмечаемые на Х-карте выборки изделий были произведены двумя различными станками, один из которых производит изделия со значением контролируемой характеристики выше среднего, а другой - ниже.

Операционные характеристики (ОХ - кривые)

Стандартные карты контроля качества обычно дополняются графиком, который носит название операционная характеристика (ОХ-кривая). При использовании стандартных контрольных карт для непрерывных переменных или для дискретных переменных возникает вопрос: насколько чувствительна используемая процедура контроля качества?   Точнее говоря, какова вероятность не обнаружить выборочную точку анализируемой характеристики (например, среднего значения на Х-карте) вне контрольных пределов (т.е. посчитать процесс производства текущим "в нормальном режиме"), когда, на самом деле, произошел сдвиг процесса на некоторую величину? Обычно эту вероятность называют вероятностью бета-ошибки ( ). Таким образом, - это вероятность ошибочно принять, что процесс (его характеристики - среднее значение, средняя процентная доля, средняя частота обнаружения дефектов и т.д.) находится в нормальном режиме. Необходимо отметить, что понятие операционной характеристики относится к вероятностям принятия ошибочного решения только для критериев, связанных с выходом выборочной точки за контрольные пределы, а не для рассмотренных выше критериев серий.

Кривые операционных характеристик оказываются исключительно полезным средством при оценивании мощности применяемой процедуры контроля качества. На практике решение об установлении объема контрольных выборок должно опираться не только на стоимость выполнения контрольной операции (т.е. на расходы в расчете на одно включенное в выборку изделие), но также на затраты, которые повлечет за собой не обнаруженное ухудшение качества. С помощью ОХ-кривых инженер может оценить вероятности необнаружения отклонений качества контролируемой продукции на определенную величину.

Индексы пригодности процесса

В случае контрольных карт для непрерывных переменных часто возникает необходимость включить в итоговый вывод результатов анализа так называемые индексы пригодности процесса. Коротко говоря, индексы пригодности процесса выражают (в виде отношения), какая часть деталей или изделий, производимых в рамках текущего производственного процесса, по своим характеристикам попадает в определенные технологами пределы (в частности, в инженерные допуски).

К примеру, так называемый индекс Cp находится следующим образом:

Cp = (ВГС-НГС)/(6*сигма)

где сигма представляет собой оценку стандартного отклонения процесса, ВГС и НГС - соответственно верхнюю и нижнюю границы плановой спецификации (инженерные допуски). Если распределение контролируемой характеристики качества или переменной (например, размер поршневых колец) подчиняется нормальному закону, и процесс абсолютно точно центрирован (т.е. среднее значение процесса соответствует положению центральной линии на контрольной карте), то данный индекс может интерпретироваться как та часть стандартной кривой нормального распределения (ширина процесса), которая находится внутри границ инженерных допусков. В случае нецентрированного процесса, вместо рассмотренного выше индекса используется уточненный индекс Cpk . Для "пригодного" процесса индекс Cp должен быть больше 1. Это означает, что для того, чтобы можно было ожидать попадание более 99% всех выпущенных деталей или изделий в рамки приемлемых инженерных спецификаций, величина интервала между контрольными пределами плановых спецификаций должна превышать 6 сигма. Более подробно обсуждение этого и других индексов приводится в модуле Анализ процессов.

Другие специализированные типы контрольных карт

Далее рассматривается ряд других наиболее широко используемых методов и соответствующих им типов контрольных карт - "рабочих лошадок" контроля качества. Однако, с приходом недорогих персональных компьютеров, все большую популярность приобретают процедуры, требующие проведения большего объема вычислений.

X-карты для данных с негауссовским распределением. Контрольные пределы для стандартных X-карт вычисляются, исходя из предположения о приблизительно нормальном распределении выборочных средних. Следовательно, для отдельных наблюдений в выборках нормальность распределения не обязательна, так как. по мере увеличения объема выборок распределение выборочных средних будет приближаться к нормальному (см. обсуждение центральной предельной теоремы в разделе Элементарные понятия статистики. Однако необходимо отметить, что при построении R-карты, S-карты и S**2-карты предполагается, что отдельные наблюдения обладают нормальным распределением). В монографии Шуарта (Shewhart, 1931) автор экспериментирует с различными негауссовскими распределениями отдельных наблюдений и оценивает полученные в результате распределения средних для выборок объема 4. В результате было обнаружено, что, на самом деле, до тех пор, пока распределение отдельных наблюдений в выборках является приблизительно нормальным, можно применять вычисленные на основе нормального распределения стандартные контрольные пределы. Введение в данный вопрос и обсуждение предположений о распределении данных при контроле качества путем построения контрольных карт можно найти в работе Hoyer and Ellis, 1996.

Однако, как отмечено в работе Ryan (1989), при малых объемах выборок и сильной асимметрии распределения наблюдений, построенные по таким данным стандартные контрольные пределы приводят как к получению большого числа ложных сигналов тревоги (т.е. росту вероятности альфа-ошибки), так и увеличению числа случаев, когда при фактически произошедшей разладке процесс продолжает считаться контролируемым (росту вероятности бета-ошибки). В программе STATISTICA существует возможность расчета контрольных пределов для X-карт (а также индексов пригодности процесса) на основе так называемых  кривых Джонсона  (Johnson, 1949), с помощью которых аппроксимируется асимметрия   и  эксцесс  большой группы негауссовских распределений (см. также раздел  Подгонка распределений  в модуле  Анализ процессов). Негауссовские X-карты рекомендуется применять в том случае, когда распределение выборочных средних обладает явной асимметрией или является негауссовским. 

Контрольная карта T**2 Хотеллинга. Когда исследуется несколько взаимосвязанных характеристик качества (заданных в виде нескольких переменных), для всех средних значений можно построить общий график, воспользовавшись для этого многомерной статистикой Хотеллинга T**2 (впервые предложена в работе Hotelling, 1947).

Контрольная карта накопленных сумм (CUSUM-карта). Контрольная карта типа CUSUM была впервые предложена в работе Page (1954). Обсуждение использующихся при ее построении математических принципов можно найти в работах Ewan (1963), Johnson (1961), а также Johnson and Leone (1962).

Если строить график накопленной суммы отклонений от плановых спецификаций для следующих друг за другом выборочных средних, то даже малые постоянные сдвиги среднего значения процесса постепенно приведут к накоплению ощутимой суммы отклонений. Поэтому данный тип контрольных карт особенно хорошо подходит для обнаружения малых постоянных сдвигов процесса, которые могут оказаться незамеченными при применении Х-карты. Например, когда из-за износа оборудования процесс медленно "выскальзывает" из-под контроля, в результате чего размеры изделий превышают плановые спецификации (или становятся ниже их), при применении контрольной карты данного типа будет получен монотонно растущий (или снижающийся) график накопленной суммы отклонений от плановых спецификаций.

Для установления контрольных пределов в CUSUM-картах в работе Barnhard (1959) было предложено использовать так называемую V-маску, которая наносится на график после построения точки для последней выборки (самой правой точки на графике). Можно считать, что V-маска представляет собой верхний и нижний контрольный пределы для накопленных сумм. Однако, вместо того, чтобы быть параллельными центральной линии, эти прямые сходятся под определенным углом вправо, образуя в результате фигуру, похожую на лежащую букву V. Если график накопленной суммы пересекает любую из линий маски, то процесс считается вышедшим из-под контроля.

Контрольная карта скользящего среднего (MA-карта). Возвращаясь к примеру с размером поршневых колец, предположим, что наибольший интерес для инженера по контролю качества представляет обнаружение малых трендов последовательных выборочных средних. Например, необходимо обнаружить износ оборудования, который приводит к медленному, но постоянному ухудшению качества (т.е. отклонению размеров изделий от требований плановой спецификации. Одним из способов отслеживания таких трендов и обнаружения незначительных постоянных сдвигов среднего значения процесса является построение описанной выше CUSUM-карты. Другой способ состоит в использовании одной из схем установления весов данных, согласно которой осуществляется суммирование нескольких средних. При движении такого взвешенного среднего вдоль выборочных точек получается контрольная карта скользящего среднего, приведення на следующем рисунке.

Контрольная карта экспоненциально взвешенного скользящего среднего (EWMA-карта). Идея построения скользящих средних для последовательных (соседних) выборочных значений может быть обобщена. В принципе, чтобы обнаружить тренд, необходимо присвоить веса следующим друг за другом выборочным значениям, получив таким образом скользящее среднее. Однако, вместо простого арифметического скользящего среднего, можно найти геометрическое скользящее среднее (соответствующая контрольная карта показана на следующем рисунке и называется картой геометрического скользящего среднего, см. работу Montgomery,1985, 1991).

В частности, можно рассчитать значения для каждой точки графика по следующей формуле:

zt = *x-ср.t + (1-)*zt-1

В данной формуле значение каждой точки  zt  рассчитывается как произведение  (лямбда) и соответствующего среднего значения x-ср.t, плюс единица минус  , умноженная на рассчитанное ранее усредненное значение для предыдущей точки графика. Параметр  (лямбда) принимает значения в интервале от  0 до 1.  Не вдаваясь в подробности (см. Montgomery, 1985, стр. 239), можно отметить, что данный метод усреднения предполагает, что вес исторически "старых" выборочных средних уменьшается по геометрическому закону при присоединении новых выборочных средних. Интерпретация контрольной карты данного типа имеет много общего с интерпретацией карты скользящего среднего. EWMA-карта позволяет обнаружить малые сдвиги исследуемых средних значений и, следовательно, ухудшение качества производственного процесса.

Регрессионные контрольные карты. Иногда может понадобиться обнаружить взаимосвязь между двумя различными параметрами производственного процесса. Например, руководство почтовой организации может захотеть узнать, сколько человеко-часов тратится на обработку некоторого объема корреспонденции. Эти две анализируемые переменные должны быть приблизительно линейно связаны друг с другом. Тогда эту взаимосвязь можно описать с помощью широко известного коэффициента корреляции Пирсона r. Описание свойств этой статистки можно найти в разделе Основные статистики. На регрессионной контрольной карте строится линия регрессии, которая выражает линейную взаимосвязь между двумя рассматриваемыми переменными. На карту также наносятся точки данных для всех наблюдений. Вокруг линии регрессии строится доверительный интервал, в который должна попадать определенная доля выборки (например, 95%). Присутствие выбросов на этом графике будет свидетельствовать о том, что для некоторых выборок не соблюдается общая тенденция взаимосвязи, которая характерна для рассматриваемых переменных.

Применения. Для регрессионных контрольных карт существует множество областей применения. Так, например, профессиональные аудиторы могут с помощью карт данного типа обнаружить, у каких розничных торговцев число наличных трансакций превышает ожидаемое для данного уровня общего объема продаж или выделить те бакалейные магазины, в которых для существующего уровня продаж число погашенных купонов, дающих покупателю право на премию из ассортимента магазина при накоплении определенного числа купонов, превышает ожидаемое. В обоих случаях выбросы на регрессионных контрольных картах (т.е. слишком большое число наличных платежей, слишком большой объем погашенных купонов) могут привлечь к себе внимание и служить основанием для более тщательной проверки.

Контрольные карты Парето. На практике оказывается, что равномерное распределение нарушения качества на различных стадиях производственного процесса или на различных предприятиях, выпускающих продукт, встречается довольно редко. Скорее, причиной большинства проблем является наличие лишь нескольких "паршивых овец в стаде". Данный принцип стал широко известен под названием принципа Парето и утверждает, что потери качества столь "плохо" распределены, что малое число возможных причин его ухудшения отвечает за большинство возникающих проблем. К примеру, вполне возможно, что в основном загрязнение воздуха возникает из-за относительно небольшого числа "грязных" автомобилей. Или, в большинстве компаний основное число убытков является следствием неудачи с одним или двумя выпускаемыми продуктами. Для выявления "паршивых овец в стаде" строят контрольные карты Парето.

Они представляют собой  гистограммы, на которых показано распределение потерь от ухудшения качества (например, в долларах) по некоторым категориям. Обычно категории - причины потери качества - приводятся в нисходящем порядке значимости (по частоте возникновения, стоимости в долларах и т.д.). Очень часто карта Парето помогает определить, на что направить усилия по улучшению качества продукта.

Все права на материалы электронного учебника принадлежат компании StatSoft

statsoft.ru

Пример построения контрольной карты Шухарта в Excel

В настоящей заметке представлены удобные шаблоны в Excel для построения контрольных карт Шухарта. Если эта тема для вас новая, предлагаю начать с книги Д. Уилер, Д. Чамберс. Статистическое управление процессами. Существует много видов контрольных карт (см., например, ГОСТ Р 50779.42-99. Статистические методы. Контрольные карты Шухарта). Но основных – два: карта средних и индивидуальных значений. Если контролируемый процесс устроен так, что некоторые значения образуют естественные группы, то рекомендуется использовать контрольную карту средних. Исходные данные следует собрать в группы, рассчитав для каждой из них среднее значение и размах (размах – разность между максимальным и минимальным значением в группе; рис. 1).

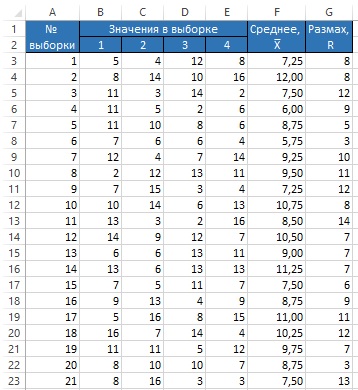
Рис. 1. Исходные данные для построения карты среднего и размаха

Скачать заметку в формате Word или pdf, примеры в формате Excel

Рекомендуется накопить 20–30 средних значений, и уже по ним строить карту. Карта среднего и размаха содержит два графика (рис. 2), на верхнем – карта среднего, на нижнем – карта размаха. На карте среднего отображают средние значения отдельных групп, а также три линии: центральную (среднее средних) и две контрольные границы – верхнюю и нижнюю. Если расчетное значение для нижней границы меньше нуля, эту границу, либо не наносят на карту, либо проводят на отметке ноль. На карте размаха, присутствуют аналогичные данные. Нижняя контрольная граница, как правило отсутствует.

Границы рассчитывают по следующим формулам:UCLX̅ = X̿ + A2R̅ – верхняя граница карты средних;CLX̅ = X̿ – центральная линия карты средних;LCLX̅ = X̿ – A2R̅ – нижняя граница карты средних;UCLR = D4R̅ – верхняя граница карты размахов;CLR = R̅ – центральная линия карты размахов;LCLR = D3R̅ – нижняя граница карты размахов.

Здесь Х̅ – среднее значение в одной выборке, X̿ – среднее по нескольким значениям средних Х̅, R̅ – среднее по размахам в нескольких выборках, A2, D3, D4 – коэффициенты, зависящие от размера выборок n (рис. 3). При построении карты на рис. 2 использованы 30 первых значений.

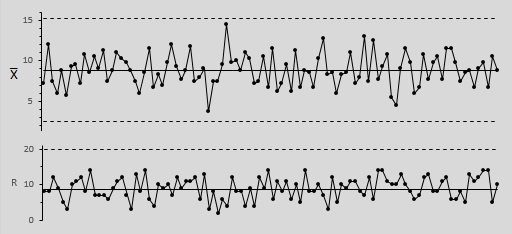
Рис. 2. Карта среднего и размаха; значение D3 для n = 4 отсутствует, поэтому нижней границы на карте размаха нет

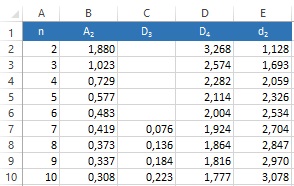
Рис. 3. Константы для контрольных карт среднего и размаха (A2, D3, D4) и индивидуальных значений (d2)

Если данные образуют некий ряд, не подлежащий группировке, применяются карты индивидуальных значений и скользящего размаха. Они получили название XmR-карт. Скользящий размах есть модуль разности последовательных значений (рис. 4; использованы данные из столбца В на рис. 1).

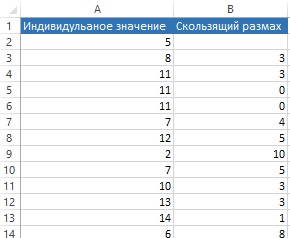
Рис. 4. Исходные данные для построения XmR-карты

Для XmR-карты границы рассчитывают по следующим формулам:

нижняя граница карты размахов отсутствует.

Здесь 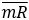 – средний скользящий размах, а значения коэффициентов d2 и D4 берутся для n = 2 (см рис. 3). Почему так? Потому что карта скользящего размаха фактически использует группы из двух последовательных измерений для вычисления размаха. Для расчета всех линий использованы первые 30 значений.

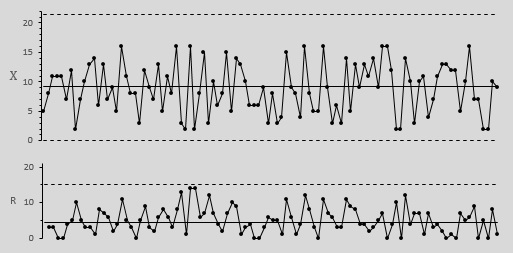
Рис. 5. XmR-карта индивидуальных значений и скользящего размаха

Если сравнить карту средних (рис. 2) и индивидуальных значений (рис. 5), видно, что последняя обладает большей волатильностью, и диапазон между нижней и верхней контрольными границами шире. Это не удивительно, так как на карте средних используется усреднение по четырем значениям. Если выполнить усреднение по еще большему числу значений, границы станут еще ближе.

Важным моментом при построении контрольных карт является использование двух статистик: средних и размахов. Часто используемый неверный способ расчета контрольных границ заключается в том, что используется лишь одна статистика. Например, при построении карты как на рис. 5, использовались бы только индивидуальные значения и их дисперсия. В этом случаев границы рассчитывались бы по следующим формулам:

Поскольку при таком подходе используется единая статистика рассеяния, карты размахов в данном случае нет. Вычисление контрольных пределов, основанное на использовании единой статистики рассеяния, приведет к неправильному результату. Подобные вычисления приводят к расширению полосы между контрольными пределами. Правильный путь вычисления контрольных пределов для карты индивидуальных значений всегда должен использовать двухточечные скользящие размахи.

Эта заметка была полностью переработана в октябре 2016 г. Оказалось, что в первоначальном варианте я предлагал неверное решение. С первоначальным вариантом, представляющим лишь исторический интерес, можно ознакомиться здесь.

Возможно вас также заинтересует:Контрольные карты Шухарта. Правила определения отсутствия управляемостиРациональная группировка данных при построении контрольной карты Шухарта

baguzin.ru

Контрольные карты

При организации любого производственного процесса возникает задача установки пределов характеристик изделия, в рамках которых произведенная продукция удовлетворяет своему предназначению. Вообще говоря, существует два "врага" качества продукции: (1) отклонения от плановых спецификаций и (2) слишком большой разброс реальных характеристик изделий (относительно плановых спецификаций). На ранних стадиях отладки производственного процесса для оптимизации этих двух показателей качества часто используются методы планирования.

Общий подход к текущему контролю качества достаточно прост. В процессе производства проводятся выборки изделий заданного объема. После этого на специально разлинованной бумаге строятся диаграммы изменчивости выборочных значений плановых спецификаций в этих выборках и рассматривается степень их близости к заданным значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или оказывается, что выборочные значения находятся вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки. Иногда такие специально разлинованные бумаги называют контрольными картами Шухарта (в честь W. A. Shewhart, который общепризнанно считается первым, применившим на практике описываемые здесь методы анализа в 1924 г).

Виды контрольный карт

по шкале измерения

• качественные
• количественные

По выборочному параметру

• среднего
• среднеквадратического отклонения
• медиана
• размах

Контрольные карты по количественным признакам(http://statmetkach.ru/lab8.html)

Контрольные карты используются для статистического контроля и регулирования технологического процесса. На контрольную карту наносят значения некоторой статистической характеристики (точки), рассчитываемые по данным выборок в порядке их получения, верхнюю и нижнюю контрольные границы Кв (или UCL) и Кн (или LCL), верхнюю и нижнюю границы технических допусков Тв и Тн (при их наличии), а также среднюю линию (CL). Иногда используют также предупредительные границы Кп. Для расчёта границ и построения контрольной карты используют обычно 20...30 точек. Пример контрольной карты представлен на рисунке 6.1.

Рис.6.1. Пример контрольной карты.

По положению точек относительно границ судят о налаженности или разлаженности технологического процесса. Обычно процесс считают разлаженным в следующих случаях:

1 Некоторые точки выходят за контрольные пределы.

2 Серия из семи точек оказывается по одну сторону от средней линии. Кроме того, если по одну сторону от средней линии находятся:

а) десять из серии в одиннадцать точек

б) двенадцать из четырнадцати точек

в) шестнадцать из двадцати точек

3  Имеется тренд (дрейф), т.е. точки образуют непрерывно повышающуюся или непрерывно понижающуюся кривую.

4 Две – три точки оказываются за предупредительными двухсигмовыми границами

5 Приближение к центральной линии. Если большинство точек находится внутри полуторасигмовых линий, это значит, что в подгруппах смешиваются данные из различных распределений

6 Имеет место периодичность, т.е. то подъём, то спад с примерно одинаковыми интервалами времени

7 Контрольные границы шире поля допуска. В идеальном случае достаточно, чтобы контрольные границы составляли ¾ величины поля допуска.

Если процесс налажен (достигнута необходимая точность и стабильность), на контрольную карту продолжают наносить точки, но через 20...30 точек пересчитывают контрольные границы. Они должны совпадать с исходными границами. Если контрольная карта показывает, что процесс разлажен, находят причины разладки и производят наладку.

Бывают контрольные карты по количественным признакам (для непрерывных значений) и по качественным признакам (для дискретных значений). По количественным признакам используют в основном следующие контрольные карты:

-карта средних арифметических значений (-карта)

-карта медиан (-карта)

-карта средних квадратичных отклонений (s-карта)

-карта размахов (R-карта)

-карта индивидуальных значений (x-карта)

Карта средних значений используется для контроля отклонения параметра от нормы и настройки на норму. Точки на контрольной карте – это средние значения небольших выборок, обычно одинакового объёма, из 3...10 элементов:

 , где n – объём выборки (подгруппы).

Для получения выборок можно также использовать результаты измерений, проводившихся через одинаковые промежутки времени, путём разбиения их на группы.

Средние значения выборок находят с одним лишним знаком по сравнению с исходными данными. Среднюю линию рассчитывают как среднее из средних значений выборок:

 , где k – число подгрупп (число точек). Обычно k = 20...30.

Контрольные границы рассчитывают по формуле

 , где  - среднее квадратичное отклонение всей совокупности данных. В этом выражении (как и при расчёте контрольных границ для других видов контрольных  карт) коэффициент 3 используется, исходя из правила трёх сигм.

Карта медиан используется вместо карты средних значений, когда хотят упростить расчёты. Точки на карте – это медианы выборок одинакового объёма из 3...10 элементов. Медиана – это при нечётном объёме выборки середина вариационного ряда, при чётном объёме выборки – среднее из двух значений середины вариационного ряда.

Средняя линия - это среднее из медиан выборок. Контрольные границы находят по формуле

Карта медиан менее точна, чем карта средних значений. При использовании для расчётов компьютера применение карты медиан вместо карты средних значений вряд ли оправдано.

Карта средних квадратичных отклонений используется для контроля рассеяния показателя. Точки на карте – средние квадратичные отклонения выборок одинакового объёма из 3...10 элементов. Средняя линия  - это среднее из СКО выборок. Контрольные границы:

         , где c2 – критерий Пирсона, n – объём выборки, a - уровень значимости. Обычно принимают a = 0,0027, что соответствует доверительной вероятности 0,9973. Часто на s-карте используют только верхнюю границу.

Карта размахов используется вместо карты средних квадратичных отклонений, когда хотят упростить расчёты. При этом карта размахов менее точна.

При построении R-карты берут 20...30 выборок одинакового объёма из 2...10 элементов. Точки ан карте – размахи выборок. Размах выборки R – это разность между максимальным xmax и минимальным xmin значениями выборки. Средняя линия  - это среднее размахов выборок. Контрольные границы рассчитывают по формулам:

При уровне значимости 0,0027 коэффициенты D3 и D4 можно найти из табл. 6.1. При n<7 нижняя контрольная граница не используется.

Таблица 6.1.

Часто при статистическом регулировании технологических процессов используют двойные карты, отражающие как отклонение параметра от нормы, так и его рассеяние. Это могут быть, например, -карты или другие.

Контрольные карты по качественным признакам

По качественным признакам (или по альтернативному признаку) различают следующие контрольные карты:

-        карта доли дефектной продукции (p-карта)

-        карта числа дефектных единиц продукции (pn-карта)

-        карта числа дефектов (c-карта)

-        карта числа дефектов на единицу продукции (u-карта)

Карта доли дефектной продукции. Применяется для контроля и регулирования технологического процесса по доле дефектных изделий в выборке. Точки на контрольной карте ставят по значениям доли дефектной продукции в выборках:

, где ni – объём i-й выборки, x – количество бракованных изделий в выборке. Выборка берётся за смену, сутки или более.

Среднюю линию рассчитывают по уравнению

, где k – число выборок. Обычно k = 20...30.

Контрольные границы находят по уравнению

Объём выборки подбирают так, чтобы в ней было в основном от 1 до 5 дефектных изделий. Если объём выборки неодинаков при каждом отборе, то контрольные границы вычисляют при каждом отборе (для каждой точки), т.е. границы в этом случае непостоянны.

Карта числа дефектных единиц продукции. Используется для контроля и регулирования технологического процесса по числу дефектных изделий в выборке. Используют выборки постоянного объёма. Объём выборки подбирают так, чтобы в ней было в основном от 1 до 5 дефектных изделий. Точки наносят на карту по количеству дефектных изделий в выборке pin. Среднюю линию рассчитывают как значение

Контрольные границы находят по уравнению , где . Если Кн<0, его не рассматривают.

Карта числа дефектов. В этих картах регистрируется число дефектов c, выявленных в установленной единице контролируемой продукции, например, в рулоне ткани или бумаги, на определённой площади пластика, стекла и т.п. Предусматривают такую единицу контролируемой продукции, чтобы она содержала в основном 1...5 дефектов.

Среднюю линию находят по уравнению

Контрольные границы 

Карта числа дефектов на единицу продукции. Используется вместо с-карты, когда параметр единицы продукции (например, площадь, длина) не является постоянной величиной, т.е объём выборки непостоянен. Точки на u-карте – это значения ui=ci/ni, где ci – число дефектов в i-й выборке. Средняя линия

Контрольные границы: . Поскольку объём выборки непостоянен, границы тоже непостоянны, и их вычисляют для каждой точки.

Разладка процесса: критерии серий

Когда точка на контрольной карте, соответствующая выборочному значению контролируемой характеристики (например, среднему значению в X-карте) оказывается вне ограниченной контрольными переделами области, это дает основания предполагать, что производственный процесс разладился. Далее, при этом необходимо отслеживать появление систематической тенденции в расположении точек (например, выборочных средних) на контрольной карте, так как наличие такой тенденции может служить свидетельством тренда среднего значения контролируемого процесса.  Эти критерии иногда называют критериями серий типа AT&T или критериями против альтернатив специального вид. Термин специальные альтернативы, как альтернатива случайным или общим причинам, был использован в работе Шухарта (Shewhart) для того, чтобы сделать разграничение между нормальным производственным процессом, вариации в котором появляются только в силу действия случайных причин, и вышедшим из-под контроля процессом , в котором вариации характеристик обусловлены некоторыми неслучайными, то есть специальными факторами (см. Montgomery, 1991, стр. 102).

Как и обсуждавшиеся ранее контрольные пределы, выраженные в единицах сигмы, критерии серий имеют в своей основе "статистическое" обоснование. Так, например, вероятность того, что любое выборочное среднее значение для X-карты окажется выше центральной линии, равна 0.5 при следующих условиях: (1) производственный процесс находится в нормальном состоянии (т.е. центральная линия проведена через значение, равное среднему контролируемой характеристики генеральной совокупности изделий), (2) средние значения следующих друг за другом выборок независимы (т.е. отсутствует автокорреляция) и (3) выборочные средние значения контролируемой характеристики распределены по нормальному закону. Проще говоря, при таких условиях для выборочного среднего значения шансы попасть выше или ниже центральной линии составляют 50 на 50. Поэтому вероятность того, что два следующих друг за другом выборочных средних окажутся выше центральной линии, будет равна 0.5, умноженному на 0.5 , т.е. 0.25.

Соответственно, вероятность того, что выборочные средние девяти последующих выборок (или серия из 9 точек контрольной карты) окажется с одной стороны от центральной линии, составит 0.59 = .00195. Заметим, что это значение приблизительно равно вероятности того, что отдельное выборочное среднее значение не попадет в интервал, ограниченный контрольными пределами в 3 сигма (при условии нормального распределения выборочных средних и нормальности производственного процесса). Поэтому, в качестве еще одного индикатора разладки производственного процесса можно рассматривать ситуацию, когда девять последовательных выборочных средних находятся с одной стороны от центральной линии.

Зоны A, B, C. Обычно для задания критериев поиска серий область контрольной карты над центральной линией и под ней делится на три "зоны".

По умолчанию, зона А определяется как область, расположенная на расстоянии от 2 до 3 сигма по обе стороны от центральной линии. Зона В определяется как область, отстоящая от центральной линии на расстояние от 1 до 2 сигма, а зона С - как область, расположенная между центральной линией по обе ее стороны и ограниченная прямой, проведенной на расстоянии одной сигма от центральной линии.

9 точек в зоне С или за ее пределами (с одной стороны от центральной линии). Если этот критерий выполняется (т.е. если на контрольной карте обнаружено такое расположение точек), то делается вывод о возможном изменении среднего значения процесса в целом. Заметим, что здесь делается предположение о симметричности распределения исследуемых характеристик качества вокруг среднего значения процесса на графике. Но это условие не выполняется, например, для R-карт, S-карт и большинства карт по альтернативному признаку. Тем не менее, данный критерий полезен для того, чтобы указать занимающемуся контролем качества инженеру на присутствие потенциальных трендов процесса. Например, здесь стоит обратить внимание на последовательные выборочные значения с изменчивостью ниже среднего, так как с их помощью можно догадаться, каким образом снизить вариацию процесса.

6 точек монотонного роста или снижения, расположенные подряд. Выполнение этого критерия сигнализирует о сдвиге среднего значения процесса. Часто такой сдвиг обусловлен изнашиванием инструмента, ухудшением технического обслуживания оборудования, повышением квалификации рабочего и т.п.

14 точек подряд в "шахматном" порядке (через одну над и под центральной линией). Если этот критерий выполняется, то это указывает на действие двух систематически изменяющихся причин, которое приводит к получению различных результатов. Например, в данном случае может иметь место использование двух альтернативных поставщиков продукции или отслеживание двух различных альтернативных воздействий.

2 из 3-х расположенных подряд точек попадают в зону A или выходят за ее пределы. Этот критерий служит "ранним предупреждением" о начинающейся разладке процесса. Заметим, что для данного критерия вероятность получения ошибочного решения (критерий выполняется, однако процесс находится в нормальном режиме) в случае Х-карт составляет приблизительно 2 %.

4 из 5-ти расположенных подряд точек попадают в зону B или за ее пределы. Как и предыдущий, этот критерий может рассматриваться в качестве индикатора - "раннего предупреждения" о возможной разладке процесса. Процент принятия ошибочного решения о наличии разладки процесса для этого критерия также находится на уровне около 2%.

15 точек подряд попадают в зону C (по обе стороны от центральной линии). Выполнение этого критерия указывает на более низкую изменчивость по сравнению с ожидаемой (на основании выбранных контрольных пределов).

8 точек подряд попадают в зоны B, A или выходят за контрольные пределы, по обе стороны от центральной линии (без попадания в зону C). Выполнение этого критерия служит свидетельством того, что различные выборки подвержены влиянию различных факторов, в результате чего выборочные средние значения оказываются распределенными по бимодальному закону. Такая ситуация может сложиться, например, когда отмечаемые на Х-карте выборки изделий были произведены двумя различными станками, один из которых производит изделия со значением контролируемой характеристики выше среднего, а другой - ниже.

yuschikev.narod.ru

Смотрите также

• 
  Контрольный журнал
• 
  Контрольных работ
• 
  Контрольное списывание
• 
  Входная контрольная
• 
  Браслеты контрольные
• 
  Контрольный кабель
• 
  Кабель контрольный
• 
  Контрольная по
• 
  Контрольный диктант
• 
  Заказать контрольную
• 
  Контрольная