ГДЗ по алгебре 9 класс контрольно-измерительные материалы Мартышова Решебник
 Решение есть!
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
- Физика
- Немецкий язык
- Украинский язык
- История
- Информатика
Контрольно измерительные материалы по алгебре, Макарычев (9 класс)
Контрольно-измерительные материалы
9 класс алгебра
Контрольная работа по теме «Функция. Квадратный трехчлен»
1 вариант
1. Дана функция f (х) = 17
f (х) =0, f (х) <0, f (х) > 0? Является ли эта функция возрастающей или убывающей?
2. Разложите на множители квадратный трехчлен:
а) х2 -14х +45; б) 3у2+7у-6.
3. Сократите дробь .
4. Область определения функции g отрезок [-2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
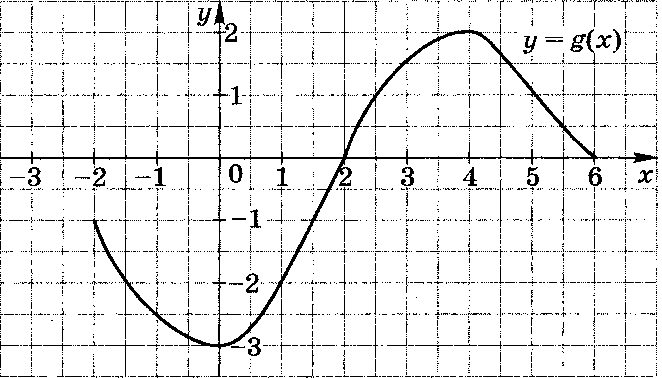
2 вариант
1. Дана функция g(х) = -13х + 65. При каких значениях аргумента g(х) = 0, g(х) <0, g(х) > 0? Является ли эта функция возрастающей или убывающей?
2. Разложите на множители квадратный трехчлен:
а) х2-10х+21; б) 5у2+9у-2.
3. Сократите дробь .
4. Область определения функции f отрезок [-5; 4]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
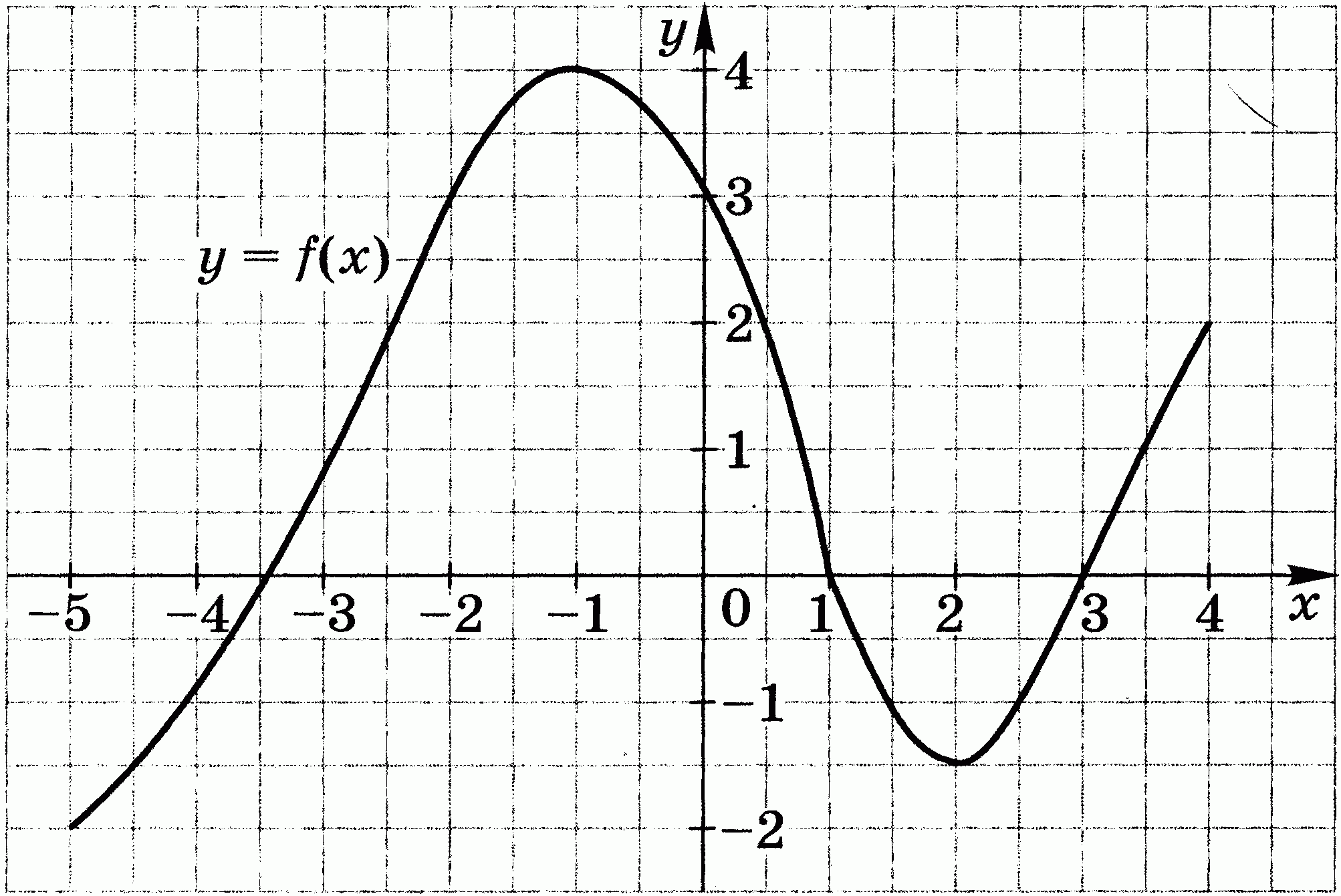
Контрольная работа по теме
«Квадратичная функция. Степенная функция»
1 вариант
1. Постройте график функции у = х2 — 6х + 5. Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = -1;
в) нули функции; промежутки, в которых у > 0 и в которых у < 0;
г) промежуток, на котором функция возрастает.
2. Изобразите схематически график функции:
а) у= — х2 +4 б) у=(х – 3)2
3. Найдите значение выражения .
4. Не выполняя построения, определите, пересекаются ли парабола у = х2и прямая у = 5х -16. Если точки пересечения существуют, то найдите их координаты.
2 вариант
1. Постройте график функции у = х2 — 8х + 12. Найдите с помощью графика:
а) значение у при х = 1,5;
б) значения х, при которых у = -2;
в) нули функции; промежутки, в которых у >0 и в которых y< 0;
г) промежуток, в котором функция убывает.
2. Изобразите схематически график функции:
а) у= х2 – 5 б) у= — (х + 1)2
3. Найдите значение выражения .
4. Не выполняя построения, определите, пересекаются ли парабола у =х2и прямая у =20-3х. Если точки пересечения существуют, то найдите их координаты.
Контрольная работа по теме
«Уравнения и неравенства с одной переменной»
1 вариант
1. Решите уравнение:
а) х3 — 81х = 0; б) х4 — 19х2 + 48 = 0; в) (х2+3х+1)(х2+3х – 9)=171.
2. Решите неравенство:
а) 2х2 — 7х – 9 < 0; б) х2> 49;
в) 1 – х > — 4х2; г) ≥0.
3. Решите уравнение
.
4. При каких значениях х имеет смысл выражение:
а) ?
2 вариант
1. Решите уравнение:
а) х3 — 64х = 0; б) х4 — 20х2 + 64 = 0; в) (х2+3х+4)(х2+3х +9)=266.
2. Решите неравенство:
а) 3х2 — 5х – 22 < 0; б) х2< 81;
в) 3х+8 < — 2х2; г) ≤0.
3. Решите уравнение
.
4. При каких значениях х имеет смысл выражение:
а) ?
Контрольная работа по теме
«Уравнения и неравенства с двумя переменными»
1 вариант
1. Решите систему уравнений:
Периметр прямоугольника равен 28 м, а его площадь равна 40 м2. Найдите стороны прямоугольника.
3. Решите графически систему уравнений:
Не выполняя построения, найдите координаты точек пересечения параболы и прямой у = 3х-4.
5. Решите систему уравнений:
2 вариант
1. Решите систему уравнений:
Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120 см2.
3. Решите графически систему уравнений:
4. Не выполняя построения, найдите координаты точек пересечения параболы и прямой у = 3х-8.
5. Решите систему уравнений:
Контрольная работа по теме «Арифметическая прогрессия»
1 вариант
Найдите двадцать шестой член арифметической прогрессии (аn), первый член которой равен 12, а разность равна — 3.
Найдите сумму тридцати восьми первых членов арифметической прогрессии (аn): 5; 12; …
Найдите первый член арифметической прогрессии (аn), если а5=64, d=0,5.
Является ли число -27 членом арифметической прогрессии (аn), в которой а1= — 4, а11= — 1,4.
Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.
2 вариант
Найдите тридцать второй член арифметической прогрессии (аn), первый член которой равен -15, а разность равна 2.
Найдите сумму сорока трех первых членов арифметической прогрессии (аn): 8; 13; …
Найдите первый член арифметической прогрессии (аn), если а6=72,
d= -2.
Является ли число -27 членом арифметической прогрессии (аn), в которой а1= 3, а11= — 5,4.
Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.
Контрольная работа по теме «Геометрическая прогрессия»
1 вариант
1. Найдите седьмой член геометрической прогрессии (bn), если b1= -32 и
q =.
2. Первый член геометрической прогрессии (bn), равен 2, а знаменатель
равен 3. Найдите сумму шести первых членов это прогрессии.
3. Найдите сумму бесконечной геометрической прогрессии: 24; -12; 6; ….
4. Найдите шестой член геометрической прогрессии (bn), если известно, что
5. Между числами -2 и -32 вставьте три числа так, чтобы получилась геометрическая прогрессия.
2 вариант
1. Найдите шестой член геометрической прогрессии (bn), если b1= 81и
q= — .
2. Первый член геометрической прогрессии (bn), равен 6, а знаменатель
равен 2. Найдите сумму семи первых членов это прогрессии.
3. Найдите сумму бесконечной геометрической прогрессии: -40; 20; -10; … .
4. Найдите шестой член геометрической прогрессии (bn), если известно, что
5. Между числами 1 и 64 вставьте пять чисел так, чтобы получилась геометрическая прогрессия.
Контрольная работа по теме
«Элементы комбинаторики и теории вероятности»
1 вариант
1. Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах.
2. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?
3. Победителю конкурса книголюбов разрешается выбрать две книги из 10 различных книг. Сколькими способами он может осуществить этот выбор?
4. В доме 90 квартир, которые распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира на первом этаже, если таких квартир 6?
5. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?
6. На четырех карточках записаны цифры 1, 3, 5, 7. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число 3157?
2 вариант
1. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 9 без повторений цифр?
2. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде. Сколькими способами можно сделать этот выбор?
3. Из 15 туристов надо выбрать дежурного и его помощника. Какими способами это можно сделать?
4. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?
5. Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала. Сколькими способами можно сделать этот выбор?
6. На пяти карточках написаны буквы а, в, и, л, с. Карточки перевернули и перемешали. Затем наугад последовательно эти карточки положили в ряд и открыли. Какова вероятность того, что в результате получится слово «слива»?
ГДЗ: Алгебра 8 класс Черноруцкий

Алгебра 8 класс
Тип: КИМ
Авторы: Черноруцкий
Издательство: Вако
Контрольно-измерительные материалы по алгебре под редакцией Черноруцкого – это пособие с тематически сгруппированными тестами. Каждое задание соответствует требованиям школьной программы. По своей структуре КИМ похожи на ЕГЭ, поэтому учителя часто используют их для подготовки к экзаменам. Каждый тест дается в нескольких вариантах, что позволяет адекватно оценить каждого школьника.
Система оценивания
КИМы по алгебре содержат следующие уровни:
- Уровень А (базовый). Состоит из 4-5 номеров с вариантами ответов. Ученики должны обвести правильный.
- Уровень Б (достаточный). Состоит из 2 упражнений на которые нужно дать краткий ответ.
- Уровень С (высокий). Состоит из 2 вопросов, на которые нужно дать развернутый ответ.
Итоговая контрольная работа построена другим образом. Здесь содержится больше номеров. Задания построены таким образом, что позволяют определить реальный уровень знаний учащихся.
Тематика тестов
В 8 классе по алгебре рассматриваются темы, связанные со свойствами дробей, возведением их в степень, функциями, рациональными и иррациональными числами и прочее. Для того чтобы проверить свои знания и подготовиться к уроку заранее, воспользуйтесь «ГДЗ по Алгебре 8 класс КИМ Черноруцкий ВАКО». В пособии содержатся ответы на все тесты. Выберите страницу и номер работы и сверьтесь с решением. Структура решебника полностью соответствует структуре КИМ. Нумерация совпадает, поэтому вы без труда найдете необходимый номер.
Наше предложение
На нашем сайте размещена онлайн-версия решебника. Используя ее для проверки, вы научитесь правильно совершать действия с цифрами, решать квадратные уравнения и осуществлять действия над ними. Пользуйтесь ГДЗ с компьютера и мобильного телефона. Издание направлено на школьников, учителей и родителей.
ГДЗ по алгебре 9 класс контрольно-измерительные материалы Мартышова Л.И.
«ГДЗ по алгебре 9 класс контрольно-измерительные материалы Мартышова (ВАКО)» сильно упростит жизнь ребят. Им не придётся часами сидеть за учебниками. Ведь так хочется веселиться с друзьями, гулять, кататься на велосипеде, дыша свежим вечерним воздухом.
Зачем школьникам предмет
От учителей часто слышна фраза: «Математика — царица всех наук». Но никогда дети не воспринимают её всерьёз. Это же такой скучный и сложный предмет. Дети сильно ошибаются, алгебра открывает для них много возможностей. С ней сейчас связано большинство важных, интересных и денежных профессий. Среди них:
- экономист;
- инженер;
- программист;
- работник банка.
Также счёт примеров и решение задач стимулируют развитие мышления и логики. Людям с такими навыками намного проще жить, даже если они не получили высшего образования. Будущим хозяевам и хозяйкам придётся вести семейный бюджет, ходить за покупками, строить себе дом или делать ремонт. Всё требует расчётов и решений. Так что, пока есть время, нужно быстрее бежать грызть гранит науки. Поможет в этом наш любимый и верный онлайн-решебник.
Что даёт ГДЗ
Пусть родители не думают, что это просто источник ответов, откуда можно быстренько списать все домашнее задание. Это многофункциональный помощник, после использование которого в дневнике будут красоваться одни пятёрки, а вся стена будет завешана грамотами и благодарностями. Заходя на сайт, дети могут:
- проверить своё решение;
- узнать новую информацию и поделиться ею с одноклассниками;
- научиться грамотно оформлять работу.
Кроме того, часто бывают ситуации, когда преподаватель намерено занижает ребёнку оценки за задания. Докажет правоту ученика решебник.
Структура и плюсы решебника по алгебре за 9 класс от Мартышовой
Открыв портал, дети приятно удивятся простоте его устройства. Вначале страницы находится поисковая строка, позволяющая без проблем найти что-либо. После представлено изображение пособия и необходимая о нём информация. Дальше идут готовые верные ответы к 25 тестам с 2 вариантами, помимо которых есть 10 контрольных работ, включая итоговую. Кроме удобной организации, «ГДЗ по алгебре 9 класс контрольно-измерительные материалы Л.И. Мартышова (ВАКО)» имеет много других достоинств. Во-впервых, на сайте представлены сканы всей тетради. Во-вторых, он мобилен в работе, без проблем переходит с одного номера на другой. В-третьих, ресурс наполнен десятками разных сборников и практикумов.
ГДЗ по алгебре 7 класс контрольно-измерительные материалы Мартышова Л.И.
В седьмом классе в расписании школьников появляются два незнакомых предмета – алгебра и геометрия. Успешно освоить программу новой дисциплины и научиться решать тематические примеры и задачи учащимся поможет «ГДЗ по Алгебре 7 класс КИМ Мартышова (ВАКО)».
Чему научит решебник
Учащиеся средней и старшей школы с каждым годом начинают использовать все больше учебно-методических пособий, чтобы добиваться высоких результатов на уроках. В контексте изучения математики особое место занимает сборник контрольно-измерительных материалов Мартышовой. В нем содержатся задания по всем темам курса, а именно:
- выражения с переменными;
- квадратичная и кубическая функции;
- арифметические действия с многочленами;
- разложение на множители;
- системы линейных уравнений с двумя переменными и др.
Подробно изучить алгоритмы решения типовых уравнений и задач ученикам поможет онлайн-сборник готовых домашних заданий к озвученному пособию.
Структура онлайн-решебника
«ГДЗ по Алгебре 7 класс КИМ Мартышова Л.И. (ВАКО)» станет отличной возможностью для семиклассников подготовиться к аттестационным работам по всем темам учебной программы. В нем ребята найдут:
- 23 тестовых блока;
- 19 самостоятельных работ;
- 10 контрольных работ, включая итоговую;
- готовые подробные решения;
- верные ответы для каждого номера.
Все перечисленные материалы ученики смогут найти на нашем сайте в режиме онлайн. Чтобы сократить время на поиск нужного варианта, решебник оснастили удобной навигацией по тематическим блокам и номерам работ. Таким образом, учащиеся смогут эффективно потренироваться в выполнении типовых упражнений, не затрачивая на это большого количества свободного времени.
Принцип работы с онлайн-решебником по алгебре за 7 класс от Мартышовой
Семиклассники могут как регулярно выполнять практические задания, так и непосредственно перед грядущим контрольным срезом. В любом случае методика работы с пособием включает в себя:
- самостоятельное выполнение работы;
- проверку собственных решений с помощью образцов из сборника;
- выявление ошибок и слабых мест;
- повторение материала, вызывающего затруднения;
- грамотное оформление правильного ответа.
Описанная практика помогает наилучшим образом ликвидировать имеющиеся пробелы в знаниях, а также повысить уверенность в собственных навыках перед сдачей аттестационных работ.
Решебник контрольно-измерительные материалы по Алгебре за 10 класс Рурукин А.Н. на Гитем ми
ГДЗ 10 класс Алгебра контрольно-измерительные материалы Рурукинавтор: Рурукин А.Н..
Данное пособие содержит решебник (ГДЗ) контрольно-измерительные материалы по Алгебре за 10 класс . Автора: Рурукин А.Н. Издательство: ВАКО. Полные и подробные ответы к упражнениям на Гитем
Тест 1. Варианты
1 2Тест 2. Варианты
1 2Тест 3. Варианты
1 2Тест 4. Варианты
1 2Тест 5. Варианты
1 2Тест 6. Варианты
1 2Тест 7. Варианты
1 2Тест 8. Варианты
1 2Тест 9. Варианты
1 2Тест 10. Варианты
1 2Тест 11. Варианты
1 2Тест 12. Варианты
1 2Тест 13. Варианты
1 2Тест 14. Варианты
1 2Тест 15. Варианты
1 2Тест 16. Варианты
1 2Тест 17. Варианты
1 2Тест 18. Варианты
1 2Тест 19. Варианты
1 2Тест 20. Варианты
1 2Тест 21. Варианты
1 2Тест 22. Варианты
1 2Тест 23. Варианты
1 2Тест 24. Варианты
1 2Тест 25. Варианты
1 2Тест 26. Варианты
1 2Тест 27. Варианты
1 2Самостоятельные работы
СР-1. Варианты
1 2СР-2. Варианты
1 2СР-3. Варианты
1 2СР-4. Варианты
1 2СР-5. Варианты
1 2СР-6. Варианты
1 2СР-7. Варианты
1 2СР-8. Варианты
1 2СР-9. Варианты
1 2СР-10. Варианты
1 2СР-11. Варианты
1 2СР-12. Варианты
1Как выучить высшую математику, не отправляясь в университет — Часть 3
В первой и второй статьях этой серии мы рассмотрели курсы, которые читаются в первой половине четырехлетнего курса бакалавриата по математике, и способы их изучения. модули самостоятельно.
В первый год мы обсудили основы — линейную алгебру, обыкновенные дифференциальные уравнения, вещественный анализ и теории вероятностей. На втором курсе мы опирались на эти основы, изучая метрические пространства, интеграл Римана, теорию групп и исчисление на векторных пространствах.
На третьем году четырехлетнего курса магистратуры, особенно курса с прикладной направленностью, который будет интересен квантам, нам нужно начать думать о более абстрактных концепциях, которые подготовят нас к изучению стохастического исчисления, вероятностной машины. Обучение и байесовская эконометрика.
Имея это в виду, важно, чтобы мы изучали такие темы, как теория меры и линейный функциональный анализ.
Оба этих курса содержат идеи, лежащие в основе теории вероятностей, анализа временных рядов и некоторых аспектов машинного обучения.Теория меры учит нас обобщению интеграла Римана до интеграла Лебега, в то время как линейный функциональный анализ обсуждает функциональные пространства, многие из которых необходимы для решения определенных дифференциальных уравнений с частными производными.
На этом уровне доступно меньше видеолекций, так как содержание становится довольно сложным. Однако до сих пор существует множество доступных учебников и конспектов лекций, многие из которых содержат вопросы и решения для проверки ваших знаний.2 + bx + c = 0 $.
Множество таких комплексных чисел обозначается $ \ mathbb {C} $. Одним из ключевых результатов комплексного анализа является Фундаментальная теорема алгебры, которая утверждает, что каждый комплексный многочлен или порядок $ n $ с коэффициентами в $ \ mathbb {C} $ содержит $ n $ корней внутри $ \ mathbb {C} $.
Комплексный анализ связан с концепциями последовательностей, серий, дифференцирования и интеграции, как и в реальном анализе. Однако тот факт, что $ \ mathbb {C} $ двумерен (каждый элемент $ z \ in \ mathbb {C} $ имеет «Реальный» и «Мнимый» компоненты) и имеет другую геометрию по сравнению с $ \ mathbb { R} $ означает, что некоторые известные результаты не совсем совпадают.п $. Однако это очень применимый предмет в различных областях, включая квантовую механику (уравнение Шредингера), гидродинамику (через конформные отображения) и электротехнику (анализ сигналов / преобразование Фурье, теорию управления и т. Д.).
В частности, для приложений количественной торговли анализ сигналов является значительной частью некоторых фондов (например, Renaissance Technology — это часто цитируемый пример!), И поэтому хорошее понимание того, как ведут себя комплексные числа, поможет вам понять инструменты, которые вы используете в гораздо более структурированный способ.
Учебные материалы
Я изучил комплексный анализ в основном из конспектов лекций в университете, а также из текстов курса Яна Стюарта и Дэвида Толла.
Книга Джона Хауи из серии Springer по математике для студентов бакалавриата (SUMS) также отлично подходит для самостоятельного изучения и написана на более простом уровне (возможно, для студентов второго курса бакалавриата).
Отличным дополнением к более «алгебраическим» подходам является геометрический подход Тристана Нидхэма в его книге «Визуальный комплексный анализ».Я сам склонен лучше понимать концепции, когда вижу их визуально, и эта книга действительно помогла мне понять основные концепции, особенно касающиеся сложных различий.
Если вы предпочитаете учиться с помощью конспектов лекций или видеокурсов, Coursera и MIT предлагают бесплатные альтернативы в формате MOOC:
Топология
Топология — это предмет изучения математики, который пытается определить конкретные свойства абстрактных пространств, которые сохраняются при непрерывных преобразованиях.«Непрерывный» аспект этих преобразований означает, что рассматриваются только такие понятия, как «растяжение» или «изгиб». Если отверстия разорваны или части «склеены», это не считается топологическими преобразованиями.
В старой математической шутке рассказывается о топологе, который не может отличить чайную чашку от пончика (пончик для тех, кто в США!), Поскольку оба имеют одно отверстие (отверстие в пончике и отверстие в ручке чашки). .
Основными предметами изучения являются топологические пространства, непрерывные преобразования между ними (гомеоморфизмы и диффеоморфизмы), а также понятия компактности и связности.
Элементарная топология ведет к некоторым увлекательным областям математики, включая дифференциальную топологию и алгебраическую топологию. Первый касается изучения многообразий и дифференциальной геометрии — глубокой области математики, имеющей тесную связь с теоретической физикой. Последний использует абстрактные алгебраические инструменты в попытке классифицировать топологические пространства через определение инвариантов.
По общему признанию, топология не является предметом, который легко допускает прямое отношение к методам количественного финансирования.Однако нельзя сказать, что это бесполезно. В частности, стартап, известный как Ayasdi, напрямую использует топологические методы для определения режима.
Следовательно, если вы хотите быть одним из лучших квантов и работать над самыми передовыми проблемами, как с другими более абстрактными областями математики, представленными в этой серии статей, это действительно помогает узнать как можно больше, поскольку это часто бывает изначально. неясно, как в конечном итоге могут быть применены некоторые области математики.
Учебные материалы
Я изучил вводную топологию из лекций, прочитанных в Университете Уорика, когда я был студентом. Основной учебник курса написан Сазерлендом (см. Ниже). Это отличная книга, которая плавно переходит от реального анализа к метрическим пространствам и полностью абстрактным топологическим концепциям.
Однако позже я решил небрежно прочитать некоторые вводные топологические концепции, чтобы заново ознакомиться с этой областью, и решил попробовать книгу Кроссли Springer Undergraduate Mathematics Series.Возможно, это лучше для самостоятельного изучения. Он идет довольно далеко, охватывая гомотопию, а также сингулярные и симплициальные гомологии.
К сожалению, топология — непростая тема для поиска видеолекций, поэтому основной путь к ее изучению — через самоизучение из учебников. При этом, учитывая, что это не часто является предпосылкой для количественных финансов, его можно легко «пропустить», если ваша единственная цель — изучить математику, достаточную для того, чтобы быть количественным.
Теория колец
На первом и втором году обучения в традиционной бакалавриате обычным делом является углубленное изучение абстрактной алгебраической концепции группы.Группы имеют огромное количество математических и физических приложений и являются одной из самых фундаментальных математических структур.
Кольцо, однако, похоже на группу, за исключением того, что это не просто набор с одной связанной операцией с двоичным набором, а набор с двумя двоичными операциями, которые пытаются обобщить концепции сложения и умножения. Мотивация для такого объекта заключается в том, что он позволяет ari
Классификация математических предметов
Классификация математических предметов 2000 Классификация предметов по математикеAMS
AMS Тематическая классификация
00-XX Общие
01-XX История и
биография [См. также классификационный номер -03
в других разделах]
03-XX Математический
логика и основы
04-XX Этот раздел удален {Для набора
теория см. 03Exx}
05-XX
Комбинаторика {Для конечных полей см. 11Txx}
06-XX Приказ,
решетки, упорядоченные алгебраические структуры [См. также 18B35]
08-XX Общие
алгебраические системы
11-XX Номер
теория
12-XX Теория поля
и многочлены
13-XX Коммутативный
кольца и алгебры
14-XX Алгебраический
геометрия
15-XX Линейные и
полилинейная алгебра; матричная теория
16-XX Ассоциативный
кольца и алгебры {Коммутативный случай см. 13-XX}
17-XX
Неассоциативные кольца и алгебры
18-ХХ Категория
теория; гомологическая алгебра {Для коммутативных колец
см. 13Dxx, для ассоциативных колец
16Exx, для групп 20Jxx,
для топологических групп и родственных структур 57Txx; см. также 55Nxx
и 55Uxx для алгебраических
топология}
19-XX $ K $ -теория
[См. Также 16E20, 18F25]
20-XX Теория групп
и обобщения
22-XX Топологический
группы, группы Ли {О группах преобразований см.
54х25, 57Sxx, 58-ХХ.Для абстрактного гармонического анализа см. 43-XX}
26-XX Реальный
функции [См. также 54C30]
28-XX Измерение и
интегрирование {Для анализа на многообразиях см. 58-XX}
30-XX Функции
комплексная переменная {Для анализа на многообразиях см.
58-XX}
31-XX Потенциал
теория {О теории вероятностного потенциала см. 60J45}
32-XX Несколько
комплексные переменные и аналитические пространства {Для бесконечных-
размерная голоморфность, см. 46G20, 58B12}
33-XX Специальный
функции (33-XX посвящены свойствам функций
как функции) {Для ортогональных функций см. 42Cxx; за
аспекты комбинаторики, см. 05Axx; для теоретико-числовых аспектов,
см. 11-XX; за
теория представлений, см. 22Exx}
34-XX Обычный
дифференциальные уравнения
35-XX Частично
дифференциальные уравнения
37-XX Динамический
системы и эргодическая теория [См. также 26A18, 34Cxx,
34Dxx, 35Bxx, 46Lxx,
58Jxx, 70-XX]
39-XX Разница
и функциональные уравнения
40-XX Последовательности,
серия, суммируемость
41-XX
Приближения и разложения {Для всей теории приближений в
сложный домен, см. 30Exx,
30E05 и 30E10; для всех тригонометрических
аппроксимация и интерполяция, см. 42Axx, 42A10 и 42A15; за
численное приближение, см. 65Dxx}
42-XX Фурье
анализ
43-XX Аннотация
гармонический анализ {Для другого анализа топологических и
Группы лжи, см. 22Exx}
44-XX Интегральный
преобразовывает, операционное исчисление {Для дробного
производные и интегралы, см. 26A33.О преобразованиях Фурье см.
42A38, 42B10. Для интегральных преобразований в
места распространения, см.
46F12. Для числовых
методы, см. 65R10}
45-XX Интегральный
уравнения
46-XX Функциональный
анализ {Для многообразий, смоделированных на топологической линейной
пробелы, см. 57N20, 58Bxx}
47-XX Оператор
теория
49-XX Исчисление
вариации и оптимальное управление; оптимизация
[См. Также 34H05, 34K35, 65Kxx, 90Cxx,
93-XX]
51-XX Геометрия
{По алгебраической геометрии см. 14-XX}
52-XX Выпуклый и
дискретная геометрия
53-XX Дифференциал
geometry {Информацию о дифференциальной топологии см. в 57Rxx.За
основные вопросы дифференцируемых многообразий, см. 58Axx}
54-XX Общие
топология {Для топологии многообразий всех размерностей
см. 57Nxx}
55-XX Алгебраический
топология
57-XX Коллекторы
и клеточные комплексы {О комплексных многообразиях см. 32Qxx}
58-XX Глобальный
анализ, анализ на коллекторах [см. также 32Cxx, 32Fxx,
32Wxx, 46-XX, 47Hxx,
53Cxx] {Для геометрического интегрирования
теория
см. 49Q15}
60-XX Вероятность
теория и случайные процессы {Для дополнительных
приложения, см. 11Kxx,
62-XX, 90-XX, 91-XX, 92-XX,
93-XX, 94-XX]
62-XX Статистика
65-XX Числовой
анализ
68-XX Компьютер
наука {Для статей, связанных с машинными вычислениями и
программы в определенной математической области, см. Раздел -04
в
та область}
70-XX Механика
частицы и системы {Для релятивистской механики
см. 83A05 и 83C10; по статистической механике см. 82-XX}
73-XX Раздел удален {Для механиков
твердых тел, см. 74-XX}
74-XX Механика
деформируемые твердые тела
76-XX Жидкость
механика {Для общей механики сплошной среды см. 74Axx или
другие части 74-ХХ}
78-XX Оптика,
электромагнитная теория {О квантовой оптике см. 81V80}
80-XX Классика
термодинамика, теплопередача {Для термодинамики
твердые тела, см. 74A15}
81-XX Квантовая
теория
82-XX Статистический
механика, строение материи
83-XX Теория относительности
и теория гравитации
85-XX Астрономия
и астрофизика {Относительно небесной механики см. 70F15}
86-XX Геофизика
[См. Также 76U05, 76V05]
90-XX Операции
исследования, математическое программирование
91-XX Теория игр,
экономика, социальные и поведенческие науки
92-XX Биология и
другие естественные науки
93-XX Системы
теория; control {Оптимальное управление см. 49-XX}
94-XX Информация
и связь, схемы
97-XX Математика
образование
| @ Как стать математиком (или статистиком) : Версия для печати: здесь [.pdf] Последняя редакция: 01.08.2009
Это как если хочешь
будь хорошим пианистом, Об этой статье:
|
| Неделя 1 | Лекция 1 | 4/6 | Введение и основные понятия | Слайды
|
| Лекция 2 | 4/8 | Настройка контролируемого обучения.Линейная регрессия. | Классные заметки
| |
| Переуступка | 4/8 | Набор задач 0.[файлы] Срок сдачи: 15 апреля в 23:59. | ||
| Раздел 1 | 4/10 | Пятничная лекция : Линейная алгебра. | Банкноты
| |
| 2 неделя | Лекция 3 | 4/13 | Взвешенные наименьшие квадраты.Логистическая регрессия. Метод Нетвона Персептрон. Экспоненциальная семья. Обобщенные линейные модели. | Классные заметки |
| Лекция 4 | 15/4 | Классные заметки | ||
| Переуступка | 15/4 | Набор задач 1.[файлы] [решения] Срок сдачи: 29 апреля в 23:59. | ||
| Раздел 2 | 17 апреля | Пятничная лекция : Вероятность | Банкноты
| |
| 3 неделя | Лекция 5 | 4/20 | Гауссовский дискриминантный анализ.Наивный байесовский. Сглаживание Лапласа. | Классные заметки
|
| Лекция 6 | 22/4 | Сглаживание Лапласа.Машины опорных векторов. | Классные заметки
| |
| Раздел 3 | 24/4 | Пятничная лекция : Python и Numpy | Банкноты | |
| пр. | 24/4 | Предложение по проекту должно быть сдано 24 апреля в 23:59. | ||
| 4 неделя | Лекция 7 | 4/27 | Машины опорных векторов. Ядра. | Классные заметки |
| Лекция 8 | 29/4 | Нейронные сети — 1 | Классные заметки
| |
| Переуступка | 29/4 | Набор задач 2.[файлы] Срок сдачи: 13 мая, 23:59. | ||
| Раздел 4 | 1/5 | Пятничная лекция : Метрики оценки | Банкноты | |
| 5 неделя | Лекция 9 | 5/4 | Нейронные сети — 2 | Классные заметки
|
| Лекция 10 | 5/6 | Bias — Дисперсия.Регуляризация. Выбор функции / модели. | Классные заметки
| |
| Раздел 5 | 5/8 | Пятничная лекция : Глубокое обучение | Банкноты | |
| 6 неделя | Лекция 11 | 5/11 | К-средних.GMM (не EM). Максимизация ожиданий. | Классные заметки
|
| Лекция 12 | 13/5 | Максимизация ожиданий (продолжение) | Классные заметки | |
| Переуступка | 13/5 | Набор задач 3. Срок сдачи: 27 мая, 23:59. | ||
| Раздел 6 | 15/5 | Пятничная лекция : Среднесрочный обзор | Классные заметки | |
| пр. | 15/5 | Основные этапы проекта должны быть выполнены 15 мая в 23:59. | ||
| 7 неделя | Лекция 13 | 18/5 | Факторный анализ. | Классные заметки |
| Среднесрочная | 5/20 | Подробности смотрите на Piazza post. | ||
| Лекция 14 | 5/20 | Анализ основных и независимых компонентов. | Классные заметки
| |
| 8 неделя | Лекция 15 | 5/25 | День памяти, без лекций. | |
| Лекция 16 | 5/27 | Слабое наблюдение | Классные заметки Дополнительный материал | |
| Переуступка | 5/27 | Набор задач 4. Срок сдачи: 10.06, 23:59 (без поздних дней). | ||
| 9 неделя | Лекция 17 | 1/6 | Марковский процесс принятия решений. Итерация значений и итерация политики. Q-Learning. Аппроксимация функции цены. | Классные заметки
|
| Лекция 18 | 6/3 | Обучение с подкреплением, продолжение | ||
| 10 неделя (последняя неделя занятий) | Лекция 19 | 6/8 | Политика поиска.Усиление. POMDP. | Классные заметки
|
| Лекция 20 | 6/10 | Резюме, справедливость, состязательность | Классные заметки | |
| пр. | 6/10 | Постер в формате PDF и видеопрезентация. Срок сдачи: 10.06, 23:59 (без поздних дней). | ||
| пр. | 6/10 | Заключительный отчет по проекту. Срок сдачи: 10.06, 23:59 (без поздних дней). | ||
Дополнительные примечания
| ||||
Другие ресурсы
| ||||
ELAC — Описание и содержание курса
Описание и содержание курса
120 Плоская геометрия (5)
Лекция, 5 часов.
Это базовый курс по основам геометрии евклидовой плоскости, который включает рассмотрение геометрических свойств и взаимосвязей. Особое внимание уделяется практике точного мышления и разработке логических доказательств.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
125 Промежуточная алгебра (5)
Лекция, 5 часов.
Примечание. Для этого класса требуется научный или бизнес-калькулятор.
Этот курс укрепляет и развивает навыки манипуляции в элементарной алгебре.Темы включают фундаментальные операции с алгебраическими выражениями, решения уравнений и неравенств, возведение в степень, графики алгебраических, экспоненциальных и логарифмических функций, системы уравнений и неравенств, а также введение в конические разделы. Приложения включены в большое количество текстовых задач.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
125S Промежуточная алгебра с опорой (5)
Лекция, 5 часов; Лаборатория, 2 часа.
Примечание. Для этого класса требуется научный или бизнес-калькулятор.
Этот курс включает обязательный лабораторный компонент для изучения тем из предалгебры и элементарной алгебры. Этот курс укрепляет и развивает навыки манипулирования элементарной алгеброй. Темы включают фундаментальные операции с алгебраическими выражениями, решения уравнений и неравенств, возведение в степень, графики алгебраических, экспоненциальных и логарифмических функций, системы уравнений и неравенств, а также введение в конические разделы.Приложения включены в большое количество текстовых задач.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
134 Ускоренная элементарная и промежуточная алгебра (6)
Лекция, 4 часа; Лаборатория, 4 часа.
Примечание. Для этого класса требуется научный или бизнес-калькулятор.
Ускоренный курс, охватывающий темы элементарной и средней алгебры. Темы включают линейные уравнения и неравенства, показатели степени, многочлены и факторинг, рациональные выражения, рациональные уравнения и неравенства, радикальные выражения и уравнения, квадратные уравнения и неравенства, построение графиков линейных и нелинейных уравнений и неравенств, системы линейных и нелинейных уравнений и неравенств, функции, экспоненциальные и логарифмические функции, коники, последовательности и ряды.Этот курс включает компонент компьютерной лаборатории и удовлетворяет всем требованиям по промежуточной алгебре.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
137 Алгебра предварительной статистики (5)
Лекция, 5 часов.
Этот курс знакомит с темами алгебры и основными элементами исследовательского анализа данных. Темы курса включают в себя: решение алгебраических уравнений, упрощение алгебраических выражений, анализ данных, статистику выборки и графики, меры центральной тенденции и распространения, функции и их графики, вероятность, последовательности и ряды, а также экспоненциальные и логарифмические функции.Этот класс предназначен для подготовки студентов, желающих изучать статистику. Студентам, желающим пройти другие курсы математики уровня 200, потребуется Math 125, Math 125S или Math 134, а предварительные условия можно найти в каталоге колледжа.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
173 Введение в математическое программирование (4) UC: CSU
Пререквизиты: математика 260.
Лекция, 3 часа; лаборатория, 2 часа.
Этот курс представляет собой введение в программирование с использованием C ++, включая теорию, приложения и программирование.Подробно обсуждаются переменные и основные типы данных, операторы, управляющие структуры, ввод и вывод, массивы, строки, функции, рекурсия, структуры, указатели, пространства имен и перегрузка. Представлены классы и объектно-ориентированное программирование. Особое внимание уделяется комментированию кода и отладке. В курс включены примеры из математики.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
192 Графический калькулятор (1) CSU
Лекция, 1 час.
Этот курс знакомит с использованием графического калькулятора.Он включает такие темы, как функции построения графиков в двух и трех измерениях, написание программ, инженерные и вычислительные приложения, решение систем уравнений с использованием матриц и анализ данных с использованием статистики.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
215 Основы математики I (3) UC: CSU (C-ID Math 120)
(Кредитный лимит UC: максимум 1 курс из: Математика 215 и 216)
Пререквизиты: математика 125 или 125S или 134.
Лекция: 3 часа.
Этот курс предназначен для тех, кто планирует преподавать математику в начальной школе. Курс охватывает язык множеств, элементарную логику, системы счисления, числа, основные операции, функции, целые числа, рациональные числа, действительные числа и алгоритмы, используемые в вычислениях.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
216 Основы математики II (3) UC: CSU
(Кредитный лимит UC: максимум 1 курс из: Математика 215 и 216)
Необходимое условие: удовлетворительное завершение математики 215.
Лекция, 3 часа.
Этот курс является вторым в последовательности, предназначенной для тех, кто планирует преподавать математику в начальной школе. Представленные темы включают основную вероятность, вводную статистику и вводную геометрию, включая конструкции, соответствие и подобие, измерения, геометрию движения и мозаику.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
227 Статистика (4) UC: CSU IGETC Area 2A (C-ID Math 110)
(Кредитный лимит UC: математика 227 в сочетании с ENG GEN 221, максимальный кредит, один курс).
Пререквизиты: математика 125 или математика 125S или математика 134 или математика 137.
Лекция, 4 часа.
Примечание. Требуется калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс представляет собой введение в вероятность, меры центральной тенденции и дисперсии, описательную и логическую статистику, включая выборку, оценку и проверку гипотез. Дисперсионный анализ, хи-квадрат и t-распределения Стьюдента; линейная корреляция и регрессионный анализ также представлены как темы.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
227S Статистика с поддержкой (4) UC: CSU IGETC Area 2A
(Кредитный лимит UC: максимум 1 курс из: MATH 227, 227S, BUS 015, ECON 020 и PSYCH 091).
Пререквизиты: математика 125 или математика 125S или математика 134 или математика 137.
Лекция, 4 часа; Лаборатория, 1 час
Примечание: Требуется калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс представляет собой введение в вероятность, меры центральной тенденции и дисперсии, описательную и логическую статистику, включая выборку, оценку и проверку гипотез. Дисперсионный анализ, хи-квадрат и t-распределения Стьюдента; линейная корреляция и регрессионный анализ также представлены как темы.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
230 Математика для студентов, изучающих гуманитарные науки (3) UC: CSU IGETC Area 2A
Пререквизиты: математика 125 или математика 125S или математика 134.
Лекция, 3 часа.
Знакомство с духом и стилем математики и ее стремлением стать человеческим делом. Темы выбираются из множества математических областей, включая логику, теорию множеств, системы счисления, теорию чисел, алгебру, метрическую систему, геометрию, математические системы, потребительскую математику, вероятность, статистику, теорию графов, голосование и распределение, которые предназначены для проиллюстрировать природу математических открытий, полезность математических приложений и красоту геометрического дизайна.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
235 Конечная математика (5) UC: CSU IGETC Area 2A (C-ID Math 130)
Пререквизиты: математика 125 или 125S или 134.
Лекция, 5 часов.
Примечание. Требуется калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс охватывает темы конечной математики с приложениями к бизнесу и общественным наукам. Среди представленных тем — системы линейных уравнений, неравенства, линейное программирование, математика финансов, матричная алгебра, вероятность, статистика и теория игр.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
236 Расчет для бизнеса и социальных наук (5) UC: CSU IGETC Area 2A (C-ID Math 140)
(Кредитный лимит UC: математика 236, объединенная математика 261 + математика 262, максимальный кредит, два курса).
Пререквизиты: математика 235 или математика 245.
Лекция, 5 часов.
Примечание: Студент должен проконсультироваться с консультантом, чтобы определить, какие предварительные условия требуются университетом, на который направлен перевод.
Примечание. Требуется калькулятор.Обратитесь к инструктору, чтобы узнать о конкретном виде.
Этот курс состоит из элементарного дифференциального и интегрального исчисления алгебраических, экспоненциальных и логарифмических функций, а также частных производных и метода множителей Лагранжа. Подчеркиваются приложения к бизнесу и общественным наукам.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
241 Тригонометрия с векторами (4) CSU
Пререквизиты: математика 125 или математика 125S или математика 134.
Лекция, 4 часа.
Примечание. Для этого класса требуется научный калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс включает изучение тригонометрических функций и их обратных; измерение углов в градусах и радианах; оценка треугольников; решения тригонометрических уравнений; проверка тригонометрических тождеств; векторы; сложные числа; построение графиков тригонометрических функций и полярных кривых.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
Тригонометрия 241S с векторами с опорой (4) CSU
Пререквизиты: математика 125 или математика 125S или математика 134.
Лекция, 4 часа; Лаборатория, 1 час
Примечание: для этого класса требуется научный калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс включает изучение тригонометрических функций и их обратных; измерение углов в градусах и радианах; оценка треугольников; решения тригонометрических уравнений; проверка тригонометрических тождеств; векторы; сложные числа; построение графиков тригонометрических функций и полярных кривых.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
245 Колледж Алгебра (3) UC: CSU IGETC Area 2A
(Лимит кредита UC: Math 245 и 260 вместе — максимум четыре единицы кредита).
Пререквизиты: математика 125 или математика 125S или математика 134.
Лекция, 3 часа; Лаборатория, 1 час
Примечание: для этого класса требуется научный калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс охватывает такие темы, как полиномиальные и рациональные функции, обратные, экспоненциальные и логарифмические функции, системы и матрицы, аналитическая геометрия, последовательности и ряды, биномиальная теорема, математическая индукция, теория счета и вероятность.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
260 Предварительный расчет (5) UC: CSU IGETC Area 2A
(Кредитный лимит UC: Math 245,260 и 260S вместе — максимальный кредит пять единиц).
Пререквизиты: математика 125 или математика 125S или математика 134.
Лекция, 5 часов.
Примечание. Требуется калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс охватывает темы алгебры колледжа, включая полиномиальные и рациональные функции, экспоненциальные и логарифмические функции, системы уравнений и неравенств, конические сечения, последовательности и ряды, а также ограничения в качестве предварительного ознакомления с исчислением.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
260S Предварительный расчет (6) UC: CSU IGETC Area 2A
(Кредитный лимит UC: Math 245,260 и 260S вместе — максимальный кредит пять единиц).
Пререквизиты: математика 125 или математика 125S или математика 134.
Лекция, 5 часов; лаборатория, 1 час
Примечание: требуется калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Этот курс охватывает темы алгебры колледжа, включая полиномиальные и рациональные функции, экспоненциальные и логарифмические функции, системы уравнений и неравенств, конические сечения, последовательности и ряды, а также ограничения в качестве предварительного ознакомления с исчислением.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
261 Исчисление I (5) UC: CSU IGETC Area 2A (C-ID Math 211)
(Кредитный лимит UC: математика 236, объединенная математика 261 + математика 262, максимальный кредит, два курса).
Пререквизиты: математика 241 или 241S и математика 260 или 260S.
Лекция, 5 часов.
Примечание. Требуется калькулятор. Обратитесь к инструктору по поводу необходимого конкретного вида.
Это первая последовательность из трех курсов по математике.Включены следующие темы: пределы и непрерывность, производные, приложения дифференцирования, интегралы, основная теорема исчисления и приложения интегрирования.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
262 Исчисление II (5) UC: CSU IGETC Area 2A (C-ID Math 221)
(Кредитный лимит UC: математика 236, объединенная математика 261 + математика 262, максимальный кредит, два курса).
Пререквизиты: математика 261.
Лекция, 5 часов.
Примечание. Требуется калькулятор.Обратитесь к инструктору по поводу необходимого конкретного вида.
Это второй из трех курсов по математике. Темы включают дифференцирование и интегрирование логарифмических, экспоненциальных, круговых и гиперболических функций и их обратных, неопределенных форм, несобственных интегралов, стандартных методов интегрирования, параметрических уравнений и полярных координат, длины дуги, площади поверхности вращения, бесконечных последовательностей и серий, и представление функций в виде степенного ряда.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
263 Исчисление III (5) UC: CSU IGETC Area 2A (C-ID Math 230)
Пререквизиты: математика 262.
Лекция, 5 часов.
Примечание. Требуется калькулятор, о конкретном типе которого можно узнать у инструктора.
Это третий из трех курсов по математике. Темы включают векторы и геометрию пространства, векторные функции, частные производные, множественные интегралы и векторное исчисление.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
270 Линейная алгебра (3) UC: CSU IGETC Area 2A (C-ID Math 250)
Пререквизиты: математика 262.
Лекция, 3 часа.
Этот курс включает изучение систем линейных уравнений и их решений, матриц, определителей, векторных пространств, линейных преобразований, ортогональности и проблем с характеристическими значениями.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
272 Методы дискретной математики (5) UC: CSU IGETC Area 2A (C-ID Math 160)
Пререквизиты: Математика 262.
Лекция, 5 часов.
Этот курс знакомит с наборами, отношениями, функциями и логикой, а также с формальными методами доказательства, такими как противоречие, противопоставление, индукция, диагонализация, рекурсия и принцип голубятни.Эти идеи и методы развиваются на основе рассмотрения проблем комбинаций и подсчета, элементарной теории чисел и теории графов. Также обсуждаются темы, связанные с раскраской карты, сложностью и криптографией.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
273 Введение в объектно-ориентированное программирование (4) UC: CSU
Пререквизиты: математика 173.
Лекция, 3 часа; лаборатория, 2 часа.
Этот курс посвящен объектно-ориентированному программированию, структурам данных и разработке алгоритмов с использованием C ++.Темы включают обзор классов и объектов, операторов и перегрузку операторов, динамическое выделение памяти, наследование классов, возможность повторного использования кода, друзей, исключения, стандартную библиотеку шаблонов, нотацию Big-O, связанные списки, стеки, очереди и деревья. , а также алгоритмы поиска и сортировки. Особое внимание уделяется комментированию и отладке кода.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
275 Обыкновенные дифференциальные уравнения (3) UC: CSU IGETC Area 2A (C-ID Math 240)
Пререквизиты: математика 263.
Лекция, 3 часа.
Примечание. Для этого класса требуется научный калькулятор.
Этот курс дает студенту базовое понимание теории и содержания обыкновенных дифференциальных уравнений. Особое внимание уделяется различным методам решения этих уравнений, особенно первого и второго порядка, а также решениям задач физических приложений. Другие затронутые темы включают теоремы существования и единственности, системы линейных дифференциальных уравнений, численные и графические методы с использованием компьютеров и преобразование Лапласа.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
280 Введение в численный анализ (3) UC: CSU IGETC Area 2A
Пререквизиты: математика 263 и ЛИБО математика 173 или общая инженерия 121 ИЛИ Компьютерные науки Информационные технологии 243 или информатика 216.
Лекция, 3 часа.
Этот курс предназначен для введения в численные методы. Представленные темы включают анализ ошибок, поиск корней нелинейных уравнений, численные методы для матричных операций, интерполяцию и аппроксимацию кривой.Также рассматриваются численные методы дифференцирования и интегрирования.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
282 Введение в абстрактную алгебру (3) UC: CSU
Пререквизиты: математика 270.
Лекция, 3 часа.
Этот курс представляет собой введение в числа, системы счисления и основные алгебраические структуры групп, колец и полей.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
284 Введение в теорию чисел (3) UC: CSU IGETC Area 2A
Пререквизиты: математика 262.
Лекция, 3 часа.
Этот курс знакомит с темами элементарной теории чисел, включая изучение простых чисел, составных чисел, алгоритма Евклида, диофантовых уравнений, сравнений, делимости, мультипликативных функций, квадратичных вычетов и непрерывных дробей
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
286 Уравнения с частными производными в естественных науках (5) UC: CSU IGETC Area 2A
Пререквизиты: математика 275.
Лекция, 5 часов.
Этот курс знакомит с линейными уравнениями в частных производных, а также краевыми и начальными задачами с особым акцентом на волновое уравнение, уравнение теплопроводности и уравнение Лапласа. Также изучаются методы разделения переменных, разложения по собственным функциям и метод характеристик для нелинейных уравнений.
СОДЕРЖАНИЕ И ЦЕЛИ КУРСА
Василий Громов — НИУ ВШЭ
Магистерские диссертации :
2018
Спецификация для алгоритмов эволюционного программирования
2017
Реляционные тензоры как способ представления информации о хаотических временных рядах
Конструктивные нейронные сети для исследования хаотических
Алгоритмы прогнозирующей кластеризации для прогнозирования хаотических временных рядов на несколько шагов вперед
Прогнозирование резких разрывов тренда
Расчетная инвариантная мера для динамической системы, заданная наблюдаемым временным рядом
2016
Подобные временные ряды в задачах хаотических временных рядов
Статистические исследования естественных языков с использованием методов самоорганизованной критичности
2015
Методы кластеризации для прогнозирования хаотических временных рядов
Прогнозная кластеризация для заблаговременного выявления популярных твитов
2014
нейронных моделей NEAT для p переписать хаотические временные ряды
2009
Идентификация поврежденных механических систем с использованием конструктивных нейронных сетей
Бакалаврские диссертации :
2018
Характеристики инвариантной меры для прогнозирования временных рядов
Конструктивные нейронные сети
9000 нейронных сетей2 Прогнозирование временных рядов на несколько шагов впередВыявление скоординированных атак в твитере
Спецификация в задаче маршрутизации транспортных средств
2017
Статистические характеристики корпуса литературных текстов
Динамика текстов в конечномерном семантическом пространстве (для англоязычного корпуса )
Статистические характеристики переключений эмоций в английских текстах
2016
Самоорганизованные методы критичности для естественного отбора в генетических алгоритмах
Графы совпадения на естественном языке в виде сложных сетей
Расчетное предсказание как Количество кластеров для предсказания хаотических временных рядов
2015
Нелинейная краевая задача и теорема суперпозиции Колмогорова
2014
Эволюционные алгоритмы прогнозирования временных рядов
..