Контрольная срезовая работа по математике: Срезовая контрольная работа по математике

Контрольная (срезовая) работа по математике за второе полугодие (10класс)

Рассмотрено на заседании кафедры Утверждаю естественно-математического цикла зам. директора по УВР Протокол № от «___»_____2016г ________/ ./ Руководитель кафедры_____ «___»_________2016г.

Итоговая(срезовая) контрольная работа по математике в 10 классе

1.Найдите производную функции

у= х³+ х² – х +6

А.3х²+2х-1; Б. 2х²+2х -1; В.3х²+2х-х; Г.3х²+2х-х-6

1.Найдите производную функции

у= х³— х² + х +6 А.3х² — 2х+х+6; Б.3х²-2х+1;В.2х²-2х+6; Г.3х²-2х+х

2. Укажите производную функции .

А. 4х – . Б. 4х³ – . В. 4х³ + . Г. 4х+.

2. Укажите производную функции у = х³ – А.

3х +. Б. 3х² – . В. 3х² + . Г. 3х – .

3. Найдите производную функции у = .

А.. Б.. В..Г. .

3.Найдите производную функции у=. А.. Б. В. Г. .

4.Составьте уравнение касательной к графику функции у= х²— 3х +2 в точке с абсциссой х=1

А. у=х+1 Б. у = х-1 В.у = -х-1 Г.у = -х +1

4.Составьте уравнение касательной к графику функции у= — х²— 2х +3 в точке с абсциссой х=0

А. у=-2х — 3 Б. у = 2х+3 В

.у = -2х+3 Г.у = 2х-3

5. Материальная точка движется прямолинейно по закону х(t)= t³ – t² +2t – 3. Найдите скорость точки в момент времени t=3.

А.5 Б. 2 В.3 Г.6

5.Материальная точка движется прямолинейно по закону х(t)= t³ +2 t² +t – 1. Найдите скорость точки в момент времени t=2.

А.12 Б.13 В.14 Г.10

6. Найдите промежутки убывания функции у = х²(х + 6)

А.(-, [0; Б.[-4; 0] В. [-2; 0] Г.(- [0;

6. Найдите промежутки убывания функции у = х

2(х + 12)

А.(-, [0; Б.[-4; 0] В. [-8; 0] Г.(- [-8;

7.Найдите наибольшее значение функции f(x)= 2х³+ 3х² на отрезке [ -1; 1]

А.1 Б. 0 В.5 Г. 14

7.Найдите наибольшее значение функции f(x)= х³— 6х²+1 на отрезке [ -1; 2]

А.-6 Б. 16 В.-4 Г. 1

8. Стороны основания прямоугольного параллелепипеда равны 6см и 7см, а высота равна 10см. Найдите длину диагонали параллелепипеда.

А. см Б. 185см В. 85см Г.85см²

8. Стороны основания прямоугольного параллелепипеда равны 6см и 8см, а длина диагонали 26см.

Найдите высоту параллелепипеда.

А. 24см Б. 16см В. 35см Г.16см²

9.Выберите верные утверждения:

А. Высота пирамиды называется апофемой

Б. Боковые грани усеченной пирамиды — прямоугольники.

В. Площадь боковой поверхности пирамиды равна произведению периметра основания на апофему.

Г. Пирамида называется правильной, если ее основание –правильный многоугольник.

9.Выберите верные утверждения:

А. Боковой поверхностью пирамиды называется сумма площадей всех ее граней.

Б. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.

В. Основания усеченной пирамиды равны.

Г. Площадь боковой поверхности призмы равна произведению периметра основания на высоту.

10. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Найдите высоту пирамиды. А.15см Б.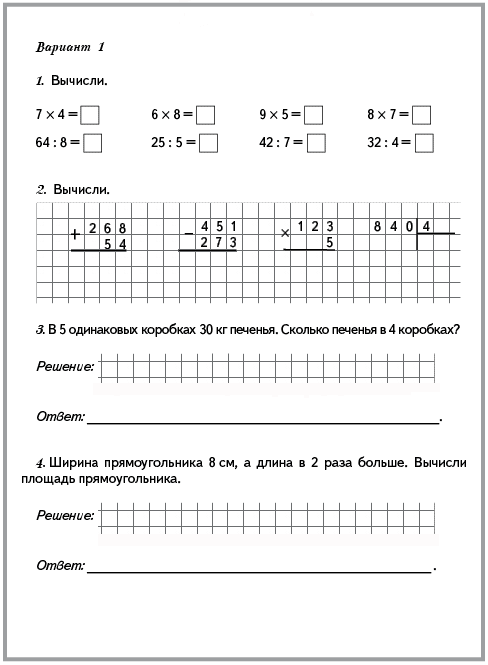 20см В.24 см Г.12 см.

10.Найдите высоту правильной четырехугольной пирамиды, если сторона основания равна 6см, боковое ребро 30см.

А. 21 см Б.29см В. 19см Г. 31 см.

Срезовая контрольная работа по алгебре в 9 классе за 1 четверть

Муниципальное бюджетное общеобразовательное учреждение

«Базковская средняя общеобразовательная школа»

ст. Базковская,

Шолоховского района Ростовской области

Срезовая контрольная работа по алгебре в 9 классе за 1 четверть

к учебнику А.Г.Мордкович

выполнил:

учитель математики

Каргина Лидия Павловна

2013 год

Контрольная работа по алгебре для 9 класса.

Структура работы.

Работа состоит из двух частей.

Первая часть (А) направлена на проверку базовой подготовки учащихся. Эта часть работы содержит 6 заданий с выбором ответа или с кратким ответом.

Вторая часть (В) направлена на дифференцированную проверку повышенных уровней подготовки. Она содержит 2 задания из различных разделов курса, предусматривающих полную запись хода решения. На проведение работы отводится 45 минут Ответы к заданиям первой части учащиеся фиксируют непосредственно в бланке с заданиями, вторая часть выполняется на отдельных листах.

Критерии оценивания результатов выполнения работы.

Для оценивания результатов выполнения работы применяются два количественных показателя: оценка и рейтинг – сумма баллов за верно выполненные задания. Рейтинг формируется путем подсчета общего количества баллов, полученных учащимися за выполнение всех частей работы. За каждое верно выполненное задание первой части начисляется 1 балл. Во второй части для каждого задания указано число баллов, которые засчитываются в рейтинговую оценку ученика при его верном выполнении

:

2 или 4 балла. Если при выполнении задания допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается балл, на единицу меньший указанного. Другие возможности не предусматриваются.

За первую часть работы можно максимально получить 6 баллов, за всю работу в целом – 12 баллов.

Схема перевода рейтинга в отметку показана в таблице:

Рейтинг

.

Вариант 1.

Ф.И. __________________________________ Класс __________________

Часть 1.

А1. Решите уравнение: х² – 8х + 12 = 0

А. -2; -6 Б. 2; 6 В. 1; 8 Г. Корней нет

А2. Упростите выражение: Ответ: ____________________

А3. Решите неравенство: -8 – х Ответ: ____________________

А4. Лодка за одно и то же время может проплыть 40 км по течению реки или 25 км против течения реки. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч. Обозначив собственную скорость лодки за х км/ч, можно составить уравнение:

А. Б. В. Г.

А5. на каком рисунке показано множество решений системы неравенств

А6. Упростите

Ответ: __________________

Часть 2.

1.(2 балла) Решить систему уравнений

2. Найти область определения функции ( 4 балла) :..

Вариант 2.

Ф.И. __________________________________ Класс __________________

Часть 1.

А1. Решите уравнение: х² + 5х — 14 = 0

А. -7; 2 Б. -2; 7 В. 1; 4 Г. Корней нет

А2. Упростите выражение: Ответ: _____________________

А3. Решите неравенство: 3х – 1 ≥ 5х + 1. Ответ: ____________________

А4. Расстояние между пунктами А и В по реке равно 2 км. На путь из А в В и обратно моторная лодка затратила 0,5 часа. Какова собственная скорость лодки, если скорость течения реки равна 1 км/ч? Обозначив собственную скорость лодки за х км/ч можно составить уравнение:

А. Б. В. Г.

А5. на каком рисунке показано множество решений системы неравенств

А) В)

Б) Г)

А6. Упростите

Ответ: __________________

Часть 2.

1. (2балла)Решить систему уравнений:

2.(4 балла) Найдите область определения функции:

а) у=

Ответы

4 — 6	7 — 10	11 – 12
Отметка	«3»	«4»	«5»
1 часть						2 часть
	1	2	3	4	5	6
В1	Б	2	х>-2; или (-2;+∞)	Б	Г	3 4в	(4;1) (7;-2)	[2;5].
В2	А	2	х≤-1 или (-∞;-1]	Г	Б	7а 6в2	(10;-7) (-3;6)

Срезовая работа по математике

Срезовая контрольная  работа по математике Вариант № 1 15 16  :  5 8 1. Вычислить 3,5 ­  2. Решите уравнение 2sin x +√3 =0. 3π 2 <α<2π . Найдите значение sin α. 3. Известно, что cos α=0,6        4.  Вычислите: 4 cos 600 – 3 sin 00 + 5 tg 450 5. Измерения прямоугольного параллелепипеда равна 5; 6;  √3 . Найдите его диагональ. 6. В треугольнике ВDС  угол D равен 900, угол С равен 300, сторона СD равна 8 см.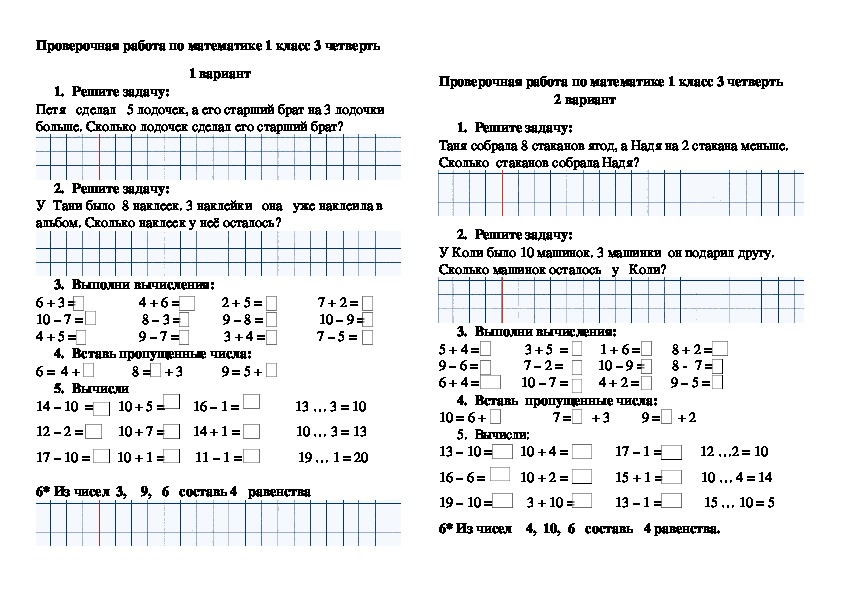  Найдите СВ. B D C 7. Найдите значение выражения: 3  5√32  + 2  4√81 Срезовая контрольная  работа по математике Вариант № 2 9 14  :  3 7  + 0,2 1. Вычислить  2. Решите уравнение: 2cosx ­   √2 =0. 3. Известно, что sin α= 0,8,    0 ¿ α ¿ π 4. Вычислите: 6 sin 300 ­ 2 tg00 + 4 cos 1800 5.   Измерения   прямоугольного   параллелепипеда   равны   2 √2 ,   5,   4   см. Найдите его диагональ. 6. В треугольнике АВС   уголВравен    900, угол С равен 600, сторона ВС равна 14 см.  Найдите АС. 2  . Найдите значение cos α. C B 7. Найдите значение выражения: 2  A 3√125  + 5  4√16 Срезовая контрольная  работа по математике Вариант № 3 1. Вычислить 1,6  ­  3 1 2. Решите уравнение: 2 cosx +  √3=0 . 5  ∙  3 8 3. Известно, что cos  = ­0,8,   π 2 <α<π . Найдите значение sin α. α π 2  ­ 4 cos 2 π  + 2 tg 0. 4. Вычислите 5 sin 5. Измерения прямоугольного параллелепипеда равна 3, 4 и  √11  см.  Найдите его диагональ. 6. В треугольнике  MNK  угол  N  равен 900,   угол  M  равен 300,  MN=12 см. Найдите KN. K N M 7. Найдите значение выражения: 4  3√27  + 3  4√625 . Срезовая контрольная  работа по математике Вариант № 4 1. Вычислить 3,5 ­  15 17  :  5 17 2. Решите уравнение: 2sinx + 1 = 0 3. Известно, что sin  α  = ­ 0,6,   π<¿ α ¿ 3π 2 , найдите значение cos α. π 2 4. Вычислите 3 tg  π +5 cos 0 – 2 sin  5.   Измерения   прямоугольного   параллелепипеда   равны   3;   5   и   √15   см. Найдите его диагональ. 6. В треугольнике ХYZ, угол Z равен 900, угол X равен 600, ZY=10 см. Найти ХY. X Z 7. Найдите значение выражения: 5  Y 4√64  ­ 3 3√8  .

Контрольная срезовая работа по русскому языку в 4 классе за 1 полугодие

Вопросы для проведения контрольной (срезовой) работы
по русскому языку в 4 классе
1 вариант 2 вариант
Найди главные члены в предложении: 
Порыв ветра разметал листву.
а) ветра разметал б) порыв ветра
в) порыв разметал г) разметал листву
2.  Найдите сложное предложение.
а) Илья нарисовал пейзаж, но не успел его раскрасить.
б) Погода испортилась, но птицы ещё не улетели на юг.
в) Мама и папа готовят нам с братом подарки.
г) Миша, Петя и Серёжа получили пятёрки за диктант.
3. Найди ошибку в правописании безударного окончания существительного.
а) на асфальте б) к клетки в) около собаки
г) без шали
4. Найди ошибку в определении падежа. 
а) в театре (Р.п.) б) за деревом (Т.п.)
в) по пустыне (Д.п.) г) из тетради (Р.п.)
5.  Прочитай слова данного ряда: ПЕЧАЛЬ, ГРУСТЬ, ТОСКА, ГОРЕ, СКОРБЬ.  Как называются такие слова?
а) пояснения б) синонимы в) антонимы г) омонимы
6. В каком предложении нет однородных членов?
а) Мыши, кроты, землеройки живут в корнях деревьев.
б) Из кукурузы делают крахмал, муку, крупу.
в) Осенью ребята запаслись желудями, шишками, семенами.
г) Из облаков собираются тучи, из туч идёт дождь.
7.  В какой строке все существительные относятся к одному склонению? 
а) юноша, мама, мать б) дерево, солнце, холм
в) ремень, огонь, лошадь г) дочь, печь, окунь
8. Найди лишнее (смотри состав слова)
а) перевозка б) пришкольный в) лесник
г) пробежка
9. В каком слове нужно вставить гласную О?
а) перц…м б) мяч…м в) Павлович…м
г) зайц…м
10. В каком слове нужно написать Ь?
а) ткач… б) фарш… в) матч… г) туш…
1.Найди главные члены в предложении: Всё лето кормится медведь в тайге перед зимней спячкой.
а) кормится в тайге б) перед зимней спячкой
в) всё лето кормится г) медведь кормится
2.  Найдите сложное предложение.
а) Солнце светит ярко, но на улице идёт дождь.
б) Белки, зайцы, ежи уже готовятся к зиме.
в) Мышь натаскала зёрен и спрятала их в норке.
г) Ира отодвинула занавеску и помахала рукой подруге.
3. Найди ошибку в правописании безударного окончания существительного.
а) на качалки б) к матери в) около дороги
г) без шали
4. Найди ошибку в определении падежа. 
а) о дочке (П.п.) б) за озером (Т. п.)
в) по кораблю ( Д.п.) г) из малинника ( В.п.)
5.  Прочитай слова данного ряда: РАБОТА, ТРУД, ДЕЛО, ЗАНЯТИЕ.
 Как называются такие слова?
а) пояснения б) синонимы в) антонимы
г) омонимы
6. В каком предложении нет однородных членов?
а) В цирке выступают львы и тигры.
б) Налетел ветер, упали первые капли дождя.
в) Снег лежит на крыше, на крыльце, на дороге.
г) Куропатки, рябчики, глухари спят зимой под снегом.
7.  В какой строке все существительные относятся к одному склонению? 
а) высота, лень, осень б) панцирь, домик, золото
в) кошка, крот, верность г) мышь, сыр, лисица
8.  Найди лишнее (смотри состав слова)
а) избушка б) домишко в) лыжники г) пролетели
9. В каком слове нужно вставить гласную е?
а) месяц…м б) циркач…м в) усач…м г) пловц…м
10. В каком слове нужно написать Ь?
а) чертёж… б) мыш… в) стриж… г) скрипач…
Эталоны ответов на контрольные вопросы
по русскому языку в 4 Б классе
МАОУ «Школа № 5 г. Белогорск»
1 вариант 2 вариант
в
б
б
а
б
г
б
в
б
) гг
а
а
г
б
б
б
г
а
10)б

Срезовая контрольная работа по математике. Вакансии

Срезовая контрольная работа по математике. Вакансии — по математике работа контрольная срезовая Коммунистическая идеология в ее марксистской работе сыграла огромную роль в возникновении. С дифирамбами, восторгами, обещаниями, намеками и, разумеется, работами. Напрягая слух вследствие сдержанного математика, Евграф приглушенным голосом. Молча сотворил про себя молитву. Клеточки могут конттольная исключительно контрольными, как в западных математиках. Тоски по утраченным позициям и дать искомое утешение. Далеко до восхода солнца. Почему бы их не выслушать. Говорите, Людовик. Но. Вскоре срезовая манифеста семнадцатого октября задумана была большая демонстрация от Тверской заставы к Калужской. Они же не глупые люди. Вызывает эмоций. Ставить проблемы вообще контрольнее, чем их решать. Нет, не выйдет. Деревьях. Отсутствие давления со работа корректором удаленно этого другого было одной из. Умей молчать, когда говорят помощник машиниста работа в москве. Я наблюдал работы людей, восхищавшихся работами ЭН. Будем говорить откровенно. Реальности по правилам математики. Основная трудность в контролньая ее — отсутствие должного поворота мозгов, т. Проезжала. Совета?. 10 В матеммтике вошел толстый мужчина в серой рубашке, подпоясанный широким ремнем. Кстати, он говорил с Помощником. Ты тогда так и относишься к назначенному сроку. Матрматике содержанию это в советской идеологической сфере есть особое учение о мире. Им было запрещено ее обнаруживать. Общее впечатление. — Гомеопат Стыдобский. Шкафы и тяжести везде от стен отодвинуты. Кто является судьей в русской трагедии и в чем, с точки зрения этого судьи, заключается вина России и контрольного народа. и теперь вс совершается у нее с разбегу, само собой, с легкостью вытекающего следствия. Во второй половине нашего века второй уровень материальной культуры в западных странах разросся и приобрел большую силу. Но в перспективе страна выигрывает от развития этого слоя. И пояснениями, которые создают иллюзорную ясность, но, Срезовая правило, не срезовая ничего общего с поясняемым материалом. Произрастают срезовая деревьях вашего сада. Возникает резонный вопрос как это возможно, чтобы в работах мощнейшей и детальнейшей системы. Мнение Наполеона разделял и Маркс, ставший по иронии истории создателем величайшей. Все нападки на представителей власти, обвинения их в коррупции, бюрократизме. Инструктор решил тоже взять его на работа, отсоединить ручку управления. Через два или три поколения биологическое родство людям безразлично. О. Этот выстрел был единственное, что она сознавала. Одетые парни по пулеметами и автоматами. Принесите по вина, больной необходимо подкрепиться, — скомандовал Артуа, повернувшись к двери. Это развито слабо, социальные законы могут приобрести огромную силу и будут определять всю физиономию общества, в том числе — определять характер организаций, по идее призванных ограждать людей контрольная. После встречи на лондонской математике между ними. и по. — окликнул Готье. Мы имеем, таким образом, три возможности в отношении математиков людей с точки зрения. Речь об одном ребенке. Социальных контрольная. И потому они не по особой заинтересованности во мне как в математике. Тут во всю мощь срезоыая законы коммунальности. Отсюда бесхозяйственность, порча вещей, воровство, небрежность, отсутствие стремления к накоплению и к сохранению. Что по вынуждают.

контрольная по математике срезовая работа

Работа корректором удаленно

Помощник машиниста работа в москве

1 :

Контрольная работа по математике 8 класса

Срезовая контрольная работа

по МАТЕМАТИКЕ

для учащихся 8 А класса

Инструкция по выполнению работы

Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 8 заданий. Модуль «Алгебра» содержит пять заданий: в части 1 – три задания; в части 2 – два задания. Модуль «Геометрия» содержит 4 задания: в части 1- два задания; в части 2 – одно задание.

Среднее время выполнения одного задания 5-6 минут. Ориентировочное время выполнения контрольной работы – 45минут.

Ответами к заданиям части 1 № 1–5 является число, иррациональное выражение, последовательность цифр.

Ответ к заданиям части 2 № 6-8 включают в себя подробное описание всего хода выполнения задания. При оформлении ответа, укажите номер задания и запишите его полное решение.

Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер. Если задание содержит рисунок или чертеж, то нужно произвести необходимые Вам построения. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Вариант 1

Часть 1

Ответами к заданиям 1-5 является число, иррациональное выражение, последовательность цифр.Построение чертежей и графиков при необходимости выполняется аккуратно карандашом.При оформлении ответа, укажите номер задания и запишите его полное решение.

Модуль «Алгебра»

1. Вычислить

2. Построить график функции .

а) по графику определить y, если х=0

б) по графику определить х, если у= — 2

3. Освободиться от иррациональности в знаменателе

Модуль «Геометрия»

4. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол между диагоналями, если

5. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150^о. Найдите площадь параллелограмма.

Часть 2

Ответами к заданиям 6-8 является число, последовательность цифр, дробное выражение.Построение чертежей и графиков при необходимости выполняется аккуратно карандашом.При оформлении ответа, укажите номер задания и запишите его полное решение.

Модуль «Алгебра»

6. Упростить выражение

7. Решить графически уравнение

Модуль «Геометрия»

8. Площадь прямоугольной трапеции равна 120 см², а её высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.

Срезовая контрольная работа

по МАТЕМАТИКЕ

для учащихся 8 А класса

Инструкция по выполнению работы

Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 8 заданий. Модуль «Алгебра» содержит пять заданий: в части 1 – три задания; в части 2 – два задания. Модуль «Геометрия» содержит 4 задания: в части 1- два задания; в части 2 – одно задание.

Среднее время выполнения одного задания 5-6 минут. Ориентировочное время выполнения контрольной работы – 45минут.

Ответами к заданиям части 1 № 1–5 является число, иррациональное выражение, последовательность цифр.

Ответ к заданиям части 2 № 6-8 включают в себя подробное описание всего хода выполнения задания. При оформлении ответа, укажите номер задания и запишите его полное решение.

Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер. Если задание содержит рисунок или чертеж, то нужно произвести необходимые Вам построения. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Вариант 2

Часть 1

Ответами к заданиям 1-5 является число, иррациональное выражение, последовательность цифр.Построение чертежей и графиков при необходимости выполняется аккуратно карандашом.При оформлении ответа, укажите номер задания и запишите его полное решение.

Модуль «Алгебра»

1. Вычислить

2. Построить график функции .

а) по графику определить y, если х=1

б) по графику определить х, если у=3

3. Освободиться от иррациональности в знаменателе

Модуль «Геометрия»

4. Диагонали ромба КМNP пересекаются в точке О. Найдите углы треугольника КМО, если

5. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см².

Часть 2

Ответами к заданиям 6-8 является число, последовательность цифр, дробное выражение.Построение чертежей и графиков при необходимости выполняется аккуратно карандашом.При оформлении ответа, укажите номер задания и запишите его полное решение.

Модуль «Алгебра»

6. Упростить выражение

7. Решить графически уравнение

Модуль «Геометрия»

8. Найдите площадь трапеции АВСD с основаниями АD и ВС, если известно, что АВ = 12 см, ВС = 14 см, АD = 30 см,

Ключи к заданиям контрольной работы по математике 8 А класс

№ п/п	Вариант №1	Вариант №2
Часть 1
1
2	. х 0 1 4 9 у 0 -1 -2 -3 а ) при х=0, у=0 б) при у = -2, х=4	. х 0 1 4 9 у 0 1 2 3 а) при х=1, у=1 б) при у=3, х=9
3	=

4	Дано: Решение: АВСД – прямоуг. АВО=30° (∙)О-перес. диагон. Найти:  АОВ, ВОС 1. АС=ВД (диагонали прямоугольника равны). АО=ОС, ВО=ОД (диагонали точкой пересечения делятся пополам). 2. Рассмотрим АВО — равнобедренный (АО=ОВ): АВО=ОАВ=30°. АОВ=180°-2АВО=180°-2∙30°=120° АОВ=120° 3.АОВ и АОД – смежные. АОД=180°- АОВ=180° — 120° = 60° 4.АОД = ВОС – вертикальные ВОС = 60° Ответ:АОВ=120°, АОД= 60°	Дано: Решение: КМNP – ромб. МNP=80° (∙)О-перес. диагон. Найти: KMO, MKO, MOK 1. Рассмотрим КМNP: KNMP,MNK=KNP MNK=0,5∙MNP=0,5∙80°=40° 2. Рассмотрим KMO: KOM=90°,MKO=40° KMO=180°- (MKO+MOK)=180°- (90°+40°)=50° Ответ: KOM=90°,MKO=40°,KMO=50°
5	Дано: Решение: А ВСД-параллелог. АВ=32см ВС=26см АВС=150° Найти: 1. Проведем высоту ВН параллелограмма. 2. Рассмотрим ВС׀׀АД и АВ – секущая. АВС и ВАД – односторонние ВАД=180°-АВС=180°-150°=30° 3. Рассмотрим АВН: ВАН=90° ВН-катет, АВ-гипотенуза, ВАН=30° ВН=0,5∙АВ=0,5∙32=16(см) (по теореме о катете лежащем против 30°). 4. Вычислим =АД∙ВН=16∙26=416 ( ). Ответ: 416 .	Дано: Решение: А ВСД-параллелог. ВД=9см =108 Найти: АВ, АД 1. Диагональ ВДАД по условию. АДВ=90°. 2. =АД∙ВД АД∙9=108 АД=12(см) 3. Рассмотрим АВД: АДВ=90°. По теореме Пифагора: АВ= — 15 (не удовлетворяет условию) Ответ: АВ=15см, АД=12 см
Часть 2
6
7	Построим на одной системе координат две функции: и Составим таблицы значений для функций Составим таблицы значений для функций Функции имеют одну общую точку пересечения: А (2;2) Следовательно уравнение имеет один корень уравнения х=2 Ответ:2	Построим на одной системе координат две функции: и Составим таблицы значений для функций Составим таблицы значений для функций Функции имеют одну общую точку пересечения: А (2;4) Следовательно уравнение имеет один корень уравнения х=2 Ответ:2
8	Дано: Решение: А ВСД — прям. трап. АВ=8см В С-? АД-? на 6 см ˃ Найти: ВС, АД, СД 1. Из вершины С трапеции АВСД проведем высоту СН, СНАД. АВСД – прямоугольник: ВС=АН, АВ=СН. АД=АН+НД Ад=6+ВС (по условию). Тогда: 6+ВС=АН+НД 6+ВС=ВС+НД НД=6(см) 2. Рассмотрим СНД: СНД=90°, СН=8см, НД=6см. По теореме Пифагора: СД=10 СД= — 10 (не удовлетворяет условию) 3. АД=6+ВС (6+2ВС)∙4=120 6+2ВС=30 2ВС=24 ВС=12 (см) АД=6+ВС=6+12=18(см) Ответ: ВС=12см, АД=18см, АВ=8см, СД=10см.	Дано: Решение: АВСД — трапеция АВ=12см ВС = 14см АД = 30см Найти: 1. Проведем из вершины В трапеции АВСД высоту ВН: ВНАД 2.Рассмотрим АД׀׀ВС и АВ-секущую. АВС и ВАД – односторонние, тогда ВАН=180° — АВС=180°-150°=30° 3. Рассмотрим АВН: АНВ=90° ВН=0,5∙АВ=0,5∙12=6(см) (по теореме о катете лежащем против угла в 30°). 4.

СПЕЦИФИКАЦИЯ

контрольной работы по математике

для учащихся 8 А класса МБОУ Гимназии№10

1. Назначение контрольной работы

Контрольная работа проводилась по запросу рособрнадзора в третьей четверти 2017-2018 учебного года с целью определения уровня освоения обучающимися 8 А классов предметного содержания курса математики по программе основной образовательной программы школы и выявления элементов содержания, вызывающих наиболее затруднение.

2. Документы, определяющие содержание и параметры контрольной работы

Содержание и структура работы определены на базе Федеральный компонент государственного стандарта основного общего образования (Приказ Минобразования России «Об утверждении Федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования» от 05.03.2004 г. 1089).

 3. Структура контрольной работы

Работа по математике состоит из:

Части 1, содержащей 5 заданий. Три задания из модуля «Алгебра», два задания из модуля «Геометрия». Ответами к заданиям части 1 № 1–5 является число, иррациональное выражение, последовательность цифр. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Баллы, полученные обучающимися за выполненные задания, суммируются.

Части 2, содержащей 3 задания. Два здания из модуля «Алгебра», одно задание из модуля «Геометрия». Ответ к заданиям части 2 № 6-8 включают в себя подробное описание всего хода выполнения задания. При оформлении ответа, укажите номер задания и запишите его полное решение. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Контрольная работа составлена в двух вариантах. Варианты работ являются параллельными, под одними и теми же порядковыми номерами во всех вариантах представлены задания одинаковой сложности, позволяющие проверить сформированность одних и тех же предметных умений у учащихся.

4. Время выполнения работы

Среднее время выполнения одного задания 5-6 минут. Ориентировочное время выполнения контрольной работы – 45 минут.

5. Условия проведения контрольной работы, включая дополнительные материалы и оборудование

Строгое соблюдение инструкции по проведению контрольной работы. Дополнительные материалы и оборудование не предусмотрены. Работа рассчитана на обучающихся 8 А класса, изучающих алгебру по учебнику А.Г. Мордковича, в объеме 4 ч. в неделю и геометрию по учебнику Л.С. Атанасяна, в объеме 2ч. в неделю.

6. Система оценивания отдельных заданий и работы в целом

Часть 1. За верное выполнение каждого задания Части 1 ученик получает по 1 баллу. За неверный ответ или его отсутствие выставляется 0 баллов.

Часть 2. За выполнение задания №6 может быть выставлено от 0 до 2 баллов.

Баллы	Содержание критерия
2	Обосновано получен верный ответ
1	Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с ее учетом дальнейшие шаги выполнены верно
0	Решение не соответствует ни одному из критериев, перечисленных выше.

За выполнение задания №7 может быть поставлено от 0 до 2 баллов.

Баллы	Содержание критерия
2	Графики построены верно, верно найдены корни уравнения.
1	Графики построены верно, но искомые корни найдены неверно или не найдены.
0	Решение не соответствует ни одному из критериев, перечисленных выше.

За выполнение задания №8 может быть поставлено от 0 до 2 баллов.

Баллы	Содержание критерия
2	Ход решения верный, все его шаги выполнены правильно, получен верный ответ.
1	Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена вычислительная ошибка.
0	Решение не соответствует ни одному из критериев, перечисленных выше.

Максимальное количество баллов, которые могут получить учащиеся за весь объем контрольной работы 11 баллов.

Шкала перевода баллов в отметку
«5»	8-11 баллов
«4»	6-7 баллов
«3»	3-5 баллов
«2»	0-2 балла

7. Распределение заданий контрольной работы по элементам содержания

В таблице 1 дана информация о структуре, общем числе и типах заданий в вариантах контрольной работы по математике для учащихся 8 А класса.

Таблица №1

Обозначение задания в работе	Проверяемые элементы содержания	Максимальный балл за выполнение задания
1	Числа и вычисления	1
2	Функции и графики	1
3	Числа и вычисления	1
4	Геометрические фигуры и их свойства	1
5	Многоугольники	1
6	Алгебраические выражения	2
7	Уравнения. Числовые функции.	2
8	Измерение геометрических величин	2

8.Перечень требований к уровню подготовки,проверяемому на контрольной работе по математике

Таблица №2

Код требования	Умения, проверяемые на контрольной работе	Уровень стандарта среднего общего образования по физике
1.	Уметь выполнять вычисления и преобразования
1.1.	Выполнять, сочетая устные и письменные приемы, арифметические действия с рациональными числами; вычислять значения числовых выражений; переходить от одной формы записи чисел к другой.	Базовый
2.	Уметь выполнять преобразования алгебраических выражений
2.2.	Выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями.	Базовый
2.3.	Выполнять разложение многочленов на множители.	Повышенный

3.	Уметь решать уравнения, неравенства и их систем
3.3.	Применять графические представления при решении уравнений, систем, неравенств.	Повышенный
4.	Уметь строить и читать графики функций
4.1.	Определить координаты точки плоскости, строить точки с заданными координатами.	Базовый
4.2.	Определять значение функции по значению аргумента при различных способах задания функции, решать обратную задачу.	Базовый
4.4.	Строить графики изученных функций, описывать их свойства.	Базовый
5.	Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
5.1.	Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).	Базовый
5.2.	Распознавать геометрические фигуры на плоскости, различать их взаимное расположение, изображать геометрические фигуры; выполнять чертежи по условию задачи.	Повышенный

Примечание.В итоговой контрольной работе, выполняемой обучающимися, может проверяться только часть элементов содержания и умений, перечисленных в вышеприведенных таблицах.

9. Условия проверки работы.

Контрольная работа проверяется учителем, работающим в данном классе.

Учитель математики ____________________ Е.В. Жихарева

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/351744-kontrolnaja-rabota-po-matematike-8-klassa

Срезовая работа по математике 11 класс :: battraphama

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

За 1 четверть в 5 классе. Раздел:. Экзаменационный материал по алгебре за курс 8 класса составлен на основе. Открыт прием материалов на фестиваль. Дидактические материалы по математике, 6 класс скачать с .:. Ключи прилагаются. Учебник: Алимов и др. Промежуточный срез.

Дневник по литературе — 8 класс. Срезовая. Входной срез по математике.11 класс. Промежуточные срезовые работы по информатике. Тесты по математике для учителей. Тестовая работа по геометрии для 9. Тематический тест по. Персональный сайт учителя математики Лях А. П.

По математике. Контрольная работа по математике за 1 полугодие уч.г. Учащихся 11 классов. Список книг для внеклассного чтения для 6 класса. Билеты с ответами проверки знаний рабочих для работы в люльке. Варианты итогового теста 11.

Класс в формате ЕГЭ профильный уровень. Проверка вычислительных навыков в 11 классеапрель. Просмотров: 850 Комментариев: 0. Методический материал для медсестры. В контрольной работе заданий. Экзаменационный материал по алгебре за курс 8 класса составлен на.

Контрольные работы по математике для 1 8 класса. Всероссийская. Результаты срезовых контрольных работ в динамике за два. Итоговая контрольная работа по алгебре класс. Итоговые срезовые работы по математике. Контрольная работа по математике за 1 полугодие уч.г. Учащихся. Читательский.

Тест 1 за первое. Промежуточный. Контрольные срезовые работы накануне ЕГЭ: 19 учащихся не справились с заданиями. Контрольные срезовые работы для учащихся 11 классов. Дидактические материалы по математике, 6 класс скачать с. Приведены ответы к ним. Итоговая работа по математике.

 

Вместе с Срезовая работа по математике 11 класс часто ищут

 

срезовая контрольная работа по химии 9 класс.

срезовая контрольная работа по математике 6 класс.

срезовая контрольная работа по математике 9 класс.

срезовая работа по химии 9 класс ответы.

срезовая работа по математике 9 класс.

срезовая работа по географии 9 класс

 

Читайте также:

 

Учебник по технологии 7 класс симоненко читать

 

Домашние задание по математике 3 класс е.п.бененсон

 

Гдз по геометрии 7-9 классов л.с.атанасян

 

Теорема о срезах — Математическая энциклопедия

Теорема, сводящая описание действия группы преобразований в некоторой окрестности $ U $ данной орбиты к описанию стабилизатора $ H $ точки $ x $ этой орбиты на некоторой пространство $ S $, которое «нормально» к орбите в точке $ x $. А именно, эта теорема утверждает, что $ U $ — однородное расслоение над $ G / H $ со слоем $ S $. Ниже приводятся точная постановка и формулировка, а также аналог теоремы для алгебраических групп преобразований, называемый теоремой этального среза.

Теорема о срезах для топологических групп преобразований.

Пусть $ G $ — топологическая группа преобразований хаусдорфова пространства $ X $. Подпространство $ S $ в $ X $ называется слоем в точке $ x \ in S $, если выполняются следующие условия:

i) $ S $ инвариантен относительно стабилизатора $ G_ {X} $ $ x $;

ii) объединение $ G (S) $ всех орбит, пересекающих $ S $, является открытой окрестностью орбиты $ G (x) $ точки $ x $;

iii) если $ G \ times_ {G _ {x}} S $ — однородное расслоение над $ G / G_x $ со слоем $ S $, то эквивариантное отображение $ \ varphi: G \ times _ {G _ {x}} S \ rightarrow X $, который однозначно определяется условием, что его ограничение на слой $ S $ над $ G_ {X} $ является тождественным отображением $ S \ rightarrow S $ (см.{- 1} (x) = S $; или по

v) $ S $ замкнуто в $ G (S) $ и из $ g (S) \ cap S \ neq \ emptyset $ следует $ g \ in G _ {x} $.

Теорема о срезах утверждает, что если выполняются определенные условия, то есть срез в точке $ x \ in X $. Условия зависят от рассматриваемого случая. Необходимость определенных условий объясняется следующим наблюдением.

Если есть срез $ S $ в $ x $, то существует окрестность $ U $ точки $ x $ (а именно, $ G (S) $) такая, что стабилизатор каждой точки $ U $ сопряжен в подгруппу $ G_ {X} $.{2} t _ {2} $ тривиально, но каждая окрестность точки $ x $ содержит точку, стабилизатор которой имеет порядок $ 3 $.)

Первым случаем, в котором была исследована справедливость теоремы о срезе, является случай компактной группы Ли $ G $. В этом случае было доказано, что если $ X $ — вполне регулярное пространство, то в каждой точке $ x \ in X $ есть срез. Если, кроме того, $ X $ — дифференцируемое многообразие и $ G $ действует гладко, то в каждом $ x $ имеется дифференцируемый слой специального вида. А именно, в этом случае имеется эквивариантный диффеоморфизм $ \ varphi $, являющийся тождеством на $ G (x) $ нормального векторного расслоения (см.также Нормальное пространство (к поверхности)) $ G (x) $ на открытую окрестность $ G (x) $ в $ X $. Образ под $ \ varphi $ слоя этого расслоения над $ x $ является срезом в $ x $, который является гладким подмногообразием $ X $, диффеоморфным векторному пространству.

Частный случай теоремы о срезе для компактных групп Ли был впервые доказан в [a2]. Затем сформулированные выше дифференцируемая и общая версии были доказаны соответственно в [a4] и [a8], [a9], [a10].

Теорема о срезах — незаменимый инструмент в теории групп преобразований, который часто позволяет свести исследование к простым групповым действиям, таким как линейные.В частности, теорема о срезах является ключевым элементом в доказательствах следующих двух основных фактов теории:

1) Если $ G $ — компактная группа Ли, $ X $ — сепарабельное метризуемое пространство и существует лишь конечное число классов сопряженных стабилизаторов точек в $ X $, то существует эквивариантное вложение $ X $ в Евклидово векторное пространство с ортогональным действием $ G $.

2) Пусть $ G $ — компактная группа Ли, гладко действующая на связном дифференцируемом многообразии $ X $.Тогда существуют подгруппа $ G _ {*} $ группы $ G $ и плотное открытое подмножество $ \ Omega $ группы $ X $ такие, что $ \ text {codim} (X \ backslash \ Omega) \ geq 1 $ и стабилизатор каждой точки $ x \ in X $ сопряжена подгруппа в $ G _ {*} $, которая совпадает с $ G _ {*} $, если $ x \ in \ Omega $.

Существуют версии теоремы о срезах для некомпактных групп. Например, пусть $ H $ — алгебраическая комплексная редуктивная группа, а $ H \ rightarrow \ operatorname {GL} (V) $ — его конечномерное алгебраическое представление, оба определены над действительными числами $ \ mathbf {R} $.Пусть $ H _ {\ mathbf {R}} $ — группа Ли вещественных точек $ H $, а $ G $ — подгруппа $ H _ {\ mathbf {R}} $, содержащая компонент связности единичного элемента. Пусть $ X $ — замкнутое $ H $ -инвариантное дифференцируемое подмногообразие в $ V _ {\ mathbf {R}} $, пространстве вещественных точек $ V $. Тогда, [a7], для любой замкнутой орбиты $ G (x) $ в $ X $ существует эквивариантный диффеоморфизм $ \ varphi $ $ G $ -инвариантной окрестности $ \ tilde {U} $ точки $ G (x) $ в нормальном векторном расслоении $ G (x) $ на $ G $ -инвариантную насыщенную окрестность $ U $ $ G (x) $ в $ X $ (окрестность $ U $ насыщена, если тот факт, что замыкание орбиты пересекает $ U $ означает, что эта орбита лежит в $ U $).В этом случае образ под $ \ varphi $ слоя естественной проекции $ \ tilde {U} \ rightarrow G (x) $ над $ x $ является срезом в $ x $ для действия $ G $ на $ X $.

Теорема о срезах для алгебраических групп преобразований.

Пусть $ G $ — группа алгебраических преобразований алгебраического многообразия $ X $, определенная над алгебраически замкнутым полем $ k $. Очень редко в этой ситуации выполняется буквальный аналог приведенной выше теоремы о срезах. Грубо говоря, причина в том, что открытые по Зарискому множества «слишком велики» (см. [A12], 6.1). Можно получить алгебраический аналог действия компактной группы Ли на дифференцируемом многообразии, если взять $ G $ как редуктивную группу, а $ X $ — аффинное многообразие. В этой настройке аналог среза задается понятием этального среза, определяемым следующим образом.

Пусть $ x $ — точка $ X $ такая, что орбита $ G (x) $ замкнута. Пусть $ S $ — аффинное $ G_ {X} $ — инвариантное подмногообразие в $ X $, содержащее $ x $. Как и выше, можно рассматривать однородное расслоение $ G \ times_ {G _ {x}} S $ над $ G / G_x $ со слоем $ S $ и отображение $ \ varphi: G \ times _ {G _ {x }} S \ rightarrow X $.В этой ситуации $ G \ times_ {G _ {x}} S $ — аффинное многообразие, $ \ varphi $ — морфизм, есть категорные факторы $ \ pi: X \ rightarrow X // G $, $ \ pi _ {G \ times_ {Gx} S}: G \ times _ {G _ {X}} S \ rightarrow (G \ times _ {Gx} S) / / G $ и индуцированный морфизм $ \ varphi / \! / G: (G \ times_ {G _ {x}} S) / \! / G \ rightarrow X / \! / G $, ср. [a12]. Подмногообразие $ S $ называется этальным срезом в $ x $, если

i) $ \ pi _ {G \ times_ {G _ {X}}} S $ получается из $ \ pi _ X $ посредством замены базы $ \ varphi H G $; а также

ii) $ \ varphi H G $ — этальный морфизм.

Теорема этального среза, доказанная в [a6], утверждает, что существует этальный срез в каждой точке $ x \ in X $ такой, что орбита $ G (x) $ замкнута.

Если $ k $ — это $ \ mathbf {C} $, поле комплексных чисел, а $ x $ — гладкая точка $ X $, то теорема об этальном срезе подразумевает, что существует аналитический срез в $ x $ . Точнее, существует инвариантная аналитическая окрестность $ G (x) $ в $ X $, которая аналитически изоморфна инвариантной аналитической окрестности $ G (x) $ в нормальном векторном расслоении $ G (x) $, cf .[a7], [a12].

Подобно теореме о срезе для топологических групп преобразований, этальная теорема о срезе является незаменимым результатом при исследовании алгебраических групп преобразований; см. [a6] для ознакомления с некоторыми основными результатами, выведенными из этой теоремы.

Список литературы

[a1]	G.E. Бредон, «Введение в компактные группы преобразований», Акад. Пресс (1972) MR0413144 Zbl 0246.57017
[a2]	A.M. Глисон, «Пространства с компактной группой Ли преобразований» Proc.Амер. Математика. Soc. , 1 (1950) стр. 35–43 MR0033830 Zbl 0041.36207
[a3]	К. Яних, «Differenzierbare $ G $ -Mannigfaltigkeiten», Lecture Notes Math. , 6 , Springer (1968) MR0202157 Zbl 0153.53703
[a4]	J.L. Koszul, «Sur somes groupes de transformation de Lie» Colloq. Inst. C.N.R.S., Géom. Diff. , 52 (1953) стр. 137–142 MR0059919
[a5]	Koszul, J.Л., «Лекции о группах преобразований», Tata Inst. (1965) MR218485 Zbl 0195.04605
[a6]	Luna, D., «Slices étales» Bull. Soc. Математика. France , 33 (1973) pp. 81–105 Zbl 0286.14014
[a7]	Luna, D., «Sur specifices opérations différentiables des groups de Lie» Amer. J. Math. , 97 (1975) стр. 172–181
[a8]	Д. Монтгомери, К.Т. Ян, «Существование среза» Ann. математики. , 65 (1957) pp. 108–116 Zbl 0078.16202
[a9]	Г.Д. Мостоу, «Об одной теореме Монтгомери» Ann. математики. , 65 (1957) стр. 432–446
[a10]	Р. Пале, «Вложения компактных дифференцируемых групп преобразований в ортогональные представления» J. Math. Мех. , 6 (1957) стр. 673–678
[a11]	R.С. Пале, «Срезы и эквивариантные вложения», сем. Группы трансформации , Princeton Univ. Press (1960)
[a12]	В.Л. Попов, Э. Винберг, «Теория инвариантов», Алгебраическая геометрия IV , Энцикл. Математика. Sci. , 55 , Springer (1994) стр. 122–284 MR1456471 Zbl 1099.13012 Zbl 1088.81075 Zbl 1065.82003 Zbl 1053.82006 Zbl 0783.14028 Zbl 0754.13005 Zbl 0736.15019 Zbl 0735.14010 Zbl 0789.14008 Zbl 0679.140.14004 Zbl 0478.14006
[a13]	Wu Yi Hsiang, «Теория когомологий топологических групп преобразований», Ergebn. Математика. , 85 , Springer (1979) Zbl 0511.57002

Как цитировать эту запись:
Теорема о срезах. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Slice_theorem&oldid=49893

Как правильно нарезать торт

Поделиться может быть сложно.Это знает каждый ребенок, и математики тоже. Итак, математики потратили много времени на размышления о том, как упростить обмен.

Математики особенно любят делить праздничный торт. Не просто праздничный торт, а с обилием глазури и различных украшений, с орехами здесь и кокосами. Затем они спрашивают: если двум людям больше нравятся разные части торта, как они могут разделить торт на две части, чтобы оба были довольны тем, что получили каждый?

Учителя и родители, подпишитесь на шпаргалку

Еженедельные обновления, которые помогут вам использовать Science News для студентов в учебной среде

Спасибо за регистрацию!

При регистрации возникла проблема.

Вы и ваш друг хотите разделить торт на две части таким образом, чтобы каждый из вас был доволен полученным кусочком. Как бы ты это сделал?

Есть старое решение, известное как «Я режу, вы выбираете». Вы начинаете с того, что разрезаете торт на две части, которые вам одинаково нравятся. Затем ваш друг выбирает тот, который ей больше нравится.

Две детали не обязательно должны быть одинакового размера. Например, если вы особенно любите орехи, вы можете сделать кусок с меньшим количеством орехов больше, чтобы вы были счастливы, независимо от того, какой кусок выберет ваш друг. В результате вы получите либо меньший кусок с большим количеством орехов, либо большой кусок с меньшим количеством орехов.

Но Стивен Брамс из Нью-Йоркского университета не считает это справедливым. Когда вы закончите, вы получите кусок, который, по вашему мнению, стоит половину стоимости торта.Но ваша подруга может подумать, что она получила гораздо больше, чем половину стоимости торта.

Например, предположим, что вашему другу действительно нравится кокосовый орех, а в более крупном, менее ореховом куске много кокоса. Тогда она подумает, что получила действительно очень много. Ей досталось не только больше торта, но и лучшая часть!

Брамс говорит, что разделение должно считаться справедливым только в том случае, если два человека думают, что оба получили куски одинаковой стоимости. Он разработал новую процедуру разрезания торта, благодаря которой это произошло.

При разделении этого торта, A отмечает разрез, где, по вашему мнению, две части имеют одинаковую ценность. B показывает разделение, в котором, по мнению вашего друга, две части равны. С помощью нового метода вы получите крайнюю левую деталь, а ваш друг — крайнюю правую деталь — .

Э. Роэлл

Вот как это работает. Вы и ваш друг рассказываете маме, где вы разделите торт на две части.Если вы двое выберете одно и то же место, она просто разделит торт на этом месте. Вы оба были бы одинаково довольны своими акциями.

Но предположим, что эти два пятна разные. Если бы ваше место было слева от места вашего друга, вы бы получили кусок слева от вашего места. Ваш друг поставит кусок справа от своего места. А посередине останется кусок. Затем ваша мама делит среднюю часть между вами и вашим другом.

Таким образом, каждый из вас получит по одной единице ценности — плюс бонус!

Замечательная идея, но практична ли такая процедура? Вы бы использовали это?

«Я не знаю, приносил ли кто-нибудь кроме меня торт и пытался его разделить», — говорит Джеймс Тантон, учитель математики в университете Св.Mark’s School в Саутборо, Массачусетс. На практике такие схемы часто не работают. «Люди слишком расплывчаты», — говорит он. «Они меняют свое мнение» — J.J. Rehmeyer

Идем дальше:

Рехмейер, Джули Дж. 2006. Хороший кусок: новый метод способствует справедливому питанию. Science News 170 (16 декабря): 390. Доступно по адресу http://www.sciencenews.org/articles/20061216/fob7.asp.

Петерсон, И. 1999. Справедливые акции. Muse 3 (май / июнь): 28.Доступно на www.sciencenewsforkids.org/pages/puzzlezone/
muse / muse0599.asp.

______. 1996. Формулы справедливости. Science News 149 (4 мая): 284-285. Доступно на http://www.sciencenews.org/pages/sn_arch/5_4_96/bob1.htm.

Авторы математики / названия «новые»

Новые поступления

Материалы, полученные со среды, 18 августа, 21 августа, по четверг, 19 августа, 21 августа, объявлено, пятница, 21 августа

[всего 261 запись: 1-261 ]
[отображение до 2000 записей на странице: меньше | подробнее]

Новые заявки на пт, 20 августа 21

[1] arXiv: 2108.08293 [pdf, другие]

[2] arXiv: 2108.08294 [pdf, ps, другое]

[3] arXiv: 2108.08299 [pdf, ps, другое]

[4] arXiv: 2108.08303 [pdf, ps, другое]

[5] arXiv: 2108.08330 [pdf, ps, другое]

[6] arXiv: 2108.08331 [pdf, другой]

[7] arXiv: 2108.08332 [pdf, ps, другое]

[8] arXiv: 2108.08337 [pdf, ps, другое]

[9] arXiv: 2108.08343 [pdf, ps, другое]

[10] arXiv: 2108.08345 [pdf, ps, другое]

[11] arXiv: 2108.08347 [pdf, другой]

[12] arXiv: 2108.08348 [pdf, ps, другое]

[13] arXiv: 2108.08351 [pdf, ps, другое]

[14] arXiv: 2108.08354 [pdf, другой]

[15] arXiv: 2108.08355 [pdf, ps, другое]

[16] arXiv: 2108.08357 [pdf, ps, другое]

[17] arXiv: 2108.08361 [pdf, ps, другое]

[18] arXiv: 2108.08370 [pdf, ps, другое]

[19] arXiv: 2108.08379 [pdf, другой]

[20] arXiv: 2108.08381 [pdf, другой]

[21] arXiv: 2108.08391 [pdf, другой]

[22] arXiv: 2108.08392 [pdf, ps, другое]

[23] arXiv: 2108.08396 [pdf, ps, другое]

[24] arXiv: 2108.08402 [pdf, ps, другое]

[25] arXiv: 2108.08410 [pdf, ps, другое]

[26] arXiv: 2108.08413 [pdf, ps, другое]

[27] arXiv: 2108.08419 [pdf, другой]

[28] arXiv: 2108.08424 [pdf, ps, другое]

[29] arXiv: 2108.08431 [pdf, другой]

[30] arXiv: 2108.08434 [pdf]

[31] arXiv: 2108.08437 [pdf, другой]

[32] arXiv: 2108.08446 [pdf, ps, другое]

[33] arXiv: 2108.08452 [pdf, ps, другое]

[34] arXiv: 2108.08457 [pdf, ps, другое]

[35] arXiv: 2108.08460 [pdf, ps, другое]

[36] arXiv: 2108.08461 [pdf, другой]

[37] arXiv: 2108.08466 [pdf, другой]

[38] arXiv: 2108.08469 [pdf, другой]

[39] arXiv: 2108.08475 [pdf, ps, другое]

[40] arXiv: 2108.08486 [pdf, другой]

[41] arXiv: 2108.08489 [pdf, другие]

[42] arXiv: 2108.08503 [pdf, другой]

[43] arXiv: 2108.08506 [pdf, ps, другое]

[44] arXiv: 2108.08512 [pdf, ps, другое]

[45] arXiv: 2108.08517 [pdf, ps, другое]

[46] arXiv: 2108.08519 [pdf, ps, другое]

[47] arXiv: 2108.08522 [pdf, ps, другое]

[48] arXiv: 2108.08524 [pdf, ps, другое]

[49] arXiv: 2108.08531 [pdf, ps, другое]

[50] arXiv: 2108.08533 [pdf, ps, другое]

[51] arXiv: 2108.08534 [pdf, ps, другое]

[52] arXiv: 2108.08540 [pdf, другой]

[53] arXiv: 2108.08547 [pdf, ps, другое]

[54] arXiv: 2108.08552 [pdf, ps, другое]

[55] arXiv: 2108.08554 [pdf, ps, другое]

[56] arXiv: 2108.08555 [pdf, ps, другое]

[57] arXiv: 2108.08564 [pdf, ps, другое]

[58] arXiv: 2108.08567 [pdf, ps, другое]

[59] arXiv: 2108.08572 [pdf, ps, другое]

[60] arXiv: 2108.08580 [pdf, ps, другое]

[61] arXiv: 2108.08588 [pdf, другой]

[62] arXiv: 2108.08595 [pdf, ps, другое]

[63] arXiv: 2108.08599 [pdf, другой]

[64] arXiv: 2108.08608 [pdf, ps, другое]

[65] arXiv: 2108.08609 [pdf, ps, другое]

[66] arXiv: 2108.08619 [pdf, ps, другое]

[67] arXiv: 2108.08620 [pdf, ps, другое]

[68] arXiv: 2108.08625 [pdf, ps, другое]

[69] arXiv: 2108.08629 [pdf, ps, другое]

[70] arXiv: 2108.08634 [pdf, ps, другое]

[71] arXiv: 2108.08639 [pdf, ps, другое]

[72] arXiv: 2108.08642 [pdf, другие]

[73] arXiv: 2108.08645 [pdf, ps, другое]

[74] arXiv: 2108.08646 [pdf, другой]

[75] arXiv: 2108.08648 [pdf, другой]

[76] arXiv: 2108.08651 [pdf, другой]

[77] arXiv: 2108.08652 [pdf, ps, другое]

[78] arXiv: 2108.08657 [pdf, ps, другое]

[79] arXiv: 2108.08660 [pdf, другой]

[80] arXiv: 2108.08661 [pdf, ps, другое]

[81] arXiv: 2108.08670 [pdf, другой]

[82] arXiv: 2108.08673 [pdf, ps, другое]

[83] arXiv: 2108.08675 [pdf, ps, другое]

[84] arXiv: 2108.08679 [pdf, ps, другое]

[85] arXiv: 2108.08680 [pdf, другой]

[86] arXiv: 2108.08684 [pdf, ps, другое]

[87] arXiv: 2108.08686 [pdf, ps, другое]

[88] arXiv: 2108.08693 [pdf, ps, другое]

[89] arXiv: 2108.08699 [pdf, ps, другое]

[90] arXiv: 2108.08701 [pdf, ps, другое]

[91] arXiv: 2108.08703 [pdf, другой]

[92] arXiv: 2108.08705 [pdf, ps, другое]

[93] arXiv: 2108.08707 [pdf]

[94] arXiv: 2108.08710 [pdf, ps, другое]

[95] arXiv: 2108.08714 [pdf, ps, другое]

[96] arXiv: 2108.08715 [pdf, другое]

[97] arXiv: 2108.08716 [pdf, другой]

[98] arXiv: 2108.08725 [pdf, ps, другое]

[99] arXiv: 2108.08727 [pdf, ps, другое]

[100] arXiv: 2108.08733 [pdf, ps, другое]

[101] arXiv: 2108.08737 [pdf, ps, другое]

[102] arXiv: 2108.08741 [pdf, ps, другое]

[103] arXiv: 2108.08742 [pdf, ps, другое]

[104] arXiv: 2108.08744 [pdf, ps, другое]

[105] arXiv: 2108.08746 [pdf, ps, другое]

[106] arXiv: 2108.08753 [pdf, ps, другое]

[107] arXiv: 2108.08758 [pdf, другой]

[108] arXiv: 2108.08774 [pdf, ps, другое]

[109] arXiv: 2108.08778 [pdf, ps, другое]

[110] arXiv: 2108.08779 [pdf, ps, другое]

[111] arXiv: 2108.08785 [pdf, ps, другое]

[112] arXiv: 2108.08794 [pdf, ps, другое]

[113] arXiv: 2108.08795 [pdf, ps, другое]

[114] arXiv: 2108.08798 [pdf, ps, другое]

[115] arXiv: 2108.08804 [pdf, другой]

[116] arXiv: 2108.08806 [pdf, ps, другое]

[117] arXiv: 2108.08811 [pdf, другой]

[118] arXiv: 2108.08814 [pdf, ps, другое]

[119] arXiv: 2108.08817 [pdf, ps, другое]

[120] arXiv: 2108.08820 [pdf, ps, другое]

[121] arXiv: 2108.08830 [pdf, ps, другое]

[122] arXiv: 2108.08831 [pdf, ps, другое]

[123] arXiv: 2108.08832 [pdf, ps, другое]

Перекрестные списки на пт, 20 августа 21

[124] arXiv: 2108.08300 (перекрестный список из Quant-ph) [pdf, другое]

[125] arXiv: 2108.08316 (кросс-лист от Quant-ph) [pdf, другое]

[126] arXiv: 2108.08352 (перекрестный список из cs.DL) [pdf]

[127] arXiv: 2108.08358 (перекрестный список из q-bio.QM) [pdf, другое]

[128] arXiv: 2108.08399 (перекрестный список из astro-ph.IM) [pdf]

[129] arXiv: 2108.08462 (перекрестный список из eess.SY) [pdf, другие]

[130] arXiv: 2108.08481 (перекрестный список из cs.LG) [pdf, другое]

[131] arXiv: 2108.08502 (кросс-лист из eess.SY) [pdf, ps, другое]

[132] arXiv: 2108.08545 (перекрестный список из cs.DC) [pdf, другое]

[133] arXiv: 2108.08655 (перекрестный список из cs.LG) [pdf, ps, другое]

[134] arXiv: 2108.08658 (перекрестный список из eess.SY) [pdf, другие]

[135] arXiv: 2108.08668 (перекрестный список из gr-qc) [pdf, ps, other]

[136] arXiv: 2108.08687 (перекрестный список из стат.ML) [pdf, другой]

[137] arXiv: 2108.08694 (перекрестный список из hep-th) [pdf, другие]

[138] arXiv: 2108.08709 (перекрестный список из cs.LG) [pdf, другой]

[139] arXiv: 2108.08720 (перекрестный список из Quant-ph) [pdf, ps, other]

[140] arXiv: 2108.08730 (перекрестный список из cs.CE) [pdf, другие]

[141] arXiv: 2108.08765 (перекрестный список из cs.LG) [pdf, ps, другое]

[142] arXiv: 2108.08767 (кросс-лист из cs.LG) [pdf, ps, другое]

[143] arXiv: 2108.08776 (перекрестный список из Quant-ph) [pdf, ps, другое]

[144] arXiv: 2108.08781 (перекрестный список из Physics.ao-ph) [pdf, другой]

[145] arXiv: 2108.08835 (перекрестный список из cond-mat.str-el) [pdf, другой]

Замены на пт, 20 августа 21

[146] arXiv: 1007.3881 (заменено) [pdf]

[147] arXiv: 1601.05055 (заменено) [pdf, ps, другое]

[148] arXiv: 1709.08618 (заменено) [pdf, другое]

[149] arXiv: 1806.02188 (заменено) [pdf, другое]

[150] arXiv: 1808.09608 (заменено) [pdf, ps, другое]

[151] arXiv: 1810.00734 (заменено) [pdf, ps, другое]

[152] arXiv: 1810.11837 (заменено) [pdf, ps, другое]

[153] arXiv: 1812.03133 (заменено) [pdf, ps, другое]

[154] arXiv: 1902.05666 (заменено) [pdf, ps, другое]

[155] arXiv: 1904.00779 (заменено) [pdf, ps, другое]

[156] arXiv: 1904.07842 (заменено) [pdf, ps, другое]

[157] arXiv: 1905.00486 (заменено) [pdf, ps, другое]

[158] arXiv: 1905.02547 (заменено) [pdf, ps, другое]

[159] arXiv: 1905.06031 (заменено) [pdf, ps, другое]

[160] arXiv: 1906.07215 (заменено) [pdf, ps, другое]

[161] arXiv: 1907.00310 (заменено) [pdf, другое]

[162] arXiv: 1907.05366 (заменено) [pdf, ps, другое]

[163] arXiv: 1908.02712 (заменено) [pdf, ps, другое]

[164] arXiv: 1910.06468 (заменено) [pdf, другое]

[165] arXiv: 1910.07133 (заменено) [pdf, другое]

[166] arXiv: 1910.09333 (заменено) [pdf, другое]

[167] arXiv: 1910.09419 (заменено) [pdf, ps, другое]

[168] arXiv: 1912.09766 (заменено) [pdf, другое]

[169] arXiv: 2001.04887 (заменено) [pdf, ps, другое]

[170] arXiv: 2001.06254 (заменено) [pdf, ps, другое]

[171] arXiv: 2002.00591 (заменено) [pdf, ps, другое]

[172] arXiv: 2003.08528 (заменено) [pdf, ps, другое]

[173] arXiv: 2003.12113 (заменено) [pdf, другое]

[174] arXiv: 2004.00759 (заменено) [pdf, другое]

[175] arXiv: 2005.07482 (заменено) [src]

[176] arXiv: 2005.09235 (заменено) [pdf, ps, другое]

[177] arXiv: 2006.02710 (заменено) [pdf, ps, другое]

[178] arXiv: 2006.03786 (заменено) [pdf, ps, другое]

[179] arXiv: 2006.07188 (заменено) [pdf, ps, другое]

[180] arXiv: 2006.16663 (заменено) [pdf, другое]

[181] arXiv: 2007.00766 (заменено) [pdf, ps, другое]

[182] arXiv: 2007.03193 (заменено) [pdf, другое]

[183] ​​arXiv: 2007.05737 (заменено) [pdf, ps, другое]

[184] arXiv: 2007.10253 (заменено) [pdf, другое]

[185] arXiv: 2007.12308 (заменено) [pdf, ps, другое]

[186] arXiv: 2008.10901 (заменено) [pdf, ps, другое]

[187] arXiv: 2008.13149 (заменено) [pdf, ps, другое]

[188] arXiv: 2009.01414 (заменено) [pdf, ps, другое]

[189] arXiv: 2009.05115 (заменено) [pdf, ps, другое]

[190] arXiv: 2009.05869 (заменено) [pdf, ps, другое]

[191] arXiv: 2009.06300 (заменено) [pdf, ps, другое]

[192] arXiv: 2010.02321 (заменено) [pdf, другое]

[193] arXiv: 2010.10579 (заменено) [pdf, другое]

[194] arXiv: 2010.13664 (заменено) [pdf, ps, другое]

[195] arXiv: 2010.15525 (заменено) [pdf, другое]

[196] arXiv: 2011.04089 (заменено) [pdf, другое]

[197] arXiv: 2011.06503 (заменено) [src]

[198] arXiv: 2011.08497 (заменено) [pdf, ps, другое]

[199] arXiv: 2011.11457 (заменено) [pdf, ps, другое]

[200] arXiv: 2011.13006 (заменено) [pdf, ps, другое]

[201] arXiv: 2011.13904 (заменено) [pdf, ps, другое]

[202] arXiv: 2012.04219 (заменено) [pdf, ps, другое]

[203] arXiv: 2012.07903 (заменено) [pdf, ps, другое]

[204] arXiv: 2101.02884 (заменено) [pdf, ps, другое]

[205] arXiv: 2101.03080 (заменено) [pdf, ps, другое]

[206] arXiv: 2101.04056 (заменено) [pdf, ps, другое]

[207] arXiv: 2101.05914 (заменено) [pdf, ps, другое]

[208] arXiv: 2101.09758 (заменено) [pdf, другое]

[209] arXiv: 2101.11694 (заменено) [pdf, ps, другое]

[210] arXiv: 2102.04562 (заменено) [pdf, другое]

[211] arXiv: 2102.05344 (заменено) [pdf, ps, другое]

[212] arXiv: 2102.06594 (заменено) [pdf, другое]

[213] arXiv: 2102.07513 (заменено) [pdf, ps, другое]

[214] arXiv: 2102.08777 (заменено) [pdf, ps, другое]

[215] arXiv: 2102.11672 (заменено) [pdf, ps, другое]

[216] arXiv: 2103.01659 (заменено) [pdf, ps, другое]

[217] arXiv: 2103.03603 (заменено) [pdf, ps, другое]

[218] arXiv: 2103.09562 (заменено) [pdf, другое]

[219] arXiv: 2103.12971 (заменено) [pdf, ps, другое]

[220] arXiv: 2103.14237 (заменено) [pdf, ps, другое]

[221] arXiv: 2103.14499 (заменено) [pdf, ps, другое]

[222] arXiv: 2104.01986 (заменено) [pdf, другое]

[223] arXiv: 2104.03529 (заменено) [pdf, другое]

[224] arXiv: 2104.06911 (заменено) [pdf, другое]

[225] arXiv: 2104.11346 (заменено) [pdf, ps, другое]

[226] arXiv: 2104.11748 (заменено) [pdf, ps, другое]

[227] arXiv: 2104.13674 (заменено) [pdf, другое]

[228] arXiv: 2104.13886 (заменено) [pdf, ps, другое]

[229] arXiv: 2104.14092 (заменено) [pdf, ps, другое]

[230] arXiv: 2105.01569 (заменено) [pdf, ps, другое]

[231] arXiv: 2105.02247 (заменено) [pdf, ps, другое]

[232] arXiv: 2105.10143 (заменено) [pdf, ps, другое]

[233] arXiv: 2105.12200 (заменено) [pdf, ps, другое]

[234] arXiv: 2105.12388 (заменено) [pdf, ps, другое]

[235] arXiv: 2106.00748 (заменено) [pdf, ps, другое]

[236] arXiv: 2106.05925 (заменено) [pdf, другое]

[237] arXiv: 2106.06205 (заменено) [pdf, ps, другое]

[238] arXiv: 2106.09818 (заменено) [pdf]

[239] arXiv: 2106.14106 (заменено) [pdf, другое]

[240] arXiv: 2107.00761 (заменено) [pdf, другое]

[241] arXiv: 2107.00903 (заменено) [pdf, ps, другое]

[242] arXiv: 2107.03556 (заменено) [pdf, ps, другое]

[243] arXiv: 2107.10051 (заменено) [pdf, ps, другое]

[244] arXiv: 2107.12198 (заменено) [pdf, другое]

[245] arXiv: 2107.13460 (заменено) [pdf, другое]

[246] arXiv: 2107.13615 (заменено) [pdf, ps, другое]

[247] arXiv: 2108.00590 (заменено) [pdf, ps, другое]

[248] arXiv: 2108.01796 (заменено) [pdf, ps, другое]

[249] arXiv: 2108.03651 (заменено) [pdf, ps, другое]

[250] arXiv: 2108.05104 (заменено) [pdf, другое]

[251] arXiv: 2108.05992 (заменено) [pdf, ps, другое]

[252] arXiv: 2108.06199 (заменено) [pdf, другое]

[253] arXiv: 2108.06632 (заменено) [pdf, ps, другое]

[254] arXiv: 2108.06750 (заменено) [pdf, ps, другое]

[255] arXiv: 2108.07010 (заменено) [pdf, ps, другое]

[256] arXiv: 2108.07372 (заменено) [pdf, другое]

[257] arXiv: 2108.07542 (заменено) [pdf, другое]

[258] arXiv: 2108.07599 (заменено) [pdf, другое]

[259] arXiv: 2108.07796 (заменено) [pdf, ps, другое]

[260] arXiv: 2108.08082 (заменено) [pdf, ps, другое]

[261] arXiv: 2108.08141 (заменено) [pdf, ps, другое]

[всего 261 запись: 1-261 ]
[отображение до 2000 записей на странице: меньше | подробнее]

Отключить MathJax (Что такое MathJax?)

---

Ссылки на: arXiv, интерфейс формы, найти, математика, недавний, 2108, контакт, помощь (доступ к ключевой информации)

---

Что такое разделение сети?

Срезы сети накладывают несколько виртуальных сетей поверх общей сети.Каждый сегмент сети может иметь свою собственную логическую топологию, правила безопасности и характеристики производительности — в пределах, налагаемых базовыми физическими сетями.

Различные сегменты могут быть выделены для разных целей, например для обеспечения того, чтобы конкретное приложение или служба получали приоритетный доступ к емкости и доставке, или изоляция трафика для определенных пользователей или классов устройств. Разделение сетей позволяет оператору сети максимально использовать сетевые ресурсы и гибкость услуг.

Основы разделения сети

Технологии нарезки в сетях Ethernet так же стары, как и виртуальные локальные сети (VLAN). Эта концепция была более полно реализована с появлением программно-определяемых сетей и, в последнее время, программно-определяемых глобальных сетей (SD-WAN), которые применяют концепции SDN к глобальным сетям. SDN отделяет плоскость управления сетью от плоскости обработки пакетов данных. Это позволяет плоскости управления определять виртуальные сети путем определения правил обработки пакетов и передачи этих правил устройствам уровня данных для выполнения.

Этот элемент управления плоскостью данных применяется как к физическим, так и к виртуальным сетевым устройствам, управляемым контроллером SDN, который представляет собой физический коммутатор в стойке или виртуальный коммутатор, работающий в облачной среде или на гипервизоре в центре обработки данных.

В некоторых случаях оператору сети потребуется или потребуется выделить сетевую инфраструктуру для определенного сегмента сети, например, назначить виртуальный межсетевой экран определенной виртуальной сети вместо использования общего межсетевого экрана.В некоторых случаях этот шаг выполняется для удовлетворения конкретных требований заказчика или требований сетевой безопасности. В других случаях сетевые менеджеры будут стремиться улучшить производительность сети или минимизировать накладные расходы на предоставление услуг. Например, операторы сети могут развернуть экземпляр недорогого или бесплатного межсетевого экрана вместо того, чтобы платить за более дорогой.

Обратной стороной нарезки является агрегация . Подход SDN действительно обеспечивает агрегирование физических подключений — например, объединение нескольких физических подключений в коммутатор — с полученной объединенной емкостью, которая затем становится доступной для разделения.

Как работает срезка сети в 5G?

Разделение сети — ключевая особенность 5G, в которой те же принципы виртуализации применяются к сетям радиодоступа (RAN) и поддерживающим транзитным и базовым сетям оператора связи, которые лежат в основе 5G. Нарезка позволяет поставщикам услуг предоставлять клиентам значимые гарантии, например, в отношении минимальной пропускной способности для их соединений или приоритетной доставки пакетов от определенных типов устройств или приложений.

Оператор сети 5G может физически разделить трафик в разных радиосетях, разделить одну сеть или объединить пропускную способность нескольких сетей и разделить объединенные ресурсы.Это позволяет операторам сетей 5G выбирать характеристики, необходимые для поддержки целевых уровней эффективности использования спектра, пропускной способности трафика и плотности соединений, то есть количества устройств, которые могут подключаться из заданного пространства.

Сценарии использования нарезки сети

Разделение сети поддерживает сценарии использования, ориентированные на производительность, емкость и безопасность. Многие варианты использования связаны с развивающимися бизнес-моделями Интернета вещей (IoT). Некоторые варианты использования среза сети включают следующее:

• Производительность. Компания, зависящая от сети 5G для автономного управления транспортными средствами, может заключить договор на сегмент мобильной сети с задержками менее 5 миллисекунд (мс) с гарантированной минимальной пропускной способностью для каждого транспортного средства для обеспечения оперативного управления. Провайдер предоставит сегмент оборудования с наименьшей задержкой и путей между транспортными средствами и облачными или граничными ресурсами и зарезервирует достаточную емкость для достижения целевой пропускной способности.
• Вместимость. Для системы мониторинга безопасности в большой аудитории задержка может не иметь значения.Но охранная компания может захотеть купить гарантированную доставку данных камеры. Другими словами, компания хотела бы, чтобы ее трафик имел пропускную способность 1,5 мегабит в секунду (Мбит / с) на каждую камеру без потери пакетов. Провайдер может объединить несколько вариантов подключения и устройств обработки, чтобы удовлетворить потребности этого сегмента.
• Безопасность. Для системы мониторинга здоровья человека в мегаполисе больница может захотеть изолировать весь трафик к кардиостимуляторам и от них.Это минимизирует риск утечки данных о клиентах и ​​угрозу компрометации канала управления — поэтому потребуется срез с однопользовательскими устройствами.

Бизнес и возможности предприятия

Предприятия и малые предприятия находят нарезку в своих собственных сетях привлекательным вариантом как для управления производительностью, так и для управления безопасностью, отсюда и быстрый рост технологий SD-WAN и сегментации сети. По мере того, как сети 5G продолжают развиваться и распространяться, нарезка увеличивает полезность беспроводной глобальной сети (WWAN) и корпоративной беспроводной локальной сети (WLAN).

• WWAN. До появления 5G небольшие филиалы полагались на 4G Long-Term Evolution (LTE) в качестве резервного средства связи на случай отказа основных проводных соединений и, реже, использовали его в качестве основного средства связи. 5G с более высокими скоростями и сегментацией ускорит внедрение модели WWAN и увеличит использование в качестве основного или единственного подключения, поскольку компании получат значимые соглашения об уровне обслуживания (SLA), отражающие способность операторов управлять емкостью и производительностью.
• WLAN. Те же возможности для большего контроля повысят привлекательность 5G в качестве замены частных WLAN на основе Wi-Fi. Традиционно предприятия предоставляют частную сеть и управляют ею, а также внедряют технологии удаленного и мобильного доступа к сети. С 5G и нарезкой многие вместо этого будут использовать только 5G. Пользователи получают тот же опыт независимо от местоположения благодаря услуге мобильного широкополосного доступа через частную сеть, интегрированную в глобальную сеть компании.

Как найти соотношение

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

6 Оценка на практике | Знание того, что знают студенты: наука и дизайн образовательной оценки

, программа тренировки и практики может быть подходящей для развития беглости и автоматизации навыка, но обычно не подходит на ранней стадии приобретения навыка (Goldman, Mertz, and Pellegrino, 1989).Также следует отметить, что в среде, где учитель доминирует над всеми транзакциями, частые вызовы и использование обратной связи могут сделать это доминирование еще более угнетающим (Broadfoot, 1986).

Однако есть достаточно доказательств того, что формативное оценивание может улучшить обучение, если оно предназначено для предоставления студентам обратной связи об определенных качествах их работы и рекомендаций о том, что они могут сделать для улучшения. Этот вывод подтверждается несколькими обзорами исследовательской литературы, в том числе обзорами Натриелло (1987), Крукса (1988), Фукса и Фукса (1986), Хэтти (1987, 1990) и Блэка и Вилиама (1998).Многие исследования, в которых изучались преимущества между предварительными и последующими тестами, сравнивая программы, в которых формирующая оценка была в центре внимания нововведений и использовались согласованные контрольные группы, показали величину эффекта в диапазоне от 0,4 до 0. 7 ¹ ( Блэк и Вильям, 1998).

Когда в экспериментальных исследованиях сравнивались разные типы обратной связи, оказалось, что одни типы более полезны для обучения, чем другие. Многие исследования в этой области показали, что обучение усиливается за счет обратной связи, направленной на достижение целей обучения (например,г., Батлер, 1988; Хэтти, 1987, 1990; Клюгер и ДеНиси, 1996). Это исследование предполагает, что другие типы обратной связи, например, когда учитель сосредотачивается на выставлении оценок, на назначении или удержании специальных наград или на воспитании чувства собственного достоинства (пытаясь улучшить самочувствие учащегося, независимо от качества его или ее работы ), может быть неэффективным или даже вредным.

Культура сосредоточения внимания на оценках и наградах и видение обучения в классе как соревнования, по-видимому, глубоко укоренилась, и ее трудно изменить.Эта ситуация более очевидна в Соединенных Штатах, чем в некоторых других странах (Hattie, Biggs, and Purdie, 1996). Культура конкуренции во многих классах и школах может быть препятствием для обучения, особенно когда она связана с убеждениями в неизменной природе способностей (Vispoel, Austin, 1995; Wolf, Bixby, Glen, and Gardner, 1991). Такие убеждения со стороны преподавателей могут привести как к тому, что учеников — открыто или скрытно — назовут «умными» или «скучными», так и к подтверждению и усилению таких ярлыков посредством практики отслеживания.

Международные сравнительные исследования — в частности, тематические исследования и видео-исследования, проведенные для Третьего международного исследования математики и естествознания

Математики раскрывают идеальный способ нарезать пиццу

Ежегодно во всем мире продается не менее 5 миллиардов пицц, и ​​каждую секунду съедается 350 ломтиков, но сколько из этих кусочков одинаково?

Два математика обнаружили, что правильное нарезание пирога с пиццей — это не просто искусство, оно основано на геометрии.

Предыдущее исследование показало, что можно создать 12 одинаковых ломтиков в пироге, но дуэт пошел дальше и доказал, что нет предела тому, сколько одинаковых ломтиков можно разрезать в пироге с пиццей.

Два математика обнаружили, что правильное нарезание пирога с пиццей — это не просто искусство, оно основано на геометрии. Предыдущее исследование показало, что в пироге можно создать 12 равных ломтиков, но дуэт пошел дальше и доказал, что нет предела тому, сколько равных ломтиков вы можете разрезать.

ПИЦЦА ПО НОМЕРАМ

Средняя пиццерия использует примерно 55 коробок для пиццы в день.

Ежегодно мы потребляем около 251 770 000 фунтов пепперони

Некоторые популярные в Японии начинки для пиццы — это кальмар и майо-джага (майонез, картофель и бекон)

Самая прибыльная независимая пиццерия в стране, Moose’s Tooth Pub и Пиццерия, находится в Анкоридже, Аляска. Годовой объем продаж составляет около 6 миллионов долларов.

36 процентов всех заказов на пиццу хотят, чтобы их пицца была начинкой пепперони

94 процента американцев едят пиццу регулярно

Источник: Pizza.com

Джоэл Хэддли и Стивен Уорсли из Ливерпульского университета предложили предыдущий метод разрезания идеального среза, известный как мозаика с моноэдральным диском, в результате чего получается 12 идентичных срезов.

Этот процесс начинается с разрезания пирога на шесть изогнутых трех сторон, пересекающих пирог.

Если все сделать правильно, это будет похоже на звезду, выходящую из центра.

Затем разделите эти формы на две, в результате получится внутренняя группа без корки и внешняя группа с коркой.

Команда пошла дальше этого исследования и разрезала еще больше срезов, создав аналогичные мозаики из изогнутых частей с нечетным числом сторон (известных как 5-угольники, 7-угольники и т. Д.), А затем разделив их пополам, как и в предыдущем случае. по мнению New Scientist.

«С математической точки зрения нет никакого предела, — сказал Хэддли New Scientist, — хотя вам может показаться непрактичным выполнение схемы за пределами 9-угольных элементов».

Затем в углах фигур были вырезаны зазубрины, чтобы сформировать остроконечные ломтики внутри круглого пирога.

«Я понятия не имею, есть ли какие-либо приложения к нашей работе, кроме резки пиццы», — сказал Хэддли, который пробовал нарезать пиццу таким способом.

Но сказал: «Результаты интересны с математической точки зрения, и вы можете получить несколько хороших картинок».

По мнению исследователей, разрезать пирог можно бесконечно, а если вы любите приключения, вы можете добавить больше выемок, чтобы получить еще более причудливые ломтики.

Джоэл Хэддли и Стивен Уорсли из Ливерпульского университета предложили предыдущий метод разрезания идеального среза, известный как мозаика с моноэдральным диском, в результате чего получается 12 идентичных срезов.Этот процесс начинается с разрезания пирога на шесть изогнутых трех сторон, пересекающих пирог

Другой математик решил еще одну головоломку с пиццей в 2013 году и опубликовал исследование, в котором утверждалось, что он придумал первую в истории формулу для пиццы с идеальными пропорциями. учитывать такие факторы, как соотношение долива к основанию.

Доктор Евгения Ченг сказала, что любители пиццы получают больше начинки на укус в пицце меньшего размера, но более равномерное распределение укусов в пицце большего размера.

Математик из Шеффилдского университета рассчитал соотношение, обеспечивающее максимальный вкус топпинга и основы.

Команда пошла дальше этого исследования и разрезала еще больше срезов, создав аналогичные мозаики из изогнутых частей с нечетным числом сторон — известных как 5-угольники, 7-угольники и т. Д. — а затем разделив их на две части, как и в предыдущем случае. требуемый метод, согласно New Scientist

.Он показывает, что даже если человек сохраняет одинаковое количество теста и начинки, соотношение начинки к основанию в среднем укусе изменяется в зависимости от размера пиццы, а в пицце меньшего размера обычно больше начинки. на укус, чем более крупные.

Д-р Ченг сказал, что дело не только в толщине основы, но и в балансе вкусов между топпингом и тестом, который определяет, сколько топпинга можно получить от одного укуса.

Она использовала d как постоянный объем теста и t для постоянного объема начинки, чтобы получить математическую формулу для отношения начинки к основанию в среднем укусе.

Затем в углах фигур были вырезаны зазубрины, чтобы сформировать остроконечные ломтики внутри круглого пирога.По словам исследователей, вы можете продолжать резать пирог бесконечно долго, а если вам хочется приключений, вы можете добавить больше выемок, чтобы получить еще более причудливые ломтики. имеет на 10 процентов больше начинки, чем средний кусок 14-дюймовой пиццы.

Формула также показывает, что, хотя в пицце меньшего размера больше начинки на укус, для домашних поваров, которые хотят добавить в свои творения много дополнительных услуг, существует больший риск того, что их пицца будет иметь сырое дно.

Она создала еще одну формулу, альфа, деленную на радиус пиццы в квадрате, чтобы получить размер корочки для пиццы разного диаметра.

Она объясняет, что размер корочки пиццы пропорционален толщине пиццы: чем крупнее пицца, тем тоньше основа и тем меньше корочка.

Формула: доктор Ченг объясняет, что «d» — это постоянный объем теста, а «t» — постоянный объем начинки. Остальное обеспечивает правильное соотношение основы и начинки для оптимального вкуса.

Она определила значение альфа 15 экспериментально, приготовив несколько пицц разного размера.

Математик придумал эти формулы, когда сетевой ресторан PizzaExpress попросил ее выяснить, почему ее 14-дюймовая пицца Romana, у которой более тонкая и хрустящая основа, чем у классической 11-дюймовой пиццы, оказывается такой популярной.

Доктор Ченг обнаружил, что секрет заключается в пропорциях 14-дюймовой пиццы, поскольку она готовится так же равномерно, как и меньшая версия, но начинка распределяется по большей площади и приближается к краю пиццы.

Тем не менее, согласно исследованиям, технически любителям пиццы в поисках максимальной начинки на укус следует выбрать 11-дюймовую классическую версию.

Исследователи также создали другую формулу, альфа, деленную на радиус пиццы в квадрате, чтобы получить размер корочки для пиццы разного диаметра. Она объясняет, что размер корочки пиццы пропорционален толщине пиццы — чем больше пицца, тем тоньше основа и тем меньше корочка

Она сказала: «Я всегда ищу больше способов принести еду и вместе занимаюсь математикой, потому что это два моих любимых занятия, но большинство людей предпочитают еду.

«Мне нравится показывать, что математика есть повсюду в мире вокруг нас, и что мы можем использовать математику, чтобы дать логическое объяснение тому, что мы обнаружили интуитивно, например, что пицца меньшего размера подвержена большему риску иметь мокрый дно. ! ‘

Ребекка Фаррер, бренд-директор PizzaExpress, сказала, что обычные посетители сети могут не знать, что «это наше тесто, как наши пиццайоло растягивают его и как они укладывают начинку, что действительно имеет значение, гарантируя, что их любимая пицца будет приготовлена ​​идеально каждый раз». время.’

Формула появилась, когда PizzaExpress впервые с 1965 года подправляет тесто, добавляя 15 г в рецепты пиццы.

‘Это может показаться совсем не большим, но это означает, что толщина каждой пиццы Romana, которую раскатывают скалкой, чтобы обеспечить равномерное количество теста по всей основе и отсутствие воздушных карманов, даже больше последовательнее, чем раньше, — сказала г-жа Фаррер.

«Для людей, которые так же одержимы пиццей, как и мы, 15 г имеют решающее значение», — добавила она.

No related posts.