МАСТЕР-КЛАСС ГЕОМЕТРИЯ 9 КЛАСС КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «ВЕКТОРЫ» Предмет
МАСТЕР-КЛАСС
ГЕОМЕТРИЯ, 9 КЛАСС, КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «ВЕКТОРЫ»
Предмет: Геометрия
Тема: Контрольная работа по теме ”Векторы”
Класс: 9 класс
Педагог: Аширбекова Лариса Александровна, заместитель директора по воспитательной работе, учитель математики и информатики.
Учреждение образования: МОУ Шуринская средняя общеобразовательная школа Кемеровской области
Город: Кемеровская область
Цель урока: контроль знаний учащихся
Ход урока.
Организационный момент: объяснить цель урока.
Контрольная работа (тестирование)
Вариант 1
1. Вектором называется направленный …. (отрезок)
2. Векторы называются равными, если они сонаправлены и … (их длины равны)
3.
Дан треугольник АВС.
Выразите через векторы = и = вектор
А) — ; б) -; в) +
ABCD — трапеция. Найдите сумму векторов ++; разность векторов —
А) ++=, -=
Б) ++=, -=
В) ++=, —=
4. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина ВС, =, = . Выразите через векторы и следующие векторы:
А) , б) , в) , г)
А) А) = +, б) = , в) = —, г) =+
Б) А) = -, б) = , в) = -, г) =-
В) А) = +, б) = , в) = +, г) =-
5.
Одно основание трапеции на 4 см больше другого, а средняя линия равна 8 см. Найдите основания трапеции
а) 6 см и 10 см
б) 6 см и 8 см
в) 8 см и 10 см
Вариант 2
1. Закончи предложение.
От любой точки М можно отложить вектор, равный данному вектору, и притом только… (один)
2. Вставь пропущенное слово.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на … прямых
3. Дан треугольник АВС. Выразите через векторы = и = вектор .
А) —
Б) +
В) —
4. ABCD — трапеция. Найдите сумму векторов +; разность векторов —
а) +=, -=
б) +=, -=
в) +=, -=
5. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, =, =. Выразите через векторы и следующие векторы: А) , б) , в) , г)
А) ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, =, =.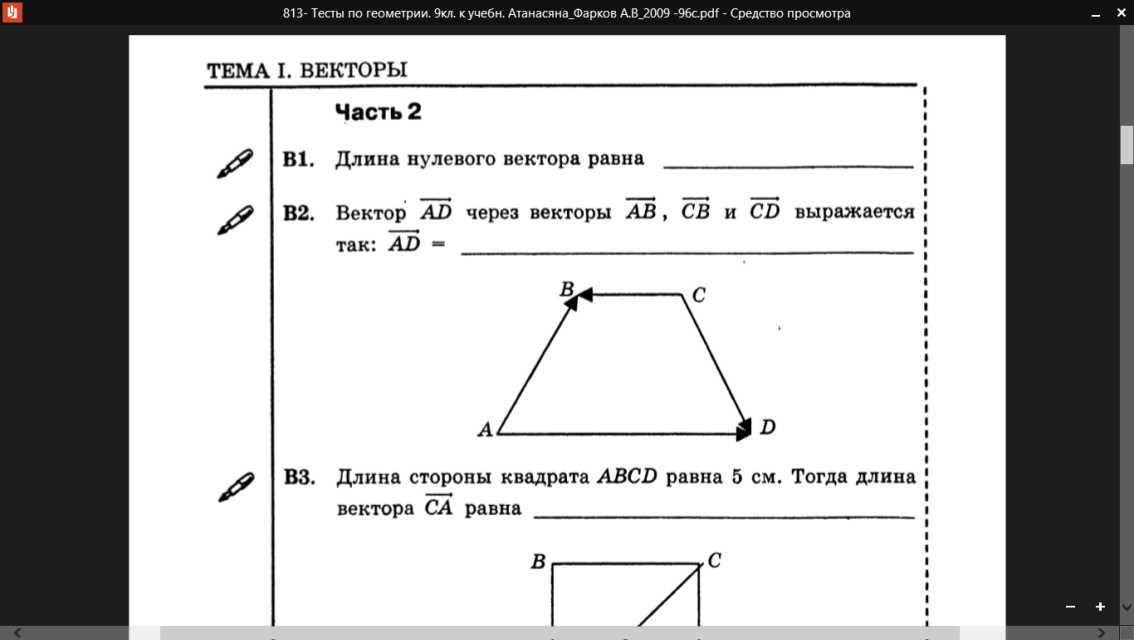
Выразите через векторы и следующие векторы: А) , б) , в) , г)
Б) а)=-, б) =, в) =-, г) =-
В) а)=+, б) =, в) =+, г) =-
Глава X. §1 Координаты вектора ( 2 часа)
Урок 7.Разложение вектора по двум неколлинеарным векторам.
Учащиеся должны:
Знать формулировку и доказательство леммы о коллинеарных векторах, и теорему о разложении по двум неколлинеарным векторам;
Уметь решать задачи, применяя полученные знания.
Ход урока
Организационный момент: назвать цели урока.
Анализ контрольной работы.
Объяснение нового материала:
План объяснения:
1. Разложение вектора по двум неколлинеарным векторам.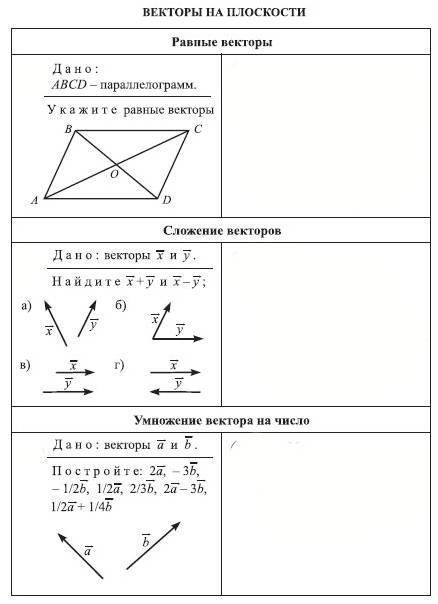
При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.
2. Лемма о коллинеарных векторах.
Лемма — это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.
Теорема:Если векторы и коллинеарны и 0, то существует такое число k, что = k.
Так как рассматриваемые векторы, по условию коллинеарны, то они могут иметь одинаковые направления. Рассмотрим два случая, когда векторы и сонаправлены и противоположно направлены.
Доказательство:
1) . Возьмем число . Так как k 0, то векторы k и сонаправлены (рисунок 1). Кроме того, их длины равны: k= k = =. Поэтому = k
2) . Возьмем число . Так как k и снова сонаправлены (рисунок2). Их длины также равны: k= k = =. Поэтому = k
рисунок2
3. Теорема о разложении вектора по двум неколлинеарным векторам.
Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Пусть и — данные неколлинеарные векторы, вектор представлен в виде
= х+у, где х и у — некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.
Доказательство:
Возможны два случая:
1) Вектор коллинеарен одному из векторов и , например, вектору (рисунок1). В этом случае по лемме о неколлинеарных векторах вектор можно представить в виде = у, где у — некоторое число, и, следовательно, =0+у, т.е. вектор разложении по векторам
и .
2) Вектор не коллинеарен ни вектору , ни вектору . Отметим какую-нибудь точку О и отложим от нее векторы = , =, = (рисунок2).
Через точку Р проведем прямую, параллельную прямой ОВ, и обозначим через А1 точку пересечения этой прямой с прямой ОА.
По правилу треугольника = + . Но векторы и коллинеарны соответственно векторам и , поэтому существует числа х и у, такие, что = х, = у. Следовательно, = х+у, т.е. вектор разложен по векторам и .
Докажем теперь, что коэффициенты х и у разложения определяются единственным образом. Допустим, что наряду с разложением = х+у имеет место другое разложение = х1+у1. Вычитая второе равенство из первого и используя правила действий над векторами, получаем =(х-х1) + (у-у1). Это равенство может выполняться только в том случае, когда коэффициенты х-х1 и у-у1 равны нулю. В самом деле, если предположить, например, что х-х1 0, то из полученного равенства найдем = -, а значит векторы и коллинеарны.
Но это противоречит условию теоремы. Следовательно, х-х1=0 и у-у1=0, откуда х=х1и у=у1. Это и означает, что коэффициенты вектора определяются единственным образом. Теорема доказана.
Выводу по теме:
1.Лемма — это вспомогательное утверждение, употребляемое при доказательстве одной или нескольких теорем.
2. Лемма (о коллинеарных векторах). Если векторы и коллинеарны и вектор 0, то существует такое число k, при котором = k
3. Пусть и — данные неколлинеарные векторы, вектор представлен в виде
= х+у, где х и у — некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.
4. Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
IV. Закрепление полученных знаний:
Тестирование:
1. Диагонали параллелограмма АВСD пересекаются в точке О. Выразите вектор через векторы и .
а) = —
б) = —
в) =+
2. №911 (а) Найдите такое число k, чтобы выполнялось равенство = k, если известно, что векторы и противоположно направлены и =0,5 см, = 2см.
а) -4
б) 4
в) 0,4
3. №911(б). Найдите такое число k, чтобы выполнялось равенство = k, если известно, что векторы и сонаправлены и =12 см, = 24 дм.
А) -20
Б) 20
В) 0,2
4. №912(а,г). Диагонали параллелограмма пересекаются в точке О, М — середина отрезка АО. Найдите, если это возможно, такое число k, чтобы выполнялось равенство: = k, = k
а) -2,
б) 2, 1
в) 2,
5. Дан произвольный треугольник АВС с медианой АD. Найдите , как вектор выражается через векторы и .
А) = +
Б) = +
В) = +
V. Подведение итогов.
VI. Задание на дом: п. 86, №№ 911 (в,г), 912 2,3 столбик), 916 (в,г)
1.Нарисовать равнобедренный АВС с основанием АС=4 см. Провести среднюю линию МD и найти её длину. 2. Найти длины указанных векторов. 3 . Найти площадь трапеции. 4 . Постройте четырехугольник АВСD по координатам его вершин: А(-5;0), В(-3;3), С(2;3), D(4;0). а) Определите вид получившейся фигуры и найдите её площадь. Ответ. Это равнобедренная трапеция. S= . б) Выпишите все коллинеарные векторы. Ответ.BCАD,CBDА, ВС DА, СВ АD в) Найдите длину средней линии. Ответ.7 | 1. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N(2; 4), К (2; — 2). а)Найдите среднюю линию МNK. Ответ. L =6:2=3. б) Найдите площадь МNK. Ответ.S=(8*6):2=24 кв.ед. 2. В равнобедренной трапеции высота делит большее основание на отрезки, равные5 и 12 см. Найдите среднюю линию трапеции. Ответ. 9,5 см. 3. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и. 4 .Найти площадь Ответ. 60 кв. 5.Сложите два вектора по правилу параллелограмма. | 1.Построить четырехугольник ABCD, если A(-4;7),B(0;1),C(-4;-5),D(-8;1). а) Определите вид получившейся фигуры и найдите её площадь. Ответ. Это ромб.S= =12*80:2=48кв.ед. 2.Найти. Ответ. 3. Начертите два неколлинеарных вектора и. Постройте вектор n, равный . 4. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции и её площадь. Ответ.L=11см. S= 5. В прямоугольном параллелепипеде известно, что ВD1=5, СС1-3, В1С1= . Найдите длину ребра АВ. Решение и ответ. ВD-4 (ученик должен увидеть пифагорову триаду), АВ=СD= = . Ответ.3. |
ед.Тематические контрольные работы по геометрии 9 класс | Тест по геометрии (9 класс):
Контрольные работы по геометрии 9 класс
Контрольная работа по теме: «Векторы.
Метод координат»
Вариант 1
- Найдите координаты и длину вектора если
- Даны координаты вершин треугольника ABC: A (-6; 1), B (2; 4), С (2; -2). Докажите, что треугольник ABC равнобедренный, и найдите высоту треугольника, проведенную из вершины A.
- Окружность задана уравнением Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат.
Вариант 2
- Найдите координаты и длину вектора если
- Даны координаты вершин четырехугольника ABCD: A (-6; 1), B (0; 5), С (6; -4),D (0; -8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
- Окружность задана уравнением Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — выполнены 3 задания, но есть ошибка;
«3» — верно выполнены 2 задания.
Контрольная работа по теме: «Соотношения между сторонами и углами треугольника.
Скалярное произведение векторов»
Вариант 1
- Найдите угол между лучом ОА и положительной полуосью Ох, если А(-1; 3).
- Решите треугольник АВС, если
- Найдите косинус угла М треугольника KLM, если К(1; 7), L(-2; 4), М(2; 0).
Вариант 2
- Найдите угол между лучом ОВ и положительной полуосью Ох, если В(3; 3).
- Решите треугольник ВСD, если
- Найдите косинус угла А треугольника АВC, если А(3; 9), В(0;6), С(4;2).
Критерии оценки:
«5» — верно выполнены все задания;
«4» — выполнены 3 задания, но есть ошибка;
«3» — верно выполнены 2 задания.
Контрольная работа по теме: «Длина окружности и площадь круга»
Вариант 1
- Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.
- Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 дм2.
- Найдите длину дуги окружности радиуса 3 см, если её градусная мера равна 150о.
Вариант 2
- Периметр правильного шестиугольника, вписанного в окружность, равен 48 см. Найдите сторону квадрата, вписанного в ту же окружность.
- Найдите длину окружности, если площадь вписанного в неё правильного шестиугольника равна .
- Найдите площадь кругового сектора, если градусная мера его дуги равна 120о, а радиус круга равен 12 см.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — выполнены 3 задания, но есть ошибка;
«3» — верно выполнены 2 задания.
Контрольная работа по теме: «Движения»
Вариант 1
- Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ.
2. Две окружности с центрами О1 и О2, радиусы которых равны, пересекаются в точках M и N. Через точку М проведена прямая, параллельная О1О2 и пересекающая окружность с центром О2 в точке D. Используя параллельный перенос, докажите, четырехугольник О1МDО2 является параллелограммом.
Вариант 2
- Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны CD.
2. Дан шестиугольник А1А2А3А4А5А6. Его стороны А1А2 и А4А5, А2А3 и А5А6, А3А4 и А6А1 попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали А1А4, А2А5, А3А6 данного шестиугольника пересекаются в одной точке.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — выполнены 2 задания, но есть ошибка;
«3» — верно выполнено 1 задание.
Контрольна робота по теми вектори 9 класс
Скачать контрольна робота по теми вектори 9 класс doc
Контрольная работа № 1 по геометрии для 9 класса.
по теме «Векторы». 2 вариант. 1. От любой точки М можно отложить вектор, равный данному вектору, и притом только (закончить предложение). 5.
Найдите площадь трапеции ABCD с боковой стороной BC = 5, если расстояния от вершин A и D до прямой BC равны 3 и 7 соответственно. По теме: методические разработки, презентации и конспекты. Контрольная работа по природоведению 5 класс; контрольная работа по географии 6 класс «Гидросфера».
Контрольная работа геометрия понятие вектора 9 itsufa.ru Скачать Посмотреть. Файл доступен только для скачивания. Когда даете методы по теме «Векторы» из учебника, то говорите, что метод параллелограмма это ЭКВИВАЛЕНТНЫЙ метод, так как в жизни никто вектора не переносит в любую точку пространства, иначе может оказаться, что сила может быть приложена к другому объекту в пространстве, а это абсурд.
Правильно говорить только о проекции векторов, все остальное с точки зрения физики приложения сил, скоростей, ускорений к объекту в пространстве смысла не имеет(не может сила одного объекта приложена к другому объекту в пространстве, если они лежат, например, на разных поверхностях).
Презентация, доклад по геометрии 9 класс Подготовка к контрольной работе №1 по теме Векторы. Презентация по геометрии 9 класс Подготовка к контрольной работе №1 по теме Векторы, предмет презентации: Геометрия.
Этот материал в формате pptx (PowerPoint) содержит 6 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Главная. Геометрия. Презентация по геометрии 9 класс Подготовка к контрольной работе №1 по теме Векторы. Слайды и текст этой презентации. Слайд 1. Текст слайда: Подготовка к контрольно. В данной презентации-проверочной работе содержится 5 заданий. В 1 — 3 заданиях отрабатывается понимание понятий сонаправленных, коллинеарных и равных векторов.
В 4-ом задании ученикам предлагается выбрать векторную величину из нескольких предложенных. Пятое задание представлено в виде утверждений, из которых нужно выбрать верное. Контрольные работы по темам: «Понятие вектора», «Метод координат», «Соотношения между сторонами и углами треугольники», «Длина окружности и площадь круга», «Движения» можно использовать для контроля знаний и умений обучающихся в конце изучения каждой темы курса геометрии за 9 класс.
Контрольные работы составлены в соответствии с рабочей программой к учебнику «Геометрия » автор Атанасян. ©. По кнопке ниже вы можете скачать методическую разработку «Контрольные работы по геометрии 9 класс» категории «Математика 9 класс» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Скачать материал Mb.
Контрольные работы по геометрии 8 класс. 2 комплект (4 варианта). Итоговый тест. Самостоятельная работа «Пропорциональные отрезки». Самостоятельная работа «Решение прямоугольных треугольников».
Творческая самостоятельная работа «Танграм». Творческая самостоятельная работа «Геометрия ножниц». Самостоятельная работа «Свойства ромба, квадрата, параллелограмма, прямоугольника». геометрия 9 класс (Атанасян). 1. Векторы. Координаты вектора. Простейшие задачи.Задачи на чертежах. 9 класс. 2. Уравнение окружности. Уравнение прямой. Задачи на чертежах. 9. Теоретические уроки, тесты и задания по предмету Векторы, 9 класс, Геометрия.
Задания составлены профессиональными педагогами. ЯКласс — онлайн-школа нового поколения. 9 класс. Учебники.
Темы обязательны для заполнения. Можно добавить 10 тем. отправить. дежурный. Контрольная работа 1. Вариант 1. № 4 ГДЗ Геометрия 9 класс Зив Б.Г. Разложите вектор по векторам. Поможете решить? Даны векторы Разложите вектор по векторам. 21 мая 1 ответ. ГДЗ Экзамены Геометрия 9 класс Зив Б. Г. 1 ответ. Роза Красникова. Пожаловаться.
ГДЗ Тема 21 Физика класс А.В.Перышкин Задание № Изобразите силы, действующие на тело. Привет всем! Нужен ваш совет, как отвечать.
PDF, txt, doc, docПохожее:
| Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 1
————————————————————————— Вариант 1
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 1
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 1
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 1
Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 2
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 2
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 2
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 2
————————————————————————— Контрольная работа №1 по теме «Векторы» (9 класс) Вариант 2
Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 1 Найдите координаты и длину вектора, еслиКонтрольная работа №2 по теме «Метод координат» (9 класс)Вариант 1 а) Докажите, что Δ MNK – равнобедренный. б) Найдите высоту, проведенную из вершины М. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 1 а) Докажите, что Δ MNK – равнобедренный. б) Найдите высоту, проведенную из вершины М. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 1 а) Докажите, что Δ MNK – равнобедренный. б) Найдите высоту, проведенную из вершины М. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 1 а) Докажите, что Δ MNK – равнобедренный. б) Найдите высоту, проведенную из вершины М. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 1 а) Докажите, что Δ MNK – равнобедренный. б) Найдите высоту, проведенную из вершины М. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 1 а) Докажите, что Δ MNK – равнобедренный. б) Найдите высоту, проведенную из вершины М. Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 2 а) Докажите, что Δ CDE – равнобедренный. б) Найдите высоту, проведенную из вершины C. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 2 а) Докажите, что Δ CDE – равнобедренный. б) Найдите высоту, проведенную из вершины C. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 2 а) Докажите, что Δ CDE – равнобедренный. б) Найдите высоту, проведенную из вершины C. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 2 а) Докажите, что Δ CDE – равнобедренный. б) Найдите высоту, проведенную из вершины C. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 2 а) Докажите, что Δ CDE – равнобедренный. б) Найдите высоту, проведенную из вершины C. ————————————————————————— Контрольная работа №2 по теме «Метод координат» (9 класс) Вариант 2 а) Докажите, что Δ CDE – равнобедренный. б) Найдите высоту, проведенную из вершины C. BestMathsВектор — это способ представления величины, имеющей размер и направление. например Полет самолета или траектория мяча для крикета Векторы также используются, чтобы показать, куда перемещается фигура при переводе. ОбозначениеВекторы иногда помечены как или. Можно представить вектор: Длина вектораДлину вектора (называемую его величиной) можно найти с помощью теоремы Пифагора. Свойства векторов Умножение на число. например Умножение вектора на число дает параллельный вектор. Умножение на отрицательного числа изменяет направление стрелки вектора. Добавление векторовВекторов можно сложить вместе. По матрицам. Добавьте соответствующие элементы. например По чертежу . Сформируйте треугольник. Второй вектор добавляется в конец первого вектора. Результирующий вектор (помеченный c) может быть отмечен двумя стрелками. Стрелки на результирующем элементе имеют направление, противоположное добавляемым векторам. например
Решение задач с помощью векторовМногие типы проблем, от физики до навигации, можно решить, нарисовав векторную диаграмму, а затем используя тригонометрию или даже масштабную диаграмму. Пример
Захватывающая и веселая практика с подшипниками — Скаляров и векторов Физика — математическая наука.Основные концепции и принципы имеют математическую основу. В ходе изучения физики мы будем сталкиваться с множеством концепций, связанных с математической основой. Хотя мы часто делаем упор на концептуальную природу физики, мы будем уделять значительное и постоянное внимание ее математическому аспекту. Движение предметов можно описать словами. Даже у человека без образования в области физики есть набор слов, которые можно использовать для описания движущихся объектов.Такие слова и фразы, как , идет быстро, , , остановился, , , замедляется, , , ускоряется, , и , так и поворачивает , обеспечивают достаточный словарный запас для описания движения объектов. В физике мы используем эти и многие другие слова. Мы будем расширять этот словарный список такими словами, как расстояние , смещение , скорость , скорость и ускорение . Как мы вскоре увидим, эти слова связаны с математическими величинами, имеющими строгие определения.Математические величины, которые используются для описания движения объектов, можно разделить на две категории. Величина может быть векторной или скалярной. Эти две категории можно отличить друг от друга по их различным определениям: Остальная часть этого урока будет посвящена нескольким примерам векторных и скалярных величин (расстояние, смещение, скорость, скорость и ускорение).По мере прохождения урока обращайте особое внимание на векторную и скалярную природу каждой величины. По мере того, как мы переходим к другим разделам Учебника по физике и знакомимся с новыми математическими величинами, обсуждение часто начинается с определения новой величины как вектора или скаляра. Проверьте свое понимание1. Чтобы проверить ваше понимание этого различия, примите во внимание следующие величины, перечисленные ниже.Отнесите каждую величину к категории векторных или скалярных. Нажмите кнопку, чтобы увидеть ответ.
Модуль 9: Векторы — пути к математикеРабочие примеры векторовПример 1 Теннисный мяч катится к стене, которая находится на расстоянии 10 м вправо. Если после удара о стену мяч откатывается еще 2.5 м по земле влево, рассчитайте результирующее смещение мяча. Обратите внимание, что результирующий вектор — это векторная сумма двух (или более) векторов. Другими словами, это результат сложения двух или более векторов вместе. Ответ Нарисуйте диаграмму в масштабе, чтобы представить ситуацию. Мы знаем, что результирующее смещение шара () равно сумме отдельных смещений шара (и): Поскольку мяч движется по прямой линии (т. Сначала выбираем положительное направление. Сделаем вправо положительное направление. Это означает, что налево становится отрицательным направлением. С правым положительным числом: Затем мы просто складываем два смещения, чтобы получить результат: Наконец, в этом случае право означает положительный результат, поэтому: Следующие видеоролики посвящены сложению двух векторов которые не противоположны друг другу по направлению (как это было в примере выше).В первом видео объясняются два метода, которые можно использовать для добавления векторов. Во втором видео рассматривается пример сложения трех векторов.
(Обратите внимание, что векторное уравнение, записанное в верхней части доски во втором видео, описывает результирующий вектор (в данном случае вектор — скорость) как сумму трех векторов с каждым вектором представлен его величиной (например, 6 м / с) и направлением (например, E30 ° N)). Пример 2 Следующий рабочий пример был взят и адаптирован со следующего веб-сайта: http: // cnx.org / content / col10322 / 1.175 Найдите полное смещение человека, который идет следующими тремя путями (смещениями) на плоском поле. Сначала она проходит 25,0 м в направлении 49,0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0 ° к югу от востока. Каждый из трех векторов смещения обозначен буквами A, B и C соответственно и представлен на диаграммах ниже. Обратите внимание, что три вектора были нарисованы на трех отдельных осях, но было бы так же уместно представить все три на одном наборе осей. Изображение: //cnx.org/resources/5d8d6294b8ed018811ba255dea7d749a/Figure_03_02_08.jpg Ответ Изобразите каждый вектор смещения графически стрелкой, обозначив C, первый A, второй B длины пропорциональны расстоянию и направлениям, указанным относительно линии восток-запад. Изображение: http://cnx.org/content/m42127/latest/Figure_03_02_11a.jpg Общее смещение R имеет величину 50,0 м и направление 7,0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0º к югу от востока. Пример 3 Тракция Гамильтона-Рассела (для восстановления правильного анатомического положения сломанной бедренной кости) Масса, подвешенная на веревке, оказывает на веревку силу натяжения (выраженную в ньютонах, Н) к силе тяжести.Натяжение тягового шнура (из-за подвешенной массы) можно определить с помощью 2-го закона Ньютона: Натяжение в шнуре = сила тяжести (Н) = подвешенная масса (кг) × 9,8 Когда шнур проходит вокруг «неподвижного шкива» «, натяжение может быть приложено в направлении, отличном от силы тяжести. Подвижные шкивы также обеспечивают механическое преимущество (результирующая сила тяги больше, чем натяжение корда). Посмотрите на рисунок тяги Гамильтона-Рассела ниже. Обратите внимание, что шнур, прикрепленный к колену, проходит через 3 фиксированных шкива и один подвижный шкив, прикрепленный к стопе.Подвешенная масса 4,25 кг натягивает шнур, поддерживающий ногу. Обратите внимание, что шкивы изменяют направление шнура, так что шнур оказывает давление на ногу в трех местах. То есть есть три силы равной величины (обозначенные на рисунке F1, F2 и F3), действующие на ногу из-за троса. Сила тяги к ноге — это сила, полученная из векторной суммы трех сил (натяжение шнура в трех местах на ноге). Удивительно, но сила тяги параллельна бедренной кости, но не какой-либо части спинного мозга. Величина каждой силы составляет 41,65 Н (= 4,25 кг × 9,8 м / с), а направление каждой силы показано стрелками силы. Величина тягового усилия больше веса подвешенной массы (за счет подвижного шкива достигается механическое преимущество). Теперь мы построим векторную диаграмму для определения величины и направления силы тяги. Нарисуйте (используя масштаб 1 см = 10 Н) вектор, представляющий натяжение (41.65 Н) в шнур, прикрепленный к колену (F1) из-за массы 4,25 кг (длина будет 4,17 см). Убедитесь, что ваш вектор параллелен стрелке, представляющей силу F1 на диаграмме. Сложите два других вектора силы (поместив их хвост на вершине предыдущего вектора силы). Нарисуйте получившийся вектор, измерьте его длину в см и преобразуйте длину в ньютоны. (Обратите внимание, что все 3 вектора силы натяжения имеют одинаковую величину и одинаковую длину). Опишите направление результирующего вектора тракции по отношению к бедренной кости. (ВНС: величина 10,5 см = 105 с. ). Напряжение отдельных мышц складывается из одинаковых векторов, чтобы получить результирующую силу. Если одна мышца повреждена, результирующая величина и направление действия других будут нарушены. Четырехглавая мышца бедра (передняя часть бедра) состоит из четырех мышц: медиальная широкая широкая мышца бедра, средняя широкая мышца бедра, латеральная широкая мышца бедра и прямая мышца бедра (см. Добавьте четыре вектора силы четырехглавой мышцы, нарисовав векторы «хвост к кончику», используя направление, указанное на диаграмме, и величины VM = 2 см, VL = 4,5 см, VI = 3,5 см и RF = 4,3 см. Какова величина результирующего вектора, проведенного от хвоста виртуальной машины к вершине RF? Ответ VM + VL + VI + RF = 2 + 4.5 + 3,5 + 4,3 = 13,8 см в направлении Вычисление результирующего вектора, включающего два вектора, расположенные под прямым углом друг к другу В то время как наши рабочие примеры до сих пор включали поиск результирующего вектора графически (путем рисования их в scale) стоит познакомить вас с алгебраическим подходом, который подходит для использования, когда два вектора расположены под прямым углом друг к другу. Пример 5 Эрик покидает базовый лагерь и отправляется в поход на 11 км на север, а затем на 11 км на восток. Определите полученное смещение Эрика алгебраически. Ответ В этой задаче требуется определить результат сложения двух векторов смещения, расположенных под прямым углом друг к другу. Результат (или результат) ходьбы на 11 км на север и 11 км на восток — это вектор, направленный на северо-восток, как показано на диаграмме справа. Поскольку смещение на север и смещение на восток расположены под прямым углом друг к другу, теорема Пифагора может использоваться для определения результирующего (т.е., гипотенуза прямоугольного треугольника). Изображение: www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Addition Следовательно, результирующее смещение составляет 15,6 км в направлении северо-восток. Практические задания1. Складываются два вектора одинаковой величины; один указывает на восток, один на запад.Величина результирующего вектора:
2. Что из следующего не является векторной величиной?
3. Лодка движется на 10 км на запад, 5 км на север и затем 10 км на восток.Смещение лодки от исходного положения составляет:
4. Вы идете 31 м на юг и 31 м на запад. Ваше перемещение примерно:
5.
6. Вектор имеет величину и __________.
7.Графическое представление векторов включает ______.
Нажмите здесь , чтобы проверить свои ответы % PDF-1.2
%
134 0 объект
>
endobj
xref
134 62
0000000016 00000 н. Решение задач с векторами Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее. Скорость:Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью. Пример : Мяч брошен с начальной скоростью 70 футов в секунду., под углом 35 год ° с горизонтальным. Найдите вертикальную и горизонтальную составляющие скорости. Позволять v представлять скорость и использовать данную информацию для записи v в форме единичного вектора: v знак равно 70 ( потому что ( 35 год ° ) ) я + 70 ( грех ( 35 год ° ) ) j Упростим скаляры, получим: v
≈
57. Поскольку скаляры — это горизонтальная и вертикальная составляющие v , Следовательно, горизонтальная составляющая равна 57,34 футов в секунду, а вертикальная составляющая 40,15 футов в секунду. Сила:Сила также представлена вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, является векторной суммой этих сил. Пример : Две силы F 1 и F 2 с величинами 20 и 30 фунт соответственно воздействуют на объект в точке п как показано. Найдите равнодействующие силы, действующие в п . Сначала мы пишем F 1 и F 2 в компонентном виде: v
≈
57. Упростим скаляры, получим: F 1 знак равно ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) j знак равно 20 ( 2 2 ) я + 20 ( 2 2 ) j знак равно 10 2 я + 10 2 j F 2 знак равно ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) j знак равно 30 ( — 3 2 ) я + 30 ( 1 2 ) j знак равно — 15 3 я + 15 j Итак, равнодействующая сила F является F знак равно F 1 + F 2 знак равно ( 10 2 я + 10 2 j ) + ( — 15 3 я + 15 j ) знак равно ( 10 2 — 15 3 ) я + ( 10 2 + 15 ) j ≈ — 12 я + 29 j Работа: Работа
W
сделано силой
F
в движении по вектору
D
является
W
знак равно
F
⋅
D
. Пример : Сила задается вектором F знак равно 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9 ) . Найдите проделанную работу. Сначала мы находим смещение. Вектор смещения D знак равно 〈 5 — 1 , 9 — 3 〉 знак равно 〈 4 , 6 〉 . Используя формулу, проделанная работа W знак равно F ⋅ D знак равно 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 знак равно 26 Если единицей силы являются фунты, а расстояние измеряется в футах, то выполненная работа 26 фут-фунт векторов, графическое представление векторов, величина вектора, направление вектора Векторы могут быть графически представлены направленными линейными сегментами. A Вектор на плоскости — это направленный отрезок прямой. Два вектора эквивалентны , если они имеют одинаковую величину и направление . Рассмотрим вектор, проведенный из точки A в точку B. Точка A называется начальной точкой вектора, а точка B называется конечной точкой . Символическое обозначение этого вектора (читай «вектор AB»). Векторы также обозначаются жирными буквами, такими как u, v и w.Четыре вектора на рисунке слева имеют одинаковую длину и направление. Таким образом, они представляют эквивалентных векторов; то есть Длина, или звездной величины , выражается как ||. Чтобы определить, эквивалентны ли векторы, мы находим их величины и направления. Пример 1 Векторы u, и w показаны на рисунке ниже. Покажем, что u = = w. Решение Сначала мы находим длину каждого вектора, используя формулу расстояния: Имейте в виду, что эквивалентность векторов требует только одинаковой величины и одного направления, а не одного и того же местоположения. Предположим, человек делает 4 шага на восток, а затем 3 шага на север. Затем он или она будет в 5 шагах от начальной точки в направлении, показанном слева.Вектор длиной 4 единицы, указывающий вправо, представляет 4 шага на восток, а вектор длиной 3 единицы и направленный вверх представляет 3 шага на север. Сумма двух векторов представляет собой вектор с 5 шагами по величине и в показанном направлении. Сумма также называется результирующим двух векторов. В общем, два ненулевых вектора u и v можно сложить геометрически, поместив начальную точку v в конечную точку u и затем найдя вектор, который имеет ту же начальную точку, что и u, и ту же конечную точку, что и v, как показано на следующем рисунке. Мы также можем описать сложение векторов, поместив вместе начальные точки векторов, завершив параллелограмм и найдя диагональ параллелограмма. (См. Рисунок слева внизу.) Это описание сложения иногда называют законом параллелограмма сложения векторов.Сложение векторов коммутативно. Как показано на рисунке справа внизу, и u + v, и v + u представлены одним и тем же направленным отрезком линии. Если две силы F 1 и F 2 действуют на объект, комбинированный эффект является суммой или равнодействующей F 1 + F 2 отдельных сил. Пример 2 Силы в 15 и 25 ньютонов действуют на объект под прямым углом друг к другу. Найдите их сумму или равнодействующую, указав величину равнодействующей и угол, который она составляет с большей силой. Решение Мы рисуем рисунок — на этот раз прямоугольник — используя v или, чтобы представить результат. Пилоты должны корректировать направление своего полета при боковом ветре. И ветер, и скорость самолета могут быть описаны векторами. Пример 3 Скорость и направление самолета. Самолет летит по пеленгу 100 ° со скоростью 190 км / ч, а ветер дует 48 км / ч со скоростью 220 °. Найдите путевую скорость самолета и направление его траектории или курса относительно земли. Раствор Сначала делаем рисунок. Для вектора w мы можем найти два других вектора u и v, сумма которых равна w.Векторы u и v называются компонентами w, а процесс их нахождения называется , разрешающим или представляющим вектор на его векторные компоненты. Когда мы разрешаем вектор, мы обычно ищем перпендикулярные компоненты. Чаще всего один компонент будет параллелен оси x, а другой — оси y. По этой причине их часто называют горизонтальными и вертикальными компонентами вектора.На рисунке ниже вектор w = разрешен как сумма u = и v =. Пример 4 Вектор w имеет величину 130 и наклонен на 40 ° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты. Решение Сначала мы сделаем чертеж, на котором показаны горизонтальные и вертикальные векторы u и v, сумма которых равна w. векторов по физике — практические контрольные вопросы и экзамен по главеСтр. 1Вопрос 1 1. В компонентной форме вектор A равен 3i + 6j, а вектор B равен i + 2j. Каково скалярное произведение этих векторов?вопрос 2 2.Каково общее определение векторного разрешения?Вопрос 3 3. Какой из следующих векторов НЕ в компонентной форме?Вопрос 4 4. Что из следующего является определением вектора?Вопрос 5 5. Как сложить векторы геометрически?Стр. 2Вопрос 6 6. Электрический лестничный подъемник прилагает силу в 600 ньютонов прямо вверх, перемещая подъемник с постоянной скоростью 0,1 метра в секунду. Мощность лестничного лифта является скалярным произведением силы и скорости.Если лестница находится под углом 60 градусов НИЖЕ ГОРИЗОНТАЛИ, сколько мощности потребляет лестничный подъемник?Вопрос 7 7. Что из следующего НЕ является примером векторной величины?Вопрос 8 8.Что из следующего НЕ является примером умножения векторов? (Другими словами, какой расчет не имеет вектора для ответа?)Вопрос 9 9. Если вы выстрелите пушечным ядром под малым углом, как будут сравниваться x- и y-компоненты его скорости?Вопрос 10 10.Вектор A имеет величину 4 единицы, вектор B имеет величину 8 единиц. Если угол между ними составляет 35 градусов, каково скалярное произведение векторов A и B?Стр. 3Вопрос 11 11. В каком из этих уравнений вам НИКОГДА НЕ потребуется вычитать два вектора?Вопрос 12 12.Какие из следующих утверждений верно?Вопрос 13 13. Когда мы используем точечные произведения?Вопрос 14 14. Если вы толкаете коробку с силой 8 ньютонов вбок в положительном направлении x, 3 ньютона вниз в отрицательном направлении y и 1 ньютон вперед в положительном направлении z, как бы вы представили эту силу в виде компонента? ?Вопрос 15 15.Пушечное ядро выстреливается со скоростью 10 м / с вверх от горизонтали и 30 м / с на запад. Каков угол и направление пушечного ядра?Стр. 4Вопрос 16 16. Если вы снимаете что-то под большим углом, как будут сравниваться компоненты x и y?Вопрос 17 17.Сила A действует на 2 ньютона на запад и на 3 ньютона на юг. Сила B действует на 5 ньютонов на запад и 2 ньютона на север. Что является результатом этих двух векторов?Вопрос 18 18. Пушечное ядро выстреливается под углом 55 градусов относительно горизонтали с силой 80 Ньютонов. Какова величина вектора силы, действующего на ядро?Вопрос 19 19.Как бы вы записали 50 ньютонов на восток и 70 ньютонов на юг в компонентной форме? (Используйте север на юг в качестве оси y и с востока на запад в качестве оси x, как в уроке.)Вопрос 20 20. Теннисный мяч движется со скоростью 20 м / с на запад и 5 м / с вверх. Какова общая величина вектора скорости теннисного мяча?Стр. 5Вопрос 21 21.Если объект движется со скоростью 4 м / с в направлении x и 2 м / с в направлении y, какова скорость объекта, записанная в терминах стандартных базисных векторов?Вопрос 22 22. Если вектор 1 имеет величину 3 единицы и направление на 30 градусов ниже отрицательной оси x, а вектор 2 имеет величину 4 единицы и направление на 80 градусов ниже отрицательной оси x, то вектор 1 минус вектор 2? (Пожалуйста, ответьте на этот вопрос геометрически, используя бумагу, карандаш и линейку.) Вопрос 23 23. Каково скалярное произведение 3i + 2j, умноженное на 4i + 8j?Вопрос 24 24. Вы толкаете тележку для покупок с силой 20 Н вниз и силой 50 Н.Какова общая величина прилагаемой силы?Вопрос 25 25. Что из следующего НЕ может представлять то же движение, что и другие?Стр. 6Вопрос 26 26. Вы толкаете багги с силой 40 ньютонов вперед и 10 ньютонов вниз. Под каким углом толкаете багги?Вопрос 27 27. Грузовик движется со скоростью 5 м / с на север и 3 м / с на запад, в то время как человек ВНУТРИ грузовика движется в определенном направлении с определенной скоростью. Общая скорость человека (комбинация скорости грузовика и скорости человека) составляет 6 м / с на север и 1 м / с на запад.Как быстро человек должен двигаться в грузовике?Вопрос 28 28. Если рассчитать кросс-произведения AxB и BxA, как будут сравниваться результаты?Вопрос 29 29. Что из следующего является определением вектора?Вопрос 30 30. Что из этого является правильным определением векторной величины?Инструкции по экзамену на главу «Векторы в физике»Выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов. Если хотите, можете пропустить вопросы и прийти назад к ним позже с помощью кнопки «Перейти к первому пропущенному вопросу». Когда вы сдали пробный экзамен, появится зеленая кнопка отправки. появляются.Щелкните его, чтобы увидеть свои результаты. Удачи! . Leave a Reply
| |
Постройте векторы, равные: а) ; 
Выразите векторы через векторы 
Выразите векторы через векторы 
Выразите векторы через векторы 
Выразите векторы через векторы 
Выразите векторы через векторы 
(2)= Задания для подготовки к контрольной работе можно предложить учащимся накануне проведения проверочной работы в качестве домашнего задания. «Геометрия. классы», рекомендованный Министерством образования и науки Российской Федерации и включенный в Федеральный перечень учебников. Каждая проверочная работа дается в четырех вариантах. Кроме того, по каждой теме дается набор заданий для подготовки к контрольной работе.
Метод координат Контрольная работа № 1 8 Соотношения между сторонами и углами треугольника. ГДЗ по геометрии 9 класс Мерзляк дидактические материалы контрольная работа вариант №1 — 1.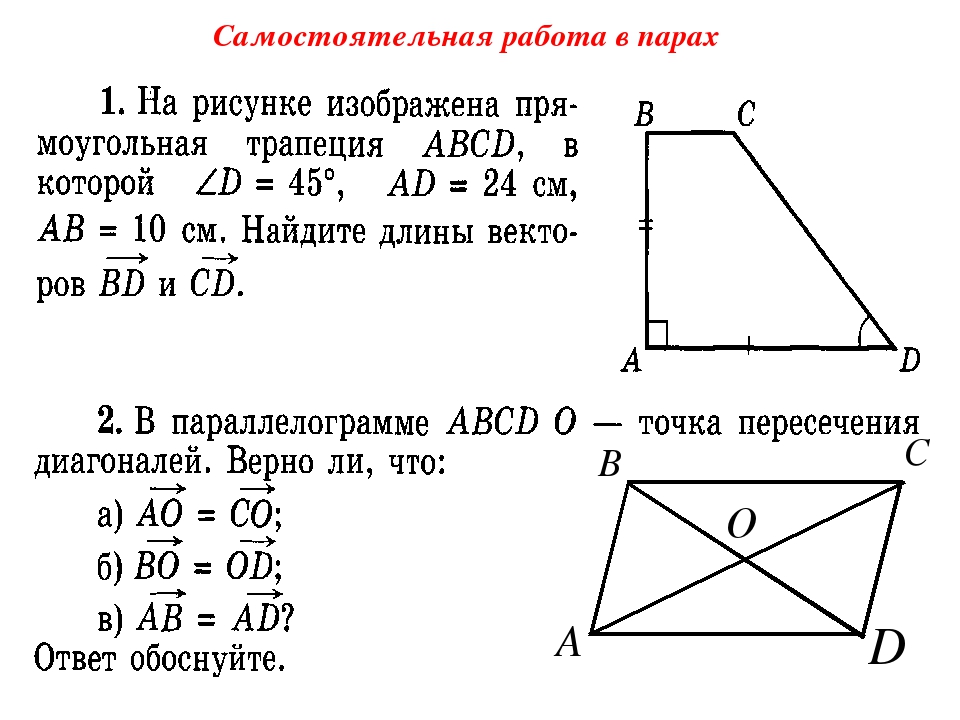
5 миль, север
е. мяч движется влево и вправо), мы можем использовать только что объясненный метод алгебраического сложения.
Описанный выше метод «голова к хвосту» даст возможность определить величину и направление результирующего смещения, обозначенного R.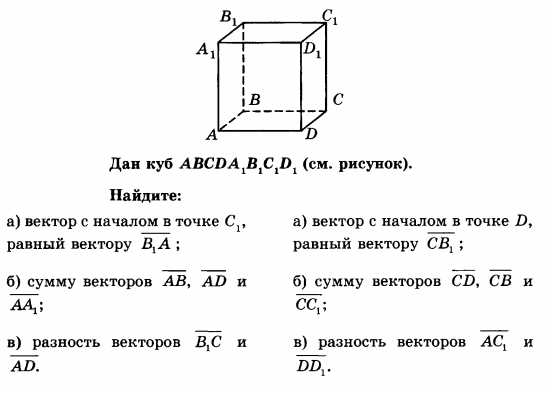
Рисунок ниже).Он разгибает ногу, чтобы сделать движение ногой. Направление силы, которую сокращение каждой из этих четырех мышц оказывает на сухожилие надколенника, можно приблизительно определить четырьмя векторами (обозначенными VM, VI, VL, RF).
В следующем примере вы можете заметить, что мы применили теорему Пифагора для вычисления результирующего вектора.
Вы также можете найти результирующее смещение, нарисовав векторы в масштабе, как это было в предыдущем методе, использованном в рабочих примерах 1-4, и сравните свои ответы.
Два футболиста ударились о блокирующие санки. Один поражает его с силой 350 Н, восток, а другой — с силой 270 Н, юг. Результирующая сила:
0000001591 00000 н.
0000001750 00000 н.
0000001854 00000 н.
0000001911 00000 н.
0000001967 00000 н.
0000002023 00000 н.
0000002082 00000 н.
0000002139 00000 п.
0000002206 00000 н.
0000002275 00000 н.
0000002332 00000 н.
0000002388 00000 н.
0000003213 00000 н.
0000003476 00000 н.
0000003646 00000 н.
0000003815 00000 н.
0000003912 00000 н.
0000004242 00000 п.
0000004410 00000 н.
0000004599 00000 н.
0000007745 00000 н.
0000008200 00000 п.
0000008406 00000 н.
0000008851 00000 н.
0000009033 00000 н.
0000009213 00000 н.
0000012695 00000 п.
0000012870 00000 п.
0000013084 00000 п.
0000013279 00000 п.
0000013460 00000 п.
0000013512 00000 п.
0000014114 00000 п.
0000014282 00000 п.
0000048701 00000 п.
0000049464 00000 п.
0000049678 00000 п.
0000049701 00000 п.
0000059677 00000 п.
0000059700 00000 п.
0000069019 00000 н.
0000069042 00000 н.
0000078454 00000 п.
0000078478 00000 п.
0000093547 00000 п.
0000093571 00000 п.
0000109074 00000 н.
0000109097 00000 н.
0000118983 00000 п.
0000119007 00000 н.
0000131678 00000 н.
0000131702 00000 н.
0000145571 00000 н.
0000145650 00000 н.
0000146508 00000 н.
0000153429 00000 н.
0000164440 00000 н.
0000170324 00000 н.
0000180486 00000 н.
0000002461 00000 н.
0000003191 00000 п.
трейлер
]
>>
startxref
0
%% EOF
135 0 объект
>
endobj
136 0 объект
[
137 0 R 138 0 R 139 0 R 140 0 R 141 0 R 142 0 R 143 0 R 144 0 R 145 0 R
146 0 руб.
]
endobj
137 0 объект
>
/ Ж 13 0 Р
>>
endobj
138 0 объект
>
/ Ж 8 0 Р
>>
endobj
139 0 объект
>
/ Ж 9 0 Р
>>
endobj
140 0 объект
>
/ Ж 38 0 Р
>>
endobj
141 0 объект
>
/ Ж 59 0 Р
>>
endobj
142 0 объект
>
/ Ж 60 0 Р
>>
endobj
143 0 объект
>
/ Ж 74 0 Р
>>
endobj
144 0 объект
>
/ Ж 64 0 Р
>>
endobj
145 0 объект
>
/ Ж 49 0 Р
>>
endobj
146 0 объект
>
/ Ж 150 0 Р
>>
endobj
194 0 объект
>
транслировать
Hb«f` Ā
34
я
+
40,15
j
34
я
+
40,15
j
Длина выбирается в соответствии с некоторым масштабом, чтобы представить величину вектора , а направление направленного отрезка линии представляет направление вектора . Например, если мы допустим, что 1 см представляет 5 км / ч, то ветер со скоростью 15 км / ч с северо-запада будет представлен направленным отрезком линии длиной 3 см, как показано на рисунке слева.
На иллюстрациях слева каждая из первых трех пар векторов не эквивалентна. Четвертый набор векторов является примером эквивалентности.
То есть, если u = и v =, то 
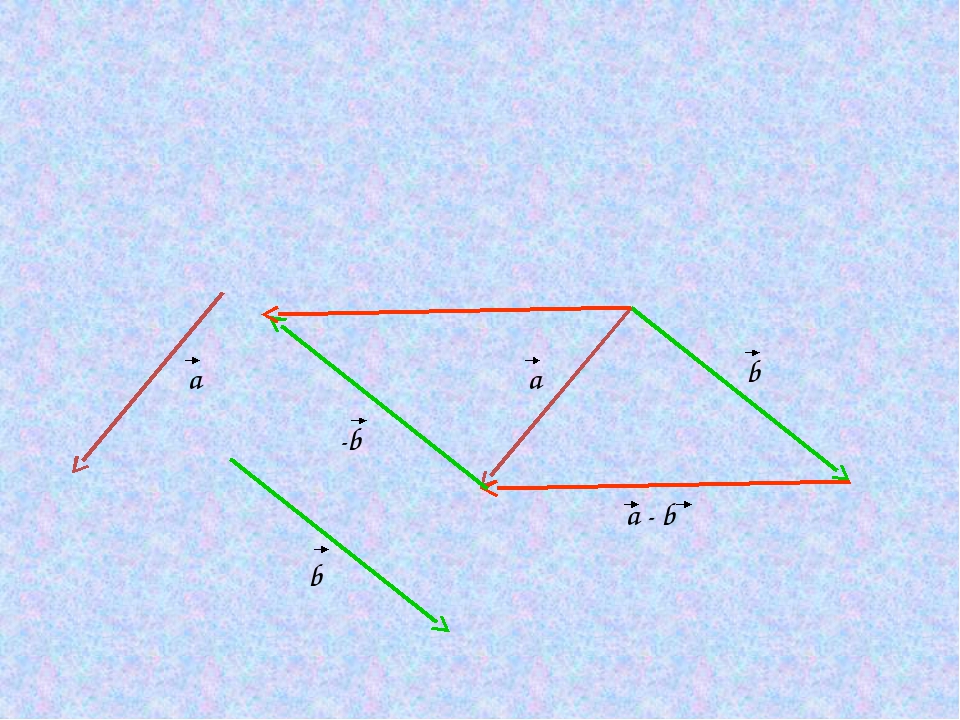Чтобы найти величину, воспользуемся теоремой Пифагора: 
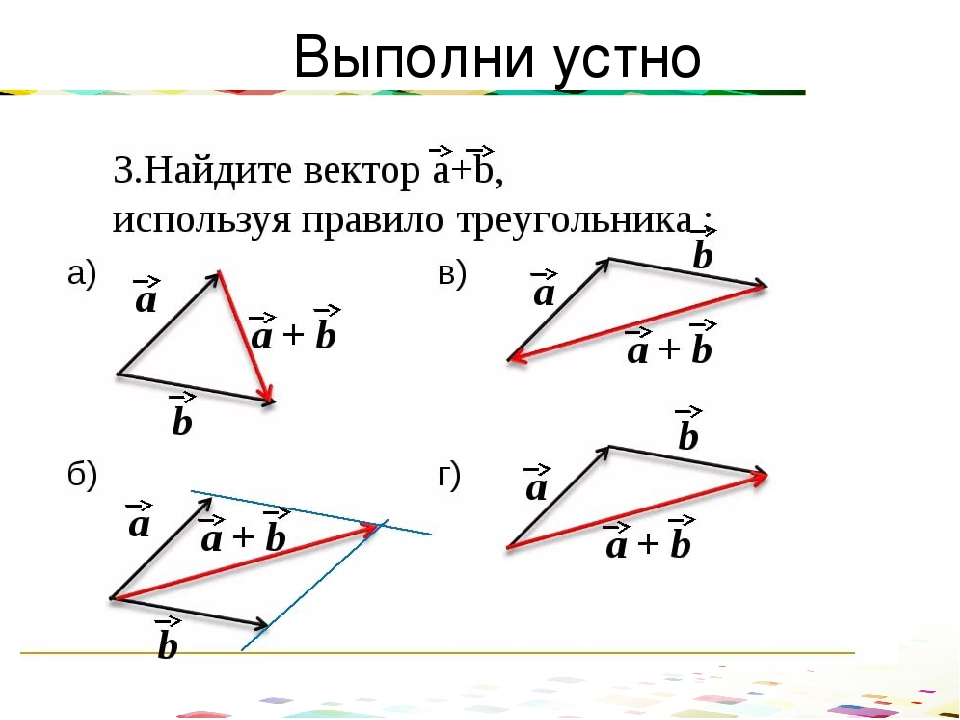Ветер представлен как, а вектор скорости самолета — как.Результирующий вектор скорости равен v, сумме двух векторов. Угол θ между v и называется углом сноса .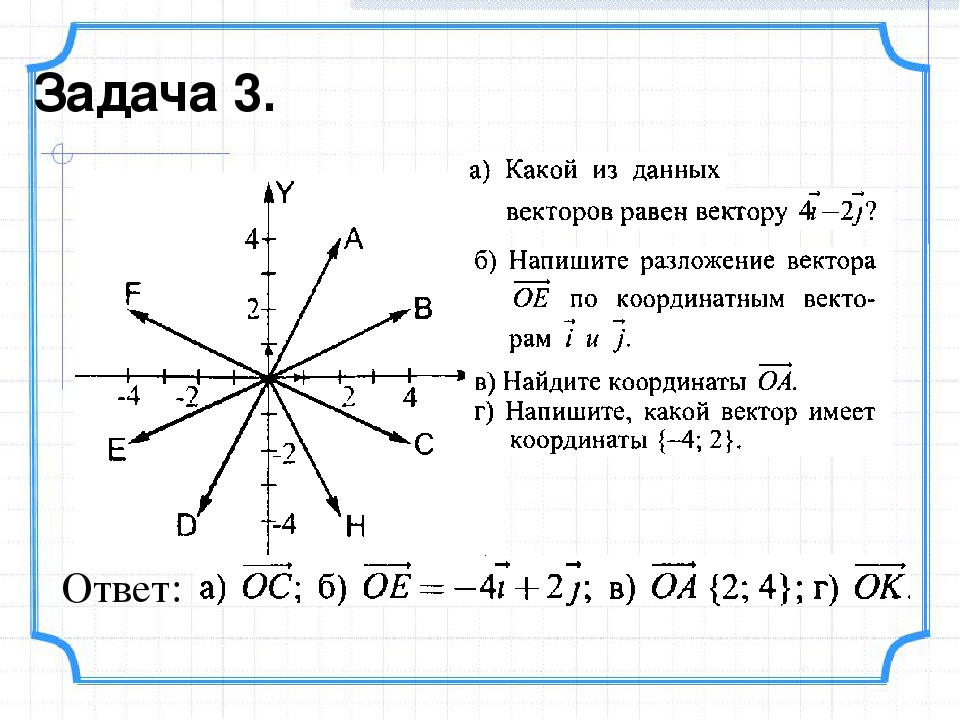 
cos40 ° ≈ 100,