Контрольная работа вариант 2 по математике: Учебно-методический материал по математике (2 класс) на тему: Контрольные работы по математике. 2 класс. Школа России

Учебно-методический материал по математике (2 класс) на тему: Контрольные работы по математике. 2 класс. Школа России

Входная контрольная работа №1

1.  Найди сумму чисел: 9 и 3.

    Найди разность чисел: 11 и 2.

    Уменьши число 8 на 2.

    Увеличь число 6 на 3.

2. Сравни (вместо точек поставь знаки >,

7 + 3 …  9

12 + 5 … 17

   

3. Вычисли:   10 – 8 + 4 =

                            6 + 4 – 3 =

   

4. Реши задачу: Сшили 5 платьев и 4 блузки. Сколько всего сшили вещей?

 

5. Реши задачу: В вазе было 10 яблок. Съели 8 яблок. Сколько яблок осталось?

 

6. Начерти два отрезка. Длина первого 4 см, а длина второго на 2 см больше.

 

7. Вырази:

        15 см = … дм …см

        1 дм 7 см = … см

Входная контрольная работа №1

1 Найди сумму чисел: 9 и 3.

    Найди разность чисел: 11 и 2.

    Уменьши число 8 на 2.

    Увеличь число 6 на 3.

2. Сравни (вместо точек поставь знаки >,

7 + 3 …  9

12 + 5 … 17

   

3. Вычисли:   10 – 8 + 4 =

                            6 + 4 – 3 =

   

4. Реши задачу: Сшили 5 платьев и 4 блузки. Сколько всего сшили вещей?

 

5. Реши задачу: В вазе было 10 яблок. Съели 8 яблок. Сколько яблок осталось?

 

6. Начерти два отрезка. Длина первого 4 см, а длина второго на 2 см больше.

 

7. Вырази:

        15 см = … дм …см

        1 дм 7 см = … см

Контрольная работа № 2

 по теме «Нумерация чисел от 1 до 100»

Вариант 1.

1. Реши задачу:

Дедушке 64года, а бабушке 60. На сколько лет дедушка старше бабушки?

2. Реши примеры:

69 + 1 =                  5 + 30 =                 56 – 50 =

40 – 1 =                   89 – 9 =                 80 – 20 =

3. Сравни, вставь вместо звёздочек знаки «» или «=»:

8 м * 7 дм                1 м * 98 см

25 мм * 4 см            53 мм * 5 см

4. Из чисел 30, 5, 13, 55, 3, 35, 15, 50. 53, 33, 51, 31 выпиши в одну строку все двузначные числа, начиная с наименьшего.

      5*.  Заполни пропуски цифрами так, чтобы записи были верными:

       7 8              3

      6* . У нашей кошки 7 котят. Некоторые из них рыжие, 2 черных и 1 белый.

       Сколько рыжих котят у кошки?

Контрольная работа № 2

 по теме «Нумерация чисел от 1 до 100»

Вариант 2.

1. Реши задачу:

Папе 32 года, а мама на 2 года моложе. Сколько лет маме?

2. Реши примеры:

6 + 40 =                   49 + 1 =               34 – 4 =

87 – 70 =                  90 – 1 =               60 – 20 =

3. Сравни, вставь вместо звёздочек знаки «» или «=»:

6 м * 9 дм                1 м * 92 см

13 мм * 2 см            68 мм * 6 см

4. Из чисел 79, 17. 7. 91, 70, 9, 97, 99, 19, 71, 90. 77 выпиши все двузначные числа, начиная с наименьшего.

5* . Заполни пропуски цифрами так, чтобы все записи были верными:

5 3                6

6* . Бабушка положила в тарелку 12 груш. После того, как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?

Контрольная работа № 3  за 1 четверть

Вариант 1

1. Реши задачу:

На стоянке такси стояло 12 автомашин. После того, как несколько машин уехало, осталось 5 автомашин. Сколько автомашин уехало?

Составь и реши задачи, обратные данной.

2. Найди значения выражений:

6 + 7 – 9 =                           15 – (3 + 5) =

10 + 3 – 4 =                          8 + (12 – 5) =    

18 – 10 + 5 =                        9 + (13 – 7) =

3. Сравни, вставь вместо звёздочек знаки «» или «=»:

4 см 2 мм * 24 мм              1 м * 100 см

7 + 4 * 19                             59 мин. * 1 ч.

4. Начерти ломаную из трёх звеньев, зная, что длина ломаной 10 см.

5. Из чисел 48, 1, 14. 4, 40. 81, 8, 18, 84, 44, 80, 88 выпиши все двузначные числа в порядке возрастания.

      6* . У Тани и Маши вместе 13 орехов. Когда Таня съела 5 орехов и Маша

     ещё  несколько, у девочек осталось 6 орехов. Сколько орехов съела Маша?    

   Контрольная работа № 3  за 1 четверть

Вариант 2.

1. Реши задачу:

Рыболовы поймали несколько окуней. Из 9 окуней они сварили уху, и у них осталось ещё 7 окуней. Сколько всего окуней поймали рыболовы?

Составь и реши задачи, обратные данной.

2. Найди значения выражений:

5 + 8 – 9 =                           14 – (2 + 5) =

10 + 5 – 6 =                          4 + (16 – 8) =    

19 – 10 + 7 =                        9 + (18 – 10) =

3. Сравни, вставь вместо звёздочек знаки «» или «=»:

3 дм 2 см * 23 см             1 см * 10 мм

8 + 5 * 14                          1 ч. * 30 мин.

4. Начерти ломаную из трёх звеньев, зная, что длина ломаной 8 см.

5. Из чисел 62, 12, 6. 66, 20, 26, 2, 21, 16, 22, 60. 61 выпиши все двузначные числа в порядке убывания.

      6* . В коробке 15 конфет. Когда Саша съел 6 конфет и несколько конфет съел его

       брат, в коробке осталось 7 конфет. Сколько конфет съел брат?  

Контрольная работа № 4 по теме

«Числа от 1 до 100. Устные приёмы сложения и вычитания»

Вариант 1.

1. Реши задачу:

В книге 25 страниц. Серёжа начал читать книгу вчера и прочитал 8 страниц, а сегодня прочитал ещё 7 страниц. Сколько книг осталось прочитать Серёже?

2. Найдите значения выражений:

40 + 5 =               30 + 20 =

26 + 2 =               70 + 13 =

76 – 70 =              28 – 8 =

60 – 40 =              37 – 6 =

3. Вычислите, указав порядок действий:

60 – (2 + 3) =                    15 + (19 – 4) =

4* . Красный шнур на 1 м длиннее зелёного и на 2 м длиннее синего. Длина зелёного шнура 5 м. Найдите длину синего шнура.

5*.  Вставь в «окошки» числа так, чтобы:

1). равенство сохранилось;

2). знак равенства изменился на знак «>».

                          52 + □ = 52 + □

       Сделай две записи.

Контрольная работа № 4 по теме

«Числа от 1 до 100. Устные приёмы сложения и вычитания»

Вариант 2.

1. Реши задачу:

В гараже было 20 машин. Сначала из гаража выехало 2 машины, а потом ещё 8. Сколько машин осталось в гараже?

2. Найдите значения выражений:

50 + 5 =               70 + 20 =

46 + 3 =               80 + 17 =

36 – 20 =              39 – 9 =

80 – 40 =              56 – 4 =

3. Вычислите, указав порядок действий:

83 + (5 — 3) =                    70 — (50 + 20) =

4* . На вешалке висят головные уборы: шляп на 1 больше, чем шапок, а шапок на 1 больше, чем беретов. Шляп 8. Сколько шапок и сколько беретов?

5*.  Вставь в «окошки» числа так, чтобы:

1). равенство сохранилось;

2). знак равенства изменился на знак «

                                                 41 + □ = 41 + □

       Сделай две записи.

Контрольная работа № 5

за 1 полугодие

Вариант 1.

1. Реши задачу:

В ёлочной гирлянде 7 красных лампочек, синих на 6 больше, чем красных, а жёлтых – столько, сколько красных и синих вместе. Сколько в гирлянде жёлтых лампочек?

2. Реши примеры:

75 + 20 =                90 – 3 =               45 – 5 + 7 =

80 + 11 =                60 – 20 =              83 – (40 + 30) =

3. Реши уравнение:

5 + х = 12

4. Найди периметр данной фигуры:

5. Вставь в «окошки» числа так, чтобы записи были верными:

6 дм 3 см =  см                  50 мм =  см

6*. Вместо звёздочек вставь знаки «+» или «- «, а в «окошки» запиши числа так, чтобы записи были верными:

 * 8

Контрольная работа № 5

за 1 полугодие

Вариант 2.

1. Реши задачу:

На новогоднюю ёлку повесили 11 шаров, сосулек на 4 меньше, чем шаров, а шишек – столько, сколько шаров и сосулек вместе. Сколько шишек повесили на ёлку?

2. Реши примеры:

54 + 30 =                80 – 4 =               34 – 4 + 6 =

70 + 12 =                40 – 10 =             95 – (60 + 20) =

3. Реши уравнение:

Х + 7 = 16

4. Найди периметр данной фигуры:

5. Вставь в «окошки» числа так, чтобы записи были верными:

5м 8 дм =  дм                  60 мм =  см

6*. Вместо звёздочек вставь знаки «+» или «-«, а в «окошки» запиши числа так, чтобы записи были верными:

11 — 7

Контрольная работа №6 по теме

«Письменные приёмы сложения и вычитания чисел от 1 до 100»

Вариант 1

1. Вычисли столбиком:

53 + 37 =                      86 – 35 =

36 + 23 =                      80 – 56 =

65 + 17 =                      88 – 81 =

2. Реши уравнения:

64 – х = 41                      30 + х = 67

3. Начерти один отрезок длиной 1 дм, а другой на 3

Самостоятельные и контрольные работы по математике. 2 класс 2 часть. Петерсон Л.Г.

Твитнуть

Поделиться

Плюсануть

Поделиться

Отправить

Класснуть

Запинить

 

Аннотация

Предлагаемые вниманию учителей самостоятельные и контрольные работы составлены в соответствии с программой по математике для начальной школы автора Л.Г.Петерсон. Содержат рекомендации по организации и проведению контроля знаний учащихся. Могут быть использованы во всех типах учебных заведений. Комплект предназначен для работы с учащимися 2 класса.

Пример из учебника

Во 2-м выпуске представлены самостоятельные и контрольные работы по 4-6 книгам из 12 книг комплекта по математике для начальной школы автора Л. Г. Петерсон. Основной принцип проведения контроля знаний – минимизация стресса детей. Атмосфера в классе должна быть спокойной и доброжелательной, а ошибки в самостоятельной работе должны восприниматься исключительно как сигнал для их устранения. Спокойная атмосфера во время контрольных работ определяется большой подготовительной работой, которая снимает все поводы для беспокойства. Кроме того, ребенок должен отчетливо ощущать веру учителя в его силы, заинтересованность в его успехах.

Задачи международного конкурса «Кенгуру»
Кенгуру – это массовый международный математический конкурс-­игра под девизом «Математика для всех>>. Главная цель конкурса – привлечь как можно больше ребят к решению математических задач, показать каждому школьнику, что обдумывание задачи может быть делом живым, увлекательным и даже весёлым.

 

Учебник можно просто читать в онлайн режиме, переходя сразу на тот параграф или раздел, который Вам сейчас нужен.

Контрольная работа по математике №2 по теме «Числа, которые больше 1000. Нумерация» (УМК Школа России)

Данная работа нацелена на проверку знаний учащихся по теме «Числа, которые больше 1000. Нумерация»

Тип урока: проверка и оценка знаний
Элементы содержания: применять полученные знания, умения и навыки на практике; работать самостоятельно; контролировать свою работу и её результат.

Просмотр содержимого документа
«Контрольная работа по математике №2 по теме «Числа, которые больше 1000. Нумерация» (УМК Школа России)»

КОНТРОЛЬНАЯ РАБОТА №2

«Числа, которые больше 1000. Нумерация»

(УМК Школа России)

Вариант I.

1.Запиши числа от 3798 до 3806

2. Вычисли:

64 000 : 1 000 = 7 800 * 10 = 3 000 + 400 + 50 + 9 =

9 000 + 5 = 5 000 + 60 + 2 = 400 376 – 400 000 – 70 =

543 605 – 500 000 – 600 = 43 879 – 43 000 =

3. Запиши числа с помощью цифр (ответы через запятую):

15 ед. III класса, 30 ед. II класса

56 дес. II класса, 306ед. I класса

168 миллионов 48 тысяч 30

27 тысяч

3 миллиарда 430 миллионов 5 тысяч 50

4. Запиши в виде суммы разрядных слагаемых число 87003

5. Реши задачу:

Токарь за семичасовой рабочий день вытачивает 63 детали, а его ученик за 6 ч. Вытачивает 30 деталей. На сколько больше деталей вытачивает за 1 час рабочий, чем его ученик?

Вариант 2

1. Запиши числа от 5697 до 5703

2.

Вычисли:

84 000 : 1 000 = 5 300 * 100 = 7 000 + 500 + 60 + 3 =

7 000 + 7 = 6 000 + 500 + 1 = 800 231 – 800 000 – 1 =

657 908 – 600 000 – 900 = 54 768 – 54 000 =

3. Запиши числа с помощью цифр (ответы через запятую):

7 ед. III класса, 506 ед. II класса

97 дес. II класса, 54 ед. I класса

118 миллионов 23 тысячи 80

38 тысяч

4 миллиарда 340 миллионов 6тысяч 90

4. Запиши в виде суммы разрядных слагаемых число: 45001

5. Реши задачу :

Пекарь за шестичасовой рабочий день выпекает 54 пирога, а его ученик за 4 часа выпекает 24 таких пирога. На сколько больше пирогов выпекает за 1 час пекарь, чем его ученик?

Исчисление II — Корневой тест

Онлайн-заметки Павла

Примечания Быстрая навигация Скачать

• Перейти к
• Примечания
• Проблемы с практикой
• Проблемы с назначением
• Показать / Скрыть
• «> Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Тест соотношения
• Стратегия для серии
• Разделы
• Параметрические уравнения и полярные координаты
• Векторы
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер для комплексных чисел
• Как изучать математику
• Шпаргалки и таблицы
• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои студенты

• Заметки Загрузки
• Полная книга
• Текущая глава
• Текущий раздел
• Practice Problems Загрузок
• Полная книга — Только проблемы
• Полная книга — Решения
• Текущая глава — Только проблемы
• Текущая глава — Решения
• Текущий раздел — Только проблемы
• Текущий раздел — Решения
• Проблемы с назначением Загрузок
• Полная книга
• Текущая глава

Calculus II — Ratio Test

Онлайн-заметки Павла

Примечания Быстрая навигация Скачать

• Перейти к
• Примечания
• Проблемы с практикой
• Проблемы с назначением
• Показать / Скрыть
• «> Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Абсолютная сходимость
• Корневой тест
• Разделы
• Параметрические уравнения и полярные координаты
• Векторы
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер для комплексных чисел
• Как изучать математику
• Шпаргалки и таблицы
• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои студенты

• Заметки Загрузки
• Полная книга
• Текущая глава
• Текущий раздел
• Practice Problems Загрузок
• Полная книга — Только проблемы
• Полная книга — Решения
• Текущая глава — Только проблемы
• Текущая глава — Решения
• Текущий раздел — Только проблемы
• Текущий раздел — Решения
• Проблемы с назначением Загрузок
• Полная книга
• Текущая глава
• Текущий раздел
• Прочие товары
• Получить URL для загружаемых элементов

• Распечатать страницу в текущем виде (по умолчанию)
• Показать все решения / шаги и распечатать страницу
• Скрыть все решения / шаги и распечатать страницу

• Дом
• Классы
• Алгебра

Как выучить высшую математику, не отправляясь в университет — Часть 2

В последней статье этой серии мы рассмотрели базовые курсы, которые часто проходят в четырехлетнем курсе математики бакалавриата. Мы увидели, что основными курсами были линейная алгебра, обыкновенные дифференциальные уравнения, вещественный анализ и теория вероятностей. На «втором курсе» нашего самостоятельного изучения математики мы будем углубляться в анализ и алгебру, обсуждая интеграл Римана, абстрактную алгебру, метрические пространства и векторное исчисление.

В формальной обстановке середина 2-го года обучения — это когда ученики начинают понимать, хотят ли они специализироваться на чистой или прикладной математике и хотят ли они сосредоточиться на анализе или алгебре.Чистая математика и алгебра — синонимы, равно как и анализ и прикладная математика. Первое связано с тем, что продвинутая чистая математика часто занимается симметрией и отношениями между разрозненными областями математики (такими как сочетание алгебры и геометрии в алгебраической геометрии). Последнее, потому что вещественные векторные пространства часто являются областью дифференциальных уравнений в частных производных, которые представляют пространственно-временные физические явления, такие как электромагнитные поля, сжимаемые жидкости и деформируемые структуры.

Весьма вероятно, что как потенциальный специалист по математике вы захотите специализироваться в прикладной математике, что приведет к курсам стохастического анализа, анализа Фурье, дифференциальных уравнений в частных производных, статистики и научных вычислений. Тем не менее, это не всегда так. Многие известные кванты начинали с чистой математики или теоретической физики, в том числе Джим Саймонс и Эмануэль Дерман.

Эта статья будет посвящена 2-му году, а предыдущая — 1-му.Еще как минимум две статьи будут посвящены 3-му и 4-му годам. В последующих статьях будет рассмотрена общая программа курса магистра финансового инжиниринга (MFE).

Год 2

Как вкратце упоминалось выше, второй год бакалавриата по математике расширяет обсуждение анализа до интеграла Римана, который является обычным интегралом, знакомым из средней школы, инженерии и физики. Это контрастирует с интегралом Лебега, который обсуждается в Теории меры в течение третьего года.

Кроме того, ослаблены дальнейшие структурные предположения, что приводит к концепции метрических пространств. Это множества, в которых также есть понятие «расстояние». Векторное исчисление расширяет возможности дифференцирования и интегрирования на векторные пространства, что очень хорошо применимо в областях электродинамики, механики сплошных сред и гидродинамики.

Теория групп получает более строгое развитие за счет введения колец, а также основных идей групп матриц (групп Ли).Многие курсы также более подробно обсуждают неевклидову геометрию. Сюда входят сферическая / эллиптическая геометрия и гиперболическая геометрия. Эти концепции в конечном итоге приводят к дифференциальной геометрии и ее применению к общей теории относительности.

Во второй год также вводятся базовые стохастические процессы, которые очень важны для профессионалов в области количественных финансов. Еще одна абсолютно важная тема, основанная на элементарной вероятности, обсуждавшейся в первом году, — это статистика. Обычно отдел статистики большинства университетов разрешает переходные модули для математиков.

Также относится к количественному анализу и обычно предлагается в качестве опции численный анализ, который пытается анализировать алгоритмы, приближающие проблемы анализа, например, с помощью дифференциальных уравнений. Поскольку многие квантовые алгоритмы в конечном итоге включают приблизительное вычисление значений функций, поиск собственных значений, решение задач регрессии или оптимизации (как в машинном обучении), его стоит изучать как модуль.

Курсы второго года обучения в значительной степени отражают расширение и консолидацию тем, введенных в первый год. Рассмотрены следующие области математики:

Вот список курсов для 1 года:

Реальный анализ — интеграл Римана

Курсы первого года по реальному анализу, как правило, концентрируются на последовательностях, рядах, функциях одной действительной переменной (например, $ f: \ mathbb {R} \ rightarrow \ mathbb {R} $), непрерывности этих функций, а также на свойствах и результаты, относящиеся к их производным.

На второй год основное внимание уделяется интегралу Римана, который является «стандартным» интегралом, который будет знаком со средней школы, а также концепциям точечной сходимости и равномерной сходимости последовательностей функций. Одна из наиболее важных обсуждаемых концепций — это Фундаментальная теорема исчисления, которая определяет, как производные и интегралы функции связаны друг с другом.

Изучение интеграла Римана абсолютно необходимо для количественного аналитика, который хочет работать в области ценообразования производных финансовых инструментов, поскольку значительная часть стохастического исчисления и теории вероятностей опирается на теоретические концепции меры, такие как интеграл Лебега, который является более общим, чем более знакомый Риман. интеграл.

Реальный анализ является обязательным условием для следующих курсов второго года по метрическим пространствам и векторному исчислению, последний из которых имеет большое значение для определенных областей машинного обучения.

Учебные материалы

Метрическое пространство

Курс метрических пространств часто является первым введением в более абстрактные идеи из области математики, известной как топология. Метрическое пространство — это математический набор, связанный с функцией двух точек в наборе, определяющий «расстояние» или «метрику» между ними.

Эта идея расстояния внутри набора позволяет обсуждать интересные свойства, такие как открытость, замкнутость, полноту, связность, а также различные формы непрерывности функций между метрическими пространствами. Эти идеи основаны на концепциях, изучаемых в реальном анализе, включая последовательности, ряды и сходимость, хотя и в параметрах более высокого измерения.

Очень знакомый пример метрического пространства — трехмерное евклидово пространство со «стандартной» евклидовой метрикой («расстояние по прямой») между двумя точками.Более абстрактный пример — расстояние Левенштейна между двумя строками текста, которое позволяет количественно измерить схожесть строк. Я могу лично засвидетельствовать, что это чрезвычайно полезно в области обработки естественного языка.

Учебные материалы

В университете я использовал «Введение в метрические и топологические пространства» Сазерленда на втором курсе курса «Метрические пространства». Тем не менее, ретроспективно я обнаружил, что книга серии Springer по математике для студентов-бакалавров «Метрические пространства» М.О’Сиркоид тоже заслуживает изучения.

Векторное исчисление

Векторное исчисление — один из наиболее практичных курсов для будущих квантов. Он имеет дело с концепцией изменения скалярных и векторных полей. Многие концепции в математике, физике и квантовых финансах можно смоделировать как поля, и поэтому механизм векторного исчисления весьма применим.

Курс векторного исчисления познакомит с множеством полезных инструментов, таких как частная производная, градиент, дивергенция, ротор и операторы Лапласа, а также ключевые теоремы Гаусса и Стокса, которые являются строительными блоками уравнений в частных производных, которые в конечном итоге моделируют электромагнитное поле. поля и потоки жидкости.

Частные производные и оператор градиента широко используются в области статистического машинного обучения, особенно когда дело доходит до оптимизации решения на поверхности оптимизации , как в алгоритме стохастического градиентного спуска.

Некоторые университетские курсы по векторному исчислению содержат темы из области комплексного анализа. Хотя большинство курсов сосредоточено исключительно на физических приложениях методов векторного исчисления, таких как электродинамика, гравитация, механика сплошных сред или гидродинамика.

Учебные материалы

Обыкновенные дифференциальные уравнения — нелинейность и хаос

Дифференциальные уравнения сами по себе являются большой областью исследований. По окончании материала первого года, который обычно завершается обсуждением линейного ОДУ второго порядка с постоянными коэффициентами, появляются более интересные ОДУ, которые можно найти в реальных приложениях. К ним относятся области механики, электроники и математической биологии. Такие ОДУ обладают нелинейным и хаотическим поведением.

При изучении дифференциальных уравнений этого типа наблюдается довольно большой скачок сложности. Акцент становится меньше на механические методы получения решений и больше на понимание границ поведения более сложных систем. Дифференциальные уравнения в конечном итоге приводят к более продвинутой области динамических систем. Однако их не часто изучают должным образом до третьего или четвертого года обучения по математике.

Обычные дифференциальные уравнения также приводят к стохастическим дифференциальным уравнениям (SDE) , которые являются ОДУ, которые содержат случайный аспект.SDE чрезвычайно важны для предполагаемого количественного анализа, который хочет изучать ценообразование деривативов и анализ временных рядов. Базовые модели движения цен акций часто моделируются как геометрические случайные блуждания, что требует использования SDE.

Учебные материалы

Как и в случае с курсами ODE первого года обучения, нет недостатка в учебниках для изучения обыкновенных дифференциальных уравнений в бакалавриате. Уловка состоит в том, чтобы найти солидный вводный текст, а затем текст, который идет немного глубже, включая обсуждение теории управления, нелинейности, хаоса и моделирования.

Springer и CUP имеют относительно хороший набор учебников по ODE. В частности, посмотрев на те, которые я рекомендовал в предыдущей статье, вы могли бы рассмотреть следующее:

Геометрия — неевклидова

Знакомая геометрия повседневной жизни — трехмерная евклидова геометрия. На втором курсе студенты часто знакомятся с проективной геометрией, эллиптической геометрией и гиперболической геометрией. Эти геометрии возникают, когда «пятый постулат» Евклида ослабляется, что позволяет параллельным линиям пересекаться или расходиться, в отличие от евклидовой геометрии.

Эти дополнительные геометрии играют большую роль в физических науках, особенно в изучении теории относительности и космологии, где риманова геометрия используется для моделирования пространства-времени в общей теории относительности. Эти геометрические формы также являются чрезвычайно интересными предметами для изучения сами по себе.

Изучение геометрии менее применимо к кванту, чем другие области математики. Однако в предыдущей статье я упоминал, что твердое понимание тригонометрических концепций было необходимо для изучения анализа Фурье, который является очень важным для квантов.

Учебные материалы

Абстрактная алгебра

В Части 1 мы увидели, что студенты часто попадают в абстрактные группы через модуль «Основы». На 2-м курсе дается более тщательное изучение абстрактной алгебры, которая охватывает более глубокие группы и часто приводит к изучению колец.

Кольцо похоже на группу, за исключением того, что в нем есть две операции, представляющие «сложение» и «умножение». У группы есть только одна операция.Возможно, наиболее распространенный пример кольца — это кольцо целых чисел ($ \ mathbb {Z} $) с добавлением и умножением.

На большинстве курсов абстрактной алгебры второго года обучения обсуждаются изоморфизмы, фактор-группы, теорема Лагранжа, абелевы группы, орбиты и стабилизаторы. Все это важные темы для дальнейшего изучения абстрактной алгебры, включая группы Ли и алгебры Ли.

Как я пояснил в Части 1, потенциальному кванту необязательно иметь глубокое понимание теоретико-групповых концепций.Эти концепции обычно не применимы к основным областям количественного финансирования. Тем не менее, группы и кольца — это увлекательные области математики, которые доставляют массу удовольствия самоучке, решившей изучать их ради самих себя.

Учебные материалы

Случайные процессы

Стохастические процессы обычно предлагается как дополнительный модуль в университете и как таковой не является «основным». Однако очевидно, что это чрезвычайно важно для количественного финансирования, особенно в области ценообразования деривативов.

Прежде чем углубленно изучать стохастическое исчисление, которое требует понимания интеграла Лебега и других теоретических концепций меры, рекомендуется рассмотреть более элементарные случайные процессы.

Такие курсы часто начинаются с обзора теории вероятностей, включая краткое обсуждение сигма-полей и вероятностных мер (но без лишних дополнительных теоретических концепций меры). Затем внимание обращается на такие процессы, как дискретные мартингалы и цепи Маркова, прежде чем вводить непрерывный случай.

Такой курс естественным образом ведет к дальнейшему изучению стохастического анализа, который вводит исчисление Ито и, в конечном итоге, ценообразование опционов.

Учебные материалы

Численный анализ

Основная цель численного анализа — представить методы решения уравнений с помощью численного метода, то есть с использованием приближенных методов, а не поиска аналитического решения. В теме также представлены методы понимания ошибок, вносимых в процесс, а также важные концепции, такие как повторение уравнений, сходимость и стабильность.

Численный анализ чрезвычайно важен для решения дифференциальных уравнений, которые широко используются в количественных финансах, гидродинамике, гравитации, механике сплошных сред и электродинамике. Изучение численного анализа позволяет понять, когда применимы определенные численные методы, а когда они могут привести к чрезмерной ошибке.

Как квант, вероятно, вы будете использовать некоторую форму численного приближения, либо Монте-Карло цепи Маркова для байесовского анализа, либо численное интегрирование для решения уравнений в частных производных при ценообразовании производных.Следовательно, изучение численного анализа стоит рассмотреть, чтобы избежать распространенных ошибок.

Учебные материалы

Статистика

Статистика, вероятно, самый востребованный количественный навык в коммерческом секторе, который можно изучать на математике. Он обеспечивает основу для понимания неопределенности и измерения риска, которые абсолютно необходимы для практики квантования.

Помимо своей ценности как инструмента управления рисками, он также обеспечивает основу, на которой построено большинство основных методов машинного обучения.Следовательно, необходимо, чтобы предполагаемая количественная статистика изучалась на уровне бакалавриата.

Статистика использует теорию вероятности, а затем основывает ее на обсуждении концепций распределения вероятностей, математического ожидания, корреляции и ковариации. После того, как эти основные концепции изложены, оставшаяся часть материала обычно состоит из объяснения классических / частотных тестов гипотез для анализа данных.

Эти тесты невероятно распространены в коммерческом мире, особенно в количественных финансах.Как количественный менеджер портфеля или аналитик рисков вы будете часто использовать их в реальных условиях. Следовательно, стоит хорошо изучить эти методы.

Курс классической / частотной статистики естественным образом ведет к курсу байесовской статистики. Последний стал популярным в последние годы из-за вычислительной управляемости лежащих в основе алгоритмов Монте-Карло цепи Маркова.

Учебные материалы

Следующие шаги

Второй год программы бакалавриата — это объединение и расширение идей первого года. Для самоучки пора начать выбирать модули, которые подходят для их собственной карьерной траектории.

Я описал многие курсы выше. Некоторые из них не важны для количественного анализа, желающего изучить «самый минимум», необходимый для работы над ценообразованием деривативов, статистическим машинным обучением или количественной торговлей.

Однако важно понимать, что роли в количественном финансировании весьма конкурентоспособны. Получение всестороннего математического образования так же важно, как и знание предпосылок для количественных финансов, особенно когда речь идет о ситуациях собеседования.Не следует отказываться от более абстрактных курсов, таких как абстрактная алгебра или неевклидова геометрия, поскольку результаты, полученные в этих областях, часто находят свое применение в более прикладных областях математики и количественных финансов.

В следующей статье, посвященной 3-му году обучения, мы рассмотрим более абстрактные области анализа, такие как теория меры и функциональный анализ. Первый очень важен для изучения вероятностного и стохастического анализа. Будут представлены многие прикладные модули, такие как байесовская статистика и гидродинамика, которые являются отличной тренировочной площадкой для обучения потенциальных квантов тому, как выполнять анализ данных и решать уравнения в частных производных.

Прочтите следующую статью из серии: Как изучать высшую математику, не отправляясь в университет — Часть 3

Статьи по теме

Level Test Upper Intermediate B2

Level Test Upper Intermediate B2 — Бесплатный тест на уровень английского

• question_answer [email protected]

Выберите один вариант для каждого вопроса, затем нажмите Результат теста , чтобы получить свой результат и уровень (35 вопросов)

• А.Выберите правильный вариант

• Б. Исправьте порядок слов

  1. Американец ее второй муж?

  • это

  • Американский

  • ее

  • секунда

  • муж

  2.он прекрасно танцует вальс

  • он

  • танцы

  • красиво

  • Вальс

  3. про какой фильм?

  4.никто серьезно не пострадал в аварии

  • никто

  • было

  • раненых

  • серьезно

  • в

  • авария

  5. что значит «Glitterati»?

  • что

  • среднее

  • да

  • ‘Glitterati’

  6. Очень нравится этот ресторан

  • Я

  • нравится

  • очень

  • много

  • это

  • ресторан

  7.почти он пропустил рейс

  • почти

  • он

  • пропущено

  • рейс

  8. он потерял ключи, вероятно,

  • он

  • имеет

  • потеряно

  • его

  • ключи

  • вероятно

  9.он не попрощался даже

  • он

  • нет

  • скажем

  • до свидания

  • четные

  10. Сколько сигарет вы обычно выкуриваете в день?

  • как

  • много

  • сигареты

  • обычно

  • вы

  • до

  • дым

  • а

  • 9000 2 дня

• С. Запутанные слова

Мы используем файлы cookie, чтобы улучшить работу в сети.

Перемещаясь по этому сайту, не изменяя своих настроек, вы даете согласие на получение файлов cookie.

Подробнее

ОК

MST125 | Основы математики 2

Счет бюджета студентов Открытого университета

The Open University Student Budget Accounts Ltd (OUSBA) предлагает удобный вариант оплаты по мере использования для оплаты взносов в OU, который является безопасным, быстрым и простым способом оплаты.Обратите внимание, что Открытый университет работает исключительно с OUSBA и не может предложить вам кредитные средства от других поставщиков. Все кредиты зависят от статуса и подтверждения того, что вы можете позволить себе выплаты.

Вы платите OU через OUSBA одним из следующих способов:

• Зарегистрируйтесь сейчас, платите позже — OUSBA оплачивает плату за модуль напрямую организационному подразделению. Затем вы выплачиваете OUSBA беспроцентную выплату в полном объеме непосредственно перед началом вашего модуля. 0% годовых представительских. Этот вариант может дать вам дополнительное время, которое может потребоваться для обеспечения финансирования для выплаты OUSBA.
• Оплата в рассрочку — OUSBA рассчитывает вашу ежемесячную плату и количество взносов на основе стоимости модуля, который вы изучаете. годовых 5,1% представительских.

Совместные кредитные заявки

Если вы чувствуете, что не сможете получить ссуду OUSBA самостоятельно из-за кредитной истории или проблем с доступностью, OUSBA предлагает возможность подать заявку на совместную ссуду с третьей стороной. Например, ваш муж, жена, партнер, родитель, брат или сестра или друг. В таких случаях OUSBA будет необходимо провести дополнительные проверки доступности по отдельности и / или коллективно для обоих совместных заявителей, которые будут нести солидарную ответственность за погашение кредита.

Поскольку при обработке совместных кредитных заявок требуются дополнительные проверки доступности, к сожалению, мгновенное решение не может быть принято. В среднем время обработки совместной кредитной заявки составляет пять рабочих дней с момента получения необходимой документации.

Узнайте больше о бюджетных счетах студентов открытого университета (OUSBA).

Кредитная / дебетовая карта

Вы можете частично или полностью оплатить обучение дебетовой или кредитной картой при регистрации на каждый модуль.

Мы принимаем карты American Express, Mastercard, Visa и Visa Electron.

Смешанные выплаты

Мы знаем, что иногда вам может понадобиться комбинировать способы оплаты. Например, вы можете оплатить часть платы за обучение с помощью дебетовой карты, а оставшуюся часть оплатить частями через счет бюджета студента Открытого университета (OUSBA).

Лучшие 20 вопросов и ответов по математике на собеседовании

1) Какие существуют классы математики и какую математику вы предпочитаете?

Различные типы математических полей: исчисление, алгебра и дроби. Я использую все виды математики, но математический анализ является основным.

2) W что такое алгебра?

Алгебра — это одна из областей математики, в которой символы и буквы используются для обозначения чисел, точек и объектов, а также взаимосвязей между ними.Он используется, чтобы знать неизвестные переменные.

Например, вы потеряли 5 ручек, и теперь у вас осталось 10 ручек, чтобы узнать общее количество ручек, которое у вас было. Вы будете использовать алгебраическое уравнение.

Х -5 = 10

X = 10 + 5 = 15 — общее количество ручек, которое у вас было.

3) Сколько места потребуется для полки на 30 чашек, если для шкафа на 12 стенок потребуется 18 футов пространства на стене?

Для оболочки 30 Cup требуется 45 футов стены

4) В учительской есть четыре стеллажа с 10 ящиками с мелками.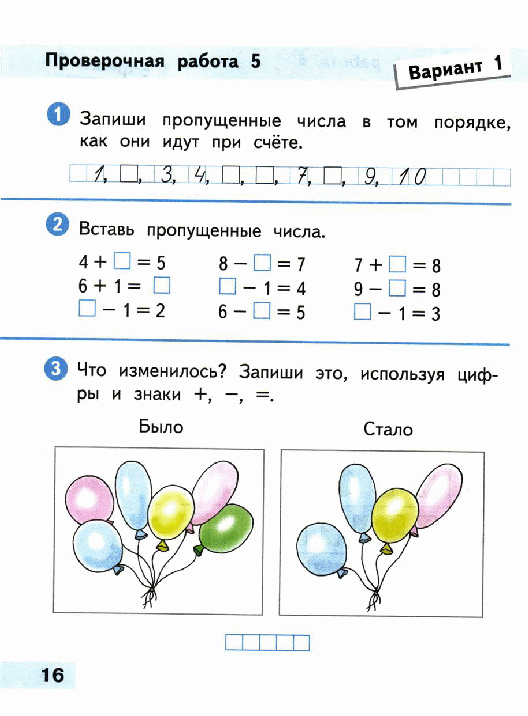 t

6) W Что такое законы коммутации, ассоциации и распределения в математике?

• Законы коммутации гласят, что мы можем поменять местами числа, и вы все равно получите то же число, если сложите, например, a + b = b + a и то же самое для умножения.

• Ассоциативные законы гласят, что не имеет значения, как мы группируем число, конечное значение останется прежним, например, (a + b) + c = (a + b) + c, и то же самое для умножения

• Законы распределения гласят, что мы можем получить тот же ответ, умножая число на группу чисел, сложенных вместе или умножая их по отдельности, а затем складывая их, например, a x (b + c) = axb + axc

7) В небольшой компании средняя зарплата трех сотрудников составляет 1000 долларов в неделю.Если один сотрудник зарабатывает 1100 долларов, а другой — 500 долларов, сколько заработает третий сотрудник?

Формула для расчета,

(e1 + e2 + e3) / 3 = 1000 долларов США

1100 + 500 + e3 = 1000 x 3

1600 + e3 = 3000

e3 = 3000-1600

= 1400

Третий сотрудник заработает 1400 долларов

8) Объясните в сложном вычислении, например, 8 + (9 x 5 ² +8), откуда вы начнете вычисление?

Чтобы избежать недоразумений, с чего начать расчет, вы должны следовать BODMAS

• B = Кронштейн первый
• O = Приказы (степени и квадратные корни)
• DM = деление и умножение
• AS = Сложение и вычитание

После того, как вы закончили с B или O, продолжайте слева направо, выполняя любые «D» или «M», как указано в задаче, а затем продолжайте слева направо, выполняя любые «A» или «S». как указано в задаче.

9) W Что такое геометрия?

Геометрию можно разделить на два класса

• Плоская геометрия: речь идет о плоских формах, таких как треугольники, линии и круги, которые можно нарисовать на листе бумаги.
• Solid Geometry: речь идет о трехмерных объектах, таких как цилиндры, кубы, призма и сферы.

10) W Какая разница между Line, Point, Plane и Solid?

• Точка не имеет размеров
• Линия одномерная
• Самолет двумерный
• Твердое тело трехмерное

11) W Что такое внешний угол в многоугольниках?

В многоугольниках угол между любой стороной фигуры и линией, продолженной от следующей стороны, называется внешними углами.Все внешние углы многоугольника в сумме составляют 360 °. Каждый внешний угол должен составлять 360 °

12) H Как вы можете преобразовать дробь в проценты?

Чтобы преобразовать дробь в проценты, рассмотрим пример для 4/9

• Первое деление 4/9 = 0,44
• Затем умножьте на 100 = 0,44 x 100 = 44,44
• Добавьте к ответу знак «%» = 44,44%

Процент от 4/9 = 44,4%

13) H Как вы можете преобразовать процент в дробь?

Чтобы преобразовать процент в дробь, скажем, 70% в дробь

• Преобразовать 70% в десятичное число = 70/100 = 0.7
• Запишите десятичную дробь «поверх» числа 1 = 0,7 / 1
• Затем умножьте верх и низ на 10 = 0,7x 10 = 7/10

Для каждого числа после десятичной запятой 1 x 10

(10 за 1, 100 за 2)

• Что даст = 7/10
• 7/10 это дробная форма

14) W как кубический метр?

Кубический метр — это стандартная единица измерения объема объекта длиной по длине. Единица записывается в м ^3.

1 м ³ (кубический метр) = 1000 литров

15) H Что такое гектар, а сколько квадратный миллиметр?

• 1 га = 100 метров с каждой стороны, поэтому на гектаре 100 м x 100 м = 10000 м ²

• Квадратный миллиметр равен миллиметрам x миллилитрам ; миллиметр — это тысяча частей метра, поэтому квадратный миллиметр составляет одну миллионную квадратного метра

1 X 1 = 1 квадратный метр

1000 1000 1000, 000

16) Если кондуктор выдает 50 билетов за 30 минут, сколько билетов он сможет выпустить за 8 часов.?

Если кондуктор выдает 50 билетов за 30 минут, значит, количество билетов выдается за 8 ч. будет

(480 x50) / 30 = 800 билетов

То есть кондуктор может оформить 800 билетов на 8 часов.

17) W что это перестановка?

Упорядоченное расположение группы объектов известно как перестановка, например, перестановка расположения из 9 шаров разного цвета в 3 разных рядах может быть выполнена ₉ P ₃ = 504 способами.

18) W Что такое линейное уравнение? Для чего это используется?

Для расчета или решения задач, связанных с расстоянием, скоростью и временем, мы используем линейное уравнение. Он также используется для поиска решений, связанных с весом, массой и плотностью. Линейное уравнение можно представить как Ax + By + Cz +… = D.

19) Приведите пример, где вы можете использовать линейное уравнение в своей повседневной жизни?

Например, если вы находитесь в офисе в 20 милях от вашего офиса, и вы достигли 8 утра, и вы знаете, что трафик движется со скоростью 40 миль в час.

Чтобы узнать, во сколько вам следует уйти из дома, используйте это уравнение

Затраченное время = расстояние / скорость движения

t = 20/40 = ½ или полчаса. Чтобы прийти в офис в 8 утра, нужно выходить из дома в 7:30 утра

.

20) W что это касательная?

Линия, которая касается кривой в одной точке, но не проходит и не пересекает ее, называется касательной.

21) W Что такое стандартное отклонение?

Стандартное отклонение — это мера разброса данных о среднем значении.Он называется сигма и представлен как символ σ.

.

No related posts.