Контрольная работа системы счисления 9 класс: Контрольная работа Системы счисления 9 класс

Содержание

Контрольная работа Системы счисления 9 класс

Контрольная работа 9 класс

Системы счисления

Вариант 1

№1 Переведите десятичное 83 в двоичную и шестеричную системы счисления.

№2 Переведите число 11111100₂ в восьмеричную ССч.

№3 Переведите число 1111111100₂ в шестнадцатеричную систему счисления.

№4 Переведите число 603₈ в двоичную ССч.

№5 Переведите число E43₁₆ в двоичную ССч.

№6 Переведите числа в десятичную ССч.:

21020_3;

_{1010110_2;}

3CE₁₆.

№7 Вычислите:

А) 1010101₂ + 10000101₂

Б) 1111011101₂ + 101101000₂

В) 1001000011₂ — 10110111₂

Г) 111011100₂ — 10010100₂

Д) 11001₂ * 1011100₂

№7 Вычислите значение суммы 43₈ + 56₁₆

Ответ запишите в десятичной СС

Вариант 2

№1 Переведите десятичное 126 в двоичную и троичную системы счисления.

№2 Переведите число 10001101₂ в восьмеричную ССч.

№3 Переведите число 11010101101₂ в шестнадцатеричную систему счисления.

№4 Переведите число 714₈ в двоичную ССч.

№5 Переведите число D27₁₆в двоичную ССч.

№6 Переведите числа в десятичную ССч.:

2314₅

;

1010011₂;

2AB₁₆.

№7 Вычислите:

А) 1101100000₂ + 10110110₂

Б) 101110111₂ + 1000100001₂

В) 1011001001₂ — 1000111011₂

Г) 1110000110₂ — 101111101₂

_{Д) 1011001₂ * 1011011₂}

№8 Вычислите значение суммы 23₈ + 67₁₆

Ответ запишите в десятичной СС

Вариант 3

№1 Переведите десятичное 202 в двоичную и пятеричную системы счисления.

№2 Переведите число 11100010₂в восьмеричную систему счисления.

№3 Переведите число 1011010111₂ в шестнадцатеричную систему счисления.

№4 Переведите число 325₈в двоичную систему счисления.

№5 Переведите число B3F₁₆ в двоичную систему счисления.

№6 Переведите числа в десятичную систему счисления:

256₇;

10101011₂;

5ЕА_16.

№7 Вычислите:

А) 101111111₂+1101110011₂

Б) 10111110₂+100011100₂

В) 1010101101₂-110011110

Г) 1010001111₂-1001001110₂

Д) 101011₂*100111₂

№8 Вычислите значение суммы 61₈+45₁₆

Ответ запишите в десятичной СС

Вариант 4

№1 Переведите десятичное 53 в двоичную и семеричную системы счисления.

№2 Переведите число 1010110₂ в восьмеричную систему счисления.

№3 Переведите число 11101011110₂ в шестнадцатеричную систему счисления.

№4 Переведите число 532₈ в двоичную систему счисления.

№5 Переведите число АОС₁₆ в двоичную систему счисления.

№6 Переведите числа в десятичную систему счисления:

3021₄;

11011001₂;

1BD₁₆.

№7 Вычислите:

А) 100101011₂+111010011₂

Б) 1001101110₂+1101100111₂

В) 1100110010₂-1001101101₂

Г) 1110001100₂-10001111₂

Д) 1010101₂*1011001₂

№8 Вычислите значение суммы 52₈+74₁₆

Ответ запишите в десятичной СС

Ответы

1010011₂

215₆

374

3FC₁₆

110000011₂

111001000011₂

21020₃=195₁₀

1010110₂=86₁₀

3CE₁₆=974₁₀

А)11011010

Б)10101000101

В)110001100

Г)101001000

Д)100011111100

121

Вар 2

1111110₂

11200₃

215₈

6AD₁₆

111001100₂

110100100111₂

2314₅=334₁₀

1010011₂=83₁₀

2AB₁₆=683₁₀

А)10000010110

Б)1110011000

В)10001110

Г)1000001001

Д)1111110100011

122

Вар 3

11001010₂

1302₅

342₈

2DC₁₆

11010101₂

101100111111₂

256₇=139₁₀

10101011₂=171₁₀

5EA₁₆=1514₁₀

А)10011110010

Б)111011010

В)100001111

Г)1000001

Д)11010001101

118

Вар 4

110101₂

104₇

126₈

75E₁₆

101011010₂

101000001100₂

3021₄=201₁₀

11011001₂=217

1BD₁₆=445₁₀

А)1011111110

Б)10111010101

В)11000101

Г)1011111101

Д)1110110001101

158

Критерии:

«5» 12 — 14

«4» 8 – 11

«3» 5 — 7

Контрольная работа по теме «Системы счисления» | Тест по информатике и икт (9 класс) по теме:

Контрольная работа по теме «Системы счисления»

Вариант 1

Задание 1.

Заполните пустые клетки таблицы

Двоичная система счисления	Восьмеричная система счисления	Десятичная система счисления	Шестнадцатеричная система счисления
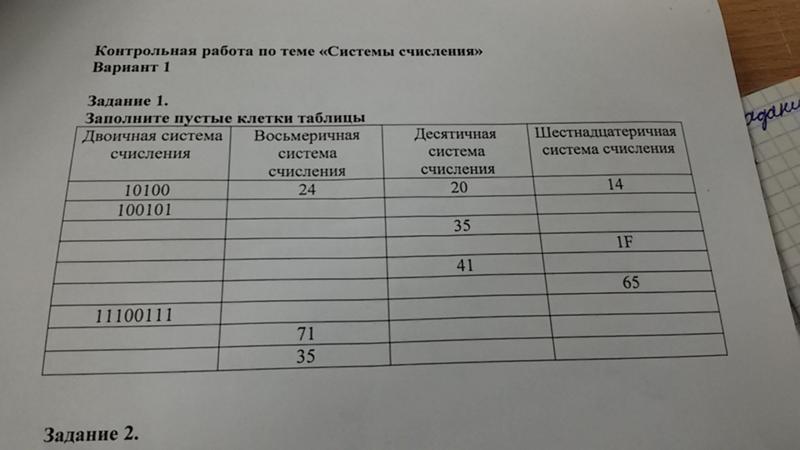
10100	24	20	14
100101
		35
			1F
		41
			65
11100111
	71
	35

Задание 2.

Выполните сложение.

а) 1001100112+100010012

б) 11111112+1000012

в) 100000012+11111112

г)10010012+1F16

д)238+6510

е)10011102+4416

Задание 3.

Расположить числа в порядке возрастания.

1112, А216, 348, 7610

Задание 4.

Решите задачу.

Ученик рассказал, что маме 14 лет, папе 26 лет, ему (сыну) 9 лет. Сумма возрастов мамы и папы – 48 лет. Какую систему счисления использовал ученик? Вычислить, сколько лет маме, папе и сыну в десятичной системе счисления.

Система счисления, использованная учеником ___________________________

Маме _____ лет, папе _____ лет, сыну ____ лет.

Контрольная работа по теме «Системы счисления»

Вариант 2

Задание 1.

Заполните пустые клетки таблицы

Двоичная система счисления	Восьмеричная система счисления	Десятичная система счисления	Шестнадцатеричная система счисления
11110	36	30	1Е
11100
		46
			2С
		53
			89
11100111
	62
	54

Задание 2.

Выполните сложение.

а) 10000011102+11001102

б) 100010012+10101012

в) 1110001112+10000012

г)110110112+2916

д)458+8110

е)11100112+FF16

Задание 3.

Расположить числа в порядке возрастания.

100012, В516, 738, 8710

Задание 4.

Решите задачу.

Ученик рассказал, что маме 36 (30) лет, папе 43 (35) лет, ему (сыну) 13 (11) лет. Сумма возрастов мамы и папы – 101 год. Какую систему счисления использовал ученик? Вычислить, сколько лет маме, папе и сыну в десятичной системе счисления.

Система счисления, использованная учеником ___________________________

Маме _____ лет, папе _____ лет, сыну ____ лет.

Тест по информатике и икт (9 класс) на тему: Контрольная работа по темам «Системы счисления. Логика» 9 класс

Контрольная работа по теме «Системы счисления и логика» 9 класс

ВАРИАНТ 1

Выполните действия:
а) 13428 + 56118
б) 100011012 * 1012
Переведите числа из одной системы счисления в другую:
а) 27210 → ?2 б) 27210 → ?8 в) 27210 → ?16
Переведите числа из одной системы счисления в другую:
а) 10011011102 → ?8
б) А16,8F16 → ?2
Запишите число -23110 в 16-и разрядном представлении.
Постройте таблицу истинности и логическую схему для выражения A+ ‾B + (‾A*C)+ ‾C.
НЕ ((x>-1) И (x 9)

1) -1 2) 5 3) 3 4) 9

Напишите 2-3 формулы упрощения логических выражений.
Водители трех транспортных средств – участники дорожно-транспортного происшествия – автобуса, легкового автомобиля и маршрутного такси – давали объяснение инспектору ГИБДД. На вопрос инспектора, кто спровоцировал аварию, водители ответили следующее:

Водитель автобуса: «Я не нарушал правил, и водитель легкового автомобиля тоже».

Водитель легкового автомобиля: «Водитель автобуса не является нарушителем, правила нарушил водитель маршрутного такси».

Водитель маршрутного такси: «Я не делал этого, правила нарушил водитель автобуса».

Известно, что один из водителей исказил оба факта, другой сказал чистую правду, а третий в одной части своего заявления солгал, а другая часть его признания истинна. Кто же виноват в аварии?

Контрольная работа по теме «Системы счисления и логика» 9 класс

ВАРИАНТ 2

Выполните действия:
а) 12758 + 43218

б) 101010012 * 1012

Переведите числа из одной системы счисления в другую:
а) 26510 → ?2 б) 26510 → ?8 в) 26510 → ?16
Переведите числа из одной системы счисления в другую:
а) 10110010102 → ?8
б) B41,2616 → ?2
Запишите число -25410 в 16-и разрядном представлении
Постройте таблицу истинности и логическую схему для выражения ‾A+ B * ‾ (‾A+C)+ ‾B.
НЕ ((x>- 4) ИЛИ (x

1) -4 2) 12 3) 17 4) 20

Напишите 2-3 формулы упрощения логических выражений.
Восемь преступников, подозреваемых в ограблении банка, были вызваны к следователю. На вопрос следователя, кто ограбил банк, были получены следующие ответы:

Соня: «Это сделал Винни».

Майкл: «Это ложь!»

Винни: «Это я ограбил!»

Бонни: «Это я сделал!».

Лиза: «Бонни не грабила».

Дик: «Ограбила либо Соня, либо Лиза!».

Ник: «Это не женская работа…»

Том: «Это Ник постарался!»

Кто ограбил банк, если известно, что из восьми высказываний истинны только два? Ответ

запишите в виде первой буквы имени.

Учебно-методический материал по информатике и икт (9 класс) на тему: Контрольная работа по теме «Системы счисления»

Контрольная работа по теме «Системы счисления»

56710 = Х3
D1016 = Х10
111012+11101001112 (перевести в восьмеричную)
1101011100112+1111101111112
1101012*111112
11101112*111011012(перевести в шестнадцатеричную)
(467+234)*11113=X7
Сколько натуральных чисел в промежутке

11111112 16

Контрольная работа по теме «Системы счисления»

55710 = Х4
A1016 = Х10
110112+110101001112(перевести в восьмеричную)
1111011100112+1101101111112
1101112*110112
11101012*111011112(перевести в шестнадцатеричную)
(468+235)*11114=X9
Сколько натуральных чисел в промежутке

2018 ≤ X 2

Контрольная работа по теме «Системы счисления»

56910 = Х3
F1016 = Х10
111012+11101001112(перевести в восьмеричную)
1111011100112+1111101111012
11011012*101112
11101112*111011102(перевести в шестнадцатеричную)
(469+236)*11115=X9
Сколько натуральных чисел в промежутке

8216 8

Контрольная работа по теме «Системы счисления»

66710 = Х5
B1016 = Х10
1110112+11101001112(перевести в восьмеричную)
11011011100112+1111101111112
1101112*1111012
111011012*111011112(перевести в шестнадцатеричную)
(467+239)*11112=X11
Сколько натуральных чисел в промежутке

2218 16

Контрольная работа по теме «Системы счисления»

59710 = Х6
A4016 = Х10
1100112+11101001112(перевести в восьмеричную)
1111011100112+11011111111012
11011012*111112
11101112*1110111012(перевести в шестнадцатеричную)
(469+237)*11114=X7
Сколько натуральных чисел в промежутке

9316 ≤ X ≤ 1010100112

Контрольная работа по теме «Системы счисления»

76710 = Х4
A2016 = Х10
1011112+11101001112(перевести в восьмеричную)
1111011100112+1111101111012
1101112*1011112
101101112*111011112(перевести в шестнадцатеричную)
(567+238)*11119=X6
Сколько натуральных чисел в промежутке

101110112 ≤ X 8

Контрольная работа по теме «Системы счисления»

56610 = Х3
D0116 = Х10
1111012+11101001112 (перевести в восьмеричную)
1101011100112+1111101100112
1101012*1101112
111011012*111011012(перевести в шестнадцатеричную)
(667+134)*12113=X7
Сколько натуральных чисел в промежутке

11111102 16

Контрольная работа по теме «Системы счисления»

56410 = Х5
A1216 = Х10
110112+1101101001112(перевести в восьмеричную)
1011011100112+1101101111112
11010112*110112
11101012*1011011112(перевести в шестнадцатеричную)
(568+435)*111314=X9
Сколько натуральных чисел в промежутке

11111012 ≤ X 16

Контрольная работа в 9 классе «Системы счисления»

Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №2» имени Баки Урманче
Нижнекамского МР Республики Татарстан

Контрольная работа в 9 классе
«Системы счисления» в 3-х вариантах
Подготовила учитель информатики
Исламова Илиза Халафовна

Нижнекамск, 2012
Представление информации в двоичной системе счисления (вариант 1)
1)Перевести число 135 из десятичной системы счисления в двоичную систему счисления
11100001
10000111
10000101
10100001

Представление информации в двоичной системе счисления (вариант 2)

1)Перевести число 165 из десятичной системы счисления в двоичную систему счисления

11100001
10100111
10010101
10100101

Представление информации в двоичной системе счисления (вариант 3)

1)Перевести число 145 из десятичной системы счисления в двоичную систему счисления

11100001
10000111
10010001
10100001

Контрольная работа по теме
«Представление информации в двоичной системе счисления

Вариант 1.

1)Перевести число 135 из десятичной системы счисления в двоичную систему счисления

2) Перевести число 0,824 из десятичной системы счисления в двоичную систему

счисления (до 4-х знаков после запятой)

3) Перевести число 671,7 из восьмеричной системы счисления в двоичную систему

счисления

4) Перевести двоичное число 1111101 в десятичную систему счисления

5) Перевести двоичное число 110111,111 в шестнадцатеричную систему счисления

6) Сложить два восьмеричных числа 165+37=?

7) Сложить два двоичных числа 1111 + 1101 = ?

8) Найти разность двоичных чисел 101010 — 1011 = ?

9) Произвести умножение двоичных чисел 1011 * 111 = ?

10) Произвести деление двоичных чисел 1101110 : 1011 = ?

Вариант 2

1)Перевести число 165 из десятичной системы счисления в двоичную систему счисления

2) Перевести число 0,8125 из десятичной системы счисления в двоичную систему

счисления (до 4-х знаков после запятой)

3) Перевести число 751,5 из восьмеричной системы счисления в двоичную систему

счисления

4) Перевести двоичное число 10000111 в десятичную систему счисления

5) Перевести двоичное число 101101,111 в шестнадцатеричную систему счисления

6) Сложить два восьмеричных числа 165+47=?

7) Сложить два двоичных числа 1001 + 1101 = ?

8) Найти разность двоичных чисел 100010 — 1011 = ?

9) Произвести умножение двоичных чисел 1101 * 111 = ?

10) Произвести деление двоичных чисел 1111001 : 1011 = ?

Вариант 3

1)Перевести число 145 из десятичной системы счисления в двоичную систему счисления

2) Перевести число 0,4375 из десятичной системы счисления в двоичную систему

счисления (до 4-х знаков после запятой)

3) Перевести число 401,5 из восьмеричной системы счисления в двоичную систему

счисления

4) Перевести двоичное число 1101101 в десятичную систему счисления

5) Перевести двоичное число 1100101,11 в шестнадцатеричную систему счисления

6) Сложить два восьмеричных числа 175+45=?

7) Сложить два двоичных числа 1111 + 1101 = ?

8) Найти разность двоичных чисел 100010 — 1101 = ?

9) Произвести умножение двоичных чисел 1110 * 111 = ?

10) Произвести деление двоичных чисел 1001101 : 1011 = ?

Таблица ответов:

Список использованной литературы

Авторская разработка

2) Перевести число 0,824 из десятичной системы счисления в двоичную систему счисления (до 4-х знаков после запятой) 0,0110 0,0111 0,1101 0,1111
3) Перевести число 671,7 из восьмеричной системы счисления в двоичную систему счисления 10000001,101 110111001,111 111111001,101 100000001,101	4) Перевести двоичное число 1111101 в десятичную систему счисления 135 144 124 125
5) Перевести двоичное число 110111,111 в шестнадцатеричную систему счисления 27,Е 65,7 55,Е 27,7	6) Сложить два восьмеричных числа 165+37=? 224 234 124 332
7) Сложить два двоичных числа 1111 + 1101 = ? 11110 11010 11100 11000	8) Найти разность двоичных чисел 101010 — 1011 = ? 11010 11111 10010 10011
9) Произвести умножение двоичных чисел 1011 * 111 = ? 1000001 1101011 1001111 1001101	10) Произвести деление двоичных чисел 1101110 : 1011 = ? 100 1101 1010 101
2) Перевести число 0,8125 из десятичной системы счисления в двоичную систему счисления (до 4-х знаков после запятой) 0,0110 0,0111 0,1101 0,1111
3) Перевести число 751,5из восьмеричной системы счисления в двоичную систему счисления 10000001,101 110111001,111 111101001,101 100000001,101	4) Перевести двоичное число 10000111 в десятичную систему счисления 135 144 124 125
5) Перевести двоичное число 101101,111 в шестнадцатеричную систему счисления 59,Е 55,7 2D,Е 5D,Е	6) Сложить два восьмеричных числа 165+47=? 224 234 124 332
7) Сложить два двоичных числа 1001 + 1101 = ? 11110 11010 11100 10110	8) Найти разность двоичных чисел 100010 — 1011 = ? 11010 10111 10010 10011
9) Произвести умножение двоичных чисел 1101 * 111 = ? 1011011 1101011 1001111 1001001	10) Произвести деление двоичных чисел 1111001 : 1011 = ? 1001 1101 1111 1011
2) Перевести число 0,4375 из десятичной системы счисления в двоичную систему счисления (до 4-х знаков после запятой) 0,0110 0,0111 0,1101 0,1111
3) Перевести число 401,5 из восьмеричной системы счисления в двоичную систему счисления 100100001,101 110001001,111 101101001,101 100000001,101	4) Перевести двоичное число 1101101 в десятичную систему счисления 110 135 109 111
5) Перевести двоичное число 1100101,11 в шестнадцатеричную систему счисления 27,Е 65,С C5,Е 145,6	6) Сложить два восьмеричных числа 175+45=? 224 234 124 242
7) Сложить два двоичных числа 1111 + 1101 = ? 11100 11001 11100 11000	8) Найти разность двоичных чисел 100010 — 1101 = ? 11010 11111 10101 10011
9) Произвести умножение двоичных чисел 1110 * 111 = ? 1100010 1101010 1001110 1001100	10) Произвести деление двоичных чисел 1001101 : 1011 = ? 110 1101 111 101
Вариант1	Вариант2	Вариант3
	10000111	10100101	10100001
	0,1101	0,1101	0,0111
	110111001,111	111101001,101	100000001,101
	125	135	109
	27,Е	2D,Е	65,С
	224	234	242
	11100	10110	11100
	11111	10111	10101
	1001101	1011011	1100010
	1010	1011	111

Контрольная работа по теме «Системы счисления»

Вариант № 1

1. Перевести число 100111₂ в десятичную систему счисления.

2. Переведите целые числа 513₁₀и 7000₁₀ в двоичную систему счисления.

3. Переведите целые числа 8700₁₀ и 9300₁₀ в восьмиричную систему счисления.

4. Переведите целые числа 287₁₀ и 1023₁₀ в шестнадцатиричную систему счисления.

5. Перевести двоичные числа в восьмиричную и шестнадцатиричную системы счисления 1010001001011 и 1011001101111.

6.Переведите числа 266₈ и 2А19₁₆в двоичную систему счисления.

7. Даны два числа 29 и 17. Перевести их в двоичную систему счисления, в которой выполнить сложение, вычитание и умножение этих чисел.

Контрольная работа №2 по теме «Системы счисления»

Вариант № 2

1. Перевести число 143511₈ в десятичную систему счисления.

2. Переведите целые числа 600₁₀ и 2304₁₀ в двоичную систему счисления.

3. Переведите целые числа 8888₁₀ и 2936₁₀ в восьмиричную систему счисления.

4. Переведите целые числа 266₁₀ и 1280₁₀ в шестнадцатиричную систему счисления.

5. Перевести двоичные числа в восьмиричную и шестнадцатиричную системы счисления 110001000100 и 101000100101.

6.Переведите числа 1270₈ и 266₁₆в двоичную систему счисления.

7. Даны два числа 27 и 14. Перевести их в двоичную систему счисления, в которой выполнить сложение, вычитание и умножение этих чисел.

Контрольная работа №2 по теме «Системы счисления»

Вариант № 3

1. Перевести число Е3В5₁₆ в десятичную систему счисления.

2. Переведите целые числа 602₁₀ и 1000₁₀ в двоичную систему счисления.

3. Переведите целые числа 295₁₀ и 8900₁₀ в восьмиричную систему счисления.

4. Переведите целые числа 2041₁₀ и 321₁₀ в шестнадцатиричную систему счисления.

5. Перевести двоичные числа в восьмиричную и шестнадцатиричную системы счисления 111001010001 и 1001111001.

6.Переведите числа 757₈ и А23₁₆в двоичную систему счисления.

7. Даны два числа 24 и 19. Перевести их в двоичную систему счисления, в которой выполнить сложение, вычитание и умножение этих чисел.

Ответы

Вариант № 1

39₁₀
1000000001₂, 1101101011000₂
20774₈, 22124₈
11F₁₆, 3FF₁₆
12113₈, 144B₁₆; 13157₈, 166F₁₆
10110110₂, 10101000011001₂
11101₂, 10001₂; 101110₂, 1100₂, 111101101₂

Вариант № 2

51017₁₀
1001011000₂, 100100000000₂
21270₈, 5570₈
10A, 500
6104,C44; 5045, A25
1010111000, 1001100110
11011, 1110; 101001, 1101, 101111010

Вариант № 3

58293
1001011010,1111101000
447, 21304
7F9, 141
7121, E51; 1171, 279
111101111, 101000100011
11000, 10011; 101011, 101, 111001000

MCQ Class 9 Number System с ответами Загрузить PDF

Вышеупомянутые NCERT CBSE и KVS MCQ для Class 9 Number System помогут вам повысить свои оценки, поскольку на экзаменах появляются вопросы с несколькими вариантами ответов. Эти MCQ системы нумерации CBSE NCERT класса 9 были разработаны опытными преподавателями сайта StudiesToday.com для учащихся 9 класса.

Преимущества MCQ CBSE NCERT для системы счисления класса 9

a) MCQ NCERT CBSE KVS по системе счисления 9 помогут детям укрепить свои представления и улучшить оценки на тестах и экзаменах.

b) Эти вопросы с несколькими вариантами ответов для класса 9 системы счисления помогут улучшить аналитические навыки и навыки декодирования сложных задач.

c) Ежедневная практика различных MCQ по различным предметам поможет развить твердое понимание каждой темы, которую вы будете помнить до даты экзамена

d) Вы также сможете правильно пересмотреть все главы системы счисления и сэкономить время во время ваши классные тесты и экзамены.

Бесплатная распечатка MCQ в формате PDF системы номеров класса 9 CBSE разработана школьными учителями в StudiesToday.com. Мы предоставляем самые эксклюзивные бесплатные печатные MCQ из базы данных в соответствии со стандартами CBSE NCERT и KVS. Все MCQ были тщательно разработаны для всех типов студентов, вы можете загрузить в формате PDF CBSE Class 9 Number System Chapter мудрые вопросы MCQ с ответами и использовать их для дальнейшего изучения. Вам также следует внимательно ознакомиться с программой для системы счисления 9 класса и загрузить MCQ по каждой изучаемых вами темах. Это очень поможет в выявлении всех ошибок в вашем понимании темы.Практикуйте CBSE Grade 10 Number System MCQ ежедневно, чтобы вы могли получить более высокие баллы на экзамене.

Щелкните по ссылкам ниже для NCERT Class 9 Number System , чтобы загрузить последние решенные образцы документов CBSE (NCERT), вопросы за прошлый год (последние десять лет) с решениями, распечатанные рабочие листы в формате pdf для Class 9 Number System NCERT Books и NCERT решения для системы счисления класса 9 NCERT на основе учебной программы и руководящих принципов, выпущенных CBSE и NCERT. Учебный материал для NCERT для системы счисления класса 9 был составлен опытными учителями ведущих школ Индии и доступен для бесплатного скачивания

CBSE 9th Maths MCQ | Вопросы с несколькими вариантами ответов по системе счисления: проверьте PDF здесь

Вопросы с несколькими вариантами ответов, MCQ составят значительную часть вопросника по математике на ежегодном экзамене CBSE Class 9 2020. Студенты могут легко набрать полные отметки по этим вопросам объективного типа с небольшим трудом. работа и хорошие практики. Мы предоставляем здесь вопросы системы счисления MCQ, которые подготовлены профильными экспертами.Все вопросы основаны на важных концепциях, затронутых в главе. Этот набор важных вопросов станет хорошим практическим тестом для студентов, который заставит их быстро пересмотреть все фундаментальные концепции.

Найдите ниже MCQ из CBSE Class 9 Maths Chapter 1 Number System:

1. Между двумя рациональными числами находится / находятся:

а) Ровно одно рациональное число

б) Бесконечно много рациональных чисел

в) Многие иррациональные числа

г) Только иррациональные числа

Ответ: (б)

New * CBSE Class 9th Science Важные MCQ для ежегодного экзамена 2020

2. Произведение рационального и иррационального чисел:

а) Всегда целое

б) Всегда рациональное число

в) Всегда иррациональное число

г) Иногда рационально, а иногда иррационально

Ответ: (c)

3. Десятичное разложение иррационального числа может быть:

а) Прекращение действия

б) Повторяющиеся

c) Завершающие или не завершающие

г) Непрерывные и единовременные

Ответ: (d)

4. Рациональное число от √2 до √3:

а) 1,9

б) (√2. √3) / 2

в) 1,5

г) 1,8

Ответ: (c)

CBSE Class 9 Maths Новый образец экзамена для ежегодного экзамена 2020

5. Что из перечисленного нерационально?

в) √5

г) √81

Ответ: (c)

6. 4√5 + 5√5 равно:

а) 9√5

б) 9√10

в) 5√10

г) 7√5

Ответ: (а)

7. Что из следующего является иррациональным?

а) 0,4014001400014…

б) 0,14

Ответ: (а)

8. √12 X √15 равно:

а) 5√6

б) 6√5

в) 10√5

г) √25

Ответ: (б)

CBSE Class 9 Maths Важные вопросы всех форматов для ежегодного экзамена 2020

9. Что из следующего равно x ²?

Ответ: (d)

а) 1/4

б) 1/2

в) 4

г) 1/16

Ответ: (б)

12. Какой будет знаменатель после рационализации 7 / (5√3 — 5√2)?

а) 19

б) 20

в) 25

d) Ни один из этих

Ответ: (d)

Практический документ по математике класса 9 CBSE для ежегодного экзамена 2020

Ответ: (а)

а) 2,732

б) 0,2679

в) 0,732

г) 0,517

Ответ: (d)

15. Значение (256) ^0,16 X (256) ^0. 09 составляет:

а) 4

б) 16

в) 64

г) 256,25

Ответ: (а)

Если вы хотите прочитать эти вопросы в автономном режиме, то PDF-файл с вопросами можно загрузить по указанной ниже ссылке:

Также проверьте следующие статьи, чтобы помочь в подготовке к 9-му ежегодному экзамену CBSE Class:

MCQ класса 9 CBSE по математике, естественным наукам, социальным наукам и экзамену по английскому языку 2020

Программа CBSE Class 9 для ежегодного экзамена 2020

CBSE Class 9 Science Exam Pattern 2020

CBSE Class 9 Social Science Exam Pattern 2020

Наука, класс 9, NCERT Книга и решения PDF

Математика NCERT Книга и решения PDF

Система счисления | Примечания, видео, контроль качества и тесты | 8 класс> Обязательная математика> Система счисления

Система счисления

Число — это математический объект, используемый для подсчета, измерения и маркировки. Целые числа — это набор действительных чисел, состоящий из натуральных чисел, их аддитивной инверсии и нуля. Исходными примерами являются натуральные (или считающие) числа: 1, 2, 3, 4, 5 и т. Д. Существует бесконечно много натуральных чисел.

Двоичная система счисления

Чтобы узнать больше о двоичной системе счисления. Для начала необходимо пересмотреть десятичную систему счисления. В десятичной системе счисления используется десять различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), расположенных с использованием позиционного обозначения.Позиционное обозначение используется, когда необходимо представить число больше 9. каждая позиция цифры означает, сколько групп из 10, 100, 1000 и т. д. содержится в этом числе. Например:

2584 = 2 х 1000 + 5 х 100 + 8 х 10 + 4 х 1

= 2 x 10³ + 5 x 10² + 8 x 10¹ + 4 x 10 °

В двоичной системе счисления всегда используются только два разных символа (цифра 0 и 1), которые расположены с использованием позиционного обозначения. Когда необходимо представить число больше 1, позиционное обозначение используется для обозначения количества групп из 2, 4, 8, содержащихся в этом числе.Например:

Рассмотрим число 30

30 ÷ 2 = 15 остаток 0

15 ÷ 2 = 7 Остаток 1

7 ÷ 2 = 3 Остаток 1

3 ÷ 2 = 1 остаток 1

1 ÷ 2 = 0 Остаток 1

Следовательно, 30 = 11110 ₂ реагирует как один ноль основания два.

Сложение двоичных чисел

Сложение двоичного числа — очень простая задача, аналогичная сложению десятичных чисел от руки. В отличие от сложения десятичных дробей, правила сложения двоичных разрядов мало что нужно запоминать.

0 + 0 = 0

1 + 0 = 1

1 + 1 = 10

1 + 1 + 1 = 11

Вычитание двоичных чисел

Мы можем вычесть двоичное число из другого двоичного числа. Для этого выровняйте два числа вверх так же, как вы вычитаете два десятичных числа: первое число вверху и второе число под ним.

0 — 0 = 0

1 — 0 = 1

1 — 1 = 0

Пятеричная система счисления

Система счисления с основанием пять известна как система счисления с пятью числами.В этой системе всего пять цифр 0, 1, 2, 3 и 4.

Пятерка означает, что каждое место по основанию 5 является степенью 5.

Рассмотрим пятеричное число 155 ₅

155 ₅ = 1 X 5² + 5 X 5¹ + 5 X5 °

= 25 + 25 + 5

= 55

Чтобы преобразовать десятичное число в пятеричное, мы должны несколько раз разделить его на 5 и записать остатки, полученные до тех пор, пока результат деления не станет 0. Пятеричное число получается путем чтения последовательности остатков в обратном порядке.Например, давайте рассмотрим число 84 ₁₀

84 ÷ 5 = 16 Остаток 4

16 ÷ 5 = остаток 1

3 ÷ 5 = остаток 0

Следовательно, 84 ₁₀ = 214 ₅

Дополнение пятых чисел

Ключ к пониманию художественной схемы в базе, отличной от 10, — это понимание обозначений, которые мы используем в базе 10. Мы записываем число тринадцать как 13, что означает 1 десятки и единицы. Это может помочь вам думать о предметах, например о палках.Идея состоит в том, чтобы сделать тринадцать палочек и сложить их в группу из десяти. Вы получаете 1 группу по десять и три дополнительных. Предположим, если вы сложите 23 и 19, вы сложите 3 группы, из которых 9 дадут 12, что составляет 1 десять и 2 дополнительных. То есть вы получите еще одну группу из десяти палочек. Это «перенос». Итак, всего у вас 2 + 1 +1 десятки и 2 единицы, на сумму 42.

В базе 5 вы хотите собирать объекты группами по пять, а не десятками. Итак, если у вас есть девять объектов, вы можете объединить их в одну группу из пяти и четырех объектов.

Теперь, чтобы сложить 2 и 3, используя запись по основанию 5, 2 + 3 = 10 по основанию 5.

Вычитание пятизначных чисел

Вычитание является прямым, поскольку вы всегда вычитаете меньшую цифру из большой цифры. Проблема состоит в том, чтобы иметь дело с заимствованиями. Давайте сначала рассмотрим проблему с основанием 10.

3 2 5

-1 3 4

1 9 1

Выпрямление в крайнем правом столбце 5 — 4 = 1, но в следующем столбце вам нужно заимствовать из следующего столбца.Поскольку это обозначение с основанием 10, вы берете десять, поэтому 3 в третьем столбце равняется 2, а прибавляя к 10 к 2, вы получаете 12 во втором столбце.

Теперь попробуем задачу с базой 5

4 3 1

— 2 4 0

1 4 1

Как и в задаче с основанием 10, первый столбец прост, 1-0 = 1. Во втором вам нужно заимствовать из третьего столбца. Поскольку числа записаны в системе счисления с основанием 5, вы берете пять, поэтому 4 в третий столбец становится 3, а добавление пяти дает восемь во втором столбце.

Система счисления | Примечания, видео, контроль качества и тесты | 8 класс> Компьютер> Система счисления

Система счисления может быть определена как комбинация различных чисел, которая помогает в расчетах. История числа начинается с первобытного возраста человека. Развитие системы счисления интегрировалось с развитием человека. В первобытные времена люди считали камни и гальку.

Двоичные числа

Двоичное число — это число из двух основных чисел.Он представлен 1 и 0. 1 или 0 называется двоичными цифрами. Мы можем сгенерировать это число с помощью комбинации 0 и 1. Оно представлено суффиксом два. Например (10101) ₂. В следующей таблице показаны некоторые десятичные числа и их эквивалентные двоичные числа **.

Десятичные (десятичные) числа

Десятичное число называется десятичным числом. Это первая система счисления, в которой выполняются все древние и современные математические вычисления. Другая система счисления образована от этого числа.Он генерируется комбинацией 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Мы можем представить эти числа с помощью суффикса два. Например, (9810) ₁₀ На следующей диаграмме показаны отношения между несколькими системами счисления, производными от десятичного числа.

Восьмеричные числа

Число с основанием восемь называется восьмеричным числом. Он обозначается буквой Q или O. Мы можем генерировать эти числа с помощью комбинации 0, 1, 2, 3, 4, 5, 6, 7. Мы можем представить эти числа с помощью суффикса восемь.Например, (5432) ₈

Шестнадцатеричные числа

Число с основанием шестнадцать называется шестнадцатеричным числом. Мы можем сгенерировать эти числа с помощью комбинации 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Где A = 10, B = 11, C = 13, D = 14, E = 15, F = 16. Мы можем представить эти числа с суффиксом шестнадцать. Например. (12AB) ₁₆ Где A = 10, B = 11. 4-битный формат двоичного файла используется для преобразования шестнадцатеричного числа в двоичное.

Эквивалентные значения для разных систем счисления

9047 9047 9047 9047 9047 9047 9047 9047 9047 9047 9047 9047 904 81 9047 9047 9047 9047 9047
Десятичное Двоичное Восьмеричное Hexadeciamal
0 0 0 9047 9047 9047 1 9047 9047 1 9047 1 1
2 10 2 2
3 11 3 3
4 5 101 5 5
6 110 6 6
7 111 7 7 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 15 D
14 1110 16 E
15 1111 17 F
ISS по анализу Эквивалентное значение 9 Важно, чтобы все тестировщики могли писать тестовые примеры, основанные на разделении эквивалентности и анализе граничных значений. Принимая это во внимание, ISTQB имеет большое значение для этой темы в экзамене на сертификат ISTQB Foundation level. Хорошая практика и логическое мышление могут упростить решение этих вопросов.
Что такое разделение эквивалентности?
Разделение на разделы эквивалентности — это метод получения тестовых примеров. В этом методе классы эквивалентности (для входных значений) идентифицируются таким образом, что каждый член класса вызывает одинаковый вид обработки и вывода.
Значения на крайних точках (начальные / конечные значения или нижние / верхние значения) такого класса известны как граничные значения. Анализ поведения системы с использованием таких значений называется Boundary Value Analysis (BVA).
Вот несколько примеров вопросов для практики из экзаменационных работ ISTQB по эквивалентному разделению и BVA. (В порядке: от простого к сложному)

Вопрос № 1)
Одно из полей формы содержит текстовое поле, которое принимает числовые значения в диапазоне от 18 до 25. Определите недопустимый класс эквивалентности.
a) 17
b) 19
c) 24
d) 21
Решение:
Текстовое поле принимает числовые значения в диапазоне от 18 до 25 (18 и 25 также являются частью класса). Итак, этот класс становится нашим действительным классом. Но вопрос в том, чтобы определить недопустимый класс эквивалентности. Классы будут следующими:
Класс I: значения <18 => недопустимый класс
Класс II: от 18 до 25 => действительный класс
Класс III: значения> 25 => недопустимый класс
17 подпадают под недопустимый класс.19, 24 и 21 подпадают под действующий класс. Итак, ответ — «А»
Вопрос № 2)
На экзамене кандидат должен набрать минимум 24 балла, чтобы сдать экзамен. Максимум, который он может набрать — 40 баллов. Определите значения действительной эквивалентности, если учащийся сдает экзамен.
a) 22,23,26
b) 21,39,40
c) 29,30,31
d) 0,15,22
Решение:
Классы будут следующими:
Class I : значения <24 => недопустимый класс
Класс II: от 24 до 40 => допустимый класс
Класс III: значения> 40 => недопустимый класс
Мы должны определить допустимые значения эквивалентности. Допустимые значения эквивалентности будут присутствовать в классе допустимой эквивалентности. Все значения должны быть из второго сорта. Итак, ответ — «C»
Вопрос № 3)
Одно из полей формы содержит текстовое поле, которое принимает буквенно-цифровые значения. Определите действительный класс эквивалентности
a) КНИГА
b) Книга
c) Boo01k
d) Книга
Решение:
Буквенно-цифровые символы представляют собой комбинацию букв и цифр. Следовательно, мы должны выбрать вариант, в котором есть и то, и другое.Допустимый класс эквивалентности будет состоять как из алфавитов, так и из чисел. Вариант «c» содержит как буквы, так и цифры. Итак, ответ — «C»
Вопрос № 4)
Коммутатор выключается, когда температура падает ниже 18, а затем включается, когда температура превышает 21. Когда температура превышает 21. • Определите значения эквивалентности, которые принадлежат к одному классу.
a) 12,16,22
b) 24,27,17
c) 22,23,24
d) 14,15,19
Решение:
Мы должны выбрать значения из того же класса ( это может быть действительный или недопустимый класс).Классы будут следующими:
Класс I: менее 18 (выключатель выключен)
Класс II: от 18 до 21
Класс III: выше 21 (выключатель включен)
Только для варианта ‘c’, все значения из одного класса. Следовательно, ответ — «C» . (Обратите внимание, что вопрос не касается допустимых или недопустимых классов. Он касается только значений в том же классе)
Вопрос № 5)
Программа проверяет числовое поле следующим образом: значения меньше 10 отклоняются, принимаются значения от 10 до 21, значения больше или равные 22 отклоняются.Какие из следующих входных значений охватывают все разделы эквивалентности?
а. 10,11,21
б. 3,20,21
с. 3,10,22
г. 10,21,22
Решение:
Мы должны выбрать значения, которые попадают во все классы эквивалентности (действительные и недопустимые). Классы будут следующими:
Класс I: значения <= 9 => недопустимый класс
Класс II: от 10 до 21 => действительный класс
Класс III: значения> = 22 => недопустимый класс
Все значения из опции ‘c’ попадает во все классы эквивалентности. Итак, ответ — «С».
Вопрос № 6)
Программа проверяет числовое поле следующим образом: значения меньше 10 отклоняются, значения от 10 до 21 принимаются, значения больше или равные 22 отклоняются. Что из перечисленного охватывает САМЫЕ граничные значения?
а. 9,10,11,22
б. 9,10,21,22
с. 10,11,21,22
г. 10,11,20,21
Решение:
Мы уже создали классы, показанные в вопросе 5.Границы можно обозначить как 9, 10, 21 и 22. Эти четыре значения указаны в опции «b». Итак, ответ — «B»
Вопрос № 7)
В системе, разработанной для расчета налога, подлежащего уплате:
У сотрудника 4000 фунтов стерлингов не облагаются налогом.
Следующие 1500 фунтов стерлингов облагаются налогом в размере 10%.
Следующие 28000 фунтов стерлингов после этого облагаются налогом по ставке 22%.
Любая дополнительная сумма облагается налогом в размере 40%.
С точностью до целого фунта какая из этих групп чисел попадает в три РАЗЛИЧНЫХ класса эквивалентности?
а) 4000 фунтов стерлингов; 5000 фунтов стерлингов; 5500 фунтов стерлингов
б) 32001 фунтов стерлингов; 34000 фунтов стерлингов; 36500 фунтов стерлингов
c) 28000 фунтов стерлингов; 28001 фунт стерлингов; 32001
фунтов стерлингов d) 4000 фунтов стерлингов; 4200 фунтов стерлингов; 5600 фунтов стерлингов
Решение:
Классы будут следующими:
Класс I: от 0 до 4000 фунтов стерлингов => без налога
Класс II: от 4001 фунтов стерлингов до 5500 фунтов стерлингов => налог 10%
Класс III: от 5501 фунтов стерлингов до фунтов стерлингов 33500 => налог 22%
Класс IV: 33501 фунт стерлингов и выше => налог 40%
Выберите значения, которые попадают в три различных класса эквивалентности.Вариант «d» имеет значения из трех разных классов эквивалентности. Итак, ответ — «Д».
Вопрос № 8)
В системе, разработанной для расчета подлежащего уплате налога:
Заработная плата сотрудника не облагается налогом в размере 4000 фунтов стерлингов.
Следующие 1500 фунтов стерлингов облагаются налогом в размере 10%.
Следующие 28000 фунтов стерлингов после этого облагаются налогом по ставке 22%.
Любая дополнительная сумма облагается налогом в размере 40%.
С точностью до целого фунта, какой из них является допустимым тестом для анализа граничных значений?
a) 28000 фунтов стерлингов
b) 33501 фунтов стерлингов
c) 32001 фунтов стерлингов
d) 1500 фунтов стерлингов
Решение:
В вопросе № 7 классы уже разделены.Мы должны выбрать значение, которое является граничным значением (начальное / конечное значение). 33501 — граничное значение. Итак, ответ — «B» .
Вопрос № 9)
Учитывая следующую спецификацию, какие из следующих значений возраста находятся в ОДНОМ разделе эквивалентности?
Если вам меньше 18 лет, вы слишком молоды, чтобы быть застрахованным.
С 18 до 30 включительно вы получите скидку 20%.
Лица старше 30 не имеют права на скидку.
a) 17, 18, 19
b) 29, 30, 31
c) 18, 29, 30
d) 17, 29, 31
Решение:
Классы будут следующими:
Класс I: возраст <18 => не застрахован
Класс II: возраст от 18 до 30 => скидка 20%
Класс III: возраст> 30 => без скидки
Здесь мы не можем определить, действительны или недействительны указанные выше классы, так как ничего не упоминается в вопросе.(Но согласно нашему предположению, мы можем сказать, что I и II действительны, а III недействительны. Но здесь это не требуется.) Мы должны выбрать значения, которые находятся в ЖЕСТКОМ разделе эквивалентности. Значения из опции «c» попадают в тот же раздел. Итак, ответ — «С».
Это несколько примеров вопросов для практики из статей ISTQB. Мы продолжим добавлять больше вопросов к ISTQB с ответами в следующих публикациях.
Об авторе:
Это гостевая статья «Н.Сандхья Рани ». Она имеет около 4 лет опыта в тестировании программного обеспечения, в основном в ручном тестировании. Она помогает многим начинающим тестировщикам программного обеспечения пройти сертификационный экзамен по тестированию ISTQB.
Задайте свои вопросы, связанные с экзаменом ISTQB, в разделе комментариев ниже.
Полный пакет ISTQB Certification Premium Study:
Уверенно явитесь и с легкостью сдайте базовый экзамен с этим комплексным учебным материалом премиум-класса.
Нажмите на изображение ниже, чтобы узнать больше:**
Как работают «новые» числовые результаты 1–9, буквенные эквиваленты и что означает сдать или не сдать
День результатов GCSE в этом году был непохож на другие, со студентами с тревогой получая оценки за экзамены, которые они так и не сдали после нескольких недель споров по поводу их оценок.
Как будто ничего не может быть более сложным, остается некоторая путаница в отношении «новой» системы числовых оценок, даже несмотря на то, что она действует уже третий год.
Чтобы облегчить дальнейшую неуверенность после дня результатов, вот все, что вам нужно знать, от эквивалентов старых денежных букв до того, почему знакомая система была упразднена.

Информационный бюллетень i по вопросам образования: новости и анализ по мере того, как школы пытаются вернуться к нормальной жизни

В этом году оценки GCSE и A-level вызвали разногласия (Фото: PA)

Каковы буквенные эквиваленты новых оценок?

Для экзаменов GCSE 2018 правительство изменило систему оценок GCSE с A * на G на числовую систему с 9 до 1 (9 — высшая оценка, а 1 — самая низкая).

Согласно приведенному ниже полезному руководству, выпущенному регулятором экзаменов Ofqual, новая система сводится к следующему:

9 = High A * grade
8 = нижний A * или высокий A
7 = Низшая оценка
6 = высокий класс B
5 = нижний B или высокий C
4 = младший класс
3 = D или высокий E
2 = нижняя E или высокая F
1 = нижний F или G
U = U остается прежним

Буквенные эквиваленты «старых денег» числовых оценок GCSE (Фото: Ofqual)

Что такое проход в цифровой системе?

Как раз тогда, когда вы думали, что все больше не может запутать, теперь у студентов есть две «проходные» оценки.

Школы будут оцениваться по доле учеников, получивших «стандартный» балл и выше, что означает 4-й класс.

Таким образом, если вам удалось получить 4 или выше по английскому языку и математике, это означает, что у вас не будет пересдать эту квалификацию в соответствии с правилами, введенными в 2015/16 году.

Тем не менее, школы также должны будут учитывать долю учеников, получивших «сильный» балл или выше, то есть 5-й класс.

Были дни протестов против неоднозначного алгоритма модерации (Фото: PA)

9 — это то же самое, что и A *?

Наивысшая оценка 9 — не совсем то же самое, что старые деньги A * — по сути, это лучше, поскольку 8 также примерно эквивалентно нижней половине диапазона A * и более высокому A.

При системе счисления относительно небольшое количество учеников должны достичь 9-го класса, поскольку они будут эффективно нормированы.

Так что, если вы набрали много классов 7-8, вы все равно можете быть очень довольны университетами и работодателями, считающими эти оценки очень хорошими.

Почему были изменены оценки?

Эта система была введена для большей дифференциации на верхнем конце шкалы оценок, позволяя шестым классам, колледжам, университетам и работодателям лучше понять, на каком уровне работают молодые люди.

Это было частью полной перестройки системы GCSE, которая была проведена, чтобы приблизить Англию к уровню лучших образовательных юрисдикций мира.

Хотя выставление оценок не более жесткое, чем при предыдущей системе, учебная программа GCSE содержала больше содержания, и некоторые вопросы в экзаменационных работах действительно сложнее. В каждой экзаменационной работе есть небольшое количество вопросов, предназначенных для выявления учащихся, желающих получить 9-й балл. Эти вопросы задаются этим учащимся намного сложнее, чем на старых экзаменах GCSE.

Согласно опросу Национального союза образования, почти девять из 10 (89 процентов) учителей считают, что изменения в оценке новых выпускных экзаменов GCSE привели к тому, что все больше учеников «чрезвычайно встревожены и подвержены стрессу».

Министр образования Гэвин Уильямсон в конце концов объявил о развороте правительства после протестов (Фото: PA)

Как рассчитываются оценки в этом году?

После резкого разворота в правительстве результаты GCSE в этом году по каждому предмету будут основаны либо на оценке, предсказанной школьными учителями, либо на оценке Ofqual, в зависимости от того, что выше.

Выступая на BBC News на следующее утро после объявления о развороте, министр образования Гэвин Уильямсон сказал: «Подросткам будет сказано, какая у них самая высокая оценка, будь то их центральные оценки или модерируемая стандартизированная оценка, которая имеет предоставлен Ofqual, и сертификация последует через неделю ».

Возникла путаница относительно того, будут ли действительно опубликованы полные результаты в четверг, 20 августа, в день запланированных результатов, или будет задержка.

Комментарии г-на Уильямсона, по-видимому, противоречат предыдущему заявлению Министерства образования о том, что «официальные результаты будут представлены учащимся на следующей неделе», а ученики узнают свои прогнозируемые оценки только в четверг.

Контрольная работа системы счисления 9 класс: Контрольная работа Системы счисления 9 класс