Контрольная работа по теме «Подобие треугольников» геометрия 9 класс
Контрольная работа № 4 по теме «Подобие треугольников».
Вариант – 1.
1.1. Заполните пропуски в тексте
а) Если , то АВС и А1В1С1 …
б) Если АВС А1В1С1, то .
в) Если АВС А1В1С1, то А = …, В1 = …
1.2. АВС А1В1С1, АВ = 10 см, ВС = 12 см, А1В1 = 5 см, В = 25. Найдите В1 и сторону В1С1.
А) 20 и 5 см Б) 70 и 10 см В) 25 и 12 см Г) 25 и 6 см.
1.3. КL М, МК = 6 см, МL = 3,6 см.
Найдите L.
L А) 13,6 см Б) 6,4 см
В) 10 см Г) 5,4 см.
К М
1.4. В СD – биссектриса С, ВС = 14 см,
АС = 7 см, АD = 3 см.
D Найдите ВD.
А) 9 см Б) 6 см
В) 4,5 см Г) 10 см.
С А
2.1. Стороны треугольника равны 6 см, 7 см и 8 см. Найдите стороны подобного ему треугольника, периметр которого равен 84 см.
2.2. Точки М и Р лежат на сторонах АВ и СВ АВС, причем МР ∥ АС. Найдите длину отрезка МР, если ВР = 20 см, РС = 5 см, АС = 15 см.
2.3. Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке М, DС : СМ = 3 : 5. Найдите основания трапеции, если их сумма равна 26 см.
3.1. Найдите две стороны треугольника, если их разность равна 28 см, а биссектриса угла между ними делит третью сторону на отрезки 43 см и 29 см.
Контрольная работа № 4 по теме «Подобие треугольников».
Вариант – 2.
1.1. Заполните пропуски в тексте
а) Если А = 90, А1 = 90, С = С1, то АВС и А1В1
б) Если АВС А1В1С1, то В = …, С1 = …
в) Если АВС А1В1С1, то .
1.2. АВС А1В1С1, АВ = 10 см, ВС = 3 см, А1В1 = 5 см, В = 43. Найдите В1 и сторону В1С1.
А) 43 и 1,5 см Б) 47 и 12 см В) 67 и 8 см Г) 57 и 4 см.
1.3. А СD АВ, АС = 8 см, АD = 6,4 см.
Найдите АВ.
D А) 16,4 см Б) 20 см
В) 10 см Г) 3,6 см.
С В
1.4. В АD – биссектриса А, АВ = 10 см,
АС = 5 см, ВD = 6 см.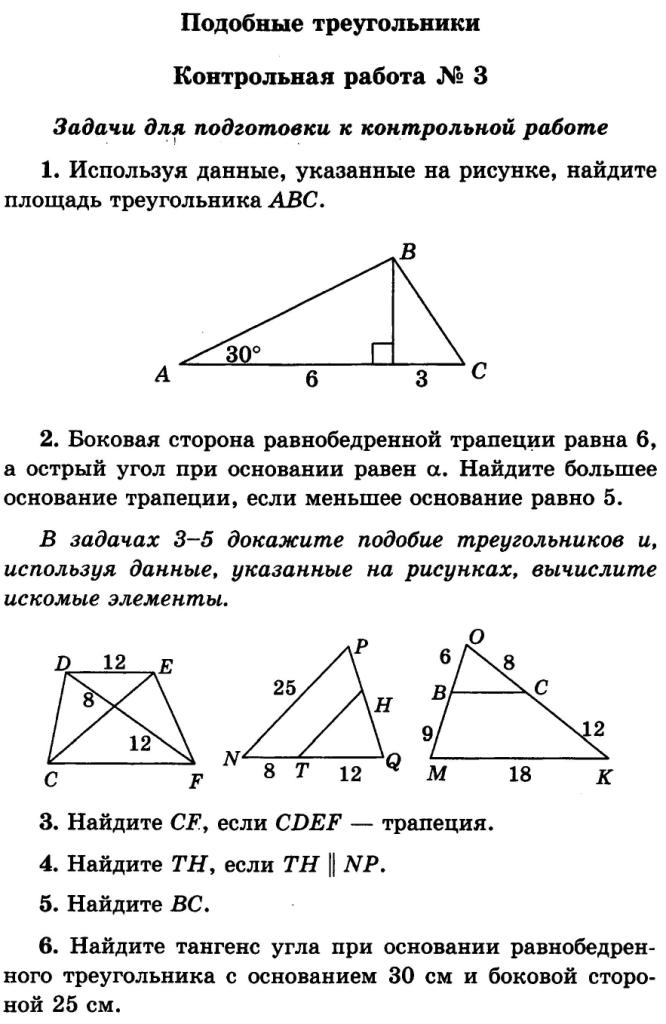
D Найдите ВС.
А) 18 см Б) 9 см
В) 3 см Г) 12 см.
А С
2.1. Стороны треугольника относятся как 2 : 5 : 6. Найдите стороны подобного ему треугольника, периметр которого равен 39 см.
2.2. Точки М и Р лежат на сторонах АВ и СВ АВС, причем МР ∥ АС. Найдите длину отрезка АС, если РС = 4 см, СВ = 12 см, МР = 6 см.
2.3. Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке F, АВ : ВF = 3 : 7. Найдите основания трапеции, если их разность равна 6 см.
3.1. Найдите две стороны треугольника, если их сумма равна 91 см, а биссектриса угла между ними делит третью сторону в отношении 5 : 8.
Сборник контрольных работ по геометрии, (9 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
9 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
.
Контрольная работа №1 9 класс.
Тема: «Векторы на плоскости».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач скалярное произведение векторов и его свойства, условия перпендикулярности и коллинеарности векторов,
находить координаты вектора и его абсолютную величину, выполнять действия с векторами;
— умение оформлять решение задачи.
I вариант. |
1.Даны точки А(-2;4) и В(5;1).Найдите координаты вектора и его абсолютную величину. 2. Дан параллелограмм АВСD. О- точка пересечения диагоналей. Найдите векторы -, +2, + + 3.Даны векторы (2;0), (1;2), (-3;m). Найдите значение m, при котором векторы А) и -2 перпендикулярны. В) + коллинеарны 4. Даны точки А(-1;4) и В(3;1), С(3;4). Найдите угол между векторами и . 5. Вычислите , если =5, =8, а угол между векторами и равен 600. |
II вариант. |
1. Даны точки А(3;-1) и В(1;4).Найдите координаты вектора АВ и его абсолютную величину. 2. Дан параллелограмм АВСD. О- точка пересечения диагоналей. Найдите векторы — 2 + + + 3. А) и 2 перпендикулярны. В) векторы — коллинеарны. 4. Даны точки А(2;-1) и В(2;3), С(-1;-1). Найдите угол между векторами и 5. Вычислите , если =3, =4, а угол между векторами и равен 600 |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Координаты вектора и его абсолютная величина. | №1, | 20 % | ||
Действия с векторами. | №2 | 20% | ||
Условия перпендикулярности и коллинеарности векторов. | №3 | 20% | ||
Скалярное произведение и его свойства. | №4 | №5 | 40 % | |
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Координаты вектора и его абсолютная величина. | Формула нахождения координат вектора. | 1 балл | 3 балла |
Формула абсолютной величины. | 1 балл | |||
Вычисления. | 1 балл | |||
2 | Действия с векто-рами. Геометричес-кий смысл. | Правило треугольника. | 1 балл | 3 балла |
Правило параллелограмма. | 1 балл | |||
Правило многоугольника. | 1 балл | |||
3 | Условия перпенди-кулярности и кол-линеарности векторов. | Условие коллинеарности векторов и вычисление . | 2 балла | 5 баллов |
Условие перпендикулярности векторов и вычисления. | 2 балла | |||
Оформление решения задачи. | 1 балл | |||
4 | Нахождение косинуса угла между векторами. | Нахождение координат вектора. | 1 балл | 5 баллов |
Знание формулы нахождения косинуса угла между векторами. | 1 балл | |||
Нахождение абсолютной величины. | 1 балл | |||
Вычисление по формуле. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
5 | Скалярное произведение и его свойства. | Скалярный квадрат. | 2 балла | 5 баллов |
ФСУ. | 1 балл | |||
Вычисление. | 1 балл | |||
Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №2 9 класс.
Тема: «Преобразования плоскости».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач свойств симметрии относительно точки и прямой, параллельного переноса;
— знание и умение применять при решении задач свойств подобия;
— умение выполнять чертежи по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1. Найдите координаты точек симметричных данным А(-2;-1), В(1;3) и С(2;0) относительно: А)оси Ох в) оси Оу С) начала координат 2. При параллельном переносе точка А(3;-1) переходит в точку А1(5,-4). В какую точку в результате данного переноса перейдет точка В(-7;0) 3.Стороны треугольника равны 6см, 7см и 8см. Найдите периметр подобного ему треугольника, периметр которого равен 84см. 4. Доказать: МВN АВС. Найти АС. А С 5. Найдите две стороны треугольника, если их сумма равна 91см, а биссектриса угла между ними делит третью сторону в отношении 5:8. |
II вариант. |
1. Найдите координаты точек симметричных данным А(0;-1), В(1;-3) и С(-2;5) относительно: А)оси Ох в) оси Оу С) начала координат 2. При параллельном переносе точка А(-3;-4) переходит в точку А1(7,3). В какую точку в результате данного переноса перейдет точка В(0;5) 3. Стороны треугольника относятся как 2:5:6. Найдите периметр подобного ему треугольника, периметр которого равен 39см. 4. Дано: АО=15см, ВО=8см, АС=27см,DO=10cм , BC=16см. Доказать: AOD COB. Найти АD. 5. Найдите две стороны треугольника, если их разность равна 28см, а биссектриса угла между ними делит третью сторону на отрезки 43см и 29см. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Симметрия относительно точки и прямой. | №1, | 20 % | ||
Параллельный перенос. | №2 | 20% | ||
Подобие треугольников. | №3,№4 | 40% | ||
Подобие треугольников. | №5 | 20 % | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Симметрия относительно точки и прямой. | Симметрия относительно оси Ох. | 1 балл | 3 балла |
Симметрия относительно оси Оу. | 1 балл | |||
Симметрия относительно начала координат. | 1 балл | |||
2 | Параллельный перенос. | Формула, задающая параллельный перенос. | 1 балл | 3 балла |
Вычисление вектора параллельного переноса. | 1 балл | |||
Нахождение точки В 1. | 1 балл | |||
3 | Подобие треугольников. | Запись сторон подобного треугольника. | 1 балл | 5 баллов |
Составление уравнения. | 1 балл | |||
Вычисление коэффициента подобия. | 1 балл | |||
Нахождение сторон подобного треугольника. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
4 | Подобие треугольников. | Применение признака подобия для доказательства. | 2 балла | 5 баллов |
Нахождение стороны. | 2 балла | |||
Оформление решения задачи. | 1 балл | |||
5 | Подобие треугольников. Свойство биссектрисы. | Знание свойства биссектрисы. | 1 балл | 5 баллов |
Выполнение чертежа по условию задачи. | 1 балл | |||
Введение неизвестного и составление уравнения. | 2 балла | |||
Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №6 9 класс.
Тема: «Многоугольники».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач пропорциональность отрезков хорд и секущих, формулы, связывающие стороны, периметр, площадь и радиусы вписанной и описанной окружностей связи величины центрального и вписанного углов
— умение выполнять чертеж по условию задачи;
— умение оформлять решение задачи..
I вариант. |
1. По данным рисунка найдите угол х (О- центр окружности. 2. Дано: AB=0.7 см, ВЕ=0.5 см, СЕ=0.4 см. Найти: DE, DC 3.Внутренний угол правильного многоугольника в 3 раза больше внешнего угла. Найдите сторону многоугольника, если периметр равен 96 см. 4.Сторона правильного треугольника, описанного около окружности, равна 12см. 5.Сторона правильного вписанного многоугольника стягивает в окружности радиуса 6 см дугу длиной 3 см. Найдите периметр многоугольника. |
II вариант. |
1. По данным рисунка найдите угол х (О- центр окружности. 2. Дано: СD=0.8 см, DЕ=0.2 см, AЕ=0.24 см Найти: BE, AB 3.Сторона правильного многоугольника равна 5 см, а его внутренний угол на 108о больше внешнего угла. Найдите периметр многоугольника. 4.Сторона правильного шестиугольника, вписанного в окружность, равна 8см. Найдите сторону квадрата описанного около данной окружность. 5. Точки касания двух соседних сторон описанного многоугольника ограничивают в окружности радиуса 6см дугу длиной 4 см. Найдите периметр многоугольника. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Центральные и вписанные углы. | №1 | 20% | ||
Пропорциональность отрезков хорд и секущих | №2 | 20% | ||
Правильные многоугольники | №3, №4 | №5 | 60% | |
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Центральные и вписанные углы. | Знание связи величины цент-рального и вписанного углов. | 1 балл | 4 балла |
Умение применять. | 1 балл | |||
Нахождение угла. | 1 балл | |||
Сопутствующие пояснения. | 1 балл | |||
2 | Пропорциональность отрезков хорд и секущих. | Знание формулы. | 1 балл | 3 балла |
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
3 | Правильные многоугольники. | Составление уравнения по условию. | 1 балл | 5 баллов |
Знание формулы нахождения уг-ла правильного многоугольника. | 1 балл | |||
Определение числа сторон многоугольника. | 1 балл | |||
Нахождение периметра | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
4 | Формулы, связы-вающие стороны, периметр, площадь и радиусы вписан-ной и описанной окружностей. | Нахождение радиуса окружности. | 2 балла | 5 баллов |
Нахождение стороны многоугольника. | 2 балла | |||
Вычисления и оформление решения задачи. | 1 балл | |||
5 | Правильные многоугольники. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
Определение количества сторон. | 2 балла | |||
Вычисления. | 1 балл | |||
Нахождение периметра. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №4 9 класс.
Тема: «Решение треугольников».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач теоремы синусов и косинусов, решать задачи на нахождение неизвестных элементов в треугольнке;
— умение оформлять решение задачи.
I вариант. |
1.В треугольнике АВС =350,=250. Укажите наибольшую сторону треугольника. Ответ объясните. 2. Две стороны треугольника равны 3см и 8см, а угол между ними равен 600. Найдите периметр треугольника. 3. Решите треугольник АВС, если=750,=450, АВ=2см. 4. Диагонали параллелограмма равны 12см и 20см, а угол между ними равен 600. Найдите стороны параллелограмма. 5. В прямоугольном треугольнике один из углов равен α, а катет, прилежащий к данному углу, равен а. Найдите биссектрису прямого угла. |
II вариант. |
1. В треугольнике АВС ⦟В=550, ⦟А=1100. Укажите наименьшую сторону треугольника. Ответ объясните. 2. Две стороны треугольника равны 3см и 5см, а угол между ними равен 1200. Найдите периметр треугольника. 3. Решите треугольник АВС, если ⦟В=300, ⦟С=1050, АС=4см. 4. Стороны параллелограмма равны 10см и 16см, а угол между ними равен 600. Найдите диагонали параллелограмма. 5. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен β. Найдите биссектрису второго острого угла. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Теорема синусов | №1, | №5 | 40% | |
Теорема косинусов | №2 | №4 | 40% | |
Решение треугольника | №3 | 20% | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Теорема синусов. | Нахождение угла треугольника. | 1 балл | 3 балла |
Знание следствия из теоремы синусов. | 1 балл | |||
Запись ответа. | 1 балл | |||
2 | Теорема косинусов. | Знание теоремы косинусов. | 1 балл | 4 балла |
Умение находить периметр. | 1 балл | |||
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
3 | Решение треугольника. | Нахождение угла треугольника. | 1 балл | 5 баллов |
Применение теоремы синусов. | 2 балла | |||
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
4 | Теорема косинусов. | Определение неизвестных элементов. | 1 балл | 5 баллов |
Нахождение катета. | 1 балл | |||
Нахождение острых углов. | 1 балл | |||
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
5 | Теорема синусов. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
Применение определения биссектрисы. | 1 балл | |||
Нахождение угла. | 1 балл | |||
Нахождение биссектрисы. | 1 балл | |||
Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №5 9 класс.
Тема: «Длина окружности и площадь круга».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач формулы площадей круга и его частей, длин окружности и дуги;
— умение оформлять решение задачи.
I вариант. |
1. Длина окружности равна 8π. Вычислить площадь круга, ограниченного данной окружностью.
2. Градусная мера дуги окружности с радиусом 6см равна 300. Вычислите площадь кругового сектора, соответствующего этой дуге. 3.Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 720, а радиус окружности равен 6см. 4. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см2. 5.Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4см, а градусная мера дуги равна 600. |
II вариант. |
1. Площадь круга равна 324π. Вычислите длину окружности, ограничивающую данный круг. 2. Градусная мера дуги окружности с радиусом 4см равна 450. Вычислите площадь кругового сектора, соответствующего этой дуге. 3. Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 360, а радиус окружности равен 12см. 4. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 см2. 5. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2см, а диаметр окружности равен 4см. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Площадь круга и его частей. Длина дуги. Длина окружности. | №1,№2 | №3, №4 | №5 | 100% |
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Площадь круга. Длина окружности. | Знание формулы длины окружности. | 1 балл | 3 балла |
Знание формулы площади круга. | 1 балл | |||
Вычисления. | 1 балл | |||
2 | Площадь кругового сектора. | Знание формулы. | 1 балл | 3 балла |
Вычисления. | 1 балл | |||
Оформление решения задачи. | 1 балл | |||
3 | Длина дуги окружности. | Выполнение чертежа по условию задачи. | 1 балл | 4 балла |
Знание формулы. |
Геометрия 9 Контрольные работы Атанасян
Геометрия 9 Контрольные работы Атанасян — контрольные работы по геометрии в 9 классе с ответами по УМК Атанасян и др. (3 уровня сложности по 2 варианта) В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 9 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Геометрия 9 класс. Контрольные работы
по учебнику Атанасяна
ГЛАВА IX. ВЕКТОРЫ
К-1. Контрольная работа по геометрии с ответами по теме «Векторы» (урок 14):
Контрольная работа № 1 + Ответы
ГЛАВА Х. МЕТОД КООРДИНАТ
К-2. Контрольная работа по геометрии с ответами по теме «Метод координат» (урок 24):
Контрольная работа № 2 + Ответы
ГЛАВА XI. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
К-3. Контрольная работа по геометрии с ответами по теме «Соотношение между сторонами и углами треугольника. Скалярное произведение векторов» (урок 38):
Контрольная работа № 3 + Ответы
ГЛАВА XII. ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
К-4. Контрольная работа по геометрии с ответами по теме
ГЛАВА XIII. ДВИЖЕНИЯ
К-5. Контрольная работа по геометрии с ответами по теме «Движения» (урок 59):
Контрольная работа № 5
ИТОГОВОЕ ПОВТОРЕНИЕ
К-6 «Итоговая контрольная работа» за курс 9 класса с ответами (урок 70)
Итоговая контрольная работа + Ответы
ПОЯСНЕНИЯ
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
Смотрите также: ВСЕ КОНТРОЛЬНЫЕ в 9 классе
Вы смотрели: Геометрия 9 Контрольные работы Атанасян — контрольные работы по геометрии в 9 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 9 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Вернуться к Списку уроков Тематического планирования в 9 классе.
Геометрия 8 класс. Контрольная работа № 3 с ответами
Контрольная работа № 3 по геометрии в 8 классе «Признаки подобия треугольников» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. Урок 38
Смотреть Список всех контрольных по геометрии в 8 классе УМК Атанасян.
Контрольная работа № 3
«Признаки подобия треугольников»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Выполнение контрольной работы
Контрольная работа по геометрии.
I уровень сложности
Вариант 1
- Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5 (рис. 7.54). Найти: а) ОВ, б) АС, BD: в) SAOC, SBOD.
- В треугольнике АВС АВ = 4 см, ВС = 1 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠A = 80°, ∠B = 60°.
- Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК||АС, ВМ : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
- * В трапеции ABCD (AD и ВС основание) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см2.
Вариант 2
- Дано: РЕ||NK, МР = 8, MN = 12, ME = 6 (рис. 7.55). Найти: а) МК; б) РЕ : NK; в) SMPE : SMNK.
- В ΔАВС АВ = 12 см, ВС = 18 см, ∠В = 70°, а в ΔMNK MN = 6 см, NK = 9 см, ∠N = 70°. Найдите сторону АС и угол С треугольника АВС, если МК = 1 см, ∠K = 60°.
- Отрезки АВ и CD пересекаются в точке О так, что ∠ACO = ∠BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.
- * В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, SBOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.
Контрольная работа по геометрии.
II уровень сложности
Вариант 1
- Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, OD = 6,3 см (рис. 7.56).
Доказать: АС||BD. Найти: a) DB : АС, б) PAOC : PDBO - Диагонали ромба ABCD пересекаются в точке О, BD = 16 см. На стороне АВ взята точка К так, что ОК ⊥ АВ и ОК = 4√3 см. Найдите сторону ромба и вторую диагональ.
- В выпуклом четырехугольнике ABCD АВ = 9 см, ВС = 8 см, CD = 16 см, AD = 6 см, BD = 12 см. Докажите, что ABCD — трапеция.
- * В равнобедренном треугольнике MNK с основанием МК, равным 10 см, MN = NK = 20 см. На стороне NK лежит точка А так, что AК : AN =1 : 3. Найдите AM.
Вариант 2
- Дано: BD = 3,1 см, BE = 4,2 см, ВА = 9,3 см, ВС = 12,6 см (рис. 7.57).
Доказать: DE||АС. Найти, a) DE : АС, б) PАВС : PDBE, в) SDBE : SABC. - Диагонали ромба ABCD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ⊥ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба.
- ABCD — выпуклый четырехугольник, АВ = 6 см, ВС = 9 см, CD = 10 см, DA = 25 см, АС = 15 см. Докажите, что ABCD — трапеция.
- * В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН.
Контрольная работа по геометрии.
III уровень сложности
Вариант 1
- К диагонали АС прямоугольника ABCD проведен перпендикуляр DE так, что АЕ = 8 см, СЕ = 4 см.
Найти: а) АВ : ВС, б) PABCD; в) SABCD. - ABCD — прямоугольная трапеция (∠A = 90°). Точка Е лежит на основании AD так, что СЕ перпендикулярен AD и АЕ = DE. Точка О — середина диагонали АС. Докажите, что ВО : ВС = = CD : AD. Найдите площадь пятиугольника ABOCD, если площадь треугольника ACD равна 20 см2.
- Диагональ BD трапеции ABCD делит ее на два подобных треугольника. Найдите BD, если основания ВС и AD равны 8 см и 12,5 см соответственно.
- * На сторонах MN и NK треугольника MNK взяты точки А и В соответственно так, что ∠ABN = ∠M. Отрезок NE является биссектрисой угла ANB, АЕ : ЕВ = 2 : 3. Найдите отношение NК к MN.
Вариант 2
- К диагонали BD прямоугольника ABCD проведен перпендикуляр АК так, что ВК = 5 см, DK = 15 см.
Найти: а) ВС : CD; б) PBCD; в) SBCD. - В прямоугольной трапеции ABCD ∠D = 90°. Точка К лежит на основании AD так, что АК = KD и ВК перпендикулярно ВС. Точка О — середина диагонали BD. Докажите, что АВ : AD = ВО : ВС. Найдите площадь треугольника ABD, если площадь пятиугольника ABOCD равна 30 см2.
- Диагональ АС трапеции ABCD равна 8 см и делит ее на два подобных треугольника. Найдите основание ВС, если AD равно 16 см.
- * На сторонах РО и PS треугольника OPS взяты точки А и В соответственно так, что ∠PAB = ∠S. Биссектриса PC треугольника OPS делит сторону OS на два отрезка так, что ОС : CS = 4 : 3. Найдите отношение РВ к РА.
3. Рефлексия учебной деятельности
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.
ОТВЕТЫ на контрольную работу:
I уровень. Вариант 1
- Ответ: а) 7,5; б) 2 : 3; в) 4 : 9.
- Ответ: 80°, 60°, 40°.
- Ответ: 5 см.
- Ответ: 5 см2.
I уровень. Вариант 2
- Ответ: а) 9; б) 2 : 3; в) 4 : 9.
- Ответ: АС = 14 см, ∠C = 60°.
- Ответ: 14 см.
- Ответ: 5 см.
II уровень. Вариант 1
- Ответ: а) 3 : 4; б) 4 : 3; в) 9 : 16.
- Ответ: АВ = 16 см, AC = 16√3.
- Смотрите решение заданий (ниже)
- Ответ: 10 см.
II уровень. Вариант 2
- Ответ: а) 1 : 3; б) 3 : 1; в) 1 : 9.
- Ответ: АС = 4√5, ВD = 8√5.
- Смотрите решение заданий (ниже)
- Ответ: 20 см.
III уровень. Вариант 1
- Ответ: а) √2/2; б) 8√3(√2 + 1) см; в) 48√2 см2.
- Ответ: 25 см2.
- Ответ: 10 см.
- Ответ: 2:3.
III уровень. Вариант 2
- Ответ: a) √3; б) 20(√3 +1) см; в) 100√3 см2.
- Ответ: 24 см2.
- Ответ: 4 см.
- Ответ: 4 : 3.
Указания к решению контрольной
I уровня сложности
Смотреть решение заданий КР 1 уровня сложности
Указания к решению контрольной
II уровня сложности
Смотреть решение заданий КР 2 уровня сложности
Указания к решению контрольной
III уровня сложности
Смотреть решение заданий КР 3 уровня сложности
Критерии оценивания результатов контрольной работы
- оценка «5» — правильно решены три задачи;
- оценка «4» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
- оценка «3» — правильно решена одна задача;
- оценка «2» — все задачи решены неправильно.
За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.
Вы смотрели: Геометрия 8 класс. Контрольная работа № 3. Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 38. Контрольная работа № 3 по теме «Признаки подобия треугольников» + ОТВЕТЫ и РЕШЕНИЯ.
Смотреть Список всех контрольных по геом
Геометрия 9 класс Контрольная № 6 Итоговая с ответами
Итоговая контрольная работа по геометрии в 9 классе с ответами и решениями (2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 9 класса (Н.Ф. Гаврилова, ВАКО). Урок 70. Геометрия 9 класс Контрольная № 6 «Итоговая за курс 9 класса».
Смотреть Список всех контрольных по геометрии в 9 классе (УМК Атанасян)
Итоговая контрольная работа
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Контрольная работа
Вариант 1
Часть I
При выполнении заданий 1—5 выберите верный ответ.
- Треугольник со сторонами 5, 9, 15:
а) остроугольный; б) тупоугольный; в) прямоугольный; г) такого треугольника не существует. - Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:
а) 25 см; б) 40 см; в) 32 см; г) 20 см. - Если один из углов ромба равен 60°, а диагональ, проведенная из вершины этого угла, равна 4√3 см, то периметр ромба равен:
а) 16 см; б) 8 см; в) 12 см; г) 24 см. - Величина одного из углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника.
а) 84°; б) 92°; в) 80°; г) 87°. - В треугольнике АВС сторона а = 7, сторона b = 8, сторона с = 5. Вычислите ∠A.
Часть II
При выполнении заданий 6—10 запишите подробное решение.
- В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.
- В треугольнике ВСЕ ∠C = 60°, СЕ : ВС = 3 : 1. Отрезок СК — биссектриса треугольника. Найдите КЕ, если радиус описанной около треугольника окружности равен 8√3.
- Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3√2, ∠KOP = 135°.
- Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если ее средняя линия равна 5.
- Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС соответственно в точках Е и D. Найдите величину угла АВС (в градусах), если известно, что АЕ = 1, BD = 3.
а) 120°; б) 45°; в) 30°; г) 60°.
Вариант 2
Часть I
При выполнении заданий 1—5 выберите верный ответ.
- Треугольник со сторонами 15, 9, 12:
а) остроугольный; б) тупоугольный; в) прямоугольный; г) такого треугольника не существует. - Если сходственные стороны подобных треугольников равны 2 см и 5 см, площадь первого треугольника равна 8 см2, то площадь второго треугольника равна:
а) 50 см2; б) 40 см2; в) 60 см2; г) 20 см2. - Если в равнобедренном треугольнике длина основания равна 12 см, а его периметр равен 32 см, то радиус окружности, вписанной в треугольник, равен:
а) 4 см; б) 3 см; в) 6 см; г) 5 см. - В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите катеты треугольника.
а) 12 см и 16 см; б) 7 см и 11 см; в) 10 см и 13 см; г) 8 см и 15 см. - Стороны прямоугольника равны а и k. Найдите радиус окружности, описанной около этого прямоугольника.
Часть II
При выполнении заданий 6—10 запишите подробное решение.
- Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается стороны ВС в точке К, причем СК : ВК = 5 : 8. Найдите площадь треугольника, если его периметр равен 72.
- Около треугольника АВС описана окружность. Медиана треугольника AM продлена до пересечения с окружностью в точке К. Найдите сторону АС, если AM = 18, МК = 8, ВК = 10.
- Найдите основание равнобедренного треугольника, если угол при основании равен 30°, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 2√3 от основания.
- Пусть М — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны АВ, AD и ВС равны между собой. Найдите угол CMD (в градусах), если известно, что DM = МС, а угол САВ не равен углу DBA.
- На боковой стороне ВС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите квадрат расстояния от вершины А до центра окружности, если AD = √3, а угол АВС равен 120°.
3. Рефлексия учебной деятельности
В конце урока учитель раздает на каждую парту ответы на задачи контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.
Ответы на контрольную работу
Вы смотрели: Геометрия 9 класс Контрольная № 6. Поурочное планирование по геометрии для 9 класса. УМК Атанасян (Просвещение). Урок 70. Итоговая контрольная работа по геометрии + ОТВЕТЫ.
Смотреть Список всех контрольных по геометрии в 9 классе по УМК Атанасян.
Вернуться к Списку уроков Тематического планирования в 9 классе.
ГДЗ геометрия / Погорелов / самостоятельные работы / С-2 А2 алгебра 9 класс самостоятельные и контрольные работы Ершова, Голобородько
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
похожих треугольников
Подобные треугольники — это треугольники, соответствующие углы которых равны. Это не означает, что соответствующие стороны также равны. Если стороны также равны, мы говорим, что треугольники конгруэнтны.
Треугольник ABC и треугольник EFG похожи по следующим причинам:
Соответствующие углы равны.
- Угол A и угол E, показанные зеленым, равны.
- Угол B и угол F, показанные красным, равны.
- Угол C и угол G, показанные темно-красным, равны.
Вообще говоря, если вы смотрите на два или более треугольников, треугольники не имеют одинакового размера, но соответствующие углы треугольников равны, тогда треугольники похожи.
Вам не обязательно иметь размер всех трех соответствующих углов, чтобы сделать вывод, что треугольники подобны.
Постулат подобия угла и угла или постулат подобия AA и аналогичные треугольники
Если два угла треугольника имеют такие же размеры, как два угла другого треугольника, тогда треугольники подобны.Почему это так?Сумма углов треугольника должна составлять 180 градусов.
Рассмотрим следующую ситуацию:
Треугольник № 1:
Угол № 1 = 30 градусов. Угол №2 = 80 градусов
Треугольник №2:
Угол №1 = 80 градусов. Угол №2 = 30 градусов
Последний угол должен быть таким же
Треугольник №1: последний угол = 180-30-80 = 70
Треугольник №2: последний угол = 180-80-30 = 70
Все 3 угла одинаковы, поэтому треугольники похожи.
Посмотрите на треугольники ниже. Согласно постулату подобия АА, они похожи.
Мы знаем, что они похожи, потому что угол A = угол D, а угол C = угол F.
На самом деле нас не волнует размер последнего угла.
Мы можем поместить маленький треугольник слева внутри треугольника справа.
Треугольники все еще похожи. Единственная разница на этот раз состоит в том, что угол C совпадает с углом F.
Специальная цифра, которая всегда дает одинаковые треугольники
На рисунке выше 3 треугольника.
Треугольник ABC, ABG и AGC.Все 3 треугольника похожи друг на друга.
Самый простой способ понять, почему они похожи на треугольники, — это подставить несколько чисел.
Допустим, угол B = 50 °
Некоторые важные вычисления:В треугольнике ABG угол, обозначенный зеленым цветом = 40 °, так как 40 ° + 50 ° + 90 ° = 180 °
Угол, выделенный коричневым цветом в треугольнике AGC = 50 °, поскольку 40 ° + 50 ° = 90 °
Угол C = 40 °, поскольку 50 ° + 40 ° + 90 ° = 180 °
Результат представлен на рисунке ниже:
Помните, все, что нам нужно для доказательства сходства, — это найти 2 соответствующих угла, которые равны.
Показать треугольник ABC аналогичен треугольнику ABG
Для треугольника ABC угол A = 90 ° и угол B = 50 °
Для треугольника ABG угол G = 90 ° и угол B = 50 °
Треугольник ABC аналогичен треугольнику ABG
Показать треугольник ABC аналогичен треугольнику AGC
Для треугольника ABC угол A = 90 ° и угол B = 50 °
Для треугольника AGC угол G = 90 ° и угол коричневого цвета = 50 °
Треугольник ABC аналогичен треугольнику AGC
Показать треугольник ABG аналогичен треугольнику AGC
Для треугольника ABG угол B = 50 ° и угол зеленого цвета = 40 °
Для треугольника AGC угол коричневого цвета = 50 ° и угол C = 40 °
Треугольник ABG аналогичен треугольнику AGC
Новые уроки математики
Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.
Примечания к редакции по математике Глава 6 — Треугольники (10-й класс)
Любой многоугольник с тремя сторонами и тремя вершинами называется треугольником .
Типы треугольников
1. Существует три типа треугольников в зависимости от длины сторон.
2. Существует три типа Треугольников на основе углов.
Центры треугольника
Есть четыре разных центра Треугольника
1.Центроид треугольника
Точка пересечения медиан трех сторон Треугольника — это центроид этого Треугольника. Он всегда будет внутри Треугольника.
2. Центр треугольника
Точка пересечения биссектрис трех углов Треугольника называется центром этого Треугольника. Это точка, откуда круг вписывается в Треугольник. Радиус определяется путем проведения перпендикуляра от центра к любой из сторон Треугольника.
3. Окружность центра треугольника
Точка пересечения серединных перпендикуляров трех вершин Треугольника называется центром описанной окружности этого Треугольника. Она не всегда находится внутри Треугольника. Он может находиться за пределами Треугольника для тупого Треугольника и падать в середине гипотенузы прямоугольного Треугольника.
4. Ортоцентр
Точка пересечения высот Треугольника — это ортоцентр этого Треугольника.Как и центр описанной окружности, она также выходит за пределы Треугольника в случае тупого Треугольника и попадает в вершину Треугольника в случае Треугольника с прямым углом.
Соответствующие и аналогичные цифры
Конгруэнт | Аналогичный | |
Уголки | Соответствующие углы такие же. | Соответствующие углы такие же. |
Стороны | Соответствующие стороны такие же. | Соответствующие стороны пропорциональны. |
Пример | ||
Пояснение | Оба квадрата имеют одинаковые углы и стороны. | Оба квадрата имеют одинаковые углы, но разные стороны. |
Символы |
Приведенное выше объяснение показывает, что если две фигуры совпадают, то они также будут подобны, но необязательно, что если две фигуры подобны, то они также будут конгруэнтными.
Подобие треугольников
В треугольниках мы также будем использовать то же условие, что два треугольника будут одинаковыми, если —
Два вышеуказанных треугольника ∆ABC и ∆DEF аналогичны-
.Если соответствующие углы двух Треугольников совпадают, то они называются равноугольными треугольниками.
Основная теорема пропорциональности (теорема Фалеса)
Согласно теореме Фалеса , если в данном Треугольнике линия проводится параллельно любой из сторон Треугольника, так что две другие стороны пересекаются в некоторой отдельной точке, то она делит две стороны в одинаковом соотношении.
В ∆KMN, если PQ║MN и пересекает KM в P и KN в Q, то
Обращение к основной теореме о пропорциональности
Это противоположность основной теоремы пропорциональности, которая гласит, что если в данном Треугольнике прямая линия делит две стороны Треугольника в одинаковом соотношении, то эта прямая линия параллельна третьей стороне Треугольника.
Критерии подобия треугольников
По сути, есть три критерия, чтобы найти сходство двух Треугольников.
1. Критерии подобия AAA (угол-угол-угол)
Если в двух данных треугольниках все соответствующие углы равны, то их соответствующие стороны также будут пропорциональны.
Это показывает, что все соответствующие углы в ∆ABC и ∆PQR одинаковы, поэтому их соответствующие стороны пропорциональны, поэтому два треугольника похожи.
Следовательно, ∆ABC ~ ∆PQR
Замечание : Если два соответствующих угла двух Треугольников равны, то, согласно сумме углов Треугольника, третий угол также будет равен.Таким образом, два треугольника будут подобны, если их два угла равны двум углам другого треугольника. Это известно как критерий AA (угол-угол) .
2. Критерии подобия SSS (Side-Side-Side)
Если в двух Треугольниках все стороны одного Треугольника находятся в таком же соотношении с соответствующими сторонами другого Треугольника, то их соответствующие углы будут равны. Следовательно, два треугольника похожи.
In ∆ABC и ∆DEF
Следовательно, ∆ABC ~ ∆DEF
Замечание : Два вышеуказанных критерия показывают, что если один из двух критериев удовлетворяет, то другой подразумевается.Таким образом, нам не нужно проверять оба условия, чтобы найти сходство двух треугольников. Если все углы равны, тогда все стороны будут пропорциональны, и наоборот.
3. Критерии подобия SAS (Side-Angle-Side)
Если в двух Треугольниках две стороны находятся в том же соотношении с двумя сторонами другого Треугольника и угол, включающий эти стороны, равен, то эти два Треугольника будут подобны.
In ∆ABC и ∆KLM
Следовательно, ∆ABC ~ ∆KLM
Площади подобных треугольников
Если даны два одинаковых Треугольника, то квадрат отношения их соответствующих сторон будет равен отношению их площади.
Если ∆ABC ~ ∆PQR, то
Теорема Пифагора (Теорема Баудхаяна)
Теорема Пифагора гласит, что в прямоугольном Треугольнике квадрат гипотенузы, т.е. сторона, противоположная прямому углу, равен сумме квадратов двух других сторон Треугольника.
Если один угол равен 90 °, то a 2 + b 2 = c 2
Пример
Найдите гипотенузу в прямоугольном треугольнике.
Решение
AB и BC — две стороны прямоугольного треугольника.
BC = 12 см и AB = 5 см
Из теоремы Пифагора имеем:
CA 2 = AB 2 + BC 2
= (5) 2 + (12) 2
= 25 + 144
Итак, AC 2 = 169
AC = 13 см
Обратное к теореме Пифагора
В Треугольнике, если сумма квадратов двух сторон равна квадрату третьей стороны, тогда данный Треугольник является Треугольником с прямым углом.
Если a 2 + b 2 = c 2 , то один угол равен 90 °.
Подобие двух прямоугольных треугольников Треугольник
В прямоугольном треугольнике, если мы проведем перпендикуляр от прямого угла к гипотенузе треугольника, то оба новых треугольника будут похожи на весь треугольник.
В приведенном выше правом углу треугольник CP является вершиной гипотенузы, поэтому
∆ACP ~ ∆ACB
∆PCB ~ ∆ACB
∆PCB ~ ∆ACP
Законы синусов и косинусов в треугольнике
Законы синусов и косинусов используются для нахождения неизвестной стороны или угла наклонного треугольника.Олигальный треугольник — это треугольник, который не является треугольником с прямым углом.
1. Закон синусов
Показывает соотношение между углом и сторонами треугольника.
Используется, когда
i) Даны два угла и одна сторона (AAS или ASA)
ii) Две стороны и угол без включения (SSA)
Закон синусов показывает, что стороны треугольника пропорциональны синусам противоположных углов.
2. Закон косинуса
Используется, когда
i) Даны две стороны и включенный угол (SAS)
ii) Даны три стороны (SSS)
Когда мы можем использовать такие законы?
Решения NCERT для математики класса 10 Глава 6
Страница № 122:
Вопрос 1:
Заполните пропуски, используя правильное слово, указанное в скобках: —
(i) Все круги __________.(соответствует, аналогично)
(ii) Все квадраты __________. (похожие, совпадающие)
(iii) Все __________ треугольники похожи. (равнобедренный, равносторонний)
(iv) Два многоугольника с одинаковым количеством сторон подобны, если (a) их соответствующие углы равны __________ и (b) их соответствующие стороны равны __________. (равный, пропорциональный)
Ответ:
(i) Аналогичный
(ii) Аналогичное
(iii) Равносторонний
(iv) (a) равно
(б) Пропорциональная
Видео решение для треугольников (Страница: 122, В.№: 1)
Решение NCERT для математики класса 10 — треугольники 122, вопрос 1
Страница № 122:
Вопрос 2:
Приведите два разных примера пары
(i) Аналогичные цифры
(ii) Не похожие цифры
Ответ:
(i) Два равносторонних треугольника со сторонами 1 см и 2 см
Два квадрата со стороной 1 см и 2 см
(ii) Трапеция и квадрат
Треугольник и параллелограмм
Видео решение для треугольников (Страница: 122, В.№: 2)
Решение NCERT для математики класса 10 — треугольники 122, вопрос 2
Страница № 122:
Вопрос 3:
Укажите, похожи ли следующие четырехугольники:
Ответ:
Четырехугольник PQRS и ABCD не похожи друг на друга, поскольку их соответствующие стороны пропорциональны, т.е.е. 1: 2, но их соответствующие углы не равны.
Видео решение для треугольников (Страница: 122, Q.No: 3)
Решение NCERT для математики класса 10 — треугольники 122, вопрос 3
Страница № 128:
Вопрос 1:
На рисунке 6.17. (i) и (ii), DE || ДО Н.Э. Найдите EC в (i) и AD в (ii).
(я)
(ii)
Ответ:
(я)
Пусть EC = x см
Принято, что DE || ДО Н.Э.
Используя основную теорему пропорциональности, получаем
(ii)
Пусть AD = x см
Принято, что DE || ДО Н.Э.
Используя основную теорему пропорциональности, получаем
Видео решение для треугольников (Страница: 128, Q.No: 1)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 1
Страница № 128:
Вопрос 2:
E и F — точки на сторонах PQ и PR соответственно ΔPQR.Для каждого из следующих случаев укажите, является ли EF || QR.
(i) PE = 3,9 см, EQ = 3 см, PF = 3,6 см и FR = 2,4 см
(ii) PE = 4 см, QE = 4,5 см, PF = 8 см и RF = 9 см
(iii) PQ = 1,28 см, PR = 2,56 см, PE = 0,18 см и PF = 0,63 см
Ответ:
(я)
Учитывая, что PE = 3,9 см, EQ = 3 см, PF = 3,6 см, FR = 2,4 см
(ii)
PE = 4 см, QE = 4.5 см, PF = 8 см, RF = 9 см
(iii)
PQ = 1,28 см, PR = 2,56 см, PE = 0,18 см, PF = 0,36 см
Видео решение для треугольников (Страница: 128, Q.No: 2)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 2
Страница № 128:
Вопрос 3:
На следующем рисунке, если LM || CB и LN || CD, докажите, что
Ответ:
На данном рисунке LM || CB
Используя основную теорему пропорциональности, получаем
Видео решение для треугольников (Страница: 128, Q.№: 3)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 3
Страница № 128:
Вопрос 4:
На следующем рисунке DE || AC и DF || AE. Докажите, что
Ответ:
In ΔABC, DE || AC
Видео решение для треугольников (Страница: 128, Q.№: 4)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 4
Стр. № 129:
Вопрос 5:
На следующем рисунке DE || OQ и DF || ИЛИ показать, что EF || QR.
Ответ:
In Δ POQ, DE || OQ
Видео решение для треугольников (Страница: 129, В.№: 5)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 5
Стр. № 129:
Вопрос 6:
На следующем рисунке A, B и C — это точки на OP, OQ и OR соответственно, такие что AB || PQ и AC || PR. Покажи, что BC || QR.
Ответ:
In Δ POQ, AB || PQ
Видео решение для треугольников (Страница: 129, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 6
Стр. № 129:
Вопрос 7:
Используя основную теорему пропорциональности, докажите, что линия, проведенная через средние точки одной стороны треугольника, параллельная другой стороне, делит третью сторону пополам. (Напомним, вы доказали это в классе IX).
Ответ:
Рассмотрим данный рисунок, на котором -1 — это линия, проведенная через среднюю точку P отрезка AB, пересекающуюся с AC в точке Q, так что.
Или, Q — средняя точка переменного тока.
Видео решение для треугольников (Страница: 129, Q.No: 7)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 7
Стр. № 129:
Вопрос 8:
Используя Обратное к основной теореме пропорциональности, докажите, что прямая, соединяющая середины любых двух сторон треугольника, параллельна третьей стороне.(Напомним, вы сделали это в IX классе).
Ответ:
Рассмотрим данный рисунок, на котором PQ — это отрезок прямой, соединяющий средние точки P и Q прямых AB и AC соответственно.
т.е. AP = PB и AQ = QC
Можно заметить, что
Следовательно, используя основную теорему пропорциональности, получаем
Видео решение для треугольников (Страница: 129, В.№: 8)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 8
Стр. № 129:
Вопрос 9:
ABCD представляет собой трапецию, в которой AB || DC и его диагонали пересекаются в точке O. Покажите, что
Ответ:
Проведите линию EF через точку O так, чтобы
В ΔADC,
Используя основную теорему пропорциональности, получаем
В ΔABD,
Итак, используя основную теорему пропорциональности, получаем
Из уравнений (1) и (2) получаем
Видео решение для треугольников (Страница: 129, В.№: 9)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 9
Стр. № 129:
Вопрос 10:
Диагонали четырехугольника ABCD пересекаются друг с другом в точке O, так что Покажите, что ABCD — трапеция.
Ответ:
Рассмотрим следующий рисунок для данного вопроса.
Нарисуйте линию OE || AB
In ΔABD, OE || AB
Используя основную теорему пропорциональности, получаем
Однако предполагается, что
⇒ EO || DC [Обратное к основной теореме пропорциональности]
⇒ AB || OE || DC
⇒ AB || CD
∴ ABCD — это трапеция.
Видео решение для треугольников (Страница: 129, В.№: 10)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 10
Стр. № 138:
Вопрос 1:
Укажите, какие пары треугольников на следующем рисунке похожи? Напишите критерий подобия, который вы использовали для ответа на вопрос, а также напишите пары похожих треугольников в символической форме:
(я)
(ii)
(iii)
(iv)
(в)
(vi)
Ответ:
(я) A = ∠P = 60 °
∠B = ∠Q = 80 °
∠C = ∠R = 40 °
Следовательно, ΔABC ∼ ΔPQR [По критерию сходства AAA]
(ii)
(iii) Данные треугольники не похожи друг на друга, так как соответствующие стороны не пропорциональны.
(iv) В ∆ MNL и ∆ QPR мы видим, что
MNQP = MLQR = 12∠M = ∠Q = 70 ° ∴∆MNL ~ ∆QPR По критерию подобия SAS
(v) Данные треугольники не похожи друг на друга, поскольку соответствующие стороны не пропорциональны.
(vi) В ΔDEF,
∠D + ∠E + ∠F = 180º
(Сумма углов треугольника 180º.)
70º + 80º + ∠F = 180º
∠F = 30º
Аналогично, в ΔPQR,
∠P + ∠Q + ∠R = 180º
(Сумма углов треугольника 180º.)
∠P + 80º + 30º = 180º
∠P = 70º
В ΔDEF и ΔPQR,
∠D = ∠P (каждые 70 °)
∠E = ∠Q (каждые 80 °)
∠F = ∠R (каждые 30 °)
∴ ΔDEF ∼ ΔPQR [По критерию сходства AAA]
Видео решение для треугольников (Страница: 138, Q.No: 1)
Решение NCERT для математики класса 10 — треугольники 138, вопрос 1
Страница № 139:
Вопрос 2:
На следующем рисунке ΔODC ∼ ΔOBA, ∠BOC = 125 ° и ∠CDO = 70 °.Найдите ∠DOC, ∠DCO и ∠OAB
.Ответ:
DOB — прямая линия.
∴ DOC + ∠COB = 180 °
⇒ ∠DOC = 180 ° — 125 °
= 55 °
В ΔDOC,
∠DCO + ∠CDO + ∠DOC = 180 °
(Сумма углов треугольника 180º.)
⇒ ∠DCO + 70º + 55º = 180 °
⇒ ∠DCO = 55 °
Задано, что ΔODC ∼ ΔOBA.
∴ ∠OAB = ∠ OCD [Соответствующие углы равны в подобных треугольниках.]
⇒ ∠OAB = 55 °
Видео решение для треугольников (Страница: 139, Q.No: 2)
Решение NCERT для математики класса 10 — треугольники 139, вопрос 2
Страница № 139:
Вопрос 3:
Диагонали AC и BD трапеции ABCD с AB || DC пересекаются друг с другом в точке O.Используя критерий подобия для двух треугольников, покажите, что
Ответ:
In ΔDOC и ΔBOA,
∠CDO = ∠ABO [Альтернативные внутренние углы как AB || CD]
∠DCO = ∠BAO [Альтернативные внутренние углы как AB || CD]
∠DOC = ∠BOA [Вертикально противоположные углы]
∴ ΔDOC ∼ ΔBOA [критерий сходства AAA]
Видео решение для треугольников (Страница: 139, В.№: 3)
Решение NCERT для математики класса 10 — треугольники 139, вопрос 3
Страница № 140:
Вопрос 4:
На следующем рисунке покажите, что
Ответ:
В ΔPQR, ∠PQR = ∠PRQ
∴ PQ = PR (i)
Дано,
Видео решение для треугольников (Страница: 140, В.№: 4)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 4
Страница № 140:
Вопрос 5:
точки S и T на сторонах PR и QR ΔPQR такие, что ∠P = ∠RTS. Покажите, что ΔRPQ ∼ ΔRTS.
Ответ:
В ΔRPQ и ΔRST,
∠RTS = ∠QPS (дано)
∠R = ∠R (Общий угол)
∴ ΔRPQ ∼ ΔRTS (по критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.№: 5)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 5
Страница № 140:
Вопрос 6:
На следующем рисунке, если ΔABE ≅ ΔACD, покажите, что ΔADE ∼ ΔABC.
Ответ:
Принято, что ΔABE ≅ ΔACD.
∴ AB = AC [По CPCT] (1)
А, AD = AE [По CPCT] (2)
В ΔADE и ΔABC,
[Разделив уравнение (2) на (1)]
∠A = ∠A [Общий угол]
∴ ΔADE ∼ ΔABC [По критерию подобия SAS]
Видео решение для треугольников (Страница: 140, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 6
Страница № 140:
Вопрос 7:
На следующем рисунке высоты AD и CE отрезка ABC пересекаются друг с другом в точке P. Покажите, что:
(i) ΔAEP ∼ ΔCDP
(ii) ΔABD ∼ ΔCBE
(iii) ΔAEP ∼ ΔADB
(в) ΔPDC ∼ ΔBEC
Ответ:
(я)
В ΔAEP и ΔCDP,
∠AEP = ∠CDP (каждый 90 °)
∠APE = ∠CPD (вертикально противоположные углы)
Следовательно, используя критерий сходства AA,
ΔAEP ∼ ΔCDP
(ii)
В ΔABD и ΔCBE,
∠ADB = ∠CEB (каждый 90 °)
∠ABD = ∠CBE (общий)
Следовательно, используя критерий сходства AA,
ΔABD ∼ ΔCBE
(iii)
В ΔAEP и ΔADB,
∠AEP = ∠ADB (каждые 90 °)
∠PAE = ∠DAB (общий)
Следовательно, используя критерий сходства AA,
ΔAEP ∼ ΔADB
(iv)
In ΔPDC и ΔBEC,
∠PDC = ∠BEC (каждый 90 °)
∠PCD = ∠BCE (Общий угол)
Следовательно, используя критерий сходства AA,
ΔPDC ∼ ΔBEC
Видео решение для треугольников (Страница: 140, В.№: 7)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 7
Страница № 140:
Вопрос 8:
E — точка на стороне AD, образованная параллелограммом ABCD, и BE пересекает CD в точке F. Покажите, что ΔABE ∼ ΔCFB
Ответ:
В ΔABE и ΔCFB,
∠A = ∠C (Противоположные углы параллелограмма)
∠AEB = ∠CBF (Альтернативные внутренние углы как AE || BC)
∴ ΔABE ∼ ΔCFB (По критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.№: 8)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 8
Страница № 140:
Вопрос 9:
На следующем рисунке ABC и AMP представляют собой два прямоугольных треугольника, расположенных под прямым углом к B и M соответственно, что доказывает:
(i) ΔABC ∼ ΔAMP
(ii)
Ответ:
In ΔABC и ΔAMP,
∠ABC = ∠AMP (каждый 90 °)
∠A = ∠A (общий)
∴ ΔABC ∼ ΔAMP (по критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.№: 9)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 9
Страница № 140:
Вопрос 10:
CD и GH являются биссектрисами ofACB и EGF соответственно, так что D и H лежат на сторонах AB и FE ΔABC и ΔEFG соответственно. Если ΔABC ∼ ΔFEG, Покажите, что:
(я)
(ii) ΔDCB ∼ ΔHGE
(iii) ΔDCA ∼ ΔHGF
Ответ:
Принято, что ΔABC ∼ ΔFEG.
∴ ∠A = ∠F, ∠B = ∠E и ∠ACB = ∠FGE
∠ACB = ∠FGE
∴ ∠ACD = ∠FGH (биссектриса угла)
А, DCB = ∠HGE (Биссектриса угла)
In ΔACD и ΔFGH,
∠A = ∠F (Доказано выше)
∠ACD = ∠FGH (Доказано выше)
∴ ΔACD ∼ ΔFGH (по критерию сходства AA)
В ΔDCB и ΔHGE,
∠DCB = ∠HGE (Доказано выше)
∠B = ∠E (Доказано выше)
∴ ΔDCB ∼ ΔHGE (по критерию сходства AA)
В ΔDCA и ΔHGF,
∠ACD = ∠FGH (Доказано выше)
∠A = ∠F (Доказано выше)
∴ ΔDCA ∼ ΔHGF (По критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.№: 10)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 10
Стр. № 141:
Вопрос 11:
На следующем рисунке E — это точка на стороне CB, образованная равнобедренным треугольником ABC с AB = AC. Если AD ⊥ BC и EF ⊥ AC, докажите, что ΔABD ∼ ΔECF
Ответ:
Принято, что ABC — равнобедренный треугольник.
∴ AB = AC
⇒ ABD = ∠ECF
В ΔABD и ΔECF,
∠ADB = ∠EFC (каждый 90 °)
∠ABD = ∠ECF (Доказано выше)
∴ ΔABD ∼ ΔECF (по критерию сходства AA)
Видео решение для треугольников (Страница: 141, Q.No .: 11)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 11
Стр. № 141:
Вопрос 12:
Стороны AB и BC и медиана AD треугольника ABC соответственно пропорциональны сторонам PQ и QR и медиане PM ΔPQR (см. Данный рисунок).Покажите, что ΔABC ∼ ΔPQR.
Ответ:
Медиана разделяет противоположную сторону.
∴
Учитывая это,
В ΔABD и ΔPQM,
(Доказано выше)
∴ ΔABD ∼ ΔPQM (по критерию подобия SSS)
⇒ ABD = ∠PQM (Соответствующие углы подобных треугольников)
В ΔABC и ΔPQR,
∠ABD = ∠PQM (Доказано выше)
∴ ΔABC ∼ ΔPQR (по критерию подобия SAS)
Видео решение для треугольников (Страница: 141, В.№: 12)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 12
Стр. № 141:
Вопрос 13:
D — точка на стороне BC треугольника ABC такая, что ∠ADC = ∠BAC. Покажи, что
Ответ:
В ΔADC и ΔBAC,
∠ADC = ∠BAC (дано)
∠ACD = ∠BCA (общий угол)
∴ ΔADC ∼ ΔBAC (по критерию сходства AA)
Мы знаем, что соответствующие стороны одинаковых треугольников пропорциональны.
Видео решение для треугольников (Страница: 141, Q.No .: 13)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 13
Стр. № 141:
Вопрос 14:
Стороны AB и AC и медиана AD треугольника ABC соответственно пропорциональны сторонам PQ и PR и медиане PM другого треугольника PQR.Покажи, что
Ответ:
Учитывая это,
Продолжим AD и PM до точек E и L соответственно, так что AD = DE и PM = ML. Затем соедините B с E, C с E, Q с L и R с L.
Мы знаем, что медианы делят противоположные стороны.
Следовательно, BD = DC и QM = MR
Также AD = DE (По конструкции)
А, ПМ = МЛ (По конструкции)
В четырехугольнике ABEC диагонали AE и BC делят друг друга пополам в точке D.
Следовательно, четырехугольник ABEC — параллелограмм.
∴ AC = BE и AB = EC (противоположные стороны параллелограмма равны)
Аналогично можно доказать, что четырехугольник PQLR является параллелограммом и PR = QL, PQ = LR
Было дано, что
∴ ΔABE ∼ ΔPQL (по критерию подобия SSS)
Мы знаем, что соответствующие углы одинаковых треугольников равны.
∴ ∠BAE = ∠QPL… (1)
Аналогично можно доказать, что ΔAEC ∼ ΔPLR и
∠CAE = ∠RPL… (2)
Складывая уравнения (1) и (2), получаем
BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ… (3)
В ΔABC и ΔPQR,
(дано)
∠CAB = ∠RPQ [Используя уравнение (3)]
∴ ΔABC ∼ ΔPQR (по критерию подобия SAS)
Видео решение для треугольников (Страница: 141, В.№: 14)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 14
Стр. № 141:
Вопрос 15:
Вертикальный столб длиной 6 м отбрасывает тень длиной 4 м на землю, и в то же время башня отбрасывает тень длиной 28 м. Найдите высоту башни.
Ответ:
Пусть AB и CD — башня и столб соответственно.
Пусть тень BE и DF будет тенью AB и CD соответственно.
В то же время световые лучи от солнца будут падать на башню и столб под одним и тем же углом.
Следовательно, ∠DCF = ∠BAE
А, DFC = ∠BEA
∠CDF = ∠ABE (Башня и столб вертикальны к земле)
∴ ΔABE ∼ ΔCDF (критерий сходства AAA)
Следовательно, высота башни составит 42 метра.
Видео решение для треугольников (Страница: 141, В.№: 15)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 15
Стр. № 141:
Вопрос 16:
Если AD и PM — медианы треугольников ABC и PQR, соответственно, где
Ответ:
Принято, что ΔABC ∼ ΔPQR
Мы знаем, что соответствующие стороны подобных треугольников пропорциональны.
∴… (1)
Также ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R… (2)
Поскольку AD и PM — медианы, они будут делить свои противоположные стороны.
∴… (3)
Из уравнений (1) и (3) получаем
… (4)
В ΔABD и ΔPQM,
∠B = ∠Q [Используя уравнение (2)]
[Используя уравнение (4)]
∴ ΔABD ∼ ΔPQM (по критерию подобия SAS)
⇒
Видео решение для треугольников (Страница: 141, В.№: 16)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 16
Страница № 143:
Вопрос 1:
Пусть и их площади будут соответственно 64 см 2 и 121 см 2 . Если EF = 15,4 см, найдите BC.
Ответ:
Видео решение для треугольников (Страница: 143, В.№: 1)
Решение NCERT для математики класса 10 — треугольники 143, вопрос 1
Страница № 143:
Вопрос 2:
Диагонали трапеции ABCD с AB || DC пересекаются друг с другом в точке O. Если AB = 2CD, найти отношение площадей треугольников AOB и COD.
Ответ:
Начиная с AB || CD,
∴ ∠OAB = ∠OCD и ∠OBA = ∠ODC (альтернативные внутренние углы)
In ΔAOB и ΔCOD,
∠AOB = ∠COD (вертикально противоположные углы)
∠OAB = ∠OCD (альтернативные внутренние углы)
∠OBA = ∠ODC (альтернативные внутренние углы)
∴ ΔAOB ∼ ΔCOD (по критерию сходства AAA)
Видео решение для треугольников (Страница: 143, В.№: 2)
Решение NCERT для математики класса 10 — треугольники 143, вопрос 2
Стр. № 144:
Вопрос 3:
На следующем рисунке ABC и DBC — это два треугольника на одном основании BC. Если AD пересекает BC в точке O, покажите, что
Ответ:
Нарисуем два перпендикуляра AP и DM на линии BC.
Мы знаем, что площадь треугольника =
.
В ΔAPO и ΔDMO,
∠APO = ∠DMO (каждый = 90 °)
∠AOP = ∠DOM (вертикально противоположные углы)
∴ ΔAPO ∼ ΔDMO (по критерию сходства AA)
Видео решение для треугольников (Страница: 144, Q.No: 3)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 3
Стр. № 144:
Вопрос 4:
Если площади двух одинаковых треугольников равны, докажите, что они равны.
Ответ:
Предположим, что ΔABC ∼ ΔPQR — два подобных треугольника.
Видео решение для треугольников (Страница: 144, Q.No: 4)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 4
Стр. № 144:
Вопрос 5:
D, E и F — это середины сторон AB, BC и CA отрезка ΔABC соответственно.Найдите соотношение площадей ΔDEF и ΔABC.
Ответ:
D и E — средние точки ΔABC.
Видео решение для треугольников (Страница: 144, Q.No: 5)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 5
Стр. № 144:
Вопрос 6:
Докажите, что отношение площадей двух одинаковых треугольников равно квадрату
отношения их соответствующих медиан.
Ответ:
Предположим, что ΔABC ∼ ΔPQR — два подобных треугольника. Пусть AD и PS — медианы этих треугольников.
ΔABC ∼ ΔPQR
… (1)
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R… (2)
Поскольку AD и PS — медианы,
∴ BD = DC =
А, QS = SR =
Алгебра (…) План урока, чтобы помочь студентам понять независимые и зависимые переменные с помощью моделирования вероятности пожара. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, зависимая, независимая, вход, выход, вероятность, переменная Студенты открывают для себя алгоритмы, сортируя фигуры в диаграммы Венна. Затем студенты сравнивают эффективность своих алгоритмов, используя коробчатые диаграммы. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгоритм , прямоугольник и ус, прямоугольная диаграмма, геометрия, узор, многоугольник, наборы, диаграмма Венна Знакомит студентов с арифметическими и геометрическими последовательностями. Учащиеся изучают дальше, создавая последовательности, варьируя начальное число, множитель и надстройку. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, график, итерация, линейные функции, умножение, множитель, отрицательное число, шаблон, положительное число, предварительное исчисление, рекурсия, рекурсивные функции, последовательности Знакомит учащихся с нанесением точек в декартовой системе координат — альтернативой «Построению графиков и координатной плоскости».« Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, функции, график, линейные уравнения, линейные функции, отрицательное число, плоскости, наклон Знакомит студентов с модульной (часовой) арифметикой и тем, как модульную арифметику можно использовать для кодирования сообщений с использованием простого сдвига, множественных и аффинных шифров. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, аффинный шифр, арифметика, шифр, криптография, дешифрование, деление, шифрование, коэффициенты, обратное, модульное, кратное, умножение, остатки, сдвиговый шифр, вычитание, время Знакомит студентов с геометрическим выводом конических сечений. Уровень оценки: 9–12 классы Связанные темы: окружности, коническое сечение, эллипс, гипербола, парабола, предварительное исчисление Исследует производные и идею бесконечности, используя геометрическую интерпретацию наклона. Уровень оценки: 9–12 классы, бакалавриат Связанные темы: исчисление, производная, дифференцировать, свойства функции, график, линейные уравнения, линейные функции, слайды, наклон, касательная Учащиеся будут отображать пары ввода / вывода на основе простой линейной функции, чтобы получить представление об основных линейных функциях. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: декартова координата, координата, координатная плоскость, функции, график, линейные функции, линии Знакомит студентов с тестом вертикальной линии для графиков функций. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: алгебра, декартова координата, константа, непрерывное распределение, координата, координатная плоскость, разрывная, свойства функции, функции, график, вход, линейные уравнения, линейные функции, линии, выход, кусочно, проверка вертикальной линии Студенты изучают основные идеи построения точек на координатной плоскости. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: алгебра, ось, декартова координата, координата, координатная плоскость, система координат, график, линейные функции, линии, отрицательное число, числовая прямая, узор, плоскости, положительное число, квадрант, наклон Демонстрирует связь между формулами и графиками. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, декартова координата, константа, координата, координатная плоскость, система координат, функции, график, вход, пересечение, линейные уравнения, линейные функции, линии, отрицательное число, выход, парабола, наклон Обучает различать возможные и невозможные графики функций, а также причины графической невозможности. Уровень оценки: 9–12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, расстояние, свойства функции, функции, график, интервалы, линейные уравнения, линейные функции, линии, узор, время, проверка вертикальной линии Студенты узнают об определенных интегралах через пределы и суммы Римана Уровень оценки: 9–12 классы, бакалавриат Связанные темы: область, исчисление, оценка, свойства функций, функции, график, бесконечность, интеграл, интегрирование, интервалы Знакомит с основными идеями, необходимыми для понимания функций. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, алгебра, арифметика, зависимые, функции, независимые, ввод, целые числа, линейные функции, умножение, вывод, шаблон, вычитание, переменная Студенты знакомятся с корреляцией между двумя переменными и линией наилучшего соответствия. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: наиболее подходящая линия, двумерная, декартова координата, координатная плоскость, корреляция, аппроксимация кривой, данные, отклонения, линейные уравнения, линейные функции, регрессия, остаток, точечная диаграмма, наклон, статистика, переменная Знакомит с основными идеями, необходимыми для понимания линейных функций. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, алгебра, арифметика, ассоциативный, коммутативный, зависимый, распределительный, деление, эквивалент, свойства функции, функции, независимый, ввод, целые числа, перехват, линейные уравнения, линейные функции, умножение, порядок операций, вывод , шаблон, наклон, вычитание, таблица, переменная Демонстрирует связи между формулами, графиками и словами. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: ускорение, алгебра, декартова координата, вогнутая, постоянная, координата, координатная плоскость, система координат, расстояние, функции, график, интервалы, линейные уравнения, линейные функции, линии, парабола, наклон, время, скорость Введение в различные алгоритмы решения линейных уравнений с одной переменной. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, алгоритм, коэффициент, дроби, обратное, умножение, переменная Студенты узнают о модульной арифметике для расшифровки зашифрованных сообщений. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, аффинный шифр, арифметика, шифр, криптография, дешифрование, деление, шифрование, модульное, кратное, умножение, шаблон, остатки, шифр сдвига, вычитание, время Знакомит студентов с концепциями преобразований. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: углов, декартова координата, координатная плоскость, система координат, размер, расстояние, переворот, геометрия, скольжение, график, шестиугольник, изображение, параллелограмм, узор, плоскости, многоугольник, предварительное изображение, отражения, вращение, квадраты , симметрия, мозаика, преобразование, перевод, транспонирование, треугольники Исчисление (…) Исследует производные и идею бесконечности, используя геометрическую интерпретацию наклона. Уровень оценки: 9–12 классы, бакалавриат Связанные темы: исчисление, производная, дифференцировать, свойства функции, график, линейные уравнения, линейные функции, слайды, наклон, касательная Студенты узнают об определенных интегралах через пределы и суммы Римана Уровень оценки: 9–12 классы, бакалавриат Связанные темы: область, исчисление, оценка, свойства функций, функции, график, бесконечность, интеграл, интегрирование, интервалы Знакомит учащихся с построением графиков в полярной координатной плоскости Уровень оценки: 9–12 классы, бакалавриат Связанные темы: исчисление , координатная плоскость, система координат, косинус, график данных, график, полярные координаты, предварительное вычисление, синус, тангенс, тригонометрия Дискретный (…) Студенты открывают для себя алгоритмы, сортируя фигуры в диаграммы Венна. Затем студенты сравнивают эффективность своих алгоритмов, используя коробчатые диаграммы. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгоритм , прямоугольник и ус, прямоугольная диаграмма, геометрия, узор, многоугольник, наборы, диаграмма Венна Знакомит студентов с арифметическими и геометрическими последовательностями. Учащиеся изучают дальше, создавая последовательности, варьируя начальное число, множитель и надстройку. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, график, итерация, линейные функции, умножение, множитель, отрицательное число, шаблон, положительное число, предварительное исчисление, рекурсия, рекурсивные функции, последовательности Знакомит студентов с модульной (часовой) арифметикой и тем, как модульную арифметику можно использовать для кодирования сообщений с использованием простого сдвига, множественных и аффинных шифров. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, аффинный шифр, арифметика, шифр, криптография, дешифрование, деление, шифрование, коэффициенты, обратное, модульное, кратное, умножение, остатки, сдвиговый шифр, вычитание, время Обозначает условную вероятность и вероятность одновременных событий. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сравнение, условная вероятность, события, экспериментальная вероятность, справедливая, дроби, независимый, умножение, проценты, вероятность, моделирование вероятности, вероятность без замены, случайное число, теоретическая вероятность Учащиеся рассматривают закономерности, возникающие из моделей агентов и геометрических фракталов. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: моделирование агентов, фракталы, паттерн, рекурсия, самоподобие Студенты узнают о факторинге, используя манипуляторы и компьютерные апплеты. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, деление, делители, множители, кратные, умножение, прямоугольники, целые числа Нахождение множителей целых чисел. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, деление, делители, множители, кратные, умножение, прямоугольники, целые числа Использует модульную (часовую) арифметику для поиска закономерностей в треугольнике Паскаля. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, деление, делители, целые числа, модульное, треугольник Паскаля, треугольник Паскаля, узор, остатки, сумма, треугольник, целые числа Использует и усиливает концепции вероятности, среднего, линейных графиков, экспериментальных данных и хаоса при анализе моделирования лесных пожаров. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: моделирование агентов, хаос, данные, десятичные дроби, события, экспериментальная вероятность, дроби, график, среднее значение, результаты, проценты, вероятность, моделирование вероятности, моделирование, теоретическая вероятность, дисперсия Знакомит студентов с моделированием вероятностей, позволяя им изучать компьютерное моделирование, одновременно изучая вероятность. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: моделирование агентов, хаос, данные, десятичные дроби, события, экспериментальная вероятность, дроби, среднее значение, результаты, проценты, вероятность, моделирование вероятности, моделирование, теоретическая вероятность, дисперсия Излагает подход к игре в хаос и его отношение к геометрическим фракталам. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: хаос, экспериментальная вероятность, фракталы, фракции, геометрическая вероятность, бесконечность, итерация, результаты, шаблон, проценты, вероятность, моделирование вероятности, случайное число, рекурсия, самоподобие, теоретическая вероятность, треугольник Рассматривает структуры данных и их приложения в теории вероятностей. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: комбинаторика, счет, деление, делители, экспериментальная вероятность, показатели, факторы, справедливый, логарифм, умножение, результаты, вероятность, моделирование вероятности, таблица, теоретическая вероятность, древовидная диаграмма, испытания Знакомит студентов с тестом вертикальной линии для графиков функций. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: алгебра, декартова координата, константа, непрерывное распределение, координата, координатная плоскость, разрывная, свойства функции, функции, график, вход, линейные уравнения, линейные функции, линии, выход, кусочно, проверка вертикальной линии Знакомит учащихся с концепциями, ведущими к вероятности. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: круговой график, подсчет, события, экспериментальная вероятность, справедливая, геометрическая вероятность, результаты, круговая диаграмма, вероятность, моделирование вероятности, случайное число, счетчик, теоретическая вероятность Обучает различать возможные и невозможные графики функций, а также причины графической невозможности. Уровень оценки: 9–12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, расстояние, свойства функции, функции, график, интервалы, линейные уравнения, линейные функции, линии, узор, время, проверка вертикальной линии Обрисовывает подход к построению фракталов путем вырезания частей плоских фигур. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: площадь, расстояние, фракталы, фракции, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, умножение, узор, проценты, периметр, рекурсия, масштаб, сегмент, самоподобие , последовательности, наборы Знакомит учащихся с идеями, связанными с пониманием фракталов. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: площадь, расстояние, фракталы, фракции, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, умножение, узор, проценты, периметр, рекурсия, масштаб, сегмент, самоподобие , последовательности, наборы Знакомит с основными идеями, необходимыми для понимания функций. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, алгебра, арифметика, зависимые, функции, независимые, ввод, целые числа, линейные функции, умножение, вывод, шаблон, вычитание, переменная Знакомит студентов с простыми понятиями вероятности. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: комбинаторика, сравнение, подсчет, события, экспериментальная вероятность, дроби, геометрическая вероятность, пересечение, результаты, проценты, вероятность, моделирование вероятности, случайное число, множества, статистика, теоретическая вероятность, испытания, объединение, диаграмма Венна Рассматривает, как могут быть созданы неправильные фракталы и как они вписываются в компьютерную графику. Уровень оценки: 9–12 классы, бакалавриат Связанные темы: хаос, измерение, фракталы, геометрические последовательности, геометрия, итерация, логарифм, узор, плоскости, многоугольник, рекурсия, масштаб, самоподобие, симметрия Знакомит студентов с модульной (часовой) арифметикой и ее использованием в решении реальных задач. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: сложение, арифметика, деление, прошедшее время, модульное, умножение, остатки, время Знакомит с основными идеями, необходимыми для понимания линейных функций. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, алгебра, арифметика, ассоциативный, коммутативный, зависимый, распределительный, деление, эквивалент, свойства функции, функции, независимый, ввод, целые числа, перехват, линейные уравнения, линейные функции, умножение, порядок операций, вывод , шаблон, наклон, вычитание, таблица, переменная Знакомит учащихся с принципом десятичной системы исчисления и с другими системами счисления. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, алгоритм, арифметика, основание, преобразование, подсчет, экспоненты, модульное, умножение, разрядное значение, вычитание Рассматривает, как можно использовать треугольник Паскаля для получения результатов, подобных треугольнику Серпинского. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь , арифметика, комбинаторика, расстояние, деление, факторы, фракталы, дроби, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, целые числа, итерация, длина, предел, линии, кратные, умножение, треугольник Паскаля, шаблон, проценты, периметр, частное, рекурсия, остатки, масштаб, сегмент, самоподобие, последовательности, множества, целые числа Знакомит учащихся с идеей поиска числовых моделей при создании нескольких различных типов фракталов. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: область, арифметика, хаос, десятичные дроби, измерение, фракталы, дроби, геометрические последовательности, геометрия, график, итерация, длина, линии, узор, теорема Пифагора, прямоугольники, рекурсия, сегмент, самоподобие, последовательности, площадь поверхности, симметрия, треугольник Показывает учащимся, что числовые шаблоны существуют в Треугольнике Паскаля, и усиливает способность учащихся определять шаблоны. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: арифметика, бином, хаос, коэффициент, комбинаторика, десятичные числа, измерение, деление, делители, коэффициенты, фракталы, дроби, геометрические последовательности, геометрия, бесконечность, целые числа, итерация, длина, линии, кратные, умножение, паскаль. треугольник, узор, вероятность, прямоугольники, рекурсия, остатки, сегмент, самоподобие, последовательности, площадь поверхности, симметрия, треугольник, целые числа Этот урок знакомит студентов с теоретической и экспериментальной вероятностью с помощью серии рабочих станций. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: гистограмма , условная вероятность, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, Монти Холл, результаты, проценты, вероятность, моделирование вероятности, вероятность с заменой, случайное число, счетчик, теоретическая вероятность, испытания Студенты узнают о вероятности, предсказывая результаты запланированных экспериментов и играя в гоночные игры. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: данные, события, экспериментальная вероятность, справедливая, дроби, результаты, проценты, вероятность, моделирование вероятности, теоретическая вероятность, испытания Учащиеся узнают, как можно представить вероятность с помощью геометрии. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: углов, площадь, круговой график, круги, подсчет, десятичные дроби, градусы, оценка, события, экспериментальная вероятность, справедливая, геометрическая вероятность, геометрия, длина, результаты, проценты, многоугольник, многогранники, вероятность, моделирование вероятности, случайное число, прямой угол, счетчик, статистика, теоретическая вероятность, объем Учащиеся узнают, как можно представить вероятность с помощью геометрии. Уровень оценки: 3-5 классы Связанные темы: углов, круговой график, круги, подсчет, десятичные дроби, оценка, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, геометрия, результаты, проценты, вероятность, моделирование вероятности, случайное число, счетчик, статистика, теоретический вероятность Рассматривает вероятностные концепции на основе статистики профессионального спорта. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: экспериментальная вероятность, вероятность, статистика, теоретическая вероятность Учащиеся используют вероятность, чтобы определить, насколько вероятно загорание каждого дерева в небольшом искусственном лесу. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: моделирование агентов, хаос, десятичные дроби, оценка, события, экспериментальная вероятность, результаты, проценты, вероятность, моделирование вероятности, моделирование, статистика, теоретическая вероятность, переменная Заключительный урок, позволяющий студентам построить рабочее определение фрактала. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: область, хаос, измерение, расстояние, экспериментальная вероятность, показатели, фракталы, дроби, генератор, геометрическая вероятность, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, логарифм, умножение, результаты , шаблон, проценты, периметр, вероятность, случайное число, рекурсия, масштаб, сегмент, самоподобие, последовательности, множества, теоретическая вероятность, треугольник Студенты учатся определять различные шаблоны с помощью последовательностей и мозаики. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, шестиугольник, итерация, умножение, узор, плоскости, многоугольник, рекурсия, рекурсивные функции, последовательности, квадраты, симметрия, мозаика, треугольник Расширяет понятие условной вероятности, обсуждая влияние замены на рисование нескольких объектов. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, арифметика, условная вероятность, делители, события, экспериментальная вероятность, справедливое, дробное, независимое, умножение, результаты, проценты, проценты, вероятность, моделирование вероятности, вероятность с заменой, вероятность без замены, случайное число, выборка, решение уравнений, теоретическая вероятность, испытания На этом уроке учащиеся изучают множества, элементы и диаграммы Венна. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: подсчет, элемент, целые числа, пересечение, шаблон, множества, объединение, диаграмма Венна, целые числа Этот урок разработан, чтобы познакомить студентов с идеей набора и с тем, что значит быть частью набора. Ученики будут экспериментировать с наборами в сочетании с диаграммой Венна. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: счет, элемент, узор, наборы, диаграмма Венна Студенты узнают о модульной арифметике для расшифровки зашифрованных сообщений. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, аффинный шифр, арифметика, шифр, криптография, дешифрование, деление, шифрование, модульное, кратное, умножение, шаблон, остатки, шифр сдвига, вычитание, время Вводит все 2 функции переменных и понятия заключенного / сбежавшего, необходимые для понимания множества Мандельброта. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: хаос, комплексное число, координата, координатная плоскость, система координат, деление, escape, экспоненты, фракталы, функции, геометрические последовательности, геометрия, бесконечность, итерация, множество Джулии, множество Мандельброта, умножение, узор, плоскости, заключенный, радиус, рекурсия, рекурсивные функции, самоподобие, множества, симметрия Представляет концепцию древовидных диаграмм как способ вычисления вероятности многоступенчатого события. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение , комбинаторика, условная вероятность, события, экспериментальная вероятность, показатели, справедливо, дроби, логарифм, кратные, умножение, результаты, проценты, вероятность, моделирование вероятности, случайное число, теоретическая вероятность, древовидная диаграмма, испытания Рассматривает вероятностные проблемы с неожиданными и неожиданными ответами. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: комбинаторика, условная вероятность, события, экспериментальная вероятность, справедливая, дроби, Монти Холл, результаты, проценты, вероятность, моделирование вероятности, вероятность с заменой, вероятность без замены, пропорция, случайное число, счетчик, статистика, стратегия , теоретическая вероятность, испытания Помогите учащимся узнать о классификации чисел по различным категориям, ответив на вопросы о диаграммах Венна. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: элемент, узор, наборы, диаграмма Венна Геометрия (…) Студенты открывают для себя алгоритмы, сортируя фигуры в диаграммы Венна. Затем студенты сравнивают эффективность своих алгоритмов, используя коробчатые диаграммы. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгоритм , прямоугольник и ус, прямоугольная диаграмма, геометрия, узор, многоугольник, наборы, диаграмма Венна Знакомит студентов с арифметическими и геометрическими последовательностями.Учащиеся изучают дальше, создавая последовательности, варьируя начальное число, множитель и надстройку. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, график, итерация, линейные функции, умножение, множитель, отрицательное число, шаблон, положительное число, предварительное исчисление, рекурсия, рекурсивные функции, последовательности Знакомит учащихся с четырехугольниками с упором на определение характеристик параллелограммов, прямоугольников и трапеций. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: углов, геометрия, параллель, параллелограмм, многоугольник, четырехугольники, прямоугольники, ромб, квадраты, дополнительные, мозаика Знакомит учащихся с острыми, тупыми и прямыми углами, а также с соотношениями между углами, образованными параллельными линиями, пересекаемыми трансверсалью. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: острый, смежный, альтернативный внешний вид, альтернативный внутренний, углы, соответствующие, геометрия, пересечение, линии, тупой, лучи, прямой угол, поперечный, вертикальный Учащиеся узнают о классификации углов по их мере и по отношению к углам, образованным двумя линиями, пересекаемыми трансверсалью. Уровень оценки: 3-5 классы Связанные темы: острый, углы, градусы, пересечение, тупой, лучи, прямой угол Сравнение форм с одинаковыми площадями, но с разными периметрами. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, сравнение, геометрия, целые числа, длина, периметр, многоугольник, прямоугольники, прямой угол, квадраты, ширина В этом уроке учащиеся исследуют области прямоугольной и неправильной формы на сетке, чтобы помочь им понять концепцию площади и единицы измерения площади. Уровень оценки: 3-5 классы Связанные темы: площадь, геометрия, длина, периметр, прямоугольники, прямой угол, квадраты, ширина Помогает учащимся понять, что существует множество способов решения задач. Этот урок также дает студентам возможность попрактиковаться в использовании различных методов для поиска участков неправильной формы. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, геометрия, длина, прямоугольники, прямой угол, квадраты, ширина Знакомит учащихся с нанесением точек в декартовой системе координат — альтернативой «Построению графиков и координатной плоскости».« Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, функции, график, линейные уравнения, линейные функции, отрицательное число, плоскости, наклон Студенты узнают о концепциях и применении хаоса. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: моделирование агентов, хаос, условная вероятность, экспериментальная вероятность, итерация, результаты, проценты, вероятность, моделирование вероятности, теоретическая вероятность Знакомит студентов с геометрическим выводом конических сечений. Уровень оценки: 9–12 классы Связанные темы: окружности, коническое сечение, эллипс, гипербола, парабола, предварительное исчисление В этом уроке используются концепции поперечных сечений трехмерных фигур для демонстрации образования двумерных форм. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: коническое сечение, геометрия, гипербола, парабола, многоугольник, предварительное вычисление, пирамида Знакомит учащихся с затраченным временем и методами его расчета. Уровень оценки: 3-5 классы Связанные темы: сложение, подсчет, прошедшее время, модульное, вычитание, время Студенты практикуются в определении времени окончания с учетом времени начала и прошедшего времени. Уровень оценки: 3-5 классы Связанные темы: сложение, арифметика, подсчет, прошедшее время, модульный, вычитание, время Учащиеся рассматривают закономерности, возникающие из моделей агентов и геометрических фракталов. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: моделирование агентов, фракталы, паттерн, рекурсия, самоподобие Использует модульную (часовую) арифметику для поиска закономерностей в треугольнике Паскаля. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, деление, делители, целые числа, модульное, треугольник Паскаля, треугольник Паскаля, узор, остатки, сумма, треугольник, целые числа Излагает подход к игре в хаос и его отношение к геометрическим фракталам. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: хаос, экспериментальная вероятность, фракталы, фракции, геометрическая вероятность, бесконечность, итерация, результаты, шаблон, проценты, вероятность, моделирование вероятности, случайное число, рекурсия, самоподобие, теоретическая вероятность, треугольник Исследует линии, плоскости, углы и многоугольники в виде мозаики. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: углы, площадь, переворот, геометрия, скольжения, шестиугольник, длина, линии, узор, периметр, плоскости, многоугольник, прямоугольники, отражения, регулярный, вращение, слайды, квадраты, симметрия, мозаика, треугольник Студенты изучают основные идеи построения точек на координатной плоскости. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: алгебра, ось, декартова координата, координата, координатная плоскость, система координат, график, линейные функции, линии, отрицательное число, числовая прямая, узор, плоскости, положительное число, квадрант, наклон Обрисовывает подход к построению фракталов путем вырезания частей плоских фигур. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: площадь, расстояние, фракталы, фракции, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, умножение, узор, проценты, периметр, рекурсия, масштаб, сегмент, самоподобие , последовательности, наборы Знакомит учащихся с идеями, связанными с пониманием фракталов. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: площадь, расстояние, фракталы, фракции, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, умножение, узор, проценты, периметр, рекурсия, масштаб, сегмент, самоподобие , последовательности, наборы Рассматривает, как могут быть созданы неправильные фракталы и как они вписываются в компьютерную графику. Уровень оценки: 9–12 классы, бакалавриат Связанные темы: хаос, измерение, фракталы, геометрические последовательности, геометрия, итерация, логарифм, узор, плоскости, многоугольник, рекурсия, масштаб, самоподобие, симметрия Знакомит студентов с длиной, периметром и площадью. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: острота, сложение, площадь, арифметика, декартовая координата, координатная плоскость, размер, расстояние, геометрия, длина, умножение, тупой, периметр, плоскости, многоугольник, теорема Пифагора, прямоугольники, вычитание, треугольник, ширина Знакомит учащихся с линиями, лучами, сегментами линий и плоскостями. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: алгебра, ось, координатная плоскость, система координат, функции, геометрия, график, бесконечность, линии, числовая прямая, плоскости, лучи, сегмент Рассматривает, как можно использовать треугольник Паскаля для получения результатов, подобных треугольнику Серпинского. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь , арифметика, комбинаторика, расстояние, деление, факторы, фракталы, дроби, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, целые числа, итерация, длина, предел, линии, кратные, умножение, треугольник Паскаля, шаблон, проценты, периметр, частное, рекурсия, остатки, масштаб, сегмент, самоподобие, последовательности, множества, целые числа Знакомит учащихся с идеей поиска числовых моделей при создании нескольких различных типов фракталов. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: область, арифметика, хаос, десятичные дроби, измерение, фракталы, дроби, геометрические последовательности, геометрия, график, итерация, длина, линии, узор, теорема Пифагора, прямоугольники, рекурсия, сегмент, самоподобие, последовательности, площадь поверхности, симметрия, треугольник Показывает учащимся, что числовые шаблоны существуют в Треугольнике Паскаля, и усиливает способность учащихся определять шаблоны. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: арифметика, бином, хаос, коэффициент, комбинаторика, десятичные числа, измерение, деление, делители, коэффициенты, фракталы, дроби, геометрические последовательности, геометрия, бесконечность, целые числа, итерация, длина, линии, кратные, умножение, паскаль. треугольник, узор, вероятность, прямоугольники, рекурсия, остатки, сегмент, самоподобие, последовательности, площадь поверхности, симметрия, треугольник, целые числа Знакомит студентов с понятием периметра. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, алгоритм, арифметика, геометрия, длина, периметр, плоскости, многоугольник, прямоугольники, квадраты, ширина Учащиеся изучают периметр и единицы измерения, используемые для измерения периметра, используя различные материалы, включая руки, ноги, линейки и компьютерные апплеты. Уровень оценки: 3-5 классы Связанные темы: арифметика, геометрия, длина, периметр, многоугольник, прямоугольники, прямой угол, масштаб, квадраты Учащиеся узнают, как можно представить вероятность с помощью геометрии. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: углов, площадь, круговой график, круги, подсчет, десятичные дроби, градусы, оценка, события, экспериментальная вероятность, справедливая, геометрическая вероятность, геометрия, длина, результаты, проценты, многоугольник, многогранники, вероятность, моделирование вероятности, случайное число, прямой угол, счетчик, статистика, теоретическая вероятность, объем Учащиеся узнают, как можно представить вероятность с помощью геометрии. Уровень оценки: 3-5 классы Связанные темы: углов, круговой график, круги, подсчет, десятичные дроби, оценка, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, геометрия, результаты, проценты, вероятность, моделирование вероятности, случайное число, счетчик, статистика, теоретический вероятность Заключительный урок, позволяющий студентам построить рабочее определение фрактала. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: область, хаос, измерение, расстояние, экспериментальная вероятность, показатели, фракталы, дроби, генератор, геометрическая вероятность, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, логарифм, умножение, результаты , шаблон, проценты, периметр, вероятность, случайное число, рекурсия, масштаб, сегмент, самоподобие, последовательности, множества, теоретическая вероятность, треугольник Студенты узнают, как работает теорема Пифагора и как ее применять. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, углы, площадь, арифметика, декартова координата, координатная плоскость, расстояние, экспоненты, геометрия, гипотенуза, длина, периметр, теорема Пифагора, прямой угол, слайды, решение уравнений, квадраты, треугольники, тригонометрия Студенты учатся определять различные шаблоны с помощью последовательностей и мозаики. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, шестиугольник, итерация, умножение, узор, плоскости, многоугольник, рекурсия, рекурсивные функции, последовательности, квадраты, симметрия, мозаика, треугольник На этом уроке учащиеся изучают множества, элементы и диаграммы Венна. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: подсчет, элемент, целые числа, пересечение, шаблон, множества, объединение, диаграмма Венна, целые числа Этот урок разработан, чтобы познакомить студентов с идеей набора и с тем, что значит быть частью набора. Ученики будут экспериментировать с наборами в сочетании с диаграммой Венна. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: счет, элемент, узор, наборы, диаграмма Венна Знакомит студентов с понятиями площади поверхности и объема. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь, арифметика, размер, геометрия, целые числа, длина, многогранники, призмы, площадь поверхности, объем Этот урок учит студентов, как определять площадь поверхности непрямоугольных призм. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь, размер, геометрия, длина, многогранники, призмы, прямоугольники, наклонная высота, площадь поверхности, треугольник, объем На этом уроке студенты узнают, как определять площадь поверхности прямоугольных призм. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь, размер, геометрия, длина, многогранники, призмы, прямоугольники, площадь поверхности Проверяет симметрию плоскости. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: углов, площадь, геометрия, скольжения, шестиугольник, иллюзия, длина, узор, плоскости, многоугольник, прямоугольники, отражения, регулярный, поворот, сегмент, квадраты, симметрия, мозаика, преобразование, перенос, треугольник Вводит все 2 функции переменных и понятия заключенного / сбежавшего, необходимые для понимания множества Мандельброта. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: хаос, комплексное число, координата, координатная плоскость, система координат, деление, escape, экспоненты, фракталы, функции, геометрические последовательности, геометрия, бесконечность, итерация, множество Джулии, множество Мандельброта, умножение, узор, плоскости, заключенный, радиус, рекурсия, рекурсивные функции, самоподобие, множества, симметрия Этот урок показывает учащимся начальной школы, как они могут наверняка узнать, что жесткие движения, такие как отражения, вращения и перемещения, создают форму, соответствующую исходной. Уровень оценки: 3-5 классы Связанные темы: конгруэнтность, отражения, вращение, преобразование, перенос Знакомит студентов с концепциями преобразований. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: углов, декартова координата, координатная плоскость, система координат, размер, расстояние, переворот, геометрия, скольжение, график, шестиугольник, изображение, параллелограмм, узор, плоскости, многоугольник, предварительное изображение, отражения, вращение, квадраты , симметрия, мозаика, преобразование, перевод, транспонирование, треугольники Студенты узнают, как найти площадь треугольника. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: площадь , декартова координата, координатная плоскость, расстояние, геометрия, длина, прямой угол, квадраты, треугольник, треугольники, ширина Изучите математическую природу искусства и мозаики и изучите роль математики в природе и нашей культуре. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: углов, площадь, контраст, геометрия, скольжения, график, шестиугольник, оттенок, иллюзия, длина, линии, узор, плоскости, многоугольник, прямоугольники, отражения, регулярный, вращение, сегмент, квадраты, симметрия, мозаика, преобразование, перевод, треугольник, значение Этот урок учит студентов, как найти объем непрямоугольных призм. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: площадь, глубина, размер, геометрия, высота, длина, умножение, многогранники, призмы, прямоугольники, наклонная высота, квадраты, площадь поверхности, треугольник, объем, ширина Этот урок учит студентов, как находить объем прямоугольных призм. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь, глубина, размер, геометрия, высота, длина, умножение, многогранники, призмы, прямоугольники, квадраты, треугольник, объем, ширина Моделирование (…) План урока, чтобы помочь студентам понять независимые и зависимые переменные с помощью моделирования вероятности пожара. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, зависимая, независимая, вход, выход, вероятность, переменная Учащиеся рассматривают закономерности, возникающие из моделей агентов и геометрических фракталов. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: моделирование агентов, фракталы, паттерн, рекурсия, самоподобие Введение в различные методы оценки посредством моделирования лесного пожара. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: оценка, вероятность, моделирование вероятности Использует и усиливает концепции вероятности, среднего, линейных графиков, экспериментальных данных и хаоса при анализе моделирования лесных пожаров. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: моделирование агентов, хаос, данные, десятичные дроби, события, экспериментальная вероятность, дроби, график, среднее значение, результаты, проценты, вероятность, моделирование вероятности, моделирование, теоретическая вероятность, дисперсия Знакомит студентов с моделированием вероятностей, позволяя им изучать компьютерное моделирование, одновременно изучая вероятность. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: моделирование агентов, хаос, данные, десятичные дроби, события, экспериментальная вероятность, дроби, среднее значение, результаты, проценты, вероятность, моделирование вероятности, моделирование, теоретическая вероятность, дисперсия Обучает различать возможные и невозможные графики функций, а также причины графической невозможности. Уровень оценки: 9–12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, расстояние, свойства функции, функции, график, интервалы, линейные уравнения, линейные функции, линии, узор, время, проверка вертикальной линии Демонстрирует связи между формулами, графиками и словами. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: ускорение, алгебра, декартова координата, вогнутая, постоянная, координата, координатная плоскость, система координат, расстояние, функции, график, интервалы, линейные уравнения, линейные функции, линии, парабола, наклон, время, скорость Номер и операции (…) Студенты открывают для себя алгоритмы, сортируя фигуры в диаграммы Венна.Затем студенты сравнивают эффективность своих алгоритмов, используя коробчатые диаграммы. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгоритм , прямоугольник и ус, прямоугольная диаграмма, геометрия, узор, многоугольник, наборы, диаграмма Венна Знакомит студентов с арифметическими и геометрическими последовательностями. Учащиеся изучают дальше, создавая последовательности, варьируя начальное число, множитель и надстройку. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, график, итерация, линейные функции, умножение, множитель, отрицательное число, шаблон, положительное число, предварительное исчисление, рекурсия, рекурсивные функции, последовательности Знакомит студентов с модульной (часовой) арифметикой и тем, как модульную арифметику можно использовать для кодирования сообщений с использованием простого сдвига, множественных и аффинных шифров. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, аффинный шифр, арифметика, шифр, криптография, дешифрование, деление, шифрование, коэффициенты, обратное, модульное, кратное, умножение, остатки, сдвиговый шифр, вычитание, время Знакомит студентов с дробями и изучает основные математические операции с дробями, сравнение дробей и преобразование дробей в десятичные числа или проценты. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сравнение, преобразование, десятичные дроби, знаменатель, деление, делители, множители, дроби, числовая строка, числитель, порядок, пропорция, рациональные числа, уменьшающая дробь, вычитание Введение в различные методы оценки посредством моделирования лесного пожара. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: оценка, вероятность, моделирование вероятности Студенты практикуются и улучшают свои навыки оценивания. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: площадь, сравнение, подсчет, оценка, длина, масштаб Знакомит студентов с оценками. Уровень оценки: 3-5 классы Связанные темы: сложение, площадь, арифметика, сравнение, подсчет, деление, оценка, длина, умножение, проценты, проценты, масштаб, вычитание Студенты узнают о факторинге, используя манипуляторы и компьютерные апплеты. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, деление, делители, множители, кратные, умножение, прямоугольники, целые числа Нахождение множителей целых чисел. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, деление, делители, множители, кратные, умножение, прямоугольники, целые числа Использует модульную (часовую) арифметику для поиска закономерностей в треугольнике Паскаля. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, деление, делители, целые числа, модульное, треугольник Паскаля, треугольник Паскаля, узор, остатки, сумма, треугольник, целые числа Излагает подход к игре в хаос и его отношение к геометрическим фракталам. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: хаос, экспериментальная вероятность, фракталы, фракции, геометрическая вероятность, бесконечность, итерация, результаты, шаблон, проценты, вероятность, моделирование вероятности, случайное число, рекурсия, самоподобие, теоретическая вероятность, треугольник Студенты узнают, как переводить дроби в десятичные. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, преобразование, десятичные дроби, знаменатель, деление, дроби, числитель, рациональные числа, уменьшающая дробь, вычитание Студенты узнают, как переводить дроби в проценты. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: преобразование, десятичные дроби, знаменатель, деление, дроби, умножение, числитель, проценты, проценты, рациональные числа, уменьшающая дробь Знакомит студентов с дробями и изучает основные математические операции с дробями, сравнение дробей и преобразование дробей в десятичные числа или проценты. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, десятичные дроби, знаменатель, деление, дроби, обратное, наименьший общий знаменатель, умножение, числитель, проценты, рациональные числа, вычитание Ученики и учитель играют в игру под названием «Король дробей», чтобы понять идею взятия дробных частей целых чисел, а затем используют манипуляторы и несколько компьютерных апплетов, чтобы закрепить эту идею. Уровень оценки: 3-5 классы Связанные темы: арифметика, сравнение, знаменатель, дроби, умножение, числовая строка, числитель, порядок, рациональные числа, вычитание Студенты практикуются в работе с преобразованием дробей, десятичных дробей и процентов, используя несколько заданий Interactivate. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: площадь, круговая диаграмма, круги, преобразование, десятичные дроби, деление, дроби, проценты, круговая диаграмма, пропорции, рациональные числа Обрисовывает подход к построению фракталов путем вырезания частей плоских фигур. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: площадь, расстояние, фракталы, фракции, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, умножение, узор, проценты, периметр, рекурсия, масштаб, сегмент, самоподобие , последовательности, наборы Знакомит учащихся с идеями, связанными с пониманием фракталов. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: площадь, расстояние, фракталы, фракции, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, умножение, узор, проценты, периметр, рекурсия, масштаб, сегмент, самоподобие , последовательности, наборы Рассматривает, как могут быть созданы неправильные фракталы и как они вписываются в компьютерную графику. Уровень оценки: 9–12 классы, бакалавриат Связанные темы: хаос, измерение, фракталы, геометрические последовательности, геометрия, итерация, логарифм, узор, плоскости, многоугольник, рекурсия, масштаб, самоподобие, симметрия Знакомит студентов с модульной (часовой) арифметикой и ее использованием в решении реальных задач. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: сложение, арифметика, деление, прошедшее время, модульное, умножение, остатки, время Усиливает навыки, связанные с умножением дробей и смешанных чисел. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: арифметика, знаменатель, деление, дроби, геометрические последовательности, график, неправильный, итерация, смешанные числа, умножение, числитель, рекурсия, последовательности, целые числа Знакомит учащихся с принципом десятичной системы исчисления и с другими системами счисления. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, алгоритм, арифметика, основание, преобразование, подсчет, экспоненты, модульное, умножение, разрядное значение, вычитание Рассматривает, как можно использовать треугольник Паскаля для получения результатов, подобных треугольнику Серпинского. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: площадь , арифметика, комбинаторика, расстояние, деление, факторы, фракталы, дроби, генератор, геометрические последовательности, геометрия, бесконечность, инициатор, целые числа, итерация, длина, предел, линии, кратные, умножение, треугольник Паскаля, шаблон, проценты, периметр, частное, рекурсия, остатки, масштаб, сегмент, самоподобие, последовательности, множества, целые числа Знакомит учащихся с идеей поиска числовых моделей при создании нескольких различных типов фракталов. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: область, арифметика, хаос, десятичные дроби, измерение, фракталы, дроби, геометрические последовательности, геометрия, график, итерация, длина, линии, узор, теорема Пифагора, прямоугольники, рекурсия, сегмент, самоподобие, последовательности, площадь поверхности, симметрия, треугольник Показывает учащимся, что числовые шаблоны существуют в Треугольнике Паскаля, и усиливает способность учащихся определять шаблоны. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: арифметика, бином, хаос, коэффициент, комбинаторика, десятичные числа, измерение, деление, делители, коэффициенты, фракталы, дроби, геометрические последовательности, геометрия, бесконечность, целые числа, итерация, длина, линии, кратные, умножение, паскаль. треугольник, узор, вероятность, прямоугольники, рекурсия, остатки, сегмент, самоподобие, последовательности, площадь поверхности, симметрия, треугольник, целые числа Студенты отрабатывают арифметические навыки.Может быть адаптирован для практики всех типов арифметики одиночных операций, начиная от простого сложения до операций с целыми и десятичными знаками. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, алгоритм, арифметика, координата, данные, десятичные дроби, деление, дроби, график, целые числа, линейные уравнения, линейные функции, умножение, вычитание Заключительный урок, позволяющий студентам построить рабочее определение фрактала. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: область, хаос, измерение, расстояние, экспериментальная вероятность, показатели, фракталы, дроби, генератор, геометрическая вероятность, геометрические последовательности, геометрия, бесконечность, инициатор, итерация, длина, предел, линии, логарифм, умножение, результаты , шаблон, проценты, периметр, вероятность, случайное число, рекурсия, масштаб, сегмент, самоподобие, последовательности, множества, теоретическая вероятность, треугольник Студенты учатся определять различные шаблоны с помощью последовательностей и мозаики. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: сложение, арифметика, арифметические последовательности, геометрические последовательности, шестиугольник, итерация, умножение, узор, плоскости, многоугольник, рекурсия, рекурсивные функции, последовательности, квадраты, симметрия, мозаика, треугольник На этом уроке учащиеся изучают множества, элементы и диаграммы Венна. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: подсчет, элемент, целые числа, пересечение, шаблон, множества, объединение, диаграмма Венна, целые числа Этот урок разработан, чтобы познакомить студентов с идеей набора и с тем, что значит быть частью набора.Ученики будут экспериментировать с наборами в сочетании с диаграммой Венна. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: счет, элемент, узор, наборы, диаграмма Венна Студенты узнают о модульной арифметике для расшифровки зашифрованных сообщений. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение, аффинный шифр, арифметика, шифр, криптография, дешифрование, деление, шифрование, модульное, кратное, умножение, шаблон, остатки, шифр сдвига, вычитание, время Вводит все 2 функции переменных и понятия заключенного / сбежавшего, необходимые для понимания множества Мандельброта. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: хаос, комплексное число, координата, координатная плоскость, система координат, деление, escape, экспоненты, фракталы, функции, геометрические последовательности, геометрия, бесконечность, итерация, множество Джулии, множество Мандельброта, умножение, узор, плоскости, заключенный, радиус, рекурсия, рекурсивные функции, самоподобие, множества, симметрия Помогите учащимся узнать о классификации чисел по различным категориям, ответив на вопросы о диаграммах Венна. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: элемент, узор, наборы, диаграмма Венна Вероятность (…) Студенты узнают о концепциях и применении хаоса. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: моделирование агентов, хаос, условная вероятность, экспериментальная вероятность, итерация, результаты, проценты, вероятность, моделирование вероятности, теоретическая вероятность Обозначает условную вероятность и вероятность одновременных событий. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сравнение, условная вероятность, события, экспериментальная вероятность, справедливая, дроби, независимый, умножение, проценты, вероятность, моделирование вероятности, вероятность без замены, случайное число, теоретическая вероятность Использует и усиливает концепции вероятности, среднего, линейных графиков, экспериментальных данных и хаоса при анализе моделирования лесных пожаров. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: моделирование агентов, хаос, данные, десятичные дроби, события, экспериментальная вероятность, дроби, график, среднее значение, результаты, проценты, вероятность, моделирование вероятности, моделирование, теоретическая вероятность, дисперсия Знакомит студентов с моделированием вероятностей, позволяя им изучать компьютерное моделирование, одновременно изучая вероятность. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: моделирование агентов, хаос, данные, десятичные дроби, события, экспериментальная вероятность, дроби, среднее значение, результаты, проценты, вероятность, моделирование вероятности, моделирование, теоретическая вероятность, дисперсия Излагает подход к игре в хаос и его отношение к геометрическим фракталам. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: хаос, экспериментальная вероятность, фракталы, фракции, геометрическая вероятность, бесконечность, итерация, результаты, шаблон, проценты, вероятность, моделирование вероятности, случайное число, рекурсия, самоподобие, теоретическая вероятность, треугольник Рассматривает структуры данных и их приложения в теории вероятностей. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: комбинаторика, счет, деление, делители, экспериментальная вероятность, показатели, факторы, справедливый, логарифм, умножение, результаты, вероятность, моделирование вероятности, таблица, теоретическая вероятность, древовидная диаграмма, испытания Знакомит учащихся с концепциями, ведущими к вероятности. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: круговой график, подсчет, события, экспериментальная вероятность, справедливая, геометрическая вероятность, результаты, круговая диаграмма, вероятность, моделирование вероятности, случайное число, счетчик, теоретическая вероятность Знакомит студентов с простыми понятиями вероятности. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: комбинаторика, сравнение, подсчет, события, экспериментальная вероятность, дроби, геометрическая вероятность, пересечение, результаты, проценты, вероятность, моделирование вероятности, случайное число, множества, статистика, теоретическая вероятность, испытания, объединение, диаграмма Венна Этот урок знакомит студентов с теоретической и экспериментальной вероятностью с помощью серии рабочих станций. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: гистограмма , условная вероятность, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, Монти Холл, результаты, проценты, вероятность, моделирование вероятности, вероятность с заменой, случайное число, счетчик, теоретическая вероятность, испытания Студенты узнают о вероятности, предсказывая результаты запланированных экспериментов и играя в гоночные игры. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: данные, события, экспериментальная вероятность, справедливая, дроби, результаты, проценты, вероятность, моделирование вероятности, теоретическая вероятность, испытания Учащиеся узнают, как можно представить вероятность с помощью геометрии. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: углов, площадь, круговой график, круги, подсчет, десятичные дроби, градусы, оценка, события, экспериментальная вероятность, справедливая, геометрическая вероятность, геометрия, длина, результаты, проценты, многоугольник, многогранники, вероятность, моделирование вероятности, случайное число, прямой угол, счетчик, статистика, теоретическая вероятность, объем Учащиеся узнают, как можно представить вероятность с помощью геометрии. Уровень оценки: 3-5 классы Связанные темы: углов, круговой график, круги, подсчет, десятичные дроби, оценка, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, геометрия, результаты, проценты, вероятность, моделирование вероятности, случайное число, счетчик, статистика, теоретический вероятность Рассматривает вероятностные концепции на основе статистики профессионального спорта. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: экспериментальная вероятность, вероятность, статистика, теоретическая вероятность Учащиеся используют вероятность, чтобы определить, насколько вероятно загорание каждого дерева в небольшом искусственном лесу. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: моделирование агентов, хаос, десятичные дроби, оценка, события, экспериментальная вероятность, результаты, проценты, вероятность, моделирование вероятности, моделирование, статистика, теоретическая вероятность, переменная Расширяет понятие условной вероятности, обсуждая влияние замены на рисование нескольких объектов. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, арифметика, условная вероятность, делители, события, экспериментальная вероятность, справедливое, дробное, независимое, умножение, результаты, проценты, проценты, вероятность, моделирование вероятности, вероятность с заменой, вероятность без замены, случайное число, выборка, решение уравнений, теоретическая вероятность, испытания Представляет концепцию древовидных диаграмм как способ вычисления вероятности многоступенчатого события. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: сложение , комбинаторика, условная вероятность, события, экспериментальная вероятность, показатели, справедливо, дроби, логарифм, кратные, умножение, результаты, проценты, вероятность, моделирование вероятности, случайное число, теоретическая вероятность, древовидная диаграмма, испытания Рассматривает вероятностные проблемы с неожиданными и неожиданными ответами. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: комбинаторика, условная вероятность, события, экспериментальная вероятность, справедливая, дроби, Монти Холл, результаты, проценты, вероятность, моделирование вероятности, вероятность с заменой, вероятность без замены, пропорция, случайное число, счетчик, статистика, стратегия , теоретическая вероятность, испытания Статистика (…) Студенты узнают, для чего используются гистограммы, как интерпретировать представленные данные и как организовать свои собственные данные с помощью гистограмм. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: гистограмма, категориальные, данные, высота, масштаб, статистика Знакомит студентов с квартилями и коробчатыми диаграммами. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: прямоугольник и усы, прямоугольная диаграмма, данные, среднее значение, меры центральной тенденции, медиана, мода, квартиль, диапазон, статистика Знакомит учащихся с нанесением точек в декартовой системе координат — альтернативой «Построению графиков и координатной плоскости».« Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, функции, график, линейные уравнения, линейные функции, отрицательное число, плоскости, наклон Введение и тонкости использования гистограмм и гистограмм. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: гистограмма, категориальная, сравнение, подсчет, данные, график, гистограмма, интервалы, длина, среднее значение, числовое, масштаб, асимметричное распределение, стандартное отклонение, статистика Обучает различать возможные и невозможные графики функций, а также причины графической невозможности. Уровень оценки: 9–12 классы Связанные темы: декартова координата, координата, координатная плоскость, система координат, расстояние, свойства функции, функции, график, интервалы, линейные уравнения, линейные функции, линии, узор, время, проверка вертикальной линии Этот урок позволяет учащимся узнать, для чего используются гистограммы, как интерпретировать представленные данные и как организовать свои собственные данные с помощью гистограмм. Уровень оценки: 3-5 классы Связанные темы: гистограмма, категориальная, круги, подсчет, данные, квадраты, статистика, треугольник Вводит статистические показатели центра. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: арифметика, гистограмма, среднее значение, меры центральной тенденции, медиана, режим, диапазон, наборы, статистика, сумма Студенты знакомятся с корреляцией между двумя переменными и линией наилучшего соответствия. Уровень оценки: 6-8 классы, 9-12 классы, бакалавриат Связанные темы: наиболее подходящая линия, двумерная, декартова координата, координатная плоскость, корреляция, аппроксимация кривой, данные, отклонения, линейные уравнения, линейные функции, регрессия, остаток, точечная диаграмма, наклон, статистика, переменная Этот урок побудит учащихся мыслить творчески, предлагая им спроектировать и построить ловушки для водяных шаров из случайного подручного материала, при этом от них потребуется учитывать множество переменных.Затем студенты построят по крайней мере две гистограммы, которые будут использоваться в рекламе, рекламирующей покупку ловушки для их группы. Уровень оценки: 3-5 классы, 6-8 классы Связанные темы: гистограмма, подсчет, данные, график, гистограмма, интервалы, линии, среднее значение, медиана, режим, круговая диаграмма, вероятность, диапазон, асимметричное распределение, стандартное отклонение, статистика Демонстрирует связи между формулами, графиками и словами. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: ускорение, алгебра, декартова координата, вогнутая, постоянная, координата, координатная плоскость, система координат, расстояние, функции, график, интервалы, линейные уравнения, линейные функции, линии, парабола, наклон, время, скорость Рассматривает концепции статистики и анализа данных на основе практических вопросов, возникающих в повседневной жизни. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: гистограмма, дроби, гистограмма, проценты, проценты, статистика Знакомит учащихся с графиками стеблей и листьев, а также с расчетом среднего, медианы и моды на основе графиков. Уровень оценки: 3-5 классы, 6-8 классы, 9-12 классы Связанные темы: арифметика, данные, график данных, график, гистограмма, среднее значение, меры центральной тенденции, медиана, режим, диапазон, статистика, ствол и лист Вводит нормальное распределение и рассматривает противоречие с кривой колокола. Уровень оценки: 9–12 классы, бакалавриат Связанные темы: площадь, арифметика, кривая колокола, непрерывное распределение, отклонения, экспериментальная вероятность, экспонента, гистограмма, бесконечность, среднее значение, меры центральной тенденции, медиана, режим, нормальное распределение, результаты, проценты, вероятность, диапазон, асимметрия распределение, квадраты, стандартное отклонение, статистика, теоретическая вероятность, испытания, дисперсия Учащиеся узнают о разнице между одномерными и двумерными данными и понимают, как выбрать лучший график для отображения данных. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: гистограмма, двумерная, прямоугольная диаграмма, прямоугольная диаграмма, декартова координата, категориальная, круговая диаграмма, круги, координата, координатная плоскость, корреляция, аппроксимация кривой, данные, график данных, отклонения, двойная гистограмма, график , гистограмма, интервалы, среднее значение, меры центральной тенденции, медиана, режим, числовое значение, выброс, проценты, проценты, круговая диаграмма, квартиль, диапазон, регрессия, остаток, шкала, диаграмма рассеяния, асимметричное распределение, стандартное отклонение, статистика, основа и лист, таблица, одномерная Тригонометрия (…) Знакомит учащихся с построением графиков в полярной координатной плоскости Уровень оценки: 9–12 классы, бакалавриат Связанные темы: исчисление , координатная плоскость, система координат, косинус, график данных, график, полярные координаты, предварительное вычисление, синус, тангенс, тригонометрия Студенты узнают, как работает теорема Пифагора и как ее применять. Уровень оценки: 6–8 классы, 9–12 классы Связанные темы: алгебра, углы, площадь, арифметика, декартова координата, координатная плоскость, расстояние, экспоненты, геометрия, гипотенуза, длина, периметр, теорема Пифагора, прямой угол, слайды, решение уравнений, квадраты, треугольники, тригонометрия Другое (…) Знакомит учащихся с затраченным временем и методами его расчета. Уровень оценки: 3-5 классы Связанные темы: сложение, подсчет, прошедшее время, модульное, вычитание, время Студенты практикуются в определении времени окончания с учетом времени начала и прошедшего времени. Уровень оценки: 3-5 классы Связанные темы: сложение, арифметика, подсчет, прошедшее время, модульный, вычитание, время |
похожих треугольников седьмой класс — Скачать PDF бесплатно
Рисование линий третьей степени симметрии
Стандарты Огайо: Геометрия соединения и тест пространственного восприятия H Определение и описание линейной и вращательной симметрии в двумерных формах и конструкциях.Индикатор 4 Проведите линии симметрии для проверки симметрии
ПодробнееГеометрические преобразования четвертый класс
Стандарты Огайо: Геометрия соединения и тест пространственного восприятия I Описывайте, идентифицируйте и моделируйте отражения, повороты и перемещения с использованием физических материалов. Показатель 7 Определите, опишите и используйте отражения
ПодробнееВ чем моя точка зрения? — Шесть класс
Приложения для чтения со стандартами Огайо: информационный, технический и убедительный текст — эталон D Выявление аргументов и методов убеждения, используемых в убедительном письме.Индикаторы 6 Определите
ПодробнееУчасток связи пятый уровень
Приложения для чтения со стандартами Огайо: эталонный тест литературного текста C Определите элементы сюжета и установите связь между элементом и будущим событием. Показатель 3 Определите основные происшествия
ПодробнееМодели фракций третий класс
Стандарты штата Огайо. Контрольный показатель числа соединений, определения чисел и операций. C. Представление часто используемых дробей и смешанных чисел с использованием слов и физических моделей.Показатель 5 Представляют дробные и смешанные
ПодробнееПонимание соотношений пятый класс
Соединение стандартов штата Огайо: число, определение числа и операции Стандартный эталон B Используйте модели и изображения, чтобы связать понятия соотношения, пропорции и процента. Показатель 1 Использование моделей и визуального представления
ПодробнееДевятый класс урбанизации
Соединение стандартов штата Огайо: Географический ориентир B Анализируйте географические изменения, вызванные деятельностью человека, используя соответствующие карты и другие географические данные.Показатель 4 Объясните причины и последствия
ПодробнееКоммутативная собственность первого уровня
Стандарты Огайо. Шаблоны соединения, функции и тест алгебры E Решайте открытые предложения и объясняйте стратегии. Индикатор 4 Решите открытые предложения, представив выражение более чем одним способом, используя
ПодробнееСравнение наборов данных восьмого уровня
Соединение стандартов штата Огайо: анализ данных и оценка вероятности C Сравните характеристики среднего, медианы и режима для данного набора данных и объясните, какой показатель центра лучше всего представляет
ПодробнееИзменения в нашем небе второго уровня
Соединение стандартов штата Огайо: эталонный показатель в науках о Земле и космосе A Наблюдайте за постоянными и меняющимися рисунками объектов в дневном и ночном небе.Показатель 2 Наблюдайте и описывайте, как Солнце, Луна и звезды
ПодробнееПищевые сети и пищевые цепи пятого класса
Соединение стандартов штата Огайо: эталонный тест B для наук о жизни Анализируйте структуры и функции растений и животных, необходимые для выживания, и описывайте поток энергии через систему, которую используют все организмы для выживания.
ПодробнееДни недели Детский сад
История Ohio Standards Connection: Benchmark A Используйте календарь, чтобы определить день, неделю, месяц и год.Показатель 1 Назовите дни недели. Краткое содержание урока: дети примут участие в разнообразии
ПодробнееScience Rocks шестой класс
Соединения стандартов Огайо: эталонный показатель в науках о Земле и космосе D Определите, что литосфера содержит горные породы и минералы, а минералы составляют горные породы. Опишите, как образуются горные породы и минералы и / или
ПодробнееДавайте измерять дошкольного возраста
Стандарты штата Огайо Стандартные контрольные измерения для измерений D Примените методы измерения для измерения длины, веса и объема (вместимости).Показатель 6 Измерить длину и объем (вместимость) нестандартным
ПодробнееНаписание простых рассказов Первый класс
Стандартные стандарты штата Огайо. Тестирование разработки приложений A. Составляйте тексты, которые передают ясное сообщение и включают хорошо подобранные детали. Показатель 1 Пишите простые рассказы с началом, серединой и концом
ПодробнееПаломничество Мансы Мусы седьмой класс
Соединение стандартов Огайо: Географический ориентир A Определите на карте расположение основных физических и человеческих особенностей каждого континента.Индикатор 2 На карте обозначьте места, связанные с историческими событиями
ПодробнееДорогие семьи 4-х классов,
Дорогие семьи 4-х классов! В течение следующих нескольких недель наш класс будет изучать геометрию. Посредством повседневной деятельности мы исследуем взаимосвязь между плоскими двухмерными фигурами и твердыми трехмерными фигурами
. ПодробнееДефицит и выбор Первый уровень
Соединение стандартов штата Огайо: экономический тест A Объясните, как нехватка ресурсов заставляет людей делать выбор, чтобы удовлетворить свои потребности.Показатель 1 Объясните, что потребности неограничены, а ресурсы
ПодробнееЭнергетические цепи седьмой степени
Соединение стандартов штата Огайо: контрольный показатель по физической науке D Опишите, что энергия принимает разные формы, некоторые формы представляют кинетическую энергию, а некоторые формы представляют потенциальную энергию; и при преобразованиях энергии
ПодробнееПринять десятый уровень экосистемного проекта
Соединение стандартов штата Огайо: эталонный показатель для наук о жизни F Объясните структуру и функции экосистем и расскажите, как экосистемы меняются с течением времени.Показатель 15 Объясните, как живые существа взаимодействуют с абиотиком
. ПодробнееВосстание революции девятый класс
Соединение стандартов Огайо: гражданские права и обязанности Контрольный показатель A Проанализируйте способы, которыми люди добиваются правительственных изменений, включая политические действия, социальный протест и революцию. Показатель 1 Анализ
ПодробнееОсновы понимания
Упражнение: TEKS: Изучение преобразований Основные понятия.(5) Инструменты геометрического мышления. Методы работы с пространственными фигурами и их свойствами важны для понимания лежащих в основе
ПодробнееДлина дуги и площади секторов
Результаты учащихся Когда учащиеся получают данные об угловом измерении дуги и длине радиуса круга, они понимают, как определить длину дуги и площадь сектора.
ПодробнееЗадачи производительности в реальном мире
Задачи по успеваемости в реальном мире Реальный мир Реальная жизнь, реальные данные, в реальном времени — Эти упражнения знакомят учащихся с реальными жизненными сценариями, в которых они используют реальные данные в реальном времени для решения задач.На самом деле
ПодробнееРАСПИСАНИЕ: МАТЕМАТИКА 2007
, K РАСПИСАНИЕ: МАТЕМАТИКА 00 СРОК МОДУЛЯ УРОВНЯ … LO ЧИСЛА, ОПЕРАЦИИ И ОТНОШЕНИЯ Способен распознавать, представлять числа и их отношения, а также подсчитывать, оценивать, вычислять и проверять
ПодробнееПроверьте мой детский сад письма
Стандартные стандарты штата Огайо. Тестирование процессов написания F Примените инструменты для оценки качества письма.Контрольный показатель D Использование стратегий и ресурсов пересмотра для улучшения идей и содержания, организации, выбора слов
ПодробнееЗадача месяца: разрезание куба
Задача месяца: Задачи месяца (POM) используются по-разному, чтобы способствовать решению проблем и способствовать внедрению первого стандарта математической практики из Common Core State Standards:
ПодробнееАкадемические стандарты Миннесоты
Соответствие академическим стандартам Миннесоты Классы K-6 G / M-204 Введение Этот документ демонстрирует высокую степень успеха, которого достигают студенты при использовании Scott Foresman Addison Wesley
ПодробнееПараллельные и перпендикулярные линии
Университет Тринити Digital Commons @ Trinity Understanding by Design: Complete Collection Understanding by Design Лето 6-12-2014 Параллельные и перпендикулярные линии Danielle R.Университет Кендрика Тринити,
ПодробнееЛичные хронологии Второй уровень
Стандарты Огайо Анализ данных о подключении и тест вероятности C Представляйте данные с помощью объектов, графических диаграмм и гистограмм. Индикаторы 3. Прочтите и постройте простые временные шкалы, чтобы упорядочить события. 5.
ПодробнееМоделирование в геометрии
Моделирование в геометрии Обзор Количество учебных дней: 8-10 (1 день = 53 минуты) Изучение материала Математические практики, которые необходимо интегрировать Используйте геометрические формы и их компоненты для представления
ПодробнееБесполое размножение шестой класс
Соединение стандартов штата Огайо: эталонный показатель B для наук о жизни Описать характеристики организма с точки зрения комбинации унаследованных признаков и признать воспроизводство характеристикой живых организмов
Подробнее7.4A / 7.4B СТУДЕНЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ № 1
7.4A / 7.4B ЗАДАНИЕ УЧАЩИХСЯ № 1 Напишите формулу, которая могла бы использоваться для определения радиуса круга, r, с учетом длины окружности, C. Формула в таблице математики для 7 класса, которая связывает
ПодробнееКлассификация треугольников урока 1
Классификация Урок 1 острый угол congruent scalene Классификация СЛОВАРЬ прямой угол равнобедренный Диаграмма Венна тупой угол равносторонний Вы классифицируете многие вещи вокруг себя.Например, вы можете выбрать
Подробнее2.1. Индуктивное рассуждение ПРИМЕР А
КОНКРЕТНЫЙ УРОК 2.1 Индуктивные рассуждения В этом уроке вы узнаете, как индуктивные рассуждения используются в естественных науках и математике. Используйте индуктивные рассуждения, чтобы делать предположения о последовательностях чисел
ПодробнееСЕРТИФИКАЦИЯ ДЛЯ НОУТБУКА MATH 60
СЕРТИФИКАЦИЯ ДЛЯ НОУТБУКА MATH 60 Глава # 1: Целые и действительные числа 1.1a 1.1b 1.2 1.3 1.4 1.8 Глава № 2: Алгебраические выражения, линейные уравнения и приложения 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
ПодробнееКонцепции / навыки. Материалы
. Золотые прямоугольники. Разделение понятий / навыков с десятичными дробями. Пропорциональное мышление. Решение задач. Материалы. TI-15. Страницы с заданиями для учащихся (стр. 75-78). Конверты, юридических и буквенных размеров. Игральные карты
. ПодробнееSAS Triangle подобие — Math Open Reference
SAS Triangle подобие — Math Open ReferenceОпределение: Треугольники подобны, если две стороны одного треугольника находятся в одинаковой пропорции с соответствующими сторонами другого, и включенный угол равны.
Это (SAS) — один из трех способов проверить, что два треугольника похожи. Список см. Подобные треугольники.
Попробуй Перетащите любую оранжевую точку на P, Q, R. Треугольник LMN изменится и останется похожим на левый треугольник PQR.
Если две стороны в одном треугольнике находятся в одинаковой пропорции с соответствующими сторонами в другом, и включенный угол между ними то же самое то треугольники похожи.
Например, в треугольнике выше сторона PQ ровно в два раза больше. пока соответствующая сторона LM в другом треугольнике, а PR вдвое меньше LN.Итак, эти две стороны находятся в одинаковой пропорции, в данном случае 2: 1 (два к одному). Так же включенные угловые углы (P и L) равны меры, и поэтому треугольники похожи.
Обратите внимание, что две стороны и угол нарисованы пурпурным цветом, чтобы показать, что они используются для проверки сходства.
Что это значит?
Поскольку две соответствующие пары сторон находятся в одинаковой пропорции, и включенный угол углы равны, мы можем быть уверены, что треугольники похожи.Потому что треугольники похожи:
- Три угла при P, Q и R равны к углам L, M и N соответственно.
- Соответствующие стороны в каждом треугольнике будут иметь одинаковую пропорцию.
Но не забывайте
Подобные треугольники можно вращать и / или зеркально отображать друг друга (отражать). (Смотрите похожие треугольники.) На рисунке выше два треугольника по-прежнему похожи, хотя один является зеркальным отражением другого и повернут.Другие похожие темы
Подобные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.


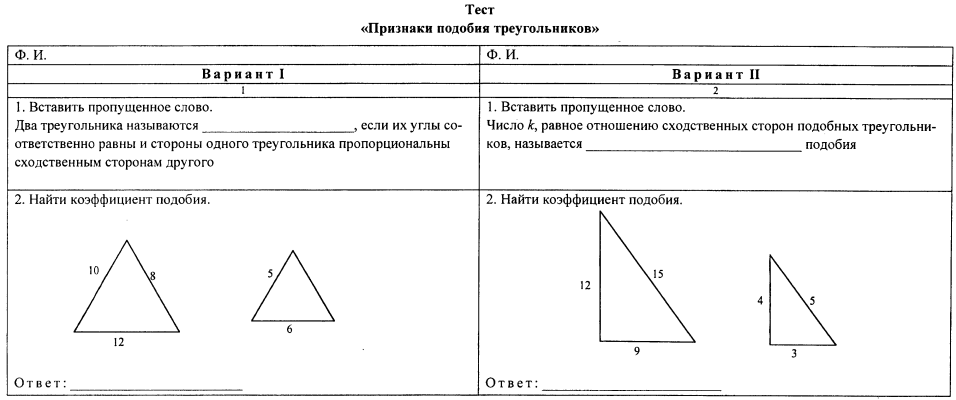 Даны векторы (2;0), (1;2), (-3;m). Найдите значение m, при котором векторы
Даны векторы (2;0), (1;2), (-3;m). Найдите значение m, при котором векторы Геометрический смысл.
Геометрический смысл.

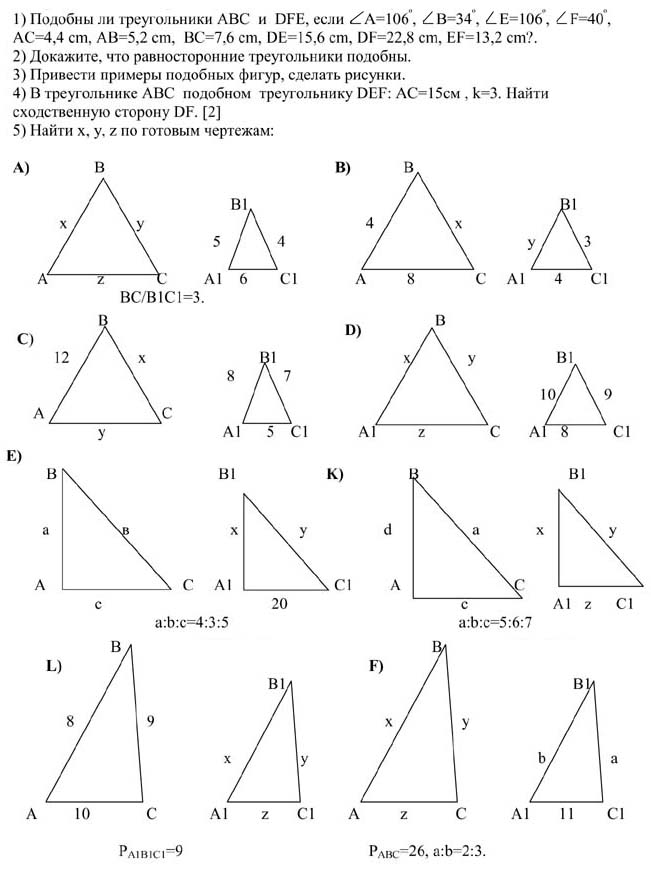
 Дано: АВ=24см, ВС=16см, МВ=15см,NC=6cм , MN=20см.
Дано: АВ=24см, ВС=16см, МВ=15см,NC=6cм , MN=20см.
 Свойство биссектрисы.
Свойство биссектрисы.

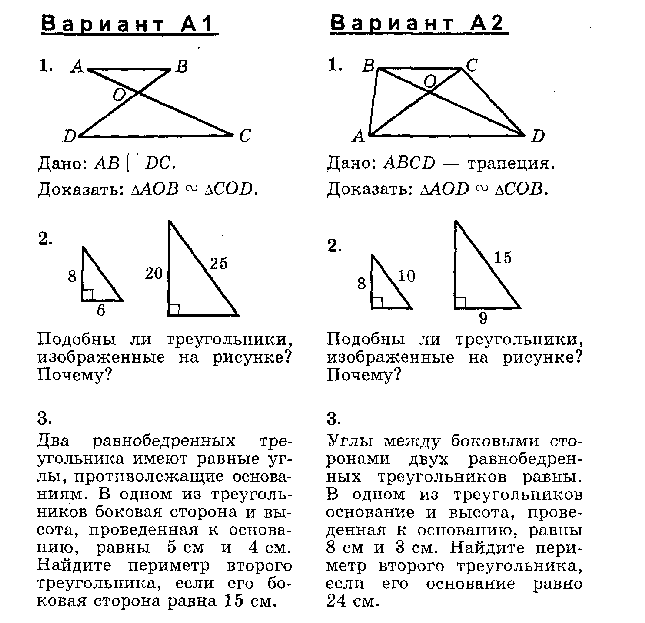
 Найдите сторону правильного шестиугольника, вписанного в данную окружность.
Найдите сторону правильного шестиугольника, вписанного в данную окружность.
