 :
:1) Какая из матриц ниже удовлетворяет матричному уравнению 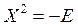 :
:
A) 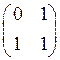
B) 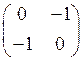
C) 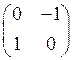
D) 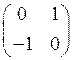
E) 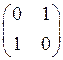
2) Какое из указанных множеств изоморфно  :
:
A) M= {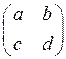 ,
, 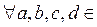
 }
}
B) M= {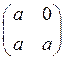 ,
, 
 }
}
C) M= {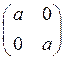 ,
, 
 }
}
D) M= {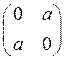 ,
, 
 }
}
E) M= {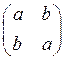 ,
, 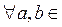
 }
}
3) В каком случае матрица вида 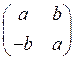 , где a,b
, где a,b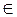
 вырождена?
вырождена?
A) 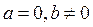
B) 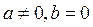
C) 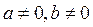
D) 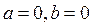
E) 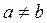
4) Пусть 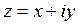 , тогда
, тогда 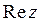 вычисляется по формуле:
вычисляется по формуле:
A) 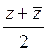 B)
B) 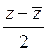 C)
C) 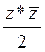 D)
D) 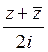 E)
E) 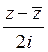
5) Модуль и аргумент комплексного числа 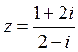 равны:
равны:
A) 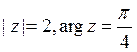
B) 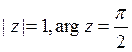
C) 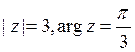
D) 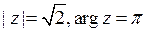
E) 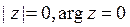
6) Значение корня 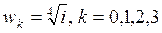 ,
, 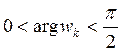 равно:
равно:
A) 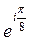 B)
B) 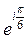 C)
C) 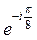 D)
D) 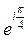 E)
E) 
7) Выберите показательную форму, соответствующую числу 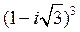 :
:
A) 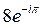
B) 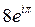
C) 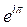
D) 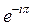
E) 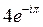
8) Пусть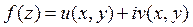 . Тогда условия Коши-Римана в точке
. Тогда условия Коши-Римана в точке 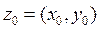 записываются как:
записываются как:
A) 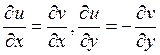
B) 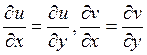
C) 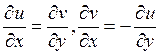
D) 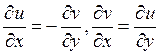
E) 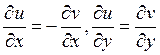
9) Функция 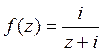 , тогда
, тогда 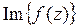 равна:
равна:
A) 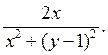
B) 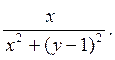
C) 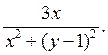
D) 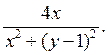
E) 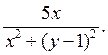
10) Значение 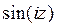 равно:
равно:
A) 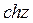 B)
B) 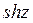 C)
C) 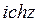 D)
D) 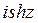 E)
E) 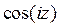
11) Найти аналитическую функцию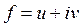 , если
, если 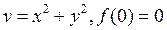 :
:
A) 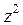
B) 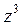
C) 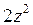
D) 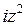
E) 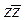
12) Если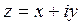 , то
, то 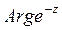 равен:
равен:
A) 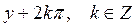
B) 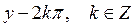
C) 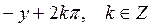
D) 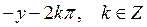
E) 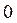
13) Решением уравнения 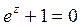 является множество:
является множество:
A) 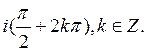
B) 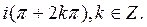
C) 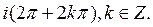
D) 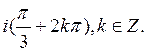
E) 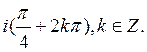
14) Функция 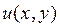 называется гармонической если:
называется гармонической если:
A) 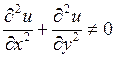
B) 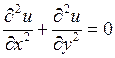
C) 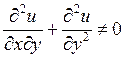
D) 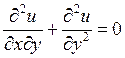
E) 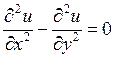
15) Коэффициент растяжения и угол поворота при отображении 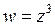 в точке
в точке 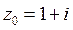 равны:
равны:
A) 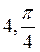
B) 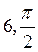
C) 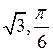
D) 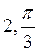
E) 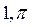
16) Коэффициент растяжения и угол поворота при отображении 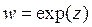 в точке
в точке 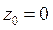 равны:
равны:
A) 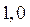
B) 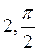
C) 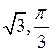
D) 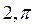
E) 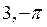
17) Коэффициент растяжения и угол поворота при отображении 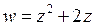 в точке
в точке 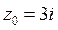 равны:
равны:
A) 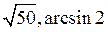
B) 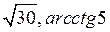
C) 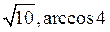
D) 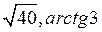
E) 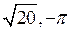
18) Интеграл 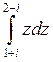 равен:
равен:
A) 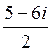
B) 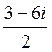
C) 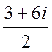
D) 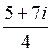
E) 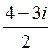
19) Интеграл 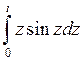 равен:
равен:
A) 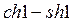
B) 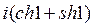
C) 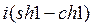
D) 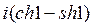
E) 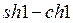
20) Интеграл 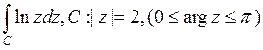 равен:
равен:
A) 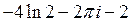
B) 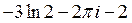
C) 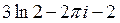
D) 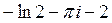
E) 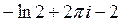
21) Интеграл 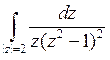 равен:
равен:
A) 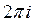 B)
B) 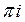 C)
C)  D)
D) 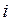 E)
E) 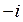
22) Интеграл 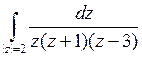 равен:
равен:
A) 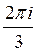
B) 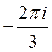
C) 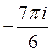
D) 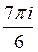
E) 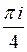
23) Интеграл 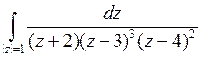 равен:
равен:
A) 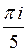
B) 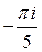
C) 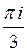
D) 0
E) 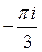
24) Определить радиус сходимости степенного ряда 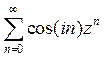 :
:
A) 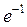
B) 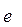
C) 
D) 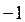
E) 1
25) Определить радиус сходимости степенного ряда 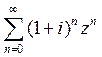 :
:
A) 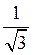
B) 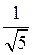
C) 1
D) 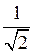
E) 0
26) Определить радиус сходимости степенного ряда 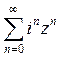 :
:
A) 1
B) 2
C) 3
D) 0
E) 4
27) Разложение 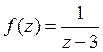 в ряд Тейлора, в окрестности точки
в ряд Тейлора, в окрестности точки 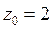 имеет вид:
имеет вид:
A) 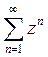
B) 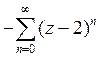
C) 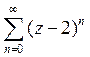
D) 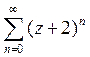
E) 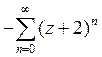
28) Функцию 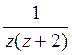 разложить в ряд Лорана в кольце
разложить в ряд Лорана в кольце 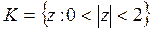 :
:
A) 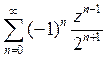
B) 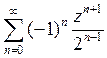
C) 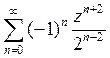
D) 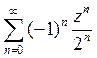
E) 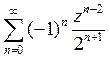
29) Вычислить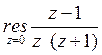 :
:
A) 1
B) 2
C) -2
D) -1
E) 0
30) Вычислить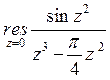 :
:
A) 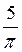
B) 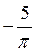
C) 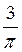
D) 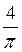
E) 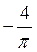
31) Вычислить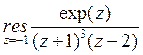 :
:
A) 0
B) 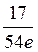
C) 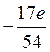
D) 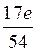
E) 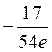
32) С помощью вычетов вычислить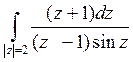 :
:
A) 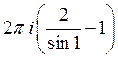 B)
B) 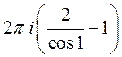 C)
C) 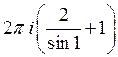 D)
D) 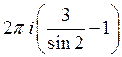 E)
E) 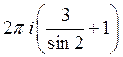
33) С помощью вычетов вычислить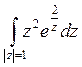 :
:
A) 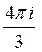 B)
B) 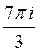 C)
C) 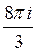 D)
D) 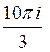 E) 0
E) 0
34) С помощью вычетов вычислить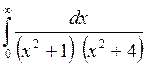 :
:
A) 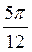
B) 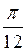
C) 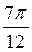
D) 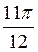
E) 0
35) С помощью теоремы Руше определить число корней уравнения 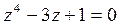 в круге
в круге 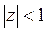 :
:
A) 2
B) 3
C) 1
D) 4
E) Нет корней
36) С помощью теоремы Руше определить число корней уравнения 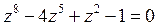 в круге
в круге 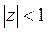 :
:
A) 3 B) 5 C) 7 D) 8 E) Нет корней
37) С помощью теоремы Руше определить число корней уравнения 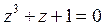 в круге
в круге 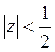 :
:
A) 2 B) 1 C) 3 D) 4 E) Нет корней
38) Указать область конформности для отображения 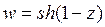 :
:
A) 
B)  {
{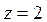 }
}
C)  {
{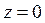 }
}
D)  {
{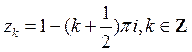 }
}
E) Нигде не конформно
39) Найти линейное отображение 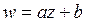 , оставляющее точку
, оставляющее точку 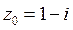 неподвижной и переводящее
неподвижной и переводящее 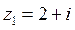 в
в 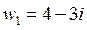 :
:
A) 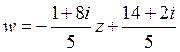
B) 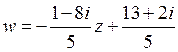
C) 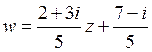
D) 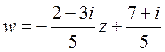
E) Не существует
40) Найти дробно-линейное преобразование, переводящее действительную ось в единичную окружность:
A) 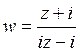 B)
B) 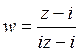 C)
C) 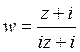 D)
D) 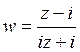 E)
E) 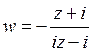


Ответы:
1) D 28) A
2) C 29) D
3) D 30) E
4) A 31) E
5) B 32) A
6) A 33) C
7) A 34) B
8) C 35) C
9) B 36) B
10) D 37) E
11) D 38) D
12) C 39) A
13) B 40) B
14) B
15) B
16) A
17) D
18) B
19) C
20) A
21) A
22) C
23) D
24) A
25) D
26) A
27) B
matematiku5.ru
Задание I. Найти все значения корня из комплексного числа. Сделать чертеж.
1. 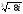 2.
2.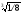 3.
3.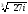 4.
4.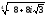 1.5.
1.5.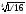
6. 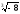 7.
7.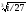 8.
8.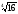 9.
9.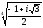 10.
10.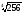
Задание II. Представить данные комплексные числа в алгебраической форме.
1. a) sin (π/4 + 2i) b) Arctg (- i/3) 2. a) cos (π/6 + 2i) b) Arcsin 4
3. a) sh (2 + iπ/4) b) Arctg (2 – i) 4. a) ch (2 + iπ/2) b) Arcsin (17/8)
5. a) sin (π/3 + i) b) Arch (3i) 6. a) cos (π/4 + i) b) Arch (-2)
7. a) sh (1 + iπ/2) b) Arccos (-5) 8. a) ch (1 – iπ) b) Arctg (-5i/3)
9. a) cos (π/4 – 2i) b) Arch (- 4i) 10. a) sh (2 – iπ) b) Arccos (- 3i)
Задание III. Начертить область, заданную неравенствами:
1. │z - 1│≤ 1; │z + 1│> 2 2. │z - 1│≥ 1 ; │z │< 2
3. │z - i│≤ 2; Re {z} > 1 4. │z + 1│≥ 1 ; │z + i│< 1
5. │z + 1│< 1; │z - i│≤ 1 6. │z + i│≤ 2 ; │z - i│> 2
7. │z – 1 - i│≤ 1; Re {z} ≥ 1; Im {z} > 1
8. │z – 1 + i│≥ 1; Re {z} < 1; Im {z} ≤ 1
9. │z - i│≤ 1; 0 < arg {z} < π/4 10. │z + i│> 1; - π/4 ≤ arg {z} < 0
Задание IV. Проверить, что u(x,y) (или v(x,y)) является действительной (или мнимой) частью аналитической функции f(z). Восстановить f(z) по известной действительной (или мнимой) части и данному значению f(z0).
1. u = x2 - y2 + x , f(0) = 0 2. u = x3 – 3xy2 + 1 , f(0) = 1
3. v = ex (y cos y + x sin y) , f(0) = 0 4. u = x2 - y2 - 2y , f(0) = 0
5. v = e-y sin x + y , f(0) = 1 6. v = ex cos y , f(0) = 1 + i
7. u = y – 2xy , f(0) = 0 8. v = x2 - y2 + 2x + 1 , f(0) = i
9. u = e-y cos x , f(0) = 1 10. v = 3x2 y – y3 , f(0) = 1
Задание V. Разложить данную функцию в ряд Лорана в окрестности точки z0 .
1. 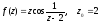 2.
2.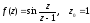
3. 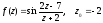 4.
4.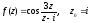
5. 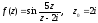 6.
6.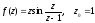
7. 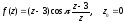 8.
8.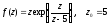
9. 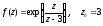 10.
10.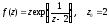
Задание VI. Вычислить определенные интегралы при помощи теории вычетов.
1. 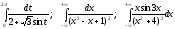
2. 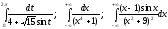
3. 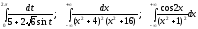
4. 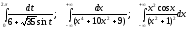
5. 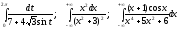
6. 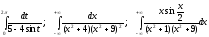
7. 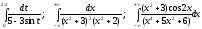
8. 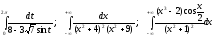
9. 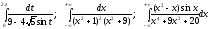
10. 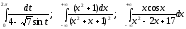
Задание I. Найти общий интеграл дифференциального уравнения с разделяющимися переменными.
1. a) 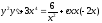 b)
b)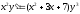
2. a) 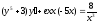 b)
b)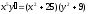
3. a) 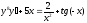 b)
b)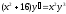
4. a) 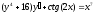 b)
b)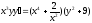
5. a) 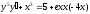 b)
b)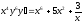
6. a) 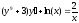 b)
b)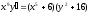
7. a) 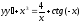 b)
b)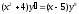
8. a) 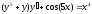 b)
b)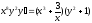
9. a) 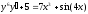 b)
b)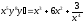
10. a) 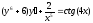 b)
b)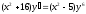
Задание II. Найти общий интеграл дифференциального уравнения первого порядка: a) однородного; b) линейного.
1. a) 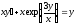 b)
b)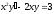
2. a) 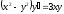 b)
b)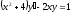
3. a) 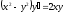 b)
b)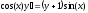
4. a) 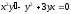 b)
b)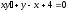
5. a) 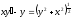 b)
b)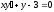
6. a) 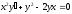 b)
b)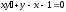
7. a) 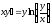 b)
b)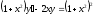
8. a) 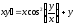 b)
b)
9. a) 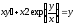 b)
b)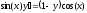
10. a) 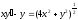 b)
b)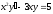
Задание III. Найти общий интеграл дифференциального уравнения высшего порядка.
1. a) 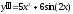 b)
b)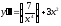
2. a) 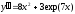 b)
b)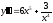
3. a) 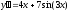 b)
b)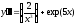
4. a) 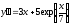 b)
b)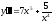
5. a) 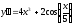 b)
b)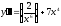
6. a) 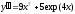 b)
b)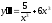
7. a) 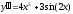 b)
b)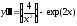
8. a) 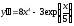 b)
b)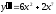
9. a) 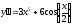 b)
b)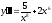
10. a) 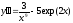 b)
b)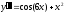
Задание IV. Найти частное решение линейного дифференциального уравнения второго порядка, удовлетворяющее заданным начальным условиям. Задача решается дважды: классическим и операционным методами.
1. 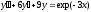 ;
;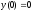
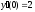
2. 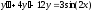 ;
;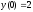
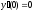
3. 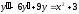 ;
;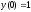
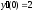
4. 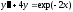 ;
;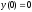
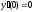
5. 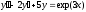 ;
;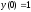
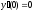
6. 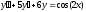 ;
;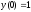
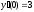
7. 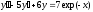 ;
;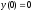
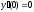
8. 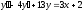 ;
;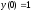
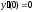
9. 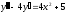 ;
;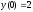
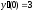
10. 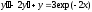 ;
;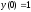
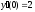
1. Письменный Д. Т. Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - 10-е изд. Испр. - М.: Айрис-пресс, 2011.- 608 с. (Эл. вариант - http://window.edu.ru/library).
2. Письменный Д. Т. Конспект лекций по высшей математике: Тридцать пять лекций. Ч. 1 / Д. Т. Письменный. - 10-е изд. - М.: Айрис-пресс, 2009.
3. Письменный Д. Т. Конспект лекций по высшей математике: Тридцать пять лекций. Ч. 1 / Д. Т. Письменный. - 9-е изд. - М.: Айрис-пресс, 2008.
4. Письменный Д. Т. Конспект лекций по высшей математике: тридцать пять лекций. Ч. 2 / Д. Т. Письменный. - 6-е изд. - М.: Айрис-пресс, 2008.
5. Кудрявцев Л. Д. Краткий курс математического анализа : учеб. для вузов. Т. 1. Дифференциальное и интегральное исчисления функций одной переменной. Ряды / Л. Д. Кудрявцев. - Изд. 3-е, перераб.- М.: Физматлит, 2008. (Эл. вариант - http://window.edu.ru/library).
6. Кудрявцев Л. Д. Краткий курс математического анализа : учеб. для вузов. Т. 2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ / Л. Д. Кудрявцев. - Изд. 3-е, перераб.- М.: Физматлит, 2008. (Эл. вариант - http://window.edu.ru/library).
7. Шипачев В. С. Основы высшей математики: учеб. пособие для вузов / В. С. Шипачев; под ред. А. Н. Тихонова. - 7-е изд. - М.: Высшее образование: Юрайт-Издат, 2009. (Эл. вариант - http://window.edu.ru/library).
8. Высшая математика в упражнениях и задачах: [учеб. пособие для втузов]: в 2 ч. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. - 7-е изд., испр. - М.: ОНИКС 21 век: Мир и Образование, 2008.
9. Высшая математика в упражнениях и задачах: В 2 ч. Ч. 2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. - 7-е изд., испр. - М.: ОНИКС 21 век: Мир и Образование, 2008.
10. Балдин К. В. Краткий курс высшей математики. — М.: ИТК «Дашков и К°», 2009 г. - 512 с. - Электронное издание. http://ibooks.ru/
studfiles.net
Контрольная работа
по теме: «ТФКП теория функций комплексного переменного» Задача 1. Найти аналитическую функцию  с известной мнимой частью
с известной мнимой частью

Решение.
Проверим, является ли функция  гармонической. Для этого вычислим частные производные:
гармонической. Для этого вычислим частные производные:
 и
и 
 , следовательно, функция
, следовательно, функция  является гармонической, и с помощью нее можно восстановить аналитическую функцию.
является гармонической, и с помощью нее можно восстановить аналитическую функцию.
Будем искать функцию  . Функция
. Функция  аналитическая, потому для функций
аналитическая, потому для функций  и
и  выполняются условия КРЭД:
выполняются условия КРЭД:
 .
.
Так как  , то
, то  .
.
Восстанавливаем функцию  с помощью интегрирования по
с помощью интегрирования по  :
:

Так как  , то
, то  .
.

Получили аналитическую функцию
 .
.

Найдем  из условия
из условия  .
.


Ответ:.  Задача 2. Вычислить интеграл, если Г – прямолинейный отрезок, соединяющий точку
Задача 2. Вычислить интеграл, если Г – прямолинейный отрезок, соединяющий точку  с точкой
с точкой  :
: 
Решение.


Найдем уравнение прямой, которая проходит через точки  :
:


Ответ: 
 , где
, где  .
. Решение.
Контур интегрирования, определяемый условием  , является окружностью с центром в точке
, является окружностью с центром в точке  и радиусом 2.
и радиусом 2.
Аналитичность подынтегральной функции  нарушается в точке
нарушается в точке  .
.
Для вычисления заданного интеграла будем использовать формулу  .
.
Найдем первую производную функции .
.


Задача 4. Разложить функцию  в ряд Лорана в каждом из колец аналитичности с центром в точке
в ряд Лорана в каждом из колец аналитичности с центром в точке  :
:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение.
Представим заданную функцию в виде суммы простых дробей:

Для нахождения неопределенных коэффициентов и приведем дроби к общему знаменателю:



1) Рассмотрим область 

Для разложения функции в ряд Лорана используем формулы убывающей геометрической прогрессии со знаменателем .
(1)
В окрестности нуля выполняется и , поэтому выполняем алгебраические преобразования функции:
.
Дроби и раскладываем по формуле (1):
Тогда для заданной функции
В области ряд Лорана функции содержит слагаемые только с положительными степенями (это правильная часть ряда Лорана).
2) Пусть область задается условием .В этой области верны оценки: и , поэтому для применения равенства (1) запишем функцию как:
.
Теперь дробь раскладывается как:
3) Пусть область задается условием .
В этой области верны оценки: и , поэтому для применения равенства (1) запишем функцию как:
Задача 5. Вычислить интеграл с помощью вычетов: .
Решение.
Найдем особые точки подынтегральной функции .
Нули знаменателя (нуль кратности 2) и (нуль кратности 1). Тогда для самой функции точка - полюс второго порядка, - простой полюс.
Точка не лежит внутри области , поэтому по основной теореме о вычетах
.
Так как точка - полюс порядка 2, то
.
Таким образом,
Задача 6. Вычислить интеграл .
Решение.
Введем замену переменной:
Знаменатель функции превращается в ноль при и . Точка лежит за пределами области .
.
Точка является простым полюсом для .
.
Ответ: .
Поделитесь с Вашими друзьями:
www.vossta.ru