Контрольная работа по геометрии четырехугольники: Контрольная работа по геометрии по теме «Четырехугольники»(8 класс)

Содержание

Контрольная работа по геометрии по теме «Четырехугольники»(8 класс)

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

1 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 40 см, а сторона АВ больше ВС на 4 см.

2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 3 раза.

3. Найти углы равнобедренной трапеции, если один из них равен 75º.

4. Найти диагонали прямоугольника АВСД, если , СД=4 см.

5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.

6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника ВОС.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

2 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 54 см, а сторона АВ больше ВС в 2 раза.

Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 120º.

4. Найти диагонали прямоугольника АВСД, если , АД=6 см.

5. В четырехугольнике сумма углов, прилежащих к каждой из двух смежных сторон, равна . Докажите, что АВСД – параллелограмм.

6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

3 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 80 см, а сторона АВ больше ВС на 5 см.

2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 4 раза.

3. Найти углы равнобедренной трапеции, если один из них равен 65º.

4. Найти диагонали прямоугольника АВСД, если , СД=15см.

5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.

6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника АОВ.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

4 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 24 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 128º.

4. Найти диагонали прямоугольника АВСД, если , АД=15 см.

5. В четырехугольнике сумма углов, прилежащих к каждой из двух смежных сторон, равна . Докажите, что MNPK– параллелограмм

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

5 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 48 см, а сторона АВ больше ВС на 6 см.

2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 5 раз.

3. Найти углы равнобедренной трапеции, если один из них равен 75º.

4. Найти диагонали прямоугольника АВСД, если , СД=17см.

5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.

6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника AОС.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

6 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 78 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 160º.

4. Найти диагонали прямоугольника АВСД, если , АД=5 см.

5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 3:4.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

7 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 36 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 140º.

4. Найти диагонали прямоугольника АВСД, если , АД=24см.

5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 3:5.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

8 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 82 см, а сторона АВ больше ВС на 3 см.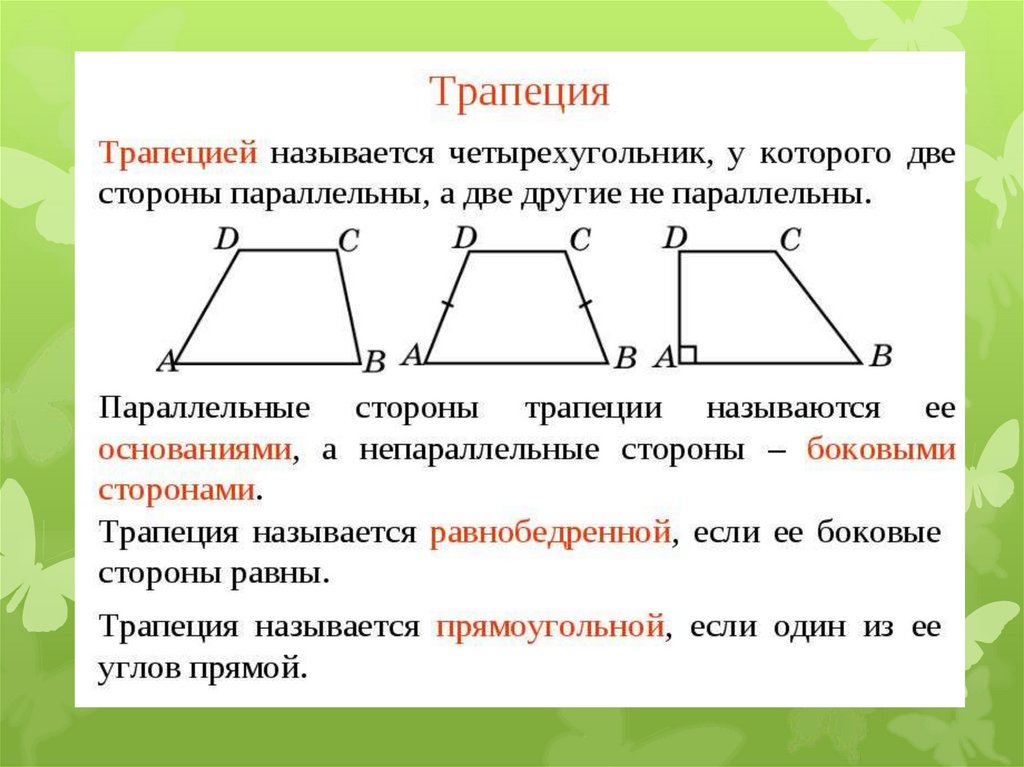

2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 9 раз.

3. Найти углы равнобедренной трапеции, если один из них равен 1 65º.

4. Найти диагонали прямоугольника АВСД, если , АД=16см.

5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.

6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника АОВ.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

10 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 42 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 100º.

4. Найти диагонали прямоугольника АВСД, если , АД=36см.

5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 1:5.

Контрольная работа по геометрии. 8 класс.

Четырехугольники

9 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 18 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 118º.

4. Найти диагонали прямоугольника АВСД, если , АД=5 см.

5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки на 6 частей.

Контрольная работа по геометрии. 8 класс.

Четырехугольники

11 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 90 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 128º.

4. Найти диагонали прямоугольника АВСД, если , АД=12 см.

5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки на 8 частей.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

12 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 60 см, а сторона АВ больше ВС в 2 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 144º.

4. Найти диагонали прямоугольника АВСД, если , АД=23 см.

5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 2:5.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

13 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 48 см, а сторона АВ больше ВС на 10 см.

2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 4 раза.

3. Найти углы равнобедренной трапеции, если один из них равен 65º.

4. Найти диагонали прямоугольника АВСД, если , СД=27см.

5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.

6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника AОС.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

14 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 60 см, а сторона АВ больше ВС в 4 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 164º.

4. Найти диагонали прямоугольника АВСД, если , АД=35 см.

5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 3:2.

Контрольная работа по геометрии. 8 класс.

Четырехугольники.

15 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 48 см, а сторона АВ больше ВС на 10 см.

2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 4 раза.

3. Найти углы равнобедренной трапеции, если один из них равен 65º.

4. Найти диагонали прямоугольника АВСД, если , СД=27см.

5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.

6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника AОС.

Контрольная работа по геометрии. 8 класс.

Четырехугольники

16 вариант.

1. Найти стороны параллелограмма АВСД, если его периметр равен 96 см, а сторона АВ больше ВС в 3 раза.

2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

3. Найти углы прямоугольной трапеции, если больший из них равен 140º.

4. Найти диагонали прямоугольника АВСД, если , АД=19 см.

5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки на 6 частей.

Контрольная работа по теме Четырехугольники по геометрии для 8 класса

УРОК 14

Контрольная работа

ЦЕЛИ:Проверить знания, умения и навыки учащихся по теме «Четырехугольник».

I Уровень (обязательный уровень).

Вариант 1

1. Диагонали прямоугольника АВСД пересекаются в точке О. найдите угол между диагоналями, если АВО=44.

2. В параллелограмме KMNP проведена биссектриса угла MKP, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник KME равнобедренный.

б) Найдите сторону KP, если ME=12см, а периметр параллелограмма равен 68 см.

Вариант 2

1. Диагонали ромба KMNP пересекается в точке О. Найдите углы треугольника КОМ, если угол MNP равен 80.

2. На стороне ВС параллелограмма АВСД взята точка М так, что АВ=ВМ.

а) Докажите, что АМ – биссектриса угла ВАД.

б) Найдите периметр параллелограмма, если длина стороны СД=8см, а СМ=4см.

II Уровень (средний уровень сложности)

Вариант 1

1. Периметр параллелограмма 50см одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.

2. Найдите углы между диагоналями прямоугольника, если каждый из них делит угол прямоугольника в отношении 4:5.

3. В трапеции АВСД диагональ ВД перпендикулярна боковой стороне АВ, АДВ=ВДС=30. Найдите длину АД, если периметр трапеции равен 60см.

4*. В параллелограмме АВСД биссектрисы углов АВС и ВСД пересекаются в точке М₁. На прямых АВ и СД взяты точки К и Р так, что А-В-К, Д-С-Р. биссектрисы углов КВС и ВСР пересекаются в точке М₂, М₁ М₂=8см. найдите АД.

Вариант 2.

1. Периметр параллелограмма 60 см. одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.

2. Угол, между диагоналями прямоугольника равен 80. Найдите угол между диагональю и меньшей стороной прямоугольника.

3. В трапеции АВСД диагональ АС перпендикулярна боковой стороне СД и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, Д=60.

4*. В параллелограмме АВСД АД=6см. биссектрисы углов АВС и ВСД пересекаются в точке М₁. На прямых АВ и СД взяты точки К и Р так, что А-В-К, Д-С-Р. Биссектрисы углов КВС и ВСР пересекаются в точке М₂. Найдите М₁ М₂.

III Уровень (сложный)

Вариант 1

1. В равнобедренной трапеции длина боковой стороны 2d, длины оснований 5d и 7d. Найдите углы трапеции.

2. В ромбе АВСД биссектриса угла ДСА перпендикулярна стороне АД. Найдите углы ромба.

3. Внутри квадрата АВСД выбрана точка М так, что треугольник АМД – равносторонний. Найдите угол АМВ.

4*. Биссектриса угла С параллелограмма АВСД пересекает сторону АД в точке М и продолжение стороны АВ за точку А в точке N. Найдите периметр параллелограмма, если АN=4см, ДМ=3см.

Вариант 2.

1. В равнобедренной трапеции боковая сторона равна меньшему основанию, а диагональ перпендикуляра боковой стороне. Найдите углы трапеции.

2. Высота ромба делит его сторону пополам. Найдите углы ромба.

3. Внутри квадрата АВСД выбрана точка N так, что треугольник ВNС равносторонний. Найдите угол NАД.

4*. В параллелограмме АВСД биссектриса угла А пересекает сторону ВС в точке F и продолжение стороны СД за точку – в точке Е. Найдите периметр параллелограмма, если ВF=2см, ЕС=3см.

Текст контрольной работы записан на доске.

Ученик выбирает уровень (по своему усмотрению).

ЗАКЛЮЧЕНИЕ.

Итак, смею надеяться, что цель моей работы достигнута – я постаралась доказать, что понимание контроля знаний учащихся предполагает широкий смысл. Систематический контроль знаний и умений учащихся – одно из основных условий повышения качества обучения.

В своей работе необходимо использовать не только общепринятые формы контроля (самостоятельные и контрольные работы и т.д.), необходимо их многообразие и разнообразие, что будет способствовать повышению заинтересованности учащихся в изучении геометрии.

Федеральное агентство по образованию

Нижегородский институт развития образования

Творческая работа:

«Контроль знаний учащихся на уроках математики»

Выполнила:

учитель математики

МОУ СОШ №6

г. Сергач

Сергачского района

Яшникова Елена Евгеньевна

г. Н.Новгород

2006г.

Приложение 1

Личные данные учителя

Яшникова Елена Евгеньевна

Дата рождения – 25 сентября 1959г.

Номер телефона для связи – 8-291-55703

Образование – Высшее педагогическое (Арзамасский государственный педагогический институт им.А.П.Гайдара)

Год окончания – 1982г.

Специальность – учитель математики

Место работы – МОУ СОШ № 6 г.Сергач

Должность — учитель математики

Квалификационная категория – первая, с 1997г.

План

Введение……………………………………………………………………1

Глава 1. Систематизация накопленных сведений по проблеме контроля знаний учащихся…………………………………………………………..2

§1. Цели контроля…………………………………………………………2

§2. Функции контроля…………………………………………………….3

п.2.1. Контролирующая функция…………………………………………3

п.2.2. Обучающая функция……………………………………………….3

п.2.3. Диагностическая функция…………………………………………4

п.2.4. Прогностическая функция…………………………………………4

п.2. 5. Развивающая функция……………………………………………..4

п.2.6. Ориентирующая функция………………………………………….4

п.2.7. Воспитывающая функция………………………………………….5

§3. Типы контроля…………………………………………………………5

п.3.1. Внешний контроль………………………………………………….5

п.3.1.1. Содержание контроля…………………………………………….6

п.3.1.2. Оценка и отметка………………………………………………….6

п.3.1.3. Формы контроля…………………………………………………..7

п.3.2. Взаимный контроль…………………………………………………8

п.3.3. Самоконтроль……………………………………………………….8

§4. Методы контроля………………………………………………………9

п.4.1. Устная проверка…………………………………………………….9

п.4.2. Проверка письменно – графических работ……………………… .9

п.4.3. Проверка практических работ…………………………………… 10

§5. Средства осуществления контроля………………………………… 10

п.5.1. Проверка домашнего задания…………………………………… 10

п.5.2. Математический диктант………………………………………… 11

п.5.3. Самостоятельная работа………………………………………….. 11

п.5.4. Контрольная работа………………………………………………. .12

ГлаваII. Использование различных форм контроля на уроках математики……………………………………………………………… ..13

§ 1. Тематическое планирование по теме «Четырехугольники»……….13

3 – 4 урокиПараллелограмм и трапеция. Свойства и признаки. (Изучение теории. Комбинированный урок с элементами беседы и упражнений закрепляющего характера)………………………………14

5 – 6 урокРешение задач по теме «Параллелограмм и трапеция» (Практикум)……………………………………………………………..18

10 урокРешение задач по теме «Прямоугольник, ромб, квадрат». (Практикум)……………………………………………………………..22

12 урокСеминар по изученной теме «Четырехугольники»…………25

13 урокЗачет по изученной теме «Четырехугольники»………..……31

14 урокКонтрольная работа (разноуровневая I-В-слабые;II-В-средние; III-В творческие задания)……………………………………………….36

Диагностика контроля………………………………………………………38

Диаграммы……………………………………………………………………40

Заключение…………………………………………………………………..42

Литература……………………………………………………………………43

Приложение 1……………………………………………………………. ….45

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/104173-kontrolnaja-rabota-po-teme-chetyrehugolniki-p

Контрольная работа по геометрии на тему Свойства четырехугольников

Контрольная работа по теме «Четырехугольники». Вариант №1.

Часть 1. В заданиях 1 – 9 вставьте пропущенные слова в определениях и теоремах.

1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков.

а) прямоугольник б) трапеция в) ромб г) четырехугольник

2.Прямоугольник – это ***, у которого все углы прямые.

а) трапеция б) четырехугольник в) ромб г) параллелограмм

3. Диагонали ромба являются *** его углов.

а) медианами б) высотами в) средними линиями г) биссектрисами

4. ***называется четырехугольник, у которого только две противолежащие стороны параллельны.

а) прямоугольник б) параллелограмм в) трапеция г) ромб

5. У параллелограмма противолежащие стороны равны, противолежащие *** равны.

а) вершины б) углы в) прямые г) отрезки

6. Ромб – это ***, у которого все стороны равны.

а) четырехугольник б) прямоугольник в) квадрат г) параллелограмм

7. *** параллелограмма пересекаются и точкой пересечения делятся пополам.

а) вершины б) стороны в) углы г) диагонали

8. Диагонали *** равны.

а) четырехугольника б) ромба в) прямоугольника г) трапеции

Часть 2. Решите задачи.

9. Один из углов параллелограмма равен 40°. Найдите остальные углы.

10. Найдите углы прямоугольной трапеции, если один из ее углов равен 20⁰

11. В ромбе одна из диагоналей равна стороне. Найдите углы ромба.

12. Найти диагонали прямоугольника АВСД, если , СД=4 см.

13.В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника ВОС.

14. Диагонали прямоугольника АВСД пересекаются в точке О, угол АВО равен 36 ⁰

Найдите угол АОД.

15. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 3 раза.

16. Диагонали ромба КМНР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МНР равен 80⁰.

17. В равнобокой трапеции сумма углов при большем основании равна 96⁰. Найдите углы трапеции.

18. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.

19. В параллелограмме КМНР проведена биссектриса угла МКР, которая пересекает сторону МН в точке Е. а) Докажите, что треугольник КМЕ равнобедренный. б) найдите периметр КМНР, если МЕ = 10 см, ЕН = 6 см.

Контрольная работа по теме: «Четырехугольники».Вариант №2.

Часть 1. В заданиях 1 – 9 вставьте пропущенные слова в определениях и теоремах.

1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков.

а) четырехугольник б) трапеция в) ромб г) прямоугольник

2.Прямоугольник – это ***, у которого все углы прямые.

а) трапеция б) параллелограмм в) ромб г) четырехугольник

3. Диагонали ромба являются *** его углов.

а) медианами б) высотами в) биссектрисами г) средними линиями

4. ***называется четырехугольник, у которого только две противолежащие стороны параллельны.

а) прямоугольник б) трапеция в) параллелограмм г) ромб

5. У параллелограмма противолежащие стороны равны, противолежащие *** равны.

а) вершины б) отрезки в) прямые г) углы

6. Ромб – это ***, у которого все стороны равны.

а) параллелограмм б) прямоугольник в) квадрат г) четырехугольник

7. *** параллелограмма пересекаются и точкой пересечения делятся пополам.

а) вершины б) диагонали в) углы г) стороны

8. Диагонали *** равны.

а) четырехугольника б) прямоугольника в) ромба г) трапеции

Часть 2. Решите задачи.

9. Один из углов параллелограмма равен 70°. Найдите остальные углы.

10. Найдите углы равнобокой трапеции, если один из ее углов равен 70⁰

11. Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 6 : 3. Найдите углы ромба.

12. Найти диагонали прямоугольника АВСД, если , АД=6 см.

13. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.

14. Диагонали прямоугольника МНКР пересекаются в точке О, угол МОН равен 64 ⁰

Найдите угол ОМР.

15. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на

16. Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол ВОА, если угол АОВ равен 65⁰.

17. В равнобокой трапеции сумма углов при меньшем основании равна 210⁰. Найдите углы трапеции.

18. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.

19. На стороне ВС параллелограмма АВСД взята точка М так, что АВ = ВМ . а) Докажите, что АМ – биссектриса угла ВАД. б) найдите периметр параллелограмма, если СД = 8 см, СМ = 6 см.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/380301-kontrolnaja-rabota-po-geometrii-na-temu-svojs

Контрольная работа по геометрии «Четырехугольники» 8 класс Макарычев

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ « ЧЕТЫРЕХУГОЛЬНИКИ». 1 ВАРИАНТ 1. Диагонали прямоугольника АВСД пересекаются в точке О, угол АВО равен 36 0 Найдите угол АОД. (3 б.) 2. Найдите углы прямоугольной трапеции, если один из ее углов равен 200.(2 б. ) 3. Диагонали ромба КМНР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МНР равен 800.(4 б.) 4. В равнобокой трапеции сумма углов при большем основании равна 960. Найдите углы трапеции.(4 б.) 5. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.(5 б.) 6. В параллелограмме КМНР проведена биссектриса угла МКР, которая пересекает сторону МН в точке Е. а) Докажите, что треугольник КМЕ равнобедренный. б) найдите периметр КМНР, если МЕ = 10 см, ЕН = 6 см.( 8 б.) критерии оценки « 3 » 5 – 8 баллов « 4 » 9 – 10 баллов « 5 » 12 – 13 баллов более 14 баллов – дополнительная оценка. КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ « ЧЕТЫРЕХУГОЛЬНИКИ». 2 ВАРИАНТ 1. Диагонали прямоугольника МНКР пересекаются в точке О, угол МОН равен 64 0 Найдите угол ОМР. (3 б.) 2. Найдите углы равнобокой трапеции, если один из ее углов равен 700.(2 б. ) 3. Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол ВОА, если угол АОВ равен 650.(4 б.) 4. В равнобокой трапеции сумма углов при меньшем основании равна 2100. Найдите углы трапеции.(4 б.) 5. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.(5 б.) 6. На стороне ВС параллелограмма АВСД взята точка М так, что АВ = ВМ . а) Докажите, что АМ – биссектриса угла ВАД. б) найдите периметр параллелограмма, если СД = 8 см, СМ = 6 см.( 8 б.) критерии оценки « 3 » 5 – 8 баллов « 4 » 9 – 10 баллов « 5 » 12 – 13 баллов более 14 баллов – дополнительная оценка.

Контрольная работа по геометрии 8 класс по теме «Четырехугольники»

Контрольная работа по теме «Четырехугольники» в логике ФГОС

Приложение 1

(для обучающихся)

На контрольной работе разрешается пользоваться:

— рабочими тетрадями;

— справочным материалом;

— таблицами и схемами;

— учебником и другой методической литературой.

Совет

Не стоит тратить много времени на поиск нужной информации вокруг. Поищите её в ячейках собственной памяти. Это может дать более продуктивный результат.

Стратегия поведения на контрольной работе

(планирование метапредметных результатов)

Просмотрите все задания контрольной работы и выпишите номера тех заданий, которые (по вашему мнению) вы решите быстро и правильно.
Выберите стратегию поведения на контрольной работе (отметьте галочкой или обведите в кружок):

А — начинаю решать контрольную работу с самых простых заданий, чтобы оставшееся время потратить на более сложные.

Б — начинаю решать более сложные задания контрольной работы, а оставшееся время я трачу на простые и легкие задания.

В — решаю все задания контрольной работы подряд, не пропуская ни одного задания.

Г — решаю задания контрольной работы подряд, а те задания, которые вызывают затруднения, пропускаю и возвращаюсь к ним только в конце.

Д — иная стратегия (опишите)________________________________________________________________________________________________________

_____________________________________________________________________________________________________________________________

3. После проверки контрольной работы поразмышляйте над тем, насколько правильную стратегию Вы избрали, помогла ли она вам в достижении желаемых результатов. Будете ли вы пользоваться этой стратегией всегда или смените её? Напишите свои выводы.

4. Внимательно изучите инструкцию

Контрольная работа по геометрии для 8 класса по теме: «Четырехугольники».

Инструкция по выполнению работы

Работа состоит из трёх частей и содержит 24 задания.

Часть I содержит 14 заданий базового уровня. Задания части I считаются выполненными, если учащийся представил верное решение (могут быть допущены пропуски в обосновании некоторых шагов решения) и ответ.

Часть II содержит 5 задания повышенного уровня и 1 задание высокого уровня сложности, соответствующих уровню возможностей обучающихся и доступных учащимся, хорошо успевающим по математике. При их выполнении надо записать полное решение и ответ.

Часть III содержит 5 задания, соответствующих уровню возможностей, но доступных учащимся с высоким уровнем математической подготовки, любящим занятия математикой. Это задания повышенной сложности, задания математических олимпиад.

На выполнение данной работы даётся 75 мин.

Проводится работа в два этапа. При этом реализуется основной принцип итоговой аттестации в основной школе: успешное выполнение заданий второй части работы не компенсирует отсутствие результата выполнения заданий первой части. Оценивание осуществляется способом «сложения» в логике ФГОС.

На первом этапе в первый день в течение 35 мин учащиеся выполняют только первую часть работы. В оставшиеся 15 минут урока после сдачи учащимися контрольных работ проводится проверка ответов и устанавливается, кто из школьников не преодолел «порог», позволяющий получить положительную отметку. Проводится анализ возможных причин затруднений школьников и допущенных ошибок.

На втором этапе во второй день в течение 40 минут учащиеся, не прошедшие «порог» в первый день, вновь пытаются это сделать, решая задания первой части (другой вариант). Остальные учащиеся выполняют задания второй и третьей части работы. При этом некоторые из них могут попытаться улучшить результат выполнения заданий первой части.

Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Система бонусов:

1 балл дополнительно за каждый новый способ решения любого задания, что дает возможность получения еще одной отметки «5» (личностный результат учащегося)

Желаем успеха!

Контрольная работа по геометрии 8 класс

Вариант 1

Часть 1 (1балл) (пишем только ответы)

1. Как называется отрезок, соединяющий две противолежащие вершины четырехугольника.

а) диагональ; б) сторона; в) медиана

2. Точка пересечения диагоналей четырехугольника является серединой каждой из них. Как называется такой четырехугольник (если диагонали не равны между собой).

а) параллелограмм; б) прямоугольник; в) трапеция

3. Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм.

а) ромб; б) прямоугольник; в) квадрат

4.АВСD – параллелограмм. Угол В равен 70°. Чему равен угол D?

а) 70° б)110° в) 35°

5.Периметр ромба равен 12 см. Чему равна длина его стороны.

а) 6 см; б) 3 см; в) 4 см

6. В параллелограмме МNКР угол N равен 150°. Чему равен угол М?

а) 50° б)30° в) 150°

7. Как называются стороны в прямоугольном треугольнике, которые образуют прямой угол.

а) катет; б) гипотенуза; в) высота

8. Запишите теорему Пифагора для прямоугольного треугольника АВС, у которого  А прямой.

а) ВС² = АВ² + АС²; б) АВ² = ВС² + АС²; в) АС² = АВ² + ВС²

Часть 2 (2 балла ) (полное решение)

1. Диагонали ромба равны 6 см и 8 см. Чему равна сторона данного ромба?

2. Один из углов параллелограмма в 3 раза больше другого. Найдите углы параллелограмма.

Критерии оценивания: 8 баллов – «3»

9 — 10 баллов – «4»

11- 12 баллов – «5»

Вариант 2

Часть 1 (1балл) (пишем только ответы)

1. Как называется отрезок, соединяющий две соседние вершины четырехугольника.

а) диагональ; б) сторона; в) медиана

2. Диагонали четырехугольника взаимно перпендикулярны. Как называется этот четырехугольник.

а) параллелограмм; б) прямоугольник; в) ромб

3. Две соседние стороны параллелограмма неравны и образуют прямой угол. Как называется такой параллелограмм.

а) ромб; б) прямоугольник; в) квадрат

4.АВСD – параллелограмм. Угол А равен 80°. Чему равен угол С?

а) 80° б) 100° в) 90°

5. Периметр ромба равен 16 см. Чему равна длина его стороны.

а) 8 см; б) 4 см; в) 5 см

6. В ромбе АВСD, угол В равен 130°. Чему равен угол А?

а) 50° б)30° в) 130°

7. Как называется сторона треугольника, лежащая против прямого угла.

а) катет; б) гипотенуза; в) высота

8. Запишите теорему Пифагора для прямоугольного треугольника MNK, у которого К прямой.

а)MN ² =KM ² +KN ²; б)KM ² =MN ² +KN ²; в)KN ² =KM ² +MN ²

Часть 2 (2 балла ) (полное решение)

1. Диагонали ромба равны 16 см и 12 см. Чему равна сторона данного ромба?

2. Один из углов параллелограмма на 50⁰ больше другого. Найдите углы параллелограмма.

Критерии оценивания: 8 баллов – «3»

9 — 10 баллов – «4»

11- 12 баллов – «5»

▶▷▶ контрольная работа по геометрии 8 класс номер 4 вариант 1

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	11-11-2018

контрольная работа по геометрии 8 класс номер 4 вариант 1 — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольные по геометрии 8 класс, Атанасян, скачать бесплатно mathematics-testscom/algebra- 8 -klass/kontrolnye Cached Контрольная работа № 1 Вариант i Часть А Запишите номера верных ответов к заданию 1 Геометрия в 7 классе, контрольные работы по Атанасяну за 1, 2 mathematics-testscom/algebra-7-klass-novoe/ Cached В 4 -й задаче третьей контрольной ( 1 вариант на параллельные прямые) сказано, что дан равнобедренный треугольник, но не указано какие именно стороны у него равны Контрольная Работа По Геометрии 8 Класс Номер 4 Вариант 1 — Image Results More Контрольная Работа По Геометрии 8 Класс Номер 4 Вариант 1 images контрольная работа по геометрии номер 1 вариант 1 9 класс wwwecaqisaxpgcombr/kontrolnaya-rabota-po-geometrii Cached Контрольная работа 1 ( вариант 1 — 4 ) Контрольная Ответы к учебнику ГДЗ по геометрии 7 класс Зив БГ 10 июн 2012 Методическая разработка (геометрия, 9 класс ) по теме: Контрольные по геометрии 9 класс Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС wwwmetod-kopilkaru/kontrolnie-raboti-po Cached Контрольная работа № 1 Г- 8 Вариант — 1 № 1 Диагонали прямоугольника abcd пересекаются в точке О, ∟АВО=36 0 Контрольные работы по геометрии 8 класс infourokru/kontrolnye_raboty_po_geometrii_ 8 Cached КОНТРОЛЬНЫЕ РАБОТЫ Геометрия 8 класс КОНТРОЛЬНАЯ РАБОТА № 1 Вариант 1 1 abcd – ромб Вычислите градусные меры углов ромба Итоговая работа по геометрии 7 класс infourokru/itogovaya_rabota_po_geometrii_7 Cached Скачать: итоговая работа по геометрии 7 класс Вариант 2 1 ) Сумма двух углов треугольника и внешнего угла к третьему равна Контрольные работы по геометрии (8 класс, УМК Атанасяна, 5 шт wwwslavkrugorg/kontrolnye-raboty-po-geometrii- 8 -klass Cached Контрольная работа № 4 1 вариант 1 ) Средние линии треугольника относятся как 2 : 2 : 4 , а периметр треугольника равен 45 см ГДЗ: Самостоятельные и контрольные работы по геометрии 7,8,9 yougdzcom/exesizephp?id=480 Cached ОПИСАНИЕ Готовые самостоятельные и контрольные работы по Геометрии для седьмого, восьмого и девятого классов от автора МА Иченская составлены в соответствии с учебником ЛС Атанасяна Контрольная работа по геометрии, 8 класс Тема: «ОКРУЖНОСТЬ» multiurokru/files/kontrol-naia-rabota-po Cached Разработка — содержание контрольной работы по геометрии для 8 класса по теме : «Окружность», 3 уровня, каждый уровень в двух вариантах Контрольная работа для 8 класса по теме: «Четырехугольники» globuss24ru/doc/kontrolynaya-rabota-dlya- 8 -k Cached Контрольная работа № 1 Четырехугольники 8 класс Вариант 1 1 На сторонах РК и МН Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 29,800 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

$AD≠AO$ а) ABOD Читать ещё Контрольные работы по геометрии 8 класса (1
( 8 класс ) урокрф › library…po_geometrii_8_klass_181759html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Читать ещё Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%)
$AD≠AO$ а) ABOD – параллелограмм б) ABOD – ромб в) AOCD – ромб г) ∠COD=∠AOD д) ∠AOD=∠BOA Часть В Запишите ответы к заданиям 2 и 3 2 Диагонали прямоугольника ABCD пересекаются в точке O Найдите периметр треугольника AOB

которые имеют 4 равнозначных по сложности варианта Во втором разделе школьники могут ознакомиться из 5-ью математическими диктантами Книга завершается 39 самостоятельными работами

применение (40%) и интеграцию (20%) предметных знаний II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Найти все углы параллелограмма 3Биссектриса угла прямоугольника делит его большую сторону пополам

9 yougdzcom/exesizephp?id=480 Cached ОПИСАНИЕ Готовые самостоятельные и контрольные работы по Геометрии для седьмого
каждый уровень в двух вариантах Контрольная работа для 8 класса по теме: «Четырехугольники» globuss24ru/doc/kontrolynaya-rabota-dlya- 8 -k Cached Контрольная работа № 1 Четырехугольники 8 класс Вариант 1 1 На сторонах РК и МН Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster
скачать бесплатно mathematics-testscom/algebra- 8 -klass/kontrolnye Cached Контрольная работа № 1 Вариант i Часть А Запишите номера верных ответов к заданию 1 Геометрия в 7 классе

контрольная работа по геометрии 8 класс номер 4 вариант 1 — Все результаты Найдите Контрольная работа 4 Вариант 1 № 3 Геометрия 8 Ответы на вопрос – Найдите Контрольная работа 4 Вариант 1 № 3 Геометрия 8 класс Зив БГ – читайте на Рамблер/класс Найдите Контрольная работа 1 Вариант 4 № 4 Геометрия 8 Ответы на вопрос – Найдите Контрольная работа 1 Вариант 4 № 4 Геометрия 8 класс Зив БГ – читайте на Рамблер/класс Найдите углы Контрольная работа 1 Вариант 1 № 1 Геометрия 8 Ответы на вопрос – Найдите углы Контрольная работа 1 Вариант 1 № 1 Геометрия 8 класс Зив БГ – читайте на Рамблер/класс ГДЗ по геометрии 8 класс самостоятельные и контрольные › Геометрия › 8 класс Решебник по геометрии за 8 класс авторы Иченская, Атанасян издательство Картинки по запросу контрольная работа по геометрии 8 класс номер 4 вариант 1 «cb»:9,»cl»:6,»ct»:9,»id»:»GvjJft67ZgNqPM:»,»ml»:»600″:»bh»:90,»bw»:130,»oh»:721,»ou»:» «,»ow»:1503,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_m3″,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcTPdnXrkjNQ5X5zji_1KH_V4L5jt3RyraBCRNFK8q_HD8p9VQSjKQ_ESm48″,»tw»:188 «cl»:6,»cr»:3,»ct»:3,»id»:»fPD9UBWZ-mxvVM:»,»ml»:»600″:»bh»:90,»bw»:88,»oh»:1585,»ou»:» «,»ow»:1510,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_m1″,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:92,»tu»:» \u003dtbn:ANd9GcQ0bX1_Y2Rsw2NzRgifoExSo7O8Rj2PXFosMUq-I0QCfDBKtUidOrjSlw»,»tw»:88 «cl»:3,»cr»:3,»ct»:6,»id»:»lzIMbF4MkUxVHM:»,»ml»:»600″:»bh»:90,»bw»:123,»oh»:1059,»ou»:» «,»ow»:1450,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_86″,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcSgDGmLNRVCLflA0aJnQx9VOEHjVIF5OmlVk25hS_AijlKd9V7s8nsvjQ»,»tw»:123 «cb»:6,»cl»:3,»cr»:3,»id»:»HuwThnqdanccgM:»,»ml»:»600″:»bh»:90,»bw»:123,»oh»:841,»ou»:» «,»ow»:1458,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_1b»,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcQcMYyFD6r3xqsFJmlT7w8UBQTUTmPnWUs-FMdIS6FGCdl3rObBnO7H94Ut»,»tw»:156 «id»:»w-pKLjomk-khCM:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:435,»ou»:» «,»ow»:1495,»pt»:»fs00infourokru/images/doc/79/96051/hello_html_7c»,»rh»:»infourokru»,»rid»:»w8Hz_iJwQvtRtM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcRmB0Ph_ra2WGpVPik4E4RgiR8dRzcwZblicr67C469b1HeTzzmt5olQDmJ»,»tw»:309 Другие картинки по запросу «контрольная работа по геометрии 8 класс номер 4 вариант 1» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Контрольные работы по геометрии 8 класс (Атанасян) — Инфоурок › Математика Похожие 21 нояб 2014 г — Скачать: контрольные работы по геометрии 8 класс (атанасян) Рейтинг материала: 4 , 1 (голосов: 88) В каждом варианте задания разделены на основной и повышенный уровень Номер материала: 142207 в решении любых вопросов связанных с работой и содержанием сайта Контрольные работы по геометрии 8 класс к учебнику Атанасяна › Математика Похожие 31 окт 2015 г — Контрольная работа № 1 Г – 8 Вариант – 4 1 Периметр параллелограмма 60 см Одна из его сторон на 6 см меньше другой Найдите Контрольные работы по геометрии 8 класс (по Атанасяну) obrazbaseru//888-kontrolnye-raboty-po-geometrii-8-klass-po-atanasyanu-2015021 Похожие Рейтинг: 4 — ‎10 голосов 13 февр 2015 г — Контрольная работа № 1 Четырехугольники; Контрольная работа №2 Площадь; Контрольная работа №3 Подобные треугольники ГДЗ, Ответы по Геометрии 8 класс Дидактические материалы Зив 23 дек 2014 г — Готовые Домашние Задания, Решебник по Геометрии 8 класс В 8-х классах, выполнение домашних работ по геометрии становится Контрольные работы К- 1 Вариант 1 Вариант 2 Вариант 3 Вариант 4 К-2 Видео 17:38 К-4 Соотношения между сторонами и углами треугольника Решайся! YouTube — 17 апр 2017 г 4:40 Контрольная работа 1 Вариант А1 Задание №3 algebra channel YouTube — 9 дек 2015 г 7:58 Контрольная работа по геометрии 8 класс Задание 1 Разбор задачи Галина Сосновская YouTube — 30 сент 2015 г Все результаты Контрольные по геометрии 8 класс, Атанасян, скачать бесплатно Рейтинг: 4 — ‎11 голосов 4 апр 2017 г — Контрольные работы по геометрии 8 класса ( 1 , 2, 3, 4 четверти) к учебнику Часть А Запишите номера верных ответов к заданию 1 1 Ответы на контрольную работу №2 для 8 класса Вариант I 1 а 2 25 3 «Итоговая контрольная работа по геометрии 8 класс» › Контрольная работа 24 мая 2017 г — Cкачать: «Итоговая контрольная работа по геометрии 8 класс » Итоговая контрольная работа по геометрии 8 класс к учебнику ЛС Атанасян по материалам ОГЭ 1 вариант 1 Найдите 4 Какое из следующих утверждений верно? 1 Все углы ромба равны 2 Номер материала, 4154 Диагностическая контрольная работа по геометрии, (8 класс) 21 нояб 2017 г — Учебно-дидактические материалы по Геометрии для 8 класса по УМК любой Вариант 1 1 Один из смежных углов на 450 больше другого 4 Периметр равнобедренного треугольника АВС с основанием ВС ГДЗ к дидактическим материаам по геометрии 8 класс Зив, Мейлер › ГДЗ › 8 класс › Геометрия › БГ Зив Похожие Решебник к дидактическим материалам по геометрии 8 класс Зив Теперь, чтоб выполнить даже простые из 8 вариантов 39 самостоятельных, не говоря уже о 4 разновидностях семи контрольных работ, нужно обращаться к ГДЗ к С- 1 1 2 3 4 5 6 7 8 С-2 1 2 3 4 5 6 7 8 С-3 1 2 3 4 5 6 7 8 С- 4 1 2 3 4 5 6 Геометрия 8 класс Контрольные работы Мельникова НБ allengorg/d/math/math2203htm Предисловие 4 Тематика контрольных работ 6 Задачи для подготовки к контрольной работе 7 Контрольная работа № 1 Четырехугольники 9 Вариант Годовая контрольная работа по геометрии для 8 класса по 1 февр 2017 г — Годовая контрольная работа по геометрии для 8 класса по учебнику ЛС Атанасян и др на 4 варианта Г – 8 Годовая контрольная работа 3 вариант 4 вариант № 1 Укажите номера неверных утверждений «Геометрия 8 класс Контрольные работы к учебнику Л С Интересные рецензии пользователей на книгу Геометрия 8 класс Рейтинг: + 1 Всего представлено 5 контрольных работ по 4 варианта в каждой Перед Сама контрольная работа содержит 6 заданий и состоит из 3 частей (1ч — задания с выбором ответа; 2ч — задачи, которые нужно / город номер Контрольные работы по геометрии 8 класс — Социальная сеть 20 мар 2012 г — Контрольная работа № 1 Четырехугольники Вариант 2 А1 Диагональ квадрата равна 4 см Сторона его равна диагонали другого [PDF] Итоговая контрольная работа по ГЕОМЕТРИИ 8 класс — Основная polaria-1ru/data/documents/Geometriya-8-kl-2018gpdf Структура варианта контрольной работы отвечает цели построения системы 4 Связь экзаменационной модели ОГЭ с моделью промежуточной аттестации Контрольная работа по геометрии содержит 8 заданий: в части 1 – 7 В ответ запишите номера выбранных утверждений без пробелов, Готовые Контрольные Работы По Геометрии 8 Класс Атанасян topikprocessweeblycom//gotovie-kontroljnie-raboti-po-geometrii-8-klass-atanasya Домашняя работа по геометрии за 8 класс к учебникам « Геометрия 7-9 по геометрии Атанасяна с ответами Варианты контрольных за 1 , 2, 3, 4 Входная контрольная работа по геометрии 8 класс — Видеоуроки 18 дек 2017 г — Контрольная работа представлена в виде теста, 2 варианта Ответы@MailRu: Пожайлуста, напишите ссылку на контрольные работы › Образование › Школы Похожие 4 ответа 3 нояб 2016 г — Тематические тесты по геометрии : 8 класс : к учебнику Л С Атанасяна и др 1 / 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK сторона МК = 8 см, RuО компанииРеклама Вакансии геометрия gkryukova40411s002edusiteru/vis_p12aa1html 1 комплект Контрольные работы по геометрии 8 класс 2 комплект ( 4 варианта ) Итоговый тест Самостоятельная работа «Пропорциональные отрезки Книга «Контрольные работы по геометрии 8 класс», Мельникова wwwbgshopru/Catalog/GetFullDescription?id=10404048&type=1 Контрольные работы по геометрии 8 класс в наличии Цена со скидкой 10% в интернет-магазине: 62 1 — 4 классы · Зачетные работы по математике Итоговая контрольная работа по геометрии в 4-х вариантах, 8 класс Похожие Итоговая контрольная работа по геометрии в 4 -х вариантах, 8 класс Скачать материал 1 вариант 8 класс 1 Площадь прямоугольника АВСD равна 15 Укажите в ответе номера верных утверждений в порядке возрастания : 1 ) 8 класса — контрольные работы по геометрии Атанасяна с ответами 8 класса — контрольные работы по геометрии Атанасяна с ответами Варианты контрольных за 1 , 2, 3, 4 четверти контрольная работа по геометрии 8 класс атанасян — SEAE Embu seaembuorg//kontrolnaia-rabota-po-geometrii-8-klass-atanasian-otvety-resheniexm контрольная работа по геометрии 8 класс атанасян ответы решение to Mail» data-nosubject=»[ No Subject]» data-timestamp=’short’ Help Account Info Yahoo Найдите Контрольная работа 4 Вариант 2 № 1 Геометрия 8 Ответы на Контрольные работы по геометрии (8 класс, УМК Атанасяна, 5 шт) uchkopilkaru//3613-kontrolnye-raboty-po-geometrii-8-klass-umk-atanasyana-5-sht Похожие 13 мар 2014 г — Катеты прямоугольного треугольника равны 6и 8 см Контрольная работа № 3 1 вариант 1 ) По рисA = B, СО = 4 , DO= 6, АО = 5 Геометрия 8 класс Контрольные работы по геоиетрии К учебнику Похожие В книжном интернет-магазине OZON можно купить учебник Геометрия 8 класс Контрольные работы по геоиетрии К учебнику Л С Атанасяна и др Итоговая аттестационная работа по геометрии 8 класс — PDF docplayerru/34103917-Itogovaya-attestacionnaya-rabota-po-geometrii-8-klasshtml Итоговая аттестационная работа по геометрии 8 класс 1 ) половине этой стороны 2) этой стороне 3) удвоенной этой стороне 4 ) сумме двух сторон треугольника 3 4 А9 Если Вы обвели не тот номер , то зачеркните обведённый номер крестиком и Контрольная работа 1 Четырехугольники Вариант 1 Контрольная работа 8 класс применение подобияdocx — Знанио Файл Контрольная работа 8 класс применение подобияdocx для Контрольная работа по геометрии «Применение подобия к решению задач» ( 8 класс ) Вариант 1 1 Значение выражения 2sin 30°- 1 равно: а) — 1 /2 ; б) – 1 4 Диагонали прямоугольника АВСD пересекаются в точке О Отрезок ОF – высота КОНТРОЛЬНАЯ РАБОТА № 1 — УРОКИ-КОНСПЕКТЫ ПО КОНТРОЛЬНАЯ РАБОТА № 1 — УРОКИ-КОНСПЕКТЫ ПО ГЕОМЕТРИИ 8 КЛАСС — подробных поурочных разработках по геометрии для 8 класса содержит варианты уроков, справочные и б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см 17 selfies that prove the stupidity knows no limit Контрольная работа по геометрии 8 класс Четырехугольники 1 Контрольная работа по геометрии 8 класса Подобие 1 вариант 1 Контрольная работа № 4 8 класс 1 вариант 1 На рисунке Найдите сторону АВ Ершова Голобородько 8 класс самостоятельные и контрольные › 8 класс › Геометрия игры · Правообладателям · ГДЗ / 8 класс / Геометрия / самостоятельные и контрольные работы ГДЗ К-10 Годовая контрольная работа 1 2 3 4 5 Контрольные работы по геометрии 8-го класса открытыйурокрф/статьи/641227/ Тематические контрольные работы по геометрии для 8-го класса составлены В части А необходимо выбрать правильный ответ из предложенных вариантов , задания Систематическое изложение курса позволяет начать работу по контрольных работ по геометрии 8 класса ( Приложения 1 , 2, 3, 4 , 5) ГДЗ по геометрии 8 класс Гусев Медяник дидактические — GDZme › 8 класс › Геометрия ГДЗ по геометрии 8 класс к дидактическим материалам Гусев Медяник, онлайн ответы из Представленные виды работ разделены на 4 варианта Рабочая программа по геометрии по учебнику ЛСАтанасян (8 7 янв 2015 г — На изучение математики в 8 классе согласно Федеральному базисному учебному плану отводится 5 часов в неделю (всего 170 часов) из них на Контрольная работа № 4 Вариант 1 Номер материала, 42336 Контрольные работы по геометрии 8 класс К учебнику Л С Похожие Контрольные работы по геометрии 8 класс К учебнику Л С Атанасяна и др Кроме того, по каждой теме дается набор заданий для подготовки к контрольной работе Каждый вариант включает задания трех видов: с выбором ответа, Часть 1 Федосова Н 275 ₽ В корзину География 9 класс Атлас Контрольные и самостоятельные работы по алгебре и геометрии 83,00 ₽ — ‎В наличии 8 класс Ко всем действующим учебникам ФГОС» (Журавлев СГ) в Издание ориентировано на работу с любыми учебниками по алгебре и геометрии из Федерального 3-й и 4 -й варианты рассчитаны на учащихся, проявляющих повышенный ISBN, 5-377-11023- 1 , 5-377-08225-5, 978-5-377 -08225-5 Геометрия 8 класс контрольная Контрольные работы по Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС Геометрия 8 класс контрольная Контрольная работа № 1 8 класс II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов Запишите номера верных ответов к заданиям 1 и 21 ГДЗ к контрольным и самостоятельным по геометрии 8 класс Зив › ГДЗ › 8 класс › Геометрия › дидактические материалы Зив Похожие Геометрия 8 класс Дидактические материалы Зив В части 1 размещены 7 разных контрольных работ, которые имеют 4 равнозначных по сложности ГДЗ по алгебре 8 класс Мордкович — онлайн решебник — uchimorg ГДЗ по алгебре 8 класс Мордкович — онлайн решебник § 1 Основные понятия § 4 Сложение и вычитание алгебраических дробей с разными знаменателями Домашняя контрольная работа № 1 Вариант 1 Вариант 2 Жохов, Чесноков, Шварцбурд — онлайн решебник · ГДЗ по геометрии 10- 11 класс Контрольная работа по геометрии 8 класс по теме — Продлёнка 22 июл 2016 г — Контрольная работа по геометрии 8 класс по теме: «Окружность» Наименование Вариант 1 Вариант 2 А1 Радиус 1 )8 2)16 3)2 4 )другой ответ А2 Найдите Укажите номера верных утверждений 1 )Длина Геометрия 9 класс: поурочные планы по учебнику А В Погорелова Киселёва Ю А — 2014 — ‎Education Ключ к тесту Задание Вариант 1 2 3 4 5 6 7 8 9 10 Вариант I 78 в 17 8 б 1 Итоговый тест по всему курсу геометрии 2 Итоговая контрольная работа 2 «РЕШУ ВПР»: математика–4 ВПР — 2019: задания, ответы Специально для наших читателей мы ежемесячно составляем варианты для самопроверки Если ваш школьный учитель составил работу и сообщил вам номер , введите его сюда 1 , 2, 3, 4 , 51, 52, 61, 62, 7, 8 , 91, 92, 10, 11 ГДЗ по алгебре для 9 класса Задачник АГ Мордкович Похожие ГДЗ к контрольным работам по алгебре за 9 класс Александрова ЛА 1 ; 2; 3; 4 ; 5; 6; 7; 8 ; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26 математика — Решим всё разворот боковой поверхности конуса сектор, с дугой 1 ,8π дм, а угловой размер дуги 120 градусов просмотры: 8 | математика класс не задан прямоугольник с периметром 4 дм, вращается вокруг прямой, на которой геометрия 7 класс Определите номер подъезда, в котором живет Слава ( L1) Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (50) Показать скрытые результаты В ответ на жалобу, поданную в соответствии с Законом США «Об авторском праве в цифровую эпоху», мы удалили некоторые результаты (1) с этой страницы Вы можете ознакомиться с жалобой на сайте LumenDatabaseorg Вместе с контрольная работа по геометрии 8 класс номер 4 вариант 1 часто ищут контрольная работа по геометрии 8 класс 4 четверть готовые контрольные работы по геометрии 8 класс атанасян готовые контрольные работы по геометрии 8 класс атанасян ответы контрольная работа по геометрии 8 класс четырехугольники контрольная работа номер 1 по геометрии 8 класс атанасян ответы контрольная работа по геометрии 8 класс номер 5 контрольная работа по геометрии 8 класс подобные треугольники годовая контрольная работа по геометрии 8 класс атанасян Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google

Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 ГДЗ по геометрии 8 класс самостоятельные eurokiorg › gdz…geometriya/8_klass…ichenskaya-274 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян В восьмом классе школьники продолжают изучать геометрию , углубляя и расширяя свои знания по предмету Если в седьмом классе элементарные понятия и аксиомы не вызывали трудностей, то 8 класс часто преподносит Читать ещё ГДЗ самостоятельные и контрольные работы по геометрии 8 класс Иченская, Атанасян В восьмом классе школьники продолжают изучать геометрию , углубляя и расширяя свои знания по предмету Если в седьмом классе элементарные понятия и аксиомы не вызывали трудностей, то 8 класс часто преподносит неприятные сюрпризы Они заключаются в неумении интегрировать формулы и доказательства в единое решение задания Как помочь восьмикласснику понять геометрию ? Отличный способ – ГДЗ по предмету Полностью решенное задание из хорошего учебного пособия поможет наработать базу, понять основные алгоритмы и принципы Скрыть 2 Контрольные работы по геометрии 8 класс к учебнику infourokru › …raboti-po-geometrii-klass…537738html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Инфоурок › Математика › Другие методич материалы › Контрольные работы по геометрии 8 класс к учебнику Контрольная работа № 1 Г- 8 Вариант — 1 № 1 Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360 Читать ещё Инфоурок › Математика › Другие методич материалы › Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС Контрольные работы по геометрии 8 класс к учебнику Атанасяна ЛС скачать материал библиотека материалов Контрольная работа № 1 Г- 8 Вариант — 1 № 1 Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360 Найдите угол AOD Скрыть 3 ГДЗ 1 контрольная работа / К-2 геометрия 8 класс GDZru › class-8/geometria/ziv-meiler/e:1-t:1-a:0/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ по геометрии 8 класс БГ Зив дидактические материалы контрольная работа / К-2 — 1 Авторы : БГ Зив, ВМ Мейлер Читать ещё ГДЗ по геометрии 8 класс БГ Зив дидактические материалы контрольная работа / К-2 — 1 Авторы : БГ Зив, ВМ Мейлер Издательство: Просвещение ← предыдущий следующий → Решебник / контрольная работа / К-2 / 1 ← предыдущий следующий → © GDZru 2018 Copyright Подписка About [email protected] google play app store Скрыть 4 Контрольная работа по геометрии 8 класс номер 4 вариант 1 — смотрите картинки ЯндексКартинки › контрольная работа по геометрии 8 класс номер 4 Пожаловаться Информация о сайте Ещё картинки 5 Контрольные работы по геометрии 8 класс infourokru › …po_geometrii_8_klass-342142htm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте КОНТРОЛЬНЫЕ РАБОТЫ Геометрия 8 класс КОНТРОЛЬНАЯ РАБОТА № 1 Вариант 1 ▲1 ABCD – ромб Вычислите градусные меры углов ромба 2 Периметр параллелограмма равен 30см Одна из его сторон больше другой на 3см 6 Геометрия 8 класс — контрольная работа 1 , вариант gdz-fiveru › Решебники › 8 класс › Геометрия › Зив › k14 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение варианта 4 контрольной работы 1 к учебнику за 8 класс по геометрии дидактические материалы авторов Зив, Мейлер ГДЗ по геометрии 8 класс Зив, Мейлер дидактические материалы, контрольная работа 1 , вариант 4 7 ГДЗ по геометрии для 8 класса Казаков В В — Тема reshebacom › gdz/geometrija/8-klass/kazakov/e:0-t…3 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробное решение Тема 1 Четырёхугольники / Контрольная работа 1 Вариант 1 4 по геометрии опорные конспекты для учащихся 8 класса , авторов Казаков В В 2016 Читать ещё Подробное решение Тема 1 Четырёхугольники / Контрольная работа 1 Вариант 1 4 по геометрии опорные конспекты для учащихся 8 класса , авторов Казаков В В 2016 показать содержание ← предыдущее Следующее → решебник / Тема 1 Четырёхугольники / Контрольная работа 1 Вариант 1 / 4 ← предыдущее Следующее → Подпишись на нашу группу Скрыть 8 Контрольные работы по геометрии 8 класса mathematics-testscom › algebra-8-klass…geometriya… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы по геометрии 8 класса (1, 2, 3, 4 четверти) к учебнику Атанасяна ЛС с ответами Контрольная работа № 1 Вариант I Часть А Запишите номера верных ответов к заданию 1 1 На рисунке ABCD – трапеция, $AB||OD$, $AO||CD$, $AD=OD$, $AD≠AO$ а) ABOD Читать ещё Контрольные работы по геометрии 8 класса (1, 2, 3, 4 четверти) к учебнику Атанасяна ЛС с ответами Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Все материалы проверены антивирусной программой Контрольная работа № 1 Вариант I Часть А Запишите номера верных ответов к заданию 1 1 На рисунке ABCD – трапеция, $AB||OD$, $AO||CD$, $AD=OD$, $AD≠AO$ а) ABOD – параллелограмм б) ABOD – ромб в) AOCD – ромб г) ∠COD=∠AOD д) ∠AOD=∠BOA Часть В Запишите ответы к заданиям 2 и 3 2 Диагонали прямоугольника ABCD пересекаются в точке O Найдите периметр треугольника AOB, если AB= 4 , AD=3, BD=5 Скрыть 9 ГДЗ к контрольным и самостоятельным по геометрии reshebacom › gdz/geometrija/8-klass/ziv Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробные решения и ответы к учебнику геометрии по контрольным и самостоятельным работам для 8 класс , авторов В части 1 размещены 7 разных контрольных работ , которые имеют 4 равнозначных по сложности варианта Во втором разделе школьники могут ознакомиться из 5-ью Читать ещё Подробные решения и ответы к учебнику геометрии по контрольным и самостоятельным работам для 8 класс , авторов БГ Зив, ВМ Мейлер, Просвещение 2014 год В части 1 размещены 7 разных контрольных работ , которые имеют 4 равнозначных по сложности варианта Во втором разделе школьники могут ознакомиться из 5-ью математическими диктантами Книга завершается 39 самостоятельными работами , которые предполагают 8 вариантов Самостоятельные работы Скрыть 10 Сборник контрольных работ по геометрии , ( 8 класс ) урокрф › library…po_geometrii_8_klass_181759html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Читать ещё Сборник Контрольных рабор по геометрии 8 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний II вариант 1 Стороны параллелограмма 4 см и 7 см Найдите периметр параллелограмма 2 Один из углов параллелограмма равен 48 Найти все углы параллелограмма 3Биссектриса угла прямоугольника делит его большую сторону пополам, меньшая сторона равна 7 см Найдите периметр прямоугольника 4 Один из углов ромба равен 120 , а диагональ, исходящая из вершины этого угла равна 12см Найдите периметр ромба 5Докажите, что если диагонали прямоугольника перпендикулярны, то он является квадратом Скрыть Гдз по Геометрии дидактические материалы за 8 класс GdzPutinacom › Гдз за 8 класс › Геометрия › Зив Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Геометрия 8 класс БГ Зив Дидактические материалы Подробные гдз и решебник по Геометрии для 8 класса дидактические материалы, авторы учебника: БГ Зив, ВМ Мейлер на 2017-2018 год Самостоятельные работы Вместе с « контрольная работа по геометрии 8 класс номер 4 вариант 1 » ищут: итоговая контрольная работа по геометрии 8 класс контрольная работа по алгебре 8 класс контрольные работы по геометрии 8 класс атанасян с ответами и решением контрольная работа по геометрии 7 класс контрольная работа по геометрии 9 класс входная контрольная работа по геометрии 8 класс атанасян диагонали прямоугольника abcd пересекаются в точке o годовая контрольная работа по геометрии 8 класс контрольная работа 1 по геометрии 8 класс гдз по геометрии 7-9 класс атанасян 1 2 3 4 5 дальше Bing Google Mailru Нашлось 373 млн результатов Дать объявление Регистрация Войти 0+ ЯндексБраузер с Алисой, которая готова поболтать Установить Закрыть Попробовать еще раз Включить Москва Настройки Клавиатура Помощь Обратная связь Для бизнеса Директ Метрика Касса Телефония Для души Музыка Погода ТВ онлайн Коллекции Яндекс О компании Вакансии Блог Контакты Мобильный поиск © 1997–2018 ООО «Яндекс» Лицензия на поиск Статистика Поиск защищён технологией Protect Вы всегда успеете к началу На Яндексе можно смотреть любимые телепередачи после эфира Перейти

Четырехугольник | Определение, формы и примеры (видео)

Определение четырехугольника

Четырехугольник — это четырехугольная плоская фигура, замыкающаяся в пространстве. Девять четырехугольников имеют названия: трапеция, трапеция, равнобедренная трапеция, параллелограмм, ромб, прямоугольник, квадрат, воздушный змей и дротик. Четырехугольники могут быть вогнутыми или выпуклыми, простыми или сложными, а также могут называться четырехугольниками.

Значение четырехугольника

Слово четырехугольник образовано из частей, состоящих из двух слов: префикса quad — , что означает четыре, и — угол .

Четырехугольник и четырехугольник — синонимы в геометрии. Четырехугольник тоже латинское, но означает «четыре стороны». Совершенно другое слово четырехугольник происходит от греческого происхождения, но также означает четырехгранную форму.

Форма четырехугольника

Четырехугольник — это четырехсторонний многоугольник с четырьмя внутренними углами. Боковые стороны прямые и соединяются, чтобы закрыть область.

Каждый раз, когда вы рисуете фигуру на плоском листе бумаги, обладающую этими свойствами, вы рисуете четырехугольник:

Четыре точки, соединенные четырьмя прямыми сторонами
Четыре внутренних угла
Закрытая территория

Угловой четырехугольник

Все выпуклые четырехугольники имеют четыре внутренних угла, диапазон измерения которых составляет от 0 ° до 180 °.Вогнутые четырехугольники будут иметь один внутренний угол, превышающий 180 °. Сумма внутренних углов для всех четырехугольников всегда равна 360 °.

В четырехугольниках, таких как прямоугольники и квадраты, внутренние углы должны составлять 90 °.

В ромбах, равнобедренных трапециях и параллелограммах внутренние углы разделятся на две пары равных углов.

В трапеции все внутренние углы будут неравными. Форму с разными размерами для каждого внутреннего угла можно также назвать неправильным четырехугольником.

Четырехугольник с одним прямым углом может быть трапецией или неправильным воздушным змеем.

Боковые четырехугольники

Каждый четырехугольник имеет четыре стороны, которые соединяют четыре вершины на плоской поверхности (плоскости), и каждая точка соединяется с двумя другими точками, образуя форму.

Длина сторон многое говорит о каждом четырехугольнике:

Если нет двух сторон одинаковой длины, у вас есть трапеция.
Если две стороны равной длины, у вас будет равнобедренная трапеция.
Если две пары противоположных сторон равны, у вас есть параллелограмм, прямоугольник или квадрат.
Если две пары соседних сторон равны, у вас воздушный змей или дротик.

Стороны должны состоять из отрезков прямых линий. Если стороны изогнутые, это не четырехугольник.

Примеры четырехугольников

Девять различных форм являются примерами четырехугольников:

Трапеция
Трапеция
Равнобедренная трапеция
Воздушный змей
Дротик
Параллелограмм
Прямоугольник
Ромб
Квадрат

Самый простой из возможных четырехугольников — это трапеция , которая должна иметь только четыре прямые стороны и закрывать пространство.

Двумя наиболее распространенными примерами четырехугольника являются квадраты и прямоугольники; оба технически являются трапециями. Эти две плоские формы имеют две пары параллельных сторон.

Виды четырехугольников

Четырехугольники могут быть вогнутыми или выпуклыми. Вогнутый четырехугольник имеет один внутренний угол больше 180 °.

Выпуклый четырехугольник не имеет внутреннего угла больше 180 °, поэтому кажется, что все его стороны выдвигаются наружу. Все остальные формы, которые мы видели, за исключением дротика, были выпуклыми четырехугольниками.

Частный случай четырехугольников может быть получен, если две стороны пересекаются друг с другом. Это сложные четырехугольники, точнее сложных четырехугольников .

Эти геометрические формы самопересекаются. У них два острых (менее 90 °) внутренних угла и два внутренних угла, превышающих 180 ° и кажущихся выходящими за пределы формы!

Четырехугольники (или четырехугольники) могут интересно сочетаться друг с другом. Например, квадрат действительно несколько вещей:

Это трапеция, потому что у нее четыре прямые стороны, закрывающиеся на участке
Это воздушный змей, потому что у него две пары совпадающих сторон, которые примыкают друг к другу.
Это ромб, потому что его четыре стороны равны по длине.
Это параллелограмм, потому что у него одна пара противоположных сторон параллельна

Однако наиболее точное описание состоит в том, что это квадрат.

Четырехугольник викторина

Трапеция — это четырехугольник?
Сколько сторон у четырехугольника?
Квадрат — это четырехугольник?
Назовите хотя бы один четырехугольник, который представляет собой , а не параллелограмм.

Мы знаем все углы. Не смотрите на ответы, пока не попробуете все вопросы!

Трапеция — это четырехугольник. Это плоская форма с четырьмя прямыми сторонами, которые закрываются в пространстве.
У четырехугольника четыре стороны.
Квадрат — это четырехугольник.
Четырехугольники, которые являются параллелограммами , а не , — это воздушные змеи, дротики, трапеции, сложные четырехугольники и трапеции.
Четырехугольник на изображении — это трапеция, потому что у него четыре прямые стороны, закрывающиеся в области. Остальные не являются четырехугольниками, потому что они не закрываются в пространстве, имеют слишком мало сторон, слишком много сторон или имеют изогнутые стороны.

Следующий урок:

Параллелограмм

Расчет длины диагонали четырехугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

UVA11455 Вот мой четырехугольник 【Геометрия】 — Программист искал

Любой квадрат — это прямоугольник, любой прямоугольник — это четырехугольник, а любой четырехугольник состоит из четырех сторон.Но не все прямоугольники являются квадратами, не все четырехугольники являются прямоугольниками, и не все наборы из четырех сторон являются четырехугольниками.
У нас длина четырех сторон. Вы должны определить, могут ли они образовывать квадрат. Если нет, определите, могут ли они образовывать прямоугольник. Если нет, определите, могут ли они образовать четырехугольник.
Входные данные
Первая строка входных данных содержит целое число, указывающее количество тестовых примеров.
Для каждого тестового примера есть строка с четырьмя положительными целыми числами от 0 до 2 ³⁰.
Выходные данные
Для каждого тестового примера выходные данные должны состоять из строки с текстом «квадрат», «прямоугольник», «четырехугольник» или «банан», если стороны соответствующего случая могут образовывать квадрат, прямоугольник , четырехугольник или нет соответственно.
Пример ввода
4
10 8 7 6
9 1 9 1
29 29 29 29
5 12 30 7
Пример вывода
четырехугольник
прямоугольник
квадрат
банан

Ссылка на вопрос ： UVA11455 Вот мой четырехугольник
Краткое описание проблемы : Учитывая 4 стороны четырехугольника, оцените фигуру, образованную им.
анализ проблем : Простые вопросы не объясняют.
Описание процедуры : (немного)
Ссылка : (немного)
Надпись : (немного)

Программа

AC на языке C ++ выглядит следующим образом:

 

# включить <бит / stdc ++. h>

используя пространство имен std;

int a [4];

int main ()
{
    int t;
    scanf ("% d", & t);
    while (t--) {
        scanf ("% d% d% d% d", & a [0], & a [1], & a [2], & a [3]);

        sort (a, a + 4);

        если (a [0] == a [1] && a [1] == a [2] && a [2] == a [3]) printf ("квадрат \ п");
        иначе, если (a [0] == a [1] && a [1]! = a [2] && a [2] == a [3]) printf ("прямоугольник \ n");
        иначе, если (a [0] + a [1] + a [2] <= a [3]) printf ("банан \ n");
        иначе printf ("четырехугольник \ п");
    }

    возврат 0;
}

Почему негоны и треугольники такие плохие?

Это вопрос, который, вероятно, задают многие новички в области 3D-моделирования: «В чем проблема с негонами и треугольниками и почему мне всегда приходится перенаправлять мою геометрию, чтобы создать четырехугольник?» Да, негры и треугольники обычно плохо отзываются, но для этого есть веская причина.Хотя изменение маршрута топологии в вашей модели иногда может показаться утомительной задачей, обычно оно того стоит, и ваша модель станет намного лучше после небольшой очистки.

Что такое нгон? Если вы не знакомы с тем, что такое негон, давайте очень быстро рассмотрим этот вопрос, чтобы вы могли лучше понять этот вопрос. Ngon - это грань или многоугольник, состоящий из пяти или более сторон или ребер, соединенных пятью или более вершинами. Все, что находится над квадратом (4 стороны), считается негоном.

Что такое треугольник? Треугольник - это то, что вы, вероятно, уже понимаете, и это грань, состоящая всего из 3 сторон или ребер, соединенных 3 вершинами. Прямо посередине этих двух многоугольников находится четырехугольник, представляющий собой грань или многоугольник, состоящий из четырех сторон или ребер, соединенных четырьмя вершинами. Вы, наверное, слышали, что это тип многоугольника, который вы должны стремиться создать. Однако по мере того, как вы добавляете контуры краев, разрешение и формируете геометрию так, чтобы сделать то, что вы хотите сделать, почти невозможно , а не , столкнуться с несколькими треугольниками или негонами.Так зачем тратить время на изменение маршрута топологии и создание сетки на основе квадратов? Давайте рассмотрим несколько основных причин, по которым следует избегать использования негонов и треугольников.

Деформации Негоны обычно вызывают множество проблем при деформации модели. Если ваша модель будет передана по конвейеру для настройки и анимации, то топология на основе квадратов является обязательной. Треугольники также могут вызывать эту проблему. Хотя треугольники немного мягче и не так плохи, как ngons, они все же могут вызывать некоторые проблемы во время анимации.Неочищенная топология означает, что модель будет отправлена вам для исправления. Хотя вы можете работать над своим собственным проектом, будучи моделистом, риггером и аниматором, вы определенно устанавливаете свои собственные правила на этапе моделирования. Но вы быстро узнаете из первых рук проблемы, которые возникают при попытке анимировать тяжелую модель ngon.

Проблемы с отрисовкой Негоны и треугольники также могут вызывать некоторые странные проблемы во время рендеринга. Хотя в области просмотра все может выглядеть хорошо, после рендеринга вы можете заметить очень странные артефакты.Единственный способ действительно избежать этого - вернуться и очистить негоны на вашей модели.

Сглаживание И негоны, и треугольники вызывают проблемы при попытке сгладить модель. Дополнительные вершины и ребра могут вызвать очень странную неровность модели, которой в противном случае не было бы, если бы модель была составлена из четырехугольников.

Квадроциклы принимаются во всех отраслях промышленности Очень важная причина, по которой следует избегать негонов и треугольников, заключается в том, что квадраты действительно являются общепринятыми полигонами.Если вы отправляете демонстрационную катушку для 3D-моделирования с наложением каркаса, а топология вашей модели состоит из несовпадения четырехугольников, треугольников и негонов с разными границами, то вы отправляете рекрутеру сообщение о том, что вы этого не сделаете. потратьте время на правильную топологию вашей модели для работы в других областях конвейера, таких как текстурирование, оснастка и анимация. Конечно, есть случаи, когда негоны можно использовать, например, на идеально ровной поверхности, и случаи, когда треугольников просто невозможно избежать, или, может быть, вы можете скрыть треугольники в месте, где зритель никогда их не увидит.Но вы должны попытаться потратить время на то, чтобы очистить вашу модель и перенаправить любые типы полигонов для решения проблем в квадраты. Если у вас есть вопросы, на которые вы хотите получить ответы, обязательно оставьте их в комментариях ниже!

Определение четырехугольника Merriam-Webster

quad · run · gle | \ ˈKwä-ˌdraŋ-gəl \

2а : 4-сторонний корпус, особенно в окружении зданий.

б : здания, окружающие четырехугольник

3 : участок страны, представленный одной из серии листов карт.

Параллелограмм, формулы параллелограмма

Четырехугольник с двумя парами параллельных сторон называется параллелограммом .
Каждая пара противоположных сторон параллелограмма равны.

Чтобы определить, является ли четырехугольник параллелограммом, мы будем использовать следующие критерии:

- если две пары противоположных сторон в четырехугольнике равны, то этот четырехугольник является параллелограммом;
- если две противоположные стороны в четырехугольнике параллельны и равны, то этот четырехугольник является параллелограммом;
- если в четырехугольнике диагонали делят друг друга пополам, то этот четырехугольник является параллелограммом;

Четырехугольник с четырьмя прямыми углами называется прямоугольником .
Справедливо следующее утверждение: Если параллелограмм является прямоугольником, то его диагонали равны по длине.
Наоборот, если диагонали параллелограмма равны по длине, то этот параллелограмм является прямоугольником.

Параллелограмм, у которого две смежные равные стороны, называется ромбом . Справедливо следующее утверждение о ромбе:
Если параллелограмм является ромбом, то его диагонали перпендикулярны.
И наоборот, если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.

Квадрат можно рассматривать как прямоугольник с равными смежными сторонами или как ромб с прямым углом.
Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.

Формулы параллелограмма

∠A + ∠B = 180 ° и ∠A + ∠D = 180 °
∠A = ∠C, ∠B = ∠D

Периметр параллелограмма:

P = 2a + 2b

Площадь параллелограмма (ромба):

$ A = AB \ cdot DE = BC \ cdot DF $
$ A = AB \ cdot AD \ sin \ alpha $
$ A = \ frac12 AC \ cdot BD \ sin \ gamma $

Соотношение сторон и диагоналей параллелограмма (ромба):

p ² + q ² = 2 (a ² + b ²)
или
AC ² + BD ² = 2 (AB ² + BC ²)

Стратегии и практические вопросы по геометрии

От 25 до 30% математического раздела SAT будет включать геометрию, и большинство этих вопросов будут касаться полигонов в той или иной форме.Многоугольники бывают разных форм и размеров, и вам нужно будет уверенно разбираться в них, чтобы справиться с вопросами SAT в день теста.

К счастью, несмотря на их разнообразие, многоугольники зачастую менее сложны, чем кажутся, и несколько простых правил и стратегий помогут вам быстро решить эти вопросы по геометрии.

Это будет ваше полное руководство по полигонам SAT - правила и формулы для различных полигонов, типы вопросов, которые вам будут задавать о них, и лучший подход к решению этих типов вопросов.

Что такое многоугольник?

Прежде чем говорить о формулах многоугольника, давайте посмотрим, что же такое многоугольник.

Многоугольник - это любая плоская замкнутая форма, состоящая из прямых линий. «Замкнутость» означает, что все линии должны соединяться, и ни одна сторона многоугольника не может быть изогнута.

Полигоны

НЕ Полигоны

Многоугольники делятся на две большие категории - правильные и неправильные. У правильного многоугольника все стороны равны и все углы равны , а у неправильных многоугольников - нет.

Правильные многоугольники

Неправильные многоугольники

(Примечание: большинство многоугольников на SAT, состоящих из пяти или более сторон, будут правильными многоугольниками, но всегда проверяйте это дважды! В вопросе вам будет сказано, является ли форма "правильной" или "неправильной". . ")

Различные типы многоугольников названы по количеству сторон и углов.Треугольник состоит из трех сторон и трех углов («три» означает три), четырехугольник состоит из четырех сторон («четырехугольник» означает четыре), пятиугольник состоит из пяти сторон («пента» означает пять), и поэтому на.

Большинство многоугольников, которые вы увидите на SAT (хотя и не все), будут либо треугольниками, либо своего рода четырехугольниками. Треугольников во всех их формах описаны в нашем полном руководстве по треугольникам SAT, поэтому давайте посмотрим на различные типы четырехугольников, которые вы увидите в тесте.

Что касается многоугольников, вы можете заметить, что многие определения подходят для других определений.

Четырехугольники

Есть много различных типов четырехугольников, большинство из которых являются подкатегориями друг друга.

Параллелограмм

Параллелограмм - это четырехугольник, в котором все противоположные стороны параллельны и конгруэнтны (равны) друг другу. Длина может отличаться от ширины, но обе ширины будут равны и обе длины будут равны.

Параллелограммы

отличаются тем, что их противоположные углы будут равны, а их смежные углы будут дополнительными (то есть любые два смежных угла в сумме дадут 180 градусов).

Прямоугольник

Прямоугольник - это особый вид параллелограмма, в котором каждый угол равен 90 градусам. Длина и ширина прямоугольника могут быть одинаковыми или отличаться друг от друга.

Площадь

Если прямоугольник имеет одинаковую длину и ширину, он называется квадратом.Это означает, что квадрат является разновидностью прямоугольника (который, в свою очередь, является разновидностью параллелограмма), но НЕ все прямоугольники являются квадратами.

Ромб

Ромб - это тип параллелограмма, в котором все четыре стороны равны, а углы могут иметь любую меру (при условии, что их смежные стороны составляют в сумме 180 градусов, а их противоположные углы равны). Подобно тому, как квадрат является разновидностью прямоугольника, но не все прямоугольники являются квадратами, ромб является разновидностью параллелограмма (но не все параллелограммы являются ромбами).

Трапеция

Трапеция - это четырехугольник, у которого есть только один набор параллельных сторон. Две другие стороны не параллельны.

Воздушный змей

Воздушный змей - это четырехугольник, у которого две пары равных сторон пересекаются друг с другом.

А вот и формулы - мвахаха!

Формулы многоугольников

Хотя существует много различных типов многоугольников, их правила и формулы основаны на нескольких простых базовых идеях.Пройдемся по списку.

Формулы площади

Большинство вопросов о многоугольниках на SAT требуют от вас найти площадь или периметр фигуры. Это самые важные формулы площади, которые вам нужно запомнить во время теста.

Площадь треугольника

$$ (1/2) bh $$

Площадь треугольника всегда равна половине основания, умноженной на высоту. В прямоугольном треугольнике высота будет равна одной из ножек. В любом другом типе треугольника вы должны опускаться на свою высоту перпендикулярно от вершины треугольника к основанию.2 \ или {lw} $$

Поскольку все стороны квадрата равны, вы можете найти площадь, умножив длину на ширину или просто возведя в квадрат одну из сторон.

Площадь прямоугольника

$$ lw $$

Для любого прямоугольника, не являющегося квадратом, вы всегда должны умножать основание на высоту, чтобы найти площадь.

Площадь параллелограмма

$$ bh $$

Определение площади параллелограмма в точности такое же, как определение площади прямоугольника.Поскольку параллелограмм может наклоняться в сторону, мы говорим, что должны использовать его основание и высоту (вместо длины и ширины), но принцип тот же.

Вы можете понять, почему эти два действия равны, если бы вы преобразовали параллелограмм в прямоугольник, опустив прямую высоту и сдвинув основание.

Площадь трапеции

$$ [(l_1 + l_2) / 2] ч $$

Чтобы найти площадь трапеции, вы должны найти среднее значение двух параллельных оснований и умножить его на высоту трапеции.

Теперь давайте посмотрим на пример:

На рисунке WXYZ представляет собой прямоугольник с $ \ ov {WA} = \ ov {BZ} = 4 $. Площадь заштрихованной области равна 32. Какова длина $ \ ov {XY} $?

[Примечание: цифра не в масштабе]

А . 6
Б . 8
С . 12
Д . 16
Е . 20

Во-первых, давайте заполним данную информацию.

Наша заштрихованная фигура представляет собой трапецию, поэтому давайте воспользуемся формулой для определения площади трапеции.

$ = [(l_1 + l_2) / 2] ч

Теперь, если мы назовем самую длинную базу q, самая короткая база будет $ q − 4−4 $ или $ q − 8 $. (Почему? Потому что самая короткая нога равна самой длинной минус две заданные нами длины, равные 4).

Это означает, что теперь мы можем подставить наши значения для длин ног. Кроме того, нам также задаются высота и площадь, поэтому мы можем подставить все наши значения в формулу, чтобы найти длину нашей самой длинной стороны q.

32 доллара = [(q + (q − 8)) / 2] 2

долларов

32 доллара = (2q + 2q − 16) / 2

долларов

$ 64 = 4q − 16 $

80 долларов = 4 кв.

долларов

$ 20 = q $

Длина $ \ ov {XY} $ (которую мы обозначили как $ q $) равна 20.

Наш окончательный ответ - E , 20.

В общем, лучший способ найти площадь различных типов многоугольников - это преобразовать многоугольник в более мелкие и более управляемые формы. Это также поможет вам, если вы забудете свои формулы в день проверки.

Например, если вы забыли формулу площади трапеции, превратите трапецию в прямоугольник и два треугольника и найдите площадь для каждого из них.

Давайте посмотрим, как решить указанную выше проблему, используя вместо этого этот метод.

Нам говорят, что площадь трапеции равна 32. Мы также знаем, что можем найти площадь треугольника, используя формулу $ {1/2} bh $. Итак, давайте найдем площади для обоих наших треугольников.

$ {1/2} bh $

$ {1/2} (4) (2)

{1/2} 8 долларов

$ 4 $

Каждый треугольник стоит 8, поэтому вместе оба треугольника будут:

$ 4 + 4 $

$ 8 $

Теперь, если мы добавим площадь наших треугольников к нашей заданной площади трапеции, мы увидим, что площадь нашего полного прямоугольника равна:

$ 32 + 8 $

$ 40 $

Наконец, мы знаем, что находим площадь прямоугольника, умножая длину на ширину.У нас задана ширина 2, поэтому длина будет:

40 долларов = lw

долларов

40 долларов = 2 литра

долларов

20 = l

Длина прямоугольника (линия $ \ ov {XY} $) будет равна 20.

И снова наш окончательный ответ - E , 20.

Всегда помните, что есть много разных способов найти то, что вам нужно, поэтому не бойтесь использовать ярлыки!

Какой бы путь решения вы ни выбрали, зависит от того, как вы предпочитаете работать.

Формулы углов

Независимо от того, является ли ваш многоугольник правильным или неправильным, сумма его внутренних градусов всегда будет соответствовать правилам этого конкретного многоугольника.Каждый многоугольник имеет разную сумму степеней, но эта сумма будет согласованной, независимо от того, насколько неправильной формы многоугольник.

Например, внутренние углы треугольника будут всегда равны 180 градусам (чтобы узнать больше об этом, обязательно ознакомьтесь с нашим руководством по треугольникам SAT), является ли треугольник равносторонним (правильный многоугольник), равнобедренным, острым , или тупой.

Все эти треугольники будут иметь общий внутренний градус 180 градусов.

Таким образом, согласно тому же самому понятию, внутренние углы четырехугольника - будь то воздушный змей, квадрат, трапеция или другой - всегда будут в сумме равняться 360 градусам.Почему? Потому что четырехугольник состоит из двух треугольников.

Например:

Один внутренний угол параллелограмма составляет 65 градусов. Если остальные углы имеют размеры $ a $, $ b $ и $ c $, каково значение $ a + b + c $?

Все четырехугольники имеют внутреннюю сумму градусов 360, поэтому:

$ a + b + c + 65 = 360 $

$ a + b + c = 295 $

Сумма $ \ bi a, \ bi b , и $ \ bi c $ равна 295 .

Сумма внутреннего угла

Вы всегда сможете найти сумму внутренних углов многоугольника одним из двух способов - запомнив формулу внутреннего угла или разделив многоугольник на ряд треугольников.

Метод 1: Формула внутреннего угла

$$ (n − 2) 180 $$

Если у вас есть $ n $ сторон в многоугольнике, вы всегда можете найти сумму внутренних степеней по формуле $ (n − 2) $, умноженной на 180 градусов.

Если вы начнете с одного угла и проведете соединительные линии с каждым другим углом, чтобы образовать треугольники, вы поймете, почему в этой формуле есть $ n − 2 $.Причина в том, что вы не можете создать треугольник, используя сразу две соединяющиеся стороны, составляющие угол - каждая из них будет просто прямой линией. Чтобы увидеть это в действии, давайте посмотрим на наш второй метод.

Метод 2. Разделение многоугольника на треугольники

Причина, по которой приведенная выше формула работает, заключается в том, что вы, по сути, делите свой многоугольник на серию треугольников. Поскольку треугольник всегда равен 180 градусам, вы можете умножить количество треугольников на 180, чтобы найти внутреннюю сумму градусов вашего многоугольника, независимо от того, является ли ваш многоугольник правильным или неправильным.

Индивидуальные внутренние углы

Если ваш многоугольник обычный , вы также сможете найти индивидуальную градусную меру каждого внутреннего угла, разделив сумму в градусах на количество углов. (Примечание: $ n $ может использоваться как для количества сторон, так и для количества углов; количество сторон и углов в многоугольнике всегда будет одинаковым.)

$$ {(n − 2) 180} / n $$

Опять же, вы можете использовать формулу или метод деления треугольника, разделив внутреннюю сумму на количество углов.

Уголки, удильщик ... одно и то же, правда?

Боковые формулы

Как мы видели ранее, у правильного многоугольника все стороны равны. А если ваш многоугольник правильный, вы можете найти количество сторон, используя формулу, обратную формуле для определения углов.

Правильный многоугольник с n сторонами имеет равные углы в 120 градусов. Сколько сторон у фигуры?

Для этого вопроса будет быстрее всего использовать наши ответы и работать в обратном направлении, чтобы найти количество сторон в нашем многоугольнике.(Чтобы узнать больше о том, как использовать технику подключения ответов, ознакомьтесь с нашим руководством по подключению ответов).

Начнем с середины с варианта ответа C.

Мы знаем из нашей формулы угла (или создавая треугольники из наших многоугольников), что пятиугольная фигура будет иметь:

$ (n − 2) 180 $

$ (5–2) 180 $

$ (3) 180 $

540 $ градусов.

Или, опять же, вы всегда можете найти сумму своей степени, составив треугольники из вашего многоугольника.

Таким образом, вы все равно получите $ (3) 180 = 540 $ градусов.

Теперь мы также знаем, что это правильный многоугольник, поэтому каждый внутренний угол будет таким же. Это означает, что мы можем найти отдельные углы, разделив общую сумму на количество сторон / углов.

Итак, давайте найдем отдельные градусы, разделив эту сумму на количество углов.

$ 540/5 = 108 $

Вариант ответа C слишком мал. И мы также знаем, что чем больше сторон у фигуры, тем больше будет каждый отдельный угол. Это означает, что мы можем вычеркнуть варианты ответа A и B (60 градусов и 90 градусов соответственно), так как эти ответы будут еще меньше.

Теперь попробуем вариант ответа D.

$ (n − 2) 180 $

$ (6−2) 180 $

$ (4) 180 $

$ 720 $

Или вы можете найти свою внутреннюю сумму градусов, еще раз построив треугольники из ваших многоугольников.

Что снова даст вам (4) 180 = 720 долларов.

Теперь разделим сумму степеней на количество сторон.

720 долларов США / 6 = 120 9000 долларов США 7

Мы нашли ответ. У фигуры 6 сторон.

Наш окончательный ответ - D , 6.

К счастью для нас, SAT предсказуем. Вам не нужен экстрасенс, чтобы понять, что вы, вероятно, увидите в день испытаний.

Типичные вопросы о многоугольниках

Теперь, когда мы ознакомились со всеми нашими правилами и формулами для многоугольников, давайте рассмотрим несколько различных типов вопросов о многоугольниках, которые вы увидите на тесте SAT.

Почти все вопросы о многоугольниках так или иначе связаны с диаграммами (особенно, если вопрос касается любого многоугольника с четырьмя или более сторонами).Немногочисленные задачи, в которых , а не используют диаграмму, обычно будут простыми задачами со словами, включающими прямоугольники.

Обычно в вопросе о многоугольнике вас просят найти одно из трех:

# 1: мера угла (или сумма двух или более углов)
# 2: периметр фигуры
# 3: площадь фигуры

Давайте посмотрим на несколько реальных математических примеров SAT для этих различных типов вопросов.

Мера угла:

Поскольку этот шестиугольник правильный, мы можем найти градус каждого из его внутренних углов.Ранее мы видели, что мы можем найти эту степень в градусах, используя формулу внутреннего угла или разделив нашу фигуру на треугольники.

Шестиугольник можно разделить на 4 треугольника, поэтому $ 180 ° * 4 = 720 $ градусов.

В шестиугольнике 6 внутренних углов, а в правильном шестиугольнике все они равны. Итак:

720 долларов США / 6 = 120 9000 долларов США 7

Теперь линия BO находится в центре фигуры, поэтому она делит внутренний угол CBA пополам. Угол CBA равен 120, что означает, что угол $ x $ будет:

$ 120/2 = 60 $

Угол $ x $ составляет 60 градусов.

Наш окончательный ответ: B , 60.

Периметр фигуры:

Нам говорят, что ABCE - это квадрат с площадью 1. Мы знаем, что мы находим площадь квадрата, умножая длину и ширину (или возводя одну сторону в квадрат), что означает, что:

$ lw = 1 $

Это означает, что:

$ l = 1 $

А,

долл. США = 1

долл. США

Мы также знаем, что в квадрате все стороны равны. Это означает, что $ \ ov {AB}, \ ov {BC}, \ ov {CE} и \ ov {AE} $ ВСЕ равны 1.

Нам также говорят, что CED - это равносторонний треугольник, что означает, что все стороны равны. Поскольку мы знаем, что $ \ ov {CE} = 1 $, мы знаем, что $ \ ov {CD} $ и $ \ ov {DE} $ также равны 1.

Таким образом, периметр многоугольника в целом, состоящий из прямых $ \ ov {AB}, \ ov {BC}, \ ov {CD}, \ ov {DE} и \ ov {EA} $, равен равно:

$ 1 + 1 + 1 + 1 + 1 = 5 $

Наш окончательный ответ: B , 5.

[Примечание: не обманывайтесь, выбирая вариант ответа C! Несмотря на то, что каждая линия на рисунке равна 1, а есть 6 линий, линия $ \ ov {CE} $ НЕ является частью периметра .Это вариант ответа, созданный для того, чтобы заманить вас, поэтому старайтесь всегда отвечать только на то, что задает вопрос.)

Площадь фигуры:

Нам говорят, что длина ковра 8 футов и что длина также на 2 фута больше ширины. Это означает, что ширина должна быть:

$ 8−2 = 6 $

Теперь мы также знаем, что находим площадь прямоугольника, умножая ширину и длину. Итак:

$ 8 * 6 = 48 $

Площадь коврика 48 квадратных футов.

Наш окончательный ответ: B , 48.

А теперь время для некоторых практических советов, от завязывания лука до решения ваших многоугольных вопросов.

Как решить вопрос о многоугольнике

Теперь, когда мы рассмотрели типичные вопросы, которые вам задают на SAT, и прошли процесс поиска ответов, мы видим, что каждый метод решения имеет несколько общих приемов.

Чтобы решить ваши полигональные задачи наиболее точно и эффективно, обратите внимание на следующие стратегии:

# 1: разбивать фигуры на более мелкие

Не бойтесь писать все диаграммы.Многоугольники - сложные фигуры, поэтому по возможности всегда разбивайте их на мелкие части. Разбейте их на треугольники, квадраты или прямоугольники, и вы сможете решить вопросы, которые иначе было бы невозможно решить.

В качестве альтернативы, вам может понадобиться расширить ваши фигуры, добавив дополнительные линии и создав новые формы, чтобы разбить вашу фигуру. Просто всегда не забывайте игнорировать эти ложные строки, когда решите проблему.

Поскольку это неудобная форма, давайте создадим новую линию и разделим фигуру на два треугольника.

Теперь давайте заменим данную информацию.

Из наших определений мы знаем, что каждый треугольник будет иметь внутренние углы, которые в сумме составляют 180 градусов. Мы также знаем, что два созданных нами угла будут равны.

Мы можем использовать эту информацию, чтобы найти недостающие равные угловые меры, вычитая наши данные из 180 градусов.

$ 180-30-20-20 $

$ 110 $

Теперь мы можем разделить это число пополам, чтобы найти измерение каждого из двух равных углов.

$ 110/2 $

$ 55 $

Теперь мы можем рассматривать меньший треугольник как отдельный независимый треугольник, чтобы найти меру угла z. Опять же, внутренние углы будут составлять 180 градусов, поэтому:

$ 180-55-55 $

$ 70 $

Угол $ z $ равен 70 градусам.

Наш окончательный ответ: B , 70.

# 2: Используйте свои ярлыки

Если вам неудобно запоминать формулы или вы беспокоитесь о том, что ошибетесь в день теста, не беспокойтесь об этом! Просто разберитесь со своими ярлыками (например, помните, что все полигоны можно разбить на треугольники), и все будет в порядке.

# 3: По возможности используйте PIA или PIN-код

Поскольку многоугольники содержат много данных, очень легко спутать ваши числа или потерять путь, по которому вам нужно спуститься, чтобы решить проблему. По этой причине он часто может помочь вам использовать либо стратегию подключения ответов (PIA), либо стратегию подключения чисел (PIN), хотя иногда это может занять больше времени (для получения дополнительной информации ознакомьтесь с нашими руководствами по PIA и ШТЫРЬ).

# 4: Организуйте свою работу

Существует много информации, которую нужно отслеживать при работе с многоугольниками (особенно если вы разбиваете фигуру на более мелкие формы). 2 = 64 $

долл. США x = 8 долл. США

долл. США

Наконец, давайте сложим все линии, составляющие периметр трапеции.

$ 17 + 20 + 15 + 20 + 8 $

$ 80 $

Наш окончательный ответ - D , 80.

2. Нам говорят, что больший многоугольник имеет равные стороны и равные углы. Мы также можем видеть, что заштрихованная фигура имеет 4 стороны и углы, что означает, что это четырехугольник.

Мы знаем, что у четырехугольника 360 градусов, поэтому давайте вычтем наши данные из 360.

$ x + y = 80 $

$ 360−80 = 280 $

Опять же, мы знаем, что многоугольник имеет все равные углы, поэтому мы можем найти отдельные градусы, разделив полученное число пополам.

$ 280/2 = 140 $

Каждый внутренний угол многоугольника будет равен 140 градусам.

Теперь мы можем найти количество сторон, изменив формулу для стороны многоугольника или подставив ответы. Давайте посмотрим на оба метода.

Метод 1: Формула

$$ {(n − 2) 180} / n $$

Мы знаем, что эта формула дает нам меру каждого внутреннего угла, поэтому давайте воспользуемся знанием нашего индивидуального внутреннего угла (наши найденные 140 градусов) и подключим его, чтобы найти n, количество сторон.

140 долларов = {(n − 2) 180} / n

долларов

$ 140n = (n − 2) 180 $

$ 140n = 180n − 360 $

$ −40n = −360 $

$ n = 9 $

У нашего многоугольника 9 сторон.

Наш ответ: B , 9.

Метод 2. Подключение ответов

Мы также можем использовать наш метод вставки ответов, чтобы найти количество сторон в нашем многоугольнике.

Как всегда, выберем вариант ответа C.

Вариант ответа C дает нам 8 сторон.Мы знаем, что многоугольник с восемью сторонами будет разбит на 6 треугольников.

Так будет:

180 долларов * 6

долларов

$ 1080 $, всего

Теперь, если мы разделим эту сумму на количество сторон, мы получим:

$ 1080/8 $

$ 135 $

Каждый внутренний угол будет 135 градусов.

Это близкий ответ, но не совсем то, что нам нужно. Мы также знаем, что чем больше сторон имеет правильный многоугольник, тем больше будет каждый внутренний угол (углы равностороннего треугольника составляют 60 градусов каждый, каждый прямоугольник - 90 градусов и т. Д.), Поэтому нам нужно выбрать многоугольник. с более чем 8 сторонами.

Давайте тогда попробуем вариант ответа B, 9 сторон.

Мы знаем, что 9-сторонний многоугольник будет состоять из 7 треугольников.

Это означает, что общая внутренняя степень будет:

180 долларов * 7

долларов

$ 1260 $

И мы знаем, что каждая угловая мера будет одинаковой, поэтому:

$ 1260/9 $

$ 140 $

Мы нашли правильный ответ - 9-сторонний многоугольник будет иметь индивидуальный угол в 140 градусов.

Наш окончательный ответ - B , девять.

3. Давайте начнем с разбивки нашей фигуры на более мелкие и более удобные многоугольники.

Мы знаем, что больший прямоугольник будет иметь площадь:

$ 2 * 1 $

$ 2 $

Меньший прямоугольник будет иметь площадь:

$ 1 * x

$ x

(Примечание: мы используем $ x $ вместо одной из меньших сторон маленьких прямоугольников, так как мы еще не знаем ее длину)

Нам сказали, что общая площадь составляет $ 9/4 $, поэтому:

$ 2 + x = 9/4 $

$ x = 9 / 4−2 $

$ x = 9 / 4-8 / 4 $

$ х = 1/4 $

Теперь, когда мы знаем длину x, мы можем найти периметр всей фигуры.

Давайте сложим все длины наших открытых сторон, чтобы найти наш периметр.

$ 1 + 2 + 1 + 0,25 + 1 + 0,25 + 1 $

$ 6.5 $

Наш периметр - 6.5 $.

Наш окончательный ответ - 6.5.

Думаю, вы заслужили подарок за продвижение по полигонам, не так ли?

На вынос

Хотя вопросы о полигонах могут показаться сложными, все полигоны подчиняются лишь нескольким правилам.Вы можете встретить многоугольники неправильной формы и многоугольники, но основные стратегии и формулы будут применяться независимо.

До тех пор, пока вы будете следовать шагам решения, хорошо организовывать свою работу и помнить свои ключевые определения, вы сможете брать на себя и решать многоугольные вопросы, которые когда-то казались совершенно непонятными.

Что дальше?

Уф! Вы выделили многоугольники, и теперь пора убедиться, что остальные ваши математические ноу-хау находятся в отличной форме.Во-первых, убедитесь, что у вас есть практические знания по всем математическим темам на SAT, чтобы вы могли понять свои сильные и слабые стороны. Затем найдите больше руководств по математике SAT по конкретным темам, подобных этому, чтобы вы могли превратить эти слабые места в сильные.

Хотите освежить в памяти вопросы о вероятности? Дроби и соотношения? Линии и углы? Независимо от того, какая тема вам нужна, мы поможем вам.

Не хватает времени на SAT математику? Посмотрите наше руководство о том, как лучше всего ускорить свое время (и свой счет!).

Беспокоитесь о тестовом дне? Посмотрите, как вам следует подготовиться к рассматриваемому дню.

Хотите получить наивысший балл? Ознакомьтесь с нашим руководством по получению 800 баллов за SAT, написанным отличным бомбардиром.

Хотите улучшить свой результат SAT на 160 баллов?

Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.

Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.

Контрольная работа по геометрии четырехугольники: Контрольная работа по геометрии по теме «Четырехугольники»(8 класс)

Контрольная работа по геометрии по теме «Четырехугольники»(8 класс)

Контрольная работа по теме Четырехугольники по геометрии для 8 класса

Вариант 1

Вариант 1

Вариант 1

Федеральное агентство по образованию

Приложение 1

Личные данные учителя

Введение……………………………………………………………………1

Контрольная работа по геометрии на тему Свойства четырехугольников

Контрольная работа по теме «Четырехугольники». Вариант №1.

Контрольная работа по геометрии «Четырехугольники» 8 класс Макарычев

Контрольная работа по геометрии 8 класс по теме «Четырехугольники»

Контрольная работа по геометрии 8 класс

▶▷▶ контрольная работа по геометрии 8 класс номер 4 вариант 1

Четырехугольник | Определение, формы и примеры (видео)

Определение четырехугольника

Значение четырехугольника

Форма четырехугольника

Угловой четырехугольник

Боковые четырехугольники

Примеры четырехугольников

Виды четырехугольников

Четырехугольник викторина

Следующий урок:

Расчет длины диагонали четырехугольника

UVA11455 Вот мой четырехугольник 【Геометрия】 — Программист искал

Почему негоны и треугольники такие плохие?

Определение четырехугольника Merriam-Webster

Параллелограмм, формулы параллелограмма

Формулы параллелограмма

Стратегии и практические вопросы по геометрии

Что такое многоугольник?

Четырехугольники

Параллелограмм

Прямоугольник

Площадь

Ромб

Трапеция

Воздушный змей

Формулы многоугольников

Формулы площади

Площадь треугольника

Площадь прямоугольника

Площадь параллелограмма

Площадь трапеции

Формулы углов

Сумма внутреннего угла

Метод 1: Формула внутреннего угла

Метод 2. Разделение многоугольника на треугольники

Индивидуальные внутренние углы

Боковые формулы

Типичные вопросы о многоугольниках

Мера угла:

Периметр фигуры:

Площадь фигуры:

Как решить вопрос о многоугольнике

# 1: разбивать фигуры на более мелкие

# 2: Используйте свои ярлыки

# 3: По возможности используйте PIA или PIN-код

# 4: Организуйте свою работу

На вынос

Что дальше?

Добавить комментарий Отменить ответ