Контрольная работа по физике прямолинейное равноускоренное движение: Контрольная работа № 1 по физике для 9 класса | Методическая разработка по физике (9 класс):

Контрольная работа № 1 по физике для 9 класса | Методическая разработка по физике (9 класс):

Контрольная работа по физике № 1

по теме: Прямолинейное равноускоренное движение. Законы Ньютона

Вариант 1

1. С каким ускорением должен затормозить автомобиль, движущийся со скоростью 36 км/ч, чтобы через 10 с остановиться?
2. За какое время велосипедист проедет 30 м, начиная движение с ускорением 0,75 м/с 2?
3. Какую скорость приобретает троллейбус за 5 с, если он трогается с места с ускорением 1,2 м/с 2?
4. С каким ускорением двигался при разбеге реактивный самолёт массой 50 т, если сила тяги двигателей 80 кН?
5. .Чему равна сила, сообщающая телу массой 3 кг ускорение 0,4 м/с2?
6.  Лыжник массой 60 кг, имеющий в конце спуска скорость 36 км/ч, остановился через 40 с после окончания спуска. Определите силу сопротивления его движению.

Контрольная работа по физике № 1

по теме: Прямолинейное равноускоренное движение. Законы Ньютона

Вариант 2

1. Поезд подходит к станции со скоростью 36 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?
2. Определите, какую скорость развивает мотоциклист за 15 с, двигаясь из состояния покоя с ускорением 1,3 м/с2?
3. Какой должна быть длина взлетной полосы, если известно, что самолёт для взлёта должен приобрести скорость 240 км/ч, а время разгона самолёта равно примерно 30 с?
4. .Вагонетка массой 200 кг движется с ускорением 0,2 м/с2. Определите силу, сообщающую вагонетке это ускорение.
5.  Чему равно ускорение, с которым движется тело массой 3 кг, если на него действует сила 12 Н?
6.  Порожний грузовой автомобиль массой 3 т начал движение с ускорением 0,2 м/с2. Какова масса этого автомобиля вместе с грузом, если при той же силе тяги он трогается с места с ускорением 0,15м/с2?

Контрольная работа по физике № 1

по теме: Прямолинейное равноускоренное движение. Законы Ньютона

Вариант 1

1. С каким ускорением должен затормозить автомобиль, движущийся со скоростью 36 км/ч, чтобы через 10 с остановиться?
2. За какое время велосипедист проедет 30 м, начиная движение с ускорением 0,75 м/с 2?
3. Какую скорость приобретает троллейбус за 5 с, если он трогается с места с ускорением 1,2 м/с 2?
4. С каким ускорением двигался при разбеге реактивный самолёт массой 50 т, если сила тяги двигателей 80 кН?
5. .Чему равна сила, сообщающая телу массой 3 кг ускорение 0,4 м/с2?
6.  Лыжник массой 60 кг, имеющий в конце спуска скорость 36 км/ч, остановился через 40 с после окончания спуска. Определите силу сопротивления его движению.

Контрольная работа по физике № 1

по теме: Прямолинейное равноускоренное движение. Законы Ньютона

Вариант 2

1. Поезд подходит к станции со скоростью 36 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?
2. Определите, какую скорость развивает мотоциклист за 15 с, двигаясь из состояния покоя с ускорением 1,3 м/с2?
3. Какой должна быть длина взлетной полосы, если известно, что самолёт для взлёта должен приобрести скорость 240 км/ч, а время разгона самолёта равно примерно 30 с?
4. . Вагонетка массой 200 кг движется с ускорением 0,2 м/с2. Определите силу, сообщающую вагонетке это ускорение.
5.  Чему равно ускорение, с которым движется тело массой 3 кг, если на него действует сила 12 Н?
6.  Порожний грузовой автомобиль массой 3 т начал движение с ускорением 0,2 м/с2. Какова масса этого автомобиля вместе с грузом, если при той же силе тяги он трогается с места с ускорением 0,15м/с2?

Тест по физике на повторение темы Равномерное и равноускоренное движение 9 класс

Тест по физике на повторение темы Равномерное и равноускоренное движение 9 класс с ответами. Тест включает в себя 2 варианта, в каждом варианте 10 заданий с выбором ответа (в части А — 7 заданий, в части В — 2 задания, в части С — 1 задание.).

1 вариант

A1. Землю можно считать материальной точкой

1) при рассмотрении движения Земли вокруг Солнца
2) при определении суточного движения точек зем­ной поверхности
3) при рассмотрении движения автомобиля по по­верхности Земли
4) при изучении движения спутника вокруг Земли

А2. Автомобиль проехал расстояние от пункта А до пункта В, равное 260 км, а затем вернулся в пункт С, находящийся на расстоянии 90 км от пункта А.

Величина перемещения автомобиля равна

1) 90 км
2) 150 км
3) 260 км
4) 350 км

А3. За 3 часа катер прошёл расстояние 86,4 км. Скорость катера равна

1) 5 м/с
2) 8 м/с
3) 29 м/с
4) 259 км/ч

А4. Скорость лифта изменилась за 2 с от 1,3 м/с до 0,1 м/с. Ускорение лифта равно

1) -0,4 м/с²
2) -0,6 м/с²
3) 0,6 м/с²
4) 0,4 м/с²

А5. Автомобиль, двигавшийся со скоростью 10 м/с, начи­нает разгоняться с ускорением 3 м/с². Путь, пройден­ный автомобилем за 2 с после начала ускорения, равен

1) 12 м
2) 26 м
3) 34 м
4) 40 м

А6. Зависимость от времени координат четырёх тел, движущихся по оси ОХ, представлена в таблице.

С постоянным ускорением двигалось тело

1) 1
2) 2
3) 3
4) 4

А7. Скорость моторной лодки в неподвижной воде равна 5 м/с, скорость течения реки 5,4 км/ч. Скорость лодки относи­тельно земли при движении вверх по реке равна

1) 3,5 м/с
2) 5 м/с
3) 6,5 м/с
4) 0,4 м/с

B1. Установите соответствие между характеристиками движения и их определениями.

Характеристики движения

А) Путь
Б) Перемещение

Определение

1) Длина траектории
2) Линия, вдоль которой движется тело
3) Вектор, соединяющий начальное и конечное положения тела

4) Проекция линии, вдоль которой движется тело
5) Проекция вектора, со­единяющего точку и на­чало координат, на ко­ординатную ось

В2. Установите соответствие между физическими вели­чинами и формулами, по которым они определяются.

Физическая величина

А) Перемещение при равноускоренном движении
Б) Перемещение при равномерном движении

Формула

1) v/t
2) v₀t + at²/2
3) v₀ + at
4) v₀ + at²/2
5) vt

C1. Автомобиль, двигавшийся со скоростью 144 км/ч, останавливается через 10 с после начала торможения. Найдите путь, пройденный автомобилем за 4 с после начала торможения.

2 вариант

A1. Автомобиль можно считать материальной точкой

1) при рассмотрении вращения колес автомобиля
2) при определении силы сопротивления воздуха, действующей на движущийся автомобиль
3) при определении средней скорости движения ав­томобиля по поверхности Земли
4) при определении условий равновесия автомобиля, стоящего на наклонной дороге

А2. Автомобиль проехал расстояние от пункта А до пункта В, равное 260 км, а затем вернулся в пункт С, находящийся на расстоянии 90 км от пункта А.

Путь автомо­биля равен

1) 170 км
2) 260 км
3) 350 км
4) 430 км

А3. За 3 часа катер прошёл расстояние 75,6 км. Скорость катера равна

1) 7 м/с
2) 10 м/с
3) 25 м/с
4) 227 км/ч

А4. Скорость лифта изменилась за 2 с от 0,2 м/с до 1 м/с. Ускорение лифта равно

1) -0,4 м/с²
2) -0,6 м/с²
3) 0,6 м/с²
4) 0,4 м/с²

А5. Автомобиль, двигавшийся со скоростью 20 м/с, начи­нает тормозить с ускорением 3 м/с². Путь, пройден­ный автомобилем через 2 с после начала торможения, равен

1) 17 м
2) 34 м
3) 40 м
4) 46 м

А6. Зависимость от времени координат четырёх тел, движущихся по оси ОХ, представлена в таблице.

С постоянной скоростью двигалось тело

1) 1
2) 2
3) 3
4) 4

А7. Скорость моторной лодки в неподвижной воде равна 5 м/с, скорость течения реки 5,4 км/ч. Скорость лодки относи­тельно земли при движении вниз по реке равна

1) 3,5 м/с
2) 5 м/с
3) 6,5 м/с
4) 10,4 м/с

B1. Установите соответствие между физическими понятиями и их определениями

Физическое понятие

А) Система отсчёта
Б) Траектория

Определение

1) Линия, вдоль которой движется тело

2) Длина траектории
3) Вектор, соединяющий начальное и конечное положения тела
4) Тело отсчёта, связанная с ним система координат и прибор для измерения времени
5) Проекция вектора, соединяюще­го точку и начало координат, на координатную ось

В2. Установите соответствие между физическими вели­чинами и формулами, по которым они определяются.

Физическая величина

А) Скорость при равномерном движении
Б) Скорость при равноускоренном движении

Формула

1) S/t
2) v₀t + at²/2
3) v₀ + at

4) v₀ + at²/2
5) St

C1. Автомобиль, двигавшийся со скоростью 108 км/ч, останавливается через 6 с после начала торможения. Найдите путь, пройденный автомобилем за 3 с после начала торможения.

Ответы на тест по физике на повторение темы Равномерное и равноускоренное движение 9 класс
1 вариант
А1-1
А2-1
А3-2
А4-2
А5-2
А6-4
А7-1
В1-13
В2-25
С1. 128 м
2 вариант
А1-3
А2-4
А3-1
А4-4
А5-2
А6-1
А7-3
В1-41
В2-13
С1. 67,5 м

Тест по физике Прямолинейное равноускоренное движение 9 класс

Тест по физике Прямолинейное равноускоренное движение 9 класс с ответами.

Тест включает в себя 2 варианта. В каждом варианте по 6 заданий.

Вариант 1

1. Координата тела, движущегося прямолинейно, ме­няется по закону: х = 32 − 8t + 2t² (м).

Укажите, какие из приведённых ниже утверждений являются верными.

А) каждую секунду скорость тела уменьшается на 2 м/с
Б) тело начало движение из точки с координатой 32 м со скоростью 8 м/с, направленной по оси ОХ

1) только А
2) только Б
3) оба утверждения верны
4) оба утверждения неверны

2. По графику зависимости проекции скорости от вре­мени определите проекцию перемещения на ось ОХ, совершённого телом за последние 6 с движения.

1) 16 м
2) 24 м
3) −24 м
4) −16 м

3. Проекция скорости велосипедиста меняется по зако­ну v = −10 + 0,8t (м/с). Чему равна проекция переме­щения велосипедиста за 10 с?

4. Координата тела, движущегося прямолинейно, за­висит от времени по закону х = −16 + 12t − 4t² (м).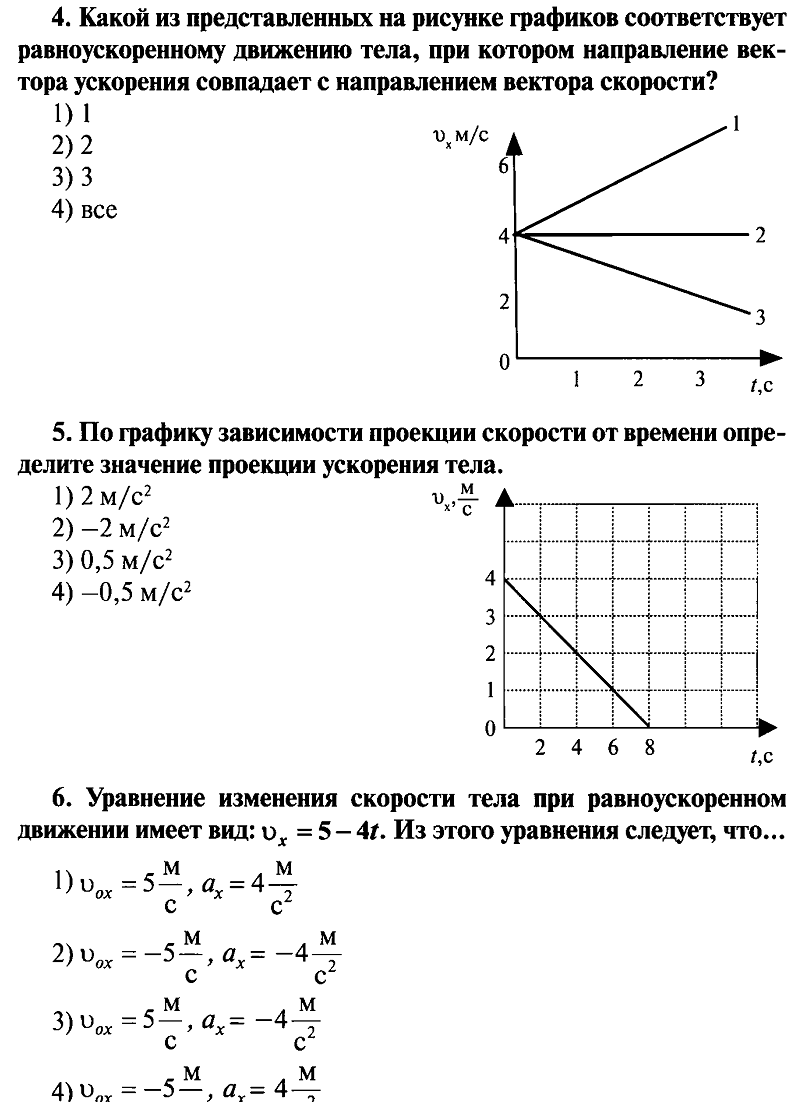 Как при движении тела в течение первой секунды меняется модуль скорости, модуль ускорения и расстояние от тела до начала координат?

Для каждой физической величины определите соот­ветствующий характер изменения.

Физическая величина

А) модуль скорости
Б) моду ль ускорения
В) расстояние до начала координат

Характер изменения

1) увеличивается
2) уменьшается
3) не изменяется

5. Шарик скатывается по наклонному жёлобу без на­чальной скорости. Положения шарика в различные моменты времени даны в виде таблицы.

s, м	0	0,05	0,2	0,45	0,8	1,25
t, с	0	0,5	1	1,5	2	2,5

Выберите из предложенного перечня

два верных утверждения.

1) ускорение шарика равно 0,4 м/с²
2) ускорение шарика равно 0,5 м/с²
3) за первую секунду движения шарик совершил перемещение в 3 раза меньшее, чем за вторую
4) в начале второй секунды скорость шарика была равна 0,2 м/с
5) за первые 2 с движения путь, пройденный ша­риком, в 3 раза больше, чем за первую

6. Запишите кратко условие задачи и решите её.

При аварийном торможении автомобиль, движу­щийся со скоростью 54 км/ч, останавливается через 4 с. Найдите тормозной путь.

Вариант 2

1. Координата тела, движущегося прямолинейно, ме­няется по закону: х = 4t + t² (м).

Укажите, какие из приведённых ниже утверждений являются верными.

А) тело движется равноускоренно с начальной ско­ростью 4 м/с, направленной по оси ОХ
Б) каждую секунду скорость тела увеличивается на 2 м/с

1) только А
2) только Б
3) оба утверждения верны
4) оба утверждения неверны

2. По графику зависимости проекции скорости от вре­мени определите проекцию перемещения на ось ОХ, совершённого телом за первые 6 с движения.

1) 24 м
2) 16 м
3) −24 м
4) −16 м

3. Проекция скорости велосипедиста меняется по зако­ну v = 14 − 1,2t (м/с). Чему равна проекция переме­щения велосипедиста за 5 с?

4. Координата тела, движущегося прямолинейно, зави­сит от времени по закону х = 16 − 20t + 4t² (м). Как при движении тела в течение первой секунды меняется модуль скорости, модуль ускорения и расстоя­ние от тела до начала координат?

Для каждой физической величины определите соот­ветствующий характер изменения.

Физическая величина

А) модуль скорости
Б) модуль ускорения
В) расстояние до начала координат

Характер изменения

1) увеличивается
2) уменьшается
3) не изменяется

5. Шарик скатывается по наклонному жёлобу без на­чальной скорости. Скорости шарика в различные моменты времени даны в виде таблицы.

v, м/с	0	0,3	0,6	0,9	1,2	1,5
t, с	0	0,5	1	1,5	2	2,5

Выберите из предложенного перечня два верных утверждения.

1) ускорение шарика равно 0,3 м/с²
2) ускорение шарика равно 0,4 м/с²
3) за первую секунду движения шарик совершил перемещение в 2 раза меньшее, чем за вторую
4) за первые 2 с движения перемещение шарика вдоль жёлоба равно 1,2 м
5) за первые 2 с движения путь, пройденный ша­риком, в 4 раза больше, чем за первую

6. Запишите кратко условие задачи и решите её.

Поезд, отойдя от станции, прошёл путь 250 м и развил скорость 18 км/ч. Найдите модуль ускорения поезда.

Ответы на тест по физике Прямолинейное равноускоренное движение 9 класс
Вариант 1
1-4
2-4
3. −60 м
4. А2 Б3 В2
5. 1 3
6. 30 м
Вариант 2
1-3
2-2
3. 55 м
4. А2 Б3 В2
5. 4 5
6. 0,05 м/c²

Прямолинейное равноускоренное движение — физика, тесты

библиотека
материалов

Содержание слайдов

Номер слайда 1

Диктант по темам. ФИЗИКА ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ. * Вам будет предложено 6 вопросов по изученным темам. На странице каждого вопроса установлен таймер времени вопроса на экране: 1 или 5 минут. По окончанию времени слайд листается самостоятельно.

Номер слайда 2

Вопрос №1 * К какому виду движения — равномерному или неравномерному — относится прямолинейное равноускоренное движение?

Номер слайда 3

Вопрос № 2 * Что понимают под мгновенной скоростью неравномерного движения?

Номер слайда 4

Вопрос №3 * Дайте определение ускорения равноускоренного движения. Какова единица ускорения?

Номер слайда 5

Вопрос №4 * Что такое равноускоренное движение?

Номер слайда 6

Вопро № 5 Что показывает модуль вектора ускорения? *

Номер слайда 7

Вопрос №6 * При каком условии модуль вектора скорости движущегося тела увеличивается; уменьшается?

Номер слайда 8

Пример оформления решения задач *

Номер слайда 9

Вопрос №7 * Автомобиль, двигавшийся со скоростью 30 м/с, начал тормозить. Чему будет равна его скорость через 1 минуту, если ускорение при торможении равно 0,3 м/с2? Обратите внимание! Проекция вектора ускорения на ось t отрицательна.

Номер слайда 10

Вопрос №8 * Санки начинают двигаться с горы с ускорением 2 м/с2. Какое расстояние они пройдут за 2 секунды?

Номер слайда 11

Вопрос №9 * Каково ускорение велосипедиста, если его скорость за 5 секунд изменилась от 7 до 2 м/с?

Номер слайда 12

* Сдаем свои работы

Тест по физике Равноускоренное движение для 9 класса

Тест по физике Равноускоренное движение для 9 класса с ответами. Тест включает два варианта, в каждом по 7 заданий.

Вариант 1

A1. Равноускоренным движением называют движение, при котором

1) тело за равные промежутки времени проходит равные расстояния
2) скорость тела за разные промежутки времени изменяется на одинаковые значения
3) скорость тела за равные промежутки времени изменяется на одинаковые значения
4) скорость тела не изменяется

А2. На рисунке показан график зависимости скорости тела от времени. Тело

1) движется равномерно
2) движется равнозамедленно
3) движется равноускоренно
4) покоится

А3. Формула для координаты тела, движущегося равноускоренно с начальной скоростью из начала координат, имеет вид

1) х = x₀ + v₀t + at²/2
2) x = v₀t
3) х = at²/2
4) х = v₀t + at²/2

А4. Мотоцикл «Yamaha R1» разгоняется с места до 200 км/ч за 8,6 с. Величина ускорения мотоцикла равна

1) 55,5 м/с²
2) 6,5 м/с²
3) 13 м/с²
4) 23,3 м/с²

А5. Поезд двигался из начала координат равномерно со скоростью 36 км/ч, после чего в точке с координатой 1500 м начал двигаться с ускорением 0,01 м/с² в течении 30 минут. С начала движения поезд прошёл путь, равный

1) 18 км
2) 34,2 км
3) 35,7 км
4) 16,2 км

А6. На рисунке показан график зависимости скорости тела от времени. Ускорение тела равно

1) 0 м/с²
2) 0,75 м/с²
3) 1 м/с²
4) 1,33 м/с²

B1. Определите, какие из величин правого столбца обозначают векторную физическую величину, а какие скалярную

А) Векторная величина Б) Скалярная величина

1) Движение 2) Время 3) Ускорение 4) Секунда 5) Метр

Вариант 2

A1. Ускорением тела называется

1) векторная величина, равная отношению изменения расстояния к промежутку времени, за которое это изменение произошло
2) векторная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло
3) скалярная величина, равная отношению изменения расстояния к промежутку времени, за которое это изменение произошло
4) скалярная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло

А2. На рисунке показан график зависимости скорости тела от времени. Тело

1) движется равномерно
2) движется равнозамедленно
3) движется равноускоренно
4) покоится

А3. Формула для координаты тела, движущегося равноускоренно без начальной скорости из произвольной точки, имеет вид

1) х = x₀ + v₀t + at²/2
2) х = x₀ + at²/2
3) х = at²/2
4) x = v₀t + at²/2

А4. Автомобиль «Nissan GT-R» разгоняется с места до 100 км/ч за 2,7 с. Ускорение автомобиля равно

1) 37 м/с²
2) 10,3 м/с²
3) 27 м/с²
4) 13,7 м/с²

А5. Моторная лодка начала движение с острова с координатой 700 м в направлении начала координат с ускорением 0,5 м/с² Лодка достигнет начала координат

1) 53 с
2) 35 с
3) 37,4 с
4) 70 с

А6. На рисунке показан график зависимости скорости тела от времени. Ускорение тела равно

1) 0 м/с²
2) -0,75 м/с²
3) 1 м/с²
4) -1 м/с²

B1. Определите, какие из величин правого столбца обозначают векторную физическую величину, а какие скалярную.

А) Векторная величина Б) Скалярная величина

1) Скорость 2) Секунда 3) Путь 4) Движение 5) Метр

Ответы на тест по физике Равноускоренное движение для 9 класса
Вариант 1
А1-3
А2-2
А3-4
А4-2
А5-3
А6-3
В1. А3 Б2
Вариант 2
А1-2
А2-3
А3-2
А4-2
А5-1
А6-2
В1. А1 Б3

Тест Прямолинейное равноускоренное движение (9 класс) по физике

Сложность: знаток.Последний раз тест пройден 14 часов назад.

1. Вопрос 1 из 10

   Какое(-ие) утверждение(-я) верно(-ы): а)равноускоренное движение является неравномерным движением; б)равноускоренное движение является равномерным движением ?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 60% ответили правильно
   • 60% ответили правильно на этот вопрос

   В вопросе ошибка?

   Следующий вопросОтветить

2. Вопрос 2 из 10

   В каких единицах измеряется ускорение в СИ?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 78% ответили правильно
   • 78% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

3. Вопрос 3 из 10

   Какая физическая величина относится к векторным величинам?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 82% ответили правильно
   • 82% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

4. Вопрос 4 из 10

   Какое(-ие) утверждение(-я) верно(-ы): а)если направление ускорения совпадает с направлением начальной скорости, то модуль скорости увеличивается; б)если направление ускорения противоположно направле­нию начальной скорости, то модуль скорости уменьшается ?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 61% ответили правильно
   • 61% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

5. Вопрос 5 из 10

   Мотоциклист начинает движение из состояния покоя. Через 30 с. он достигает скорости 54 км/ч. С каким ускорением происходит движение?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 63% ответили правильно
   • 63% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

6. Вопрос 6 из 10

   Санки съехали с одной горки и въехали на другую. Во время подъема на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с. При этом ускорение равно

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 54% ответили правильно
   • 54% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

7. Вопрос 7 из 10

   Во время подъема в гору скорость велосипедиста, двигающегося прямолинейно и равноускоренно, изменилась за 8 с от 5 м/с до 10,8 км/ч. При этом модуль ускорения велосипедиста был равен

   • Правильный ответ
   • Неправильный ответ
   • Вы ответили лучше 60% участников
   • 40% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

8. Вопрос 8 из 10

   Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста 0,5 м/с². Сколько времени длится спуск?

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 54% ответили правильно
   • 54% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

9. Вопрос 9 из 10

   Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с². На этом спуске его скорость увеличилась на 18 м/с. Велосипедист заканчивает свой спуск после его начала через

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 65% ответили правильно
   • 65% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

10. Вопрос 10 из 10

    Вагон наехал на тормозной башмак при скорости 4,5 км/ч. Через 3 с вагон остановился. Определите тормозной путь

    • Правильный ответ
    • Неправильный ответ
    • Вы ответили лучше 62% участников
    • 38% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

ТОП-5 тестовкоторые проходят вместе с этим

Изучение ряда тем по физике имеет огромное значение для того, чтобы школьник мог успешно знакомиться с основами этой науки, а потому тест «Прямолинейное равноускоренное движение» (9 класс) может стать особенно важен для всех, кто хочет хорошо или отлично успевать по предмету. Он содержит в себе десять вопросов разной степени сложности; задания с выбором правильного ответа требуют знания теории («равноускоренное движение», «ускорения», «единицы СИ») и умения описывать физические опыты и решать небольшие по объему задачи (например, на поиск ускорения).

Тесты по физике «Равноускоренное движение» пригодятся не только девятиклассникам; они могут быть очень удобны и для старшеклассников, которые повторяют изученное перед экзаменом ЕГЭ. Пригодятся они также родителям или учителям, которым требуется провести урок контроля знаний.

Рейтинг теста

Средняя оценка: 3.5. Всего получено оценок: 579.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

MCQ с равномерным ускорением движения — викторина, вопросы и ответы

Uniformly Accelerated Motion Multiple Choice Questions (MCQ), викторина с равномерным ускорением движения отвечает в формате PDF для изучения онлайн-курса физики. Изучите прикладную физику: движение и силу. Вопросы и ответы с множественным выбором (MCQ), вопросы викторины «Равномерно ускоренное движение» и ответы для онлайн-программ бакалавриата. Изучите смещение в физике, формулу скорости, импульс в физике, подготовку к тесту по физическим уравнениям.

«На поверхность Земли, где воздушное трение незначительно, объекты падают с помощью« вопросов с множественным выбором »(MCQ) при равномерно ускоренном движении с выбором разное ускорение, та же скорость, такое же ускорение и та же скорость для онлайн-программ бакалавриата . Практический тест оценки стипендий, онлайн-обучение равномерно ускоренных вопросов викторины движения для конкурсных экзаменов по специальностям физики для классов подготовки к тесту SAT. Видео с равномерным ускорением

MCQ по равномерно ускоренному движению Скачать PDF

MCQ: На поверхность Земли, где воздушное трение незначительно, объекты падают вместе с

1. разное ускорение
2. такая же скорость
3. такое же ускорение
4. такая же скорость

MCQ: Из уравнений расстояния правильным является

.

1. V _f = V _i + 2as
2. V _f ² = V _i ² + as
3. V _f ² = V _i ² + 2a
4. V _f ² = V _i ² + 2as

MCQ: Правильное уравнение расстояния —

1. V _i = V _f + при
2. V _f = V _i + при
3. V _f = V _i + t
4. V _f = V _i + a

MCQ: Скорость вертикально брошенного шара со временем будет

.

1. вверх положительный
2. вниз отрицательное
3. вверх отрицательное
4. положительный вниз

6.2: Равномерно ускоренное движение — Physics LibreTexts

Перед изучением движения в сопротивляющейся среде может быть уместно сделать краткий обзор равномерно ускоряющегося движения. То есть движение, в котором сопротивление равно нулю. Любые формулы, которые мы разрабатываем для движения в сопротивляющейся среде, должны переходить к формулам для равноускоренного движения, когда сопротивление приближается к нулю.

Можно представить себе ситуацию, когда тело начинает со скоростью \ (v_ {0} \), а затем ускоряется со скоростью \ (a \).2 + 2акс. \ tag {6.2.3} \ label {eq: 6.2.3} \]

Поскольку ускорение равномерное, нет необходимости использовать исчисление для его получения. Первое следует непосредственно из значения ускорения. Пройденное расстояние — это площадь под графиком скорость: время. На рисунке VI.1 показан график скорость: время для постоянного ускорения, и уравнение \ (\ ref {eq: 6.2.2} \) очевидно с первого взгляда на график. Уравнение \ (\ ref {eq: 6.2.3} \) может быть получено путем исключения \ (t \) между уравнениями \ (\ ref {eq: 6.2.1} \) и \ (\ ref {eq: 6.2.2} \). (Это также можно вывести из соображений энергии, хотя это скорее ставит телегу впереди лошади.)

Тем не менее, хотя в расчетах нет необходимости, поучительно посмотреть, как их можно использовать для анализа равномерно ускоренного движения, поскольку расчет будет необходим в менее простых ситуациях. 2_ {0} + 2акс.\ tag {6.2.8} \ label {eq: 6.2.8} \]

Это пространственный интеграл.

Примеры.

Вот несколько простых примеров проблем при равномерно ускоренном движении. Вероятно, будет хорошей идеей поработать с алгеброй и получить алгебраических решений для каждой задачи. То есть, даже если вам говорят, что начальная скорость составляет 15 мс ^-1 , назовите ее \ (v_ {0} \) или, если вам сказали, что высота составляет 900 футов, назовите ее \ (h \ ). Возможно, вам будет полезно рисовать графики зависимости расстояния от времени или скорости от времени в большинстве задач.{2} = 4ac \).

Пример \ (\ PageIndex {1} \)

Тело выпало из состояния покоя. Последняя треть расстояния до падения на землю покрывается за время T. Покажите, что время, затрачиваемое на все падение на землю, составляет 5,45T.

Пример \ (\ PageIndex {2} \)

The Lady находится в 8 метрах от автобусной остановки, когда Автобус, трогаясь с остановки на автобусной остановке, трогается с места с ускорением 0,4 м с ^-2 . С какой наименьшей скоростью должна бежать леди, чтобы успеть на автобус?

Ответ: 2.53мс ^-1 .

Пример \ (\ PageIndex {3} \)

Парашютист спускается с постоянной скоростью 10 футов в секунду. Когда она находится на высоте 900 футов, ее друг, находящийся прямо под ней, бросает ей яблоко. С какой наименьшей скоростью он должен бросить яблоко, чтобы оно достигло ее? Сколько времени нужно, чтобы добраться до нее, на каком росте она тогда и какова относительная скорость парашютиста и яблока? Предположим, что \ (g \) = 32 фута с ^-2 . Пренебрегать сопротивлением воздуха для яблока (но не для парашютиста!)

Ответ: 230ft ^-1 , 7.5s, 825 футов, 0 футов ^-1 .

Пример \ (\ PageIndex {4} \)

Лунный исследователь проводит на Луне следующий эксперимент, чтобы определить там гравитационное ускорение \ (g \). Он подбрасывает лунный камень вверх с начальной скоростью 15 м с ^-1 . Через восемь секунд он подбрасывает еще один камень вверх с начальной скоростью 10 м с ^-1 . Он отмечает, что камни сталкиваются через 16,32 секунды после запуска первого камня. Вычислите g, а также высоту столкновения.

Ответ: 1,64 мс ^-2 , 26,4 м

Равномерное ускоренное прямолинейное движение — вкл. + Ускоренное прямолинейное движение … Равномерно ускоренное прямолинейное движение … Как решать кинематические задачи: текстовое поле p232

UUnit 3: Kinematics

Равномерное прямолинейное движение Унифицированное ускоренное движение

14 графики: наклон линии

наклон = подъем / бег

если y vs x, тогда наклон = y / x

Если график представляет собой смещение в зависимости от времени: наклон = d / t = d2 — d1 / t2 — t1 = скорость

Если график представляет собой зависимость скорости от времени: наклон = v / t = v2 — v1 / t2 — t1 = ускорение

UniformMotion:

Constantspeed: anobjectmovesequaldistancesinequaltimeintervals

GraphiteMoves3 (: anobjectmoves3)

VelocityvsTime: uniformmotion

v

t

запомнить постоянную скорость на смещение mentvstimegraph?

d

t

Ускорение

изменение скорости с течением времени

a = v / t = м / с2

при изменении скорости грузовика с 5 м / ст. 50 м / с, за 60 секунд, что такое ускорение?

50 м / с 5 м / с / 60 с = 45/60 м / с 2

=.75 м / с2

Равномерно ускоренное прямолинейное движение

скорость больше не постоянная (более реальная) скорость меняется от момента к моменту

ti = начальное время (с) tf = конечное время (с) xi = начальное положение (м) xf = конечное положение (м) vi = начальная скорость (м / с) vf = конечная скорость (м / с) a = ускорение (м / с2)

Мгновенная скорость

скорость в точный момент времени

На графике: положение в зависимости от времени, если скорость не постоянна, у нас есть кривая.Скорость — это наклон, но когда кривая меняется, что нам делать ?????

d

t

возьмем тангенс кривой

d

t

a = y2 — y1x2 — x1

speedvstimegraphs

vjectcity

при изменении скорости

а = v / t =?

p228229

Обратите внимание, как скорость представлена ​​в виде вектора в вопросе №7. Они являются направленными, «восточными» (+) или «западными» (-). Длина ошибки пропорциональна spped.

Может ли автомобиль иметь положительное ускорение и отрицательное направление?

Отрицательное ускорение и положительное направление?

Уравнения равномерного ускорения

Уравнение 1: a = v / t = v2 — v1 / ta * t = v2 — v1 a * t + v1 = v2

v2 = v1 + at

Уравнение 3: xf = xi + v1t + at2

Уравнение 2: xf = xi + (vi + vf) t

Уравнение 4: vf2 = vi2 + 2ax

Уравнение 1:

Как решать кинематические задачи: текстовое поле p232

draw начало оси x диаграммы, в начальной точке, xi = 0 id ti и tf id известные параметры (обязательно укажите знаки (+ или -). Найдите одно из 4 уравнений, в котором искомая величина является единственной неизвестной

Пример:

Водитель автомобиля, движущегося на восток со скоростью 25 м / с, нажимает на тормоза и начинает замедляться на скорости 2. 0 м / с2

Как далеко машина уезжает за 8,0 с?

a = -2,0 м / с2

vi = 25 м / ст = 8,0 с

d =?

какая формула?

d = vit + 1/2 a t2

d = 25 (8.0) + 1/2 (-2.0) (8.02) d = 200 — 64d = 136 м (+)

Примеры в тексте книга p 232

A:

B:

Практика: Раздел 10.2p. 234

стр. 2341. Что мы знаем?

d = 402 м vi = 0 м / с t = 6.2) 402 = 1/2 (a * 36) 804 = 36aa = 22,3 м / с2 = 22 м / с2

vfvf2 = vi2 + 2axvf2 = 0 + 2 * 22,3 * 402

vf = 17929,2 vf = 133,9 м / с = 130 м / с

старый учебник

стр. 213 1п217

стр. 220-222

Страница 1: 31 января — 8:19 PM Страница 2: 31 января — 8:22 PM Страница 3: 31 января — 8:32 PM Страница 4: 31 января-8: 36 PM Страница 5: 10-7 января : 30 PM Страница 6: Янв 10-7: 04 PM Страница 7: Янв 10-7: 15 PM Страница 8: Ян 31-8: 39 PM Страница 9: Янв 10-7: 19 PM Страница 10: Янв 31-8: 42 PM Страница 11: 31 января — 9: 08 Страница 12: 2 — 3 февраля: 45 Страница 13: 31 января — 8: 17 Страница 14: 10 — 7: 41 января Страница 15: 31 января — 21:14 Страница 16: 31-9 января: 18 PM Страница 17: 31 января — 21:21 Страница 18: 2 — 3 февраля: 46 PM Страница 19: 2 — 4 февраля 12 PM Страница 20: 31 января — 9: 22 PM Страница 21: 2 — 3 февраля: 22 PM

.