Контрольная работа номер 2 степенная функция: Контрольная работа №2 по теме «Степенная функция»

Контрольная работа №2 по теме «Степенная функция»

Инфоурок › Алгебра ›Другие методич. материалы›Контрольная работа №2 по теме «Степенная функция»

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп.

образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-957529

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Алгебра 9 Дорофеев К-2 . Контрольная работа и ответы

Контрольная работа по алгебре № 2.
9 класс (УМК Дорофеев и др.).

Алгебра 9 Дорофеев К-2. Контрольная работа по алгебре в 9 классе «Квадратичная функция» с ОТВЕТАМИ. В учебных целях использованы цитаты из пособия «Алгебра. Контрольные работы 9 класс» (авт. Л.В. Кузнецова и др.), которое используется в комплекте с учебником «Алгебра 9 класс / Г.В. Дорофеев и др. — М.: Просвещение». При постоянном использовании контрольных необходимо купить указанное пособие.

---

Контрольная работа «Квадратичная функция»

В контрольной работе проверяются умения:

• использовать функциональную терминологию и символику;
• читать график, описывающий реальный процесс;
• находить нули функции, заданной формулой;
• строить график квадратичной функции;
• по графику отвечать на вопросы, касающиеся свойств квадратичной функции;
• находить область определения функции, заданной формулой;
• решать квадратные неравенства.

---

 

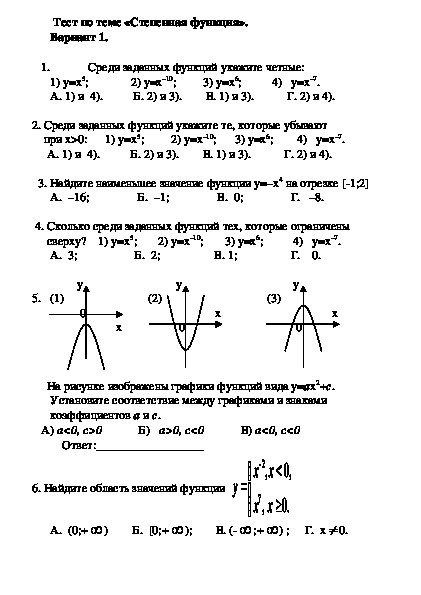
Контрольная работа по алгебре К-2

OCR-версия заданий (транскрипт)

Алгебра 9 Дорофеев К-2.  Вариант 1

1. Мяч подбросили вертикально вверх с высоты 1,5 м, придав ему начальную скорость 10 м/с. По графику изменения высоты его полёта в зависимости от времени движения ответьте на вопросы: а) Через какое время мяч достиг максимальной высоты? б) На какой высоте находился мяч через 0,5 с после начала полёта?
2. Функция задана формулой у = 3х2 + 2х — 5. а) Найдите значение функции при х = -2. б) При каких значениях х функция принимает значение, равное -5? в) Найдите нули функции.
3. а) Постройте график функции у = х2 + 2х — 8. б) Укажите значения аргумента, при которых функция принимает отрицательные значения. в) Укажите промежуток, на котором функция убывает.
4. Решите неравенство х2 — 3х + 2 > 0.
5. Найдите область определения выражения
6. Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = -х2 вдоль оси х на 4 единицы вправо и вдоль оси у на 2 единицы вверх.
7. При каких значениях b и с вершина параболы у = 2х2 + bх + с находится в точке (-1; 3)?

Дополнительное задание
8. На рисунке изображён график функции у = ах2 + bх + с. Определите знаки коэффициентов а, b и с.

Алгебра 9 Дорофеев К-2.  Вариант 1

1. Мяч подбросили вертикально вверх с высоты 1,5 м, придав ему начальную скорость 10 м/с. По графику изменения высоты его полёта в зависимости от времени движения ответьте на вопросы: а) Через какое время мяч достиг максимальной высоты? б) На какой высоте находился мяч через 0,5 с после начала полёта?
2. Функция задана формулой у = 3х2 + 2х — 5. а) Найдите значение функции при х = -2. б) При каких значениях х функция принимает значение, равное -5? в) Найдите нули функции.
3. а) Постройте график функции у = х2 + 2х — 8. б) Укажите значения аргумента, при которых функция принимает отрицательные значения. в) Укажите промежуток, на котором функция убывает.
4. Решите неравенство х2 — 3х + 2 > 0.
5. Найдите область определения выражения
6. Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = -х2 вдоль оси х на 4 единицы вправо и вдоль оси у на 2 единицы вверх.
7. При каких значениях b и с вершина параболы у = 2х2 + bх + с находится в точке (-1; 3)?

Дополнительное задание
8. На рисунке изображён график функции у = ах2 + bх + с. Определите знаки коэффициентов а, b и с.

 

Решения и ОТВЕТЫ
на контрольную работу

Вариант 1. Смотреть ответы

Вариант 2. Смотреть ответы

Вариант 3. Смотреть ответы

Вариант 4. Смотреть ответы

 

Вернуться к Списку контрольных работ по алгебре 9 класс (УМК Дорофеев)

---

Алгебра 9 Дорофеев К-2. Контрольная работа по алгебре «Квадратичная функция» в 9 классе с ответами. Цитаты из пособия для учащихся «Алгебра. Контрольные работы» (авт. Л.В. Кузнецова и др.) использованы в учебных целях.

 

Контрольная работа по алгебре «Степенная функция» (9 класс)

1 вариант                                                                                                                          2 вариант Контрольная работа № 3 по теме «Степенная функция» 1.  Найти область определения функции: 1) у =  15 х 6      2) у =  18 1) у = 5х8 – 4х2        2) у =                                                  1) у =  22 х 2. Исследовать функцию на четность и нечетность: 2 х 2 х                                            1) у = 9х6 + 2х2        2) у =  х7        2)  у =  1 8 х 2 х 2 48  23 х 3. В одной системе координат построить графики данных функций и найти точки их пересечения: 2 2           у =  8 х                                                                                           у =  1 х           у = х2                                                                                           у = х3 4. Решить уравнение:  = х – 1                                                                                    11х 3х  = х – 5               у =  х2 + 3х – 1                                                                            у = х2 – х – 4 5. Не строя графики функций, решить систему уравнений:             у =  3 х                                                                                            у =  4 х       1 вариант                                                                                                                          2 вариант Контрольная работа № 3 по теме «Степенная функция» 1.

 Найти область определения функции: 1) у =  15 х 6      2) у =  18 1) у = 5х8 – 4х2        2) у =                                                  1) у =  22 х 2. Исследовать функцию на четность и нечетность: 2 х 2 х                                            1) у = 9х6 + 2х2        2) у =  х7        2)  у =  1 8 х 2 х 2 48  23 х 3. В одной системе координат построить графики данных функций и найти точки их пересечения:           у =  8 х                                                                                           у =  1 х           у = х2                                                                                           у = х3 4. Решить уравнение:  = х – 1                                                                                    11х 3х  = х – 5               у =  х2 + 3х – 1                                                                            у = х2 – х – 4 5. Не строя графики функций, решить систему уравнений:             у =  3 х                                                                                            у =  4 х 1 вариант                                                                                                                          2 вариант Контрольная работа № 3 по теме «Степенная функция» 1.

 Найти область определения функции: 1) у =       2) у =  18  22 х   3) у =                               1) у =  2 х7        2)  у =  48  23 х    3) у =  15 х 6                                       1) у = 5х8 – 4х2        2) у =  2. Исследовать функцию на четность и нечетность: 2 х 2 х      3) у =  2х +    х           1) у = 9х6 + 2х2        2) у =  1 8 х 2 х 2     3) у = х3 ­    х 3. В одной системе координат построить графики данных функций и найти точки их пересечения:     1)   у =  8 х                        2)       у =    х + 1                              1)      у =  1 х                       2)      у =    х + 2           у = х2                                  у = х3                                                у = х3   у = х2 1 вариант                                                                                                                          2 вариант Контрольная работа № 3 по теме «Степенная функция» 1. Найти область определения функции: 1) у =       2) у =  18  22 х   3) у =                               1) у =  15 х 6                                       2 х7        2)  у =  48  23 х    3) у =  1) у = 5х8 – 4х2        2) у =  2.  Исследовать функцию на четность и нечетность: 2 х 2 х      3) у =  2х +    х           1) у = 9х6 + 2х2        2) у =  1 8 х 2 х 2     3) у = х3 ­    х 3. В одной системе координат построить графики данных функций и найти точки их пересечения:     1)   у =  8 х                        2)       у =    х + 1                              1)      у =  1 х                       2)      у =    х + 2           у = х2                                  у = х3                                                у = х3   у = х2 1 вариант                                                                                                                          2 вариант Контрольная работа № 3 по теме «Степенная функция» 1. Найти область определения функции: 1) у =       2) у =  18  22 х   3) у =                               1) у =  15 х 6                                       2 х7        2)  у =  48  23 х    3) у =  1) у = 5х8 – 4х2        2) у =  2. Исследовать функцию на четность и нечетность: 2 х 2 х      3) у =  2х +    х           1) у = 9х6 + 2х2        2) у =  1 8 х 2 х 2     3) у = х3 ­    х 3.  В одной системе координат построить графики данных функций и найти точки их пересечения:     1)   у =  8 х                        2)       у =    х + 1                              1)      у =  1 х                       2)      у =    х + 2           у = х2                                  у = х3                                                у = х3   у = х2

Контрольные работы по алгебре. 9-й класс

Контрольные работы по алгебре составлены к учебнику алгебры 9-гокласса Ю. Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С. Б. Суворовой,  но могут быть использованы и при изучении алгебры по учебникам других авторов.

1. Контрольная работа №1 Квадратный трехчлен. Квадратичная функция. (Приложение 1)
2. Контрольная работа №2 «Уравнения  и  неравенства  с одной переменной» (Приложение 2)
3. Контрольная работа № 3Системы уравнений с двумя переменными. (Приложение 3)
4. Контрольная работа № 4 Арифметическая прогрессия. (Приложение 4)
5. Контрольная работа №5 Геометрическая прогрессия ( Приложение 5)
6. Контрольная работа № 6 Степенная функция. Корень n-й степени. (Приложение 6)
7. Контрольная работа №7 Степень с рациональным показателем и ее свойства. (Приложение 7)

Литература:

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. «Алгебра 9»  издательство «Просвещение», 2008;
2. Математика.  9 класс. Тематические тесты для подготовке к ГИА-9. Под редакцией Ф.Ф.Лысенко,  С.Ю.Кулабуховой, Легион-М, Ростов-на-Дону. 2011
3. Алгебра. 9 класс. Тематические тесты. Ю.П.Дудницын, В. Л.Кронгауз  М. Просвещение. 2011.
4. Дидактические материалы. Алгебра. 9 класс. Макарычев Ю.Н., Миндюк Н.Г.,Крайнева Л.Б.   издательство «Просвещение», 2012;
5. Государственная итоговая аттестация. Тематические тренировочные задания. 9 класс. Базовый уровень, под редакцией Е.А. Семенко, М.,«Экзамен», 2011.
6. КИМ по алгебре 9 класс. Мартышова Л.И.,М. «Вако», 2010г.

Контрольная работа № 6 по математике (степенная функция) для 9-го класса от Ассоциации учителей в 2017 году

Ответы

Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Статистика и загрузка

Скачать

Если загрузка не началась автоматически, повторите попытку или нажмите сюда!

Просмотров	495	201	Загрузок
Добавил	Гость	09. 06.2018	Дата
День	Суббота	00:51	Время

Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.

Все материалы сайта представлены исключительно в ознакомительных целях.

---

Источник/автор материала: Сайт Ассоциации учителей математики Цумадинского района

---

Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.

Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.

---

Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]

Справочные материалы

Загрузка формул…

Загрузка тестирования…

Обсуждения

Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Контрольная работа №2 «Квадратичная функция. Степенная функция» (9 класс) Вариант Постройте график функции. Найдите с помощью графика

Контрольная работа №2 «Квадратичная функция. Степенная функция» (9 класс) Вариант — страница №1/1

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 1.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наименьшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 1.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наименьшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 1.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наименьшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 1.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наименьшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 1.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наименьшее значение функции .

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 2.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наибольшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 2.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наибольшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 2.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наибольшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 2.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наибольшее значение функции .

———————————————————————————————————————————-

Контрольная работа № 2 «Квадратичная функция. Степенная функция» (9 класс)

Вариант 2.

1. Постройте график функции . Найдите с помощью графика:

а) нули функции;

б) промежутки, в которых y > 0 и в которых y ;

в) промежутки, на которых функция возрастает, убывает;

г) наименьшее значение функции.

2. Вычислите:

3. Решите уравнение: а) б) в)

4. Является ли четной или нечетной функция а) ; б) .

5. Найдите наибольшее значение функции .

5.2 Функции мощности и полиномиальные функции — College Algebra

Цели обучения

В этом разделе вы:

• Определите степенные функции.
• Определите конечное поведение степенных функций.
• Определите полиномиальные функции.
• Укажите степень и старший коэффициент полиномиальных функций.

Рисунок 1 (кредит: Джейсон Бэй, Flickr)

Предположим, что на небольшом острове процветает определенный вид птиц.Его население за последние несколько лет показано в таблице 1.

Год	20092009	20102010	20112011	20122012	20132013
Популяция птиц	800800	897897	992992	1,0831,083	1,1691,169

Таблица 1

Население можно оценить с помощью функции P (t) = — 0. 3t3 + 97t + 800, P (t) = — 0,3t3 + 97t + 800, где P (t) P (t) представляет популяцию птиц на острове через tt лет после 2009 года. Мы можем использовать эту модель для оценки максимального количества птиц. население и когда это произойдет. Мы также можем использовать эту модель, чтобы предсказать, когда популяция птиц исчезнет с острова. В этом разделе мы рассмотрим функции, которые мы можем использовать для оценки и прогнозирования этих типов изменений.

Определение функций питания

Прежде чем мы сможем понять проблему с птицами, будет полезно понять другой тип функции.Степенная функция — это функция с одним членом, который является произведением действительного числа, коэффициента , и переменной, возведенной в фиксированное действительное число.

В качестве примера рассмотрим функции для площади или объема. Функция для площади круга радиусом rr является

и функцию объема шара радиусом rr это

Оба они являются примерами степенных функций, потому что они состоят из коэффициента ππ или 43π, 43π, умноженного на переменную rr, возведенную в степень.

Функция мощности

Степенная функция — это функция, которая может быть представлена ​​в форме

где kk и pp — действительные числа, а kk известен как коэффициент.

Вопросы и ответы

Является ли f (x) = 2xf (x) = 2x степенной функцией?

Нет. Степенная функция содержит переменную базу, возведенную в фиксированную степень. Эта функция имеет постоянную базу, возведенную в переменную степень. Это называется экспоненциальной функцией, а не степенной функцией.

Пример 1

Определение функций питания

Какие из следующих функций являются степенными?

f (x) = 1 Константа f (x) = x Идентификация функции f (x) = x 2 Квадратичная функция f (x) = x 3 Кубическая функция f (x) = 1x Обратная функция f (x) = 1x 2 Возведенная в квадрат функция f (x) = x Функция квадратного корня f (x) = x3Кубическая функция f (x) = 1Константная функция f (x) = x Идентификация функции f (x) = x2 Квадратная функция f (x) = x3 Кубическая функция f (x) = 1xРеципрокная функцияf (x) = 1×2Взаимная функция в квадрате f (x) = xКвадратная функция f (x) = x3 Функция кубического корня

Решение

Все перечисленные функции являются степенными.

Постоянные и тождественные функции являются степенными функциями, потому что их можно записать как f (x) = x0f (x) = x0 и f (x) = x1f (x) = x1 соответственно.

Квадратичная и кубическая функции являются степенными функциями с целыми степенями f (x) = x2f (x) = x2 и f (x) = x3.f (x) = x3.

Обратные и обратные квадраты функций являются степенными функциями с отрицательными целыми степенями, поскольку их можно записать как f (x) = x − 1f (x) = x − 1 и f (x) = x − 2.f (x ) = х − 2.

Функции квадратного и кубического корня являются степенными функциями с дробными степенями, потому что они могут быть записаны как f (x) = x12f (x) = x12 или f (x) = x13.f (х) = х13.

Попробуй # 1

Какие функции являются степенными?

f (x) = 2x⋅4x3g (x) = — x5 + 5x3h (x) = 2×5−13×2 + 4f (x) = 2x⋅4x3g (x) = — x5 + 5x3h (x) = 2×5−13×2 + 4

Определение конечного поведения степенных функций

На рисунке 2 показаны графики f (x) = x2, g (x) = x4f (x) = x2, g (x) = x4 и h (x) = x6, h ( x) = x6, которые являются степенными функциями с четными целочисленными степенями. Обратите внимание, что эти графики имеют похожие формы, очень похожие на квадратичную функцию в наборе инструментов.Однако по мере увеличения мощности графики несколько сглаживаются вблизи начала координат и становятся круче при удалении от начала координат.

Рис. 2 Четно-степенные функции

Чтобы описать поведение при увеличении и увеличении числа, мы используем идею бесконечности. Мы используем символ ∞∞ для положительной бесконечности и −∞ − ∞ для отрицательной бесконечности. Когда мы говорим, что «xx стремится к бесконечности», что может быть символически записано как x → ∞, x → ∞, мы описываем поведение; мы говорим, что xx неограниченно увеличивается.

С положительной функцией четной степени, когда входное значение неограниченно увеличивается или уменьшается, выходные значения становятся очень большими положительными числами. Точно так же мы могли бы описать это поведение, сказав, что по мере приближения xx к положительной или отрицательной бесконечности значения f (x) f (x) неограниченно увеличиваются.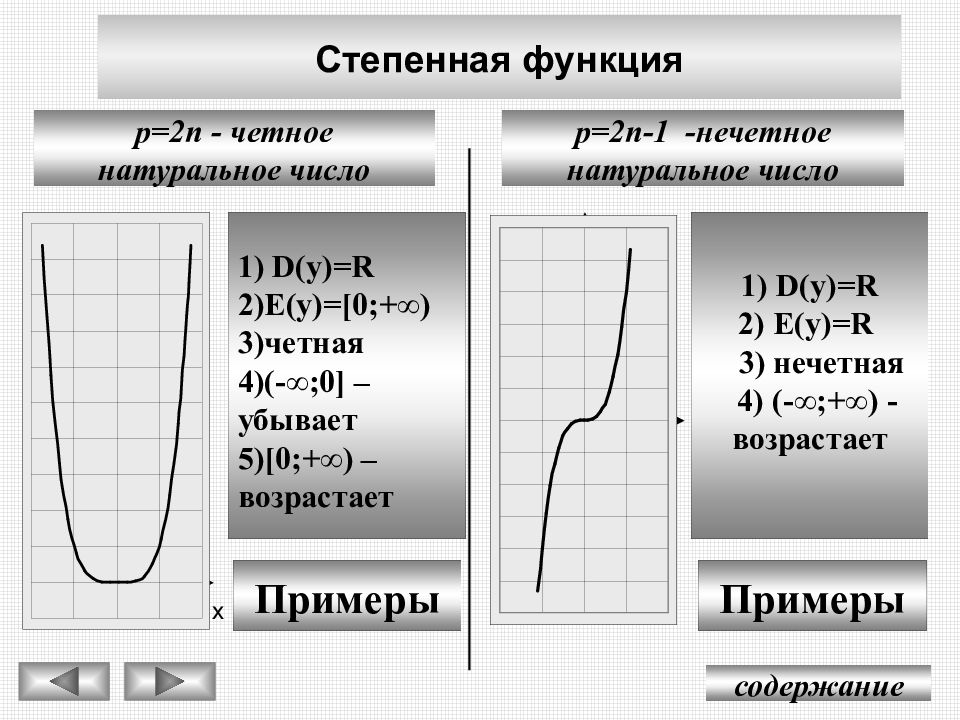 В символической форме мы могли бы записать

как x → ± ∞, f (x) → ∞ при x → ± ∞, f (x) → ∞

На рисунке 3 показаны графики f (x) = x3, g (x) = x5, f (x) = x3, g (x) = x5 и h (x) = x7, h (x) = x7, которые являются степенными функциями с нечетными целочисленными степенями.Обратите внимание, что эти графики похожи на кубическую функцию в наборе инструментов. Опять же, по мере увеличения мощности графики сглаживаются около начала координат и становятся более крутыми по мере удаления от начала координат.

Рисунок 3 Функции нечетной степени

Эти примеры показывают, что функции вида f (x) = xnf (x) = xn обнаруживают симметрию того или иного вида. Во-первых, на рисунке 2 мы видим, что четные функции вида f (x) = xn, nf (x) = xn, n even симметричны относительно оси y-y. На рисунке 3 мы видим, что нечетные функции вида f (x) = xn, nf (x) = xn, n odd, симметричны относительно начала координат.

Для этих функций нечетной степени, как xx стремится к отрицательной бесконечности, f (x) f (x) убывает неограниченно. Как xx стремится к положительной бесконечности, f (x) f (x) неограниченно увеличивается. В символической форме пишем

при x → −∞, f (x) → −∞ при x → ∞, f (x) → ∞ при x → −∞, f (x) → −∞ при x → ∞, f (x) → ∞

поведение графика функции, когда входные значения становятся очень маленькими (x → −∞x → −∞) и становятся очень большими (x → ∞x → ∞), называется конечным поведением функции. Мы можем использовать слова или символы для описания конечного поведения.

На рисунке 4 показано конечное поведение степенных функций в форме f (x) = kxnf (x) = kxn, где nn — неотрицательное целое число, зависящее от степени и константы.

Рисунок 4

Как это сделать

Для данной степенной функции f (x) = kxnf (x) = kxn, где nn — неотрицательное целое число, определите конечное поведение.

1. Определите, является ли степень четной или нечетной.
2. Определите, является ли константа положительной или отрицательной.
3. Используйте рисунок 4 для определения конечного поведения.

Пример 2

Определение конечного поведения функции мощности

Опишите конечное поведение графика f (x) = x8.f (x) = x8.

Решение

Коэффициент равен 1 (положительный), а показатель степенной функции равен 8 (четное число). Когда xx приближается к бесконечности, выход (значение f (x) f (x)) неограниченно увеличивается. Запишем x → ∞, f (x) → ∞.x → ∞, f (x) → ∞. Когда xx приближается к отрицательной бесконечности, выход неограниченно увеличивается.В символической форме при x → −∞, f (x) → ∞.x → −∞, f (x) → ∞. Мы можем графически представить функцию, как показано на рисунке 5.

Рисунок 5

Пример 3

Определение конечного поведения функции мощности.

Опишите конечное поведение графика f (x) = — x9.f (x) = — x9.

Решение

Показатель степенной функции равен 9 (нечетное число).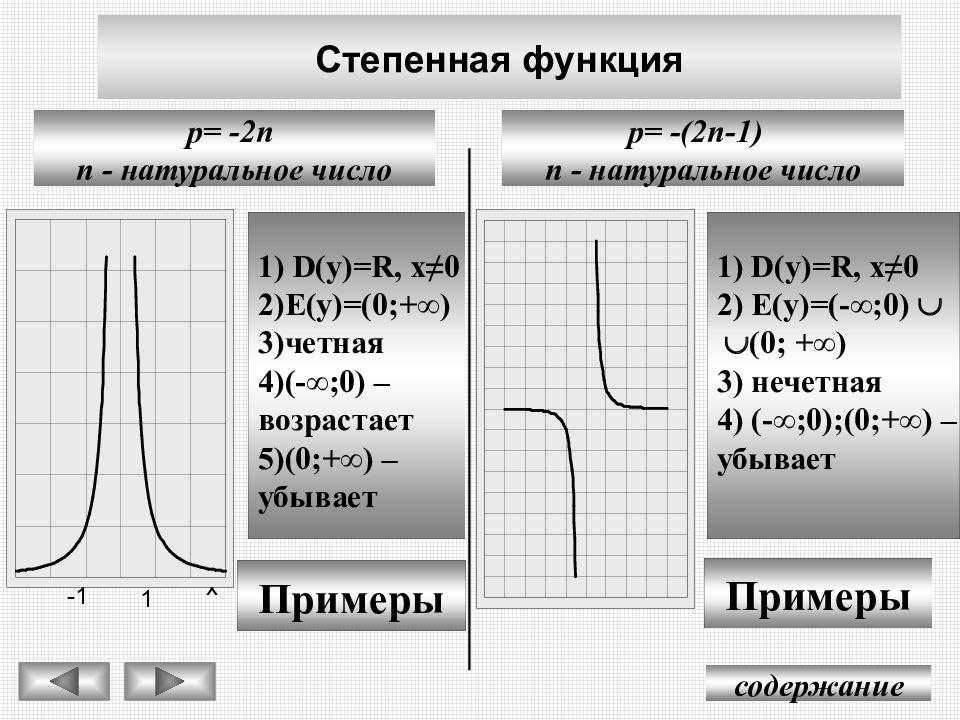 Поскольку коэффициент равен –1–1 (отрицательный), график является отражением относительно оси x-x графика f (x) = x9.е (х) = х9. На рисунке 6 показано, что по мере приближения xx к бесконечности выход неограниченно уменьшается. Когда xx приближается к отрицательной бесконечности, выход неограниченно увеличивается. В символической форме мы бы написали

при x → −∞, f (x) → ∞ при x → ∞, f (x) → −∞ при x → −∞, f (x) → ∞ при x → ∞, f (x) → −∞

Рисунок 6

Анализ

Мы можем проверить нашу работу, используя функцию таблицы в графической утилите.

х х	е (х) е (х)
–10	1 000 000 000
–5	1 953 125
0	0
5	–1,953,125
10	–1 000 000 000

Таблица 2

Из таблицы 2 видно, что когда мы подставляем очень маленькие значения для x, x, результат очень большой, а когда мы заменяем очень большие значения x, x, вывод очень маленький. (означает, что это очень большое отрицательное значение).

Попробуй # 2

Опишите словами и символами конечное поведение f (x) = — 5×4.f (x) = — 5×4.

Определение полиномиальных функций

В Мексиканском заливе прорвался нефтепровод, в результате чего образовалось нефтяное пятно примерно круглой формы. В настоящее время радиус пятна составляет 24 мили, но каждую неделю этот радиус увеличивается на 8 миль. Мы хотим написать формулу для площади, покрытой нефтяным пятном, объединив две функции. Радиус rr разлива зависит от количества недель ww что прошло.Эта связь линейна.

Мы можем объединить это с формулой для площади AA круга.

Составление этих функций дает формулу для площади в неделях.

A (w) = A (r (w)) = A (24 + 8w) = π (24 + 8w) 2A (w) = A (r (w)) = A (24 + 8w) = π (24+ 8w) 2

Умножение дает формулу.

A (w) = 576π + 384πw + 64πw2A (w) = 576π + 384πw + 64πw2

Эта формула является примером полиномиальной функции . Полиномиальная функция состоит либо из нуля, либо из суммы конечного числа ненулевых членов, каждое из которых является произведением числа, называемого коэффициентом члена, и переменной, возведенной в неотрицательную целую степень.

Полиномиальные функции

Пусть nn быть неотрицательным целым числом. Полиномиальная функция — это функция, которую можно записать в виде

f (x) = тревога + … + a2x2 + a1x + a0f (x) = тревога + … + a2x2 + a1x + a0

Это называется общей формой полиномиальной функции. Каждый aiai является коэффициентом и может быть любым действительным числом, но anan cannot = 0. Каждое выражение aixiaixi является членом полиномиальной функции.

Пример 4

Определение полиномиальных функций

Какие из следующих полиномиальных функций?

f (x) = 2×3⋅3x + 4g (x) = — x (x2−4) h (x) = 5x + 2f (x) = 2×3⋅3x + 4g (x) = — x (x2−4) h (х) = 5х + 2

Решение

Первые две функции являются примерами полиномиальных функций, потому что их можно записать в форме f (x) = dancingn +… + a2x2 + a1x + a0, f (x) = тревога + … + a2x2 + a1x + a0, где степени — неотрицательные целые числа, а коэффициенты — действительные числа.

• f (x) f (x) может быть записано как f (x

3.3 Функции мощности и полиномиальные функции — Precalculus

Перейти к содержаниюPrecalculusPrecalculus3.3 Функции мощности и полиномиальные функции и обозначение функций

1.2 Домен и диапазон

1.3 Скорости изменений и поведение графиков

1.4 Состав функций

1.5 Преобразование функций

1.6 Абсолютные функции

1.7 Обратные функции

Обзор главы

1. Ключевые термины
2. Ключевые уравнения
3. Ключевые концепции

Упражнения

1. Упражнения на обзор
2. Практический тест

2 Линейные функции

1. Введение в линейные функции
2. 2.1 Линейные функции
3. 2.2 Графики линейных функций
4. 2.3 Моделирование с помощью линейных функций
5. 2.4 Подгонка линейных моделей к данным
6. Обзор главы
   1. Ключевые термины
   2. Ключевые уравнения
   3. Ключевые концепции
Обзор

Упражнения

Практический тест

3 Полиномиальные и рациональные функции

1. Введение в полиномиальные и рациональные функции
2. 3.1 Комплексные числа
3. 3.2 Квадратичные функции
4. 3.3 Функции степеней и полиномиальные функции
5. 3.4 Графы полиномиальных функций
6. 3.5 Делительные полиномы
7. 3.6 Нули полиномиальных функций
8. 3.7 Рациональные функции
10. Радиационные функции
3.80008 Рациональные функции
11. Моделирование с использованием вариации
12. Обзор главы
    1. Ключевые термины
    2. Ключевые уравнения
    3. Ключевые концепции
13. Упражнения
    1. Обзор упражнений
    2. Практический тест

4 Экспоненциальные и логические функции Функции

4.1 Экспоненциальные функции

4.2 Графики экспоненциальных функций

4.3 Логарифмические функции

4.4 Графики логарифмических функций

4.5 Логарифмические свойства

Calculus II — Power Series and Functions

Онлайн-заметки Павла

Примечания Быстрая навигация Скачать

• Перейти к
• Примечания
• Проблемы с практикой
• Проблемы с назначением
• Показать / Скрыть
• Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Серия Power
• Серия Тейлор
• Разделы
• Параметрические уравнения и полярные координаты
• Векторы
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер комплексных чисел

POWER функция — служба поддержки Office

Допустим, вы хотите рассчитать чрезвычайно малый уровень допуска для обработанной детали или огромное расстояние между двумя галактиками.2.

Пример

Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.

Формула	Описание	R esult
= МОЩНОСТЬ (5,2)	5 кв.	25
= МОЩНОСТЬ (98.6,3.2)	98,6 возведен в степень 3,2.	2401077.222
= МОЩНОСТЬ (4,5 / 4)	4 в степени 5/4.	5.656854249

Числовые функции — PowerQuery M

• 07.04.2020
• 3 минуты на чтение

В этой статье

Эти функции создают числовые значения и управляют ими.

Число

Константы

Информация

Преобразование и форматирование

Функция	Описание
Байт.С	Возвращает 8-битное целое число из заданного значения.
Валюта. От	Возвращает значение валюты из заданного значения.
Десятичный. Из	Возвращает десятичное число из заданного значения.
Двойной. Из	Возвращает значение типа Double из заданного значения.
внутр. Из	Возвращает 8-битовое целое число со знаком из заданного значения.
Внутр.16. Из	Возвращает 16-битное целочисленное значение из заданного значения.
Внутр.32. Из	Возвращает 32-битное целочисленное значение из заданного значения.
Внут64. С	Возвращает 64-битное целочисленное значение из заданного значения.
Номер от	Возвращает числовое значение из значения.
Number.FromText	Возвращает числовое значение из текстового значения.
Number.ToText	Возвращает текстовое значение из числового значения.
Процент от	Возвращает процентное значение от заданного значения.
Одноместный. С	Возвращает одно числовое значение из заданного значения.

Округление

Функция	Описание
Номер Круглый	Возвращает число (n), допускающее значение NULL, если значение является целым числом.
Number.RoundAwayFromZero	Возвращает Number.RoundUp (значение), если значение> = 0, и Number.RoundDown (значение), если значение <0.
Номер.Круглый вниз	Возвращает наибольшее целое число, меньшее или равное числовому значению.
Number.RoundTowardZero	Возвращает Number.RoundDown (x), если x> = 0, и Number.RoundUp (x), если x <0.
Номер. Раунд вверх	Возвращает большее целое число, большее или равное числовому значению.

Операции

Функция	Описание
Номер ABS	Возвращает абсолютное значение числа.
Число комбинаций	Возвращает количество комбинаций заданного количества элементов для необязательного размера комбинации.
Кол-во Exp	Возвращает число, представляющее e в степени.
Номер.Факториал	Возвращает факториал числа.
Number.IntegerDivide	Делит два числа и возвращает целую часть полученного числа.
Номер Ln	Возвращает натуральный логарифм числа.
Номер журнала	Возвращает логарифм числа по основанию.
Номер. Журнал10	Возвращает десятичный логарифм числа.
Номер.Мод	Делит два числа и возвращает остаток от полученного числа.
Число перестановок	Возвращает количество общих перестановок заданного количества элементов для необязательного размера перестановки.
Кол. Мощность	Возвращает число, возведенное в степень.
Номер Знак	Возвращает 1 для положительных чисел, -1 для отрицательных чисел или 0 для нуля.
Номер.Sqrt	Возвращает квадратный корень числа.

Случайно

Функция	Описание
Число Случайное	Возвращает случайное дробное число от 0 до 1.
Number.RandomBetween	Возвращает случайное число между двумя заданными числовыми значениями.

Тригонометрия

байт

Как возвести число в степень в Excel с помощью формулы и оператора

Часто пользователям нужно возвести число в степень.Как это сделать правильно с помощью «Excel»?

В этой статье мы постараемся разобраться в популярных вопросах пользователей и дадим инструкции, как правильно пользоваться системой. MS Office Excel позволяет выполнять ряд математических функций: от самых простых до самых сложных. Эта универсальная программа рассчитана на все случаи жизни.

Взаимодействие с другими людьми

как возвести в степень в excel?

Прежде чем искать нужную функцию, обратите внимание на математические законы:

1. «1» останется «1» в любой степени.».

Мы построили 8 в «квадрат» (то есть до второй степени) и получили результат вычисления в ячейку «A2».

Вариант 2. Использование функции

В Microsoft Office Excel есть удобная функция «МОЩНОСТЬ», которую вы можете активировать для простых и сложных математических вычислений.

Функция выглядит так:

= МОЩНОСТЬ (Число, Степень)

ВНИМАНИЕ!

1. Цифры в этой формуле указываются без пробелов и других знаков.
2. Первая цифра — это значение «число». Это основа (то есть фигура, которую мы строим). Microsoft Office Excel позволяет вводить любое действительное число.
3. Вторая цифра — величина «градус». Это индикатор, в котором мы строим первую фигуру.
4. Значения обоих параметров могут быть меньше нуля (со знаком «-»).

Взаимодействие с другими людьми

Формула возведения в степень в Excel

Примеры использования функции = МОЩНОСТЬ ().

Использование мастера функций:

1. Запустите мастер функций с помощью комбинации горячих клавиш SHIFT + F3 или щелкните кнопку в начале строки формулы «fx» (вставка функции). Из выпадающего списка «Или выберите категорию:» выберите «Math & Trig», а в нижнем поле «Select a function:» укажите нужную нам функцию «POWER» и нажмите OK. Или выберите: «ФОРМУЛЫ» — «Библиотека функций» — «Math & Trig» — «POWER».
2. В появившемся диалоговом окне заполните поля аргументами.Например, нам нужно возвести «2» в степень до «3». Затем в первом поле введите «2», а во втором — «3».
3. Нажимаем кнопку «ОК» и получаем в ячейке, в которую была введена формула, нужное нам значение. В этой ситуации в «кубе» стоит «2», т.е. 2 * 2 * 2 = 8. Программа все рассчитала правильно и выдала вам результат.

Если вам кажется, что лишние клики — сомнительное удовольствие, предлагаем один вариант попроще.

Ввод функции вручную:

1. В строке формулы ставим знак «=» и начинаем вводить название функции.Обычно достаточно написать «= po…» — и система сама угадает, что предложит вам полезный вариант.
2. Как только вы увидели такую ​​подсказку, просто нажмите клавишу «Tab». Или вы можете продолжить писать, вручную вводя каждую букву. Затем в скобках укажите обязательные параметры: два числа, разделенных точкой с запятой.
3. После этого нажимаем «Enter» — и в ячейке появляется вычисленное значение 8.

Последовательность действий простая, а результат пользователь получает достаточно быстро.В аргументах вместо чисел можно указать ссылки на ячейки.

Степень квадратного корня в Excel

Для извлечения корня по формулам Microsoft Excel мы используем немного другой, но очень удобный способ вызова функций:

1. Перейти на вкладку «ФОРМУЛЫ». В разделе «Библиотека функций» панели инструментов щелкните инструмент «Math & Trig». И из выпадающего списка выберите опцию «SQRT».
2. Введите аргумент функции по запросу системы.В нашем случае нужно было найти корень из «25», поэтому вводим его в строку. После ввода номера просто нажмите кнопку «ОК». В ячейке отразится цифра, полученная в результате математического расчета корня.

ВНИМАНИЕ! Если нам нужно знать корень степени в Excel, мы не используем функцию = SQRT (). Напомним теорию из математики:

«Корнем n-й степени числа a является число b, n-я степень которого равна a», то есть:
ⁿ √a = b; b ⁿ = a
«Корень n-й степени из числа a будет равен увеличению степени того же числа a на 1 / n», то есть:
ⁿ √a = a ^{1 / n}
Отсюда следует, что для вычисления математической формулы корня в n-й степени например:
⁵ √32 = 2

В Excel вы должны написать по этой формуле: = 32 ^ (1/5), то есть: = a ^ (1 / n) — где a — число; N-степень:

Или через эту функцию: = МОЩНОСТЬ (32,1 / 5)

В аргументах формулы и функции вы можете указать ссылки на ячейки вместо чисел.

Как в Excel записать число в градусе?

Для вас часто важно, чтобы число в градусе правильно отображалось при печати и красиво смотрелось в таблице. Как в Excel записать число в степень? Здесь вам нужно использовать вкладку Формат ячеек. В нашем примере мы записали «3» в ячейку «А1», которая должна быть представлена ​​с точностью до -2.

Последовательность действий следующая:

1. Щелкните правой кнопкой мыши ячейку с номером и выберите во всплывающем меню вкладку «Формат ячеек».Если не получилось — найдите вкладку «Формат ячеек» в верхней панели или нажмите CTRL + 1.
2. В появившемся меню выберите вкладку «Число» и установите формат для ячейки «Текст». Щелкните ОК.
3. В ячейке A1 введите «-2» рядом с «3» и выберите его.
4. Опять вызываем формат ячеек (например, нажав горячие клавиши CTRL + 1) и теперь только нам доступна вкладка «Шрифт», где мы ставим галочку напротив «Надстрочный индекс». И жмем ОК.
5. Результат должен иметь следующее значение:

Использовать функции Excel просто и удобно.

No related posts.