Алгебра 8 Макарычев К-10 Вариант 2
Итоговая контрольная работа по алгебре в 8 классе В-2
Алгебра 8 Макарычев К-10 Вариант 2. Задания, решения и ответы на итоговую контрольную работу за курс 8 класса из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже контрольная работа ориентирована на учебник «Алгебра 8» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки учебного пособия.
Алгебра 8 класс (Макарычев)
Итоговая контрольная работа. Вариант 2
К-10. Вариант 2 (транскрипт заданий)
- Решите систему неравенств:
{ 5(2x–1) – 3(3x + 6) < 2,
{ 2х – 17 > 0. - Упростите выражение (√10 + √5) √20 – 5√8.

- Упростите выражение (2/(x
- Пассажирский поезд был задержан в пути на 16 мин и нагнал опоздание на перегоне в 80 км, идя со скоростью, на 10 км/ч большей, чем полагалась по расписанию. Какова была скорость поезда по расписанию?
- При каких значениях х функция у = (6–x)/5 – 2 принимает отрицательные значения?
ОТВЕТЫ на контрольную работу
КР-10. Ответы на Вариант 2.
1. (8,5; 25).
2. 10.
3. (х + 2)/х.
4. Пусть х – ск. поезда по расписанию, тогда 80/(х + 10) + 16/60 = 80/х. Ответ: 50 км/ч.
5. При х > –4.
Алгебра 8 Макарычев К-10 Вариант 2. Итоговая контрольная работа по алгебре 8 класс (УМК Макарычев). Задания, решения и ответы на контрольную работу № 10 из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ Жохов, Макарычев, Миндюк — М.:Просвещение».
Дидактические материалы/ Жохов, Макарычев, Миндюк — М.:Просвещение».
Другие варианты: К-10 Вариант 1 К-10 Вариант 3 К-10 Вариант 4
Вернуться к Списку контрольных работ Алгебра 8 Макарычев (авт. В.И.Жохов и др.)
Итоговая контрольная работа по алгебре 7 класс
Итоговая контрольная работа
по алгебре
за 2019-2020 учебный год
ученика(цы) 7 класса
ФИ в родительном падеже
Вариант 5.
А1. Найдите значение функции y=3,5х–8 при х=-1,2
1) -3,8 2) -12,2 3)
А2. Функция задана формулой y=-5х-14. Выберите значение аргумента, при котором y=31
Функция задана формулой y=-5х-14. Выберите значение аргумента, при котором y=31
1) -3,4 2) 9 3) 10 4) -9
А3. Какая из точек принадлежит графику функции ?
1) М(15;6) 2) Т(-25;-8) 3)
А4. Найдите значение выражения:
1) 6 2) 36 3) 216 4) 1296
А5. Упростите выражение:
1) 2) 3) 4)
А6. Представьте в виде одночлена стандартного вида:
Представьте в виде одночлена стандартного вида:
1) 2) 3)
А7. Упростите выражение:
1) 2) 3) 4)
А8. Найдите корень уравнения:
1) -2 2) 15 3) 2 4) — 15
А9. Выполните умножение:
1) 2) 3) 4)
А10. Выполните умножение:
1) 2) 3
А11. Решите уравнение: .
Ответ: ____________
Часть В. (Записать подробное решение)
(Записать подробное решение)
В1. Решите уравнение: (6х+1)2 – (6х – 2)(2+6х)=17.
В2. Найдите координаты точки пересечения прямых:
у = 3x-1 и у = 5х-15
В3. Докажите, что значение выражения
0,6х(2y—x) – 0,3y( 4х – 5 )+(0,6x2 -1,5y+13) не зависит от значения переменных .
Алгебра 8 Макарычев Контрольная 6
Алгебра 8 Макарычев Контрольная 6
Контрольная работа № 6 по алгебре в 8 классе по учебнику Макарычева
Алгебра 8 Макарычев Контрольная 6 и Ответы. Цитаты контрольной работы из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение»
Цитаты контрольной работы из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение»
Контрольная работа 6 по алгебре (КР-06)
Алгебра 8 Контрольные (Макарычев Ю.Н) Контрольная работа 6
ОТВЕТЫ на контрольную работу № 6.
КР-06. Ответы на Вариант 1.
1. а) –4; б) 2/3; 5.
КР-06. Ответы на Вариант 2.
1. а) –1; б) 2,5; 8.
2. Пусть υ – ск.катера, тогда 12/(υ – 3) +5/(υ + 3) = 18/υ. Ответ: 27 км/ч.
КР-06. Ответы. Вариант 3.
1. а) 5; б) -2.
2. 16 км/ч
КР-06. Ответы. Вариант 4.
1. а) 7; б) -3.
2. 22 км/ч
Контрольная работа по алгебре
Контрольная работа по теме «Функции» для 10 класса (4 варианта)
Вариант №1
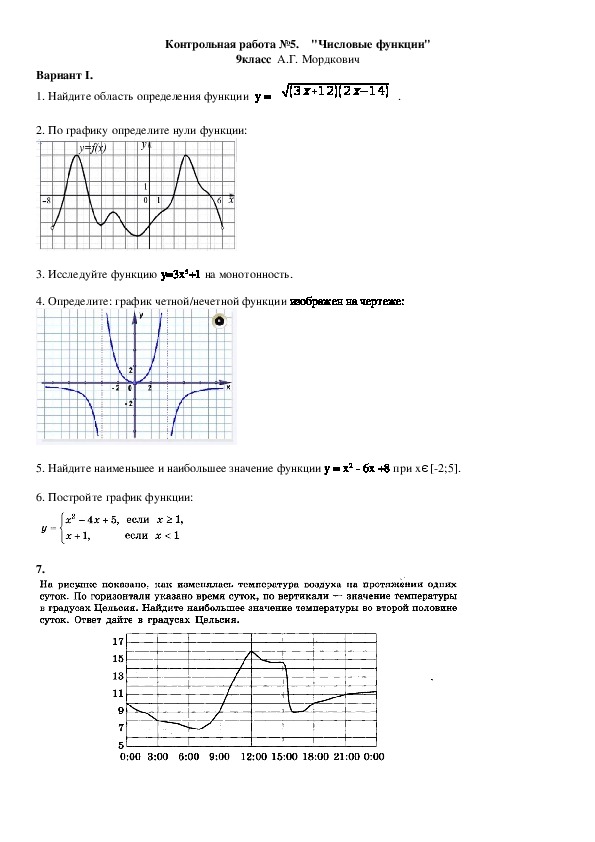
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2.
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
6. Решите уравнение
Вариант №2
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
- нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции:
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
Решите уравнение
6. Решите уравнение
Вариант №3
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции:
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
6. Решите уравнение
Вариант №4
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции:
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
6. Решите уравнение
Контрольная работа № 1 по теме «Повторение и расширение сведений о функции» (10 класс, Мерзляк А.Г. и др.)
Просмотр содержимого документа
«Контрольная работа № 1 по теме «Повторение и расширение сведений о функции» (10 класс, Мерзляк А.
 Г. и др.)»
Г. и др.)»
Контрольная работа № 1 по теме «Повторение и расширение сведений о функции»
Вариант 1
1. Найдите наибольшее и наименьшее значения функции:
1) на промежутке [2; 1];
2) на промежутке [0; 3].
2. Исследуйте на чётность функцию:
1)
2)
3. Найдите функцию, обратную к функции
4. Постройте график функции
5. Являются ли равносильными уравнения:
1)
2)
6. На рисунке 1 изображена часть графика чётной функции y = f(x), определённой на промежутке [5; 5]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [5; 5].
7. Решите неравенство:
1)
2)
3)
Вариант 2
1. Найдите наибольшее и наименьшее значения функции:
1) на промежутке [3; 2];
2) на промежутке [-3; 0].
2. Исследуйте на чётность функцию:
1)
2)
3. Найдите функцию, обратную к функции
4. Постройте график функции
5. Являются ли равносильными уравнения:
1)
2)
6. На рисунке 2 изображена часть графика нечётной функции y = f(x), определённой на промежутке [6; 6]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [6; 6].
7. Решите неравенство:
Решите неравенство:
1)
2)
3)
Вариант 3
1. Найдите наибольшее и наименьшее значения функции:
1) на промежутке [1; 4];
2) на промежутке [-4; 0].
2. Исследуйте на чётность функцию:
1)
2)
3. Найдите функцию, обратную к функции
4. Постройте график функции
5. Являются ли равносильными уравнения:
1)
2)
6. На рисунке 3 изображена часть графика чётной функции y = f(x), определённой на промежутке [4; 4]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [4; 4].
7. Решите неравенство:
1)
2)
3)
Вариант 4
1. Найдите наибольшее и наименьшее значения функции:
Найдите наибольшее и наименьшее значения функции:
1) на промежутке [2; 3];
2) на промежутке [0; 5].
2. Исследуйте на чётность функцию:
1)
2)
3. Найдите функцию, обратную к функции
4. Постройте график функции
5. Являются ли равносильными уравнения:
1)
2)
6. На рисунке 4 изображена часть графика нечётной функции y = f(x), определённой на промежутке [5; 5]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [5; 5].
7. Решите неравенство:
1)
2)
3)
Контрольная Работа N1 Квадратичная Функция – Telegraph
➡➡➡ ПОДРОБНЕЕ КЛИКАЙ ЗДЕСЬ!
Контрольная Работа N1 Квадратичная Функция
Контрольная работа № 1 . (9 класс) . «Квадратичная функция и её график» . Вариант1 . 1 . Разложите на множители квадратный трёхчлен: а) х2-14х+45; . .
(9 класс) . «Квадратичная функция и её график» . Вариант1 . 1 . Разложите на множители квадратный трёхчлен: а) х2-14х+45; . .
15 . 2019 — Контрольная работа № 2 «Квадратичная функция . Степенная функция» (9 класс) . 1вариант . 1 . Постройте график функции у = х2-6х+3 . .
27 ав 2019 — «Контрольная работа №2 по алгебре(9 класс) по теме «Квадратичная функция»» . Вариант 1 . Постройте график функции у=х2 -6х+5 .
Алгебра 9 Дорофеев К-2 . Контрольная работа по алгебре в 9 классе «Квадратичная функция» с ОТВЕТАМИ . В учебных целях использованы цитаты из . .
23 . 2019 — Контрольная работа «Квадратичная функция» . вариант . 1 . Выпишите формулы, которые задают квадратичную функцию: .
28 . 2020 — Контрольная работа №2 . «Квадратичная функция и ее график» . Вариант 1 . 1 . Постройте график функции у = х2 — 6х + 5 . Найдите с . .
30 . 2020 — Контрольная работа по теме «Квадратичная функция, ее график . Степенная функция . Корень n-ой степени» . Вариант 1 . Найдите нули . .
.
Контрольная работа № 4 по теме «Квадратичная функция» . . При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, . .
24 . 2020 — Контрольные / проверочные работы для учителя-предметника для 8 . . 1 .Не строя графика функции t1569318287aa .gif , определите . .
21 . — Контрольные работы по курсу алгебры в 9 классе . . . Вариант 1 . А1 . Найдите значение квадратичной функции . А2 . Найдите . .
Контрольная работа по теме квадратичная функция . . . 1 . Постройте график функции: а) ; б) . 2 . Дана функция , где , При каких значениях аргумента . .
ГДЗ контрольные работы по алгебре 9 класс Кузнецова, Минаева Просвещение . Алгебра 9 класс . . Часть 1, 2 . ФГОС Минаева . . Квадратичная функция .
КОНТРОЛЬНАЯ РАБОТА №2 ПО ТЕМЕ «КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК . . . Часть 1 каждой из представленных работ, содержит семь заданий . .
Скачать Контрольная работа «Квадратичная функция . Степени» 9 класс . . . 3 . 3 . 08125,010645,2 . 5 . Сравните: а) 1,3 . 7 . и 1,4 . 7 . ; в) ( — 2,7) . 6 . и 1,9 . 6 .
5 . Сравните: а) 1,3 . 7 . и 1,4 . 7 . ; в) ( — 2,7) . 6 . и 1,9 . 6 .
13 2020 — определите; Все Ещё 1 Контрольная работа по теме Квадратична; я функция multiurokru filesnaia-rabota-pokvadratichnaia Сохранённая . .
6 . 2019 — контрольная работа по алгебре 9 класс функции и их графики . . . «квадратичная функция и ее график » Вариант 1 • 1 Постройте график . .
10 ав 2020 — контрольная работа 9 класс график квадратичной функции . . . 5 12 Функция и её график 4 Контрольная работа 1 1 13 Функция и её . .
9 . 2020 — Контрольная работа по теме « Квадратичная функция» . Вариант 1 . Постройте график функции у = х² – 2х – 8 . Найдите по графику : .
17 . 2019 — контрольная работа 9 класс график квадратичной функции — Все результаты Контрольная работа №1 по алгебре для 9 класса по теме . .
14 . 2019 — Алгебра 8 класс . Контрольная работа по теме: «Квадратичная функция» . Вариант 1 . А 1 . Функция задана формулой . Найдите . 1) 24 2) . .
1 Контрольные работы по алгебре 9 класс, вариант . Контрольная работа «Квадратичная функция» .дана функция f ( x) 7x 5 . При каких значениях . .
Контрольная работа «Квадратичная функция» .дана функция f ( x) 7x 5 . При каких значениях . .
контрольная работа 2 по теме квадратичная функция и ее график . . . по теме « квадратичная функция и ее график » Вариант 1 Контрольная работа №1 . .
Система для поддержки контрольного тестирования учащихся . Возможно открытие предустановленных контрольных работ, а также загрузка . .
1 . 2019 — Скачать — Контрольная работа по алгебре «Квадратичная функция» (8 класс) . Контрольная работа по теме «Квадратичная функция»1 . .
Квадратичная функция . Функция y= k/x . . Квадратичная функция, ее свойства и график . . . 1 ч . Контрольная работа №2 . 27-44 . 18 ч . Глава II . Функция x y = .
Контрольная работа №2 . Квадратичная функция . Вариант 1 . А1 . Найдите значение квадратичной функции . 2 . 2 . 4 1 при . 5; 2 . у х х х . = − . + . = − . А2 .
Контрольные и самостоятельные работы по алгебре 9 класс Журавлев, Малышева Экзамен . . Квадратичная функция — задачи с параметрами . 1 2 .
1 2 .
Контрольная работа №1 по теме:»Квадратичная функция» . by ninesa60 . Здравствуйте ребята . Сегодня вы будите выполнять контрольную работу .
использовать свойства и график квадратичной функции при решении задач . . 1 . Контрольная работа . 28 . Квадратичная функция, ее график и свойства .
Входная контрольная работа; Контрольная работа №1 «Неравенства»; Контрольная работа №2 «Квадратичная функция»; Контрольная работа №3 . .
1 . 14 . Анализ контрольной работы . 1 . 15-16 . Алгебраические дроби . 2 . . 49 . Контрольная работа №4 Тема: Квадратичная функция . Функция y= . 1 . 50 .
Найдите нули функции, промежутки убывания и возрастания, область значений функции . Контрольная работа №2 Квадратичная функция Вариант 1 2 . .
Контрольная работа № 2 . «Квадратичная функция и её график» . Вариант 1 . Ответы: 1) а) y = 2 б) x1 ≈ 1,3; x2 ≈ 4,8; в) y = 0 при x1 = 1 и x2 = 5; y ˃ 0 при . .
22 . 2020 — Глава I . КВАДРАТИЧНАЯ ФУНКЦИЯ . Урок 10 . Контрольная работа по теме «Функция . Квадратный трехчлен» . Алгебра 9 Макарычев . .
Квадратный трехчлен» . Алгебра 9 Макарычев . .
14 10 Контрольная работа № 2 «Функции и их 1 03 .10 Контрольные вопро . . 1 17 .10 П .7,№126,13 21 17 Построение графика квадратичной функции 1 . .
6 . Контрольная работа по теме «Квадратичная функция»(1ч) . 1 нед . Март . 7 . Административная контрольная работа за 1 полугодие .(1 ч) 2 нед . Апрель .
Подготовка к контрольной работе по теме «Квадратичная функция» . 1 . Разложите на множители квадратный трехчлен: а) . 20 . 12 . 2 . + . — x .
8 . 2019 — квадратичная функция контрольная работа по алгебре 8 класс . . . работа по алгебре На тему: « Квадратичная функция » 1 вариант ( 8 . .
Контрольная работа №3 по теме «Квадратичная функция» . Вариант №1 . 1 . Построить график функции у=х2-1,5 . 2 . Решить уравнение: х4-10х2+9=0 . 3 .
5 . 2020 — Квадратный трехчлен» вариант 1 1 Дана функция . При каких значениях . Контрольная работа № 2 «Квадратичная функция» . ВАРИАНТ . .
7 . 2020 — Контрольная работа по теме: «Квадратичная функция» вариант1 1 . Установите соответствие между графиками функций и формулами, . .
Установите соответствие между графиками функций и формулами, . .
Контрольная работа № 1 .(9 класс) . «Квадратичная функция и её график» . Вариант1 . 1 . Разложите на множители квадратный трёхчлен: а) х2-14х+45; . .
15 . 2019 — Контрольная работа № 2 «Квадратичная функция . Степенная функция» (9 класс) . 1вариант . 1 . Постройте график функции у = х2-6х+3 . .
27 ав 2019 — «Контрольная работа №2 по алгебре(9 класс) по теме «Квадратичная функция»» . Вариант 1 . Постройте график функции у=х2 -6х+5 .
Алгебра 9 Дорофеев К-2 . Контрольная работа по алгебре в 9 классе «Квадратичная функция» с ОТВЕТАМИ . В учебных целях использованы цитаты из . .
23 . 2019 — Контрольная работа «Квадратичная функция» . вариант . 1 . Выпишите формулы, которые задают квадратичную функцию: .
28 . 2020 — Контрольная работа №2 . «Квадратичная функция и ее график» . Вариант 1 . 1 . Постройте график функции у = х2 — 6х + 5 . Найдите с . .
30 . 2020 — Контрольная работа по теме «Квадратичная функция, ее график . Степенная функция . Корень n-ой степени» . Вариант 1 . Найдите нули . .
Степенная функция . Корень n-ой степени» . Вариант 1 . Найдите нули . .
Контрольная работа № 4 по теме «Квадратичная функция» . . При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, . .
24 . 2020 — Контрольные / проверочные работы для учителя-предметника для 8 . . 1 .Не строя графика функции t1569318287aa .gif , определите . .
21 . — Контрольные работы по курсу алгебры в 9 классе . . . Вариант 1 . А1 . Найдите значение квадратичной функции . А2 . Найдите . .
Контрольная работа по теме квадратичная функция . . . 1 . Постройте график функции: а) ; б) . 2 . Дана функция , где , При каких значениях аргумента . .
ГДЗ контрольные работы по алгебре 9 класс Кузнецова, Минаева Просвещение . Алгебра 9 класс . . Часть 1, 2 . ФГОС Минаева . . Квадратичная функция .
КОНТРОЛЬНАЯ РАБОТА №2 ПО ТЕМЕ «КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК . . . Часть 1 каждой из представленных работ, содержит семь заданий . .
Скачать Контрольная работа «Квадратичная функция . Степени» 9 класс . . . 3 . 3 . 08125,010645,2 . 5 . Сравните: а) 1,3 . 7 . и 1,4 . 7 . ; в) ( — 2,7) . 6 . и 1,9 . 6 .
Степени» 9 класс . . . 3 . 3 . 08125,010645,2 . 5 . Сравните: а) 1,3 . 7 . и 1,4 . 7 . ; в) ( — 2,7) . 6 . и 1,9 . 6 .
13 2020 — определите; Все Ещё 1 Контрольная работа по теме Квадратична; я функция multiurokru filesnaia-rabota-pokvadratichnaia Сохранённая . .
6 . 2019 — контрольная работа по алгебре 9 класс функции и их графики . . . «квадратичная функция и ее график » Вариант 1 • 1 Постройте график . .
10 ав 2020 — контрольная работа 9 класс график квадратичной функции . . . 5 12 Функция и её график 4 Контрольная работа 1 1 13 Функция и её . .
9 . 2020 — Контрольная работа по теме « Квадратичная функция» . Вариант 1 . Постройте график функции у = х² – 2х – 8 . Найдите по графику : .
17 . 2019 — контрольная работа 9 класс график квадратичной функции — Все результаты Контрольная работа №1 по алгебре для 9 класса по теме . .
14 . 2019 — Алгебра 8 класс . Контрольная работа по теме: «Квадратичная функция» . Вариант 1 . А 1 . Функция задана формулой . Найдите . 1) 24 2) . .
1 Контрольные работы по алгебре 9 класс, вариант . Контрольная работа «Квадратичная функция» .дана функция f ( x) 7x 5 . При каких значениях . .
контрольная работа 2 по теме квадратичная функция и ее график . . . по теме « квадратичная функция и ее график » Вариант 1 Контрольная работа №1 . .
Система для поддержки контрольного тестирования учащихся . Возможно открытие предустановленных контрольных работ, а также загрузка . .
1 . 2019 — Скачать — Контрольная работа по алгебре «Квадратичная функция» (8 класс) . Контрольная работа по теме «Квадратичная функция»1 . .
Квадратичная функция . Функция y= k/x . . Квадратичная функция, ее свойства и график . . . 1 ч . Контрольная работа №2 . 27-44 . 18 ч . Глава II . Функция x y = .
Контрольная работа №2 . Квадратичная функция . Вариант 1 . А1 . Найдите значение квадратичной функции . 2 . 2 . 4 1 при . 5; 2 . у х х х . = − . + . = − . А2 .
Контрольные и самостоятельные работы по алгебре 9 класс Журавлев, Малышева Экзамен . . Квадратичная функция — задачи с параметрами . 1 2 .
Контрольная работа №1 по теме:»Квадратичная функция» . by ninesa60 . Здравствуйте ребята . Сегодня вы будите выполнять контрольную работу .
использовать свойства и график квадратичной функции при решении задач . . 1 . Контрольная работа . 28 . Квадратичная функция, ее график и свойства .
Входная контрольная работа; Контрольная работа №1 «Неравенства»; Контрольная работа №2 «Квадратичная функция»; Контрольная работа №3 . .
1 . 14 . Анализ контрольной работы . 1 . 15-16 . Алгебраические дроби . 2 . . 49 . Контрольная работа №4 Тема: Квадратичная функция . Функция y= . 1 . 50 .
Найдите нули функции, промежутки убывания и возрастания, область значений функции . Контрольная работа №2 Квадратичная функция Вариант 1 2 . .
Контрольная работа № 2 . «Квадратичная функция и её график» . Вариант 1 . Ответы: 1) а) y = 2 б) x1 ≈ 1,3; x2 ≈ 4,8; в) y = 0 при x1 = 1 и x2 = 5; y ˃ 0 при . .
22 . 2020 — Глава I . КВАДРАТИЧНАЯ ФУНКЦИЯ . Урок 10 . Контрольная работа по теме «Функция . Квадратный трехчлен» . Алгебра 9 Макарычев . .
14 10 Контрольная работа № 2 «Функции и их 1 03 .10 Контрольные вопро . . 1 17 .10 П .7,№126,13 21 17 Построение графика квадратичной функции 1 . .
6 . Контрольная работа по теме «Квадратичная функция»(1ч) . 1 нед . Март . 7 . Административная контрольная работа за 1 полугодие .(1 ч) 2 нед . Апрель .
Подготовка к контрольной работе по теме «Квадратичная функция» . 1 . Разложите на множители квадратный трехчлен: а) . 20 . 12 . 2 . + . — x .
8 . 2019 — квадратичная функция контрольная работа по алгебре 8 класс . . . работа по алгебре На тему: « Квадратичная функция » 1 вариант ( 8 . .
Контрольная работа №3 по теме «Квадратичная функция» . Вариант №1 . 1 . Построить график функции у=х2-1,5 . 2 . Решить уравнение: х4-10х2+9=0 . 3 .
5 . 2020 — Квадратный трехчлен» вариант 1 1 Дана функция . При каких значениях . Контрольная работа № 2 «Квадратичная функция» . ВАРИАНТ . .
7 . 2020 — Контрольная работа по теме: «Квадратичная функция» вариант1 1 .Установите соответствие между графиками функций и формулами, . .
Контрольная Работа Номер 1 По Теме Механика
Предмет Философии Контрольная Работа
Контрольная Работа Основные Тригонометрические Функции
Системный Анализ В Экономике Контрольная Работа Проблема
Контрольная Работа Номер 1 Функции
ГДЗ Алгебра 8 класс Потапов, Шевкин
Многие школьники недооценивают важность такого предмета, как математика. А ведь не зря ее называют царицей наук. Без математических вычислений был бы невозможен технический прогресс. В основе всех естественных наук лежат различные закономерности и уравнения. Поэтому вне зависимости от профильных предпочтений учеников забывать о математике не стоит.
Большинство трудностей с предметом возникают по нескольким причинам: от банальной невнимательности до непонятного изложения материала учителем. И когда дело доходит до проверочных работ, неминуемо совершаются ошибки. В восьмом классе алгебра полна важных тем и разделов, которые будут отражены в ОГЭ через год, а значит в обучении не должно быть места пробелам.
Как научиться легко решать математические задачи
С каждым учебным годом возрастает объем самостоятельной работы. Помимо выполнения многочисленных домашних заданий, школьники начинают изучать и дополнительные учебные пособия для лучшего понимания предмета. Среди них есть и те, что позволяют значительно сэкономить время для подготовки. Одним из таких актуальных пособий станет «ГДЗ по Алгебре 8 класс Дидактические материалы Потапов, Шевкин (Просвещение)».
Какие материалы содержит сборник ГДЗ
Во многих российских школах для отработки полученных знаний по математике используются дидактические материалы под редакцией Потапова. «ГДЗ по Алгебре 8 класс Потапов» представляет собой онлайн-решебник по оригинальной рабочей тетради и содержит следующие материалы:
- 28 самостоятельных работ по темам курса;
- 7 промежуточных контрольных работ;
- описание решения всех заданий;
- правильные ответы.
Благодаря им, ученики смогут самостоятельно разобраться с непонятной темой, научиться решать конкретные примеры, уравнения и задачи. На страницах ГДЗ вы найдете задания по следующим темам: графики функций, преобразование выражений, системы рациональных уравнений, теорема Виета и др.
Преимущества онлайн-решебника
Помимо очевидной возможности уверенно справляться с домашними заданиями, восьмиклассники получают следующие преимущества:
- Повышение уверенности в себе, благодаря способности проверить ход своего решения;
- Быстрая отработка пропущенной темы;
- Оперативный поиск правильных ответов в режиме онлайн;
- Подготовка к контрольным и проверочным работам.
Данный сборник неоднократно отмечался учениками и преподавателями алгебры, как наиболее эффективный в рамках изучения предмета в восьмом классе, а также подготовки к контрольным работам и экзаменам.
|
Последовательности и серии: терминология и обозначения
Purplemath
«Последовательность» (называемая «прогрессией» в британском английском) — это упорядоченный список чисел; числа в этом упорядоченном списке называются «элементами» или «элементами» последовательности.
«Серия» — это то, что вы получаете, когда складываете все члены последовательности; сложение, а также результирующее значение называются «суммой» или «суммированием». Например, «1, 2, 3, 4» — это последовательность с терминами «1», «2», «3» и «4»; соответствующий ряд представляет собой сумму «1 + 2 + 3 + 4», а значение ряда равно 10.
Последовательность может быть названа или обозначена заглавной буквой, такой как «A» или «S». Термины последовательности обычно называются примерно так: « a i » или « a n », причем нижняя буква « i » или « n » является «индексом» или прилавок.Таким образом, второй член последовательности может быть назван « a 2 » (произносится «ау-суб-два»), а « a 12 » будет обозначать двенадцатый член.
MathHelp.com
Последовательность также можно записать в терминах.Например, последовательность терминов a i с индексом от i = 1 до i = n , может быть записана как:
Последовательность терминов, начинающихся с индекса 3 и продолжающихся бесконечно, может быть записана как:
В некоторых книгах используются скобки; другие используют обозначение фигурных скобок. В любом случае, они говорят о списках терминов. Начальное значение счетчика называется «нижним индексом»; конечное значение называется «верхним индексом».Форматирование соответствует английскому: нижний индекс пишется под верхним, как показано выше. (Множественное число от «index» — «индексы», произносится как INN-duh-seez.)
Примечание. Иногда последовательности начинаются с индекса n = 0, поэтому первый член на самом деле a 0 . Тогда второй член будет a 1 . Первый указанный термин в таком случае будет называться термином «нулевой эталон». Этот метод нумерации терминов используется, например, в массивах Javascript.Или, как во втором примере выше, последовательность может начинаться со значением индекса больше 1. Не предполагайте, что каждая последовательность и ряд будут начинаться с индекса n = 1.
Когда последовательность не имеет фиксированного числового верхнего индекса, а вместо этого «уходит в бесконечность» («бесконечность» обозначается символом «восьмерки», ∞), последовательность называется «бесконечной» последовательностью. Бесконечные последовательности обычно имеют конечные нижние индексы. То есть они начнут с некоторого конечного счетчика, например i = 1.
Как упоминалось выше, последовательность A с терминами a n также может называться «{ a n }», но вопреки тому, что вы, возможно, узнали в других контекстах, этот «набор «на самом деле является упорядоченным списком, а не неупорядоченным набором элементов. (В вашей книге могут использоваться другие обозначения, отличные от тех, которые я показываю здесь. К сожалению, они, похоже, еще не полностью стандартизированы для этой темы. Просто старайтесь всегда проверять, какой бы ресурс вы ни использовали, что вы четкое определение терминов и символов этого ресурса.) В наборе нет определенного порядка элементов, и повторяющиеся элементы обычно отбрасываются как бессмысленные дубликаты. Таким образом, следующий набор:
… уменьшится до (и эквивалентно):
С другой стороны, следующая последовательность:
{ a n } = {1, 2, 1, 2, 1, 2, 1, 2}
…не может быть изменено или «упрощено» каким-либо образом.
Термины последовательности могут быть просто перечислены, как показано выше, или же они могут быть определены правилом. Часто это правило связано с индексом. Например, в последовательности A = { a i } = {2 i + 1} член i определяется правилом «2 i + 1», поэтому первые несколько терминов:
a 1 = 2 (1) + 1 = 3
а 2 = 2 (2) + 1 = 5
а 3 = 2 (3) + 1 = 7
…и так далее. Иногда правило для последовательности таково, что следующий член в последовательности определяется в терминах предыдущих терминов. Этот тип последовательности называется «рекурсивной» последовательностью, а правило называется «рекурсией». Самая известная рекурсивная последовательность — это последовательность Фибоначчи (fibb-oh-NAH-chee). Его правило рекурсии следующее:
a 1 = a 2 = 1;
a n = a n –1 + a n –2 для n ≥ 3
Это правило гласит, что первые два члена последовательности равны 1; тогда каждый термин после первых двух находится путем добавления двух предыдущих терминов.Таким образом, третий член, a 3 , находится путем добавления a 3–1 = a 2 и a 3–2 = a 1 . Первые несколько членов последовательности Фибоначчи:
Для обозначения серии мы используем либо заглавную латинскую букву «S», либо греческую букву, соответствующую заглавной «S», которая называется «сигма» (SIGG-muh):
Чтобы показать суммирование, скажем, с первого по десятый членов последовательности { a n }, мы должны написать следующее:
Как и в терминологии для последовательностей, « n = 1» называется «нижним индексом», говоря нам, что « n » является счетчиком и что счетчик начинается с «1»; «10» называется «верхним индексом», говоря нам, что a 10 будет последним термином, добавленным в этой серии; « a n » обозначает термины, которые мы добавим.Все это произносится как «сумма от n равняется от одного до десяти a-sub-n». Символ суммирования выше означает следующее:
a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + a 7 + а 8 + а 9 + а 10
Вышеописанная форма называется «развернутой» формой серии, в отличие от более компактной «сигма» нотации.
Для индекса можно использовать любую букву, но i , j , k , m и n , вероятно, используются чаще, чем любые другие буквы.
Есть несколько правил, которые могут помочь упростить или оценить ряды. Если каждый член в серии умножается на одно и то же значение, вы можете вынести это значение из ряда. Это означает следующее:
Это означает, что, если вам сказали, что сумма некоторого конкретного ряда имеет значение, скажем, 15, и что каждый член в серии умножается, скажем, на 2, вы можете найти значение как:
Другое правило для рядов состоит в том, что, если члены ряда являются суммами, вы можете разделить ряд сумм на сумму рядов.Другими словами:
Если вы складываете только первые несколько членов ряда, а не все (возможно, бесконечно много) из них, это называется «взятием (или нахождением) частичной суммы». Если, скажем, вам сказали найти сумму только первых восьми членов ряда, вы бы «нашли восьмую частичную сумму».
Последовательности и серии наиболее полезны, когда есть формула для их членов.Например, если формула для терминов a n последовательности определяется как « a n = 2 n + 3», то вы можете найти значение любого члена, вставив значение n в формулу. Например, a 8 = 2 (8) + 3 = 16 + 3 = 19. Словами « a n = 2 n + 3» можно читать как « n . -й срок дает два-энн плюс три ». Слово « n -th» произносится как «ENN-eth» и означает просто «общий термин a n , где я еще не указал значение n .«
Конечно, не содержит в качестве формулы для n -го члена последовательности. Значения членов могут быть совершенно случайными, не имея отношения между n и значением a n . Но с последовательностями со случайными терминами трудно работать, и они в целом менее полезны, поэтому вы вряд ли увидите многие из них в своих классах.
URL: https: // www.purplemath.com/modules/series.htm
Нахождение числа перестановок n различных объектов
Принцип умножения можно использовать для решения различных типов задач. Один тип проблем связан с размещением объектов по порядку. Мы расставляем буквы в слова и цифры в числа, выстраиваем в очередь фотографии, украшаем комнаты и многое другое. Порядок объектов называется перестановкой .
Нахождение числа перестановок
n отдельных объектов с использованием принципа умноженияДля решения задач перестановки часто бывает полезно нарисовать отрезки линии для каждого варианта. Это позволяет нам определить количество каждой опции, чтобы мы могли умножить. Например, предположим, что у нас есть четыре картины, и мы хотим найти количество способов, которыми мы можем повесить три картины по порядку на стене. Мы можем нарисовать три линии, чтобы обозначить три места на стене.
Есть четыре варианта для первого места, поэтому мы пишем 4 в первой строке.
После того, как первое место было заполнено, есть три варианта для второго места, поэтому мы пишем 3 во второй строке.
После того, как второе место было заполнено, есть два варианта для третьего места, поэтому мы пишем 2 в третьей строке. Наконец-то находим товар.
Есть 24 возможных перестановки картин.
Как сделать: учитывая различные варианты [latex] n [/ latex], определите, сколько существует перестановок.
- Определите, сколько вариантов существует для первой ситуации.
- Определите, сколько вариантов осталось для второй ситуации.
- Продолжайте, пока все точки не будут заполнены.
- Умножьте числа.
Пример 2: Нахождение числа перестановок с использованием принципа умножения
На соревнованиях по плаванию участвуют девять пловцов.
- Сколько способов они могут разместить первое, второе и третье места?
- Сколько способов они могут занять первое, второе и третье место, если пловец по имени Ариэль занял первое место? (Предположим, что есть только один участник по имени Ариэль.)
- Какими способами все девять пловцов могут выстроиться в очередь для фото?
Анализ решения
Обратите внимание, что в части c мы обнаружили 9! способы выстроиться в очередь для 9 человек. Количество перестановок различных объектов [latex] n [/ latex] всегда можно найти с помощью [latex] n! [/ Latex].
Семья из пяти человек фотографируется. Используйте принцип умножения, чтобы найти следующее.
Попробовать 3
Какими способами семья может выстроиться для портрета?
Решение
Попробовать 4
Сколько способов фотограф может выстроить в ряд из 3 членов семьи?
Решение
Попробовать 5
Сколько способов семья может выстроиться для портрета, если родители должны стоять по бокам?
Решение
Нахождение числа перестановок
n отдельных объектов с помощью формулыДля некоторых задач перестановки неудобно использовать принцип умножения, потому что нужно умножить очень много чисел.К счастью, мы можем решить эти проблемы с помощью формулы. Прежде чем изучать формулу, давайте рассмотрим два распространенных обозначения перестановок. Если у нас есть набор объектов [latex] n [/ latex] и мы хотим выбрать объекты [latex] r [/ latex] из набора по порядку, мы пишем [latex] P \ left (n, r \ right) [/латекс]. Другой способ записать это — [латекс] {n} _ {} {P} _ {r} [/ latex], обозначение, обычно встречающееся на компьютерах и калькуляторах. Чтобы вычислить [латекс] P \ left (n, r \ right) [/ latex], мы начинаем с нахождения [latex] n! [/ Latex], количества способов выстроить все [латекс] n [/ latex] объекты.Затем мы делим на [latex] \ left (n-r \ right)! [/ Latex], чтобы исключить элементы [latex] \ left (n-r \ right) [/ latex], которые мы не хотим выстраивать в линию.
Давайте посмотрим, как это работает, на простом примере. Представьте себе клуб из шести человек. Им нужно избрать президента, вице-президента и казначея. Шесть человек могут быть избраны президентом, любой из пяти оставшихся человек может быть избран вице-президентом, а любой из оставшихся четырех человек может быть избран казначеем. Это можно сделать разными способами: [латекс] 6 \ умножить на 5 \ умножить на 4 = 120 [/ латекс].Используя факториалы, мы получаем тот же результат.
[латекс] \ frac {6!} {3!} = \ Frac {6 \ cdot 5 \ cdot 4 \ cdot 3!} {3!} = 6 \ cdot 5 \ cdot 4 = 120 [/ латекс]
Есть 120 способов выбрать 3 офицера по порядку из клуба с 6 членами. Мы называем это перестановкой 6, взятых по 3 за раз. Общая формула следующая.
[латекс] P \ left (n, r \ right) = \ frac {n!} {\ Left (n-r \ right)!} [/ Latex]
Обратите внимание, что формула по-прежнему работает, если мы выбираем всех [latex] n [/ latex] объектов и размещаем их по порядку.В этом случае мы будем делить на [latex] \ left (nn \ right)! [/ Latex] или [latex] 0! [/ Latex], что, как мы сказали ранее, равно 1. Таким образом, количество перестановок [ latex] n [/ latex] объектов, взятых [latex] n [/ latex] за раз — это [latex] \ frac {n!} {1} [/ latex] или просто [latex] n! \ text {.} [ / латекс]
Общее примечание: формула для перестановок
n отдельных объектовДля различных объектов [latex] n [/ latex] количество способов выбрать объекты [latex] r [/ latex] из набора по порядку составляет
[латекс] P \ left (n, r \ right) = \ frac {n!} {\ Left (n-r \ right)!} [/ Latex]
Практическое руководство. Учитывая проблему со словом, оцените возможные перестановки.
- Определите [латекс] n [/ латекс] по данной информации.
- Определите [латекс] r [/ латекс] по данной информации.
- Заменить [латекс] n [/ латекс] и [латекс] r [/ латекс] в формуле с заданными значениями.
- Оценить.
Пример 3: Нахождение числа перестановок по формуле
Профессор создает экзамен из 9 вопросов из банка тестов из 12 вопросов. Сколько способов она может выбрать и расставить вопросы?
Решение
Заменить [латекс] n = 12 [/ latex] и [latex] r = 9 [/ latex] в формулу перестановки и упростить.
[латекс] \ begin {array} {l} \ text {} P \ left (n, r \ right) = \ frac {n!} {\ Left (nr \ right)!} \ Hfill \\ P \ left (12,9 \ right) = \ frac {12!} {\ Left (12–9 \ right)!} = \ Frac {12!} {3!} = 79 \ text {,} 833 \ text {,} 600 \ hfill \ end {array} [/ latex]
Существует 79 833 600 возможных перестановок экзаменационных вопросов!
Анализ решения
Мы также можем использовать калькулятор, чтобы найти перестановки. Для этой проблемы мы должны ввести 15, нажать функцию [latex] {} _ {n} {P} _ {r} [/ latex], ввести 12, а затем нажать знак равенства.Функция [latex] {} _ {n} {P} _ {r} [/ latex] может находиться в меню MATH с командами вероятности.
Вопросы и ответы
Можно ли было решить, используя принцип умножения?
Да. Мы могли бы умножить [латекс] 15 \ cdot 14 \ cdot 13 \ cdot 12 \ cdot 11 \ cdot 10 \ cdot 9 \ cdot 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 [/ latex] , чтобы найти тот же ответ .
В спектакле 7 актеров готовятся к выходу на занавес. Используйте формулу перестановки, чтобы найти следующее.
Попробовать 6
Какими способами могут выстроиться 7 актеров?
Решение
Попробовать 7
Какими способами можно выбрать 5 из 7 актеров, чтобы они выстроились в линию?
Решение
Регрессия с матричной алгеброй
Регрессия с матричной алгебройРегрессия с матричной алгеброй
Опишите решение для весов регрессии для необработанных оценок, используя матричную алгебру.
Опишите решение для стандартизированных весов регрессии из корреляционной матрицы с использованием матричной алгебры.
Опишите выборочные распределения весов b, и бета.
Что означает ковариационная или корреляционная матрица весов b ? Как это используется?
В исходной форме уравнение регрессии:
Это говорит о том, что Y, наша зависимая переменная, состоит из линейной части и ошибки. Линейная часть состоит из точки пересечения, a и k независимых переменных, X 1 …X k вместе с соответствующими весами регрессии необработанных оценок b 1 … b k .
В матричных терминах то же уравнение можно записать:
y = X b + e
и = | Х | б + | e |
Н x 1 | Н х (1 + к) | (1 + к) х 1 | Н x 1 |
Здесь говорится, что для получения Y для каждого человека необходимо умножить каждое X i на соответствующие b, , , сложить их, а затем добавить ошибку.Матрицы выглядят так:
Y 1 | 1 | Х 11 | Х 12 | . | . | . | х 1к | а | e 1 | |||
Y 2 | = | 1 | Х 21 | Х 22 | х 2к | б 1 | + | e 2 | ||||
. | . | . | . | . | б 2 | |||||||
. | . | . | . | . | . | |||||||
. | . | . | . | . | . | |||||||
Да Нет | 1 | х N1 | х N2 | . | . | . | Х Nk | б к | e N |
Используя необработанные оценки, мы создаем расширенную матрицу плана X, в которой есть дополнительный столбец единиц для перехвата.Для каждого человека 1 используется для добавления точки пересечения в первую строку вектора-столбца b .
Если мы решим для весов b , мы найдем, что
b = (X’X) -1 X’y
Чтобы понять, почему это выглядит так, сначала вспомните уравнение регрессии:
y = Xb + e
Предположим, что ошибка будет в среднем равна нулю, и забудем набросать доказательство:
y = Xb
Теперь мы хотим найти b , поэтому нам нужно избавиться от X .Сначала мы превратим X в красивую квадратную симметричную матрицу, предварительно умножив обе части уравнения на X ‘:
X’y = X’Xb
И теперь у нас есть квадратная симметричная матрица, которая, если повезет, имеет обратную, которую мы назовем (X’X) -1 . Умножаем обе стороны на это обратное, и получаем
.(X’X) -1 X’y = (X’X) -1 (X’X) b
Получается, что матрица, умноженная на обратную ей, является единичной матрицей ( A -1 A = I ):
(X’X) -1 X’y = Ib
, а матрица, умноженная на единичную матрицу, есть сама ( AI = IA = A ):
(X’X) -1 X’y = b
, что является желаемым результатом.
Числовой пример с одной независимой переменной
Предположим, наши данные выглядят так:
Мы можем представить проблему регрессии как:
b = (X’X) -1 X’y
| -1 | |||||||||||||||||
1 | 6 | 1 | |||||||||||||||
1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 2 | |||||
6 | 7 | 8 | 9 | 7 | 1 | 8 | 6 | 7 | 8 | 9 | 7 | 3 | |||||
1 | 9 | 3 | |||||||||||||||
1 | 7 | 4 | |||||||||||||||
| Х ‘ | Х | Х ‘ | y | ||||||||||||||
5 | 37 | ||||||||
| X’X = | N | S X | |||||||
37 | 279 | ||||||||
S X | S X 2 |
13 | |
| X’y = | S Y |
99 | |
S XY |
Теперь найдем обратное X’X .
Если X — это матрица 2 на 2, то обратная величина — это простая функция элементов, каждый из которых делится на определитель.
Предположим, A имеет следующие элементы:
А = | а | б | |
| с | д | ||
Тогда | A | это ad-bc.Обратное к X —
.А -1 = | д / | X | | — b / | X | | |
— c / | X | | а / | X | | ||
или
А -1 = | д / (ад-бк) | -b / (ad-bc) |
| -c / (ad-bc) | а / (ad-bc) |
В нашем примере
и
(X’X) -1 = | 10.73 | -1,42 | (округлено) |
-1,42 | ,19 |
Чтобы найти b , находим
b = (X’X) -1 X’y
10.7308 | -1,42308 | 13 | -1.38 | |||
-1,42308 | .1 | |||||
99 | = | .54 | ||||
| (X’X) -1 | X’y | б |
Следовательно, a = -1.38 и b = 0,54. Уравнение регрессии:
Y ‘= -1,38 + .54X.
Показатели отклонения и 2 IV
Показанные выше вычисления исходных оценок — это то, что обычно используют статистические пакеты для вычисления множественной регрессии.
Однако мы также можем использовать матричную алгебру для определения весов регрессии, используя (а) оценки отклонения вместо исходных оценок и (б) просто корреляционную матрицу. Конечно, теперь нам придется сделать и то, и другое.
Формулировка оценки отклонения хороша тем, что матрицы в этом подходе содержат сущности, которые концептуально более интуитивно понятны.Итак, давайте предположим, что мы вычли среднее значение Y из каждого значения Y и среднее значение каждого X из его столбца. В этом случае у нас
b = (X d ‘X d ) -1 X d y d
, что является тем же уравнением, что и для исходных оценок, за исключением того, что нижний индекс d обозначает оценки отклонения. Матрица проекта X не содержит начального столбца с единицами, потому что точка пересечения для этой модели будет равна нулю. (Почему точка пересечения равна нулю?) Поскольку оценки представляют собой оценки отклонения, матрица X’X будет матрицей SSCP:
… | ||||
| X’X = | … | сим | ||
… | … | |||
… |
И матрица X’y будет матрицей сумм перекрестных произведений:
Для задачи с двумя переменными решение для гирь b выглядит следующим образом:
–1 | ||||
| б = | ||||
| X’X | X’y |
Это означает, что умножьте матрицу перекрестных произведений x и y на обратную матрицу SSCP, чтобы найти веса b .
Определитель X’X находится путем умножения элементов главной диагонали и вычитания произведения недиагональных элементов. Обратное к X’X является простой функцией элементов X’X , каждый из которых делится на определитель.
Веса b будут найдены умножением приведенной выше матрицы на X’y :
| б = | ||||
| X’X -1 | X’y |
| б = |
Обратите внимание, что эти формулы соответствуют тем, которые я дал вам ранее, без матричной алгебры.
Вспомните нашу задачу с двумя переменными, в которой мы предсказали
оценок эффективности работы механиков Chevy на основе оценок способностей к работе и добросовестности. Одним из первых, что мы сделали, было вычисление следующей матрицы:
л | х1 | х2 | |
Я | 29,75 | 139,5 | 90.25 |
х1 | 0,77 | 1091,8 | 515,5 |
х2 | 0,72 | 0,68 | 521,75 |
В приведенной выше таблице есть суммы квадратов, перекрестные произведения и корреляции:
Чтобы решить для гирь b , берем следующие части:
–1 | ||||
| б = | ||||
| X’X | X’y |
–1 | ||||
1091.8 | 515,5 | 139,5 | ||
| б = | 515,5 | 521,75 | 90,25 | |
| X’X | X’y |
.0017 | -.0016 | 139,5 | = | .086 | ||
| б = | -.0016 | .0036 | 90,25 | .087 | ||
| X’X -1 | X’y | = | б |
Обратите внимание, что этот результат согласуется с нашими предыдущими оценками, вычисленными без матричной алгебры.
Получение b-весов из корреляционной матрицы
С двумя стандартизованными переменными наше уравнение регрессии составляет
z y ‘= b 1 z 1 + b 2 z 2
Чтобы найти вес бета-версии, мы просто находим:
b
= -1 рандов, где R — корреляционная матрица предикторов (переменные X), а r — вектор-столбец корреляций между Y и каждым X.
Вспомните нашу предыдущую матрицу:
л | х1 | х2 | |
Я | 29,75 | 139,5 | 90,25 |
х1 | 0,77 | 1091,8 | 515,5 |
х2 | 0.72 | 0,68 | 521,75 |
Матрица R :
А матрица r :
Следовательно, наши бета-веса:
1.86 | -1,26 | ,77 | = | ,52 | ||
| б = | -1,26 | 1,86 | ,72 | .37 | ||
| Р -1 | р | = | б |
Обратите внимание, что этот результат согласуется с нашими предыдущими оценками бета-весов, вычисленных без матричной алгебры.
Если все предикторы ортогональны, тогда матрица R является единичной матрицей I , и тогда R -1 будет равно R . В таком случае веса b будут равны простым корреляциям (мы отметили ранее, что r и b одинаковы, когда независимые переменные не коррелированы). Обратная матрица обесценивает корреляции в r , чтобы придать им веса, соответствующие уникальным частям каждого предиктора, то есть b весов.Обратная операция в некотором смысле делает предсказатели ортогональными.
Выборочная ковариация регрессионных весов
Мы можем определить популяцию, в которой уравнение регрессии описывает отношения между Y и некоторыми предикторами, например,
Y ‘ JP = a + b 1 MC + b 2 C,
Где Y — результативность работы, a и b — параметры совокупности, MC — результаты теста на понимание текста, а C — результаты теста на добросовестность. Если мы возьмем повторные выборки из нашей совокупности и оценим b 1 и b 2, у нас будет два выборочных распределения, по одному для каждой оценки наклона.Каждое из распределений наклона будет иметь дисперсию, известную как дисперсия выборки (эта дисперсия используется для построения доверительных интервалов и критериев значимости). Поскольку все переменные в этом уравнении измеряются на одних и тех же людях, измерения зависят. Между двумя оценками наклона будет ковариация. Другими словами, две оценки наклона являются зависимыми и могут изменяться (коррелироваться) между выборками. Предположим, наши параметры популяции следующие:
r (популяционные корреляции) | Я | Х1 | Х2 |
Я | 1 | ||
Х1 | .45 | 1 | |
Х2 | ,50 | .80 | 1 |
Вес нашей бета-версии будет:
1 | ,8 | –1 | ,45 | |
.8 | 1 | ,50 | ||
| R | р |
2,78 | -2,22 | ,45 | = | .1389 | ||
= | -2,22 | 2,78 | ,50 | .3889 | ||
| Р -1 | р | б |
(Примечание: эти веса b являются бета-версиями как в смысле стандартизации, так и в смысле значений совокупности.) Я взял 1000 образцов размером 100 из этой популяции. Распределение выборки для beta1 выглядит так:
Его среднее значение составляет 0,1376, что близко к ожидаемому значению 0,1388, а его стандартное отклонение составляет 0,1496.
Распределение выборки для beta2:
Среднее значение распределения составляет 0,3893, что близко к ожидаемому значению 0,3889, а стандартное отклонение составляет 0,1482.
Диаграмма разброса пар бета-весов для 1000 выборок:
Как видите, существует отрицательная корреляция между бета-весами.Когда один относительно большой, другой относительно мал. Это происходит всякий раз, когда предикторы коррелируют. Когда предикторы коррелированы, один предиктор имеет тенденцию получать больше, чем его доля в данной выборке. Коррелированные предикторы — свиньи — они зависят от дисперсии в Y.
.Ковариационная матрица дисперсии весов b :
, который представляет собой дисперсию оценки (среднеквадратичную невязку), умноженную на обратную матрицу SSCP (обратная величина оценок отклонения, умноженная на транспонирование оценок отклонения).Диагональные элементы этой матрицы представляют собой выборочные дисперсии весов b . Если мы возьмем квадратные корни из этих элементов, мы получим стандартные ошибки весов b , которые используются при их проверке. Недиагональные элементы C являются ковариациями гирь b .
В нашем примере сумма квадратов ошибки составила 9,88. Df составлял 20-2-1 = 17. Следовательно, дисперсия оценки составляет 9,88 / 17 = 0,58. Обратное к нашей матрице SSCP —
..0017 | -.0016 |
-.0016 | .0036 |
| (X’X) -1 |
Следовательно, наша ковариационная матрица дисперсии C равна
.0001 | -.0001 |
-.0001 | .0002 |
| С |
Стандартная ошибка b1 равна sqrt (c11) = 0,031.
Стандартная ошибка b2 равна sqrt (c22) = 0,046.
Тестовая статистика для b1 и b2 —
t = b1 / s1 = 0,086 / 0,031 = 2,81.
t = b2 / s2 = 0,087 / 0,046 = 1,89.
Эти значения t согласуются с нашими предыдущими вычислениями, выполненными без матричной алгебры в пределах ошибки округления.
Для проверки разницы между наклонами (например, b 1 равно b 2 ) включает члены как для дисперсии весов b , так и для ковариации весов b . В частности,
Этот тест аналогичен двухвыборочному t-критерию, в котором стандартная ошибка разницы определяется как
.Разница в том, что дисперсия ошибок для двух средних независима, поэтому ковариация между ними равна нулю.Веса b являются зависимыми, поэтому нам нужно включить ковариацию, чтобы быть точными.
В нашем примере
Примечание. Этот тест имеет смысл только в том случае, если обе гири b одного типа и измеряются на одной шкале. Например, если бы один IV был очками, набранными командой хозяев, а другой был очками, набранными командой гостей за тот же тип игры, это было бы нормально. Но если бы один был за доллары, а другой — на несколько дней, это было бы неправильно, потому что размер блока влияет на размер веса b .
Два средних значения совокупности с неизвестными стандартными отклонениями — вводная статистика
- Две независимые выборки представляют собой простые случайные выборки из двух различных популяций.
- Для двух разных популяций:
- если размеры выборки малы, распределения важны (должны быть нормальными)
- если размер выборки большой, распределения не важны (не обязательно должны быть нормальными)
ПРИМЕЧАНИЕ
Тест, сравнивающий два независимых средних значения совокупности с неизвестными и, возможно, неравными стандартными отклонениями совокупности, называется t-критерием Аспина-Велча.Формула степеней свободы была разработана Аспином-Велчем.
Сравнение двух средних значений численности населения очень распространено. Разница между двумя образцами зависит как от средних значений, так и от стандартных отклонений. Совершенно разные средства могут возникнуть случайно, если между отдельными образцами есть большие различия. Чтобы учесть вариацию, мы берем разницу средних значений выборки — и делим на стандартную ошибку, чтобы стандартизировать разницу. Результатом является статистика теста t-score.
Поскольку нам неизвестны стандартные отклонения генеральной совокупности, мы оцениваем их, используя два стандартных отклонения выборки из наших независимых выборок. Для проверки гипотезы мы вычисляем оценочное стандартное отклонение или стандартную ошибку , разность средних значений выборки , -.
Стандартная ошибка:Статистика теста ( т -балл) рассчитывается следующим образом:
где:
- s 1 и s 2 , стандартные отклонения выборки, представляют собой оценки σ 1 и σ 2 , соответственно.
- σ 1 и σ 1 — неизвестные стандартные отклонения генеральной совокупности.
- и являются образцом. μ 1 и μ 2 — средние по совокупности.
Число степеней свободы ( df ) требует довольно сложного вычисления. Однако компьютер или калькулятор легко рассчитают. df не всегда целое число. Вычисленная ранее статистика теста аппроксимируется распределением Стьюдента t с df следующим образом:
Степени свободыКогда оба размера выборки n 1 и n 2 равны пяти или больше, приближение Стьюдента t будет очень хорошим.Обратите внимание, что выборочные отклонения ( s 1 ) 2 и ( s 2 ) 2 не объединяются. (Если возникает вопрос, не объединяйте отклонения.)
ПРИМЕЧАНИЕ
Нет необходимости вычислять это вручную. Калькулятор или компьютер легко вычислит это.
Независимые группы
Считается, что среднее количество времени, которое мальчики и девочки в возрасте от семи до 11 лет каждый день проводят за занятиями спортом, одинаково. Проведено исследование и собраны данные, в результате чего данные представлены на (Рисунок).Каждая популяция имеет нормальное распределение.
| Размер выборки | Среднее количество часов занятий спортом в день | Стандартное отклонение выборки | |
|---|---|---|---|
| Девочки | 9 | 2 | |
| Мальчики | 16 | 3,2 | 1,00 |
Есть ли разница в среднем количестве времени, которое мальчики и девочки в возрасте от семи до 11 лет занимаются спортом каждый день? Тест на 5% уровне значимости.
Стандартные отклонения населения неизвестны. Пусть g будет нижним индексом для девочек и b будет нижним индексом для мальчиков. Тогда μ g — среднее значение для девочек и μ b — среднее значение для мальчиков. Это тест двух независимых групп , две популяции означает .
Случайная переменная: = разница в среднем количестве времени, в течение которого девочки и мальчики занимаются спортом каждый день.
H 0 : μ g = μ b H 0 : μ g — μ b = 0
H a : μ g ≠ μ b H a : μ g — μ b ≠ 0
Слова «то же самое» говорят вам H 0 имеет знак «=».Поскольку нет других слов для обозначения H a , предположим, что здесь сказано, что «отличается». Это двусторонний тест.
Распределение для теста: Используйте t df , где df рассчитывается с использованием формулы df для независимых групп, двух средних значений совокупности. Используя калькулятор, df составляет приблизительно 18,8462. Не объединять отклонения.
Вычислите значение p , используя распределение Стьюдента t : p -value = 0.0054
График:
Итак, = 2 — 3,2 = –1,2
Половина значения p ниже –1,2, а половина — выше 1,2.
Принять решение: Поскольку α > p -значение, отклонить H 0 . Это означает, что вы отклоняете μ g = μ b . Средства разные.
Нажмите STAT . Перейдите к ТЕСТЫ и нажмите 4: 2-SampTTest .Перейдите к Статистике и нажмите ВВОД . Стрелкой вниз введите 2 для первого выборочного среднего, для Sx1, 9 для n1, 3,2 для второго выборочного среднего, 1 для Sx2 и 16 для n2. Стрелка вниз к µ1: и стрелка к не равняется µ2. Нажмите ENTER . Стрелка вниз к Pooled: и № . Нажмите ENTER . Стрелка вниз до Рассчитайте и нажмите ENTER . Значение p равно p = 0.0054, dfs составляет приблизительно 18,8462, а статистика теста -3,14. Повторите процедуру еще раз, но вместо «Вычислить» сделайте Draw.
Заключение: На уровне значимости 5% данные выборки показывают, что имеется достаточно доказательств, чтобы сделать вывод о том, что среднее количество часов, в течение которых девочки и мальчики в возрасте от семи до 11 лет занимаются спортом в день, различается (среднее количество часов мальчиков в от семи до 11 занятий спортом в день больше, чем среднее количество часов, которые играют девочки, ИЛИ среднее количество часов, которое девочки в возрасте от семи до 11 занимаются спортом в день, больше, чем среднее количество часов, которые играют мальчики).
Попробуй
Два образца показаны на (Рисунок). Оба имеют нормальное распределение. Считается, что средства для двух популяций одинаковы. Есть разница в средствах? Тест на 5% уровне значимости.
| Размер выборки | Среднее значение | Стандартное отклонение выборки | |
|---|---|---|---|
| Население A | 25 | 5 | 1 |
| Население B | 16 | 4.7 | 1,2 |
ПРИМЕЧАНИЕ
Когда сумма размеров выборки больше 30 ( n 1 + n 2 > 30), вы можете использовать нормальное распределение для аппроксимации t Стьюдента.
Группа сообщества в двух соседних колледжах проводит исследование, чтобы определить, какой из них выпускает студентов с большим количеством классов математики. Колледж А составляет 11 выпускников Их среднее значение — четыре класса математики со стандартным отклонением 1.5 классов математики. Колледж Б отбирает девять выпускников. В среднем они составляют 3,5 урока по математике со стандартным отклонением в один класс по математике. Общественная группа считает, что студент, окончивший колледж A , посещал больше уроков математики, в среднем человек. Обе популяции имеют нормальное распределение. Проверьте уровень значимости 1%. Ответьте на следующие вопросы.
а. Это проверка двух средств или двух пропорций?
г. Известны или неизвестны стандартные отклонения популяций?
г.Какой дистрибутив вы используете для проведения теста?
г. Что такое случайная величина?
г.
e. Каковы нулевая и альтернативная гипотезы? Напишите нулевую и альтернативную гипотезы словами и символами.
e.
ф. Это тест: правосторонний, левосторонний или двусторонний?
ф.
правый
ч. Вы отвергаете или не отвергаете нулевую гипотезу?
и.На уровне значимости 1%, исходя из данных выборки, нет достаточных доказательств, чтобы сделать вывод о том, что студент, окончивший колледж A, в среднем посещал больше уроков математики, чем студент, окончивший колледж B.
Попробуй
Было проведено исследование, чтобы определить, удерживает ли компания A своих работников дольше, чем компания B. Компания A отбирает 15 работников, и их среднее время работы в компании составляет пять лет со стандартным отклонением 1,2. Компания B отбирает 20 рабочих, и их среднее время работы в компании составляет 4 человека.5 лет со стандартным отклонением 0,8. Популяции распределены нормально.
- Известны ли стандартные отклонения населения?
- Проведите соответствующую проверку гипотезы. Каков ваш вывод на уровне значимости 5%?
Профессор крупного местного колледжа хотел определить, есть ли разница в средних оценках итоговых экзаменов между студентами, которые посещали его онлайн-курс статистики, и студентами, которые посещали его очные статистические занятия.Он считал, что средний балл итоговых экзаменов в онлайн-классе будет ниже, чем в очном. Прав ли профессор? 30 произвольно выбранных финальных экзаменов из каждой группы перечислены на (Рисунок) и (Рисунок).
| 67,6 | 41,2 | 85,3 | 55,9 | 82,4 | 91,2 | 73,5 | 94,1 | 64,7 | 64,7 |
| 70.6 | 38,2 | 61,8 | 88,2 | 70,6 | 58,8 | 91,2 | 73,5 | 82,4 | 35,5 |
| 94,1 | 88,2 | 64,7 | 55,9 | 88,2 | 97,1 | 85,3 | 61,8 | 79,4 | 79,4 |
| 77,9 | 95,3 | 81.2 | 74,1 | 98,8 | 88,2 | 85,9 | 92,9 | 87,1 | 88,2 |
| 69,4 | 57,6 | 69,4 | 67,1 | 97,6 | 85,9 | 88,2 | 91,8 | 78,8 | 71,8 |
| 98,8 | 61,2 | 92,9 | 90,6 | 97,6 | 100 | 95,3 | 83.5 | 92,9 | 89,4 |
Является ли средняя оценка за итоговый экзамен онлайн-класса ниже, чем средняя оценка за итоговый экзамен очного занятия? Проверьте уровень значимости 5%. Ответьте на следующие вопросы:
- Это проверка двух средних или двух пропорций?
- Известны или неизвестны стандартные отклонения генеральной совокупности?
- Какой дистрибутив вы используете для тестирования?
- Что такое случайная величина?
- Каковы нулевая и альтернативная гипотезы? Запишите нулевую и альтернативную гипотезы словами и символами.
- Этот тест правый, левый или двусторонний?
- Что такое значение p ?
- Вы отвергаете или не отвергаете нулевую гипотезу?
- На уровне значимости ___, из выборочных данных, ______ (есть / нет) достаточных доказательств, чтобы сделать вывод, что ______.
(см. Заключение на (рисунок) и напишите свое аналогичным образом)
Сначала поместите данные для каждой группы в два списка (например, L1 и L2). Нажмите STAT. Перейдите к ТЕСТЫ и нажмите 4: 2SampTTest.Убедитесь, что данные выделены, и нажмите ENTER. Стрелка вниз и введите L1 для первого списка и L2 для второго списка. Стрелка вниз на μ 1 : и стрелка на ≠ μ 2 (не равно). Нажмите Ввод. Стрелка вниз к объему: Нет. Нажмите ENTER. Стрелка вниз, чтобы рассчитать, и нажмите ENTER.
Примечание
Будьте осторожны, чтобы не перепутать информацию для группы 1 и группы 2!
- два средства
- неизвестно
- Студенческая т
- H 0 : μ 1 = μ 2 Нулевая гипотеза: средние оценки итоговых экзаменов равны для классов онлайн-статистики и очной статистики.
- H a : μ 1 < μ 2 Альтернативная гипотеза: средняя оценка итоговых экзаменов в онлайн-классе меньше, чем средняя оценка итоговых экзаменов очных занятий класс лица.
- левый хвост
- p -значение = 0,0011
- Отклонить нулевую гипотезу
- Профессор был прав. Факты показывают, что средний балл итоговых экзаменов в онлайн-классе ниже, чем в очном.
На уровне значимости 5% , исходя из выборочных данных, есть (есть / нет) достаточные доказательства, чтобы сделать вывод о том, что среднее значение итоговых экзаменов для онлайн-класса меньше среднего итогового экзаменационного результата. очного занятия.
Коэна для малых, средних и больших размеров эффекта Стандарты Коэна d — это мера величины эффекта, основанная на разнице между двумя средними значениями. Коэн d , названный в честь статистика США Джейкоба Коэна, измеряет относительную силу различий между средними значениями двух популяций на основе данных выборки.Рассчитанное значение величины эффекта затем сравнивается со стандартами Коэна для малых, средних и больших величин эффекта.
| Размер эффекта | д |
|---|---|
| Малый | 0,2 |
| средний | 0,5 |
| Большой | 0,8 |
d Коэна — это мера разницы между двумя средними, деленная на объединенное стандартное отклонение: где
Рассчитайте d Коэна для (Рисунок).Размер эффекта маленький, средний или большой? Объясните, что означает размер эффекта для этой проблемы.
μ 1 = 4 с 1 = 1,5 n 1 = 11
μ 2 = 3,5 с 2 = 1 n 2 = 9
d = 0,384
Эффект небольшой, потому что 0,384 находится между значением Коэна 0,2 для небольшого размера эффекта и 0,5 для среднего размера эффекта.Размер различий средних значений для двух колледжей невелик, что указывает на то, что между ними нет существенной разницы.
Рассчитайте d Коэна для (Рисунок). Размер эффекта маленький, средний или большой? Объясните, что означает размер эффекта для этой проблемы.
d = 0,834; Большой, потому что 0,834 больше, чем 0,8 по Коэну для большого размера эффекта. Разница между средними показателями итогового экзамена онлайн-студентов и студентов очного обучения велика, что указывает на значительную разницу.
Попробуй
Взвешенная альфа — это показатель доходности акций с поправкой на риск за год. Высокая положительная взвешенная альфа означает, что цена акции выросла, а небольшая положительная взвешенная альфа указывает на неизменную цену акций в течение периода времени. Взвешенная альфа используется для выявления компаний с сильными восходящими или нисходящими тенденциями. Взвешенная альфа для 30 крупнейших акций банков на северо-востоке и западе, определенная Nasdaq 24 мая 2013 г., указана на (Рисунок) и (Рисунок), соответственно.
| 94,2 | 75,2 | 69,6 | 52,0 | 48,0 | 41,9 | 36,4 | 33,4 | 31,5 | 27,6 |
| 77,3 | 71,9 | 67,5 | 50,6 | 46,2 | 38,4 | 35,2 | 33,0 | 28,7 | 26,5 |
| 76,3 | 71,7 | 56.3 | 48,7 | 43,2 | 37,6 | 33,7 | 31,8 | 28,5 | 26,0 |
| 126,0 | 70,6 | 65,2 | 51,4 | 45,5 | 37,0 | 33,0 | 29,6 | 23,7 | 22,6 |
| 116,1 | 70,6 | 58,2 | 51,2 | 43,2 | 36.0 | 31,4 | 28,7 | 23,5 | 21,6 |
| 78,2 | 68,2 | 55,6 | 50,3 | 39,0 | 34,1 | 31,0 | 25,3 | 23,4 | 21,5 |
Есть ли разница в взвешенной альфе акций 30 крупнейших банков на северо-востоке и западе? Проверьте уровень значимости 5%. Ответьте на следующие вопросы:
- Это проверка двух средних или двух пропорций?
- Известны или неизвестны стандартные отклонения генеральной совокупности?
- Какой дистрибутив вы используете для тестирования?
- Что такое случайная величина?
- Каковы нулевая и альтернативная гипотезы? Запишите нулевую и альтернативную гипотезы словами и символами.
- Этот тест правый, левый или двусторонний?
- Что такое значение p ?
- Вы отвергаете или не отвергаете нулевую гипотезу?
- На уровне значимости ___, из выборочных данных, ______ (есть / нет) достаточных доказательств, чтобы сделать вывод, что ______.
- Вычислите d Коэна и интерпретируйте его.
Обзор главы
Два средних значения совокупности из независимых выборок, где стандартные отклонения генеральной совокупности неизвестны
- Случайная переменная: = разница средств выборки
- Распределение: t -распределение Стьюдента со степенями свободы (отклонения не объединяются)
Обзор формулы
Стандартная ошибка: SE =
Статистика теста ( т -балл): т =
степеней свободы:
где:
s 1 и s 2 — стандартные отклонения выборки, а n 1 и n 2 — размеры выборки.
и являются образцом.
Коэна d — мера величины эффекта:
где
Используйте следующую информацию, чтобы ответить на следующие 15 упражнений: Укажите, предназначена ли проверка гипотезы для
- известные средние по независимой группе, стандартные отклонения и / или дисперсии
- средние значения независимых групп, стандартные отклонения совокупности и / или дисперсии неизвестны
- сопоставленные или парные образцы
- среднее значение
- две пропорции
- одинарная пропорция
Считается, что 70% мужчин сдают тест водителей с первой попытки, а 65% женщин сдают тест с первой попытки.Интересно, равны ли на самом деле пропорции.
Новый стиральный порошок протестирован на потребителях. Обращает на себя внимание доля потребителей, которые предпочитают новый бренд лидирующему конкуренту. Для проверки этого проводится исследование.
Новая обработка лобового стекла утверждает, что она более эффективно отталкивает воду. Десять ветровых стекол испытываются путем имитации дождя без новой обработки. Затем обрабатываются те же лобовые стекла, и эксперимент проводится снова. Проводится проверка гипотез.
совпадающих или парных выборок
Известное стандартное отклонение в заработной плате для всех профессионалов среднего звена в финансовой индустрии составляет 11 000 фунтов стерлингов. Компания A и компания B работают в финансовой сфере. Предположим, что взяты образцы профессионалов среднего звена из компании A и из компании B. Выборочная средняя заработная плата профессионалов среднего звена в компании A составляет 80 000 фунтов стерлингов. Выборочная средняя заработная плата для специалистов среднего звена в компании B составляет 96 000 фунтов стерлингов. Руководство компании A и компании B хочет знать, по-разному ли в среднем платят их специалистам среднего звена.
Средний рабочий в Германии получает восемь недель оплачиваемого отпуска.
Согласно телевизионной рекламе, 80% стоматологов согласны с тем, что зубная паста Ultrafresh — лучшая на рынке.
Считается, что средняя оценка за сочинение по английскому языку в определенной школьной системе у женщин выше, чем у мужчин. Случайная выборка из 31 женщины имела средний балл 82 со стандартным отклонением три, а случайная выборка из 25 мужчин имела средний балл 76 со стандартным отклонением четыре.
средние по независимой группе, стандартные отклонения и / или дисперсии по совокупности неизвестны
Среднее значение по лиге составляет 0,280 с известным стандартным отклонением 0,06. Гремучители и Викинги принадлежат к лиге. Среднее значение ватина для выборки из восьми Rattlers составляет 0,210, а среднее значение ватина для выборки из восьми викингов — 0,260. 24 игрока на Rattlers и 19 игроков на Vikings. Различаются ли статистически средние показатели Рэттлеров и Викингов?
В случайной выборке из 100 лесов в США 56 были хвойными или содержали хвойные породы.В случайной выборке из 80 лесов в Мексике 40 были хвойными или содержали хвойные породы. Является ли доля хвойных пород в США статистически больше, чем доля хвойных пород в Мексике?
Говорят, что новое лекарство улучшает сон. Случайным образом выбираются восемь субъектов, которым дается лекарство. Среднее количество часов сна каждого человека регистрировалось до начала приема лекарства и после него.
Считается, что подростки в среднем спят больше взрослых. Для подтверждения этого проводится исследование.Выборка из 16 подростков имеет среднее время сна 8,9 часа и стандартное отклонение 1,2. Выборка из 12 взрослых имеет среднее время сна 6,9 часа и стандартное отклонение 0,6.
средние по независимой группе, стандартные отклонения и / или дисперсии по совокупности неизвестны
Универсиады тренируются в среднем пять раз в неделю.
Выборка из 12 государственных программ аспирантуры в школе A имеет среднюю плату за обучение в размере 64 000 фунтов стерлингов со стандартным отклонением 8 000 фунтов стерлингов. В школе B выборка из 16 программ магистратуры штата имеет среднее значение 80 000 фунтов стерлингов со стандартным отклонением 6 000 фунтов стерлингов.В среднем отличается ли средняя плата за обучение?
средние по независимой группе, стандартные отклонения и / или дисперсии по совокупности неизвестны
Потребителям предлагается новый усилитель диапазона Wi-Fi. Исследователь тестирует собственный диапазон 12 различных маршрутизаторов в одинаковых условиях. Диапазоны записываются. Затем исследователь использует новый усилитель диапазона WiFi и записывает новые диапазоны. Лучше ли работает новый усилитель диапазона Wi-Fi?
Директор средней школы утверждает, что 30% студентов-спортсменов едут в школу сами, а 4% не-спортсменов едут в школу сами.В выборке из 20 студентов-спортсменов 45% ездят в школу сами. В выборке из 35 студентов, не занимающихся спортом, 6% ездят в школу самостоятельно. Является ли процент студентов-спортсменов, которые ездят в школу самостоятельно, больше, чем процент не спортсменов?
Используйте следующую информацию, чтобы ответить на следующие три упражнения: Проводится исследование, чтобы определить, какой из двух безалкогольных напитков содержит больше сахара. В образце 13 банок напитка А и шесть банок напитка Б. Среднее количество сахара в напитке А составляет 36 граммов со стандартным отклонением 0.6 грамм. Среднее количество сахара в напитке B составляет 38 граммов со стандартным отклонением 0,8 грамма. Исследователи считают, что в напитке B в среднем больше сахара, чем в напитке A. Обе популяции имеют нормальное распределение.
Стандартные отклонения известны или неизвестны?
Что такое случайная величина?
Случайная величина — это разница между средним количеством сахара в двух безалкогольных напитках.
Это односторонний или двусторонний тест?
Используйте следующую информацию, чтобы ответить на следующие 12 упражнений: The U.Центр контроля заболеваний С. сообщает, что средняя продолжительность жизни составляла 47,6 года для белых, родившихся в 1900 году, и 33,0 года для небелых. Предположим, вы произвольно просматриваете записи о смерти людей, родившихся в 1900 году в определенном округе. Из 124 белых средняя продолжительность жизни составила 45,3 года со стандартным отклонением 12,7 года. Средняя продолжительность жизни из 82 небелых составила 34,1 года со стандартным отклонением 15,6 года. Проведите проверку гипотезы, чтобы увидеть, была ли средняя продолжительность жизни в округе одинаковой для белых и небелых.
Это тест на средства или пропорции?
Сформулируйте нулевую и альтернативную гипотезы.
- H 0 : __________
- H a : __________
Это правосторонний, левосторонний или двусторонний тест?
В символах, какая случайная переменная представляет интерес для этого теста?
На словах определите интересующую случайную переменную для этого теста.
разница между средней продолжительностью жизни белых и небелых
Какое распределение (нормальное или распределение Стьюдента t ) вы бы использовали для этой проверки гипотезы?
Объясните, почему вы выбрали именно тот дистрибутив (рисунок).
Это сравнение двух средних значений совокупности с неизвестными стандартными отклонениями совокупности.
Рассчитайте статистику теста и значение p .
Нарисуйте график ситуации. Обозначьте горизонтальную ось. Отметьте предполагаемую разницу и разницу в выборке. Заштрихуйте область, соответствующую значению p .
Проверить решение учащегося.
При заранее заданном α = 0,05, каково ваше:
- Решение:
- Причина решения:
- Заключение (выпишите полным предложением):
- Отклонить нулевую гипотезу
- p -значение <0.05
- Недостаточно доказательств на уровне значимости 5%, чтобы поддержать утверждение о том, что продолжительность жизни в 1900-х годах различается между белыми и небелыми.
Похоже, что средства те же? Почему или почему нет?
Домашнее задание
УКАЗАНИЯ: Для каждой задачи со словом используйте лист с решениями для проверки гипотезы. Лист решения находится в Приложении E. Пожалуйста, делайте копии листов решения. Для онлайн-версии книги рекомендуется скопировать файл.doc или файлы .pdf.
ПРИМЕЧАНИЕ
Если вы используете распределение ученика t для следующей задачи домашнего задания, в том числе для парных данных, вы можете предположить, что основная совокупность распределена нормально. (Однако при использовании этих тестов в реальной ситуации вы должны сначала доказать это предположение.)
Считается, что среднее количество курсов английского языка, которые проходят за двухлетний период студентами колледжей мужского и женского пола, примерно одинаково.Проведен эксперимент и собраны данные от 29 мужчин и 16 женщин. Мужчины прошли в среднем три курса английского языка со стандартным отклонением 0,8. Женщины прошли в среднем четыре курса английского языка со стандартным отклонением 1,0. Статистически ли средние значения одинаковы?
Студент четырехлетнего колледжа утверждает, что средний набор в четырехлетние колледжи выше, чем в двухгодичных колледжах в Соединенных Штатах. Проведены два опроса. Из 35 обследованных двухгодичных колледжей среднее число учащихся составило 5 068 человек со стандартным отклонением 4 777 человек.Из 35 опрошенных четырехлетних колледжей среднее число учащихся составило 5 466 человек со стандартным отклонением 8 191 человек.
Индексы: 1: двухгодичные колледжи; 2: четырехлетние колледжи
- H 0 : μ 1 ≥ μ 2
- H a : μ 1 < μ 2
- — это разница между средней посещаемостью двухгодичных и четырехлетних колледжей.
- Студенческая — т
- статистика теста: -0,2480
- p -значение: 0,4019
- Проверить решение учащегося.
- Альфа: 0,05
- Решение: не отклонять
- Причина решения: p -значение> альфа
- Заключение. При уровне значимости 5% имеется достаточно доказательств, чтобы сделать вывод о том, что средний набор учащихся в четырехлетние колледжи выше, чем в двухгодичных колледжах.
На вечеринке по случаю дня рождения Рэйчел 11 th восемь девушек были приурочены к тому, чтобы посмотреть, как долго (в секундах) они смогут задерживать дыхание в расслабленном положении.После двухминутного отдыха они рассчитали время во время прыжка. Девочки думали, что средняя разница между их прыжками и расслаблением будет равна нулю. Проверьте свою гипотезу.
| Время расслабления (секунды) | Время прыжка (секунды) |
|---|---|
| 26 | 21 |
| 47 | 40 |
| 30 | 28 |
| 22 | 21 |
| 23 | 25 |
| 45 | 43 |
| 37 | 35 |
| 29 | 32 |
Предполагается, что средняя заработная плата начального уровня выпускников колледжей со степенью инженера-механика и инженера-электрика примерно одинакова.Военкомат считает, что средняя зарплата инженера-механика на самом деле ниже средней зарплаты инженера-электрика. Кадровая служба произвольно опрашивает 50 инженеров-механиков начального уровня и 60 инженеров-электриков начального уровня. Их средняя заработная плата составляла 46 100 и 46 700 евро соответственно. Их стандартные отклонения составили 3450 и 4210 фунтов соответственно. Проведите проверку гипотез, чтобы определить, согласны ли вы с тем, что средняя зарплата начинающего инженера-механика ниже, чем средняя зарплата электротехника начального уровня.
Индексы: 1: машиностроение; 2: электротехника
- H 0 : µ 1 ≥ µ 2
- H a : µ 1 < µ 2
- — это разница между средней заработной платой инженеров-механиков и инженеров-электриков начального уровня.
- т 108 Статистика теста
- : т = –0.82
- p -значение: 0.2061
- Проверить решение учащегося.
- Альфа: 0,05
- Решение: Не отвергать нулевую гипотезу.
- Причина решения: p -значение> альфа
- Заключение. При уровне значимости 5% недостаточно доказательств, чтобы сделать вывод о том, что средняя начальная заработная плата инженеров-механиков ниже, чем у инженеров-электриков.
Маркетинговые компании собрали данные, свидетельствующие о том, что девочки-подростки используют больше рингтонов на своих сотовых телефонах, чем мальчики.В одном конкретном исследовании с участием 40 случайно выбранных девочек и мальчиков-подростков (по 20 каждого) с сотовыми телефонами среднее количество мелодий звонка для девочек составило 3,2 со стандартным отклонением 1,5. Среднее значение для мальчиков составило 1,7 при стандартном отклонении 0,8. Проведите проверку гипотезы, чтобы определить, совпадают ли средние значения или среднее значение девочек выше среднего значения мальчиков.
Используйте информацию из (Рисунок), чтобы ответить на следующие четыре упражнения.
Используя данные только первого круга, проведите проверку гипотезы, чтобы определить, является ли среднее время прохождения круга в гонках таким же, как и на практике.
- H 0 : µ 1 = µ 2
- H a : µ 1 ≠ µ 2
- — это разница между средним временем прохождения круга в гонках и на тренировках.
- т 20,32
- статистика теста: –4,70
- p -значение: 0,0001
- Проверить решение учащегося.
- Альфа: 0,05
- Решение: отклонить нулевую гипотезу.
- Причина решения: p -значение <альфа
- Заключение: При уровне значимости 5% имеется достаточно доказательств, чтобы сделать вывод о том, что среднее время прохождения круга в гонках отличается от такового на практике.
Повторите тест из упражнения 10.83, но на этот раз объедините данные из 1 и 5 кругов.
- H 0 : µ 1 = µ 2
- H a : µ 1 ≠ µ 2
- — это разница между средним временем прохождения круга в гонках и на тренировках.
- т 40.94
- статистика теста: –5,08
- p -значение: ноль
- Проверить решение учащегося.
- Альфа: 0,05
- Решение: отклонить нулевую гипотезу.
- Причина решения: p -значение <альфа
- Заключение: При уровне значимости 5% имеется достаточно доказательств, чтобы сделать вывод о том, что среднее время прохождения круга в гонках отличается от такового на практике.
В двух-трех полных предложениях подробно объясните, как вы можете использовать данные Терри Фогель, чтобы ответить на следующий вопрос. «Терри Фогель едет быстрее на гонках, чем на тренировках?»
Используйте следующую информацию, чтобы ответить на следующие два упражнения. В конференциях Высшей и Западной футбольной лиги есть новый резервный дивизион, который позволяет новым игрокам развивать свои навыки. Данные за случайно выбранную дату показали следующие годовые цели.
| Западный | Восточная |
|---|---|
| Лос-Анджелес 9 | округ Колумбия Юнайтед 9 |
| Даллас 3 | Чикаго 8 |
| Чивас США 4 | Колумбус 7 |
| Реал Солт-Лейк 3 | Новая Англия 6 |
| Колорадо 4 | MetroStars 5 |
| Сан-Хосе 4 | Канзас-Сити 3 |
Проведите проверку гипотез, чтобы ответить на следующие два упражнения.
точное распределение для проверки гипотезы:
- нормальное распределение
- Студенческая т -распределение
- равномерное распределение
- экспоненциальное распределение
Если уровень значимости 0,05, вывод:
- Имеется достаточно доказательств, чтобы сделать вывод о том, что команды W в среднем забивают меньше голов, чем команды E
- Недостаточно доказательств, чтобы сделать вывод о том, что команды W в среднем забивают больше голов, чем команды E .
- Недостаточно доказательств, чтобы сделать вывод о том, что команды W в среднем забивают меньше голов, чем команды E .
- Невозможно определить
Предположим, инструктор по статистике считает, что нет существенной разницы между средними баллами дневных студентов по статистике на Экзамене 2 и статистических вечерних студентов на Экзамене 2. Она берет случайные выборки из каждой популяции. Среднее значение и стандартное отклонение для 35 студентов дневного отделения статистики составили 75.86 и 16.91. Среднее значение и стандартное отклонение для 37 студентов-статистиков-вечерников составили 75,41 и 19,73. Нижний индекс «день» относится к студентам-дневникам статистики. Нижний индекс «ночь» относится к статистике вечерних школьников. Заключительное заявление:
- Имеется достаточно доказательств, чтобы сделать вывод о том, что статистические данные среднего учащихся дневного отделения по экзамену 2 лучше, чем статистические данные среднего учащихся дневного отделения по экзамену 2.
- Недостаточно доказательств, чтобы сделать вывод о том, что статистика дневных учеников по Экзамену 2 лучше, чем статистика ночных учеников по экзамену 2.
- Недостаточно доказательств, чтобы сделать вывод о значительном различии между средними значениями статистики дневных и вечерних студентов на экзамене 2.
- Имеется достаточно доказательств, чтобы сделать вывод о значительном различии между средними значениями статистики дневных и вечерних учащихся на экзамене 2.
Исследователи опросили уличных проституток в Канаде и США. Средний возраст 100 канадских проституток на момент занятия проституцией составлял 18 лет со стандартным отклонением шесть.Средний возраст 130 проституток в США, когда они начали заниматься проституцией, составлял 20 лет со стандартным отклонением восемь. Является ли средний возраст занятия проституцией в Канаде ниже, чем средний возраст в Соединенных Штатах? Проверьте уровень значимости 1%.
Тест: два независимых средних значения выборки, стандартные отклонения генеральной совокупности неизвестны.
Случайная переменная:
Распределение: H 0 : μ 1 = μ 2 H a : μ 1 < μ 2 Средний возраст начала проституции в Канада ниже среднего возраста в Соединенных Штатах.
График: левосторонний
p -значение: 0,0151
Решение: Не отклонять H 0 .
Заключение. При уровне значимости 1%, основанном на данных выборки, нет достаточных доказательств, чтобы сделать вывод о том, что средний возраст начала проституции в Канаде ниже, чем средний возраст в Соединенных Штатах.
Порошковая диета протестирована на 49 человек, а жидкая диета — на 36 различных людях. Интересно, приводит ли жидкая диета к более высокой средней потере веса, чем порошковая диета.В группе с порошковой диетой средняя потеря веса составила 42 фунта со стандартным отклонением 12 фунтов. В группе с жидкой диетой средняя потеря веса составила 45 фунтов со стандартным отклонением 14 фунтов.
Предположим, инструктор по статистике считает, что нет существенной разницы между средними баллами дневных студентов по статистике на Экзамене 2 и статистических вечерних студентов на Экзамене 2. Она берет случайные выборки из каждой популяции. Среднее значение и стандартное отклонение для 35 студентов дневного отделения статистики составили 75.86 и 16,91 соответственно. Среднее значение и стандартное отклонение для 37 студентов-статистиков-вечерников составили 75,41 и 19,73. Нижний индекс «день» относится к студентам-дневникам статистики. Нижний индекс «ночь» относится к статистике вечерних школьников. Подходящая альтернативная гипотеза для проверки гипотезы:
- мкм день > мкм ночь
- мкм день < мкм ночь
- мкм день = мкм ночь
- мкм день ≠ мкм ночь
Глоссарий
- Степени свободы ( df )
- количество объектов в выборке, которые могут изменяться.
- Стандартное отклонение
- Число, равное квадратному корню из дисперсии и измеряющее, насколько далеко значения данных отличаются от своего среднего; обозначение: s для стандартного отклонения выборки и σ для стандартного отклонения генеральной совокупности.
- Переменная (случайная переменная)
- характеристика интереса к изучаемому населению. Общее обозначение переменных — заглавные латинские буквы X , Y , Z ,… Общее обозначение для определенного значения из домена (набор всех возможных значений переменной) — строчные латинские буквы x , y , z ,….Например, если X — это количество детей в семье, тогда x представляет собой конкретное целое число 0, 1, 2, 3,…. Переменные в статистике отличаются от переменных в промежуточной алгебре двумя следующими способами.
- Область случайной величины (RV) не обязательно является числовым набором; домен может быть выражен словами; например, если X = цвет волос, то домен будет {черный, светлый, серый, зеленый, оранжевый}.
- Мы можем сказать, какое именно значение x случайной величины X принимает только после проведения эксперимента.
| ’62 Центр театра и танца, ’62 Центр | ||
| касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Academic Resources, Парески | 597-4672 | 597-4959 факс |
| Службы поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Affirmative Action, Hopkins Hall | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотография Студия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Студия скульптуры, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / фотостудия, Spencer Studio Art | 597-3193 | |
| Asian Studies, Hollander | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, Физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочный домик, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическая культура | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
| Центр экологических исследований, класс 1966 г. Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория наук об окружающей среде, Морли | 597-2380 | |
| Исследования окружающей среды | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабоведение, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Холландер | 597-2391 | 597-3028 факс |
| лингафонный кабинет | 597-3260 | |
| Россия, Холландер | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Chemistry, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| College Marshal, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс-Вест | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс-Уэст | 597-4151 | 597-4178 факс |
| Почтовые службы для выпускников / разработчиков, Мирс-Уэст | 597-4369 | |
| Девелопмент, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Фогт | 597-3538 | 597-4039 факс |
| Grants Office, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Фонд родителей, Фогт | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Mears | 597-4119 | 597-4178 факс |
| Начало и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Парески | 597-2591 | 597-4748 факс |
| Запросы Elm Tree House, Mt.Хоуп Фарм | 597-2591 | |
| Офис контролера, Хопкинс Холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Financial Information Systems, Hopkins Hall | 597-4023 | |
| Карты покупок, Хопкинс Холл | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Davis Center (бывший Многокультурный центр), Jenness | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Кондитерская, Парески | 597-4511 | |
| Общественное питание, факультет | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Парески | 597-2889 | |
| Economics, Schapiro | 597-2476 | 597-4045 факс |
| Английский, Холландер | 597-2114 | 597-4032 факс |
| Сооружения, служебное здание | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы на работу производственных помещений | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Факультетский клуб, Факультетский дом / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Geosciences, Clark Hall | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Аспирантура по истории искусств, Кларк | 458-2317 факс | |
| Health and Wellness Services, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Санитарное просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с угрозой жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Лес Хопкинса | 597-4353 | |
| Розенбург Центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Погодная линия (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курса, Drop Box для офисных услуг | 597-4090 | |
| Центр ссуды на оборудование, Додд Приложение | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [адрес электронной почты защищен] | 597-4090 | |
| Мультимедийные службы и справочная служба | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / Телефоны | 597-4090 | |
| Междисциплинарные исследования, Холландер | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Справедливость и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Хопкинс-холл | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Performance Studies, ’62 Center | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр старой обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс-холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Жилье для преподавателей / сотрудников | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 Дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Каталогизация / Службы метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Вовлеченность студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Паресский почтовый кабинет | 597-2150 | |
| Устойчивое развитие / Центр Зилха, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямса | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| VP for Campus Life, Hopkins Hall | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| вице-президент по финансам и администрированию, Хопкинс-холл | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Уильямс Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Хопкинс-холл | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
Статистика: сила из данных! Организационные данные: стеблевые и листовые участки
Архивный контент
Информация, помеченная как архивная, предназначена для справки, исследования или ведения записей.Он не регулируется веб-стандартами правительства Канады и не изменялся и не обновлялся с момента его архивирования. Свяжитесь с нами, чтобы запросить формат, отличный от доступных.
График стебля и листа или график ствола — это метод, используемый для классификации дискретных или непрерывных переменных . График стебля и листа используется для организации данных по мере их сбора.
График стебля и листа выглядит как гистограмма. Каждое число в данных разбито на стержень и лист, отсюда и название.Основа числа включает все цифры, кроме последней. Лист числа всегда будет однозначным.
Хороший стебельно-листовой участок
- показывает первые цифры числа (тысячи, сотни или десятки) как основание и показывает последнюю цифру (единицы) как лист .
- обычно использует целые числа. Все, что имеет десятичную точку, округляется до ближайшего целого числа. Например, результаты испытаний, скорости, высоты, веса и т. Д.
- выглядит как гистограмма, когда он повернут на бок.
- показывает, как распределяются данные — то есть наибольшее число, наименьшее число, наиболее распространенное число и выбросы (число, лежащее за пределами основной группы чисел).
Начало страницы
После того, как вы решили, что график стебля и листа — лучший способ показать ваши данные, нарисуйте его следующим образом:
- В левой части страницы запишите тысячи, сотни или десятки (все цифры, кроме последней).Это будут ваши стебли.
- Проведите линию справа от этих стержней.
- На другой стороне линии запишите единицы (последняя цифра числа). Это будут твои листья.
Например, если наблюдаемое значение равно 25, тогда стебель равен 2, а лист — 5. Если наблюдаемое значение равно 369, то стебель равен 36, а лист равен 9. Если наблюдения точны до одного или нескольких десятичных разрядов, например 23,7, стержень равен 23, а лист — 7. Если диапазон значений слишком велик, число 23.7 можно округлить до 24, чтобы ограничить количество стержней.
На делянках стволов и листьев отметки не требуются, поскольку используются фактические данные.
Не совсем понимаете? Попробуйте выполнить упражнения.
Пример 1 — Создание участка стебля и листа
Каждое утро учитель задавал в классе 20 вопросов по географии. Класс ставил их вместе, и каждый записывал свои личные баллы. По прошествии года каждый студент пытался улучшить свои оценки викторины.Каждый день Эллиот записывал свои контрольные отметки на участке стебля и листа. Вот как выглядели его отметки на графике:
| 0 | 3 6 5 |
|---|---|
| 1 | 0 1 4 3 5 6 5 6 8 9 7 9 |
| 2 | 0 0 0 0 |
Проанализируйте график стебля и листа Эллиота. Какой у него самый частый результат в викторинах по географии? Какая у него самая высокая оценка? Его самый низкий балл? Поверните участок стебля и листа на бок так, чтобы он выглядел как гистограмма.Большинство оценок Эллиота составляют 10, 20 или меньше 10? По сюжету трудно понять, улучшился ли Эллиот или нет, потому что мы не знаем порядок этих оценок.
Попробуйте сделать свой собственный участок стебля и листа. Используйте оценки чего-то вроде всех ваших результатов экзаменов в прошлом году или очков, набранных вашей спортивной командой в этом сезоне.
Начало страницы
Основное преимущество графика ствола и листа заключается в том, что данные сгруппированы, а также отображаются все исходные данные.В Примере 3 о сроке службы батареи в разделе Таблицы распределения частот таблица показывает, что два наблюдения произошли в интервале от 360 до 369 минут. Однако таблица не сообщает вам, что это за фактические наблюдения. График стебля и листа покажет эту информацию. Без графика ствола и листа два значения (363 и 369) можно найти только путем поиска по всем исходным данным — утомительная задача, когда у вас много данных!
При просмотре набора данных каждое наблюдение можно рассматривать как состоящее из двух частей — стебля и листа.Чтобы построить график стебля и листа, каждое наблюдаемое значение необходимо сначала разделить на две части:
- Основа — это первая цифра или цифры;
- Лист — это последняя цифра значения;
- Каждая основа может состоять из любого количества цифр; но
- На каждом листе может быть только одна цифра.
Начало страницы
Пример 2 — Создание участка стебля и листа
Учительница спросила 10 своих учеников, сколько книг они прочитали за последние 12 месяцев.Их ответы были следующие:
12, 23, 19, 6, 10, 7, 15, 25, 21, 12
Подготовьте график стебля и листа для этих данных.
Совет: Число 6 можно записать как 06, что означает, что у него на ножке 0 и на листе 6.
Участок стебля и листа должен выглядеть так:
| 0 | 6 7 |
|---|---|
| 1 | 2 9 0 5 2 |
| 2 | 3 5 1 |
В таблице 2:
- стержень 0 представляет интервал классов от 0 до 9;
- шток 1 представляет интервал классов от 10 до 19; и
- стержень 2 представляет интервал классов от 20 до 29.
Обычно участок стебля и листа имеет порядок как , что просто означает, что листья расположены в порядке возрастания слева направо. Кроме того, нет необходимости разделять листья (цифры) знаками препинания (запятыми или точками), поскольку каждый лист всегда представляет собой одну цифру.
Используя данные из Таблицы 2, мы сделали заказанный участок стебля и листа , показанный ниже:
| 0 | 6 7 |
|---|---|
| 1 | 0 2 2 5 9 |
| 2 | 1 3 5 |
Начало страницы
Пример 3 — Создание упорядоченного участка стебля и листа
Пятнадцать человек спросили, как часто они ездят на работу более 10 рабочих дней.Каждый человек водил машину следующим образом:
5, 7, 9, 9, 3, 5, 1, 0, 0, 4, 3, 7, 2, 9, 8
Сделайте для этого стола заказанный участок стебля и листа.
Его необходимо нарисовать следующим образом:
| 0 | 0 0 1 2 3 3 4 5 5 7 7 8 9 9 9 |
|---|
Организация этого участка стебля и листа не дает много информации о данных.Имея только один стебель, листья переполнены. Если листья становятся слишком скученными, может быть полезно разделить каждый стебель на два или более компонентов. Таким образом, интервал 0–9 можно разделить на два интервала 0–4 и 5–9. Точно так же стержень 0–9 можно разделить на пять интервалов: 0–1, 2–3, 4–5, 6–7 и 8–9.
В этом случае участок стебля и листа должен выглядеть следующим образом:
| 0 (0) | 0 0 1 2 3 3 4 |
|---|---|
| 0 (5) | 5 5 7 7 8 9 9 9 |
Примечание: Стержень 0 (0) означает все данные в интервале 0–4.Ствол 0 (5) означает все данные в интервале 5–9.
Начало страницы
Пример 4 — Разделение стеблей
Бритни готовится к соревнованиям по плаванию. Количество 50-метровых кругов, которые она проплавала каждый день в течение 30 дней, составляет:
22, 21, 24, 19, 27, 28, 24, 25, 29, 28, 26, 31, 28, 27, 22, 39, 20, 10, 26, 24, 27, 28, 26, 28, 18 , 32, 29, 25, 31, 27
- Подготовить заказанный участок стебля и листа. Кратко прокомментируйте, что он показывает.
- Нарисуйте участок стебля и листа заново, разделив стебли на интервалы по пять единиц. Кратко прокомментируйте, что показывает новый сюжет.
- Диапазон наблюдений составляет от 10 до 39, поэтому на участке стебля и листа должны быть стебли 1, 2 и 3. Упорядоченный участок стебля и листа показан ниже:
График стебля и листа показывает, что Бритни обычно проплывает от 20 до 29 кругов на тренировке каждый день.Таблица 6. Круги, пройденные Бритни за 30 дней 1 0 8 9 2 0 1 2 2 4 4 4 5 5 6 6 6 7 7 7 7 8 8 8 8 8 9 9 3 1 1 2 9 - Разделение стеблей на интервалы по пять единиц дает следующий участок стебля и листа:
Таблица 7. Круги, пройденные Бритни за 30 дней 1 (0) 0 1 (5) 8 9 2 (0) 0 1 2 2 4 4 4 2 (5) 5 5 6 6 6 7 7 7 7 7 8 8 8 8 8 9 9 3 (0) 1 1 2 3 (5) 9 Примечание: Стержень 1 (0) означает все данные от 10 до 14, 1 (5) означает все данные от 15 до 19 и т. Д.
Пересмотренный график стебля и листа показывает, что Бритни обычно плавает от 25 до 29 кругов на тренировках каждый день. Значения 1 (0) 0 = 10 и 3 (5) 9 = 39 можно рассматривать как выбросы — концепция, которая будет описана в следующем разделе.
Начало страницы
Пример 5 — Разделение стержней с использованием десятичных значений
Вес (с точностью до десятых килограмма) 30 студентов был измерен и записан следующим образом:
59.2, 61.5, 62.3, 61.4, 60.9, 59.8, 60.5, 59.0, 61.1, 60.7, 61.6, 56.3, 61.9, 65.7, 60.4, 58.9, 59.0, 61.2, 62.1, 61.4, 58.4, 60.8, 60.2, 62.7, 60.0, 59,3, 61,9, 61,7, 58,4, 62,2
Подготовьте упорядоченный график стебля и листа для данных. Кратко прокомментируйте, что показывает анализ.
Ответ
В этом случае стебли будут целыми числами, а листья — десятичными значениями. Диапазон данных от 56,3 до 65,7, поэтому стержни должны начинаться с 56 и заканчиваться на 65.
| 56 | 3 |
|---|---|
| 57 | |
| 58 | 4 4 9 |
| 59 | 0 0 2 3 8 |
| 60 | 0 2 4 5 7 8 9 |
| 61 | 1 2 4 4 5 6 7 9 9 |
| 62 | 1 2 3 7 |
| 63 | |
| 64 | |
| 65 | 7 |
В этом примере не было необходимости разделять стебли, потому что листья не скапливаются на слишком малом количестве стеблей; также не было необходимости округлять значения, поскольку диапазон значений невелик.Этот график стебля и листа показывает, что группа с наибольшим количеством зарегистрированных наблюдений — это группа от 61,0 до 61,9.
Начало страницы
Выброс — это экстремальное значение данных. Это значение наблюдения, которое значительно отличается от остальных данных. В наборе данных может быть несколько выбросов.
Иногда выбросы являются важной информацией, и их не следует игнорировать. В других случаях они возникают из-за ошибки или дезинформации, и их следует игнорировать.
В предыдущем примере 56,3 и 65,7 можно было считать выбросами, поскольку эти два значения сильно отличаются от других значений.
Игнорируя эти два выброса, график стебля и листа из предыдущего примера можно перерисовать, как показано ниже:
| 58 | 4 4 9 |
|---|---|
| 59 | 0 0 2 3 8 |
| 60 | 0 2 4 5 7 8 9 |
| 61 | 1 2 4 4 5 6 7 9 9 |
| 62 | 1 2 3 7 |
При использовании участка стебля и листа определение выброса часто является вопросом суждения.Это связано с тем, что, за исключением случаев использования коробчатых диаграмм (объясненных в разделе, посвященном прямоугольным диаграммам и диаграммам усов), нет строгого правила относительно того, насколько далеко должно быть значение от остальной части набора данных, чтобы считаться выбросом.
Начало страницы
Когда вы оцениваете общий образец любого распределения (который представляет собой образец, сформированный всеми значениями конкретной переменной), обратите внимание на следующие особенности:
- количество вершин
- общая форма (косая или симметричная)
- центр
- спред
Количество вершин
Линейные графики полезны, потому что они легко показывают некоторые характеристики данных.(Подробнее об этом типе графиков см. В разделе о линейных графиках.)
Первая характеристика, которую можно легко увидеть на линейном графике, — это количество высших точек или пиков, которые имеет распределение.
В то время как большинство распределений, которые встречаются в статистических данных, имеют только один главный пик (одномодальный), другие распределения могут иметь два пика (бимодальный) или более двух пиков (мультимодальный).
Примеры унимодальных, бимодальных и мультимодальных линейных графиков показаны ниже:
Общая форма
Вторая основная характеристика распределения — это степень симметричности .
Совершенно симметричная кривая — это такая кривая, в которой обе стороны распределения будут точно соответствовать друг другу, если фигура будет сложена над ее центральной точкой. Пример показан ниже:
Симметричное унимодальное колоколообразное распределение — относительно обычное явление — называется нормальным распределением.
Если распределение является асимметричным, говорят, что оно искажено .
Говорят, что распределение смещено вправо или смещено положительно, , когда большая часть данных сосредоточена в левой части распределения.Распределения с положительным перекосом встречаются чаще, чем с отрицательным перекосом.
Доход является одним из примеров положительно искаженного распределения. Большинство людей зарабатывают менее 40 000 долларов в год, но некоторые зарабатывают немного больше, а меньшее число зарабатывает многие миллионы долларов в год. Следовательно, положительный (правый) хвост на линейном графике дохода простирается довольно далеко, тогда как отрицательный (левый) косой хвост останавливается на нуле. Правый хвост явно идет дальше от центра распределения, чем левый, как показано ниже:
Говорят, что распределение смещено влево или смещено отрицательно, , если большая часть данных сосредоточена справа от распределения.Левый хвост явно простирается дальше от центра распределения, чем правый, как показано ниже:
Центр и разворот
Определение центра (медиана , ) распределения можно выполнить, отсчитав половину наблюдений от наименьшего. Очевидно, что этот метод неприменим для очень больших наборов данных. Однако диаграмма ствола и листа упрощает это, поскольку данные расположены в порядке возрастания. Среднее значение — еще одна мера центральной тенденции.(Подробнее см. Главу о центральной тенденции.)
Величину разброса распределения и любые большие отклонения от общей картины (выбросы) можно быстро определить на графике.
График стебля и листа — это простой вид графика, который состоит из самих чисел. Это средство отображения основных характеристик дистрибутива. Если график стебля и листа повернуть на бок, он будет напоминать гистограмму или гистограмму и предоставлять аналогичную визуальную информацию.
Начало страницы
Пример 6 — Использование графиков стебля и листьев в качестве графика
Результаты тестов по математике 41 студента (с максимальным баллом 70) приведены ниже:
31, 49, 19, 62, 50, 24, 45, 23, 51, 32, 48, 55, 60, 40, 35, 54, 26, 57, 37, 43, 65, 50, 55, 18, 53 , 41, 50, 34, 67, 56, 44, 4, 54, 57, 39, 52, 45, 35, 51, 63, 42
- Является ли переменная дискретной или непрерывной? Объяснять.
- Подготовьте упорядоченный график стебля и листа для данных и кратко опишите, что на нем показано.
- Есть ли выбросы? Если да, то какие?
- Посмотрите на участок стебля и листа сбоку. Опишите основные особенности дистрибутива, такие как:
- количество вершин
- симметрия
- значение в центре распределения
Ответы
- Оценка за тест — это дискретная переменная. Например, невозможно получить результат теста 35.74542341 ….
- Наименьшее значение — 4, а максимальное — 67. Таким образом, график стебля и листа, охватывающий этот диапазон значений, выглядит следующим образом:
Таблица 10. Баллы 41 студента по математике 0 4 1 8 9 2 3 4 6 3 1 2 4 5 5 7 9 4 0 1 2 3 4 5 5 8 9 5 0 0 0 1 1 2 3 4 4 5 5 6 7 7 6 0 2 3 5 7 Примечание: Обозначения 2 | 4 представляют стержень 2 и лист 4.
График стебля и листа показывает, что большинство студентов набрали от 50 до 59 баллов. Большое количество студентов, получивших высокие результаты, может означать, что тест был слишком легким, что большинство студентов хорошо знали материал, или сочетание того и другого. .
- Результат 4 может быть выбросом, поскольку существует большой разрыв между этим и следующим результатом, 18.
- Если перевернуть стебель и листовой участок на бок, он будет выглядеть следующим образом:
Распределение имеет единственный пик в интервале 50–59.
Хотя имеется всего 41 наблюдение, распределение показывает, что большинство данных сгруппированы справа. Левый хвост простирается дальше от центра обработки данных, чем правый. Следовательно, распределение смещено влево или отклонено на отрицательно.
Поскольку имеется 41 наблюдение, центр распределения (медианное значение) будет находиться в 21-м наблюдении. Если отсчитать 21 наблюдение от наименьшего, центр будет 48.
