Контрольные работы по математике 10 класс (Колягин, Атанасян) | Учебно-методический материал по математике (10 класс) на тему:
А-10 (авт. Ю.М. Колягин) Контрольная работа №3
Степень с действительным показателем
Базовый уровень
В – 1 В — 2
1. Вычислить:
1) 1)
2) 2)
2. Упростить выражение при
1) 1)
2) 2)
3. Сократить дробь 3. Сократить дробь
4. Сравнить числа:
1) 1)
2) и 1. 2) и 1.
5. Найти сумму бесконечно убывающей
геометрической прогрессии,
если
5. Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен
А – 10 (Ю.М. Колягин) Базовый уровень Контрольная работа №4
Степенная функция
Вариант 1
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х7 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (0,95)7; 2) сравнить и .
3. Решить уравнение:
1) 2) ; 3)
4. Установить, равносильны ли неравенства и
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Контрольная работа №4
Степенная функция
Вариант 2
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х6 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (1,001)6; 2) сравнить и .
3. Решить уравнение: 1) 2) .
3)
4. Установить, равносильны ли неравенства и .
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
А-10 (Ю.М. Колягин) Базовый уровень Контрольная работа №5
Показательная функция
Вариант 1
1. Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство >
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Контрольная работа №5
Показательная функция
Вариант 2
1. Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство .
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
(Дополнительно) Решить уравнение
А – 10 Колягин Контрольная работа № 6 Логарифмическая функция
Вариант 1
1. Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Контрольная работа № 1.4 Логарифмическая функция
Вариант 2
1. Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
А – 10 Колягин Контрольная работа №7
Тригонометрические формулы Вариант 1
1. Найти значение выражения: 1) 2) 3)
2. Вычислить:
3. Упростить выражение:
4. Доказать тождество:
5. Решить уравнение
Контрольная работа № 7
Тригонометрические формулы Вариант 2
1. Найти значение выражения: 1) 2) 3)
Найти значение выражения: 1) 2) 3)
2. Вычислить:
3. Упростить выражение:
4. Доказать тождество:
5. Решить уравнение
А – 10 Колягин Контрольная работа № 8
Тригонометрические уравнения
Вариант 1
1. Решите уравнение:
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
; в)
4. Решите уравнение:
а)
Контрольная работа № 8
Тригонометрические уравнения
Вариант 2
1. Решите уравнение:
а)
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
в)
4. Решите уравнение:
а)
Контрольная работа по математике 10 класса за первое полугодие. УМК Колягин Ю.М.
Контрольная работа за 1 полугодие по математике в 10 классе
1 вариант Часть 1
Модуль «Алгебра»
А1.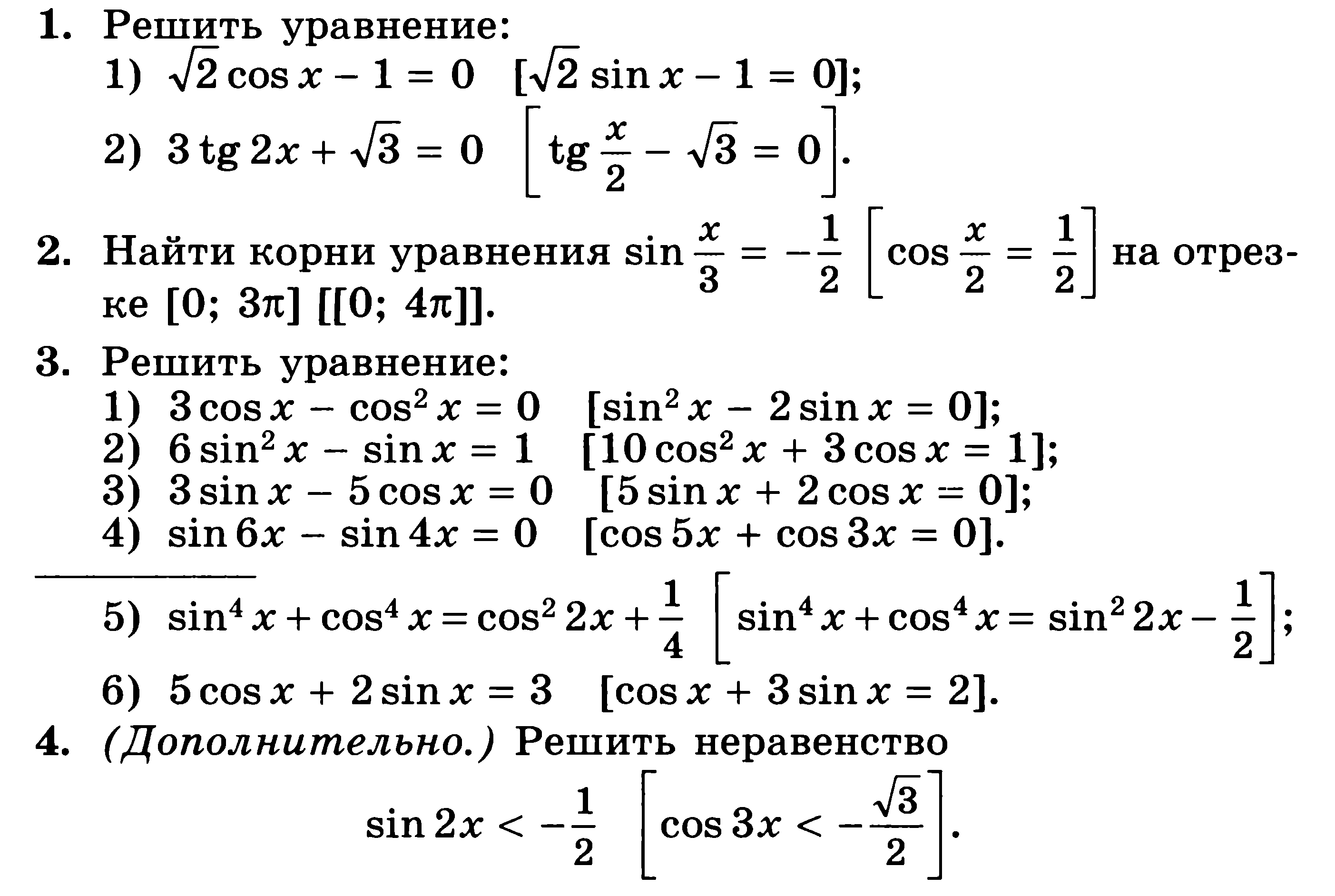 Найдите значение выражения: (7,6 – 3,1)∙6,8.
Найдите значение выражения: (7,6 – 3,1)∙6,8.
Ответ:__________________________________________________
А2.Найдите значение выражения:.
Ответ:__________________________________________________
А3.Не выполняя деления, найти остаток от деления многочлена
Р(х) = х4+3х3– х+2 на двучлен х+1.
Ответ:___________________________________________________
А4. Извлечь корень: .
Ответ:___________________________________________________
А5. Найдите значение выражения:
А6. Найти область определения функции у =
Ответ:___________________________________________________
А7. Найдите корень уравнения
Ответ:___________________________________________________
Модуль «Геометрия»
А8. Какие из следующих утверждений верны?
а) Любые четыре точки лежат в одной плоскости;
б) Любые три точки не лежат в одной плоскости;
в) Любые четыре точки не лежат в одной плоскости;
г) Любые три различные точки лежат в одной плоскости.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ:____________________________________
А9.Дан тетраэдр ДАВС. Какое из ребер в основании тетраэдра пересекается с прямой MN.
Ответ:_______________________
А10.В параллелепипеде укажите ребро, скрещивающееся с ребром АВ.
Ответ:____________________________________
А11. В параллелепипеде ребра, выходящие из одной вершины равны соответственно 5 см, 6см и 7 см. Найдите сумму длин всех ребер.
Ответ:_____________________________________
Часть 2
Модуль «Алгебра»
В1. Решите уравнение: х3 – 6х2+3х+10=0.
С1. Решите систему уравнений:
Модуль «Геометрия»
В1.Плоскость пересекает стороны АВ и ВС треугольника АВС в
точках Д и Е соответственно, причем АС параллельна плоскости Найдите АС, если ВД:АВ=3:7,ДЕ=10.
С1.Через точку К, не лежащую между параллельными плоскостями
и , проведены прямые l и m. Прямая l пересекает плоскости и в точках А и А соответственно, прямая
Контрольная работа за 1 полугодие по математике в 10 классе
2 вариант Часть 1
Модуль «Алгебра»
А1.Найдите значение выражения: (1,2+2,3)∙23.
Ответ:__________________________________________________
А2.Найдите значение выражения:.
Ответ:__________________________________________________
А3.Не выполняя деления, найти остаток от деления многочлена
Р(х) = 2х3+5х2+х – 2 на двучлен х+2.
Ответ:___________________________________________________
А4. Извлечь корень: .
Ответ:___________________________________________________
А5. Найдите значение выражения:
Найдите значение выражения:
Ответ:___________________________________________________
А6. Найти область определения функции у =
Ответ:___________________________________________________
А7. Найдите корень уравнения
Ответ:___________________________________________________
Модуль «Геометрия»
А8. Какие из следующих утверждений верны?
а) Через любые три точки проходит плоскость и притом только одна;
б) Если две точки прямой лежат в одной плоскости, то и вся прямая лежит в этой плоскости;
в) Через прямую и точку, лежащую на ней, проходит единственная плоскость;
г) Нельзя провести плоскость через две параллельные прямые.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ:____________________________________
А9.Какое из ребер в основании параллелепипеда пересекается с прямой КL?
Ответ:_______________________
А10.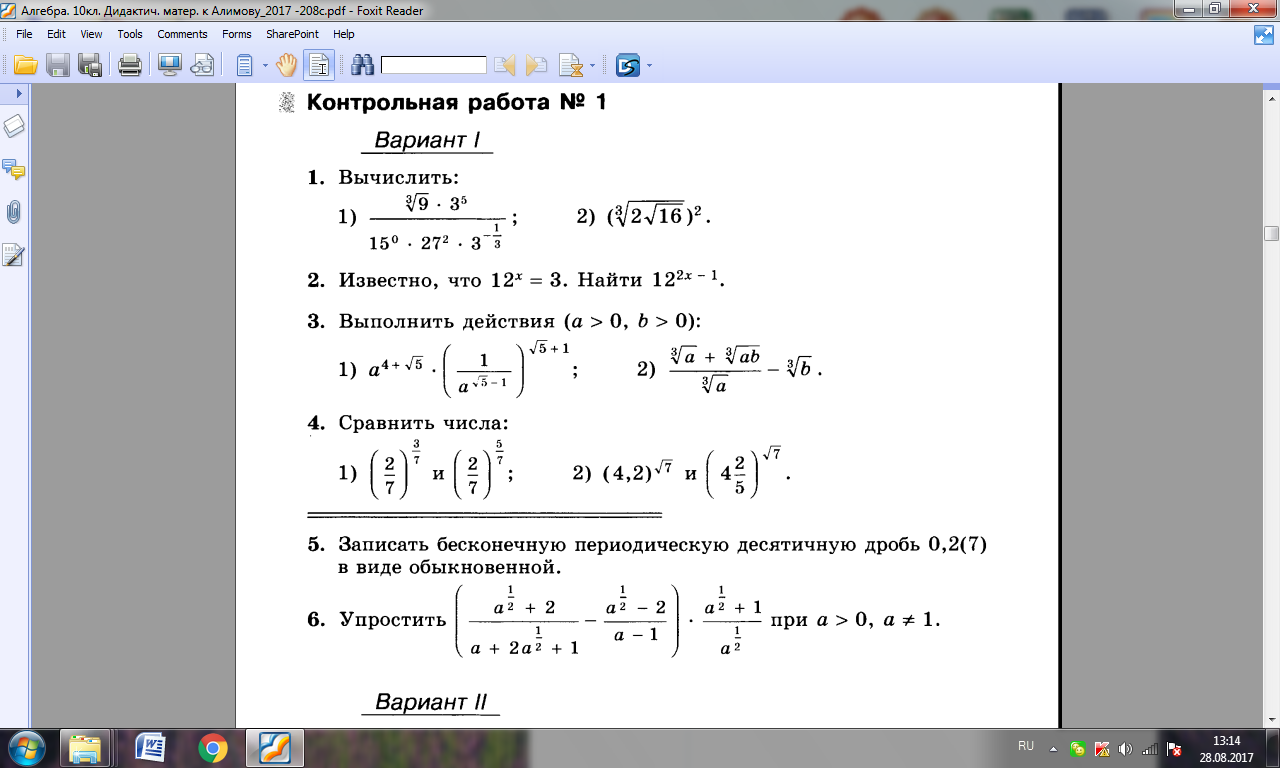 В тетраэдре укажите пару скрещивающихся ребер.
В тетраэдре укажите пару скрещивающихся ребер.
Ответ:____________________________________
А11. Определите сумму всех ребер, если это правильный тетраэдр и длина его ребра равна 4 см.
Ответ:_____________________________________
Часть 2
Модуль «Алгебра»
В1. Решите уравнение: х3+4х2 – 7х-10=0.
С1. Решите систему уравнений:
Модуль «Геометрия»
В1.Плоскость пересекает стороны MP и KP треугольника MPK соответственно в точках N и E, причем сторона MK параллельна плоскости , MK=12, МР:NP = 8:5.Найдите NE.
С1.Через точку М, лежащую между параллельными плоскостями и , проведены прямые
Спецификация диагностической работы за 1 полугодие по математике в 10 классе
Контрольная работа предназначается для проверки уровня усвоения обучающимися 10класса предметного содержания курса математики за 1 полугодие.
Анализдиагностической работы
№ | Баллы | Проверяемое содержание | Планируемые результаты | Умения | ||||
Часть 1 | ||||||||
Модуль «Алгебра» | ||||||||
1 | 1 | Арифметические действия с десятичными дробями. | Оперировать понятием десятичной дроби, выполнять вычисления с десятичными дробями | Умение выполнять действия с десятичными дробями. | ||||
2 | 1 | Степень числа с натуральным показателем | Владение понятием степени с натуральным показателем | Умение выполнять действия со степенью с натуральным показателем | ||||
3 | 1 | Многочлен Р(х). Теорема Безу | Применять теорему Безу для отыскания остатка при делении многочлена на линейный двучлен | Уметь находить остаток с помощью применения теоремы Безу | ||||
4 | 1 | Квадратные корни | Оперировать понятием квадратных корней, их свойствами | Уметь выполнять преобразования выражений, содержащих квадратные корни | ||||
5 | 1 | Степень числа с рациональным показателем | Владение понятием степени с рациональным показателем | Умение выполнять действия со степенью с рациональным показателем | ||||
6 | 1 | Функция | Владение понятием функции, область определения функции | Умение находить область определения функции | ||||
7 | 1 | Уравнение | Применение свойства равенства степеней с одинаковым основанием и разными показателями | Умение решать показательны уравнения с неизвестным в показателе степени | ||||
Модуль «Геометрия» | ||||||||
8 | 1 | Анализ геометрических высказываний | Применение теоретических знаний | Умение выбрать правильный ответ | ||||
9 | 1 | Тетраэдр | Понятие тетраэдра, его элементов | Уметь находить элементы тетраэдра | ||||
10 | 1 | Параллелепипед | Понятие параллелепипеда, его элементов | Уметь находить элементы параллелепипеда | ||||
11 | 1 | Тетраэдр, параллелепипед | Понятие тетраэдра, параллелепипеда, его элементов | Уметь находить сумму длин ребер тетраэдра и параллелепипеда. | ||||
Часть 2 | ||||||||
Модуль «Алгебра» | ||||||||
12 | 2 | Алгебраическое уравнение | Применять алгоритм решения алгебраического уравнения с использованием следствий из теоремы Безу | Уметь решать алгебраические уравнения | ||||
13 | 2 | Решение систем уравнений | Применять способы решения систем уравнений способом подстановки | Уметь решать системы уравнений | ||||
Модуль «Геометрия» | ||||||||
14 | 2 | Параллельность прямых, прямой и плоскости | Применять теоремы, выражающие признаки параллельности прямых, прямой и плоскости | По условию задачи составлять чертеж. | ||||
15 | 2 | Параллельность плоскостей | Применять теоремы, выражающие признаки параллельности прямой и плоскости, параллельность плоскостей | По условию задачи составлять чертеж. Умение доказывать параллельность прямых, сопоставлять с признаками и свойствами, делать выводы и вычисления. | ||||
Критерии к заданию С
Задания12 – 15 учитель выставляет от 0 до 2 баллов в зависимости от правильности и полноты решения.
Содержание верного ответа и указание по оцениванию задания Сконтрольного теста | баллы |
даны полные пояснения к действиям нет вычислительных ошибок записан полный ответ | 2 |
даны полные пояснения к действиям допущена вычислительная ошибка, с ее учетом решение доведено до ответа или не записан ответ | 1 |
Другие случаи, не соответствующие указанным выше критериям | 0 |
Шкала пересчета суммарного балла за выполнение экзаменационной работы в целом в отметку по математике:
«2» | «3» | «4» | «5» |
0 – 6 | 7 -10 | 11-15 | 16 — 19 |
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» в отметку по алгебре:
«2» | «3» | «4» | «5» |
0 – 3 | 4 – 7 | 8 – 10 | 11 – 12 |
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» в отметку по геометрии:
«2» | «3» | «4» | «5» |
0 – 2 | 3 – 4 | 5 – 6 | 7 – 8 |
Алгебра и начала математического анализа.
 10 класс. Дидактические материалы к учебнику Ю.М.Колягина, Шабунин М.И. | ISBN: 978-5-09-050896-4
10 класс. Дидактические материалы к учебнику Ю.М.Колягина, Шабунин М.И. | ISBN: 978-5-09-050896-4Шабунин М.И.
Аннотация
Книга содержит материалы к каждой теме курса алгебры и начал математического анализа для 10 класса для базового и углублённого уровней и дополняет систему упражнений учебника и дидактические материалы тех же авторов, предназначенные для базового уровня. Каждая глава содержит примеры и задачи с подробными решениями, задания для самостоятельной работы, контрольные работы и ответы к заданиям.
Каждая глава содержит примеры и задачи с подробными решениями, задания для самостоятельной работы, контрольные работы и ответы к заданиям.
Дополнительная информация
| Регион (Город/Страна где издана): | Москва |
| Год публикации: | 2017 |
| Тираж: | 2500 |
| Страниц: | 142 |
| Формат: | 60×90/16 |
| Ширина издания: | 145 |
| Высота издания: | 215 |
Вес в гр. : : | 140 |
| Язык публикации: | Русский |
| Тип обложки: | Мягкий / Полужесткий переплет |
| Цвета обложки: | Синий |
| Возраст от: | 12 |
| Полный список лиц указанных в издании: | Шабунин М.И. |
№ параграфа | Содержание материала | Дата проведения | |
Глава I. Действительные числа | |||
1 | 1 | Целые и рациональные числа | |
2 | 2 | Бесконечно убывающая геометрическая прогрессия | |
3 | 3 | Действительные числа | |
4 | 4 | Арифметический корень натуральной степени | |
5 | 5 | Степень с рациональным показателем | |
6, 7 | 6 | Степень с действительным показателем | |
8 | Урок обобщения и систематизации знаний по теме «Действительные числа» | ||
9 | Контрольная работа № 1 по теме «Действительные числа» | ||
Глава II. | |||
10 | 7 | Показательная функция, её свойства и график | |
11,12 | 8 | Показательные уравнения | |
13,14 | 8 | Показательные неравенства | |
15 | Урок обобщения и систематизации знаний по теме «Показательная функция» | ||
16 | Контрольная работа № 2 по теме «Показательная функция» | ||
Глава III. Степенная функция | |||
17 | 9 | Степенная функция, её свойства и график | |
18 | 10 | Взаимно обратные функции | |
19 | 11 | Равносильные уравнения | |
20 | 11 | Равносильные неравенства | |
21 | 12 | Иррациональные уравнения | |
22 | 13 | Иррациональные неравенства | |
23 | Урок обобщения и систематизации знаний по теме «Степенная функция» | ||
24 | Контрольная работа № 3 по теме «Степенная функция» | ||
Глава IV. | |||
25 | 14 | Логарифмы | |
26 | 15 | Свойства логарифмов | |
27 | 16 | Десятичные и натуральные логарифмы | |
28 | 17 | Логарифмическая функция, её свойства и график | |
29,30 | 18 | Логарифмические уравнения | |
31, 32 | 19 | Логарифмические неравенства | |
33 | Урок обобщения и систематизации знаний по теме «Логарифмическая функция» | ||
34 | Контрольная работа № 4 по теме «Логарифмическая функция» | ||
Глава V. | |||
35 | 20 | Способ подстановки | |
36 | 21 | Способ сложения | |
37 | 22 | Решение систем уравнений различными способами | |
38 | 23 | Решение задач с помощью систем уравнений | |
39 | Урок обобщения и систематизации знаний по теме «Системы уравнений» | ||
40 | Контрольная работа № 5 по теме «Системы уравнений» | ||
Тригонометрические формулы | |||
41 | 24 | Радианная мера угла | |
42 | 25 | Поворот точки вокруг начала координат | |
43 | 26 | Определение синуса, косинуса и тангенса угла | |
44 | 27 | Знаки синуса, косинуса и тангенса | |
45 | 28 | Зависимость между синусом, косинусом и тангенсом одного и того же угла | |
46 | 29 | Тригонометрические тождества | |
47 | 30 | Синус, косинус и тангенс углови — | |
48 | 31 | Формулы сложения | |
49 | 32 | Синус, косинус и тангенс двойного угла | |
50 | 33 | Синус, косинус и тангенс половинного угла | |
51 | 34 | Формулы приведения | |
52 | 35 | Сумма и разность синусов. | |
53 | 36 | Произведение синусов и косинусов | |
54 | Урок обобщения и систематизации знаний по теме «Тригонометрические формулы» | ||
55 | Контрольная работа № 6 по теме «Тригонометрические формулы» | ||
Глава VI. Тригонометрические уравнения | |||
56,57 | 37 | Уравнение cos x = а | |
58,59 | 38 | Уравнение sin x = а | |
60 | 39 | Уравнение tg x = а | |
61 | 40 | Уравнение ctg x = а | |
62 | 41 | Уравнения, сводящиеся к квадратным | |
63 | 42 | Уравнения, однородные относительно sin x и cos x | |
64 | 43 | Уравнение, линейное относительно sin x и cos x | |
65 | 44 | Решение уравнений методом замены неизвестного | |
66 | 45 | Решение уравнений методом разложения на множители | |
67 | 46 | Различные приёмы решения тригонометрических уравнений | |
68 | 47 | Уравнения, содержащие корни и модули | |
69 | 48 | Системы тригонометрических уравнений | |
70 | 49 | Появление посторонних корней и потеря корней тригонометрического уравнения | |
71 | Урок обобщения и систематизации знаний по теме «Тригонометрические уравнения» | ||
72 | Контрольная работа № 7 по теме «Тригонометрические уравнения» | ||
Глава VII. | |||
73 | Периодичность тригонометрических функций | ||
74,75 | Свойства функции y = sin x и её график | ||
76,77 | Свойства функции y = cos x и её график | ||
79 | Свойства функции y = tg x и y = ctg x их свойства и графики | ||
80 | Обратные тригонометрические функции | ||
81 | Урок обобщения и систематизации знаний по теме «Тригонометрические функции» | ||
82 | Контрольная работа № 1 по теме «Тригонометрические функции» | ||
83-86 | Повторение. | ||
ГДЗ по Алгебре 10 класс Колягин Базовый и углубленный уровень
Авторы: Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И..
Авторы создавали ГДЗ по алгебре за 10 класс Колягин базовый и углубленный уровень для того, чтобы ученик закреплял свои навыки. Бывает много случав, когда ребенок плохо запомнил урок, а на дом задана лабораторная по непонятой ему теме, родители же не могут помочь ему, поскольку заняты своей работой.
Спасением в такой ситуации будет решебник с готовыми ответами. Учащийся сам имеет возможность разобрать любое упражнение, пользуясь данным ресурсом. Каждый раздел содержит подробное решение заданий, идентичных тем, которые представлены в основном учебнике. Пользуясь данным пособием, ребенок получит дополнительные плюсы в освоении школьного материала.
Помимо разборов, методичка содержит тесты, познавательные задачи, схемы, таблицы, а также терминологические правила задач. К каждому заданию прилагаются правильные ответы. Школьник может тренироваться, писать типовые проверочные работы, а также контрольные работы, которые предусматривает учебный процесс по школьному предмету.
К каждому заданию прилагаются правильные ответы. Школьник может тренироваться, писать типовые проверочные работы, а также контрольные работы, которые предусматривает учебный процесс по школьному предмету.
Почему стоит использовать ГДЗ по алгебре за 10 класс Колягина (базовый и углубленный уровень)
Использовать этот сайт-помощник следует по нескольким причинам:
- решения изложены простым и понятным языком, рассчитанным на восприятие информации десятиклассника;
- если дети что-то не понимают, родители сами сумеют разобрать с ними любой номер, не прибегая к полномасштабному изучению учебного пособия;
- даже учителя-предметники смогут найти полезную информацию, чтобы использовать ее в качестве исходника для составления дополнительного тестирования в соответствии с ФГОС;
- репетиторы также смогут извлечь пользу для себя, и узнать что-то нового.
Задачи в старших классах довольно сложные, вызывают большие затруднения у учащихся. Каждая новая ступень в школе дополняется усиленной терминологией. Пользование решебником по алгебре для 10 класса базового и углубленного уровня (авторы: Колягин Ю. М., Ткачева М. В., Федорова Н. Е., Шабунин М. И.) позволит не запустить учебу и хорошо подготовиться к дальнейшим экзаменам и ЕГЭ.
Каждая новая ступень в школе дополняется усиленной терминологией. Пользование решебником по алгебре для 10 класса базового и углубленного уровня (авторы: Колягин Ю. М., Ткачева М. В., Федорова Н. Е., Шабунин М. И.) позволит не запустить учебу и хорошо подготовиться к дальнейшим экзаменам и ЕГЭ.
Решебник к дидактическим материалам по алгебре для 10 класса Шабунина М.И. ОНЛАЙН
Решения самостоятельных и контрольных работ по алгебре и началам математического анализа из дидактических материалов для 10 класса Шабунина М.И. — Рукопись. — 2014.
Настоящее пособие содержит решения самостоятельных и контрольных работ из сборника «Алгебра и начала математического анализа. Дидактические материалы. 10 класс : базовый уровень / [М. И. Шабунин, М. В. Ткачёва, Н. Е. Фёдорова, Р. Г. Газарян]. — М.: Просвещение, 2010.— 207 с.»
Пособие адресовано родителям, которые смогут проконтролировать детей, а в случае необходимости помочь им в выполнении домашней работы по алгебре.
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы. Как листать слайды — читайте на странице https://gdz.math-helper.net/kak-prosmatrivat-slaydyi/
Внимание! Рукопись не проверялась, возможны ошибки
Содержание
Материал для повторения курса алгебры 7—9 классов
Общие теоретические сведения
1. Квадратные уравнения
2. Квадратичная функция
3. Решение квадратных неравенств с помощью графика квадратичной функции
4. Метод интервалов
5. Уравнения и неравенства, содержащие неизвестное под знаком модуля
Глава I. Действительные числа
§ 1. Целые и рациональные числа
§ 2. Действительные числа
§ 3. Бесконечно убывающая геометрическая прогрессия
§ 4. Арифметический корень натуральной степени
§ 5. Степень с рациональным и действительным показателями
Контрольная работа № 1
Глава II. Степенная функция
§ 6. Степенная функция, её свойства и график
§ 7. Взаимно обратные функции
Взаимно обратные функции
§ 8. Равносильные уравнения и неравенства
§ 9. Иррациональные уравнения
§ 10. Иррациональные неравенства
Контрольная работа № 2
Глава III. Показательная функция
§ 11. Показательная функция, её свойства и график
§ 12. Показательные уравнения
§ 13. Показательные неравенства
Контрольная работа № 3
Глава IV. Логарифмическая функция
§ 15. Логарифмы
§ 16. Свойства логарифмов
§ 17. Десятичные и натуральные логарифмы. Формула перехода
§ 18. Логарифмическая функция, её свойства и график
§ 19. Логарифмические уравнения
§ 20. Логарифмические неравенства
Контрольная работа № 4
Глава V. Тригонометрические формулы
§ 21. Радианная мера угла
§ 22. Поворот точки вокруг начала координат
§ 23. Определение синуса, косинуса и тангенса угла
§ 24. Знаки синуса, косинуса и тангенса
§ 25. Зависимость между синусом, косинусом и тангенсом одного и того же угла
§ 26. Тригонометрические тождества
Тригонометрические тождества
§ 27. Синус, косинус и тангенс углов а и -а
§ 28. Формулы сложения
§ 29. Синус, косинус и тангенс двойного угла
§ 30. Синус, косинус и тангенс половинного угла
§ 31. Формулы приведения
§ 32. Сумма и разность синусов. Сумма и разность косинусов
Контрольная работа № 5
Глава VI. Тригонометрические уравнения
§ 33. Уравнение cos x = а
§ 34. Уравнение sin x = а
§ 35. Уравнение tg x = а
§ 36. Решение тригонометрических уравнений
§ 37*. Примеры решения простейших тригонометрических неравенств
Контрольная работа № 6
ВНИМАНИЕ! Все права на публикацию рукописей принадлежат сайту gdz.math-helper.ru. Копирование и распространение материалов запрещено!
ИСКРА Учебно-методические пособия
Учебник полностью соответствует программе Ш.А. Алимова для старших классов и является органичным продолжением учебников алгебры для 7-9 классов («Просвещение»), подготовленных авторским коллективом в составе Ш. А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и других. Традиционный программный материал курса дополнен углублением теоретических сведений, демонстрацией прикладных аспектов вводимых понятий, исторической справкой.
А. Алимова, Ю.М. Колягина, Ю.В. Сидорова и других. Традиционный программный материал курса дополнен углублением теоретических сведений, демонстрацией прикладных аспектов вводимых понятий, исторической справкой.
В учебнике представлен в целостном виде раздел по тригонометрии с разными типами тригонометрических уравнений и методами их решения. Много внимания уделяется алгебраическим, показательным и логарифмическим примерам и задачам. Содержится избыточная и разделенная по трем уровням сложности система задач и упражнений. Дополнительно разбираются задачи вступительных экзаменов в различные вузы.
ОГЛАВЛЕНИЕ:
- ГЛАВА 1. Действительные числа. Степень с действительным показателем.
- ГЛАВА 2. Показательная функция.
- ГЛАВА 3. Степенная функция.
- ГЛАВА 4. Логарифмическая функция.
- ГЛАВА 5.
 Системы уравнений.
Системы уравнений. - ГЛАВА 6. Тригонометрические формулы.
- ГЛАВА 7. Тригонометрические уравнения.
- ГЛАВА 8. Тригонометрические функции.
См. также методические рекомендации к данному учебнику.
Из раздела РАСПРОДАЖА.
| Издатель (производитель) | Мнемозина |
| Период обучения | 10 класс |
| ISBN | 5-346-00733-4 |
| Автор(ы) (Составитель) |
Колягин Ю. М., Сидоров Ю.В., Федорова Н.Е.,Ткачева М.В., Шабунин М.И. М., Сидоров Ю.В., Федорова Н.Е.,Ткачева М.В., Шабунин М.И.
|
| Год издания | 2007 |
| Издание | 6-е |
| Вид издания | Учебник |
| Формат издания | 60х90/16 (145х215мм) средний |
| Обложка |
7Бц – Твердый переплет.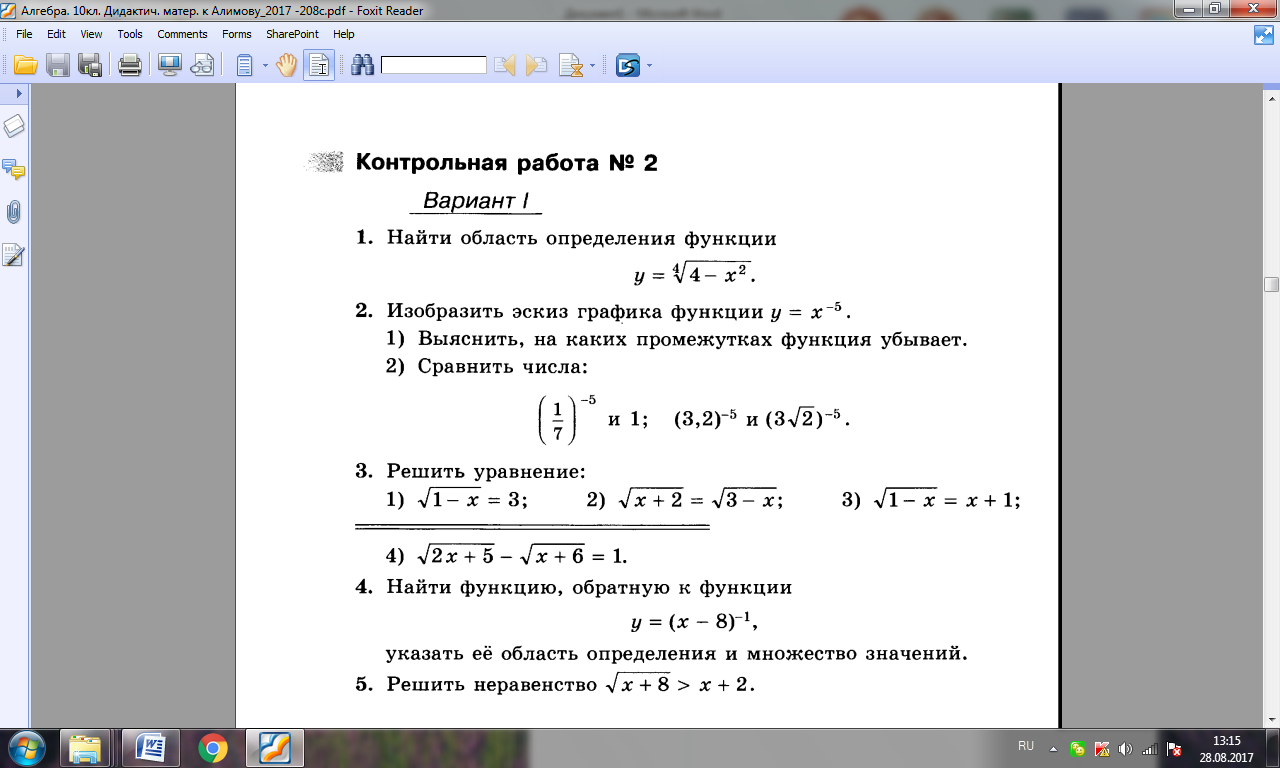 Целлофанированная или лакированная. Целлофанированная или лакированная.
|
| Вес (с упаковкой) | 470 г |
| Кол-во страниц | 364 |
| Возрастная категория | 12 + |
| Тип издания (жанр) | Учебное издание |
| Язык | русский |
| Иллюстрации | черно-белые |
Категории: Алгебра и начала анализа РАСПРОДАЖА !!!
Теги: распродажа уравнения Мнемозина Алгебра Алгебра и начала анализа Колягин Учебник 10 класс профильный уровень Сидоров Ткачева Федорова Шабунин действительные числа функции тригонометрия Алимов Тригонометрические функции Системы уравнений логарифмы степень углубленное изучение показательные функции степенные функции
Практические тесты по английскому языку для 10-х классов
All Common Core: ресурсы по английскому языку для 10-х классов
Пройдите бесплатный диагностический тест Varsity Learning Tools для Common Core: 10th Grade English Language Arts, чтобы определить, какой академический
концепции, которые вы понимаете, а какие требуют вашего постоянного внимания. Каждая задача Common Core: 10th Grade English Language Arts связана с основной концепцией, которая проходит тестирование.Общее ядро: результаты диагностического теста по английскому языку 10-го класса показывают, как вы справились с каждым разделом теста.
Затем вы можете использовать результаты для создания индивидуального учебного плана, основанного на вашей конкретной области потребностей.
Каждая задача Common Core: 10th Grade English Language Arts связана с основной концепцией, которая проходит тестирование.Общее ядро: результаты диагностического теста по английскому языку 10-го класса показывают, как вы справились с каждым разделом теста.
Затем вы можете использовать результаты для создания индивидуального учебного плана, основанного на вашей конкретной области потребностей.
Вопросы : 24
Среднее затраченное время : 12 часов 41 минута
Вопросы : 24
Среднее время работы : 9 часов 39 минут
All Common Core: ресурсы по английскому языку для 10-х классов
Наши совершенно бесплатные практические тесты Common Core: 10th Grade English Language Arts — идеальный способ улучшить свои навыки. Брать
один из наших многочисленных практических тестов Common Core: 10th Grade English Language Arts для выполнения часто задаваемых вопросов. Ты
получат невероятно подробные результаты по окончании практического теста Common Core: 10th Grade English Language Arts
поможет вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов Common Core: 10th Grade English Language Arts
и начнем!
Брать
один из наших многочисленных практических тестов Common Core: 10th Grade English Language Arts для выполнения часто задаваемых вопросов. Ты
получат невероятно подробные результаты по окончании практического теста Common Core: 10th Grade English Language Arts
поможет вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов Common Core: 10th Grade English Language Arts
и начнем!
Практические тесты по концепции
common_core_10th_grade_english_language_arts-languageВопросы : 2
Сложность теста :
Среднее затраченное время : 15 минут
common_core_10th_grade_english_language_arts-values-of-unknown-and-multi-value-words-and-phrases-ccss-ela-literacy-l-9-10-4Вопросы : 1
Сложность теста :
Среднее затраченное время : 1 час 9 минут
common_core_10th_grade_english_language_arts-use-common-grade-Соответствующие-греческие или латинские-аффиксы-и-корни-для-определения-значений-слов-ccss-ela-literacy-l-9-10-4-bВопросы : 1
Сложность теста :
Среднее затраченное время : 17 часов 54 минуты
common_core_10th_grade_english_language_arts-use-context-clues-to-definition-word-values-ccss-ela-literacy-l-9-10-4-aВопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-verify-предварительные определения-значений-слов-ccss-ela-literacy-l-9-10-4-dВопросы : 2
Сложность теста :
Среднее затраченное время : 4 минуты
common_core_10th_grade_english_language_arts-понять-нюансы-значения-слова-и-отношения-ccss-ela-literacy-l-9-10-5Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-интерпретировать-фигуры-речи-в-контексте-ccss-ela-literacy-l-9-10-5-aВопросы : 1
Сложность теста :
Среднее затраченное время : 24 секунды
common_core_10th_grade_english_language_arts-чтение-информационный-текствопросов : 10
Сложность теста :
Среднее затраченное время : 1 час 52 минуты
common_core_10th_grade_english_language_arts-analysis-how-an-author-структур-и-приказов-обсуждение-событий-или-идей-ccss-ela-literacy-ri-9-10-3Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-how-specific-sizes of the-text-develop-the-author-s-idea-ccss-ela-literacy-ri-9-10-5Вопросы : 2
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-key-историко-литературные-тексты-ccss-ela-literacy-ri-9-10-9Вопросы : 1
Сложность теста :
Среднее затраченное время : 1 минута 4 секунды
common_core_10th_grade_english_language_arts-analysis-the-strong-рассуждения-валидность-и-релевантность-заявлений-при оценке-письменных-аргументов-ccss-ela-literacy-ri-9-10-8Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-cite-strong-подробные-доказательства-в поддержку-текстового-анализа-и-выводы-ccss-ela-literacy-ri-9-10-1Вопросы : 1
Сложность теста :
Среднее затраченное время : 2 мин 41 сек
common_core_10th_grade_english_language_arts-define-a-main-idea-analysis-its-development-through-details-and-objectively-summarize-a-text-ccss-ela-literacy-ri-9-10-2Вопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 38 секунд
common_core_10th_grade_english_language_arts-define-authorial-point-of-view-and-analysis-support-rhetoric-ccss-ela-literacy-ri-9-10-6Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-определение-образный-коннотативный-и-технический-значения-слова-и-анализ-совокупные-эффекты-выбора-слова-ccss-ela-literacy-ri-9-10-4Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-read-and-comprehend-grade-Соответствующие-информационные-тексты-ccss-ela-literacy-ri-9-10-10Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-чтение-литератураВопросы : 7
Сложность теста :
Среднее затраченное время : 2 часа 25 минут
common_core_10th_grade_english_language_arts-analysis-a-subject-s-image-in-two-media-ccss-ela-literacy-rl-9-10-7Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-a-theme-s-development-in-relative-to-specific-details-and-objectively-summarize-a-text-ccss-ela-literacy-rl-9-10-2Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-how-a-work-uses-and-transforms-source-material-ccss-ela-literacy-rl-9-10-9Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-how-complex-characters-drive-a-story-ccss-ela-literacy-rl-9-10-3Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-how-textual-structure-order-of-events-and-timelines-create-value-ccss-ela-literacy-rl-9-10-5Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-analysis-the-point-of-view-of-a-a-world-Literate-ccss-ela-literacy-rl-9-10-6Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-cite-strong-подробные-доказательства-в поддержку-текстового-анализа-и-выводы-ccss-ela-literacy-rl-9-10-1Вопросы : 1
Сложность теста :
Среднее затраченное время : 27 секунд
common_core_10th_grade_english_language_arts-определение-образное-и-коннотативное-значение-слова-и-анализ-совокупные-эффекты-выбора-слова-ccss-ela-literacy-rl-9-10-4Вопросы : 1
Сложность теста :
common_core_10th_grade_english_language_arts-read-and-comprehend-grade-Соответствующие-литературные-тексты-ccss-ela-literacy-rl-9-10-10Вопросы : 1
Сложность теста :
All Common Core: ресурсы по английскому языку для 10-х классов
Практические тесты
common_core_10th_grade_english_language_arts_4Вопросы : 12
Сложность теста :
Среднее затраченное время : 1 час 42 минуты
common_core_10th_grade_english_language_arts_3Вопросы : 12
Сложность теста :
Среднее затраченное время : 2 часа 2 минуты
common_core_10th_grade_english_language_arts_2Вопросы : 12
Сложность теста :
Среднее затраченное время : 1 час 39 минут
common_core_10th_grade_english_language_arts_1Вопросы : 12
Сложность теста :
Среднее время работы : 22 часа 37 минут
Общие основные государственные стандарты © Copyright 2010. Центр передового опыта Национальной ассоциации губернаторов и Совет директоров государственных школ. Все права защищены.
Центр передового опыта Национальной ассоциации губернаторов и Совет директоров государственных школ. Все права защищены. Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie.
 Если вы подозреваете это, попробуйте другой браузер.
Если вы подозреваете это, попробуйте другой браузер. - Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или уточнить у системного администратора.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файлах cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Second Geometry, Первое издание — AbeBooks
Второе и значительно расширенное издание, In Contemporary Calf MOORE, Jonas. Математический компендиум; или «Полезные практики в арифметике, геометрии и астрономии, географии и навигации, расстановке и расквартировании армий, укреплении и артиллерийском строительстве, калибровке и измерении». Объяснение логарифмов с новыми индексами; Непаир S стержни или кости, совершающие движения, и применение маятников; С проекцией сферы для универсального дьяла и т. Д.Сэр Джонас Мур, Knt. покойный генеральный инспектор ордена Его Величества. Издание второе, с любыми крупными дополнениями. Лондон: Отпечатано для Роберта Харфорда, 1681 г. [С отдельным титульным листом, но непрерывным сопоставлением]: Таблица искусственных синусов и касательных для каждого градуса и минуты квадранта, подобранная по размеру логарифмов. Лондон: Отпечатано для Роберта Харфорда, 1679 г. Второе, значительно расширенное издание. Две части в одном двенадцатимесячном томе (5 x 2 7/8 дюйма; 125 x 73 мм). 24, 120, [178], [2, реклама] стр.С одной выгравированной складной пластиной (часто отсутствующей) и шестью выгравированными пластинами в тексте, две из которых откидываются и складываются. С многочисленными таблицами с надписью «Логарифмы Бригга». С окончательным рекламным листом. Первая титульная страница в двояковую рамку. Складные пластины представляют собой складной вечный календарь с гравировкой, установленный на A1r; складная шкала, установленная на F5v; складная гравированная пластина с расчетами широты, выходящая после страницы 120. Это второе издание с «множеством крупных дополнений» почти на 100 страниц больше, чем первое издание.
Издание второе, с любыми крупными дополнениями. Лондон: Отпечатано для Роберта Харфорда, 1681 г. [С отдельным титульным листом, но непрерывным сопоставлением]: Таблица искусственных синусов и касательных для каждого градуса и минуты квадранта, подобранная по размеру логарифмов. Лондон: Отпечатано для Роберта Харфорда, 1679 г. Второе, значительно расширенное издание. Две части в одном двенадцатимесячном томе (5 x 2 7/8 дюйма; 125 x 73 мм). 24, 120, [178], [2, реклама] стр.С одной выгравированной складной пластиной (часто отсутствующей) и шестью выгравированными пластинами в тексте, две из которых откидываются и складываются. С многочисленными таблицами с надписью «Логарифмы Бригга». С окончательным рекламным листом. Первая титульная страница в двояковую рамку. Складные пластины представляют собой складной вечный календарь с гравировкой, установленный на A1r; складная шкала, установленная на F5v; складная гравированная пластина с расчетами широты, выходящая после страницы 120. Это второе издание с «множеством крупных дополнений» почти на 100 страниц больше, чем первое издание. Полный современный пестрый теленок, возвращенный к стилю. Доски двунаправленные в слепую. Края в крапинку красные. На корешке золотые буквы. Углы слегка выбиты. Финальный рекламный лист немного обрезан по переднему краю. В целом очень хорошая, чистая копия. Что касается первого издания, то «его записи были отредактированы его вторым клерком по артиллерийскому делу, Николасом Стефенсоном, в виде записной книжки« Mathematical Compendium »(1674)». (DNB) «Справочник по прикладной математике, впервые опубликованный в 1674 году, включая инструкции по использованию элементарного механического вычислительного устройства, известного как« Кости Напьера », далекого предшественника компьютера, разработанного в начале 1600-х годов Джоном Напье, изобретателем логарифмов.«(Swann Galleries)» Сэр Джонас Мур (1617–1679) был математиком-практиком, учителем и писателем, который, будучи неспособным зарабатывать на жизнь репетитором и профессором математики, добился выдающегося положения при дворе Реставрации Карла II.
Полный современный пестрый теленок, возвращенный к стилю. Доски двунаправленные в слепую. Края в крапинку красные. На корешке золотые буквы. Углы слегка выбиты. Финальный рекламный лист немного обрезан по переднему краю. В целом очень хорошая, чистая копия. Что касается первого издания, то «его записи были отредактированы его вторым клерком по артиллерийскому делу, Николасом Стефенсоном, в виде записной книжки« Mathematical Compendium »(1674)». (DNB) «Справочник по прикладной математике, впервые опубликованный в 1674 году, включая инструкции по использованию элементарного механического вычислительного устройства, известного как« Кости Напьера », далекого предшественника компьютера, разработанного в начале 1600-х годов Джоном Напье, изобретателем логарифмов.«(Swann Galleries)» Сэр Джонас Мур (1617–1679) был математиком-практиком, учителем и писателем, который, будучи неспособным зарабатывать на жизнь репетитором и профессором математики, добился выдающегося положения при дворе Реставрации Карла II. после демонстрации своей ценности как геодезиста и картографа. После назначения на высокий пост главного инспектора Королевской артиллерии, он использовал свой доход и влияние на короля, чтобы стать покровителем навигационной астрономии. Способный математик (он наиболее известен своими работами в области тригонометрии и разработкой функции cos.’в математических уравнениях), его непреходящая важность проистекает из его сильной поддержки математики и астрономии, которая сделала возможными многие другие математические и астрономические достижения »(DNB). ESTC R269. Wing M2573. HBS 68247. $ 3000. Лондон Отпечатано для Роберта Харфорда, 1681.
после демонстрации своей ценности как геодезиста и картографа. После назначения на высокий пост главного инспектора Королевской артиллерии, он использовал свой доход и влияние на короля, чтобы стать покровителем навигационной астрономии. Способный математик (он наиболее известен своими работами в области тригонометрии и разработкой функции cos.’в математических уравнениях), его непреходящая важность проистекает из его сильной поддержки математики и астрономии, которая сделала возможными многие другие математические и астрономические достижения »(DNB). ESTC R269. Wing M2573. HBS 68247. $ 3000. Лондон Отпечатано для Роберта Харфорда, 1681.
Полимеры | Бесплатный полнотекстовый | Гибридные материалы на основе поли-3-амин-7-метиламин-2-метилфеназина и наночастиц магнетита, иммобилизованных на однослойных углеродных нанотрубках
1. Введение
Современные технологии требуют создания материалов нового поколения с улучшенными функциональными характеристиками. Гибридные наноматериалы, описанные здесь, имеют комбинацию органических и неорганических компонентов, обеспечивающую ряд требуемых свойств [1,2,3]. В этом отношении гибридные наноматериалы, в которых органический компонент представляет собой сопряженный полимер, а неорганический компонент представлен магнитными наночастицами, представляют особый интерес для исследователей во всем мире [4]. Гибридные наноматериалы на основе полисопряженных систем и магнитных наночастиц представляются очень перспективными для современных технологий благодаря сочетанию их электрических и магнитных свойств.Такие электромагнитные нанокомпозиты могут быть использованы в качестве катодных материалов для химических батарей [5,6], в качестве антикоррозионных покрытий [7,8,9,10] и гетерогенных каталитических систем [11], в медицинских целях [12], а также в качестве эффективных сорбентов. для очистки питьевой воды [13,14,15,16,17,18], а также в качестве материалов, эффективно поглощающих электромагнитное излучение [19,20,21,22,23].
Гибридные наноматериалы, описанные здесь, имеют комбинацию органических и неорганических компонентов, обеспечивающую ряд требуемых свойств [1,2,3]. В этом отношении гибридные наноматериалы, в которых органический компонент представляет собой сопряженный полимер, а неорганический компонент представлен магнитными наночастицами, представляют особый интерес для исследователей во всем мире [4]. Гибридные наноматериалы на основе полисопряженных систем и магнитных наночастиц представляются очень перспективными для современных технологий благодаря сочетанию их электрических и магнитных свойств.Такие электромагнитные нанокомпозиты могут быть использованы в качестве катодных материалов для химических батарей [5,6], в качестве антикоррозионных покрытий [7,8,9,10] и гетерогенных каталитических систем [11], в медицинских целях [12], а также в качестве эффективных сорбентов. для очистки питьевой воды [13,14,15,16,17,18], а также в качестве материалов, эффективно поглощающих электромагнитное излучение [19,20,21,22,23]. Таким образом, создание новых нанокомпозитных материалов на основе полимеров с системой полисопряжения и магнитных наночастиц не утратило актуальности.В последние годы большое внимание привлекли новые тройные гибридные нанокомпозиты, которые содержат, помимо сопряженных полимеров и магнитных наночастиц, углеродные наноматериалы. Однако существует лишь несколько работ, описывающих синтез и свойства тройных наноматериалов, содержащих сопряженные полимеры, магнитные наночастицы и углеродные компоненты. Существует два подхода к получению тройных нанокомпозитов: окислительная полимеризация in situ анилина в присутствии многослойных углеродных нанотрубок ( MWCNT), или оксид графена с последующим осаждением наночастиц магнетита на их поверхность [19,20,24]; окислительная полимеризация анилина или пиррола in situ в присутствии наночастиц магнетита, прикрепленных к MWCNT или восстановленному оксиду графена [21,22].При высокой дисперсности магнитных наночастиц тройные нанокомпозиты являются суперпарамагнитными [19,20,21].
Таким образом, создание новых нанокомпозитных материалов на основе полимеров с системой полисопряжения и магнитных наночастиц не утратило актуальности.В последние годы большое внимание привлекли новые тройные гибридные нанокомпозиты, которые содержат, помимо сопряженных полимеров и магнитных наночастиц, углеродные наноматериалы. Однако существует лишь несколько работ, описывающих синтез и свойства тройных наноматериалов, содержащих сопряженные полимеры, магнитные наночастицы и углеродные компоненты. Существует два подхода к получению тройных нанокомпозитов: окислительная полимеризация in situ анилина в присутствии многослойных углеродных нанотрубок ( MWCNT), или оксид графена с последующим осаждением наночастиц магнетита на их поверхность [19,20,24]; окислительная полимеризация анилина или пиррола in situ в присутствии наночастиц магнетита, прикрепленных к MWCNT или восстановленному оксиду графена [21,22].При высокой дисперсности магнитных наночастиц тройные нанокомпозиты являются суперпарамагнитными [19,20,21].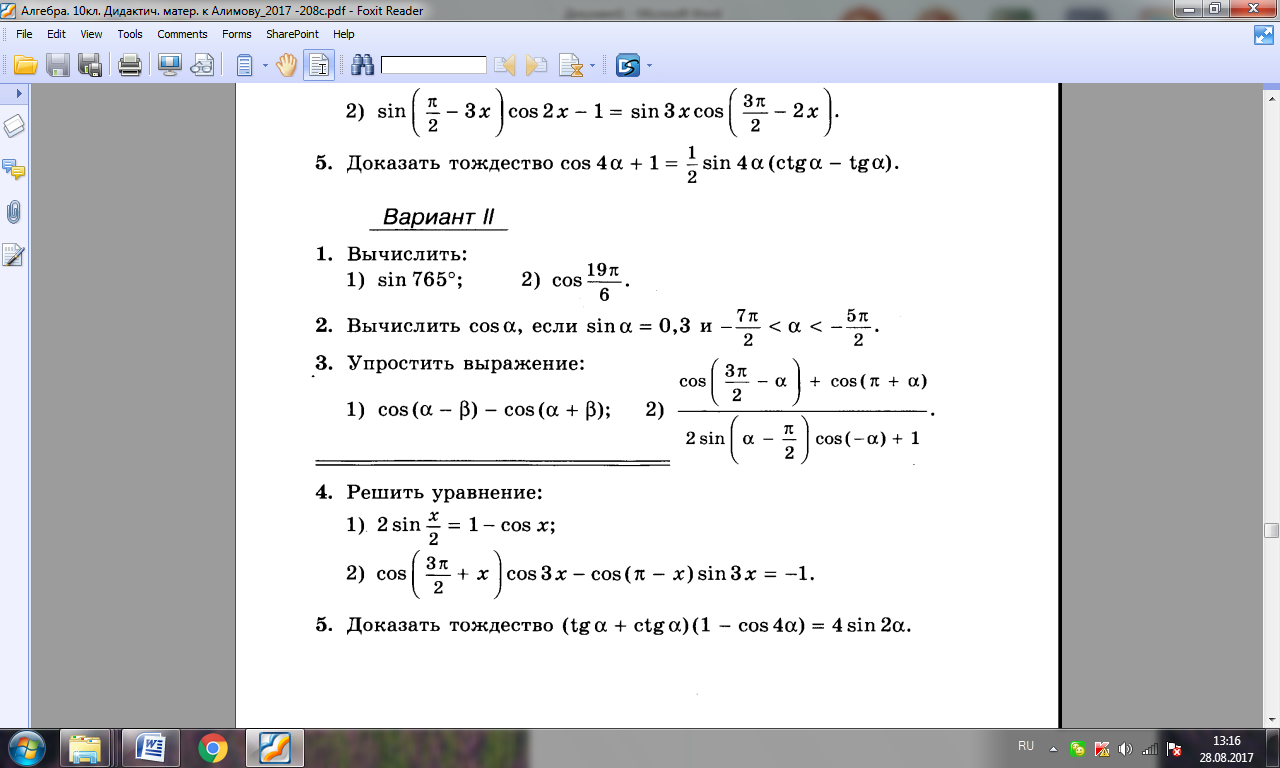 Величина намагниченности насыщения зависит от содержания магнитных наночастиц. Агрегация наночастиц Fe 3 O 4 определяет ферромагнитное поведение нанокомпозита [22]. Полученные наноматериалы могут эффективно поглощать электромагнитное излучение. В данной работе предлагается метод синтеза новых гибридных полимер-металл-углеродных нанокомпозитных материалов на основе наночастиц Fe 3 O 4 , иммобилизованных на поверхности однослойных углеродных нанотрубок. (SWCNT).Полимерный компонент гибридного наноматериала представляет собой поли-3-амин-7-метиламин-2-метилфеназин (ПАММП), который впервые был синтезирован авторами методом окислительной полимеризации 3-амин-7-диметиламина-2. -метилфеназина гидрохлорид (ADMPC), также известный как нейтральный красный [25]. ПАММП представляет собой полулестничный гетероциклический термостабильный полимер, в котором атомы азота участвуют в общей полисопряженной системе. Анализ результатов спектральных исследований с помощью FTIR и электронной спектроскопии, рентгеновской фотоэлектронной спектроскопии, твердотельной HRMAS (вращение под магическим углом высокого разрешения) и спектроскопии ЯМР 13 C [25] позволяет представить химическую структуру PAMMP, как показано на рисунке 1.
Величина намагниченности насыщения зависит от содержания магнитных наночастиц. Агрегация наночастиц Fe 3 O 4 определяет ферромагнитное поведение нанокомпозита [22]. Полученные наноматериалы могут эффективно поглощать электромагнитное излучение. В данной работе предлагается метод синтеза новых гибридных полимер-металл-углеродных нанокомпозитных материалов на основе наночастиц Fe 3 O 4 , иммобилизованных на поверхности однослойных углеродных нанотрубок. (SWCNT).Полимерный компонент гибридного наноматериала представляет собой поли-3-амин-7-метиламин-2-метилфеназин (ПАММП), который впервые был синтезирован авторами методом окислительной полимеризации 3-амин-7-диметиламина-2. -метилфеназина гидрохлорид (ADMPC), также известный как нейтральный красный [25]. ПАММП представляет собой полулестничный гетероциклический термостабильный полимер, в котором атомы азота участвуют в общей полисопряженной системе. Анализ результатов спектральных исследований с помощью FTIR и электронной спектроскопии, рентгеновской фотоэлектронной спектроскопии, твердотельной HRMAS (вращение под магическим углом высокого разрешения) и спектроскопии ЯМР 13 C [25] позволяет представить химическую структуру PAMMP, как показано на рисунке 1. В процессе синтеза ПАММП может образовывать пленочные покрытия на поверхности субстрата, добавляемого в реакционный раствор. Синтез гибридных наноматериалов Fe 3 O 4 / SWCNT / ПАММП проводили в водных растворах ацетонитрила или ДМФА путем химической окислительной полимеризации in situ ADMPC на поверхности ранее синтезированного нанокомпозита металл-углерод Fe 3 O 4 / SWCNT. Способы формирования гибридного дисперсного наноматериала Fe 3 O 4 / SWCNT / PAMMP включают иммобилизацию мономера на поверхности нанокомпозита металл-углерод Fe 3 O 4 / SWCNT и последующую окислительную полимеризацию in situ в нейтральная среда в присутствии персульфата аммония в качестве окислителя (рис. 2).Исследованы магнитные, термические и электрические свойства полученных наноматериалов.
В процессе синтеза ПАММП может образовывать пленочные покрытия на поверхности субстрата, добавляемого в реакционный раствор. Синтез гибридных наноматериалов Fe 3 O 4 / SWCNT / ПАММП проводили в водных растворах ацетонитрила или ДМФА путем химической окислительной полимеризации in situ ADMPC на поверхности ранее синтезированного нанокомпозита металл-углерод Fe 3 O 4 / SWCNT. Способы формирования гибридного дисперсного наноматериала Fe 3 O 4 / SWCNT / PAMMP включают иммобилизацию мономера на поверхности нанокомпозита металл-углерод Fe 3 O 4 / SWCNT и последующую окислительную полимеризацию in situ в нейтральная среда в присутствии персульфата аммония в качестве окислителя (рис. 2).Исследованы магнитные, термические и электрические свойства полученных наноматериалов.2. Экспериментальный образец
Персульфат аммония (ч. Д. До н. Э.) Очищали перекристаллизацией из дистиллированной воды, как описано ранее [26]. 3-амин-7-диметиламин-2-метилфеназин гидрохлорид (C 15 H 17 CIN 4 ) (ADMPC) (нейтральный красный), водный раствор аммиака (х.ч.), FeCl 3 · 6H 2 О (сорт высокой чистоты) и FeSO 4 · 7H 2 О (сорт высокой чистоты), а также ацетонитрил и ДМФ (все от Acros Organics, Geel, Бельгия) использовали без какой-либо дополнительной очистки.Водные растворы реагентов готовили на дистиллированной воде. ОСУНТ производства ООО «Карбон Чг» (Москва, Россия) были получены методом электродугового разряда с катализатором Ni / Y (d = 1,4–1,6 нм, l = 0,5–1,5 мкм). ПАММП был получен окислительной полимеризацией в водном растворе ацетонитрила [25]. Синтез наночастиц Fe 3 O 4 , иммобилизованных на поверхности ОСУНТ (металл-углеродный нанокомпозит Fe 3 O 4 / ОСУНТ). проводили гидролизом солей железа (II) и (III), взятых в соотношении 1: 2, в растворе гидроксида аммония [27] в присутствии ОСУНТ при 60 ° C.
3-амин-7-диметиламин-2-метилфеназин гидрохлорид (C 15 H 17 CIN 4 ) (ADMPC) (нейтральный красный), водный раствор аммиака (х.ч.), FeCl 3 · 6H 2 О (сорт высокой чистоты) и FeSO 4 · 7H 2 О (сорт высокой чистоты), а также ацетонитрил и ДМФ (все от Acros Organics, Geel, Бельгия) использовали без какой-либо дополнительной очистки.Водные растворы реагентов готовили на дистиллированной воде. ОСУНТ производства ООО «Карбон Чг» (Москва, Россия) были получены методом электродугового разряда с катализатором Ni / Y (d = 1,4–1,6 нм, l = 0,5–1,5 мкм). ПАММП был получен окислительной полимеризацией в водном растворе ацетонитрила [25]. Синтез наночастиц Fe 3 O 4 , иммобилизованных на поверхности ОСУНТ (металл-углеродный нанокомпозит Fe 3 O 4 / ОСУНТ). проводили гидролизом солей железа (II) и (III), взятых в соотношении 1: 2, в растворе гидроксида аммония [27] в присутствии ОСУНТ при 60 ° C. Для этого 0,86 г FeSO 4 · 7H 2 O и 2,35 г FeCl 3 · 6H 2 O растворяли в 20 мл дистиллированной воды. 0,038 г SWCNT (10 мас.% От веса ADMPC) добавляли к реакционной среде, которую затем нагревали до 60 ° C; Затем добавляли 5 мл NH 4 OH. Полученную суспензию нагревали на водяной бане до 80 ° C и перемешивали в течение 0,5 часа. Суспензию охлаждали при комнатной температуре при непрерывном интенсивном перемешивании в течение 1 ч. Полученный нанокомпозит Fe 3 O 4 / SWCNT отфильтровывали, промывали дистиллированной водой для удаления остаточных количеств гидроксида аммония до тех пор, пока значение pH фильтрата не достигло 7, и сушили над КОН в вакууме до постоянной массы.Выход Fe 3 O 4 / SWCNT составил 1.072 г с C Fe = 61,2% (по данным AAS). Проведен синтез нанокомпозита Fe 3 O 4 / SWCNT / PAMMP. в нейтральной среде следующим образом. Свежеприготовленный нанокомпозит Fe 3 O 4 / SWCNT в желаемой концентрации (таблица 1) промывали дистиллированной водой до нейтральной реакции и без предварительной сушки добавляли прямо в раствор ADMPC в ацетонитриле (0,02 моль / л.
Для этого 0,86 г FeSO 4 · 7H 2 O и 2,35 г FeCl 3 · 6H 2 O растворяли в 20 мл дистиллированной воды. 0,038 г SWCNT (10 мас.% От веса ADMPC) добавляли к реакционной среде, которую затем нагревали до 60 ° C; Затем добавляли 5 мл NH 4 OH. Полученную суспензию нагревали на водяной бане до 80 ° C и перемешивали в течение 0,5 часа. Суспензию охлаждали при комнатной температуре при непрерывном интенсивном перемешивании в течение 1 ч. Полученный нанокомпозит Fe 3 O 4 / SWCNT отфильтровывали, промывали дистиллированной водой для удаления остаточных количеств гидроксида аммония до тех пор, пока значение pH фильтрата не достигло 7, и сушили над КОН в вакууме до постоянной массы.Выход Fe 3 O 4 / SWCNT составил 1.072 г с C Fe = 61,2% (по данным AAS). Проведен синтез нанокомпозита Fe 3 O 4 / SWCNT / PAMMP. в нейтральной среде следующим образом. Свежеприготовленный нанокомпозит Fe 3 O 4 / SWCNT в желаемой концентрации (таблица 1) промывали дистиллированной водой до нейтральной реакции и без предварительной сушки добавляли прямо в раствор ADMPC в ацетонитриле (0,02 моль / л. , 0.38 г). Содержание углеродных нанотрубок C SWCNT = 10 и 20 мас.% Относительно массы мономера. Этот процесс иммобилизации мономера на поверхности Fe 3 O 4 / SWCNT проводили при 60 ° C при непрерывном интенсивном перемешивании в течение 1 ч. Суспензию охлаждали при комнатной температуре при интенсивном перемешивании в течение 1 ч. После этого для проведения in situ окислительной полимеризации ADMPC на поверхности металл-углерод Fe 3 O 4 / SWCNT водный раствор (30 мл) персульфата аммония (0.04 моль / л, 0,548 г) по каплям добавляли к суспензии Fe 3 O 4 / SWCNT / ADMPC в ацетонитриле, предварительно охлажденной до 15 ° C с помощью криотермостата LOIP FT-311-25 (Санкт-Петербург , Россия). Объемное соотношение органической и водной фаз составляло 1: 1 (V всего = 60 мл). Синтез продолжали 4 ч при интенсивном перемешивании при 15 ° C. По окончании синтеза смесь осаждали пятикратным избытком дистиллированной воды.
, 0.38 г). Содержание углеродных нанотрубок C SWCNT = 10 и 20 мас.% Относительно массы мономера. Этот процесс иммобилизации мономера на поверхности Fe 3 O 4 / SWCNT проводили при 60 ° C при непрерывном интенсивном перемешивании в течение 1 ч. Суспензию охлаждали при комнатной температуре при интенсивном перемешивании в течение 1 ч. После этого для проведения in situ окислительной полимеризации ADMPC на поверхности металл-углерод Fe 3 O 4 / SWCNT водный раствор (30 мл) персульфата аммония (0.04 моль / л, 0,548 г) по каплям добавляли к суспензии Fe 3 O 4 / SWCNT / ADMPC в ацетонитриле, предварительно охлажденной до 15 ° C с помощью криотермостата LOIP FT-311-25 (Санкт-Петербург , Россия). Объемное соотношение органической и водной фаз составляло 1: 1 (V всего = 60 мл). Синтез продолжали 4 ч при интенсивном перемешивании при 15 ° C. По окончании синтеза смесь осаждали пятикратным избытком дистиллированной воды. Полученный продукт отфильтровывали, многократно промывали дистиллированной водой для удаления остаточных количеств реагента и сушили над КОН в вакууме до постоянного веса.Окислительная полимеризация ADMPC в присутствии нанокомпозита Fe 3 O 4 / SWCNT также может быть проведена в водном растворе ДМФ. Выход Fe 3 O 4 / SWCNT / PAMMP составил 1.23 г при C Fe = 45.7% (по данным AAS) (таблица 1).
Полученный продукт отфильтровывали, многократно промывали дистиллированной водой для удаления остаточных количеств реагента и сушили над КОН в вакууме до постоянного веса.Окислительная полимеризация ADMPC в присутствии нанокомпозита Fe 3 O 4 / SWCNT также может быть проведена в водном растворе ДМФ. Выход Fe 3 O 4 / SWCNT / PAMMP составил 1.23 г при C Fe = 45.7% (по данным AAS) (таблица 1). Для синтеза композитного материала SWCNT / PAMMP ADMPC (0,02 моль / л, 0,38 г) растворяли в ацетонитриле (30 мл). К полученному раствору добавляли 0,0114 г SWCNT (3 мас.% По отношению к массе мономера).Процесс проводили при 60 ° C при непрерывном интенсивном перемешивании в течение 1 ч. Полученную суспензию SWCNT / ADMPC перемешивали в ультразвуковой бане при комнатной температуре в течение 0,5 часа. Затем для проведения окислительной полимеризации ADMPC in situ в присутствии SWCNT водный раствор (30 мл) персульфата аммония (0,04 моль / л, 0,548 г) по каплям добавляли к суспензии SWCNT / ADMPC, предварительно охлажденной до 15 ° C. ° C. Объемное соотношение органической и водной фаз составляло 1: 1 (V всего = 60 мл). Синтез продолжали 4 ч при интенсивном перемешивании при 15 ° C.По окончании синтеза смесь осаждали пятикратным избытком дистиллированной воды. Полученный продукт отфильтровывали, многократно промывали дистиллированной водой для удаления остаточных количеств реагента и сушили над КОН в вакууме до постоянного веса. Выход ОСУНТ / ПАММП составил 0,23 г.
° C. Объемное соотношение органической и водной фаз составляло 1: 1 (V всего = 60 мл). Синтез продолжали 4 ч при интенсивном перемешивании при 15 ° C.По окончании синтеза смесь осаждали пятикратным избытком дистиллированной воды. Полученный продукт отфильтровывали, многократно промывали дистиллированной водой для удаления остаточных количеств реагента и сушили над КОН в вакууме до постоянного веса. Выход ОСУНТ / ПАММП составил 0,23 г.
FTIR образцов измерены на FTIR-спектрометре Bruker IFS 66v (Карлсруэ, Германия) в диапазоне 400–4000 см –1 . Образцы были приготовлены в виде прессованных таблеток KBr. ИК-спектры ослабленного полного отражения (НПВО) в режиме ослабленного полного отражения регистрировали с помощью ИК-микроскопа HYPERION-2000 (Bruker, Карлсруэ, Германия) в сочетании с ИК-Фурье-спектрометром Bruker IFS 66v в диапазоне 600–4000 см -1. (150 сканов, кристалл ZnSe, разрешение 2 см −1 ).
(150 сканов, кристалл ZnSe, разрешение 2 см −1 ).
Электронно-микроскопическое исследование было выполнено с использованием просвечивающего электронного микроскопа LEO 912 AB OMEGA (Bioz Inc., Лос-Альтос, Калифорния, США) и автоэмиссионный сканирующий электронный микроскоп Zeiss Supra 25 FE-SEM (Carl Zeiss AG, Йена, Германия). Для приготовления образцов ПЭМ нанокомпозиты тщательно растирались в агатовой ступке и диспергированный порошок наносился на поддерживающую сетку. Разрешение получаемых изображений составляет 1-2 нм. Размер наночастиц определяется с помощью программного обеспечения EsiVision (eVision Software, Гаага, Нидерланды).
Испытание площади поверхности по БЭТ проводили на Micromeritics ASAP 2020 (Micromeritics Corporate, Норкросс, Джорджия, США) методом капиллярной конденсации азота при 77 К в области относительного давления (P / P 0 ) от 0.01 до 0,99. Поправочный коэффициент площади поверхности составил ± 1. Дегазация образца проводилась при 120 ° C в течение 2 ч.
Для исследования магнитных характеристик систем использовался вибрационный магнитометр. Ячейка вибрационного магнитометра была выполнена в виде проточного кварцевого микрореактора, что позволило изучать химические превращения «in situ» [29]. Измерялась удельная намагниченность в зависимости от величины магнитного поля; определены магнитные характеристики образцов при комнатной температуре. Электропроводность по постоянному току при комнатной температуре определяли с помощью стандартной 4-точечной процедуры на приборе Loresta-GP MCP-T610 (Mitsubishi, Shimotsuruma, Япония). Электропроводность по переменному току измерялась прецизионным LCR-метром 6367A (Microtest, New Taipei City, Тайвань) в диапазоне частот 0,1 Гц – 1,15 МГц.
Термогравиметрический анализ (ТГА) выполнен на приборе Mettler Toledo TGA / DSC1 (Giessen, Германия) в динамическом режиме в диапазоне 30–1000 ° C на воздухе и в токе аргона. Масса образцов 100 мг, скорость нагрева 10 ° С / мин, скорость потока аргона 10 мл / мин.Прокаленный оксид алюминия использовали в качестве эталона. Образцы анализировали в тигле Al 2 O 3 .
Дифференциальную сканирующую калориметрию (DSC) проводили на калориметре Mettler Toledo DSC823 ee (Giessen, Германия). Образцы нагревали со скоростью 10 ° C / мин в атмосфере азота при скорости потока азота 70 мл / мин. Результаты измерений обрабатывались с помощью сервисной программы STARe, поставляемой с прибором.
3. Результаты и обсуждение
Образование Fe 3 O 4 / SWCNT и Fe 3 O 4 / SWCNT / PAMMP нанокомпозитных материалов было подтверждено просвечиванием (TEM) и сканированием (FE-SEM ) электронная микроскопия, ИК-Фурье спектроскопия, дифракция рентгеновских лучей и атомно-абсорбционная спектрометрия (ААС).
 97 °, 54,1 °, 66,69 °, 84,57 °, 90,97 ° и 102,16 ° (CrK α -излучение) (Рисунок 5) [30,31]. Все эти дифракционные пики соответствуют кубической структуре Fe 3 O 4 (JCPDS 19-0629) и относятся к индексам Миллера (220), (311), (400), (422), (511), и (440) [32]. Отсутствие дифракционного пика углеродной фазы на дифрактограмме нанокомпозита Fe 3 O 4 / ОСУНТ объяснялось невозможностью получения дифракционной картины от одной плоскости ОСУНТ.
97 °, 54,1 °, 66,69 °, 84,57 °, 90,97 ° и 102,16 ° (CrK α -излучение) (Рисунок 5) [30,31]. Все эти дифракционные пики соответствуют кубической структуре Fe 3 O 4 (JCPDS 19-0629) и относятся к индексам Миллера (220), (311), (400), (422), (511), и (440) [32]. Отсутствие дифракционного пика углеродной фазы на дифрактограмме нанокомпозита Fe 3 O 4 / ОСУНТ объяснялось невозможностью получения дифракционной картины от одной плоскости ОСУНТ. На основе полученного металл-углеродного Fe 3 O 4 / нанокомпозит SWCNT, гибрид полимер-металл-углерод Fe 3 O 4 наноматериалы / SWCNT / PAMMP были синтезированы путем окислительной полимеризации in situ ADMPC в водный раствор ацетонитрила. Для иммобилизации ADMPC на поверхности нанокомпозита Fe 3 O 4 / SWCNT, свежеприготовленные наночастицы магнетита осаждались на SWCNT и промывались до нейтральной реакции без предварительной сушки, затем добавлялись в реакционно-нейтральную среду Fe 3 O 4 / Синтез наноматериалов SWCNT / PAMMP.
 Интенсивные полосы при 1606 и 1499 см −1 соответствуют валентным колебаниям связей ν C – C в ароматических кольцах. Полосы поглощения при 1342, 1312 и 1226 см −1 относятся к валентным колебаниям связей ν C – N . Полосы при 1194 и 1143 см −1 характерны для плоских изгибных колебаний δ связей C – H ароматического кольца [33,34,35,36,37]. Полосы при 1033 и 1011 см –1 вызваны изгибными колебаниями δ C – H ароматического кольца вне плоскости.Полосы при 731 и 714 см −1 связаны с внеплоскостными изгибными колебаниями δ связей C – H в тризамещенном бензольном кольце концевых групп. Наличие полос поглощения при 820 и 1287 см — 1 (внеплоскостные изгибные колебания δ связей C – H в 1,2,4,5-замещенном бензольном кольце) указывает на то, что полимерные цепи растут за счет связи C – N между 3-аминогруппами и пара-положение фенильных колец по отношению к азоту.
Интенсивные полосы при 1606 и 1499 см −1 соответствуют валентным колебаниям связей ν C – C в ароматических кольцах. Полосы поглощения при 1342, 1312 и 1226 см −1 относятся к валентным колебаниям связей ν C – N . Полосы при 1194 и 1143 см −1 характерны для плоских изгибных колебаний δ связей C – H ароматического кольца [33,34,35,36,37]. Полосы при 1033 и 1011 см –1 вызваны изгибными колебаниями δ C – H ароматического кольца вне плоскости.Полосы при 731 и 714 см −1 связаны с внеплоскостными изгибными колебаниями δ связей C – H в тризамещенном бензольном кольце концевых групп. Наличие полос поглощения при 820 и 1287 см — 1 (внеплоскостные изгибные колебания δ связей C – H в 1,2,4,5-замещенном бензольном кольце) указывает на то, что полимерные цепи растут за счет связи C – N между 3-аминогруппами и пара-положение фенильных колец по отношению к азоту. Такой тип связывания наблюдается в процессе полимеризации анилина (тип «голова к хвосту») [33,38,39].Характерным изменением спектров FTIR нанокомпозита по сравнению со спектром полимера является то, что увеличение содержания углеродных нанотрубок приводит к гипсохромному сдвигу частоты каркасных колебаний ПАММП на 7–9 см −1 в спектрах НПВО FTIR нанокомпозита Fe 3 O 4 / SWCNT / PAMMP (Рисунок 6). В полосах поглощения этот сдвиг указывает на π – π * взаимодействие феназиновых звеньев ПАММП с ароматическими структурами ОСУНТ. В процессе окислительной полимеризации АДМФК in situ на поверхности нанокомпозита Fe 3 O 4 / ОСУНТ, Феназиновые звенья ПАММП обеспечивают образование полимерных цепей в непосредственной близости от поверхности металл-углерод Fe 3 O 4 / SWCNT.Согласно данным ПЭМ и FE-SEM, ПАММП формируется на поверхности нанокомпозита Fe 3 O 4 / ОСУНТ (рис. 3 и рис. 7).
Такой тип связывания наблюдается в процессе полимеризации анилина (тип «голова к хвосту») [33,38,39].Характерным изменением спектров FTIR нанокомпозита по сравнению со спектром полимера является то, что увеличение содержания углеродных нанотрубок приводит к гипсохромному сдвигу частоты каркасных колебаний ПАММП на 7–9 см −1 в спектрах НПВО FTIR нанокомпозита Fe 3 O 4 / SWCNT / PAMMP (Рисунок 6). В полосах поглощения этот сдвиг указывает на π – π * взаимодействие феназиновых звеньев ПАММП с ароматическими структурами ОСУНТ. В процессе окислительной полимеризации АДМФК in situ на поверхности нанокомпозита Fe 3 O 4 / ОСУНТ, Феназиновые звенья ПАММП обеспечивают образование полимерных цепей в непосредственной близости от поверхности металл-углерод Fe 3 O 4 / SWCNT.Согласно данным ПЭМ и FE-SEM, ПАММП формируется на поверхности нанокомпозита Fe 3 O 4 / ОСУНТ (рис. 3 и рис. 7). Это также подтверждается данными испытаний площади поверхности BET. Удельная поверхность нанокомпозита Fe 3 O 4 / SWCNT / PAMMP (58,8 м 2 / г) намного меньше, чем у SWCNT (1067,3 м 2 / г) и ближе к удельной поверхности полимер (15,9 м 2 / г) (таблица 2). Согласно данным XRD, полимерный компонент в нанокомпозите является аморфным (Рисунок 5 и Рисунок 8).Дифракционные картины нанокомпозита Fe 3 O 4 / SWCNT / PAMMP четко идентифицируют дифракционные пики Fe 3 O 4 при углах рассеяния 2θ = 46,1 °, 54,2 °, 66,9 °, 84,8 °, 91,2 ° и 102,2 ° (CrK α -излучение) (рисунок 5 и рисунок 8). Эти дифракционные пики относятся к индексам Миллера (220), (311), (400), (422), (511) и (440) [32]. Согласно данным TEM и FE-SEM, размер наночастиц Fe 3 O 4 , определенный с помощью программного обеспечения EsiVision, находится в пределах диапазона 2 (Рис. 3 и Рис.
Это также подтверждается данными испытаний площади поверхности BET. Удельная поверхность нанокомпозита Fe 3 O 4 / SWCNT / PAMMP (58,8 м 2 / г) намного меньше, чем у SWCNT (1067,3 м 2 / г) и ближе к удельной поверхности полимер (15,9 м 2 / г) (таблица 2). Согласно данным XRD, полимерный компонент в нанокомпозите является аморфным (Рисунок 5 и Рисунок 8).Дифракционные картины нанокомпозита Fe 3 O 4 / SWCNT / PAMMP четко идентифицируют дифракционные пики Fe 3 O 4 при углах рассеяния 2θ = 46,1 °, 54,2 °, 66,9 °, 84,8 °, 91,2 ° и 102,2 ° (CrK α -излучение) (рисунок 5 и рисунок 8). Эти дифракционные пики относятся к индексам Миллера (220), (311), (400), (422), (511) и (440) [32]. Согласно данным TEM и FE-SEM, размер наночастиц Fe 3 O 4 , определенный с помощью программного обеспечения EsiVision, находится в пределах диапазона 2 (Рис. 3 и Рис. 7).По данным ААС, в зависимости от условий синтеза содержание C Fe = 17,6–45,7% (табл. 1). На рисунке 9 показано распределение по размерам областей когерентного рассеяния в наночастицах Fe 3 O 4 . В нанокомпозите Fe 3 O 4 / SWCNT / PAMMP кривые распределения кристаллитов Fe 3 O 4 по размерам узкие. Около 95–97% кристаллитов Fe 3 O 4 имеют размер до 8 нм. Как видно на рисунке 9, нанокомпозит Fe 3 O 4 / ОСУНТ имеет более широкую кривую распределения по размерам.Только около 85% кристаллитов Fe 3 O 4 имеют размер до 8 нм. Согласно данным ПЭМ, размер наночастиц Fe 3 O 4 в нанокомпозите Fe 3 O 4 / ОСУНТ находится в пределах диапазона, указанного на рис. 3а). Это объясняется тем, что полимер на поверхности Fe 3 O 4 / SWCNT снижает агрегацию наночастиц в процессе синтеза наноматериала Fe 3 O 4 / SWCNT / PAMMP.
7).По данным ААС, в зависимости от условий синтеза содержание C Fe = 17,6–45,7% (табл. 1). На рисунке 9 показано распределение по размерам областей когерентного рассеяния в наночастицах Fe 3 O 4 . В нанокомпозите Fe 3 O 4 / SWCNT / PAMMP кривые распределения кристаллитов Fe 3 O 4 по размерам узкие. Около 95–97% кристаллитов Fe 3 O 4 имеют размер до 8 нм. Как видно на рисунке 9, нанокомпозит Fe 3 O 4 / ОСУНТ имеет более широкую кривую распределения по размерам.Только около 85% кристаллитов Fe 3 O 4 имеют размер до 8 нм. Согласно данным ПЭМ, размер наночастиц Fe 3 O 4 в нанокомпозите Fe 3 O 4 / ОСУНТ находится в пределах диапазона, указанного на рис. 3а). Это объясняется тем, что полимер на поверхности Fe 3 O 4 / SWCNT снижает агрегацию наночастиц в процессе синтеза наноматериала Fe 3 O 4 / SWCNT / PAMMP. Исследованы магнитные свойства наноматериалов Fe 3 O 4 / SWCNT и Fe 3 O 4 / SWCNT / PAMMP и измерены значения их основных магнитных характеристик. Зависимость намагниченности от напряженности магнитного поля при комнатной температуре показана на рисунках 10 и 11. Исследовано влияние концентрации железа на магнитные свойства наноматериала Fe 3 O 4 / SWCNT / PAMMP. Намагниченность насыщения M S зависит от концентрации железа и достигает 47.24 emu / g при C Fe = 45,7% (таблица 1), что значительно выше, чем у других подобных материалов, о которых сообщалось в предыдущих исследованиях [20,22]. Коэффициент прямоугольности петли гистерезиса κ S = M R / M S ~ 0 указывает на суперпарамагнитное поведение гибридного наноматериала [29,40]. Как видно на рисунке 11, в нанокомпозите Fe 3 O 4 / ОСУНТ коэффициент прямоугольности петли гистерезиса немного выше (κ S = 0.
Исследованы магнитные свойства наноматериалов Fe 3 O 4 / SWCNT и Fe 3 O 4 / SWCNT / PAMMP и измерены значения их основных магнитных характеристик. Зависимость намагниченности от напряженности магнитного поля при комнатной температуре показана на рисунках 10 и 11. Исследовано влияние концентрации железа на магнитные свойства наноматериала Fe 3 O 4 / SWCNT / PAMMP. Намагниченность насыщения M S зависит от концентрации железа и достигает 47.24 emu / g при C Fe = 45,7% (таблица 1), что значительно выше, чем у других подобных материалов, о которых сообщалось в предыдущих исследованиях [20,22]. Коэффициент прямоугольности петли гистерезиса κ S = M R / M S ~ 0 указывает на суперпарамагнитное поведение гибридного наноматериала [29,40]. Как видно на рисунке 11, в нанокомпозите Fe 3 O 4 / ОСУНТ коэффициент прямоугольности петли гистерезиса немного выше (κ S = 0. 01). Остаточная намагниченность M R чистого Fe 3 O 4 / SWCNT составляет 0,45 ЭМЕ / г, а коэрцитивная сила H C составляет 6 Э. Суперпарамагнитное поведение нанокомпозитов при относительно высоких концентрациях магнитных наночастиц определяется небольшими размерами и высокой дисперсностью магнитных наночастиц. Так или иначе, полученные значения M R / M S для Fe 3 O 4 / SWCNT / PAMMP и Fe 3 O 4 / нанокомпозиты SWCNT характерны для одноосных однодоменных частиц.Критический размер перехода в однодоменное состояние для Fe 3 O 4 составляет 128 нм [29,40]. Для исследования термической стабильности Fe 3 O 4 использовались методы ТГА и ДСК. / Нанокомпозит SWCNT / ПАММП. На рисунке 12 показана температурная зависимость от потери массы в нанокомпозите Fe 3 O 4 / SWCNT / PAMMP по сравнению с PAMMP при нагревании до 1000 ° C в потоке аргона и на воздухе.
01). Остаточная намагниченность M R чистого Fe 3 O 4 / SWCNT составляет 0,45 ЭМЕ / г, а коэрцитивная сила H C составляет 6 Э. Суперпарамагнитное поведение нанокомпозитов при относительно высоких концентрациях магнитных наночастиц определяется небольшими размерами и высокой дисперсностью магнитных наночастиц. Так или иначе, полученные значения M R / M S для Fe 3 O 4 / SWCNT / PAMMP и Fe 3 O 4 / нанокомпозиты SWCNT характерны для одноосных однодоменных частиц.Критический размер перехода в однодоменное состояние для Fe 3 O 4 составляет 128 нм [29,40]. Для исследования термической стабильности Fe 3 O 4 использовались методы ТГА и ДСК. / Нанокомпозит SWCNT / ПАММП. На рисунке 12 показана температурная зависимость от потери массы в нанокомпозите Fe 3 O 4 / SWCNT / PAMMP по сравнению с PAMMP при нагревании до 1000 ° C в потоке аргона и на воздухе. Содержание нанокомпозита углеродных нанотрубок C SWCNT = 10 мас.% По отношению к массе мономера.По данным AAS, содержание C Fe 3 O 4 = 23,5%. В таблице 3 приведены основные термические свойства полученных материалов. Как видно на рисунке 12, характер кривых потери веса не меняется до 320 ° C. Потеря веса при низких температурах связана с удалением влаги, что подтверждается данными ДСК (Рисунок 13).
Содержание нанокомпозита углеродных нанотрубок C SWCNT = 10 мас.% По отношению к массе мономера.По данным AAS, содержание C Fe 3 O 4 = 23,5%. В таблице 3 приведены основные термические свойства полученных материалов. Как видно на рисунке 12, характер кривых потери веса не меняется до 320 ° C. Потеря веса при низких температурах связана с удалением влаги, что подтверждается данными ДСК (Рисунок 13).Термостойкость нанокомпозита Fe 3 O 4 / SWCNT / PAMMP немного выше, чем у PAMMP.В инертной среде выше 320 ° C потеря веса образцов происходит постепенно. ПАММП теряет половину своего первоначального веса в инертной атмосфере при 865 ° C. Для нанокомпозита при этой температуре потеря веса составляет всего 44%, а при 1000 ° C остаток составляет 51%. Процессы термоокислительной деструкции начинаются при 315 ° C. Потеря веса 50% наблюдается при 475 ° C для полимера и при 485 ° C для нанокомпозита.
Изучена частотная зависимость от проводимости на переменном токе (σ ac ) в нанокомпозите Fe 3 O 4 / SWCNT / PAMMP. Нанокомпозит Fe 3 O 4 / SWCNT / PAMMP демонстрирует слабую частотную зависимость от проводимости σ ac в диапазоне 0,1–5,0 × 10 4 Гц. При увеличении частоты переменного тока в диапазоне 7,7 × 10 3 –1,15 × 10 6 Гц проводимость увеличивается с 8,3 × 10 –6 См / см до 2,4 × 10 –5 См. Между тем частотная зависимость от проводимости на переменном токе (σ ac ) в нанокомпозите ОСУНТ / ПАММП, не содержащем наночастиц магнетита, демонстрирует постепенное увеличение электропроводности во всем исследованном диапазоне частот ( кривая 2 на рисунке 14).По мере увеличения частоты электрическая проводимость возрастает до значения 3,4 × 10 -7 См / см. Согласно предыдущим исследованиям [41,42], такой характер частотной зависимости от проводимости указывает на прыжковый механизм переноса заряда. Таким образом, присутствие наночастиц Fe 3 O 4 изменяет характер электропроводности нанокомпозита.
Нанокомпозит Fe 3 O 4 / SWCNT / PAMMP демонстрирует слабую частотную зависимость от проводимости σ ac в диапазоне 0,1–5,0 × 10 4 Гц. При увеличении частоты переменного тока в диапазоне 7,7 × 10 3 –1,15 × 10 6 Гц проводимость увеличивается с 8,3 × 10 –6 См / см до 2,4 × 10 –5 См. Между тем частотная зависимость от проводимости на переменном токе (σ ac ) в нанокомпозите ОСУНТ / ПАММП, не содержащем наночастиц магнетита, демонстрирует постепенное увеличение электропроводности во всем исследованном диапазоне частот ( кривая 2 на рисунке 14).По мере увеличения частоты электрическая проводимость возрастает до значения 3,4 × 10 -7 См / см. Согласно предыдущим исследованиям [41,42], такой характер частотной зависимости от проводимости указывает на прыжковый механизм переноса заряда. Таким образом, присутствие наночастиц Fe 3 O 4 изменяет характер электропроводности нанокомпозита. Согласно предыдущим исследованиям [41,42], частотная зависимость от проводимости на переменном токе в металлсодержащих полимерных композитах описывается следующим образом: оценка: где ω = 2πf — угловая частота, A и p зависят от температуры и объемной доли проводящего металлсодержащего компонента.На низких частотах основной вклад в проводимость дает составляющая σ dc . В этом случае его вклад тем больше, чем выше содержание металла [43]. Измерения проводимости σ dc показали, что проводимость Fe 3 O 4 / SWCNT / PAMMP σ dc = 8,3 × 10 −6 См / см на 6 порядков выше, чем проводимость PAMMP. в основном виде (σ dc = 1,2 × 10 −12 См / см) и SWCNT / PAMMP (σ dc = 4.4 × 10 −12 См / см). Таким образом, наночастицы магнетита вносят существенный вклад в проводимость нанокомпозита σ dc . Ионная составляющая проводимости также играет важную роль в области низких частот.
Согласно предыдущим исследованиям [41,42], частотная зависимость от проводимости на переменном токе в металлсодержащих полимерных композитах описывается следующим образом: оценка: где ω = 2πf — угловая частота, A и p зависят от температуры и объемной доли проводящего металлсодержащего компонента.На низких частотах основной вклад в проводимость дает составляющая σ dc . В этом случае его вклад тем больше, чем выше содержание металла [43]. Измерения проводимости σ dc показали, что проводимость Fe 3 O 4 / SWCNT / PAMMP σ dc = 8,3 × 10 −6 См / см на 6 порядков выше, чем проводимость PAMMP. в основном виде (σ dc = 1,2 × 10 −12 См / см) и SWCNT / PAMMP (σ dc = 4.4 × 10 −12 См / см). Таким образом, наночастицы магнетита вносят существенный вклад в проводимость нанокомпозита σ dc . Ионная составляющая проводимости также играет важную роль в области низких частот.

 Умение сравнивать числа.
Умение сравнивать числа.
 Умение доказывать параллельность прямых, сопоставлять с признаками и свойствами, делать выводы и вычисления, используя теоретические знания из планиметрии
Умение доказывать параллельность прямых, сопоставлять с признаками и свойствами, делать выводы и вычисления, используя теоретические знания из планиметрии Ю.Магрычев/
Ю.Магрычев/ Показательная функция
Показательная функция Логарифмическая функция
Логарифмическая функция Системы уравнений
Системы уравнений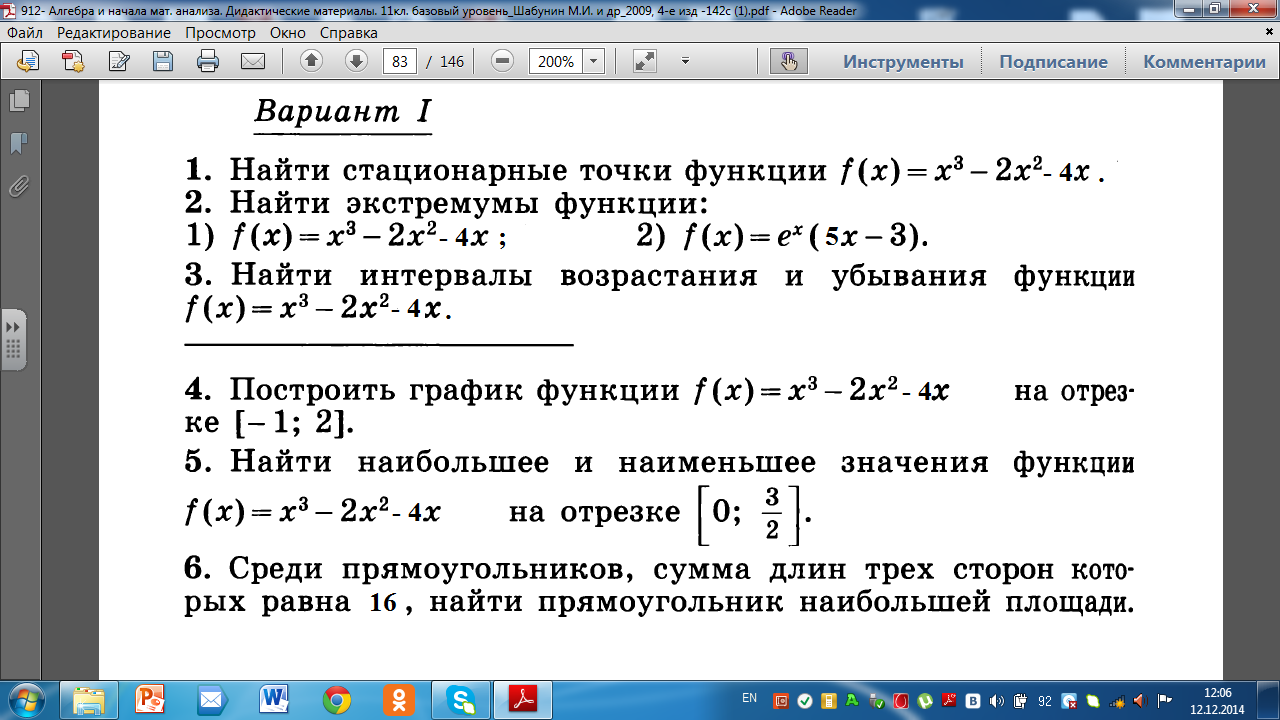 Сумма и разность косинусов
Сумма и разность косинусов Тригонометрические функции
Тригонометрические функции Решение задач
Решение задач