Контрольна робота интеграл — concert-market.ru
Скачать контрольна робота интеграл fb2
Сборник онлайн калькуляторов для решения интегралов. Решение интегралов. Интеграл является одним из самых важных понятий математического анализа. Данное понятие появляется тогда, когда необходимо решить задачи о нахождении площади под кривой, массы неоднородного тела.
Также интеграл помогает в решении задач, которые касаются восстановления функции по ее производной. Контрольная работа «Интеграл», состоящая из двух вариантов. Интеграл Вариант 1. Найдите площади криволинейных трапеций.
f(х)=x2,x=0,x=2, y=0. Определенный интеграл. Вид работы: Контрольная работа. Предмет: Математика. Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.
Контрольная работа по алгебре 11 класса по теме «Первообразная и. интеграл». I вариант II вариант.
Вариант 1. Вычислите: а) б). Определенный интеграл. Вариант 2. Вычислите: а) б). Определенный интеграл. Вариант 3. Вычислите: а) б) в). Определенный интеграл. Вариант 4. Вычислите: а) б) в). Определенный интеграл. Вариант 5. Вычислите: а) б) в). Определенный интеграл. Вариант 6. Вычислите: а) б) в).
Определенный интеграл. Вариант 7.
Інтеграл, контрольні роботи, 11 клас. Определенный интеграл. Вид работы: Контрольная работа. Предмет: Математика. Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.
1. Организационный момент.
2. Контрольная работа. Вариант 1. 1) Докажите, что функция есть первообразная для функции на промежутке. 2) Известно, что функция есть первообразная для функции f(x) на промежутке. Найти f(x). 3) Для функции найдите: а) общий вид первообразных.
Похожее:
Новости Курилова Ирина Владиславовна
16
января
2019
домашняя контрольная работа по алгебре 9 классДевятиклассникам предлагается решить работу, проверить свои знания. Ответы присылайте в комментариях до понедельника 21.01.2019.Удачи!
https://yadi.sk/i/LagelYkueOhLZA
января
2019
Домашняя контрольная работа по теме «Первообразная и интеграл», 11 класс24 января 2019 годв вы пишете контрольную работу по теме «Интеграл».
Есть возможность к ней подготовиться. Ответы на домашнюю работу принимаю до 21.01.2019г.
https://yadi.sk/i/MqZbFEP73RNUkx
30
апреля
2018
Результаты конкурса ФГОСТЕСТ, апрель 2018фгостест апрель2018
По этой ссылке можно посмотреть результаты участия в апрельской сессии олимпиады ФГОСТЕСТ
16
марта
2018
Результаты участия в математическом конкурсе «Лига чисел»Результаты конкукрса «Лига чисел»
08
марта
2018
Домашняя контрольная работа для 11 классаКонтрольная работа по теме рациональные уравнения
15 марта состоится контрольная работа по теме «Рациональные уравнения». Предлагаю одиннадцатиклассникам потренироваться.
31
января
2018
Разбор демоварианта ЕГЭ-2018 по математикеРазбор демо варианта ЕГЭ по математике
Вниманию выпускников! Предлагаю посмотреть полезное видео
10
января
2018
Для обучающихся 10,11 классовПредлагаю обучающимся 10-11 класса попробовать свои силы и пройти онлайн ЕГЭ базового уровня и результаты прислать в комментариях.
http://www.examen.ru/tests/matematika-bazovaya-ege-2018
10
января
2018
Для учащихся 11 класса25 января 2018 года вы пишете контрольную работу по теме «Первообразная. Интеграл». Предлагаю вариант пробной контрольной работы. Ответы принимаю до 20 января в комментариях. Желаю успеха. И.В.
Контрольная по интегралам
10
января
2018
Для обучающихся 10 класса29 января 2018 года вы будете писать контрольную работу по теме «Логарифмы. Логарифмические и показательные уравнения и неравенства». Предлагаю Вам работу, позволяющую подготовиться к контрольной работе. Ответы принимаю в комментариях до 25 января. Можно присылать ответы по каждому заданию ( по мере изучения материала). И.В.
Проверочная по логарифмам
25
декабря
2017
Результаты олимпиады ФГОСТЕСТК сведению участников олимпиады.
По ссылке можно узнать свои результаты.https://fgostest.ru/PC/Results.aspx?id=9d739c1b-3cb7-4d1e-89e8-56071094060d
08
декабря
2017
Результаты олимпиад «Олимпис. Осенняя сессия, 2017»К сведению участников олимпиад «Олимпис». По ссылке можно узнать свои результаты. Дипломы и призы организаторы обещают в феврале 2018 года.
Олимпис,2017
01
декабря
2017
К сведению обучающихся!В декабре с 6 по 20 пройдет Всероссийская олимпиада (физико-математический цикл) Центра дистанционной сертификации ФГОСТЕСТ. По вопросам регистрации обращаться к Куриловой И.В.
25
октября
2017
Регистрация на Международные олимпиады Олимпис С 1 по 30 ноября 2017 года пройдут Международные онлайн олимпиады «Олимпис». Учащиеся 1-4 классов могут пройти 5 олимпиад по: математике, русскому, английскому языкам, информатике и окружающему миру.
01
сентября
2017
неделя мониторинга по математикеС 11 по 17 сентября 2017 года Электронная школа Знаника проводит традиционную Всероссийскую неделю мониторинга. В рамках мероприятия школьники смогут проверить свои знания по математике.Генеральным партнером Недели впервые стала Корпорация «Российский учебник», разработав комплекс контрольно-измерительных материалов по русскому языку для основной школы и математике и русскому языку для начальной школы.
Принять участие может любой желающий: школа, учитель с классом, школьник с родителем.
Мониторинг абсолютно бесплатный.
Мероприятие очное: учитель скачивает задания, печатает и в классе раздаёт их для решения, отводя на работу 45 минут.
Контрольная работа по теме “Первообразная, интеграл, площадь криволинейной трапеции”
Контрольная работа по теме
“Первообразная, интеграл, площадь криволинейной трапеции”
Найти:
В1В2
1.2×5-3×2 dx 1.5×4+2×3 dx2.12(2x+3×2)dx 2. 34(2×3- 3x)dx
у= x2 — 8x + 18y = -x2 + 10x — 16
y = -2x + 18y = x + 2
В3 В4
Найти:
1.2×8-7×3 dx 1.5×6+2×3 dx2.12(2×2+3×7)dx 2. 35(4×3- 3x)dx
3.sin4x-3dx 3.cos5x+6dx4.14x-1 dx 4.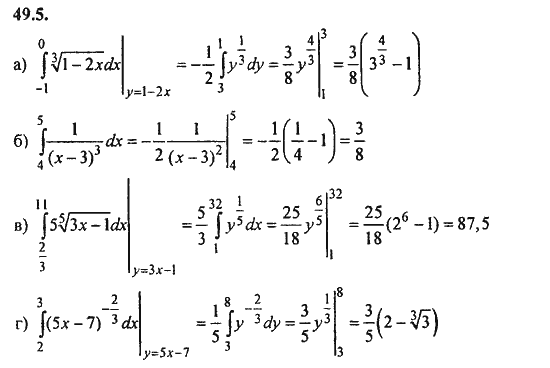
y = x2 – 2x + 3 y = 0.5×2 – 4x + 10
y = 3x – 1 y = x + 2
B5B6
1.Найти:
1.3×6-4×2 dx 1.6×3-3×3 dx2.03(4x+3×3)dx 2. 25(4×5- 4x)dx
3.sin4x+4dx 3.cos5x-4dx4.13x-1 dx 4. 54x+2 dx5. 23(4x+1)2 dx 5.23(8x-4)2 dx2.Найти площадь фигуры, ограниченной линиями
У=х2-2х+3у=х2+2х+1
У=3х-1 у=1-х
В7 В8
Найти:
1.2×2-5×2 dx 1.8×4+4×2 dx2.14(3x+4×2)dx 2. 45(3×3- 6x)dx
3.
sin4x-2dx 3.cos5x-3dx4.14x+2 dx 4. 28x+1 dx5. 24(3x-1)3 dx 5.24(3x+9)2 dxНайти площадь фигуры, ограниченной линиями
y = 4x – x2 y= x2+2 y = 4 – xy = 4x + 2
В9В10
Найти:
1.3×5+4×2 dx 1.6×4-3×3 dx2.33(5x-2×2)dx 2. 35(8×2- 43x)dx
3.sin8x-4dx 3.cos4x+5dx4.2x+1 dx 4. 44x-2 dx5. 34(3x-1)2 dx 5.25(5x+1)2 dx2.Найти площадь фигуры, ограниченной линиями
y = 6x – x2 y = 4 – x2
y = x + 4 y = x + 2
В11B12
1.Найти:
1.2×4-5×2 dx 1.5×4+2×3 dx2.02(3x+3×3)dx 2.
34(2×3- 3x)dx
3.sin5x-3dx 3.cos3x-4dx4.13x-1 dx 4. 34x-1 dx5. 12(8x+1)2 dx 5.13(4x+2)2 dx2.Найти площадь фигуры, ограниченной линиями
y = x2 + 2x + 1 y = x2 + 4x + 4
y = 1 – x y = x + 2
Приложенные файлы
- 585718
Размер файла: 34 kB Загрузок: 8
курсов Gooroo: сравнительный тест пределов
Обзор
Этот курс будет охватывать тест прямого сравнения, тест сравнения пределов и тест нулевой бесконечности. Исчисление — это математика изменения и движения. Исчисление было независимо разработано в конце 17 века Исааком Ньютоном и Готфридом Вильгельмом Лейбницем. Исчисление II — это интегральное исчисление. В основном в этом курсе мы изучаем множество методов для решения множества различных проблем с приложениями.
Пройдя этот курс, вы сможете настраивать и оценивать интегралы, чтобы находить площади и объемы и решать реальные проблемы, вычислять интегралы вручную, используя различные методы, включая подстановки, части, частичные дроби и гиперболическую тригонометрию, анализировать сходимость последовательностей, рядов,
и степенные ряды, решают элементарные задачи векторного анализа Этот курс состоит из четырех основных глав: 1. Применение интегралов: использование интегралов для поиска площадей и объемов и решения реальных задач.
2.Вычисление интегралов вручную: оценивайте интегралы вручную, используя различные методы, включая подстановки, части, частичные дроби и гиперболическую тригонометрию.
3. Анализ сходимости последовательностей, рядов и степенных рядов.
4. Векторный анализ: решение элементарных задач векторного анализа
Инструктор
Миюран Д.
Кандидат математических наук
Я доктор.
Миуран Денсил, профессиональный математик, в настоящее время работает доцентом. Я получил степень магистра и доктора математики в 2016 и 2020 годах в Техасском технологическом университете, Техас, США. Во время учебы в колледже я выиграл очень престижную президентскую стипендию для выпускников на 5 лет, которую получают самые лучшие аспиранты школы. Я был приглашенным спикером на многие признанные конференции и выиграл много грантов на свои исследования. Моя диссертация была посвящена геометрическим свойствам специальных функций и связанных с ними квадратичных дифференциалов.Мои исследовательские интересы включают уравнения в частных производных и теорию чисел. Я окончила Университет Келании, Шри-Ланка, в 2011 году со степенью бакалавра, то есть специальной степенью по математике с отличием первого класса.
Преподавание — моя страсть и призвание! Кроме того, математика — это весело и интерактивно! Я начал преподавать математику в очень молодом возрасте. У меня более 16 лет опыта преподавания и преподавания математики в детском саду старшеклассникам, на уровне колледжа и на уровне выпускников.
После получения степени бакалавра я работал преподавателем в Университете Келании с 2011 по 2013 год, а затем работал преподавателем в университете Моратува с 2013 по 2015 год. Затем я поступил в аспирантуру Техасского технологического университета, работая ассистентом GPTI / исследователем в 2015-2020 годах.
Я преподавал: исчисление I, II, III + Pre-Cal, AP Cal AB / AP Cal BC, тригонометрия, линейная алгебра, геометрия, ODE / PDE, алгебра 1,2, численные методы, действительный / расширенный анализ, комплексные числа , Дискретная математика, Теория групп / Теория колец / Теория чисел, Интегрирование / Уравнения Лапласа / Преобразование рядов Фурье, Математика для степеней, Механика / Движение частицы / Силовое равновесие / Гармоническое движение, Тренажер для экзаменов, таких как SAT, разделы математики GRE .
За 16 лет опыта преподавания и долгой академической жизни я нашел методы, которые помогли мне понять и решить любую проблему быстрее и точнее. Теперь я готов преподавать их вам, поскольку я считаю, что нет ничего слишком сложного, если ученик хочет учиться.
Поскольку математика является интерактивным и увлекательным предметом, она позволяет студентам получить дополнительную практику и обеспечивает индивидуальную учебную атмосферу для студентов, чтобы отточить их аналитическое мышление и технику решения проблем.
Отличные новости! Миюран хочет помочь тебе раскрыть свой потенциал. Виртуальное обучение теперь доступно в несколько кликов.
11.4: Интегральный тест — математика LibreTexts
Как правило, довольно сложно, а зачастую и невозможно точно определить значение ряда. Во многих случаях можно по крайней мере определить, сходится ли ряд или нет, и поэтому мы потратим большую часть времени на решение этой проблемы.
Если все члены \ (a_n \) в серии неотрицательны, то очевидно, что последовательность частичных сумм \ (s_n \) не убывает. Это означает, что если мы можем показать, что последовательность частичных сумм ограничена, ряд должен сходиться.
Мы знаем, что если ряд сходится, члены \ (a_n \) стремятся к нулю, но это не означает, что \ (a_n \ ge a_ {n + 1} \) для каждого \ (n \). Однако это свойство есть во многих полезных и интересных сериях, и они являются одними из самых простых для понимания. Давайте посмотрим на пример.2 \) и т. Д. — иными словами, именно члены ряда. Частичная сумма \ (s_n \) — это просто сумма площадей первых \ (n \) прямоугольников. Поскольку все прямоугольники лежат между кривой и осью \ (x \), любая сумма площадей прямоугольников меньше, чем соответствующая площадь под кривой, и поэтому, конечно, любая сумма площадей прямоугольников меньше площади под всей кривая, то есть вплоть до бесконечности. Есть небольшая проблема на левом конце, где есть асимптота, но мы можем легко это обойти.\ infty {1 \ над x} \, dx = 1 + \ infty. \]
Проблема в том, что несобственный интеграл не сходится. Обратите внимание: это не , а не доказывает, что \ (\ sum 1 / n \) расходится, просто это конкретное вычисление не может доказать, что оно сходится.
2 \] с точностью до двух десятичных знаков.2} \, dx = {1 \ over N}, \), поэтому \ (N = 100 \) — хорошая отправная точка. Сложение первых 100 членов дает примерно \ (1,634983900 \), а плюс \ (1/100 \) равен \ (1.644983900 \), поэтому аппроксимация ряда значением, находящимся на полпути между ними, будет не более \ (1/200 = 0,005 \) по ошибке. Средняя точка равна \ (1.639983900 \), но хотя это верно для \ (\ pm0.005 \), мы не можем сказать, является ли правильное двухзначное приближение \ (1.63 \) или \ (1.64 \).
Нам нужно сделать \ (N \) достаточно большим, чтобы уменьшить гарантированную ошибку, возможно, примерно до \ (0.2/6 \ приблизительно1.644934068 \), который округляется до \ (1.64 \) (едва) и действительно ниже верхней границы \ (1.644965982 \), опять же едва. Часто приближения будут даже лучше, чем «гарантированная» точность, но не всегда, как показывает этот пример.
Архив 2019-2020 / Архив 2019-20 Математика
Курс № 5491/5492
Класс: 9-12
Предварительные условия: Успешное завершение курса алгебры 8Этот курс охватывает фундаментальные темы алгебры, необходимые учащимся для обучения на курсах математики в старших классах, а также для дальнейшей карьеры и образования.
Обсуждаемые темы включают: квадратные уравнения, правила экспонент, дроби с переменными, работу функций, системы линейного программирования и члены полиномиальных функций. Для этого курса требуется графический калькулятор. (Вернуться наверх)
Курс: 5111/5112
Класс: 9–12Пререквизиты: Успешное завершение алгебры 9B
Геометрия — это изучение логических рассуждений, линий, плоскостей и их взаимосвязи с треугольниками, четырехугольниками, кругами и другими плоскими фигурами.Особое внимание уделяется написанию дедуктивных доказательств. Студенты будут применять концепции формы, пространства и измерения, чтобы иллюстрировать и описывать физический мир и решать проблемы. Студенты будут использовать измерения прямо или косвенно, изучать уравнения алгебры и графики в двух измерениях.
(Вернуться наверх)
Алгебра IIA / B
Курс: 5031/5032
Оценка: 9-12
Предпосылка: Успешное завершение геометрии B
Этот курс включает изучение линейных, квадратичных, рациональных, полиномиальных, экспоненциальных и логарифмических уравнений. Для этого курса учащиеся должны иметь графический калькулятор, эквивалентный TI-83 или лучше. * Студентам рекомендуется завершить этот курс до конца 11 класса, чтобы подготовиться к государственному экзамену MCA по математике.
(Вернуться наверх)
Курс: 5245/5246/5247
Класс: 10-12Пререквизиты: Алгебра IIB
Предварительные исчисления A, B и C предназначены в первую очередь для студентов, которые очень заинтересованы в изучении математики или тех, кто знает, что ему / ей потребуется больше курсов по математике или наука в его / ее образовательном развитии за пределами средней школы.В этом курсе рассматриваются следующие темы: система счисления, математическая индукция, ряды, последовательности, пределы, аналитическая геометрия, функции, комплексные числа, доказательство, процедуры построения графиков, абсолютное значение, функции наклона и тригонометрия.
После успешного завершения Pre-Calculus студент будет иметь тригонометрические знания, чтобы перейти к Calculus. Для этого курса учащиеся должны иметь графический калькулятор, эквивалентный TI-83 или лучше. (Вернуться наверх)
AP Calculus I A / B
Курс: 5255/5256
Класс: 11-12
Расширенный расчетный курс разработан как расширение и обзор всех ранее пройденных курсов математики, объединяющий их и применяющий интересными способами.Основная часть этого курса состоит в том, чтобы определить и использовать деривации для поиска уклонов, связанных скоростей и решения задач по максимуму-минимуму. Также будет сосредоточено внимание на антипроизводных и интегралах, нахождение площади под кривыми, длины кривых и изучение трансцендентных функций (триггеры, экспоненты, логарифмы и т. Д.). Цель состоит в том, чтобы подготовиться к экзамену Advanced Placement, который проводится в середине мая, что позволит тем, кто имеет проходные баллы, получить кредит колледжа за этот курс.
Для этого курса учащиеся должны иметь графический калькулятор, эквивалентный TI-83 или лучше.Студенты будут готовы к сдаче экзамена AP Calculus AB. (Вернуться наверх)
AP Calculus II A / B
Курс: 5258/5259
Класс: 11-12
Темы, охваченные AP Calculus BC, включают все темы AP Calculus A и AP Calculus B. Этот курс является расширением предыдущих курсов по математическому анализу. Дополнительные темы, которые будут рассмотрены: полярные, параметрические и векторные функции с использованием производных и интегралов, разработка приближений с использованием рядов Эйлера, Тейлора и Маклорена, правило Л’Опиталса для проверки сходимости, первообразные по частям и частичные дроби, поиск сходимости геометрических, гармонических и чередующийся ряд, радиус и интервал сходимости степенного ряда, оценка ошибки Лагранжа для полиномов Тейлора. После успешного завершения этого курса студенты сдают весенний экзамен AP Calculus BC, который может принести студентам дополнительные кредиты колледжа.
Они получат оценку за этот тест и дополнительную оценку за уже пройденный тест AP Calculus. Для этого курса требуется графический калькулятор. Студенты будут готовы к сдаче экзамена AP Calculus BC. (Вернуться наверх)
Тригонометрия
Курс: 5330
Оценка: 10-12Предварительные условия: Успешное завершение Алгебры II B
Тригонометрия — это изучение взаимосвязи между сторонами и углами прямоугольного треугольника.Этот курс разработан, чтобы расширить предварительные знания студентов об этом исследовании из геометрии, используя тригонометрические функции и отношения в приложениях и идентичностях. Тригонометрия предназначена для студентов, которые хотят продолжить изучение математики и / или подготовиться к следующему курсу. Для этого курса у студентов должен быть графический калькулятор.
(Вернуться наверх)
Расширенные функции, статистика и геометрия A / B
Курс: 5350/5351
Оценка: 10–12Предварительные условия: Успешное завершение Алгебры II A и B
Расширенные функции, статистика и геометрия предназначена для усиления и расширения знаний учащихся в области геометрии, статистики и алгебры II.
Рассмотренные концепции включают функции, вероятность, статистику и геометрию. Этот курс предназначен для дальнейшей подготовки студентов к экзамену ACT и служит отличным курсом подготовки к экзамену ACT. Пройдя этот курс, студенты обретут уверенность в продолжении обучения в математике и / или смежных областях. Для этого курса учащиеся должны иметь графический калькулятор, эквивалентный TI-83 или лучше. * Студенты могут сдавать AFSG-A или AFSG-B, либо оба. (Вернуться наверх)
Колледж СНГ Алгебра через моделирование A / B
Курс: 5425/5426
Оценка: (11-12)Необходимое условие: Успешное завершение алгебры II A и B с оценкой C или выше.
Высший 50–20-й процентильный класс, или рекомендация учителя
Этот курс знакомит студентов с искусством математического прогнозирования посредством алгебраического моделирования и элементарной теории вероятностей. Класс охватывает методы представления поведения реальных данных с помощью алгебраических уравнений, включая линейные, полиномиальные, экспоненциальные и логарифмические функции.
Студенты научатся разрабатывать уравнения, которые точно представляют поведение реальных данных. Задачи взяты из разных дисциплин.В то время как студенты практикуют традиционные алгебраические методы, они также будут широко использовать программу электронных таблиц Excel, чтобы исследовать поведение наборов данных. Класс также укрепит способность студентов общаться и оценивать математические рассуждения. Этот курс удовлетворяет требованиям университетского математического мышления. Успешное завершение этого курса может позволить студентам получить 3 семестровых кредита в Университете Миннесоты. (CI 1806 College Algebra через моделирование) (Вернуться к началу)
Введение в C ++
Курс: 5436
Класс: 9-12Пререквизиты: Успешное завершение алгебры 9 A и B
Этот курс научит студентов писать программы на C ++.C ++ — это структурированный язык высокого уровня, позволяющий писать программы для приложений любого типа и размера.
Курс будет охватывать шесть основных элементов программирования: ввод, операции с данными, вывод, условное выполнение, циклы и функции. (Вернуться наверх)
AP Computer Science A / B
Курс: 5445/5446
Класс: 11-12
Это курс информатики на уровне колледжа.Он предназначен для высокомотивированных студентов, интересующихся темами информатики. Информатика включает в себя совокупность технических навыков и научных методов, которые можно использовать для создания высококачественных компьютерных решений реальных проблем. Студенты научатся свободно кодировать в хорошо структурированной манере, используя язык Java. По окончании студенты смогут: применять известные алгоритмы и структуры данных, читать и понимать большие программы, а также понимать процесс проектирования и разработки, ведущий к большой программе.
Студентам будет предложено пройти тест Advanced Placement Test, который проводится в середине мая. Многие колледжи и университеты предоставляют зачетные единицы за высокие достижения по тесту AP. AP Computer Science будет предлагаться только при достаточном количестве учащихся. AP Computer Science не засчитывается как зачет по математике. (Вернуться наверх)
Статистика AP A / B
Курс: 5449/5450
Класс: 10-12
Цель этого курса — познакомить студентов с основными концепциями и инструментами для сбора, анализа и вывода на основе данных.Студенты знакомятся с четырьмя широкими концептуальными темами: изучение данных, выборка и экспериментирование, прогнозирование закономерностей и статистический вывод. Студенты должны зарегистрироваться на оба семестра и сдают AP Exam в мае. Студенты должны иметь графический калькулятор, эквивалентный TI 83 или TI 84.
(Вернуться наверх)
Курс: 5030
Класс: 11-12(Требуется рекомендация учителя)
Потребительская математика применяет знания ученика по арифметике и алгебре в повседневных ситуациях.Темы будут включать личные финансы, валовой и чистый доход, банковское дело для физических лиц, транспорт, потребительский кредит, налоги, жилье, инвестиции и страхование.
(Вернуться наверх)
Базовая и прикладная статистика СНГ A / B
Курс: 5451/5452
Класс: 10-12
Базовая и прикладная статистика — это вводный курс по статистике, предназначенный для привлечения студентов с использованием методов моделирования и симуляции. Он подчеркивает понимание и применение статистических концепций и процедур с использованием визуальных и количественных методов для представления и анализа данных с использованием методов вывода.
Успешное завершение этого курса может позволить студентам получить 3 семестровых кредита в Университете Миннесоты. (Вернуться наверх)
% PDF-1.3
%
129 0 объект
>
endobj
xref
129 73
0000000016 00000 н.
0000001811 00000 н.
0000003821 00000 н.
0000004039 00000 н.
0000004356 00000 п.
0000004542 00000 н.
0000004696 00000 н.
0000004918 00000 н.
0000005138 00000 п.
0000005553 00000 н.
0000005777 00000 н.
0000006001 00000 п.
0000006390 00000 н.
0000006720 00000 н.
0000006928 00000 н.
0000006969 00000 н.
0000007191 00000 н.
0000007380 00000 н.
0000007680 00000 н.
0000007834 00000 н.
0000008255 00000 н.
0000008784 00000 н.
0000008806 00000 н.
0000009595 00000 н.
0000009954 00000 н.
0000010158 00000 п.
0000010362 00000 п.
0000010571 00000 п.
0000010593 00000 п.
0000011145 00000 п.
0000011498 00000 п.
0000011850 00000 п.
0000012054 00000 п.
0000012273 00000 п.
0000012295 00000 п.
0000012850 00000 п.
0000012872 00000 п.
0000013427 00000 п.
0000013633 00000 п.
0000014115 00000 п.
0000014137 00000 п.
0000014703 00000 п.
0000014856 00000 п.
0000015169 00000 п.
0000015191 00000 п.
0000015810 00000 п.
0000015832 00000 п.
0000016384 00000 п.
0000016406 00000 п.
0000016963 00000 п.
0000017184 00000 п.
0000018982 00000 п.
0000021053 00000 п.
0000032608 00000 п.
0000034570 00000 п.
0000042603 00000 п.
0000042818 00000 п.
0000050984 00000 п.
0000052469 00000 п.
0000054269 00000 п.
0000054473 00000 п.
0000054552 00000 п.
0000057230 00000 н.
0000057455 00000 п.
0000062027 00000 н.
0000062263 00000 п.
0000062468 00000 п.
0000064036 00000 п.
0000066960 00000 п.
0000071140 00000 п.
0000074430 00000 п.
0000001908 00000 н.
0000003798 00000 н.
трейлер
]
>>
startxref
0
%% EOF
130 0 объект
>
endobj
200 0 объект
>
транслировать
Hb«f« / a`g` Ȁ
Базовый анализ: японский сорт 11
Базовый анализ: японский язык 11 класс
Список ключевых слов базового кода продукта: mawrld; MAWRLD; mawrld / 11; MAWRLD / 11; mawrld-11; MAWRLD-11
Распечатать код продукта: MAWRLD / 11
Код продукта в Интернете: MAWRLD / 11.
E
Заголовок (HTML): Базовый анализ: японский язык 11 класс
Ярлык автора / редактора (необязательно): Отредактировано
Автор (ы) (дисплей продукта): Кунихико Кодайра
Принадлежность (а) (HTML): Университет Гакушуин, Токио, Япония
Название серии книг: Математический мир
Объем: 11
Месяц и год публикации: 1996-08-27
Год авторского права: 1996 г.
Количество страниц: 184
Тип обложки: Мягкое покрытие
Печатать ISBN-13: 978-0-8218-0580-0
Интернет ISBN 13: 978-1-4704-2477-0
Печатать ISSN: 1055-9426
Интернет ISSN: 1055-9426
Первичный МСК: 00
Учебник ?: ложный
Прикладная математика ?: ложный
Книга MAA ?: ложный
Обучение на основе запросов ?: ложный
Электронные СМИ?: ложный
Одежда или подарок: ложный
Тема SXG: GI
Интернет-цена 1 этикетка: Список
Интернет-цена 1: 30.
00
Цена печати за 1 этикетку: Список
Цена печати 1: 32.00
Этикетка с ценой в Интернете 2: Член AMS
Интернет-цена 2: 24.00
Цена печати 2 Этикетка: Член AMS
Цена печати 2: 25,60
Этикетка с ценой в Интернете 3: Член МАА
Интернет-цена 3: 27.00
Этикетка с ценой 3 печати: Член МАА
Цена печати 3: 28,80
Стоимость пакета 1 Наклейка: Список
Стоимость пакета 1: 47.00
Ярлык цены пакета 2: Член AMS
Стоимость пакета 2: 37,60
Стоимость пакета 3: 42,30
Этикетка с ценой 3 пакета: Член МАА
Печать URL-адреса добавления в корзину: / some / url / at / AMS / MAWRLD-11
Электронный URL добавления в корзину: /some/url/at/AMS/MAWRLD-11.E
Печать доступна для заказа: истинный
Обзорная копия: https://www.ams.org/exam-desk-review-request?&eisbn=978-1-4704-2477-0&pisbn=978-0-8218-0580-0&epc=MAWRLD/11.
E & ppc = MAWRLD / 11 & title = Basic% 20Analysis% 3A% 20Japanese% 20Grade% 2011 & author = Kunihiko% 20Kodaira & type = R
Ссылка на разрешения CCC: https://www.copyright.com/openurl.do?isbn=9780821805800&WT.mc.id=American%20Mat Mathematical%20Society
| Семестр | Дата | Инструктор | Темы | Текстовые разделы | Решения |
|---|---|---|---|---|---|
| W16 | 02.05.16 | Balcomb | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | нет |
| W16 | 11.03.16 | Balcomb | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | нет |
| W16 | 02. 05.16 | Отт | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| W16 | 11.03.16 | Отт | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W16 | 13.04.16 | Отт | Финал: все экзамены с 02.05 и 03.11 (кроме работы, разделения переменных и вероятности) плюс последовательности, ряды, тесты сходимости, степенные ряды, ряд Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 8.1-8.4, 9.1-9.2, 10.1-10.2, 11.1-11.7 | да |
| W16 | 03.02.16 | Таун | отзыв к экзамену 1 | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| W16 | 09. 03.16 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W16 | 11.04.16 | Таун | Обзордля финала, часть I | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 10.1, 10.3 | да |
| W16 | 12.04.16 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| F15 | 02.10.15 | Balcomb | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | нет |
| F15 | 11.06.15 | Balcomb | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | нет |
| F15 | 16. 12.15 | Balcomb | Финал: все экзамены 10.02 и 11.06 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| F15 | 02.10.15 | Coulombe | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| F15 | 11.06.15 | Coulombe | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F15 | 16.12.15 | Coulombe | Финал: все экзамены 10.02 и 11.06 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5. 4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| F15 | 02.10.15 | Отт | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| F15 | 11.06.15 | Отт | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F15 | 16.12.15 | Отт | Финал: все экзамены 10.02 и 11.06 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| F15 | 30.09.15 | Таун | отзыв к экзамену 1 | (O / Z) 5. 4, 6.1-6.2, 7.1-7.4 | да |
| F15 | 11.04.15 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F15 | 14.12.15 | Таун | Обзордля финала, часть I | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 10.1, 10.3 | да |
| F15 | 15.12.15 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| W15 | 06.02.15 | Balcomb | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | нет |
| W15 | 13.03.15 | Balcomb | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8. 1-8.4, 9.1-9.2, 10.1-10.3 | нет |
| W15 | 15.04.15 | Balcomb | Финал: все экзамены 02/06 и 03/13 плюс последовательностей, серий, тестов сходимости, степенных рядов, серии Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| W15 | 06.02.15 | Jayawant | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| W15 | 13.03.15 | Jayawant | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W15 | 06.02.15 | Вонг | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5. 4, 6.1-6.2, 7.1-7.4 | да |
| W15 | 13.03.15 | Вонг | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W14 | 15.04.15 | Вонг | Финал: все экзамены 02/06 и 03/13 плюс последовательностей, серий, тестов сходимости, степенных рядов, серии Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| W15 | 02.04.15 | Таун | отзыв к экзамену 1 | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| W15 | 11.03.15 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W15 | 13.04.15 | Таун | Обзордля финала, часть I | (O / Z) 5. 4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 10.1-10.3 | да |
| W15 | 14.04.15 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| F14 | 26.09 / 14C | Монтгомери | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| F14 | 26.09 / 14D | Монтгомери | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| F14 | 31.10 / 14C | Монтгомери | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9. 1-9.2, 10.1-10.3 | да |
| F14 | 31.10 / 14D | Монтгомери | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F14 | 10.12.14 | Монтгомери | Final (Версия 1): все экзамены с 26.09 и 31.10 плюс последовательностей, серий, тестов сходимости, степенных рядов, серии Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| F14 | 10.12.14 | Монтгомери | Final (Версия 2): все экзамены с 26.09 и 31.10 плюс последовательностей, серий, тестов сходимости, степенных рядов, серии Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| F14 | 26.09.14 | Росс | (Экзамен 1) подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем | (O / Z) 5. 4, 6.1-6.2, 7.1-7.2 | да |
| F14 | 31.10.14 | Росс | (экзамен 2) интегрирование по частям, частичное интегрирование, тригонометрическое интегрирование, полиномы Тейлора, несобственные интегралы | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.2 | да |
| F14 | 10.12.14 | Росс | (Заключительный экзамен) все экзамены 26.09 и 31.10 плюс последовательностей, серий, тестов сходимости, степенных рядов, серии Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 8.1-8.4, 9.1-9.2, 10.1-10.2, 11.1-11.7 | да |
| F14 | 24.09.14 | Таун | отзыв к экзамену 1 | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| F14 | 29.10.14 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F14 | 08.12.14 | Таун | Обзордля финала, часть I | (O / Z) 5. 4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 10.1, 10.3 | да |
| F14 | 12.09.14 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| W14 | 31.01.14 | Jayawant | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.4 | да |
| W14 | 07.03.14 | Jayawant | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W14 | 09.04.14 | Jayawant | Финал: все экзамены 31.01 и 03.07 плюс последовательностей, рядов, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7. 4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| W14 | 31.01.14 | Вонг | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| W14 | 07.03.14 | Вонг | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W14 | 09.04.14 | Вонг | Финал: все экзамены 31.01 и 03.07 плюс последовательностей, рядов, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| W14 | 29.01.14 | Таун | отзыв к экзамену 1 | (O / Z) 5. 4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| W14 | 05.03.14 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W14 | 07.04.14 | Таун | Обзордля финала, часть I | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 10.1, 10.3 | да |
| W14 | 08.04.14 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| F13 | 27.09.13 | Harkleroad | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | нет |
| F13 | 01.11.13 | Harkleroad | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8. 1-8.4, 9.1-9.2, 10.1-10.3 | нет |
| F13 | 11.12.13 | Harkleroad | Финал: все экзамены 27.09 и 01.11 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| F13 | 27.09.13 | Jayawant | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| F13 | 01.11.13 | Jayawant | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F13 | 11.12.13 | Jayawant | Финал: все экзамены 27.09 и 01.11 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5. 4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| F13 | 27.09.13 | Вонг | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| F13 | 01.11.13 | Вонг | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F13 | 11.12.13 | Вонг | Финал: все экзамены 27.09 и 01.11 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | нет |
| F13 | 25.09.13 | Таун | отзыв к экзамену 1 | (O / Z) 5. 4, 6.1-6.2, 7.1-7.4 | да |
| F13 | 30.10.13 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| F13 | 12.09.13 | Таун | Обзордля финала, часть I | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 10.1, 10.3 | да |
| F13 | 10.12.13 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| W13 | 01.02.13 | Jayawant | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, разделение переменных | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| W13 | 08.03.13 | Jayawant | интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 8. 1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W13 | 10.04.13 | Jayawant | Финал: все экзамены с 01.02 и 03.08 плюс последовательностей, рядов, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| W13 | 01.02.13 | Росс | (Экзамен 1) подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем | (O / Z) 5.4, 6.1-6.2, 7.1-7.2 | да |
| W13 | 08.03.13 | Росс | (экзамен 2) интегрирование по частям, дробей, тригонометрическое интегрирование, полиномы Тейлора, несобственные интегралы, вероятность | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W13 | 10.04.13 | Росс | (Заключительный экзамен) все экзамены с 01.02 по 03.08 плюс последовательностей, серий, тестов сходимости, степенных рядов, серии Тейлора | (O / Z) 5. 4, 6.1-6.2, 7.1-7.2, 8.1-8.4, 9.1-9.2, 10.1-10.3, 11.1-11.7 | да |
| W13 | 30.01.13 | Таун | отзыв к экзамену 1 | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4 | да |
| W13 | 06.03.13 | Таун | отзыв к экзамену 2 | (O / Z) 8.1-8.4, 9.1-9.2, 10.1-10.3 | да |
| W13 | 08.04.13 | Таун | Обзордля финала, часть I | (O / Z) 5.4, 6.1-6.2, 7.1-7.2, 7.4, 8.1-8.4, 10.1, 10.3 | да |
| W13 | 09.04.13 | Таун | Обзордля финала, часть II | (O / Z) 9.1-9.2, 10.2, 11.1-11.7 | да |
| F12 | 28.09.12 | Coulombe | подстановка, числовые интегралы и их границы погрешности, площадь, длина дуги, объем, работа | (O / Z) 5.4, 6.1-6.2, 7.1-7.3 | да |
| F12 | 02. 11.12 | Coulombe | разделение переменных, интегрирование по частям, дробей, тригонометрическое интегрирование, многочлены Тейлора, несобственные интегралы, вероятность | (O / Z) 7.4, 8.1-8.4, 9.1, 10.1-10.3 | да |
| F12 | 12.12.12 | Coulombe | Финал: все экзамены от 28.09 и 02.11 плюс последовательностей, серий, тестов сходимости, степенных рядов, рядов Тейлора | (O / Z) 5.4, 6.1-6.2, 7.1-7.3, 8.1-8.4, 9.1, 10.1-10.3, 11.1-11.7 | да |
Математика · The Park School of Baltimore
Годовые курсы математики
Математика 9
Оценка: 9
В курсах математики для 9-х классов изучаются алгебра, геометрия и связи между ними.Повсюду делается упор на решение проблем, рассуждения и доказательства. Студенты разделены по интересам и способностям, — с разными классами, различающимися по темпам и уровню абстракции.
Математика 9-1
В этом курсе изучаются сложные алгебраические и геометрические аспекты с упором на решение проблем, рассуждения и доказательства. Темы включают теорию графов, законы экспонент и радикалов, алгебру рациональных выражений, квадратные уравнения, евклидову и координатную геометрию и тригонометрию единичного круга.
Математика 9-2, 9-3, 9-4
Эти курсы исследуют алгебру, геометрию и связи между ними, уделяя особое внимание развитию у студентов способности решать проблемы с помощью различных подходов. Темы включают алгебру, координатную геометрию, системы уравнений, тригонометрию, квадратичные функции и комбинаторику с постоянным упором на рассуждения и доказательства.
Математика 10
Grade 10 — Обязательно
Этот курс требуется на одном из трех уровней: математика 10-1, математика 10-2 или математика 10-3.
Математика 10-1
Студенты расширяют понимание алгебры и геометрии, полученные в математике 9-1.
Они исследуют экспоненциальные и логарифмические функции, комбинаторику, последовательности и ряды, графические преобразования, полиномы и рациональные функции, круговое движение и тригонометрические функции, тригонометрические тождества, комплексные числа и начинают изучение бесконечно малых процессов.
Математика 10-2, математика 10-3 и математика 10-4
Эти курсы изучают алгебру, геометрию и дискретную математику, но более глубоко, чем в прошлом году, с постоянным акцентом на развитие способности студентов решать задачи с помощью различных подходов.Темы могут включать в себя теорию графов, геометрические последовательности и ряды, радикалы и законы показателей, алгебру рациональных выражений, экспоненциальные функции, дальнейшее изучение квадратных уравнений, полиномиальных функций и комплексных чисел, статистику и евклидову геометрию.
Математика 11-2 +, Математика 11-2 и Математика 11-3
11 класс
Эти курсы подчеркивают приложения математики и могут включать следующие области: алгоритмы, экспоненциальные функции, логарифмы, тригонометрические функции, преобразования функций, полиномиальные функции, тригонометрические тождества, комбинаторику и вероятность, а также другие темы по геометрии.
Исчисление (ускоренное)
11–12 классы
Представлены концепции и приложения дифференциального и интегрального исчисления. Для юниоров завершающим курсом является месячный заключительный проект, требующий значительной самостоятельной работы. Студенты, успешно завершившие курс, готовы к сдаче экзамена Advanced Placement Calculus AB.
Необходимое условие: математика 10-1 или разрешение текущего учителя математики.
Расширенный расчет (ускоренный)
12 класс
В «Исчислении» учащиеся знакомятся с концепцией пределов и узнают, как их можно применить для развития теории дифференциации (скорости изменения) и интеграции (накопления), которая завершается изучением фундаментальных теорем исчисления.Advanced Calculus развивает методы дифференцирования и интегрирования и служит основой для таких классов, как дифференциальные уравнения, многомерное исчисление и линейная алгебра. Учебная программа разработана таким образом, чтобы включать: неопределенные формы; логарифмическое и неявное дифференцирование; соответствующие ставки; интеграция по частям; частичное разложение фракций; несобственные интегралы; параметрические и полярные уравнения; векторное исчисление применительно к положению, скорости и ускорению; дифференциальные уравнения и модели населения; последовательности; Тейлор и степенной ряд.
Эти темы охватывают весь материал экзамена Advanced Placement (AP) Calculus BC и обеспечат прочную основу для студентов, заинтересованных в прохождении теста. В дополнение к основным темам, упомянутым ранее, класс может время от времени относиться к другим областям высшей математики. Эти темы могут включать разные системы счисления; «размеры» бесконечности; математическая физика и теория относительности; многомерное исчисление и геометрия; и ряды Фурье.
Предпосылка: исчисление
Advanced Elective: линейная алгебра (ускоренный курс)
9–12 классы
Линейная алгебра — замечательный элемент математики: она живёт прямо в том золотом уголке, где пересекаются красота и «крайняя полезность».Предмет начинается с глубокого исследования стратегий решения систем линейных уравнений, переходя к мощной сфере векторов, векторных пространств и линейных преобразований. Прикладная линейная алгебра расширяет возможности большинства современных вычислительных наук, таких как знаменитый алгоритм Google PageRank, компьютерная графика и анимация, а также компьютерная аксиальная томография (например, компьютерная томография).
Этот класс обеспечит баланс теории, приложения и вычислений.
Пререквизиты: Разрешение кафедры
Курсы математики осеннего семестра
Исчисление I
12 класс
Студенты начнут курс с рассмотрения «проблемы касательной», а затем изучат пределы и разработают определение производной.В то же время они будут изучать рациональные функции, используя язык и методы ограничений, чтобы помочь понять графики этих функций. Прежде чем применять производную к реальным задачам, студенты изучат различные техники получения производных, одновременно укрепляя свои навыки алгебры.
Необходимое условие: математика 11-2 или разрешение отдела. Студенты, изучавшие математику и моделирование в прошлом году, не имеют права на этот курс.
Исчисление 2 (ускоренное)
12 класс
Этот курс исследует как теорию, так и применение дифференциального исчисления, и предназначен для углубления и расширения понимания тем, изученных в математике и моделировании в прошлом году.
Это включает в себя обширное исследование пределов, построение кривых, логарифмическое дифференцирование и правило L’Hospital, а также множество реальных приложений, включающих связанные скорости и оптимизацию.Он заканчивается введением в антидифференциацию и интеграцию.
Предварительные требования: Расчет и моделирование
Дискретная математика I
10–12 классы
Дискретная математика — это современный раздел математики, который фокусируется на различных задачах, темах и алгоритмах, которые часто имеют целочисленные результаты. Темы основаны на реальных приложениях. Этот курс фокусируется на математической перспективе справедливости, ценности и индивидуального восприятия.Студенты изучают широкий спектр методов голосования и изучают алгоритмы «справедливого раздела» через призму прав на владение недвижимостью, распределения для руководящих органов и множества непрерывных дел.
Статистика I
10–12 классы
Студенты изучают темы описательной статистики: отображение данных, описание наборов данных в соответствии с центром, формой и распространением, нормальное распределение, корреляция, экспериментальный план и систематическая ошибка выборки.
Весенние семестровые курсы
Исчисление 2
12 класс
Студенты продолжат использовать призму исчисления для изучения функций и их графиков.Темы могут включать неявное дифференцирование, проблемы оптимизации, связанные проблемы скорости, площадь под кривой, определение интеграла и фундаментальную теорему исчисления.
Предпосылка: Исчисление 1
Исчисление 3 (ускоренное)
12 класс
Этот курс исследует теорию и применение интегрального исчисления — антидифференцирование, определенные интегралы, фундаментальную теорему исчисления и интеграл как аккумулятор, а также ряд приложений, таких как площадь под кривой, движение частиц , и дифференциальные уравнения во многих повседневных контекстах.Курс завершится обширным исследованием бесконечных рядов и несобственных интегралов.
Необходимое условие: Calculus 2 (ускоренный)
Дискретная математика 2 (ускоренная)
10–12 классы
Дискретная математика 2 сосредоточится в первую очередь на приложениях, которые можно анализировать с помощью матриц.