Контрольная работа геометрии 7 класс: ГДЗ самостоятельные и контрольные работы по геометрии 7 класс Иченская, Атанасян Просвещение

ГДЗ Геометрия 7 класс Мельникова

В 7 классе каждому ребёнку необходимо получить прочную базу знаний по геометрии. Без этого фундамента могут возникнуть серьёзные трудности в более старших классах.

Что будут проходить на уроках геометрии?

• Введение в курс предмета и изучение начальных сведений;
• Простые фигуры: треугольники (и соотношение между его углами и сторонами), параллельные прямые, лучи, точка;
• Задачи с применением вышеперечисленных фигур.

Обращайте внимание на основные признаки равенства треугольников и на задачи с доказательством различных теорем.

Почему стоит выбрать именно эту тетрадь

Эти контрольные работы составлены к учебнику Атанасян по геометрии для 7 — 9 классов. Уже не одно поколение детей занимается по данной программе. Знания, которые получает ребёнок в процессе обучения, помогают с легкостью сдать ему экзамен по математике в 9 классе. Т. к. «Контрольные работы по геометрии 7 класс» пользуются популярностью среди школьников, мы предлагаем вам воспользоваться нашим онлайн-решебнком.

О решебнике

«ГДЗ по Геометрии 7 класс Тетрадь для контрольных работ Мельникова» состоит из 5 частей-разделов. Каждый раздел имеет своё название и включает в себя 4 варианта самостоятельных работ и один итоговый контроль.

Для того, чтобы перейти на страницу с ответом нажмите на интересующую вас работу. Сайт автоматически покажет решение. Если вы допустили ошибку, пролистайте страницу в начало и выберите другой раздел.

Кому пригодится решебник

Во-первых, гдз необходим тем, кто самостоятельно занимается дома. У учителей не всегда есть возможность проверить все задания, поэтому ученики используют самопроверку.

Во-вторых, он нужен тем, кто хочет просто списать. И, в-третьих, некоторые школьники много пропускают по разным причинам, поэтому вынуждены таким образом догонять материал.

Контрольная работа вариант 1 — 2 гдз по геометрии 7 класс Мерзляк, Полонский дидактические материалы

Условие / контрольная работа / вариант 1 / 2

Контрольная работа № 2 Тема. Треугольники 1. Докажите равенство треугольников MBF и DBF (рис. 266), если ∠MBF = ∠DBF, ∠MFB = ∠DFB. 2. Найдите стороны равнобедренного треугольника, если его периметр равен 84 см, а боковая сторона на 18 см больше основания. 3. На рисунке 267 DP = РЕ, DK = КЕ. Докажите равенство углов KDM и КЕМ. 4. На боковых сторонах АВ и ВС равнобедренного треугольника ABC отметили соответственно точки Е и F такие, что АЕ — CF. Докажите, что ZACE — ZCAF. 5. Серединный перпендикуляр стороны АВ треугольника ABC пересекает его сторону АС в точке D. Найдите периметр треугольника BDC, если АС = 8 см, ВС = 6 см.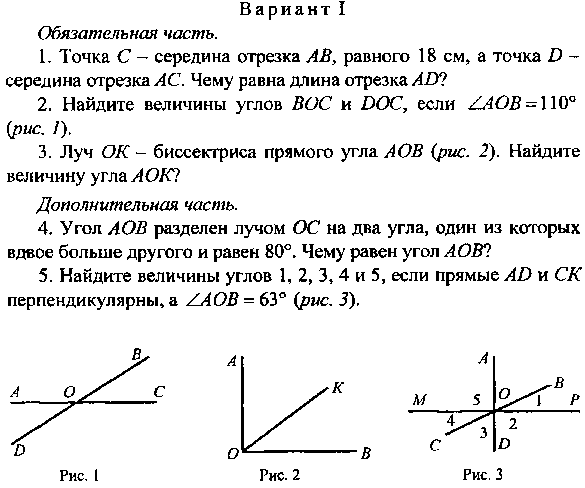

Решебник / контрольная работа / вариант 1 / 2

Видеорешение / контрольная работа / вариант 1 / 2

Годовая контрольная работа по геометрии , 7 класс

УТВЕРЖДАЮ:

Руководитель МО математики_______________ Фирсова С.В.

МБОУ «Лицей №2» г. Михайловск

«___» ____________ 2021 г.

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

по геометрии 2020-2021 уч.год 7 класс

Разработала:

Бережнова Н.Н.

учитель математики

Пояснительная записка

1.ВИД КОНТРОЛЯ– тестовая работа

2.СОДЕРЖАНИЕ КОНТРОЛЯ:

Проверяются следующие темы:

Основные понятия планиметрии;

Сумма углов треугольника;

Неравенство треугольника;

Смежные углы;

Вертикальные углы;

Параллельные прямые;

Углы, образованные двумя параллельными прямыми и секущей;

Прямоугольный треугольник.

3. Цель: контроль освоения обучающимися образовательной программы, уровня сформированности следующих навыков по изученным темам: начальные геометрические сведения, треугольники, параллельные прямые, соотношения между сторонами и углами треугольника.

4. Работа ориентирована на проверку выполнения требований к уровню подготовки по геометрии обучающихся 7 класса.

5. Текст контрольной работы взят из учебно-методического пособия к учебнику Л.С.Атанасяна «Геометрия 7-9»: автор Н.Б. Мельникова «Контрольные работы по геометрии 7класс».М.: «Экзамен», 2019.

Контрольная работа представлена в двух вариантах и содержит 9 заданий.

На выполнение работы отводится 40 минут.

6. Критерии оценивания

За верное выполнение каждого задания – 1 балл

Максимальное количество баллов –9.

Критерии выставления оценок

№Количество балловШкольная оценка

1.6-9 «5»

2.4-5 «4»

3.3 «3»

4.Менее 3-х «2»

 

1 вариант 1). Найти смежные углы. если один из углов больше другого на 52 градуса. 2) Сумма вертикальных углов равна 162 градуса. Найти градусные меры этих углов. 3). Найдите углы треугольника АВС, если ∠А : ∠В : ∠С = 1 : 2 : 3 4). Периметр равнобедренного треугольника равен 25 см. Боковая сторона в 2 раза больше основания. Найдите длины сторон. 5). В равнобедренном треугольнике один из углов равен 35 . Чему равны остальные углы ? 6).Доказать, что треугольники равны. 7). Найти сторону АВ 8). Выберите верное утверждение: а) Смежные углы равны. б) Через любые три точки можно провести прямую, и притом только одну. в) Часть прямой, ограниченная двумя точками, называется отрезком. г) Тупой угол равен 180 градусов

2 вариант 1) Найти смежные углы, если один из углов меньше другого на 32 градуса 2) Сумма накрест лежащих углов равна 84 градуса. Найти градусные меры этих углов 3). Найдите углы треугольника АВС, если ∠А : ∠В : ∠С = 2 : 3 : 4 4). Периметр равнобедренного треугольника равен 24 см. Боковая сторона в 2 раза меньше основания. Найдите длины сторон. 5). В равнобедренном треугольнике один из углов равен 70 . Чему равны остальные углы? 6). Доказать, что треугольники равны 7). Найти сторону ВС. 8). Выберите верное утверждение: а) Две прямые имеют множество общих точек, в этой ситуации говорят, что прямые параллельны. б) Развернутый угол равен 90 градусов. в) Сумма вертикальных углов равна 180 градусов. г) Через любые две точки можно провести прямую, и притом только одну.

Контрольные работы по геометрии 7 класс

Контрольная работа № 1 (7 класс)

по теме «Начальные геометрические сведения» (глава I, п.п. 1-13)

Вариант 1

Три точки В,С, и D лежат на одной прямой а. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезкаВС?

Сумма вертикальных углов MOE и DOC, образованных при пересечении прямыхМС и DЕ, равна 204°. Найдите угол МОD.

С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла. Укажите равные углы.

4* На рисунке прямая АВ перпендикулярна к прямой СD,

луч ОЕ биссектриса угла АОD. Найдите угол СОЕ.

_____________________________________________________________________________

Контрольная работа № 1 (7 класс)

по теме «Начальные геометрические сведения» (глава I, п.п. 1-13)

Вариант 2

Три точки М,N, и K лежат на одной прямой а. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МK?

Сумма вертикальных углов АОВ и COD, образованных при пересечении прямыхАD и ВС, равна 108°. Найдите угол ВОD.

С помощью транспортира начертите угол, равный 132°, и проведите биссектрису смежного с ним угла. Укажите равные углы.

4* На рисунке прямая АС перпендикулярна к прямой ВD,

луч ОМ биссектриса угла АОВ. Найдите угол СОМ.

Контрольная работа № 2 (7 класс)

по теме «Треугольники. Задачи на построение» (глава II, п.п. 14-23)

Вариант 1

Отрезки АВ и СD пересекаются в точке О, являющейся серединой каждого из них. Докажите, что: а) треугольники АОD и ВОС равны; б) AО = СВО.

Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что ADB = ADC. Докажите, что АВ = АС.

Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ₁ к боковой стороне АС.

4* Как с помощью циркуля и линейки построить угол в 11°15′?

_____________________________________________________________________________

Контрольная работа № 2 (7 класс)

по теме «Треугольники. Задачи на построение» (глава II, п. п. 14-23)

Вариант 2

Отрезки МЕ и РК пересекаются в точке D, являющейся серединой каждого из них. Докажите, что: а) треугольники РDЕ и КDМ равны; б) PED = KMD.

На сторонах углаD отмечены точки М и К так, что DM = DK. Точка Р лежит внутри угла D и РК = РМ. Докажите, что луч DР – биссектриса угла MDK.

Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту АН из вершины угла А.

4* Как с помощью циркуля и линейки построить угол в 67°30′?

Контрольная работа № 3 (7 класс)

по теме «Параллельные прямые» (глава III, п.п. 24-29)

Вариант 1

На рисунке прямыеa и b параллельны, 1 = 55°. Найдите 2.

Отрезки АС и BD пересекаются в их общей середине точкеО. Докажите, что прямые АВ и CD параллельны.

Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная сторонеCD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если СDЕ =68°.

4*. В треугольникеАВСА =67°, С =35°, BD – биссектриса угла АВС. Через вершину В

проведена прямаяMNAC. Найдите угол MBD. (Указание. Для каждого из возможных случаев сделайте чертеж.)

____________________________________________________________________________

Контрольная работа № 3 (7 класс)

по теме «Параллельные прямые» (глава III, п.п. 24-29)

Вариант 2

На рисунке прямыеa и b параллельны, 1 = 115°. Найдите 2.

Отрезки АD и BC пересекаются в их общей середине точкеМ. Докажите, что прямые АС и ВD параллельны.

Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная сторонеAB и пересекающая сторону AC в точке F. Найдите углы треугольника ADF, если BAC =72°.

4*. В треугольникеCDEС =59°, Е =37°, DК – биссектриса угла CDE. Через вершину D

проведена прямаяABCE. Найдите угол ADK. (Указание. Для каждого из возможных случаев сделайте чертеж.)

Контрольная работа № 4 (7 класс)

по теме «Сумма углов треугольника. Соотношения между сторонами и углами треугольника» (глава IV, п.п. 30-33)

Вариант 1

В треугольникеАВСАВ > ВС > АС. Найдите А, В, С, если известно, что один из углов треугольника равен 120°, а другой 40°.

В треугольникеCDE точка М лежит на стороне СЕ, причем CMD острый. Докажите, что DE > DM.

Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

4*. На сторонах углаА, равного 45°, отмечены точки В и С, а во внутренней области угла –

точка D так, что ABD = 95°, ACD = 90°. Найдите угол BDC.

____________________________________________________________________________

Контрольная работа № 4 (7 класс)

по теме «Сумма углов треугольника. Соотношения между сторонами и углами треугольника» (глава IV, п.п. 30-33)

Вариант 2

В треугольникеАВСАВ < ВС < АС. Найдите А, В, С, если известно, что один из углов треугольника прямой, а другой равен 30°.

В треугольникеMNP точка K лежит на стороне MN, причем NKP острый. Докажите, что KP<MP.

Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

4*. На сторонах углаА, равного 125°, отмечены точки В и С, а внутри угла – точка D так,

что ABD = 65°, ACD = 40°. Найдите угол BDC.

Контрольная работа № 5 (7 класс)

по теме «Прямоугольный треугольник. Построение треугольника по трем элементам» (глава IV, п.п. 34-38)

Вариант 1

Дано: , AB = CD (Рис. 1).

Доказать: .

В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние ОН от точки О до прямой MN.

Постройте прямоугольный треугольник по гипотенузе и острому углу.

4*. С помощью циркуля и линейки постройте угол, равный 105°.

____________________________________________________________________________

Контрольная работа № 5 (7 класс)

по теме «Прямоугольный треугольник. Построение треугольника по трем элементам» (глава IV, п.п. 34-38)

Вариант 2

Дано: , AD = BC (Рис. 2).

Доказать: AB = DC.

В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние FH от точки F до прямой DE.

Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.

4*. С помощью циркуля и линейки постройте угол, равный 165°.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/378817-kontrolnye-raboty-po-geometrii-7-klass

Геометрия 7 класс Контрольные работы КИМ

Контрольные работы по геометрии в 7 классе с ответами для любого УМК. В учебных целях использованы цитаты из учебного издания «Контрольно-измерительные материалы. Геометрия 7 класс» (составитель вопросов — Н.Ф.Гаврилова, издательство ВАКО). Представлено 6 работ в 2-х вариантах. Геометрия 7 класс Контрольные работы. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия. Затем представлены ответы на оба варианта контрольной. При постоянном использовании данных контрольных работ лучше всего КУПИТЬ книгу Геометрия 7 класс Контрольно-измерительные материалы. Е-класс. ФГОС (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки учебного издания.

 

Геометрия 7 класс

Контрольные работы (КИМ):

 

Контрольная 1. Основные свойства простейших геометрических фигур. Смежные и вертикальные углы

Контрольная работа № 1 К-1 + ответы

 

Контрольная 2. Треугольники

Контрольная работа № 2 К-2 + ответы

 

Контрольная 3. Параллельные прямые

Контрольная работа № 3 К-3 + ответы

 

Контрольная 4. Сумма углов треугольника. Соотношения между сторонами и углами треугольника

Контрольная работа № 4 К-4 + ответы

 

Контрольная 5. Прямоугольный треугольник. Построение треугольника по трем элементам

Контрольная работа № 5 К-5 + ответы

 

Итоговая контрольная работа за 7 класс

Итоговая контрольная работа К-6 + ответы

 

---

Вы смотрели страницу «Геометрия 7 класс Контрольные работы КИМ». Задания и ответы по учебному пособию «Контрольно-измерительные материалы. Геометрия 7 класс» (составитель вопросов — Н.Ф.Гаврилова, издательство ВАКО). Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Вернуться на страницу «Геометрия 7 класс»

 

---

Другие контрольные работы по математике в 7 классе:

 

Полугодовая контрольная работа по геометрии 7 класс, Александров

Полугодовая контрольная работа по геометрии 7 класс

I

вариант Часть 1

1. Укажите номера верных утверждений. 1) Сумма смежных углов равна 90⁰. 2) Биссектриса треугольника – это луч, который делит угол пополам 3) Через любую точку проходит более одной прямой. 4) Любые два равнобедренных треугольника равны. 5) Медиана- это отрезок соединяющий вершину с серединой противоположной стороны. 2. Укажите смежные углы. 1) 2) 3)

3. Установите соответствие треугольниками и названиями.

А Б В 1. Тупоугольный

2. Равносторонний

3. Равнобедренный

В ответ запиши получившееся число.

4. В каком треугольнике медиана основания является биссектрисой и высотой?

А ) в разностороннем. Б) в прямоугольном. В) в равнобедренном.

Часть 2. Решите задачи.

1. Найдите меньший смежный угол, если один из них на 20 градусов меньше другого.

2. Сумма двух углов образованных при пересечении двух прямых равна 150 градусам. Найдите все углы.

3. Определите есть ли на рисунке 1 равные треугольники, если есть, докажите их равенство.

4. В равнобедренном треугольнике АВС основание АС в три раза меньше его боковой стороны АВ, а периметр равен 28см. Найдите боковую сторону АВ.

Рис1.

Полугодовая контрольная работа по геометрии 7 класс

II вариант Часть 1

1. Укажите номера верных утверждений. 1) Сумма вертикальных углов равна 90⁰. 2) В треугольнике медианы пересекаются в одной точке. 3) Через любую точку проходит не более одной прямой. 4) Любые два равносторонних треугольника равны. 5) Сумма смежных углов равна 180⁰

2. Укажите вертикальные углы. 1) 2) 3)

3. Найдите соответствие между свойствами и углами.

А) Сумма равна 180

0. Б) Углы равны В) Угол равен 90⁰.

1. Прямой 2. Смежные 3. Вертикальные

В ответ запиши получившееся число.

4. В каком треугольнике биссектриса основания является медианой и высотой?

А ) в равностороннем. Б) в прямоугольном. В) в равнобедренном.

Часть 2. Решите задачи.

1. Найдите больший смежный угол, если один из них в 3 раза больше другого.

2. Сумма двух углов образованных при пересечении двух прямых равна 108 градусам. Найдите все углы.

3. Определите есть ли на рисунке 1 равные треугольники, если есть, докажите их равенство.

Рис1

4. В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2:3. Найдите стороны треугольника.

Рис1

Оценивание

	На «3»	На «4»	На «5»
Выполнено верно часть 1	4 задания	4 задания	4 задания
Выполнено верно часть 2	1 задача	2 задачи	3-4 задачи

Рабочие листы по геометрии — Мистер Кокерхэм-Математика 7 класс

Обновление . .. ĉ Angle Application.doc (60k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:51 ĉ B3 Quiz 2 Review G1-G4.doc (61k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:51 ĉ Challenging Angle Questions.docx (87k) Джошуа Кокерхэм, 25 марта 2014 г., 4:23 ĉ Circum и Площадь кругов.docx (97k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:51 ĉ Джошуа Кокерхэм, 3 февраля 2014 г., 8:35 ĉ Джошуа Джошуа , 3 февраля 2014 г., 8:36 ĉ Geometric Concepts Quiz.doc (232k) Joshua Cockerham, 21 марта 2014 г., 11:46 ĉ Geometry Quiz 4 B3.doc ( 113k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:37 ĉ Тест геометрии I.doc (109k) Joshua Cockerham, 3 февраля 2014 г., 8:37 AM ĉ Geometry Test III B1 и B2.doc (156k) Джошуа Кокерхэм, 3 февраля 2014 г. , 8 : 38 AM ĉ Geometry Test III Review.doc (73k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:37 AM ĉ Geometry and Probability EOG.doc (121k) Джошуа Cockerham, 3 февраля 2014 г., 8:36 ĉ Введение в геометрию поперечного сечения.docx (133k) Джошуа Кокерхэм, 10 апреля 2014 г., 4:32 ĉ Примечания к масштабному коэффициенту.doc (26k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:50 ĉ Джошуа Кокерхэм, 3 февраля 2014 г., 8:50 ĉ Проблемы со словом поверхности и объема.doc (420 КБ) Джошуа Кокерхэм, 3 февраля 2014 г., 8:52 AM ĉ Площадь и объем поверхности.doc (29k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:52 AM ĉ Обзор теста Конец 9 недель.docx (34k) Joshua Cockerham, 26 марта 2014 г., 12:25 ĉ Объем и площадь поверхности.doc (66k) Joshua Cockerham, 3 февраля 2014 г., 8: 56 AM ĉ Формулы объема и площади поверхности.doc (29k) Джошуа Кокерхэм, 3 февраля 2014 г., 8:56

Common Core Math 7 класс — Геометрия: углы, площади и объемы — Видео и уроки

Дополните свое преподавание Common Core State Standards для учащихся 7 класса этими уроками геометрии и викторинами.Превратите уроки в задания и проекты, чтобы ваши ученики полностью усвоили концепции углов, площади и объема, обсуждаемые в видеороликах.

Стандарт : Знать формулы площади и длины окружности и использовать их для решения задач; дают неформальный вывод отношения между окружностью и площадью круга. (CCSS.Math.Content.7.G.B.4)

Стандарт : Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре.(CCSS.Math.Content.7.G.B.5)

Стандарт : Решение реальных и математических задач, касающихся площади, объема и площади поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм. (CCSS.Math.Content.7.G.B.6)

Об этой главе

Когда ученики полностью поймут, как измерять площадь, они смогут делать это для многих типов фигур. Они также могут получить знания о различных типах углов.На этих уроках ваши ученики могут узнать следующее:

• Расчет площади и длины окружности
• Типы измерения углов
• Определение площади различных форм, таких как треугольники, прямоугольники, параллелограммы, многоугольники, ромбы и трапеции.
• Определите характеристики четырехугольника
• Понимание процессов, используемых для определения области сложных форм
• Примените формулу, используемую для расчета площади поверхности
• Расчет объема и площади призмы

Эти простые уроки могут оказаться полезными для тех учащихся, которые испытывают трудности с некоторыми понятиями площади и объема и могут реагировать на изучение геометрии визуально.Освоение этого стандарта подготовит учащихся к изучению более сложных геометрических предметов в средней школе и колледже.

Как использовать эти уроки в классе

Вы можете комбинировать эти предложения с вашими обычными учебными планами, чтобы соответствовать стандартам Common Core.

Идентификация формы

Выбирайте различные формы в классе, например, рабочий стол (прямоугольник), часы (круглые) и плитки для пола (квадрат).Измерьте углы, площадь и объем каждой из этих фигур.

Создание группового действия

Пусть ваши ученики объединятся в небольшие группы. Скажите каждой группе, что у них ночевка, и что все они будут спать в одной комнате. Раздайте листы, на которых вы нарисовали квадрат или прямоугольник. Меняйте размеры фигур на каждом листе. Попросите своих учеников определить площадь комнаты и смогут ли они уместить всех членов своей группы в одну комнату для этой фиктивной ночевки.

Назначьте конкурентоспособные углы, области и объемы домашнего задания Проект

Попросите каждого ученика создать таблицу с заголовками «Объект» и «Измерения». Попросите учащихся найти в своем доме предметы различной формы, например коробку с хлопьями, велосипедную шину, книжный шкаф и т. Д. Попросите учащихся вычислить площадь, окружность, углы и объем каждой из этих форм. Сообщите ученикам, что побеждает тот, у кого больше всего предметов!

Common Core Math 7 класс — Геометрия: геометрическое построение — Видео и уроки

Используйте видеоуроки и практические тесты из этого сборника геометрических построений, чтобы помочь своим ученикам седьмого класса соответствовать Общим основным государственным стандартам по математике.Есть также советы и предложения о том, как использовать уроки и узнать, когда ваши ученики усвоили эти концепции.

Стандарт: Решение задач, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей из масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе. (CCSS.MATH.CONTENT.7.G.A.1)

Стандарт: Нарисуйте (от руки, линейкой и транспортиром, а также технологией) геометрические фигуры в заданных условиях.Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника. (CCSS.MATH.CONTENT.7.G.A.2)

Стандарт: Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид. (CCSS.MATH.CONTENT.7.G.A.3)

Об этой главе

Учащиеся, усвоившие эти стандарты Common Core, смогут рисовать, описывать и конструировать геометрические фигуры, а также описывать отношения между ними.Используйте уроки из этого сборника, чтобы научить своих учеников следующим навыкам:

• Применение масштабных коэффициентов к площади, объему и периметру подобных фигур
• Чтение и интерпретация масштабных чертежей
• Изготовление геометрических конструкций
• Построение типов треугольников
• Обозначение трехмерных фигур сверху, сбоку и спереди

Когда ваши ученики овладеют этими стандартами, вы узнаете, когда они смогут решать задачи, которые включают в себя масштабные чертежи геометрических фигур, рисовать или конструировать геометрические фигуры с использованием заданных условий и описывать двумерные формы, получаемые в результате нарезания трех частей. Фигуры D.

Как использовать эти уроки в классе

Вот несколько советов по включению материалов коллекции в ваши планы уроков:

Построение геометрических фигур

Для работы в классе попробуйте создать некоторые конструкции, описанные в видео «Практика создания геометрических конструкций с помощью инструментов». Предложите учащимся работать в небольших группах, чтобы они могли обмениваться инструментами и давать советы друг другу. После этого попросите каждого ученика записать название своих конструкций и размеры, которые они использовали.

Сделайте масштабную модель Великой пирамиды в Гизе

Посмотрите уроки по масштабным коэффициентам и построению геометрических фигур. Затем создайте точную копию пирамиды Гизы, используя картон или плотную бумагу, ножницы и скотч. Измерения пирамид легко получить в Интернете. Предложите учащимся использовать полученные знания для уменьшения масштаба. Используйте линейку, чтобы измерить и нарисовать стороны пирамиды, а затем вырежьте и соберите формы.

Назначьте уроки и викторины домашним заданием

Дополните регулярные задания видео и викторинами из этого сборника.Студенты могут просмотреть видео в качестве напоминания перед тем, как ответить на практические вопросы, соответствующие каждому уроку. В качестве бонусного задания предложите студентам придумывать собственные вопросы и отвечать на них на основе вопросов в практических тестах.

Геометрия — 7 класс по математике

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Математика, 7 класс, Конструкции и углы, предварительная оценка

Это задание позволяет оценить работу студентов и определить, с какими трудностями они сталкиваются. Результаты самопроверки помогут вам определить, какие учащиеся должны работать в Галерее, а какие учащиеся выиграют от проверки перед экзаменом.Попросите учащихся поработать над самопроверкой индивидуально.

Попросите учащихся представить вам свои работы. Делайте заметки о том, что их работа показывает об их текущем уровне понимания и различных подходах к решению проблем.

Не оценивать работы студентов. Поделитесь с каждым учеником наиболее подходящими Вмешательствами, чтобы направлять их мыслительный процесс. Также отметьте учащихся, у которых возникла конкретная проблема, чтобы вы могли поработать с ними на следующем уроке «Собираем все вместе».

Проверьте вопросы, связанные с этой работой.

Студент неправильно вычисляет mÀ1.

• Какова сумма углов в треугольнике?
• Какова сумма известных вам угловых мер?

Студент неправильно вычисляет мÀ2.

• Как найти размер ∠ FGE ?
• Какова сумма углов в треугольнике?

Студент не видит, что ∠3 и ∠ BGC (27 °) являются дополнительными углами.

• Какой тип угла образуют ∠ BGC и ∠ CGE ?

Студент дает плохое объяснение, например, объяснение расчетов, а не математическое объяснение.

• Какова сумма углов в треугольнике?
• Что вы знаете об углах, образованных двумя пересекающимися прямыми?

Студент предлагает адекватное решение всех вопросов

• Найдите другой способ решения проблемы.

1. Измерение ∠1 составляет 63 °.
   Измерение ∠2 составляет 135 °.
   Измерение ∠3 составляет 153 °.
   Измерение ∠4 составляет 45 °.
   Измерение ∠5 составляет 27 °.

2. Решения могут отличаться. Учащиеся могут использовать следующие понятия, чтобы найти угловые меры:

   • Дополнительные углы, чтобы найти m∠1
   27 ° + m∠1 = 90 °
   m =1 = 63 °

   • Сумма углов треугольника равна 180 ° найти m∠2 (и m∠1).
   18 ° + 27 ° + м∠2 = 180 °
   м∠2 = 135 °

   • Дополнительные углы для нахождения м∠3
   27 ° + м∠3 = 180 °
   м∠3 = 153 °

   • Последовательные углы параллелограмма являются дополнительными для нахождения m∠4.
   м∠2 + m∠4 = 180 °
   135 ° + m∠4 = 180 °
   м∠4 = 45 °

   • Противоположные углы параллелограмма совпадают, чтобы найти m∠5.
   18 ° + m∠5 = m∠4
   18 ° + m∠5 = 45 °
   m∠5 = 27 °
   

3. Сумма углов в шестиугольнике составляет 720 °. Есть 6 сторон, поэтому используйте общее правило:

s = (6 — 2) 180 °

s = 4⋅180 °

s = 720 °

Студенты также могут сложить измерения каждого из углов шестиугольника, чтобы найти сумму.

Формирующее оценивание

Пройдите эту самопроверку самостоятельно.

Большая фигура представляет собой шестиугольник. Фигуры ABGF и CDEF представляют собой параллелограммы.

1. Найдите меры ∠1, ∠2, ∠3, ∠4 и ∠5.
2. Объясните, как вы определяли каждую угловую меру.
3. Какова сумма углов шестиугольника? Откуда вы знаете?

Рабочие листы MAP для 7-х классов

Ищете БЕСПЛАТНЫЕ печатные вопросы и упражнения по MAP для 7-го класса, которые помогут вашим ученикам изучить и применить математические концепции MAP для 7-го класса?

Ищете практические вопросы по математике, чтобы измерить готовность ваших учеников 7-го класса к экзаменам? Если так, то не смотрите дальше.Вот обширная коллекция бесплатных упражнений и рабочих листов, которые помогут вашим ученикам в подготовке и практике MAP Math 7-го класса.

Загрузите наши бесплатные рабочие листы по математике для 7-го класса MAP Math.

Надеюсь, вам понравится!

ВАЖНАЯ ИНФОРМАЦИЯ: УСЛОВИЯ АВТОРСКОГО ПРАВА: Эти рабочие листы предназначены для личного использования. Рабочие листы нельзя загружать в Интернет ни в какой форме, включая учебные / личные веб-сайты или сетевые диски. Вы можете скачать рабочие листы и распечатать их столько, сколько вам нужно.У вас есть разрешение распространять печатные копии среди ваших учеников, учителей, репетиторов и друзей.

У вас НЕТ разрешения отправлять эти рабочие листы кому-либо каким-либо образом (по электронной почте, текстовым сообщениям или другими способами). Они ДОЛЖНЫ загрузить рабочие листы сами. Вы можете отправить адрес этой страницы своим ученикам, преподавателям, друзьям и т. Д.

Абсолютно лучшая рабочая тетрадь

для обзора 7-го класса MAP Математические концепции!

MAP для 7-го класса Основные понятия по математике

Дроби и десятичные знаки

Вещественные и целые числа

Пропорции, соотношения и процент

Алгебраические выражения

Уравнения и неравенства

Линейные функции

Экспоненты и радикалы

Геометрия и твердые фигуры

Статистика и вероятность

КАРТА 7 класса Упражнения по математике

Дроби и десятичные знаки

Упрощение дробей

Сложение и вычитание дробей

Умножение и деление дробей

Добавление смешанных чисел

Вычесть смешанные числа

Умножение смешанных чисел

Деление смешанных чисел

Сравнение десятичных знаков

Округление десятичных знаков

Сложение и вычитание десятичных знаков

Умножение и деление десятичных знаков

Преобразование дробей, десятичных и смешанных чисел

Факторинговые номера

Наибольший общий делитель

Наименьший общий множитель

Вещественные и целые числа

Сложение и вычитание целых чисел

Умножение и деление целых чисел

Порядок целых чисел и чисел

Упорядочивание, порядок и сравнение целых чисел

Порядок операций

Смешанные целочисленные вычисления

Целые числа и абсолютное значение

Пропорции и соотношения

Соотношения записи

Коэффициенты упрощения

Создать пропорцию

Подобные рисунки

Проблемы с соотношением и ставками в словах

Смешанные целочисленные вычисления

процентов

Расчет процентов

Процент проблем

Наценка, скидка и налог

Алгебраические выражения

Выражения и переменные

Упрощение выражений переменных

Упрощение полиномиальных выражений

Переведите фразы в алгебраическое утверждение

Распределительная собственность

Оценка одной переменной

Оценка двух переменных

Объединение похожих терминов

Уравнения и неравенства

Одношаговые уравнения

Двухступенчатые уравнения

Многоступенчатые уравнения

Графическое отображение неравенств с одной переменной

Одноэтапные неравенства

Двухэтапные неравенства

Многоступенчатые неравенства

Линейные функции

Нахождение наклона

Графические линии с использованием формы наклона – пересечения

Графические линии с использованием стандартной формы

Написание линейных уравнений

Графическое изображение линейных неравенств

Поиск середины

Определение расстояния двух точек

Полиномы

Упрощение полиномов

Сложение и вычитание многочленов

Умножение одночленов

Умножение и деление одночленов

Умножение многочлена на одночлен

Умножение биномов

Факторинг трехчленов

Операции с многочленами

Системы уравнений

Решение систем уравнений подстановкой

Решение систем уравнений методом исключения

Системы уравнений Word Задачи

Экспоненты и радикалы

Свойство умножения экспонент

Свойство деления экспонент

Полномочия продуктов и коэффициентов

Нулевые и отрицательные экспоненты

Отрицательные экспоненты и отрицательные основания

Научная нотация

Статистика

Круговая диаграмма или круговая диаграмма

Вероятность проблем

Среднее (Среднее)

Геометрия

Теорема Пифагора

Площадь треугольников

Периметр полигонов

Площадь и окружность кругов

Площадь квадратов, прямоугольников и параллелограммов

Площадь трапеций

Сплошные фигуры

Объем кубиков

Объем прямоугольных призм

Площадь поверхности кубиков

Площадь поверхности прямоугольной призмы

Объем цилиндра

Площадь поверхности цилиндра

Ищете лучшие ресурсы, которые помогут вашим ученикам повторить и практиковать темы MAP Math в 7-м классе?

The Best Books

to Ace the 7 Grade MAP Math Test!

Реза — опытный преподаватель математики и специалист по подготовке к экзаменам, который занимается со студентами с 2008 года.Он помог многим студентам поднять результаты стандартизированных тестов и поступить в колледжи своей мечты. Он работает со студентами индивидуально и в группах, преподает как живые, так и онлайн-курсы по математике и математическую часть стандартизированных тестов. Он предлагает индивидуальный индивидуальный план обучения и индивидуальное внимание, которое влияет на то, как ученики относятся к математике.

3 месяца назад

Пойди по математике, 7 класс. Ответ на ключ. Глава 8. Моделирование геометрических фигур. Пойди по математике. Ответим ключ

.

Идите по математике для 7 класса. Ключ ответов на вопросы Глава 8 Моделирование геометрических фигур: Присоединяйтесь к списку лучших учащихся, используя ключ ответов для 7 класса.Получите доступ к бесплатной загрузке Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures. Мы должны подготовить решения таким образом, чтобы все студенты могли легко понять концепцию. Быстрое и легкое обучение возможно только с помощью нашего ключа ответов HMH Go Math.

Иди по математике, 7 класс. Ключевой ответ Глава 8 Моделирование геометрических фигур

Мы предлагаем студентам обратиться к Главе 8 «Моделирование геометрических фигур» по математике для 7 класса, чтобы получить наивысший балл на экзаменах.Это вызывает у студентов интерес к изучению математики. Изучите концепции геометрических фигур таким образом, чтобы подготовить вопросы самостоятельно. Нажмите на прикрепленные ниже ссылки и получите пошаговое объяснение.

Глава 8 — Моделирование геометрических фигур — Урок: 1

Глава 8 — Моделирование геометрических фигур — Урок: 2

Глава 8 — Моделирование геометрических фигур — Урок: 3

Глава 8 — Моделирование геометрических фигур — Урок: 4

Глава 8 — Моделирование геометрических фигур

Практическое руководство — стр.240

Вопрос 1.
Размер комнаты на чертеже составляет 3 дюйма: 5 футов. Стена на том же чертеже имеет размер 18 дюймов. Заполните таблицу.

а. Какова длина самой стены?

______ футов

Ответ: 30 футов

Пояснение:
Мы заполняем таблицу, используя прямую пропорциональность.
3 дюйма: 5 футов.
Стена на том же чертеже имеет размер 18 дюймов на 30 футов.

Вопрос 1.
б. Окно в комнате имеет фактическую ширину 2,5 фута. Найдите ширину окна на чертеже.
______ дюймов

Ответ: 1,5 дюйма

Пояснение:
Мы определяем количество дюймов, соответствующее 1 футам на реальном окне
3 дюйма / 5 дюймов
Умножаем и делим на 5
(3 дюйма ÷ 5) / (5 футов ÷ 5) = 0,6 / 1 фут
Таким образом, 1 фут соответствует 0,6 дюйма, поэтому ширина окна в таблице составляет
2,5 × 0,6 = 1,5 дюйма

Вопрос 2.
Масштаб чертежа составляет 2 дюйма: 4 фута. Каковы длина и ширина фактического помещения? Найдите площадь реальной комнаты.

Ширина: _________ футов
Длина: _________ футов
Площадь: _________ квадратных футов

Ответ:
Ширина: 28 футов
Длина: 14 футов
Площадь: 392 кв. Футов

Пояснение:
Мы определяем количество футов, соответствующее 1 дюйму на чертеже
2 дюйма / 4 дюйма = (2 дюйма ÷ 2) / (4 дюйма ÷ 2) = 1/2
Таким образом, 1 дюйм соответствует 2 футам от реальных габаритов помещения.
Определяем реальную длину комнаты, обозначенную на чертеже 14 дюймами.
14 × 2 = 28 футов
Определяем реальную ширину комнаты, обозначенную на чертеже как 7 дюймов.
7 × = 14 футов
Мы вычисляем площадь реальной комнаты:
28 × 14 = 392 квадратных фута.

Вопрос 3.
Масштаб на чертеже 2 см: 5 м. Какова фактическая длина и ширина комнаты? Найдите площадь реальной комнаты.

Ширина: _________ м
Длина: _________ м
Площадь: _________ кв.м

Ответ:
Ширина: 25 м
Длина: 15 м
Площадь: 375 кв.м

Пояснение:
Определяем количество метров, соответствующее 1 сантиметру на чертеже:
2 см / 5 см = (2 см ÷ 2) / (5 см ÷ 2) = 1 см / 2.5 м
Определяем реальную длину помещения, обозначенную на чертеже 10 см:
10 × 2,5 = 25 м
Определяем реальную ширину помещения, обозначенную на чертеже 6 см:
6 × 2,5 = 15 м
Вычисляем площадь комнаты:
25 × 15 = 375 квадратных футов.

Вопрос 4.
Чертеж столовой в масштабе нарисован на бумаге с сантиметровой сеткой, как показано. Масштаб 1 см: 4 м.
а. Нарисуйте прямоугольник на бумаге с сантиметровой сеткой в ​​масштабе 1 см: 6 м.

Тип ниже:
_____________

Ответ:

Вопрос 4.
г. Какова фактическая длина и ширина кафетерия при исходных масштабах? Каковы реальные размеры кафетерия при использовании новых весов?
Длина: _________ м
Ширина: _________ м

Ответ:
В исходном масштабе размеры на чертеже равны
l1 = 9 см
w1 = 6 см
Реальную длину определяем по оригинальному масштабу:
9 × 4 = 36
Фактическую ширину определяем с помощью исходный масштаб:
6 × 4 = 24
Во втором масштабе размеры на чертеже равны
l2 = 6 см
w1 = 4 см
Реальную длину определяем, используя исходный масштаб:
6 × 6 = 36
We Определите фактическую ширину, используя исходную шкалу:
4 × 6 = 24
Таким образом, длина составляет 36 м
Ширина составляет 24 м

Регистрация основных вопросов

Вопрос 5.
Если у вас есть точный, полный чертеж в масштабе и масштабе, какие размеры объекта чертежа вы можете найти?
Тип ниже:
_____________

Ответ:
Если у нас есть точный, полный чертеж в масштабе и масштабе, мы можем определить все размеры объекта, потому что все они пропорциональны размерам на чертеже, а соотношение является масштабом.

Независимая практика — стр. № 241

Вопрос 6.
Art
У Мари есть уменьшенная копия знаменитой картины Рене Магритта «Школьный учитель».Ее копия имеет размеры 2 на 1,5 дюйма. Масштаб копии — 1 дюйм: 40 см.
а. Найдите размеры оригинальной картины.
Длина: _________ см
Ширина: _________ см

Ответ:
Длина: 80 см
Ширина: 60 ​​см

Пояснение:
Нам даны данные
Масштаб: 1 дюйм: 40 см
Копия l1 = 2 дюйма
w1 = 1,5 дюйма
Определяем длину l оригинальной картины
l = 2 × 40 = 80см
Определяем ширина w оригинальной картины
w = 1.5 × 40 = 60 см

Вопрос 6.
б. Найдите область оригинальной картины.
_____________ кв см

Ответ: 4800 кв. См

Пояснение:
Определяем ширину w оригинальной картины
A = l.w
A = 80 × 60 = 4800 кв. См

Вопрос 6.
c. Поскольку 1 дюйм равен 2,54 см, найдите размеры оригинальной картины в дюймах.
Длина: _________ дюймов
Ширина: _________ дюймов

Ответ:
Определяем длину l оригинальной картины в дюймах:
1 дюйм.= 2,54 см
l = 80 / 2,54 см ≈ 31,5 дюйма
Определяем ширину w исходной картины в дюймах:
w = 60 / 2,54 ≈ 23,6 дюйма

Вопрос 6.
г. Найдите площадь оригинальной картины в квадратных дюймах
_____________ квадратных дюймов

Ответ: 743,4 квадратных дюйма

Пояснение:
Мы находим площадь оригинальной картины в квадратных дюймах:
l × w = 31,5 × 23,6 = 743,4 квадратных дюйма
Таким образом, площадь оригинальной картины равна 743.4 квадратных дюйма.

Вопрос 7.
Пол игровой комнаты составляет 120 на 75 футов. В масштабном чертеже пола на сетке используется масштаб 1 единица: 5 футов. Каковы размеры чертежа в масштабе?
Длина: _________ шт.
Ширина: _________ шт.

Ответ:
Длина: 24 шт.
Ширина: 15 шт.

Пояснение:
Нам даны данные:
Масштаб: 1 единица: 5 футов
Фактические размеры: l = 120 футов, w = 75 футов
Мы определяем количество единиц на чертеже, соответствующее 1 футу, исходя из фактических размеров.
1 единица / 5 футов
(1 единица ÷ 5) / (5 футов ÷ 5) = 0,2 единицы / 1 фут
Определяем длину чертежа в масштабе:
120 × 0,2 = 24 единицы
Определяем ширину чертеж в масштабе:
75 × 0,2 = 15 шт.

Вопрос 8.
Множественные представления
Длина стола 6 футов. На чертеже в масштабе длина составляет 2 дюйма. Напишите три возможных масштаба рисунка.
Тип ниже:
_____________

Ответ:
l = 6 футов
l1 = 2 дюйма
l = фактическая длина
l1 = длина на чертеже в масштабе
2 дюйма: 6 футов
1 дюйм: 3 фута
2/6 × 12 = 2/72 = 1/36
1 см: 36 см

Вопрос 9.
Анализ взаимосвязей
Масштаб чертежа в масштабе составляет 10 см: 1 мм. Что больше, реальный объект или масштабный рисунок? Объяснять.
_____________

Ответ:
Нам дан масштаб
10 см: 1 мм
100 мм: 1 м
Это означает, что соответствующий фактический размер для 100 мм чертежа составляет 1 мм, поэтому большему на чертеже соответствует меньший фактический размер. расстояние, поэтому масштаб чертежа больше.

Вопрос 10.
Архитектура
Масштабная модель здания 5.4 фута высотой.
а. Если первоначальное здание было 810 метров в высоту, в каком масштабе была сделана модель?
______ футов: ______ м

Ответ: 1 фут: 150 м

Пояснение:
Отметим:
h2 = высота на масштабе модели
h = фактическая высота
Нам даны данные
h2 = 5,4 фута
h = 810 метров
Определяем масштаб для модели
h2 / h = 5,4 фута / 810 м = (5,4 фута ÷ 5,4) / (810 ÷ 5,4)
1 фут / 150 м
1 фут: 150 м

Вопрос 10.
г. Если модель сделана из крошечных кирпичей, каждый размером 0,4 дюйма, сколько кирпичей в высоту эта модель?
___________ кирпич

Ответ: 14 кирпичей

Пояснение:
Определяем масштаб для модели:
х2 / 0,4 = 5,4 / 0,4 = 13,5
Количество кирпичей: 14

Стр. № 242

Вопрос 11.
Вас попросили построить масштабную модель вашей школы из зубочисток. Представьте, что ваша школа имеет высоту 30 футов. Ваш масштаб — 1 фут: 1.26 см.
а. Если высота зубочистки 6,3 см, сколько зубочисток будет у вашей модели?
______ зубочистки

Ответ: 6

Пояснение:
Учитывая, что
h = 30 футов
1 фут: 1,26 см
h2 = высота на масштабной модели
h = фактическая высота
Определяем высоту h2 модели:
h2 = 30 × 1,26 = 37,8 см
h2 / 6,3 = 37,8 / 6,3 = 6
Таким образом, количество зубочисток = 6

Вопрос 11.
б. У вашей матери закончились зубочистки, и она предлагает вам использовать вместо них ватные палочки.Вы их измеряете, а они высотой 7,6 см. Сколько ватных тампонов высотой будет у вашей модели?
______ ватные палочки

Ответ: 5

Пояснение:
Находим количество хлопковых мазков
h2 / 7,6 = 37,8 / 7,6 ≈ 5
Таким образом, количество хлопковых мазков = 5

H.O.T.

Фокус на мышлении высшего порядка

Вопрос 12.
Выводы по розыгрышу
Площадь квадратного пола на чертеже в масштабе составляет 100 квадратных сантиметров, а масштаб чертежа составляет 1 см: 2 фута.Какова фактическая площадь пола? Каково соотношение площади на чертеже к фактической площади?
Площадь = ______ кв. Футов

Ответ: 400 кв. Футов

Пояснение:
A1 = площадь чертежа
A = площадь фактического пола
Приведены данные:
A1 = 100 см²
1 см: 2 фута
1 см соответствует 2 футам
1 см × 1 см соответствует 2 футам × 2 футам
1 см² соответствует 4 футам²
A = 100. 4 = 400 фут²
Мы определяем отношение площади на чертеже к фактической площади:
1 фут = 0.3048 м = 30,48 см
A1 / A = 100/400 × 30,48² ≈ ​​0,0003

Вопрос 13.
Множественные представления
Опишите, как перерисовать масштабный чертеж с новым масштабом.
Тип ниже:
_____________

Ответ:
Чтобы перерисовать масштабный чертеж с новым масштабом, мы выполняем 2 шага:
1. Мы находим, во сколько раз новый масштаб больше или меньше старого.
2. Мы умножаем этот коэффициент масштабирования на размеры старого чертежа в масштабе, чтобы получить новый чертеж.

Вопрос 14.
Представление реальных проблем
Опишите, как несколько рабочих мест или профессий могут использовать масштабные чертежи на работе.
Тип ниже:
_____________

Ответ:
Масштабные чертежи чрезвычайно полезны в работах, которые должны представлять большие площади на небольших устройствах, таких как
1. Архитектура / конструкции
2. Медицина
3. Сельское хозяйство
4. Туризм
5. Транспорт

Практическое руководство — стр. № 245

Укажите, создает ли каждая фигура условия для образования уникального треугольника, более одного треугольника или отсутствия треугольника.

Вопрос 1.

Введите ниже:
_____________

Ответ: Уникальный треугольник

Пояснение:
Нам даны два угла и включенная сторона, таким образом, получается уникальный треугольник, поскольку стороны, выходящие из B и A, пересекаются в единственной точке.

Вопрос 2.

Введите ниже:
_____________

Ответ: Нет треугольника

Пояснение:
Даны три стороны треугольника. Мы проверяем, больше ли сумма любых двух сторон другой.
4 + 11 = 15> 3
11 + 3 = 14> 4
3 + 4 = 7 не больше 11.
Поскольку одно неравенство не проверено, треугольник не существует.

Вопрос 3.

Введите ниже:
_____________

Ответ: Уникальный треугольник

Пояснение:
Нам даны два угла и включенная сторона, таким образом, получается уникальный треугольник, поскольку стороны, выходящие из B и A, пересекаются в единственной точке.

Вопрос 4.

Введите ниже:
_____________

Ответ: Уникальный треугольник

Пояснение:
Даны три стороны треугольника.Мы проверяем, больше ли сумма любых двух сторон другой.
6 + 12 = 18> 7
12 + 7 = 19> 6
6 + 7 = 13> 12
Поскольку все неравенства проверены, существует единственный треугольник.

Регистрация основных вопросов

Вопрос 5.
Опишите длины трех сегментов, которые нельзя использовать для образования треугольника.
Тип ниже:
_____________

Ответ:
Найдите длины трех отрезков, которые не должны быть сторонами треугольника, по крайней мере одна сумма двух сторон должна быть меньше другой стороны.
Пусть a, b, c — длины трех сегментов.
a + b не> a + b + k = c

Независимая практика

Вопрос 6.
На отдельном листе бумаги попробуйте нарисовать треугольник с длиной стороны 3 и 6 сантиметров и включенным углом 120 °. Определите, образуют ли данные сегменты и угол уникальный треугольник, более одного треугольника или нет треугольника.
Тип ниже:
_____________

Ответ: Уникальный треугольник

Пояснение:
∠A = 120 °
AB = 6
AC = 3

Рисуем отрезок AB, угол A и отрезок AC, затем соединяем B и C.В результате получился уникальный треугольник.

Вопрос 7.
Ландшафтный архитектор представил заказчику проект цветочного сада треугольной формы с длиной сторон 21 фут, 37 футов и 15 футов. Объясните, почему архитектор не был нанят для создания цветника.
Тип ниже:
_____________

Ответ:
Нам даны стороны треугольника
21 + 37 = 58> 15
37 + 15 = 52> 21
15 + 21 = 36 not> 37
Мы проверили три треугольника, неравенства
Таким образом, треугольник не существуют, поэтому архитектора не наняли для создания цветника.

Стр. № 246

Вопрос 8.
Сделайте предположение
Углы на реальном дорожном знаке треугольной формы имеют размер 60 °. Углы на чертеже знака в масштабе имеют размер 60 °. Объясните, как вы можете использовать эту информацию, чтобы решить, можно ли использовать три заданные угловые меры для образования уникального треугольника или более чем одного треугольника.

Тип ниже:
_____________

Ответ: Три заданные угловые меры, сумма которых равна 180 °, могут быть использованы для образования бесконечности треугольников, имеющих свойство пропорциональности их соответствующих сторон.

H.O.T.

Фокус на мышлении высшего порядка

Вопрос 9.
Сообщайте математические идеи
На рисунке слева показан отрезок линии длиной 2 дюйма, образующий угол 45 °, с пунктирной линией, длина которой не указана. На рисунке справа показан компас, установленный на ширину 1 \ (\ frac {1} {2} \) дюймов с точкой на верхнем конце 2-дюймового сегмента. Строится дуга, дважды пересекающая пунктирную линию.

Объясните, как вы можете использовать этот рисунок, чтобы решить, можно ли использовать две стороны и угол, не входящий между ними, для образования уникального треугольника, более одного треугольника или без треугольника.
Тип ниже:
_____________

Ответ:
Тринагла не существует, потому что одна сторона короче двух других. Круг пересекает пунктирную линию только один раз, так что один угол составляет 45 °, поэтому есть только одно решение. Круг с центром в точке B дважды пересекает пунктирную линию, таким образом, образуются два треугольника.

Вопрос 10.
Критическое мышление
Две стороны равнобедренного треугольника имеют длину 6 дюймов и 15 дюймов соответственно.Найдите длину третьей стороны. Объясните свои рассуждения.
_______ дюймов

Ответ: 15 дюймов

Пояснение:
Даны две стороны равнобедренного треугольника
a = 6
b = 15
Есть две возможности, третья сторона равна a или b. Давайте изучим их оба.
Случай 1: a = c = 6, b = 15
a + c = 6 + 6 = 12 не более 15 = b
Мы проверим три неравенства треугольника
a + b = 6 + 15 = 21> 15 = c
a + c = 6 + 15 = 21> 15 = b
b + c = 15 + 15 = 30> 6 = a
Случай 2: a = 6, b = c = 15
Таким образом, третий сторона треугольника равна 15.

Практическое руководство — стр. № 249

Опишите каждое поперечное сечение.

Вопрос 1.

Введите ниже:
_____________

Ответ: Треугольник / Четырехугольный треугольник
Данное поперечное сечение в кубе представляет собой треугольник / равносторонний треугольник.

Вопрос 2.

Введите ниже:
_____________

Ответ: Прямоугольник
Данное поперечное сечение цилиндра представляет собой прямоугольник.

Вопрос 3.

Введите ниже:
_____________

Ответ: Треугольник

Пояснение:
Поперечное сечение призмы — треугольник.

Вопрос 4.

Введите ниже:
_____________

Ответ: Кривая в форме радуги
Данное сечение конуса представляет собой кривую в форме радуги.

Регистрация основных вопросов

Вопрос 5.
Каков первый шаг в описании того, что получается, когда данная плоскость пересекает данную трехмерную фигуру?
Тип ниже:
_____________

Ответ:
Первый шаг в описании того, какая фигура получается, когда данная плоскость пересекает данную трехмерную фигуру, — это установить количество сторон, которые имеет поперечное сечение.

Независимая практика

Вопрос 6.
Опишите различные способы пересечения плоскостью цилиндра и полученное поперечное сечение.

Тип ниже:
_____________

Ответ:
Поперечное сечение может быть:
1. круг
2. эллипс
3. прямоугольник

Стр. № 250

Вопрос 7.
Сделайте гипотезу
Какие поперечные сечения вы можете увидеть, когда плоскость пересекает конус, чего вы не увидите, когда плоскость пересекает пирамиду или призму?
Тип ниже:
_____________

Ответ:
Сечение может быть:
1.окружность
2. эллипс
3. парабола
4. гипербола
5. треугольник

H.O.T.

Фокус на мышлении высшего порядка

Вопрос 8.
Критическое мышление
Две цифры слева внизу показывают, что вы можете сформировать поперечное сечение куба, представляющего собой пятиугольник. Представьте себе плоскость, разрезающую куб под углом таким образом, чтобы разрезать пять из шести граней куба. Нарисуйте пунктирные линии на третьем кубе, чтобы показать, как образовать поперечное сечение, представляющее собой шестиугольник.

Тип ниже:
_____________

Ответ:
Рисуем плоскость, разрезающую куб так, чтобы сечение было шестиугольником: для этого берем середину из 6 смежных сторон:

Вопрос 9.
Анализировать взаимосвязи
Сфера имеет радиус 12 дюймов. Горизонтальная плоскость проходит через центр сферы.
а. Опишите поперечное сечение, образованное плоскостью и сферой.
Тип ниже:
_____________

Ответ: Круг

Пояснение:
Нам дана сфера и поперечное сечение, проходящее через центр сферы:
Поперечное сечение, проходящее через центр сферы, представляет собой круг с радиусом, равным радиусу сферы.

Вопрос 9.
б. Опишите поперечные сечения, образованные, когда плоскость пересекает внутреннюю часть сферы, но удаляется от центра.
Тип ниже:
_____________

Ответ: Поперечные сечения, образованные плоскостью, пересекающей внутреннюю часть сферы за пределами центра, представляют собой окружности.

Вопрос 10.
Сообщайте математические идеи
Правая прямоугольная призма пересекается горизонтальной плоскостью и вертикальной плоскостью. Поперечное сечение, образованное горизонтальной плоскостью и призмой, представляет собой прямоугольник размером 8 дюймов.и 12 дюймов. Поперечное сечение, образованное вертикальной плоскостью и призмой, представляет собой прямоугольник с размерами 5 дюймов и 8 дюймов. Опишите грани призмы, включая их размеры. Затем найдите его объем.
Тип ниже:
_____________

Ответ: 480 куб. Дюймов

Пояснение:
Горизонтальное сечение имеет размеры 8 × 12, а вертикальное — 5 × 8.
Призма имеет размеры:
5 дюймов, 8 дюймов, 12 дюймов
Находим объем призмы:
5 × 8 × 12 = 480 кубических дюймов

Вопрос 11.
Представление реальных проблем
Опишите реальную ситуацию, которая может быть представлена ​​плоскостями, разрезающими трехмерную фигуру для формирования поперечных сечений.
Тип ниже:
_____________

Ответ:
Примеры реальных ситуаций, которые могут быть представлены плоскостями, разрезающими трехмерные фигуры для образования поперечных сечений:
— электрические провода
— водопроводные / газовые трубы
— проект дома
— геология
— сейсмология

Практическое руководство — стр.256

Для 1–2 используйте рисунок.

Вопрос 1.
Словарь
Сумма измерений ∠UWV и ∠UWZ равна 90 °, поэтому UWV и ∠UWZ равны _____ углам.
Тип ниже:
_____________

Ответ: Дополнительные углы

Пояснение:
Сумма ∠UWV и ∠UWZ равна 90 °, поэтому UWV и ∠UWZ являются дополнительными углами.

Вопрос 2.
Словарь
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — это _____ углы.
Тип ниже:
_____________

Ответ: Смежные углы

Пояснение:
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — смежные углы.

Для 3–4 используйте рисунок.

Вопрос 3.
∠AGB и ∠DGE — это _____ углы, поэтому m∠DGE = _____.
Тип ниже:
_____________

Ответ: ∠AGB и ∠DGE — вертикальные углы, поэтому m∠DGE = m∠AGB = 30 °

Вопрос 4.
Найдите меру ∠EGF.
_______ °

Ответ: 100 °

Пояснение:
m∠CGD + m∠DGE + m∠EGF = 180 °
50 ° + m∠AGB + m∠EGF = 180 °
50 ° + 30 ° + 2x = 180 °
2x = 180 ° — 80 °
2x = 100 °
мм EGF = 2x = 100 °

Вопрос 5.
Найдите значение x и меру ∠MNQ.

x = _______ °
мMNQ = _______ °

Ответ:
∠MNQ + ∠QNP = 90 °
3x — 13 ° + 58 ° = 90 °
3x = 90 ° + 13 ° — 58 °
3x = 45 °
x = 15 °
м∠MNQ = 3x — 13 °
= 3 × 15 ° — 13 °
= 45 ° — 13 °
= 32 °

Регистрация основных вопросов

Вопрос 6.
Предположим, что вы знаете, что ∠T и ∠S являются дополнительными и что m∠T = 3 (m∠S). Как найти m∠T?
Тип ниже:
_____________

Ответ:
m∠T + m∠S = 180 °
m∠T = 3 (m∠S)
m∠S = m∠T / 3
Сформируем второе уравнение, запишем m∠S через m∠ T
m∠T + m∠T / 3 = 3 × 180 °
3m∠T + m∠T = 3 × 180 °
4m∠T = 540 °
m∠T = 540 ° / 4
m∠T = 135 °

Независимая практика — стр. № 257

Для 7–11 используйте цифру.

Вопрос 7.
Назовите пару смежных углов. Объясните, почему они рядом.
Тип ниже:
_____________

Ответ:
Пара смежных углов:
∠SUR и ∠RUN (общая вершина U и одна общая сторона — UR — без перекрытия)
∠NUQ и ∠QUP (общая вершина U и одна общая сторона — UQ — без перекрытия. )
∠PUT и ∠TUS (общая вершина U и одна общая сторона — UT — без перекрытия)

Вопрос 8.
Назовите пару острых вертикальных углов.
Тип ниже:
_____________

Ответ:
Глядя на рисунок выше, мы можем сказать, что ∠SUR и ∠PUQ — это вертикальные углы.

Вопрос 9.
Назовите пару дополнительных углов.
Тип ниже:
_____________

Ответ:
На рисунке выше показано, что ∠SUR и ∠RUQ являются дополнительными углами.

Вопрос 10.
Обоснуйте рассуждение
Найдите m∠QUR. Обосновать ответ.
_______ °

Ответ:
Мы должны найти m∠QUR.
∠SUR и ∠QUR — дополнительные уголки.
м∠SUR + m∠QUR = 180 °
м∠QUR + 41 ° = 180 °
м∠QUR = 180 ° — 41 °
м∠QUR = 139 °

Вопрос 11.
Выводы по розыгрышу
Что больше, m∠TUR или m∠RUQ? Объяснять.
Тип ниже:
_____________

Ответ:
m∠QUR = 139 °
m∠TUR = m∠TUS + m∠SUR
90 ° + 41 ° = 131 °
Находим m∠TUR
139 °> 131 °
m∠QUR> m∠

тур.

Для 12–13 используйте цифру. Велосипедная дорожка пересекает дорогу, как показано. Решите для каждой указанной меры или переменной угла.

Вопрос 12.
x =?
_______ °

Ответ: x = 21 °

Пояснение:
KMI и ∠HMG расположены вертикально, поэтому совпадают.
Определяем x:
84 ° = 4x
4x = 84 °
x = 84 ° / 4
x = 21 °

Вопрос 13.
м∠KMH =?
_______ °

Ответ: 96 °

Пояснение:
KMI и ∠KMH являются дополнительными.
Определяем m∠KMH:
м∠KMH + m∠KMI = 180 °
м∠KMH + 84 ° = 180 °
м∠KMH = 180 ° — 84 °
м∠KMH = 96 °

Для 14–16 используйте рисунок. Решите для каждой указанной угловой меры.

Вопрос 14.
m∠CBE =?
_______ °

Ответ: 118 °

Пояснение:
Определяем m∠CBE:
м∠CBE + m∠EBF = 180 °
м∠CBE + 62 ° = 180 °
м∠CBE = 180 ° — 62 °
м∠CBE = 118 °

Вопрос 15.
м∠ABF =?
_______ °

Ответ: 28 °

Пояснение:
Определяем m∠ABF
m∠ABF + m∠EBF = 90 °
м∠ABF + 62 ° = 90 °
м∠ABF = 90 ° — 62 °
м∠ABF = 28 °

Вопрос 16.
m∠CBA =?
_______ °

Ответ: 152 °

Пояснение:
Определяем m∠CBA
m∠CBA = m∠DBF = m∠DBE + m∠EBF
90 ° + 62 ° = 152 °
м∠CBA = 152 °

Вопрос 17.
Размер ∠A на 4 ° больше меры B.Эти два угла дополняют друг друга. Найдите размер каждого угла.
мА = __________ °
мБ = __________ °

Ответ:
мА = 47 °
мБ = 43 °

Пояснение:
Нам даны данные:
m∠A = m∠B + 4 °
m∠A + m∠B = 90 °
m∠B + 4 ° + m∠B = 90 °
2m∠B = 90 ° — 4 °
2m∠B = 86 °
m∠B = 86 ° / 2
m∠B = 43 °
m∠A = m∠B + 4 °
m∠A = 43 ° + 4 °
м∠A = 47 °

Вопрос 18.
Измерение ∠D в 5 раз больше меры ∠E.Два угла являются дополнительными. Найдите размер каждого угла.
мД = __________ °
мЭ = __________ °

Ответ:
mD = 150 °
mE = 30 °

Пояснение:
Нам даны данные
m∠D = 5 (m∠E)
m∠D + m∠E = 180 °
5 (m∠E) + m∠E = 180 °
6 m∠E = 180 °
м∠E = 180 ° / 6
м∠E = 30 °
м∠D = 5 (м∠E)
м∠D = 5 × 30 °
м∠D = 150 °

Стр. № 258

Вопрос 19.
Астрономия
Иногда астрономы используют угловые меры, разделенные на градусы, минуты и секунды.Один градус равен 60 минутам, а одна минута равна 60 секундам. Предположим, что ∠J и ∠K дополняют друг друга, а величина ∠J составляет 48 градусов, 26 минут, 8 секунд. Какова мера ∠K?
_______ ° _______ ‘_______”

Ответ: 41 ° 33 ‘52 ″

Пояснение:
Нам даны данные
м∠Дж + м∠К = 90 °
м∠Дж = 48 ° 26 ‘8 ″
90 ° — 48 ° 26′ 8 ″
89 ° 60 ‘- 48 ° 26 ‘8 ″
89 ° 59’60 ”- 48 ° 26′ 8 ″ = 41 ° 33 ’52 ″
Таким образом, размер ∠K составляет 41 ° 33′ 52 ″

H.О.

Фокус на мышлении высшего порядка

Вопрос 20.
Представляют проблемы реального мира
Железнодорожные пути пересекаются с дорогой, как показано. Город разрешит парковку под углом K, если угол K больше 38 °. Можно ли построить автостоянку под углом К? Почему или почему нет?

_______

Ответ:
m∠K = 180 ° — 50 ° — 90 ° = 40 °
Поскольку m∠K = 40 °> 38 °, парковка может быть построена.

Вопрос 21.
Обоснование рассуждений
Кендра говорит, что она может нарисовать ∠A и ∠B так, чтобы m∠A равнялось 119 °, а ∠A и ∠B — дополнительные углы.Ты согласен или несогласен? Объясните свои рассуждения.
_______

Ответ:
Нам даны данные
m∠A = 119 °
m∠A + m∠B = 90 °
m∠B = 90 ° — m∠A
= 90 ° — 119 ° = -29 °
Поскольку m∠B <0, Кендра ошибается, она не может рисовать углы.

Вопрос 22.
Вывод выводов
Если два угла дополняют друг друга, каждый угол называется дополнением другого. Если два угла являются дополнительными, каждый угол называется добавлением другого.
а. Предположим, что m∠A = 77 °.Какова мера дополнения к ∠A? Объяснять.
_______ °

Ответ: 77 °

Пояснение:
90 ° — (90 ° — m∠A) = 90 ° — (90 ° — 77 °)
90 ° — 77 ° = 13 °
77 °

Вопрос 22.
б. Какой вывод можно сделать о дополнении угла? Объяснять.
Тип ниже:
_____________

Ответ:
Дополнением к углу является сам угол:
90 ° — (90 ° — m∠A)
90 ° — 90 ° + m∠A

8.1 Подобные формы и чертежи в масштабе — Стр. № 259

Вопрос 1.
План дома имеет масштаб 1 дюйм: 4 фута. Длина и ширина каждой комнаты в реальном доме показаны в таблице. Заполните таблицу, найдя длину и ширину каждой комнаты на чертеже.

Тип ниже:
_____________

Ответ:

Таким образом, на каждые 4 фута в фактическом измерении на чертеже приходится 1 дюйм.

8.2 Геометрические чертежи

Вопрос 2.
Можно ли сформировать треугольник со сторонами 8 см, 4 см и 12 см?
______

Ответ:
Нам даны длины сторон
8 + 12 = 20> 4
4 + 12 = 16> 8
8 + 4 not> 12
Поскольку одно из неравенств не проверено, три заданные длины сторон не могут образовать треугольник.

Вопрос 3.
Треугольник имеет длину стороны 11 см и 9 см. Каким может быть значение третьей стороны, 20 см или 15 см?
______

Ответ: 15 см

Пояснение:
Нам даны длины сторон
11, 9
11 + 9 = 20 not> 20
Мы проверяем неравенства треугольника, если добавляем третью сторону 20 см
Поскольку одно из неравенств не проверено, три заданная длина сторон не может образовывать треугольник.
11, 9, 15
11 + 9 = 20> 15
11 + 15 = 26> 9
15 + 9 = 24> 11
Проверяем, что неравенства треугольника проверены, 15 может быть значением третьей стороны.

8,3 Поперечные сечения

Вопрос 4.
Назовите одно возможное поперечное сечение сферы.
Тип ниже:
_____________

Ответ: Круг
Одно из возможных поперечных сечений сферы — это круг.

Вопрос 5.
Назовите хотя бы две формы, которые являются поперечными сечениями цилиндра.
Тип ниже:
_____________

Ответ: Три возможных поперечных сечения цилиндра — это круг, эллипс и прямоугольник.

Регистрация основных вопросов

Вопрос 5.
Как можно моделировать геометрические фигуры для решения реальных задач?
Тип ниже:
_____________

Ответ: Вы можете моделировать геометрию для постройки зданий и небоскребов, а также магазинов.

8.4 Угловые отношения

Вопрос 6.
∠BGC и ∠FGE — _____ углы, поэтому m∠FGE = _____

_____ °

Ответ: ∠BGC и ∠FGE — вертикальные углы, поэтому m∠FGE = m∠BGC = 90 ° — 40 ° = 50 °

Вопрос 7.
Предположим, вы знаете, что ∠S и ∠Y дополняют друг друга и что m∠S = 2 (m∠Y) — 30 °. Найдите MY.
м? Y = _____ °

Ответ: 40 °

Пояснение:
m∠S + m∠Y = 90 °
m∠S = 2 (m∠Y) — 30 °
Заменим выражение m∠S из второго уравнения на первое, мы можем найти m∠Y
2 (m∠Y) — 30 ° + m∠Y = 90 °
3m∠Y = 90 ° + 30 °
3m∠Y = 120 °
m∠Y = 120 ° / 3
m∠Y = 40 °

Выбранный ответ — стр.260

Вопрос 1.
Какое число можно добавить к 15, чтобы получить сумму 0?
Опции:
а. -10
б. -15
с. 0
г. 15

Ответ: -15

Пояснение:
Число, которое мы добавляем к числу, чтобы получить нулевую сумму, является его противоположностью. В любом случае мы должны добавить -15 к 15.
15 + (-15) = 0
Таким образом, правильный ответ — вариант B.

Вопрос 2.
Ученики рисуют задник для школьного спектакля. Фон имеет ширину 15 футов и высоту 10 футов.Каждые 16 дюймов на масштабном чертеже представляют 5 футов на заднем плане. Какова площадь чертежа в масштабе?
Опции:
а. 150 в ²
б. 6 в ²
с. 3096
г. 1536 в ²

Ответ: 1536 в ²

Пояснение:
Нам даны размеры l и w фона и масштаб чертежа:
l = 15 футов
w = 10 футов
16 дюймов: 5 футов
16 дюймов / 5 футов = (16 дюймов ÷ 5 ) / (5 футов ÷ 5) = 3,2 дюйма / 1 фут
l1 = 15 × 3.2 = 48 дюймов
w1 = 10 × 32 = 320 дюймов
l1 × w1 = 48 × 32 = 1536 квадратных дюймов
Таким образом, правильный ответ — вариант D.

Вопрос 3.
Размер двух сторон треугольника составляет 8 см и 12 см. Что из перечисленного НЕ МОЖЕТ быть мерой третьей стороны?
Опции:
а. 4
г. 12
г. 8
г. 16

Ответ: 4 см

Пояснение:
Даны две стороны треугольника
a. 4
4 + 8 не> 12
б. 12
12 + 8> 12
12 + 12> 8
c.8
8 + 8> 12
8 + 12> 12
д. 16
8 + 12> 16
8 + 16> 12
12 + 16> 8
Таким образом, единственное измерение, которое не может быть мерой третьей стороны треугольника, составляет 4 см.
Таким образом, правильный ответ — вариант А.

Вопрос 4.
Поперечное сечение — это пересечение трехмерной фигуры и _____.
Опции:
а. пункт
б. самолет
c. линия
д. набор

Ответ: Самолет

Пояснение:
Поперечное сечение — это взаимодействие трехмерной фигуры и плоскости.
Таким образом, правильный ответ — вариант Б.

Для 5–6 используйте диаграмму.

Вопрос 5.
Каков показатель ∠BFC?
Опции:
а. 18
г. 108
г. 72
г. 144

Ответ: 108 °

Пояснение:
∠BFC + ∠BFA = 180 °
∠BFC + 72 ° = 180 °
∠BFC = 180 ° — 72 °
∠BFC = 108 °
Углы ∠BFC и ∠BFA являются дополнительными. Определяем ∠BFC.
Таким образом, правильный ответ — вариант Б.

Вопрос 6.
Что описывает отношения между ∠BFA и ∠CFD?
Опции:
а. прилегающие углы
б. дополнительные углы
c. дополнительные уголки
d. вертикальные углы

Ответ: вертикальные углы

Пояснение:
Углы ∠BFA и ∠CFD являются вертикальными углами, потому что они представляют собой противоположные углы, образованные на пересечении двух прямых.
Таким образом, правильный ответ — вариант D.

Вопрос 7.
Вся одежда уценена на 15%. Какое выражение представляет новую розничную цену?
Опции:
а.0,85x
б. 1.15x
c. 1.85x
г. 0,15 х

Ответ: 0,85x

Пояснение:
x = начальная цена
Поскольку цена снизилась на 15%, новая цена будет уменьшена на 15/100 x
x — 0,15x = 0,85x
Таким образом, правильный ответ — вариант A.

Мини-задачи

Вопрос 8.
Ира построила модель Великой пирамиды в Египте для школьного проекта. Великая пирамида имеет квадратное основание со сторонами длиной 756 футов. Высота Великой пирамиды 481 фут.Ира построил свою модель пирамиды в масштабе 1 дюйм: 20 футов.
а. Какова длина каждой стороны основания пирамиды Иры?
_____ в

Ответ: 37,8 дюйма
Мы вычисляем количество дюймов, соответствующее 1 футу, исходя из фактических размеров:
1 дюйм / 20 фут = (1 дюйм ÷ 20) / (20 футов ÷ 20) = 0,05 дюйма / 1 фут.
0,05 дюйма на 1 фут.
Определяем длину основания пирамиды Иры:
756 × 0,05 = 37,8 дюйма

Вопрос 8.
б. Какова площадь основания пирамиды Иры?
_____ квадратных дюймов

Ответ: 1428.84 квадратных дюйма

Пояснение:
Определяем площадь основания пирамиды Иры:
37,8 × 37,8 = 1428,84 квадратных дюйма.

Вопрос 8.
c. Какова высота пирамиды Иры?
_____ в

Ответ:
Определяем высоту пирамиды Иры:
481 × 0,05 = 24,05 дюйма

Вопрос 8.
г. Ира построила свою модель, используя поперечные сечения, вырезанные параллельно основанию. Какой формы было каждое поперечное сечение?
Тип ниже:
____________

Ответ: Поперечные сечения, параллельные основанию, имеют форму квадрата.

Заключение:

Поэтому подготовьте своих детей, заставив их попрактиковаться в тесте с помощью Go Math Grade 7 Answer Key Глава 8 Моделирование геометрических фигур. Получите ответы на все вопросы с помощью простых приемов для всех глав Go Math Answer Key.