Контрольная работа № 1 по теме «Числовая окружность»
Контрольная работа № 1 (1 час)
Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Вариант 1
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 1, 3, –1;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
4. Задайте аналитически и постройте график функции у которой
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция убывает на R. Решите неравенство
Вариант 2
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках –4, –2, 0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
Сделайте чертёж.
4. Задайте аналитически и постройте график функции у которой
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция возрастает на R. Решите неравенство
Вариант 3
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках –1, 0, 2, 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа
 Сделайте чертёж.
Сделайте чертёж.4. Задайте аналитически и постройте график функции у которой
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция убывает на R. Решите неравенство
Вариант 4
1. Задает ли указанное правило функцию
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках –6, –3, 0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге PB. Сделайте чертёж.
Сделайте чертёж.
4. Задайте аналитически и постройте график функции у которой
5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.
6. Известно, что функция возрастает на R. Решите неравенство
Рекомендации по оцениванию контрольной работы
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума – до первой черты, задания среднего уровня – между первой и второй чертой, задания уровня выше среднего – после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума – оценка «3»; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) – оценка «4»; за успешное выполнение заданий всех трех уровней – оценка «5».
Решение контрольной работы
Вариант 1
1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.
В случае
условия не соблюдаются: f(0) = 0 и f(0) = –1.
б)
Контрольная работа по алгебре 10 класс на тему Числовая окружность
Контрольная работа № 1 (Алгебра, 10 класс)
1 вариант
Дана функция :
а) найдите область определения функции;
б) вычислите значения функции в точках -2; 1; 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на чётность.
Задайте аналитически и постройте график функции, у которой
Найдите функцию, обратную функции Постройте на одном чертеже графики данной и полученной функций.
На числовой окружности взяты точки MN( ). Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
Контрольная работа № 1 (Алгебра, 10 класс)
2 вариант
Дана функция :
а) найдите область определения функции;
б) вычислите значения функции в точках -3; 2; 6;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на чётность.
Задайте аналитически и постройте график функции, у которой
Найдите функцию, обратную функции Постройте на одном чертеже графики данной и полученной функций.
На числовой окружности взяты точки MN( ). Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
______________________________________________________________________
Контрольная работа № 1 (Алгебра, 10 класс)
3 вариант
Дана функция :
а) найдите область определения функции;
б) вычислите значения функции в точках -1; 0; 10;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на чётность.
Задайте аналитически и постройте график функции, у которой
Найдите функцию, обратную функции Постройте на одном чертеже графики данной и полученной функций.
На числовой окружности взяты точки MN( ). Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
Контрольная работа № 1 (Алгебра, 10 класс)
4 вариант
Дана функция :
а) найдите область определения функции;
б) вычислите значения функции в точках -0,75; 0; 3;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на чётность.
Задайте аналитически и постройте график функции, у которой
Найдите функцию, обратную функции Постройте на одном чертеже графики данной и полученной функций.
На числовой окружности взяты точки MN( ). Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
Сделайте чертёж.
______________________________________________________________________
Контрольная работа № 1 (Алгебра, 10 класс)
5 вариант
Дана функция :
а) найдите область определения функции;
б) вычислите значения функции в точках ; 1; –3,5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на чётность.
Задайте аналитически и постройте график функции, у которой
Найдите функцию, обратную функции Постройте на одном чертеже графики данной и полученной функций.
На числовой окружности взяты точки MN(2 ). Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
______________________________________________________________________
Контрольная работа № 1 (Алгебра, 10 класс)
6 вариант
Дана функция :
а) найдите область определения функции;
б) вычислите значения функции в точках ; 7; –1;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на чётность.
Задайте аналитически и постройте график функции, у которой
Найдите функцию, обратную функции Постройте на одном чертеже графики данной и полученной функций.
На числовой окружности взяты точки MN( ). Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.
______________________________________________________________________
| 1. |
Единичная окружность, квадранты
Сложность: среднее |
1 |
2.
|
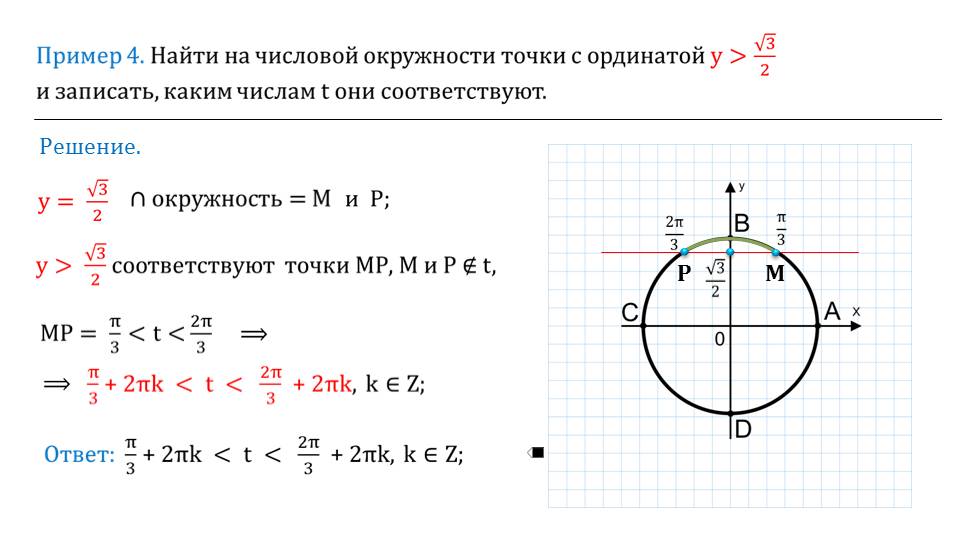
Числовая окружность
Сложность: лёгкое |
5 |
| 3. |
Определение чисел, соответствующих точке
Сложность: лёгкое |
1 |
4.
|
Соответствие точек числовой окружности числам
Сложность: лёгкое |
1 |
| 5. |
Определение координат точек
Сложность: лёгкое |
1 |
6.
|
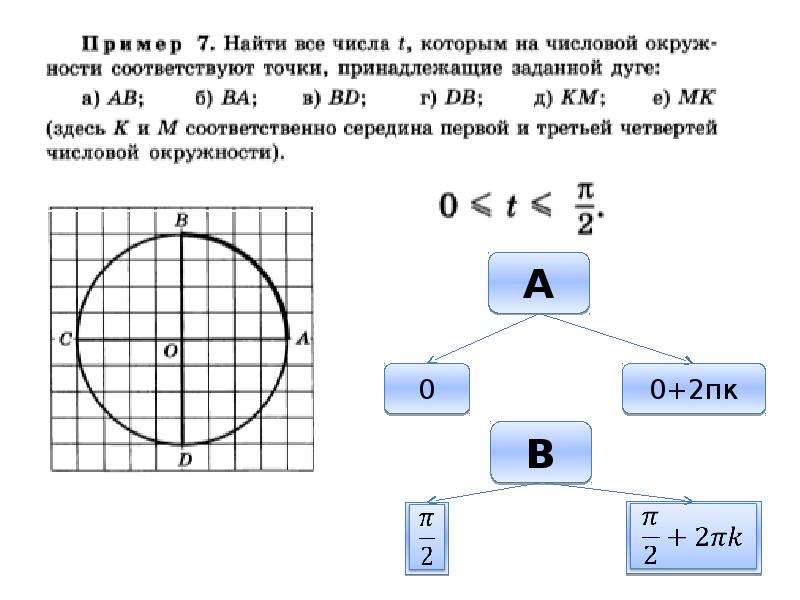
Длина дуги на числовой окружности, разделённой точками
Сложность: среднее |
3 |
| 7. |
Длина дуги на числовой окружности
Сложность: среднее |
1 |
8.
|
Симметрия точек на числовой окружности
Сложность: среднее |
2 |
| 9. |
Принадлежность точек числовой окружности
Сложность: среднее |
1 |
10.
|
Расположение точек на числовой окружности
Сложность: сложное |
3 |
| 11. |
Сравнение абсциссы и ординаты точки
Сложность: сложное |
3 |
12.
|
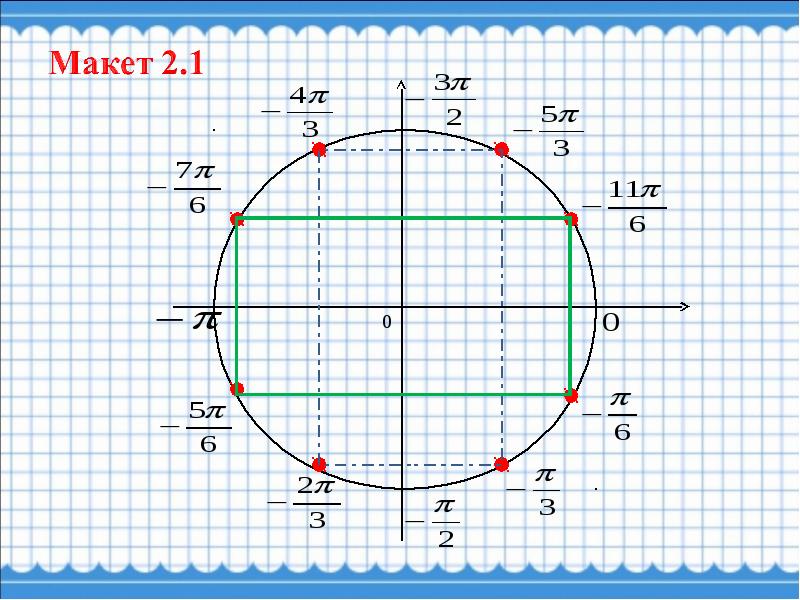
Соответствие между числами и точками числовой окружности
Сложность: сложное |
4 |
Числовая окружность в координатной плоскости — урок. Алгебра, 10 класс.
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок.
Начальная точка числовой окружности \(A\) совмещена с точкой \((1;0)\).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты.
Найдём сначала координаты тех точек координатной плоскости, которые получены на макетах числовой окружности.
Точка Mπ4 — середина \(I\) четверти. Опустим перпендикуляр \(MP\) на прямую \(OA\) и рассмотрим треугольник \(OMP\). Так как дуга \(AM\) составляет половину дуги \(AB\), то ∡MOP=45°.
Значит, треугольник \( OMP \) — равнобедренный прямоугольный треугольник и \(OP = MP\), т. е. у точки \(M\) абсцисса и ордината равны: \(x = y\).
Так как координаты точки \(M(x;y)\) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений: x2+y2=1x=y |
Подставив \(x\) вместо \(y\) в первое уравнение системы, получим следующее решение:
x2+x2=1;2×2=1;x2=12;x=12=22;y=x=22.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π4, будут Mπ4=M22;22.
Аналогично можно получить координаты и других точек первого макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
| \(0\) | π4 | π2 | 3π4 | π | 5π4 | 3π2 | 7π4 | 2π |
Абсцисса \(x\) | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) | 22 | \(1\) |
Ордината \(y\) | \(0\) | 22 | \(1\) | 22 | \(0\) | −22 | \(-1\) | −22 | \(0\) |
Рассуждаем аналогично для точки \(M\), если теперь она соответствует числу π6.
Треугольник \(MOP\) прямоугольный. Так как дуга \(AM\) составляет третью часть дуги \(AB\), то ∡MOP=30°.
Катет \(MP\) лежит против угла \(30\) градусов в прямоугольном треугольнике, значит, равен половине гипотенузы, т. е. ордината точки \(M\) равна MP=12;y=12 |
Абсциссу \(x\) точки \(M\) найдём, решив уравнение:
x2+y2=1;
x2=1−122=1−14=34;x=32.
При решении учитываем, что абсцисса точки \(M\) положительна.
Получили, что координаты точки \(M\), соответствующей числу π6, будут Mπ6=M32;12.
Аналогично можно получить координаты и других точек второго макета числовой окружности, учитывая только знаки координат в каждой четверти.
Полученные результаты запишем в таблицу.
Точка окружности |
π6 | π3 | 2π3 | 5π6 | 7π6 | 4π3 | 5π3 | 11π6 | |
Абсцисса \(x\) | 32 | 12 | −12 | −32 | −32 | −12 | 12 | 32 |
Ордината \(y\) | 12 | 32 | 32 | 12 | −12 | −32 | −32 | −12 |
Самостоятельная работа по математике (числовая окружность на координатной плоскости) для 10-го класса от школы Пифагора в 2018 году
Ответы
Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 275 | 81 | Загрузок |
|---|---|---|---|
| Добавил | Гость | 30.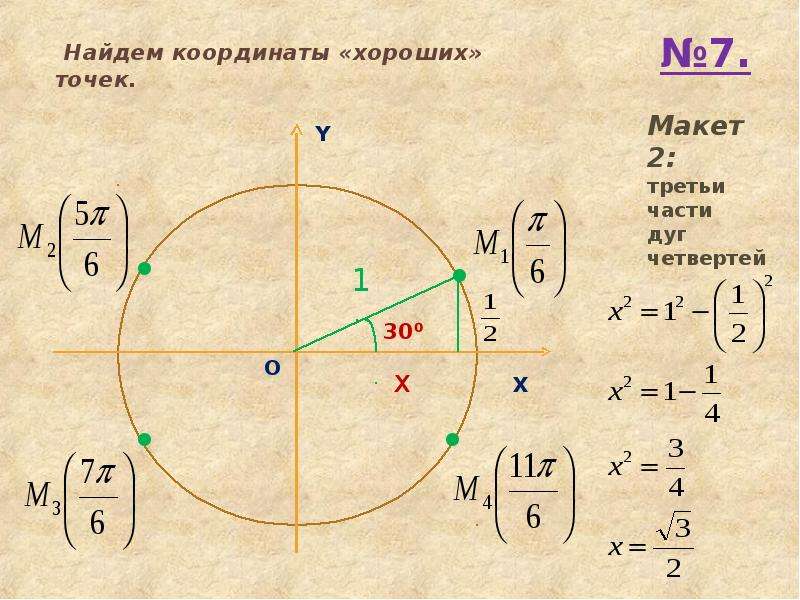 11.2019 11.2019 | Дата |
| День | Суббота | 22:09 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: школа Пифагора — уроки в школе
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено.
Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Справочные материалы
Загрузка формул…
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ
Урок:
Числовая окружность
на координатной пЛОСКОСТИ
УМК Алгебра и начала математического анализа, 10-11 классы. В 2. Ч.1. Учебник для общеобразовательных учреждений (базовый уровень) /А.Г. Мордкович. – 10-еизд., стер.- М.: Мнемозина,2013. Ч.2. Задачник для общеобразовательных учреждений (базовый уровень) /[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10-еизд., стер.- М.: Мнемозина,2013.
Уровень обучения. Базовый
Цели: ввести понятие модели числовой окружности в декартовой и
криволинейной системе координат; формировать умение находить декартовы
координаты точек числовой окружности и выполнять обратное действие: зная
декартовы координаты точки, определять её числовое значение на числовой
окружности.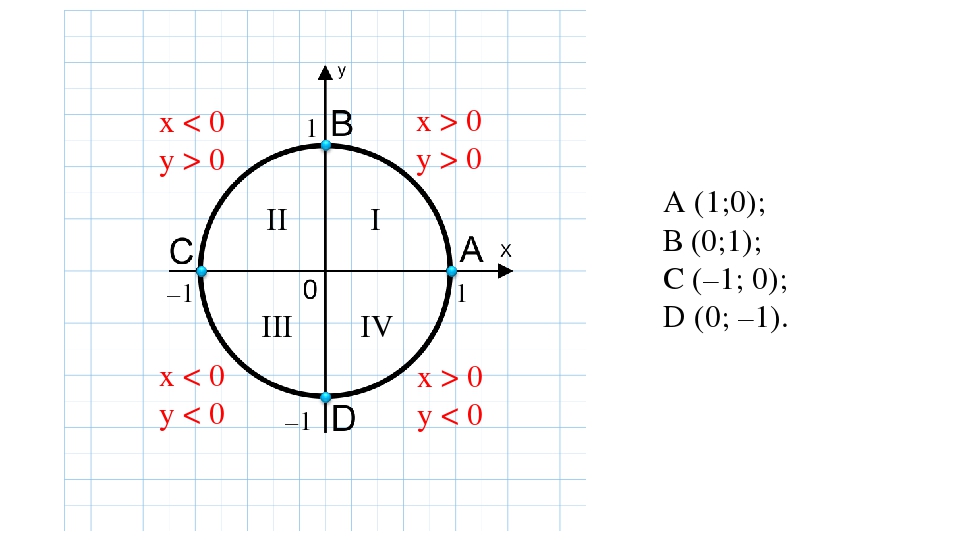
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите координаты точек плоскости:
2. Назовите число, соответствующее заданной точке на числовой окружности.
III. Объяснение нового материала.
1. Объяснение проводи согласно пункту учебника. Разместив числовую окружность в декартовой системе координат, подробно разбираем свойства точек числовой окружности, находящихся в различных координатных четвертях.
Точка M(π4) середина I четверти.
Опустим перпендикуляр MP на прямую OA и рассмотрим треугольник OMP.
Так как дуга AM составляет половину дуги AB, то ∡MOP=45°
Значит, треугольник OMP — равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M
абсцисса и ордината равны: x=y.
Так как координаты точки M(x;y) удовлетворяют уравнению числовой окружности x2+y2=1, то для их нахождения нужно решить систему уравнений:
x2+x2=1
2x2=1
x2=1/2
у=x=2√2
Получили, что координаты точки M, соответствующей числу π/4 будут M(π/4)=M(2√2;2√2)
Треугольник MOP прямоугольный. Так как дуга AM составляет третью часть дуги AB, то ∡MOP=30°.
Катет MP лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен
половине гипотенузы, т.е. ордината точки M равна
MP=1/2 y=1/2
Абсциссу x точки M найдём, решив уравнение:
x2+y2=1
x2=1−(1/2)2=1−1/4=3/4 x=3√2
При решении учитываем, что
абсцисса точки M положительна.
Получили, что координаты точки M, соответствующей числу π/6 будут M(π/6)=M(3√2;1/2)
2. Методическая «игра» – отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М(t) к М (х; у). (презентация слайд 1)
3. Методическая «игра» – отыскание знаков координат «плохих» точек числовой окружности. Если, например, М(2) = М (х; у), то х < 0; у > 0. (презентация слайд 2)
IV. Формирование умений и навыков.
1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).
Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.
Решение:
№ 5.1 (а).
2. № 5.4 (а; б), № 5.5 (а; б).
Эта
группа заданий направлена на формирование умений находить криволинейные
координаты точки по её декартовым координатам.
Решение:
№ 5.5 (б).
3. № 5.10 (а; б).
Данное упражнение направлено на формирование умения находить декартовы координаты «плохих» точек.
V. Итоги урока.
Вопросы учащимся:
– Что собой представляет модель – числовая окружность на координатной плоскости?
– Как, зная криволинейные координаты точки на числовой окружности, найти её декартовы координаты и наоборот?
Домашнее задание: № 5.1 (в; г) – 5.5 (в; г), № 5.10 (в; г).
Кругов: Круги на координатной плоскости Учебное пособие
Мы можем описать окружность в координатной плоскости с помощью уравнения. Но прежде чем мы туда поедем, мы немного упростим задачу. Начнем с рассмотрения круга с центром в начале координат и радиусом 5 единиц. Вот он, на координатной плоскости.
Обратите внимание, что круг проходит через точки (5, 0), (0, 5), (-5, 0) и (0, -5).
Мы пытаемся найти уравнение, связывающее координаты общей точки на окружности ( x , y ).Обратите внимание, что по природе декартовой системы мы можем легко нарисовать прямоугольный треугольник на основе любой точки ( x , y ).
Одна нога горизонтальная и имеет длину x . Другая нога вертикальная и имеет длину х . Гипотенуза соединяет ( x , y ) и начало координат. Если ( x , y ) находится на окружности, а центр окружности находится в начале координат, тогда гипотенуза имеет длину, равную радиусу окружности.В данном случае это 5 единиц.
Пифагор говорит нам, что x 2 + y 2 = 5 2 .
Но радиус круга с центром в начале координат не обязательно должен быть 5 единиц. Это могло быть 6, 7, 50 или даже миллион единиц. Покроем все наши базы и назовем это r единиц. Итак, у нас есть уравнение x 2 + y 2 = r 2 .
Вот и все.Теперь у нас есть уравнение, которое связывает координаты x и y любой точки на окружности с радиусом r с центром в начале координат. Разве это не было просто?
Вы можете заметить, что мы оставили члены x и y на одной стороне уравнения, вместо того, чтобы решать для y , как мы обычно делаем для линейных уравнений. (Помните те, что из алгебры?) Формула со всеми переменными на одной стороне называется неявно , а формула, которая была решена для одной переменной в терминах другой (например, y = mx + b ) называется явным .
Давайте попробуем решить наше неявное уравнение для y . В итоге вы получите беспорядочный плюс-минус квадратный корень. Мы будем придерживаться красивого, чистого и простого уравнения, которое у нас есть. Кроме того, это семейный сайт. Мы не хотим здесь никакого явного содержания.
Пример задачи
Какова формула для круга с центром в начале координат и окружностью 25,1 дюйма?
Мы знаем, что формула для круга: x 2 + y 2 = r 2 .Все, что нам нужно для завершения, это длина радиуса, которую мы можем найти с помощью окружности. Если мы просто вспомним формулу C = 2π r , мы можем вставить 25,1 дюйма для C и решить для r ≈ 4 дюйма. Таким образом, наше окончательное уравнение: x 2 + y 2 = 4 2 или x 2 + y 2 = 16.
Наша формула определенно хороша, чистый и простой, но это полезно, только если наш круг находится в начале координат.Как мы можем описать такой круг за пределами Сиднея?
Мы все еще можем нарисовать прямоугольный треугольник, поэтому Пифагор все еще может нам помочь. Гипотенуза по-прежнему имеет длину, равную радиусу окружности, поскольку ее концы — это центр окружности и точка на окружности. Мы знаем, что радиус Сиднейского круга составляет 5 км.
Но длины ножек уже не просто старые x и y . Мы должны скорректировать «смещение» центра круга от начала координат.Таким образом, длины горизонтальных и вертикальных сторон нашего прямоугольного треугольника равны x -4 и y -3 соответственно. Теперь мы можем подставить эти длины в теорему Пифагора, чтобы получить ( x -4) 2 + ( y -3) 2 = 5 2 .
И вот наша формула для Сиднейского круга с x и y в километрах (потому что австралийцы, как и весь остальной мир, используют метрическую систему).
В общем случае неявная формула для окружности с центром ( h , k ) и радиусом r :
( x — h ) 2 + ( y — k ) 2 = r 2
Теперь у нас есть вся информация, необходимая для определения любого круга в красивой компактной формуле.Вы можете использовать его для описания чего угодно, от орбиты космического корабля до печенья на листе печенья. Совершенно верно: математическая технология, необходимая для вывода спутника на орбиту, не более сложна, чем та, которая необходима для изготовления сникердудлей дома. Более менее.
Пример задачи
Каково уравнение для окружности с центром (6, -2) и радиусом 18 единиц?
Неявная формула для круга с центром ( h , k ) и радиусом r имеет вид ( x — h ) 2 + ( y — k ) 2 = r 2 .Нам даны центр и радиус, поэтому все, что нам нужно сделать, это вставить информацию в нужные места. У нас должно получиться ( x -6) 2 + ( y — (-2)) 2 = 18 2 , или ( x -6) 2 + ( y + 2) 2 = 324 в упрощенном виде.
Как построить график круга
- Образование
- Математика
- Исчисление
- Как построить график круга
Первое, что вам нужно знать, чтобы изобразить уравнение круга, — это место на плоскости центр расположен.Уравнение круга отображается как
Это называется формой с центральным радиусом (или стандартной формой), потому что она дает вам обе части информации одновременно. Значения h и v представляют центр окружности в точке ( h , v ), а r обозначают радиус. В частности, h представляет собой горизонтальное смещение — насколько далеко влево или вправо центр окружности падает от оси y .Переменная v представляет вертикальное смещение — насколько далеко выше или ниже центр падает от оси x . Вы можете отсчитывать от центра r единиц (радиус) по горизонтали в обоих направлениях и по вертикали в обоих направлениях. Это даст вам четыре разных точки, все на одинаковом расстоянии от центра. Соедините эти четыре точки с лучшей кривой, которую вы можете нарисовать, чтобы получить график круга.
Центр в начале координат
Самый простой круг для построения графика имеет центр в начале координат (0, 0).Поскольку и h, , и v равны нулю, они могут исчезнуть, и вы можете упростить стандартное уравнение круга, чтобы оно выглядело как
Например, чтобы построить круг
выполните следующие действия:
Осознайте, что центр круга находится в начале координат (№ h и v ), и поместите эту точку там.
Рассчитайте радиус, решив для r .
Установить r -квадрат = 16.В этом случае получается r = 4.
Нанесите точки радиуса на координатную плоскость.
Вы отсчитываете по 4 в каждом направлении от центра (0, 0): влево, вправо, вверх и вниз.
Соедините точки, чтобы построить круг, используя плавную круглую кривую.
На рисунке показан этот круг на плоскости.
Центр от начала координат
Построить график круга в любом месте координатной плоскости довольно просто, если его уравнение представлено в форме центрального радиуса.Все, что вам нужно сделать, это построить центр круга в точке ( h , k ), а затем отсчитать от центра r единиц в четырех направлениях (вверх, вниз, влево, вправо). Затем соедините эти четыре точки красивым круглым кружком. К сожалению, хотя построить круги в начале координат намного проще, очень немногие из них столь же просты и понятны, как эти. В pre-calc вы работаете с преобразованием графиков всех форм и размеров (для вас это не новость, правда?). К счастью, все эти графики построены по одному и тому же шаблону для горизонтального и вертикального смещения, поэтому вам не нужно запоминать множество правил.
Не забудьте поменять знак у h и v внутри скобок в уравнении. Это необходимо, потому что h и v находятся внутри символов группировки, а это означает, что сдвиг происходит противоположно тому, что вы могли бы подумать.
Например, чтобы построить график уравнения
Найдите центр окружности из уравнения ( h , v ).
Поместите центр круга в точку (3, –1).
Рассчитайте радиус, решив для r .
Нанесите точки радиуса на координатную плоскость.
Отсчитайте 5 единиц вверх, вниз, влево и вправо от центра в (3, –1). Это означает, что у вас должны быть точки (8, –1), (–2, –1), (3, –6) и (3, 4).
Соедините точки с графиком круга с круглой плавной кривой.
Рисунок дает вам визуальное представление об этом круге.
Unit Circle | Ресурсы Wyzant
Автор: Шу Джен В.
На приведенном выше рисунке показан график единичной окружности на оси координат X — Y.
Из графика видно, что единичная окружность определяется как имеющая радиус (r) = 1.
При переходе от квадранта I к квадранту IV против часовой стрелки координаты на оси единичного круга следующие:
(1, 0), (0, 1), (-1, 0) и (0, -1)
Это важно помнить, когда мы определяем координаты X и Y вокруг единичной окружности.Единичный круг составляет 360 °. На приведенном выше графике единичный круг разделен на 4 квадранта, которые делят единичный круг на 4 равные части. Каждая деталь ровно 90 °.
Вопрос: Почему каждая секция / квадрант равен 90 °?
Также можно показать, что единичный круг состоит из четырех углов 90 °, что в сумме составляет 360 °:
Теперь мы собираемся разделить единичный круг на углы 30 °, 45 ° и 60 °. Это особые углы, которые очень важно запомнить.
Начнем с квадранта I, так как это основы, а координаты X и Y положительны. Увидеть ниже.
Затем мы переходим к квадранту II, который начинается с 90 ° и продолжается до 180 °. На диаграмме ниже каждый угол в квадранте II составляет 30 °, 45 ° и 60 ° внутри этого квадранта. Однако, поскольку углы имеют точку отсчета на отметке 0 ° в квадранте I, они маркируются в соответствии с углом, который они составляют от квадранта I к квадранту II.Например, 45 ° в квадранте II обозначено как 135 °, потому что это угол, который он составляет от 0 ° в квадранте I до угла 45 ° в квадранте II. Кроме того, из графика видно, что угол 45 ° в квадранте II попадает между 90 ° и 180 ° на единичной окружности. Это делается для углов 30 °, 45 ° и 60 ° в каждом квадранте. Увидеть ниже.
График ниже показывает градусы единичного круга во всех 4-х квадрантах от 0 ° до 360 °.
Теперь мы добавим радианы к единичной окружности. Радианы — это стандартная единица измерения углов.
Формула для вычисления радианов:
Мы будем вычислять радианы для каждого градуса на единичной окружности, отмеченной выше.
| Градусов | Формула | Радианы (упрощенные) |
| 0 ° | (0 °) * ( π / 180 ° ) | 0 |
| 30 ° | (30 °) * ( π / 180 ° ) = 30π / 180 ° радиан | π / 6 |
| 45 ° | (45 °) * ( π / 180 ° ) = 45π / 180 ° радиан | π / 4 |
| 60 ° | (60 °) * ( π / 180 ° ) = 60π / 180 ° радиан | π / 3 |
| 90 ° | (90 °) * ( π / 180 ° ) = 90π / 180 ° радиан | π / 2 |
| 120 ° | (120 °) * ( π / 180 ° ) = 120π / 180 ° радиан | 2π / 3 |
| 135 ° | (135 °) * ( π / 180 ° ) = 135π / 180 ° радиан | 3π / 4 |
| 150 ° | (150 °) * ( π / 180 ° ) = 150π / 180 ° радиан | 5π / 6 |
| 180 ° | (180 °) * ( π / 180 ° ) = 180π / 180 ° радиан | π / 1 |
| 210 ° | (210 °) * ( π / 180 ° ) = 210π / 180 ° радиан | 7π / 6 |
| 225 ° | (225 °) * ( π / 180 ° ) = 225π / 180 ° радиан | 5π / 4 |
| 240 ° | (240 °) * ( π / 180 ° ) = 240π / 180 ° радиан | 4π / 3 |
