1 вариант. 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и . 3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции. 4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и . | 2 вариант 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и 3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. 4. * В треугольнике МNK О – точка пересечения медиан, . Найдите число k. | 1 вариант. 1. Найдите координаты и длину вектора , если . 2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2). 3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что Δ— равнобедренный; б) Найдите высоту, проведённую из вершины М. 4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ). | 2 вариант. 1). Найдите координаты и длину вектора , если . 2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что Δ— равнобедренный; б) Найдите биссектрису, проведённую из вершины С. 4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ). | 1 вариант
В = 600, ВС = Найдите АС.
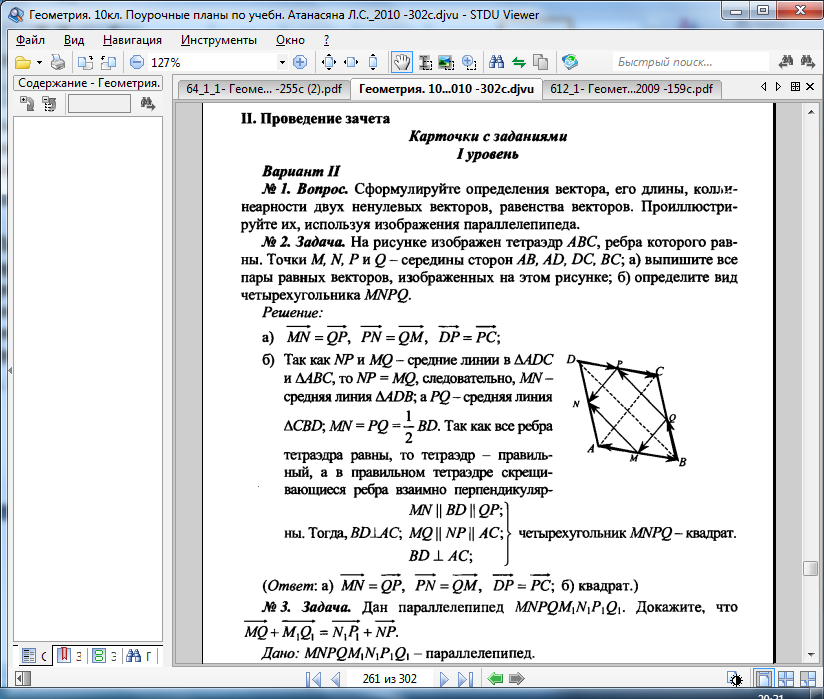
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
| 2 вариант
D = 450, СЕ =Найдите DE.
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
| 1 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. 3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности. | 2 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см. 2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность. | 1 вариант 1. Начертите ромб АВСD. Постройте образ этого ромба: а) при симметрии относительно точки С; б) при симметрии относительно прямой АВ; в) при параллельном переносе на вектор ; г) при повороте вокруг точки D на 600 по часовой стрелке. 2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр. 3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой. | 2 вариант 1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма: а) при симметрии относительно точки D; б) при симметрии относительно прямой CD; в) при параллельном переносе на вектор ; г) при повороте вокруг точки А на 450 против часовой стрелки. 2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей. 3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой. |
Контрольная работа по геометрии «Векторы», ФГОС
1 вариант
Найдите координаты и длину вектора , если
Найдите координаты вектора , если A(1,-3), B(0,-6)
Начертите два неколлинеарных вектора и . Постройте
Найдите координаты вектора , если , если
В трапеции основания равны 9 и 14. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(-1,2), проходящей через точку B(0,1)
2 вариант
Найдите координаты и длину вектора , если
Найдите координаты вектора , если A(6,-4), B(1,-6)
Начертите два неколлинеарных вектора и . Постройте
Найдите координаты вектора , если , если
В трапеции основания равны 12 и 7. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(2,-3), проходящей через точку B(-1,-2)
1 вариант
Найдите координаты и длину вектора , если
Найдите координаты вектора , если A(1,-3), B(0,-6)
Начертите два неколлинеарных вектора и . Постройте
Постройте
Найдите координаты вектора , если , если
В трапеции основания равны 9 и 14. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(-1,2), проходящей через точку B(0,1)
2 вариант
Найдите координаты и длину вектора , если
Найдите координаты вектора , если A(6,-4), B(1,-6)
Начертите два неколлинеарных вектора и . Постройте
Найдите координаты вектора , если , если
В трапеции основания равны 12 и 7. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(2,-3), проходящей через точку B(-1,-2)
1 вариант
Найдите координаты и длину вектора , если
Найдите координаты вектора , если A(1,-3), B(0,-6)
Начертите два неколлинеарных вектора и . Постройте
Найдите координаты вектора , если , если
В трапеции основания равны 9 и 14. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(-1,2), проходящей через точку B(0,1)
2 вариант
Найдите координаты и длину вектора , если
Найдите координаты вектора , если A(6,-4), B(1,-6)
Начертите два неколлинеарных вектора и . Постройте
Постройте
Найдите координаты вектора , если , если
В трапеции основания равны 12 и 7. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(2,-3), проходящей через точку B(-1,-2)
Контрольная работа № 1. Векторы | |
1 вариант. 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и . 3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции. 4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и . | 2 вариант 1. Начертите два неколлинеарных вектора и . а) ; б) 2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и 3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции. 4. * В треугольнике МNK О – точка пересечения медиан, . Найдите число k. |
Контрольная работа № 2. Метод координат. | |
1 вариант. 1. Найдите координаты и длину вектора , если . 2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2). 3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите высоту, проведённую из вершины М. 4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ). | 2 вариант. 1). Найдите координаты и длину вектора , если . 2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите биссектрису, проведённую из вершины С. 4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ). |
Контрольная работа № 3. Соотношения между сторонами и углами треугольника. | |
1 вариант
В = 600, ВС = Найдите АС.
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
| 2 вариант
D = 450, СЕ =Найдите DE.
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
|
Контрольная работа № 4. Длина окружности и площадь круга. | |
1 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. 3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности. | 2 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см. 2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность. |
Контрольная работа № 5. Движения. | |
1 вариант 1. Начертите ромб АВСD. Постройте образ этого ромба: а) при симметрии относительно точки С; б) при симметрии относительно прямой АВ; в) при параллельном переносе на вектор ; г) при повороте вокруг точки D на 600 по часовой стрелке. 2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр. 3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой. | 2 вариант 1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма: а) при симметрии относительно точки D; б) при симметрии относительно прямой CD; в) при параллельном переносе на вектор ; г) при повороте вокруг точки А на 450 против часовой стрелки. 2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей. 3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой. |
Контрольная работа по геометрии. 9 класс. Тема: Векторы
- Подробности
- Категория: Контрольные работы по геометрии.
 9 класс
9 класс
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ
9 КЛАСС
ТЕМА: ВЕКТОРЫ
ВАРИАНТ 1
1. ABCD — параллелограмм,
K принадлежит ВС, L принадлежит AD, BK : KC = 2 : 3, AL : LD = 3 : 2. Найдите разложение вектора
по неколлинеарным векторам
Ответ:
2. Дана трапеция ABCD с основаниями AD = 20 и ВС = 8, О — точка пересечения диагоналей. Разложите вектор
по векторам
Ответ:
3. Диагонали ромба АС = а, BD = b. Точка К принадлежит BD и ВК : KD = 1 : 3. Найдите величину
Ответ:
4. В равнобедренной трапеции острый угол равен 60
Ответ: 24 см.
5. В прямоугольнике ABCD известно, что AD = a, DC = b, O — точка пересечения диагоналей. Найдите величину
Найдите величину
Ответ:
ВАРИАНТ 2
1. ABCD — параллелограмм,
К принадлежит ВС, L принадлежит AD, BK : KC = 3 : 4, AL : LD = 4 : 3. Найдите разложение вектора
по неколлинеарным векторам
Ответ:
2. Дана трапеция ABCD с основаниями AD = 15 и ВС = 10, О — точка пересечения диагоналей. Разложите вектор
по векторам
Ответ:
3. Диагонали ромба АС = а, BD = b. Точка К принадлежит АС и АК : КС = 2 : 3. Найдите величину
Ответ:
4. В равнобедренной трапеции острый угол равен 60°, боковая сторона равна 10 см, меньшее основание равно 14 см. Найдите среднюю линию трапеции.
Ответ: 19 см.
5. В прямоугольнике ABCD известно, что АВ = а, ВС = b, О — точка пересечения диагоналей. Найдите величину
Ответ:
9 класс Контрольная работа №1 Вариант 1
9 класс Контрольная работа №2(геометрия)
Вариант1(1уровень)
1. Напишите
уравнение окружности а)с центром в
точке О (2;3) и R=4,
б) с центром в начале
Напишите
уравнение окружности а)с центром в
точке О (2;3) и R=4,
б) с центром в начале
координат и R=5.
2.Даны точки А (2;5) и В (4;7). Найдите а) координаты точки С, если С- середина АВ;
б) координаты вектора АВ; в) расстояние между точками А и В.
3.Напишите уравнение прямой, проходящей через точки А (2;5) и В (4;7).
9 класс Контрольная работа №2(геометрия)
Вариант2(1уровень)
1.Напишите уравнение окружности а)с центром в точке О (3;2) и R=9, б) с центром в начале
координат и R=7.
2.Даны точки А (3;8) и В (5;6). Найдите а) координаты точки С, если С- середина АВ;
б) координаты вектора АВ; в) расстояние между точками А и В.
3.Напишите уравнение прямой, проходящей через точки А (3;8) и В (4;7).
9 класс Контрольная работа №2(геометрия)
Вариант1(2уровень)
1. Напишите
уравнение окружности : а)с центром в
точке О (2;3) и проходящей через точку
Напишите
уравнение окружности : а)с центром в
точке О (2;3) и проходящей через точку
А (0;4), б) с центром в начале координат и R=5.
2. Даны точки А (3;8), В (5;6) и С (-6;2) . Найдите: а) длину медианы АМ, б) координаты
вектора АС.
3. Напишите уравнение прямой, проходящей через точки А (-3;8) и В (4;7).
9 класс Контрольная работа №2(геометрия)
Вариант2(2уровень)
1.Напишите уравнение окружности : а)с центром в точке О (2;-3) и проходящей через точку
А (4;0), б) с центром в начале координат и R=9.
2. Даны точки А (3;-8), В (5;7) и С (-6;2) . Найдите: а) длину медианы ВМ, б) координаты
вектора АВ.
3. Напишите уравнение прямой, проходящей через точки А (-3;8) и В (-4;3).
9класс Контрольная работа №3 Вариант 1. Тема «Решение треугольников» 1. 2. В ΔАВС: АВ=8, ВС=5, В=60˚. Найдите: АС, А, С. 3. Найдите соsМ, соsL, cosK в ΔКLМ, если К(1;7), L(-2;4), M(2;0). 4. Найдите скалярное произведение векторов а и b, если |а|=9, |b|=10, a угол между ними равен 125˚. | 9класс Контрольная работа №3 Вариант 2. Тема «Решение треугольников» 1. В ΔАВС: ВС=, В=45˚, А=60˚. Найдите: АС, АВ, С. 2. В ΔАВС: АС=6, ВС=5, С=60˚. Найдите: АВ, А, В. 3. Найдите соsА, соsВ, cosС в ΔАВС, если А(3;9), В(0;6), С(4;2). 4. Найдите скалярное произведение векторов а и b, если |а|=8, |b|=5, a угол между ними равен 115˚. |
9класс Контрольная работа № 4 Вариант 1 Тема:
«Длина окружности. 1. Дуга в 150˚ имеет радиус 3см. Найдите длину этой дуги. 2. Периметр правильного треугольника, вписанного в окружность, равен 45см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность. 3. Найдите площадь круга и длину окружности, если площадь вписанного в неё квадрата равна 49см2. 4. Найдите длину окружности и площадь круга, если радиус равен 5,1см. | 9класс Контрольная работа № 4 Вариант 2 Тема: «Длина окружности. Площадь круга» 1. Найдите площадь кругового сектора, если градусная мера его дуги равна 120˚, а радиус круга равен 12см. 2. Периметр правильного шестиуголь-ника, вписанного в окружность, равен 48см. Найдите сторону квадрата, вписанного в ту же окружность. 3.
Найдите площадь круга и длину
окружности, если периметр вписанного
в неё квадрата равна 48см. 4. Найдите длину окружности и площадь круга, если радиус равен 3,6см. |
9 класс Контрольная работа Вариант 1 Тема: «Движения» 1)Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция а)при симметрии относительно прямой, содержащей боковую сторону АВ; б) при симметрии относительно точки, являющейся серединой боковой стороны СD в) при повороте вокруг точки А на угол, равныйDАВ, по часовой стрелке; г) при параллельном переносе на вектор . 2) Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О . Докажите, что ∆АВС= ∆А1В1С1 | 9 класс Контрольная работа Вариант 2 Тема: «Движения» 1)Дана
трапеция АВСD
с основаниями АD
и ВС. а) при симметрии относительно прямой, содержащей боковую сторону СD ; б) при симметрии относительно точки, являющейся серединой боковой стороны АВ в) при повороте вокруг точки D на угол, равный СDА, по часовой стрелке; г) при параллельном переносе на вектор DА. 2) Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О. Докажите, что ∆АВС= ∆А1В1С1 |
9 класс Самостоятельная работа Вариант 1 Тема : «Простейшие задачи в координатах» 1. Найдите координаты середины отрезка АВ, если А(-2;3), В(6;-3) 2. Найдите длину отрезка ЕН, если Е(-3;8), Н(2;-4) 3. Найдите длину вектора {-4; -3} 4.
Вершины ∆АВС имеют координаты А(8;-3),
В(5;1), С(12;0). 5.Найдите длину вектора,если А(3;-6),В(-4; -7). | 9 класс Самостоятельная работа Вариант 2 Тема : «Простейшие задачи в координатах» 1. Найдите координаты середины отрезка ВС, если С(3;-4), В(-6; 3) 2. Найдите длину отрезка КВ, если К(-6;-3), В(2;3) 3. Найдите длину вектора {-6; 8} 4. Вершины четырехугольника АВСD имеют координаты А(-3; -1), В(1; 2), С(5; -3), D(1; -4). Докажите АВСD-ромб. Найдите S∆АВСD 5.Найдите длину вектора,если А(-3;6), В(4; 7). |
9 класс Самостоятельная работа Тема: « Уравнение окружности и прямой»
Вариант 1 | Вариант 2 |
1.Напишите
уравнение окружности с центром в точке
А и радиуса R,
если А (4;-5), R=3. 2.Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (-2;3). 3. Напишите уравнение прямой, проходящей через две точки М (-2;-1) и N (3;1). | 1.Напишите уравнение окружности с центром в точке А и радиуса R, если А (-7;8), R=9. 2.Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (6;-8). 3. Напишите уравнение прямой, проходящей через две точки М (-1;-2) и N (1;3). |
9 класс Самостоятельная работа Тема: «Решение треугольников» Вариант 1.(1ур) 1) Дано: а=5см, В=30˚,С=50˚ Найдите: b, с, А, SАВС 2) Дано: а =6см, с =7см, В= 40˚. Найдите:
b,
А. | 9 класс Самостоятельная работа Тема: «Решение треугольников» Вариант 2.(1ур) 1) Дано: а=6см, В=40˚,С=60˚ Найдите: b, с, А, SАВС. 2) Дано: а =5см, с =8см, В= 30˚. Найдите: b, С. |
9 класс Самостоятельная работа Тема: «Решение треугольников» Вариант 1.(2ур) 1) Дано: АС=0,59см, В=40˚,С=35˚ Найдите: ВС, АВ, А. 2) Дано: ВС =27см, АВ =16см, В= 140˚. Найдите:
АС,
А,
С,
SАВС. | 9 класс Самостоятельная работа Тема: «Решение треугольников» Вариант 2.(2ур) 1) Дано: ВС=0,75см, А=40˚,С=20˚ Найдите: АС, АВ, В. 2) Дано: АС =13см, АВ =42см, А= 100˚. Найдите: ВС, В, С, SАВС |
9класс Самостоятельная работа Вариант1 Тема «Скалярное произведение векторов» 1. Вычислите скалярное произведение векторов а и b, если =2, =3, а угол между ними равен 120˚. 2. Вычислите скалярное произведение векторов а и b, если , . 3. Вычислите косинус угла между векторами а и b, если , 4. | 9класс Самостоятельная работа Вариант2 Тема «Скалярное произведение векторов» 1. Вычислите скалярное произведение векторов m и n, если =3, =4, а угол между ними равен 135˚. 2. Вычислите скалярное произведение векторов m и n, если, . 3.Вычислите косинус угла между векторами m и n , если m , n . 4. При каком значении у вектора m и n перпендикулярны, если m, n/ |
9 класс Самостоятельная работа Вариант 1 Тема: «Правильные многоугольники» 1) Найдите угол правильного десятиугольника. 2) Найдите сторону правильного ∆ , если радиус описанной около него окружности равен 2см. 3)Найдите
радиус окружности, вписанной в квадрат,
если радиус описанной около него
окружности равен 2м. 4) Найдите площадь правильного ∆ , если расстояние от его центра до вершины равно 2м. | 9 класс Самостоятельная работа Вариант 2 Тема: «Правильные многоугольники» 1) Найдите угол правильного девяностоугольника. 2) Найдите сторону квадрата, если расстояние от его центра до вершины равно 2м. 3) Найдите радиус окружности, вписанной в правильный ∆ , если радиус описанной около него окружности равен 2м. 4) Найдите площадь квадрата, если радиус описанной около него окружности равен 2см. |
9 класс Самостоятельная работа « Синус, косинус, тангенс угла»
Вариант1 | Вариант2 |
1.Найти: а)tg, если sin= 0,6 , 90˚< <180; б)sin,если
cos=-0,4;
в)cos,
если sin=
. 2.Могут ли одновременно выполняться: а)sin=0,7, cos=0,3; б) sin=0,8 , cos=0,6? | 1.Найти: а)tg, если sin= 0,7 , 90˚< <180; б)sin,если cos=-0,6; в)cos, если sin= . 2. Могут ли одновременно выполняться: а)sin=0,2, cos=0,8; б) sin= , cos=? |
9класс Самостоятельная работа Вариант 1 Тема: «Площадь круга. Длина окружности» 1. Найдите длину окружности и площадь круга, если радиус равен 3,5см. (3) 2. Длина окружности равна 22π см. Найдите площадь соответствующего ей круга. (4) 3. Найдите площадь кругового сектора радиуса 6м, если градусная мера его дуги равна150˚.(3) 4. Длина дуги равна 62,8 м, а её радиус 36м. Найдите градусную меру дуги.(5) 5.
Сторона правильного шестиугольника,
описанного около окружности равна
4см. | 9класс Самостоятельная работа Вариант 2 Тема: «Площадь круга. Длина окружности» 1. Найдите длину окружности и площадь круга, если радиус равен 5,3см. (3) 2. Площадь круга равна 225πсм2. Найдите длину окружности, соответст-вующей этому кругу.(4) 3. Дуга в 110˚ имеет радиус 36см. Найдите длину этой дуги. (3) 4. Площадь кругового сектора равна 3,24см2, его радиус равен 0,18см. Найди-те градусную меру дуги сектора.(5) 5. Сторона правильного треугольника, описанного около окружности равна 4см. Найдите длину этой окружности.(5) |
9 класс Самостоятельная работа Вариант 1 Тема: « Отображение плоскости на себя» | 9 класс Самостоятельная работа Вариант 2 Тема: « Отображение плоскости на себя» |
1. | 1.Постройте точку А1, симметрич-ную точке А относительно прямой а |
2. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О (центр). | 2. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О (центр). |
3. Постройте отрезок А1В1, полученный параллельным переносом отрезка АВ на вектор а. | 3. Постройте отрезок А1В1, полученный параллельным переносом отрезка АВ на вектор а. |
9 класс Самостоятельная работа Вариант 3 Тема: « Отображение плоскости на себя» | 9 класс Самостоятельная работа Вариант 4 Тема: « Отображение плоскости на себя» |
1. | 1.Постройте прямоугольник А1В1С1D1, симметричный прямоугольнику АВС D, относительно прямой а. |
2. Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О (центр). | 2. Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О (центр). |
3. Постройте трапецию А1В1С1D1, полученную, параллельным переносом трапеции АВСD на вектор ВD | 3. Постройте трапецию А1В1С1D1, полученную, параллельным переносом трапеции АВСD на вектор АС |
4. | 4. Постройте точку А1, получен-ную из точки А поворотом вокруг точки О по часовой стрелке на угол 120˚ |
9 класс Самостоятельная работа Вариант 5 Тема: « Отображение плоскости на себя» | |
1.Постройте квадрат А1В1С1D1, симметричный квадрату АВС D, относительно прямой а. | 9 класс Самостоятельная работа Вариант 2 Тема: « Отображение плоскости на себя» |
2. Постройте ∆А1В1С1, симметрич-ный ∆АВС относительно точки О (центр). | 1.Постройте точку А1, симметрич-ную точке А относительно прямой а |
3. | 2. Постройте отрезок А1В1, симметричный отрезку АВ относительно точки О (центр). |
4. Постройте точку А1, получен-ную из точки А поворотом вокруг точки О против часовой стрелки на угол 150˚ | 3. Постройте отрезок А1В1, полученный параллельным переносом отрезка АВ на вектор а. |
Геометрия 9 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 9 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 9 класс. Дидактические материалы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах, а также есть набор заданий по каждой теме для подготовки к контрольным работам. Структура контрольных работ и форма заданий соответствуют структуре и форме заданий Основного государственного экзамена (ОГЭ).
9 класс. Дидактические материалы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах, а также есть набор заданий по каждой теме для подготовки к контрольным работам. Структура контрольных работ и форма заданий соответствуют структуре и форме заданий Основного государственного экзамена (ОГЭ).
Контрольные работы по геометрии в 9 классе:
Контрольная работа 1 К-1. Векторы. Метод координат
Контрольная работа 2 К-2. Соотношения в треугольнике
Контрольная работа 3 К-3. Длина окружности и площадь круга
Контрольная работа 4 К-4. Движения
Контрольная работа 5 К-5. Начальные сведения из стереометрии
Контрольная работа 6 К-6. ИТОГОВАЯ за 9 класс
Контрольная работа 7 К-7. ИТОГОВАЯ за 7-9 классы
Структура контрольной работы
Каждая контрольная работа рассчитана на один урок. Все работы составлены в четырех вариантах одинакового уровня сложности (только в пособии). Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.
Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.
В часть А включаются задания с выбором ответа. Учащимся нужно выбрать из предложенных вариантов либо верное утверждение, либо нужный рисунок. При этом верных ответов может быть несколько, и учащимся необходимо записать номера ответов, которые, по их мнению, верны. Заметим, что, вообще говоря, в заданиях с выбором ответа применяются два подхода. При первом подходе среди предлагаемых вариантов ответа имеется только один правильный. При втором — верных ответов может быть несколько, и результатом решения задачи является не один номер, а все номера верных ответов. При этом задание считается выполненным верно, если указаны номера всех верных ответов.
В часть В входят вычислительные задачи, которые необходимо решить и записать число, которое получилось в результате вычислений.
При выполнении частей А и В контрольной работы учащиеся не записывают ни обоснования, ни вычисления, нужные для решения задач. Все записи или рисунки учащиеся, в случае необходимости, могут делать в черновике. Черновик не сдается учителю и не влияет на оценку за выполнение работы.
Все записи или рисунки учащиеся, в случае необходимости, могут делать в черновике. Черновик не сдается учителю и не влияет на оценку за выполнение работы.
В части С имеются и задачи на доказательство, и задачи на вычисление геометрических величин. Решение этих задач должно быть оформлено письменно, как в традиционной контрольной работе. Следует иметь в виду, что при записи решения вычислительных задач, так же как и при решении задач на доказательство, необходимо приводить обоснования с использованием изученных геометрических фактов.
Последняя задача, в каждом варианте отмеченная звездочкой, предназначена для наиболее подготовленных учащихся, успевающих достаточно быстро выполнить все предыдущие задания. В зависимости от уровня подготовленности класса эту задачу можно считать дополнительной и оценивать ее решение отдельно.
Перед проведением первой контрольной работы необходимо проинструктировать учащихся о том, как они должны оформить решение задач. Полезно привести пример, показывающий, как должны выглядеть ответы на задачи частей А и В.
Следует напомнить эти инструкции и при проведении каждой последующей контрольной работы.
Дифференцированный подход к учащимся осуществляется за счет того, что в работах представлены задания разного уровня, которые, как правило, расположены по мере возрастания уровня сложности. Стереометрический материал может изучаться в ознакомительном плане без обязательной проверки его усвоения. Поэтому контрольную № 5 по усмотрению учителя можно не проводить или полученные за нее оценки выставлять в журнал по желанию учащегося.
Номера заданий обязательного уровня, посильных для менее подготовленных учащихся, отмечены кружком. Такие задания представлены во всех трех частях работы.
Следует заметить, что при традиционном письменном оформлении решения задач предлагаемое в контрольных работах количество задач было бы нереально решить за один урок. Однако нужно иметь в виду, что задания с выбором ответа и с кратким ответом не требуют времени на оформление решения и очень часто ответы на них могут быть получены устно. Поэтому основные затраты времени будут связаны с решением задач части С.
Поэтому основные затраты времени будут связаны с решением задач части С.
Тематика контрольных работ
Каждая тематическая контрольная работа направлена на проверку усвоения материала главы учебника. Одна из итоговых контрольных работ проверяет усвоение материала, изучавшегося в 9 классе, другая составлена по материалу всего курса планиметрии. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах.
Контрольная работа № 1. Векторы. Метод координат
• равенство векторов, координаты и модуль вектора, сложение векторов и умножение вектора на число;
• координаты середины и длина отрезка, заданного координатами концов;
• уравнение окружности;
• средняя линия трапеции.
Контрольная работа № 2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Скалярное произведение векторов
• теорема синусов, теорема косинусов;
• формула площади треугольника;
• скалярное произведение векторов.
Контрольная работа № 3. Длина окружности и площадь круга
• правильные многоугольники;
• длина окружности и длина дуги окружности;
• площадь круга и кругового сектора.
Контрольная работа № 4. Движения
• понятие движения;
• симметрия относительно прямой, симметрия относительно точки, параллельный перенос; поворот.
Контрольная работа № 5. Начальные сведения из стереометрии
• геометрические тела: призма, параллелепипед, пирамида, цилиндр, конус;
• свойства правильной призмы и правильной пирамиды;
• объемы тел, боковая поверхность цилиндра и конуса;
• сечение прямоугольного параллелепипеда плоскостью.
Итоговая контрольная работа за курс 9 класса
• координаты середины отрезка, заданного координатами концов;
• равенство векторов, модуль вектора;
• скалярное произведение векторов;
• теорема синусов, теорема косинусов;
• длина окружности и площадь круга;
• площадь правильного многоугольника.
Итоговая контрольная работа за курс 7-9 классов
• свойства параллелограмма, прямоугольника и ромба;
• признаки подобия треугольников;
• средняя линия треугольника;
• формулы площади треугольника;
• теорема Пифагора и определения синуса, косинуса и тангенса острого угла прямоугольного треугольника;
• теорема синусов, теорема косинусов.
Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.
1.Нарисовать равнобедренный АВС с основанием АС=4 см. Провести среднюю линию МD и найти её длину. 2. Найти длины указанных векторов. 3 . Найти площадь трапеции. 4 . Постройте четырехугольник АВСD по координатам его вершин: А(-5;0), В(-3;3), С(2;3), D(4;0). а) Определите вид получившейся фигуры и найдите её площадь. Ответ. Это равнобедренная трапеция. S= . б) Выпишите все коллинеарные векторы. Ответ.BCАD,CBDА, ВС DА, СВ АD в) Найдите длину средней линии. Ответ.7 | 1. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N(2; 4), К (2; — 2). а)Найдите среднюю линию МNK. Ответ. L =6:2=3. б) Найдите площадь МNK. Ответ.S=(8*6):2=24 кв.ед. 2. В равнобедренной трапеции высота делит большее основание на отрезки, равные5 и 12 см. Найдите среднюю линию трапеции. Ответ. 9,5 см. 3. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и. 4 .Найти площадь Ответ. 60 кв.ед. 5.Сложите два вектора по правилу параллелограмма. | 1.Построить четырехугольник ABCD, если A(-4;7),B(0;1),C(-4;-5),D(-8;1). а) Определите вид получившейся фигуры и найдите её площадь. Ответ. Это ромб.S= =12*80:2=48кв.ед. 2.Найти. Ответ. 3. Начертите два неколлинеарных вектора и. Постройте вектор n, равный . 4. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции и её площадь. Ответ.L=11см. S= 5. В прямоугольном параллелепипеде известно, что ВD1=5, СС1-3, В1С1= . Найдите длину ребра АВ. Решение и ответ. ВD-4 (ученик должен увидеть пифагорову триаду), АВ=СD= = . Ответ.3. |
Решение задач с векторами
Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.
Скорость:
Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью.
Пример :
Мяч брошен с начальной скоростью 70 футов в секунду., под углом 35 год ° с горизонтальным. Найдите вертикальную и горизонтальную составляющие скорости.
Позволять v представлять скорость и использовать данную информацию для записи v в форме единичного вектора:
v знак равно 70 ( потому что ( 35 год ° ) ) я + 70 ( грех ( 35 год ° ) ) j
Упростим скаляры, получим:
v ≈ 57.34 я + 40,15 j
Поскольку скаляры являются горизонтальной и вертикальной составляющими v ,
Следовательно, горизонтальная составляющая равна
57,34
футов в секунду, а вертикальная составляющая
40,15
футов в секунду.
Сила:
Сила также представлена вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, является векторной суммой этих сил.
Пример :
Две силы F 1 а также F 2 с величинами 20 а также 30 фунт соответственно воздействуют на объект в точке п как показано. Найдите равнодействующие силы, действующие в п .
Сначала мы пишем F 1 а также F 2 в компонентном виде:
v ≈ 57.34 я + 40,15 j
Упростим скаляры, получим:
F 1 знак равно ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) j знак равно 20 ( 2 2 ) я + 20 ( 2 2 ) j знак равно 10 2 я + 10 2 j F 2 знак равно ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) j знак равно 30 ( — 3 2 ) я + 30 ( 1 2 ) j знак равно — 15 3 я + 15 j
Итак, равнодействующая сила F является
F знак равно F 1 + F 2 знак равно ( 10 2 я + 10 2 j ) + ( — 15 3 я + 15 j ) знак равно ( 10 2 — 15 3 ) я + ( 10 2 + 15 ) j ≈ — 12 я + 29 j
Работа:
Работа
W
сделано силой
F
в движении по вектору
D
является
W
знак равно
F
⋅
D
.
Пример :
Сила задается вектором F знак равно 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9 ) . Найдите проделанную работу.
Сначала мы находим Displacement.
Вектор смещения
D знак равно 〈 5 — 1 , 9 — 3 〉 знак равно 〈 4 , 6 〉 .
Используя формулу, проделанная работа
W знак равно F ⋅ D знак равно 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 знак равно 26
Если единицей силы являются фунты, а расстояние измеряется в футах, то выполненная работа 26 фут-фунт
векторов по физике — практические контрольные вопросы и экзамен по главе
Стр.
 1
1Вопрос 1 1. В компонентной форме вектор A равен 3i + 6j, а вектор B равен i + 2j. Каково скалярное произведение этих векторов?
Ответы:вопрос 2 2.Каково общее определение векторного разрешения?
Ответы:Вопрос 3 3. Какой из следующих векторов НЕ в компонентной форме?
Ответы:Вопрос 4 4.Что из следующего является определением вектора?
Ответы:Вопрос 5 5. Как сложить векторы геометрически?
Ответы:Стр. 2
Вопрос 6 6.Электрический лестничный подъемник прилагает силу в 600 ньютонов прямо вверх, перемещая подъемник с постоянной скоростью 0,1 метра в секунду.
 Мощность, используемая лестничным лифтом, является скалярным произведением силы и скорости. Если лестница расположена под углом 60 градусов НИЖЕ ГОРИЗОНТАЛИ, сколько мощности потребляет лестничный подъемник? Ответы:
Мощность, используемая лестничным лифтом, является скалярным произведением силы и скорости. Если лестница расположена под углом 60 градусов НИЖЕ ГОРИЗОНТАЛИ, сколько мощности потребляет лестничный подъемник? Ответы:Вопрос 7 7.Что из следующего НЕ является примером векторной величины?
Ответы:Вопрос 8 8. Что из перечисленного НЕ является примером умножения векторов? (Другими словами, какой расчет не имеет вектора для ответа?)
Ответы:Вопрос 9 9.Если вы выстрелите пушечным ядром под малым углом, как будут сравниваться x- и y-компоненты его скорости?
Ответы:Вопрос 10 10. Вектор A имеет величину 4 единицы, вектор B имеет величину 8 единиц.
 Если угол между ними составляет 35 градусов, каково скалярное произведение векторов A и B? Ответы:
Если угол между ними составляет 35 градусов, каково скалярное произведение векторов A и B? Ответы:Стр. 3
Вопрос 11 11.В каком из этих уравнений вам НЕ понадобится вычитать два вектора?
Ответы:Вопрос 12 12. Какие из следующих утверждений является верным?
Ответы:Вопрос 13 13.Когда мы используем точечные произведения?
Ответы:Вопрос 14 14. Если вы толкаете коробку с силой 8 ньютонов вбок в положительном направлении оси x, 3 ньютона вниз в отрицательном направлении оси y и на 1 ньютон вперед в положительном направлении оси z, как бы вы представили эту силу в виде компонента? ?
Ответы:Вопрос 15 15.
 Пушечное ядро выстреливается со скоростью 10 м / с вверх от горизонтали и 30 м / с на запад. Каков угол и направление пушечного ядра? Ответы:
Пушечное ядро выстреливается со скоростью 10 м / с вверх от горизонтали и 30 м / с на запад. Каков угол и направление пушечного ядра? Ответы:стр. 4
Вопрос 16 16. Если вы снимаете что-то под большим углом, как будут сравниваться компоненты x и y?
Ответы:Вопрос 17 17.Сила А действует на 2 ньютона на запад и на 3 ньютона на юг. Сила B действует на 5 ньютонов на запад и на 2 ньютона на север. Каков результат этих двух векторов?
Ответы:Вопрос 18 18. Пушечное ядро выстреливается под углом 55 градусов относительно горизонтали с силой 80 Ньютонов. Какова величина вектора силы, действующего на ядро?
Ответы:Вопрос 19 19.
 Как бы вы записали 50 ньютонов на восток и 70 ньютонов на юг в компонентной форме? (Используйте север на юг в качестве оси Y и с востока на запад в качестве оси X, как в уроке.) Ответы:
Как бы вы записали 50 ньютонов на восток и 70 ньютонов на юг в компонентной форме? (Используйте север на юг в качестве оси Y и с востока на запад в качестве оси X, как в уроке.) Ответы:Вопрос 20 20. Теннисный мяч движется со скоростью 20 м / с на запад и 5 м / с вверх. Какова общая величина вектора скорости теннисного мяча?
Ответы:стр. 5
Вопрос 21 21.Если объект движется со скоростью 4 м / с в направлении x и 2 м / с в направлении y, какова скорость объекта, записанная в терминах стандартных базисных векторов?
Ответы:Вопрос 22 22.
Если вектор 1 имеет величину 3 единицы и направление на 30 градусов ниже отрицательной оси x, а вектор 2 имеет величину 4 единицы и направление на 80 градусов ниже отрицательной оси x, то вектор 1 минус вектор 2?
(Пожалуйста, ответьте на этот вопрос геометрически, используя бумагу, карандаш и линейку. )
)
Вопрос 23 23. Каково скалярное произведение 3i + 2j, умноженное на 4i + 8j?
Ответы:Вопрос 24 24. Вы толкаете тележку для покупок с силой 20 Н вниз и силой 50 Н.Какова общая величина прилагаемой силы?
Ответы:Вопрос 25 25. Что из следующего НЕ может представлять то же движение, что и другие?
Ответы:Стр. 6
Вопрос 26 26.Вы толкаете багги с силой 40 ньютонов вперед и 10 ньютонов вниз. Под каким углом толкаете багги?
Ответы:Вопрос 27 27. Грузовик движется со скоростью 5 м / с на север и 3 м / с на запад, в то время как человек ВНУТРИ грузовика движется в определенном направлении с определенной скоростью.
 Общая скорость человека (комбинация скорости грузовика и скорости человека) составляет 6 м / с на север и 1 м / с на запад.Как быстро человек должен двигаться в грузовике? Ответы:
Общая скорость человека (комбинация скорости грузовика и скорости человека) составляет 6 м / с на север и 1 м / с на запад.Как быстро человек должен двигаться в грузовике? Ответы:Вопрос 28 28. Если рассчитать кросс-произведения AxB и BxA, как будут сравниваться результаты?
Ответы:Вопрос 29 29.Что из следующего является определением вектора?
Ответы:Вопрос 30 30. Что из этого является правильным определением векторной величины?
Ответы:«Векторы в физике» Инструкция к экзамену
Выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов.Вы можете пропустить вопросы, если хотите, и приходите
назад
к ним позже с помощью кнопки «Перейти к первому пропущенному вопросу». Когда вы сдадите пробный экзамен, появится зеленая кнопка отправки.
появляться.
Щелкните его, чтобы увидеть свои результаты. Удачи!
Когда вы сдадите пробный экзамен, появится зеленая кнопка отправки.
появляться.
Щелкните его, чтобы увидеть свои результаты. Удачи!
Скаляров и векторов
Физика — математическая наука. Основные концепции и принципы имеют математическую основу. В процессе изучения физики мы будем сталкиваться с множеством концепций, связанных с математической базой.Хотя мы часто делаем упор на концептуальную природу физики, мы будем уделять значительное и постоянное внимание ее математическому аспекту.
Движение предметов можно описать словами. Даже у человека без образования в области физики есть набор слов, которые можно использовать для описания движущихся объектов. Такие слова и фразы, как , идет быстро, , , остановился, , , замедляется, , , ускоряется, , и , поворачивает, , обеспечивают достаточный словарный запас для описания движения объектов.В физике мы используем эти и многие другие слова. Мы будем расширять этот словарный список такими словами, как расстояние , смещение , скорость , скорость и ускорение . Как мы вскоре увидим, эти слова связаны с математическими величинами, имеющими строгие определения. Математические величины, которые используются для описания движения объектов, можно разделить на две категории. Величина может быть векторной или скалярной.Эти две категории можно отличить друг от друга по их различным определениям:
Мы будем расширять этот словарный список такими словами, как расстояние , смещение , скорость , скорость и ускорение . Как мы вскоре увидим, эти слова связаны с математическими величинами, имеющими строгие определения. Математические величины, которые используются для описания движения объектов, можно разделить на две категории. Величина может быть векторной или скалярной.Эти две категории можно отличить друг от друга по их различным определениям:
- Скаляры — это величины, которые полностью описываются только величиной (или числовым значением).
- Векторы — это величины, которые полностью описываются величиной и направлением.
Остальная часть этого урока будет посвящена нескольким примерам векторных и скалярных величин (расстояние, смещение, скорость, скорость и ускорение).По мере прохождения урока обращайте особое внимание на векторную и скалярную природу каждой величины. По мере того, как мы переходим к другим разделам Учебного пособия по физике и знакомимся с новыми математическими величинами, обсуждение часто начинается с определения новой величины как вектора или скаляра.
Проверьте свое понимание
1. Чтобы проверить ваше понимание этого различия, примите во внимание следующие величины, перечисленные ниже.Классифицируйте каждую величину как вектор или скаляр. Нажмите кнопку, чтобы увидеть ответ.
| Кол-во | Категория |
|---|---|
| а. 5 м | |
| б. 30 м / сек, Восток | |
| г. 5 миль, север | |
| г. 20 градусов Цельсия | |
| e.256 байт | |
| ф. 4000 калорий |
Сложение и вычитание векторов: аналитические методы
Цели обучения
К концу этого раздела вы сможете:
- Изучите правила сложения и вычитания векторов с помощью аналитических методов.
- Применяйте аналитические методы для определения вертикальных и горизонтальных составляющих векторов.

- Примените аналитические методы, чтобы определить величину и направление результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации.Однако аналитические методы более краткие, точные и точные, чем графические методы, которые ограничены точностью, с которой можно сделать рисунок. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Разрешение вектора на перпендикулярные компоненты
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (помимо прочего) движения в перпендикулярных направлениях независимы. Нам очень часто требуется разделить вектор на перпендикулярные составляющие.Например, имея такой вектор, как A на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора, A x и A y , сложить, чтобы получить его.
Рис. 1. Вектор A с хвостом в начале системы координат x, y показан вместе с его компонентами x и y, A x и A y . Эти векторы образуют прямоугольный треугольник. Аналитические соотношения между этими векторами кратко изложены ниже.
A x и A y определены как компоненты A вдоль осей x — и y -осей. Три вектора A , A x и A y образуют прямоугольный треугольник:
A x + A y = A
Обратите внимание, что эта взаимосвязь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление).Это соотношение не распространяется только на величины. Например, если A x = 3 м на восток, A y = 4 м на север и A = 5 м на северо-восток, то верно, что векторы A x + A y = A. Однако не верно, что сумма модулей векторов также равна. То есть
Однако не верно, что сумма модулей векторов также равна. То есть
[латекс] 3 \ text {m} + 4 \ text {m} \ ne 5 \ text {m} \\ [/ latex]
Таким образом, A x + A y ≠ A Если вектор A известен, то его величина A (длина) и угол θ ( его направление) известны.Чтобы найти A x и A y , его x — и y -компоненты, мы используем следующие отношения для прямоугольного треугольника.
[латекс] A_ {x} = A \ cos \ theta \\ [/ латекс]
и
[латекс] A_ {y} = A \ sin \ theta \\ [/ latex]
Рис. 2. Величины компонентов вектора Ax и A y могут быть связаны с результирующим вектором A и углом θ с тригонометрическими тождествами.Здесь мы видим, что [латекс] A_ {x} = A \ cos \ theta \\ [/ latex] и [latex] A_ {y} = A \ sin \ theta \\ [/ latex].
Предположим, например, что A — это вектор, представляющий полное перемещение человека, идущего по городу, рассматриваемое в Кинематике в двух измерениях: Введение и Сложение и вычитание векторов: Графические методы.
Рис. 3. Мы можем использовать отношения [латекс] A_ {x} = A \ cos \ theta \\ [/ latex] и [latex] A_ {y} = A \ sin \ theta \\ [/ latex] для определения величина горизонтальных и вертикальных составляющих векторов в этом примере.{\ circ}) = 5.0 \ text {blocks} \\ [/ latex]
Вычисление результирующего вектора
Если известны перпендикулярные компоненты A x и A y вектора A , то A также можно найти аналитически. Чтобы найти звездную величину A и направление θ вектора из его перпендикулярных компонентов A x и A y , мы используем следующие отношения:
[латекс] A = \ sqrt {{A} _ {x ^ 2} + {A_ {y ^ 2}}} \\ [/ latex]
θ = tan — 1 ( A y / A x ). {2}} \ text {= 10} \ text {.} 3 \\ [/ latex] блока, опять же в соответствии с примером человека, идущего по городу. Наконец, направление θ = tan –1 (5/9) = 29,1º, как и раньше.
{2}} \ text {= 10} \ text {.} 3 \\ [/ latex] блока, опять же в соответствии с примером человека, идущего по городу. Наконец, направление θ = tan –1 (5/9) = 29,1º, как и раньше.
Уравнения [латекс] A_ {x} = A \ cos \ theta \\ [/ latex] и [latex] A_ {y} = A \ sin \ theta \\ [/ latex] используются для нахождения перпендикулярных компонентов вектор, то есть переход от A и θ к A x и A y .{2}} \\ [/ latex] и θ = tan –1 ( A y / A x ) используются для нахождения вектора из его перпендикулярных компонентов — то есть перейти от A x и A y к A и θ . Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
Добавление векторов с помощью аналитических методов
Чтобы увидеть, как складывать векторы с использованием перпендикулярных компонентов, рассмотрим рисунок 5, на котором векторы A и B складываются для получения результирующего R .
Рис. 5. Векторы A и B — это два этапа шага, а R — результирующее или полное смещение. Вы можете использовать аналитические методы, чтобы определить величину и направление R .
Если A и B представляют два этапа шага (два смещения), то R — это полное смещение. Человек, идущий на прогулку, получает чаевые рэндов. Есть много способов прийти к одной и той же точке.{2}} \\ [/ latex] и θ = tan –1 ( A y / A x ). Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Шаг 1. Определите оси x и y, которые будут использоваться в задаче. Затем найдите компоненты каждого вектора, которые нужно добавить вдоль выбранных перпендикулярных осей . Используйте уравнения A x = A cos θ и A y = A sin θ , чтобы найти компоненты.На рисунке 6 эти компоненты: A x , A y , B x и B y . Углы, которые образуют векторы A и B с осью x , составляют θ A и θ B соответственно.
Рисунок 6. Чтобы сложить векторы A и B, сначала определите горизонтальные и вертикальные компоненты каждого вектора.Это пунктирные векторы A x , A y , B x и B y , показанные на изображении.
Шаг 2. Найдите компоненты результирующего по каждой оси, сложив компоненты отдельных векторов по этой оси . То есть, как показано на рисунке 7,
R x = A x + B x
и
R y = A y + B y .
Рис. 7. Величина векторов A, , x и B , x суммируется, чтобы получить величину R x результирующего вектора в горизонтальном направлении. Аналогично, величины векторов A, , x и B, , y складываются, чтобы получить величину R y результирующего вектора в вертикальном направлении.
Компоненты, расположенные вдоль одной оси, например, , x , -ось, являются векторами на одной линии и, таким образом, могут складываться друг с другом как обычные числа. {2}} \\ [/ latex]
{2}} \\ [/ latex]
Шаг 4. Чтобы получить направление результата:
θ = tan −1 ( R y / R x ).
Следующий пример иллюстрирует эту технику добавления векторов с использованием перпендикулярных компонентов.
Пример 1. Добавление векторов аналитическими методами
Добавьте вектор A к вектору B , показанному на рисунке 8, используя перпендикулярные компоненты вдоль осей , x , и , y, , .Оси x и y расположены вдоль направлений восток-запад и север-юг соответственно. Vector A представляет собой первый этап прогулки, на которой человек проходит 53,0 м в направлении 20,0º к северу от востока. Вектор B представляет собой вторую ногу, смещение 34,0 м в направлении 63,0º к северу от востока.
Рисунок 8.
Vector A имеет звездную величину 53,0 м и направление 20,0º к северу от оси x .Вектор B имеет звездную величину 34,0 м и направление 63,0º к северу от оси x . Вы можете использовать аналитические методы, чтобы определить величину и направление R .
СтратегияКомпоненты A и B вдоль осей x и y представляют собой движение на восток и на север, чтобы добраться до той же конечной точки. Найденные, они объединяются для получения результата.
Раствор Следуя описанному выше методу, мы сначала находим компоненты A и B по осям , x , и , y, , . Обратите внимание, что A = 53,0 м, θ A = 20,0 º, B = 34,0 м и θ B = 63,0 º. Мы находим x -компоненты, используя [latex] A_ {x} = A \ cos \ theta \\ [/ latex], что дает
Мы находим x -компоненты, используя [latex] A_ {x} = A \ cos \ theta \\ [/ latex], что дает
[латекс] \ begin {array} {c} A_ {x} = A \ cos \ theta_ {A} = (53.{\ circ}) \\ = (34,0 м) (0,891) = 30,3 \ text {m} \ end {array} [/ latex]
Компоненты x и y результирующего, таким образом, равны
R x = A x + B x = 49,8 м + 15,4 м = 65,2 м
и
R y = A y + B y = 18.{2} \ text {m}} \\ [/ latex]
, так что
R = 81,2 м.
Наконец, находим направление результирующего:
θ = tan −1 ( R y / R x ) = + tan −1 (48,4 / 65,2).
Таким образом,
θ = tan -1 (0,742) = 36,6º.
Рис. 9. Используя аналитические методы, мы видим, что величина R равна 81.2 м и направление 36,6º к северу от востока.
ОбсуждениеЭтот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонентов очень похоже — это просто добавление отрицательного вектора. Вычитание векторов осуществляется добавлением отрицательного вектора. То есть A — B ≡ A + ( –B ). Таким образом, метод вычитания векторов с использованием перпендикулярных компонентов идентичен методу сложения .Компоненты –B являются отрицаниями компонентов B . Компоненты x и y результирующего A — B = A , таким образом, равны
.[латекс] R_ {x} = A_ {x} + (-B_ {x}) \\ [/ latex]
и
[латекс] R_ {y} = A_ {y} + (-B_ {y}) \\ [/ latex]
, а остальная часть описанного выше метода идентична методу сложения. (См. Рисунок 10.)
Анализ векторов с использованием перпендикулярных компонентов очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга.Следующий модуль, Projectile Motion, является одним из многих, в которых использование перпендикулярных компонентов помогает сделать изображение четким и упрощает физику.Рисунок 10. Вычитание двух векторов, показанных на рисунке 5. Компоненты –B являются отрицательными значениями компонентов B. Метод вычитания такой же, как и для сложения.
Исследования PhET: добавление векторов
Узнайте, как складывать векторы. Перетащите векторы на график, измените их длину и угол и просуммируйте их.Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
- Шаги для сложения векторов A и B с использованием аналитического метода следующие:
Шаг 1: Определите систему координат для векторов.Затем определите горизонтальные и вертикальные компоненты каждого вектора, используя уравнения
.[латекс] \ begin {массив} {lll} {A} _ {x} & = & A \ text {cos} \ theta \\ {B} _ {x} & = & B \ text {cos} \ theta \ end {array} \\ [/ latex]
и
[латекс] \ begin {array} {lll} {A} _ {y} & = & A \ text {sin} \ theta \\ {B} _ {y} & = & B \ text {sin} \ theta \ text {.} \ end {array} \\ [/ latex]
Шаг 2: Добавьте горизонтальные и вертикальные компоненты каждого вектора, чтобы определить компоненты R x и R y результирующего вектора, R :
[латекс] {R} _ {x} = {A} _ {x} + {B} _ {x} \\ [/ latex]
и
[латекс] {R} _ {y} = {A} _ {y} + {B} _ {y} \\ [/ latex]
Шаг 3: Используйте теорему Пифагора, чтобы определить величину R результирующего вектора R :
[латекс] R = \ sqrt {{{R} _ {x}} ^ {2} + {{R} _ {y}} ^ {2}} \\ [/ latex]
Шаг 4: Используйте тригонометрическую идентичность для определения направления [латекс] \ тета \ [/ латекс] R :
[латекс] \ theta = {\ text {tan}} ^ {- 1} \ left ({R} _ {y} / {R} _ {x} \ right) [/ latex].
Концептуальные вопросы
1. Предположим, вы складываете два вектора A и B . Какое относительное направление между ними дает результирующую с наибольшей величиной? Какая максимальная величина? Какое относительное направление между ними дает наименьшую величину равнодействующей? Какая минимальная величина?
2. Приведите пример ненулевого вектора с нулевой компонентой.
3. Объясните, почему вектор не может иметь компонент, превышающий его собственную величину.
4. Если векторы A и B перпендикулярны, какова составляющая A в направлении B ? Каков компонент B в направлении A ?
Задачи и упражнения
1. Найдите следующее для пути C на рисунке 12: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца. В этой части задачи явно покажите, как вы следуете шагам аналитического метода сложения векторов.
Рис. 12. Различные линии представляют собой пути, по которым идут разные люди в городе. Все блоки имеют ширину 120 м.
2. Найдите следующее для пути D на рисунке 12: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца. В этой части задачи явно покажите, как вы следуете шагам аналитического метода сложения векторов.
3. Найдите северную и восточную составляющие смещения от Сан-Франциско до Сакраменто, показанные на рисунке 13.
Рисунок 13.
4. Решите следующую задачу, используя аналитические методы. Предположим, вы идете 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от начальной точки и каково направление по компасу линии, соединяющей исходную точку и конечное положение? (Если вы представляете два этапа прогулки как векторные смещения A и B , как на рисунке 14, то в этой задаче вам предлагается найти их сумму R = A + B .)
Рис. 14. Два смещения A и B складываются, чтобы получить общее смещение R, имеющее величину R и направление θ .
Обратите внимание, что вы также можете решить эту проблему графически. Обсудите, почему аналитический метод решения этой проблемы потенциально более точен, чем графический метод.
5. Повторите упражнение 4, используя аналитические методы, но поменяйте порядок двух этапов прогулки и покажите, что вы получите тот же конечный результат.(Эта задача показывает, что добавление их в обратном порядке дает тот же результат, то есть B + A = A + B .) Обсудите, как другой путь для достижения той же точки может помочь преодолеть препятствие, блокирующее вам другой путь.
6. Вы ведете [латекс] 7 \ text {.} \ Text {50 км} [/ latex] по прямой в направлении 15º к востоку от севера. (а) Найдите расстояния, на которые вам нужно проехать прямо на восток, а затем прямо на север, чтобы добраться до той же точки. (Это определение эквивалентно нахождению компонентов смещения в восточном и северном направлениях.) (b) Покажите, что вы все еще прибываете в одну и ту же точку, если восточный и северный этапы меняются местами.
7. Снова выполните упражнение 4, используя аналитические методы, и измените второй этап прогулки на 25,0 м прямо на юг. (Это эквивалентно вычитанию B из A , то есть нахождению R ‘ = A — B ) (b) Повторите еще раз, но теперь вы сначала идете на 25,0 м на север, а затем на 18,0 м на восток. (Это эквивалентно вычитанию A из B, то есть поиску 30.8 м, 35,8 к западу от севера. Это согласуется с вашим результатом?)
8. У нового землевладельца есть треугольный участок плоской земли, который она хочет оградить. Начиная с западного угла, она измеряет длину первой стороны 80,0 м, а следующей — 105 м. Эти стороны представлены как векторы смещения A от B на рисунке 15. Затем она правильно вычисляет длину и ориентацию третьей стороны C. Каков ее результат?
Рисунок 15.
9.Вы летите 32,0 км по прямой в неподвижном воздухе в направлении 35º к югу от запада. (а) Найдите расстояния, на которые вам придется лететь прямо на юг, а затем прямо на запад, чтобы прибыть в ту же точку. (Это определение эквивалентно нахождению компонентов смещения в южном и западном направлениях.) (B) Найдите расстояния, на которые вам придется пролететь сначала в направлении 45,0º к югу от запада, а затем в направлении 45,0º к западу от севера. . Это компоненты смещения по другому набору осей — одна повернута на 45 °.
10. Фермер хочет отгородить свой четырехсторонний участок плоской земли. Он измеряет первые три стороны, показанные как A, B и C на рисунке 16, а затем правильно вычисляет длину и ориентацию четвертой стороны D. Каков его результат?
Рисунок 16.
11. Пытаясь сбежать со своего острова, Гиллиган строит плот и отправляется в море. В течение дня ветер сильно меняется, и его дует по следующим прямым линиям: 2,50 км 45,0 ° к северу от запада; затем 4.70 км 60,0º к югу от востока; затем 1,30 км 25º к югу от запада; затем 5,10 км прямо на восток; затем 1,70 км 5,00º к востоку от севера; затем 7.20 к югу от запада; и, наконец, 2,80 км, 10,0 ºсеверо востока. Каково его окончательное положение относительно острова?
12. Предположим, пилот летит 40,0 км в направлении 60º к северу от востока, а затем летит 30,0 км в направлении 15º к северу от востока, как показано на рисунке 17. Найдите его общее расстояние R от начальной точки и направление θ. прямого пути до конечной позиции.Обсудите качественно, как этот полет будет изменен ветром с севера и как влияние ветра будет зависеть как от скорости ветра, так и от скорости самолета относительно воздушной массы.
Рисунок 17.
Глоссарий
- аналитический метод:
- Метод определения величины и направления результирующего вектора с использованием теоремы Пифагора и тригонометрических тождеств
Избранные решения проблем и упражнения
1.(а) 1,56 км (б) 120 м на восток
3. Северная составляющая 87,0 км, восточная составляющая 87,0 км
5. 30,8 м, 35,8 к западу от севера
7. (a) 30,8 м, 54,2º к югу от запада (b) 30,8 м, 54,2º к северу от востока
9. 18,4 км к югу, затем 26,2 км к западу (b) 31,5 км под углом 45,0º к югу от запада, затем 5,56 км под углом 45,0º к западу от севера
11. 7,34 км, 63,5º к югу от востока
Векторов
Это вектор:
Вектор имеет величину , (размер) и направление :
Длина линии показывает ее величину, а стрелка указывает направление.
Мы можем сложить два вектора, соединив их голова к хвосту:
И неважно, в каком порядке мы их добавляем, результат будет тот же:
Пример: самолет летит на север, но дует ветер с северо-запада.
Два вектора (скорость, создаваемая воздушным винтом, и скорость ветра) приводят к немного более низкой путевой скорости при движении немного к востоку от севера.
Если бы вы смотрели на самолет с земли, казалось бы, он немного поскользнулся.
Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.
Скорость, ускорение, сила и многое другое — векторы.
Вычитание
Мы также можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- , затем добавьте их как обычно:
a — b
Обозначение
Вектор часто пишется полужирным шрифтом , например, a или b .
| Вектор также может быть записан как буквы его головы и хвоста со стрелкой над ним, например: |
Расчеты
А теперь … как нам делать расчеты?
Самый распространенный способ — сначала разбить векторы на части x и y, например:
Вектор a разбит на
два вектора a x и a y
(Позже мы увидим, как это сделать.)
Добавление векторов
Затем мы можем сложить векторы на , добавив части x и , добавив части y :
Вектор (8, 13) и вектор (26, 7) складываются в вектор (34, 20)
Пример: складываем векторы
a = (8, 13) и b = (26, 7)c = a + b
c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)
Когда мы разбиваем вектор таким образом, каждая часть называется компонентом :
Вычитание векторов
Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.
Пример: вычесть
k = (4, 5) из v = (12, 2)a = v + — k
a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| a |
ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):
|| a ||
Для его вычисления мы используем теорему Пифагора:
| a | = √ (х 2 + y 2 )
Пример: какова величина вектора
b = (6, 8)?| b | = √ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против скалярного
Скаляр имеет звездную величину (размер) только .
Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.
Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому c — вектор, он имеет величину и направление
- , но c — это просто значение, например 3 или 12.4
Пример: k
b на самом деле является скаляром, умноженным на k, вектор b .Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы меняем размер вектора.
Пример: умножить вектор
m = (7, 3) на скаляр 3| a = 3 м = (3 × 7, 3 × 3) = (21, 9) |
Он все еще указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (скалярное произведение и перекрестное произведение)
Как умножить два вектора вместе? Есть несколько способов! (Подробности см. На этих страницах.) |
Более двух измерений
Векторы также отлично работают в трех и более измерениях:
Вектор (1, 4, 5)
Пример: складываем векторы
a = (3, 7, 4) и b = (2, 9, 11)c = a + b
с = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)
Пример: какова величина вектора
w = (1, −2, 3)?| w | = √ (1 2 + (−2) 2 + 3 2 ) = √ (1 + 4 + 9) = √14
Вот пример с 4-мя измерениями (но его сложно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)
Звездная величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины по осям x и y (или наоборот):
| <=> | ||
| Вектор a в полярных координатах Координаты | Вектор a в декартовой системе координат Координаты |
Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:
| От полярных координат (r, θ ) до декартовых координат (x, y) | От декартовых координат (x, y) до полярных координат (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут ящик.
- Сэм тянет с силой 200 Ньютонов при 60 °
- Алекс тянет с усилием 120 Ньютонов под углом 45 °, как показано на рисунке
Что такое объединенная сила и ее направление?
Давайте сложим два вектора голова к хвосту:
Первое преобразование из полярной системы в декартовую (до 2 десятичных знаков):
Вектор Сэма:
- x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
- y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21
Вектор Алекса:
- x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
- y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85
Теперь у нас:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ действителен, но давайте вернемся к полярному, поскольку вопрос был в полярном:
- r = √ (x 2 + y 2 ) = √ (184.85 2 + 88,36 2 ) = 204,88
- θ = tan -1 (y / x) = tan -1 (88,36 / 184,85) = 25,5 °
И у нас есть (округленный) результат:
А для Сэма и Алекса это выглядит так:
Они могли бы получить лучший результат, если бы стояли плечом к плечу!
графических методов — физика колледжа: OpenStax
Сводка
- Ознакомьтесь с правилами сложения, вычитания и умножения векторов.
- Применяйте графические методы сложения и вычитания векторов для определения смещения движущихся объектов.
Вектор — величина, имеющая величину и направление.Например, смещение, скорость, ускорение и сила — это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (то есть системы координат), используя стрелку, имеющую длину, пропорциональную величине вектора, и указывающую в направлении вектора.
На рисунке 2 показано такое графическое представление вектора вектора , используя в качестве примера общее смещение человека, идущего по городу, рассмотренному в главе 3.1 Кинематика в двух измерениях: введение. Мы будем использовать обозначение, что жирный символ, такой как [latex] \ textbf {D} [/ latex], обозначает вектор. Его величина обозначается курсивом [латекс] \ boldsymbol {D}, [/ latex], а направление — [латексом] \ boldsymbol {\ theta}. [/ Latex]
ВЕКТОРОВ В ЭТОМ ТЕКСТЕ
В этом тексте мы представим вектор с переменной жирным шрифтом. Например, мы представим количественную силу вектором [latex] \ textbf {F}, [/ latex], который имеет как величину, так и направление.Величина вектора будет представлена переменной курсивом, например [latex] \ boldsymbol {F}, [/ latex], а направление переменной будет задано углом [latex] \ boldsymbol {\ theta}. . [/ латекс]
Рис. 2. Человек идет 9 кварталов на восток и 5 кварталов на север. Смещение составляет 10,3 блока под углом 29,1 o севернее востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, рассматриваемому на рисунке 2, нарисуйте стрелку, представляющую вектор полного смещения D .Используя транспортир, нарисуйте линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна величине вектора и измеряется вдоль линии с помощью линейки. В этом примере величина вектора D составляет 10,3 единицы, а направление θ составляет 29,1 o к северу от востока.Метод «голова к хвосту» — это графический способ добавления векторов, описанный на рисунке 4 ниже и в следующих шагах.Хвост вектора является начальной точкой вектора, а конец (или вершина) вектора является конечным заостренным концом стрелки.
Рис. 4. Метод «голова к хвосту» : Метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, направленного на восток.(c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы сформировать сумму или результирующего вектора D . Длина стрелки D пропорциональна величине вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, составляет 29,1 0 .Шаг 1. Нарисуйте стрелку для обозначения первого вектора (9 блоков на восток) с помощью линейки и транспортира .
Рисунок 5.Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 блоков к северу). Поместите хвост второго вектора в начало первого вектора .
Рисунок 6.Шаг 3. Если имеется более двух векторов, продолжить этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас только два вектора, поэтому мы закончили размещать стрелки от конца к хвосту .
Шаг 4. Нарисуйте стрелку от хвоста первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рис. 7.Шаг 5. Чтобы получить звездную величину полученного результата, измерьте его длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление результирующего, измерьте угол, который он образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть сделаны чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1: Добавление векторов графическим методом «голова к хвосту»: женщина на прогулке
Используйте графическую технику для добавления векторов, чтобы найти полное смещение человека, который идет следующими тремя путями (смещениями) на плоском поле.о} [/ латекс] к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0 ° к югу от востока.
Стратегия
Изобразите каждый вектор смещения графически стрелкой, обозначив первый [latex] \ textbf {A}, [/ latex], второй [latex] \ textbf {B}, [/ latex] и третий [latex] \ textbf { C}, [/ latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» дает возможность определить величину и направление результирующего смещения, обозначенного [latex] \ textbf {R}.[/ латекс]
Решение
(1) Нарисуйте три вектора смещения.
Рис. 8.(2) Поместите векторы голова к хвосту, сохраняя как их начальную величину, так и направление.
Рисунок 9.(3) Нарисуйте результирующий вектор, [latex] \ textbf {R}. [/ Latex]
Рис. 10.(4) Используйте линейку для измерения величины [latex] \ textbf {R}, [/ latex] и транспортир для измерения направления [latex] \ textbf {R}. [/ Latex ] Хотя направление вектора можно указать разными способами, самый простой способ — измерить угол между вектором и ближайшей горизонтальной или вертикальной осью.о} [/ латекс] к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результат не зависит от порядка добавления векторов. Следовательно, мы можем складывать векторы в любом порядке, как показано на рисунке 12, и мы все равно получим то же самое решение.
Рисунок 12.Здесь мы видим, что когда одни и те же векторы добавляются в другом порядке, результат тот же.Эта характеристика верна во всех случаях и является важной характеристикой векторов. Сложение вектора — , коммутативное . Векторы можно добавлять в любом порядке.
[латекс] \ boldsymbol {\ textbf {A} + \ textbf {B} = \ textbf {B} + \ textbf {A}}. [/ Latex]
(Это верно и для сложения обычных чисел — вы получите тот же результат независимо от того, добавляете ли вы [латекс] \ boldsymbol {2 + 3} [/ latex] или [латекс] \ boldsymbol {3 + 2}, [/ латекс] например).
Вычитание векторов — это прямое расширение векторного сложения.Чтобы определить вычитание (скажем, мы хотим вычесть [latex] \ textbf {B} [/ latex] из [latex] \ textbf {A}, [/ latex] написано [latex] \ boldsymbol {\ textbf {A} — \ textbf {B}} [/ latex], мы должны сначала определить, что мы подразумеваем под вычитанием. Отрицательное значение вектора [latex] \ textbf {B} [/ latex] определяется как [latex] \ boldsymbol {- \ textbf {B}}; [/ latex] то есть графически негатив любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, [latex] \ textbf {B} [/ latex] имеет ту же длину, что и [latex] \ boldsymbol {- \ textbf {B}}, [/ latex], но указывает в противоположном направлении.По сути, мы просто переворачиваем вектор, чтобы он указывал в противоположном направлении.
Рис. 13. Негатив вектора — это просто еще один вектор той же величины, но указывающий в противоположном направлении. Итак, B — это отрицательное значение -B ; он имеет ту же длину, но противоположное направление.Вычитание вектора [latex] \ textbf {B} [/ latex] из вектора [latex] \ textbf {A} [/ latex] тогда просто определяется как добавление [latex] \ boldsymbol { — \ textbf {B}} [/ latex] в [latex] \ textbf {A}.[/ latex] Обратите внимание, что вычитание вектора — это сложение отрицательного вектора. Порядок вычитания не влияет на результаты.
[латекс] \ boldsymbol {\ textbf {A} — \ textbf {B} = \ textbf {A} + (- \ textbf {B})}. [/ Latex]
Аналогично вычитанию скаляров (где, например, [latex] \ boldsymbol {5-2 = 5 + (- 2)} [/ latex]). Опять же, результат не зависит от порядка, в котором выполняется вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.о} [/ латекс] к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном направлению , на втором этапе пути, где она окажется? Сравните это местоположение с расположением дока.
Рисунок 14.Стратегия
Мы можем представить первый этап путешествия вектором [latex] \ textbf {A}, [/ latex], а второй этап путешествия вектором [latex] \ textbf {B}. [/ Latex] док-станция расположена по адресу [latex] \ boldsymbol {\ textbf {A} \: + \: \ textbf {B}}.о} [/ латекс] к югу от востока. Мы представляем это как [latex] \ boldsymbol {- \ textbf {B}}, [/ latex], как показано ниже. Вектор [latex] \ boldsymbol {- \ textbf {B}} [/ latex] имеет ту же величину, что и [latex] \ textbf {B} [/ latex], но в противоположном направлении. Таким образом, она окажется в местоположении [latex] \ boldsymbol {\ textbf {A} + (- \ textbf {B})}, [/ latex] или [latex] \ boldsymbol {\ textbf {A} — \ textbf {B}}. [/ Латекс]
Рис. 15.Мы выполним векторное сложение, чтобы сравнить местоположение док-станции, [latex] \ boldsymbol {\ textbf {A} + \ textbf {B}}, [/ latex] с местоположением, в котором ошибочно женщина прибывает, [латекс] \ boldsymbol {\ textbf {A} + (- \ textbf {B})}.[/ латекс]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [latex] \ textbf {A} [/ latex] и [latex] \ boldsymbol {- \ textbf {B}}. [/ Latex]
(2) Поместите векторы головой к хвосту.
(3) Нарисуйте результирующий вектор [latex] \ textbf {R}. [/ Latex]
(4) Используйте линейку и транспортир, чтобы измерить величину и направление [латекса] \ textbf {R}. [/ Latex]
Рисунок 16.В данном случае [latex] \ boldsymbol {\ textbf {R} = 23.о} [/ латекс] к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от пристани, если она поедет в противоположном направлении на втором этапе пути.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и для сложения.
Если бы мы решили пройти в три раза дальше на первом этапе пути, рассмотренном в предыдущем примере, то мы прошли бы [латекс] \ boldsymbol {3 \ times 27.о} [/ латекс] к северу от востока. Это пример умножения вектора на положительный скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору противоположного направления . Например, если вы умножите на –2, величина удвоится, но направление изменится. Мы можем резюмировать эти правила следующим образом: Когда вектор [latex] \ textbf {A} [/ latex] умножается на скаляр [latex] \ boldsymbol {c}, [/ latex]
- величина вектора становится абсолютным значением [latex] \ boldsymbol {cA}, [/ latex]
- если [latex] \ boldsymbol {c} [/ latex] положительный, направление вектора не меняется,
- если [latex] \ boldsymbol {c} [/ latex] отрицательное значение, направление меняется на противоположное.
В нашем случае [latex] \ boldsymbol {c = 3} [/ latex] и [latex] \ boldsymbol {\ textbf {A} = 27.5 \ textbf {m}}. [/ Latex] Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление — это обратное умножение. Например, деление на 2 аналогично умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и для деления; просто рассматривайте делитель как скаляр от 0 до 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора.Однако во многих случаях нам нужно будет сделать наоборот. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, производят его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например x — и y -компонентов или компонентов север-юг и восток-запад.
Например, мы можем знать, что общее перемещение человека, идущего по городу, равно 10.o} [/ latex] к северу от востока и хотите узнать, сколько кварталов на восток и север нужно было пройти. Этот метод называется , , поиск компонентов (или частей) , смещения в восточном и северном направлениях, и это процесс, обратный процессу, которому следуют для определения общего смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, в которых это полезно. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим сил и в главе 4 «Динамика: законы движения Ньютона».Большинство из них включает поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для поиска компонентов вектора.
ФЕТ ИССЛЕДОВАНИЯ: ИГРА В ЛАБИРИНТ
Узнайте о положении, скорости и ускорении в «Arena of Pain». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру.Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Лабиринт.- Графический метод добавления векторов [latex] \ textbf {A} [/ latex] и [latex] \ textbf {B} [/ latex] включает рисование векторов на графике и добавление их с помощью команды head-to- хвостовой метод. Результирующий вектор [latex] \ textbf {R} [/ latex] определяется таким образом, что [latex] \ boldsymbol {\ textbf {A} + \ textbf {B} = \ textbf {R}}. [/ Latex] Величина и направление [latex] \ textbf {R} [/ latex] затем определяется с помощью линейки и транспортира соответственно.
- Графический метод вычитания вектора [latex] \ textbf {B} [/ latex] из [latex] \ textbf {A} [/ latex] включает добавление противоположности вектора [latex] \ textbf {B}, [ / latex], который определяется как [latex] \ boldsymbol {- \ textbf {B}}. [/ latex] В этом случае [latex] \ boldsymbol {\ textbf {A} — \ textbf {B} = \ textbf { A} + (- \ textbf {B}) = \ textbf {R}}. [/ Latex] Затем метод сложения «голова к хвосту» выполняется обычным способом для получения результирующего вектора [latex] \ textbf {R}. [/ Латекс]
- Сложение векторов равно коммутативному , так что [latex] \ boldsymbol {\ textbf {A} + \ textbf {B} = \ textbf {B} + \ textbf {A}}.[/ латекс]
- Метод «голова к хвосту» добавления векторов включает в себя рисование первого вектора на графике и последующее размещение хвоста каждого последующего вектора в начале предыдущего вектора. Результирующий вектор затем рисуется от хвоста первого вектора к голове последнего вектора.
- Если вектор [latex] \ textbf {A} [/ latex] умножается на скалярную величину [latex] \ boldsymbol {c}, [/ latex], величина продукта определяется как [latex] \ boldsymbol {cA }. [/ latex] Если [latex] \ boldsymbol {c} [/ latex] положительное значение, направление продукта указывает в том же направлении, что и [latex] \ textbf {A}; [/ latex] if [latex] \ boldsymbol {c} [/ latex] имеет отрицательное значение, товар указывает в противоположном направлении, как [latex] \ textbf {A}.[/ латекс]
Концептуальные вопросы
1: Что из следующего является вектором: рост человека, высота на горе. Эверест, возраст Земли, точка кипения воды, стоимость этой книги, население Земли, ускорение свободного падения?
2: Приведите конкретный пример вектора, указав его величину, единицы измерения и направление.
3: Что общего у векторов и скаляров? Чем они отличаются?
4: Два отдыхающих в национальном парке выходят из своей хижины в одно и то же место на озере, каждый идет своим путем, как показано ниже.Общее расстояние, пройденное по пути 1, составляет 7,5 км, а по маршруту 2 — 8,2 км. Каково окончательное смещение каждого кемпера?
Рисунок 19.5: Если пилоту самолета приказывают пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на рисунке 20. Какую еще информацию ему нужно получить в Сакраменто?
Рисунок 20.6: Предположим, вы сделали два шага [latex] \ textbf {A} [/ latex] и [latex] \ textbf {B} [/ latex] (то есть два ненулевых смещения).При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут складываться, чтобы дать ноль? Максимальное расстояние, которое вы можете пройти от начальной точки [latex] \ boldsymbol {\ textbf {A} + \ textbf {B}} [/ latex], является суммой длин двух шагов?
7: Объясните, почему нельзя добавить скаляр к вектору.
8: Если вы сделаете два шага разного размера, сможете ли вы прийти к исходной точке? В более общем смысле, могут ли два вектора с разными величинами складываться к нулю? Можно трое и больше?
Задачи и упражнения
Используйте графические методы для решения этих проблем.Вы можете предположить, что данные, взятые с графиков, имеют точность до трех цифр.
1: Найдите следующее для пути A на рисунке 21: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
Рис. 21. Различные линии представляют собой пути, по которым идут разные люди в городе. Все блоки имеют ширину 120 м.2: Найдите следующее для пути B на рисунке 21: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
3: Найдите северную и восточную составляющие смещения для туристов, показанных на рисунке 19.
4: Предположим, вы идете 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от начальной точки и каково направление по компасу линии, соединяющей исходную точку и конечное положение? (Если вы представите две части прогулки как векторные смещения [latex] \ textbf {A} [/ latex] и [latex] \ textbf {B}, [/ latex], как на рисунке 22, то в этой задаче вас попросят найдите их сумму [латекс] \ boldsymbol {\ textbf {R} = \ textbf {A} + \ textbf {B}} [/ latex].о} [/ латекс] к югу от запада. Как далеко вы находитесь от начальной точки и каково направление по компасу линии, соединяющей исходную точку и конечное положение? (Если вы представите две части прогулки как векторные смещения [latex] \ textbf {A} [/ latex] и [latex] \ textbf {B}, [/ latex], как на рисунке 23, то эта задача находит их сумму [латекс] \ boldsymbol {\ textbf {R} = \ textbf {A} + \ textbf {B}} [/ latex].)
Рисунок 23.6: Повторите описанную выше задачу, но поменяйте порядок двух этапов ходьбы; покажите, что вы получите тот же конечный результат.{\ prime}} [/ latex]). Покажи, что это так.
8: Покажите, что порядок сложения трех векторов не влияет на их сумму. Покажите это свойство, выбрав любые три вектора [latex] \ textbf {A}, \: \ textbf {B}, [/ latex] и [latex] \ textbf {C}, [/ latex], имеющих разную длину и направление. Найдите сумму [latex] \ boldsymbol {\ textbf {A} + \ textbf {B} + \ textbf {C}} [/ latex], затем найдите их сумму при добавлении в другом порядке и покажите, что результат тот же.(Есть пять других порядков, в которых можно добавить [latex] \ textbf {A}, \ textbf {B}, [/ latex] и [latex] \ textbf {C} [/ latex]; выберите только один.)
9: Покажите, что сумма векторов, рассмотренных в примере 2, дает результат, показанный на рисунке 17.
10: Найдите величины скоростей [latex] \ boldsymbol {v_A} [/ latex] и [latex] \ boldsymbol {v_B} [/ latex] на Рисунке 24
Рис. 24. Две скорости v A и v B складываются, чтобы получить общее v к .o} [/ latex] против часовой стрелки относительно изображений на Рисунке 24.Глоссарий
- компонент (двумерного вектора)
- кусок вектора, указывающий либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух вертикальных и горизонтальных векторных компонентов
- коммутативный
- относится к взаимозаменяемости порядка в функции; сложение векторов коммутативно, потому что порядок, в котором векторы складываются вместе, не влияет на окончательную сумму
- направление (вектора)
- ориентация вектора в пространстве
- голова (вектора)
- конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»
- метод «голова к хвосту»
- метод сложения векторов, в котором хвост каждого вектора помещается в начало предыдущего вектора
- звездная величина (вектора)
- длина или размер вектора; величина — скалярная величина
- результат
- сумма двух или более векторов
- результирующий вектор
- векторная сумма двух или более векторов
- скаляр
- величина с величиной, но без направления
- хвост
- начальная точка вектора; напротив наконечника или наконечника стрелки
Решения
Задачи и упражнения
1:
(а) [латекс] \ boldsymbol {480 \ textbf {m}} [/ латекс]
(b) [латекс] \ boldsymbol {379 \ textbf {m}}, \ boldsymbol {18.o} [/ latex] относительно оси x .
11:
x -компонент 4,41 м / с
y -компонент 5,07 м / с
Как сложить и вычесть векторы алгебраически
Введение
В этой статье мы рассмотрим вектор. Векторы — в отличие от простых чисел (скаляров), которые имеют только величину — имеют как величину (длину), так и направление. Мы рассмотрим, как представлять векторные величины, а также как их складывать и вычитать.
Ключевые термины
Цели
Отдельные числа, то есть значения, имеющие только (положительную или отрицательную) величину, называются скалярами. Числа 0, –3, π, i, 1,3, e, и т. Д. — все это примеры скаляров. Другой тип значения, который часто используется в математике, — это вектор. Вектор — это величина, имеющая направление как величиной , так и направление . В этой статье мы рассмотрим некоторые математические характеристики векторов. Векторы имеют широкое применение, например, в физике.
Введение в векторы
Чтобы понять разницу между скаляром и вектором, полезно вспомнить физические примеры.Рассмотрим, например, температуру. Вы можете использовать термометр для измерения температуры воздуха в разных местах. В каждом случае вы получите некоторое число (и единицу) — скажем, 65 ° F. Это величина, но с ней не связано никакого направления; таким образом, это скалярная величина. Теперь рассмотрим измерения ветра в тех же местах. Когда вы измеряете ветер, вы, вероятно, измеряете и скорость, и направление. Таким образом, ваши измерения ветра составляют вектор. Мы могли бы выразить этот вектор в виде стрелки, указывающей в направлении ветра, причем длина стрелки пропорциональна скорости ветра.Ниже показаны два измерения ветра, сделанные в разных точках; стрелки представляют векторы, связанные с этими измерениями.
Векторы имеют величину и направление, но сами по себе не имеют назначенного местоположения. То есть, пока сохраняется направление и длина «стрелки», мы можем перемещать ее куда угодно, не меняя ее. Это важная характеристика, которая позволит нам активно работать с векторами.
Представление векторов
Наша первая задача — найти способ четко и последовательно представлять векторы. Графически это просто: поскольку мы можем перемещать вектор куда угодно, давайте всегда располагаем «хвост» вектора в начале координатной плоскости. (Обратите внимание, что «голова» и «хвост» вектора определены, как показано ниже.)
Теперь, когда хвост вектора помещен в начало координат (помните, мы можем перемещать вектор куда угодно, если сохраняем его направление и длину), мы можем количественно определить его как координаты головы.Пример показан ниже для вектора v . (Обратите внимание, что чтобы отличать символы, представляющие векторы, от символов, представляющих скаляры, мы используем жирный шрифт. Другой распространенный метод — использовать небольшую стрелку над символом: например, вектор.)
Таким образом, вектор v — это просто координаты точки в (2, 3). Обратите внимание, что все векторы, показанные ниже, равны (2, 3) — наше соглашение заключается в том, что вектор описывается координатами точки в его голове только , когда его хвост расположен в начале координат.
Хотя мы показали вектор только в двух измерениях, этот подход можно обобщить на любое количество измерений. Например, в трех измерениях вектор будет иметь форму ( x, y, z ). Все свойства двумерных векторов можно легко расширить до трех измерений.
Но как нам «переместить» вектор с числовой точки зрения? Например, скажем, вектор v имеет голову в (3, 2) и хвост в (1, 4).
Ответ заключается в перемещении (или перемещении) головы и хвоста на эквивалентное расстояние и в одном направлении. Это преобразование должно привести к тому, что хвост вектора переместится в начало координат — простой процесс, который включает вычитание каждой координаты хвоста из себя. В приведенном выше примере результат (3–3, 2–2) = (0, 0). Чтобы перевести голову, аналогичным образом вычтите координаты хвоста из координат головы — это удовлетворяет нашему критерию, что перевод имеет фиксированное расстояние и направление.Таким образом, голову нужно двигать следующим образом: (1 — 3, 4 — 2) = (–2, 2). Таким образом, в общем случае, чтобы найти значение произвольно расположенного вектора, вычтите координаты хвоста из координат головы. Этот процесс проиллюстрирован ниже.
Обратите внимание, что вектор (0, 0), иногда называемый нулевым вектором , имеет длину 0, но не имеет определенного направления. (То есть независимо от того, какое направление вы выберете, нулевой вектор будет одинаковым.)
Практическая задача: Определите значение каждого вектора, показанного на графике ниже.
Решение: В каждом случае можно найти координатное выражение для вектора, вычитая координаты хвоста из соответствующих координат головы. Это работает, даже если хвост находится в начале координат, имеющем координаты (0, 0). Но если хвост находится в начале координат, вектор также просто равен координатам головы. Если это вам поможет, перерисуйте векторы так, чтобы хвосты располагались в начале координат.
a = (–1, 4)
b = (–3, –3)
c = (3 — 3, 2 — 0) = (0, 2)
d = (3 — 2, –4 — [–1]) = (1, –3)
Сложение и вычитание векторов
Как и в случае со скалярами, мы можем складывать и вычитать векторы. Процесс аналогичен, но с одной или двумя оговорками. Чтобы сложить или вычесть два вектора a и b , добавьте или вычтите соответствующие координаты вектора.То есть, где a и b определены следующим образом, вот правила сложения и вычитания.
Обратите внимание, что, как и в случае со скалярами, сложение векторов коммутативно, а вычитание — нет. Графически мы складываем два вектора a и b , помещая хвост b в начало a , а затем создавая новый вектор, начинающийся с хвоста a и заканчивающийся в голове b. .Координаты этого нового вектора определяются так же, как и раньше: путем размещения его хвоста в начале координат. Этот процесс проиллюстрирован ниже для векторов a = (4, 1) и b = (-1, 2).
Обратите внимание, что
Вычитание векторов следует в основном той же процедуре, что и сложение, за исключением того, что вычитаемый вектор «меняет направление».Рассмотрим те же векторы a и b , как указано выше, за исключением того, что мы вычислим a — b. (Обратите внимание, что это то же самое, что и , где — b имеет ту же длину, что и b , но имеет противоположное направление.)
Практическая задача: Выполните следующие векторные операции.
а. (3, 2) — (4, 5) б.(-1, 5) + (10, -6) с. (-1, 0) — (0, 0)
Решение: В каждом случае сложите или вычтите соответствующие координаты, чтобы найти результат.

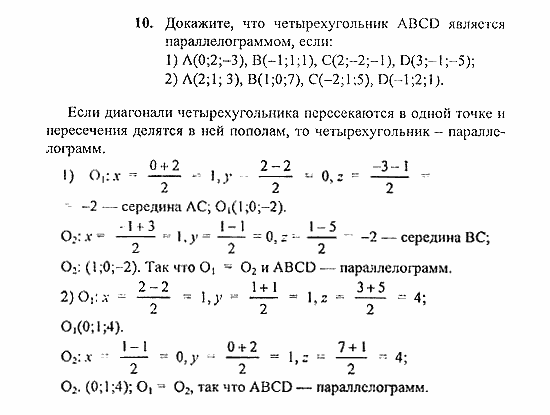 Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.

 Чему равна площадь соответствующего данной дуге кругового сектора?
Чему равна площадь соответствующего данной дуге кругового сектора?

 Постройте векторы, равные:
Постройте векторы, равные:

 Чему равна площадь соответствующего данной дуге кругового сектора?
Чему равна площадь соответствующего данной дуге кругового сектора?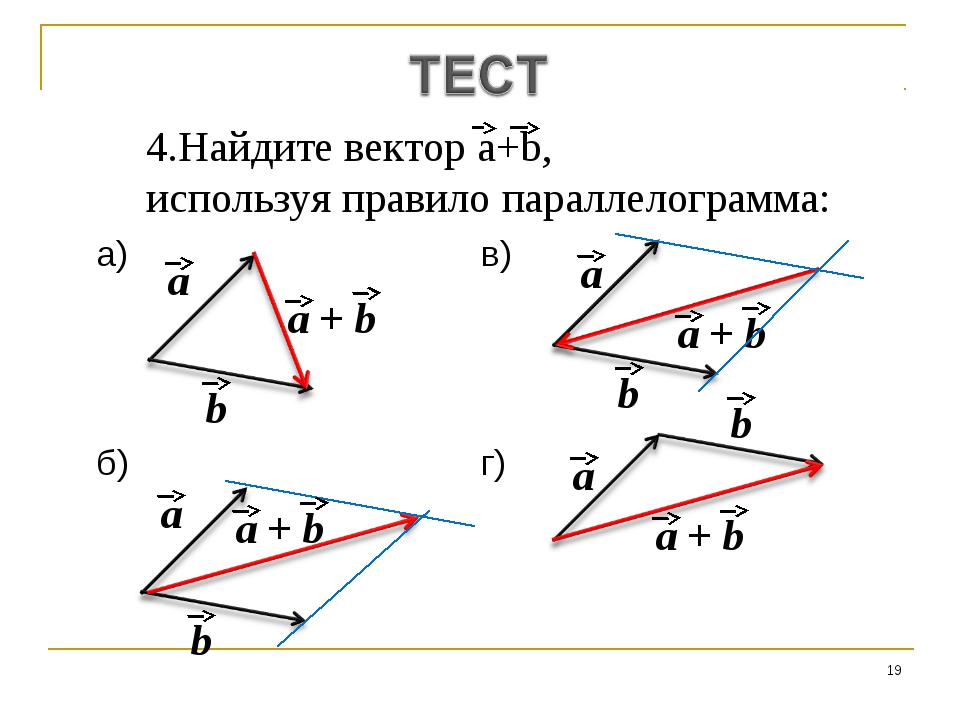
 В ΔАВС: ВС=3,
В=30˚,
С=75˚.
Найдите: АС, АВ,
А.
В ΔАВС: ВС=3,
В=30˚,
С=75˚.
Найдите: АС, АВ,
А. Площадь круга»
Площадь круга»

 Докажите
В=С.
Найдите S∆АВС
Докажите
В=С.
Найдите S∆АВС


 При каком значении х вектора а и b
перпендикулярны, если,
.
При каком значении х вектора а и b
перпендикулярны, если,
.

 Найдите длину этой окружности.(5)
Найдите длину этой окружности.(5) Постройте
точку А1,
симметрич-ную точке А относительно
прямой а
Постройте
точку А1,
симметрич-ную точке А относительно
прямой а Постройте
квадрат А1В1С1D1,
симметричный квадрату АВС D,
относительно прямой а.
Постройте
квадрат А1В1С1D1,
симметричный квадрату АВС D,
относительно прямой а. Постройте точку А1,
получен-ную из точки А поворотом вокруг
точки О против часовой стрелки на угол
120˚
Постройте точку А1,
получен-ную из точки А поворотом вокруг
точки О против часовой стрелки на угол
120˚ Постройте трапецию А1В1С1D1,
полученную, параллельным переносом
трапеции АВСD
на вектор DВ
Постройте трапецию А1В1С1D1,
полученную, параллельным переносом
трапеции АВСD
на вектор DВ