Контрольная работа 2 по геометрии: Контрольная работа №2 по геометрии

Контрольная работа по геометрии для 7 класса № 2

Контрольная работа № 2 Вариант 1 А1. В треугольнике ВСМ провели отрезок ВА так, что образовался прямой угол ВАМ. Как называется отрезок ВА? А) биссектрисой В) высотой С) медианой Д) основанием В1. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВD. Найдите угол АВС, если угол АВD=25º. В2. В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2. Найти стороны треугольника. В3. Сторона CD треугольника CDE равна 24 см, сторона СЕ в 3 раза меньше стороны CD, а сторона DЕ на 7 см больше стороны CD. Найти периметр треугольника CDЕ. В4. Выберите и запишите номера верных утверждений. В любом треугольнике медианы пересекаются в одной точке. В равнобедренном треугольнике все углы равны. Медиана равнобедренного треугольника, проведенная к основанию, является биссектрисой. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. Если высота треугольника совпадает с его биссектрисой, то треугольник разносторонний. В5. АС является биссектрисой BАD, AB = AD. Найти отрезок KD, если КВ = 5 С1. Отрезки АВ и СD пересекаются в точке О, являющейся серединой каждого из них. Докажите, что: а) треугольники АОD и ВОС равны; б) AО = СВО С2. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.

Контрольная работа № 2 Вариант 2 А1. Сколько медиан можно провести в треугольнике? а) 1 б) 2 в) 3 г) бесконечное множество В1. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВD. Найдите угол АВС, если угол АВD=35º. В2. В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3. Найти стороны треугольника. В3. Сторона МР треугольника МРE равна 18 см, сторона МЕ в 2 раза меньше стороны МР, а сторона РЕ на 9 см больше стороны МР. Найти периметр треугольника МРЕ. В4. Выберите и запишите номера верных утверждений: В равных треугольниках против равных сторон лежат равные углы. Из точки, не лежащей на прямой, можно провести два перпендикуляра к этой прямой. Биссектриса угла равнобедренного треугольника, проведенная к основанию этого треугольника, является высотой. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. Сумма длин трёх сторон треугольника называется периметром треугольника. В5. BD = AC, АDB = DAC. Найти BАD, если СDА = 105о С1. Отрезки МЕ и РК пересекаются в точке D, являющейся серединой каждого из них. Докажите, что: а) треугольники РDЕ и КDМ равны; б) PED = KMD С2. Начертите равнобедренный треугольник АВС с основанием AС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.

Геометрия 7 Контрольная 2 (Мерзляк) . 4 варианта

Геометрия 7 Контрольная 2 (Мерзляк). Контрольная работа по геометрии в 7 классе «Треугольники» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Ответов нет.

Геометрия 7 класс (УМК Мерзляк)
Контрольная работа № 2

Треугольники

Вариант 1

1. Докажите равенство треугольников ABF и CBD (рис. 42), если AB = BC и BF = BD.
2. Найдите стороны равнобедренного треугольника, если его периметр равен 33 см, а основание на 3 см меньше боковой стороны.
3. На боковых сторонах AB и BC равнобедренного треугольника ABC отметили соответственно точки D и E так, что ∠ACD = ∠CAE. Докажи те, что AD = CE.
4. Известно, что EK = FK и EC = FC (рис. 43). Докажите, что ∠EMK = ∠FMK.
5. Серединный перпендикуляр стороны AB треугольника ABC пересекает его сторону AC в точке M. Найдите сторону AC треугольника ABC, если BC = 8 см, а периметр треугольника MBC равен 25 см.

Вариант 2

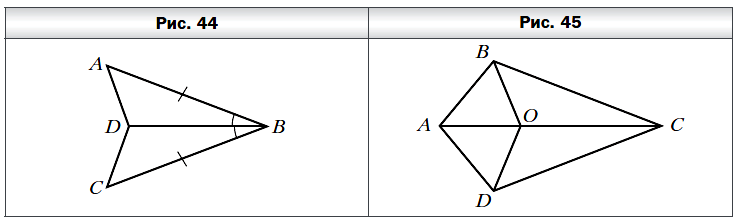
1. Докажите равенство треугольников ABD и CBD (рис. 44), если AB = BC и ∠ABD = ∠CBD.
2. Найдите стороны равнобедренного треугольника, если его периметр равен 30 см, а боковая сторона на 6 см меньше основания.
3. На основании AC равнобедренного треугольника ABC отметили точки M и K так, что ∠ABM = ∠CBK, точка M лежит между точками A и K. Докажите, что AM = CK.
4. Известно, что AB = AD и BC = DC (рис. 45). Докажите, что BO = DO.
5. Медиана BM треугольника ABC перпендикулярна его биссектрисе AD. Найдите сторону AC, если AB = 7 см.

Вариант 3

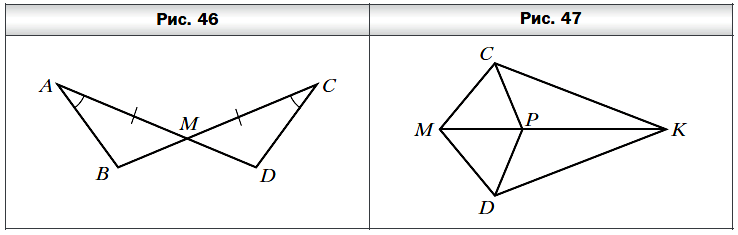
1. Докажите равенство треугольников ABM и CDM (рис. 46), если AM = CM и ∠BAM = ∠DCM.
2. Найдите стороны равнобедренного треугольника, если его периметр равен 49 см, а основание на 7 см больше боковой стороны.
3. На боковых сторонах AB и BC равнобедренного треугольника ABC отметили соответственно точки M и K так, что BM = BK. Докажите, что ∠BAK = ∠BCM.
4. Известно, что CK = DK и ∠CKP = ∠DKP (рис. 47). Докажите, что ∠MCP = ∠MDP.
5. Серединный перпендикуляр стороны AC треугольника ABC пересекает его сторону BC в точке D. Найдите периметр треугольника ABD, если AB = 10 см, BC = 15 см.

Вариант 4

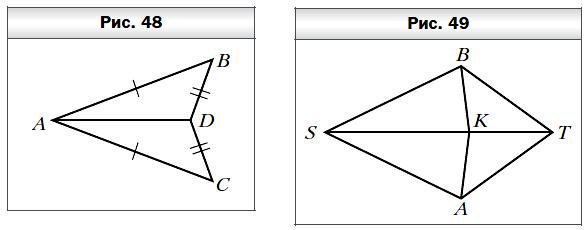
1. Докажите равенство треугольников ABD и ACD (рис. 48), если AB = AC и BD = CD.
2. Найдите стороны равнобедренного треугольника, если его периметр равен 40 см, а боковая сторона на 2 см больше основания.
3. На основании AC равнобедренного треугольника ABC отметили точки D и E так, что AD = CE, точка D лежит между точками A и E. Докажите, что ∠ABD = ∠ CBE.
4. Известно, что ∠BST = ∠AST и ∠STB = ∠STA (рис. 49). Докажите, что BK = AK.
5. Прямая, проведённая через вершину A треугольника ABC, перпендикуляр на его медиане CM и делит её пополам. Найдите сторону AC, если AB = 18 см.

 

---

Вернуться к Списку контрольных работ по геометрии 7 класс (Мерзляк)

Вы смотрели: Геометрия 7 Контрольная 2 (Мерзляк). Контрольная работа по геометрии в 7 классе «Треугольники» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Цитаты из пособия «Геометрия 7 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Геометрия 8 Атанасян К-2 В-2

Контрольная работа № 2 по геометрии в 8 классе «Теорема Пифагора. Площадь» с ответами и решениями к учебнику Л.С. Атанасяна. Вариант 2. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей. Геометрия 8 Атанасян К-2 В-2

Геометрия 8 класс (Атанасян)
Контрольная работа № 2. Вариант 2.

К-2 «Теорема Пифагора. Площадь» (транскрипт заданий)

Часть 1. Запишите номера верных ответов к заданию 1.
1°. Используя данные, указанные на рисунке, найдите площадь треугольника.
1) 42;   2) 13;   3) 21;   4) 28.

Часть 2. Запишите ответ к заданию 2.
2°. Одна из сторон прямоугольника равна 8 см, а диагональ 17 см. Чему равна вторая сторона прямоугольника?

Часть 3. Запишите обоснованное решение задач 3–5.
3°. Найдите сторону ромба, если его диагонали равны 12 см и 16 см.
4. Найдите площадь равнобедренной трапеции, если ее меньшее основание равно 7 см, боковая сторона – 13 см, высота – 12 см.
5. На рисунке ABCD – прямоугольник, CH⊥BD, сторона АВ в 3 раза меньше диагонали. Найдите СН, если ВС = 20.

---

 

Геометрия 8 Атанасян К-2 В-2
ОТВЕТЫ на контрольную работу:

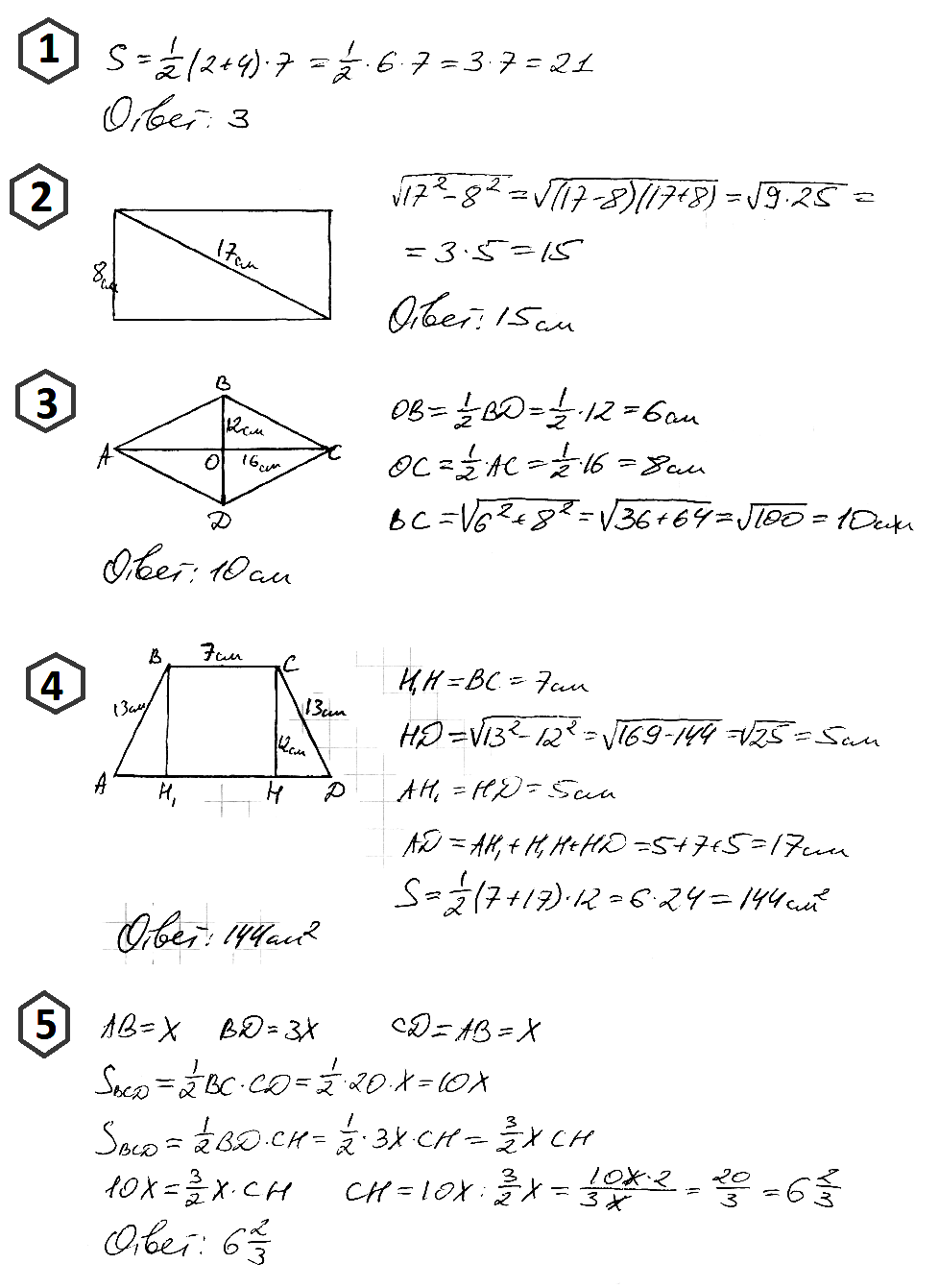
№ 1. Ответ: 3.

№ 2. Ответ: 15 см.

№ 3. Ответ: 10 см.

№ 4. Ответ: 144 см².

№ 5. Ответ: 20/3.

Смотреть образец РЕШЕНИЯ заданий в тетради

 

---

Вы смотрели: Контрольная работа «Теорема Пифагора. Площадь» по геометрии в 8 классе с ответами и решениями для УМК Атанасян. Дидактические материалы (упражнения) для учителей, учащихся и родителей.

К-2. Вариант 0  К-2. Вариант 1  К-2. Вариант 2  К-2. Вариант 3  К-2. Вариант 4

 

---

Вернуться на страницу: Контрольные работы по геометрии в 8 классе УМК Атанасян.

Перейти на страницу: Контрольные работы по геометрии в 8 классе УМК Мерзляк.

Цитаты (упражнения) из учебного пособия «Геометрия 8 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова) использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.

Геометрия 7 Атанасян К-2 В-3

Контрольная работа № 2 «Треугольники» по геометрии в 7 классе с ответами для УМК Атанасян. Вариант 3. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей. Геометрия 7 Атанасян К-2 В-3.

 

Геометрия 7 класс (Атанасян)
Контрольная работа № 2. Вариант 3.

К-2 «Треугольники» (транскрипт заданий)

Часть А. Запишите номера верных ответов к заданию 1.
№ 1. Используя рисунок, укажите верные утверждения: 1) PN — биссектриса треугольника МРК. 2) PN — высота треугольника МРК. 3) ЕК — биссектриса треугольника DEC. 4) ВМ — медиана треугольника CBD. 5) ВМ — биссектриса треугольника CBD.

Часть В. Запишите ответ к заданию 2.
№ 2. Треугольник РОВ — равнобедренный с основанием PR. Чему равен ∠1, если ∠2 = 42°?

Часть С. Запишите обоснованное решение задач 3-5.
№ 3. Луч КС — биссектриса угла DKB, а отрезок DK равен отрезку ВК. Докажите, что ΔKDC = ΔКВС.
№ 4. На основании NK равнобедренного треугольника NBK отложены отрезки NA = КС. Докажите, что ∠NBA= ∠KBC.
№ 5*. В окружности с центром О проведены диаметр АС и хорда BD, пересекающиеся в точке М, причем ВМ = DM. ∠BAC = 35°. Найдите ∠BAD.

---

 

Геометрия 7 Атанасян К-2 В-3
ОТВЕТЫ на контрольную работу:

№ 1.   1, 4.

№ 2.   42°.

№ 3.   См.решения.

№ 4.   См.решения.

№ 5.   70°.

Смотреть РЕШЕНИЯ заданий Варианта 3 в тетради

  

 

---

Вы смотрели: Контрольная работа № 2 «Треугольники» по геометрии в 7 классе с ответами для УМК Атанасян. Дидактические материалы (упражнения) для учителей, учащихся и родителей.

К-2. Вариант 0  К-2. Вариант 1  К-2. Вариант 2  К-2. Вариант 3  К-2. Вариант 4

 

---

Вернуться на страницу: Контрольные работы по геометрии в 7 классе УМК Атанасян.

Перейти на страницу: Контрольные работы по геометрии в 7 классе УМК Мерзляк.

Цитаты (упражнения) из учебного пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова) использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.

Контрольная работа №2 по геометрии 7 класс | Материал по геометрии (7 класс) на тему:

Вариант 1.

Теоретическая часть

1. Три точки, не лежащие на одной прямой, соединенные отрезками, образуют геометрическую фигуру:

а) треугольник

б) угол

в) нет правильного ответа.

2. Утверждение « Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны», является:

а) первым признаком равенства треугольников

б) вторым признаком равенства треугольников

в) нет правильного ответа

3. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется:

а) медианой

б) биссектрисой

в) высотой.

4. Отрезок, соединяющий две точки окружности называется:

а) радиусом

б) диаметром

в) хордой.

5. В равнобедренном треугольнике:

а) углы при основании равны

б) биссектриса, проведенная к основанию, является медианой и высотой

      в) стороны равны

Практическая часть.

Построить окружность с радиусом 2 см. Построить хорду АВ, диаметр CD  и радиус ОК.

Задачи.

1. Отрезки АВ и СD имеют общую середину О. Докажите, что .

2. Луч АD – биссектриса угла А. на сторонах угла А отмечены точки В и С так, что  . Докажите, что АВ = АС

Вариант 2.

Теоретическая часть.

1. Утверждение «Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны», является:

а) первым признаком равенства треугольников

б) вторым признаком равенства треугольников

в) нет правильного ответа.

2. В равных треугольниках против ………………  равных углов лежат равные:

а) стороны

б) углы

       в) нет правильного ответа

3. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называются:

а) медианой

б) биссектрисой

в) высотой.

4. Отрезок, соединяющий центр с какой-либо точкой окружности называется

а) радиусом

б) диаметром

в) хордой.

5.   В равнобедренном треугольнике:

а) высота, проведенная к основанию, является медианой и биссектрисой

б) стороны равны

в) углы при основании равны.

Практическая часть.

Построить окружность с радиусом 3 см. Построить хорду АВ, диаметр CD  и радиус ОК.

Задачи.

1. Отрезки МЕ и  РК точкой D делятся пополам . Докажите, что
2.  На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.

Тест по геометрии (11 класс): Контрольная работа № 2 по теме «Цилиндр, конус, шар»

Геометрия 11 класс Контрольная работа № 2  по теме «Цилиндр, конус, шар»

Вариант 1

В заданиях 1–5 отметьте один правильный, по вашему мнению, ответ.

1. Диагональ осевого сечения цилиндра равна 13 см. Найдите площадь этого сечения, если радиус цилиндра равен 6 см

А) 36                        Б) 60                        В) 48                              Г) 78

2. Радиус основания конуса равен 5 см, угол между образующей и высотой конуса равен 30°. Найдите образующую конуса

А) 5                        Б) 5                        В) 10                      Г) 10        

3. Найдите площадь основания конуса, в котором высота равна 1 см, а образующая составляет  см

А)                          Б) 2                В) 3                       Г)         

4. Найдите площадь осевого сечения усеченного конуса, если высота усеченного конуса равна 10 см, а радиусы оснований составляют 1 см и 3 см

А)  20                        Б) 30                В) 40                      Г) 50

5. Шар с центром в точке О касается плоскости   в точке А (рисунок). Точка В лежит в плоскости , причем AB = d,  ∠ABO =  . Найдите длину отрезка АO

 А)  d tg        Б) d ctg                В) d cos              Г) d sin        

К задачам  6 – 8 запишите полное решение

6. Разверткой боковой поверхности цилиндра является прямоугольник АВСD, где BD=8 см, угол ABD=600 . Найдите площадь полной поверхности цилиндра, если СD – высота цилиндра.

7.  Диаметр шара равен 20. Через конец диаметра сферы проведена плоскость под углом 450 к нему. Найдите площадь сечения, полученного при пересечении шара данной плоскостью.

8. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 1200 .

Найдите:

а) площадь боковой поверхности конуса

б) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 300 .

Геометрия 11 класс Контрольная работа № 2  по теме «Цилиндр, конус, шар»

Вариант 2

В заданиях 1–5 отметьте один правильный, по вашему мнению, ответ.

1. Диагональ осевого сечения цилиндра равна 17 см. Найдите площадь этого сечения, если высота цилиндра равна 8 см

А) 240                Б) 60                        В) 120                     Г) 150

2. Радиус основания конуса равен 5 см, угол между образующей и высотой конуса равен 30°. Найдите высоту конуса

А) 5                        Б) 5                        В) 10                      Г) 10        

3. Найдите площадь основания конуса, в котором высота равна 1 см, а образующая составляет  см

А)                          Б) 2                В) 3                       Г)         

4. Найдите площадь осевого сечения усеченного конуса, если высота усеченного конуса равна 10 см, а радиусы оснований составляют 2 см и 3 см

А)  20                        Б) 30                В) 40                      Г) 50

5. Шар с центром в точке О касается плоскости   в точке А (рисунок). Точка В лежит в плоскости , причем AB = d,  ∠BOA =  . Найдите длину отрезка ВO

 А)  d tg        Б) d sin                В) d cos              Г)          

К задачам  6 – 8 запишите полное решение

6. Диагональ осевого сечения цилиндра равна 8 см и составляет с образующей цилиндра угол 600 . Найдите площадь полной поверхности данного цилиндра.

7.  Диаметр сферы равен 20. Через конец диаметра сферы проведена плоскость под углом 300 к нему.  Найдите длину линии пересечения сферы этой плоскостью.

8. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 300 .

Найдите:

а) площадь боковой поверхности конуса

б) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 600 .

Критерии оценивания:

1-5 задания оцениваются в 1 балл за каждое верное

6-7 по 2 балла за каждое верное

8 – 3 балла (по 1,5 балла на каждый пункт) за каждое верное

Перевод баллов в оценки:

«3» — 4 – 7 баллов

«4» — 8 – 10 баллов

«5» — 11 – 12 баллов

Геометрия — test2.Wikipedia

Геометрия — это математика, используемая для работы с формами.

Содержание

• 1 Примеры фигур в геометрии
• 2 Геометрические измерения
• 3 Как используется геометрия?
• 4 Откуда появилась геометрия?
• 5 простых геометрических идей

Примеры фигур в геометрии [править]

В геометрии есть плоские и твердые формы.Квадраты, круги и треугольники — одни из самых простых фигур в плоской геометрии. Кубы, цилиндры, конусы и сферы — это простые формы в твердой геометрии.

Измерение в геометрии [править]

Геометрия может использоваться для измерения площади и периметра плоской формы.
Его также можно использовать для измерения объема и площади твердого тела.

Как используется геометрия? [Править]

Многие предметы имеют геометрические формы. Геометрию можно использовать для измерения многих вещей, если мы видим, что я состоит из геометрических фигур.Например, геометрия может помочь людям найти:

• Площадь поверхности дома, поэтому можно купить нужное количество краски
• объем ящика, чтобы убедиться, что он достаточно большой, чтобы вместить литр еды
• Площадь фермы, поэтому ее можно разделить на равные части
• расстояние по краю пруда, чтобы узнать, сколько ограждений купить.

Откуда взялась геометрия? [Править]

Геометрия началась как искусство измерения формы земли, чтобы люди могли справедливо разделить ее между собой.Это значит измерить землю. Из этого она превратилась в одну из важнейших частей математики. Его создал греческий математик Евклид.

Некоторые простые идеи в геометрии [править]

В математике геометрия начинается с нескольких простых идей:

Точка отображается на бумаге путем прикосновения к ней карандашом или ручкой без каких-либо боковых движений. Мы знаем, где находится точка, но у нее нет размера.

Прямая линия — это кратчайшее расстояние между двумя точками.Например, Джон туго натягивает веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.

Плоскость — это плоская поверхность, которая не останавливается ни в каком направлении. Шар, помещенный в любое место на этой плоской поверхности, не будет двигаться, если сила тяжести на поверхности постоянна.

Задач с углами — Викторина по геометрии

— Смежные углы — углы, которые имеют общую сторону и имеют общую вершину

— Дополнительные углы — углы, которые складываются, чтобы получить 90

o

— Дополнительные углы — углы, которые складываются в 180 °

— Противоположные углы — когда две линии пересекаются, они образуют две пары противоположных углов.Противоположные углы равны.

— острые углы — углы меньше 90 ^o

— прямые углы — углы равные 90 ^o

— тупые углы — углы больше 90 ^o , но меньше 180 ^o

Вопрос 1. Значение угла BMC на рисунке ниже:

15 ^o

30 ^o

40 ^o

45 ^o

Вопрос 2: Если AC и BD — диагонали прямоугольника ABCD, а треугольник EAB равносторонний, то что значение угла ADE?

40 ^o

30 ^o

25 ^o

20 ^o

Вопрос 3: На рисунке ниже AMB = 100 ^o , ∡BMD = 40 ^o и ∡CME = 60 ^o .В чем ценность ∡CMD?

40 ^o

30 ^o

25 ^o

20 ^o

Вопрос 4: Рассчитайте сумму углов a и b на рисунке ниже:

160 ^o

200 ^o

240 ^o

260 ^o

Вопрос 5: Учитывая две параллельные линии a и b , каково значение угла α в рисунок ниже?

105 ^o

135 ^o

145 ^o

150 ^o

Вопрос 6: Какое дополнение к углу 36 ^o ?

54 ^o

90 ^o

136 ^o

144 ^o

Вопрос 7. Что является дополнением к углу 79 ^o ?

11 ^o

21 ^o

101 ^o

97 ^o

Вопрос 8: Какова сумма внутренних углов геометрической фигуры ниже?

180 ^o

360 ^o

540 ^o

720 ^o

Нажмите кнопку «Отправить», чтобы увидеть результаты.

Страница не найдена · GitHub Pages

Страница не найдена · GitHub Pages

Файл не найден

Сайт, настроенный по этому адресу, не содержать запрошенный файл.

Если это ваш сайт, убедитесь, что регистр имени файла соответствует URL-адресу.
Для корневых URL (например, http://example.com/ ) вы должны предоставить index.html файл.

Прочтите полную документацию для получения дополнительной информации об использовании GitHub Pages .

СЕГОДНЯ В ГЕОМЕТРИИ…  СТАТИСТИКА к гл. 2 Тест  Цель обучения: 3.1 Определить пары линий и углов, образованных пересекающимися линиями  Независимая практика / возврат.

Презентация на тему: «СЕГОДНЯ В ГЕОМЕТРИИ…  СТАТИСТИКА к тесту в главе 2  Цель обучения: 3.1 Определить пары линий и углов, образованных пересекающимися линиями  Независимая практика / возвращение» — стенограмма презентации:

1 СЕГОДНЯ В ГЕОМЕТРИИ…  СТАТИСТИКА к гл.2 Тест  Цель обучения: 3.1 Определить пары линий и углов, образованных пересекающимися линиями  Независимая практика / возврат Глава 2 Тесты

2 КАК ВЫ «СОЗДАЛИ» ?? Результаты для ВСЕХ моих классов по геометрии: УЧЕБНОЕ КОЛИЧЕСТВО УЧАЩИХСЯ, ПРОШИВШИХ ТЕСТ CH.2 (32 балла) 1 ST ПЕРИОД3 RD ПЕРИОД5 TH ПЕРИОД6 TH ПЕРИОД ВСЕГО A277622 B5911631 C684725 D451616 F602210 Среднее 22.5425.9726.7024.9125.03

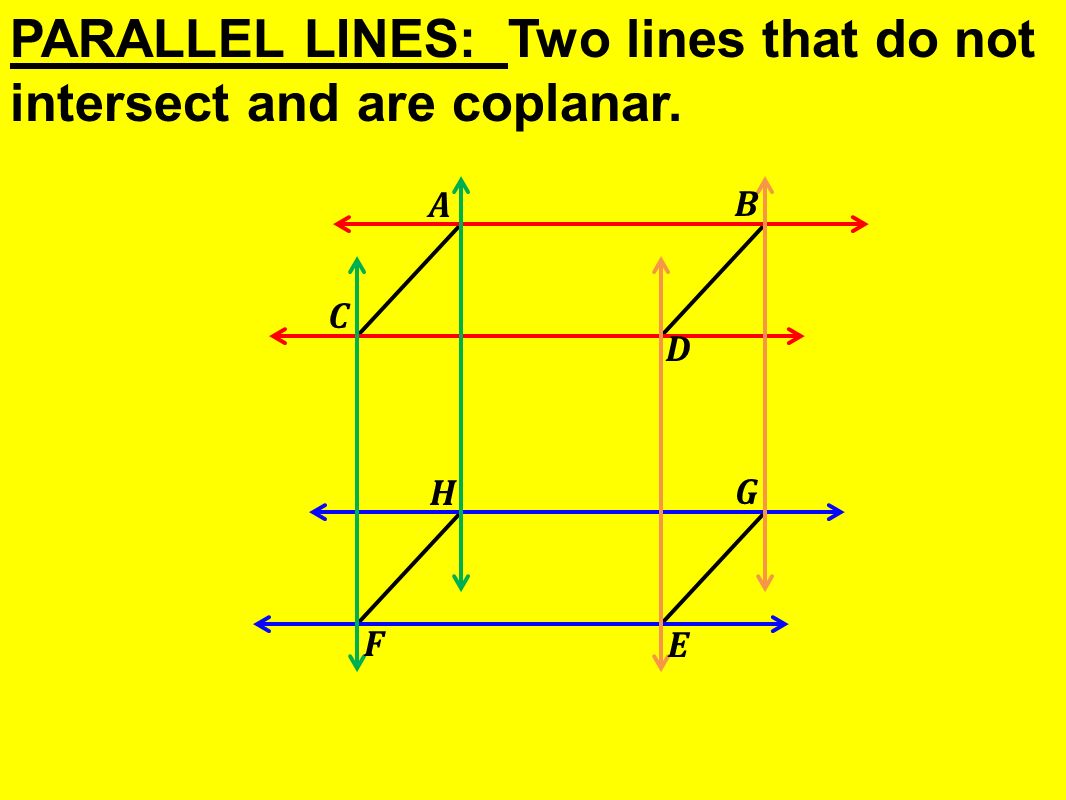
3 ПАРАЛЛЕЛЬНЫЕ ЛИНИИ: две линии, которые не пересекаются и находятся в одной плоскости.

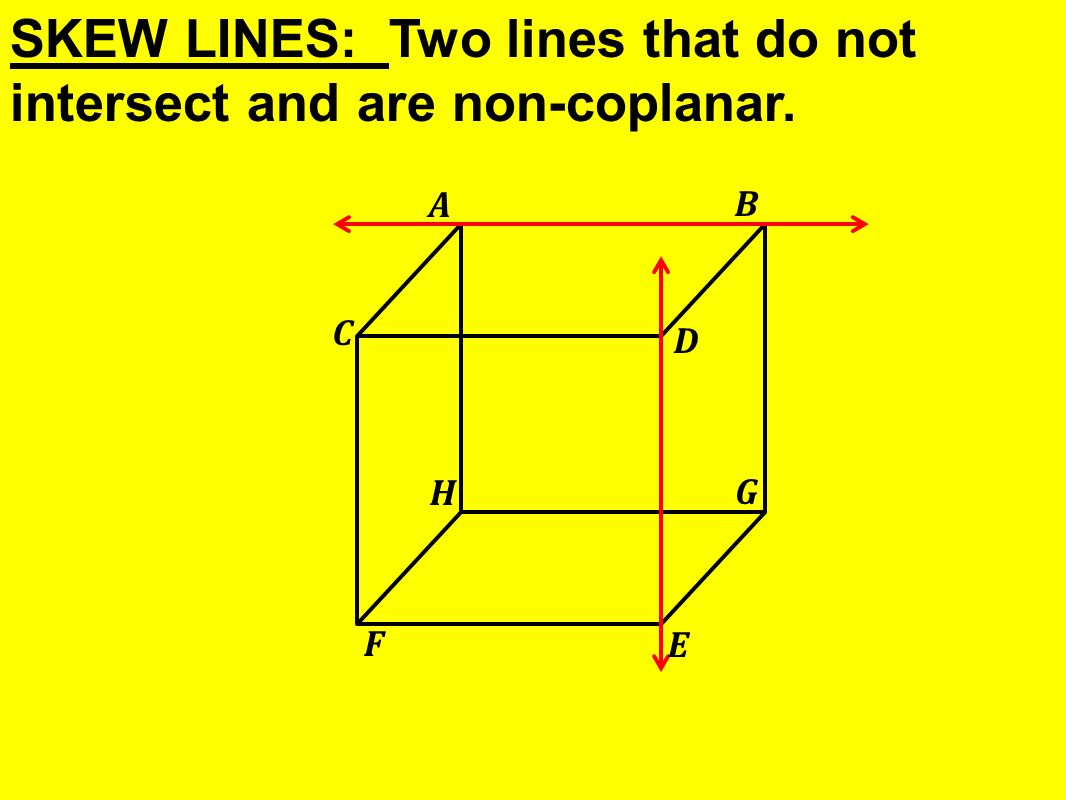
4 ЛИНИИ НАКЛОНА: две линии, которые не пересекаются и не компланарны.

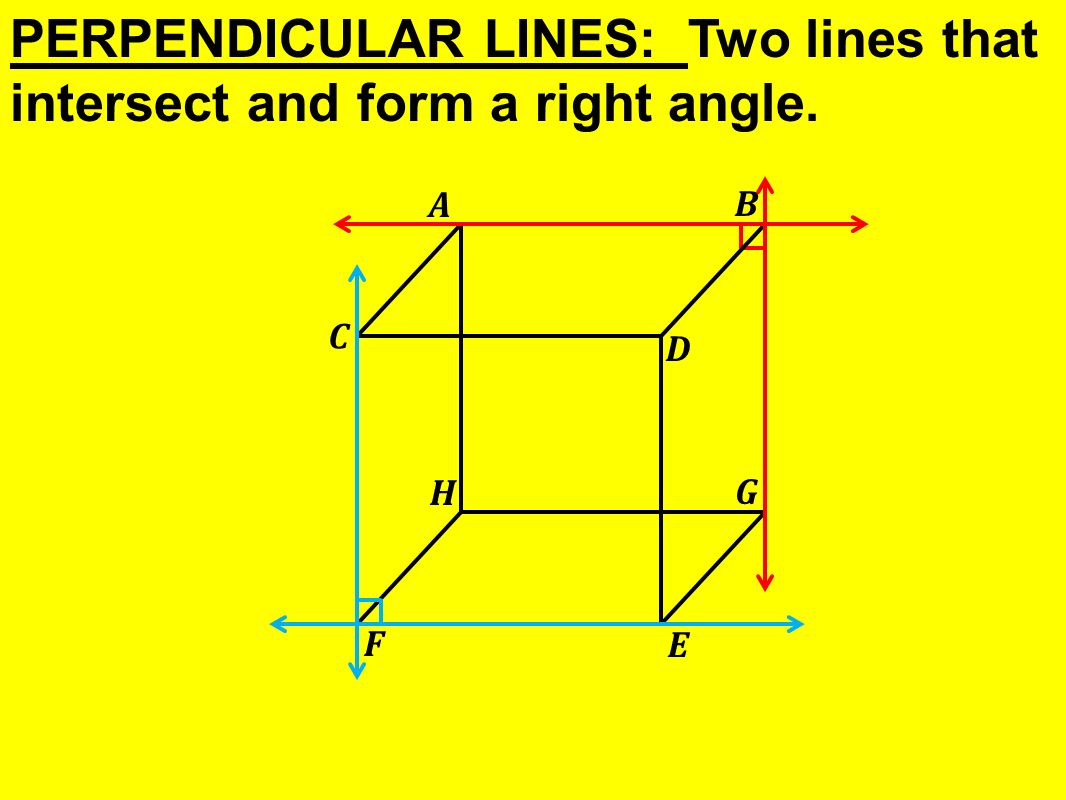
5 ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ: две линии, которые пересекаются и образуют прямой угол.

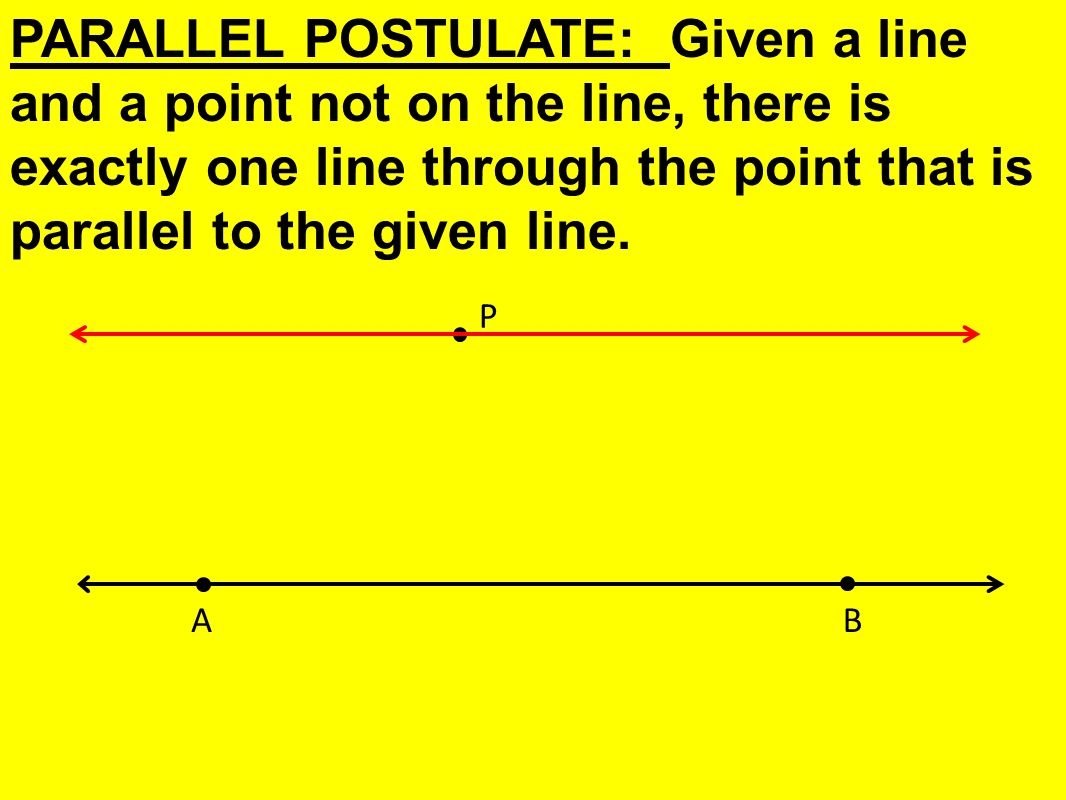
6 ПАРАЛЛЕЛЬНЫЙ ПОСТУЛАТ: дана линия и точка не на этой линии, через точку проходит ровно одна линия, параллельная данной линии.AB P

7 ПЕРПЕНДИКУЛЯРНЫЙ ПОСТУЛАТ: дана линия и точка не на этой линии, через точку проходит ровно одна линия, перпендикулярная данной линии. AB P

8 1 2 3 4 56 7 8 ПОПЕРЕЧНАЯ ПОПЕРЕЧНАЯ: линия, пересекающая две или более копланарных линий.

9 СООТВЕТСТВУЮЩИЕ УГЛЫ (CA): углы в одном и том же положении.1 2 3 4 56 7 8 Углы одного цвета — соответствующие углы. 1 2 3 4 56 7 8 ПОПЕРЕЧНЫЙ

10 АЛЬТЕРНАТИВНЫЕ ВНУТРЕННИЕ УГЛЫ (AIA): Углы, которые лежат между двумя линиями и на противоположных сторонах поперечной. 1 2 3 4 56 7 8 Углы одного цвета — это чередующиеся внутренние углы. 3 4 56 ПОПЕРЕЧНЫЙ Внутренние углы находятся в пространстве между двумя черными линиями.

11 АЛЬТЕРНАТИВНЫЕ НАРУЖНЫЕ УГЛЫ (AEA): углы, которые лежат вне двух линий и на противоположных сторонах поперечной.1 2 3 4 56 7 8 Углы одного цвета — соответствующие углы. 1 2 7 8 ПОПЕРЕЧНАЯ Внешние углы находятся в пространстве за пределами двух черных линий.

Страница не найдена · GitHub Pages

Страница не найдена · GitHub Pages

Файл не найден

Сайт, настроенный по этому адресу, не содержать запрошенный файл.

Если это ваш сайт, убедитесь, что регистр имени файла соответствует URL-адресу.
Для корневых URL (например, http://example.com/ ) вы должны предоставить index.html файл.

Прочтите полную документацию для получения дополнительной информации об использовании GitHub Pages .

.