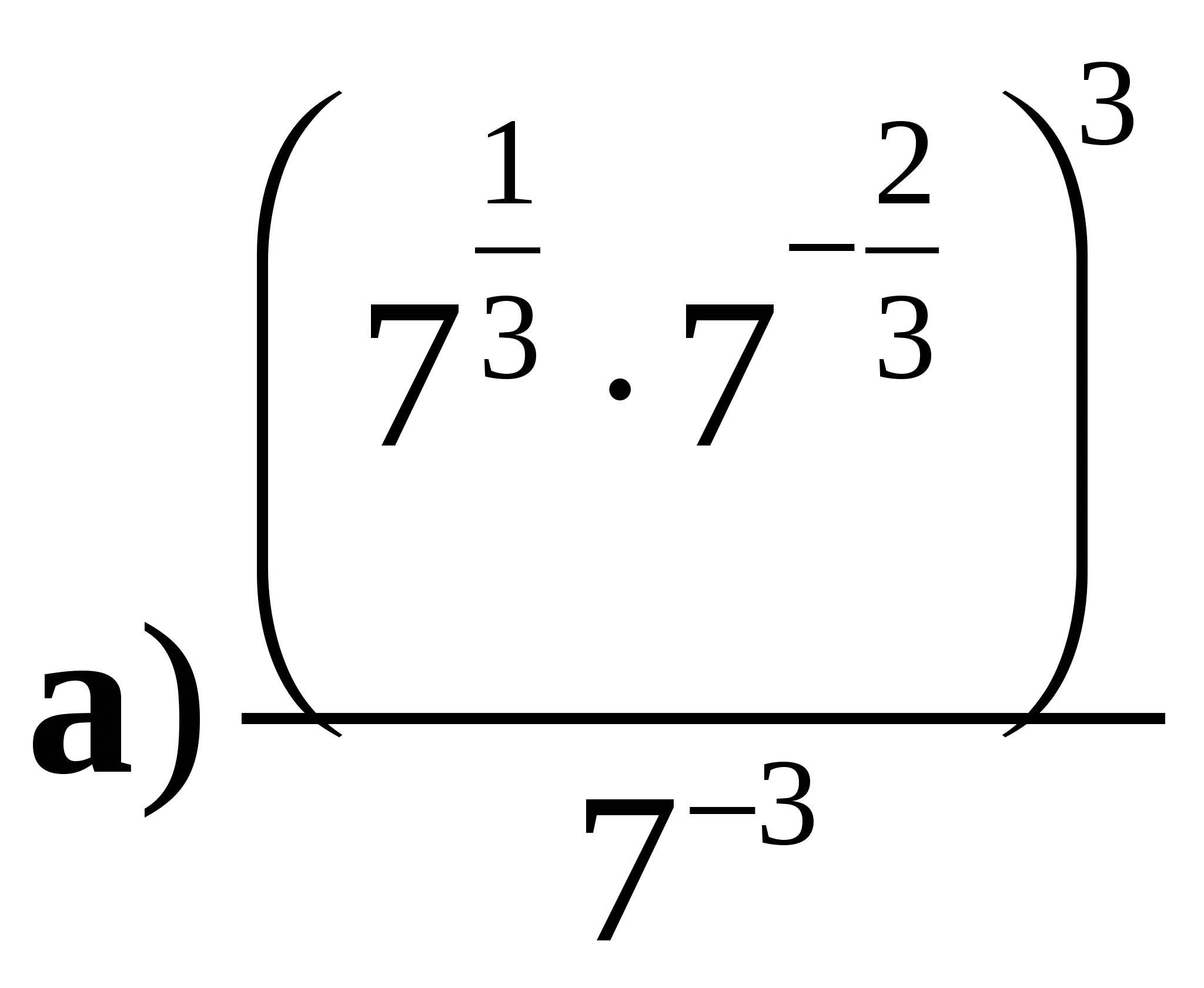 ;
; 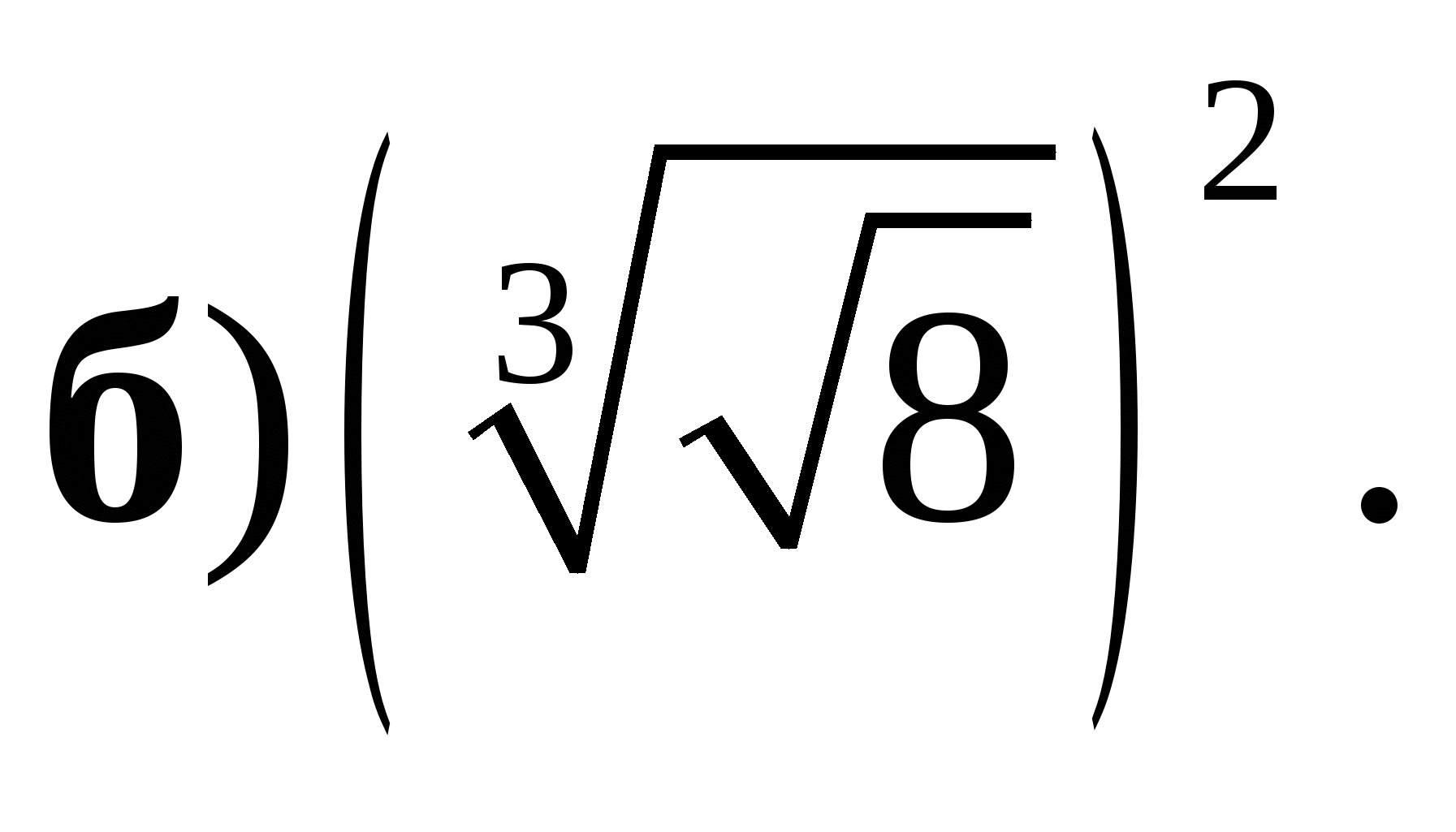
А-10 Контрольная работа №1. Действительные числа
Вариант 1
1. Вычислите: 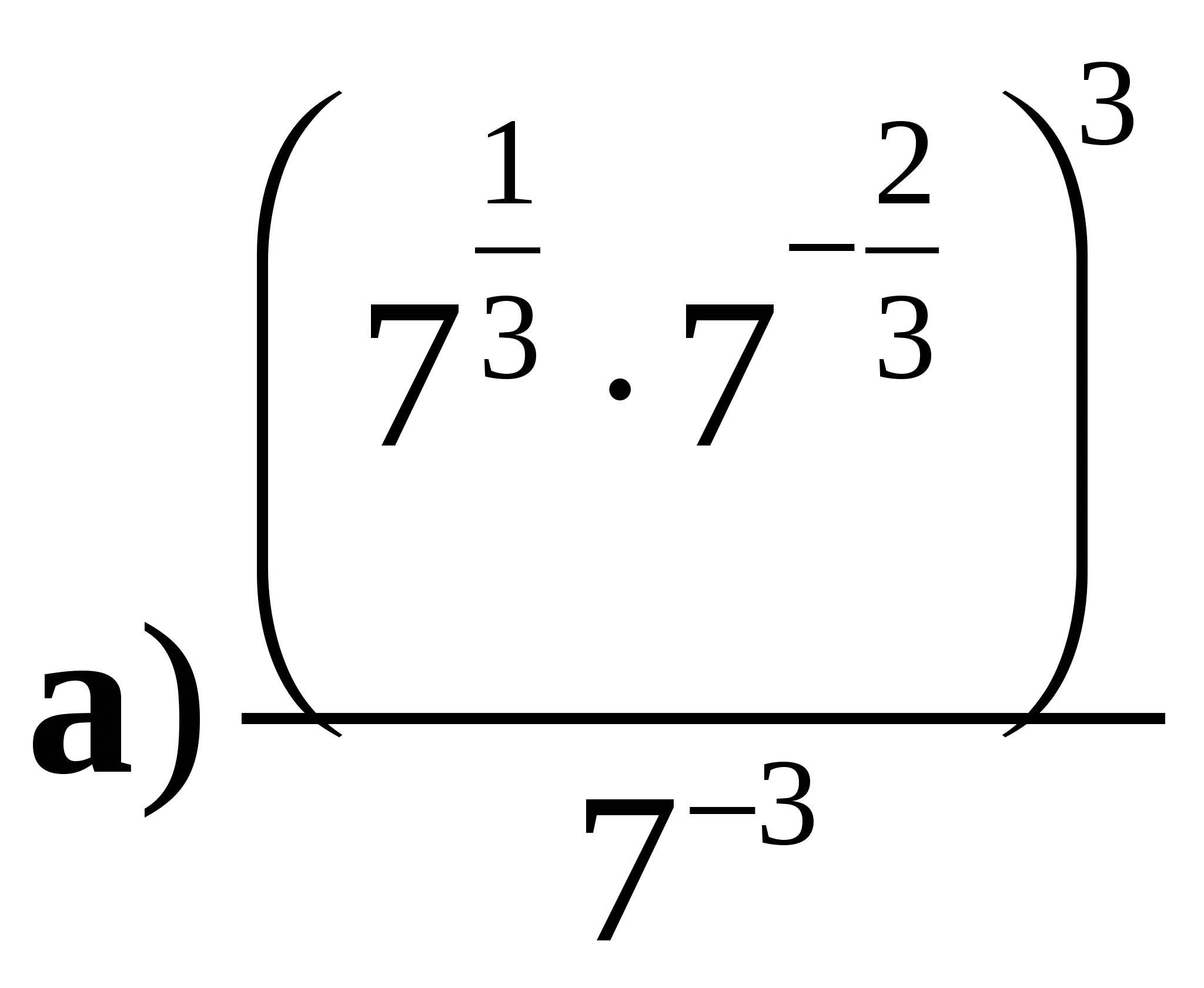 ;
; 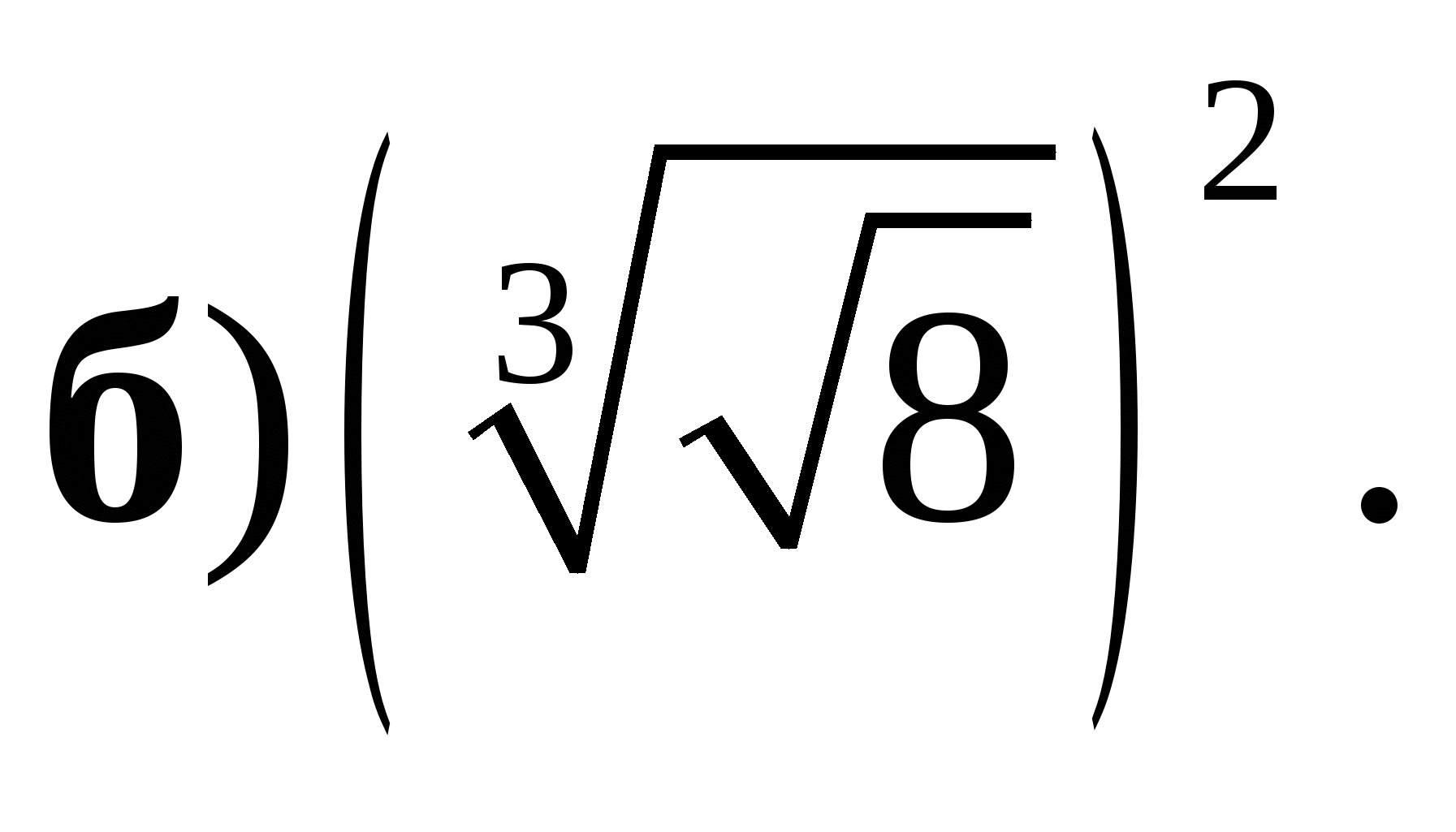
2. Упростите выражение 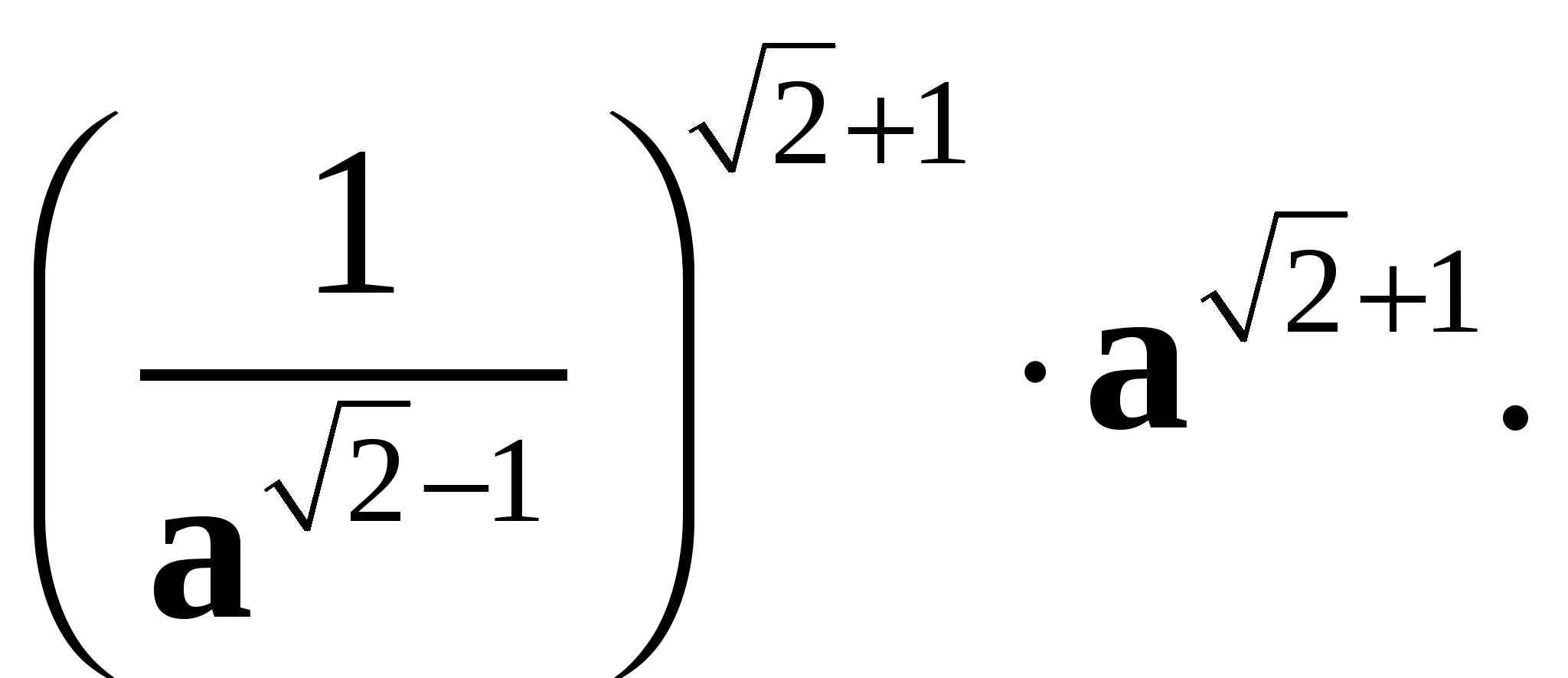
3. Решите уравнение 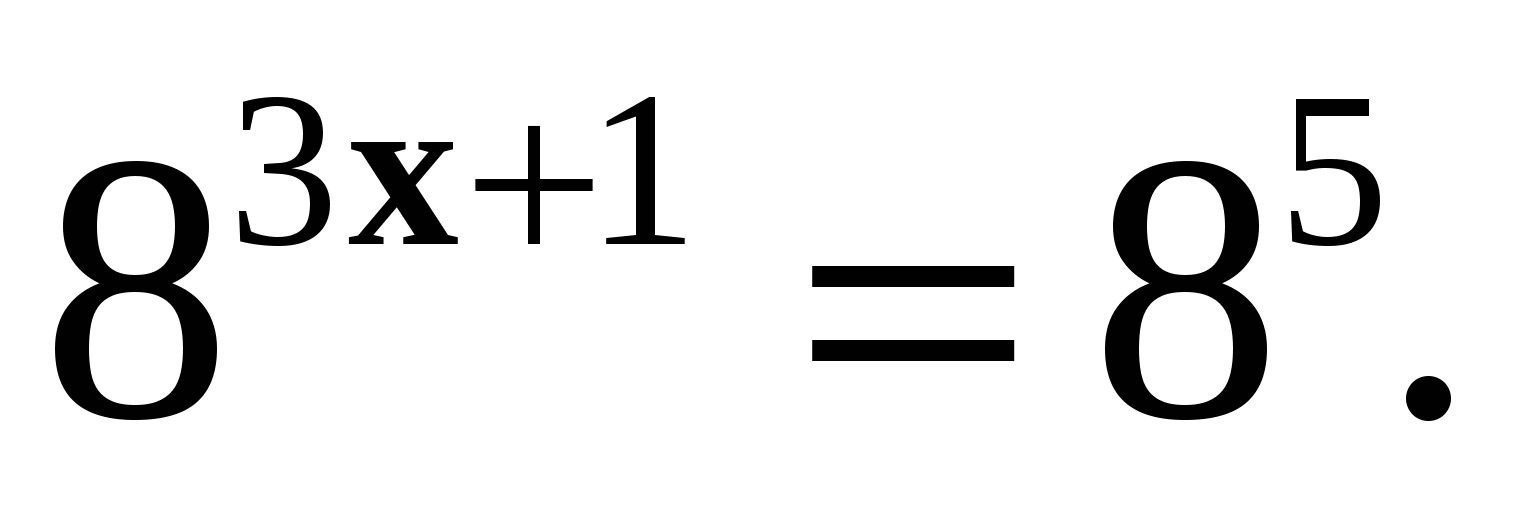
4. Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби.
5. Сократите дробь 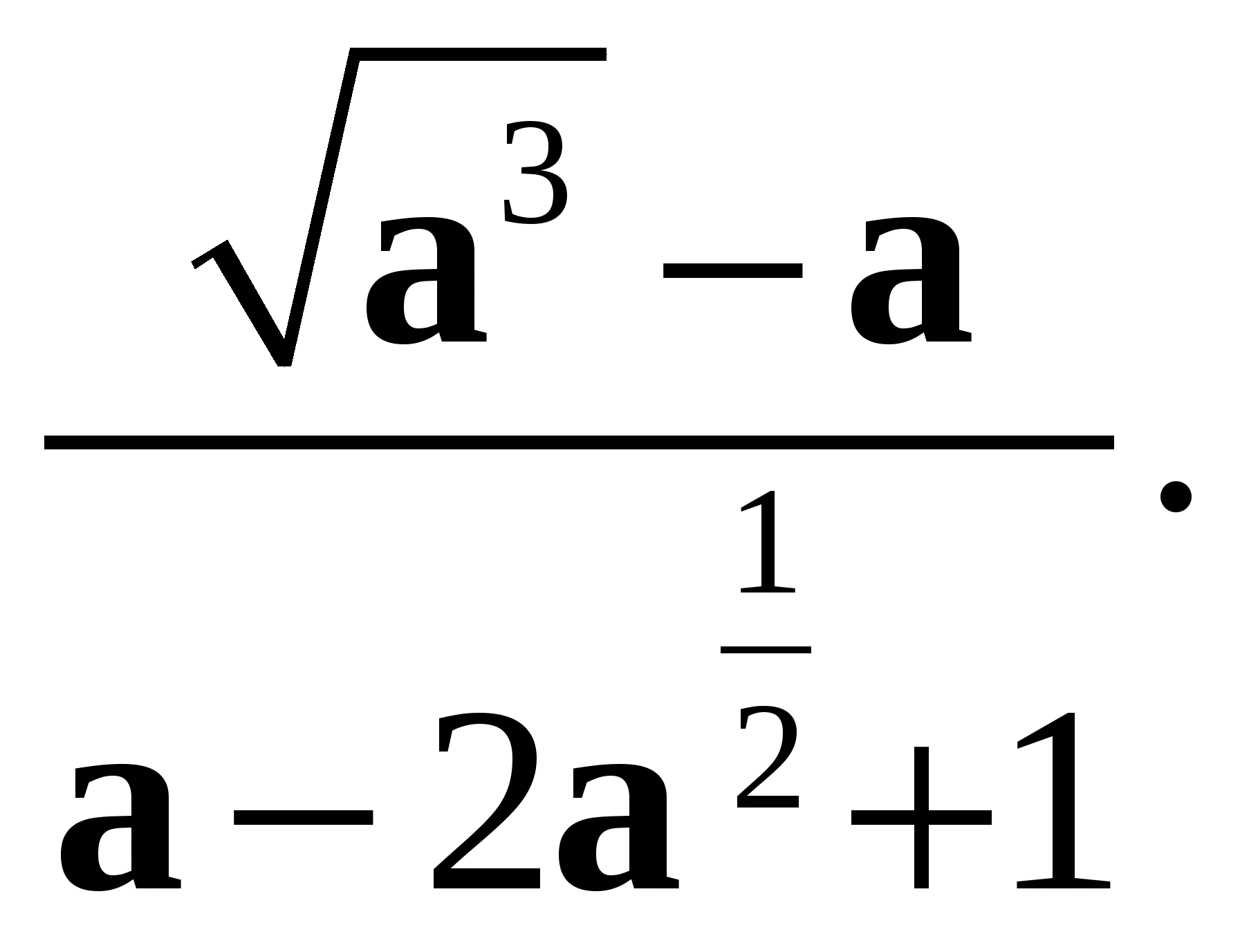
6. Сравните числа: 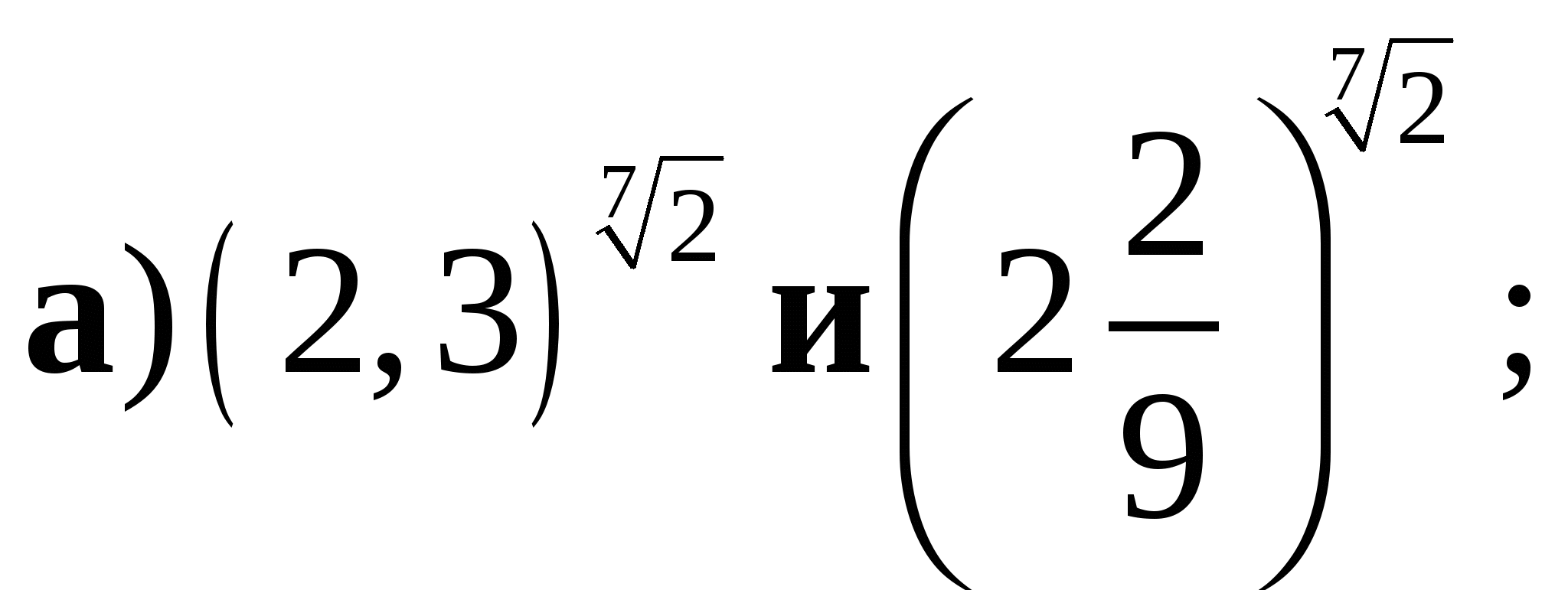
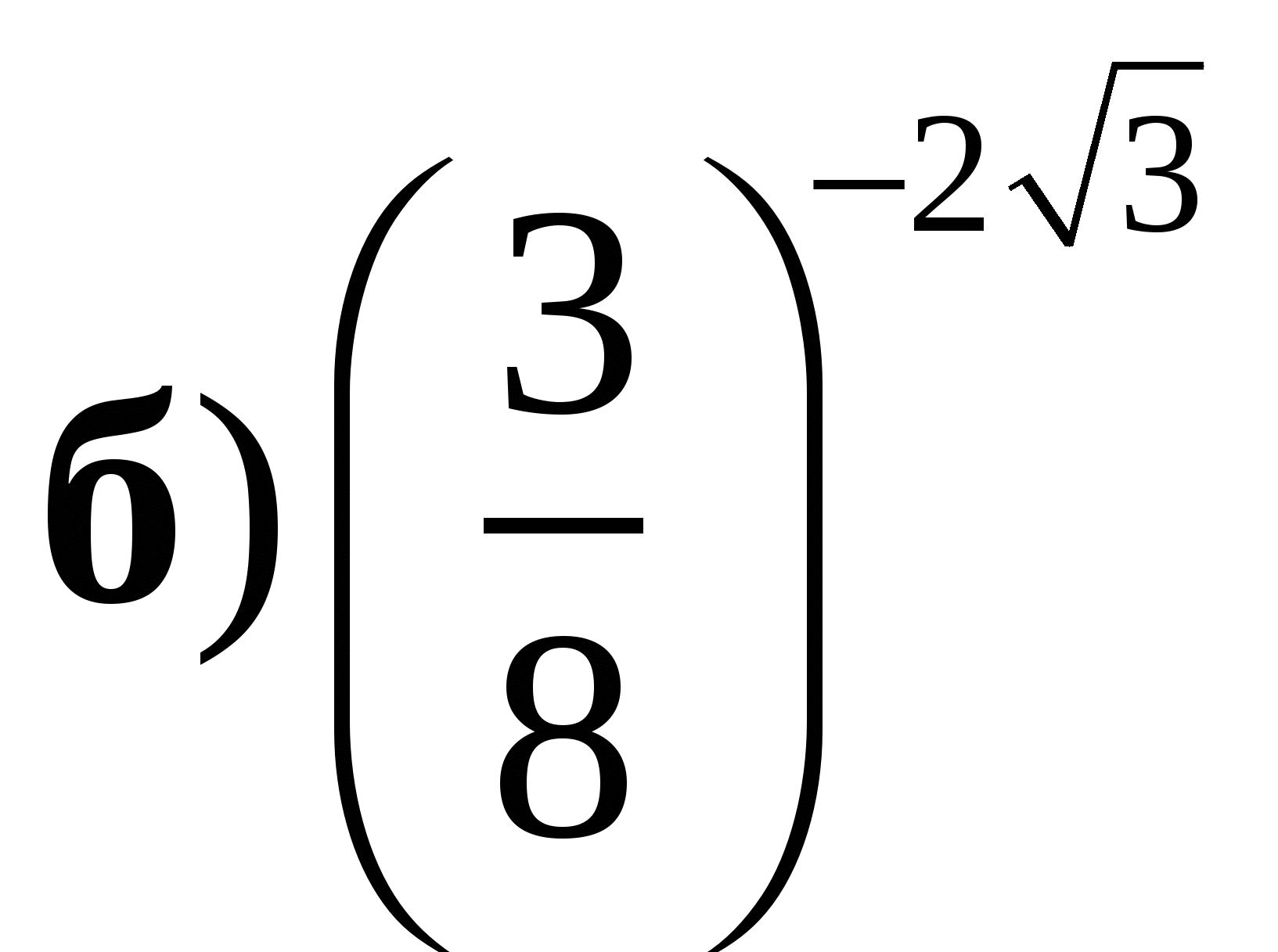 и 1;
и 1; 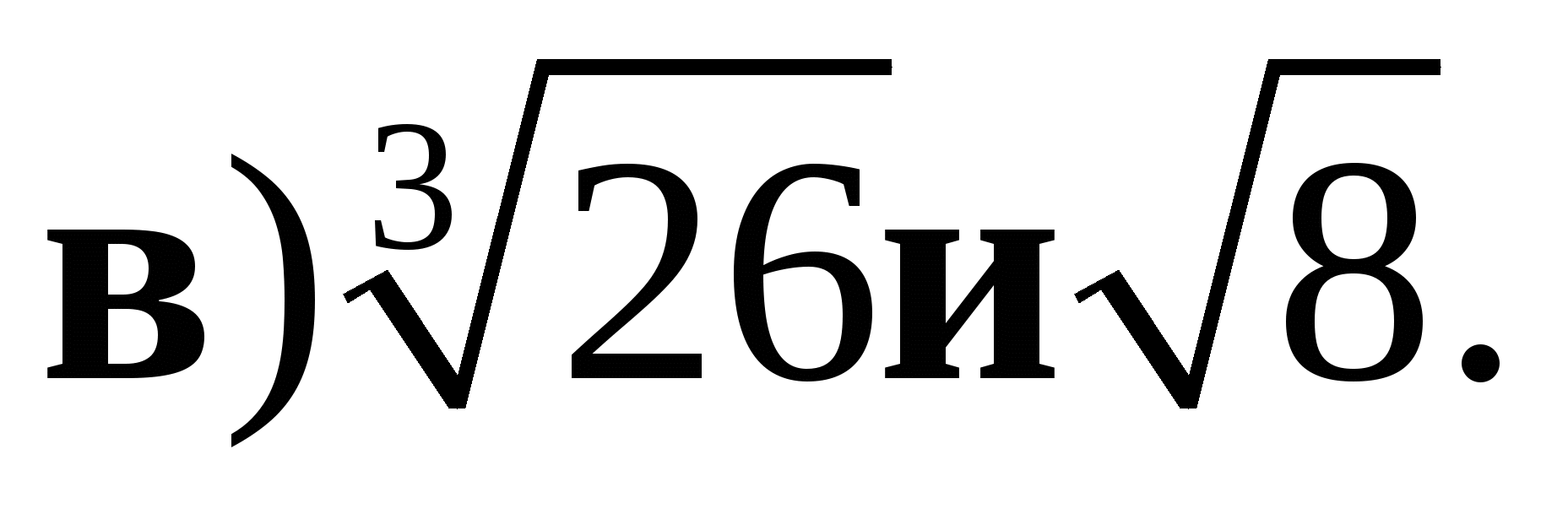
7*. Упростите выражение 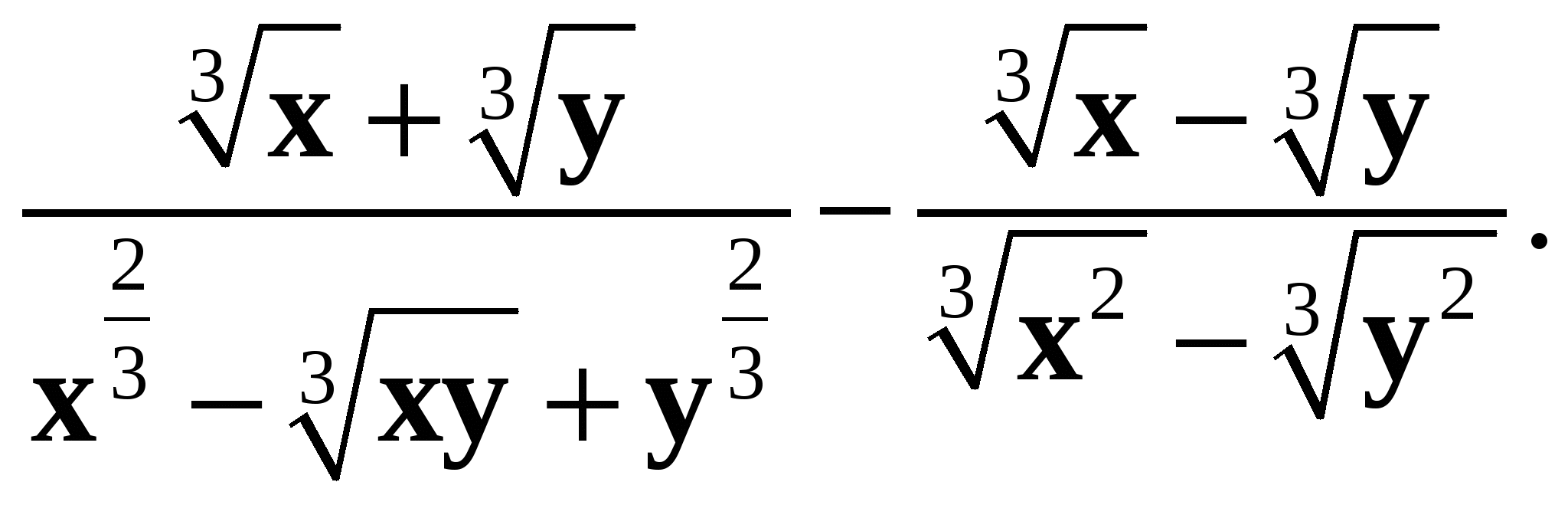
Контрольная работа №1. Действительные числа
Вариант 2
1. Вычислите: 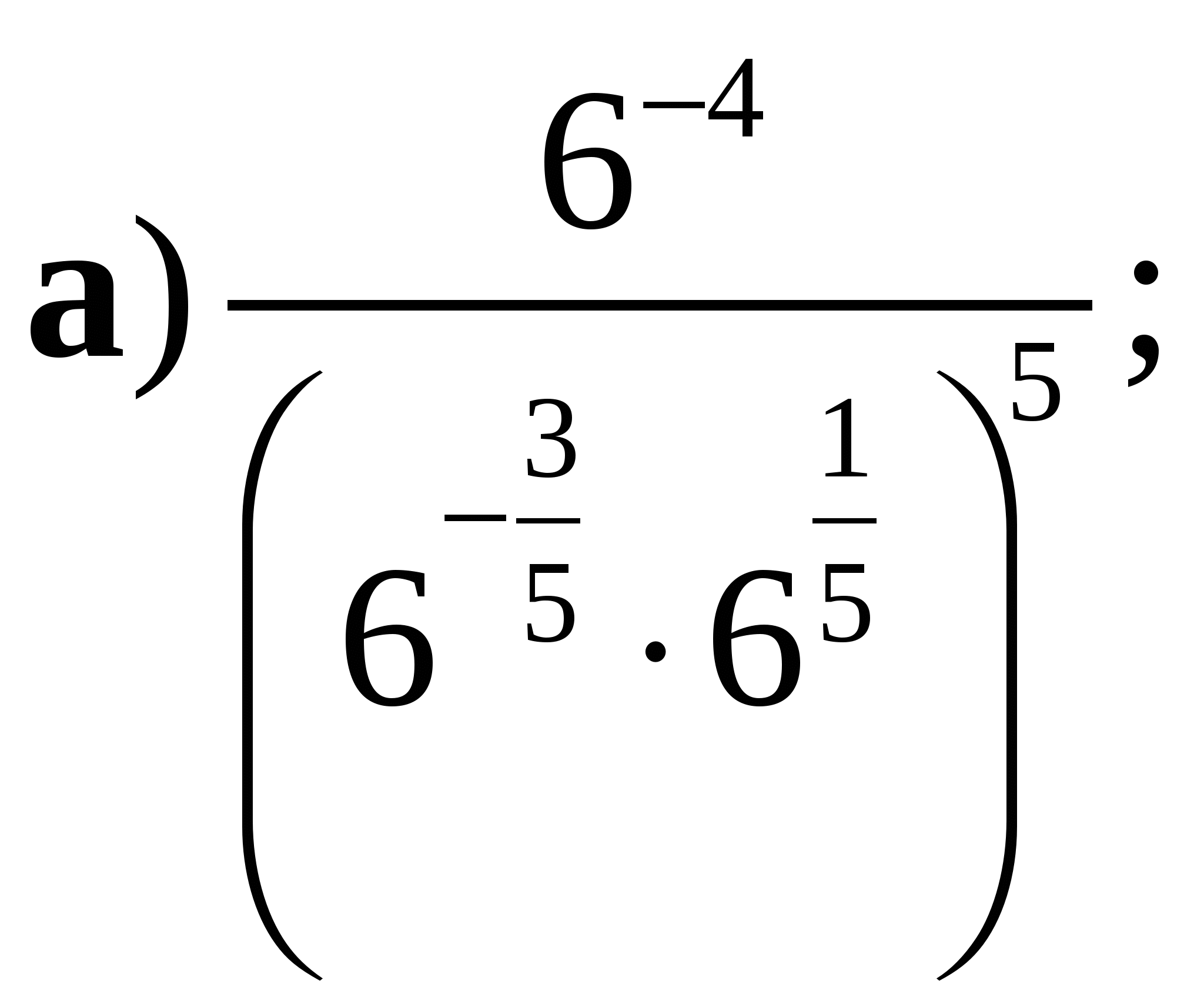
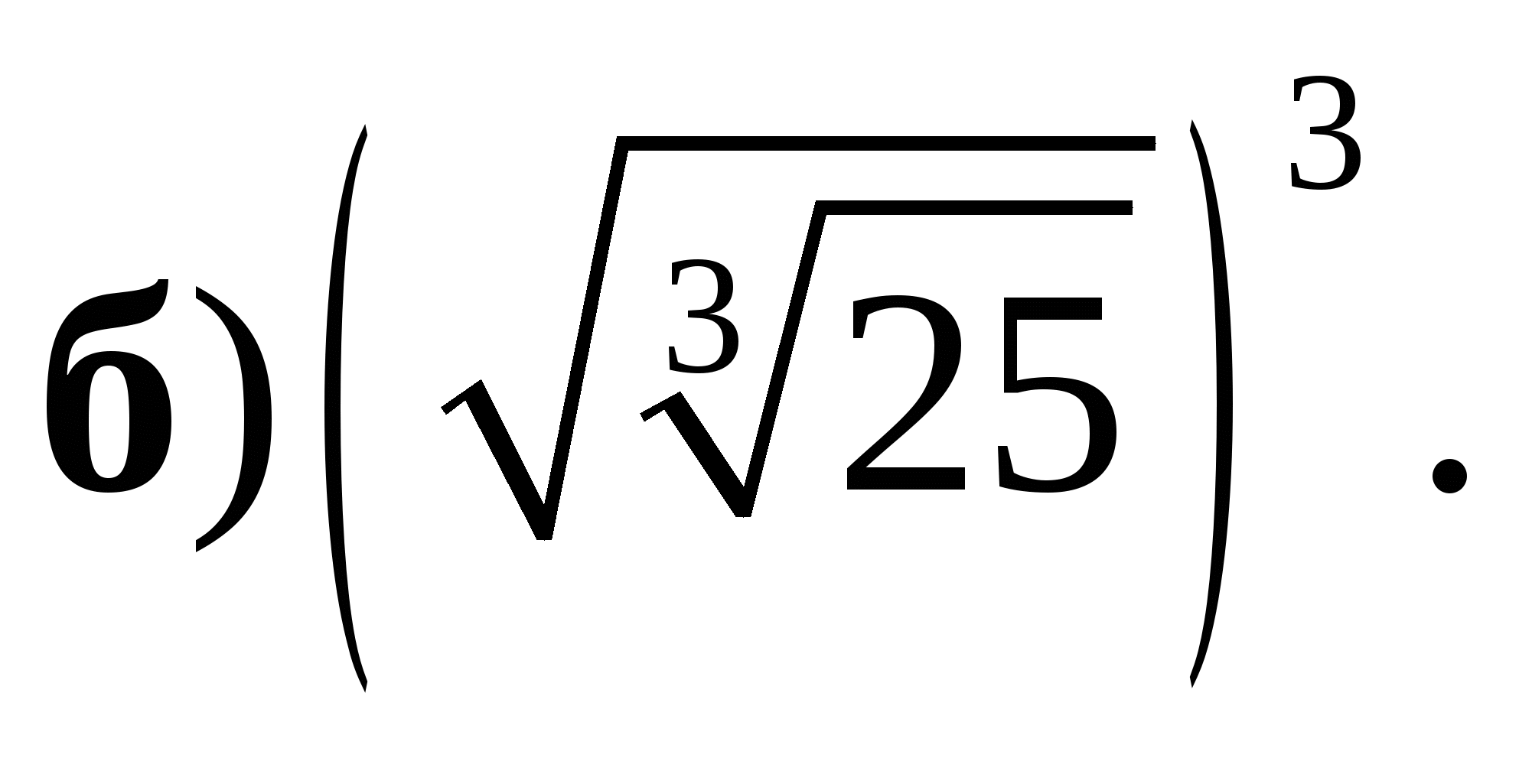
2. Упростите выражение 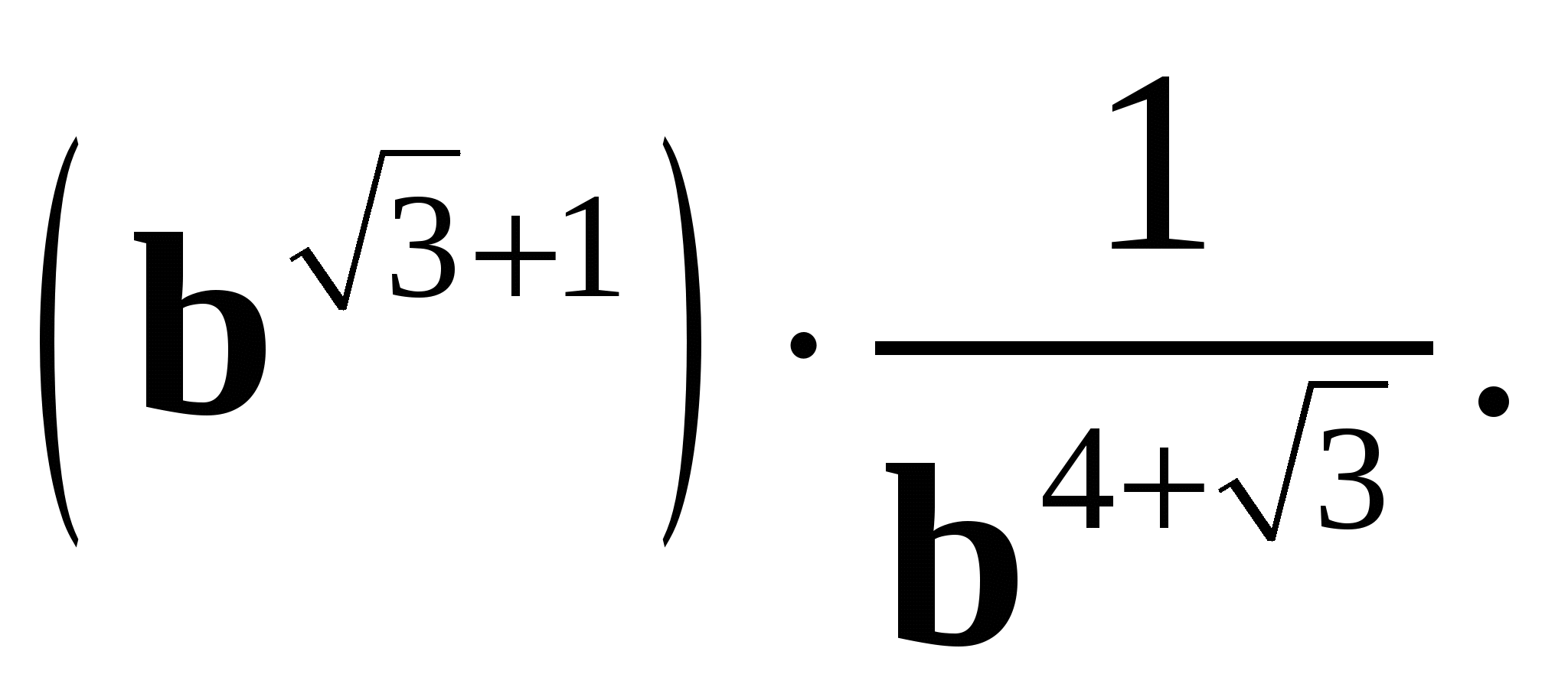
3. Решите уравнение 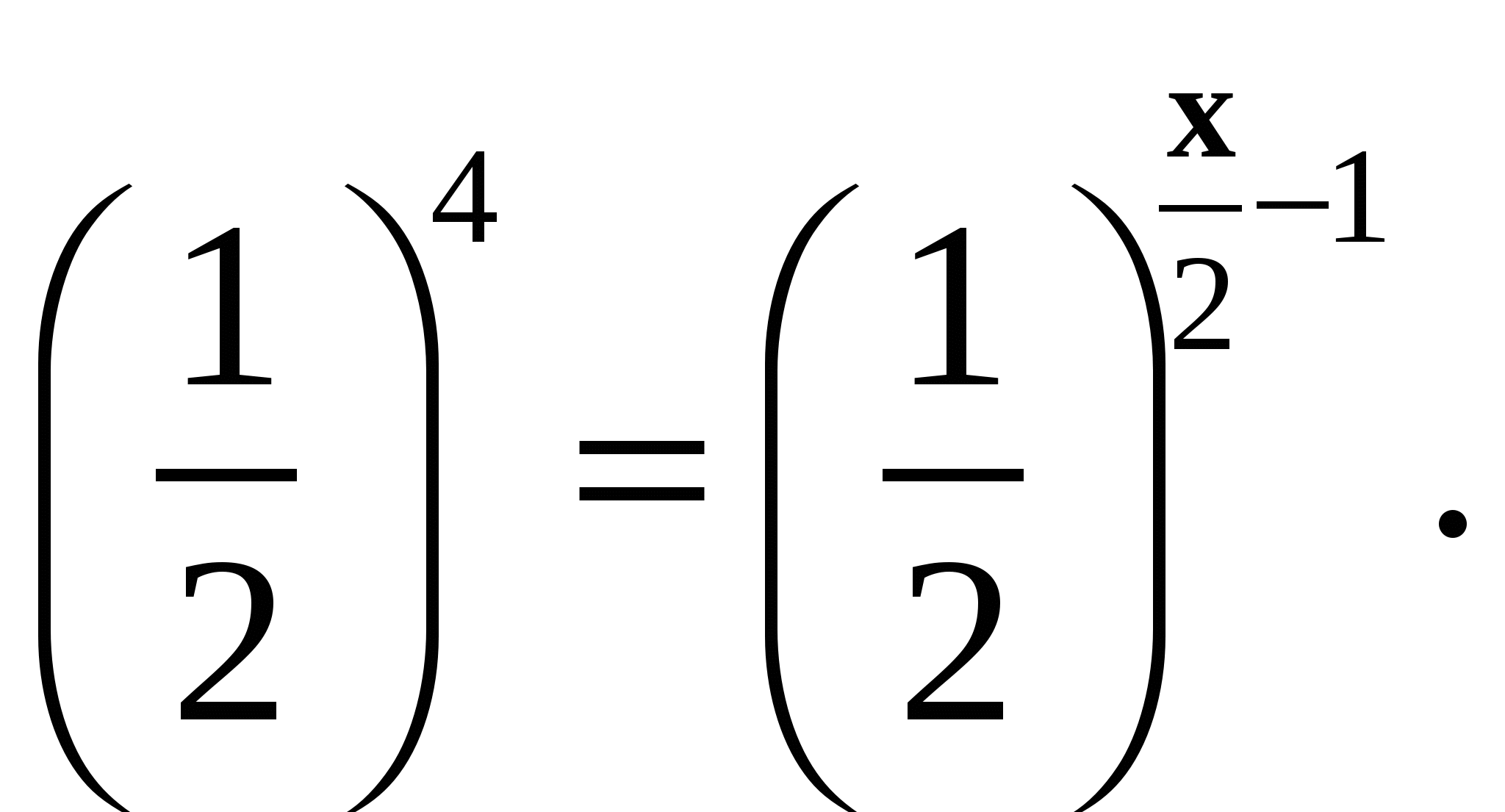
4. Запишите бесконечную периодическую дробь 0,3(6) в виде обыкновенной дроби.
5. Сократите дробь 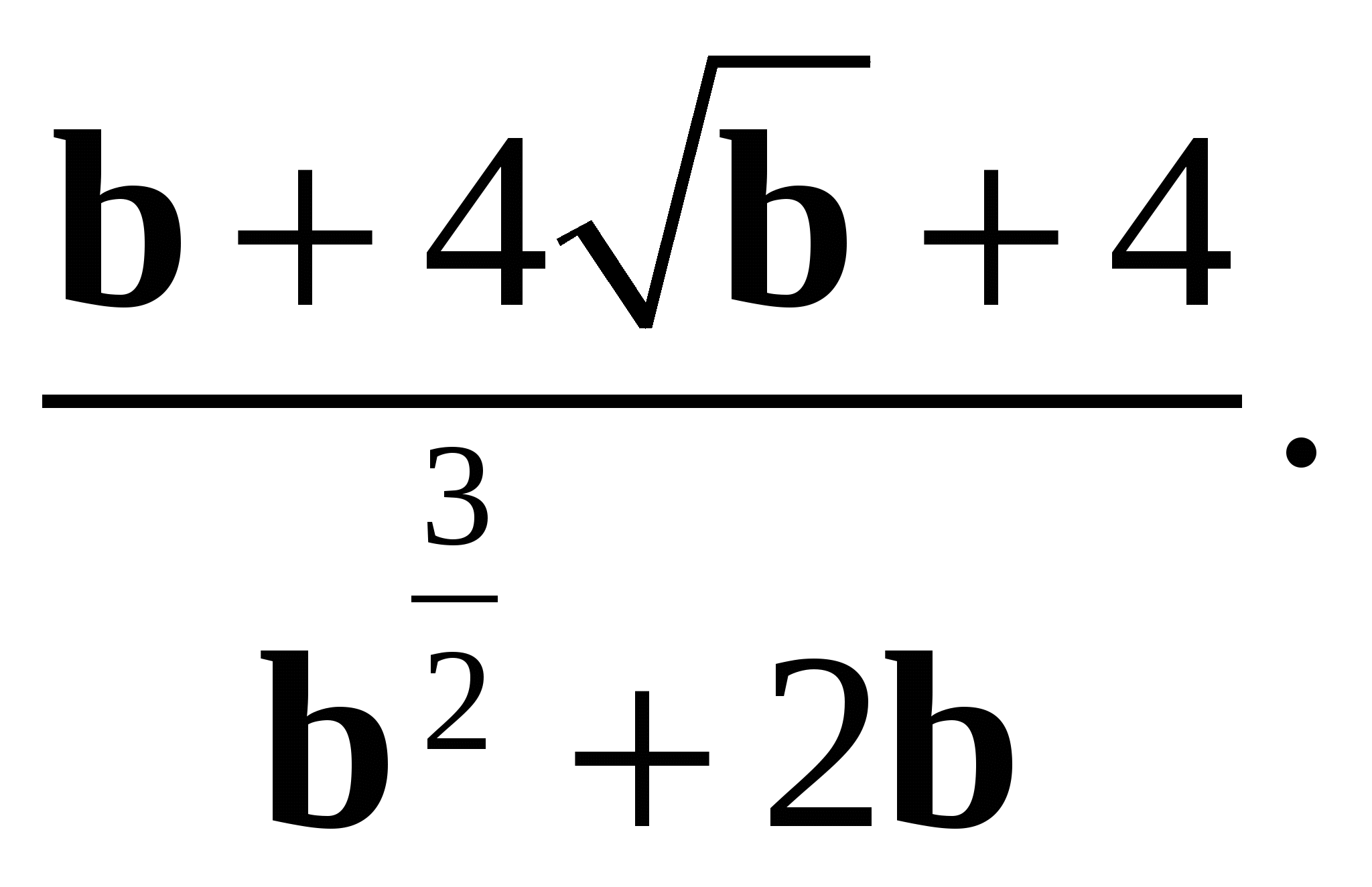
6. Сравните числа: 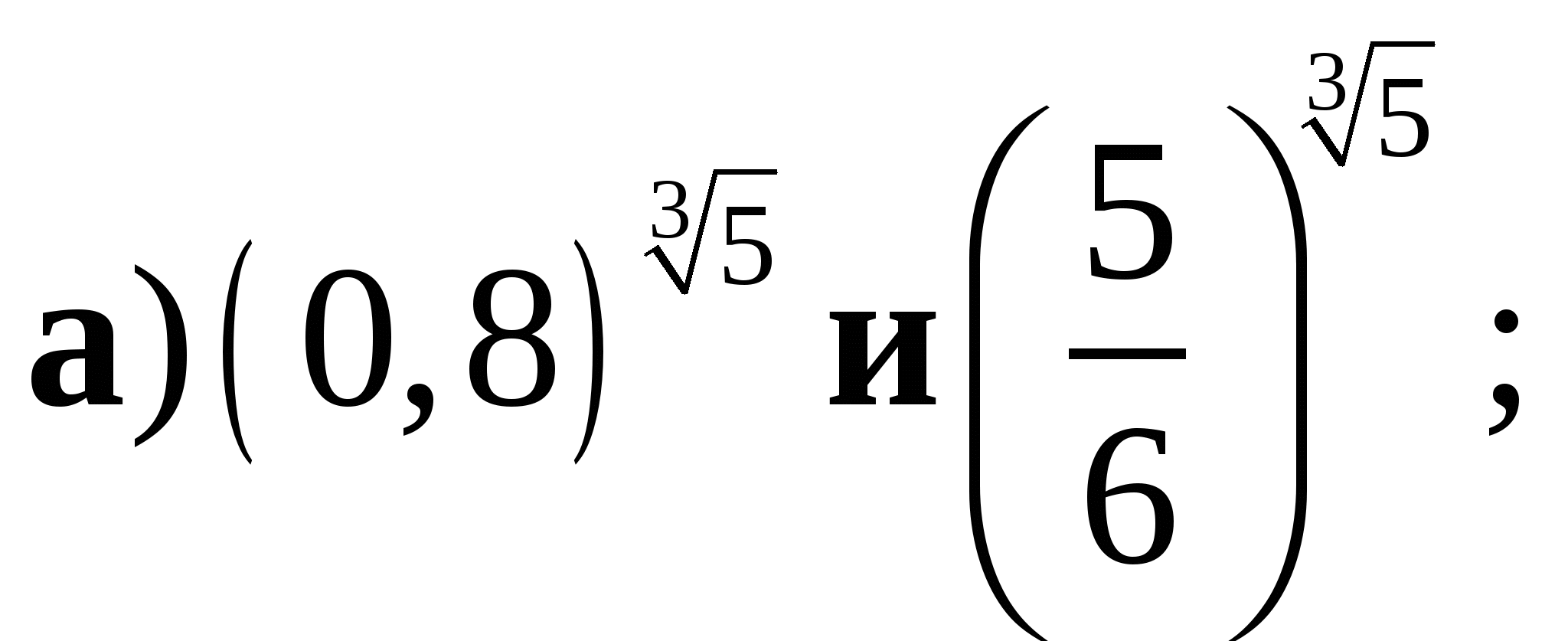
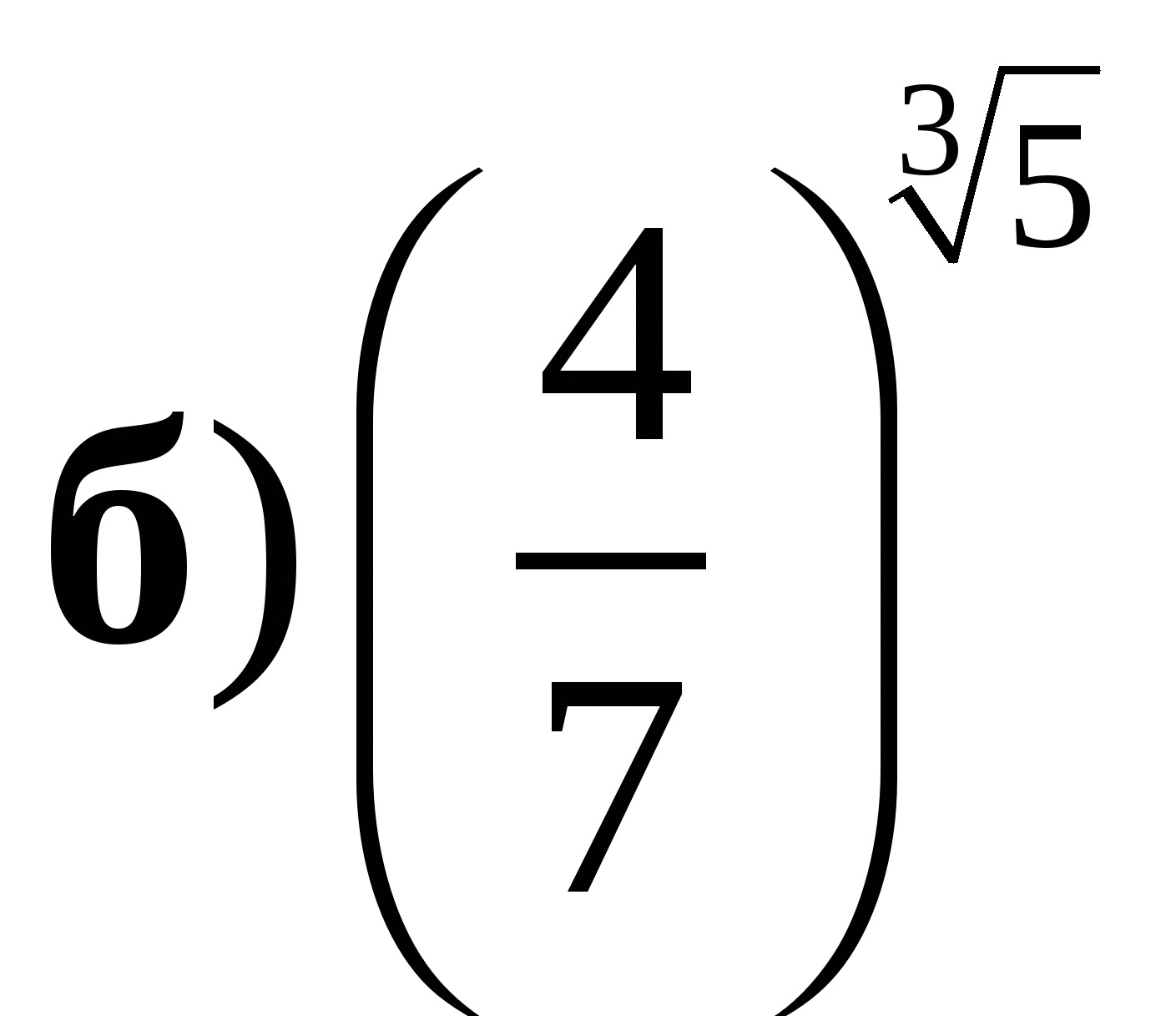 и 1;
и 1; 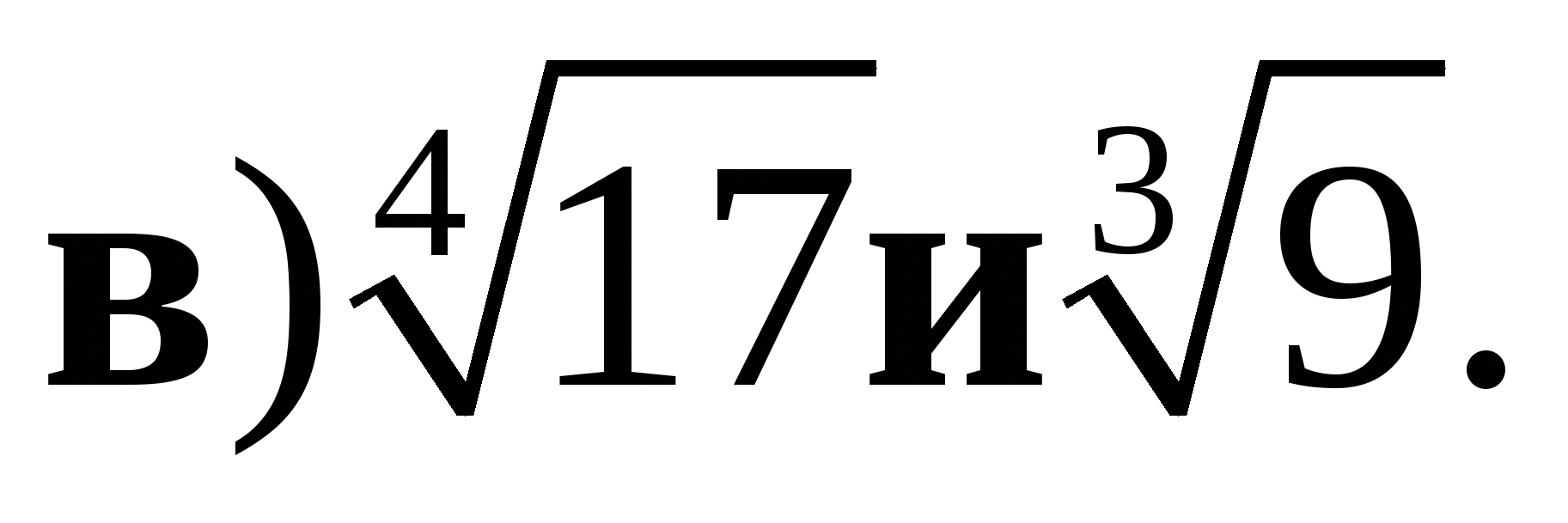
7*. Упростите выражение 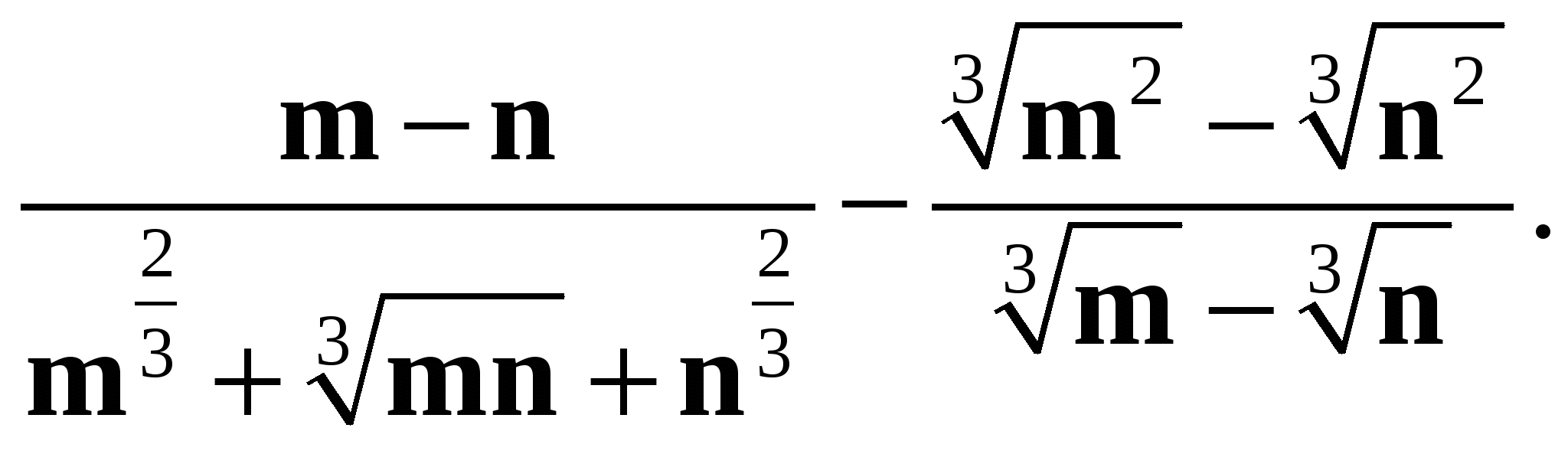
А – 10 Контрольная работа № 2
Степенная функция
Вариант 1
1. Найдите область определения функции 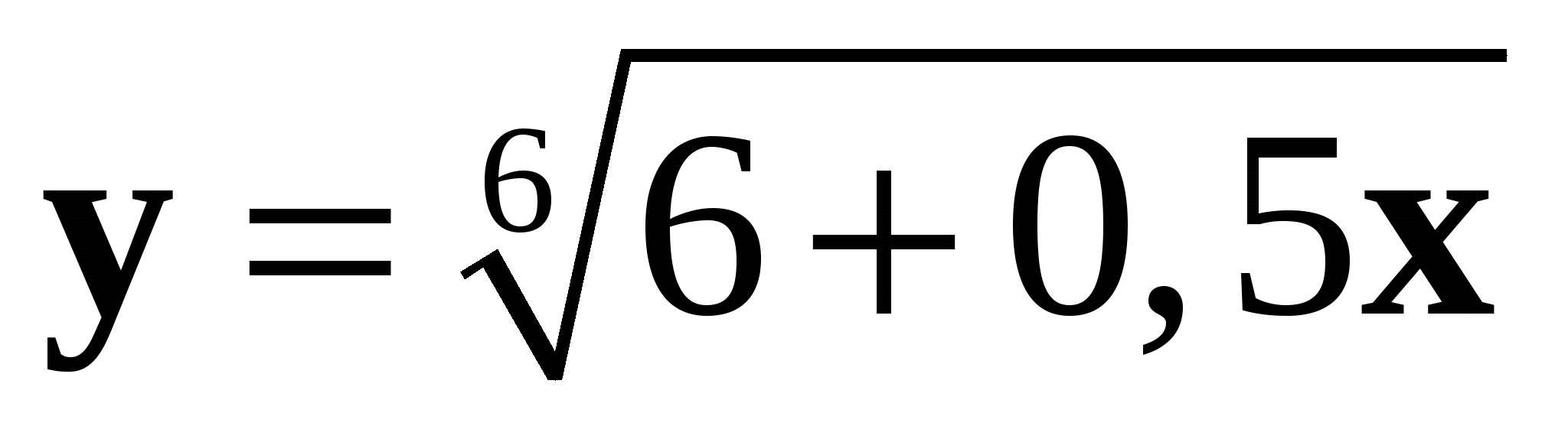 .
.
2. Схематически изобразите график функции 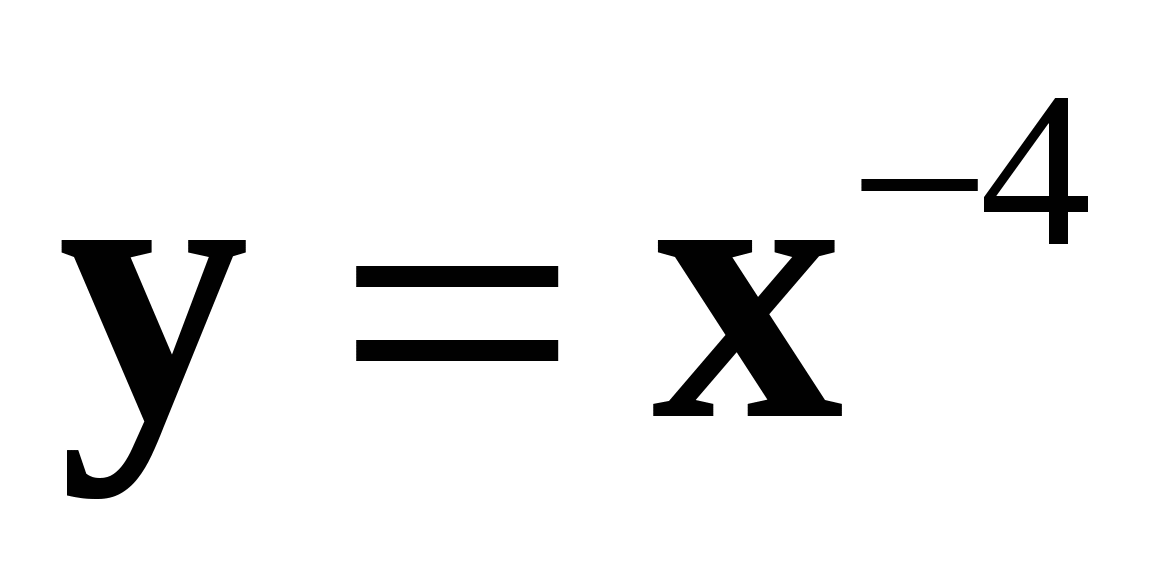 и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:
и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:
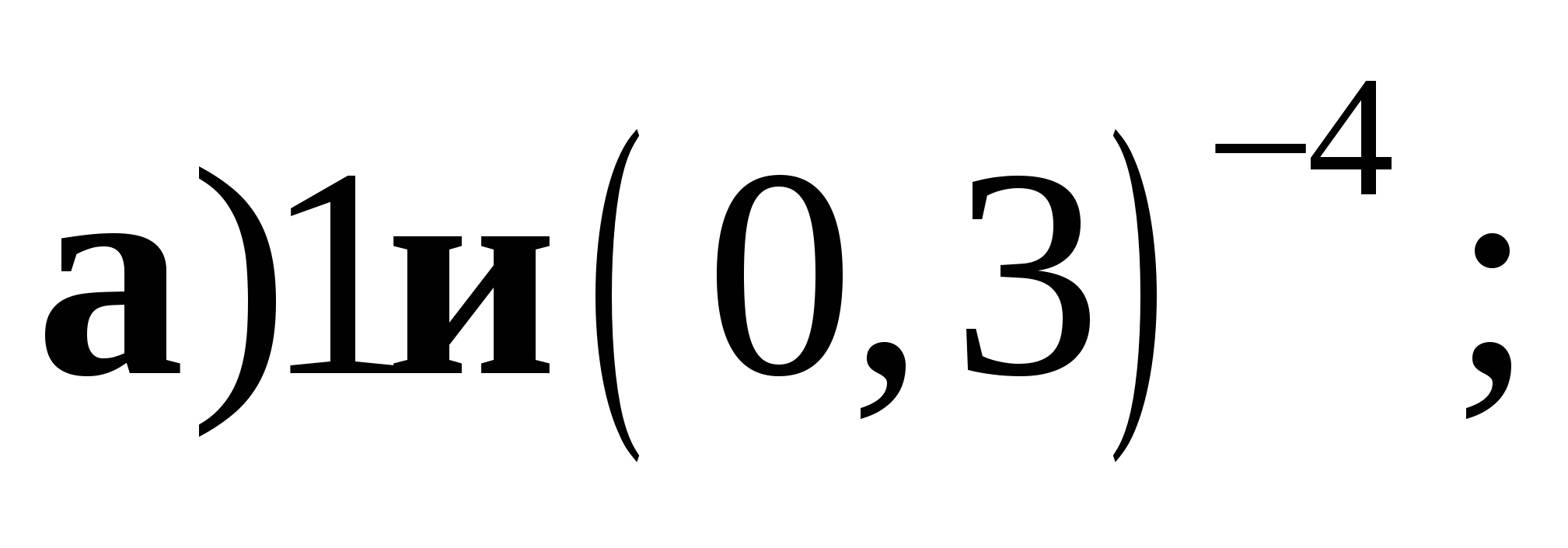
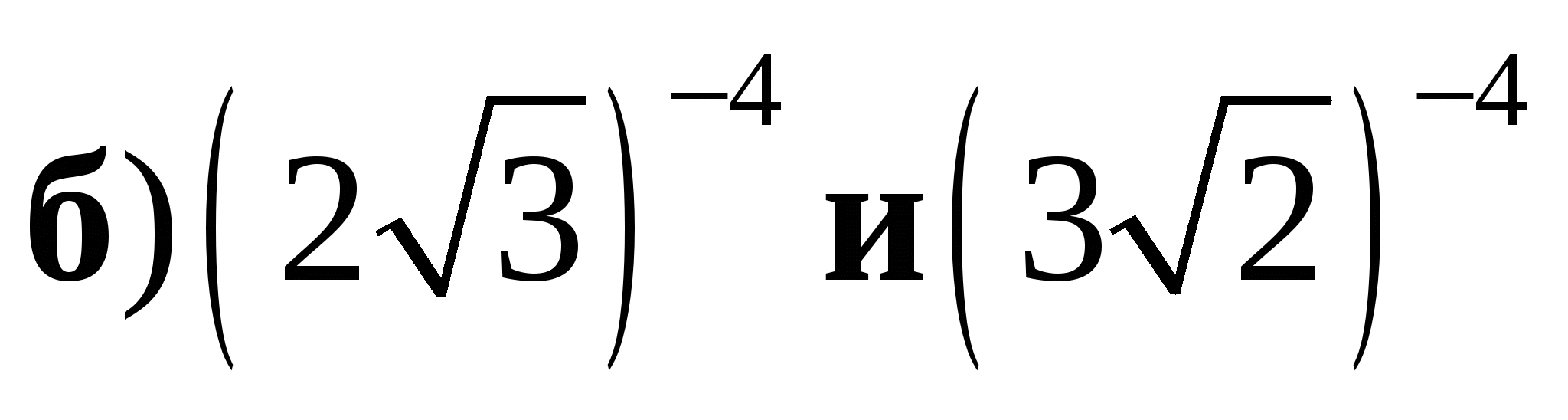 .
.
3. Решите уравнение 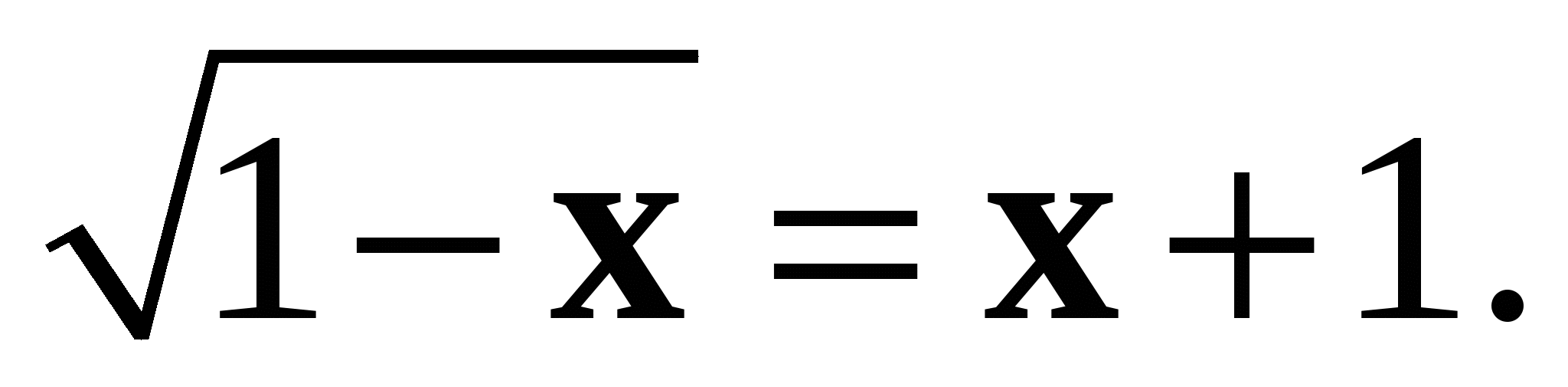
4. Решите уравнение 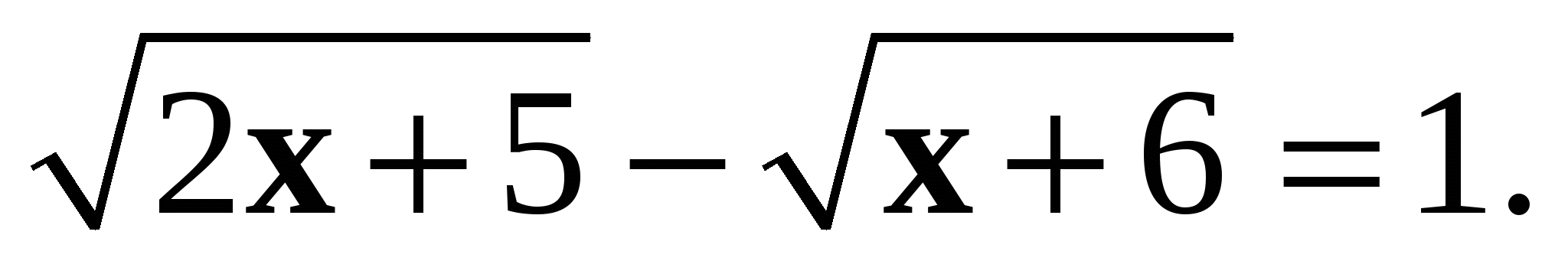
5. Установите, равносильны ли неравенства 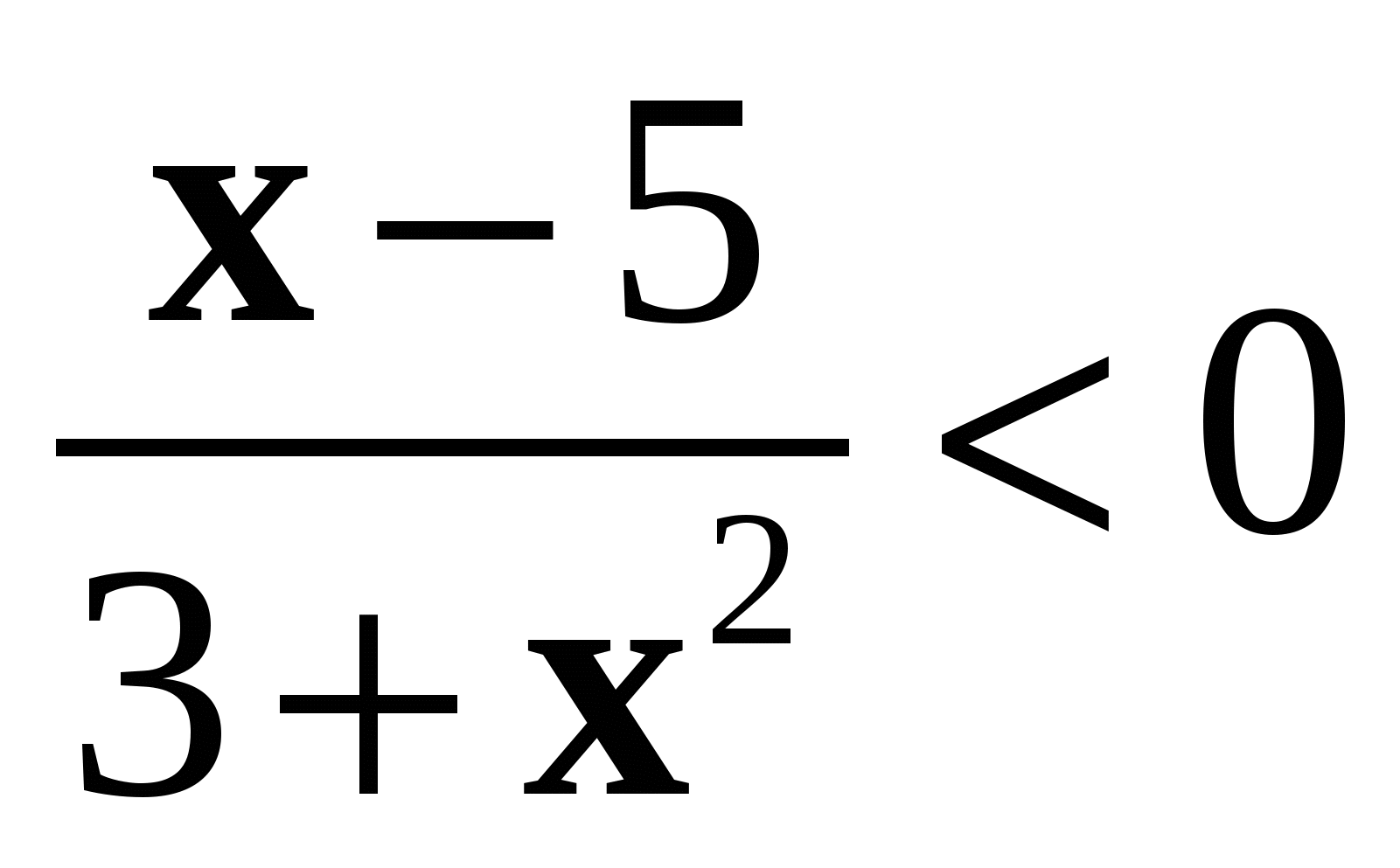 и
и 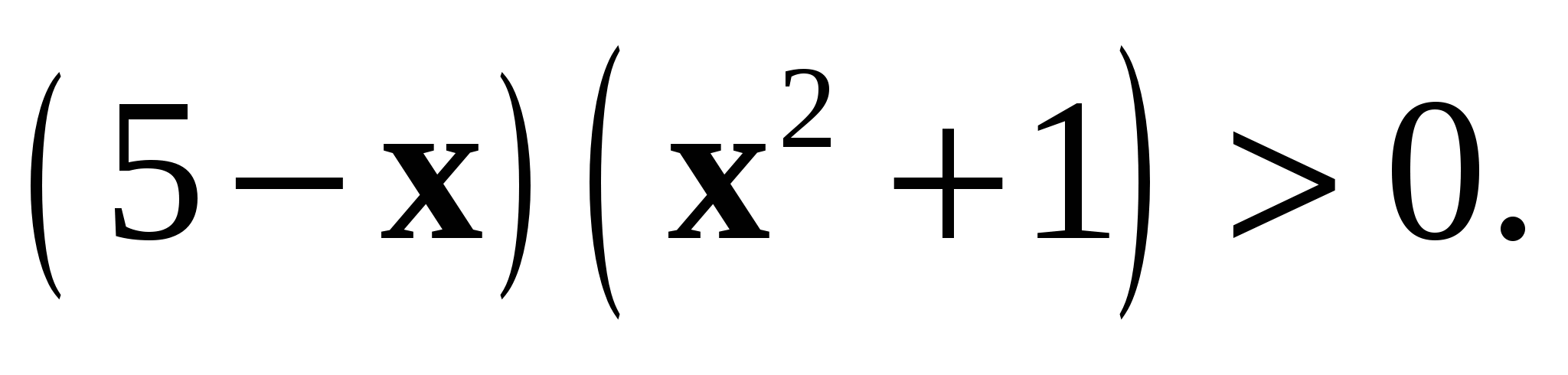
6. Найдите функцию, обратную функции 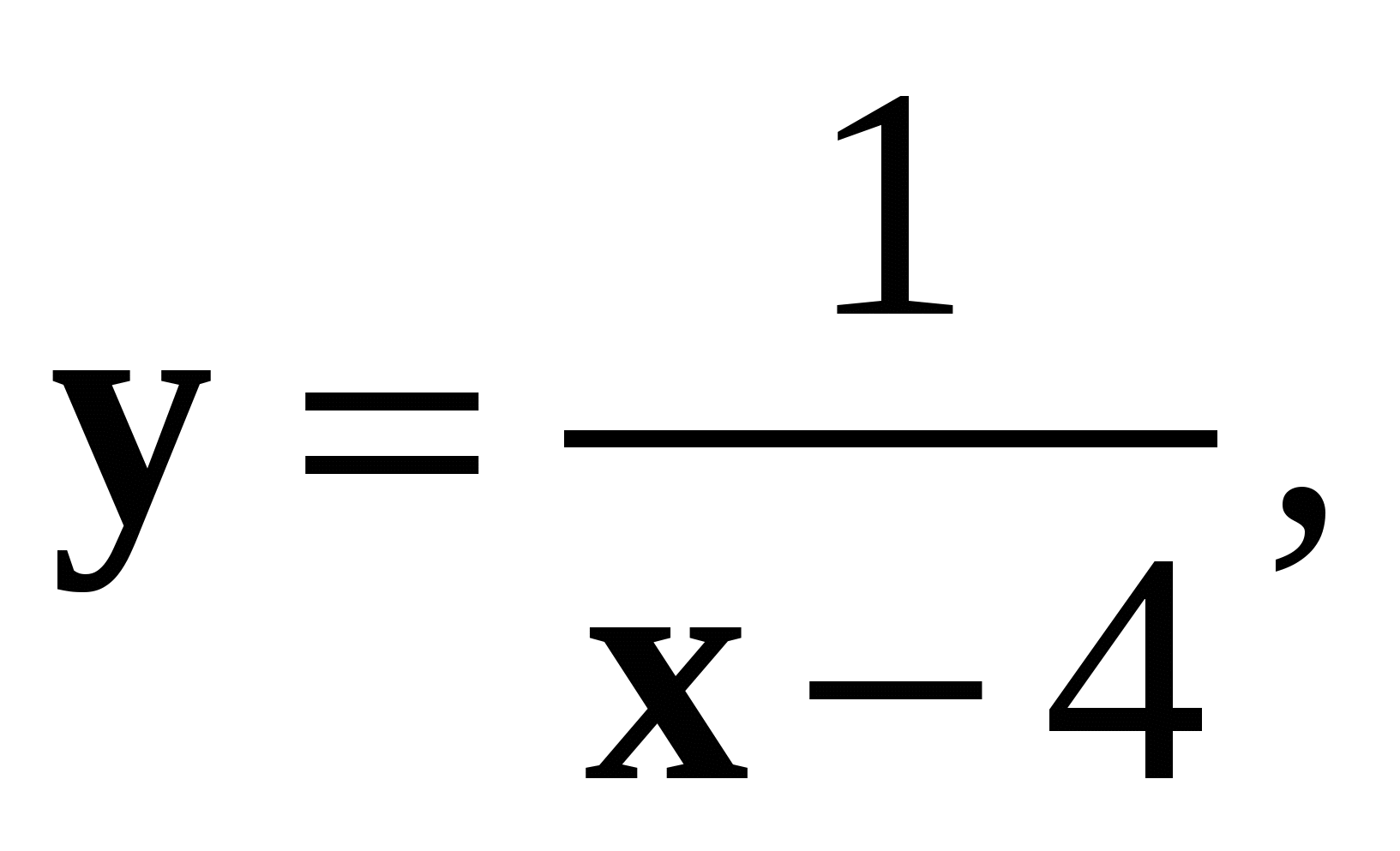 и укажите её область определения и множество значений.
и укажите её область определения и множество значений.
7*. Решите неравенство 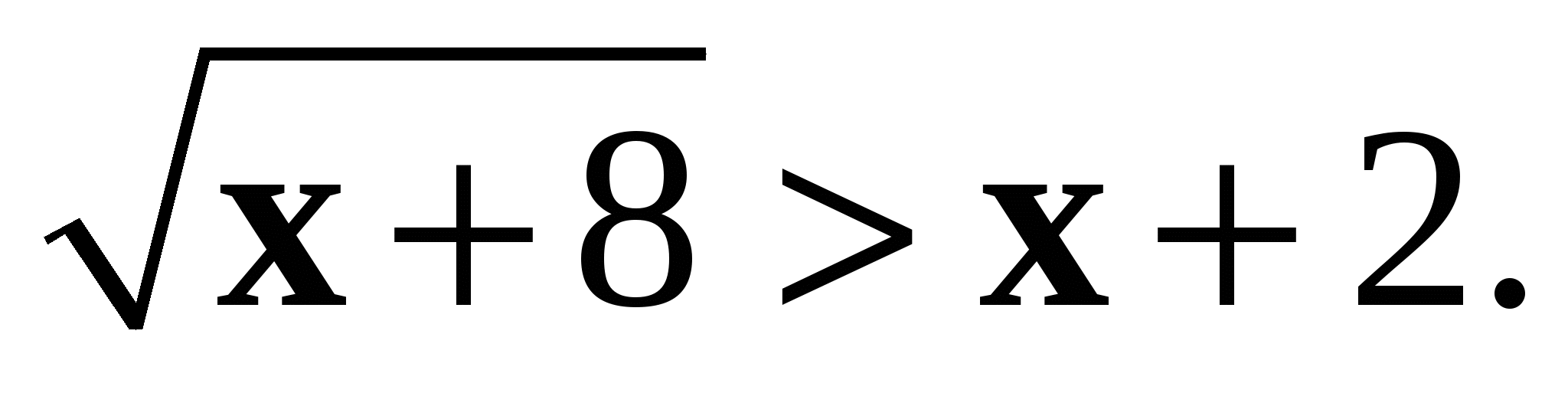
Контрольная работа № 2
Степенная функция
Вариант 2
1. Найдите область определения функции 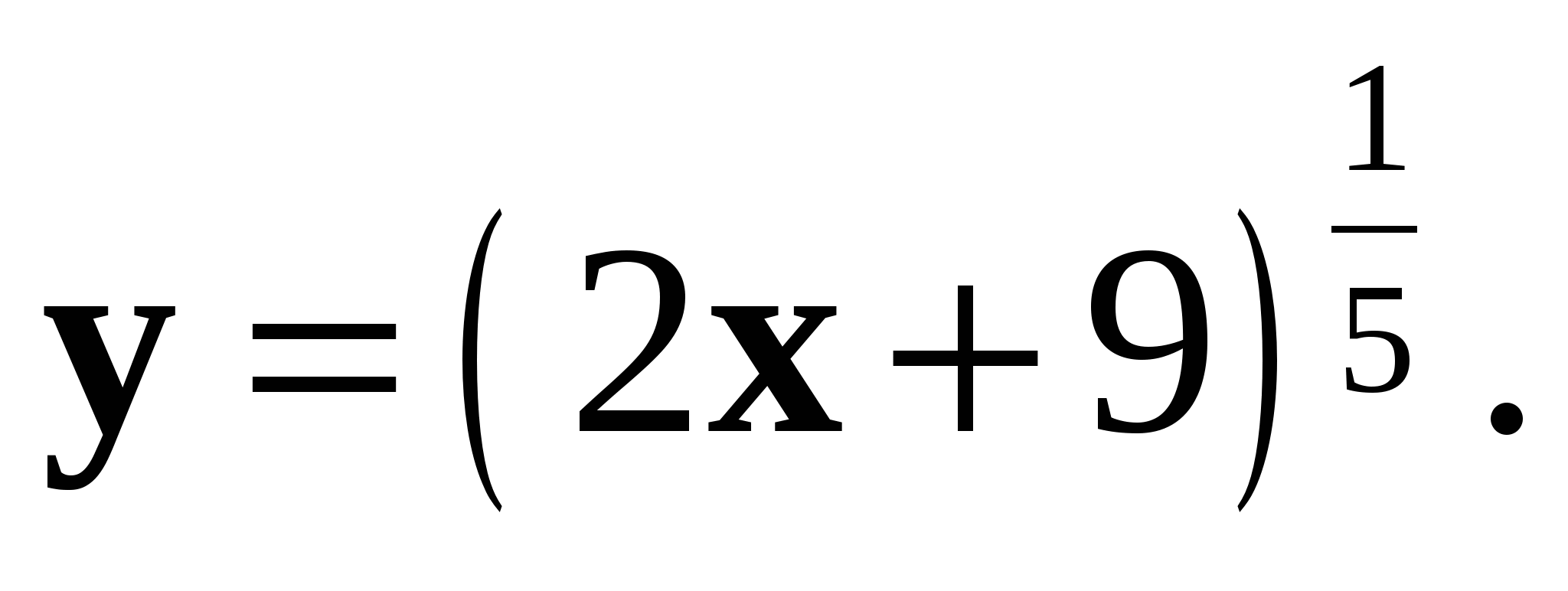
2. Схематически изобразите график функции 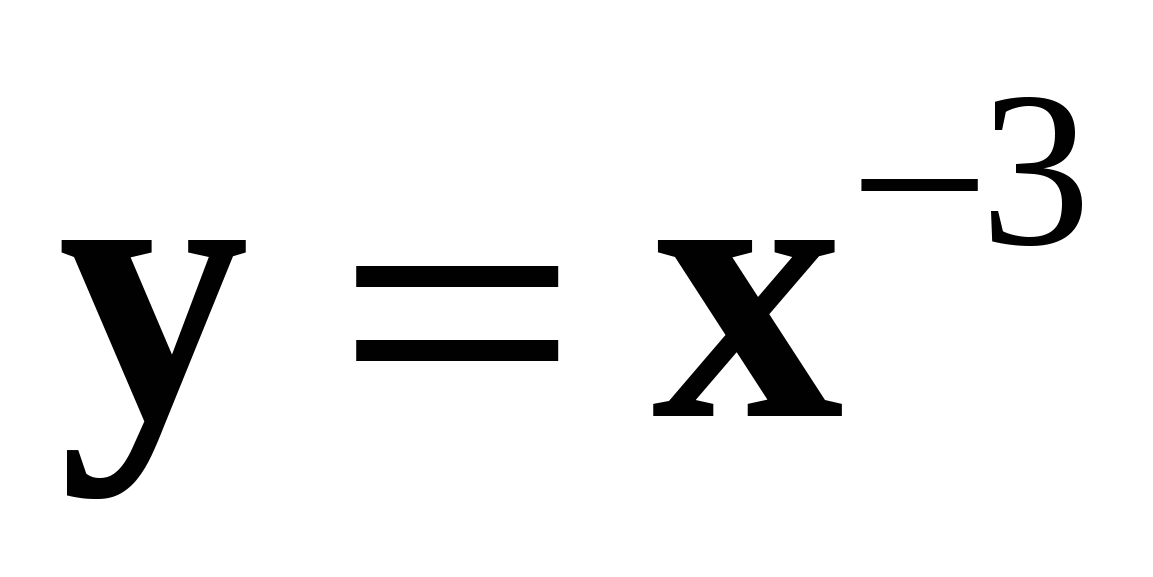 и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:
и перечислите её основные свойства. Пользуясь свойствами этой функции, сравните:
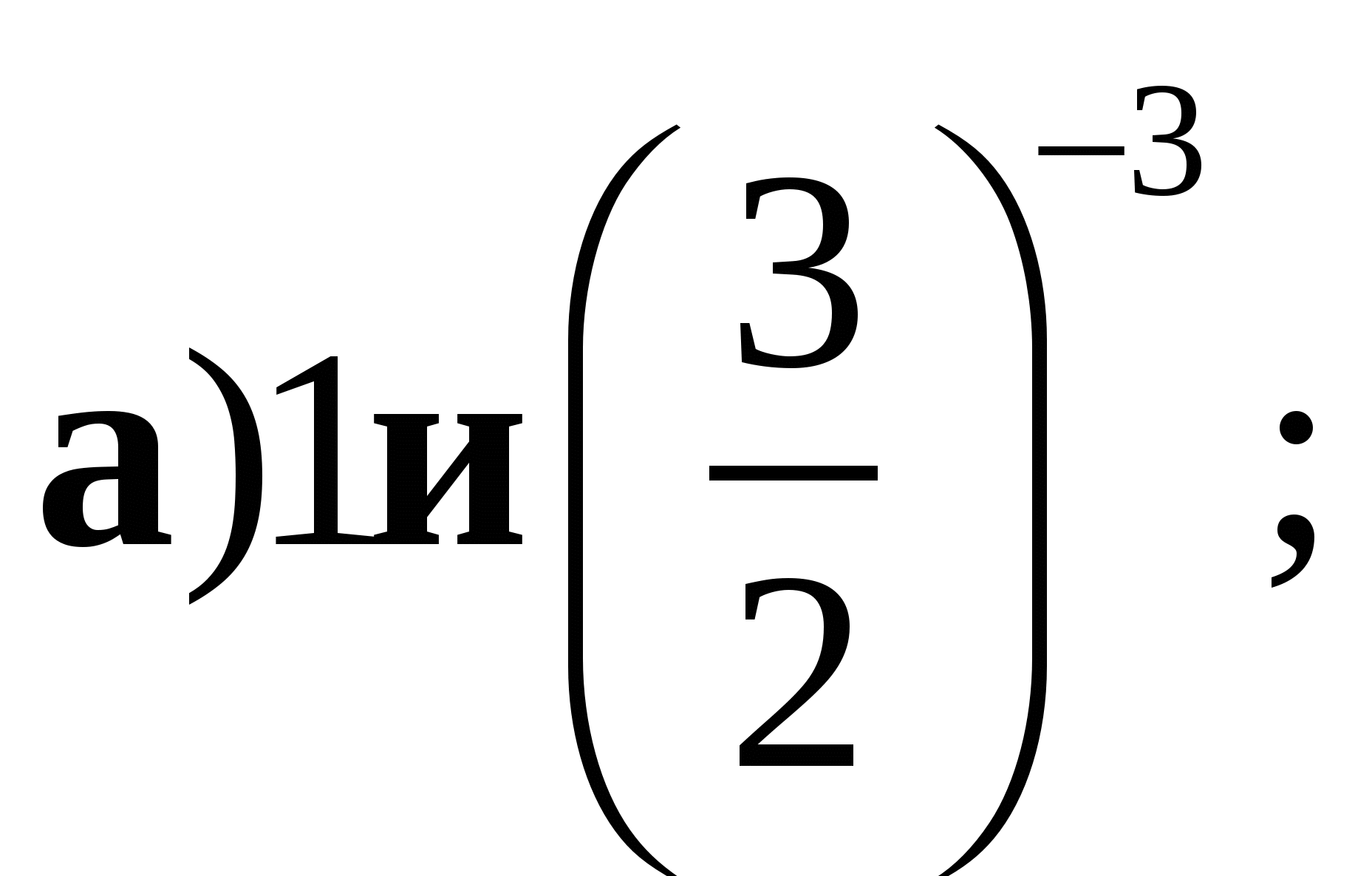
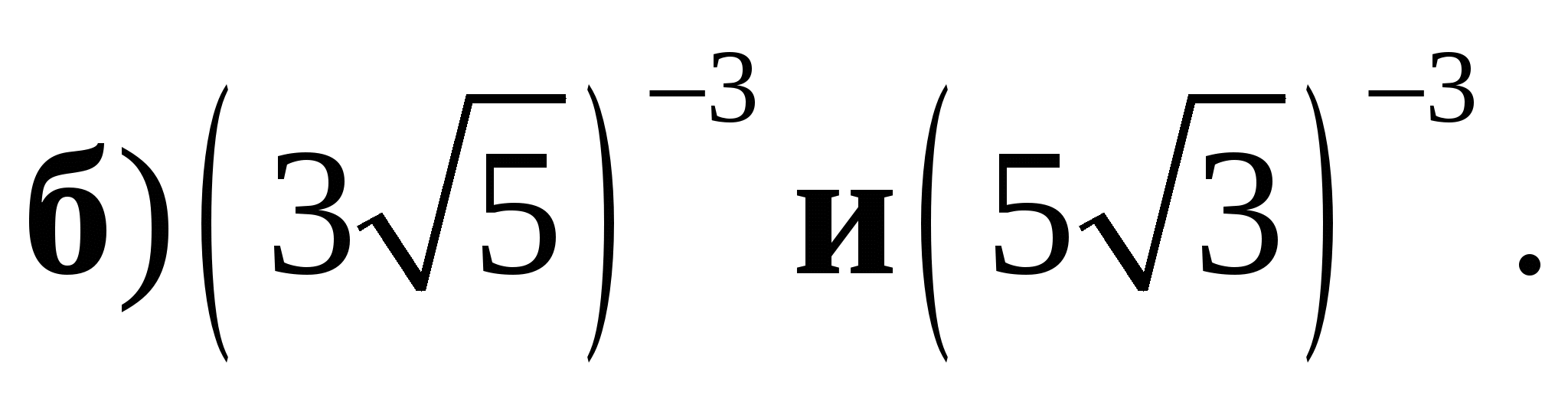
3. Решите уравнение 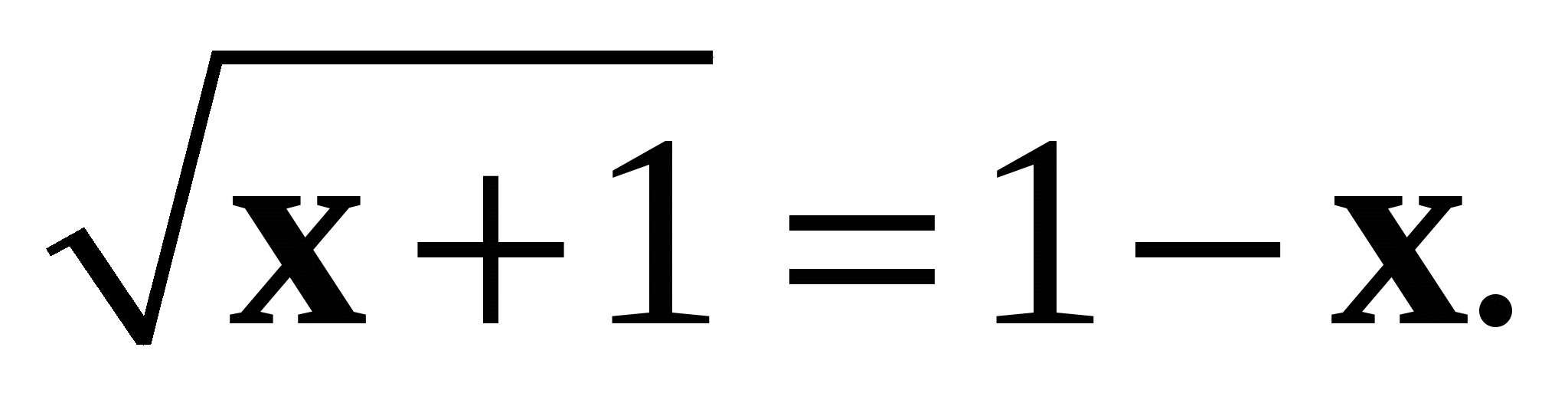
4. Решите уравнение 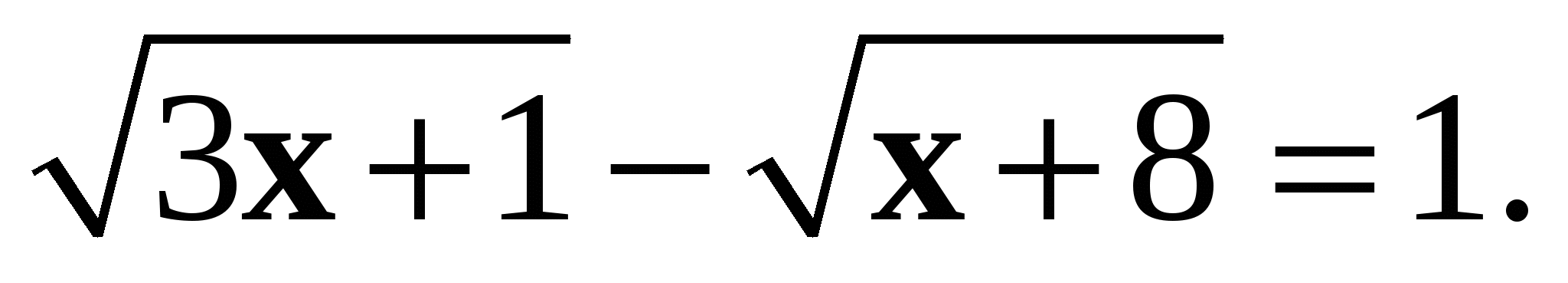
5. Установите, равносильны ли неравенства 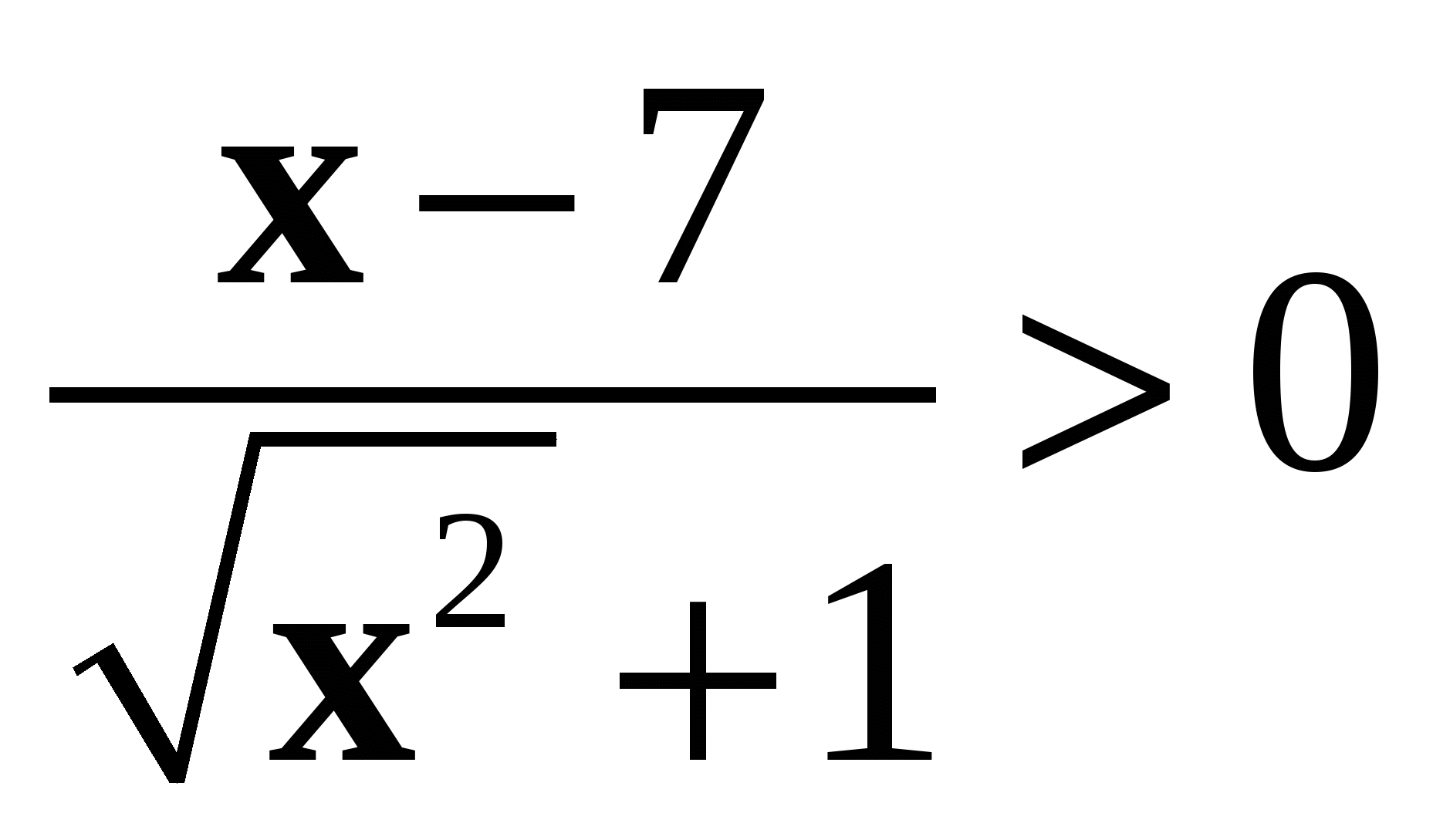 и
и 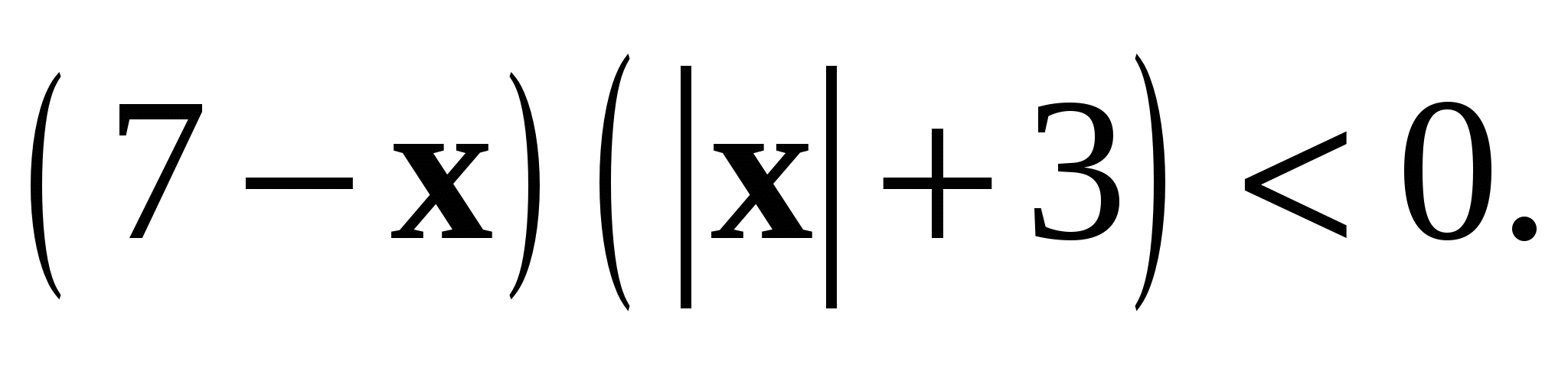
6. Найдите функцию, обратную функции 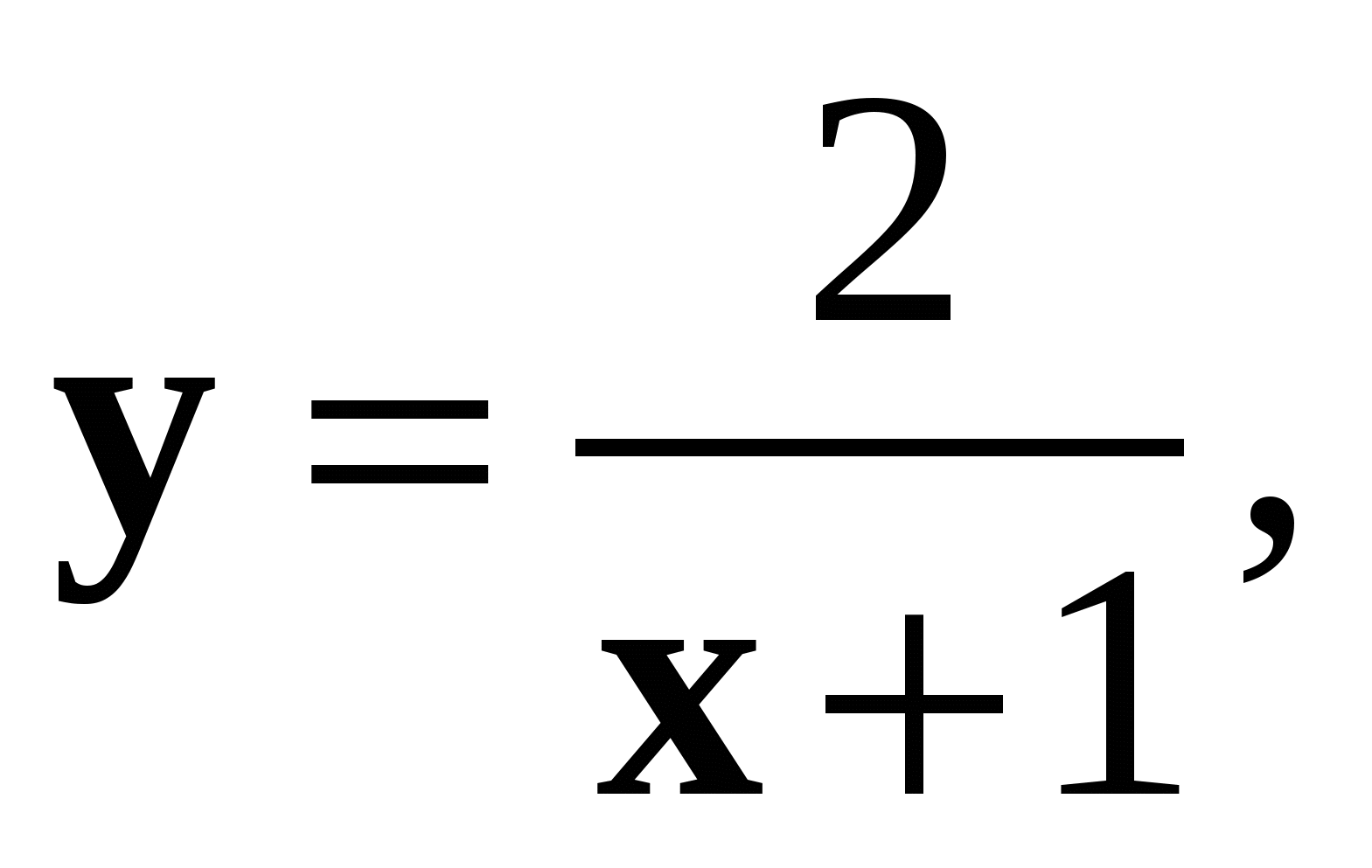 и укажите её область определения и множество значений.
и укажите её область определения и множество значений.
7*. Решите неравенство 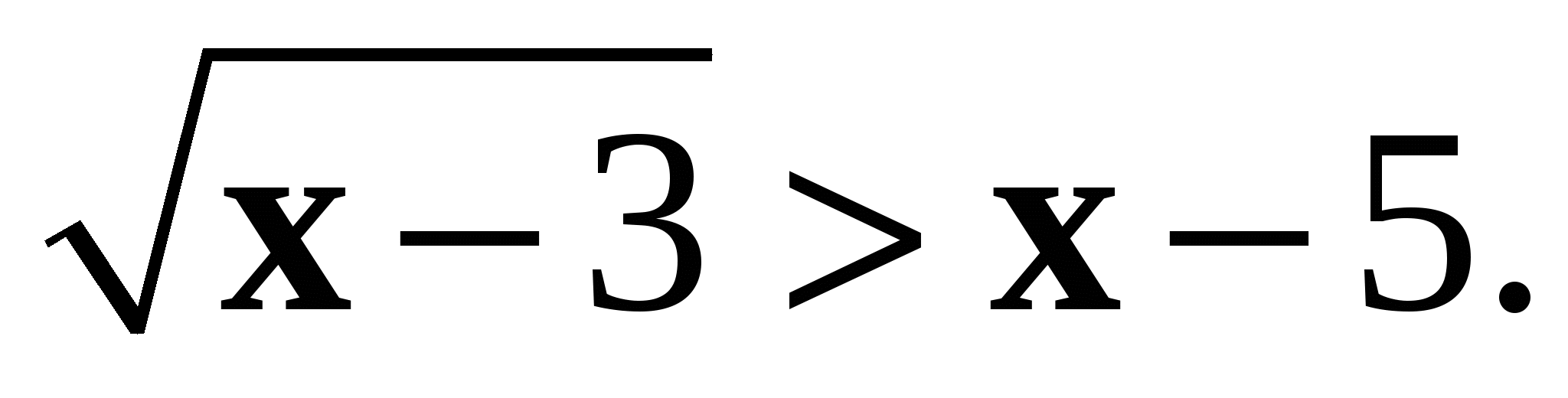
А – 10 Контрольная работа № 3
Показательная функция
Вариант 1
1. Сравните числа: 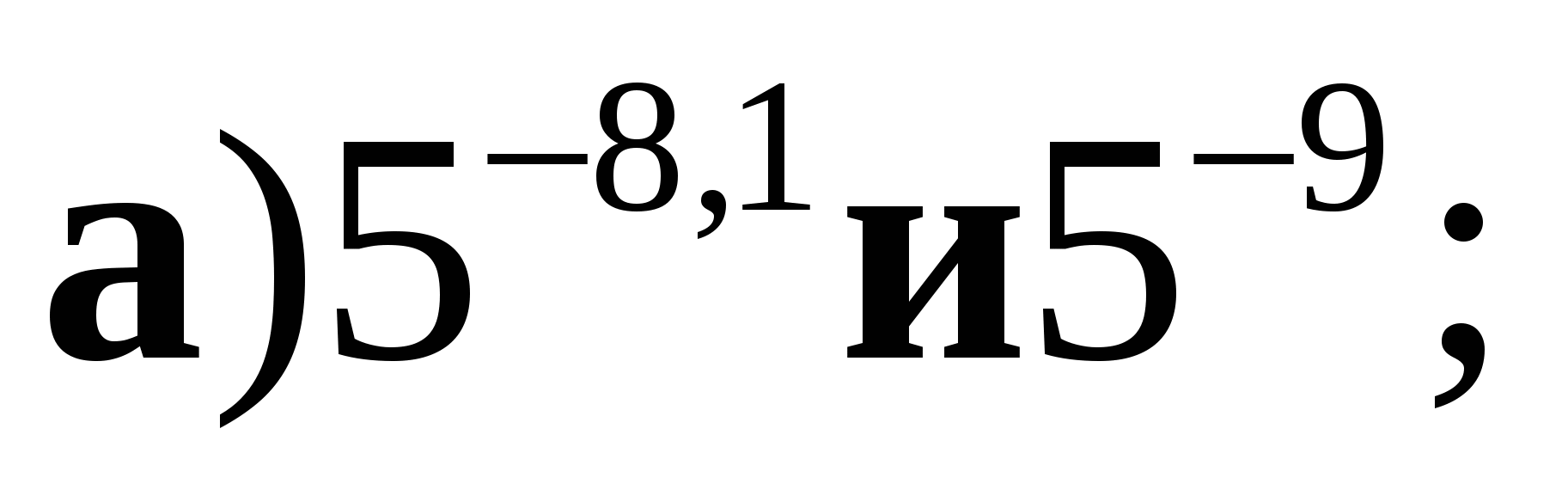 б)
б) 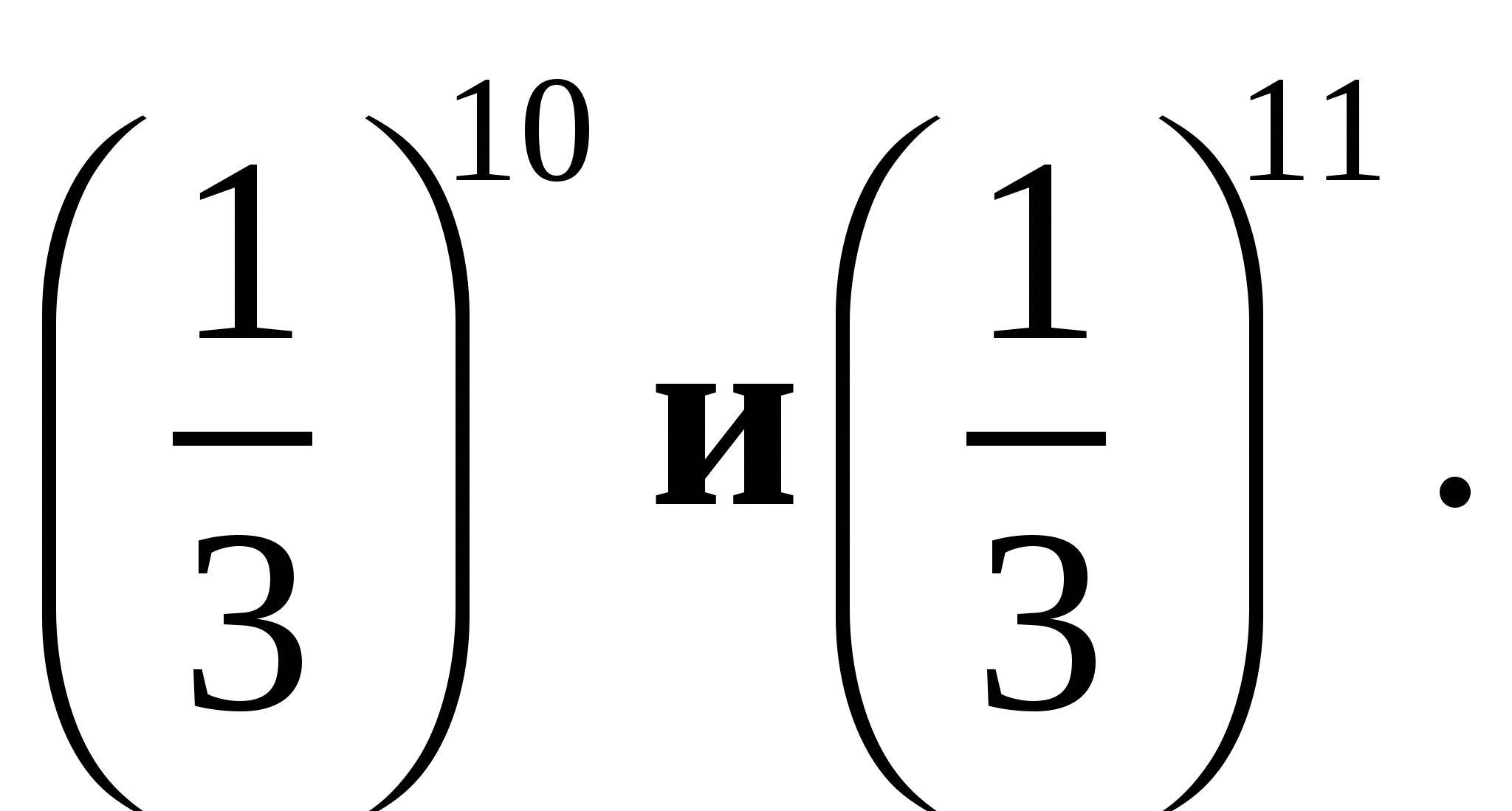
2. Решите уравнение 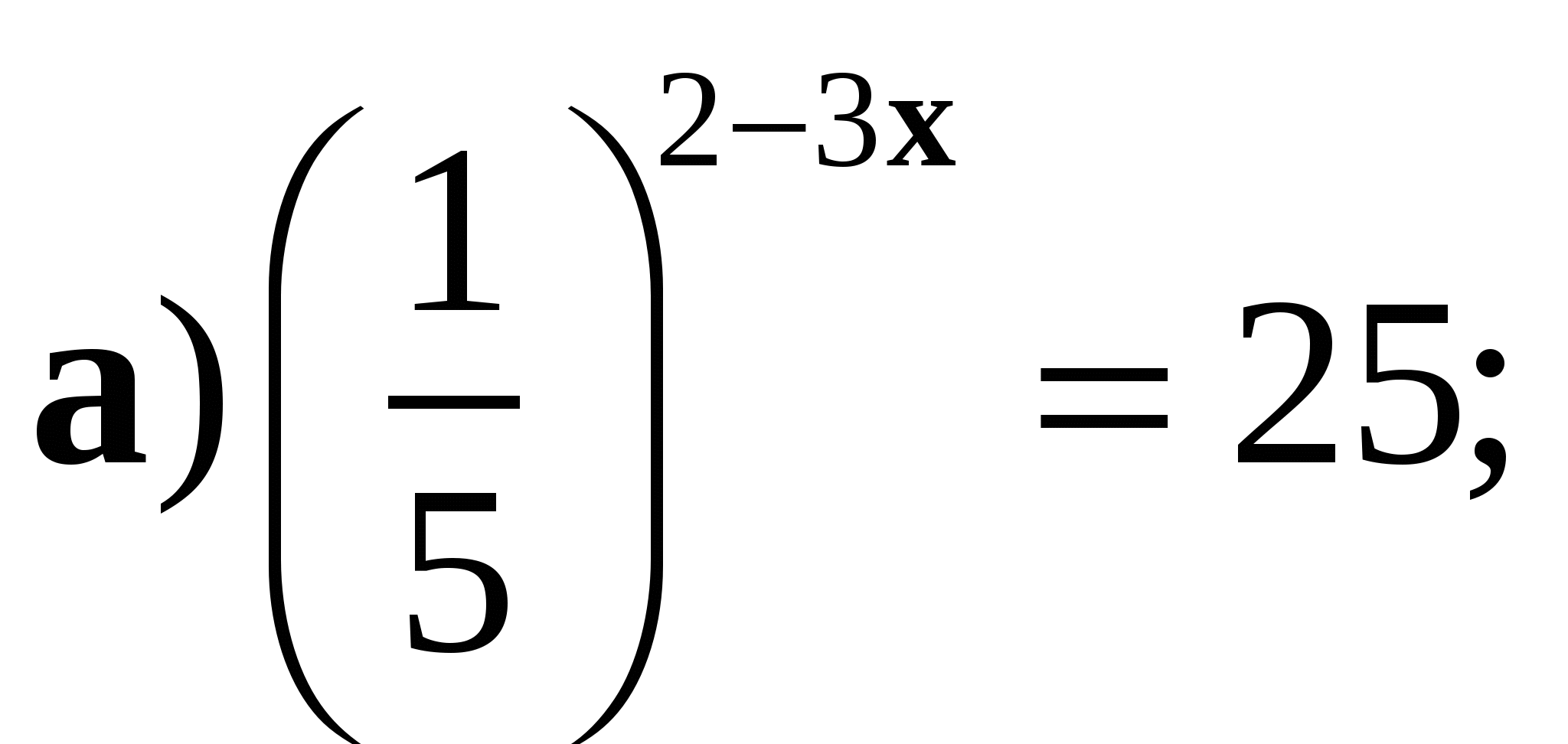
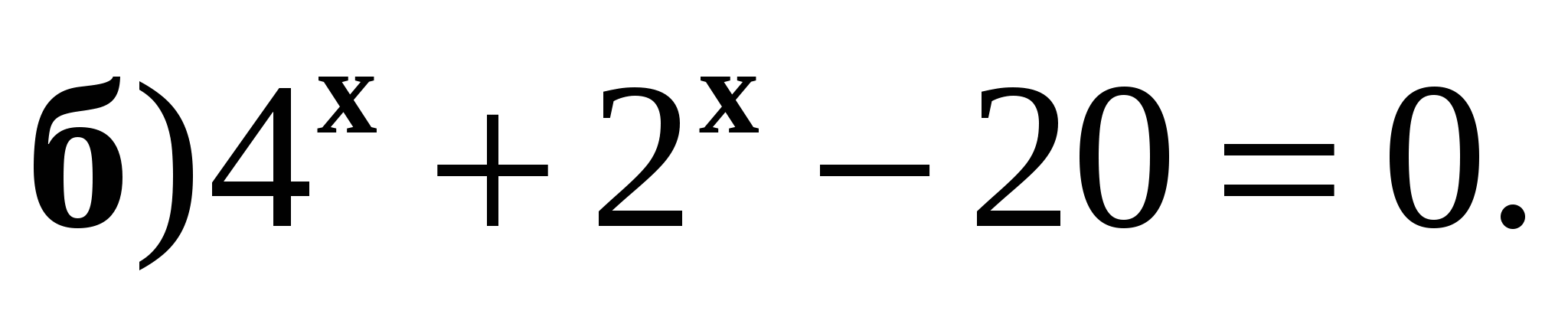
3. Решите неравенство 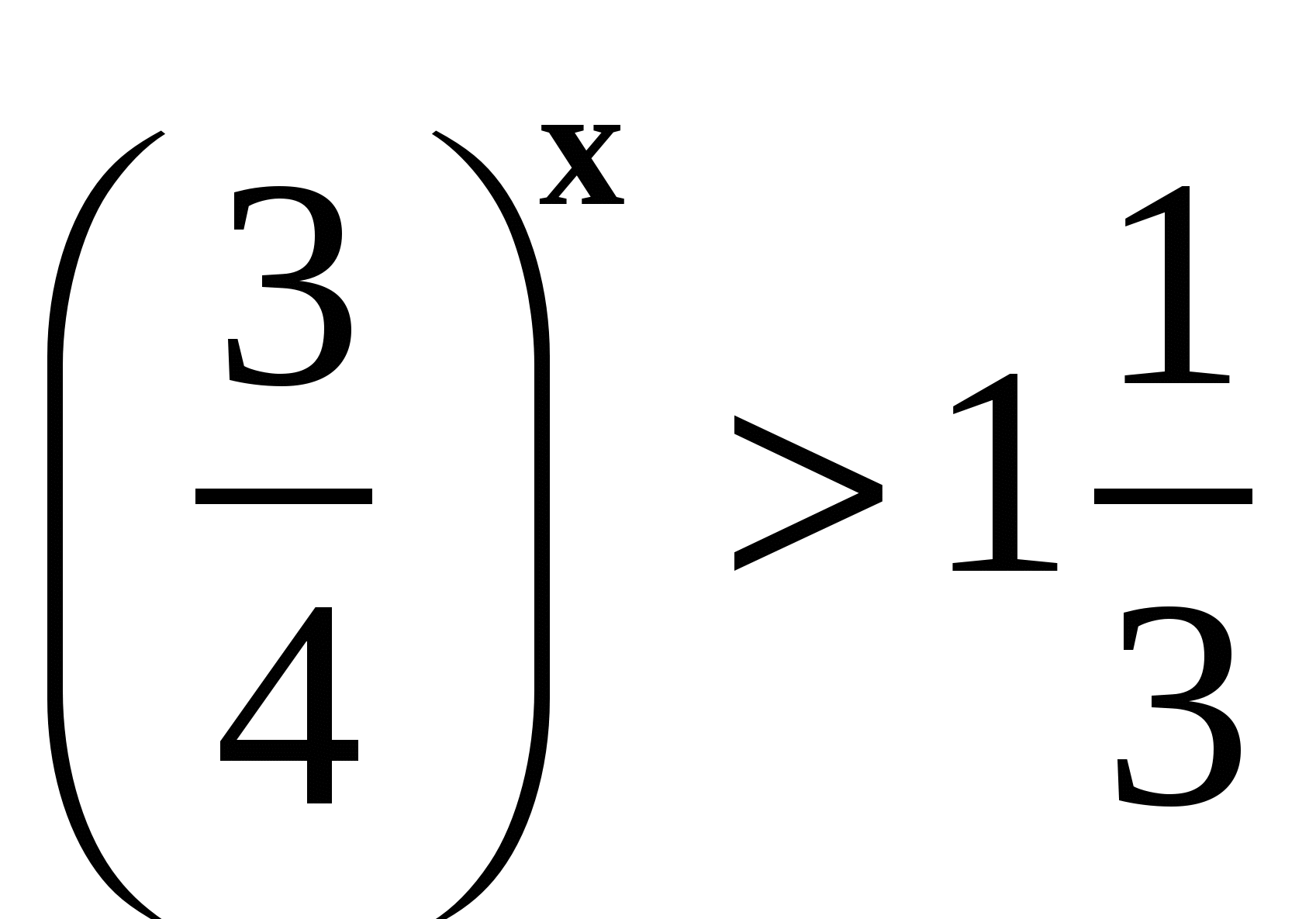 .
.
4. Решите неравенство: 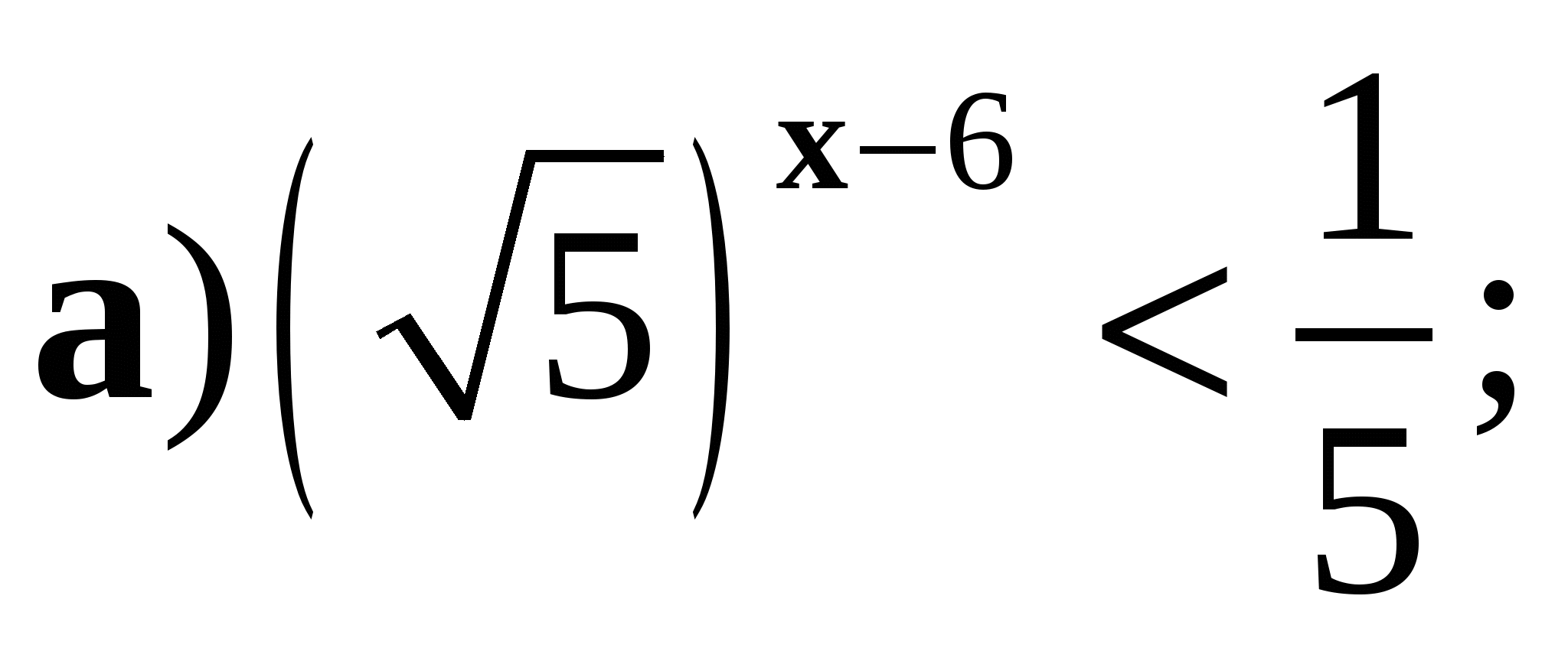
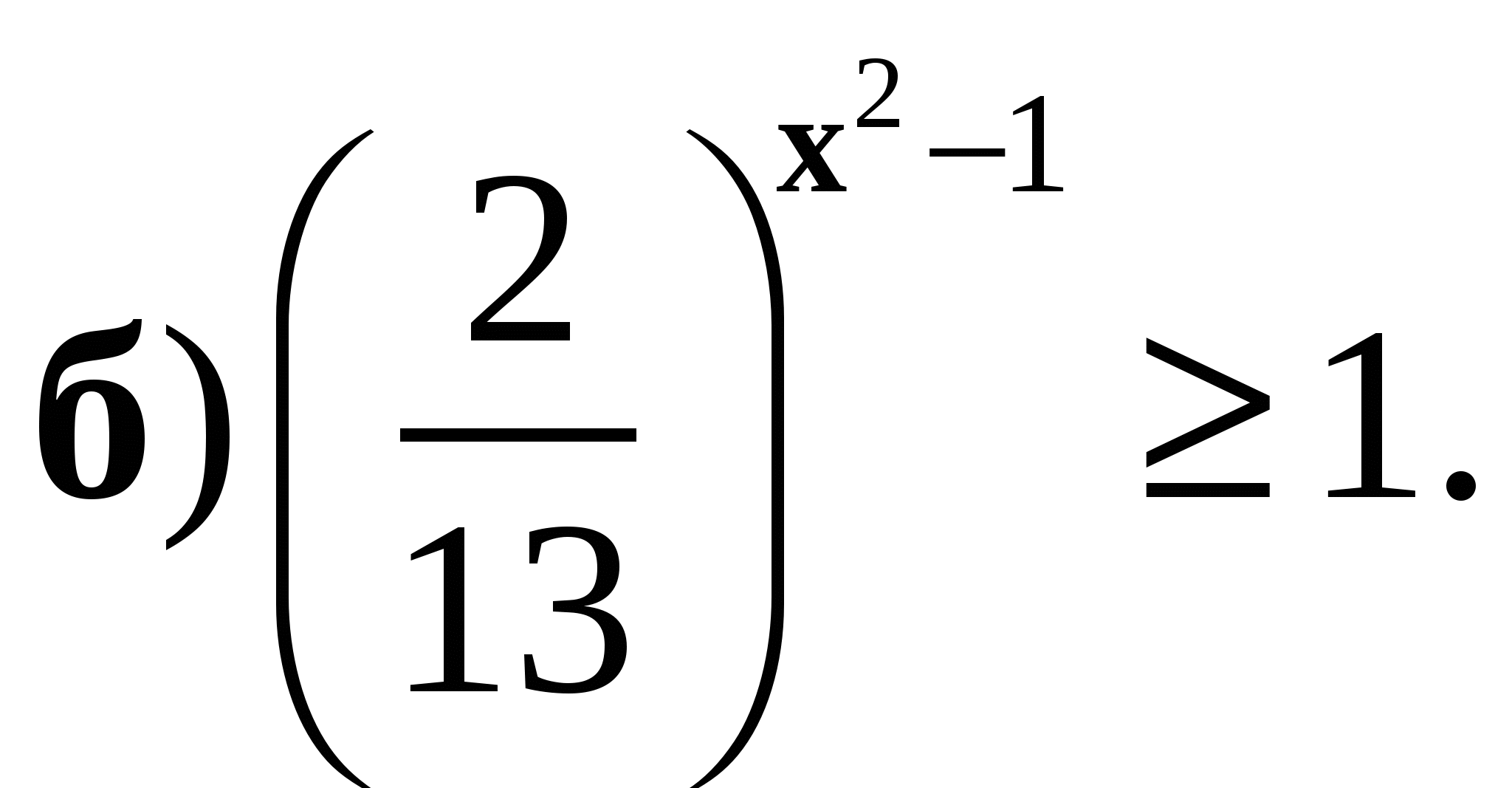
5. Решите систему уравнений 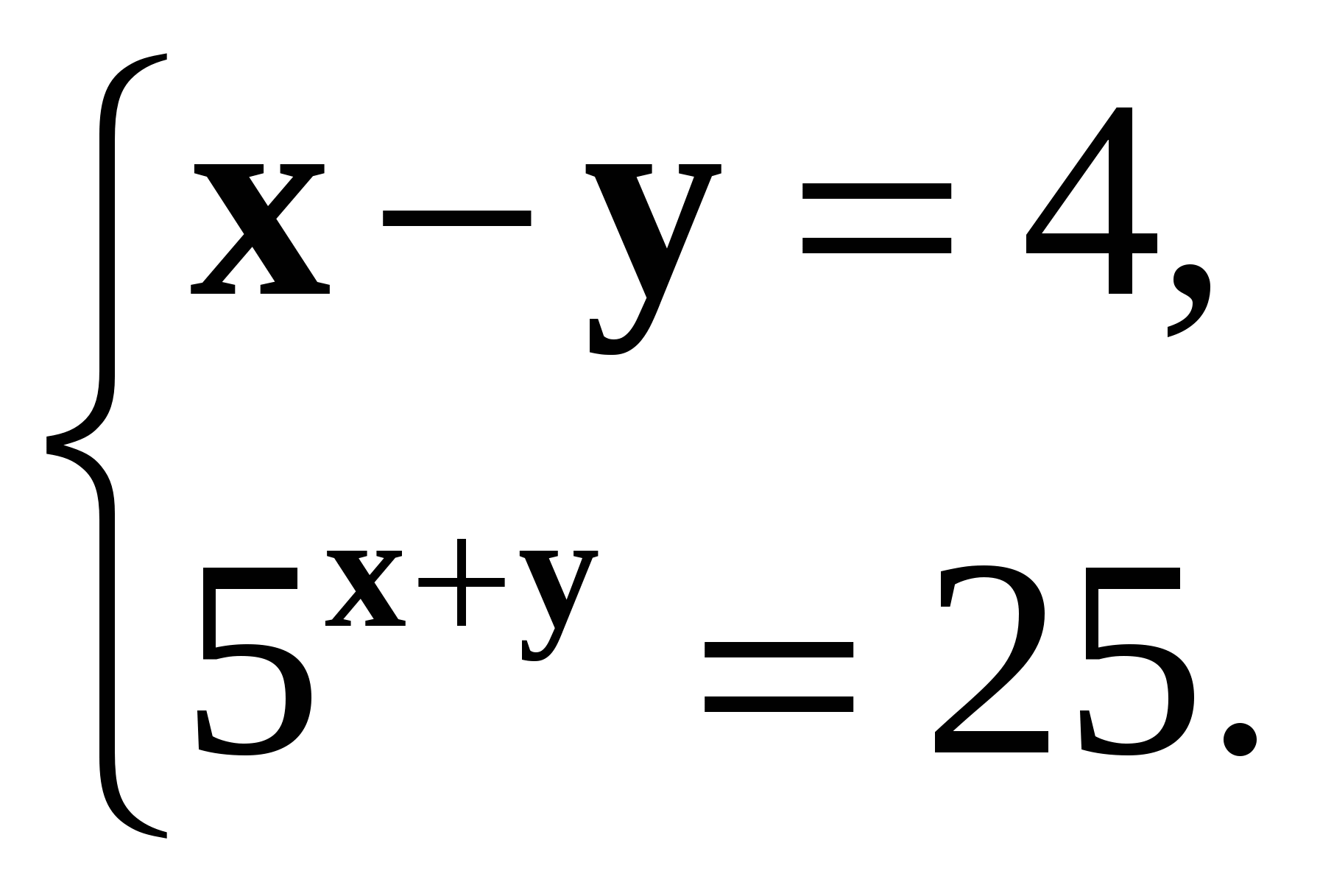
6. Решите уравнение:
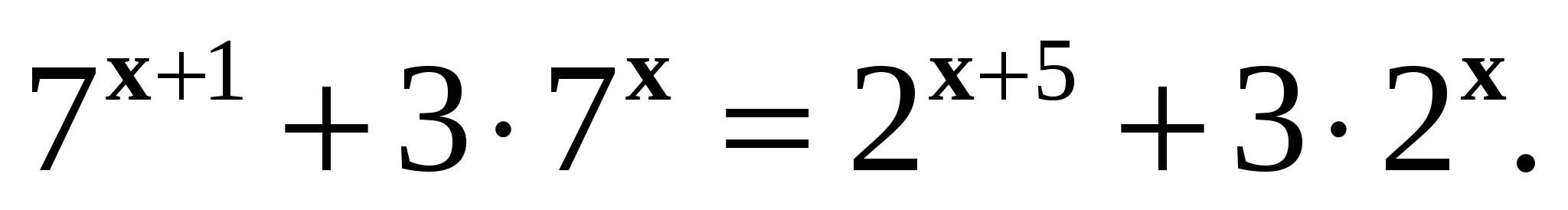
Контрольная работа № 3
Показательная функция
Вариант 2
1. Сравните числа: 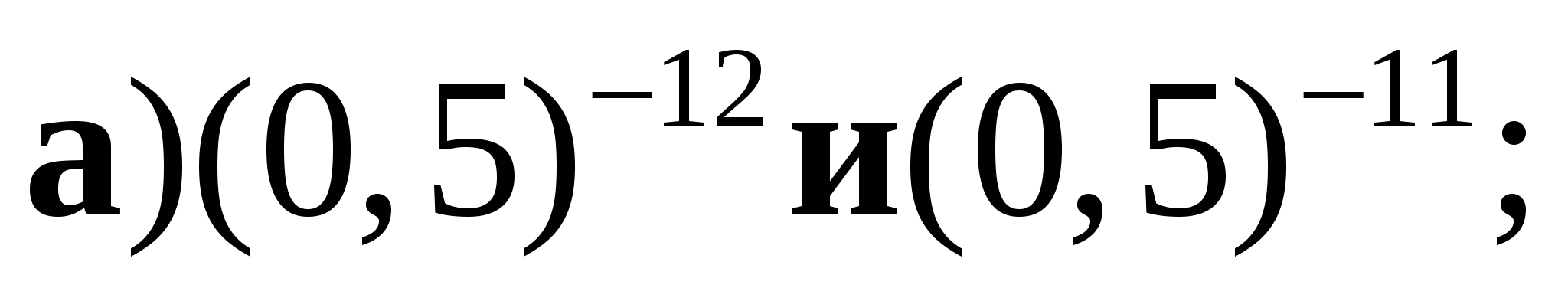 б)
б) 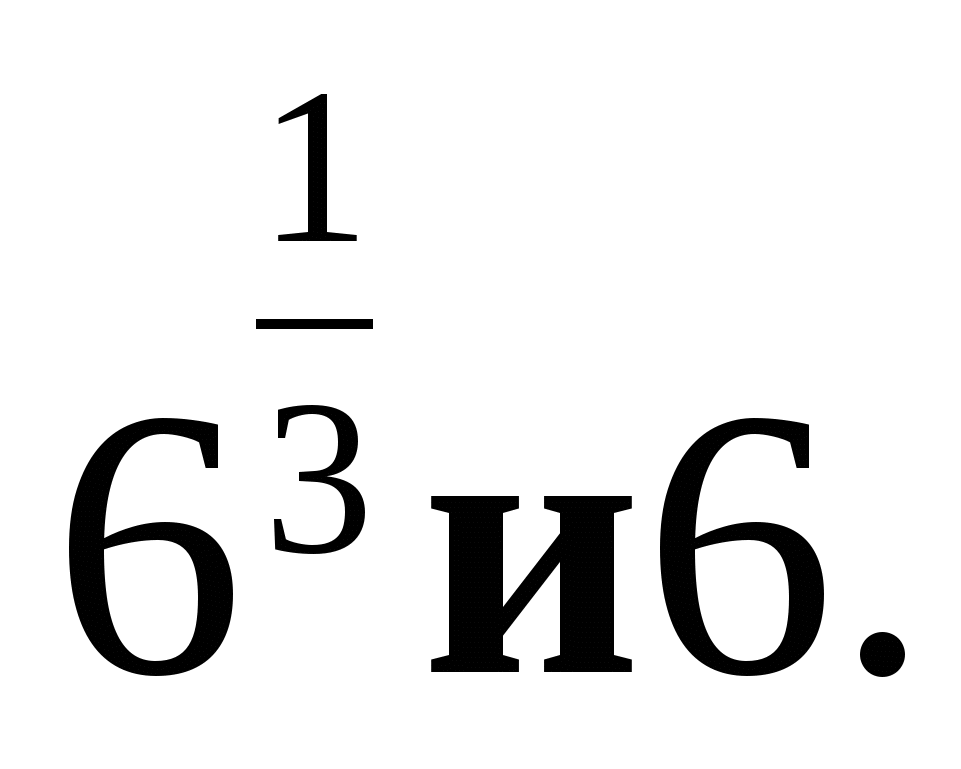
2. Решите уравнение 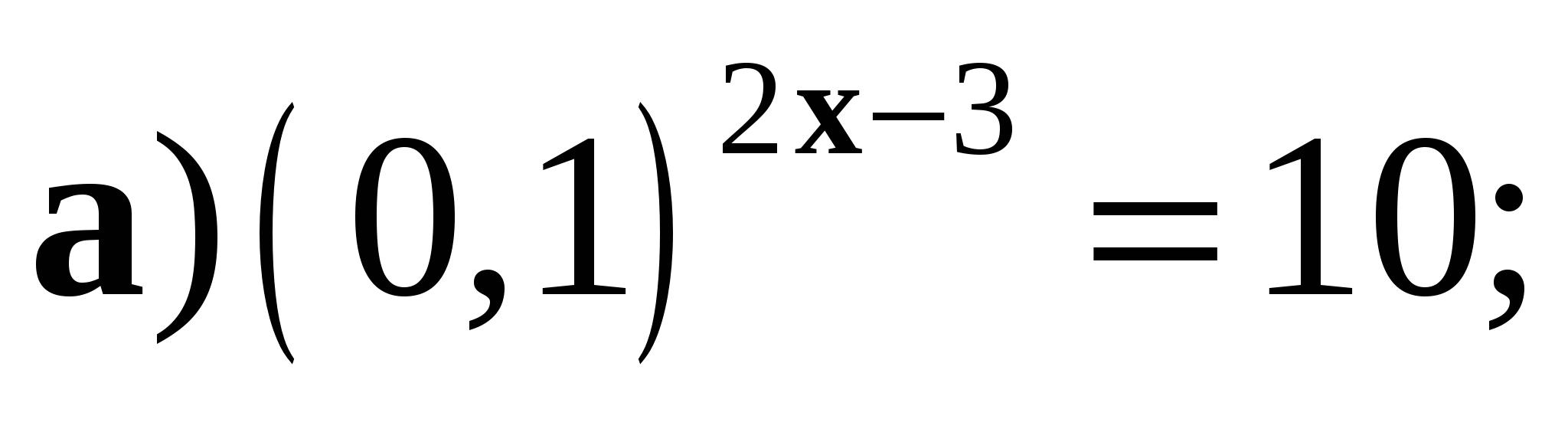
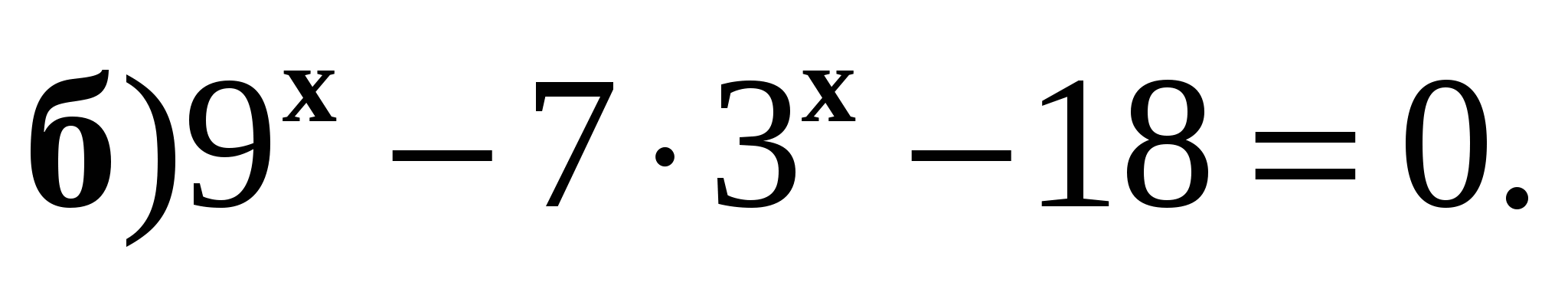
3. Решите неравенство 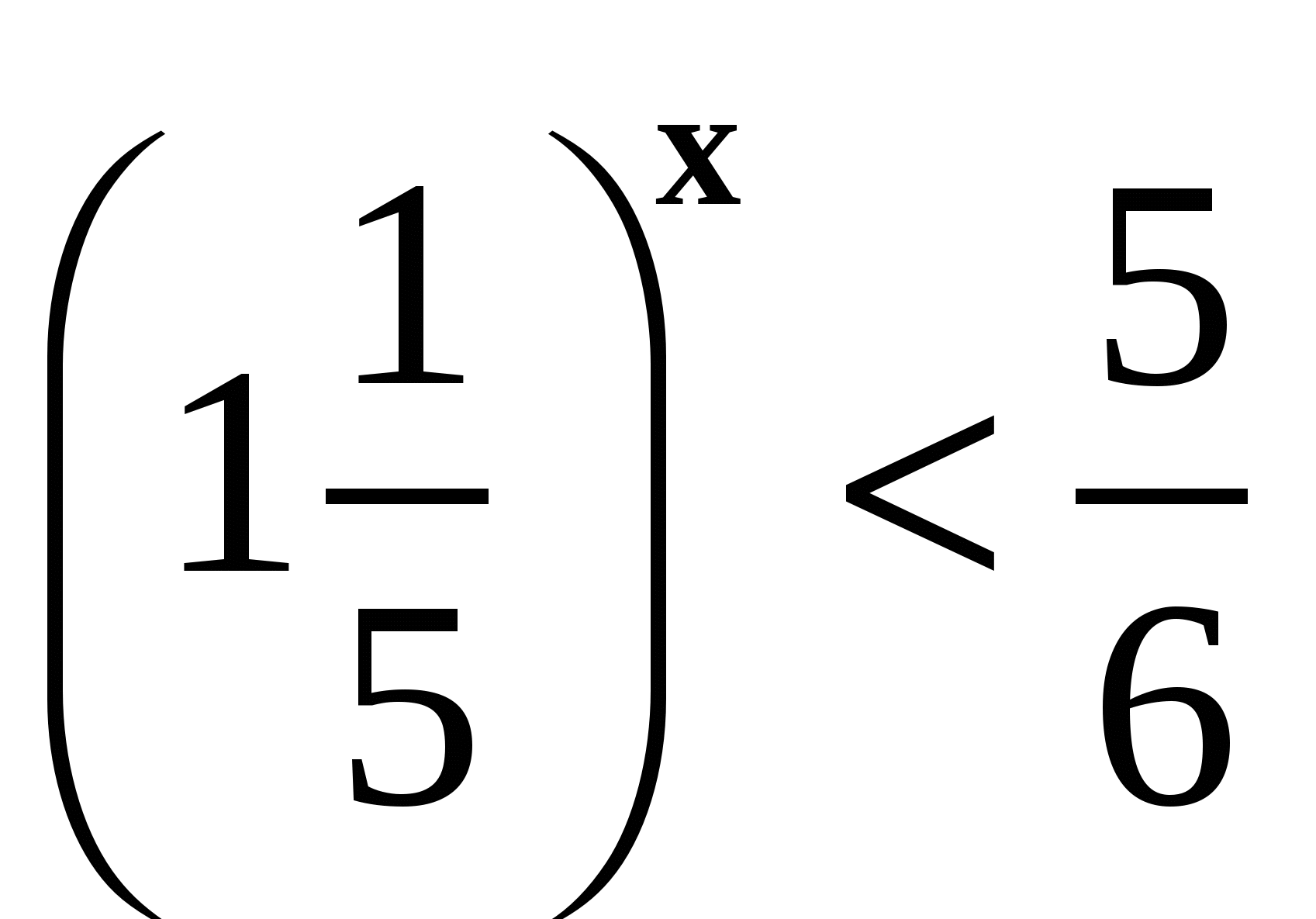 .
.
4. Решите неравенство: 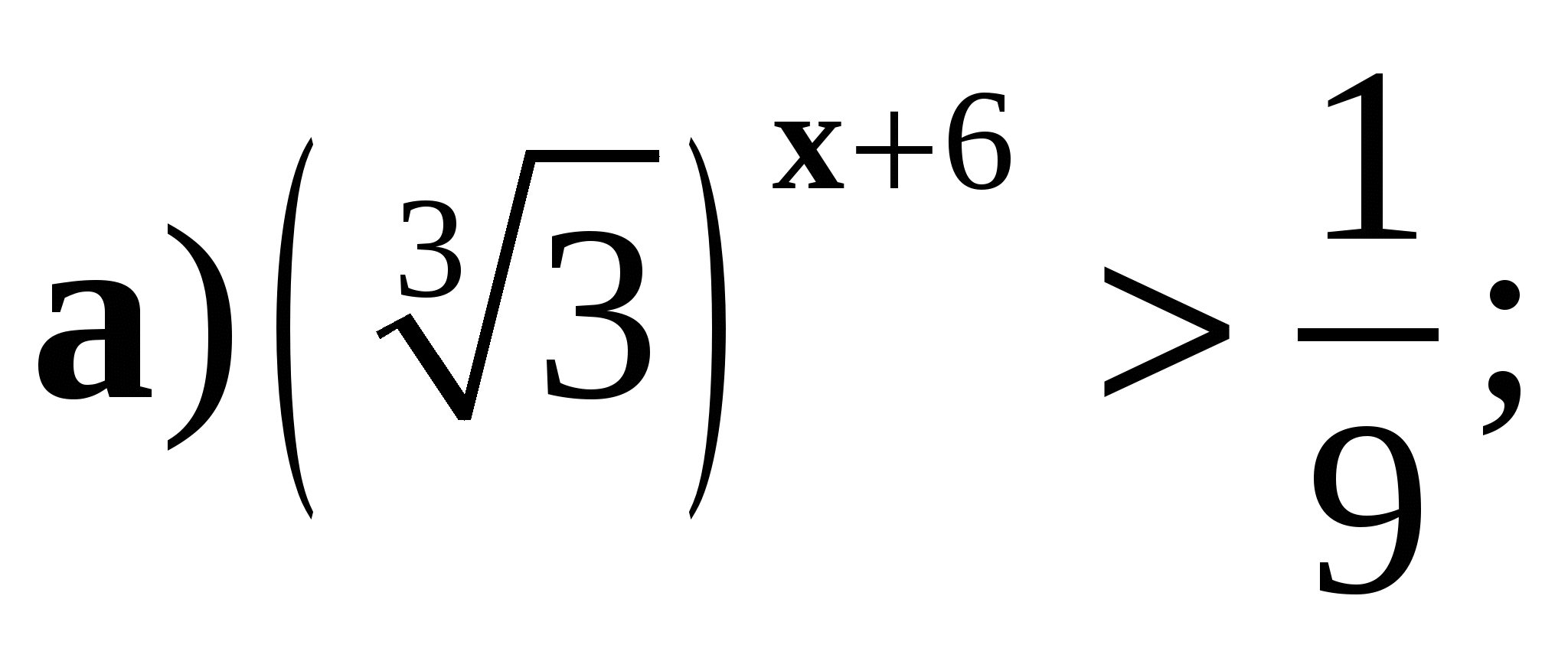
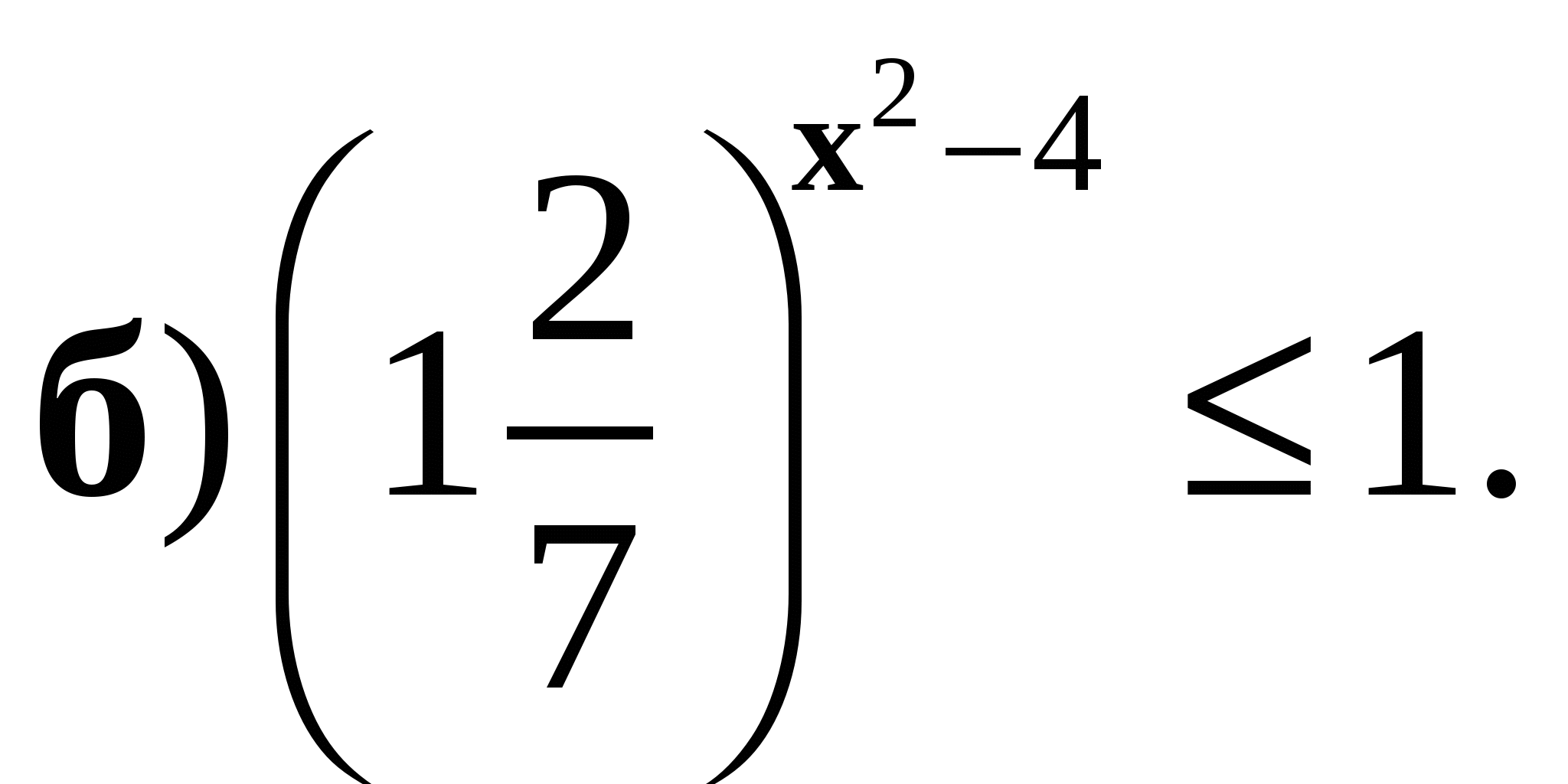
5. Решите систему уравнений 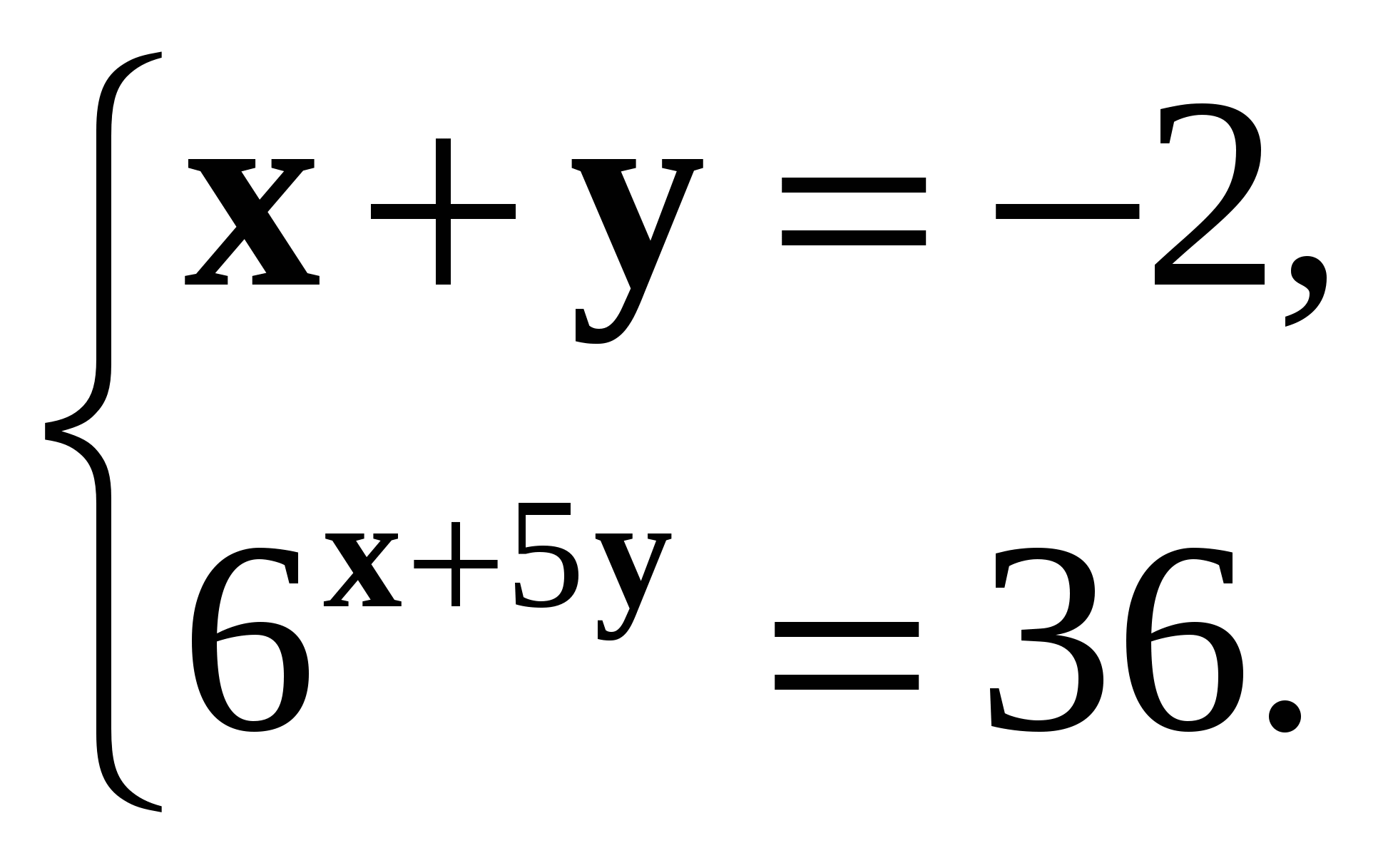
6. Решите уравнение:
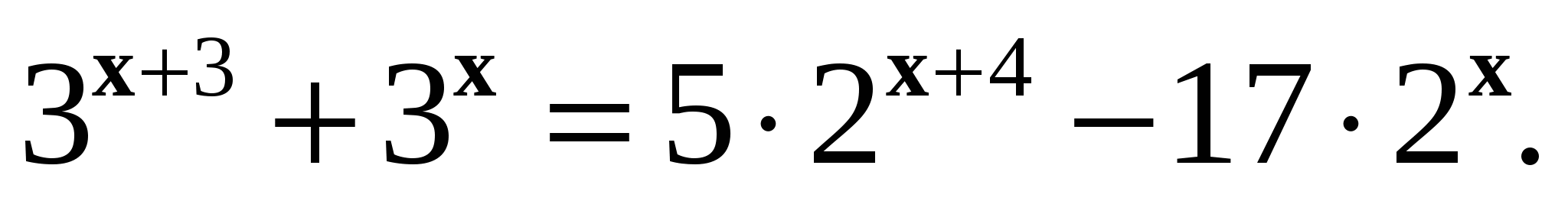
А – 10 Контрольная работа № 4
Логарифмическая функция
Вариант 1
1. Вычислите:
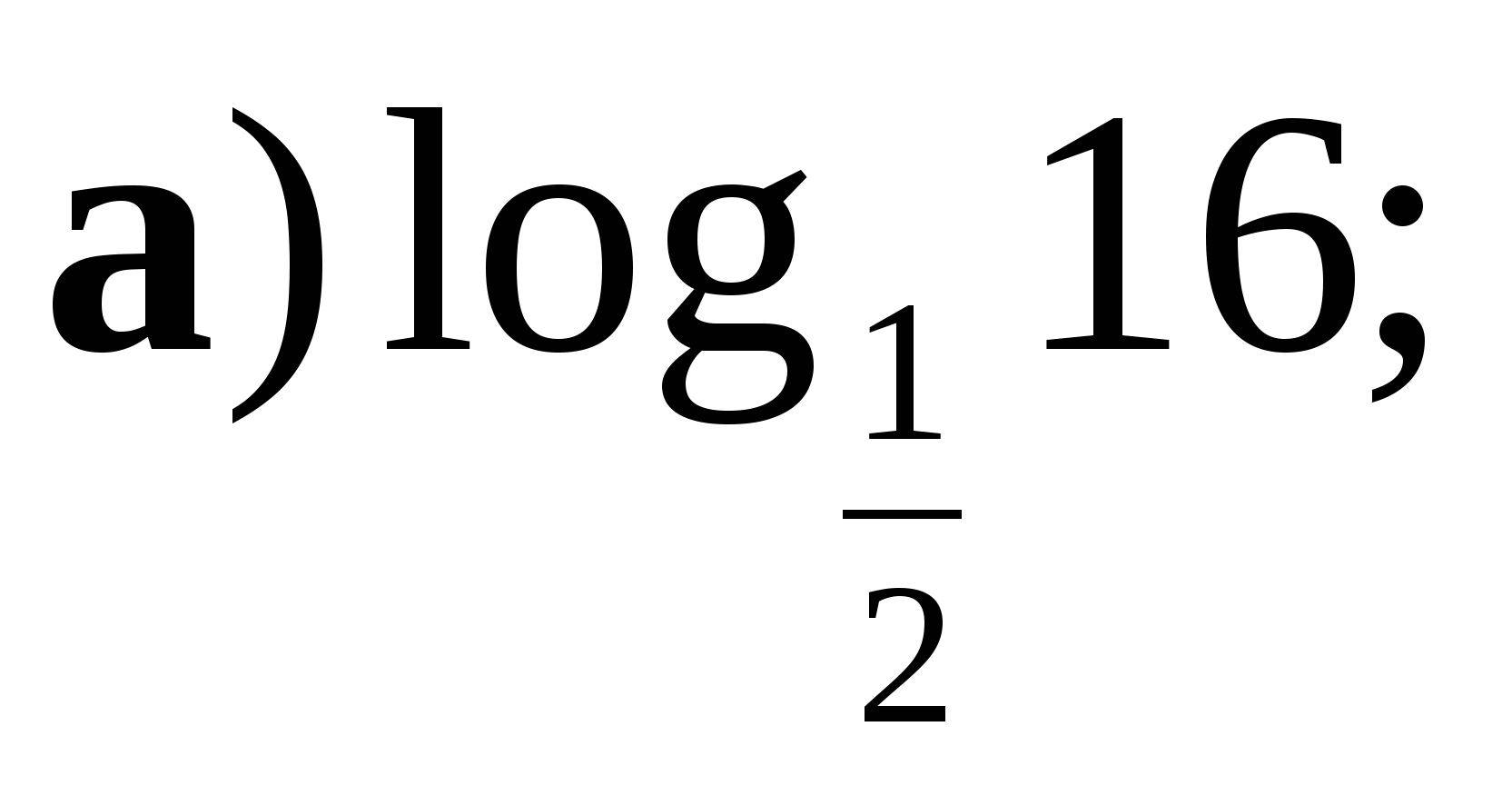
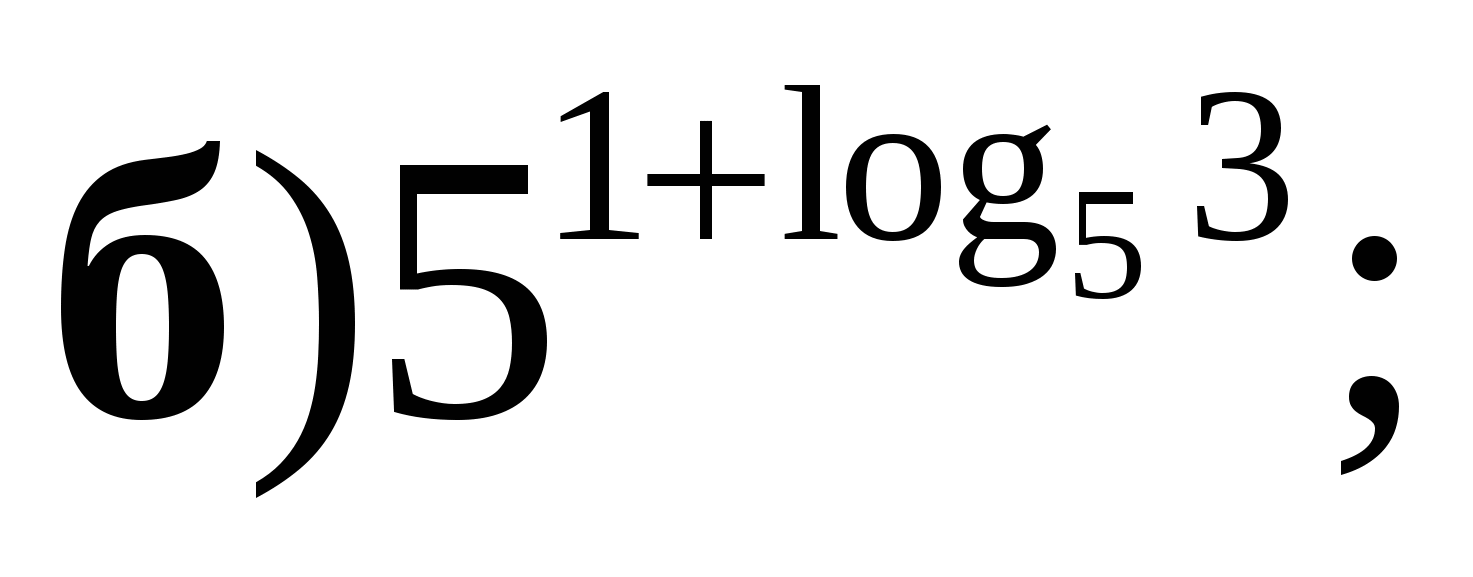
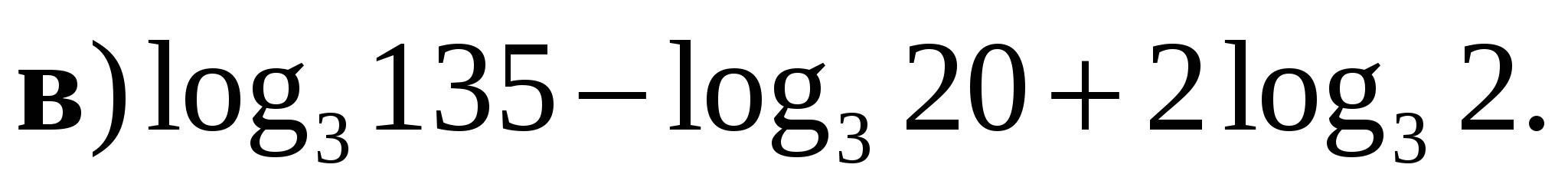
2. Сравните числа 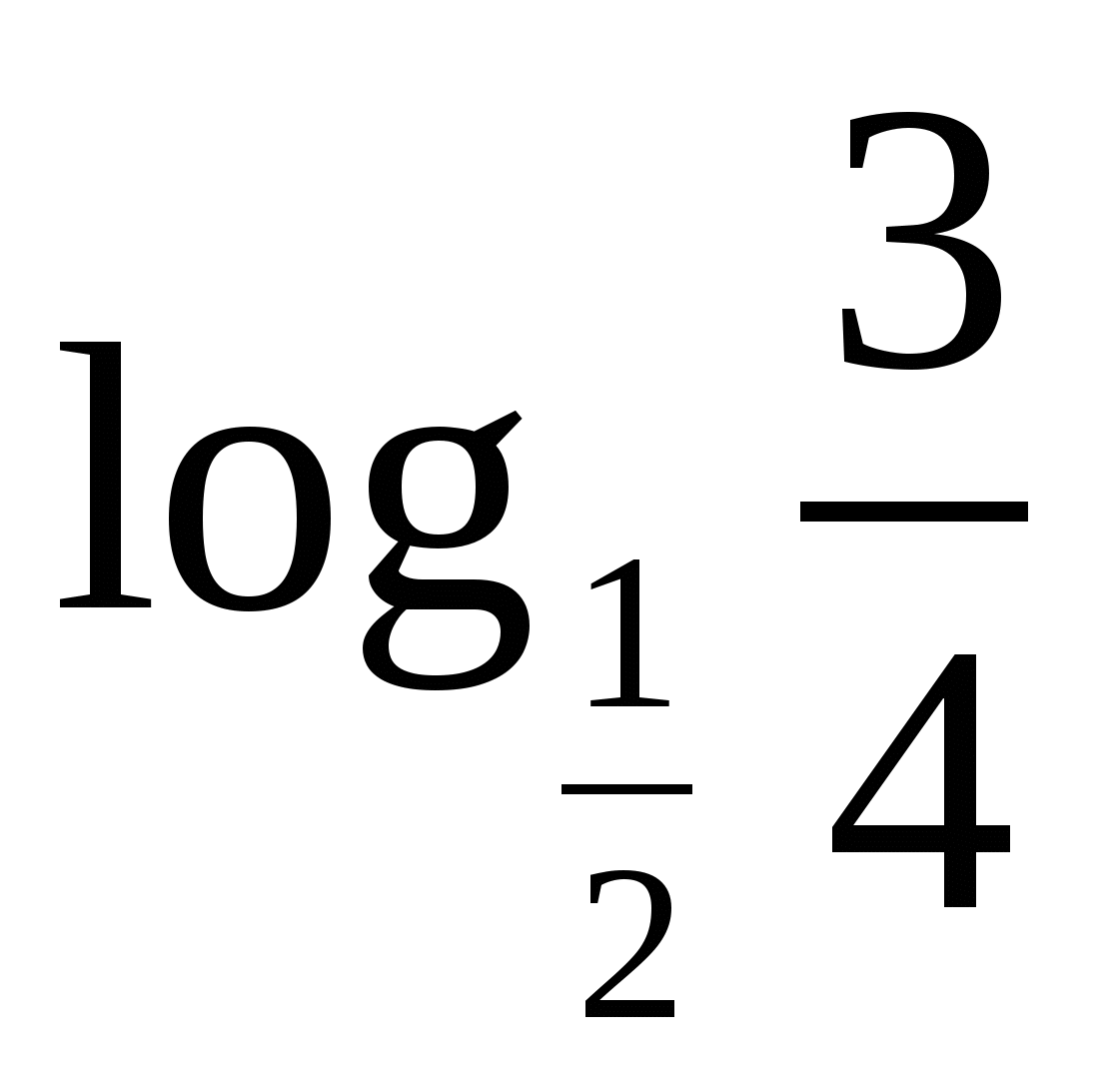 и
и 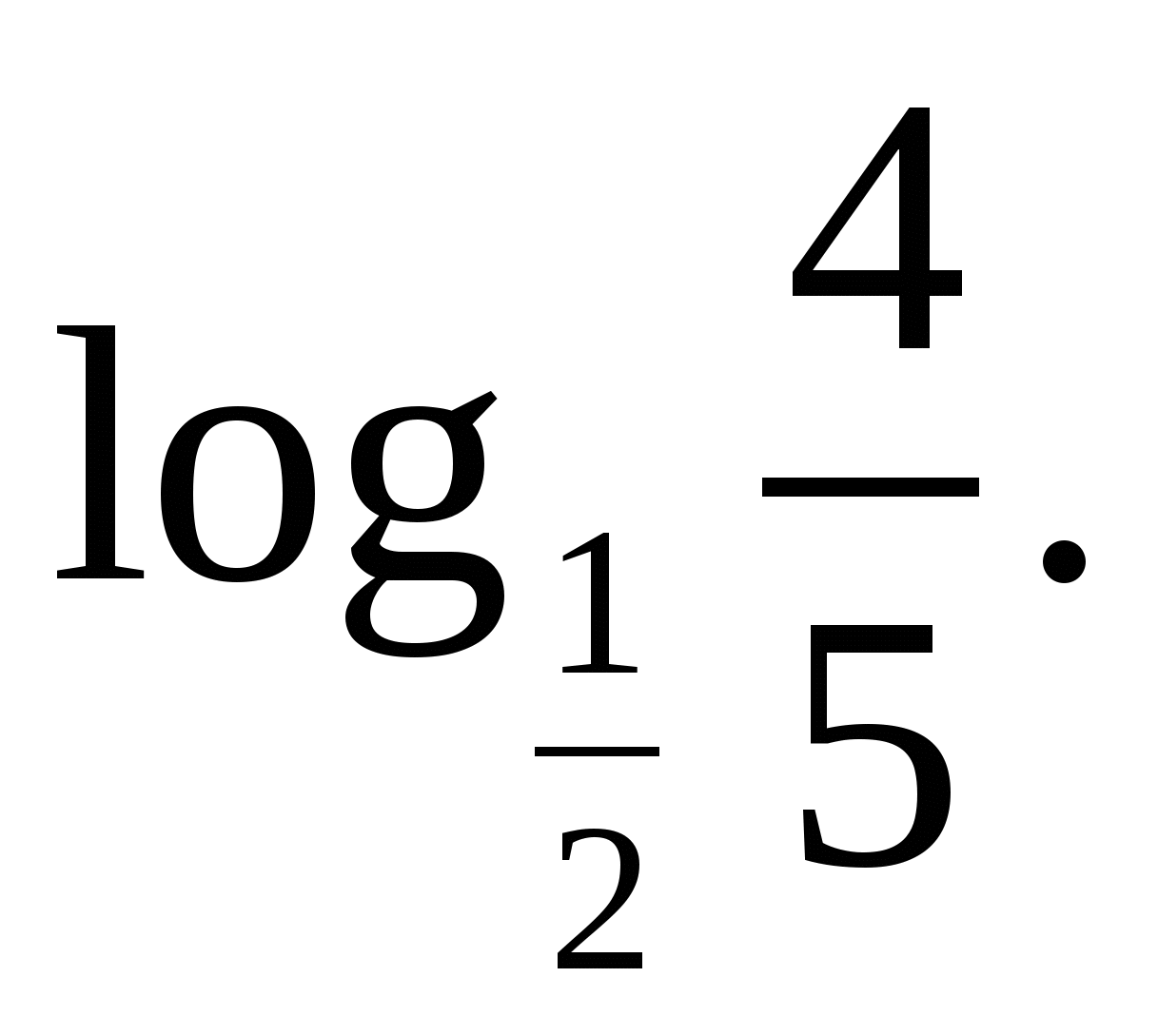
3. Решите уравнение 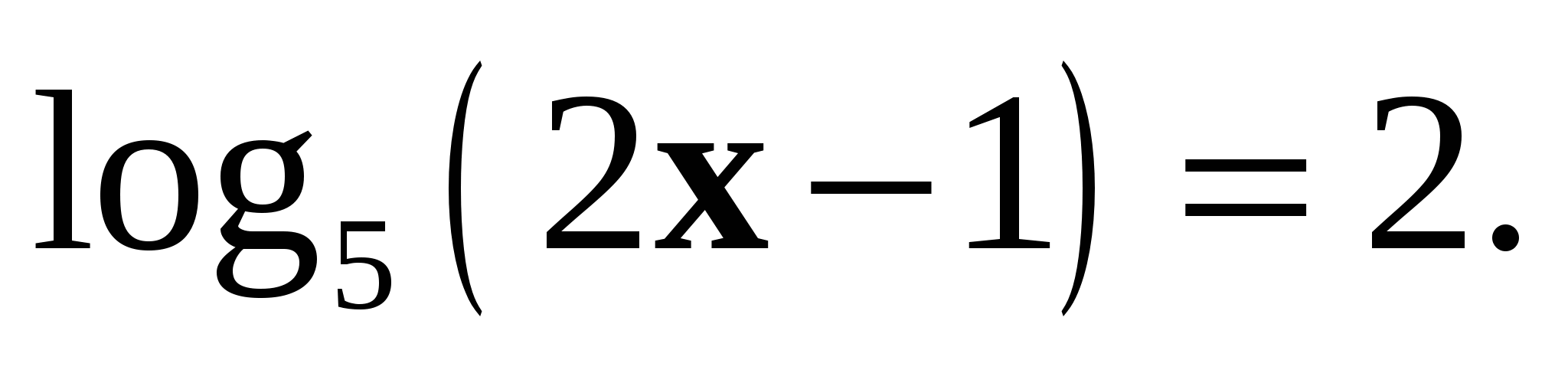
4. Решите неравенство 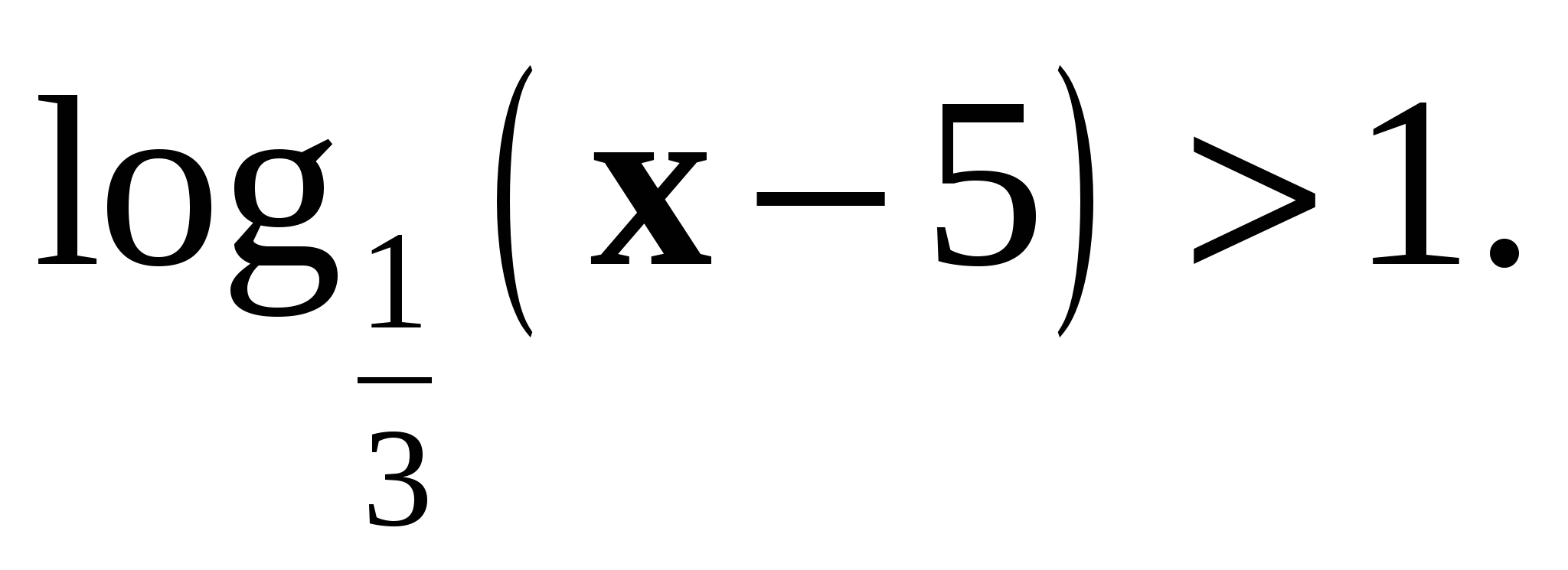
5. Решите уравнение 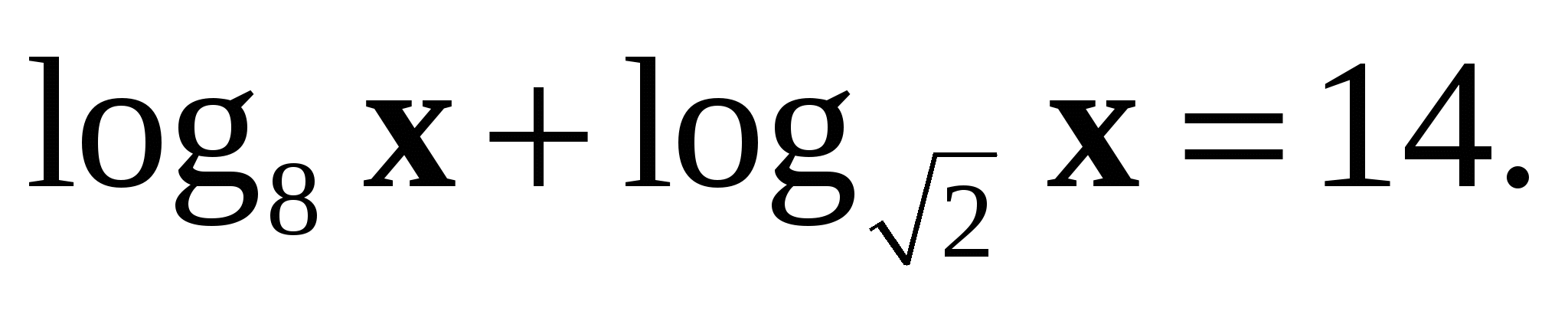
6. Решите неравенство:
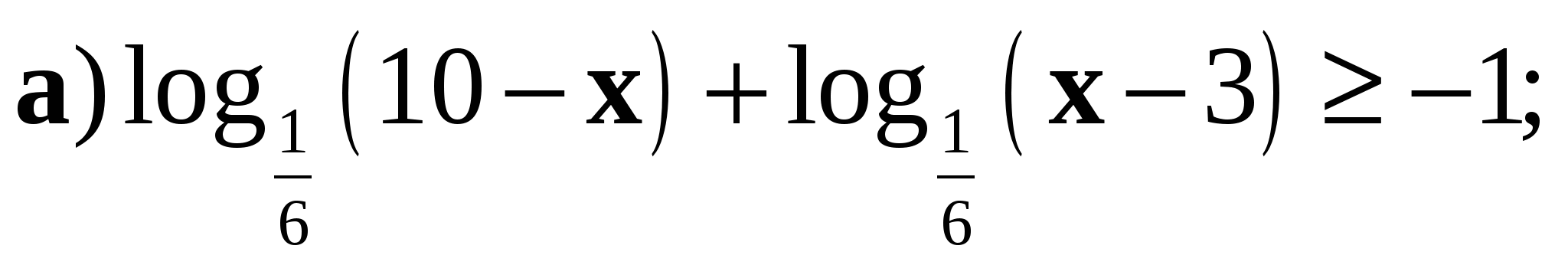
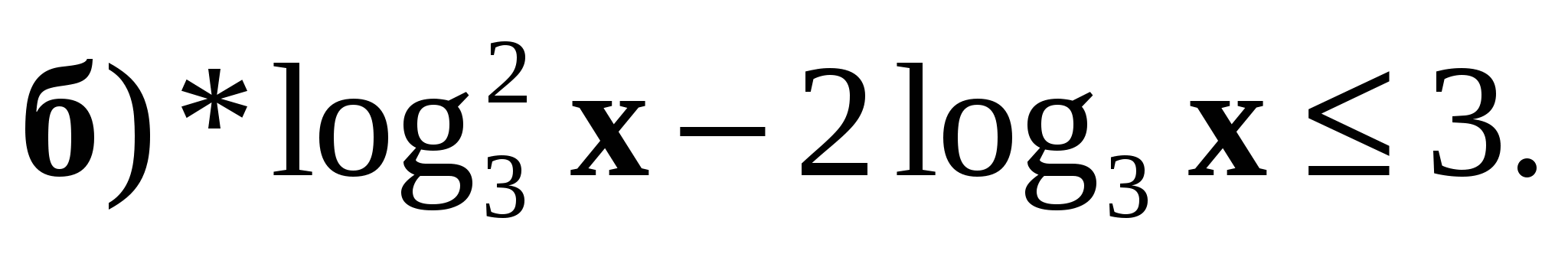
Контрольная работа № 4
Логарифмическая функция
Вариант 2
1. Вычислите:
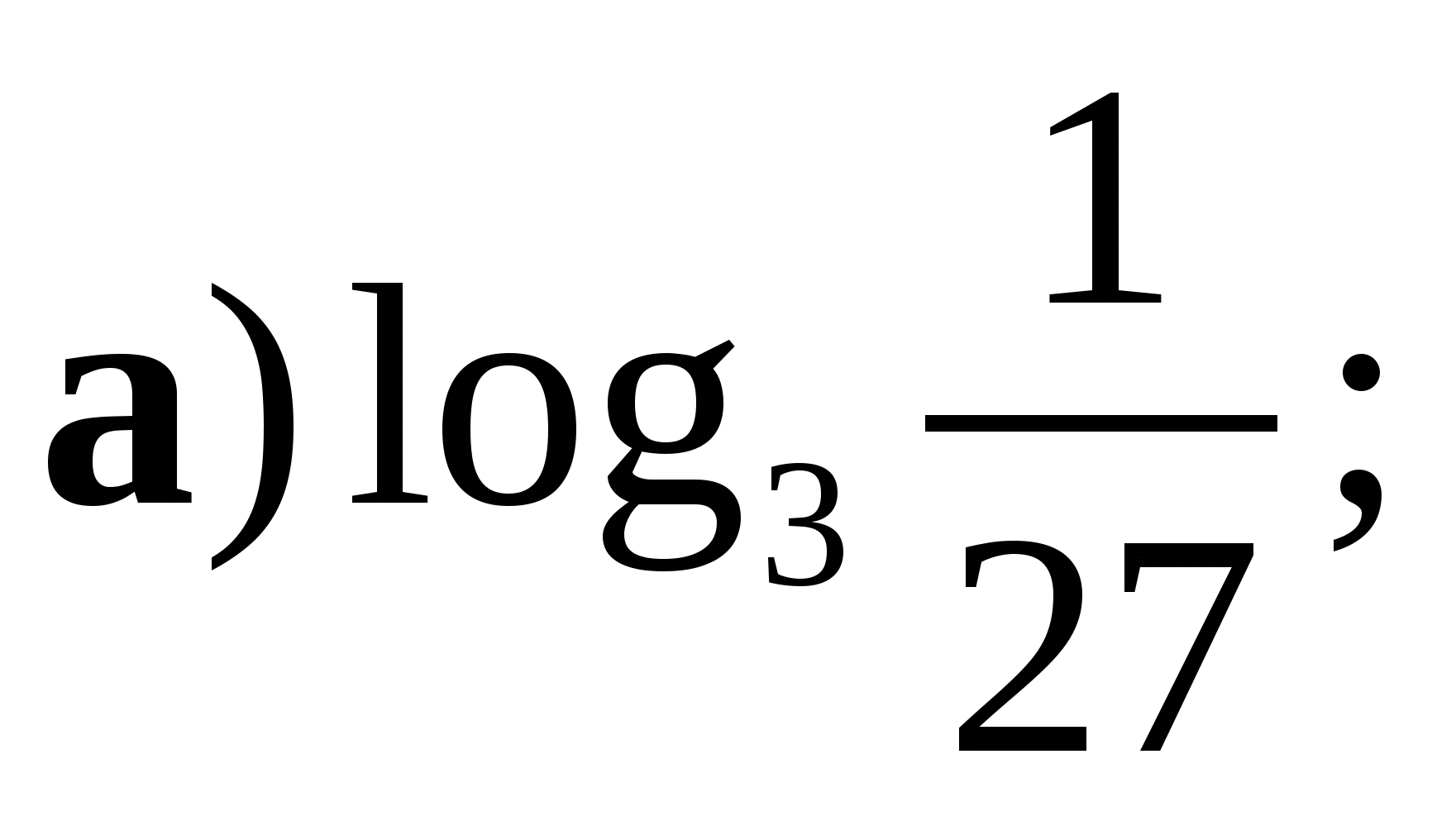
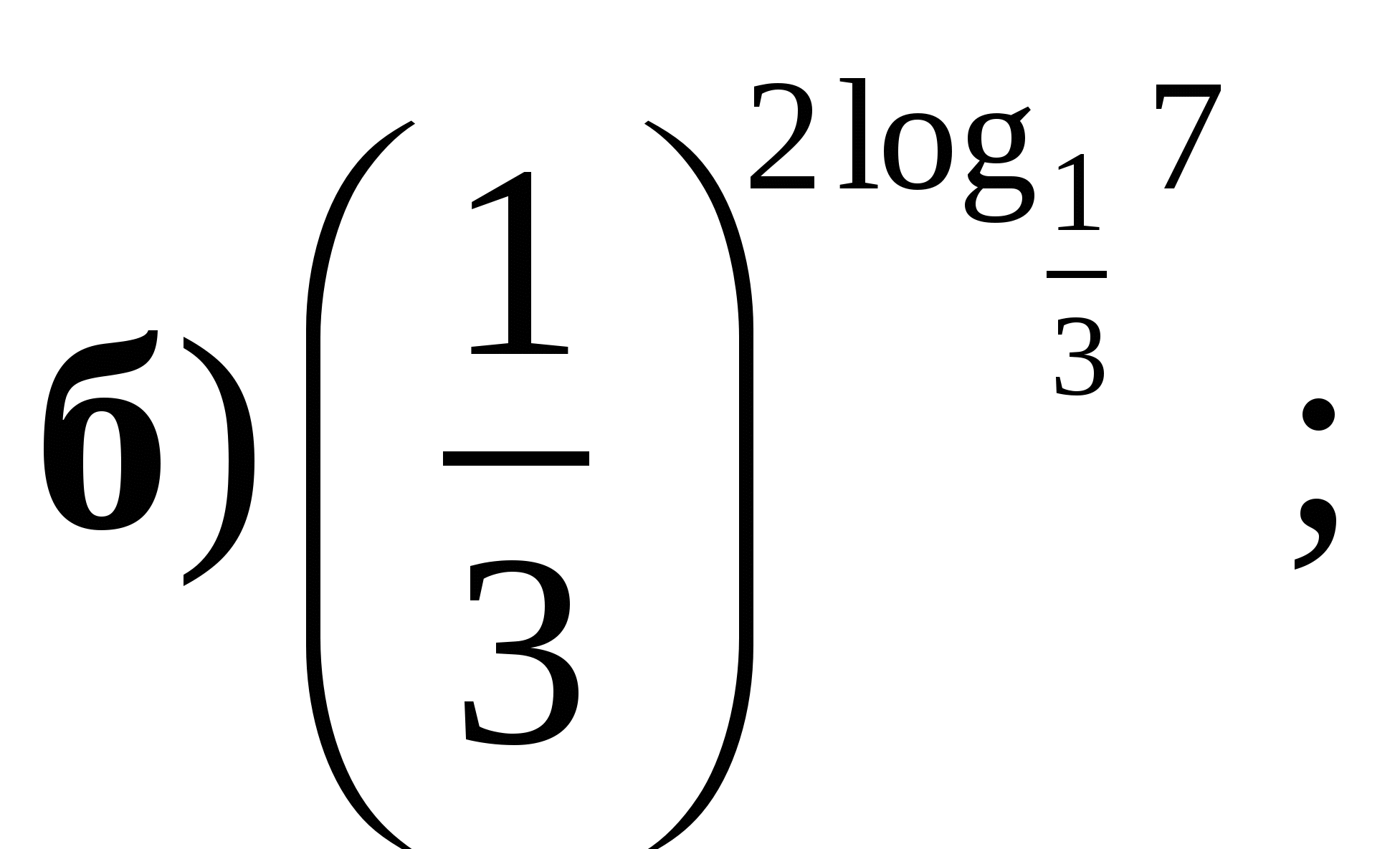
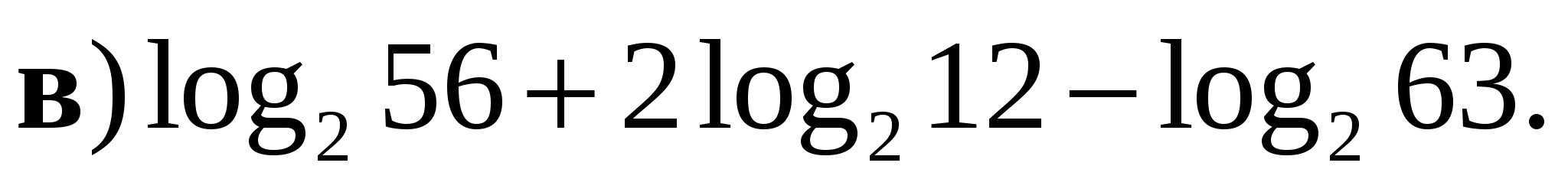
2. Сравните числа 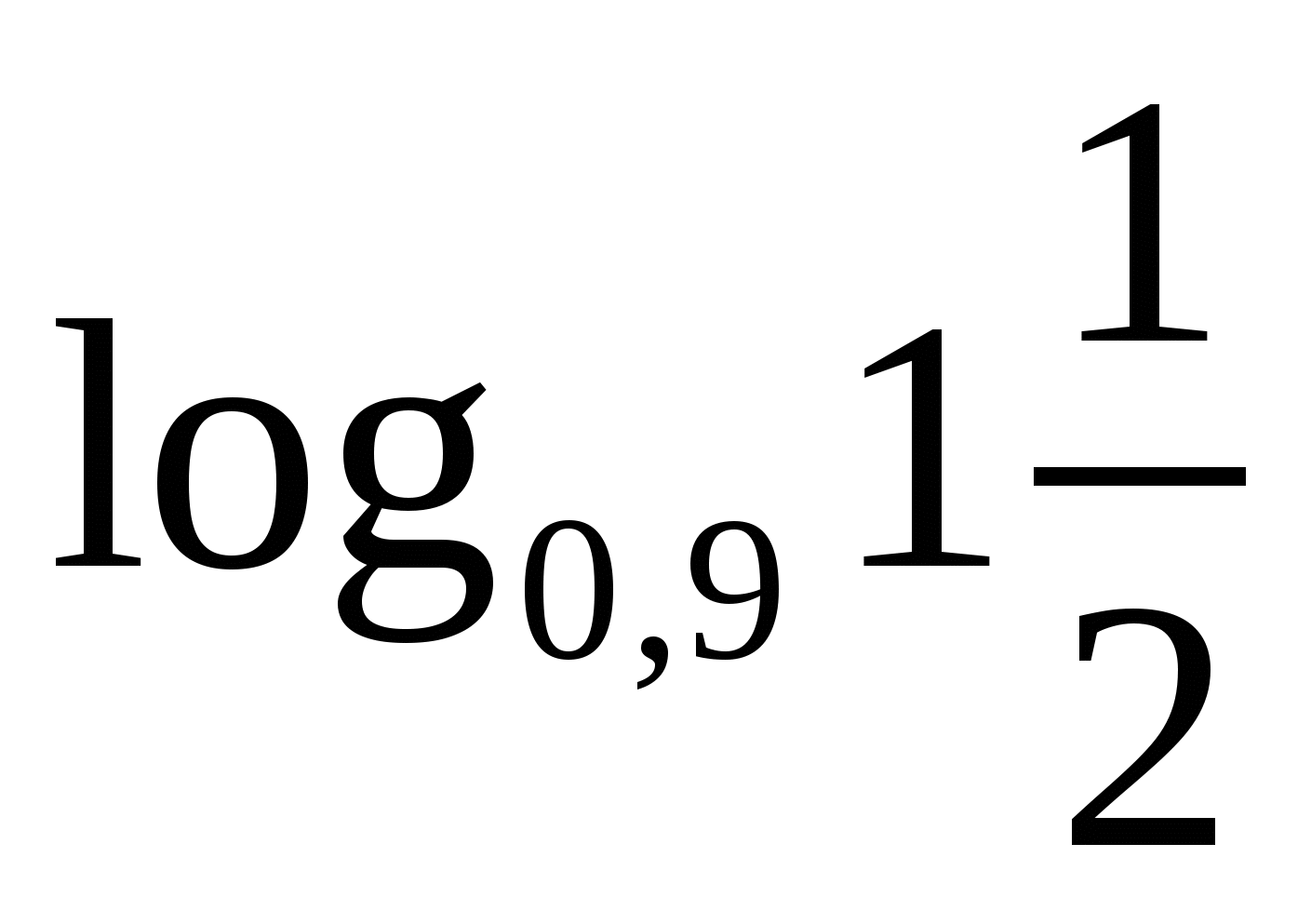 и
и 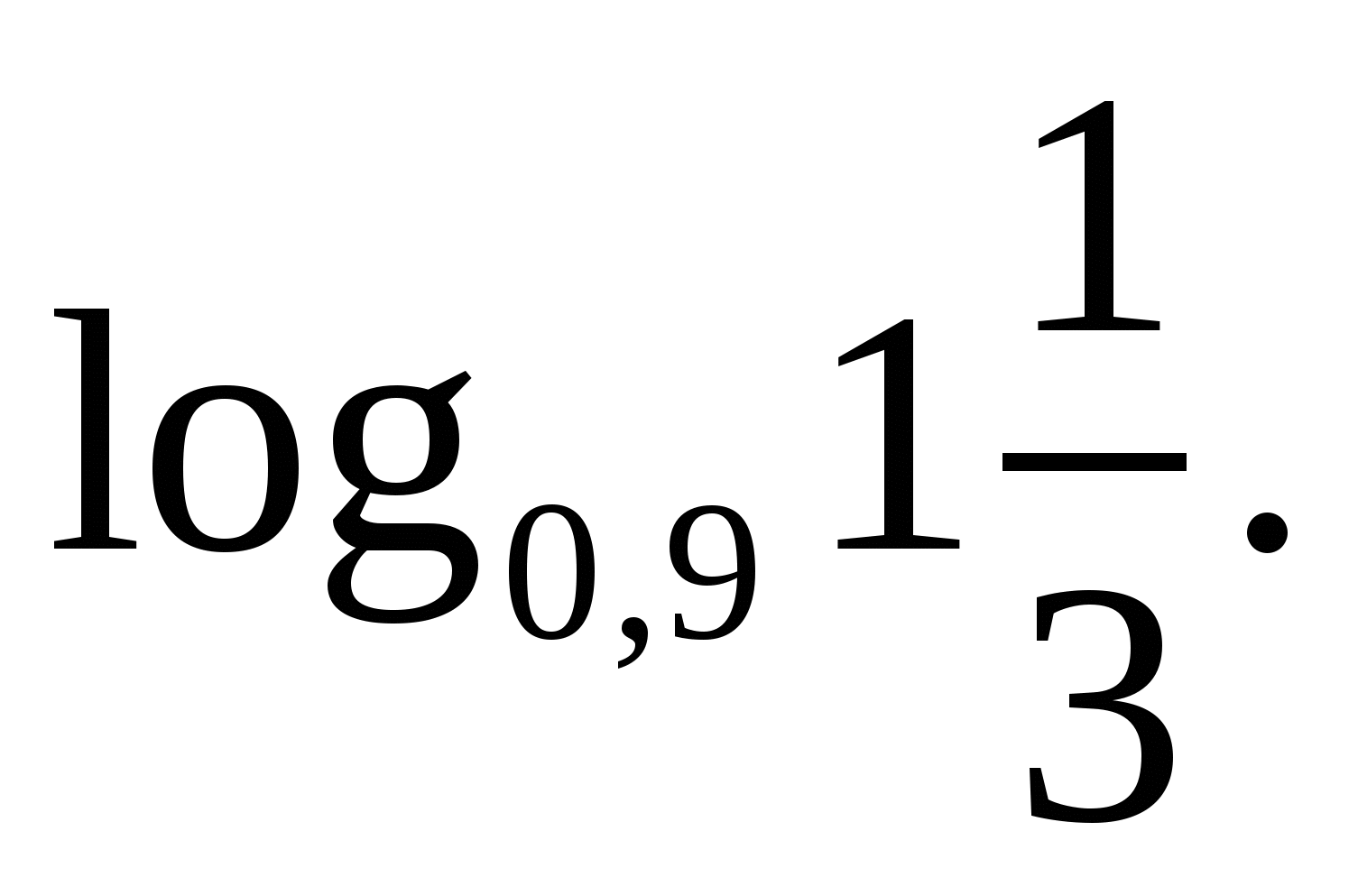
3. Решите уравнение 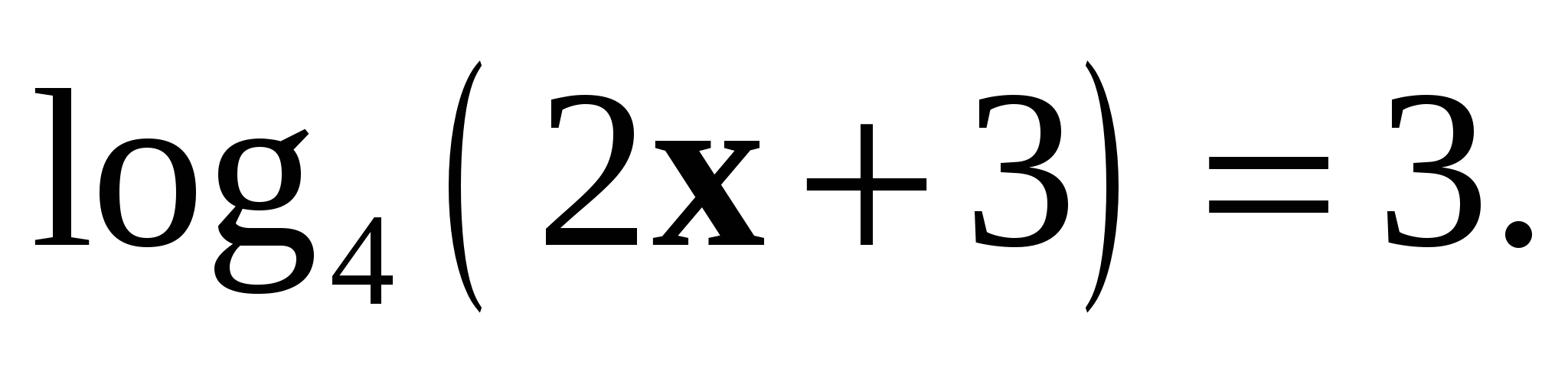
4. Решите неравенство 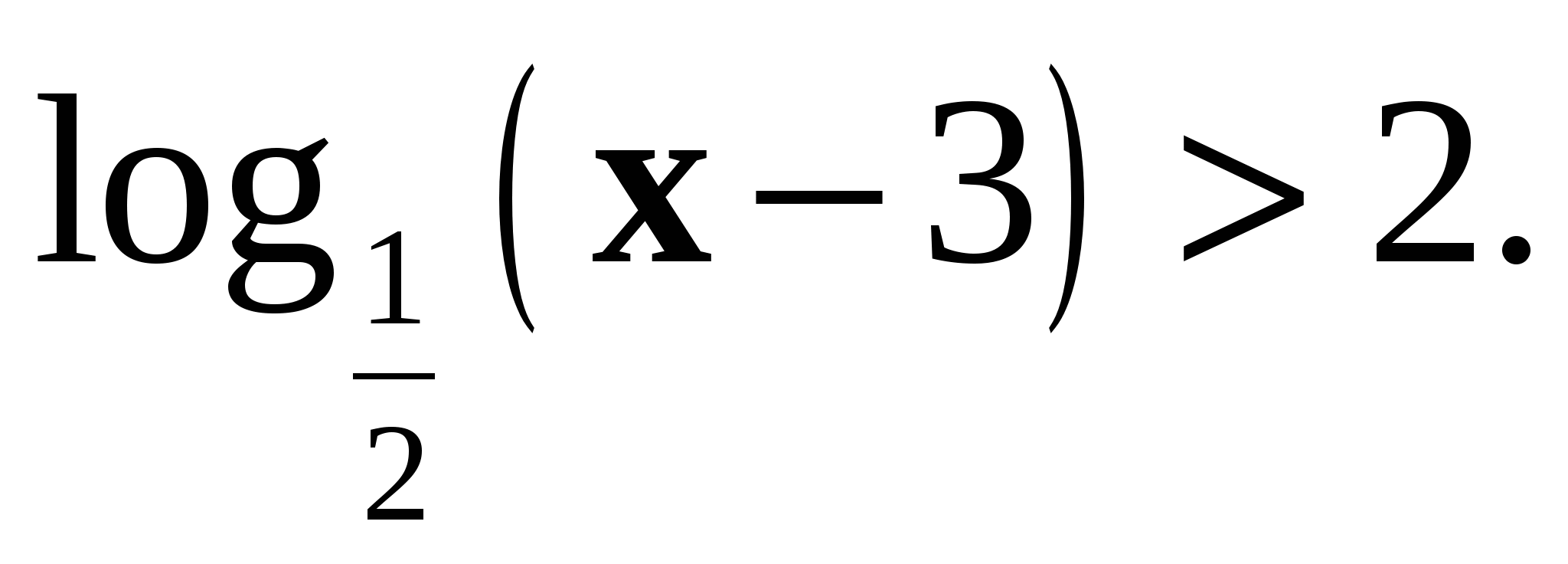
5. Решите уравнение 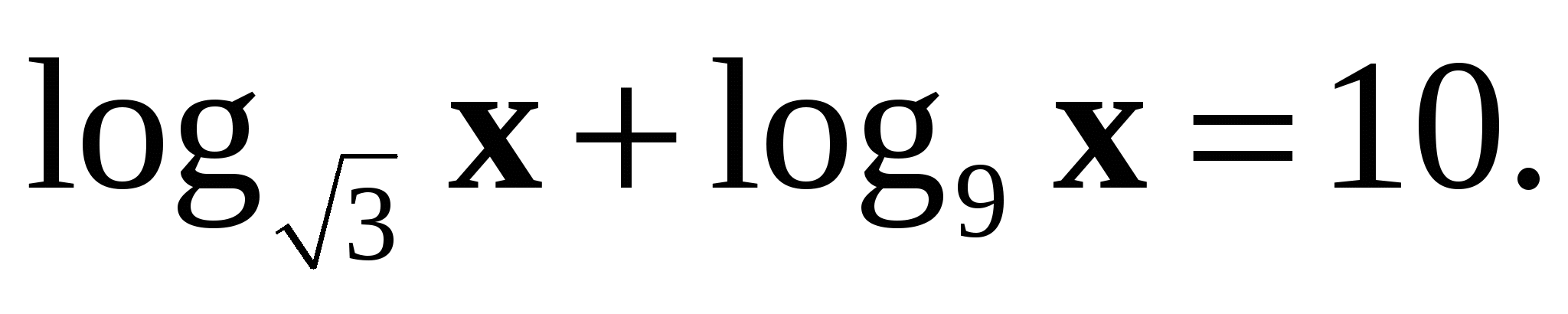
6. Решите неравенство:
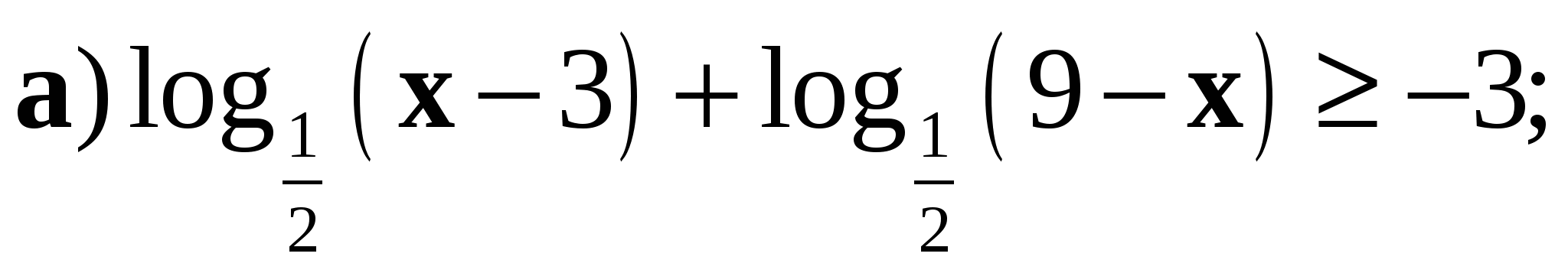
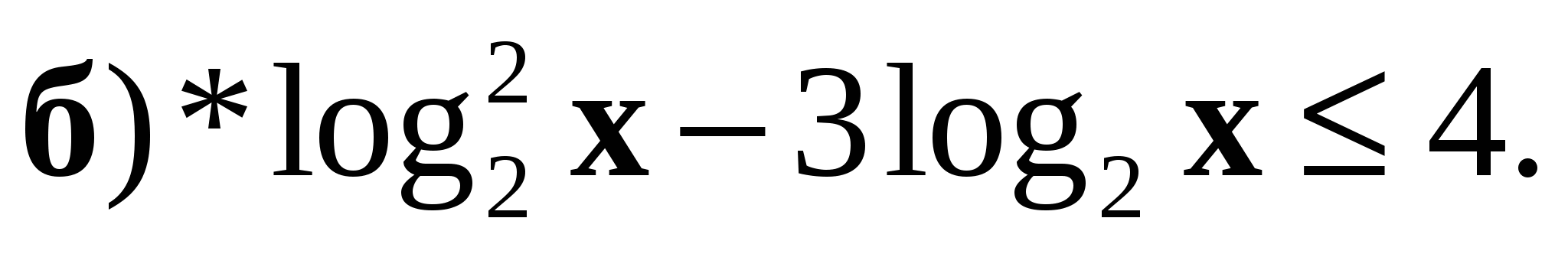
А – 10 Контрольная работа №5
Тригонометрические формулы
Вариант 1
1. Вычислите: 
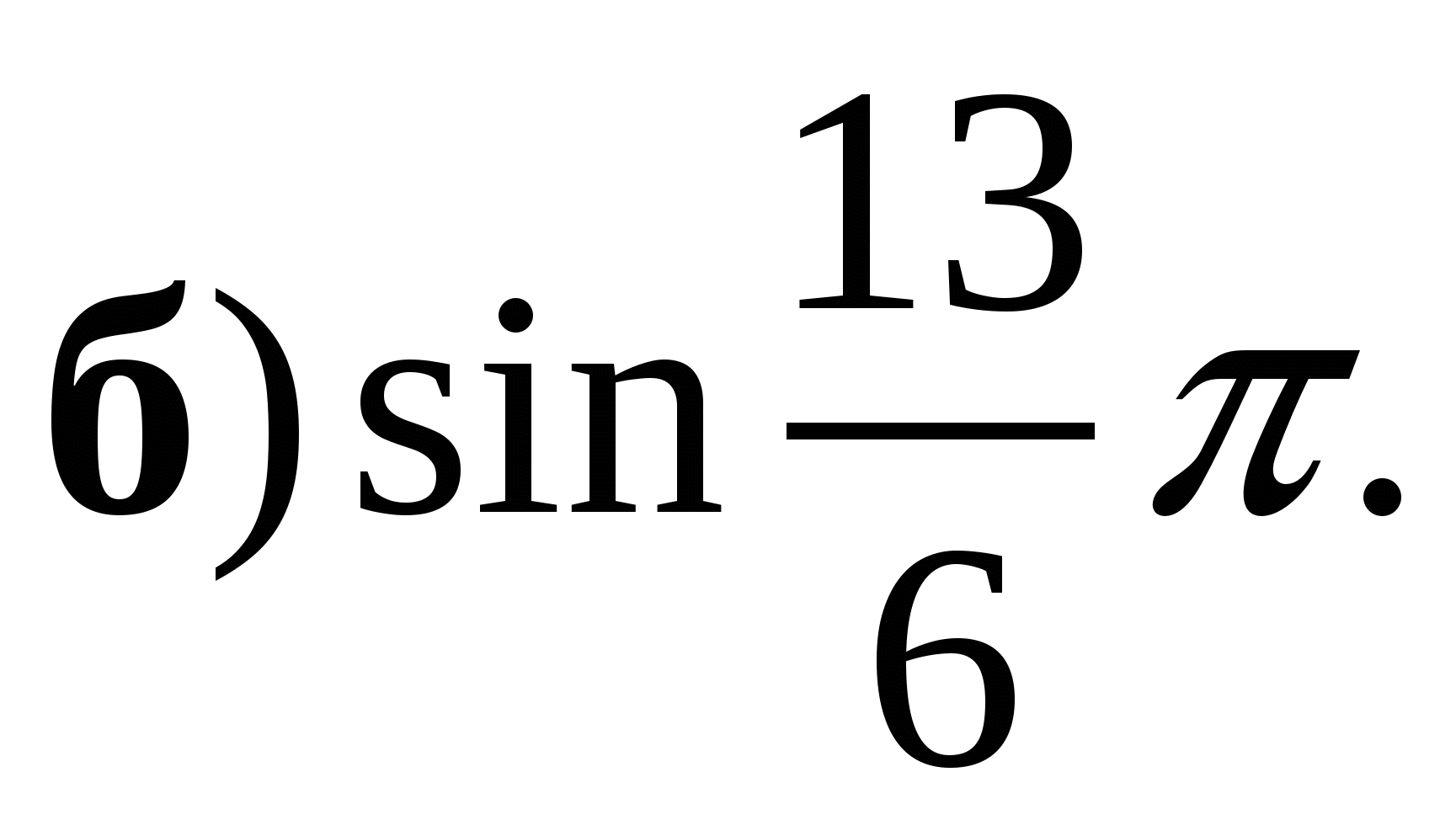
2. Вычислите sinα, если 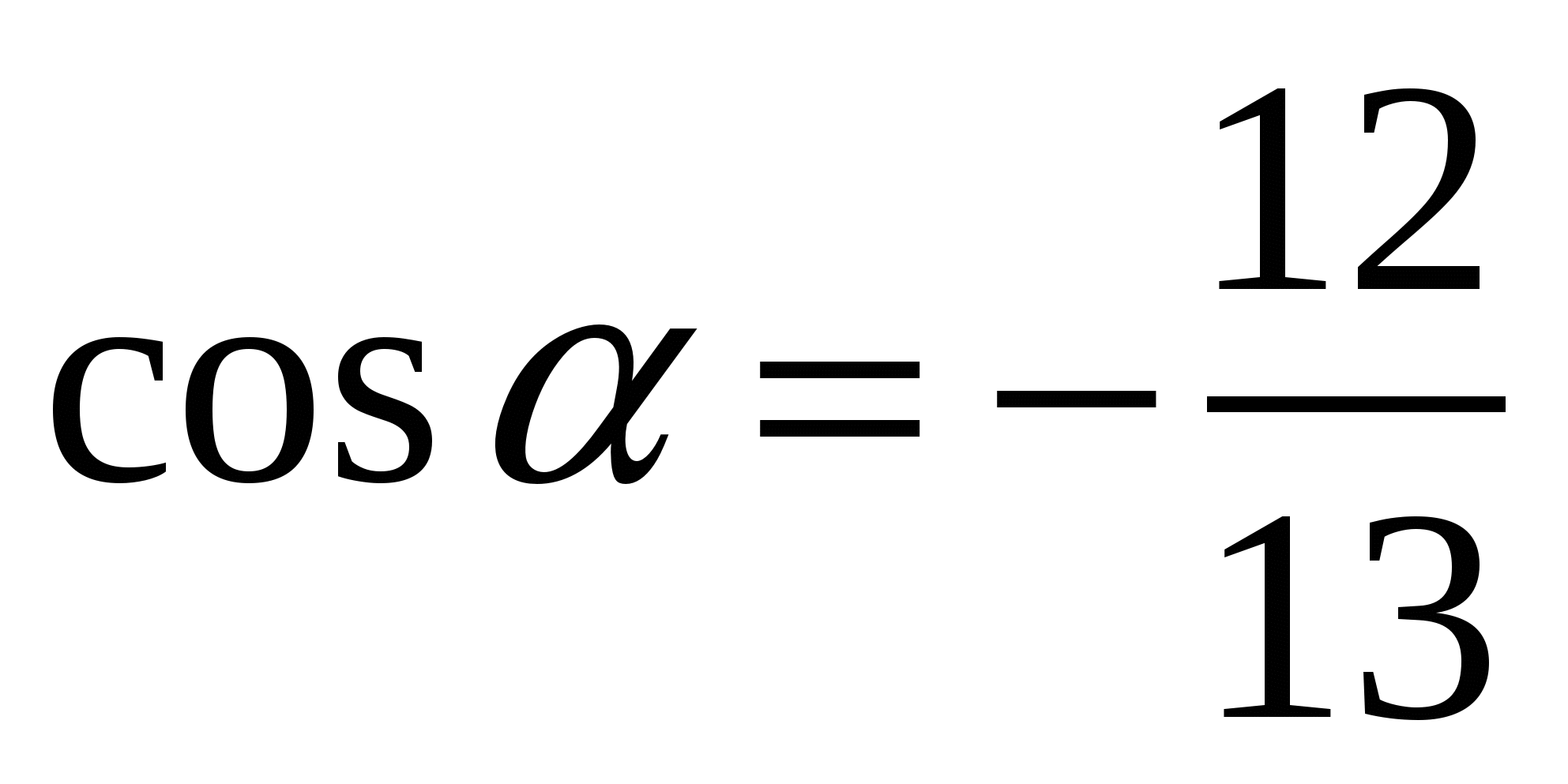 и
и 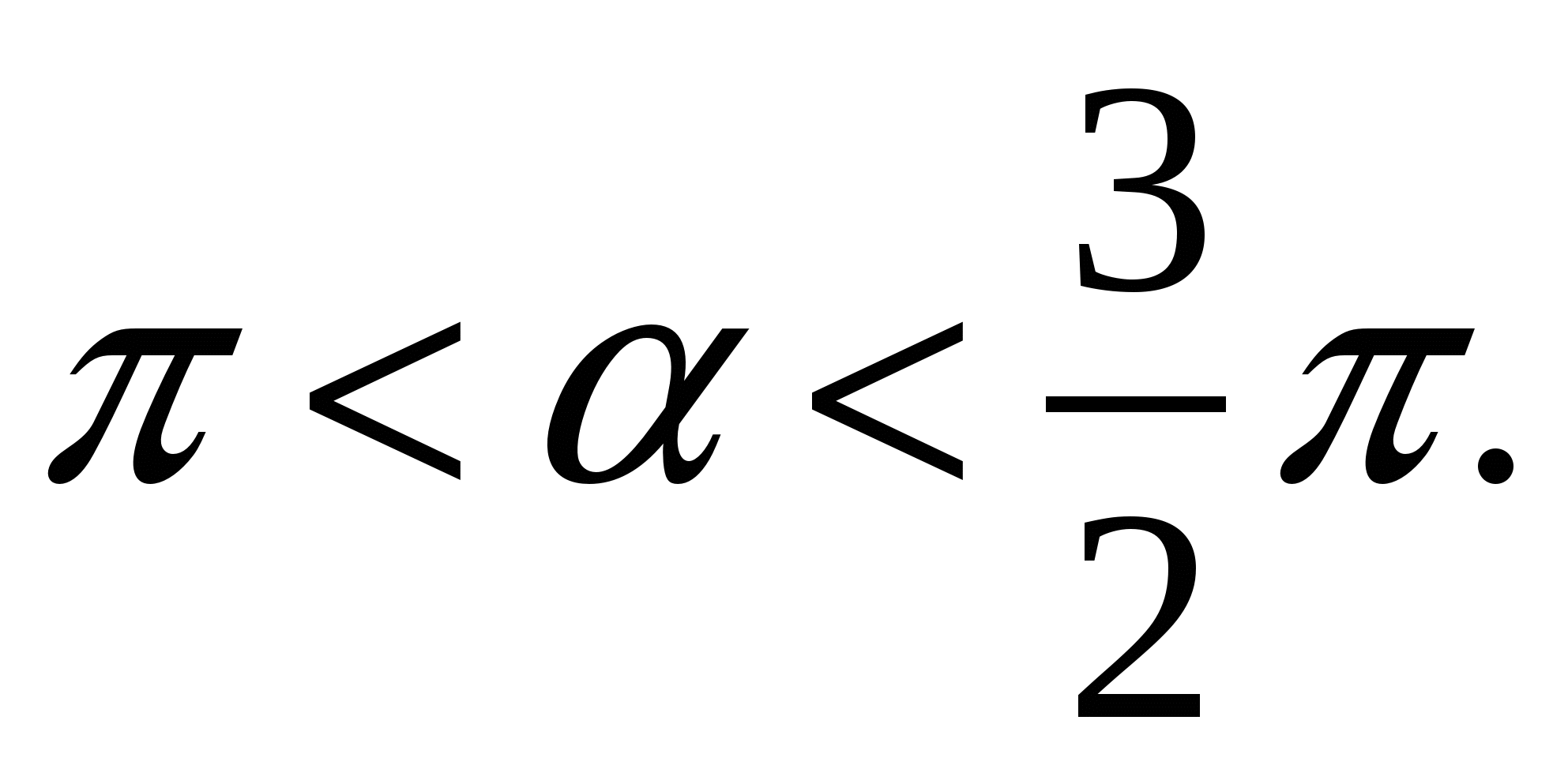
3. Упростите выражение:
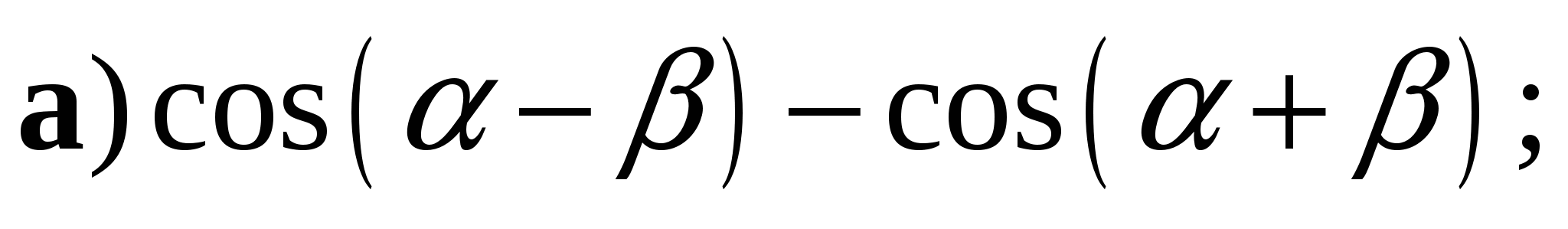
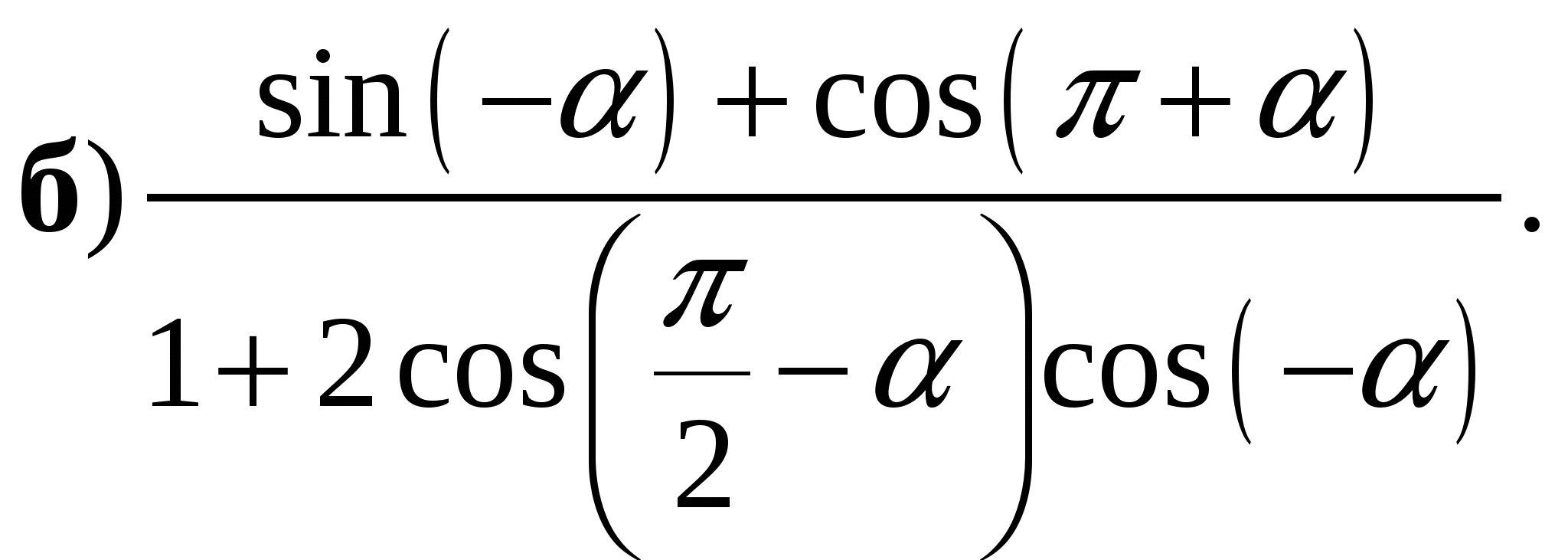
4. Решите уравнение 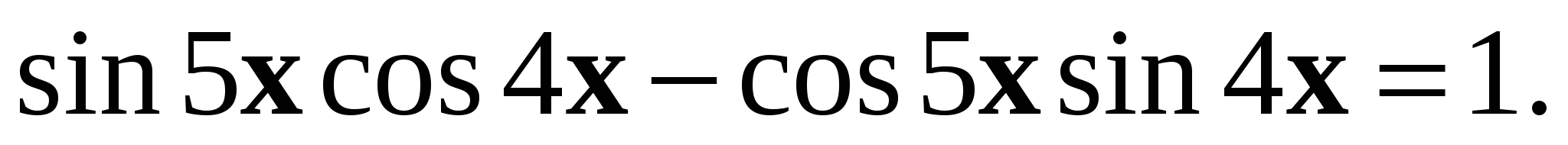
5. Докажите тождество 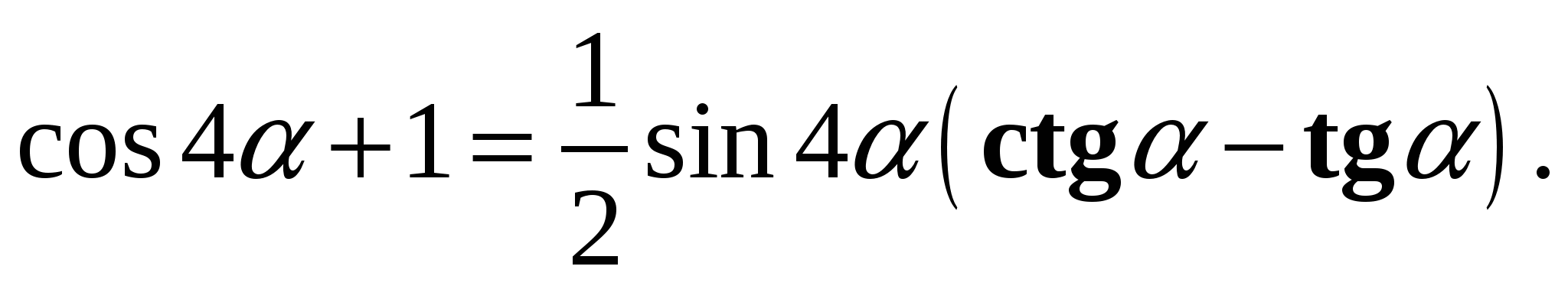
Контрольная работа №5
Тригонометрические формулы
Вариант 2
1. Вычислите: 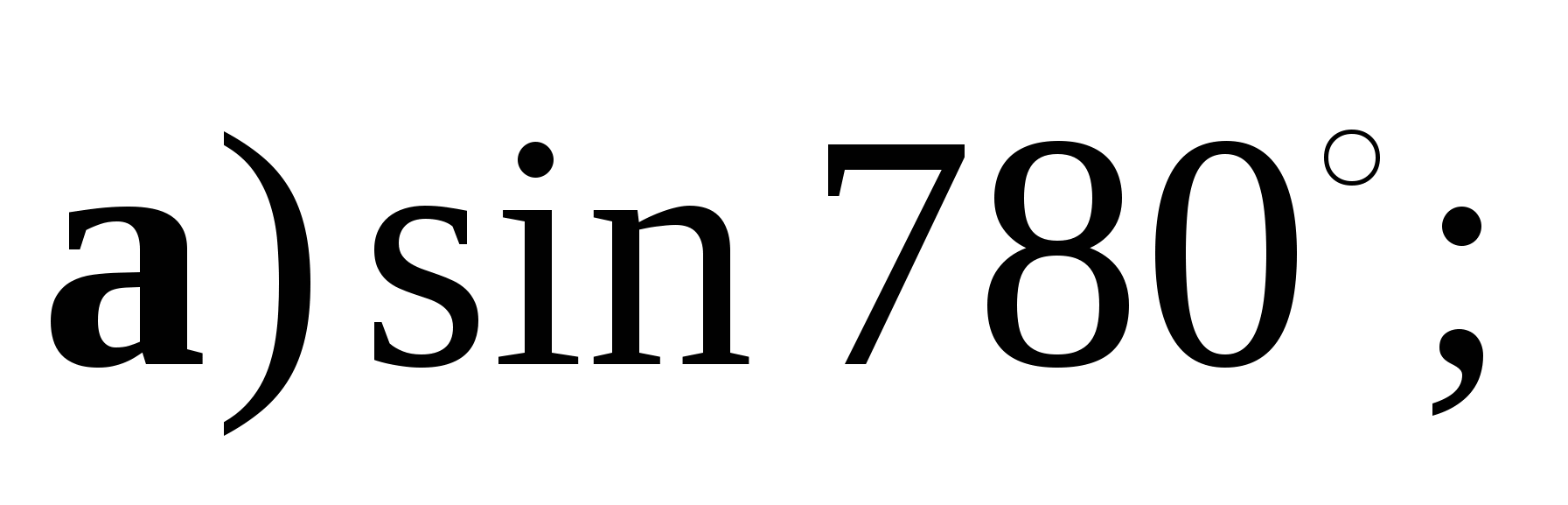
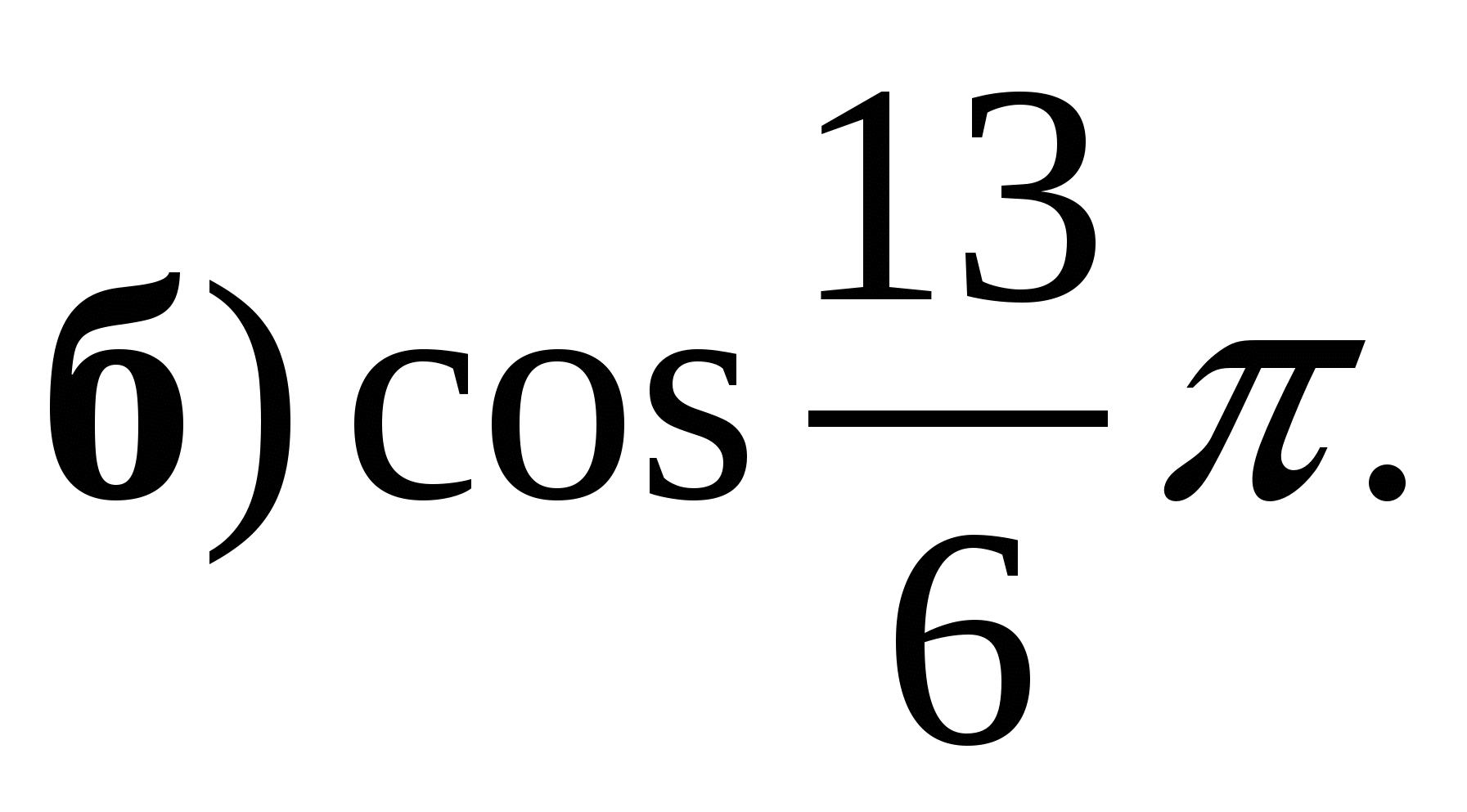
2. Вычислите cosα, если 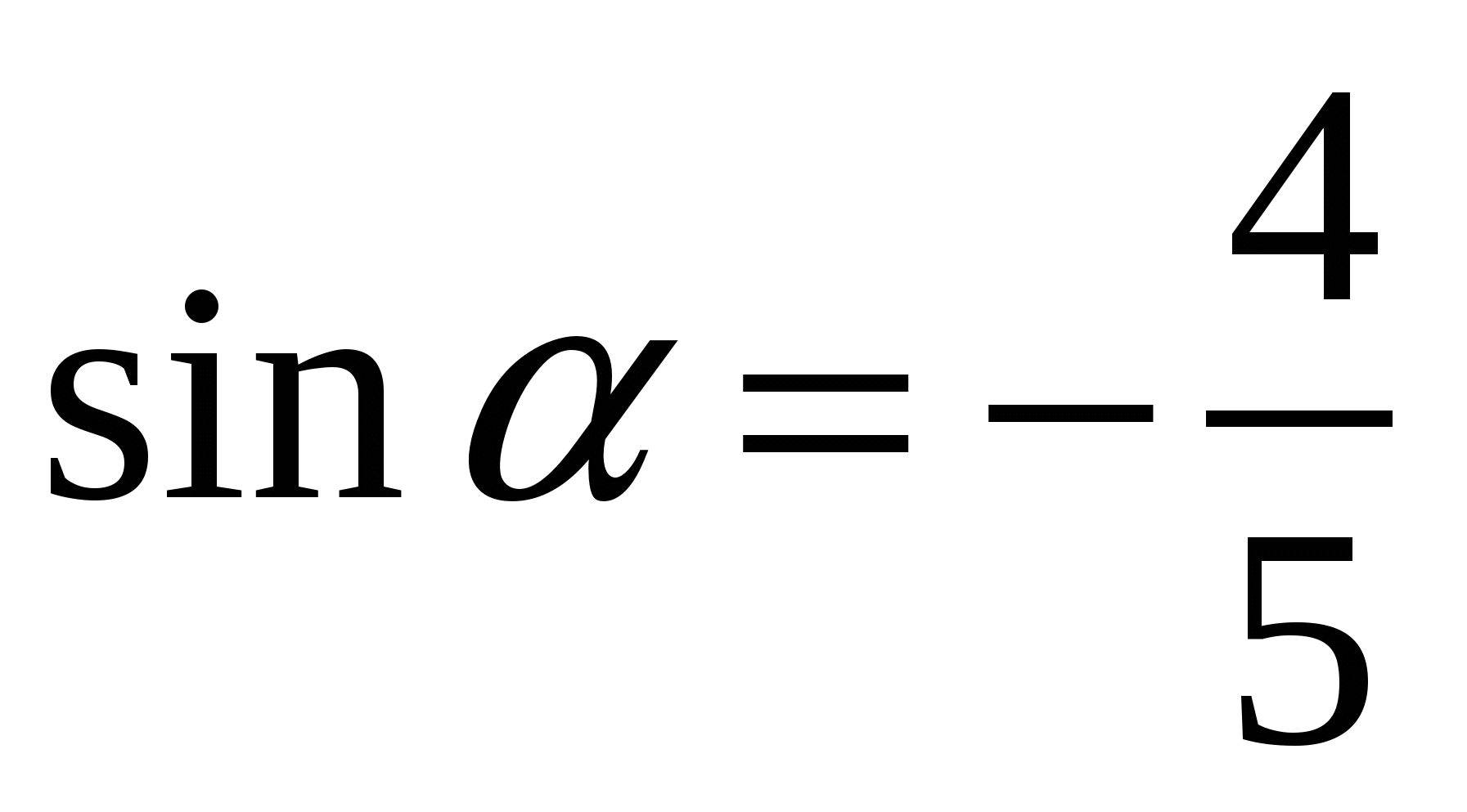 и
и 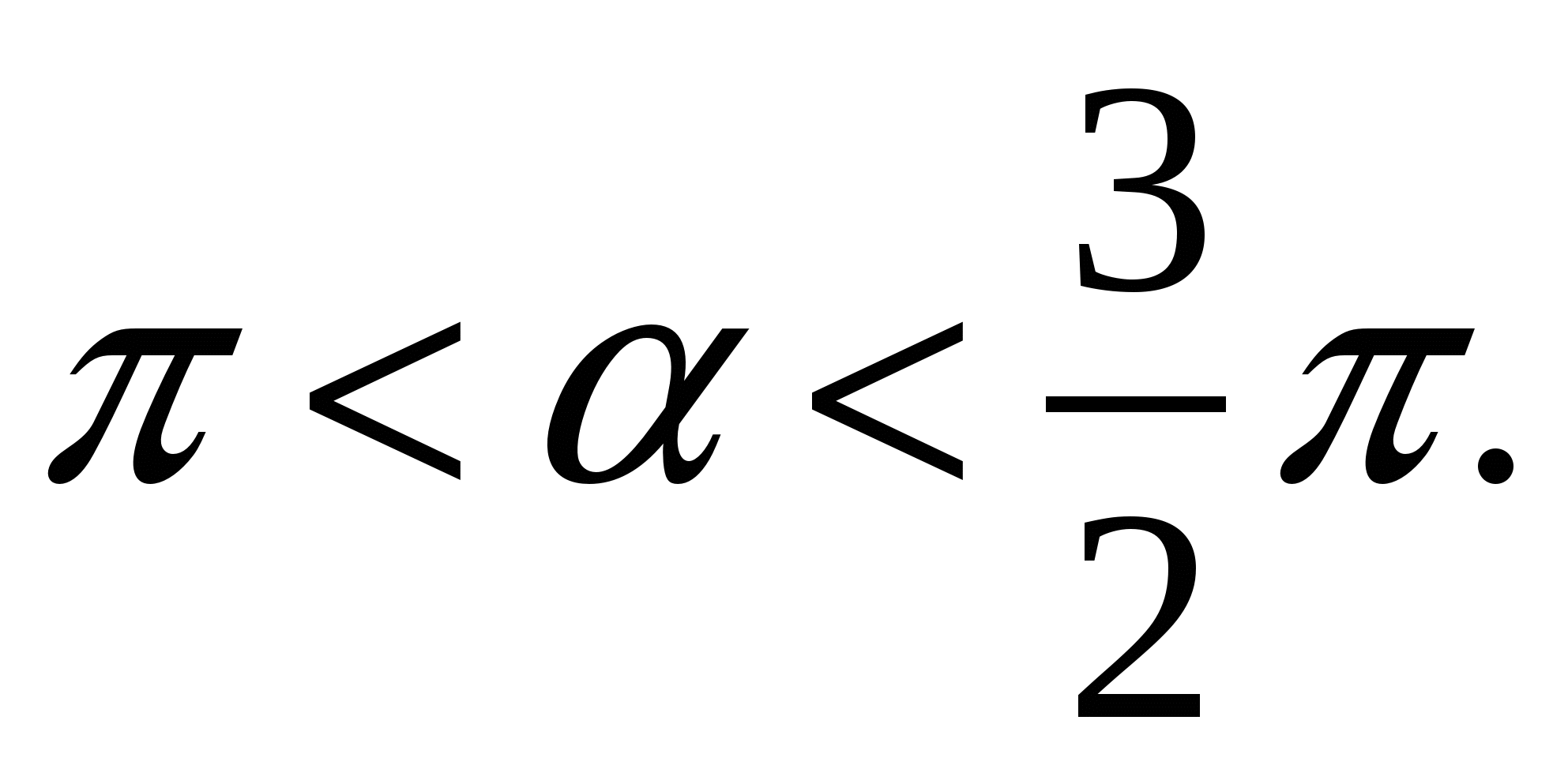
3. Упростите выражение:
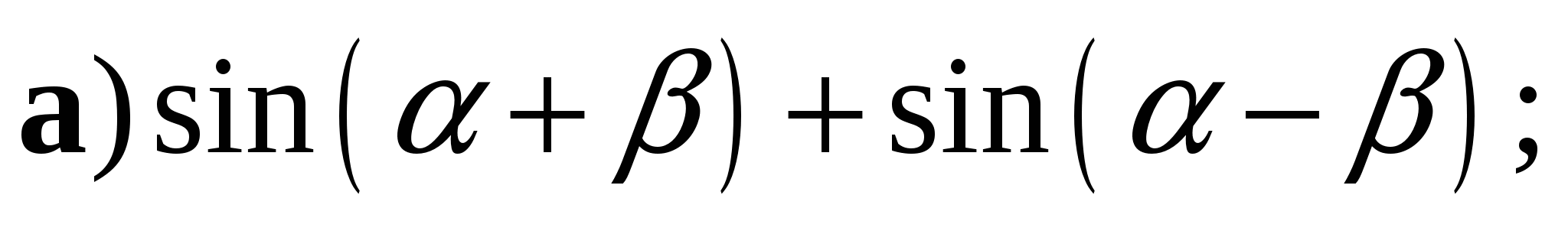
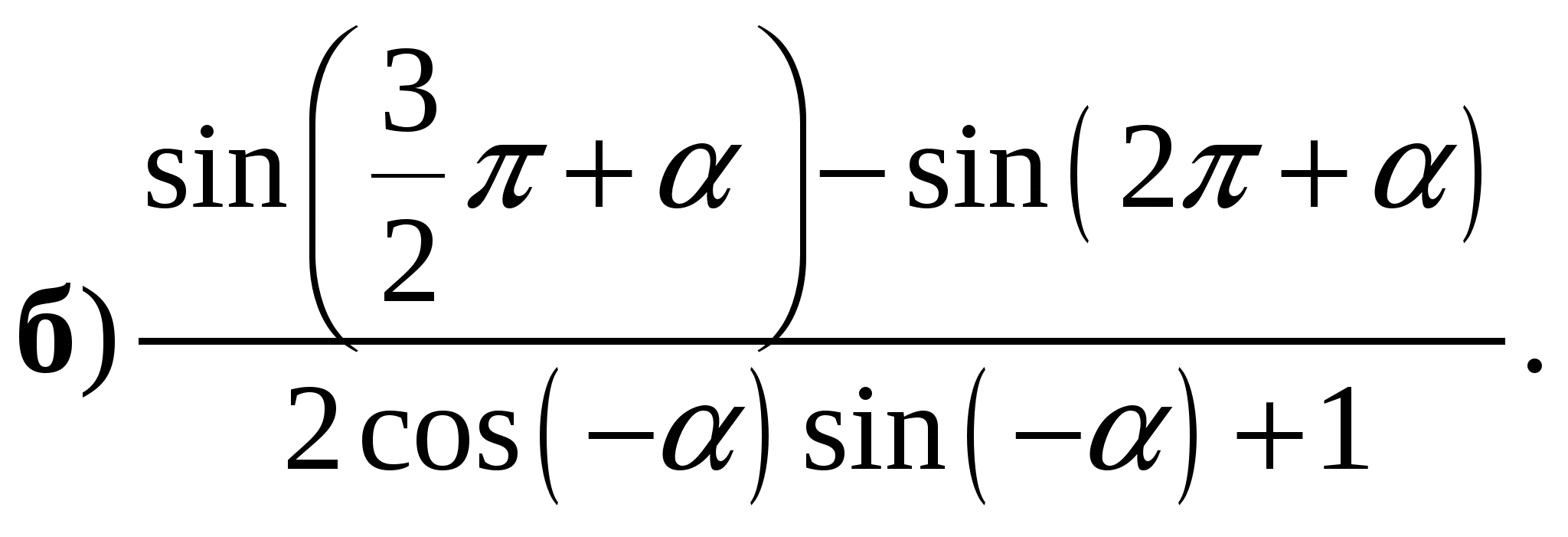
4. Решите уравнение 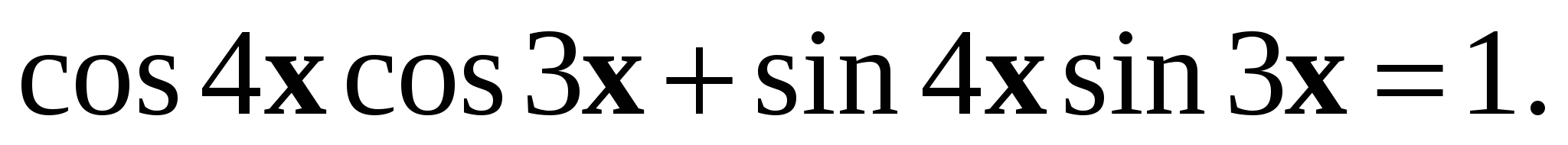
5. Докажите тождество 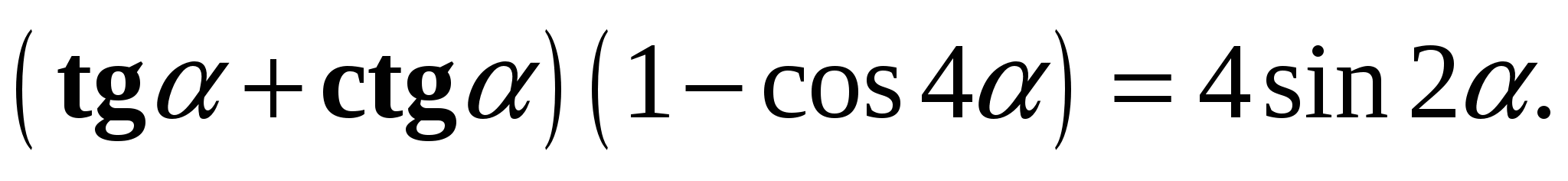
А – 10 Контрольная работа № 6
Тригонометрические уравнения
Вариант 1
1. Решите уравнение:
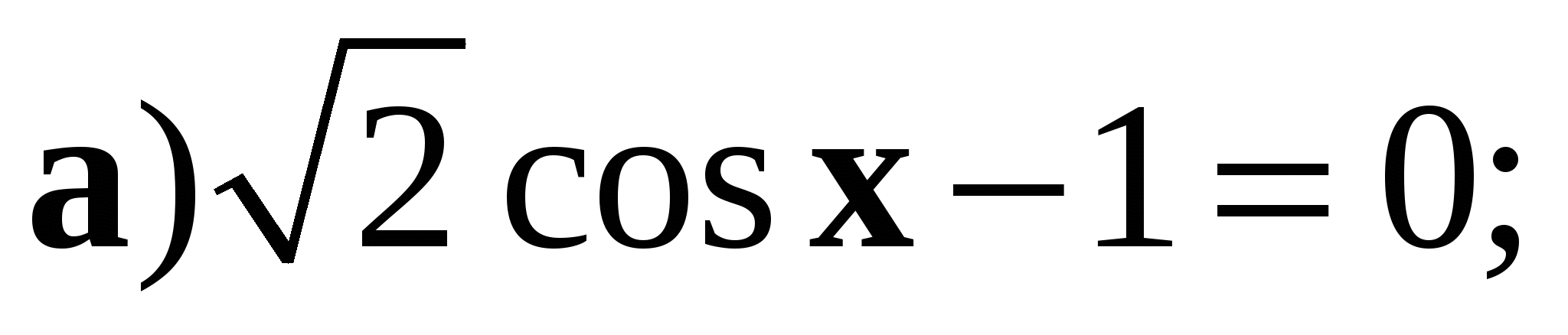
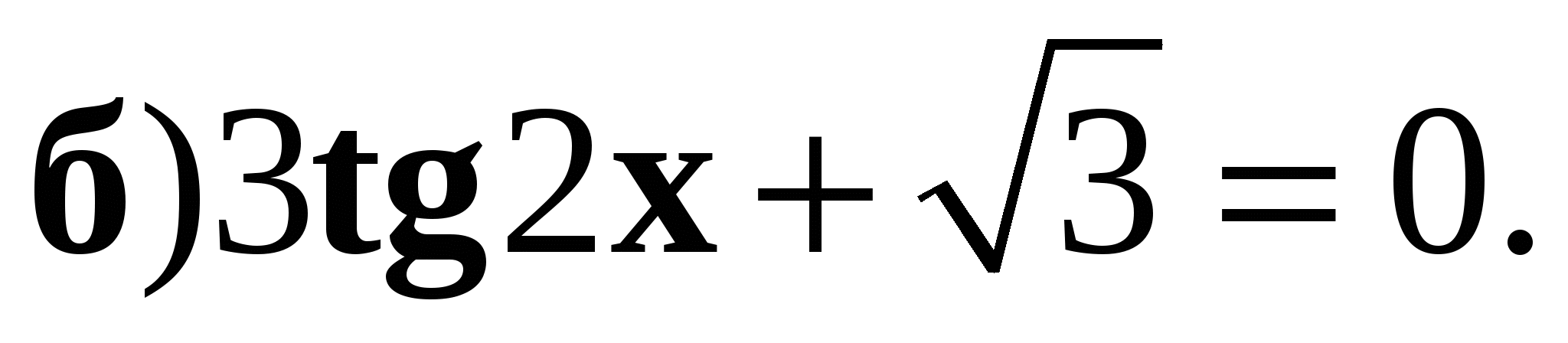
2. Найдите решение уравнения 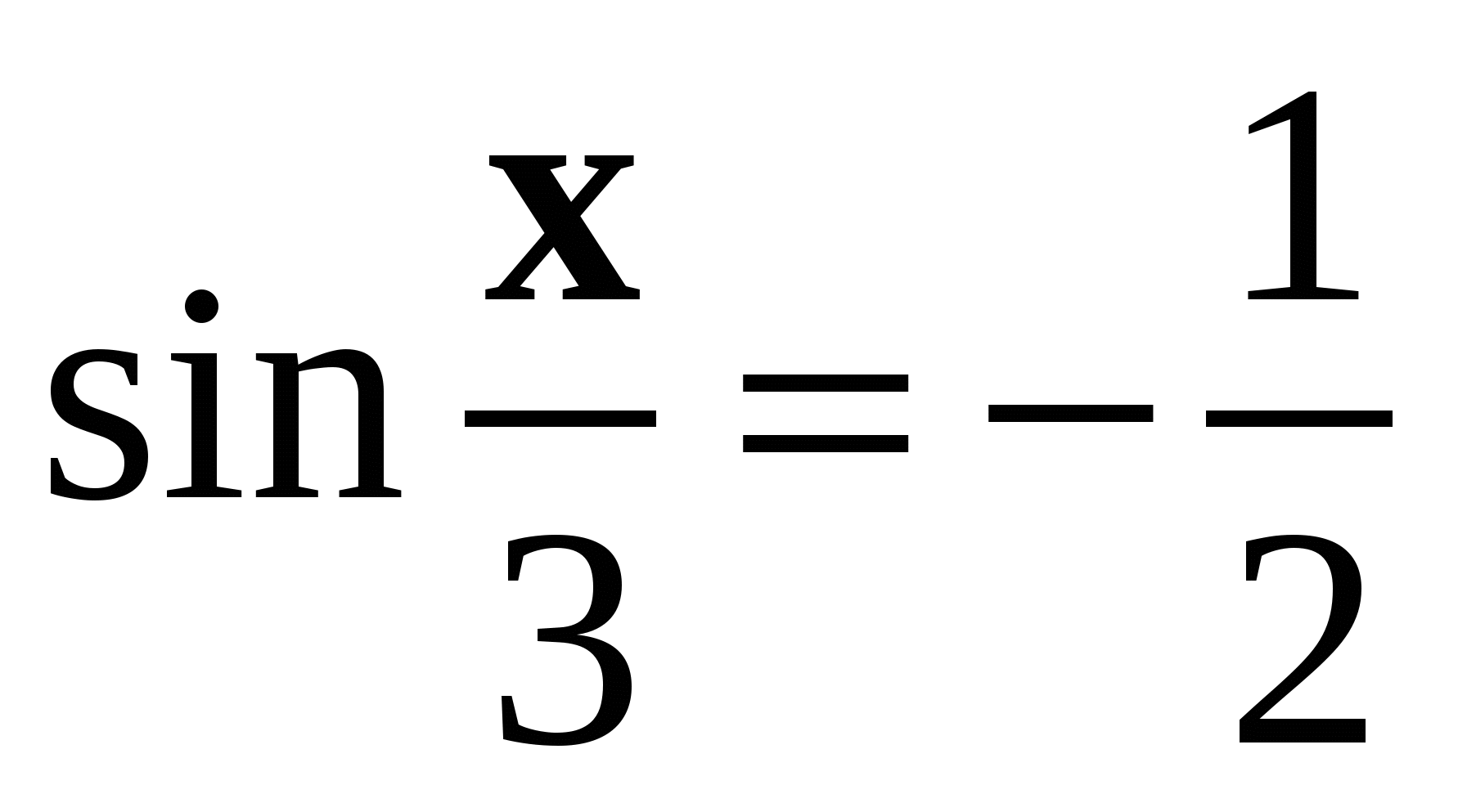 на отрезке
на отрезке 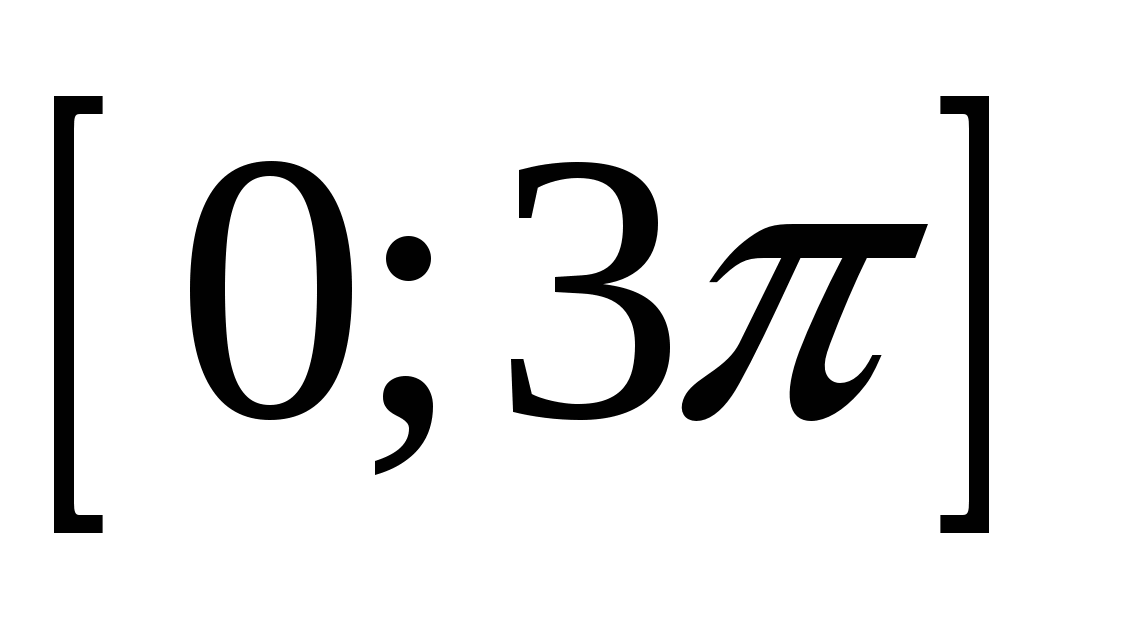 .
.
3. Решите уравнение:
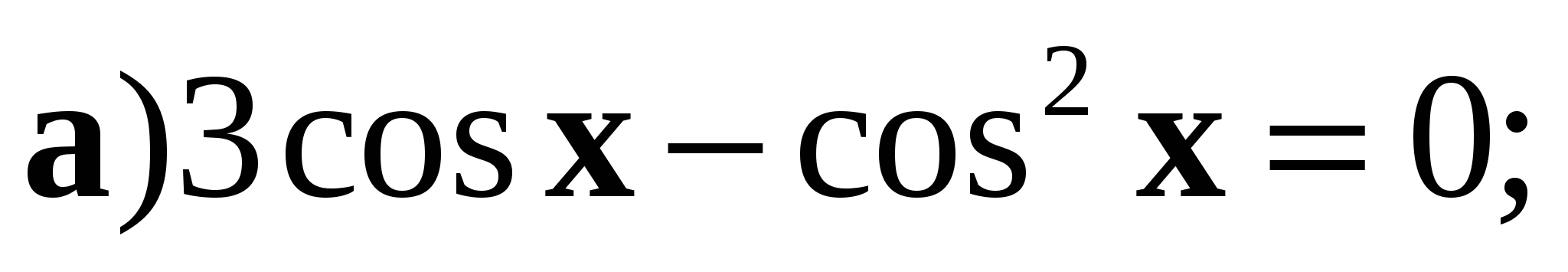
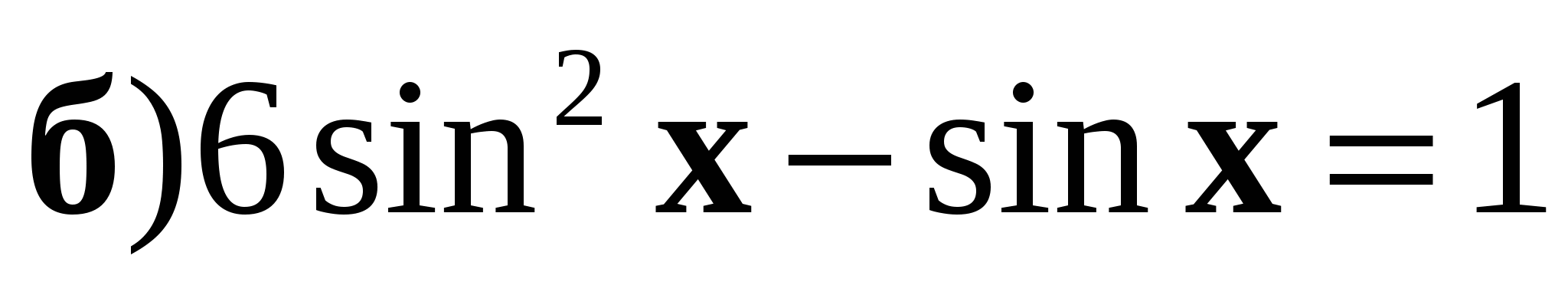 .
.
4. Решите уравнение:
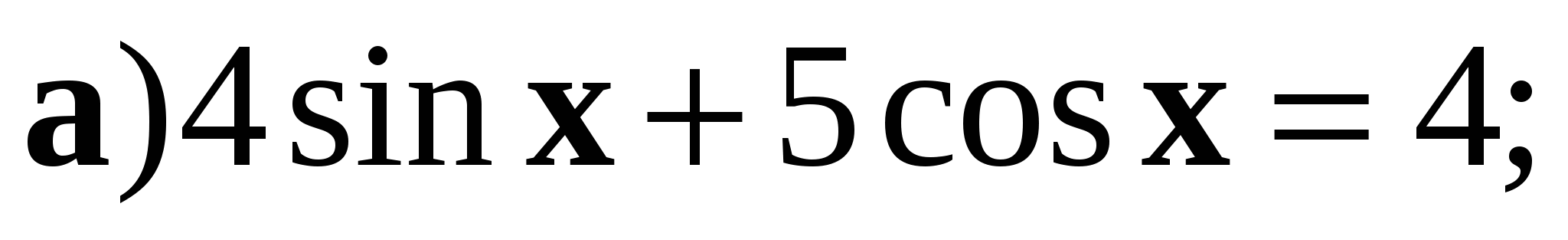
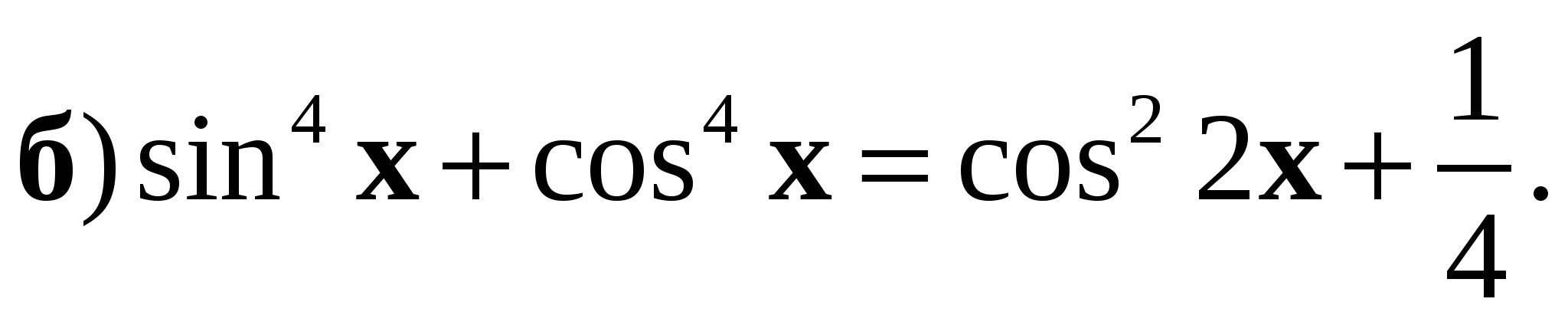
Контрольная работа № 6
Тригонометрические уравнения
Вариант 2
1. Решите уравнение:
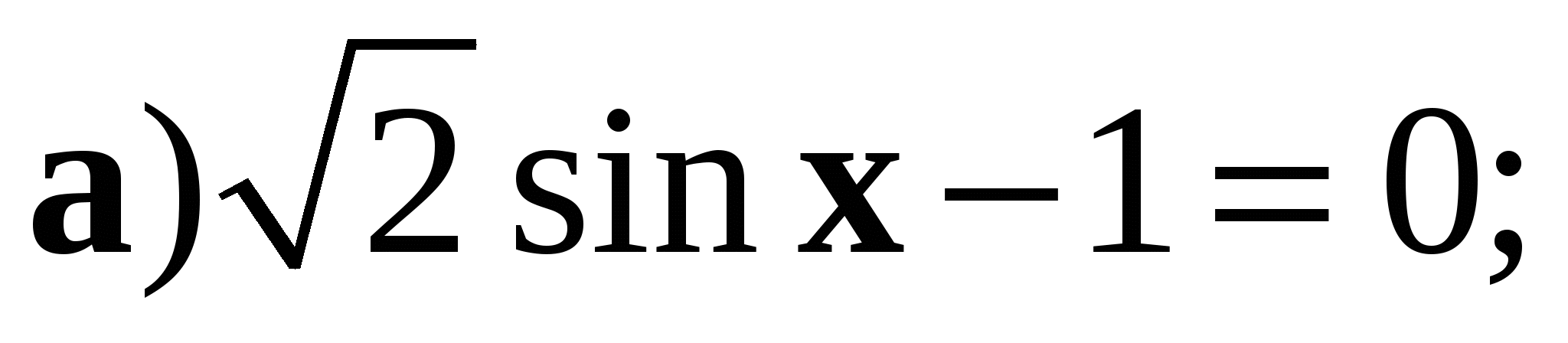
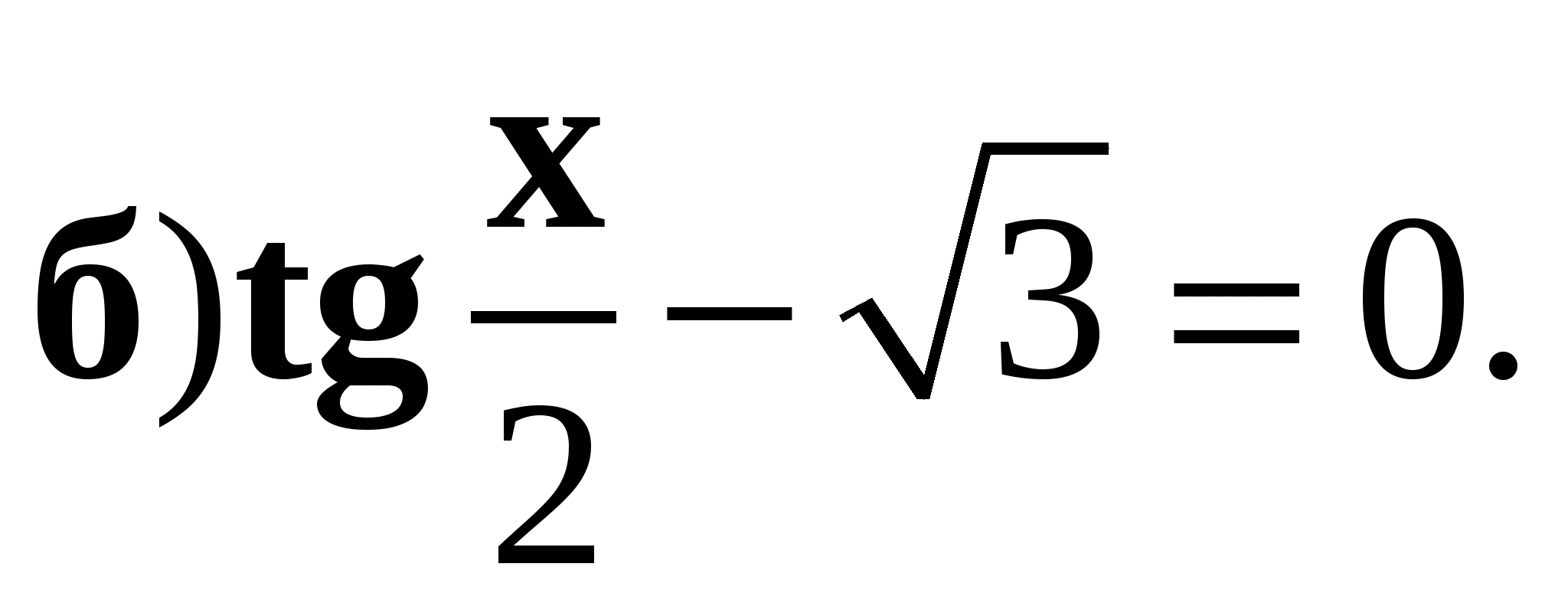
2. Найдите решение уравнения 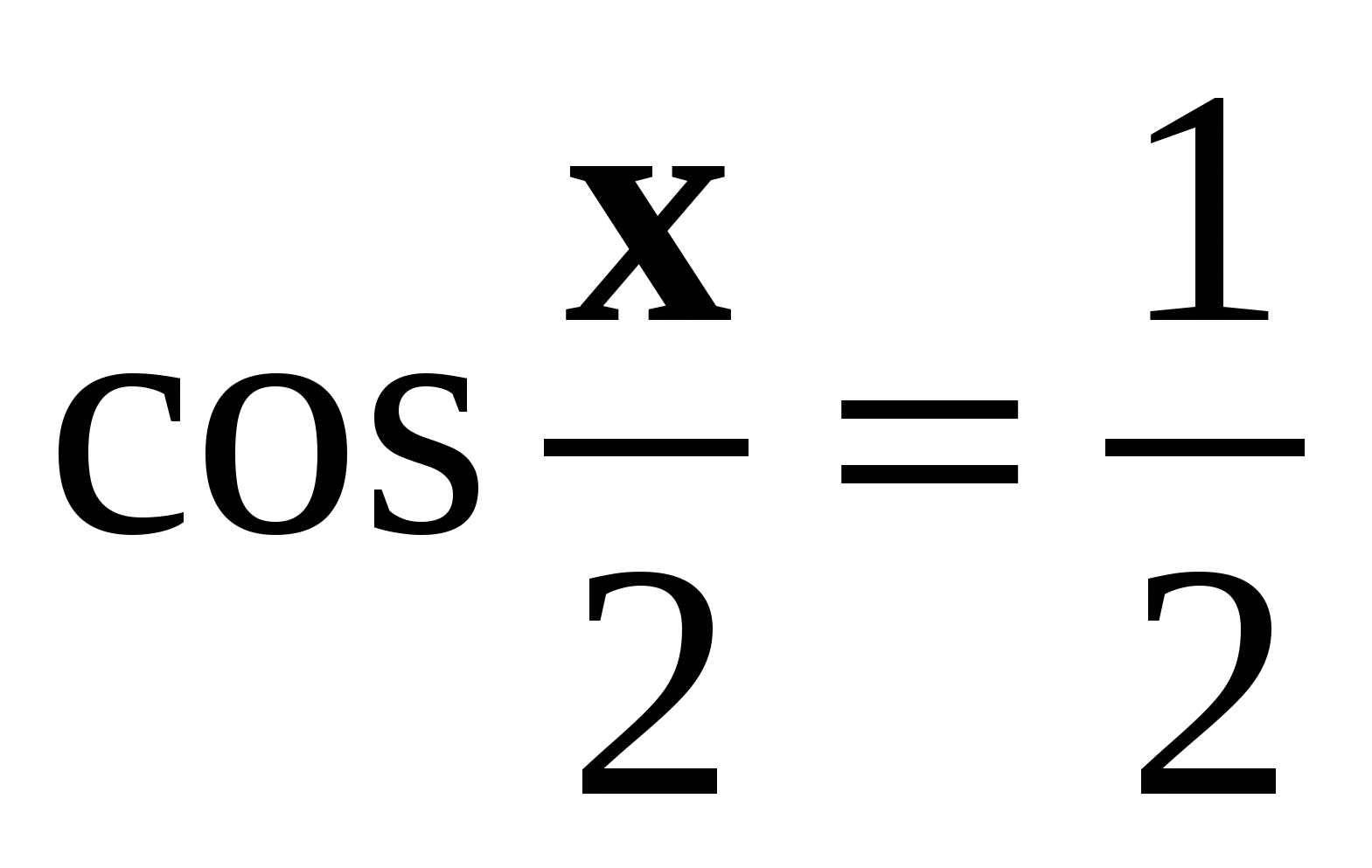 на отрезке
на отрезке 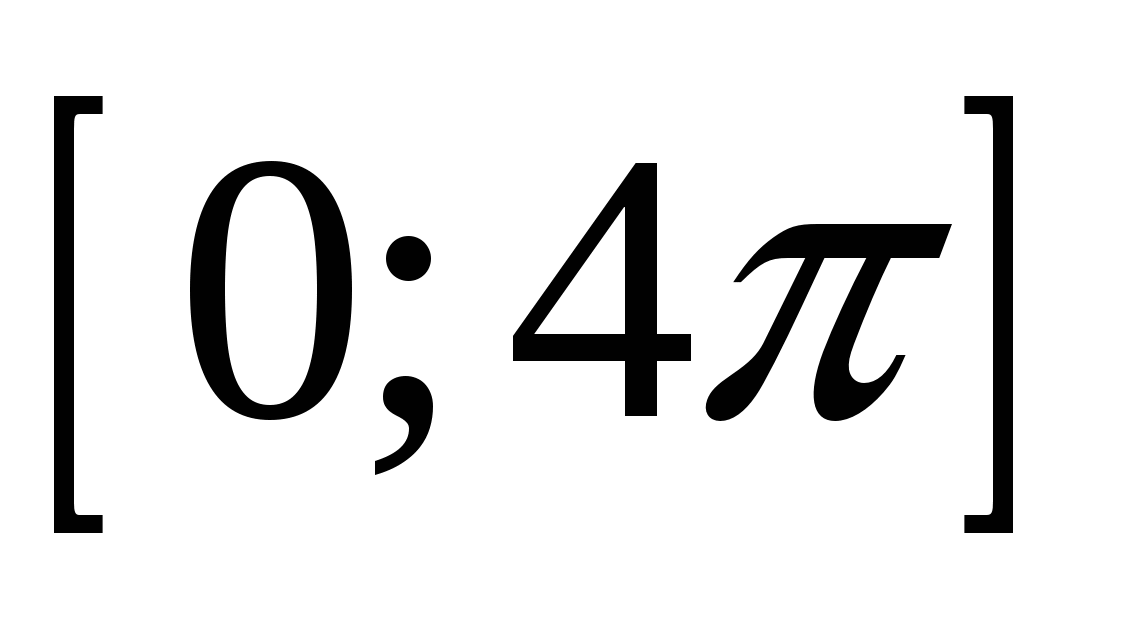 .
.
3. Решите уравнение:
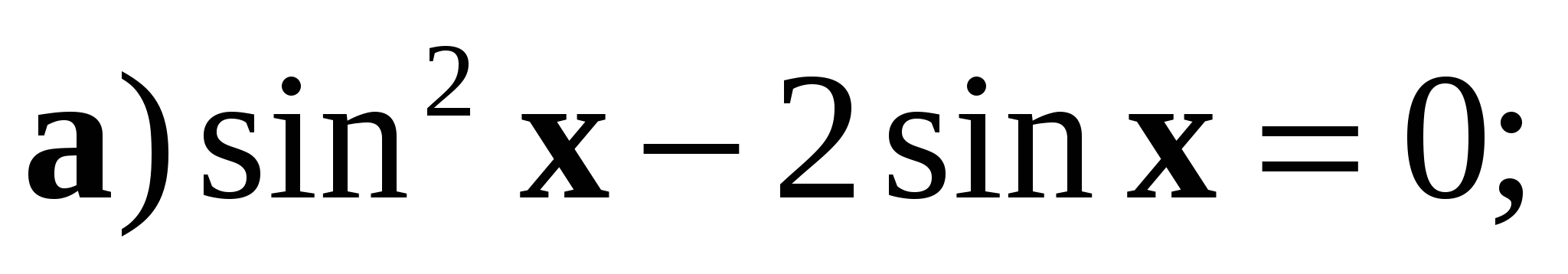
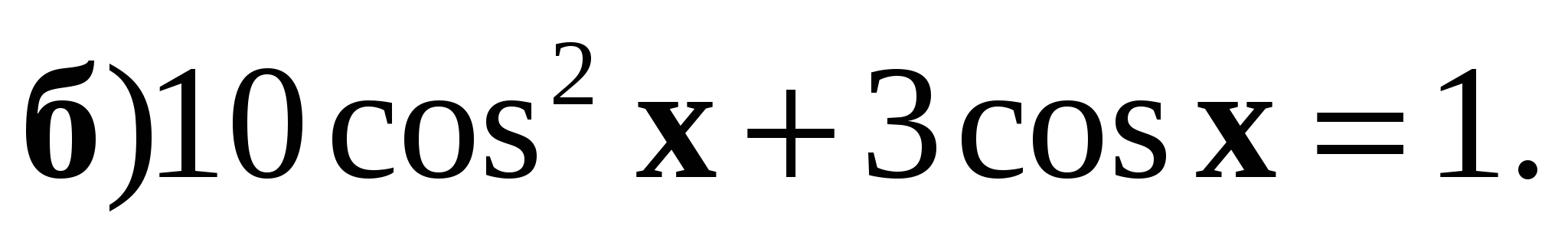
4. Решите уравнение:
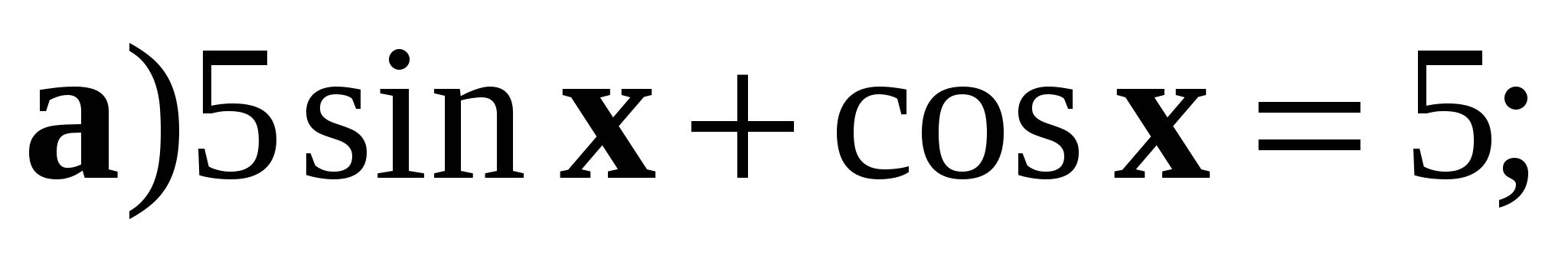
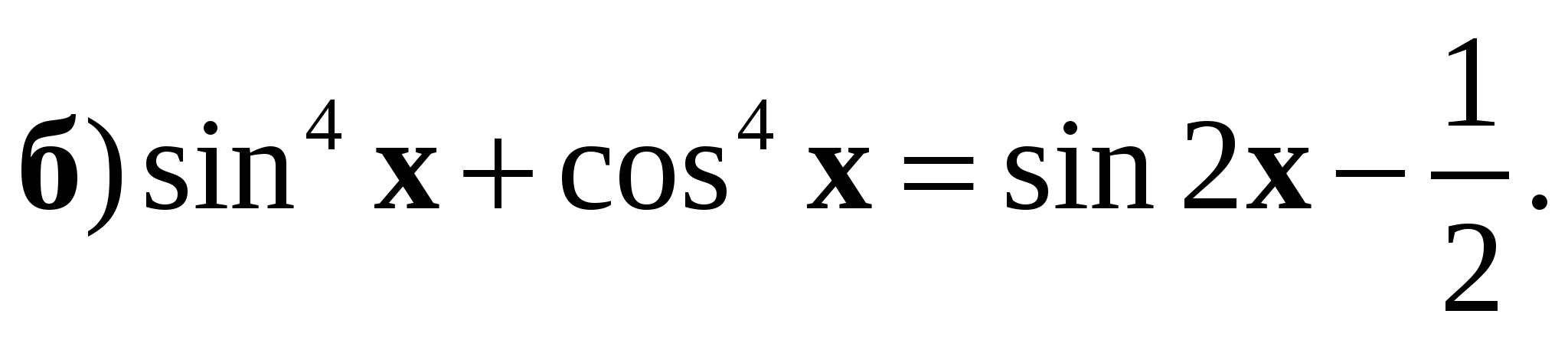
Контрольная работа № 7
Элементы комбинаторики
1. Вычислите: 

2. Сколько существует способов для обозначения вершин четырехугольника с помощью букв A, B, C, D, E, F?
3. Запишите разложение бинома 
Контрольная работа №7
1.Из урны, содержащей 15 белых, 10 красных и 5 синих шаров, наугад выбирают один шар. Какова вероятность того, что шар окажется: а) красного цвета; б) зеленого цвета?
2.Бросаются монета и игральная кость. Какова вероятность того, что появится решка и 5 очков?
3. Вероятность попадания по мишени равна 0.7. Какова вероятность того, что, не попав по мишени при первом выстреле, стрелок попадет при втором?
infourok.ru
| К-1 по теме «Действительные числа. Рациональные уравнения и неравенства» (10 класс) I вариант | К-1 по теме «Действительные числа. Рациональные уравнения и неравенства» (10 класс) II вариант |
| 1.Упростите выражение:
2.Решите уравнение: 3.Решите неравенство: а) 4*. а) Упростите выражение:
б) Найдите значение полученного выражения при n= -1. 5*.Докажите справедливость неравенства: а) б) в) 6*.Решите уравнение : 7*.К трехзначному числу приписали цифру 2 сначала справа, потом слева, получились два числа, разность которых равна 4113. Найдите это трехзначное число. | 1.Упростите выражение:
2.Решите уравнение: 3.Решите неравенство: а) 4*. а) Упростите выражение:
б) Найдите значение полученного выражения при n= -1. 5*.Докажите справедливость неравенства: а) б) в) 6*.Решите уравнение : 7*.К трехзначному числу приписали цифру 3 сначала справа, потом слева, получились два числа, разность которых равна 3114. Найдите это трехзначное число. |
К-1 по теме «Действительные числа. Рациональные уравнения и неравенства»
(10 класс)
III вариант
К-1 по теме «Действительные числа. Рациональные уравнения и неравенства»
(10 класс)
IV вариант
1.Упростите выражение:
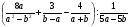 .
.
2.Решите уравнение: 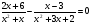 .
.
3.Решите неравенство:
а) 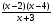 <0; б)
<0; б) 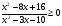 .
.
4*. а) Упростите выражение:
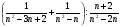 .
.
б) Найдите значение полученного выражения при n= 2.
5*.Докажите справедливость неравенства:
а) 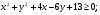
б) 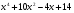 >0;
>0;
в) 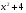 >
>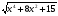 .
.
6*.Решите уравнение:  .
.
7*.К двузначному числу приписали цифру 4 сначала справа, потом слева, получились два числа, разность которых равна 432. Найдите это двузначное число.
1.Упростите выражение:
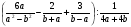 .
.
2.Решите уравнение: 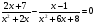 .
.
3.Решите неравенство:
а) 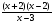 <0; б)
<0; б) 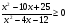 .
.
4*. а) Упростите выражение:
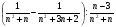 .
.
б) Найдите значение полученного выражения при n= 0.
5*.Докажите справедливость неравенства:
а) 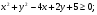
б) 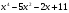 >0;
>0;
в)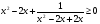 .
.
6*.Решите уравнение: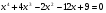 .
.
7*.К двузначному числу приписали цифру 1 сначала справа, потом слева, получились два числа, разность которых равна 234. Найдите это двузначное число.
К-2 по теме «Корень степени n» (10 класс)
I вариант
К-2 по теме «Корень степени n» (10 класс)
II вариант
1.Верно ли равенство:
а) 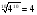 ; б)
; б) 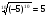 ;
;
в) 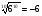 ; г)
; г) 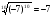 ?
?
2.Избавьтесь от иррациональности в знаменателе дроби:
а) 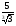 ; б)
; б) 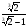 ; в)
; в) 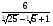 .
.
3.Вычислите:
а) 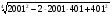 ;
;
б) 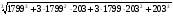
4.Упростите выражение:
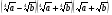 .
.
5*.Вычислите:
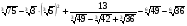
6*.Найдите значение выражения: 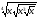 при
при 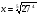 .
.
7*.Моторная лодка проходит расстояние между пристанями А и В по течению реки за 20 мин, а против течения за 1 ч. Во сколько раз собственная скорость моторной лодки больше скорости течения реки?
1.Верно ли равенство:
а) 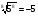 ; б)
; б) 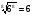 ;
;
в) 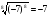 ; г)
; г) 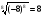 ?
?
2.Избавьтесь от иррациональности в знаменателе дроби:
а) 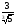 ; б)
; б) 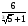 ; в)
; в) 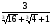 .
.
3.Вычислите:
а) 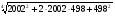 ;
;
б) 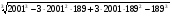 .
.
4.Упростите выражение:
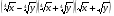 .
.
5*.Вычислите:
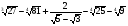
6*.Найдите значение выражения: 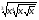 при
при 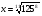 .
.
7*.Моторная лодка проходит расстояние между пристанями А и В по течению реки за 25 мин, а против течения за 50 мин. Во сколько раз собственная скорость моторной лодки больше скорости течения реки?
К-2 по теме «Корень степени n» (10 класс)
III вариант
К-2 по теме «Корень степени n» (10 класс)
IV вариант
1.Верно ли равенство:
а) 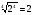 ; б)
; б) 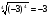 ;
;
в) 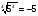 ; г)
; г) 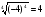 ?
?
2.Избавьтесь от иррациональности в знаменателе дроби:
а) 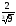 ; б)
; б) 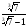 ; в)
; в) 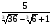 .
.
3.Вычислите:
а) 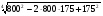 ;
;
б) 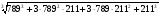 .
.
4.Упростите выражение:
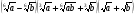 .
.
5*.Вычислите:
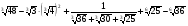
6*.Найдите значение выражения: 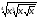 при
при 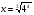 .
.
7*.Велосипедист и мотоциклист отправились одновременно из пункта А в пункт В. Скорость мотоциклиста была в 3 раза больше скорости велосипедиста, но в пути он сделал остановку для устранения поломки мотоцикла и поэтому в пункт В прибыл на 5 мин позже велосипедиста, который на весь путь затратил 60 мин. Сколько минут мотоциклист устранял поломку мотоцикла?
1.Верно ли равенство:
а) 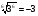 ; б)
; б) 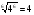 ;
;
в) 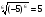 ; г)
; г) 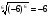 ?
?
2.Избавьтесь от иррациональности в знаменателе дроби:
а) 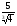 ; б)
; б) 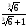 ; в)
; в) 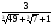 .
.
3.Вычислите:
а) 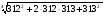 ;
;
б) 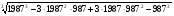
4.Упростите выражение:
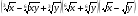 .
.
5*.Вычислите:
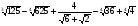
6*.Найдите значение выражения: 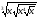 при
при 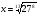 .
.
7*.Велосипедист и пешеход отправились одновременно из пункта А в пункт В. Скорость велосипедиста была в 2 раза больше скорости пешехода, но в пути он сделал остановку для устранения поломки велосипеда и поэтому в пункт В прибыл лишь на 5 мин раньше пешехода, который на весь путь затратил 40 мин. Сколько минут велосипедист устранял поломку велосипеда?
К-3 по теме «Степень положительного числа» (10 класс)
I вариант
К-3 по теме «Степень положительного числа» (10 класс)
II вариант
1.Найдите значение выражения: 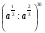 при
при 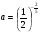 .
.
2.Вычислите: 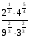 .
.
3.Постройте график функции и перечислите свойства этой функции:
а) 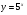 ; б)
; б) 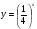 .
.
4.Упростите выражение:
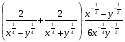 .
.
5*.Упростите выражение
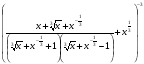
и найдите его значение при х=0,125.
6*. На четырех старых станках, работающих совместно с одинаковой производительностью, выполнили задание за некоторый срок. На одном новом и одном старом станках, работающих совместно, выполнили бы это задание за 0,8 того же срока. Во сколько раз производительность нового станка больше производительности старого станка?
1.Найдите значение выражения: 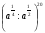 при
при 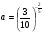 .
.
2.Вычислите: 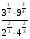 .
.
3.Постройте график функции и перечислите свойства этой функции:
а) 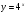 ; б)
; б) 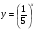 .
.
4.Упростите выражение:
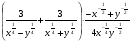 .
.
5*.Упростите выражение
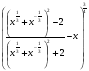
и найдите его значение при х=0,9919.
6*. Четыре ученика, работая совместно с одинаковой производительностью, выполнили задание за некоторый срок. Один мастер и один ученик, работая совместно, выполнили бы это задание за 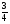 того же срока. Во сколько раз производительность мастера больше производительности ученика?
того же срока. Во сколько раз производительность мастера больше производительности ученика?
К-3 по теме «Степень положительного числа» (10 класс)
III вариант
К-3 по теме «Степень положительного числа» (10 класс)
IV вариант
1.Найдите значение выражения 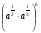 при
при 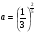 .
.
2.Вычислите: 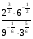 .
.
3.Постройте график функции и перечислите свойства этой функции:
а) 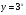 ; б)
; б) 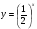 .
.
4.Упростите выражение:
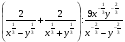 .
.
5*.Упростите выражение
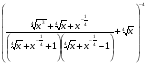
и найдите его значение при х=0,0125.
6*. Мотоциклист и велосипедист отправились одновременно из пунктов А и В навстречу друг другу и встретились через некоторое время. Если бы они отправились одновременно из тех же пунктов в одном направлении, то, для того чтобы догнать велосипедиста, мотоциклисту потребовалось бы в 2 раза больше времени, чем они потратили до встречи при движении навстречу друг другу. Во сколько раз скорость мотоциклиста больше скорости велосипедиста?
1.Найдите значение выражения 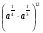 при
при 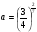 .
.
2.Вычислите: 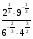 .
.
3.Постройте график функции и перечислите свойства этой функции:
а) 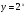 ; б)
; б) 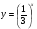 .
.
4.Упростите выражение:
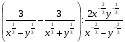 .
.
5*.Упростите выражение

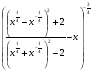
и найдите его значение при х=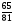 .
.
6*. Велосипедист и пешеход отправились одновременно из пунктов А и В навстречу друг другу и встретились через некоторое время. Если бы они отправились одновременно из тех же пунктов в одном направлении, то, для того чтобы догнать пешехода, велосипедисту потребовалось бы в 5 раз больше времени, чем они потратили до встречи при движении навстречу друг другу. Во сколько раз скорость велосипедиста больше скорости пешехода?
| К-4 по теме «Показательные и логарифмические уравнения и неравенства» (10 класс) I вариант | К-4 по теме «Показательные и логарифмические уравнения и неравенства» (10 класс) II вариант |
| 1.Вычислите: а) б) 2.Решите уравнение: а) 3.Решите неравенство: а) б) 4*.Докажите числовое равенство:
5*.Вычислите значение числового выражения:
6*.Решите уравнение: 7*.Некоторое число деталей токарь должен обточить к намеченному сроку. За 4 ч он выполнил две трети задания, а остальные детали обточил его ученик, который обтачивал на 5 деталей в час меньше, чем токарь. В результате задание было выполнено на 1 ч 15 мин позже намеченного срока. Сколько деталей обточил токарь и его ученик вместе? | 1.Вычислите: а) б) 2.Решите уравнение: а) 3.Решите неравенство: а) б) 4*.Докажите числовое равенство
5*.Вычислите значение числового выражения:
6*.Решите уравнение: 7*.Некоторое число деталей токарь должен обточить к намеченному сроку. За 6 ч он выполнил три четверти задания, а остальные детали обточил его ученик, который обтачивал на 6 деталей в час меньше, чем токарь. В результате задание было выполнено на 1 ч 20 мин позже намеченного срока. Сколько деталей обточил токарь и его ученик вместе? |
К-4 по теме «Показательные и логарифмические уравнения и неравенства»
(10 класс)
III вариант
К-4 по теме «Показательные и логарифмические уравнения и неравенства»
(10 класс)
IV вариант
1.Вычислите:
а) 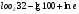 ;
;
б) 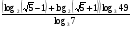 .
.
2.Решите уравнение:
а) 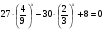 ;
;
б) 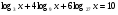 .
.
3.Решите неравенство:
а) 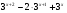 <12;
<12;
б) 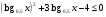 .
.
4*.Докажите числовое равенство
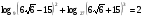 .
.
5*.Вычислите значение числового выражения
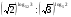 .
.
6*.Решите уравнение 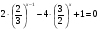 .
.
7*.Проехав за 2 ч две трети расстояния между городами А и В, водитель уменьшил скорость на 15 км/ч, поэтому остаток пути он проехал за 1 ч 20 мин. Определите расстояние между городами А и В.
1.Вычислите:
а) 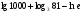 ;
;
б) 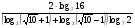 .
.
2.Решите уравнение:
а) 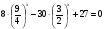 ;
;
б) 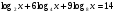 .
.
3.Решите неравенство:
а) 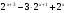 <12;
<12;
б) 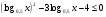 .
.
4*.Докажите числовое равенство
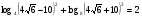 .
.
5*.Вычислите значение числового выражения
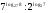 .
.
6*.Решите уравнение
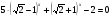 .
.
7*. Проехав за 1 ч три четверти расстояния между городами А и В, водитель увеличил скорость на 20 км/ч, поэтому остаток пути он проехал за 15 мин. Определите расстояние между городами А и В.
К-5 по теме «Синус, косинус, тангенс и котангенс угла» (10 класс)
I вариант
К-5 по теме «Синус, косинус, тангенс и котангенс угла» (10 класс)
II вариант
1.Вычислите:а) sin30°+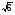 cos45°sin60°-tg30°ctg150°+ctg45°;
cos45°sin60°-tg30°ctg150°+ctg45°;
б) 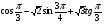 .
.
2.Упростите выражение:
а) 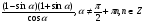 ;
;
б)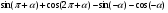 .
.
3.Вычислите:
а) 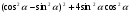 ;
;
б) 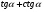 , если
, если 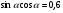 .
.
4. Найдите все такие углы 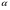 , для каждого из которых выполняется равенство:
, для каждого из которых выполняется равенство:
а) 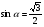 ; б)
; б) 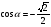 ;
;
в) 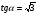 ; г)
; г) 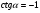 .
.
5*.Вычислите:
а) 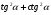 , если
, если 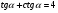 ;
;
б) 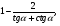 если
если 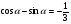 .
.
6*.Вычислите: 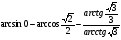 .
.
7*.Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 75% большей. На сколько процентов время движения оказалось меньше запланированного?
1.Вычислите:а) cos30°-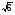 cos30°sin45°-ctg30°tg150°-tg45°;
cos30°sin45°-ctg30°tg150°-tg45°;
б) 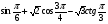 .
.
2.Упростите выражение:
а) 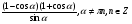 ;
;
б)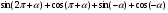 .
.
3.Вычислите:
а) 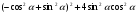 ;
;
б) 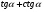 , если
, если 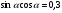 .
.
4.Найдите все такие углы 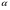 , для каждого из которых выполняется равенство:
, для каждого из которых выполняется равенство:
а) 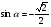 ; б)
; б) 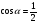 ;
;
в) 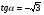 ; г)
; г) 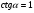 .
.
5*.Вычислите:
а) 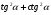 , если
, если 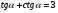 ;
;
б) 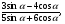 если
если 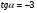 .
.
6*.Вычислите: 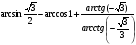
7*.Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 60% большей. На сколько процентов время движения оказалось меньше запланированного?
К-5 по теме «Синус, косинус, тангенс и котангенс угла» (10 класс)
III вариант
К-5 по теме «Синус, косинус, тангенс и котангенс угла» (10 класс)
IV вариант
1.Вычислите:а) 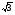 sin60°+cos60°sin30°-tg45°ctg135°+ctg90°;
sin60°+cos60°sin30°-tg45°ctg135°+ctg90°;
б) 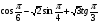 .
.
2.Упростите выражение:
а) 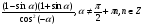 ;
;
б)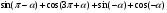 .
.
3.Вычислите:
а) 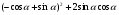 ;
;
б) 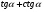 , если
, если 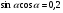 .
.
4. Найдите все такие углы 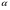 , для каждого из которых выполняется равенство:
, для каждого из которых выполняется равенство:
а) 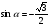 ; б)
; б) 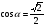 ;
;
в) 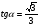 ; г)
; г) 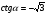 .
.
5*.Вычислите:
а) 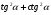 , если
, если 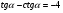 ;
;
б) 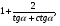 если
если 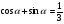 .
.
6*.Вычислите: 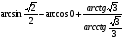 .
.
7*.В пансионате в прошлом году отдыхали 700 мужчин и женщин и 100 детей. В этом году число мужчин уменьшилось на 10%, а число женщин увеличилось на 10%, число детей увеличилось на 10. В результате общее число отдыхающих не изменилось. Сколько мужчин и сколько женщин отдыхало в пансионате в этом году?
1.Вычислите:а) 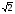 sin45°cos30°sin60°+
sin45°cos30°sin60°+
сtg30°tg135°-tg0°;
б) 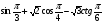 .
.
2.Упростите выражение:
а) 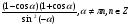 ;
;
б)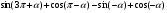 .
.
3.Вычислите:
а) 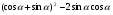 ;
;
б) 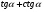 , если
, если 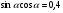 .
.
4. Найдите все такие углы 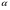 , для каждого из которых выполняется равенство:
, для каждого из которых выполняется равенство:
а) 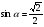 ; б)
; б) 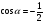 ;
;
в) 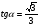 ; г)
; г) 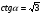 .
.
5*.Вычислите:
а) 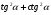 , если
, если 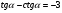 ;
;
б) 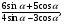 если
если 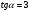 .
.
6*.Вычислите: 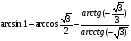 .
.
7*.В прошлом году в городской думе заседали 50 депутатов от двух партий и 5 независимых депутатов. После выборов в этом году общее число депутатов не изменилось, но число депутатов первой партии увеличилось на 10%, число депутатов второй партии уменьшилось на 10%, число независимых депутатов увеличилось на 1. Сколько депутатов от каждой из этих партий избрано в городскую думу в этом году?
К-6 по теме: «Тригонометрические формулы»
1 вариант
К-6 по теме: «Тригонометрические формулы»
2 вариант
1.Упростите выражение:
а) sin(α-β) - 2cosαsinβ, если α + β = π;
б) 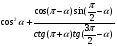 ,
, 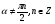 .
.
2.Вычислите:
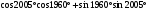 .
.
3.Известно, что 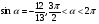 .
.
Вычислите: а)cos α; б)sin 2α;
в)cos 2α.
4.Постройте график функции: 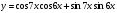 .
.
5.Вычислите: 2cos37°cos23˚-sin76˚.
6. Докажите справедливость равенства: 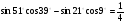 .
.
7. Из города А в город В вышел пешеход. Через 3 ч после его выхода из города А в город В выехал велосипедист, а еще через час вслед за ним выехал мотоциклист. Все участники двигались равномерно и в какой-то момент времени оказались в одной точке маршрута. Мотоциклист прибыл в город В на 2 ч раньше велосипедиста. Через сколько часов после велосипедиста пешеход пришел в город В?
1.Упростите выражение:
а) sin(α+β) + 2sinβcosα, если α – β =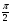 ;
;
б) 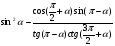 ,
, 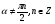 .
.
2.Вычислите:
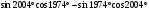 .
.
3.Известно, что 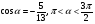 .
.
Вычислите: а)sin α; б)sin 2α;
в)cos 2α.
4. Постройте график функции: 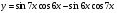 .
.
5.Вычислите: 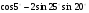 .
.
6. Докажите справедливость равенства: 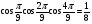 .
.
7. Велосипедист и мотоциклист одновременно отправились навстречу друг другу из городов А и В. После встречи мотоциклист прибыл в город В через 1 ч, а велосипедист прибыл в город А через 9 ч. Во сколько раз скорость мотоциклиста больше скорости велосипедиста?
К-6 по теме: «Тригонометрические формулы»
3 вариант
К-6 по теме: «Тригонометрические формулы»
4 вариант
1.Упростите выражение:
а) cos(α+β) + 2sinαsinβ, если α - β = π;
б) 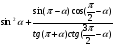 ,
, 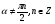
2.Вычислите:
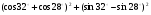 .
.
3.Известно, что 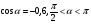 .
.
Вычислите: а)sin α; б)sin 2α; в)cos 2α.
4. Постройте график функции: 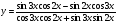 .
.
5.Вычислите: 2sin34˚sin26˚-sin82˚.
6. Докажите справедливость равенства: 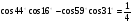 .
.
7. Велосипедист выехал из города А в город В. Через час после этого навстречу ему выехал мотоциклист из города В в город А. Через час после своего выезда мотоциклист встретился с велосипедистом, а через 0,5 ч после встречи прибыл в город А. Сколько времени в пути был велосипедист?
1.Упростите выражение:
а) sin(α-β) + 2sinβcosα, если α + β = π;
б) 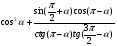 ,
, 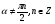
2.Вычислите:
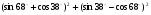 .
.
3.Известно, что 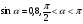 .
.
Вычислите: а)cos α; б)sin 2α; в)cos 2α.
4. Постройте график функции: 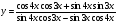 .
.
5.Вычислите: sin10˚+2sin25˚cos35˚.
6. Докажите справедливость равенства: 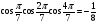 .
.
7. Пешеход вышел из города А в город В. Через час после этого навстречу ему выехал велосипедист из города В в город А. Через 2 ч после своего выезда велосипедист встретился с пешеходом, а через 1 ч после встречи прибыл в город А. Сколько времени был в пути пешеход?
К-7 по теме: «Тригонометрические уравнения и неравенства»
1 вариант
К-7 по теме: «Тригонометрические уравнения и неравенства»
2 вариант
Решите уравнения (1-5).
1. а) cos x = 1; б) sin x = 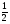 ;
;
в) ctg x =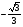 .
.
2. а) 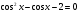 ; б)
; б) 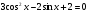
3. а) 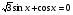 ;
;
б) 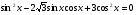 .
.
4. а) sin x = -0,5; б) cos x = 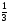 ; в) tg x = -3.
; в) tg x = -3.
5. а) 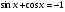 ; б)
; б) 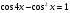 .
.
6. Решите неравенство:
а) sin x > 0,5; б) cos x < 0,5; в) tg x ≥ -3.
7. Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В в город А выехал велосипедист. Через час после выхода пешехода вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Мотоциклист прибыл в город В через 3 ч после выезда из него велосипедиста, но за 2 ч до прибытия пешехода в город В. Через сколько часов после выезда мотоциклиста велосипедист прибыл в город А?
Решите уравнения (1-5).
1. а) sin x = 1; б) cos x = 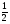 ;
;
в) tg x = 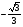 .
.
2. а) 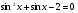 ; б)
; б) 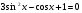 .
.
3. а) 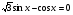 ;
;
б) 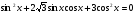 .
.
4. а) cos x = -0,5; б) sin x = 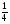 ; в) tg x = 2.
; в) tg x = 2.
5. а) 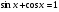 ; б)
; б) 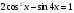 .
.
6. Решите неравенство:
а) sin x < -0,5; б) cos x > -0,5; в) tg x ≤ 2.
7. Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В в город А выехал велосипедист, а еще через час вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Пешеход пришел а город В через 6 ч после выезда мотоциклиста, а мотоциклист прибыл в город А через 4 ч после выхода пешехода из города А. Через сколько часов после мотоциклиста велосипедист прибыл в город А?
К-7 по теме: «Тригонометрические уравнения и неравенства»
3 вариант
К-7 по теме: «Тригонометрические уравнения и неравенства»
4 вариант
Решите уравнения (1-5):
1. а) cos x = -1; б) sin x = 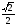 ;
;
в) ctg x = 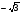 .
.
2. а) 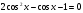 ;
;
б)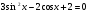 .
.
3. а) 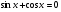 ;
;
б) 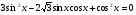 .
.
4. а) sin x = -0,6; б) cos x = 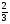 ;
;
в) tg x = -4.
5. а) 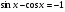 ; б)
; б) 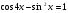 .
.
6. Решите неравенство:
а) sin x < 0,5; б) cos x > 0,5; в) tg x ≤ -3.
7. Из города А в город В вышел пешеход. Через 3 ч после его выхода из города А в город В выехал велосипедист, а еще через 2 ч вслед за ним выехал мотоциклист. Все участники двигались равномерно и в какой-то момент времени оказались в одной точке маршрута. Велосипедист прибыл в город В на 1 ч раньше пешехода. Через сколько часов после мотоциклиста велосипедист приехал в город В?
Решите уравнения (1-5):
1. а) sin x = -1; б) cos x = 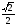 ;
;
в) tg x = 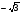 .
.
2. а) 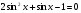 ;
;
б) 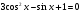 .
.
3. а) 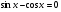 ;
;
б) 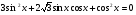 .
.
4. а) cos x = -0,7; б) sin x = 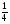 ;
;
в) tg x = 5.
5. а) 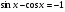 ; б)
; б) 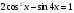 .
.
6. Решите неравенство:
а) sin x > -0,5; б) cos x < -0,5; в) tg x ≥ 2.
7. Из города А в город В вышел пешеход. Через 3 ч после его выхода из города А в город В выехал велосипедист, а еще через час вслед за ним выехал мотоциклист. Все участники двигались равномерно и в какой-то момент времени оказались в одной точке маршрута. Мотоциклист прибыл в город В на 2 ч раньше велосипедиста. Через сколько часов после велосипедиста пешеход пришел в город В?
infourok.ru
Контрольная работа № 1
1 вариант
1). Для функции f (х) = х3 + 2х2 – 1.
Найти f (0), f (1), f (-3), f (5).
2). Найти D(у), если:

3). Построить график функции:
а).у = – х + 5
б).у = х2 – 2
По графику определить :
а). Монотонность функции;
б). Ограниченность функции;
в). Минимальное ( максимальное ) значение функции
4). Для заданной функции найти обратную:

2 вариант
1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5).
2). Найти D(у), если:

3). Построить график функции:
а).у = х – 7
б).у = – х2 + 2
По графику определить :
а). Монотонность функции;
б). Ограниченность функции;
в). Минимальное ( максимальное ) значение функции
4). Для заданной функции найти обратную:

Контрольная работа № 2 по теме: «Тригонометрические функции числового и углового аргумента»
1 вариант
1). Вычислите:


2). Упростите:

3).Известно, что:  .
.
Вычислить  .
.
4). Решите уравнение:  .
.
5). Докажите тождество:  .
.
2 вариант
1). Вычислите:


2). Упростите:

3). Известно, что:
 .
.
Вычислить  .
.
4). Решите уравнение:
 .
.
5). Докажите тождество:
 .
.
Контрольная работа № 3 по теме: «Тригонометрические функции»
1 вариант
1). Найти наименьшее и наибольшее значения функций:
 на отрезке
на отрезке  ;
;
 на отрезке
на отрезке .
.
2). Упростить выражение:


3). Исследуйте функцию на четность:
4). Постройте график функции:

5). Известно, что . Докажите, что .
2 вариант
1). Найти наименьшее и наибольшее значения функций:
 на отрезке
на отрезке  ;
;
 на отрезке
на отрезке .
.
2). Упростить выражение:


3). Исследуйте функцию на четность:
4). Постройте график функции:

5). Известно, что . Докажите, что .
Контрольная работа № 4 по теме: «Тригонометрические уравнения»
1 вариант
1). Решить уравнение:

2). Найти корни уравнения  на отрезке
на отрезке  .
.
3). Решить уравнение:

4). Найти корни уравнения , принадлежащие отрезку
, принадлежащие отрезку  .
.
2 вариант
1). Решить уравнение:

2). Найти корни уравнения  на отрезке
на отрезке  .
.
3). Решить уравнение:

4). Найти корни уравнения , принадлежащие отрезку
, принадлежащие отрезку  .
.
Контрольная работа № 5 по теме: «Преобразование тригонометрических выражений»
1 вариант
1). Вычислить:

2). Упростить выражение:

3). Доказать тождество:

4). Решить уравнение
а).
5). Зная, что и
, найти
.
2 вариант
1). Вычислите:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение
а).
5). Зная, что и
, найти
.
Контрольная работа № 6 по теме: «Производная. Уравнение касательной к графику функции»
1 вариант
1). Найдите производную функции:
а). ; б).
;
в). ; г).
;
д). .
2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1.
3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени
с.
4). Дана функция .
Найдите:
а). Промежутки возрастания и убывания функции;
б). Точки экстремума;
в). Наибольшее и наименьшее значения функции на отрезке .
2 вариант
1). Найдите производную функции:
а). ; б).
;
в). ; г).
;
д). .
2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1.
3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с.
4). Дана функция .
Найдите:
а). Промежутки возрастания и убывания функции;
б). Точки экстремума;
в). Наибольшее и наименьшее значения функции на отрезке .
Контрольная работа № 8 (итоговая)
1 вариант
1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой
. Установить, в каких точках промежутка
касательная к графику данной функции составляет с осьюОхугол 600.
2). Решите уравнение:
3). Упростите выражение:
а).;
б). .
4). Постройте график функции с полным исследованием функции .
2 вариант
1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой
. Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке
.
2). Решите уравнение:
3). Упростите выражение:
а).;
б). .
4). Постройте график функции с полным исследованием функции .
kopilkaurokov.ru
Контрольная работа № 1
1 вариант
1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а). Каково взаимное расположение прямых
ЕF и АВ?
б). Чему равен угол между прямыми ЕF и АВ,
если АВС = 1500?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а). Выполните рисунок к задаче;
б). Докажите, что полученный четырех –
угольник – ромб.
2 вариант
1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DС.
а). Каково взаимное расположение прямых
РК и АВ?
б). Чему равен угол между прямыми РК и
АВ, если АВС = 400 и ВСА = 80?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К D, DА : ЕС = 1 : 2, DК : КА = 1 : 2.
а). Выполните рисунок к задаче;
б). докажите, что четырехугольник МNЕК –
трапеция.
Контрольная работа № 2
1 вариант
1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3). Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
2 вариант
1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3). Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
Контрольная работа № 3
1 вариант
1). Диагональ куба равна 6 см. Найдите:
а). Ребро куба;
б). Косинус угла между диагональю куба и
плоскостью одной из его граней.
2). Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии 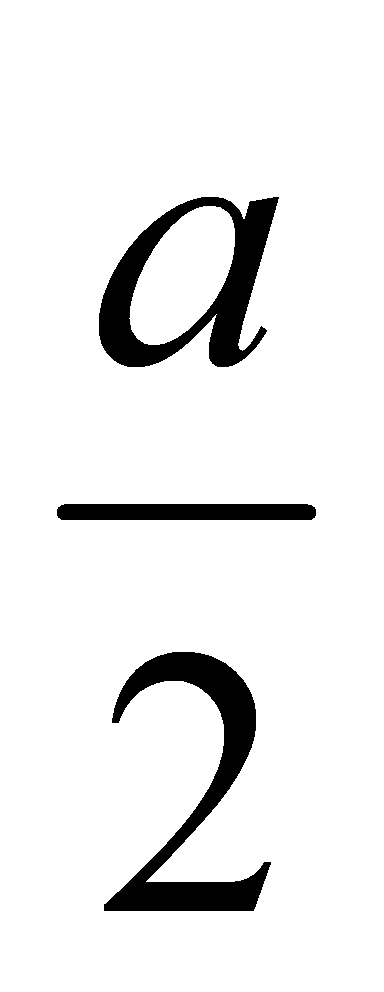 от точки D.
от точки D.
а). Найдите расстояние от точки С до плоскости α;
б). Покажите на рисунке линейный угол двугранного угла DABM, М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
2 вариант
1). Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна 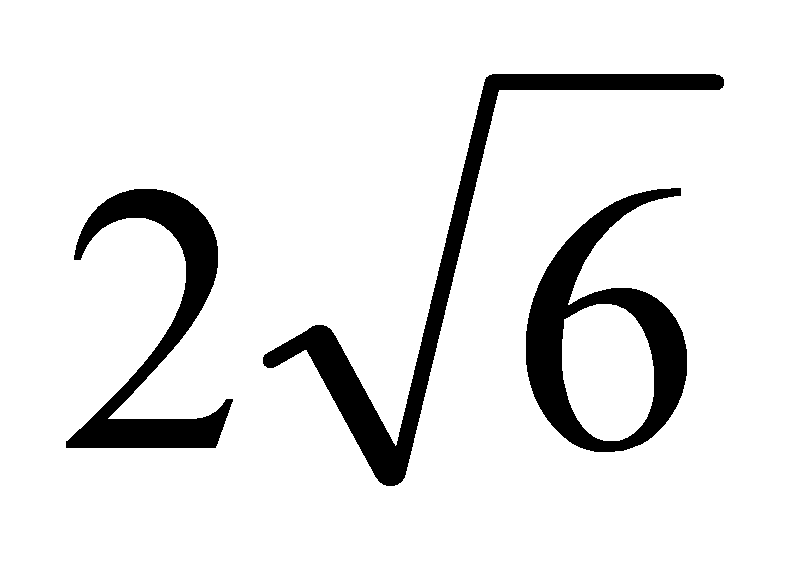 см, а его измерения относятся как 1:1:2. Найдите:
см, а его измерения относятся как 1:1:2. Найдите:
а). Измерения параллелепипеда;
б). Синус угла между диагональю параллеле –
пипеда и плоскостью его основания.
2). Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии 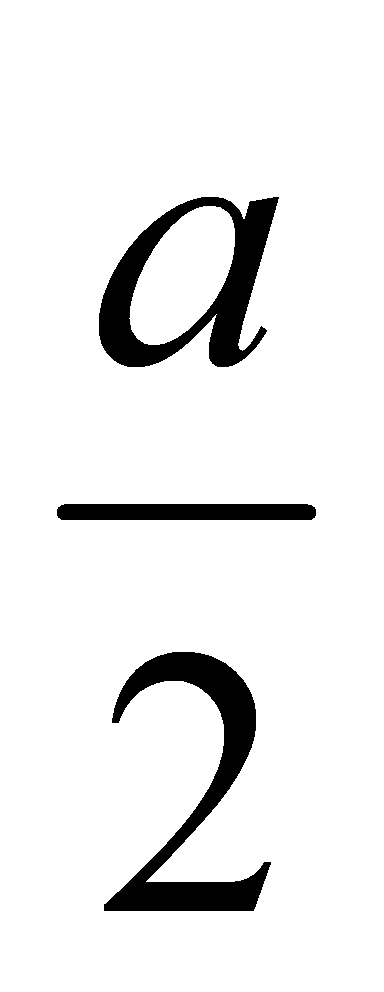 от точки В.
от точки В.
а). Найдите расстояние от точки С до плоскости α.
б). Покажите на рисунке линейный угол
двугранного угла BADM, М α.
в). Найдите синус угла между плоскостью
квадрата и плоскостью α.
Контрольная работа № 4
1 вариант
1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
2 вариант
1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны 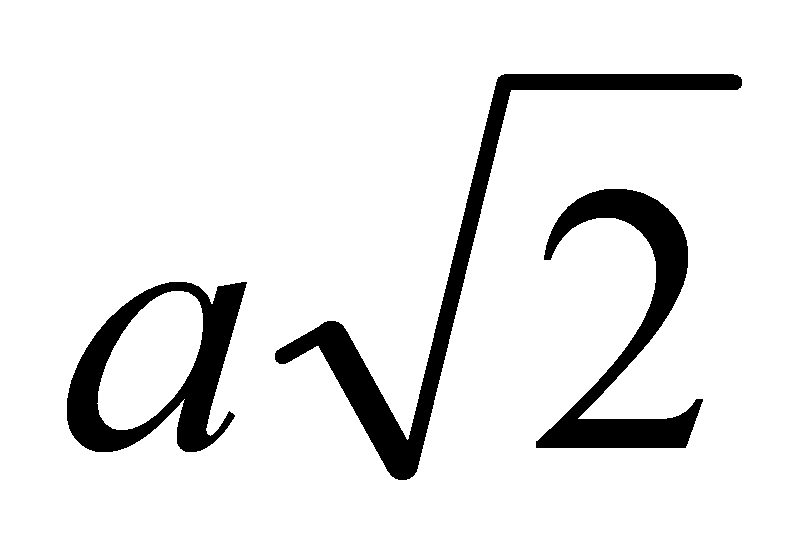 и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а). меньшую высоту параллелограмма;
б). угол между плоскостью АВС1 и плоскостью основания;
в). площадь боковой поверхности параллелепипеда;
г). площадь поверхности параллелепипеда.
infourok.ru
Составила:
учитель первой категории
МБОУ «СОШ №16»
г. Братска, Иркутской области
Сальникова Татьяна Владимировна
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данная контрольная работа содержит темы курса алгебры и начал анализа курса 10 класса (учебник А.Г. Мордкович). Содержание контрольной работы находится в рамках обязательного минимума содержания образования по алгебре и началу анализа. Тест составлен из заданий ЕГЭ по математике разных лет.
Этот же тест можно использовать и в сентябре, как вводный контроль для учащихся 11 класса.
Контрольная работа составлена в 2-х вариантах.
Время выполнения 60 минут.
Цель проведения промежуточной аттестации – установление соответствия уровня и качества подготовки обучающихся 10 класса по алгебре и начала анализа в объеме, установленном обязательным минимумом содержания основного общего образования Государственного образовательного стандарта.
Основные умения, проверяемые в работе:
умение выполнять вычисления и преобразование тригонометрических выражений;
умение решать тригонометрические уравнения;
умение проводить выборку корней тригонометрических уравнений;
умение вычислять производные по формулам;
знание геометрического и физического смысла производной;
умение читать график производной функции;
умение применять производную в ходе исследования функции.
Структура работы: отвечает цели построения дифференцированного обучения.
Работа состоит из двух частей.
Часть А составляют 7 заданий базового уровня сложности. При выполнении заданий части А учащиеся должны продемонстрировать базовую математическую компетентность. В этой части проверяется владение алгоритмами, знание и понимание ключевых элементов содержания курса алгебры 10 класса: математических понятий, их свойств, приемов решения.
Задания представлены в трех формах:
с выбором одного ответа из четырех предложенных;
с кратким ответом;
Часть В (3 задания) направлена на проверку владения материалом на повышенном и высоком уровнях. Все задания требуют полной записи решения и ответа. Задания части В направлены на проверку следующих качеств математической подготовки учащихся:
уверенное владение формально-оперативным алгебраическим аппаратом;
умение математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования.
Система оценивания выполнения отдельных заданий и работы в целом.
Оценивание работы осуществляется по принципу «сложения», оно зависит от количества и уровня сложности заданий, которые учащийся выполнил верно.
За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Задание первой части считается выполненным верно, если обведена цифра, которая соответствует правильному ответу (в заданиях с выбором ответа), или записан правильный ответ в специально отведенное для этого месте.
Задания второй части работы оцениваются в зависимости от правильности хода решения, формы его записи и отсутствия ошибок в вычислениях согласно критериям. (Замечание: В части В задание 1 оценивается в 4 баллов, задание 2 – в 4 бала, задание 3 – в 4 балла.
В целом максимальное количество баллов за работу равно 19.
Критерии оценивания заданий 2 части
| Содержание верного ответа и указания по оцениванию (допускаются различные способы оформления решения, не искажающие его смысла) | Баллы |
| Выполнены следующие условия: | |
| -задача решалась правильным методом -нет ошибок в вычислениях -ответ записан, верно | 4 |
| -задача решалась правильным методом -нет ошибок в вычислениях -неверно записан ответ | 3 |
| -задача решалась правильным методом -имеются ошибки в вычислениях | 1 |
| В остальных случаях | 0 |
Критерии оценивания итогового тестирования
| Количество набранных тестовых баллов | 7-10 баллов | 11-16 баллов | 17-19 баллов |
| Оценка | «3» удовлетворительно | «4» хорошо | «5» отлично |
| Ι вариант 1. Найдите множество значений функции у = 4 – 2cosx. 1) [-1;1] 2) [2;6] 3) [-2;2] 4)[-∞;∞] 2.Найдите производную функции у = 3. Найдите угловой коэффициент касательной, проведенной к графику функции у = 3х2 – 2х+1 в его точке с абсциссой х0 = 1. 1) 4 2) 1 3) 2 4) 5 4. Решите уравнение 2sin2x = – 5. Упростите выражение 1) 3ctgx 2) tgx 3) 3tgx 4) 2tgx+ctgx 6. Материальная точка движется прямолинейно по закону s(t) = 3t3+36t+12, где s(t) – координата точки в момент времени t. В какой момент времени скорость точки будет равна 45? 1) 4 2) 1 3) 5 4) 2 7. Найдите сумму целых значений, принадлежащих промежутку возрастания функции у = х2 –
1. Функция у = f(x) определена на промежутке (-2;7). На рисунке изображен график ее производной. Укажите на данном интервале для функции у = f(x): а) количество экстремумов; б) точку минимума функции; в) число точек графика функции, в которых касательная к графику наклонена под угол 450 к положительному направлению оси абсцисспод ненау функциильная с положительным направлением оси Ох составляет угол 45; г) число точек графика функции, в которых касательные к графику функции параллельны прямой у = 3 – 2,5х или совпадают с ней. д) число точек графика функции, в которых касательные к графику функции параллельны прямой у = 2,5 или совпадают с ней.
ЧАСТЬ В
2.a) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие 3. Найдите точку максимума функции f(x) = | ΙΙ вариант 1. Найдите наибольшее целое значений функции у = 5sinx – 2,3. 1) 3,3 2) 2,7 3) 2 4) 3 2.Найдите производную функции у = (3х – 1) 3. Укажите абсциссу точки графика функции у = 4х2 – 12х – 9, в которой угловой коэффициент касательной равен 12. 1) 0 2) 3 3) 4 4) -3 4. Решите уравнение 2cos 5. Упростите выражение cos2x – sin( 1) sinx 2) cosx 3) sin2x 4) – sin2x 6. Координата материальной точки измеряется с течением времени по закону х(t) = t5 – t4 + 6. Найдите скорость точки в момент времени t = 2. 1) 48 2) 54 3) 70 4) 88 7. Найдите количество целых значений, принадлежащих промежутку убывания функции у =
1. Функция у = f(x) определена на промежутке (-2;7). На рисунке изображен график ее производной. Укажите на данном интервале для функции у = f(x): а) количество экстремумов; б) точку максимума функции; в) число точек графика функции, в которых касательная к графику наклонена под угол 1350 к положительному направлению оси абсцисспод ненау функциильная с положительным направлением оси Ох составляет угол 45; г) число точек графика функции, в которых касательные к графику функции параллельны прямой у = 3 +2,5х или совпадают с ней. д) число точек графика функции, в которых касательные к графику функции параллельны прямой у = – 3,5 или совпадают с ней.
ЧАСТЬ В
2. а) Решите уравнение 2cos³x – 2cosx + sin²x = 0; б) Найдите корни этого уравнения, принадлежащие 3. Найдите наибольшее значение функции f(x) = (х – 2)2 ∙ (х -4) + 5 на отрезке [1; 3] . |
xn--j1ahfl.xn--p1ai