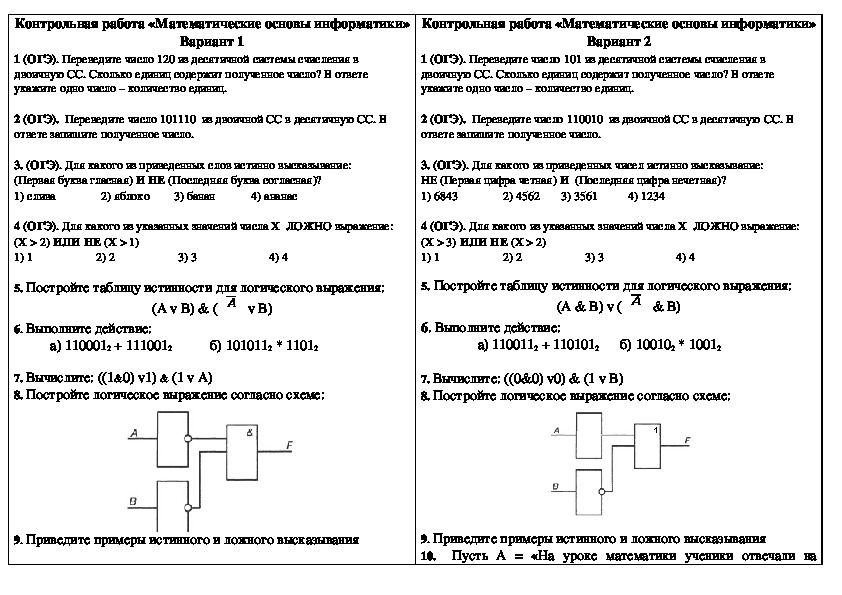
Контрольная работа «Математические основы информатики»
МКОУ Ясенковская СОШ
Административная контрольная работа по информатике
за I
По теме: «Математические основы информатики»
8 класс
Учитель информатики ВКК
Дегтярева Людмила Ивановна
Административная контрольная работа по информатике за I полугодие
«Математические основы информатики», 8 класс
- Дайте определение понятию «Система счисления»
-
Перечислите три вида систем счисления.
- Перечислите три вида логических операций, укажите обозначения и начертите таблицу истинности для каждой логической операции.
- Перечислите три типа логических элементов. Начертите схему к каждому.
- Запишите в развернутом виде следующие числа:
a) А10 = 361,105;
b) A16 = 224;
c) А8 = 521;
-
Переведите в десятичную систему счисления число 101010101
- Переведите в двоичную систему счисления число 12310. Запишите в ответе количество единиц.
- Переведите в восьмеричную систему счисления число 77710
- Переведите в шестнадцатеричную систему число 12310
- Переведите в десятичную систему счисления число 9АB16
-
Сложите числа 1101102 и 1010102. Сколько единиц содержит полученное число?
-
Какие предложения являются высказываниями?
- Бейрут – столица Перу.
- Бегемоты порхают с цветка на цветок.
- Чебурашка – мой самый любимый персонаж.
- Поднимите мне веки!
- На улице солнечная погода?
- На улице солнечная погода.
- Угостить тебя чаем?
- Бананы растут до десяти килограмм!
- F = B & (A v B)
- F = A & (B v B)
- F = A & (A v B v C)
-
Вычислите: ((0 & 0) 0) & (1V0).
- Для какого из приведённых значений числа X истинно высказывание:
Сколько единиц содержит полученное число?
НЕ (X > 5) И (X > 4)?
- Для какого из данных слов истинно высказывание:
НЕ (третья буква гласная) И (последняя согласная)?
- Слива b. инжир
- Ананас d. киви
- Определите значение сигнала на выходе логической схемы.
- Решите логическую задачу.
1 апреля три подружки Аня, Света и Оля решили разыграть одноклассников и договорились, что одна из них будет говорить только ложь, другая – только правду, а третья – через раз ложь, то правду.
Аня: Я всегда прогуливаю классный час, а Света скажет вам неправду.
Света: Я сегодня первый раз прогуляла классный час.
Оля: Аня сегодня говорит только чистую правду. Классный руководитель догадалась, кто из девочек сегодня выступает в какой роли. Догадайтесь и вы (ответ обоснуйте с помощью таблицы истинности).
Контрольная работа №1 «Математические основы информатики»
Контрольная работа №1 «Математические основы информатики»
1 вариант
1) Выберите правила сложения двоичных чисел:
a) 0+0=0; 0+1=1; 1+0=1; 1+1=10
b) 0+0=0; 0+1=1; 1+0=1; 1+1=2
c) 0+0=0; 0+1=10; 1+0=1; 1+1=1
d) 0+0=0; 0+1=0; 1+0=10; 1+1=0
2) Выберите правила умножения двоичных чисел:
a) 0*0=0; 0*1=1; 1*0=0; 1*1=1
b) 0*0=0; 0*1=0; 1*0=1; 1*1=1
c) 0*0=0; 0*1=0; 1*0=0; 1*1=1
d) 0*0=0; 0*1=1; 1*0=1; 1*1=1
3) В какой системе счисления справедливо равенство 513+64=610
a) В шестеричной
b) В семеричной
c) В восьмеричной
d) В десятичной
4) Известно, что X=D116, Y=718.
Сколько единиц содержит полученное число? В ответе укажите одно
число — количество единиц.
6) Выполните арифметические операции:
a) 111110010+10101100
b) 110101000+1100111
c) 1001*101
d) 11011*11
7) Для какого из указанных значений числа X истинно высказывание:
(X < 3) И НЕ (X < 2)?
1) 1 2) 2 3) 3 4) 4
8) Для какого из приведённых имён ложно высказывание:
(Третья буква гласная) ИЛИ НЕ (Последняя буква гласная)?
1) Елена 2) Татьяна 3) Максим 4) Станислав 9) 1(11)1
10) Три друга — Иван, Дмитрий, Степан преподают различные предметы (химию,
литературу, физику) в школах Москвы, Калининграда и Перми. Известно: Иван
работает не в Москве, а Дмитрий не в Калининграде; москвич преподает не
физику; тот, кто работает в Калининграде, преподает химию; Дмитрий преподает
не литературу. Какой предмет и в каком городе преподает каждый из
товарищей?
Контрольная работа №1 «Математические основы информатики»
3 вариант
1) Выберите правила сложения двоичных чисел:
a) 0+0=0; 0+1=1; 1+0=1; 1+1=10
b) 0+0=0; 0+1=1; 1+0=1; 1+1=2
c) 0+0=0; 0+1=10; 1+0=1; 1+1=1
d) 0+0=0; 0+1=0; 1+0=10; 1+1=0
2) Выберите правила умножения двоичных чисел:
a) 0*0=0; 0*1=1; 1*0=0; 1*1=1
b) 0*0=0; 0*1=0; 1*0=1; 1*1=1
c) 0*0=0; 0*1=0; 1*0=0; 1*1=1
d) 0*0=0; 0*1=1; 1*0=1; 1*1=1
3) В какой системе счисления справедливо равенство 344+21=420
a) В шестеричной
b) В семеричной
c) В восьмеричной
d) В пятеричной
4) Известно, что X=4110, Y=110100012.
Чему равна сумма X+Y в шестнадцатеричной
системе счисления:
a) FA16
b) AF16
c) F016
d) FD16
5) Переведите число 305 из десятичной системы счисления в двоичную систему счис
ления. Сколько единиц содержит полученное число? В ответе укажите одно
число — количество единиц.
6) Выполните арифметические операции:
a) 110001010+110000111
b) 1011011100+11101111
c) 1001*10111
d) 101101*11
7) Для какого из приведённых значений числа X ложно высказывание: НЕ (X < 7)
ИЛИ (X < 6)?
1) 4 2) 5 3) 6 4) 7 8) Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква согласная) ИЛИ НЕ (Последняя буква гласная)?
1) Егор 2) Тимур 3) Вера 4) Любовь
9) ((10)(11))(01)
10) В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и
Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что: Смит – самый высокий. Играющий на скрипке меньше ростом
играющего на флейте.
Играющие на скрипке и флейте и Браун любят пиццу. Когда
между альтистом и трубачом возникает ссора, Смит мирит их. Браун не умеет
играть ни на трубе, ни на гобое. На каких инструментах играет каждый из
музыкантов, если каждый владеет двумя инструментами?Тест с ответами: «Математические основы информатики»
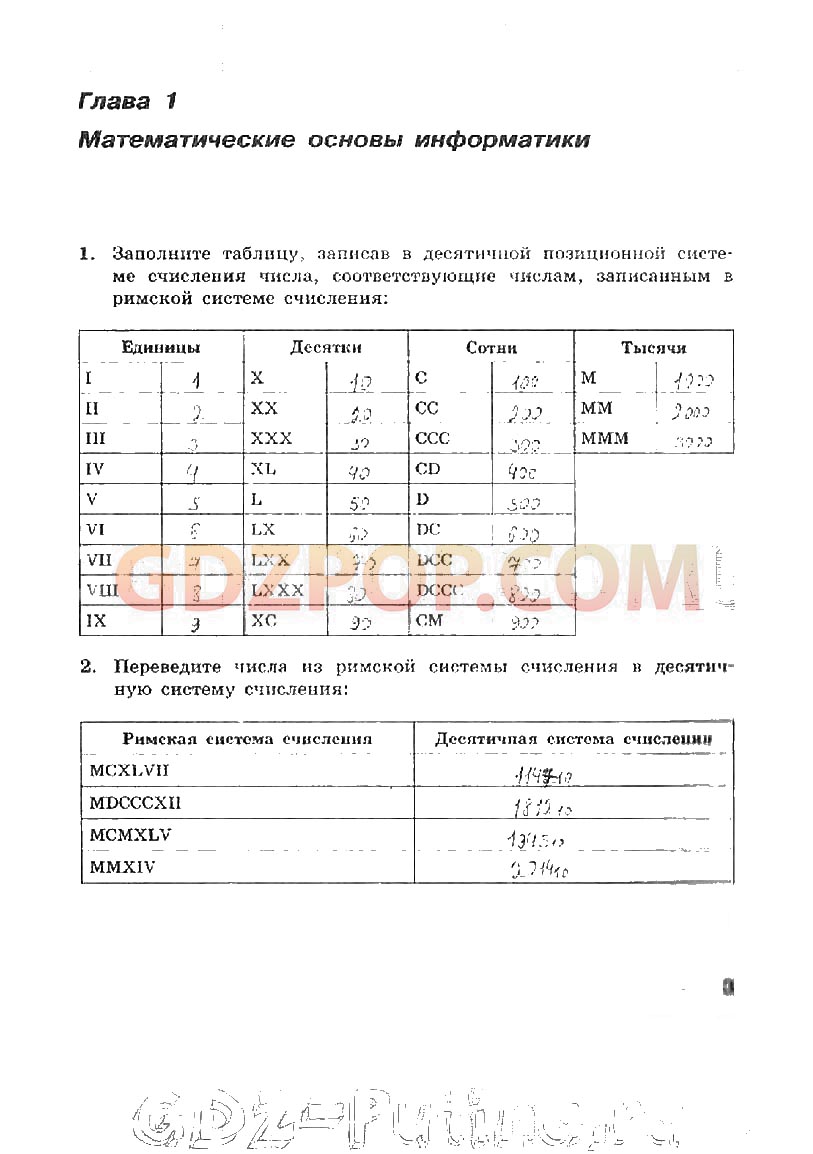
1. Совокупность знаков, с помощью которых записываются числа, называется:
а) алфавитом системы счисления +
б) цифрами системы счисления
в) системой счисления
2. Чему равен результат сложения двух чисел, записанных римскими цифрами: MCM+LXVIII:
а) 2168
б) 1968 +
в) 1168
3. Число 301011 может существовать в системах счисления с основанием:
а) 6
б) 10
в) 4 +
4. Число 301011 может существовать в системах счисления с основанием:
а) 8 +
б) 2
в) 3
5. Двоичное число 100110 в десятичной системе счисления записывается как:
а) 48
б) 68
в) 38 +
6.
(( X<2) v (X<1)):
а) 4
б) 3
в) 1 +
8. Какое высказывание является не верным:
а) Знаком v обозначается логическая операция конъюнкция. +
б) Дизъюнкцию также называют логическим сложением
в) Логическую операцию ИЛИ также называют логическим сложением
9. Вещественные числа представляются в компьютере:
а) в развёрнутой форме
б) в естественной форме
в) в экспоненциальной форме с нормализованной мантиссой +
10. В знаковый разряд ячейки для отрицательных чисел заносится:
а) +
б) 1 +
в) –
11. Количество разрядов, занимаемых двухбайтовым числом, равно:
а) 16 +
б) 8
в) 4
12. Ячейка памяти компьютера состоит из однородных элементов называемых:
а) коэффициентами
б) разрядами +
в) кодами
13. Сколько цифр 1 в двоичном представлении десятичного числа 15:
а) 4 +
б) 3
в) 2
14. Как называется раздел информатики, использующий математические приемы и методы представления информации в компьютере:
а) вычислительная математика
б) алгебра логики
в) теория кодирования +
15.
Математическая логика включает в себя такое направление информатики:
а) теорию автоматов +
б) теорию массового обслуживания
в) теорию информации
16. Раздел информатики, занимающийся созданием моделей:
а) математическая логика
б) имитационное моделирование +
в) теория информации и кодирования
17. К какой группе относятся дисциплины, которые занимаются созданием методов, ориентированных на реализацию вычислений в компьютерах:
а) математической логики
б) теории принятия решений
в) вычислительной математики +
18. Как называется дисциплина, занимающаяся разработкой специальных приемов для описания физических процессов в реальных объектах в виде математических моделей:
а) теория принятия решений
б) имитационное моделирование +
в) теория информации и кодирования
19. Как называется дисциплина, занимающаяся созданием ситуаций в условиях конфликта и противоречий для выработки единой оптимальной стратегии:
а) теория информации
б) теория исследования операций
в) теория игр +
20.
Он первым разработал абстрактную вычислительную машину, которая стала прообразом современного компьютера:
а) Шеннон
б) Тьюринг +
в) Буль
21. Как называется дисциплина, занимающаяся изучением свойств и методов построения алгоритмов, для решения задач, по которым известны начальные условия и методы решения:
а) теория алгоритмов +
б) теория принятия решений
в) теория вероятности
22. Как называется дисциплина, которая занимается изучением абстрактных вычислительных машин, представленных в виде математических моделей:
а) теория алгоритмов
б) теория автоматов +
в) теория игр
23. Слово «бит» для обозначения наименьшей единицы информации предложил этот ученый:
а) Тьюринг
б) Буль
в) Шеннон +
24. В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа):
а) зависит от ее позиции в записи числа
б) не зависит от ее позиции в записи числа +
в) зависит от формы в записи числа
25.
Любая позиционная система счисления характеризуется своим:
а) продолжением
б) окончанием
в) основанием +
26. Количество различных цифр, используемых для изображения чисел в данной системе счисления:
а) окончание позиционной системы счисления
б) основание позиционной системы счисления +
в) началом позиционной системы счисления
27. Целые числа в любой системе счисления порождаются с помощью:
а) правила счета +
б) правила расположения
в) правила вида
28. Одна из систем с основанием, являющаяся целой степенью числа:
а) главная
б) одинарная
в) двоичная +
29. Одна из систем с основанием, являющаяся целой степенью числа:
а) восьмеричная +
б) четверичная
в) основная
30. Одна из систем с основанием, являющаяся целой степенью числа:
а) восемнадцатеричная
б) шестнадцатеричная +
в) тридцатидвуричная
Фондов информатики Сертификат об окончании
Обзор
Сертификат выпускника «Основы информатики» обеспечивает прочный курс изучения математических основ вычислений, а также важных аспектов компьютерного программирования.
- Изучите основные элементы теории вычислений, включая логику, методы доказательства, комбинаторику, анализ алгоритмов, модели дискретных данных (множества, отношения, деревья) и конечные автоматы
- Изучите различные парадигмы программирования, а также принципы построения объектно-ориентированного программного обеспечения
Планируйте свои основы в области компьютерных наук Дорожная карта сертификата выпускника
Срок действия сертификата составляет девять месяцев, однако на его заполнение может уйти до трех лет.Курсы доступны осенью, зимой и весной:
- Осенний квартал: CS103, CS107, CS154, CS157
- Winter Quarter: CS108, CS110, CS161
- Spring Quarter: CS109
Примечание: предложения курсов могут быть изменены. Для прохождения курсов не нужно получать сертификат. Вы можете записаться на любые курсы, если вы соответствуете требованиям.
Кто должен подавать заявку
Практикующие специалисты, стремящиеся закрепить свое понимание основ информатики в теории и на практике.
Получение сертификата
- Получите сертификат в любой академической четверти, где предлагается соответствующий курс, при соблюдении предварительных условий
- Пройдите курсы для получения зачетных единиц и получения оценки
- Получите B (3,0) или выше за каждый курс
Предварительные требования
- Опыт работы в методологии программирования и абстракциях (CS106A и CS106B или эквивалентные).
- Присваивается степень бакалавра со средним баллом 3 по бакалавриату.0 или лучше.
Заявление
Чтобы получить сертификат об окончании высшего образования, вам необходимо подать заявление.
Подать заявку
Стоимость обучения
Стоимость обучения зависит от количества взятых вами единиц. Дополнительную информацию см. В разделе «Обучение на аспирантуре » на нашей странице «Стоимость обучения и сборы».
Срок выполнения сертификата
В среднем 1-2 года
Максимум 3 года для завершения
Вопросы
Отправьте запрос, чтобы получить дополнительную информацию.
Что происходит в математических науках
«Что происходит в математических науках» — это серия публикаций, в которых сообщается о последних математических исследованиях в понятной и понятной форме как математикам, так и нематематикам.
Оглавление каждой и полный текст выбранных статей приведены ниже.
- Содержание, том 11
- Содержание, Том 10
- Содержание, Том 9
- Содержание, Том 8
- Содержание, Том 7
- Содержание, Том 6
- Содержание, Том 5
- Содержание, Том 4
- Содержание, Том 3
- Содержание, Том 2
- Содержание, Том 1
Заказать Что происходит в математических науках, том 11 в книжном магазине AMS
Содержание, Том 11
Джерримандеринг: математика на испытании
Дана Маккензи
Расчет калорий
Дана Маккензи
Когда черные дыры сталкиваются
Дана Маккензи
Форма данных
Дана Маккензи
Игра «Set®» встретила свое совпадение
Дана Маккензи
Математика поездок на работу
Дана Маккензи
Расширяющиеся горизонты
Дана Маккензи
Квантовые компьютеры и Золотые ворота
Дана Маккензи
Иголки в бесконечном стоге сена
Дана Маккензи
Заказать Что происходит в математических науках, том 10 в книжном магазине AMS
Содержание, Том 10
Оригами: открывая будущее
, Дана Маккензи
Древнее японское искусство складывания бумаги становится высокотехнологичным, поскольку инженеры изобретают новые устройства, которые разворачивают или откладывают складывание.
Эти изобретения, в свою очередь, приводят к возникновению сложных математических проблем, касающихся путей сборки, дефектов и криволинейных складок в плоских материалах.
Основные кластеры и разрывы: перебор экспертов
Дана Маккензи
Математика получила реальную историю Уолтера Митти в 2013 году, когда Итан Чжан шокировал теоретиков чисел первой конечной верхней границей минимального размера пробелов между простыми числами. Одна из старейших проблем теории чисел, гипотеза простого близнеца, теперь может быть в пределах досягаемости.
Плата за истину установит
Барри Сипра
Когда вы платите незнакомцу, особенно онлайн, за помощь, как вы можете быть уверены, что получаете честные ответы? Новая теория информатики показывает, как рациональный личный интерес согласуется с насущной потребностью в надежных вычислениях.
Климат: прошлое, настоящее и будущее
Дана Маккензи
Куда бы вы ни посмотрели в климате Земли, перемены происходят всегда.
Во всей науке о климате математические модели помогают разобраться в том, что произошло (массовые вымирания), что происходит (таяние ледяных щитов) и что может произойти (переломные моменты).
По следам Шерлока Холмса
Дана Маккензи
В рассказе, опубликованном в 1905 году, Шерлок Холмс неправильно определил, куда ехал велосипед, на основании его следов. Тонкая взаимосвязь между передними и задними гусеницами велосипеда недавно помогла математикам решить еще одну проблему викторианской эпохи, касающуюся работы планиметров.
Quod Erat Demonstrandum
, автор — Барри Сипра
Доказательство — это своего рода математическая поэма, а иногда и эпическая.Два недавнего доказательство, каждый год в создании, показывает длину, к которой математики будут идти в упорной погоне за истину, в том числе, в эти дни, заручившись компьютерами перепроверить свою логику.
Проблема Кадисона-Зингера: точный баланс
Дана Маккензи
Большие проблемы под разными масками.
Проблема Кадисона-Зингера, впервые представленная как проблема теоретической физики, возникла во многих других математических контекстах более чем за полвека, пока не была окончательно решена в 2013 году теоретиками графов.
Пятиугольный поиск окупается
Барри Сипра
Найти формы, покрывающие плоскость, несложно. Найти их всех сложнее. Математики до сих пор не знают, сколько различных выпуклых пятиугольников способны разбить плоскость. Но список, который долго останавливался на отметке 14 лет, постепенно увеличивался благодаря новому алгоритму и компьютерному поиску.
Дивный новый мир спортивной аналитики
Дана Маккензи
В последние несколько лет профессиональный спорт захлестнула новая волна статистических методов или «аналитики».Эти методы в сочетании с новыми источниками данных, такими как видеозахват, позволяют количественно оценить неуловимые навыки и оспаривать заветные предположения об игровой стратегии.
Содержание, Том 9
Массовый прорыв
В 1963 году Питер Хиггс предсказал существование поля Хиггса, что объясняет, почему многие субатомные частицы имеют ненулевую массу.
Это предсказание было основано на простой странице математических расчетов и вдохновенной аналогии с теорией фазовых переходов Ландау-Гинзбурга.Почти полвека и более 9 миллиардов долларов спустя физики-экспериментаторы в ЦЕРНе наконец-то выследили бозон Хиггса, самый неуловимый карьер в физике. Это открытие восполнило последнюю недостающую часть Стандартной модели квантовой физики и убедительно подтвердило использование абстрактных принципов симметрии для открытия новых физических явлений.
НКТ через гиперпространство
В 2012 году геометры в быстрой последовательности решили три открытые проблемы, касающиеся оптимальной геометрии торов (внутренних трубок).Гипотеза Уиллмора определила тор с наименьшей энергией изгиба; Гипотеза Лоусона определила тор в гиперсфере (сфере в четырехмерном пространстве) с наименьшей площадью поверхности; и гипотеза Пинкалла-Стерлинга классифицировала все торы в гиперсфере, которые минимизируют площадь с учетом ограничения объема. С тюбингом еще никогда не было так весело!
Цунами: уроки математики, уроки прошлого
Великое японское цунами 2011 года унесло жизни более 15 000 человек в стране, которая была лучше подготовлена к цунами, чем любая другая страна в мире.
Трагедия высветила пробелы в нашем научном понимании этого чрезвычайно разрушительного природного явления, и тем более в понимании общества. Он также указал на некоторые способы, которыми математические модели сделали это правильно, но недостаточно быстро.
Сегодняшний прогноз: вероятность кражи со взломом десять процентов
Междисциплинарная группа из Калифорнийского университета в Лос-Анджелесе обнаружила, как адаптировать математическую модель, разработанную для прогнозирования землетрясений, для определения вероятных «горячих точек» преступности. Два полевых испытания их программного обеспечения были ошеломляющими, а прогнозирование полицейской деятельности было признано журналом Time и другими СМИ одним из главных научных открытий 2011 года.
Топологи вычеркнули четыре из «Ведерного списка»
Три десятилетия назад трехмерная топология казалась дикими, необузданными джунглями разрозненных примеров. Затем Уильям Терстон предложил ряд предположений, которые внесли некоторый порядок в хаос.
В 2012 году, всего за несколько месяцев до смерти Терстона, гипотеза виртуального Хакена и гипотеза виртуального расслоения были окончательно доказаны, показав, что почти все трехмерные многообразия произошли от шаблонов, построенных элементарным образом.
Математики делают поворот
Кубик Рубика, любимая игрушка математиков, продолжает привлекать новых поклонников и вдохновлять на новые исследования. В то время как «спидкуберы» разработали новые алгоритмы (и ловкость рук), чтобы собрать куб менее чем за 10 секунд, математики доказали, что всеведущие существа всегда могут собрать классический куб 3 на 3 на 3 за 20 ходов или меньше.
Правильная эпидемия в нужное время
В 2009 году мир пережил первую за сорок лет пандемию гриппа.К счастью, он оказался намного мягче, чем три великие пандемии двадцатого века, но предоставил идеальную возможность протестировать различные математические модели в реальном времени. Выводы: моделирование работало довольно хорошо, и связь между разработчиками моделей и полевыми работниками была отличной, но поздняя доставка вакцины потерпела бы фиаско в случае более серьезной эпидемии.
Мыслить тематически
Тематическое моделирование — это новый статистический метод, названный в честь его способности определять темы (такие как генетика или изменение климата) в большом объеме документов.Хотя он еще только зарождается, он оказался чрезвычайно популярным в области «цифровых гуманитарных наук» и может позволить веб-сайтам социальных сетей автоматически и анонимно реагировать на кибер-издевательства.
Тропическое мышление
Благословенная (или, возможно, проклятая?) С броским названием тропическая геометрия позволяет математикам решать сложные задачи классической алгебраической геометрии, создавая простые комбинаторные модели, очень похожие на фигурки из палочек. Этот новый тип геометрии также имеет удивительные приложения к теории струн в физике, эволюционным деревьям в биологии и составлению расписания движения поездов.
К сожалению, 9-й том больше не доступен.
Содержание, Том 8
Учет вкуса
Netflix, компания по прокату фильмов, предложила приз в миллион долларов за компьютерный алгоритм, который может значительно улучшить способность компании предсказывать симпатии и антипатии своих клиентов.
Чрезвычайно успешное соревнование опровергло некоторые общепринятые представления в области машинного обучения и наглядно продемонстрировало силу «краудсорсинга».«
Дивный новый симплектический мир
Тридцать лет назад Алан Вайнштейн предположил, что определенные виды динамических систем с двумя степенями свободы, такие как маятник, который может свободно как растягиваться, так и качаться, всегда имеют периодические (повторяющиеся) решения. В то время никто не знал, как доказать свою гипотезу. Но это было до «симплектических верблюдов» и «сумасшедшей» теории гомологии, основанной на уравнениях для магнитного монополя. Вывод: периодические орбиты существуют. (Магнитные монополи все еще не работают.)
Математика и финансовый кризис
В первое десятилетие 2000-х инвесторы использовали кредитные деривативы: умный, основанный на формуле метод, позволяющий разделить риск субстандартных кредитов и прибыль от быстрорастущего рынка жилья. Но они забыли — или предпочли проигнорировать — что математическая модель хороша ровно настолько, насколько хороши ее допущения.
Лучшая бильярдная игра
В вывернутой наизнанку версии бильярда, которая не может поместиться в вашем гараже (или даже в Млечном Пути), две группы исследователей находят разные способы вонзить биток в лузу на бесконечности.
SimPatient
Математические модели популяций пациентов начали дополнять или заменять клинические испытания в тех случаях, когда испытания было бы трудно или невозможно провести. В 2009 году комиссия общественного здравоохранения использовала шесть моделей рака груди, чтобы прийти к противоречивой рекомендации о том, что женщинам в возрасте 40-49 лет больше не следует рекомендовать проходить ежегодную маммографию.
Мгновенная случайность
Сколько времени нужно, чтобы смешать молоко в кофейной чашке, нейтроны в атомном реакторе, атомы в газе или вращение электронов в магните? В модели магнетизма Изинга математики рассчитали уникальное время отсечки, когда система резко переходит от практически несмешанной к почти полностью перемешанной.
Такое же поведение ожидается и для других систем, описываемых теорией цепей Маркова.
В поисках квантового хаоса
Классический бильярдный шар на столе с изогнутыми «расходящимися» сторонами движется по хаотической траектории, которая существенно меняет положение шара в долгосрочной перспективе. Однако при низких энергиях квантовые бильярдные шары не хаотичны. Стремительно сочетая чистую теорию чисел с физикой, математики доказали, что квантовый хаос действительно возникает при высоких энергиях.
3-х мерные сюрпризы
Даже в двадцать первом веке математика все еще может открывать новые явления в обычном трехмерном пространстве. Пункт 1: потрясающе эффективный способ упаковки тетраэдров. Пункт 2: Gömböc, однородное тело, которое автоматически исправляет (и ошибается) себя.
Когда заканчивается одна героическая эпоха, начинается новая
Открытие Джоном Милнором «экзотических сфер» в 1956 году открыло новую эру многомерной топологии с новыми мощными инструментами, такими как теория обрамленных кобордизмов, теория стабильной гомотопии и хирургия.
Но один вопрос, названный проблемой неизменяемого Кервера, оставался без ответа более 40 лет, пока три тополога не нашли «кратчайший путь к Эвересту».
К сожалению, 8-й том больше не доступен.
Заказать Что происходит в математических науках, том 7 в книжном магазине AMS
Содержание, Том 7
Новый поворот в теории узлов
(846 КБ)
Два, казалось бы, не связанных между собой вида узлов — модульные узлы и узлы Лоренца — оказываются одинаковыми.Для теоретиков чисел выплата — это новый взгляд на старую концепцию модульной поверхности. Для теоретиков динамических систем это новый способ понять истоки хаоса.
Рулетка с ошибочными терминами и гипотеза Сато-Тейт
Пятнадцать лет назад Эндрю Уайлс доказал Великую теорему Ферма, решив тем самым самую известную математическую задачу. Афтершоки все еще ощущаются. Команда теоретиков чисел, включая соавтора Уайлса Ричарда Тейлора, адаптирует аппарат Уайлса, чтобы отшлифовать еще одну знаменитую нерешенную проблему теории чисел.
Решение на пятьдесят один процент
(846 КБ)
Перси Диаконис, Сьюзан Холмс и Ричард Монтгомери расскажут, как повысить шансы в вашу пользу в следующий раз, когда вы подбросите монетку. И нет, вам не нужно обманывать.
Домино, кто-нибудь?
Невинная головоломка о том, как выложить шахматную доску домино, в конечном итоге приводит к новой модели случайных поверхностей. Теория и достаточно проста, чтобы быть точно решаемой, и достаточно сложная, чтобы включать фазовые переходы между «твердым», «жидким» и «газообразным» состояниями — комбинация, которой раньше никогда не было в статистической физике.
Не видеть — значит верить
Новые «метаматериалы» могут вскоре принести плащи-невидимки — а также плащи-невидимки — из царства фантастики в реальность. В отличие от мантии Гарри Поттера, эти устройства будут работать строго по принципам математики, а не магии.
Начало работы с программой (Мори)
В алгебраической геометрии программа минимальных моделей Мори представляет собой амбициозную попытку согласовать геометрию поверхностей, определяемых полиномиальными уравнениями, с их алгеброй.После 100 лет выполнения программы по одному измерению, алгебраические геометры стремительно поднимаются на вершину лестницы.
Книга, которую время не могло стереть
Более 1000 лет назад неизвестный писец скопировал некоторые работы Архимеда на пергамент. Но 200 лет спустя другой писец стер их и написал поверх молитвенника. За последние десять лет высокотехнологичные методы визуализации преодолели ущерб, нанесенный веками пренебрежения и злоупотреблений, чтобы раскрыть то, что на самом деле написал Архимед, величайший математик Древней Греции.
Картирование 248-мерного мира
Гоняясь против времени и неизлечимой болезни одного из своих коллег, команда из двадцати теоретиков групп составляет подробный обзор «самой красивой структуры в математике» — исключительной группы Ли E8.
Сжатое зондирование делает каждый пиксель на счету
(878 КБ)
Доказывая, что больше не всегда лучше, математики показывают, что «разреженные» или «сжимаемые» сигналы, такие как цифровые фотографии и сообщения сотового телефона, могут быть восстановлены на основе гораздо меньшего количества измерений, чем предполагали инженеры ранее.В качестве крайнего доказательства принципа инженеры создали первую в мире камеру с одним пикселем.
Заказать Что происходит в математических науках, том 6 в книжном магазине AMS
Содержание, Том 6
См. Ссылки на рассказы Сипры и Маккензи по теме каждой главы.
Первая из семи проблем тысячелетия близится к завершению
, автор Barry Cipra (1 МБ)
прослушать подкаст, интервью с автором
В 2002 году Григорий Перельман объявил о решении гипотезы Пуанкаре, топологической задачи, выбранной в 2000 году как одна из семи главных математических задач тысячелетия.
После более чем трех лет тщательных исследований математики осторожно принимают его доказательство, в котором используется геометрическое уравнение в частных производных, называемое «поток Риччи», впервые изученное Ричардом Гамильтоном.Классификация гиперболических многообразий — все хорошо, что хорошо кончается
Дана Маккензи (1,62 МБ)
прослушать подкаст, интервью с автором
Пока трехмерные топологи ждали вердикта по гипотезе Пуанкаре (которая имеет дело с замкнутыми многообразиями), некоторые из них разрешили набор давних гипотез о концах открытых многообразий.
цифр числа Пи
, автор Barry Cipra (317 КБ)
послушать интервью с автором подкаста
любители пи возрадуйтесь! Теперь вы можете вставить палец в число Пи и вытащить любую цифру (скажем, триллионную) без необходимости вычислять все предыдущие цифры. Единственная загвоздка в том, что вам нужно считать шестнадцать.
Комбинатористы решают опасную проблему
, автор Barry Cipra (415 КБ)
послушать интервью подкаста с автором
Вопрос, заданный студентом — может ли диаграмма Венна быть осесимметричной? — приводит к красивым «салфеткам», сложной математике и (через сорок лет) решению, найденному другим студентом.
Новые сведения о простых числах
Барри Сипра (послушайте интервью с автором подкаста)
числа удивили теоретиков чисел. Группа индийских математиков, включая двух студентов, обнаруживает первый алгоритм с полиномиальным временем для проверки, является ли число простым. Американские, турецкие и венгерские математики сотрудничают, чтобы показать, что небольшие промежутки между последовательными простыми числами возникают гораздо чаще, чем кто-либо ранее доказывал.Другое международное сотрудничество находит равномерно распределенные (но не следующие друг за другом) простые последовательности любой желаемой длины.
От кубика Рубика к квадратичным числовым полям … и выше
Даны Маккензи (послушайте интервью с автором подкаста)
Манджул Бхаргава начал с простой идеи складывать числа в квадрат. В конечном итоге из коробки появился совершенно новый способ комбинирования и подсчета объектов в алгебраической теории чисел.
Вихри в уравнениях Навье-Стокса
Барри Сипра (послушайте интервью с автором подкаста)
От Большого Красного Пятна Юпитера до водоворотов в потоке — вихри — привычная черта потока жидкости. Математики получили новое понимание образования и долговременного выживания вихрей как в двух-, так и в трехмерных жидкостях.
Гидродинамика объясняет тайны движения насекомых
Дана Маккензи (735 КБ)
прослушать подкаст, интервью с автором
Как водомеры движутся по поверхности, почти не имеющей трения? Как парят стрекозы? Эти и другие загадки биологии могут быть объяснены математикой уравнений Навье-Стокса.
Броуновское движение, фазовые переходы и конформные карты
Даны Маккензи (послушайте интервью с автором подкаста)
Новый случайный процесс, называемый эволюцией Шрамма-Лёвнера, оказывается хорошей моделью для множества физических явлений, от случайных колебаний молекул воздуха до фазовых переходов магнитного материала. Ключевое математическое свойство этих систем, доказанное в одних случаях и все еще предполагаемое в других, — конформная инвариантность.
Плавные ходы
Барри Сипра (послушайте интервью с автором подкаста)
Некоторые алгоритмы информатики, такие как симплексный алгоритм решения задач линейного программирования, работают лучше, чем предполагалось. Новый показатель сложности, называемый сглаженным анализом, показывает, почему стандартные наихудшие сценарии так вводят в заблуждение.
Заказать Что происходит в математических науках, том 5 в книжном магазине AMS
Содержание, Том 5
Новые высоты теории чисел
Прогресс стремительно развивается в постферматовском мире эллиптических кривых и модульных форм.
Математический поворот к сворачиванию белков
Мощные статистические методы помогают исследователям выяснить трехмерную структуру наиболее важных молекул жизни.
Ничто в сфере, кроме самой сферы
Многовековая проблема — гипотеза Кеплера — подтолкнула к новым открытиям и некоторым упорным вычислениям.
Конечная математика
Конечна ли вселенная? Наблюдения за космическим микроволновым фоном и новый математический алгоритм могут дать ответ.
Математика пробок
Компьютерные модели помогают исследователям понять, откуда берутся пробки и, возможно, что с ними делать.
История перезаписи
Плимптон 322 — одна из любимых клинописных табличек математиков. Но что это значило для писца, составившего его?
Это маленький, большой, маленький, большой мир
Исследователи пришли к выводу, что от теории к приложениям в исследовании сетей малого мира совсем немного.
A Celestial Па-де-Труа
Новые методы открыли множество решений старой проблемы небесной механики: орбитального движения трех тел.
Думай и богатей
Математический институт Клэя выделил семь важных задач математики с призовым фондом в 1 миллион долларов за каждую.
Изинг на торте
Новая теорема помогает объяснить, почему статистической физике так трудно решить одну из своих центральных проблем.
Заказать Что происходит в математических науках, том 4 в книжном магазине AMS
Содержание, Том 4
Голубой день компьютерных шахмат
Победа Deep Blue над Гарри Каспаровым — это конец долгого пути в компьютерных шахматах, но математическому изучению «идеальной» игры в комбинаторных играх предстоит пройти еще более долгий путь.
Первобытный случай хаоса
Квантовые хаологи и теоретики аналитических чисел нацелены на загадочный математический объект: дзета-функцию Римана.( Обратите внимание: Эта статья доступна в формате PDF.)
Доказательство примером: математик математик
Пол Эрдеш, «Джонни Эпплсид» в математике, вдохновил сотни коллег и оставил богатое наследие математических задач и решений.
Компьютеры возвращают алгебраическую геометрию к истокам
Мощь компьютеров вернула на передний план алгоритмические вопросы алгебраической геометрии.
Так же просто, как EQP
Автоматическому доказательству теорем удается разрешить многолетнюю гипотезу символической логики. Что остается делать человеческому уму?
Beetlemania: Хаос в экологии
Сотрудничество математиков и биологов привело к первому экспериментальному доказательству хаотической динамики в популяции.
От проводного к странному
Математические открытия формируют исследования потенциально революционного вида вычислений, основанных на принципах квантовой механики.
Истории из криптосистемы
Прорыв в теории вычислительной сложности имеет значение для криптографических систем с «гарантированной» безопасностью.
Но это математика?
Математика и искусство имеют больше общего, чем принято считать. Два художника двадцатого века, М. К. Эшер и Марсель Дюшан, использовали математику как источник вдохновения для своих произведений искусства.
Математическое открытие (Анри Пуанкаре)
Мысли Анри Пуанкаре о мышлении, написанные в начале двадцатого века, стоит повторить в конце века.
Заказать Что происходит в математических науках, том 3 в книжном магазине AMS
Содержание, Том 3
Теорема Ферма — наконец!
Эндрю Уайлс завершил удивительный тест tour de force , который решает самую известную задачу в математике.
Его доказательство — осуществление детской мечты.История двух теорий
Прорыв в теоретической физике упростил печально известную сложную теорию 4-мерной геометрии и дал математикам много поводов для размышлений.
Компьютерные науки открывают ДНК
Будут ли компьютеры будущего созданы с помощью биоинженерии? Это возможность.
Разделяй и властвуй
Томас Хорошенько решил изучить простые числа, встречающиеся в парах. Попутно он обнаружил, что чип Intel Pentium не может делиться. ( Обратите внимание: Эта статья доступна в формате PDF.)
Мягкое искусство контроля
Современные технологии опираются на математическую теорию управления, чтобы поддерживать равновесие.Как уравнения знают, что делать?
Вычислительная гидродинамика — на грани турбулентности
Математические методы, более быстрые компьютеры и лучшие алгоритмы получают все большее распространение в изучении сложных потоков жидкости.
Для некоторых исследователей вычислительная турбулентность — буквально несбыточная мечта.Клеточные автоматы предлагают новый взгляд на жизнь, Вселенную и все остальное
Постоянно увеличивающаяся мощность компьютеров позволила исследователям взглянуть на мир незаметно.Теоретики стремятся объяснить часто наблюдаемые сложные закономерности.
Насколько простодушны теоретики групп?
Исследователи упорно трудятся, чтобы упростить один из самых сложных доказательств в математической истории — классификацию простых групп.
Тайная жизнь больших чисел
Вычислительная задача в теории чисел была решена значительно раньше, чем предполагалось через 20 000 лет.
В математике мы доверяем
Теорема о многомерной интеграции может найти применение на Уолл-стрит. Вы могли бы назвать это схемой быстрого обогащения.
Содержание, Том 2
«Поистине замечательное доказательство»
Объявление о доказательстве Великой теоремы Ферма в прошлом году ошеломило математический мир. Доказательство Эндрю Уайлса, хоть и неполное, тем не менее получило восторженные отзывы.
От узла к узлу
Какой самый быстрый способ развязать узел? Исследователи раскрыли значительную часть ответа.
Математика новой волны
Пройдут ли компактные волны по информационным супермагистралям будущего? Теоретически это возможно.
Математические идеи для медицинской визуализации
Группа математиков, компьютерных ученых и инженеров разработала новую технологию медицинской визуализации, основанную на безопасном применении электрического тока
Parlez-vous Вейвлеты?
Математики и ученые быстро учатся говорить на новом языке.
Результаты вызывают большой фурор.Случайные алгоритмы оставляют мало шансов
Ученые-компьютерщики сделают все, чтобы избежать узких мест и ускорить вычисления. Но делать ставку на результат? Вы делаете ставку!
Мыльный раствор
Студенты программы летних математических исследований нашли отличные ответы на некоторые старые проблемы, касающиеся геометрии мыльных пузырей.
Выпрямление нелинейных кодов
Сложный класс кодов с исправлением ошибок внезапно стал намного проще в использовании.
Совершенно легко
Комбинаторная задача, долгое время считавшаяся сложной, наконец-то решена — с удивительной легкостью.
(Вектор) Поле мечты
Умная конструкция «отключает» гипотезу 40-летней давности о топологии векторных полей.
К сожалению, Том 2 больше не доступен.
Содержание, Том 1
Уравнения оживают в математической биологии
Математики работают с биологами, чтобы вникнуть в некоторые из самых сложных проблем современной биологии, от понимания иммунной системы человека до «вычисления» человеческого сердца.
Новые компьютерные идеи из «прозрачных» доказательств
Можно ли доверять компьютеру, если он выдает настолько длинные и сложные доказательства, что никто не может проверить их детали? Теоретики придумали новый способ узнать, верны ли компьютерные доказательства.
Не всегда можно услышать форму барабана
Вы слышите форму барабана? Это известная проблема, в которой спрашивается, могут ли два барабана, которые выглядят по-разному, издавать один и тот же звук.После десятилетий ломания головы математики пришли к ответу.
Экологически безопасная математика
Математики объединились с учеными для работы над решением экологических проблем, от моделирования океана до работы с опасными отходами.
Опровержение очевидного в более высоких измерениях
Интуиция о нашем трехмерном мире может удивительно вводить в заблуждение, когда дело касается высших измерений, как показывают два недавних результата по геометрии.
Сотрудничество завершается закрытыми геодезическими
Необычное сочетание дифференциальной геометрии и динамических систем привело к важному теоретическому результату о количестве замкнутых «геодезических» кривых на искаженных сферах.
Crystal Clear Computations
Выращивание кристаллов — на компьютере? Математики помогают материаловедам лучше понять природу кристаллов, одновременно решая сложные математические задачи.
Геометрия лагеря
Группа талантливых и любознательных студентов «ночевала» прошлым летом в Центре геометрии. Используя сложную компьютерную графику и собственное воображение, они придумали увлекательную математику.
Теоретики чисел раскрывают множество простых самозванцев
Как это ни странно звучит, существуют составные числа, которые «маскируются» под простые числа. Группа математиков, пытающихся выследить этих простых самозванцев, в конечном итоге доказала, что их бесконечно много.
Теоретики раскраски карт смотрят на новые миры
Сколько цветов нужно, чтобы различать соседние цвета на карте? Несмотря на знаменитую теорему о четырех цветах, это сложная проблема в теории графов, особенно если ваши карты не плоские.
К сожалению, Том 1 больше не доступен.
Бакалавр компьютерных наук и математики | Бакалавриат
- перейти к содержанию
- Перейти к основной глобальной навигации
- Перейти к дополнительной глобальной навигации
- Перейти к навигации по сайту
Поиск Идти
Выберите место для поискаВсе
Студенческие курсы
Степень магистра
Возможности PhD
- Ученики
- Штат сотрудников
- Выпускников
- Вакансии
- Исследование
- Исследование
- Бизнес
- Спорт
- Новости и события
- Около
- Курсы
- Дни открытых дверей
- Заказать проспект
Поиск курса Идти
Меню- Дом университета
- Учись у нас
- Бакалавриат
- Курсы
- А-Я бакалавриата
- Компьютерные науки и математика Бакалавр наук
Курсы
Зачем учиться здесь
Посетите нас
Проживание
Тематические области
Сборы и финансирование