А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 2. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+4)2, если -5≤x≤-2; Y= 2x, если -2< x<2; (x-4)2, если 2≤x≤5. №3. Исследуйте функцию на четность-нечетность А)y=3x4-4x2+1; Б) y=. №4 Найдите функцию, обратную функции y=x2+3, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 1. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+3)2, если -5≤x≤-2; Y= x+1, если -2< x<3; (x-5)2, если 3≤x≤6. №3. Исследуйте функцию на четность-нечетность А)y=4x -2x3 +6x5; Б) y=. №4 Найдите функцию, обратную функции y=x2+4, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 2. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+4)2, если -5≤x≤-2; Y= 2x, если -2< x<2; (x-4)2, если 2≤x≤5. №3. Исследуйте функцию на четность-нечетность А)y=3x4-4x2+1; Б) y=. №4 Найдите функцию, обратную функции y=x2+3, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 1. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+3)2, если -5≤x≤-2; Y= x+1, если -2< x<3; (x-5)2, если 3≤x≤6. №3. Исследуйте функцию на четность-нечетность А)y=4x -2x3 +6x5; Б) y=. №4 Найдите функцию, обратную функции y=x2+4, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 2. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+4)2, если -5≤x≤-2; Y= 2x, если -2< x<2; (x-4)2, если 2≤x≤5. №3. Исследуйте функцию на четность-нечетность А)y=3x4-4x2+1; Б) y=. №4 Найдите функцию, обратную функции y=x2+3, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 1. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+3)2, если -5≤x≤-2; Y= x+1, если -2< x<3; (x-5)2, если 3≤x≤6. №3. Исследуйте функцию на четность-нечетность А)y=4x -2x3 +6x5; Б) y=. №4 Найдите функцию, обратную функции y=x2+4, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 2. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+4)2, если -5≤x≤-2; Y= 2x, если -2< x<2; (x-4)2, если 2≤x≤5. №3. Исследуйте функцию на четность-нечетность А)y=3x4-4x2+1; Б) y=. №4 Найдите функцию, обратную функции y=x2+3, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. | А-10 Контрольная работа№1 по теме: Числовые функции. Вариант 1. №1. Найдите область определения функции: А) y= ; Б) y= . №2 Постройте график функции и прочитайте его: -(x+3)2, если -5≤x≤-2; Y= x+1, если -2< x<3; (x-5)2, если 3≤x≤6. №3. Исследуйте функцию на четность-нечетность А)y=4x -2x3 +6x5; Б) y=. №4 Найдите функцию, обратную функции y=x2+4, x≤0. Постройте на одном чертеже графики этих взаимно обратных функций. |
Контрольная работа по теме «Числовые функции» 9 класс.
Контрольная работа по алгебре 9 класс «Числовые функции»
Вариант 1 1..Постройте график функции у = х6. На отрезке найдите наименьшее и наибольшее значения функции. 2..Определите число корней уравнения -х4 = х – 4. 3.Опишите свойства функции, изображенной на рисунке. 4. Найдите наибольшее и наименьшее значения функции У = (х — 2)3 + 4 на отрезке . | Вариант 2 1. Постройте график функции у = х8. На отрезке найдите наименьшее и наибольшее значения функции.2. Определите число корней уравнения х3 = 2 — х. 3. Опишите свойства функции, изображенной на рисунке. 4. Найдите наибольшее и наименьшее значения функции У = (х + 3)4 — 4 на отрезке . |
Вариант 1 1..Постройте график функции у = х6.На отрезке найдите наименьшее и наибольшее значения функции. 2..Определите число корней уравнения -х4 = х – 4. 3.Опишите свойства функции, изображенной на рисунке. 4. | Вариант 2 1. Постройте график функции у = х8. На отрезке найдите наименьшее и наибольшее значения функции.2. Определите число корней уравнения х3 = 2 — х. 3. Опишите свойства функции, изображенной на рисунке. 4. Найдите наибольшее и наименьшее значения функции У = (х + 3)4 — 4 на отрезке . |
Вариант 1 1..Постройте график функции у = х6.На отрезке найдите наименьшее и наибольшее значения функции. 2..Определите число корней уравнения -х4 = х – 4. 3.Опишите свойства функции, изображенной на рисунке. 4. Найдите наибольшее и наименьшее значения функции У = (х — 2)3 + 4 на отрезке . | Вариант 2 1. Постройте график функции у = х8. На отрезке найдите наименьшее и наибольшее значения функции. 2. Определите число корней уравнения х3 = 2 — х. 3. Опишите свойства функции, изображенной на рисунке. 4. Найдите наибольшее и наименьшее значения функции У = (х + 3)4 — 4 на отрезке . |
Уроки 12-13. Контрольная работа по теме «Числовые функции»
Цель: проверить знания учащихся с использованием разноуровневых вариантов.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика контрольной работы
Контрольная работа составлена в шести вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» – четырех задач и оценка «3» – трех задач. Одна задача является резервной (или запасной) и дает некоторую возможность выбора учащимся. При таких же критериях оценки в случае вариантов 3, 4 дается дополнительно 0,5 балла и в случае вариантов 5, 6 – дополнительно 1 балл (учитывая более высокую сложность этих вариантов). Поэтому в случае вариантов 5, 6 оценку «5» можно получить за правильное решение четырех задач.
Одна задача является резервной (или запасной) и дает некоторую возможность выбора учащимся. При таких же критериях оценки в случае вариантов 3, 4 дается дополнительно 0,5 балла и в случае вариантов 5, 6 – дополнительно 1 балл (учитывая более высокую сложность этих вариантов). Поэтому в случае вариантов 5, 6 оценку «5» можно получить за правильное решение четырех задач.
Выбор вариантов может быть сделан учителем или учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
III. Варианты работы
Вариант 1
1. Найдите промежутки возрастания и убывания, наименьшее значение функции у = x2- 4х – 5.
2. Определите четность или нечетность функции
3. Для функции f(х) = 3х + 2 найдите обратную функцию f-1(х).
4. Найдите значение функции
5. Постройте график функции:
Вариант 2
1. Найдите промежутки возрастания и убывания, наибольшее значение функции у = 7 – 6х – х2.
2. Определите четность или нечетность функции
3. Для функции f(x) = 5х – 1 найдите обратную функцию f-1(х).
4. Найдите значение функции
5. Постройте график функции:
Вариант 3
1. Найдите промежутки возрастания и убывания, наименьшее значение функции
2. Определите четность или нечетность функции
3. Для функции найдите обратную функцию f-1(х).
4. Найдите значение функции f(х), если
5. Постройте график функции:
Вариант 4
1. Найдите промежутки возрастания и убывания, наибольшее значение функции
2. Определите четность или нечетность функции
3. Для функции найдите обратную функцию f-1(х).
4. Найдите значение функции f(x), если
5. Постройте график функции:
Вариант 5
1. Найдите промежутки возрастания и убывания, наибольшее значение функции
2. Определите четность или нечетность функции
3. Для функции найдите обратную функцию f-1(х).
4. Дана функция Найдите f(4) и f(6) и сравните числа f(f(4)) иf(f(6)).
Вариант 6
1. Найдите промежутки возрастания и убывания, наименьшее значение функции
2. Определите четность или нечетность функции
3. Для функции найдите обратную функцию f-1(х).
4. Дана функция Найдите f(8) и f(-4) и сравните числа f(f(8)) иf(f(-4)).
5. Постройте график функции:
Контрольная работа №2 на тему «Функция. Квадратный трёхчлен и его корни»
Контрольная работа № 1
Тема. Функция: область определения, множество значений, свойства функции Квадратный трёхчлен и его корни.
Вариант 1.
В заданиях 1 – 5 запишите правильный ответ
1. Функция задана формулой f(x) = -2 + 6. Найдите f(-3).
2. Найдите значения х, при котором функция, заданная формулой g(x) = 0,8х – 3 принимает значение равное 1.
3. Укажите область определения функции, заданной формулой φ(х) = .
4. Найдите нули функции, если они существуют g(x) = .
5. Функция задана формулой f(x) = -4x + 12. При каких
значениях х f(x) > 0.
Задания 6 – 7 выполните с кратким решением
6. Докажите, что при любом значении х, квадратный трёхчлен
принимает положительное значение
7. Сократите дробь .
Задание 8 выполните с полным объяснением
8. Постройте график функции и перечислите её свойства.
у = 1,5х – 6.
Контрольная работа № 1
Тема. Функция: область определения, множество значений, свойства функции Квадратный трёхчлен и его корни.
Вариант 2.
В заданиях 1 – 5 запишите правильный ответ
1. Функция задана формулой f(x) = 4 — 8. Найдите f(-2).
Функция задана формулой f(x) = 4 — 8. Найдите f(-2).
2. Найдите значения х, при котором функция, заданная формулой g(x) = — 0,6х + 5 принимает значение равное -1.
3. Укажите область определения функции, заданной формулой φ(х) = .
4. Найдите нули функции, если они существуют g(x) = .
5. Функция задана формулой f(x) = -5x — 7. При каких значениях х f(x) < 0.
Задания 6 – 7 выполните с кратким решением
6. Докажите, что при любом значении х, квадратный трёхчлен
принимает неотрицательное значение.7. Сократите дробь .
Задание 8 выполните с полным объяснением
8. Постройте график функции и перечислите её свойства.
у = — 0,6х + 3.
Контрольные работы по алгебре 7-9 класс
Контрольные работы по алгебре, 7-9 класс
Приведено по два варианта контрольных
работ по алгебре для 7 класса, ориентированных
на новые версии учебных комплектов
А. Г.Мордковича и др. Алгебра-7 Часть 1.
Учебник; часть 2. Задачник. Мнемозина,
2007.
Г.Мордковича и др. Алгебра-7 Часть 1.
Учебник; часть 2. Задачник. Мнемозина,
2007.
7 класс
Контрольная работа № 1
1 вариант
Найдите значение числового выражения:
а) б)
Решите уравнение: а) б)
Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Открытый луч с началом в точке (–9)». Сколько отрицательных целых чисел принадлежит данному открытому лучу?
Упростите алгебраическое выражение и найдите его значение:
при
Решите задачу, выделяя три этапа математического моделирования:
В книге 140 страниц. В пятницу Знайка прочитал в 1,2 раза меньше страниц, чем в субботу, и на 20 страниц больше, чем в воскресенье. Сколько страниц прочитал Знайка в субботу?
2 вариант
Найдите значение числового выражения:
а) б)
Решите уравнение: а) б)
Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Луч с концом в точке 7».
 Сколько натуральных
чисел принадлежит данному лучу?
Сколько натуральных
чисел принадлежит данному лучу?
_______________________________________________________________
Упростите алгебраическое выражение и найдите его значение:
при .
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
Капитан Врунгель загрузил на свой корабль в трех ящиках 39 кг авокадо. В первом ящике было в 1,5 раза больше авокадо, чем во втором, а во втором на 4 кг меньше, чем в третьем. Сколько килограммов авокадо в первом ящике?
Контрольная работа № 2
1 вариант
Постройте график линейной функции
С помощью графика найдите:
а) наименьшее и наибольшее значения функции на отрезке
б) значения переменной , при которых
Найдите координаты точки пересечения прямых и
а) Найдите координаты точек пересечения графика линейного уравнения с осями координат;
б) Определите, принадлежит ли графику
данного уравнения точка
.
_______________________________________________________________
а) Задайте линейную функцию формулой, если известно, что ее график параллелен прямой
_______________________________________________________________
При каком значении решением уравнения является пара чисел ?
2 вариант
Постройте график линейной функции
С помощью графика найдите:
а) наименьшее и наибольшее значения функции на отрезке
б) значения переменной , при которых
Найдите координаты точки пересечения прямых и
а) Найдите координаты точек пересечения графика линейного уравнения с осями координат;
_______________________________________________________________
а) Задайте линейную функцию формулой, если известно, что ее график параллелен прямой
б) Определите, возрастает или убывает
заданная функция. Ответ объясните.
Ответ объясните.
_______________________________________________________________
При каком значении решением уравнения является пара чисел ?
Контрольная работа № 3
1 вариант
Решите систему уравнений графическим методом:
Решите систему уравнений методом подстановки:
Решите систему уравнений методом алгебраического сложения:
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
В туристический поход ребята взяли двухместные и трехместные палатки. Сколько человек разместилось в трехместных палатках, если на 26 человек ребята взяли 10 палаток?
_______________________________________________________________
При каком значении , график уравнения пройдет через точку пересечения прямых и ?
2 вариант
Решите систему уравнений графическим методом:
Решите систему уравнений методом подстановки:
Решите систему уравнений методом алгебраического сложения:
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
Одна сторона прямоугольника на 4 см
больше другой. Если меньшую сторону
увеличить в 2 раза, а большую оставить
без изменения, то периметр нового
прямоугольника будет равен 56 см. Найдите
стороны данного прямоугольника.
Если меньшую сторону
увеличить в 2 раза, а большую оставить
без изменения, то периметр нового
прямоугольника будет равен 56 см. Найдите
стороны данного прямоугольника.
_______________________________________________________________
При каком значении , график уравнения пройдет через точку пересечения прямых и ?
Контрольная работа № 4
1 вариант
Упростите выражение:
а) в)
б) г)
Вычислите
Сравните значения выражений и
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
Длина прямоугольника составляет его ширины. Найдите стороны прямоугольника, если его площадь равна 120см.
_______________________________________________________________
Решите уравнение
2 вариант
Упростите выражение:
а) в)
б) г)
Вычислите
Сравните значения выражений и
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
Стороны прямоугольника относятся как
7:6, а его площадь равна 168см.
Найдите стороны прямоугольника.
_______________________________________________________________
Решите уравнение
Контрольная работа № 5
1 вариант
Найдите многочлен и запишите его в стандартном виде, если , где
Преобразуйте выражение в многочлен стандартного вида:
а) б) в)
Упростите выражение, используя формулы сокращенного умножения:
_______________________________________________________________
Найдите три последовательных натуральных числа, если известно, что квадрат большего из них на 34 больше произведения двух других.
_______________________________________________________________
Докажите, что значение выражения не зависит от значения переменной.

2 вариант
Найдите многочлен и запишите его в стандартном виде, если , где
Преобразуйте выражение в многочлен стандартного вида:
а) б) в)
Упростите выражение, используя формулы сокращенного умножения:
_______________________________________________________________
Найдите три последовательных натуральных числа, если известно, что квадрат меньшего из них на 47 меньше произведения двух других.
_______________________________________________________________
Докажите, что значение выражения не зависит от значения переменной.
Контрольная работа № 6
1 вариант
Разложите многочлен на множители:
а) в)
б) г)
Сократите дробь: а) б)
Решите уравнение
_______________________________________________________________
Докажите тождество .

_______________________________________________________________
Вычислите наиболее рациональным способом
2 вариант
Разложите многочлен на множители:
а) в)
б) г)
Сократите дробь: а) б)
Решите уравнение
_______________________________________________________________
Докажите тождество .
_______________________________________________________________
Вычислите наиболее рациональным способом
Контрольная работа № 7
1 вариант
Постройте график функции .
С помощью графика найдите:
а) значения функции при значении аргумента, равном
б) значения аргумента, если значение функции равно 4;
в) наибольшее и наименьшее значения функции на отрезке
Решите графически уравнение
Дана функция , где При каких значениях аргумента верно равенство ?
_______________________________________________________________
4. Дана функция
,
где
Дана функция
,
где
а) Найдите
б) Постройте график функции .
_______________________________________________________________
5. Постройте график функции
2 вариант
Постройте график функции .
С помощью графика найдите:
а) значения функции при значении аргумента, равном
б) значения аргумента, если значение функции равно ;
в) наибольшее и наименьшее значения функции на отрезке
Решите графически уравнение
Дана функция , где При каких значениях аргумента верно равенство ?
_______________________________________________________________
4. Дана функция , где
а) Найдите
б) Постройте график функции .
_______________________________________________________________
5. Постройте график функции
Итоговая контрольная работа
1 вариант
Постройте график функции
С помощью графика определите:
а) наибольшее и наименьшее значения функции на отрезке
б) значения аргумента, при которых
Решите уравнение
Сократите дробь:
а) б)
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
Расстояние между двумя пристанями по
реке равно 27км. Катер проплывает его по
течению реки за 1,5ч, а против течения за
2ч15м. Найти собственную скорость катера
и скорость течения реки.
Катер проплывает его по
течению реки за 1,5ч, а против течения за
2ч15м. Найти собственную скорость катера
и скорость течения реки.
_______________________________________________________________
Постройте график функции , где
С помощью графика определите, при каких значениях график функции пересекает прямую в двух точках.
2 вариант
Постройте график функции
С помощью графика определите:
а) наибольшее и наименьшее значения функции на отрезке
б) значения аргумента, при которых
Решите уравнение
Сократите дробь:
а) б)
_______________________________________________________________
Решите задачу, выделяя три этапа математического моделирования:
Катер за 1ч20м проплывает по течению реки
24км, а против течения за 1,5ч на 3км меньше. Найти скорость течения реки и собственную
скорость катера.
Найти скорость течения реки и собственную
скорость катера.
_______________________________________________________________
Постройте график функции , где
С помощью графика определите, при каких значениях график функции пересекает прямую в двух точках.
ГДЗ по алгебре 7-9 класс Контрольные Мордкович углубленный
Постоянные проверочные и промежуточные аттестации требуют от учащегося должной подготовки и хороших знаний предмета, ведь именно это определяет уровень знаний школьника. Самостоятельные, тесты, ВПР и т. д. – это то, что ставит некоторых учеников, имеющих проблемы с учебой, в ступор. Чтобы справиться со всеми предстоящими испытаниями, рекомендуется использовать ГДЗ по алгебре контрольные работы 7-9 классы Мордкович углубленный уровень.
Пособие разработано как в печатном издании, так и в онлайн-версии. Электронный вариант намного удобней и практичней, т. к. это облегчает заданную на дом работу. Правильные ответы можно открыть в интернете, где бы вы не находились. Сайт адаптирован под любое устройство (будь то хоть компьютер, хоть телефон или планшет).
Правильные ответы можно открыть в интернете, где бы вы не находились. Сайт адаптирован под любое устройство (будь то хоть компьютер, хоть телефон или планшет).
Какими еще достоинствами обладают ГДЗ по алгебре к контрольным работам для 7-9 классов Мордковича (Углубленный уровень)
Сборник с готовыми домашними заданиями обеспечивает должную поддержку любому ученику и имеет ряд плюсов, благодаря которым им и пользуются семиклассники:
- круглосуточная и бесперебойная работа портала;
- интуитивно понятный поиск по странице;
- подробно расписанные решения с рисунками и графиками;
- попутные комментарии к особым случаям;
- оформление в соответствии с ФГОС и др.
Материал на сайте постоянно обновляется в связи с изменениями в государственном стандарте. Это позволяет не беспокоиться о неправильном ответе, все задания и решения всегда актуальны для данного года.
Учителя несомненно отметят такой порыв к знаниям и вскоре в дневнике и журнале будут блистать только положительные оценки. Это станет еще одни поводом для гордости родителей, а в классе вы – явный авторитет. По статистике, к таким школьникам чаще обращаются за помощью сверстники, а это в свою очередь – один из способов завоевать уважение.
Это станет еще одни поводом для гордости родителей, а в классе вы – явный авторитет. По статистике, к таким школьникам чаще обращаются за помощью сверстники, а это в свою очередь – один из способов завоевать уважение.
Какие темы входя с решебник по алгебре для контрольных работ за 7-9 класс (автор: Мордкович А. Г.)
Учебно-методический комплекс состоит из тех же разделов, что и главное пособие. А именно вам встретятся следующие главы:
- неравенства с одной переменной;
- системы уравнений;
- числовые функции и т. д.
Таким образом, регулярно применяя в своей практике решебник, учащиеся всегда будут иметь возможность блеснуть своими знаниями перед одноклассниками. Такие школьники чаще остальных занимают призовые места на олимпиадах, что выделяет их среди своих сверстников.
Учеба покажется легкой и интересной вместе с пособием от издания «Мнемозина». Так что учитесь и не переживайте за свои оценки!
Алгебра 8 Никольский Контрольная 1 с ответами
Контрольная работа № 1 по алгебре в 8 классе с ответами (4 варианта) по УМК Никольский и др. Цитаты из пособия: «Алгебра. Дидактические материалы. 8 класс / Потапов, Шевкин» использованы в учебных целях. Ответы на контрольные работы адресованы родителям. Алгебра 8 Никольский Контрольная 1 + ответы.
Цитаты из пособия: «Алгебра. Дидактические материалы. 8 класс / Потапов, Шевкин» использованы в учебных целях. Ответы на контрольные работы адресованы родителям. Алгебра 8 Никольский Контрольная 1 + ответы.
Контрольная работа № 1 по алгебре
8 класс, УМК Никольский и др.
К-1. Вариант 3 (транскрипт заданий)
- Даны числовые промежутки А = [– 5; 7) и В = (– 4; 8]. Запишите числовые промежутки A ∪ В и А ∩ В, изобразите их на координатной оси.
- Дана функция у = 1/х.
а) Принадлежат ли точки А(– 10; 0,1), Б(– 0,5; – 2), С(– 4; – 0,25) графику этой функции?
б) Какому числовому промежутку принадлежат значения у, если х ∈ [– 3; –1]? - Постройте график функции у = х2.
а) Докажите, что эта функция является убывающей на промежутке (–∞; 0].
б) Какому числовому промежутку принадлежат значения у, если х ∈ [– 5; 7]? - Какому числовому промежутку принадлежат значения выражения А = …, если а ∈ (1/9; 2/9) ?
- * Первая, вторая и третья бригады, работая отдельно, выполнят задание за а, b и с дней соответственно, а при совместной работе они выполнят то же задание за t дней.
 Какому числовому промежутку наименьшей длины принадлежат значения t, если 3 ≤ а ≤ 5, 8 ≤ b ≤ 10 и 24 ≤ с ≤ 30?
Какому числовому промежутку наименьшей длины принадлежат значения t, если 3 ≤ а ≤ 5, 8 ≤ b ≤ 10 и 24 ≤ с ≤ 30?
К-1. Вариант 4 (транскрипт заданий)
- Даны числовые промежутки А = [– 6; 3) и В = (– 5; 7]. Запишите числовые промежутки A ∪ В и А ∩ Б, изобразите их на координатной оси.
- Дана функция у = х2.
а) Принадлежат ли точки А(–11; –121), B(9; 81), С(– 12; 144) графику этой функции?
б) Какому числовому промежутку принадлежат значения у, если x ∈ [– 2; 6]? - Постройте график функции y = 1/x.
а) Докажите, что эта функция является убывающей на промежутке (–∞; 0).
б) Какому числовому промежутку принадлежат значения у, если х ∈ [–7; –5]? - * Какому числовому промежутку принадлежат значения выражения А = …, если a ∈ (3/8; 3/4)?
- * Первая, вторая и третья трубы, работая отдельно, наполнят бассейн за а, b и с ч соответственно, а при совместной работе они наполнят бассейн за t ч. Какому числовому промежутку наименьшей длины принадлежат значения t, если 8 ≤ а ≤ 9, 12 ≤ b ≤ 18 и 24 ≤ с ≤ 30?
ОТВЕТЫ на контрольную работу:
Вы смотрели: Контрольная работа № 1 по алгебре в 8 классе с ответами по УМК Никольский и др. Цитаты из пособия: «Алгебра. Дидактические материалы. 8 класс / Потапов, Шевкин» использованы в учебных целях. Ответы на контрольные работы адресованы родителям.
Цитаты из пособия: «Алгебра. Дидактические материалы. 8 класс / Потапов, Шевкин» использованы в учебных целях. Ответы на контрольные работы адресованы родителям.
Вернуться к списку контрольных работ по алгебре 8 класс (Никольский)
Практический тест по основным математическим функциям (примеры вопросов)
Функции интерпретации
1. Функция f определяется как f (x) = √x-3. Его область определения x ≥ 3, а диапазон — f (x) ≥ 0. Что из следующего верно для f?- Если x ≥ 3, то f (x) ≥ 0.
- Каждому положительному значению x присваивается ровно одно значение.
- Диапазон функции: f (3) .
- Значение f (3) не определено.
- г (2) = 8
- г (2) = 9
- г (2) = 13
- г (2) = 17
 Функция S (r) = 4 rπ 2 дает площадь поверхности сферы радиусом r . Какова площадь поверхности сферы радиуса 4?
Функция S (r) = 4 rπ 2 дает площадь поверхности сферы радиусом r . Какова площадь поверхности сферы радиуса 4? - 8 π
- 16π
- 32π
- 64 π
Строительные функции
4.Театр продаст 500 билетов на спектакль, если будет взимать 10 долларов за билет. Более того, каждый раз, когда он поднимает цену на один доллар, он будет продавать на 50 билетов меньше, потому что некоторые люди сочтут это слишком дорогим. Какая из следующих функций t (d) представляет количество билетов, которые театр продаст, если будет взимать d долларов за билет?- t (d) = 50 d + 10
- t (d) = 50 d + 1000
- t (d) = 50 d
- t ( г) = 50 г + 10
- c (d) = 3,55 + 0,70d
- c (d) = 3,55 + 0,70 (d — 1)
- c (d) = 4,25 + 0,70d
- c (d) = 4,25 + 0,70 ( г — 1)
Линейные, квадратичные и экспоненциальные модели
6. Экспоненциальные функции растут на равные коэффициенты через равные интервалы.Во сколько раз экспоненциальная функция f (x) = 3-2 x увеличивается на каждом интервале, длина которого равна 3?
Экспоненциальные функции растут на равные коэффициенты через равные интервалы.Во сколько раз экспоненциальная функция f (x) = 3-2 x увеличивается на каждом интервале, длина которого равна 3? - В 6 раз.
- В 8 раз.
- В 18 раз.
- . В 24 раза.
- 25 o C
- 30 o C
- 40 o C
- 50 o C
Тригонометрические функции
8. На рисунке ниже кружком O обозначена единица измерения. окружности, а мера AOB равна π / 3.- π / 6
- π / 3
- 2π / 3
- π
.png) На координатной плоскости ниже изображены единичный круг и угол.
На координатной плоскости ниже изображены единичный круг и угол.Используйте график для вычисления значения sin.
- sin θ = 0,8
- sin θ = 0,6
- sin θ = 0,6
- sin θ = 0,8
10. Вычислите значение tan π / 6 ?.
- tan π / 6? = 1/2
- tan π / 6? = √3 / 3
- tan π / 6 = √3
- tan π / 6 = 2
Ответы и пояснения
Функции интерпретации
1. A: Функция f назначает каждому элементу домена ровно один элемент диапазона.Следовательно, если x находится в области x ≥ 3, то значение f находится в диапазоне f (x) ≥ 0. Следовательно, правильный ответ — вариант A. С другой стороны, вариант B неверен, потому что f не определен для некоторых положительных значений x, например x = 1. Вариант C неверен, потому что диапазон f равен f (x) ≥ 0, а не f (3). Наконец, выбор D неверен, потому что значение f (3) определено, поскольку x = 3 находится в области определения f.
2. C: Чтобы оценить g (2), подставьте 2 для каждого вхождения x в уравнении g (x) = 3x + x + 5.Затем упростите результат, используя порядок операций:
г (2) = 3 (2) + (2) + 5
= 6 + 2 + 5
= 13
3. D: Площадь поверхности будет определяться как выражение S (4). Чтобы вычислить это значение, подставьте 4 вместо r в уравнении S (r) = 4πr 2 . Затем упростите результат, используя порядок операций:
S (4) = 4π (4) 2
= 4π — 16
= 64 π Следовательно, площадь поверхности сферы равна 64π.
Функции здания
4.B: Поскольку театр продаст 500 билетов, если будет стоить 10 долларов за билет, мы знаем, что t (10) = 500. Кроме того, поскольку цена билета влияет на продажу билетов, t должна быть линейной функцией, которая уменьшается на 50 каждый время d увеличивается на 1. Следовательно, d-член функции равен 50d, поэтому функция принимает вид t (d) = 50d + c. Чтобы найти значение c, подставьте 10 вместо d и 500 вместо t (10) и решите относительно c.
Чтобы найти значение c, подставьте 10 вместо d и 500 вместо t (10) и решите относительно c.
t (10) = 50 (10) + c
500 = 500 + c
1000 = c
Таким образом, функция t (d) = 50d + 1000.
5. D: Стоимость поездки на такси складывается из двух функций: постоянной функции для первой мили и линейной функции для оставшейся части поездки. Постоянная функция: c 1 (d) = 4,25, поскольку стоимость первой мили составляет 4,25 доллара. Для линейной части вычтите 1 из d, чтобы исключить первую милю, а затем умножьте результат на 0,70, так как это стоит 0,70 доллара за милю. Результат: c 2 (d) = 0,70 (d-1). Наконец, напишите функцию для общей стоимости поездки на такси, добавив две функции.
c (d) = c 1 (d) + c 2 (d)
= 4,25 + 0,70 (d — 1)
Линейные, квадратичные и экспоненциальные модели
6. B: Длина интервала — это разница между его конечными точками. Например, длина интервала [2, 4] равна 2. Чтобы определить, как данная функция растет на интервале длиной 3, определите значение f в каждой конечной точке этого интервала. Поскольку экспоненциальные функции растут на равные коэффициенты за равные интервалы, вы можете использовать любой интервал длиной 3, и ваш ответ будет применяться ко всем таким интервалам.Например, вы можете использовать интервал [0,3]:
Чтобы определить, как данная функция растет на интервале длиной 3, определите значение f в каждой конечной точке этого интервала. Поскольку экспоненциальные функции растут на равные коэффициенты за равные интервалы, вы можете использовать любой интервал длиной 3, и ваш ответ будет применяться ко всем таким интервалам.Например, вы можете использовать интервал [0,3]:
f (0) = 3-2 (0)
= 3 — 1
= 3
f (3) = 3-2 (3 )
= 3-8
= 24
Так как f (0) = 3 и f (3) = 24, функция увеличивается в раз на 24 / 3 = 8 за этот интервал .
7. C: Линейные функции растут на равные разности (а не на равные множители) на равных интервалах. Другими словами, если линейная функция c (f) преобразует температуру f из Фаренгейта в Цельсия, то интервалы равной длины (в f) приводят к одинаковому увеличению значения функции c (f).Из задачи мы знаем, что c (32) = 0 и c (68) = 20. Таким образом, мы можем заключить, что интервалы длиной 36 (например, интервал [32,68]) приводят к увеличению на 20, поскольку 20 0 = 20. Кроме того, поскольку длина [68,104] равна 36, функция c (f) также увеличивается на 20 на этом интервале. Используйте эту информацию для вычисления c (104).
Таким образом, мы можем заключить, что интервалы длиной 36 (например, интервал [32,68]) приводят к увеличению на 20, поскольку 20 0 = 20. Кроме того, поскольку длина [68,104] равна 36, функция c (f) также увеличивается на 20 на этом интервале. Используйте эту информацию для вычисления c (104).
c (104) = c (68) + 20 = 20 + 20 = 40
Следовательно, мы можем заключить, что 104 F эквивалентно 40 o C.
Тригонометрические функции
8.B: Дуга — это часть круга. На рисунке AB — это часть окружности, которая начинается в точке A и заканчивается в B. Обычно длина дуги s определяется как s = θR, где R — радиус окружности, содержащей дугу, а? — угол между радиусами, проведенными к концам дуги. В единичном круге длина дуги — это просто мера угла (в радианах), образуемого этим углом. Следовательно, длина дуги AB равна величине ∠ AOB, поэтому ее длина составляет π / 3 .
9. A: В единичном круге тригонометрические функции могут быть представлены с учетом углов, которые начинаются с положительной стороны оси x и измеряются против часовой стрелки вокруг круга. Для таких углов синус угла — это координата y точки, где сторона угла пересекает единичный круг. Поскольку одна сторона угла пересекает единичную окружность в точке (0,6, 0,8), значение sin θ; составляет 0,8.
Для таких углов синус угла — это координата y точки, где сторона угла пересекает единичный круг. Поскольку одна сторона угла пересекает единичную окружность в точке (0,6, 0,8), значение sin θ; составляет 0,8.
10. B: Угол π / 6 выражается в радианах.Чтобы преобразовать его в градусы, умножьте на 180 / π .
π / 6 — 180 / π = 30 o
Следовательно, tan π / 6 = tan 30 o . Чтобы вычислить это значение, нарисуйте треугольник 30-60-90, который представляет собой особый треугольник, пропорции которого вы, возможно, запомнили. Сделать гипотенузу длиной в одну единицу проще, хотя в этом нет необходимости, если пропорции те же.
Согласно SOH-CAH-TOA, касательная функция определяется как напротив / рядом с в прямоугольном треугольнике.Следовательно, значение tan 30 o равно 1/2 / √3 / 2 . Упростите эту дробь:
Упростите эту дробь:
tan π / 6 = 1/2 / √3 / 2
= 1 / √3
= √3 / 3
Альтернативно, помните, что tan θ = (sin θ) / (cos θ). Вы могли запомнить синус и косинус 30 ° как 1/2 и √3 / 2 соответственно. Это то же деление, что и выше, и дает тот же ответ.
Calculus II — Ratio Test
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-10: Проверка соотношения
В этом разделе мы собираемся взглянуть на тест, который мы можем использовать, чтобы увидеть, является ли ряд абсолютно сходящимся или нет.Напомним, что если ряд абсолютно сходится, мы также будем знать, что он сходится, и поэтому мы часто будем использовать его, чтобы просто определить сходимость ряда.
Прежде чем продолжить тест, давайте напомним факториалы. Этот тест будет особенно полезен для серий, содержащих факториалы (и мы увидим некоторые из них в приложениях), поэтому давайте удостоверимся, что мы можем с ними справиться, прежде чем мы столкнемся с ними в примере.
Если \ (n \) — такое целое число, что \ (n \ ge 0 \), то \ (n \) факториал определяется как,
\ [\ begin {align *} п! & = n \ left ({n — 1} \ right) \ left ({n — 2} \ right) \ cdots \ left (3 \ right) \ left (2 \ right) \ left (1 \ right) & \ hspace {0. 15 дюймов} & {\ mbox {if}} n \ ge 1 \\ 0! & = 1 & \ hspace {0,15 дюйма} & {\ mbox {по определению}} \ end {align *} \]
15 дюймов} & {\ mbox {if}} n \ ge 1 \\ 0! & = 1 & \ hspace {0,15 дюйма} & {\ mbox {по определению}} \ end {align *} \]Давайте быстро вычислим пару.
\ [\ begin {align *} & 1! = 1 \\ & 2! = 2 \ влево (1 \ вправо) = 2 \\ & 3! = 3 \ влево (2 \ вправо) \ влево (1 \ вправо) = 6 \\ & 4! = 4 \ влево (3 \ вправо) \ влево (2 \ вправо) \ влево (1 \ вправо) = 24 \\ & 5! = 5 \ left (4 \ right) \ left (3 \ right) \ left (2 \ right) \ left (1 \ right) = 120 \ end {align *} \]Обратите внимание, что в последнем вычислении мы можем переписать факториал несколькими способами.Например,
\ [\ begin {align *} 5! & = 5 \ underbrace {\ left (4 \ right) \ left (3 \ right) \ left (2 \ right) \ left (1 \ right)} _ {4!} = 5 \ cdot 4! \\ 5! & = 5 \ left (4 \ right) \ underbrace {\ left (3 \ right) \ left (2 \ right) \ left (1 \ right)} _ {3!} = 5 \ left (4 \ right) \ cdot 3! \ end {выровнять *} \] В общем, мы всегда можем «вычеркнуть» термины из факториала следующим образом.
Нам нужно будет делать это при случае, так что не забывайте об этом.
Также, имея дело с факториалами, мы должны быть очень осторожны с скобками. Например, \ (\ left ({2n} \ right)! \ Ne 2 \, \, n! \), Как мы можем видеть, выписывая каждый из следующих факториалов.
\ [\ begin {align *} \ left ({2n} \ right)! & = \ left ({2n} \ right) \ left ({2n — 1} \ right) \ left ({2n — 2} \ right) \ cdots \ left (3 \ right) \ left (2 \ right) \ влево (1 \ вправо) \\ 2 \, \, п! & = 2 \ left [{\ left (n \ right) \ left ({n — 1} \ right) \ left ({n — 2} \ right) \ cdots \ left (3 \ right) \ left (2 \ right) \ left (1 \ right)} \ right] \ end {align *} \] Мы снова встретим факториалы со скобками, поэтому не опускайте их. Часто это одна из наиболее распространенных ошибок, которые делают студенты, когда впервые сталкиваются с факториалами.
Часто это одна из наиболее распространенных ошибок, которые делают студенты, когда впервые сталкиваются с факториалами.
Хорошо, теперь мы готовы к тесту.
Тест соотношения
Предположим, у нас есть ряд \ (\ displaystyle \ sum {{a_n}} \). Определить,
\ [L = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left | {\ frac {{{a_ {n + 1}}}} {{{a_n}}}} \ right | \]Затем,
- , если \ (L <1 \), ряд абсолютно сходится (а значит, сходится).
- , если \ (L> 1 \) ряд расходится.
- , если \ (L = 1 \), ряд может быть расходящимся, условно сходящимся или абсолютно сходящимся.
Доказательство этого теста находится в конце раздела.
Обратите внимание, что в случае \ (L = 1 \) тест отношения практически бесполезен, и нам придется прибегнуть к другому тесту, чтобы определить сходимость ряда.
Также абсолютно необходимы полосы абсолютного значения в определении \ (L \). 2} \ left ({n + 2} \ right)}}} \ right | \\ & = \ frac {{10}} {{16}} \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {{n + 1}} {{n + 2}} \\ & = \ frac {{10}} {{16}}
2} \ left ({n + 2} \ right)}}} \ right | \\ & = \ frac {{10}} {{16}} \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {{n + 1}} {{n + 2}} \\ & = \ frac {{10}} {{16}}
Итак, \ (L <1 \) и так по коэффициенту Проверить серию сходится абсолютно и, следовательно, будет сходиться.
Как видно из предыдущего примера, в них обычно происходит много отмен. Убедитесь, что вы отменили это. Если вы не сделаете такую отмену, это может значительно затруднить ограничение.n}}} {{n!}}} \ right | = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {{\ left ({n + 1} \ right)!}} {{5 \, \, n!}} \]
Чтобы сделать это ограничение, нам нужно будет исключить факториалы. Мы просто не можем достичь предела с факториалами в нем. Чтобы исключить факториалы, мы вспомним из нашего обсуждения факториалов выше, что мы всегда можем «вырезать» термины из факториалов. Если мы сделаем это с числителем (в данном случае потому, что он больший из двух), мы получим
\ [L = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {{\ left ({n + 1} \ right) \, \, n!}} {{5 \, \, n !}} \], после чего мы можем отменить \ (n \)! для числителя знаменатель получить,
\ [L = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {{\ left ({n + 1} \ right)}} {5} = \ infty> 1 \] Итак, по Ratio Test эта серия расходится. n}}}} \ right | \\ & = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left | {\ frac {{9 \, n}} {{\ left ({- 2} \ right) \, \ left ({n + 1} \ right)}}} \ right | \\ & = \ frac {9 } {2} \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {n} {{n + 1}} \\ & = \ frac {9} {2}> 1 \ end {align * } \]
n}}}} \ right | \\ & = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left | {\ frac {{9 \, n}} {{\ left ({- 2} \ right) \, \ left ({n + 1} \ right)}}} \ right | \\ & = \ frac {9 } {2} \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {n} {{n + 1}} \\ & = \ frac {9} {2}> 1 \ end {align * } \]
Следовательно, по тесту на соотношение эта серия расходится.
В предыдущем примере столбцы абсолютных значений требовались для получения правильного ответа. Если бы мы не использовали их, мы получили бы \ (L = — \ frac {9} {2} <1 \), что означало бы сходящийся ряд!
Теперь давайте рассмотрим пару примеров, чтобы увидеть, что происходит, когда мы получаем \ (L = 1 \).\ infty {\ frac {{n + 2}} {{2n + 7}}} \] Показать решение
Вот предел.
\ [L = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left | {\ frac {{n + 3}} {{2 \ left ({n + 1} \ right) + 7}} \, \, \ frac {{2n + 7}} {{n + 2}}} \ право | = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {{\ left ({n + 3} \ right) \ left ({2n + 7} \ right)}} {{\ left ({ 2n + 9} \ right) \ left ({n + 2} \ right)}} = 1 \] Опять же, тест соотношения здесь нам ничего не говорит..png) Тем не менее, мы можем быстро использовать здесь тест дивергенции.Фактически, это, вероятно, должно было быть нашим первым выбором в любом случае.
Тем не менее, мы можем быстро использовать здесь тест дивергенции.Фактически, это, вероятно, должно было быть нашим первым выбором в любом случае.
По тесту дивергенции эта серия расходится.
Итак, как мы видели в предыдущих двух примерах, если мы получим \ (L = 1 \) из теста отношения, ряд может быть либо сходящимся, либо расходящимся.
Перед тем, как перейти к следующему разделу, мы должны отметить еще одну вещь, касающуюся теста отношения.Последняя серия была полиномом, деленным на полином, и мы увидели, что получили \ (L = 1 \) из теста отношения. Это всегда будет происходить с рациональным выражением, включающим только многочлены или многочлены под радикалами. Так что в будущем даже не стоит пробовать тест на соотношение для такого рода задач, поскольку теперь мы знаем, что получим \ (L = 1 \).
Кроме того, в предпоследнем примере мы видели пример чередующейся серии, в которой положительный член был рациональным выражением, включающим многочлены, и снова мы всегда будем получать \ (L = 1 \) в этих случаях.
Давайте закроем раздел доказательством теста соотношения.
Проверка соотношения
Во-первых, обратите внимание, что мы можем предположить без ограничения общности, что серия будет начинаться с \ (n = 1 \), как мы это делали для всех наших серийных тестовых доказательств.
Давайте начнем здесь доказательство с предположения, что \ (L <1 \), и нам нужно будет показать, что \ (\ sum {{a_n}} \) абсолютно сходится. Для этого сначала отметим, что, поскольку \ (L <1 \) существует некоторое число \ (r \) такое, что \ (L Теперь вспомните, что , и поскольку мы также выбрали \ (r \) такое, что \ (L Далее рассмотрим следующее: Итак, для \ (k = 1,2,3, \ ldots \) мы имеем \ (\ left | {{a_ {N + k}}} \ right | <{r ^ k} \ left | {{ a_N}} \ right | \). Затем нам нужно предположить, что \ (L> 1 \), и нам нужно будет показать, что \ (\ sum {{a_n}} \) расходится. Напоминая, что, и поскольку \ (L> 1 \) мы знаем, что должно быть некоторое \ (N \) такое, что если \ (n \ ge N \) у нас будет, Однако, если \ (\ left | {{a_ {n + 1}}} \ right |> \ left | {{a_n}} \ right | \) для всех \ (n \ ge N \), то мы знаем, что , , потому что условия становятся больше и гарантированно не будут отрицательными. Это, в свою очередь, означает, что Следовательно, по тесту дивергенции \ (\ sum {{a_n}} \) расходится. Для следующих упражнений определите, является ли каждое из следующих соотношений функцией. {(2,1), (3,2), (- 1,1), (0, −2)} {(2,1), (3,2), (- 1,1), (0 , −2)} Для следующих упражнений вычислите функцию f (x) = — 3×2 + 2xf (x) = — 3×2 + 2x
на данном входе. Покажите, что функция f (x) = — 2 (x − 1) 2 + 3f (x) = — 2 (x − 1) 2 + 3 не взаимно однозначна. Запишите область определения функции f (x) = 3 − xf (x) = 3 − x в интервальной записи. Дано f (x) = 2×2−5x, f (x) = 2×2−5x, найти f (a + 1) −f (1) .f (a + 1) −f (1). Постройте график функции f (x) = {x + 1 if − 2 Найдите среднюю скорость изменения функции f (x) = 3−2×2 + xf (x) = 3−2×2 + x, найдя f (b) −f (a) b − af (b) −f (a ) b − a. Для следующих упражнений используйте функции f (x) = 3−2×2 + x и g (x) = xf (x) = 3−2×2 + x и g (x) = x, чтобы найти составные функции. Выразите H (x) = 5×2−3x3H (x) = 5×2−3×3 как композицию двух функций, ff и g, g, где (f∘g) (x) = H (x). (F∘g) (х) = Н (х). Для следующих упражнений нарисуйте функции в виде графика, переведя, растягивая и / или сжимая функцию набора инструментов. f (x) = 1x + 2−1f (x) = 1x + 2−1 В следующих упражнениях определите, являются ли функции четными, нечетными или никакими. f (x) = — 5×2 + 9x6f (x) = — 5×2 + 9×6 f (x) = — 5×3 + 9x5f (x) = — 5×3 + 9×5 Постройте график функции абсолютного значения f (x) = — 2 | x − 1 | + 3. f (x) = — 2 | x − 1 | +3. Решите | 2x − 3 | = 17. | 2x − 3 | = 17. Решить — | 13x − 3 | ≥17.− | 13x − 3 | ≥17. Выразите решение в виде интервалов. Найдите обратную функцию для следующих упражнений. Для следующих упражнений используйте график gg, показанный на рисунке 1. Рисунок 1 На каких интервалах функция увеличивается? На каких интервалах функция убывает? Приблизительно локальный минимум функции. Выразите ответ в виде упорядоченной пары. Приблизительно локальный максимум функции. Выразите ответ в виде упорядоченной пары. Для следующих упражнений используйте график кусочной функции, показанный на рисунке 2. Рисунок 2 Напишите уравнение для кусочной функции. Для следующих упражнений используйте значения, перечисленные в таблице 1. Таблица 1 Решите уравнение F (x) = 5. F (x) = 5. График увеличивается или уменьшается в своей области? Является ли функция однозначно представленной на графике? Найдите F − 1 (15) .F − 1 (15). Дано f (x) = — 2x + 11, f (x) = — 2x + 11, найти f − 1 (x) .f − 1 (x). Эта статья знакомит с числовыми функциями и их использованием в Tableau. Он также демонстрирует, как создать числовое вычисление на примере. Числовые функции позволяют выполнять вычисления над значениями данных в ваших полях. Числовые функции можно использовать только с полями, содержащими числовые значения. Для получения дополнительной информации см. Типы данных. Например, у вас может быть поле, содержащее значения отклонения в вашем бюджете, под названием «Отклонение бюджета». Расчет может выглядеть примерно так: Следовательно, ABS (-7) = 7. АБС Возвращает абсолютное
значение данного числа. Примеры: Второй пример возвращает
абсолютное значение для всех чисел, содержащихся в поле ACOS Возвращает арккосинус числа.
данный номер.Результат выражается в радианах. Пример: ASIN Возвращает арксинус
данный номер. Пример: ATAN Возвращает арктангенс числа.
заданное число.Результат выражается в радианах. Пример: ATAN2 Возвращает
арктангенс двух заданных чисел (x и y). Пример: ПОТОЛОК Округляет число до ближайшего целого равного или большего значения. Пример: COS Возвращает косинус угла. Пример: СОТ Возвращает котангенс угла.Укажите угол в радианах. Пример: ГРАДУСОВ Преобразует заданное число
в радианах в градусы. Пример: РАЗД. ДЕЛ (целое1, целое2) Возвращает целую часть операции деления, в которой integer1 делится на integer2. Пример: Опыт Возврат e во власти
данного номера. Примеры: ЭТАЖ Округляет число до ближайшего целого равного или меньшего значения. Пример: HEXBINX Сопоставляет координаты x, y с координатой x ближайшего шестиугольного интервала. HEXBINX и HEXBINY — это функции биннинга и построения графиков для шестиугольных бинов. Шестиугольные ячейки — это эффективный и элегантный вариант для визуализации данных в плоскости x / y, такой как карта. Поскольку ячейки имеют шестиугольную форму, каждая ячейка приближается к кругу и минимизирует изменение расстояния от точки данных до центра ячейки. Это делает кластеризацию более точной и информативной. Пример: HEXBINY Сопоставляет координаты x, y с координатой y ближайшего шестиугольного интервала. Пример: LN Возвращает натуральный логарифм.
числа.Возвращает ЖУРНАЛ Возвращает логарифм. МАКС Возвращает максимум
из двух аргументов, которые должны быть одного типа.Возвращает Примеры: МИН Возвращает минимум
из двух аргументов, которые должны быть одного типа. Примеры: PI Возвращает числовую константу «пи»:
3. МОЩНОСТЬ Повышает число
до указанной мощности.2 = МОЩНОСТЬ (5,2) =
25 РАДИАНЫ Преобразует данное число
от градусов до радианов. Пример: КРУГЛЫЙ Число раундов
до указанного количества цифр.Аргумент Пример: Этот пример раундов
каждые Некоторые базы данных, такие как SQL Server, позволяют указывать отрицательную длину ЗНАК Возвращает знак числа:
Возможные возвращаемые значения: -1, если число отрицательное, 0, если
число равно нулю или 1, если число положительное. Пример: Если среднее значение поля прибыли отрицательное, то ЗНАК ГРЕХ Возвращает синус угла. Примеры: SQRT Возвращает квадратный корень из
число. Пример: ПЛОЩАДЬ Возвращает квадрат
количество. Пример: TAN Возвращает тангенс угла.Укажите угол в радианах. Пример: ЗН Возвращает выражение
если он не равен нулю, в противном случае возвращает ноль. Пример: Следуйте инструкциям ниже, чтобы узнать, как произвести числовое вычисление. В Tableau Desktop подключитесь к сохраненному источнику данных Sample - Superstore , который поставляется с Tableau. Перейдите к рабочему листу и выберите «Анализ»> «Создать вычисляемое поле». В открывшемся редакторе вычислений выполните следующие действия: Новое числовое вычисление отображается в разделе Показатели на панели Данные . Когда «Минимальные продажи» помещены в текст на карточке «Метки» на рабочем листе, его имя изменяется на AGG (Минимальные продажи), что указывает на то, что он не может быть агрегирован дальше, поскольку он уже агрегирован до самого низкого уровня детализации ( наименьшая продажная стоимость для всех записей). В этом примере показаны минимальные продажи по категории. Когда подкатегория отображается в представлении, отображаются минимальные продажи для каждой подкатегории. Функции в Tableau Табличные функции (по алфавиту) Табличные функции (по категориям) Форматирование вычислений в Таблице Цели: В этом руководстве определение функции является непрерывным.
в какой-то момент дается.Отмечается, что это определение требует проверки
из трех условий. Приведены некоторые примеры применения этого определения.
Приводится несколько теорем о непрерывных функциях. Некоторые примеры
функции, не являющиеся непрерывными в некоторой точке, получают соответствующие
определены разрывы. Проработав эти материалы, студент должен уметь Модули: должен существовать. и левый предел существуют, но L и M разные.
Затем мы говорим, что функция имеет разрыв скачка при x = a . Функции могут быть постоянными: увеличиваться при увеличении [latex] x [/ latex] или уменьшаться при увеличении [latex] x [/ latex]. Применить определения функций увеличения и уменьшения, чтобы определить, увеличивается ли функция, уменьшается или нет в заданном интервале В рамках исследования того, как изменяются функции, мы можем определить интервалы, в течение которых функция изменяется определенным образом. Мы говорим, что функция - это , увеличивающая в интервале, если значения функции увеличиваются по мере увеличения входных значений в пределах этого интервала.Точно так же функция - , уменьшающая на интервале, если значения функции уменьшаются по мере увеличения входных значений в течение этого интервала. В терминах линейной функции [латекс] f (x) = mx + b [/ latex], если [latex] m [/ latex] положительное значение, функция увеличивается, если [latex] m [/ latex] отрицательное значение, оно уменьшается, и если [latex] m [/ latex] равно нулю, функция является постоянной функцией. Средняя скорость изменения возрастающей функции положительна, а средняя скорость изменения убывающей функции отрицательна.3−12x [/ latex] увеличивается по оси [latex] x [/ latex] от отрицательной бесконечности до [latex] -2 [/ latex], а также от [latex] 2 [/ latex] до положительной бесконечности. Обозначение интервалов записывается как: [latex] (- ∞, −2) ∪ (2, ∞) [/ latex]. Функция убывает на интервале: [latex] (−2, 2) [/ latex]. В математике постоянная функция ion - это функция, значения которой не меняются, независимо от ввода в функцию. Функция является постоянной функцией, если [latex] f (x) = c [/ latex] для всех значений [latex] x [/ latex] и некоторой константы [latex] c [/ latex].График постоянной функции [latex] y (x) = c [/ latex] представляет собой горизонтальную линию в плоскости, проходящую через точку [latex] (0, c). [/ Latex] Константа Функция: График [latex] f (x) = 4 [/ latex] иллюстрирует постоянную функцию. Посмотрите на график слева направо по оси [latex] x [/ latex]; первая часть кривой убывает от бесконечности до [latex] x [/ latex] -значения [latex] -1 [/ latex], а затем кривая увеличивается.Кривая увеличивается на интервале от [латекс] -1 [/ латекс] до [латекс] 1 [/ латекс], а затем снова уменьшается до бесконечности. График функции возрастания и убывания: Для функции, изображенной выше, кривая убывает в интервалах: [latex] (- \ infty, -1) \ cup (1, \ infty) [/ latex] и увеличивается в интервале [латекс] (-1,1) [/ латекс]. Относительные минимумы и максимумы - это точки наименьшего и наибольшего значений в их окрестностях соответственно. Определить локальные и глобальные максимумы и минимумы заданной функции Минимумы и максимумы широко используются в задачах оптимизации и искусственного интеллекта, где, учитывая ряд ограничений на ресурсы, мы хотим наилучшим образом использовать наши ресурсы.Например, мы можем захотеть максимизировать нашу прибыль, учитывая предметы, которые мы можем производить, и наши доступные ресурсы. В области искусственного интеллекта мы можем захотеть выяснить, какой план действий наименее затратный для робота (т. Е. Кратчайший путь). В идеале вам нужно найти глобальные минимумы для планов. Однако, поскольку времени для определения правильного плана не существует, искусственный интеллект часто просто находит локальные минимумы. В математике максимум и минимум функции (известные вместе как экстремумы ) - это наибольшее и наименьшее значение, которое функция принимает в точке либо в данной окрестности (локальный или относительный экстремум), либо в пределах области функции в ее целостность (глобальный или абсолютный экстремум). Примеры относительных и глобальных экстремумов : Этот график содержит примеры всех четырех возможностей: относительного (локального) максимума и минимума, а также глобального максимума и минимума. В то время как некоторые функции увеличиваются (или уменьшаются) во всей своей области, многие другие нет. Значение входа, при котором функция изменяется от увеличения к уменьшению (по мере того, как мы идем слева направо, то есть по мере увеличения входной переменной), называется относительным максимумом. Если функция имеет более одного, мы говорим, что у нее есть локальные максимумы.Точно так же значение входа, при котором функция изменяется от уменьшения к увеличению по мере увеличения входной переменной, называется относительным минимумом. Форма множественного числа - локальные минимумы. Функция также не возрастает и не убывает в экстремумах. Обратите внимание, что мы должны говорить о локальных экстремумах, потому что любой данный локальный экстремум, как здесь определено, не обязательно является наивысшим максимумом или наименьшим минимумом во всей области определения функции. График минимума локального максимума: Для изображенной функции локальный максимум находится при значении [latex] y [/ latex], равном 16, и он возникает, когда [latex] x = -2 [/ latex]. Локальный минимум находится при значении [latex] y [/ latex], равном −16, и возникает, когда [latex] x = 2 [/ latex]. Функция имеет глобальных (или абсолютных) максимум точек в [latex] x [/ latex] *, если [latex] f (x ∗) ≥ f (x) [/ latex] для всех [latex] x [/латекс]. Точно так же функция имеет глобальных (или абсолютных) минимальных точек в [латекс] x [/ latex], если [latex] f (x ∗) ≤ f (x) [/ latex] для всех [latex] x [/латекс]. Глобальные экстремумы также являются относительными экстремумами. Функции не могут иметь экстремумов, таких как линия [latex] y = x [/ latex]. Эта линия увеличивается к бесконечности и убывает к отрицательной бесконечности и не имеет относительных экстремумов. График относительных максимумов и минимумов: Эта кривая показывает относительный минимум при [латексе] (- 1, -2) [/ латекс] и относительный максимум при [латексе] (1,2) [/ латексе]. График достигает локального максимума в [latex] (1,2) [/ latex], потому что это самая высокая точка в открытом интервале вокруг [latex] x = 1 [/ latex]. Локальный максимум - это координата y при [latex] x = 1 [/ latex], которая равна [latex] 2 [/ latex]. График достигает локального минимума в [latex] (- 1, -2) [/ latex], потому что это самая низкая точка в открытом интервале около [latex] x = -1 [/ latex]. Локальный минимум - это координата y [latex] x = -1 [/ latex], которая равна [latex] -2 [/ latex]. Глобальный график максимальных и минимальных значений: Для функции, изображенной выше, абсолютный максимум происходит дважды при [latex] y = 16 [/ latex], а абсолютный минимум - при [latex] (3, -10) [/ latex] . График достигает абсолютного максимума в двух местах, [latex] x = -2 [/ latex] и [latex] x = 2 [/ latex], потому что в этих местах граф достигает своей наивысшей точки в домене. функции. Абсолютный максимум - координата y , которая равна [латекс] 16 [/ латекс]. График достигает абсолютного минимума при [latex] x = 3 [/ latex], потому что это самая низкая точка в области графика функции. Абсолютный минимум - координата y , которая равна [латекс] -10 [/ латекс]. Кусочная функция определяется несколькими подфункциями, каждая из которых применяется к отдельным интервалам ввода Практика построения графиков кусочных функций и определение их областей и диапазонов В математике кусочная функция - это функция, в которой используется более одной формулы для определения выходных данных для разных частей домена. Кусочные функции определяются с использованием общей функциональной записи, где тело функции представляет собой массив функций и связанных интервалов. Мы используем кусочные функции для описания ситуаций, в которых правило или отношение изменяется, когда входное значение пересекает определенные «границы». [латекс] \ displaystyle \ left | x \ right | = \ left \ {\ begin {matrix} -x, & if \ x <0 \\ x, & if \ x \ geq0 \ end {matrix} \ right.[/ латекс] Для всех значений [latex] x [/ latex] меньше нуля, используется первая функция [latex] (- x) [/ latex], которая отменяет знак входного значения, делая выходные значения положительными. Допустим [латекс] y = f (x) [/ latex], где [latex] f (x) = | x | [/ latex], некоторые примеры упорядоченных пар [latex] (x, | x |) [/ latex ]: [латекс] \ displaystyle (-2,2) \\ (-1,1) \\ (-0,5,0,5) [/ латекс] Для всех значений [latex] x [/ latex], больших или равных нулю, используется вторая функция [latex] (x) [/ latex], делая выходные значения равными входным значениям.Вот некоторые примеры упорядоченных пар: [латекс] \ displaystyle (2,2) \\ (1,1) \\ (0,5,0,5) [/ латекс] После нахождения и построения некоторых упорядоченных пар для всех частей («частей») функции результатом является V-образная кривая функции абсолютного значения, представленной ниже. Кусочная функция: абсолютное значение: Кусочная функция, [латекс] \ left | x \ right | = \ left \ {\ begin {matrix} -x, & if \ x <0 \\ x, & if \ x \ geq0 \ end {matrix} \ right. [/ latex], является графиком функция абсолютного значения.2 [/ latex]: [латекс] \ Displaystyle f (-2) = 4 \\ f (-1) = 1 \\ f (0) = 0 \\ f (1) = 1 [/ латекс] Эти точки удовлетворяют первой части функции и образуют следующие упорядоченные пары: [латекс] \ displaystyle (-2,4) \\ (-1,1) \\ (0,0) \\ (1,1) [/ латекс] Для средней части (части), [latex] f (x) = 3 [/ latex] (постоянная функция) для области [latex] 1 [латекс] \ displaystyle (1.5,3) \\ (1.8, 3) \\ (2,3) [/ latex] Для последней части (кусок) [latex] f (x) = x [/ latex] для домена [latex] x> 2 [/ latex] несколько упорядоченных пар: [латекс] \ displaystyle (2.2, & if \ x \ leq 1 \\ 3, & if \ 1 Обратите внимание на открытые и темные кружки на графике. Это связано с конкретными доменами для каждой части функции. Открытый кружок в конце интервала означает, что конечная точка не входит в интервал, т.е. строго меньше или строго больше чем. Закрашенный кружок означает, что конечная точка включена (равно). Область определения функции начинается с отрицательной бесконечности и продолжается через каждую часть без пробелов до положительной бесконечности. Поскольку в [latex] x = 1 [/ latex] есть закрытая И открытая точка, функция там кусочно непрерывна. Когда [latex] x = 2 [/ latex], функция также кусочно-непрерывная. Следовательно, область определения этой функции - это набор всех действительных чисел, [latex] \ mathbb {R} [/ latex]. Диапазон начинается с самого низкого значения [latex] y [/ latex], [latex] y = 0 [/ latex] и продолжается до положительной бесконечности.2 [/ latex] включает эти значения. Следовательно, диапазон кусочной функции - это также набор всех действительных чисел, больших или равных [latex] 0 [/ latex], или всех неотрицательных значений: [latex] y \ geq 0 [/ latex]. Функция взаимно однозначного соответствия, также называемая инъективной функцией, никогда не отображает отдельные элементы своего домена в один и тот же элемент его кодомена. Используйте свойства взаимно-однозначных функций, чтобы определить, является ли данная функция взаимно-однозначной Функция взаимно однозначного соответствия , также называемая инъективной функцией, никогда не отображает отдельные элементы своей области в один и тот же элемент ее совместной области. Другими словами, каждый элемент диапазона функции соответствует ровно одному элементу ее домена. Иногда инъективная функция от [latex] X [/ latex] до [latex] Y [/ latex] обозначается [latex] f: X \ mapsto Y [/ latex] с помощью стрелки с заостренным хвостом. {2} [/ latex] (без ограничений домена) взаимно однозначной? Один из способов проверить, является ли функция взаимно однозначной, - это построить график функции и выполнить тест горизонтальной линии.2 [/ latex] не проходит проверку горизонтальной линии и, следовательно, не является однозначной функцией. Если горизонтальная линия может проходить через две или более точек на графике функции, то функция не взаимно однозначна. Другой способ определить, является ли функция взаимно однозначной - составить таблицу значений и проверить, соответствует ли каждый элемент диапазона ровно одному элементу домена. Список упорядоченных пар для функции: [латекс] \ displaystyle (-2,4) \\ (-1,1) \\ (0,0) \\ (1,1) \\ (2,4) [/ латекс] Упорядоченные пары [latex] (- 2,4) [/ latex] и [latex] (2,4) [/ latex] не проходят определение «один к одному», потому что элемент [latex] 4 [/ латекс] диапазона соответствует [латексу] -2 [/ латексу] и [латексу] 2 [/ латексу].Каждый уникальный вход должен иметь уникальный выход, поэтому функция не может быть взаимно однозначной. Также обратите внимание, что эти две упорядоченные пары образуют горизонтальную линию; что также означает, что функция не является взаимно однозначной, как было сказано ранее. Это функция абсолютного значения, которая изображена на графике ниже. Обратите внимание, что он не проходит тест горизонтальной линии. Поскольку каждый уникальный вход не имеет уникального выхода, эта функция не может быть взаимно однозначной. График абсолютных значений: График функции, [латекс] f (x) = \ left | x \ right | [/ latex], не проходит проверку горизонтальной линии и, следовательно, не является однозначной функцией. Два объекта обладают симметрией, если один объект может быть получен из другого преобразованием. Определить, демонстрирует ли данное отношение некоторую форму симметрии В математике объект, такой как форма или функция, обладает симметрией, если он может быть преобразован каким-либо образом, сохраняющим свойства математического объекта.В геометрии геометрическая форма или объект являются симметричными, если их можно разделить на две или более идентичных части, которые расположены организованным образом. S означает, что объект является симметричным, если есть преобразование, которое перемещает отдельные части объекта, но не Не меняю общую форму. Для функций функция демонстрирует симметрию, если каждая точка функции может быть изменена в соответствии с математическим правилом без изменения общей функции. Определение симметрии может включать построение графика функции или ее алгебраическое вычисление. Функции и отношения могут быть симметричными относительно точки, линии или оси. Они также могут иметь симметрию после отражения. Чтобы определить, имеет ли отношение симметрию, постройте график отношения или функции и посмотрите, является ли исходная кривая отражением самой себя над точкой, линией или осью. На изображении ниже показаны примеры отражения функции по оси [latex] x [/ latex] (вертикальное отражение) и по оси [latex] y [/ latex] (горизонтальное отражение). Отражение : функция может быть отражена по оси [latex] x [/ latex] или [latex] y [/ latex]. Если функция выглядит так же после отражения, функция симметрична по этой оси. На следующем графике ниже квадратичные функции обладают симметрией относительно линии, называемой осью симметрии. Ось делит U-образную кривую на две части кривой, которые отражаются над осью симметрии. 2 + 4x + 3 [/ latex] показывает ось симметрии относительно линии [latex] x = -2 [/ latex].Кривая разделена на две эквивалентные [латексные] 2 [/ латексные] половины. Обратите внимание, что точки пересечения [latex] x [/ latex] являются отраженными точками над осью симметрии и находятся на одинаковом расстоянии от оси. Симметрия относительно точки: Приведенный выше график имеет симметрию, поскольку помеченные точки отражаются относительно начала координат. График имеет симметрию относительно начала координат или точки [latex] (0,0) [/ latex].Указанные точки [латекс] (1,3) [/ латекс] и [латекс] (- 1, -3) [/ латекс] отражаются поперек начала координат. Функции, которые имеют аддитивную инверсию, могут быть классифицированы как нечетные или четные в зависимости от их свойств симметрии. Определить, является ли функция четной, нечетной или ни одной из них Функции могут быть классифицированы как «нечетные» или «четные» в зависимости от их состава. Эти метки коррелируют со свойствами симметрии функции. Термины «нечетный» и «четный» могут применяться только к ограниченному набору функций. Чтобы функция была классифицирована как одна или другая, она должна иметь аддитивную обратную функцию. Следовательно, он должен иметь номер, который при добавлении к нему равен [latex] 0 [/ latex].3 \ right | [/ latex] имеет показатель степени, который является нечетным целым числом, [latex] 3 [/ latex], но также является четной функцией. Как мы можем проверить, четная или нечетная функция? Давайте посмотрим на их характеристики. Четные функции алгебраически определяются как функции, в которых для всех значений [latex] x [/ latex] выполняется следующее соотношение: [латекс] \ displaystyle f (x) = f (-x) [/ latex] Чтобы проверить, является ли функция четной, любое выбранное значение [latex] x [/ latex] должно давать такое же выходное значение при подстановке в функцию как [latex] -x [/ latex].4 + 2x [/ latex], изображенный выше, не является даже потому, что график не является симметричным относительно оси [latex] y [/ latex]. Например, точка [latex] (- 1, -1) [/ latex] не отражается на точке [latex] (1, -1) [/ latex]. Мы можем подтвердить это графически: функции, удовлетворяющие требованию четности, симметричны относительно оси [latex] y [/ latex]. Следовательно, для каждой точки [latex] (x, y) [/ latex] на графике соответствующая точка [latex] (- x, y) [/ latex] или наоборот также находится на графике. Нечетные функции алгебраически определяются как функции, в которых для всех значений [latex] x [/ latex] выполняется следующее соотношение: [латекс] \ displaystyle -f (x) = f (-x) [/ latex] Это отношение также может быть выражено как: [латекс] \ displaystyle f (x) + f (-x) = 0 [/ латекс] Чтобы проверить, является ли функция нечетной, отрицание функции (обязательно отрицание всех членов функции) должно привести к тому же результату, что и замена значения [latex] -x [/ latex]. 3-9x [/ latex] нечетная, поскольку график симметричен относительно начала координат.Также можно проверить, что любая точка симметрична относительно начала координат: например, [latex] (- 1,8) [/ latex] дает [latex] (1, -8) [/ latex]? Да, эти две точки симметричны относительно начала координат. Все представленные продукты и услуги выбраны WikiJob независимо друг от друга. Когда вы совершаете покупку по ссылкам на этой странице, мы можем получать комиссию. Числовые тесты мышления используются работодателями для измерения вашей способности выполнять задачи, связанные с числами, и являются одним из основных разделов любого психометрического оценочного теста. Вопросы варьируются от простых арифметических операций, таких как сложение и вычитание, до более сложных вопросов, где вам нужно интерпретировать числовую информацию, представленную в виде таблиц, диаграмм и графиков. Тесты на числовые способности популярны среди работодателей, потому что многие рабочие места требуют от вас работы с числами хотя бы часть времени. Если вы подаете заявление о приеме на работу, которая предполагает повседневную работу с цифрами, работодатель будет рассматривать ваши численные способности как ценный показатель вашей эффективности на работе. В тестах численного мышления вы обычно будете иметь дело с графиками, таблицами, числовыми последовательностями и текстом . Они будут содержать необработанные данные, необходимые для ответа на письменный вопрос, но вам часто придется выполнить несколько операций с этими данными, чтобы получить ответ. Они также могут включать вопросы, в которых математическая задача сформулирована словами, и ваша задача - применить необходимую логику для поиска решения. На экзаменах для выпускников и руководителей часто ожидается, что вы ответите на вопросов интерпретации данных .Они имеют форму диаграмм и графиков, которые вам необходимо понять, а затем интерпретировать. Другими словами, вам нужно решить, как получить ответ, а не какие вычисления применить. Чтобы помочь вам понять, что включает в себя тест на числовые способности, вот практический тест, с которого вы начнете: Пройдите еще один тест Есть два типа числовых вопросов, которые регулярно появляются в психометрических тестах: Вопросы о скорости - При неограниченном времени большинство людей, проходящих эти тесты, могут успешно ответить на все вопросы.Однако время, отведенное на выполнение теста, настолько короткое, что даже от самого способного человека не ожидается его завершения. Это означает, что результат зависит от количества правильных ответов, сделанных за относительно короткое время. Power test - содержит вопросы разной сложности; ни от кого не ожидается, что он получит правильные ответы на все вопросы, даже при наличии неограниченного времени. На практике для испытаний мощности устанавливается определенное, но достаточное время. Некоторые более редкие формы числовых тестов не имеют ограничений по времени и / или не имеют отрицательной оценки (неправильные ответы вычитаются из вашей общей оценки, а не просто 0). В зависимости от провайдера, тесты числового мышления можно сдать дома или в центре оценки; иногда и то, и другое - многие организации используют метод борьбы с мошенничеством, который требует от кандидатов лично пройти еще один тест в центре оценки. Если домашний счет и очный счет сильно различаются, то начинают звонить тревожные звонки. Продолжительность любого теста на числовые способности, который вас попросят пройти, будет зависеть от нескольких факторов, включая количество других тестов, которые вы будете проходить в день.Однако большинство тестов длятся от 30 до 40 минут и содержат от 30 до 40 вопросов. Вопросы, используемые в тестах на числовые оценки, можно разделить на четыре основных типа: Числовые вычисления - Эти вопросы включают основные принципы арифметики, включая сложение, вычитание, умножение, деление, проценты, отношения, дроби и десятичные дроби. Чтобы получить высокие баллы по этим вопросам, вам необходимо быстро и точно рассчитать без использования калькулятора. Числовая оценка - Числовая оценка важна во многих технических работах, когда вам нужно быстро и точно оценить количество материалов и т. Д. Эти вопросы требуют от вас быстрой оценки ответов на простые числовые вопросы. Вы не должны пытаться вычислить ответы; это займет слишком много времени и помешает вам ответить на достаточно вопросов, чтобы получить хорошую оценку. Числовое мышление - Эти вопросы проверяют вашу способность к рассуждению, а не способность выполнять вычисления.Другими словами, вам нужно решить, как получить ответ, а не просто сказать, какие вычисления применить. Они всегда включают некоторые вопросы числовой серии, где вам нужно выяснить, какое число или числа отсутствуют в этой серии. Они также включают текстовые вопросы, в которых математическая задача формулируется словами, и ваша задача - применить необходимую логику, чтобы найти ответ. Интерпретация данных - Большинство управленческих и надзорных работ требуют от вас интерпретации данных, представленных в диаграммах, таблицах и графиках, для принятия повседневных решений.В этих тестах обычно используются круговые диаграммы, линейные графики, диаграммы рассеяния и таблицы данных, которые необходимо интерпретировать, чтобы ответить на вопросы. Более сложные вопросы могут отображать данные в одном формате (например, в таблице), а часть этих данных - в другом формате (например, в виде круговой диаграммы). Чтобы ответить на вопросы, вы должны иметь возможность логически связать эти два элемента. Эта статья была разработана таким образом, чтобы вам было легче практиковать те области, в которых вы чувствуете себя наиболее слабыми, что дает вам наибольшую пользу в кратчайшие сроки.Таким образом, каждый тест содержит больше вопросов каждого типа, чем вы получили бы в реальном тесте. Это также гарантирует, что вы получите максимальное внимание к как можно большему разнообразию стилей и типов вопросов. Важно помнить, что настоящий тест будет содержать вопросы разных типов. Психометрические тесты имеют долгую историю исследований. Сильная корреляция между результатами этих тестов и производительностью на рабочем месте привела к тому, что компании во всем мире инвестируют в них как в важную часть процесса найма. Многим работодателям необходимо знать, что у вас есть прочный фундамент из базовых математических навыков . Эти навыки (расчет процентов, соотношений, дробей, прибыли, выручки и т. Д.) Имеют решающее значение практически в любой сфере бизнеса. Работодатели используют тесты на числовые способности главным образом по следующим причинам: По этим и другим причинам многие работодатели даже говорят, что они ценят эти тесты на пригодность больше, чем университетские степени. Рекрутеры компании знают, что их новые сотрудники не обязательно обладают хорошими отраслевыми или специальными знаниями. Вот что приходит с опытом. Ключевым моментом для них является отбор кандидатов, у которых есть основы, позволяющие им адаптироваться к окружающей среде и приобретать необходимые им навыки и знания. Компании в первую очередь заинтересованы в вашем понимании основ. Они также следят за тем, как быстро вы сможете работать под давлением. Такой вид арифметики должен быть таким, чтобы вы могли делать это быстро и точно, когда это необходимо. Тесты на числовые способности часто являются самым сложным типом проверки способностей для многих кандидатов. Это происходит по нескольким ключевым причинам, которые мы опишем здесь: В среднем у вас обычно есть от 45 секунд до 2 минут, чтобы ответить на каждый вопрос. В нижней части шкалы это действительно сложно. Есть много испытаний, в которых дойти до конца - само по себе подвиг. Обладать способностями и уверенностью в том, чтобы иметь возможность интерпретировать данные, решать, что нужно сделать, а затем быстро выполнять эти операции, является сложной задачей, поэтому практика очень важна.Мы рекомендуем пакеты числовой практики от JobTestPrep . Подготовка к тестам на числовые возможности с помощью JobTestPrep На многие вопросы нет однозначного ответа. Например, вам не нужно просто умножить два числа, чтобы найти решение. Это навык, о котором часто забывают, который приходит только на практике. Вы можете быть гением в фактическом сложении, умножении, процентах и т. Д., Но вы все равно останетесь позади, если не сможете быстро и точно определить, какие операции вам нужно выполнить и в каком порядке. Иногда математические навыки сами по себе могут быть трудными, особенно если математика не является вашей самой сильной стороной. Если учесть две предыдущие трудности - ограничение по времени и понимание того, как ответить на вопрос, - давление ситуации может очень легко помешать хорошей работе. Не все численные тесты одинаковы. Хотя все они стремятся проверить одинаковый набор навыков, у каждого создателя тестов будут свои собственные идеи о том, как лучше всего это сделать. В рамках подготовки, если вы узнаете, какого поставщика услуг тестирования использует компания, к которой вы обращаетесь, вы сможете еще больше сфокусировать свою практику. Основные поставщики: Двумя основными поставщиками тестов являются SHL и Pearson , одни из старейших компаний в отрасли. Их тесты, как правило, устанавливают отраслевой стандарт, и многие поставщики тестов следуют их примеру и вносят лишь относительно незначительные изменения в формат. Если вы сомневаетесь, вы не ошибетесь, практикуя их тесты. С учетом сказанного, некоторые провайдеры действительно встряхивают. Например, в Talent Q есть инновационный тест, который адаптируется к вашей работе. Ваши правильные и неправильные ответы помогают проинформировать тест о вашем уровне навыков и соответственно корректировать вопросы. Это позволяет сделать тест гибким и коротким. cut-e также выделяется из общей массы. С очень короткими тестами, продолжительностью от 5 до 12 минут, его вопросы сосредоточены на более абстрактных математических элементах, а не на графиках и диаграммах.Это может сбить с толку кандидатов, которые привыкли работать с более практичными вопросами. Какого поставщика использует компания, иногда зависит от конкретной роли и отдела. Конечно, вы всегда должны помнить, что компании могут в любой момент сменить поставщика. Всегда следите за тем, чтобы вы развили основные навыки, необходимые для выполнения любого теста числового мышления. Проверяются именно те навыки, а не конкретные знания о конкретном тесте. Большинство работодателей также будет стремиться к тому, чтобы думать на ногах и адаптироваться к изменениям. Численные вычисления вопросов включают математические термины и методы, а также основные принципы арифметики, такие как: Этот тип теста можно отнести к категории теста скорости и используется для определения вашей базовой математической грамотности. Вам не разрешат пользоваться калькулятором. Если вы очень плохо разбираетесь в арифметике, попробуйте заново выучить таблицу умножения до 12 и потренироваться в умножении, делении и вычислении процентов.Практика может улучшить ваши результаты по всем типам тестов, поэтому попробуйте как можно больше примеров. Эти вопросы непосредственно применимы ко многим административным и канцелярским должностям, но также могут появляться в качестве компонента выпускных и управленческих тестов. Скорость, с которой вы можете ответить на эти вопросы, является критическим критерием, так как большинство людей может получить очень высокий балл, если у вас будет неограниченное время для ответа. Таким образом, вы можете рассчитывать на 25–35 вопросов за 20–30 минут. Вы можете значительно улучшить свои результаты, тренируясь в мысленной арифметике, пока вы не станете одновременно быстрым и уверенным. Ваш результат в простых тестах на скорость будет во многом зависеть от вашей способности быстро и точно складывать, вычитать, умножать и делить. В типичном тесте, состоящем из 60 смешанных вопросов, вам может потребоваться выполнить более 200 отдельных операций умножения и деления. Важно знать свои таблицы умножения (до десятикратной таблицы умножения) и уметь мгновенно ответить на любую операцию. Ключевое слово здесь - «мгновенный». Большинство людей могут дать мгновенные ответы примерно на 80% этих операций и потратить несколько секунд на то, чтобы подумать об остальном. Эти дополнительные несколько секунд складываются в течение теста, когда ответ на один вопрос может включать три или четыре таких простых действия. Если вы побрите несколько секунд здесь и там, у вас будет время ответить на четыре или пять дополнительных вопросов в типичном тесте - и это будет иметь большое значение для вашего окончательного результата. У вас вряд ли возникнут какие-либо проблемы с таблицами умножения на 1, 2, 5 и 10, поэтому вы, вероятно, можете их игнорировать. Возьмите лист бумаги формата A4 и перечислите числа 3, 4, 6, 7, 8, 9 в столбце в левой части страницы и вдоль верхнего поля, как показано: Работа с слева направо и сверху вниз по сетке, вписывая каждый ответ. Если вы остановитесь хотя бы на секунду, чтобы обдумать ответ, поставьте прочерк и продолжайте. Не переставай думать. Либо напишите ответ сразу, либо поставьте прочерк. Вы должны выполнить это упражнение менее чем за 40 секунд. В результате обычно получается лист с несколькими черточками, правильный ответ на который приходит в голову не сразу. Вам нужно будет потратить немного времени на освежение памяти для этих операций - делайте это в течение нескольких дней, тратя пару минут за раз, пока они не станут мгновенными. Когда вы будете полностью довольны, попробуйте снова сетку - вы сможете правильно заполнить ее менее чем за 40 секунд. Правила выполнения основных арифметических операций с целыми числами (целыми числами) должны быть вам знакомы, хотя вы можете обнаружить, что некоторые вещи вы забыли. Например: Умножение или деление двух целых чисел с разными знаками дает отрицательный результат; например, 5 x –3 = –15 Умножение или деление двух отрицательных целых чисел дает положительный результат; например, –3 x –3 = 9 Есть несколько советов и приемов, которые помогут вам с мысленной арифметикой, которые стоит потратить время на их практику.Все они немного повлияют на вашу общую скорость; если вы сможете освоить несколько из них, и все они просты, то совокупный эффект позволит вам ответить на еще несколько вопросов в отведенное время. Как вы уже знаете, эти несколько дополнительных оценок могут иметь большое значение в том, как вас будут воспринимать как кандидата на работу. Рассмотрим сумму: a - b . Есть три подхода к этому виду расчета: Когда все цифры «b» меньше, чем цифры «a», расчет может производиться цифра за цифрой. Например: Оцените 862 - 41, просто вычтя 1 из 2 в разряде единиц и 4 из 6 в разряде десятков. Это равно 821. Если описанная выше ситуация не применима, проблему иногда можно изменить: Если только одна цифра в «b» больше, чем соответствующая цифра в «a», уменьшите неправильную цифру в «b» до тех пор, пока она не станет равной соответствующей цифре в «a». Затем вычтите еще раз, что величина «b» была уменьшена на «a». Например: Чтобы вычислить 872–92, превратите задачу в 872–72 = 800. Затем вычтите 20 из 800 = 780. Если более одной цифры в «b» больше, чем соответствующая цифра в «a», может быть легче найти, сколько нужно добавить к «b», чтобы получить «a». Например: Чтобы вычислить 8192–732, мы можем прибавить 8 к 732 (в результате получится 740), затем прибавить 60 (чтобы получить 800), затем 200 (для 1000). Затем прибавьте 192, чтобы получить 1192, и, наконец, прибавьте 7000, чтобы получить 8192.Наш окончательный ответ - 7460. Этот метод можно использовать для вычитания чисел слева направо, и после небольшой практики он может значительно ускорить мысленное вычитание. Одно место обрабатывается слева направо. Пример: 4075 Тысяч: 4 - 1 = 3, посмотрите направо, 075 <844, нужно взять взаймы. 3 - 1 = 2, скажем, «Две тысячи» Сотни: 0-8 = отрицательные числа здесь недопустимы 10-8 = 2 75> 44, поэтому не нужно брать в долг, скажем, «двести» Десятки: 7-4 = 3 5> 4, поэтому не нужно брать в долг, скажем, «тридцать» Единицы: 5–4 = 1, скажем, «Один» Это дает 2231 в качестве ответа. Расчет продуктов: a x b В этом случае продукт можно рассчитать по цифрам. Это не совсем так, потому что остаток возможен. Если есть остаток, он всегда равен 1, что значительно упрощает ситуацию. Все-таки произведение надо рассчитывать справа налево: 2 x 167 - это 4 с остатком, затем 2 (то есть 3) с другим остатком, затем 2 (то есть 3). Таким образом, получаем 334. Чтобы умножить число на 5, умножьте это число на 10, а затем разделите на 2. Следующий алгоритм является быстрым способом получить этот результат: Сначала добавьте ноль справа от нужного числа Затем, начиная с крайней левой цифры, разделите на 2 и добавьте каждый результат в соответствующем порядке, чтобы получить новое число Дроби ответов следует округлить до ближайшего целого числа Например, если вы намеревались умножить 176 на 5, вы должны сначала добавить ноль к 176, чтобы получить 1760. Затем разделите 1 на 2, чтобы получить 0,5, округленное в меньшую сторону до 0 Разделите 7 на 2, чтобы получить 3,5, округляем до 3 Разделите 6 на 2, чтобы получить 3 0 делить на 2 просто 0 Получается номер 0330 Последний шаг включает прибавление 5 к числу, которое следует за любой отдельной цифрой в этом новом числе, которое было нечетным до деления на два; это лучше понять на примере: В исходном номере 176 первое место - 1, что является нечетным.Поэтому мы добавляем 5 к цифре после первого разряда в нашем недавно построенном числе (0330), что составляет 3: 3 + 5 = 8 Цифра на втором месте 176, 7 тоже нечетная. Следовательно, число-место после соответствующей цифры в построенном числе (0830) также увеличивается на 5. 3 + 5 = 8 Число на третьем месте 176, 6 четное, поэтому окончательное число 0 в нашем ответе не изменилось. Последний ответ - 0880. Крайний левый ноль можно опустить, оставив 880. Итак, 176 x 5 = 880 Поскольку 9 = 10 - 1, для умножения на 9 умножьте число на 10, а затем вычтите исходное число из этого результата. Например, 9 x 27 = 270 - 27 = 243 Чтобы легко перемножить двузначные числа от 11 до 19, вы можете использовать этот простой метод сетки: Рассмотрим расчет 1a x 1b xx = a + b Это можно представить как: Так, например, расчет 17 x 16 может быть визуализирован как: Добавление столбцов в сетку дает ответ 272, например: Чтобы легко перемножить любые двузначные числа вместе, простой алгоритм выглядит следующим образом: ab x cd 100 x (a x c) + 10 x (b x c) + 10 x (a x d) + b x d Например, 23 x 47 можно уменьшить до: 800 (что составляет 2 x 4 x 100) Сложение дает 1081. Вам нужно будет несколько раз попрактиковаться в этих методах, чтобы стать профессионалом, но они могут значительно сэкономить время, отвечая на вопросы о числовых вычислениях и оценках. Дробь - это число в форме a / b, где «a» и «b» - целые числа. «a» называется числителем дроби, а «b» - знаменателем. Например, 3/5 - это дробь, числителем которой является «3», а знаменателем - «5». Это можно представить как 3, разделенные на 5. Если числитель и знаменатель дроби умножить на одно и то же целое число, полученная дробь будет эквивалентной. Если числитель и знаменатель дроби умножить на 5, получится 15/25. Следовательно, 3/5 = 15/25 Чтобы сложить две дроби с одинаковым знаменателем, вы просто складываете числители и оставляете знаменатель неизменным. 3/5 + 1/5 = 4/5 Если знаменатели не совпадают, вам нужно сделать их такими же, прежде чем выполнять сложение.Для этого нужно получить наименьший общий знаменатель . В математике наименьший общий знаменатель (сокращенно LCD) - это наименьшее общее кратное знаменателей набора дробей. То есть это наименьшее (ненулевое) число, кратное знаменателям. Например, ЖК-дисплей 1/2 и 1/4 равен 4, потому что наименьшее общее кратное 2 и 4 равно 4. Помните, знаменатель говорит о том, на что делится числитель. Любое число, разделенное на 4, будет меньше, чем если бы оно было разделено на 2.Следовательно, 4 - это наименьший общий знаменатель. Аналогично, ЖК-дисплей 1/2 и 1/3 равен 6, потому что наименьшее (ненулевое) число, кратное 2 и 3, равно 6. Использование ЖК-дисплея (или любого кратного ему числа) в качестве знаменателя позволяет складывать, вычитать или сравнивать дроби. Например: 1/2 + 1/4 = 2/4 + 1/4 = 3/4 1/2 - 1/3 = 3/6 - 2/6 = 1/6 1/3 <2/5 с 15.05 <15.06 Процесс вычитания дробей, по сути, такой же, как и процесс их сложения - найдите общий знаменатель и замените каждую дробь на эквивалентную дробь с выбранным общим знаменателем. Получившаяся дробь будет иметь этот знаменатель, а ее числитель будет результатом вычитания числителей исходных дробей. Например: 2/3 - 1/2 = 4/6 - 3/6 = 1/6 Чтобы умножить две дроби, умножьте два числителя и умножьте два знаменателя (знаменатели не обязательно должны быть одинаковыми). Например: 3/4 x 1/2 = 3/8 Если у вас есть четверть торта и вы умножите ее на три, то в итоге вы получите три четверти.Мы можем записать это численно следующим образом: 3 x 1/4 = 3/4 В качестве другого примера предположим, что пять человек работают по три часа из семи часов в день (т. Е. Три седьмых рабочего дня). В общей сложности они будут работать 15 часов (5 х 3 часа каждый) или 15 седьмых дней в день. Поскольку семь седьмых дня - это целый день, 14 седьмых - это два дня. Тогда в общей сложности они проработают два дня и одну седьмую дня. Численно: 5 x 3/7 = 15/7 = 2 1/7 Снова рассмотрим пример торта; если у вас есть четверть торта, и вы умножите количество на треть, вы получите двенадцатую часть торта. Другими словами, треть четверти (или треть четверти) равна двенадцатой. Это потому, что каждая четверть делится на три части, а четыре четверти умноженные на три составляют 12 частей (или двенадцатых). Мы можем записать это численно следующим образом: 1/3 x 1/4 = 1/12 Когда дроби умножаются на дроби, просто умножьте два числителя (верхние числа) и умножьте два знаменателя (нижние числа). Например: Чтобы разделить одну дробь на другую, инвертируйте дробь, на которую вы делите, и действуйте, как при умножении. Например: 3/4 ÷ 1/2 = 3/4 x 2/1 = 6/4 = 1½ В приведенном выше примере такое выражение, как 1½, называется смешанным числом . Это означает 1 плюс 1/2. Например, у вас может быть два целых торта и три четверти другого торта. Целая и дробная части числа пишутся рядом друг с другом: 2 + 3/4 = 2¾ Когда вас просят произвести вычисления со смешанными числами, вам может быть проще преобразовать смешанное число в неправильную дробь. Неправильная дробь можно рассматривать как еще один способ записать смешанное число; В приведенном выше примере «2¾» представьте, что два целых торта разделены на четыре части. Каждый торт составляет 4/4 от общей суммы, поэтому 4/4 + 4/4 + 3/4 = 11/4 - это еще один способ написать 2¾. Смешанное число можно преобразовать в неправильную дробь за три шага: Аналогичным образом неправильную дробь можно преобразовать в смешанное число: Например, если вас попросят решить следующее: 7–2 Преобразуем 7 в неправильную дробь: 57/8 Преобразовать 2 ¾ в неправильную дробь: 11/4 Определите ЖК-дисплей: который равен 8 Преобразовать: 11/4 в 22/8 Вычислить: 57/8 - 22/8 = 35/8 Преобразовать: 35/8 в 4⅜ Следовательно, 7⅛ - 2¾ = 4⅜ Все числа можно выразить в десятичной форме с помощью основания 10.Используется десятичная точка, и значение разряда для каждой цифры соответствует степени 10, в зависимости от ее положения относительно десятичной точки. Например, число 62,437 состоит из 5 цифр, где: ‘6’ - цифра десятков; значение позиции для «6» - 10 «3» - это «сотые» цифры; значение разряда для «3» - 1/100 «7» - это «тысячные доли»; значение позиции для "7" составляет 1/1000 Следовательно, 82.537 - это краткое написание 60 + 2 + 0,4 + 0,03 + 0,007 Эта система счисления имеет значение для основных операций. Для сложения и вычитания вы всегда должны помнить о выравнивании десятичных знаков: Например: 126,5 + 68,231 = 194,731 можно записать с выровненными десятичными точками как: Для умножения десятичных знаков нет необходимости выравнивать десятичные точки. Чтобы определить правильную позицию десятичной точки, вы просто добавляете количество цифр справа от десятичных знаков умножаемых десятичных знаков. Например: 15,381 x 0,14 = 2,15334 В этом примере у первого числа три десятичных знака, у второго числа два десятичных знака, и, следовательно, ответ должен состоять из пяти десятичных знаков. Чтобы разделить десятичную дробь на другую, например 62,744 ÷ 1,24, сначала переместите десятичную точку в делителе вправо, пока делитель не станет целым числом, затем переместите десятичную точку в делимом на такое же количество разрядов. Это дает 6274.4 ÷ 124 Эта процедура определяет правильную позицию десятичной точки в частном (как показано). После этого разделение может продолжаться как обычно. Преобразование заданной десятичной дроби в эквивалентную дробь выполняется просто. Поскольку каждое разрядное значение представляет собой степень десяти, каждое десятичное число можно легко преобразовать в целое число, разделенное на степень десяти. Например: 84,1 = 841/10 Последний пример можно свести к наименьшим членам, разделив числитель и знаменатель на 4, что является их наибольшим общим множителем. Наибольший общий делитель двух ненулевых целых чисел - это наибольшее положительное целое число, которое делит оба числа без остатка. Итак, 612/4 = 153 и 1000/4 = 250 Следовательно, 0,612 = 153/250 Любую дробь можно преобразовать в эквивалентную десятичную дробь. Поскольку дробь a / b означает «a», деленное на «b», мы можем разделить числитель дроби на ее знаменатель, чтобы преобразовать дробь в десятичную дробь. Процент - это способ выражения чисел как дробей от 100 и часто обозначается знаком процента (%). Например, 45,1% (читается как «сорок пять целых один процент») равно 0,451. Проценты используются, чтобы выразить, насколько велика одна величина по сравнению с другой величиной. В этом случае первое количество обычно является частью или изменением второго количества. Например, увеличение на 0,15 доллара по сравнению с ценой в 2,50 доллара - это увеличение на 0,15 / 2,50 = 0,06. Таким образом, в процентах это увеличение на 6%. Из-за непоследовательного использования из контекста не всегда ясно, каков процент относительно.Когда говорят о «10% -ном росте» или «10% -ном падении» количества, обычное толкование состоит в том, что это связано с начальным значением этого количества. Например, 10% -ное увеличение товара, изначально оцененного в 200 долларов, составляет 20 долларов, что дает новую цену в 220 долларов. Для многих любое другое использование неверно. В случае процентных ставок, однако, обычная практика заключается в использовании процентного изменения по-другому: Предположим, что начальная процентная ставка задана в виде процента, например, 10%.Допустим, процентная ставка вырастет до 15%. Это можно охарактеризовать как увеличение на 50%, измеряя увеличение относительно начального значения процентной ставки. Однако на практике многие говорят: «Процентная ставка выросла на 5%». Чтобы избежать этой путаницы, иногда используется единица «процентные пункты», когда речь идет о разнице в процентах. Итак, в предыдущем примере «Процентная ставка увеличилась на 5 процентных пунктов» было бы недвусмысленным выражением того, что ставка теперь составляет 15%. С изменениями процент может иметь любое положительное значение. Например, 100% рост является синонимом удвоения; прирост 100%, начиная с 200 единиц, составляет 200 единиц, увеличивая общее количество до 400. Распространенная ошибка при использовании процентов - представить, что процентное увеличение отменяется, когда за ним следует такое же процентное уменьшение. Увеличение на 50% от 100 равно 100 + 50, или 150 Снижение на 50% со 150 составляет 150 - 75, или 75 Результат меньше 100, с которой мы начали. Это явление связано с изменением начального значения после первого расчета. В этом примере первое начальное значение - 100, а второе - 150. В общем, чистый эффект равен: (1 + x) (1 - x) = 1 - x2, то есть чистое уменьшение, пропорциональное квадрату процентного изменения. Чтобы использовать конкретный пример, биржевые маклеры пришли к пониманию, что даже если акция упала на 99%, она все равно может упасть еще на 99%. Кроме того, если акция растет на большой процент, трейдер все равно теряет всю стоимость акции, если акция впоследствии упадет на 100%, что означает, что она имеет нулевую стоимость. Пройдите еще один тест Числовая оценка вопросов проверяют вашу способность быстро оценивать ответы на довольно простые числовые вопросы. Чтобы получить высокие баллы по этим вопросам, вам нужно будет быстро дать ответ. Вы должны избегать ловушки точного ответа, которая отнимет слишком много времени и помешает вам ответить на достаточно вопросов, чтобы получить хорошую оценку. Числовая оценка жизненно важна во многих ремесленных и технических работах, где важна способность быстро и точно оценить количество материалов. Тем не менее, способность делать быстрые оценки - полезный навык, которым нужно обладать, даже если вы сдаетесь на экзамен для выпускников или на профессиональный уровень, поскольку это позволит вам примерно проверить свои ответы на вопросы интерпретации данных. Скорость, с которой вы можете ответить на эти вопросы, является критическим критерием, так как большинство людей может получить очень высокий балл, если у вас будет неограниченное время для ответа.Таким образом, вы можете ожидать от 25 до 35 вопросов примерно за 10 минут. Несмотря на то, что вопросы числовой оценки кажутся простыми, может потребоваться некоторое время, чтобы найти оптимальный компромисс между скоростью и точностью. Пример вопроса: 29 + 41 + 38 + 31 =? A) 130 Чтобы оценить ответ на этот вопрос, быстро округлите каждое число в большую или меньшую сторону, чтобы облегчить их сложение. 30 + 40 + 40 + 30 = 140 Следовательно, правильный ответ: E Прежде чем вы попытаетесь ответить на каждый вопрос, посмотрите на диапазон доступных ответов и спросите себя, насколько точной должна быть ваша оценка. Например, достаточно ли порядка величины или нужно вычислить ответ до ближайшего целого числа? Если у вас нет опыта в арифметике, попробуйте заново выучить таблицу умножения до 12 и потренироваться в грубых и готовых вычислениях умножения, деления и процентов. Практика может улучшить ваши результаты тестов по всем типам тестов на способности, но численная оценка - это одна из областей, где она может иметь значение, поэтому попробуйте как можно больше примеров. Пройдите еще один тест Тесты на числовое мышление требуют, чтобы вы интерпретировали некоторую заданную информацию, а затем применили соответствующую логику для ответа на вопросы. Другими словами, вам нужно решить, как получить ответ, а не какие вычисления применить. Иногда вопросы предназначены для того, чтобы приблизиться к типу рассуждений, необходимых на рабочем месте. Самый популярный тип вопросов для числовых рассуждений - это вопросы с числовыми рядами. Вопросы с числовым обоснованием очень часто используются при отборе выпускников и руководителей. Обычно вы можете ожидать от 15 до 20 вопросов за 20-30 минут. Численное обоснование становится все более популярным способом оценки кандидатов в процессе отбора вакансий.Многие люди, которые какое-то время не посещали систему образования или не используют математику изо дня в день, испытывают страх перед такими тестами. Важно помнить, что вам не нужно изучать математику на высоком уровне, чтобы хорошо сдать эти тесты. В первую очередь это тесты на способность рассуждать, а необходимые математические вычисления неизменно просты. Сказав это, вам, возможно, придется разобраться с процентами, соотношениями, пропорциями, дробями и десятичными знаками. Обычно вам разрешается использовать калькулятор для таких вопросов, и неплохо было бы инвестировать в калькулятор, который может обрабатывать дроби и проценты. Вам также следует попробовать проработать несколько практических работ по числовым вычислениям, чтобы вернуться к размаху этих типов вычислений. Эти вопросы требуют, чтобы вы нашли недостающее число в последовательности чисел. Этот недостающий номер может быть в начале или в середине, но обычно он находится в конце. Например: 1. Найдите следующее число в серии 4, 8, 16, 32… A) 48 2. Найдите недостающий номер в серии 54, 49,…, 39, 34 A) 47 Эти числовые последовательности могут быть довольно простыми, как в приведенных выше примерах.Однако вы часто будете видеть более сложные вопросы, в которых интервалы между числами являются ключом к последовательности. 3. Найдите следующее число в серии 3, 6, 11, 18… A) 30 4. Найдите следующее число в серии 48, 46, 42, 38… A) 32 Эти простые числовые последовательности обычно состоят из четырех видимых чисел плюс одно отсутствующее число.Это связано с тем, что разработчику тестов необходимо создать последовательность, в которую может поместиться только одно число. Необходимость избегать какой-либо двусмысленности означает, что, если числовая последовательность основана на более сложном шаблоне, тогда должно быть больше видимых чисел. Например: 5. Найдите недостающий номер в серии 4, 3, 5, 9, 12, 17,… A) 32 6.Найдите недостающие числа в серии 5, 6, 7, 8, 10, 11, 14,…,… A) 19 Ответы: 1. B - Числа каждый раз удваиваются Для эффективного решения этих вопросов числовой последовательности вы должны сначала проверить взаимосвязь между самими числами, ища простую арифметическую взаимосвязь. Затем посмотрите на интервалы между числами и посмотрите, есть ли там связь. Если нет, и особенно если видно более четырех чисел, то могут быть чередованы две числовые последовательности. Иногда в этих последовательностях можно встретить умножение, деление или степени, но разработчики тестов стараются избегать их, поскольку эти операции вскоре приводят к большим числам, которые трудно вычислить без калькулятора. Другой тип вопросов последовательности, который появляется в этих тестах, включает замену букв алфавита на числа. Например: A = 1, B = 2 и т. Д. Может показаться странным рассматривать их как вопросы числового мышления, но они работают точно так же, как только вы снова замените их числами. 1. Найдите следующую букву в серии B, E, H, K,… i) L 2. Найдите следующую букву в серии A, Z, B, Y,… i) C Ответы: 1.iii - Две буквы отсутствуют между каждой, поэтому N следующий Поскольку арифметические операции с буквами выполнять нельзя, в этих вопросах меньше места для двусмысленности. Это означает, что чередующиеся последовательности могут использоваться с меньшим количеством видимых букв, чем в вопросах, в которых используются числа. В этих вопросах «алфавитной последовательности» подразумевается, что последовательность «зацикливается» и начинается снова.Важно понимать это, поскольку обычно об этом не говорится явно - от вас просто ожидается, что вы это знаете. Если вы видите более одного из этих вопросов в тесте, почти наверняка стоит потратить время на то, чтобы написать буквы алфавита с их порядковыми номерами под ними. После этого вы можете рассматривать эти вопросы так же, как вопросы о числовой последовательности. Это может сэкономить много времени и избежать простых ошибок. Пройдите еще один тест Способность интерпретировать данные, представленные в таблицах, графиках и диаграммах, является общим требованием для многих управленческих и профессиональных должностей. Если вы подаете заявку на работу, которая включает анализ или принятие решений на основе числовых данных, вы можете рассчитывать на то, что вам придется ответить на вопросы интерпретации данных. Проблемы интерпретации данных обычно требуют двух основных шагов: Во-первых, вы должны прочитать диаграмму или график, чтобы получить определенную информацию Затем вы должны применить или изменить информацию, чтобы получить ответ В этих вопросах часто используются очень конкретные иллюстрации; например, в вопросе могут быть представлены финансовые данные.Однако понимание финансов не потребуется, чтобы ответить на этот вопрос. Обычно вы можете ожидать от 20 до 25 вопросов в течение 20–30 минут. Кандидаты, которые какое-то время не посещали систему образования или которым не нужно ежедневно интерпретировать графики, круговые диаграммы, диаграммы разброса и таблицы данных, могут испытывать страх перед вопросами такого типа. Важно помнить, что вам не нужно изучать математику на высоком уровне, чтобы добиться успеха.Эти вопросы в первую очередь являются тестами на интерпретацию, а необходимые математические вычисления неизменно просты. Обычно разрешается использовать калькулятор в тестах интерпретации данных. Пройдите еще один тест Большинство тестов присваивают одну оценку каждому правильному ответу. - нет дифференциальной оценки. Это означает, что вы получите одну оценку за вычисление процента или дроби, и вы получите одну оценку за понимание некоторых данных, представленных в графическом виде, и за ответ на вопрос о них. Следовательно, имеет смысл сконцентрироваться на улучшении своей ментальной арифметики и убедиться, что вы знакомы с процентами, дробями, отношениями и т. Д., Поскольку они могут дать вам легкие оценки. Кроме того, не зацикливайтесь на вопросах, которые кажутся вам трудными - если можете, ответьте на все те, на которые легко сможете ответить, а затем вернитесь и заполните пробелы. Самый первый шаг - изучить свой тест. Прочтите все, что можно, о численных тестах в целом и посмотрите, сможете ли вы узнать, какие именно тесты использует компания, к которой вы подаете заявку. Также посетите форумы или спросите совета у друзей, прошедших тест. Это поможет вам сосредоточить свою практику и сделать ее намного более эффективной, а также привыкнуть к формату, с которым вам придется столкнуться. Когда вы думаете, что хорошо понимаете, с чем сталкиваетесь, следующим шагом будет просто практика, практика и практика. Просмотрите образцы вопросов и полные пробные тесты, такие как undefined. Practive with JobTestPrep По крайней мере, для некоторых из ваших практик вам следует отвечать на вопросы в условиях тестовых условий .В частности, вам нужно привыкнуть к тому, чтобы рассчитывать время самостоятельно и придерживаться строгих временных рамок. Если у вас есть 30 минут, чтобы ответить на 30 вопросов, вам нужно убедиться, что вы в среднем не тратите больше минуты на каждый вопрос. Это можно сделать с помощью секундомера. Каждый раз, когда он достигает минуты (или любого другого среднего времени), сбрасывайте его и двигайтесь дальше. Вернитесь к тем, которые вы не закончили, если у вас будет время в конце. Это поможет вам не волноваться из-за давления самого теста. Когда вы привыкнете к формату и вопросам, настоящий тест - это просто вопрос сохранения спокойствия и выполнения его. Всегда полезно широко искать ресурсы, которые помогут вам подготовиться к оценке числового обоснования. Вот некоторые из наших предложений по дополнительным ресурсам, на которые стоит обратить внимание: Приложения - Мы создали приложение для психометрических тестов, доступное как для Apple, так и для Android. Он содержит вопросы, имитирующие вопросы, опубликованные, в частности, SHL, Kenexa, CAPP и Cubiks.Он имеет встроенный таймер, и после этого вы можете проверить решения, чтобы научиться и развиваться. Практические онлайн-тесты - Помимо наших собственных тестов на способности, WikiJob рекомендует неопределенные. JobTestPrep предлагает широкий спектр профессионально разработанных пакетов практических навыков численного мышления, вопросов, тестов и ресурсов. Вопросы структурированы в профессиональном формате, как и настоящие. Практические численные тесты также предлагаются другими провайдерами, такими как Psychometric Success. Во-первых, убедитесь, что вы выспались, много воды и что-нибудь поесть. Не забудьте взять с собой следующее: Если вы проводите тест дома, найдите тихую уединенную комнату, в которой вы можете посидеть. Убедитесь, что вас никто не побеспокоит, и проверьте стабильность вашего интернета. Сделайте глубокий вдох, успокойтесь и начните тест. Если вы хорошо потренировались и подготовились, то, надеюсь, сдача настоящего экзамена покажется вам знакомой. Просто с чуть большим давлением. Делайте то, что вы подготовили. Подсчитайте среднее время, которое у вас есть на один вопрос, и используйте секундомер, чтобы успевать вовремя. Вот несколько вещей, которые следует помнить при прохождении теста: Используйте практические вопросы в полной мере. - Часто в начале теста вам будет предложено несколько вопросов-примеров, чтобы вы узнали о формате и сориентировались.Как ставятся вопросы? На что похожи данные? Какие расчеты нужно сделать? Запишите все, что, по вашему мнению, может помочь вам в будущем. Это также будет ваш последний шанс задать какие-либо вопросы до начала теста. Внимательно прочтите вопросы - Не позволяйте ограничениям по времени мешать вам внимательно читать. Это особенно важно, потому что недопонимание часто является причиной того, что вы забываете выполнить конкретный шаг в вычислении или не отвечаете на вопрос.Прочтите каждый вопрос дважды и убедитесь, что вы внимательно прочитали предоставленную информацию. Не делайте предположений - Помните, что все, что вам нужно для ответа на вопрос, находится на странице и нигде больше. Если вам посчастливилось вспомнить цифру или факт из своего исследования, который кажется важным, проигнорируйте его. Также используйте эти знания, чтобы ободрить себя. Если ответ найти невозможно, вы точно знаете, что это возможно, основываясь только на том, что написано на странице. Используйте процесс исключения - Если вы действительно застряли, посмотрите на некоторые из предложенных вам ответов с несколькими вариантами ответов и работайте в обратном направлении. Посмотрите, есть ли какие-либо ответы, которые определенно выглядят так, как будто они не могут быть ответом, и сначала устраните их. Focus - Ключевой навык, который необходимо проверить при численной оценке, - это ваша способность сканировать данные и оттачивать то, что важно. Вот почему вы должны внимательно прочитать вопрос, чтобы знать, что вам нужно выяснить.Затем внимательно прочтите контекст. Какие данные содержит таблица? Что показывает график? Выясните, какие данные вы можете игнорировать, и заботьтесь только о той информации, которая поможет вам ответить на вопрос. Сделайте заметки - Держите под рукой свою макулатуру и используйте ее. Жонглировать большим количеством данных и информации в голове может быстро стать непосильной задачей. Избавьте себя от хлопот и запишите факты, которые, по вашему мнению, важны, когда будете работать над вопросом. Всегда проверяйте единицы измерения, валюты и базы. - Очень распространенная ошибка в числовых тестах - спутать единицы измерения, валюты и т. Д. Иногда вам нужно будет конвертировать между валютами. Использование двух цифр, как если бы они были одной и той же валютой, приведет вас к неправильному ответу. То же самое и с графиками, таблицами и диаграммами. Всегда проверяйте оси, что они представляют и есть ли какие-либо сокращения (например, запись «10» на графике, когда ось объясняет, что это означает «10 миллионов»).Это кажется очевидным, но об этом легко забыть. Игнорировать других участников теста - Если вы проходите тест лично в центре оценивания, вероятно, вы не останетесь один в комнате. Не позволяйте этому добраться до вас. Другие кандидаты могут вздыхать, ерзать, шуршать бумагой или оглядываться. Это не имеет значения - вы пришли только на свой тест. Некогда отвлекаться, поэтому держите голову опущенной и сосредоточьтесь на собственном числовом тесте. В общем, лучше всего стремиться к точности. Даже если вы проходите тест на скорость, точность не менее важна. Для большинства тестов работодатель получит оценку точности, а также ваш исходный балл. Их больше заинтересует кандидат, который потратил немного больше времени, но был намного точнее, чем кандидат, который прошел, но был небрежным. Какие отзывы вы получаете и когда сильно различаются от компании к компании.Некоторые не дают вам обратной связи, некоторые - только в случае успеха, некоторые предлагают резюме всем кандидатам. В зависимости от типа предлагаемой обратной связи это может произойти сразу после завершения теста (автоматическая система обратной связи) или в любое время от нескольких дней до нескольких недель после завершения теста. Если вы не уверены, получите ли вы обратную связь или когда ее следует получить, просто спросите отдел кадров компании. При прохождении теста скорости, такого как численная оценка или численное вычисление, вам не разрешается использовать калькулятор.Эти тесты требуют, чтобы вы быстро ответили на простые вопросы по математике и проверили свои умственные арифметические операции. Обычно вам разрешается использовать калькулятор для числовых рассуждений и вопросов интерпретации данных. Для большинства тестов, проводимых лично в центре оценки, есть калькуляторы, но на всякий случай всегда берите с собой свои. Всегда лучше использовать знакомый калькулятор. Тип используемого вами калькулятора может помочь или помешать вам в достаточной степени, чтобы повлиять на ваши результаты.В частности, калькулятор, который вы используете, должен: Возможно, вам не разрешат пройти тест лично, но это все равно не поможет. Тесты разработаны таким образом, что все, что вам нужно, это ваш калькулятор и ваши собственные числовые навыки. Нет времени искать ответы в Google или на форумах. Плохая идея. Если вы попросите кого-нибудь пройти тест для вас, это может помочь вам пройти онлайн-тесты без надзора и перейти к следующему этапу процесса (при условии, конечно, что этот человек действительно лучше справляется с тестом, чем вы), но работодатели не согласны с этим. это не глупо, и в конечном итоге их не обмануть. Очень часто на этапе оценивания вас просят пройти еще один набор тестов на способности лично и под наблюдением. Результат этого теста будет сравнен с вашим исходным онлайн-тестом и проанализирован. Если вы обманули, то, скорее всего, на этом этапе вас обнаружат. И это лишь один из многих методов борьбы с мошенничеством, которые есть у работодателей. Многие из них не разглашаются, потому что, если бы они были, мошенники могли бы искать способы их обойти. Не рискуй.Практика - гораздо более эффективная и полезная стратегия. Тесты на числовые способности обычно не требуют математических навыков, кроме сложения, вычитания, умножения, деления, соотношений и процентов. Компании в первую очередь заинтересованы в вашем понимании основ. Они спрашивают: «Уверен ли этот человек в работе с числами в целом?». Однако от вас ожидается, что вы будете выполнять такие арифметические действия быстро и точно.Вы будете испытывать давление как из-за жестких временных рамок, так и из-за важности теста. \ infty {{a_n}} \) абсолютно сходится.
\ infty {{a_n}} \) абсолютно сходится. \ infty {\ frac {1} {n}} & \ hspace {0,5 дюйма} & {\ mbox {divergent}} \ end {align *} \]
\ infty {\ frac {1} {n}} & \ hspace {0,5 дюйма} & {\ mbox {divergent}} \ end {align *} \] гл. 1 Практический тест — Precalculus
Практический тест


х х 0 1 2 3 4 5 6 7 8 f (x) f (x) 1 3 5 7 9 11 13 15 17 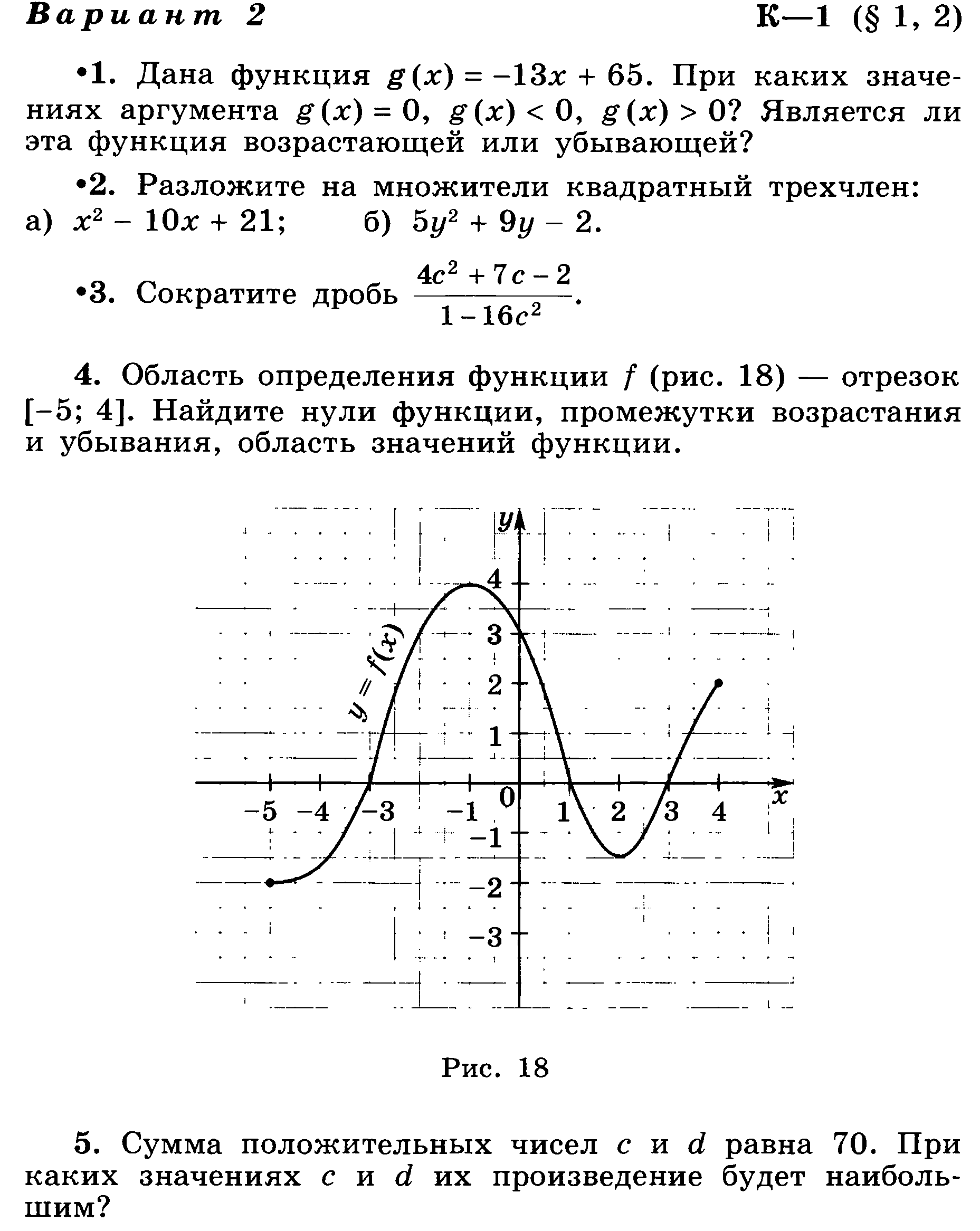
Числовые функции — Таблица
Зачем нужны числовые функции
 Одно из этих значений может быть -7.Вы можете использовать функцию ABS, чтобы вернуть абсолютное значение этого числа и всех других чисел в этом поле.
Одно из этих значений может быть -7.Вы можете использовать функцию ABS, чтобы вернуть абсолютное значение этого числа и всех других чисел в этом поле. ABS [Отклонение от бюджета] Числовые функции, доступные в Tableau
Функция
Синтаксис
Описание
ABS (номер) 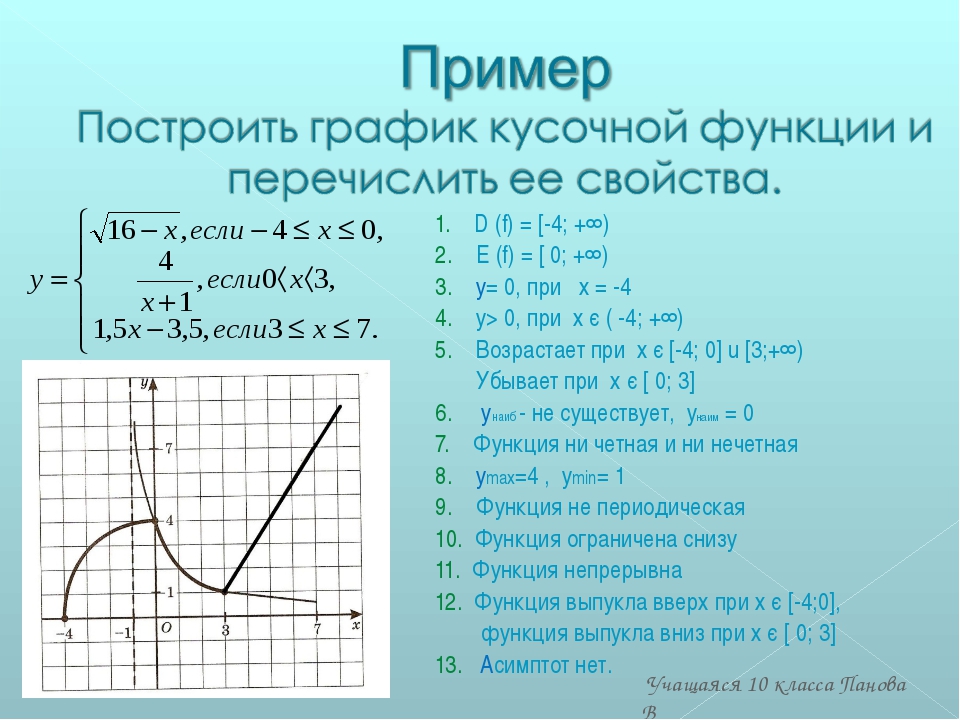
ABS (-7) = 7
ABS ([отклонение бюджета]) Отклонение бюджета . ACOS (номер) ACOS (-1)
= 3,141558979
ASIN (номер)  Результат выражается в радианах.
Результат выражается в радианах. ASIN (1) = 1,5707963267949 ATAN (номер) ATAN (180)
= 1,5652408283942 ATAN2 (число y, число x)  Результат выражается в радианах.
Результат выражается в радианах. ATAN2 (2, 1) = 1,10714871779409 ПОТОЛОК (номер) ПОТОЛОК (3,1415) = 4 Наличие по источнику данных:
Источник данных Поддержка Microsoft Access Не поддерживается Microsoft Excel Поддерживается Текстовый файл Поддерживается Статистический файл Поддерживается Tableau Server Поддерживается Actian Vector Не поддерживается Amazon Aurora для MySQL Не поддерживается Amazon EMR Hadoop Hive Поддерживается Amazon Redshift Не поддерживается База данных Aster Не поддерживается Cloudera Hadoop Поддерживается DataStax Enterprise Поддерживается EXASOL Не поддерживается Firebird Не поддерживается Google Analytics Поддерживается Google BigQuery Поддерживается Google Cloud SQL Не поддерживается Google Таблицы Не поддерживается Hortonworks Hadoop Hive Поддерживается IBM BigInsights Не поддерживается IBM DB2 Не поддерживается КПК IBM (Netezza) Не поддерживается MapR Hadoop Hive Поддерживается MarkLogic Не поддерживается Службы Microsoft Analysis Services Не поддерживается Microsoft PowerPivot Не поддерживается Microsoft SQL Server Поддерживается MySQL Не поддерживается Оракул Не поддерживается Oracle Essbase Не поддерживается Actian Matrix (ParAccel) Не поддерживается Пивотал Гринплум Не поддерживается PostgreSQL Не поддерживается Прогресс OpenEdge Не поддерживается Salesforce Поддерживается SAP HANA Не поддерживается SAP Sybase ASE Не поддерживается SAP Sybase IQ Не поддерживается Spark SQL Поддерживается Splunk Не поддерживается Терадата Не поддерживается Разъем Teradata OLAP Не поддерживается Vertica Не поддерживается COS (номер)  Укажите угол в радианах.
Укажите угол в радианах. COS (PI () / 4) = 0,707106781186548 COT (номер) COT (PI () / 4) = 1 ГРАДУСОВ (число) 
ГРАДУСОВ (PI () / 4) = 45,0 DIV (11,2) = 5 EXP (номер) 
EXP (2) = 7,389
EXP (- [Рост
Оценить] * [Время]) ЭТАЖ (номер) ЭТАЖ (3,1415) = 3 Наличие по источнику данных:
Источник данных Поддержка Microsoft Access Не поддерживается Microsoft Excel Поддерживается Текстовый файл Поддерживается Статистический файл Поддерживается Tableau Server Поддерживается Actian Vector Не поддерживается Amazon Aurora для MySQL Не поддерживается Amazon EMR Hadoop Hive Поддерживается Amazon Redshift Не поддерживается База данных Aster Не поддерживается Cloudera Hadoop Поддерживается DataStax Enterprise Поддерживается EXASOL Не поддерживается Firebird Не поддерживается Google Analytics Поддерживается Google BigQuery Поддерживается Google Cloud SQL Не поддерживается Hortonworks Hadoop Hive Поддерживается IBM BigInsights Не поддерживается IBM DB2 Не поддерживается IBM Netezza Не поддерживается MapR Hadoop Hive Поддерживается MarkLogic Не поддерживается Службы Microsoft Analysis Services Не поддерживается Microsoft PowerPivot Не поддерживается Microsoft SQL Server Поддерживается MySQL Не поддерживается Оракул Не поддерживается Oracle Essbase Не поддерживается ParAccel Не поддерживается Пивотал Гринплум Не поддерживается PostgreSQL Не поддерживается Прогресс OpenEdge Не поддерживается Salesforce Поддерживается SAP HANA Не поддерживается SAP Sybase ASE Не поддерживается SAP Sybase IQ Не поддерживается Spark SQL Поддерживается Splunk Не поддерживается Терадата Не поддерживается Разъем Teradata OLAP Не поддерживается Vertica Не поддерживается HEXBINX (число, число)  Бины имеют длину стороны 1, поэтому входные данные могут нуждаться в соответствующем масштабировании.
Бины имеют длину стороны 1, поэтому входные данные могут нуждаться в соответствующем масштабировании. HEXBINX ([Долгота], [Широта]) HEXBINY (число, число)  Бины имеют длину стороны 1, поэтому входные данные могут нуждаться в соответствующем масштабировании.
Бины имеют длину стороны 1, поэтому входные данные могут нуждаться в соответствующем масштабировании. HEXBINY ([Долгота], [Широта]) LN (номер) Null , если число меньше
или равно 0. ЖУРНАЛ (номер [, основание])  номера для данной базы.Если базовое значение опущено, основание 10
используется.
номера для данной базы.Если базовое значение опущено, основание 10
используется. МАКС (число, число) Null , если
любой аргумент — Null . MAX банка
также может применяться к отдельному полю при агрегированном вычислении. МАКС. (4,7)
MAX (продажи, прибыль)
МАКС ([Первый
Имя], [Фамилия]) MIN (число, число)  Возвращает
Возвращает Null , если
любой аргумент — Null . MIN банка
также может применяться к отдельному полю при агрегированном вычислении. МИН (4,7)
МИН (продажи, прибыль)
MIN ([Первый
Имя], [Фамилия]) PI () 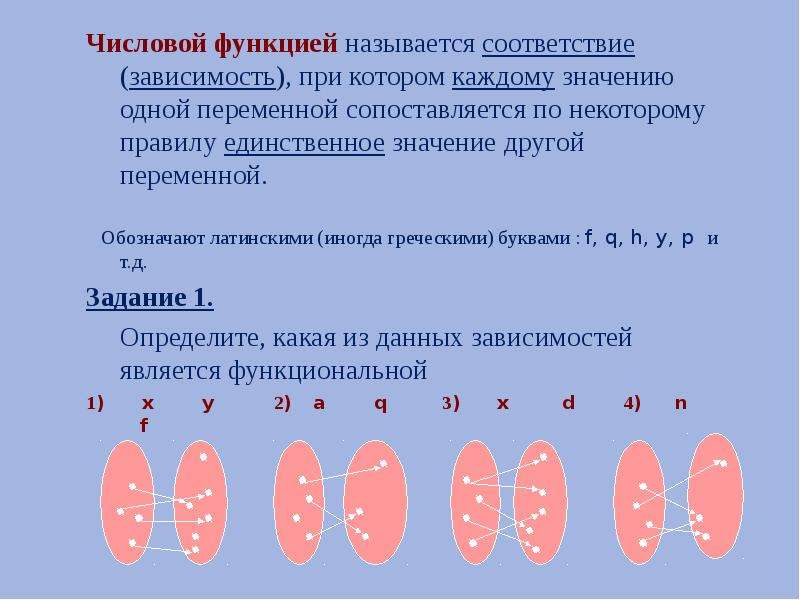 14159.
14159. МОЩНОСТЬ (число, мощность) РАДИАНЫ (число) 
РАДИАНОВ (180) = 3,14159 ОКРУГЛ (число, [десятичные знаки]) десятичных дробей указывает, сколько десятичных знаков точности следует включать в
конечный результат. Если десятичных знаков — это
опущено, число округляется до ближайшего целого числа. Продажи значение до целого числа: ТУР (Продажа) ,
где -1 округляет число до десятков, -2 округляет до сотен,
и так далее. Это верно не для всех баз данных.
Например, это не относится к Excel или Access.
Это верно не для всех баз данных.
Например, это не относится к Excel или Access. ЗНАК (номер) (СРЕДНЯЯ (прибыль))
= -1 SIN (номер)  Укажите угол в радианах.
Укажите угол в радианах. ГРЕХ (0)
= 1,0
SIN (PI () / 4) = 0,707 106781186548 SQRT (номер) КОРЕНЬ (25) = 5 ПЛОЩАДЬ (число) 
КВАДРАТ (5) = 25 TAN (номер) TAN (PI
() / 4) = 1,0 ZN (выражение)  Используйте эту функцию, чтобы
используйте нулевые значения вместо нулевых значений.
Используйте эту функцию, чтобы
используйте нулевые значения вместо нулевых значений. ZN ([Прибыль]) = [Прибыль] Создать числовой расчет
 Как и другие ваши поля, вы можете использовать его в одной или нескольких визуализациях.
Как и другие ваши поля, вы можете использовать его в одной или нескольких визуализациях. См. Также
непрерывных функций - 5
непрерывных функций - 5 Определение. Функция f является непрерывной на при x = a тогда и только тогда, когда Определение. Предположим, что у нас есть функция типа f или h выше, который имеет разрыв в x = , так что можно переопределить
функция в этой точке, как с k выше, так что новая функция является непрерывной в х = .Затем мы говорим, что функция имеет устранимый разрыв при x = a . Теорема A. Многочлен непрерывен для каждого действительного числа. Рациональная функция непрерывна в каждой точке своей области определения. Теорема B. Предположим, что f и g - функции, непрерывные в точке x = a и
Предположим, что k - постоянная величина. потом Теорема C. Предположим, что g - функция
которая непрерывна при x = a , и предположим, что f является
функция, которая непрерывна при x = g (a) , то
Состав f и g является непрерывным при x = a . Определение. Функция f непрерывна на интервале I если он непрерывен в каждой точке I . Если I имеет конечную точку a , тогда f является непрерывным на a , если Определение. Предположим, что у нас есть функция как в предыдущем блокноте
такой, что правый предел Теорема D. Следующие функции непрерывны в каждой точке своей области определения:
Если f - функция, непрерывная в каждой точке своего домена, и если f имеет обратный, тогда обратный f -1 также
непрерывно в каждой точке своей области. Свойства функций | Безграничная алгебра
Увеличивающие, убывающие и постоянные функции
Цели обучения
Ключевые выводы
Ключевые моменты
Ключевые термины
Графическое поведение функций
Постоянные функции
Определение поведения функции
Пример 1: Определите интервалы, в которых функция увеличивается, уменьшается или остается постоянной.
Относительные минимумы и максимумы
Цели обучения
Ключевые выводы
Ключевые моменты
Ключевые термины
Определения минимумов и максимумов: относительные и глобальные
Разделение относительного и глобального максимума и минимума
Пример 1: Найдите все максимумы и минимумы на графике ниже:
Пример 2:
Найдите все глобальные максимумы и минимумы на графике ниже: Кусочные функции
Цели обучения
Ключевые выводы
Ключевые моменты
Ключевые термины
Графические кусочные функции
Пример 1: Рассмотрим кусочное определение функции абсолютного значения:
Индивидуальные функции
Цели обучения
Ключевые выводы
Ключевые моменты
Ключевые термины
Свойства однозначной функции
Пример 2: Функция [латекс] f (x) = \ left | x \ right | [/ latex] один к одному?
Симметрия функций
Цели обучения
Ключевые выводы
Ключевые моменты
Ключевые термины
Симметрия
Симметричные типы функций
Определение симметрии
Пример: Симметрия функции ниже?
Четные и нечетные функции
Цели обучения
Ключевые выводы
Ключевые моменты
Ключевые термины
Четные и нечетные определения
Четные функции
Нечетные функции
100 бесплатных вопросов и советов 2021
Мини-тест числовых способностей
Чего ожидать от теста на числовые способности
Почему работодатели используют эти тесты?
Что затрудняет тесты на числовые способности?
Срок
Несколько операций
Математика
Различные поставщики тестов численного мышления
Вопросы о численных вычислениях
Простая арифметика
Вычитание
- 1844 Умножение
yy = a x b
120 (что составляет 3 x 4 x 10)
140 (что составляет 7 x 2 x 10)
21 (что составляет 7 x 3) Дроби
Десятичные
«2» - это цифра «единиц»; значение разряда для «2» - 1
«4» - это десятая цифра; значение позиции для «4» - 1/10
9,17 = 917/100
0,612 = 612/1000 В процентах
Практический тест числовых вычислений
Вопросы по численной оценке
B) 120
C) 160
D) 110
E) 140 Практический тест числового оценивания
Вопросы по числовому мышлению
Что такое числовые последовательности
B) 64
C) 40
D) 46
B) 44
C) 45
D) 46
B) 22
C) 27
D) 29
B) 30
C) 33
D) 34
B) 30
C) 24
D) 26
B) 17
C) 15
D) 16
2. B - Числа уменьшаются на 5 каждый раз
3. C - Интервал, начинающийся с 3, увеличивается каждый раз на 2
4. B - Интервал, начинающийся с 2, увеличивается на 2 и вычитается каждый раз
5.D - Каждое число является суммой предыдущего и цифры 3 слева
6. C, A - Есть две простые чередующиеся последовательности 5, 7, 10, 14, 19 и 6, 8, 11, 15 Буквы алфавита как числа
ii) M
iii) N
iv) O
ii) X
iii) D
iv) Y
2. i - Есть две чередующиеся последовательности A, B, C и Z, Y, поэтому C - следующий Практический тест численного мышления
Вопросы по интерпретации данных
Практический тест интерпретации данных
Численное мышление: советы и методы
Практика перед тестом
Непосредственно перед тестом
Эффективные стратегии при прохождении теста
Часто задаваемые вопросы
1. Что лучше: закончить тест или сосредоточиться на точности?
2. Когда мне следует узнать, как прошел тест?
3. Могу ли я использовать калькулятор?
4.Могу ли я использовать свой мобильный телефон во время теста?
5. Я подумываю, чтобы кто-нибудь еще сдал за меня тест
Последние мысли

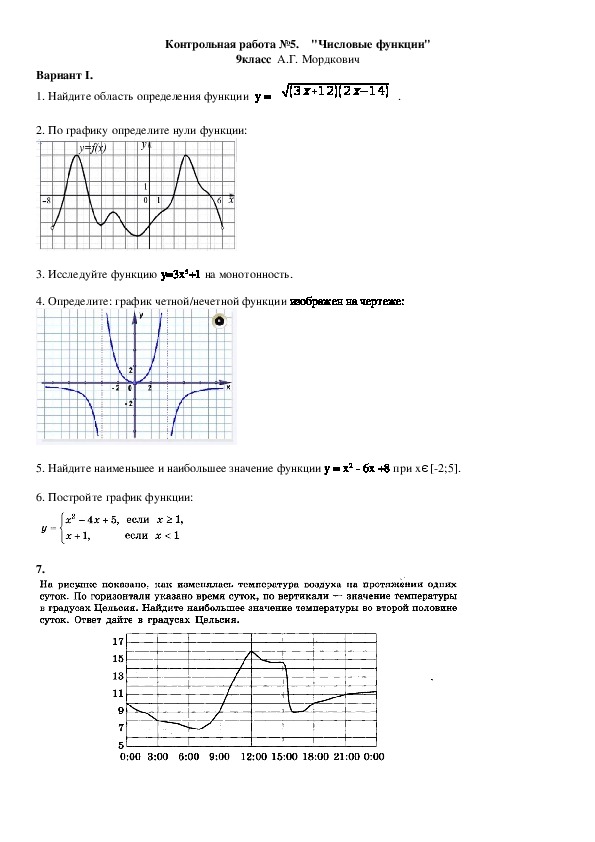



 Найдите наибольшее и наименьшее значения функции У = (х — 2)3 + 4 на отрезке .
Найдите наибольшее и наименьшее значения функции У = (х — 2)3 + 4 на отрезке .