Контрольная по теме векторы 9 класс: Контрольная работа по геометрии 9 класс по теме «Векторы»

Контрольная работы по теме: Векторы 9 класс

Контрольная работа по теме: «Векторы» Вариант 1 Начертите три неколлинеарных вектора , и. Постройте векторы, равные: 1)+ 2; 3)- 2)+ 3; 4) – 2.На стороне NP ромба MNPS точка H так, что NH=HP, О – точка пересечения диагоналей. Выразите векторы , ,  через векторы = и =. 3.В равнобедренной трапеции высота делит большее основание на отрезки, равные 24 и 11 см. Найдите среднюю линию трапеции. 4.В треугольнике MNK О – точка пересечения медиан. Выразите вектор  через векторы = =. 5.Закончите предложение: «Вектор – это…» 6.Запишите кратко: вектор a 7.Запишите обозначение вектора с концом в точке М и началом в точке Р. 8.Модулем вектора называется … 9.Начертите вектор CD сонаправленный вектору AB, но не равный ему. 10.Что можно сказать о направлении двух равных векторов? 11.Сочетательный закон сложения векторов 12.Найдите сумму векторов ВС и СА. 13.Найдите разность векторов МК и МР 14.Изобразите векторы ВС и ВК и их сумму 15.ВСМК – параллелограмм. Чему равна сумма векторов ВС и ВК? 16.Произведением вектора a на число t называется… 17.Длина вектора а равна 5. Изобразите вектор -3а. 18.Вычислите: МК +КР –МХ -РХ

Контрольная работа по теме: «Векторы» Вариант 2 Начертите три неколлинеарных вектора , и . Постройте векторы, равные: 1)+ 2; 2)-; 3)+ 4 3– 2.На стороне KL квадрата MNKL лежит точка E так, что KE=EL, О – точка пересечения диагоналей. Выразите векторы , ,  через векторы = и =. 3.В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 16 см, а меньшее основание 14 см. Найдите среднюю линию трапеции. 4. В треугольнике MNK О – точка пересечения медиан. Выразите вектор  через векторы = =. 5. Вектором называется… 6. Запишите кратко: вектор b 7. Запишите обозначение вектора с концом в точке А и началом в точке С. 8. Векторы а и b коллинеарны, но не одинаково направлены. Изобразите такие векторы. 9. Длиной вектора называется … 10. Запишите в виде равенства, чему равна длина нулевого вектора 11. Переместительный закон сложения векторов 12. Найдите сумму векторов МЕ и EА. 13. Найдите разность векторов ВК и ВЕ. 14. Изобразите векторы РС и РК и их сумму. 15. АВСР – параллелограмм. Чему равна сумма векторов АВ и АР? 16. Вектором, противоположным вектору a, называется … . 17. Длина вектора а равна 4. Изобразите вектор -2а. 18. Вычислите: МЕ – МС + ЕХ – ХС

Контрольная работа по теме «Понятие вектора. Средняя линия трапеции, средняя линия треугольника», 9 класс.

1.Нарисовать равнобедренный АВС с основанием АС=4 см. Провести среднюю линию МD и найти её длину. 2. Найти длины указанных векторов. 3 . Найти площадь трапеции. 4 . Постройте четырехугольник АВСD по координатам его вершин: А(-5;0), В(-3;3), С(2;3), D(4;0). а) Определите вид получившейся фигуры и найдите её площадь. Ответ. Это равнобедренная трапеция. S= . б) Выпишите все коллинеарные векторы. Ответ.BCАD,CBDА, ВС  DА, СВ АD в) Найдите длину средней линии. Ответ.7

1. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N(2; 4), К (2; — 2). а)Найдите среднюю линию МNK. Ответ. L =6:2=3. б) Найдите площадь МNK. Ответ.S=(8*6):2=24 кв.ед. 2. В равнобедренной трапеции высота делит большее основание на отрезки, равные5 и 12 см. Найдите среднюю линию трапеции. Ответ. 9,5 см. 3. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и. 4 .Найти площадь Ответ. 60 кв.ед. 5.Сложите два вектора по правилу параллелограмма.

1.Построить четырехугольник ABCD, если A(-4;7),B(0;1),C(-4;-5),D(-8;1). а) Определите вид получившейся фигуры и найдите её площадь. Ответ. Это ромб.S= =12*80:2=48кв.ед. 2.Найти. Ответ. 3. Начертите два неколлинеарных вектора и. Постройте вектор n, равный . 4. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции и её площадь. Ответ.L=11см. S= 5. В прямоугольном параллелепипеде известно, что ВD1=5, СС1-3, В1С1= . Найдите длину ребра АВ. Решение и ответ. ВD-4 (ученик должен увидеть пифагорову триаду), АВ=СD= = . Ответ.3.

ГДЗ Геометрия 9 класс Мельникова

Большую часть подготовки к государственной итоговой аттестации занимает именно математика, ведь именно этот предмет считается одним из самых сложных и трудно запоминаемых. Особая сложность выпадает на раздел геометрии, а это значит, что учить и запоминать все правила нужно с самого начала изучения этой дисциплины. Для того, чтобы эффективней подготовиться к экзаменам, школьникам предлагаются различные рабочие тетради и пособия. Учителя стараются максимально упрощать материал, ведь информации очень много, а времени для рассмотрения каждой мало. В рабочих тетрадях есть много тематических заданий, которые помогут ученикам улучшить свои знания. Правильные ответы предоставит решебник к учебнику «Геометрия 9 класс Тетрадь для контрольных работ Мельникова» от издательства «Экзамен».

Хорошие стороны этого ГДЗ

Сам решебник содержит множество готовых онлайн-ответов на все упражнения и номера из тетради. Также его плюсами можно назвать следующее:

1. Решебник содержит четкие ответы, без лишних дополнений.
2. Можно сверить свой ответ с правильным. Самопроверка всегда считалась плюсом для учащегося.
3. Имеются ответы на задания, где нужно вписать в предложение слово или формулу.

Какими будут результаты работы с решебником

Если научится правильно пользоваться тетрадью с готовыми ответами, то и результаты будут положительными. Обычное списывание никогда ничем не помогало, ибо переписывая ответ никаких знаний не появится. Школьник должен самостоятельно написать решение, такое, какое он считает правильным, а потом посмотреть в решебник и узнать, верный ли ответ. В таком случае ученики научатся правильно подбирать формулы к номерам и задачам.

Новые темы в девятом классе

В самом начале года девятиклассники познакомятся с такой темой, как «Вектор». Она довольно сложная и будет часто использоваться в будущем, поэтому понять ее нужно в начале изучения. Позже будет подробное рассматривание этой темы и разбор ее по частям. Например, «Координаты вектора» и «Операции с векторами».

Урок-игра «Векторы пословицы», геометрия 9 класс

 

 

Карта для решения примеров

 

 

 

 

 

 

Ключ к расшифровке

 

Задания (надо начертить символ вектора)

1

AC +CB

FA – DA +DE

CA +AD

2

 FA – FB

CE + EB

BF – CF

3

DB + BA – EA

EF + FC + CD

DE + EB – CB

EC – FC

4

BD + BA

FE – AE

ED + EA

AC + CE

 

5

BA + BD

EF +FA

EA +ED

AC + CD – FD

6

DE + EB

BE – FE

BA + AF – DF

DE +DB

FE – BE

BA + DB + AE

 

7

AB + AE

EA + AC

DB + DE

CD – ED

 

1

AC +CB

FA – DA +DE

CA +AD

2

 FA – FB

CE + EB

BF – CF

3

DB + BA – EA

EF + FC + CD

DE + EB – CB

EC – FC

4

BD + BA

FE – AE

ED + EA

AC + CE

 

5

BA + BD

EF +FA

EA +ED

AC + CD – FD

6

DE + EB

BE – FE

BA + AF – DF

DE +DB

FE – BE

BA + DB + AE

 

7

AB + AE

EA + AC

DB + DE

CD – ED

 

 

 

 

МАСТЕР-КЛАСС ГЕОМЕТРИЯ 9 КЛАСС КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «ВЕКТОРЫ» Предмет

МАСТЕР-КЛАСС

ГЕОМЕТРИЯ, 9 КЛАСС, КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «ВЕКТОРЫ»

Предмет: Геометрия

Тема: Контрольная работа по теме ”Векторы”

Класс: 9 класс
Педагог: Аширбекова Лариса Александровна, заместитель директора по воспитательной работе, учитель математики и информатики.

Учреждение образования: МОУ Шуринская средняя общеобразовательная школа Кемеровской области
Город: Кемеровская область

Цель урока: контроль знаний учащихся

Ход урока.

1. Организационный момент: объяснить цель урока.

2. Контрольная работа (тестирование)

Вариант 1

1. Вектором называется направленный …. (отрезок)

2. Векторы называются равными, если они сонаправлены и … (их длины равны)

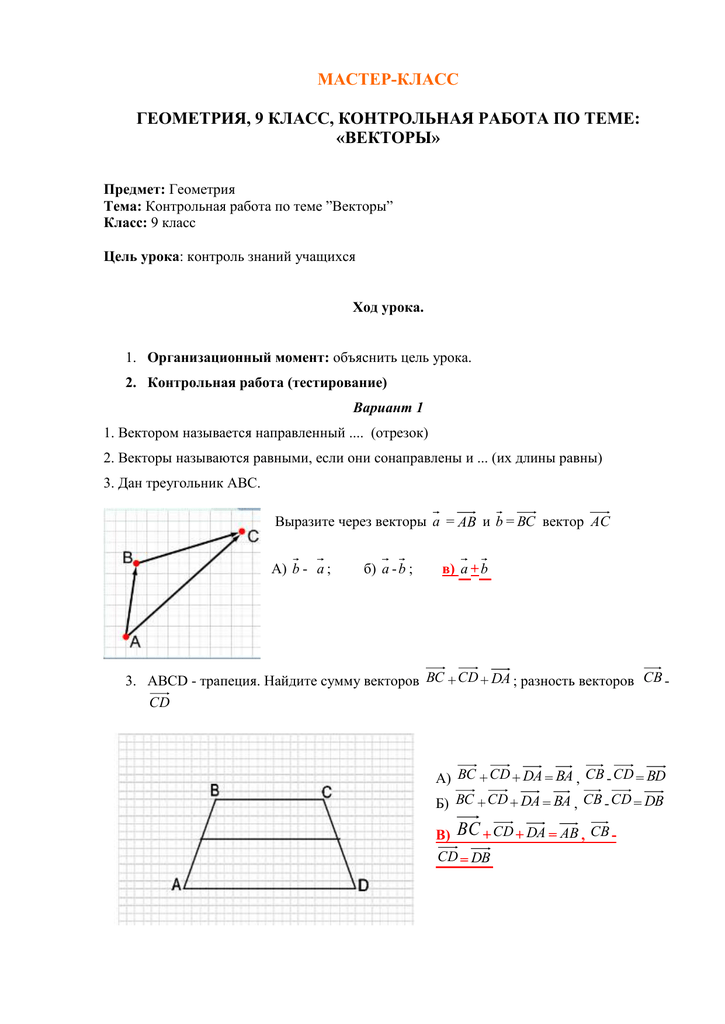
3. Дан треугольник АВС.

Выразите через векторы = и = вектор

А) — ; б) -; в) +

3. ABCD — трапеция. Найдите сумму векторов ++; разность векторов —

А) ++=, -=

Б) ++=, -=

В) ++=, —=

4.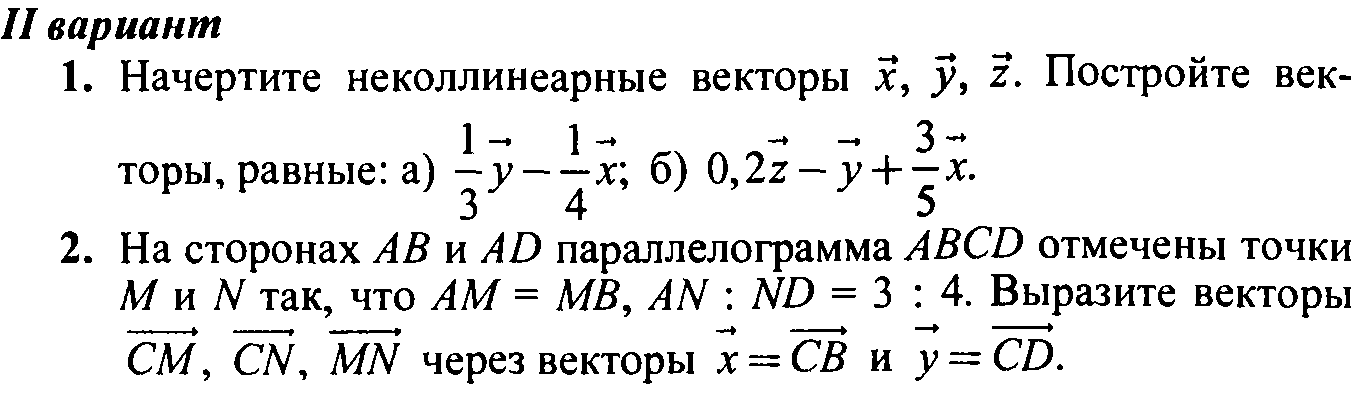 ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина ВС, =, = . Выразите через векторы и следующие векторы:

А) , б) , в) , г)

А) А) = +, б) = , в) = —, г) =+

Б) А) = -, б) = , в) = -, г) =-

В) А) = +, б) = , в) = +, г) =-

5. Одно основание трапеции на 4 см больше другого, а средняя линия равна 8 см. Найдите основания трапеции

а) 6 см и 10 см

б) 6 см и 8 см

в) 8 см и 10 см

Вариант 2

1. Закончи предложение.

От любой точки М можно отложить вектор, равный данному вектору, и притом только… (один)

2. Вставь пропущенное слово.

Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на … прямых

3. Дан треугольник АВС. Выразите через векторы = и = вектор .

А) —

Б) +

В) —

4. ABCD — трапеция. Найдите сумму векторов +; разность векторов —

а) +=, -=

б) +=, -=

в) +=, -=

5. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, =, =. Выразите через векторы и следующие векторы: А) , б) , в) , г)

А) ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, =, =. Выразите через векторы и следующие векторы: А) , б) , в) , г)

Б) а)=-, б) =, в) =-, г) =-

В) а)=+, б) =, в) =+, г) =-

Глава X. §1 Координаты вектора ( 2 часа)

Урок 7.Разложение вектора по двум неколлинеарным векторам.

Учащиеся должны:

Знать формулировку и доказательство леммы о коллинеарных векторах, и теорему о разложении по двум неколлинеарным векторам;

Уметь решать задачи, применяя полученные знания.

Ход урока

1. Организационный момент: назвать цели урока.

2. Анализ контрольной работы.

3. Объяснение нового материала:

План объяснения:

1. Разложение вектора по двум неколлинеарным векторам.

При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.

2. Лемма о коллинеарных векторах.

Лемма — это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.

Теорема:Если векторы и коллинеарны и 0, то существует такое число k, что = k.

Так как рассматриваемые векторы, по условию коллинеарны, то они могут иметь одинаковые направления. Рассмотрим два случая, когда векторы и сонаправлены и противоположно направлены.

Доказательство:

1) . Возьмем число . Так как k 0, то векторы k и сонаправлены (рисунок 1). Кроме того, их длины равны: k= k = =. Поэтому = k

2) . Возьмем число . Так как k и снова сонаправлены (рисунок2). Их длины также равны: k= k = =. Поэтому = k

рисунок2

3. Теорема о разложении вектора по двум неколлинеарным векторам.

Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Пусть и — данные неколлинеарные векторы, вектор представлен в виде

= х+у, где х и у — некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.

Доказательство:

Возможны два случая:

1) Вектор коллинеарен одному из векторов и , например, вектору (рисунок1). В этом случае по лемме о неколлинеарных векторах вектор можно представить в виде = у, где у — некоторое число, и, следовательно, =0+у, т.е. вектор разложении по векторам

и .

2) Вектор не коллинеарен ни вектору , ни вектору . Отметим какую-нибудь точку О и отложим от нее векторы = , =, = (рисунок2).

Через точку Р проведем прямую, параллельную прямой ОВ, и обозначим через А₁ точку пересечения этой прямой с прямой ОА. По правилу треугольника = + . Но векторы и коллинеарны соответственно векторам и , поэтому существует числа х и у, такие, что = х, = у. Следовательно, = х+у, т.е. вектор разложен по векторам и .

Докажем теперь, что коэффициенты х и у разложения определяются единственным образом. Допустим, что наряду с разложением = х+у имеет место другое разложение = х₁+у₁. Вычитая второе равенство из первого и используя правила действий над векторами, получаем =(х-х₁) + (у-у₁). Это равенство может выполняться только в том случае, когда коэффициенты х-х₁ и у-у₁ равны нулю. В самом деле, если предположить, например, что х-х₁ 0, то из полученного равенства найдем = -, а значит векторы и коллинеарны. Но это противоречит условию теоремы. Следовательно, х-х₁=0 и у-у₁=0, откуда х=х₁и у=у₁.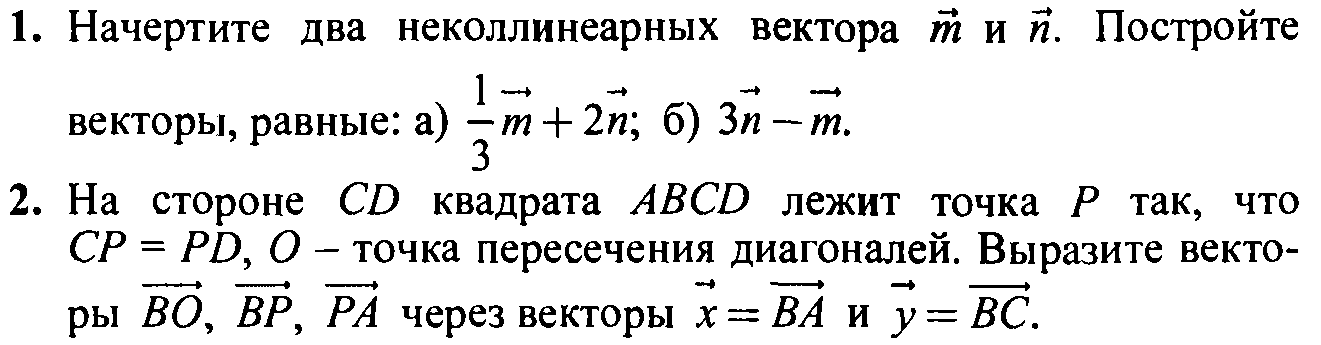 Это и означает, что коэффициенты вектора определяются единственным образом. Теорема доказана.

Выводу по теме:

1.Лемма — это вспомогательное утверждение, употребляемое при доказательстве одной или нескольких теорем.

2. Лемма (о коллинеарных векторах). Если векторы и коллинеарны и вектор 0, то существует такое число k, при котором = k

3. Пусть и — данные неколлинеарные векторы, вектор представлен в виде

= х+у, где х и у — некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.

4. Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

IV. Закрепление полученных знаний:

Тестирование:

1. Диагонали параллелограмма АВСD пересекаются в точке О. Выразите вектор через векторы и .

а) = —

б) = —

в) =+

2. №911 (а) Найдите такое число k, чтобы выполнялось равенство = k, если известно, что векторы и противоположно направлены и  =0,5 см,  = 2см.

а) -4

б) 4

в) 0,4

3. №911(б). Найдите такое число k, чтобы выполнялось равенство = k, если известно, что векторы и сонаправлены и  =12 см,  = 24 дм.

А) -20

Б) 20

В) 0,2

4. №912(а,г). Диагонали параллелограмма пересекаются в точке О, М — середина отрезка АО. Найдите, если это возможно, такое число k, чтобы выполнялось равенство: = k, = k

а) -2,

б) 2, 1

в) 2,

5. Дан произвольный треугольник АВС с медианой АD. Найдите , как вектор выражается через векторы и .

А) = +

Б) = +

В) = +

V. Подведение итогов.

VI. Задание на дом: п. 86, №№ 911 (в,г), 912 2,3 столбик), 916 (в,г)

Векторы

На данной онлайн странице электронного справочника по математике для школьников представлены следующие готовые домашние задания, гдз по предмету «Геометрия» из решебника за 9 класс:

• – задачи 1 — 8 показывают примеры решений и ответы по математике, изученных на материале курса геометрии 8 класса. Здесь рассматриваются тесты и задания по таким разделам, как средняя линия треугольника, параллелограмм, площадь треугольника, равнобедренная трапеция, вписанные и описанные окружности;
• – в тестах с номерами 9 — 12 рассматривается, как решать геометрию по теме «Коллинеарные векторы»;
• – решения векторов представлены в теме «Разложение вектора по двум неколлинеарным векторам». Контрольные работы 13 — 15;
• – тема «Координаты вектора» объясняется в работах 16 — 22 учебника. В данной рабочей тетради показываются ответы к вопросам, как решать задачи, если требуется найти координаты суммы, разности векторов и произведения вектора на число.

Задача 1.

Дано:

Четырехугольник ABCD

M, N, K, E – середины сторон AB, BC, DC, AD

 

Доказать:

Четырехугольник MNKE – параллелограмм

Доказательство:

Соединим точку А и точку С.

Получим треугольник Δ ABC, где MN – средняя линия треугольника Δ ABC и треугольник Δ ADC, где EK – средняя линия треугольника Δ ADC.

 

По свойству средней линии треугольника Δ следует, что

MN || AC – параллельны и MN= AC,

EK || AC – параллельны и EK= AC.

Тогда MN || EK – параллельны и MN=EK, поэтому

MNKE – параллелограмм (по первому признаку параллелограмма).

***

 

Задача 2.

Дано:

Треугольник Δ ABC

Сторона треугольника AB = 8,5 см

Сторона треугольника AC = 5 см

Высота AH = 4 см, т.е отрезок AH перпендикулярен стороне BC

HBC, т.е. точка H лежит на стороне BC

 

Найти:

Площадь треугольника S _ΔABC – ?

 

Решение:

S _ΔABC = BC • AH

По теореме Пифагора

BH = = = = 7,5 см

 

По теореме Пифагора

CH = = = 3 см

BC = BH + CH = 3 +7,5 = 10,5 см

S _ΔABC = • 10,5 • 4 = 21

Ответ: S _ΔABC = 21

***

 

Задача 3.

Доказать, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.

Дано:

ABCD – равнобедренная трапеция

 

Доказать: NE KM =

Доказательство:

Проведем перпендикуляры BH и CH₁, то есть BHAD перпендикулярны; также CH₁AD перпендикулярны.

Но BH и CH₁ проходят через NE тогда перпендикулярны BRNE и CR₁NE.

Стороны BH = CH₁ равны параллельны BH || CH₁

Поэтому BH = KM = CH₁ равны параллельны BH KM CH₁ как отрезок, заключенный между параллельными прямыми.

Следовательно углы равны KON = NR₁C = 90° как соответственные.

ТогдаKON = EOM = 90°, как вертикальные.

***

 

Задача 4.

Дано:

AB – отрезок

AC = CB

O – произвольная точка

 

Доказать:

Вектор OC равен половине суммы двух других векторов OA и OB, исходящих из одной и той же точки O

Доказательство: По правилу треугольника

(1)

+

(2)

Сложив выражения (1) и (2), получаем

***

 

Задача 5.

Дано:

векторы a, b, c

Три вектора и – неколлинеарные векторы.

Построить:

Суммы и разности векторов.

 

Построение:

По правилу многоугольника

a)

б)

=

 

 

 

 

 

***

 

Задача 6.

Доказать, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.

Дано:

четырехугольник ABCD – равнобедренная трапеция

 

Доказать: EF NM = , т.е. угол пересечения двух отрезков в равнобедренной трапеции равен 90°.

Доказательство:

Проведем параллельные прямые

MK || AB

MR || CD

 

Получим равнобедренный треугольник ΔMKR

AB=MK, так как трапеция равнобедренная,

CD=MR, т.к. трапеция равнобедренная.

Следовательно, EF – средняя линия треугольника ΔMKR, поэтому

MH=HR и OK=MO.

BM=MC=AK=RD, т. к. ABMK и MCDR – параллелограммы.

Поэтому HR=KO.

Тогда MN – медиана, биссектриса и высота равнобедренного треугольника ΔMKR.

Т.к. MN – высота, то отрезки MNAD – перпендикулярны.

По свойству средней линии треугольника Δ следует, что

EF || KR.

Тогда EF NM =

***

Задача 7.

Доказать, что центр окружности, вписанной в равнобедренный треугольник, лежит на медиане, проведенной к основанию.

 

Дано:

вписанная окружность в равнобедренном треугольнике

ΔABC – равнобедренный треугольник

BH₂ – медиана

 

Доказать: O BH₂, т.е. центр вписанной окружности лежит на медиане равнобедренного треугольника

Доказательство:

Проведем перпендикуляры OH₁ ; OH₂ ; OH₃ к сторонам BC, AC, AB.

Здесь из двух точек проведен один и тот же перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.

Следовательно, что O BH₂

***

 

Задача 8.

Доказать, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию или на ее продолжение.

 

Дано:

Описанная окружность около равнобедренного треугольника

Δ ABC – вписанный равнобедренный треугольник

BH₃ – медиана

Доказать: O BH₃

 

Доказательство:

Проведем из центра окружности перпендикуляры

OH₁ ; OH₂ ; OH₃ к сторонам BC, AC, AB.

Здесь проведен из двух точек перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.

Следовательно, что O BH₃

***

Наверх

Коллинеарные векторы

Лемма – теорема, вспомогательная для доказательства следующей теоремы.

 

Лемма о коллинеарных векторах:

Если векторы и коллинеарны (где ), то можно найти такое число k, что верно равенство (вектор равен произведению числа k на вектор )

 

Дано: вектор a, вектор b

Векторы и – коллинеарные, т. е. вектор b коллинеарен вектору a

 

Доказать: есть такое число k, что верно равенство

Доказательство:

1 случай. Пусть векторы a и b — сонаправленные векторы, т.е.

 

, где k>0,т.к. . Тогда и сонаправленные векторы.

Значит,

***

 

2 случай.

Пусть a, b — противоположные векторы, т.е.

Возьмем , где k<0

 

Следовательно,

***

 

Задача 9.

Дано:

вектор m, вектор n

1) – противоположно направленные векторы ,

= 0,5 см, = 2 см

2) – сонаправленные векторы ,

= 12 см, = 240 см

 

Найти: k – ?

Решение: 1) Т.к. , то k<0. Тогда

= – = – 4

Ответ: k = – 4.

Решение: 2) Т.к. , то k>0. Тогда = = 20.

Ответ: k = 20.

***

 

Задача 10.

Дано:

ABCD – параллелограмм

BD AC = O

M – середина отрезка AO

1)

2)

Найти: k – ?

Решение:

1) Т. к. , то k>0.

По свойству параллелограмма

, тогда

Ответ: k=

2) Т.к. , то k<0. , – коллинеарные, т.к. лежат на одной прямой. Найдем середину OC и обозначим ее точкой N.

Тогда AM=MO=ON=NC

Т.к. k<0, то

Ответ: k=

***

 

Задача 11.

Дано:

1) – противоположно направленные векторы,

= 400 мм, = 4дм = 400мм

2) – сонаправленные векторы , = , =

 

Найти: k – ?

Решение: 1) Т.к. , то k<0. Тогда

= – = –1

Ответ: k = –1.

 

Решение: 2) Т.к. , то k>0. Тогда = = =5.

Ответ: k = 5.

***

 

Задача 12.

Решить уравнение: найти значения x, y.

Решение: 1)

y=3

Ответ: x=0, y=3

***

 

Решить уравнение: найти значения x, y.

Решение: 2)

–3y = –1 , x= –1

y =

Ответ: x= – 1, y=

***

 

 

Наверх

Разложение вектора по двум неколлинеарным векторам

Определение: Если , где и – данные векторы, x и y – некоторые числа, то говорят, что вектор разложен на векторы и , причем x и y – коэффициенты разложения

 

Выразить вектор:

через векторы и

через и

через и

через и

 

Решение:

а) По правилу параллелограмма (x= 1, y= 1)

б) , (x=y= 2)

в) = + , = 2 – (x= 2, y = –1)

г) Т. к. = 2 – = 2 +

= – 2(x= 1, y = –2)

***

Задача 13.

Дано: ABCD – параллелограмм

;

M; AM : MC = 4 : 1

 

Найти:

Решение:

По правилу параллелограмма

или

Но , тогда

Ответ:

***

 

Задача 14.

Дано: векторы и – неколлинеарные

а)

б)

 

Найти: коэффициенты разложения x, y – ?

Решение:

а)

3 – y = 0, x+1=0 y= 3, x= – 1

б)

4 – x = 0, 5+y=0 x = 4, y= –5

Ответ: a) x= –1, y= 3 б) x = 4, y= –5

***

 

Задача 15.

Дано: ABCD – трапеция

EF – средняя линия трапеции

 

Доказать: EFAD — т.е. средняя линия трапеции параллельна её основанию,

— т.е. длина средней линии трапеции равна полусумме основанию трапеции.

Доказательство:

По правилу многоугольника

+

Сложив оба выражения, получаем

Т. к. E и F – середины сторон AB и CD, тогда

Т.к. , то , а

Поэтому EF || AD и

***

 

Теорема: Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

 

Дано:

вектор a, вектор b

и – неколлинеарные векторы

 

Доказать:

Доказательство:

Через точку А и точку В проведем прямые, параллельные прямым, содержащих векторы и . Найдем точку С.

Тогда по правилу треугольника

Заметим, что векторы и – коллинеарные, также векторы и – коллинеарные

По лемме о коллинеарных векторах

,

Тогда

 

Единственность разложения

Доказательство:

Знаем, что (1)

Пусть есть (2)

В результате разности выражений (1) и (2) получаем

Это равенство возможно

;

Т.е ;

***

 

Наверх

Координаты вектора

Определение: Единичным вектором называется вектор, длина которого равна единице.

i и j – координатные векторы

Т.к. и – неколлинеарные векторы, то любой вектор можно разложить через векторы и .

Т.е. , где x и y – координаты вектора.

{1:2}

{2:–3}

{0;0}

 

Если и ,

то , если и

***

 

Задача 16.

Найти координаты векторов.

Решение:

{2;3}

{–2;3}

{2;0}

{–3;–4}

{2;–2}

{–4;–5}

***

 

Задача 17.

Найти координаты векторов.

Решение:

{2;3}

{–;–2}

{8;0}

{1;–1}

{0;–2}

{–1;0}

***

 

Задача 18.

Найти сумму вектора по его координатам.

Решение:

{–3;}

{–2;–3}

{–1;0}

{0;3}

{0;1}

***

 

Правила, позволяющие по координатам векторов находить координаты суммы, разности векторов и произведения вектора на число.

1. Суммой векторов и с координатами (a₁;a₂) и (b₁;b₂) называется вектор с координатами (a₁+ b₁;a₂ +b₂).

 

Дано:

{a₁;a₂}; {b₁;b₂};

 

Доказать: { a₁+ b₁;a₂ +b₂}

— сумма координат вектора, т.е. формула, как найти координаты вектора через сложение

Доказательство:

{ a₁+ b₁;a₂ +b₂}

***

 

Пример 1 — сложение векторов, как найти координаты векторов:

Если даны координаты векторов {3;2}; {2;5}, то

 

2. Разностью векторов и с координатами {a₁; a₂} и {b₁; b₂} называется вектор с координатами {a₁ – b₁; a₂ – b₂}.

3. Произведением вектора с координатами {a₁; a₂} на произвольное число k называется вектор с координатами {ka₁; ka₂}.

Дано:

{a₁;a₂}

k – произвольное число

 

Доказать: {ka₁; ka₂}

— умножение вектора на число

Доказательство:

Значит, вектор {ka₁; ka₂}

 

Пример 2 — как находить координаты вектора:

Найти координаты вектора , если

{1;2}; {0;3}; {–2;3}

Решение:

{0;6}

{0;6}

Ответ: {0;6}

***

 

Задача 19.

Найти координаты вектора , если даны векторы

{–7;–1}; {–1;7}; {4;–6}

Решение:

= {–21;–14}

Ответ: {–21;–14}

***

 

Задача 20.

Дано:

1)

2)

Найти: коэффициенты разложения x, y – ?

Решение:

1)

По теореме о разложении вектора по двум неколлинеарным векторам:

x=–3, y=7

2)

По теореме о разложении вектора по двум неколлинеарным векторам:

x= –4, y=0

***

 

Задача 21.

Дано: координаты векторов

1) {3;6}; {4;–3}

2) {–5;–6}; {2;–4}

Найти: разность векторов –

Решение:

1) –= = {–1;9}

–{–1;9}

2) –= ={–7;–2}

–{–7;–2}

***

 

Задача 22.

Дано: координаты векторов

{–2;–3}; {2;–3}; {0;5}

Найти: координаты векторов, противоположных данным.

Решение:

{–2;–3}{2;3}

{2;–3}{–2;3}

{0;5}{0;–5}

***

 

MCV4U — Исчисление и векторные изображения для 12-го класса — Примечания к экзамену— onstudynotes

12 класс — Исчисление и векторы

Тест на геометрические векторы

Векторы

• Вектор : величина, имеющая направление и величину
• Скаляр: — это величина, имеющая только величину
.
• Истинный пеленг: — это направленное измерение компаса, начиная с севера и вращаясь по часовой стрелке.
• Квадрантный пеленг: — это компас, измеренный к востоку или западу от линии север-юг
• Эквивалентные векторы: равны по величине и направлению.
  • Векторы могут быть переведены в любую точку одной плоскости и при этом будут эквивалентными
• Противоположные векторы: равны по величине, но противоположны по направлению
• Векторы могут быть

Сложение и вычитание векторов

• Так как векторы остаются эквивалентными независимо от того, куда они переводятся, их можно перемещать, чтобы построить диаграммы, более удобные для решения.
• Добавление векторов с использованием метода «хвост к голове» с использованием треугольника или «хвост к хвосту», метод с использованием параллелограмма.
• Результат — это вектор, соединяющий начало первого вектора с хвостом последнего вектора
• Если 2 вектора a и b параллельны в одном направлении, | a + b | = | а | + | b | и в том же направлении
• Если a и b имеют противоположные направления и | а | > | b |, то | а + б | = | а | — | б | и a + b находится в том же направлении, что и a.
• Вычесть векторы, добавив противоположный вектор
• Нулевой вектор: означает, что нет величины или направления. Сложение двух противоположных векторов
• Векторы следуют коммутативным, ассоциативным, и идентичности свойств
  • Их можно складывать в любом порядке
  • Упрощение векторных выражений аналогично упрощению целочисленных выражений

Скалярное умножение векторов

• Когда вектор умножается на скаляр, величина умножается на скаляр, и векторы параллельны.Направления остаются неизменными, если скаляр положительный, и становятся противоположными, если скаляр отрицательный.
• Умножение векторов подчиняется правилу распределения и ассоциативности
  • Их можно расширить с помощью FOIL
  • Их можно умножать в любом порядке
• Линейная комбинация векторов может быть сформирована путем добавления скалярных кратных 2 или более векторов.

Приложения геометрических векторов

• 2 Векторы, которые перпендикулярны друг другу и суммируются, чтобы получить вектор v, называются компонентами прямоугольного вектора v.
• При решении результирующих вы можете использовать векторные операции, теорему Пифагора или тригонометрию.
• Equilibriant Vector : противоположность результирующего

12 класс — Исчисление и векторы

Тест декартовых векторов

Векторы

• Единичные векторы: i = [1, 0], j = [0,1] имеют величину 1 и хвосты в начале координат.
• Декартов вектор — это представление вектора на декартовой плоскости, где конечными точками являются точки на декартовой плоскости.
• Если вектор u транслируется так, что хвост находится в 0,0, то этот вектор называется вектором положения . Позиционные векторы представлены в квадратных скобках, где точки — [u1, u2].
• Величина u = [u1, u2] равна | u | = √ (u1 ² + u2 ² )
• Горизонтальные и вертикальные компоненты вектора u можно обозначить как [u1, 0] и [0, u1] соответственно
• Для векторов u = [u1, u2] и v = [v1, v2] и скаляра k,
  • u + v = [u1 + v1, u2 + v2]
  • u — v = [u1 — v1, u2 — v2]
  • кв = [кв1, кв2]
• Декартов вектор между двумя точками P1 (x1, y1) и P2 (x2, y2) равен P1P2 = [x2 — x1, y2 — y1]
• Геометрические векторы также можно записать как:
  • v = [| v | cosX, | v | sinX], где X — угол, составляющий v относительно положительной оси x

Точечный продукт

• Скалярное произведение определяется как a ∙ b = | a | | б | cos X, где X — угол между a и b.
• Точечное произведение дает скаляр.
• Для любых векторов u, v и w и скаляра k,
  • u и v не могут быть нулевыми, перпендикулярны тогда и только тогда, когда u ∙ v = 0
  • Коммутативная собственность
  • Ассоциативное свойство
  • Распределительная собственность
  • u ∙ u = | u | ²
  • ед ∙ 0 = 0
• Если u = [u1, u2] и v = [v1, v2], то u ∙ v = u1 * v1 + u2 * v2

Применения точечного произведения

• Для любых двух векторов u и v с углом X между ними проекция v на u является векторной составляющей v в направлении u.
  • proj _u v = | v | cos X (1 / | u | * | u |) или proj _u v = (v ∙ u / u ∙ u) u
  • | proj _u v | = | v | cos X, если 0
  • | proj _u v | = — | v | cos X если 90
  • | proj _u v | = | u ∙ v / | u | |
• На основании угла между u и v вы можете определить направление проекции.

Векторы в 3-м пространстве

• Те же свойства и формулы, что и у векторов в пространстве 2
• Ортогонально: Если 2 вектора ортогональны, угол между ними составляет 90 градусов.

Перекрестное произведение

• Перекрестное произведение между двумя векторами найдет вектор, перпендикулярный между ними обоими
• Используется для определения крутящего момента
• Направление определяется с помощью правила правой руки. Пальцы указывают на вектор r, затем наклоняются к вектору f, большой палец указывает в направлении векторного произведения
• a X b = (| a | | b | sin X) n где n — единичный вектор, ортогональный как a, так и b согласно правилу правой руки для направления, а X — угол между векторами.
• Для декартовых векторов:
  • Если v = [v1, v2, v3] и u = [u1, u2, u3]
  • u X v = [u2v3 — u3v1, u3v1 — u1v3, u1v2 — u2v1]
• | a X b | = | а | | б | грех X
  • Это также вычисляет площадь параллелограмма
• Жилье
  • u X v = — (v X u)
  • Распределительная собственность
  • ассоциативное свойство
  • коммутативная собственность
  • Если u! = 0 и v! = 0, u X v = 0 тогда и только тогда, когда u = mv, другими словами, они должны быть коллинеарны, чтобы это произошло.

Приложения перекрестного продукта

• Крутящий момент — это произведение длины гаечного ключа на прилагаемую силу
• Формулы для проекционных работ в 3D и 2D
• Тройное скалярное произведение: a * b X c
  • Перекрестное произведение должно быть выполнено до того, как будет выполнено скалярное произведение
• Объем параллелограмма составляет: V = | w * u X v |
• Работа против силы тяжести — это скалярное произведение только с осью z для силы тяжести.

12 класс — Исчисление и векторы

Испытание линий и плоскостей

Уравнение линий 2-х и 3-х пространств

• В двухмерном пространстве линию можно определить четырьмя способами: наклонная форма пересечения оси y, векторное уравнение, параметрическая форма или скалярная форма.
  • Наклон формы Y-пересечения: y = mx + b
    • м — уклон
    • b — точка пересечения по оси y
  • Векторная форма: r = r ₀ + tm
    • или: [x, y] = [x ₀ , y ₀ ] + t [m ₁ , m ₂ ]
    • [x, y] — вектор положения в любую точку на линии
    • [x ₀ , y ₀ ] — вектор положения в любую точку на линии
    • [m ₁ , m ₂ ] — вектор направления для линии
  • Параметрическая форма:
    • x = x _o + tm ₁ или x = x ₀ + t [m ₁ ]
    • y = y ₀ + tm ₂ или y = y ₀ + t [m ₂ ]
    • Те же определения, что и в векторной форме, получены из векторной формы
  • Скалярная форма: ax + by + c = 0
    • n = [a, b] — вектор нормали к линии
    • Если вектор направления d = [a, b], то вектор нормали n = [-b, a]

• В 3-пространстве линия может быть определена с помощью векторного уравнения или параметрического уравнения
  • Векторная форма: r = r ₀ + tm
    • или: [x, y, z] = [x ₀ , y _0, z ₀ ] + t [m ₁ , m _{2 ,} м ₃ ]
    • [x, y, z] — вектор положения в любую точку на линии
    • [x ₀ , y _0, z ₀ ] — вектор положения в любую точку на линии
    • [m ₁ , m _2, m ₃ ] — вектор направления для линии
  • Параметрическая форма:
    • x = x _o + tm ₁ или x = x ₀ + t [m ₁ ]
    • y = y ₀ + tm ₂ или y = y ₀ + t [m ₂ ]
    • z = z ₀ + tm ₃ или y = z ₀ + t [m ₃ ]
    • Те же определения, что и в векторной форме, получены из векторной формы
• Вектор нормали — это линия, перпендикулярная этой линии
• Для определения линии необходимы 2 точки или точка и вектор направления
• Для линий в двухместном пространстве точка и вектор нормали также могут определять линию

Уравнения плоскостей

• В двухмерном пространстве скалярное уравнение определяет линию.В трехмерном пространстве скалярное уравнение определяет плоскость
• В 3-пространстве плоскость может быть определена с помощью векторного уравнения, параметрического уравнения или скалярного уравнения.
  • Векторная форма: r = r ₀ + tm
    • или: [x, y, z] = [x ₀ , y _0, z ₀ ] + t [a ₁ , a _{2 ,} a ₃ ] + s [b ₁ , b _2, b ₃ ]
    • [x, y, z] — вектор положения для любой точки на плоскости
    • [x ₀ , y _0, z ₀ ] — вектор положения для любой точки на плоскости
    • [a ₁ , a _2, a ₃ ] и [b ₁ , b _2, b ₃ ] должны быть непараллельными векторами на плоскости
  • Параметрическая форма:
    • x = x _o + ta ₁ + tb ₁ или x = x ₀ + t [a ₁ ] + s [b ₁ ]
    • y = y ₀ + ta ₂ + tb ₂ или y = y ₀ + t [a ₂ ] + s [b ₂ ]
    • z = z ₀ + ta ₃ + tb ₃ или y = z ₀ + t [a ₃ ] + s [b ₃ ]
    • Те же определения, что и в векторной форме, получены из векторной формы
  • Скалярная форма: ax + by + cz + d = 0
    • Где [a, b, c] — вектор, нормальный к плоскости
• Плоскость может быть определена 3 неколлинеарными точками или точкой и 2 непараллельными векторами направления
• Перехват самолета
  • Пересечение плоскости по оси X находится путем задания y = z = 0 и решения относительно x
  • Пересечения Y и Z одинаковы, если установить другие 2 переменные на ноль

Пересечение линий в 2-м и 3-м пространствах

• В 2-Space пересечение двух линий имеет 3 возможности.
  • (1) Линии пересекаются ровно в одной точке
  • (2) Линии совпадают, значит решений бесконечно много
  • (3) Линии параллельны, решений нет
• В 3-пространстве пересечение двух линий может иметь 4 возможности
  • (1) Они пересекаются в одной точке
  • (2) Они совпадают
  • (3) Они параллельны
  • (4) Это перекошенных линий , где они не параллельны и не имеют решения
• Чтобы найти расстояние между двумя наклонными линиями, формула:
  • d = | (P ₁ P ₂ точка n / n) |
  • , где P ₁ и P ₂ — любые точки на каждой линии, а n = m ₁ x m ₂ .
• Чтобы найти пересечение, просто приравняйте каждую пару линий в параметрической форме и решите для X, Y и Z в каждом наборе.

Пересечение плоскостей и линий

• В 3-пространстве пересечение плоскостей и линий имеет 3 возможности
  • (1) Прямая пересекает плоскость в одной точке
  • (2) Прямая совпадает с плоскостью в бесконечном количестве точек
  • (3) Линия параллельна и не касается плоскости, решений нет
• Расстояние между точкой P и плоскостью:
  • d = | n точек PQ | / | n |
    • где n — вектор нормали к плоскости, Q — любая точка на плоскости
• Чтобы найти пересечение, подставьте каждый X, Y и Z параметрического уравнения в уравнение плоскости.Затем после того, как t будет найдено, подставьте его обратно в строку, чтобы найти каждое значение X Y и Z.

Пересечение плоскостей

• Есть 3 возможности пересечения 2-х плоскостей
  • (1) Плоскости пересекаются по линии
  • (2) Плоскости совпадают, решений бесконечно много
  • (3) Плоскости параллельны, решений нет
• С 2 самолетами:
  • 1) Проверить параллельность нормалей
  • 2) Попробуйте решить на основе параллельности нормалей
    • Если они параллельны, вы получите бесконечное число решений или их отсутствие.
    • Если они не параллельны, в качестве решения вы получите линию

• Есть 7 возможностей пересечения 3-х плоскостей:
  • Если их нормали параллельны
    • (1) Все 3 плоскости совпадают, если все нормали одинаковы
    • (2) Все 3 плоскости параллельны, если все нормали различны
    • (3) 2 плоскости совпадают и 1 параллельна, если 2 нормали различны
    • (4) 1 плоскость пересекает 2 плоскости, совпадающие или параллельные, если 2 нормали совпадают
  • Если их нормали не параллельны
    • Если тройное скалярное произведение (n1 x n2) * n3 = 0
      • (5) Треугольная призма сформирована без пересечения (0x + 0y = c)
      • (6) «Вращающаяся дверь» образована пересечением линий (0x + 0y = 0)
    • Если тройное скалярное произведение не равно 0
      • (7) Все плоскости пересекаются в точке
• Для пересечения карусельной двери и пересечения двух плоскостей на одной линии, параметр z = t должен использоваться для определения линии пересечения.

12 класс — Исчисление и векторы

Тест на скорость изменений

Темпы изменения и наклон кривой

• Средняя скорость изменения: означает скорость изменения функции за интервал. Он соответствует наклону секущей, соединяющей две конечные точки интервала
.
• Мгновенная скорость изменения: относится к скорости изменения в определенной точке.Он соответствует наклону касательной, проходящей через единственную точку или точку касания на графике функции.
  • Оценка мгновенной скорости изменения может быть получена путем вычисления средней скорости изменения на наименьшем интервале, для которого доступны данные.
  • Его также можно определить, нарисовав касательную на графике

Темпы изменения с использованием уравнений

• Для заданной функции y = f (x) мгновенная скорость изменения при x = a оценивается путем вычисления наклона секущей на очень небольшом интервале, a <= x <= a + h, так что h очень маленькое число
• Выражение f (a + h) — f (a) / h, где h not = 0, называется коэффициентом разности
  • Используется для вычисления наклона секущей между (a, f (a)) и (a + h, f (a + h)).Это позволит вам оценить наклон касательной при приближении h к 0.

Лимиты

• Последовательность — это функция, f (n) = t _n , доменом которой является набор натуральных чисел N
Предел
• , когда x приближается к a для f (x), существует, если выполняются следующие условия:
  • существует предел, когда x приближается к a- для f (x) (существует левый предел)
  • существует предел, когда x приближается к a + для f (x) (существует правый предел)
  • правая граница и левая граница равны
• Если они не равны и критерии не соблюдаются, то ограничение не существует
• Пределы могут быть бесконечным действительным числом
• Функция продолжается со значением, если они верны:
  • f (a) существует
  • предел, когда x приближается к существует
  • Предел, когда x приближается к a и f (a) одинаковы

Ограничения и непрерывность

• Предел функции при x = a может существовать, даже если функция является разрывной при x = a.
• Короче говоря, график прерывистой функции невозможно нарисовать, не подняв карандаш
• Есть 3 вида прерывания: прыжок, съемный и бесконечный
• Если прямая подстановка x = a приводит к неопределенному пределу 0/0, определите эквивалентную функцию, которая представляет f (x).
• Разрыв может быть устранен путем разложения на множители, рационализации числителя или знаменателя, расширения и упрощения.

Введение в производные инструменты

• Производные y = f (x) — это новая функция y = f ‘(x), которая представляет наклон касательной или мгновенную скорость изменения в любой точке кривой y = f (x). .
• Производная функция определяется определением первых принципов для производной, f ’(x) = lim h -> 0 f (x + h) — f (x) / h, если предел существует
• Различные обозначения для производной y = f (x) следующие: y = f ’(x), y’, dy / dx и d / dx f (x).
• Если производная не существует в точке кривой, функция недифференцируема в этом значении x. Это может происходить в точках, где функция является прерывистой, или в случаях, когда функция имеет резкое изменение, которое представлено острием или углом на графике.

12 класс — Исчисление и векторы

Тест деривативов

Производные полиномиальной функции

• Правила производных упрощают процесс дифференцирования многочленов с использованием первых принципов
• При дифференцировании радикалов мы записываем радикалы в дробной форме
• Чтобы дифференцировать степень x, стоящую в знаменателе, сначала выразите ее как степень с отрицательной экспонентой
• Правило производной: x ⁿ = nx ^n-1
• Сумма производных: (f (x) + g (x)) ’= f’ (x) + g ’(x)
• Разница производных: (f (x) — g (x)) ’= f’ (x) — g ’(x)

Правило продукта

• Правило продукта: (f (x) * g (x)) = f ’(x) g (x) + f (x) g’ (x)
• Обозначение Лейбница: d / dx [f (x) g (x)] = d / dx [f (x)] g (x) + f (x) d / dx [g (x)]

Скорость, ускорение и секундные производные

• Вторая производная функции определяется путем дифференцирования первой производной функции
• Для заданной функции положения s (t) ее функция скорости равна v (t) или s ’(t), а ее ускорение равно a (t), v’ (t) или s ’’ (t)
• Когда v (t) = 0, объект покоится.Есть много случаев, когда объект временно находится в состоянии покоя при изменении направления.
• Когда v (t)> 0, объект движется в положительном направлении
• Когда v (t) <0, объект движется в отрицательном направлении
• Когда a (t)> 0, скорость объекта увеличивается
• Когда a (t) <0, скорость объекта уменьшается
• Объект ускоряется, если a (t) x v (t)> 0, и замедляется, если v (t) x a (t) <0.

Правило цепочки

• Используется для различения составных функций, f = g o h.
• Для данной функции правило цепочки:
  • (f (g (x))) ’= f’ (g (x) * g ’(x)
• В обозначениях Лейбница,

Правило частного

• Чтобы найти производную частного:
  • q (x) = f ’(x) g (x) — f (x) g’ (x) / g ² (x)

Скорость изменения проблем

• Функция спроса или цены p (x) — это цена, по которой может быть продано x единиц продукта или услуги
• Функция дохода R (x) — это общий доход от продажи x единиц продукта или услуги.R (х) = х * P (х)
• Функция затрат C (x) — это общие затраты на производство x единиц продукта или услуги
• Функция прибыли, P (x) равно P (x) = R (x) — C (x)
• C ’(x) — функция предельных затрат
• R ’(x) — функция предельного дохода
• P ’(x) — функция предельной прибыли

12 класс — Исчисление и векторы

Тест построения эскиза кривой

Интервал увеличения и уменьшения

• Функция увеличивается, если наклон касательной положительный на всем интервале
• Функция уменьшается, если наклон касательной отрицателен на всем интервале
• Интервалы, в течение которых функция увеличивается или уменьшается, можно определить, найдя производную f ’(x) и решив неравенства f’ (x) <= 0 или f ’(x)> = 0.

Максимумы и минимумы

• Если f ’(x) изменяется с положительного на ноль на отрицательное, то всякий раз, когда он равен 0, будет точка локального максимума
• Если f ’(x) изменяется с отрицательного на ноль на положительный, то всякий раз, когда он равен 0, будет точка локального минимума
• Абсолютные максимальные и минимальные значения находятся в локальных экстремумах или в конечных точках интервала
• Критическое число — это число в области определения функции, где f ’(a) = 0 или f’ (a) существует.

Тест на вогнутость и вторые производные

• Вторая производная — это производная от первой производной.Это скорость изменения наклона касательной
  • Функция является вогнутой на интервале, если вторая производная положительна на этом интервале
  • Функция вогнута вниз на интервале, если вторая производная отрицательна
  • Функция имеет точку перегиба в точке, где вторая производная меняет знак, где f ’’ (x) = 0
• Критические точки можно классифицировать, используя вторую производную или исследуя график f ’’ (x)
  • Если f ’(a) = 0 и f’ ’(a)> 0, существует локальный минимум в (a, f (a))
  • Если f ’(a) = 0 и f’ ’(a) <0, существует локальный максимум в (a, f (a))
  • Если f ’(a) = 0 и f’ ’(a) = 0, а f’ ’(x) меняет знак в x = a, то есть POI в (a, f (a))

Простые рациональные функции

• Вертикальные асимптоты — это значения x, при которых знаменатель равен нулю
• Учитывать ВА при поиске интервалов увеличения или уменьшения вогнутости

Эскиз кривой

• При рисовании кривой не забудьте включить область, асимптоты, точки пересечения, критические значения от первой производной, критические значения второй производной, локальные и абсолютные экстремумы, точки перегиба, интервалы увеличения и уменьшения и вогнутость.

Проблемы оптимизации

• Определите, в чем проблема
• Определите переменные и создайте диаграмму, если это помогает
• Определите количество, которое нужно оптимизировать, и напишите уравнение
• Определить независимую переменную
• Определить функцию
• Определение и ограничения функции
• Определите функции и классифицируйте критические точки
• Проверьте, соответствует ли решение заданному вопросу и соответствует ли оно вопросу

12 класс — Исчисление и векторы

Синусоидальные и логарифмические производные

Производные функции синуса и косинуса

• Производная y = sin x: y ’= cos x
• Производная y = cos x: y ’= -sin x
• Производная y = sin (f (x)): y ’= cos (f (x)) * f’ (x)
• Производная y = cos (f (x)): y ’= -sinx (f (x)) * f’ (x)
• Производная y = sin ² (f (x)) равна y ’= 2 cos (f (x)) * f’ (x)
• Производная y = cos ² (f (x)) равна y ’= -2 sin (f (x)) * f’ (x)

Простые задачи тригонометрических приложений с гармоническим движением

• 1-я производная, используемая для нахождения скоростей
• 2-я производная, используемая для определения ускорения, а также максимальной / минимальной скорости
• Чтобы найти период из его уравнения, это 360 / k или 2 Pi / k для радианов

Номер e

• Символ e определяется как предел, когда n -> бесконечность (1 + 1 / n) ⁿ .Значение ~ 2.71
• Скорость изменения экспоненциальной функции также является экспоненциальной
• Производная y = e ^x равна y = e ^x (то же, что и исходная функция)

Натуральный логарифм

• Lnx = бревно _e x
• Функции y = lnx и y = e ^x являются обратными

Производные от экспонент

• Производная y = b ^x : y ’= b ^x * lnx
• Производная y = b ^{f (x)} равна y ’= b ^{f (x)} * ln b * f’ (x)
• Производная y = e ^{f (x)} равна y ’= e ^{f (x)} * f’ (x)
• Вы решаете большинство логарифмов, применяя ln или записывая обе стороны и изолировав переменную.

Правописание для 9-х классов, списки, игры и задания

Списки правописания, игры и мероприятия для 9-х классов

Подпишитесь на Home Spelling Words!

Практикуйтесь, используя наши списки правописания для 9-го класса или составляйте свои собственные списки для 9-го класса, вводя слова в ваш аккаунт. Вы также можете импортировать наши списки и добавлять свои собственные списки. Наш сайт проверки орфографии чрезвычайно гибкий.9-й класс — идеальное время, чтобы расширить словарный запас вашего ученика с помощью этого веб-сайта, введя определение предложения со списками лексики. Мы выбрали несколько довольно сложных орфографических слов для 9-го класса для нашего списки, чтобы ваш ученик получил настоящую задачу. Убедись, что ты завести аккаунт так что вы можете сохранить свои результаты! Сдавайте тесты и тренируйтесь сколько угодно раз. Помните, практикуйтесь делает совершенным.

Орфографические игры, списки и задания для 9-х классов

Создавайте собственные списки правописания

Создавайте собственные списки правописания, зарегистрировавшись в своей учетной записи Home Spelling Words.Мы не продаем и не передаем вашу информацию и не отправляем вам нежелательные электронные письма. После регистрации просто введите название своего списка (пример: Список 1), затем каждое правописание и предложение для практики, если хотите. Как только вы закончите, опубликуйте свой список и немедленно начните практиковаться. Вы также можете сдавайте тесты или играйте в орфографические игры со своими списками. Наш сайт — полезный инструмент для для домашних школ с их собственной учебной программой или студентов, которые получают еженедельный список правописания из школы.Правописание — это просто и весело!

Что говорят родители …
Возможность войти в списки из школы и практиковаться в Интернете стала для детей намного веселее. чем заставлять их записывать свои слова снова и снова.
Рассвет К.

Мы использовали домашнее правописание для изучения словарного запаса, и это было действительно полезно. Это простая программа, которой легко пользоваться.
Рэйчел П.

Орфографические игры

• Игра с заполнением пустого места Каждый раз создается новая игра, так что вы можете играть всю неделю и не скучать!
• Поиск слова Случайным образом создает новое слово для вашего ученика каждый раз, используя слова из его списка правописания.
• Spelling Soup Поймайте правильно написанное слово своей тарелкой для супа и заработайте очки.

Хеш-тестовые векторы

В криптографии хеш-значения вычисляются путем применения хеш-функции определенного типа (MD5, SHA-1, CRC32 и т. Д.) в последовательность данных, создавая выходные данные фиксированной длины, которые представляют исходные данные неуникальным образом. Впоследствии дайджесты сообщений можно использовать для проверки целостности или подлинности данных.

Перейти к…

Тестовые векторы

Каждая хеш-функция генерирует различное криптографическое хеш-значение. В таблице ниже представлены тестовые векторы для всех хэш-функций, поддерживаемых калькулятором контрольной суммы хеша и CRC.

1 · Быстрая коричневая лисица…

Тестовый вектор для Hash («Быстрая коричневая лисица перепрыгивает через ленивую собаку») · 43 байта

Быстрая коричневая лиса перепрыгивает через ленивую собаку
CRC32 (): 414fa339
MD2 (): 03d85a0d629d2c442e987525319fc471
MD4 (): 1bee69a46ba811185c194762abaeae90
MD5 (): 9e107d9d372bb6826bd81d3542a419d6
SHA-1 (): девяносто один тысячу четыреста сорок пять 2fd4e1c67a2d28fced849ee1bb76e7391b93eb12
SHA-224 (): 730e109bd7a8a32b1cb9d9a09aa2325d2430587ddbc0c38bad 5
SHA-256 (): + d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592
SHA-384 (): 91 466 ca737f1014a48f4c0b6dd43cb177b0afd9e5169367544c49 4011 e3317dbf9a509cb1e5dc1e85a941bbee3d7f2afbc9b1
SHA-512 (): + 07e547d9586f6a73f73fbac0435ed76951218fb7d0c8d788a309d785436bbb64 2e93a252a954f23 7d1e8a3b5ed6e1bfd7097821233fa0538f3db854fee6
RIPEMD-128 (): 3fa9b57f053c053fbe2735b2380db596
RIPEMD-160 (): 37f332f68db77bd9d7edd4969571ad671cf9dd3b
RIPEMD-256 (): c3b0c2f764ac6d576a6c430fb61a6f2255b4fa833e094b1ba8c1e29b6353036f
RIPEMD-320 (): e7660e67549435c62141e51c9ab1dcc3b1ee9f65 c0b3e561ae8f58c5dba3d21997781cd1cc6fbc34
ГИДРОМАССАЖ (): b97de512e91e3828b40d2b0fdce9ceb3c4a71f9bea8d88e75c4fa854df36725f d2b52eb6544edcacd6f8beddfea403cb55ae31f03ad62a5ef54e42ee82c3fb35
Тайгер-192 (): 6d12a41e72e644f017b6f0e2f7b44c6285 f06dd5d2c5b075

2 · Тестовый вектор из…

Тестовый вектор для Hash («Тестовый вектор из febooti.com «) · 28 байт

Тестовый вектор с febooti.com
CRC32 (): 0c877f61
MD2 (): 820d 9d1408 ): 6578f2664bc56e0b5b3f85ed26ecc67b
MD5 (): 500ab6613c6db7fbd30c62f5ff573d0f
SHA-1 (): a7631795f6d59cd6d14ebd0058a6394a4b93d868
SHA-224 (): + 3628b402254caa96827e3c79c0a559e4558da8ee2b65f1496578137d
SHA-256 (): 91 584 077b18fe29036ada4890bdec192186e10678597a678802df70df4bac9ab
SHA-384 (): 388bb2d487de48740f45fcb44152b0b665428c49def1aaf7 девяносто одна тысяча пятьсот девяносто один c7f09a40c10aff1cd7c3fe3325193c4dd35d4eaa032f49b0
SHA-512 (): 09fb898bc97319a243a63f697 девяносто одна тысяча пятьсот девяносто девять 1747f8e102481fb8d5346c55cb44855adc2e0e9 8f304e552b0db1d4eeba8a5c8779f6a3010f0e1a2beb5b9547a13b6edca11e8a
RIPEMD-128 (): ab076efaab01d30d16bb57f88d63c073
RIPEMD-160 (): 4e1ff644ca9f6e86167ccb30ff27e0d84ceb2a61
RIPEMD-256 (): девяносто одна тысяча шестьсот двадцать один 3bcbe8d6c9cf2cff39fb53e0dcef37f1554223da45d941d95836e1f5f84677eb
RIPEMD-320 (): девяносто одна тысяча шестьсот двадцать восемь 7ae55f027f08f354a53515b9d6df00746ddeb1e7 c8bbe8ee2c5ff8428aca0ad7d24eb64562b2e6c9
ГИДРОМАССАЖ (): e006fb0f4817f501 177e61a575057cbd486ce2d28d882aa23624440ada5 7c0913cc7b016f6315f612a9320203e0b5fa32b510c42d03bfc7b96c2769a740
Тайгер-192 (): девяносто один тысячу шестьсот сорок четыре 382599758b759db703d4940c08c3393182adad7e9a7e590f

3 · Пустой

Тестовый вектор для Hash («») · 0 байт

cdf26213a150dc3ecb610f18f6b38b46 02ba4c4e5f8ecd1877fc52d64d30e37a2d9774fb1e5d026380ae0168e3c5522d 3293ac630c13f0245f92bbb1766e16167a4e58492dde73f3 91 524

Автоматизировать хеширование?

Необходимо автоматически вычислять контрольные суммы? Как только файл будет скопирован или перемещен? По SFTP или по расписанию? Имена файлов Unicode и путь к файлу до 32 КБ? Мы вас прикрыли!
См. Решение о том, как автоматически вычислять контрольные суммы файлов и получать результаты.

Нужна помощь?

Если у вас есть вопросы, не стесняйтесь обращаться в нашу службу поддержки.

Один образец и парный (с примером)

• Home

• Testing

  • • Back
    • Agile Testing
    • BugZilla
    • Cucumber
    • Тестирование базы данных
    • ETL Testing
    • Jmeter
    • JIRA
  • Назад
  • JUnit
  • LoadRunner
  • Ручное тестирование
  • Мобильное тестирование
  • Mantis
  • Почтальон
  • QTP
  • Назад
  • Центр качества (ALM)
  • RPA
  • SAP Testing
  • Selenium
  • SoapU
  • Управление тестированием
  • TestLink

SAP

• • Назад
  • ABAP 9001 8
  • APO
  • Начинающий
  • Basis
  • BODS
  • BI
  • BPC
  • CO
  • Назад
  • CRM
  • Crystal Reports
  • FICO
  • HANA
  • HR
  • MM
  • QM
  • Заработная плата
  • Назад
  • PI / PO
  • PP
  • SD
  • SAPUI5
  • Безопасность
  • Менеджер решений
  • Successfactors
  • Учебники SAP

Интернет

• • Назад
  • Apache
  • AngularJS
  • ASP.Net
  • C
  • C #
  • C ++
  • CodeIgniter
  • СУБД
  • JavaScript
  • Назад
  • Java
  • JSP
  • Kotlin
  • Linux
  • MariaDB
  • MS Access
  • MYSQL
  • Node. js
  • Perl
  • Назад
  • PHP
  • PL / SQL
  • PostgreSQL
  • Python
  • ReactJS
  • Ruby & Rails
  • Scala
  • SQL
  • SQLite
  • Назад
  • SQL Server
  • UML
  • VB.Net
  • VBScript
  • Веб-службы
  • WPF

Обязательно изучите!

• • Назад
  • Учет
  • Алгоритмы
  • Android
  • Блокчейн
  • Бизнес-аналитик
  • Создание веб-сайта
  • Облачные вычисления
  • COBOL
  • Дизайн компилятора
  • Назад
  • E

.

No related posts.

Leave a Reply

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

Пустой
CRC32 (): девяносто одна тысяча шестьсот шестьдесят семь 00000000
MD2 (): 91 674 8350e5a3e24c153df2275c9f80692773
MD4 (): + 31d6cfe0d16ae931b73c59d7e0c089c0
MD5 ( ): d41d8cd98f00b204e9800998ecf8427e
SHA-1 (): da39a3ee5e6b4b0d3255bfef95601890afd80709
SHA-224 (): d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42f
SHA-256 (): e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
SHA-384 (): 38b060a751ac96384cd9327eb1b1e36a21fdb71114be0743 4c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95b
SHA-512 (): + cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce 4 7d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e
RIPEMD-128 ():
RIPEMD-160 (): + 9c1185a5c5e9fc54612808977ee8f548b2258d31
RIPEMD-256 ():
RIPEMD- 320 (): 22d65d5661536cdc75c1fdf5c6de7b41b9f27325 девяносто одна тысяча семьсот пятьдесят-три ebc61e8557177d705a0ec880151c3a32a00899b8
ГИДРОМАССАЖ (): + 19fa61d75522a4669b44e39c1d2e1726c530232130d407f89afee0964997f7a7 3e83be698b288febcf88e3e03c4f0757ea8964e59b63d93708b138cc42a66eb3
Тайгер-192 ():