
Контрольная тестовая работа по геометрии в 8 классе
Подготовила: учитель математики высшей квалификационной категории МБОУ СОШ с.Маркелово Шегарского района Томской области Исмухамедова Татьяна Алексеевна.
Пояснительная записка
Контрольная тестовая работа по геометрии предназначена для выходного контроля уровня знаний обучающихся 8-х классов.
Назначение работы – оценить уровень овладения обучающимися программным материалом по геометрии 8 класса. Курс геометрии изучается по учебнику "Геометрия 7 - 9" авторов Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк. Уроки геометрии проводятся 2 ч. в неделю, всего за год - 70 ч.
Тестовая часть работы направлена на проверку достижения уровня обязательной подготовки. Входящих в нее заданиях №1, 2, 3 необходимо из предложенных трех ответов выбрать один правильный и обвести кружком его номер. При решении заданий № 4 и № 5 требуется записать полученный краткий ответ. С помощью этих заданий проверяется умение владеть основными понятиями, знание алгоритмов при выполнении определенных действий, а также применение изученного в простейших практических ситуациях.
Вторая часть - задания № 6, 7, 8 и № 9, направлена на проверку повышенного уровня владения программным материалом. При выполнении этой части проверяется способность учащихся проанализировать условие, правильно выполнить чертеж к задаче, применять различные приемы рассуждений, грамотно обосновать свое решение.
Система оценивания
На выполнение работы отводится 1 урок. Первая часть выполняется в бланке с текстами заданий. В заданиях с выбором ответа ученик отмечает тот ответ, который считает верным; в заданиях с кратким ответом – вписывается ответ в отведенное место. Задания второй части выполняются на листах с выполненным чертежом и записью хода решения.
Для оценивания результатов выполнения работы применяются отметки «2», «3», «4», «5».
Задание первой части считается выполненным, если верно обведен номер ответа, или верно записан ответ. Задание второй части считается выполненным верно, если обучающийся выбрал правильный путь решения и получил верный ответ.
правильно решено
0-4 заданий
5- 6 заданий
7-8 заданий
9 заданий
отметка
«2»
«3»
«4»
«5»
Итоговая тестовая работа по геометрии. 8 класс
В - I
Фамилия, имя_____________________________________ Класс__________
1. Периметр параллелограмма равен 24 см. Чему равна сумма двух соседних сторон?

С
а) 16 см б) 12 см в) 18 см2
В
D
. Найдите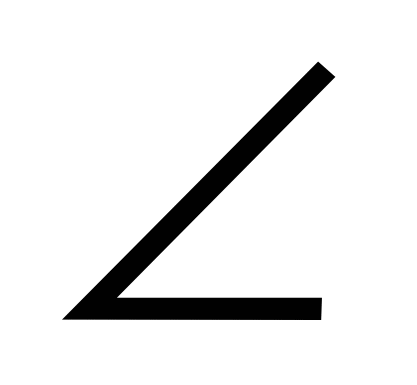 А,
А, 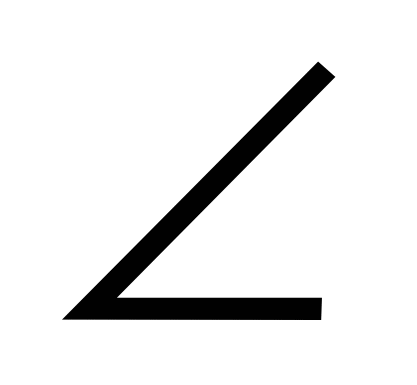 В,
В,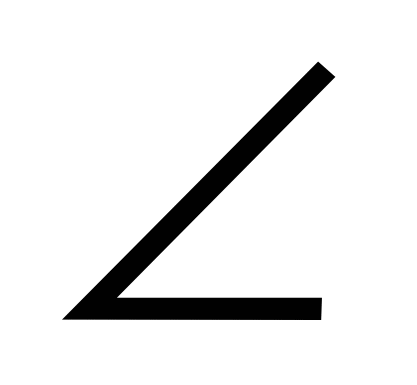 С ромба АВСD, если
С ромба АВСD, если 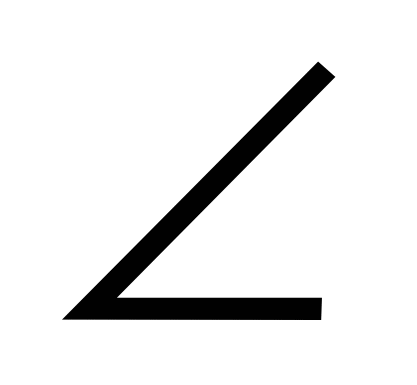 D = 70º.
D = 70º. А
а) 110º, 70º, 110º б) 140º, 70º, 140º в) 55º, 70º, 55º 
В
С
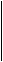
3. Найдите площадь параллелограмма АВСD,
А
30º
если АВ = 4см, ВС = 7см, А = 30º.
А = 30º. D
а) 28см2 б) 14см2 в) 56см24
В
. Найдите периметр Δ FEK, образованный средними линиями Δ АВС, если 
F
E
АВ = 14cм, ВС = 16см, АС = 20см?
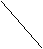
С
А

K
Ответ:________________ 5. Найдите площадь Δ СМЕ, если CМ = 8см, СЕ = 10см, 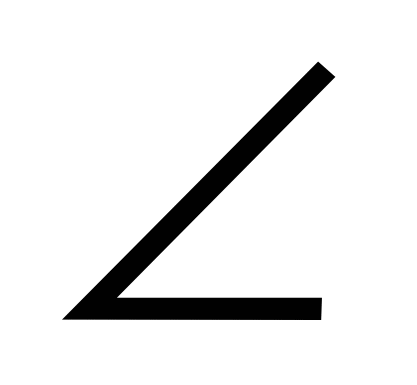 С = 45º.
С = 45º.
Ответ:_________________
6. Боковая сторона равнобедренного треугольника АВС равна 29см, а высота
 составляет 21см. Чему равно основание АС этого треугольника?
составляет 21см. Чему равно основание АС этого треугольника?
7
?м
. Фонарь освещает дерево высотой 2,8м,  находящееся от него на расстоянии 6м,
находящееся от него на расстоянии 6м,
2,8м
 длина тени, отбрасываемой этим деревом - 4м.
длина тени, отбрасываемой этим деревом - 4м. На какой высоте висит фонарь?
4м
6м

8. В равнобедренный треугольник вписана окружность. Точка касания этой
окружности делит боковую сторону на отрезки 6см и 8см, считая от основания.
В
Найдите периметр треугольника. 
9

А
. Прямая АD касается окружности в точке А, вписанный  АСВ равен 20º. Найдите
АСВ равен 20º. Найдите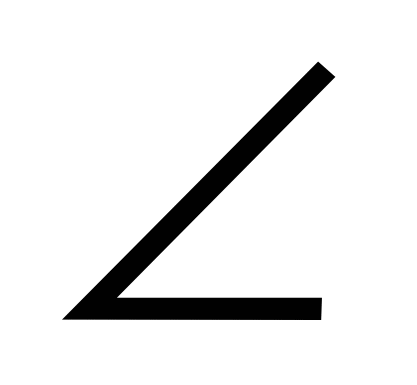 ВАD.
ВАD.


С
D
О
Итоговая тестовая работа по геометрии. 8 класс
В - II
Фамилия, имя_____________________________________ Класс__________
1. Сумма двух соседних сторон параллелограмма равна 10 см. Чему равен его
периметр?

N
а) 10 см б) 40 см в) 20 см2
М
К
. Найдите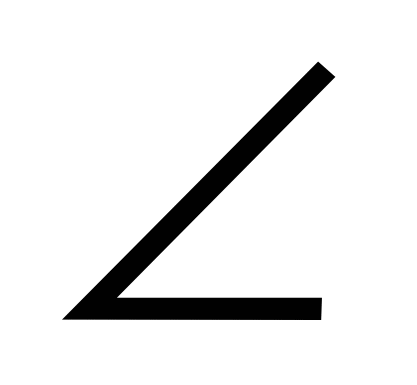 М,
М, 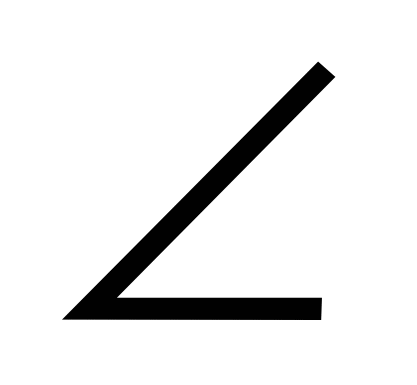 N,
N, К ромба МNКС, если
К ромба МNКС, если  С = 100º.
С = 100º. С
а) 80º,100º, 80º б) 130º, 100º, 130º в) 100º, 80º, 100º 
К
С
3. Найдите сторону МD параллелограмма МКСD, если его
30º
площадь равна 36см2, а МК = 6см, М = 30º.
М = 30º. М
D
а) 6смб) 12см в) 3см4
В
. Найдите периметр Δ АВС, если средние линии его равны 
Р
D
РD = 8cм, РК = 12см, DК = 10см?
С
А

K
Ответ:________________ 5. Найдите площадь Δ МСК, если МК = 12см, СК = 14см,  К = 60º.
К = 60º.
Ответ:_________________
6. Высота равнобедренного треугольника АВС равна 15см, длина основания АС

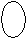 равна 16 см. Чему равна боковая сторона этого треугольника?
равна 16 см. Чему равна боковая сторона этого треугольника?

7. Дерево стоит в 8 м от столба, на котором закреплен фонарь.

7,5м
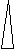 Фонарь висит на высоте 7,5 м, длина тени, отбрасываемой
Фонарь висит на высоте 7,5 м, длина тени, отбрасываемой ?м
этим деревом - 2м. Найдите высоту дерева?
2м
8м
8. В равнобедренный треугольник вписана окружность. Точка касания этой
окружности делит боковую сторону на отрезки 7см и 9см, считая от основания.
М
D
Найдите периметр треугольника.9
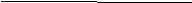
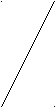
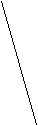 . Прямая DМ касается окружности в точке D,
. Прямая DМ касается окружности в точке D, 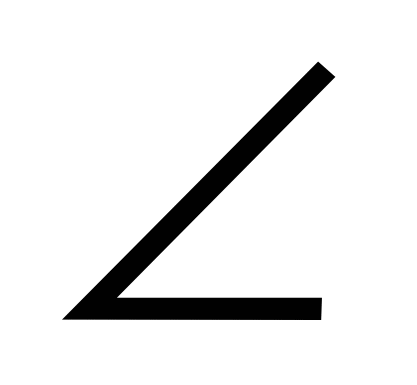 MDK
MDK
равен 130º. Найдите вписанный 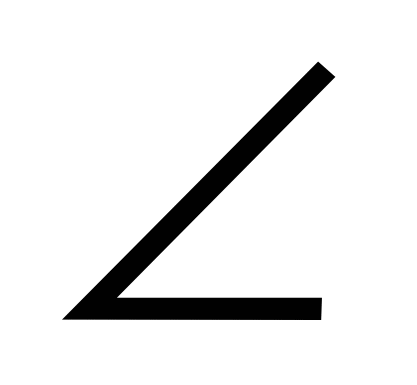 DCК.
DCК.


О
К
С
Ответы тестовой работы:
№ задания
1
2
3
4
5
6
7
8
9
1
вариант
б
а
б
Р=25см
S=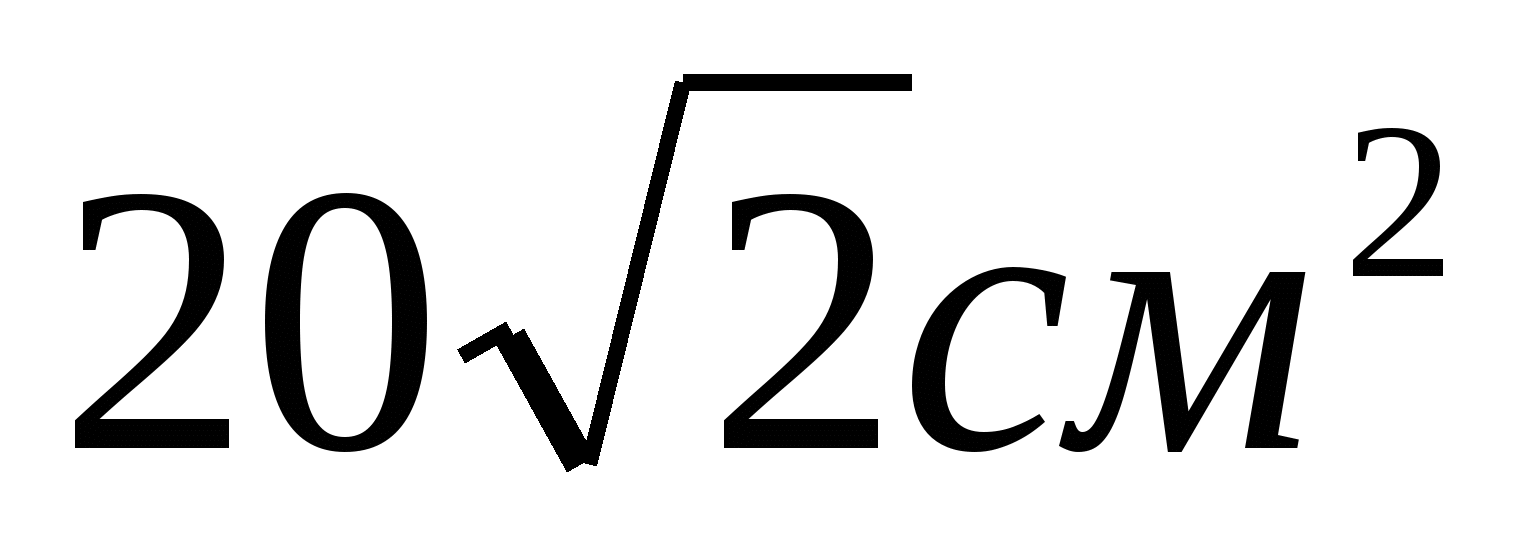
АС=40см
h= 7м
Р =40см
=40см
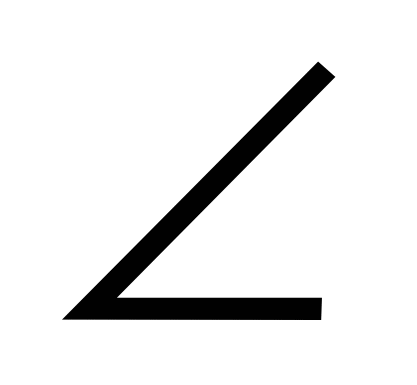 ВАD=160º
ВАD=160º
2
вариант
в
а
б
Р=60см
S=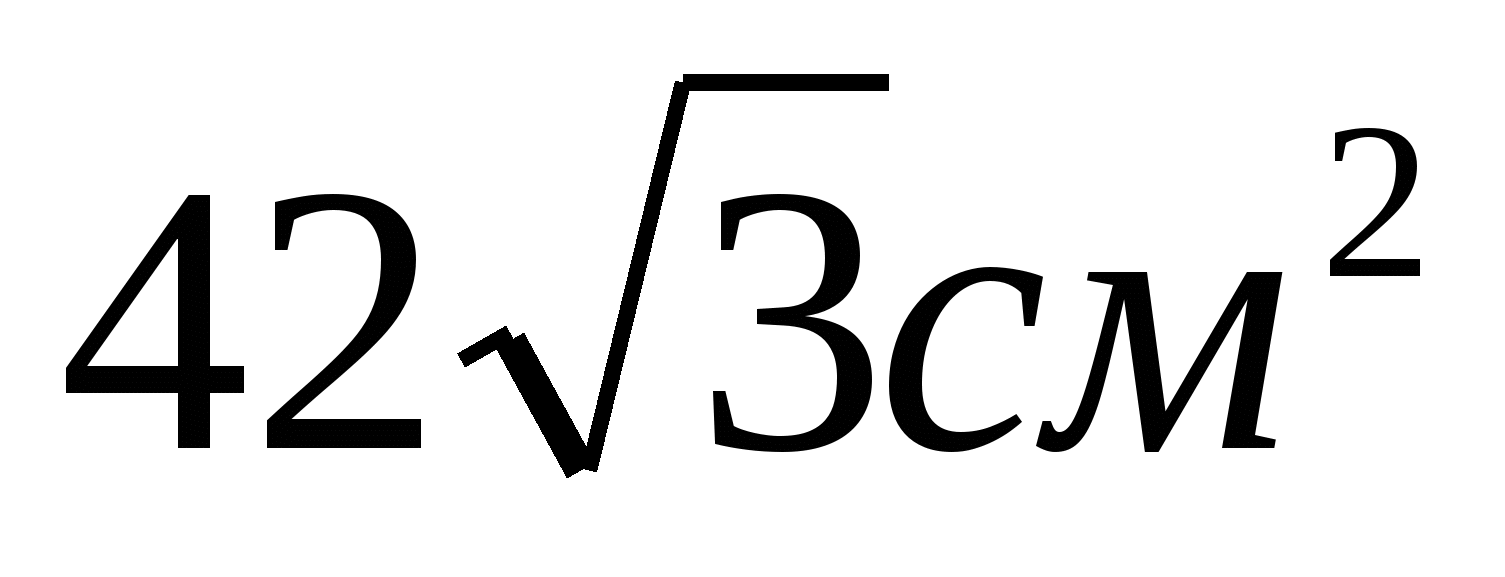
АВ=17см
h=1,5м
Р =46см
=46см
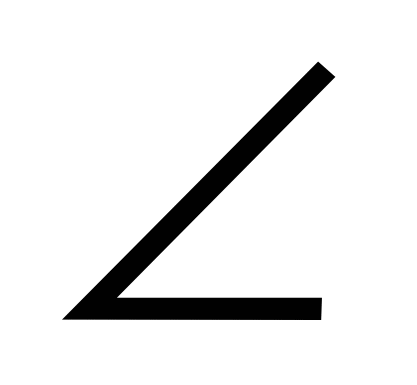 DОК=50º
DОК=50º
Литература:
1. Учебник Л. С. Атанасян, В. Ф. Бутузов и др. Геометрия 7-9 класс. М,
Просвещение, 2010
2. Д.А. Мальцев и др. ГИА 2012, 9 класс. Ростов- на - Дону.
Издатель Мальцев Д.А., 2012 г.
infourok.ru
| Контрольная работа №1. Векторы. | Контрольная работа №1. Векторы. |
| Вариант 1. | Вариант 2. |
| 1. ABCD – параллелограмм, 2. Дана трапеция ABCD с основаниями AD=20 и BC=8, О -точка пересечения диагоналей. Разложите вектор 3. Диагонали ромба АС = а, BD = b. Точка K 4. В равнобедренной трапеции острый угол равен 60 5. В прямоугольнике ABCD известно, что AD=a, DC=b, O точка пересечения диагоналей. Найдите величину | 1. ABCD – параллелограмм, 2. Дана трапеция ABCD с основаниями AD=15 и BC=10, О -точка пересечения диагоналей. Разложите вектор 3. Диагонали ромба АС = а, BD = b. Точка K 4. В равнобедренной трапеции острый угол равен 60 5. В прямоугольнике ABCD известно, что AB=a, BC=b, O точка пересечения диагоналей. Найдите величину |
Контрольная работа №2.
Метод координат.
Контрольная работа №2.
Метод координат.
Вариант 1.
Вариант 2.
1. Установите связь между векторами 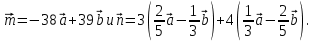
2. Векторы 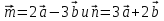 разложены по неколлинеарным векторам
разложены по неколлинеарным векторам 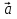 и
и 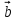 . Разложите векторы
. Разложите векторы 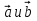 по векторам
по векторам 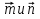 .
.
3. Четырехугольник имеет вершины с координатами А (1;1), В (3;5), С (9;-1), D(7;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
4. Напишите уравнение окружности с центром в точке С (-3;1), проходящей через точку А (2;3).
5. Прямая l проходит через точки А (-3;1) и В (1;-7). Напишите уравнение прямой m, проходящей через точку С(5;6) и перпендикулярной прямой l.
1. Установите связь между векторами 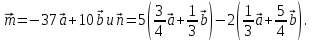
2. Векторы 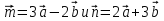 разложены по неколлинеарным векторам
разложены по неколлинеарным векторам 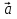 и
и 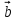 . Разложите векторы
. Разложите векторы 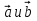 по векторам
по векторам 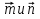 .
.
3. Четырехугольник имеет вершины с координатами А (-6;1), В (2;5), С (4;-1), D(-4;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
4. Напишите уравнение окружности с центром в точке С (2;-3), проходящей через точку А (-1;-2).
5. Прямая l проходит через точки А (2;-1) и В (-3;9). Напишите уравнение прямой m, проходящей через точку С(3;10) и перпендикулярной прямой l.
Контрольная работа №3.
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов.
Контрольная работа №3.
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов.
Вариант 1.
Вариант 2.
1. Упростите выражение
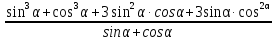
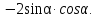
2. В треугольнике АВС 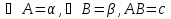 . Найдите площадь треугольника и радиус окружности, описанной около него.
. Найдите площадь треугольника и радиус окружности, описанной около него.
3. В параллелограмме ABCD даны стороны АВ=4 см, AD=5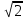 см и угол
см и угол 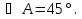 Найдите диагонали параллелограмма и его площадь.
Найдите диагонали параллелограмма и его площадь.
4. Найдите координаты вектора 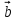 , если
, если 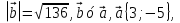 а угол между вектором
а угол между вектором 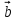 и положительным направлением оси абсцисс острый.
и положительным направлением оси абсцисс острый.
5. Вычислите скалярное произведение векторов 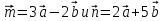 , если
, если 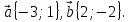
1. Упростите выражение
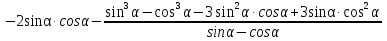
2. В треугольнике АВС  . Найдите площадь треугольника и радиус окружности, описанной около него.
. Найдите площадь треугольника и радиус окружности, описанной около него.
3. В параллелограмме ABCD даны стороны АВ=8 см, AD=3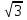 см и угол
см и угол 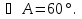 Найдите диагонали параллелограмма и его площадь.
Найдите диагонали параллелограмма и его площадь.
4. Найдите координаты вектора 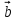 , если
, если 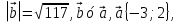 а угол между вектором
а угол между вектором 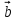 и положительным направлением оси абсцисс тупой.
и положительным направлением оси абсцисс тупой.
5. Вычислите скалярное произведение векторов 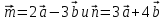 , если
, если 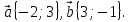
Контрольная работа №4. Длина окружности и площадь круга.
Контрольная работа №4. Длина окружности и площадь круга.
Вариант 1.
Вариант 2.
1. Три последовательные стороны четырехугольника, описанного около окружности, относятся как 3:4:5. Периметр этого четырехугольника равен 48 см. Найдите длины его сторон.
2. Около правильного шестиугольника описана окружность и в него вписана окружность. Длина большей окружности равна 4π. Найдите площадь кольца и площадь шестиугольника.
3. Хорда окружности равна 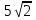 и стягивает дугу в 90
и стягивает дугу в 90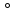 . Найдите длину дуги и площадь соответствующего сектора.
. Найдите длину дуги и площадь соответствующего сектора.
4. Найдите радиус сектора, если площадь соответствующего сегмента равна
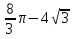 .
.
5. В треугольник вписана окружность радиуса 3 см. Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 3 см.
1. Три последовательные стороны четырехугольника, описанного около окружности, относятся как 4:5:6. Периметр этого четырехугольника равен 80 см. Найдите длины его сторон.
2. Около правильного треугольника описана окружность и в него вписана окружность. Длина меньшей окружности равна 8π. Найдите площадь кольца и площадь треугольника.
3. Хорда окружности равна 6 и стягивает дугу в 60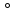 . Найдите длину дуги и площадь соответствующего сектора.
. Найдите длину дуги и площадь соответствующего сектора.
4. Найдите радиус сектора, если площадь соответствующего сегмента равна
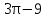 .
.
5. В треугольник вписана окружность радиуса 4 см. Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 5 см.
Контрольная работа №5. Движения.
Контрольная работа №5. Движения.
Вариант 1.
Вариант 2.
1. Точка А (-2;3) симметрична точке А1 (6;-9) относительно точки В. Найдите координаты точки В.
2. Дан треугольник АВС с вершинами А(2;1), В(-6;1), С(-1;5). Треугольник А1В1С1 симметричен треугольнику АВС относительно прямой, заданной уравнением х=1. Найдите координаты вершин А1, В1, С1.
3. Найдите вектор 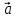 параллельного переноса, при котором прямая у=3х-2 переходит в прямую у=3х+4, а прямая 3х+2у=2 переходит в прямую 6х+4у=3.
параллельного переноса, при котором прямая у=3х-2 переходит в прямую у=3х+4, а прямая 3х+2у=2 переходит в прямую 6х+4у=3.
4. В результате поворота вокруг точки В(1;2) на 60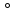 против часовой стрелки точка А(4;2) перешла в точку А1. Найдите координаты этой точки.
против часовой стрелки точка А(4;2) перешла в точку А1. Найдите координаты этой точки.
5. Прямая m задана уравнением 3х+2у-5=0. Прямая n симметрична прямой m относительно точки В(2;3). Напишите уравнение прямой n.
1. Точка А (-3;1) симметрична точке А1 (9;-5) относительно точки В. Найдите координаты точки В.
2. Дан треугольник АВС с вершинами А(-4;5), В(1;5), С(-3;-1). Треугольник А1В1С1 симметричен треугольнику АВС относительно прямой, заданной уравнением у=1. Найдите координаты вершин А1, В1, С1.
3. Найдите вектор 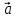 параллельного переноса, при котором прямая у=2х-1 переходит в прямую у=2х+3, а прямая 2х+3у=1 переходит в прямую 4х+6у=5.
параллельного переноса, при котором прямая у=2х-1 переходит в прямую у=2х+3, а прямая 2х+3у=1 переходит в прямую 4х+6у=5.
4. В результате поворота вокруг точки В(2;1) на 30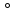 против часовой стрелки точка А(6;1) перешла в точку А1. Найдите координаты этой точки.
против часовой стрелки точка А(6;1) перешла в точку А1. Найдите координаты этой точки.
5. Прямая m задана уравнением 2х+3у-7=0. Прямая n симметрична прямой m относительно точки В(3;2). Напишите уравнение прямой n.
Контрольная работа №6.
Итоговая по программе 9 класса.
Контрольная работа №6.
Итоговая по программе 9 класса.
Вариант 1.
Вариант 2.
1. В параллелограмме ABCD точка E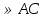 , AE:EC=1:5. Разложите вектор
, AE:EC=1:5. Разложите вектор 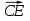 по векторам
по векторам 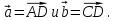
2. Найдите косинус угла между векторами 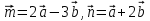 , если
, если 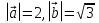 и угол между векторами
и угол между векторами 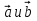 равен 30
равен 30 .
.
3. Около круга радиусом R описан правильный шестиугольник. Найдите разность между площадью шестиугольника и круга.
4. Напишите уравнение окружности, симметричной относительно точки А (-1;3) окружности, заданной уравнением х2+у2-4х+6у=0
5. Первая окружность радиуса 4 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 8 см и 12 см.
1. В параллелограмме ABCD точка E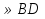 , BE:ED=1:4. Разложите вектор
, BE:ED=1:4. Разложите вектор 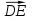 по векторам
по векторам 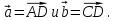
2. Найдите косинус угла между векторами 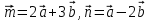 , если
, если 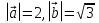 и угол между векторами
и угол между векторами 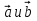 равен 30
равен 30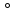 .
.
3. Около круга радиусом R описан правильный треугольник. Найдите разность между площадью треугольника и круга.
4. Напишите уравнение окружности, симметричной относительно точки А (-2;3) окружности, заданной уравнением х2+у2+6х-4у=0
5. Первая окружность радиуса 9 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 18 см и 20 см.
Контрольная работа № 7. Итоговая по курсу геометрии (7-9 классы)
Контрольная работа № 7. Итоговая по курсу геометрии (7-9 классы)
Вариант 1.
Вариант 2.
1. В равнобедренный треугольник с основанием 10 см и боковой стороной 5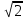 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
2. Найдите площадь круга, вписанного в ромб с диагоналями, равными 12 см и 16 см.
3. Найдите длину медианы ВМ треугольника АВС, если координаты вершин треугольника А (2;5), В (0;0), С(4;3).
4. Точка М является серединой боковой стороны АВ трапеции ABCD. Найдите площадь трапеции, если площадь треугольника MCD равна 28 см2.
5. Окружность радиуса 2 см, центр О которой лежит на гипотенузе АС прямоугольного треугольника АВС, касается его катетов. Найдите площадь треугольника АВС, если ОА=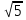 см.
см.
1. В равнобедренный треугольник с основанием 14 см и боковой стороной 7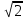 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
2. Найдите площадь круга, вписанного в ромб с диагоналями, равными 16 см и 30 см.
3. Найдите длину медианы СР треугольника АВС, если координаты вершин треугольника А (-3;-2), В (-13;14), С(0;0).
4. Точка М является серединой боковой стороны АВ трапеции ABCD. Найдите площадь треугольника MCD, если площадь трапеции равна 38 см2.
5. Окружность радиуса 3 см, центр О которой лежит на гипотенузе АС прямоугольного треугольника АВС, касается его катетов. Найдите площадь треугольника АВС, если ОА=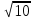 см.
см.
infourok.ru
|
Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. |
| Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2. |
| Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции. | Контрольная работа № 2. Г-8 Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. |
| Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см. |
| Контрольная работа № 3. Г-8. Вариант-1. B № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D № 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2. | Контрольная работа №3. Г-8. Вариант-2. N № 1. Рисунок 1. P Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN. M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. |
| Контрольная работа № 3. Г-8. Вариант-3. № 1. Рисунок 1. D B Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD. Найти: а) DВ : АС; б) РАОС : РDBO ; в) SDBO : SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4. № 1. Рисунок 1. B Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. D E Доказать: DЕ ║АС. Найти: а) DЕ : АС; б) РABC : РDBE ; в) SDBE : SABC. A C № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН. |
Контрольная работа № 4. Г-8.
Вариант-1.
№ 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника.
№ 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см.
№ 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см,
ВС = 5√3 см. Найдите угол В и гипотенузу АВ.
№ 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН.
№ 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см.
Контрольная работа №4. Г-8.
Вариант-2.
№ 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника.
№ 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см.
№3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см,
КТ= 7 см. Найдите угол К и гипотенузу КР.
№ 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС.
№ 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если
NK = 7 см.
Контрольная работа № 4. Г-8.
Вариант-3.
№ 1. На стороне ВС треугольника АВС выбрана точка D так, что
ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина
отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК.
№ 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см,
СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ.
№ 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции.
№ 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см.
№ 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10,
СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ.
Контрольная работа № 4. Г-8.
Вариант-4.
№ 1. На стороне АМ треугольника АВМ отмечена точка Н так, что
АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и
угол ВНМ.
№ 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см,
NК =6√3 см, КD- медиана. Найдите угол КDN.
№ 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции.
№ 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника.
№ 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ.
Контрольная работа № 5. Г-8.
Вариант-1.
№ 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см.
№ 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12.
Найдите ∟ВСА, ∟ВАС.
B A
130O
C
№ 3. Хорды MN и PK пересекаются точке E так, что ME =12 см,
NE =3 см, PE=KE. Найдите PK.
№ 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника.
Контрольная работа № 5. Г-8.
Вариант-2.
№ 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см.
№ 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3.
Найдите ∟ВОС, ∟АВС.
A B
60O
C O
№ 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см,
ВF =16 см, СF=DF. Найдите CD.
№ 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. Найдите стороны MN и NK треугольника.
Контрольная работа № 5. Г-8.
Вариант-3.
№ 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника
№ 2. Точки А и В делят окружность с центром О на дуги АВМ и
АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ.
№ 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности.
№ 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
Контрольная работа № 5. Г-8.
Вариант-4.
№ 1. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см.
№ 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН.
№ 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см,
NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности.
№ 4. В равнобедренном треугольнике основание равно 10 см, а высота,
Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
Ответы.
№ 1
№ 2
№ 3
№ 4
№ 5
Контрольная работа № 1.
Вариант-1
∟АОD=72
900 , 900,
1600, 200
5см, 10см,
5см, 10см
480, 480,
1320, 1320
DВ=6см
Вариант-2
∟ОМР=32
750, 1050,
1050, 750
5см, 15см,
5см, 15см
660, 1140,
900, 900
АМ=3см
Вариант-3
10см, 15см,
10см, 15см
800
450, 1350
450,1350
AD=24см
AD=8см
Вариант-4
18см, 12см,
18см, 12см
500
300, 300,
1500, 1500
АВ= 7см
М1 М2 =6см
Контрольная работа № 2.
Вариант-1
24см2
10см, 24см2
Р=4√41см, S= 40cм2
S АВСК= 13,5см2
-
Вариант-2
24см2
5см, 30см2
Р=4√61см, S= 60cм2
S АВСD= 24√3см2
-
Вариант-3
780cм2
SABCD = 160cм2
SABK =33,6см2,
SCBK =50,4см2
6см
-
Вариант-4
154см2
SABCD = 100cм2
SKPT=36см2,
SMPT =18см2
3см
-
Контрольная работа № 3.
Вариант-1
а) 7,5; б)  ;
;
в) 
800, 600,400
5см
S = 5см2
-
Вариант-2
а) 9; б)  ;
;
в) 
AC=14см,
∟С=600
14см
5см2
-
Вариант-3
а) ; б)
; б)  ; в)
; в) 
АВ=6см; АС= 16√3
-
10см
-
Вариант-4
а)  ; б) 3; в)
; б) 3; в) 
АС=4√5; ВD=8√5
-
20см
Контрольная работа № 5.
Вариант-1
15см
∟ВСА=550,
∟ВАС=600
РЕ=6см, РК= 12см
АВ=16√3см,
ВС= 16√2см
-
Вариант-2
12см
∟ВОС=1200,
∟АВС=450
СF=8см, СD=16см
МN=12√3см;
NК=12√2см
-
Вариант-3
6см, 8см, 10 см
∟АМВ=600, ∟АВМ=900, ∟ АСВ=1050
СD=21см, 19,5см
3см, 6,25см
Вариант-4
6см, 8см, 10см
∟ЕКА=90, ∟ЕАН=670 30١, ∟ЕКН=1120 30١
РК=16см, 9,5см
3см, 7см
www.metod-kopilka.ru
Контрольная работа №2
1 вариант.
1. Периметр равнобедренного треугольника равен 10,6 см. Основание треугольника на 1 см длиннее его боковой стороны. Найдите стороны треугольника.
2. Отрезки АВ и СD пересекаются в точке О, причем АО=ОВ, СО=ОD. Доказать, что Δ СОВ равен Δ АОD.
3. АВС – равнобедренный треугольник с основанием АС,  С= 40о,
С= 40о,  В = 100о. В треугольнике проведена медиана ВD. Найдите углы треугольника АВD.
В = 100о. В треугольнике проведена медиана ВD. Найдите углы треугольника АВD.
4. АВС – равнобедренный треугольник. Точка D - середина основания АС. Эту точку соединили с вершиной В, образовавшийся угол АDВ равен 90о. Длина стороны АС равна 6,5 см. Сторона АВ в два раза больше АС. Найдите сторону ВС.
Контрольная работа №2
2 вариант.
1. Периметр равнобедренного треугольника равен 11,9 см. Основание треугольника на 2 см длиннее его боковой стороны. Найдите стороны треугольника.
2. Отрезки АВ и СD пересекаются в точке О, причем АВ=СD,  DАВ =
DАВ =  DСВ. Доказать, что Δ DСВ равен Δ ВАD
DСВ. Доказать, что Δ DСВ равен Δ ВАD
3.Дан равнобедренный треугольник ОАВ с основанием ОВ,  В= 30о,
В= 30о,  А = 120о. В треугольнике проведена медиана АК. Найдите углы треугольника ОАК.
А = 120о. В треугольнике проведена медиана АК. Найдите углы треугольника ОАК.
4. АВС – равнобедренный треугольник. Точка D - середина основания АС. Эту точку соединили с вершиной В, образовавшийся угол АDВ равен 90о. Длина стороны АС равна 7 см. Сторона АВ в два раза больше АС. Найдите сторону ВС.
Контрольная работа № 3
Вариант 1.
1. Параллельные прямые а и в пересечены секущей с,
 1 = 120о. Найдите
1 = 120о. Найдите  2.
2.

2. В равнобедренном треугольнике MNK с основанием
МК угол при вершине N равен 40о. Найдите углы при
основании.
3. В прямоугольном треугольнике ABD проведена
биссектриса ВС. Чему равен угол СBD, если
 BAD=50о?
BAD=50о?
4. В треугольнике ABС угол А равен 35о. Угол В равен
80о, проведена биссектриса ВD. Найдите углы ADB,
BDС и AСB .
5. Найдите величины углов, образованных при
пересечении двух параллельных прямых третьей
прямой, если сумма внутренних накрест лежащих углов
равна 230о.
Контрольная работа № 3.
Вариант 2.
1. Параллельные прямые а и в пересечены прямой с,
 1 = 78о. Найдите
1 = 78о. Найдите  2.
2.

2. В равнобедренном треугольнике АВС с основанием АС
угол при вершине В равен 70о. Найдите углы при
основании.
3. В прямоугольном треугольнике АВС проведена
биссектриса ВD . Чему равен угол ВDС, если
 BAС=40о?
BAС=40о?
4. В треугольнике ОАВ угол О равен 30о. Угол А равен 85о
АК- биссектриса угла А. Найдите углы ОКА, АКВ и
ОВА.
5. Найдите величины углов, образованных при
пересечении двух параллельных прямых третьей
прямой, если сумма внутренних накрест лежащих
углов равна 260о
Контрольная работа.
( Задачи на построение. Окружность.)
1 вариант
1. Постройте треугольник АВС и проведите
а) из одной вершины биссектрису угла;
б) Из другой вершины медиану на противоположную
сторону;
в) из третьей вершины высоту.
2. Постройте треугольник по трем сторонам: а = 6см;
в = 7см; с = 5см.
3. Как расположены окружности, если их радиусы равны
40мм и 12мм, расстояние между их центрами 45мм?
Начертить чертеж.
Контрольная работа.
( Задачи на построение. Окружность.)
2 вариант
1. Постройте треугольник АВС и проведите
а) из одной вершины биссектрису угла;
б) Из другой вершины медиану на противоположную
сторону;
в) из третьей вершины высоту.
2. Постройте треугольник по трем сторонам: а = 6см;
в = 3см; с = 5см.
3. Как расположены окружности, если их радиусы равны
3см и 5см, расстояние между их центрами 5см?
Начертить чертеж.
Контрольная работа №1.
1 вариант
1. Длина отрезка СD равна 8 см. Длина отрезка ВС равна 2 см. Точка В лежит на отрезке СD .
Найдите длину отрезка ВD.
2. Луч ОС делит угол АОВ на два угла. Угол АОВ равен 1000. Градусная мера угла АОС больше градусной меры угла СОВ на 400. Найдите градусную меру угла СОВ.
3. ВЕ- биссектриса угла АВD . Угол АВD равен 1300 . Найдите градусную меру угла АВЕ.
4. Один из углов, образованных при пересечении двух прямых, равен 1450. Найдите остальные углы.
5. Вычислите:
А) 50471 + 90221=
Б) 320201 – 70451=
В) выразите в градусах и минутах: 1351, 6201.
2 вариант
1. Точка D лежит на отрезке АВ. DА=3см. DВ=5см. Найдите длину отрезка АВ.
2. СD – биссектриса угла АСВ. СЕ – биссектриса угла АСD. Угол ЕСD =200. Найдите градусную меру угла ЕСВ.
3. Луч ОК делит угол DОВ на два угла. Угол КОВ равен 150. Градусная мера угла DОК больше градусной меры угла КОВ в три раза. Найдите градусную меру угла DОВ.
4. Найдите угол, который равен 3 смежного с ним угла.
7
5. Вычислите:
А) 100451 + 170 271=
Б) 540351 – 5041=
В) выразите в градусах и минутах: 2151, 8701.
kopilkaurokov.ru