Контрольная работа по геометрии по теме «Четырехугольники»(8 класс)
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
1 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 40 см, а сторона АВ больше ВС на 4 см.
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 3 раза.
3. Найти углы равнобедренной трапеции, если один из них равен 75º.
4. Найти диагонали прямоугольника АВСД, если , СД=4 см.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника ВОС.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
2 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 54 см, а сторона АВ больше ВС в 2 раза.
2.
3. Найти углы прямоугольной трапеции, если больший из них равен 120º.
4. Найти диагонали прямоугольника АВСД, если , АД=6 см.
5. В четырехугольнике сумма углов, прилежащих к каждой из двух смежных сторон, равна . Докажите, что АВСД – параллелограмм.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
3 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 80 см, а сторона АВ больше ВС на 5 см.
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 4 раза.
3. Найти углы равнобедренной трапеции, если один из них равен 65º.
4. Найти диагонали прямоугольника АВСД, если , СД=15см.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника АОВ.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
4 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 24 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 128º.
4. Найти диагонали прямоугольника АВСД, если , АД=15 см.
5. В четырехугольнике сумма углов, прилежащих к каждой из двух смежных сторон, равна . Докажите, что MNPK– параллелограмм
.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
5 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 48 см, а сторона АВ больше ВС на 6 см.
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 5 раз.
3. Найти углы равнобедренной трапеции, если один из них равен 75º.
4. Найти диагонали прямоугольника АВСД, если , СД=17см.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника AОС.
Контрольная работа по геометрии. 8 класс.
6 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 78 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 160º.
4. Найти диагонали прямоугольника АВСД, если , АД=5 см.
5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 3:4.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
7 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 36 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 140º.
4. Найти диагонали прямоугольника АВСД, если , АД=24см.
5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 3:5.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
8 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 82 см, а сторона АВ больше ВС на 3 см.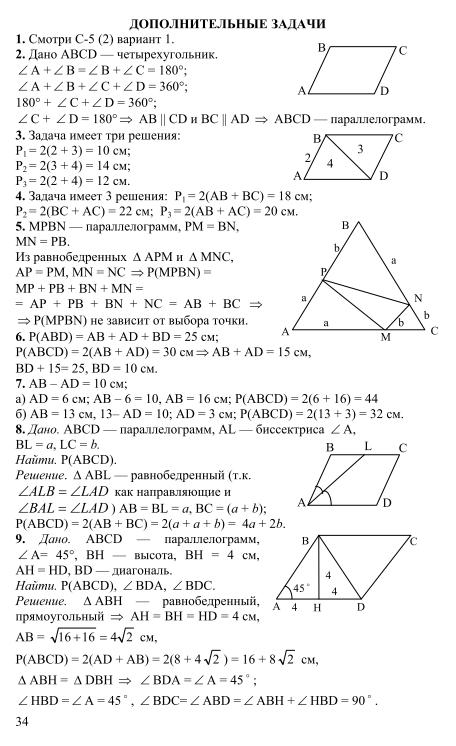
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 9 раз.
3. Найти углы равнобедренной трапеции, если один из них равен 1 65º.
4. Найти диагонали прямоугольника АВСД, если , АД=16см.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника АОВ.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
10 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 42 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 100º.
4. Найти диагонали прямоугольника АВСД, если , АД=36см.
5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 1:5.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники
9 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 18 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 118º.
4. Найти диагонали прямоугольника АВСД, если , АД=5 см.
5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки на 6 частей.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники
11 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 90 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 128º.
4. Найти диагонали прямоугольника АВСД, если , АД=12 см.
5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки на 8 частей.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
12 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 60 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 144º.
4. Найти диагонали прямоугольника АВСД, если , АД=23 см.
5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 2:5.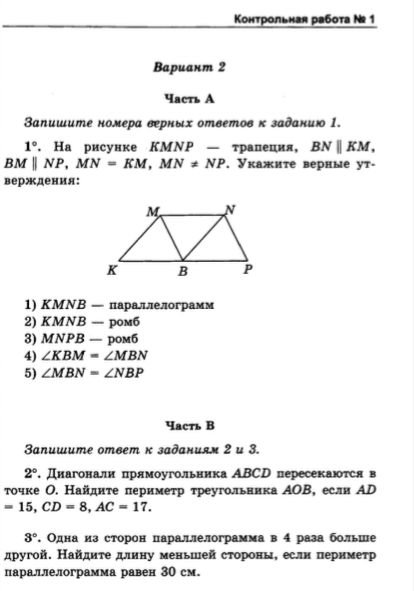
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
13 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 48 см, а сторона АВ больше ВС на 10 см.
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 4 раза.
3. Найти углы равнобедренной трапеции, если один из них равен 65º.
4. Найти диагонали прямоугольника АВСД, если , СД=27см.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника AОС.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
14 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 60 см, а сторона АВ больше ВС в 4 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 164º.
4. Найти диагонали прямоугольника АВСД, если , АД=35 см.
5. . Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки в отношении 3:2.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии. 8 класс.
Четырехугольники.
15 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 48 см, а сторона АВ больше ВС на 10 см.
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 4 раза.
3. Найти углы равнобедренной трапеции, если один из них равен 65º.
4. Найти диагонали прямоугольника АВСД, если , СД=27см.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника AОС.
Контрольная работа по геометрии. 8 класс.
Четырехугольники
16 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 96 см, а сторона АВ больше ВС в 3 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 140º.
4. Найти диагонали прямоугольника АВСД, если , АД=19 см.
5. Начертите произвольный отрезок. Разделите его с помощью циркуля и линейки на 6 частей.
6. В ромбе MHPK с тупым углом K диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен . Найти углы ромба.
Контрольная работа по геометрии по теме » Четырёхугольники»,8 класс
Контрольная работа по геометрии по теме « Четырёхугольники»,8 класс
Вариант 1
І часть (5 баллов)
Задания 1-5 имеют по четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.
Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.
Многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины, называется:
Правильным
Неправильным
Выпуклым
Невыпуклым
Сумма углов равна 360º:
Во всех ниже перечисленных
В параллелограмме
В квадрате
В трапеции
Четырехугольник, у которого две противолежащие стороны параллельны, называется:
Ромб
Трапеция
Параллелограмм
прямоугольник
4.Если в трапеции один из углов равен 90º, то она называется:
Правильной
Равнобокой
Равнобедренной
Прямоугольной
Периметр параллелограмма равен 24 см, а одна из сторон в два раза больше другой.
 Чему равна наименьшая из его сторон:
Чему равна наименьшая из его сторон:4 2) 12 3 ) 9 4) 6
ІІ часть (4 балла)
Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами
6. В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции
7.Найдите сумму углов выпуклого двадцати пятиугольника.
ІІІ часть (3 балла)
Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами
8.В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке F . Найдите периметр параллелограмма, если BF = 13,6 см, ЕС = 9 см.
Контрольная работа по геометрии по теме « Четырёхугольники»,8 класс
Вариант 2
І часть (5 баллов)
Задания 1-5 имеют по четыре варианта ответа, из которых только один верный. Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.
Выберите верный ответ. Верный ответ каждого задания оценивается одним баллом.
Сумма углов равна 360º:
В прямоугольнике
В параллелограмме
В ромбе
Во всех перечисленных выше фигурах
Фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков называется:
Трапеция
Прямоугольник
Четырехугольник
Квадрат
Четырехугольник, у которого противоположные стороны параллельны называется:
Квадрат
Параллелограмм
Трапеция
прямоугольник
4.Если боковые стороны трапеции равны, то она называется:
Правильной
Равнобедренной
Равносторонней
Равнобокой
5.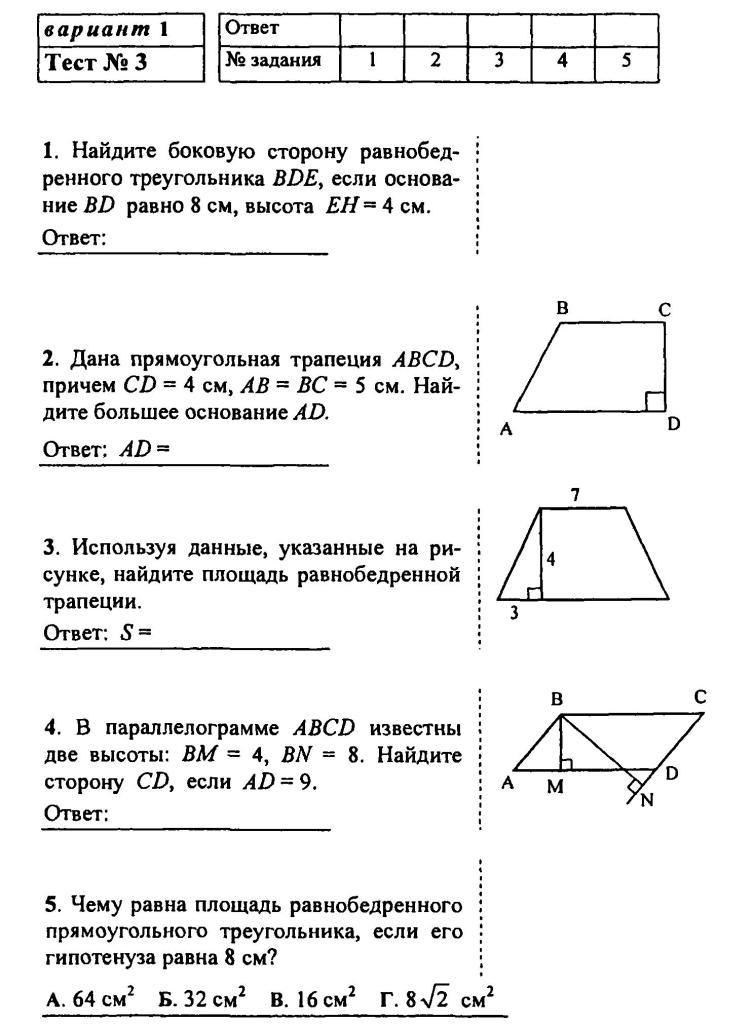 Периметр параллелограмма равен 40 см, а две из его сторон относятся как 3 :1. Чему равна наибольшая из его сторон?
Периметр параллелограмма равен 40 см, а две из его сторон относятся как 3 :1. Чему равна наибольшая из его сторон?
6 2.) 4 3)10 4.)15
ІІ часть (4 балла)
Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами
6.В равнобокой трапеции сумма углов при меньшем основании равна 236°. Найдите углы трапеции.
7.Найдите сумму углов выпуклого семнадцати угольника.
ІІІ часть (3 балла)
Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами
8.В прямоугольнике ABCD биссектриса угла А пересекает сторону ВС в точке N . Найдите периметр параллелограмма, если BN = 8,6 см, NС = 4,8 см.
Контрольная работа по геометрии «Четырехугольники»
Разноуровневая самостоятельная работа. 8 класс «Четырехугольники»
8 класс «Четырехугольники»
Имеет 3 уровня сложности.
Уровень 1
В треугольнике АВС параллельно стороне ВС проведена прямая DF. Определите вид четырехугольника CDFB.
В параллелограмме разность двух углов равна 320, Определите, могут ли эти углы быть противоположными.
Найдите углы прямоугольной трапеции, если один из ее углов равен 200.
Периметр ромба АВСD равен 64 см. Найти его сторону.
Найдите углы параллелограмма, если один из его углов равен 140.
Имеет ли оси симметрии: а) равносторонний треугольник; б) ромб; в) окружность. Сделать соответствующие чертежи.
Уровень 2
В окружности с центром О проведены диаметры АB и СD. Определите вид четырехугольника BDАC.
В равнобокой трапеции сумма углов при большем основании равна 960. Найдите углы трапеции.
Периметр параллелограмма 50 см.
 Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.
Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.В равнобедренной трапеции АВСD АВ=ВС=СD= 4 см, АD = 8 см. Найдите угол С.
В ромбе АВСD тупой угол АВС равен 1200, диагональ BD равна 8 см. Найти периметр ромба.
Постройте фигуру, симметричную квадрату АВСД относительно одной из его вершин. Какая получилась фигура?
Уровень 3
Два угла четырехугольника, прилежащие к одной стороне, прямые. Определите, является ли данный четырехугольник прямоугольником
Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма.
В параллелограмме АВСД периметр равен 60см. ∠С=30°, а перпендикуляр к прямой СД равен 7см. Найти углы и стороны параллелограмма.
Найти боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 1200.
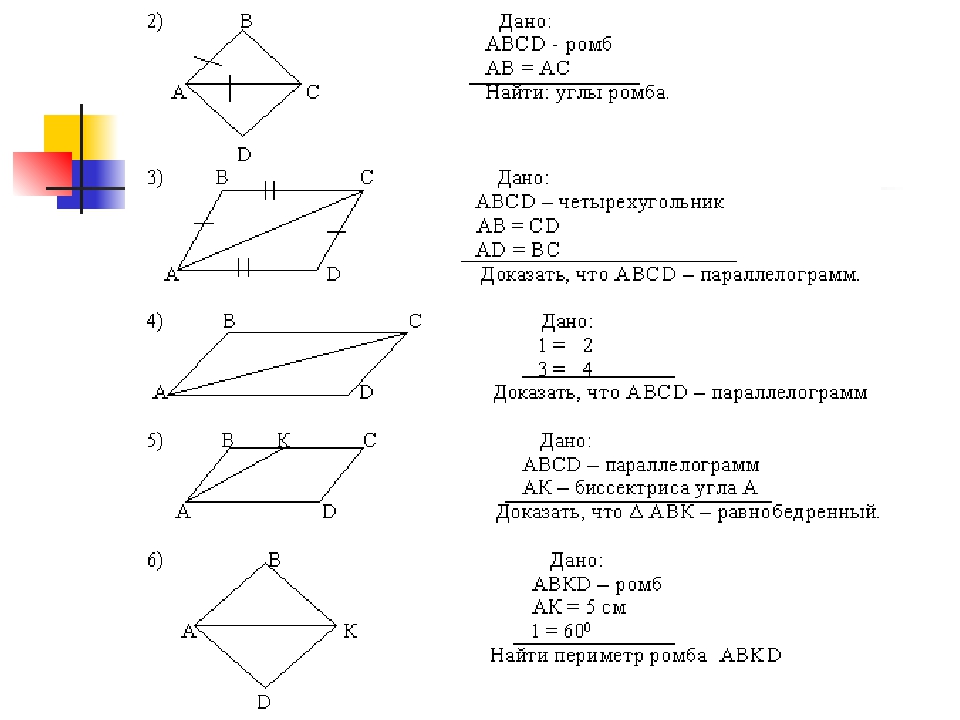
Боковая сторона равнобедренной трапеции в 2 раза меньше большего основания, и в 2 раза больше меньшего основания. Найти стороны, если периметр трапеции равен 36 м.
Треугольник ABD равносторонний. Постройте точку С симметричную точке А относительно стороны BD и определите вид четырехугольника ABCD.
Разноуровневая контрольная работа. 8 класс. «Четырехугольники»
Часть А.
Точка пересечения отрезков BF и DC делит каждый из них пополам. Определите вид четырехугольника BDFC. (2б)
В квадрате АВСD проведены диагонали, которые пересекаются в точке О. Найти углы треугольника АОВ. (2б)
Найти диагонали прямоугольника АВСД, если , СД=4 см. (2б)
Часть В.
Диагонали прямоугольника АВСД пересекаются в точке О, угол АВО равен 36 .Найдите угол АОД. (4б)
Сторона AD параллелограмма ABCD равна 9 см, а его диагонали равны 14 см и 10 см.
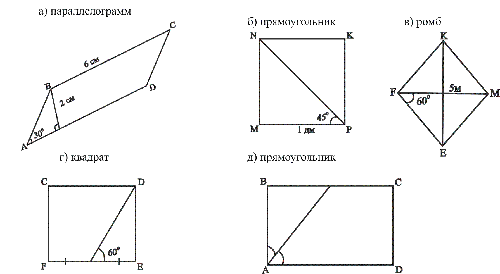 Точка О является точкой пересечения диагоналей. Найти периметр треугольника ВОС. (4б)
Точка О является точкой пересечения диагоналей. Найти периметр треугольника ВОС. (4б)
Часть С.
6. В параллелограмме КМНР проведена биссектриса угла МКР, которая пересекает сторону МН в точке Е.
а) Докажите, что треугольник КМЕ равнобедренный.
б) найдите периметр КМНР, если МЕ = 10 см, ЕН = 6 см.
( 6 б.)
критерии оценки
« 3 » — 4 – 9 баллов
« 4 » — 10 – 14 баллов
« 5 » — 15 – 20 баллов
Контрольный тест по теме «Четырехугольники»
Тема: Контрольный тест по теме «Четырехугольники»
Предмет: геометрия
Класс: 8
Учебник: «Геометрия 7-9 класс» автор Атанасян Л.С., Бутузов В.Ф. и др.
Инструкция к тесту
Тест состоит из 14 заданий, включающих теоретические вопросы, а так же практические задачи. Для ответа на вопрос надо выбрать правильный ответ из четырех предложенных вариантов. Вопрос предполагает только один вариант ответа. В №6 и №11 следует записать ответ.
В №6 и №11 следует записать ответ.
Критерии оценивания:
Каждый правильный ответ- 1балл.
За 13-14 баллов выставляется отметка «5»
За 9-12 баллов отметка «4»
За 6-8 баллов отметка «3»
В остальных случаях ставится отметка «2»
Ключ к тесту:
Вариант 1:
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
ответ | 4 | 3 | 2 | 3 | 2 | ромб | 2 | 3 | 4 | 4 | 8 | 2 | 3 | 2 |
Вариант 2:
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
ответ | 3 | 1 | 3 | 2 | 4 | квадрат | 3 | 2 | 1 | 1 | 16 | 4 | 2 | 1 |
Контрольная работа по теме «Четырехугольники»
Вариант 1
- Сумма углов равна 360º:
- В прямоугольнике
- В параллелограмме
- В ромбе
- Во всех перечисленных выше фигурах
- Фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков называется:
- Трапеция
- Прямоугольник
- Четырехугольник
- Квадрат
- Четырехугольник, у которого противоположные стороны параллельны называется:
- Квадрат
- Параллелограмм
- Трапеция
- прямоугольник
- По второму свойству параллелограмма:
- Диагонали делятся пополам
- Диагонали равны
- Диагонали в точке пересечения делятся пополам
- Диагонали делят параллелограмм пополам
- Если боковые стороны трапеции равны, то она называется:
- Правильной
- Равнобедрен
Геометрия 8 Атанасян К-1 В-3
Контрольная работа № 1 по геометрии в 8 классе «Четырехугольники» с ответами и решениями к учебнику Л. С. Атанасяна. Вариант 3. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей. Геометрия 8 Атанасян К-1 В-3.
С. Атанасяна. Вариант 3. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей. Геометрия 8 Атанасян К-1 В-3.
Геометрия 8 класс (Атанасян)
Контрольная работа № 1. Вариант 3.
К-1 «Четырехугольники» (транскрипт заданий)
Часть 1. Запишите номера верных ответов к заданию 1.
1°. На рисунке KMNP – трапеция, СМ || РК, СК || MN, MN = КМ, КМ ≠ КР. Укажите верные утверждения:
1) РКМС – параллелограмм; 2) РКМС – ромб; 3) CKMN – ромб; 4) ∠KCM = ∠MCN; 5) ∠PCK = ∠KCM.
Часть 2. Запишите ответ к заданиям 2 и 3.
2°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника ВОС, если АВ = 15, AD = 20, ВD = 25.
3°. Одна из сторон параллелограмма в 5 раз больше другой. Найдите длину меньшей стороны, если периметр параллелограмма равен 36 см.
Часть 3. Запишите обоснованное решение задач 4–6.
4°. На рисунке ABCD – ромб, ∠ABC = 120°. Найдите углы треугольника ВОС.
На рисунке ABCD – ромб, ∠ABC = 120°. Найдите углы треугольника ВОС.
5. Начертите прямоугольный треугольник АВС, на гипотенузе АВ отметьте точку N, не являющуюся ее серединой. Постройте фигуру, симметричную треугольнику АВС относительно точки N.
6. В параллелограмме BCDE биссектриса угла D пересекает сторону ВС в точке М, причем ВМ = 7, МС = 10. Найдите периметр параллелограмма.
Геометрия 8 Атанасян К-1 В-3
ОТВЕТЫ на контрольную работу:
№ 1. Ответ: 1,3, 4.
№ 2. Ответ: 45.
№ 3. Ответ: 3 см.
№ 4. Ответ: 60°, 30°, 90°.
№ 5. см. рисунок
№ 6. Ответ: 54.
Смотреть образец РЕШЕНИЯ заданий в тетради
Вы смотрели: Контрольная работа «Четырехугольники» по геометрии в 8 классе с ответами и решениями для УМК Атанасян. Дидактические материалы (упражнения) для учителей, учащихся и родителей.
К-1. Вариант 0 К-1. Вариант 1 К-1. Вариант 2 К-1. Вариант 3 К-1. Вариант 4
Вернуться на страницу: Контрольные работы по геометрии в 8 классе УМК Атанасян.
Перейти на страницу: Контрольные работы по геометрии в 8 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Геометрия 8 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова) использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.
Контрольная работа по геометрии 8 класс по теме «Четырехугольники»
Контрольная работа по теме «Четырехугольники» в логике ФГОС
Приложение 1
(для обучающихся)
На контрольной работе разрешается пользоваться:
— рабочими тетрадями;
— справочным материалом;
— таблицами и схемами;
— учебником и другой методической литературой.
Совет
Не стоит тратить много времени на поиск нужной информации вокруг. Поищите её в ячейках собственной памяти. Это может дать более продуктивный результат.
Стратегия поведения на контрольной работе
(планирование метапредметных результатов)
- Просмотрите все задания контрольной работы и выпишите номера тех заданий, которые (по вашему мнению) вы решите быстро и правильно.
- Выберите стратегию поведения на контрольной работе (отметьте галочкой или обведите в кружок):
А — начинаю решать контрольную работу с самых простых заданий, чтобы оставшееся время потратить на более сложные.
Б — начинаю решать более сложные задания контрольной работы, а оставшееся время я трачу на простые и легкие задания.
В — решаю все задания контрольной работы подряд, не пропуская ни одного задания.
Г — решаю задания контрольной работы подряд, а те задания, которые вызывают затруднения, пропускаю и возвращаюсь к ним только в конце.
Д — иная стратегия (опишите)________________________________________________________________________________________________________
_____________________________________________________________________________________________________________________________
3. После проверки контрольной работы поразмышляйте над тем, насколько правильную стратегию Вы избрали, помогла ли она вам в достижении желаемых результатов. Будете ли вы пользоваться этой стратегией всегда или смените её? Напишите свои выводы.
4. Внимательно изучите инструкцию
Контрольная работа по геометрии для 8 класса по теме: «Четырехугольники».
Инструкция по выполнению работы
Работа состоит из трёх частей и содержит 24 задания.
Часть I содержит 14 заданий базового уровня. Задания части I считаются выполненными, если учащийся представил верное решение (могут быть допущены пропуски в обосновании некоторых шагов решения) и ответ.
Часть II содержит 5 задания повышенного уровня и 1 задание высокого уровня сложности, соответствующих уровню возможностей обучающихся и доступных учащимся, хорошо успевающим по математике. При их выполнении надо записать полное решение и ответ.
Часть III содержит 5 задания, соответствующих уровню возможностей, но доступных учащимся с высоким уровнем математической подготовки, любящим занятия математикой. Это задания повышенной сложности, задания математических олимпиад.
На выполнение данной работы даётся 75 мин.
Проводится работа в два этапа. При этом реализуется основной принцип итоговой аттестации в основной школе: успешное выполнение заданий второй части работы не компенсирует отсутствие результата выполнения заданий первой части. Оценивание осуществляется способом «сложения» в логике ФГОС.
На первом этапе в первый день в течение 35 мин учащиеся выполняют только первую часть работы. В оставшиеся 15 минут урока после сдачи учащимися контрольных работ проводится проверка ответов и устанавливается, кто из школьников не преодолел «порог», позволяющий получить положительную отметку. Проводится анализ возможных причин затруднений школьников и допущенных ошибок.
В оставшиеся 15 минут урока после сдачи учащимися контрольных работ проводится проверка ответов и устанавливается, кто из школьников не преодолел «порог», позволяющий получить положительную отметку. Проводится анализ возможных причин затруднений школьников и допущенных ошибок.
На втором этапе во второй день в течение 40 минут учащиеся, не прошедшие «порог» в первый день, вновь пытаются это сделать, решая задания первой части (другой вариант). Остальные учащиеся выполняют задания второй и третьей части работы. При этом некоторые из них могут попытаться улучшить результат выполнения заданий первой части.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Система бонусов:
1 балл дополнительно за каждый новый способ решения любого задания, что дает возможность получения еще одной отметки «5» (личностный результат учащегося)
Желаем успеха!
Определение четырехугольника Merriam-Webster
quad · ran · gle | \ ˈKwä-ˌdraŋ-gəl \2a : четырехстороннее ограждение, особенно в окружении зданий
b : четырехугольные здания
3 : участок страны, представленный одним из листы карты
Другие слова из четырехугольник
четырехугольник \ kwä- ˈdraŋ- gyə- lər \ прилагательноеПримеры четырехугольника в предложении
Поскольку погода была солнечной, собрание проводилось на улице в четырехугольнике колледжа
Последние примеры в сети Школа была спроектирована вокруг четырехугольника (изобретение Оксфорда-Кембриджа), которое буквально содержит студенческую жизнь, отделенную от внешней среды, но связаны внутри. —
Ян Богост, The Atlantic , «Америка пожертвует всем ради учебы в колледже», 20 октября 2020 г. К ветерану присоединились его дочь, зять, внук и внучка на церемонии, которая прошла в здании . четырехугольник в Виндзорском замке.
—
Бьянка Бетанкур, Harper’s BAZAAR , «Королева Елизавета досрочно покинула свадьбу принцессы Беатрис для важной рыцарской церемонии», 17 июля 2020 г. Превосходство чернокожих в Говарде указывает на бесчисленных знаковых афроамериканских выпускников, которые пересекли его исторический четырехугольник в центре кампуса Двор.-
Дана Скотт, Республика Аризона , «Макур Мейкер из Hillcrest может привлечь новобранцев средней школы в Аризоне, деньги для HBCU», 11 июля 2020 г. Однако Букингемский дворец опубликовал новую фотографию королевской четы в честь дня рождения Филиппа, сделанную на прошлой неделе. в четырехугольнике внутри Виндзорского замка.
—
Ян Богост, The Atlantic , «Америка пожертвует всем ради учебы в колледже», 20 октября 2020 г. К ветерану присоединились его дочь, зять, внук и внучка на церемонии, которая прошла в здании . четырехугольник в Виндзорском замке.
—
Бьянка Бетанкур, Harper’s BAZAAR , «Королева Елизавета досрочно покинула свадьбу принцессы Беатрис для важной рыцарской церемонии», 17 июля 2020 г. Превосходство чернокожих в Говарде указывает на бесчисленных знаковых афроамериканских выпускников, которые пересекли его исторический четырехугольник в центре кампуса Двор.-
Дана Скотт, Республика Аризона , «Макур Мейкер из Hillcrest может привлечь новобранцев средней школы в Аризоне, деньги для HBCU», 11 июля 2020 г. Однако Букингемский дворец опубликовал новую фотографию королевской четы в честь дня рождения Филиппа, сделанную на прошлой неделе. в четырехугольнике внутри Виндзорского замка. — NBC News , «Принцу Филиппу, патриарху британской королевской семьи, тихо исполняется 99 лет» 10 июня 2020 года. Хотя детали, конечно, вымышлены, этот четырехугольник , по-видимому, настоящий.-
Эмма Дибдин, Harper’s BAZAAR , «Давайте разберемся, принц Чарльз, Камилла Шанд, принцесса Анна и Эндрю Паркер-Боулз любят четырехугольник», 18 ноября 2019 г. Итак, кто этот неотъемлемый четвертый член хитрого четырехугольника королевской любви , настоящий военный ветеран и бывший муж герцогини Корнуоллской?
—
Эрика Гонсалес, Harper’s BAZAAR , «Кто такой Эндрю Паркер Боулз в The Crown?», 23 ноября.2019 В отеле Lalit Hotel, который активно выступает за гендерное разнообразие на рабочем месте, ярмарка вакансий прошла в открытом четырехугольнике солнечным днем.
—
Манави Капур, Quartz India , «Первая ярмарка вакансий LGBTQI в Дели была только первым шагом к разнообразию рабочих мест», 27 февраля 2020 г.
— NBC News , «Принцу Филиппу, патриарху британской королевской семьи, тихо исполняется 99 лет» 10 июня 2020 года. Хотя детали, конечно, вымышлены, этот четырехугольник , по-видимому, настоящий.-
Эмма Дибдин, Harper’s BAZAAR , «Давайте разберемся, принц Чарльз, Камилла Шанд, принцесса Анна и Эндрю Паркер-Боулз любят четырехугольник», 18 ноября 2019 г. Итак, кто этот неотъемлемый четвертый член хитрого четырехугольника королевской любви , настоящий военный ветеран и бывший муж герцогини Корнуоллской?
—
Эрика Гонсалес, Harper’s BAZAAR , «Кто такой Эндрю Паркер Боулз в The Crown?», 23 ноября.2019 В отеле Lalit Hotel, который активно выступает за гендерное разнообразие на рабочем месте, ярмарка вакансий прошла в открытом четырехугольнике солнечным днем.
—
Манави Капур, Quartz India , «Первая ярмарка вакансий LGBTQI в Дели была только первым шагом к разнообразию рабочих мест», 27 февраля 2020 г. На литературном фестивале в Хенли в 2016 году королевский биограф Пенни Джунор, по-видимому, обсудил четырехугольник королевской любви .-
Эми Маккельден, Harper’s BAZAAR , «Корона не оправдывает отношения принцессы Анны в реальной жизни», 4 декабря 2019 г.
На литературном фестивале в Хенли в 2016 году королевский биограф Пенни Джунор, по-видимому, обсудил четырехугольник королевской любви .-
Эми Маккельден, Harper’s BAZAAR , «Корона не оправдывает отношения принцессы Анны в реальной жизни», 4 декабря 2019 г.Эти примеры предложений автоматически выбираются из различных источников новостей в Интернете, чтобы отразить текущее использование слова «четырехугольник». Взгляды, выраженные в примерах, не отражают мнение компании Merriam-Webster или ее редакторов. Отправьте нам отзыв.
ПодробнееПервое известное использование четырехугольника
XV век в значении, определенном в смысле 1
История и этимология четырехугольника
Среднеанглийский, от среднефранцузского, от позднего латинского quadriangulum , от латинского, средний от quadriangulus quadrangular, от quadri- + angulus angle
Узнать больше о четырехугольник
Статистика для четырехугольника
Процитируйте эту статью
«Четырехугольник. ” Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/quadrangle. По состоянию на 22 ноября 2020 г.
” Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/quadrangle. По состоянию на 22 ноября 2020 г.
Дополнительные определения для quadrangle
quad · ran · gle | \ ˈKwäd-ˌraŋ-gəl \
Детское определение четырехугольника
Комментарии к четырехугольнику
Что заставило вас посмотреть на четырехугольник ? Сообщите, пожалуйста, где вы это читали или слышали (включая цитату, если возможно).
определение четырехугольника по The Free Dictionary
Благослови вас, если вы войдете в четырехугольник с этой штукой, я не знаю, что бы произошло ». Сама идея была совершенно недоступна молодому Мастеру Востока, и он выглядел невыразимо. Дальше были врата, которые вели в Королевскую школу, и он стоял в четырехугольнике, вокруг которого находились различные здания. Снежный четырехугольник перед домом озарился светом в окнах спальни его старой няни Агафеи Михайловны, выполнявшей обязанности экономки. в его доме.Тогда я заметил, что пума в клетке и груда свертков были размещены у входа в этот четырехугольник. Однако ни ветер, ни солнце не благоприятствовали Staple Inn в один декабрьский полдень около шести часов, когда он был заполнен туманом. и свечи проливают темные и размытые лучи через окна всех его комнат, занятых тогда; особенно из ряда комнат в угловом доме в маленьком внутреннем четырехугольнике, где черным и белым над уродливым порталом была изображена таинственная надпись: «Луна только что очищала крыши ряда жилищ, ограничивающих четырехугольник с востока».Сомс, мы прогуляемся по четырехугольнику, пожалуйста ». Посреди леса находилась священная площадка« хула-хула », выделенная для празднования фантастического религиозного ритуала этих людей, включающая обширную продолговатый пи-пи, оканчивающийся на обоих концах высоким террасным алтарем, охраняемым рядами отвратительных деревянных идолов, а с двух оставшихся сторон, окруженных хребтами бамбуковых навесов, открывающихся внутрь четырехугольника, образованного таким образом.
в его доме.Тогда я заметил, что пума в клетке и груда свертков были размещены у входа в этот четырехугольник. Однако ни ветер, ни солнце не благоприятствовали Staple Inn в один декабрьский полдень около шести часов, когда он был заполнен туманом. и свечи проливают темные и размытые лучи через окна всех его комнат, занятых тогда; особенно из ряда комнат в угловом доме в маленьком внутреннем четырехугольнике, где черным и белым над уродливым порталом была изображена таинственная надпись: «Луна только что очищала крыши ряда жилищ, ограничивающих четырехугольник с востока».Сомс, мы прогуляемся по четырехугольнику, пожалуйста ». Посреди леса находилась священная площадка« хула-хула », выделенная для празднования фантастического религиозного ритуала этих людей, включающая обширную продолговатый пи-пи, оканчивающийся на обоих концах высоким террасным алтарем, охраняемым рядами отвратительных деревянных идолов, а с двух оставшихся сторон, окруженных хребтами бамбуковых навесов, открывающихся внутрь четырехугольника, образованного таким образом. имел ряд дверей, а с другой стороны освещались окнами, которые Кэтрин только успела обнаружить, заглядывала в четырехугольник, прежде чем мисс Тилни вошла в комнату и, едва оставаясь надеяться, что ей будет удобно, оставила ее с тревожной мольбой, чтобы она как можно реже меняла свое платье.Узкий проход привел нас в четырехугольник, вымощенный флагами и обсаженный ужасными жилищами. Дом есть в любую погоду, и дом, как она выражается, «это то, на что она смотрит». Она сидит в своей комнате (в боковом проходе на первом этаже, с арочным окном, возвышающимся над гладким четырехугольником, который через равные промежутки времени украшают гладкие круглые деревья и гладкие круглые блоки камня, как если бы деревья собирались играть в шары с Камни), и весь дом покоится в ее сознании. Замок был их, и ревущее пламя хлынуло из окон и мерцало высоко над башнями по обе стороны четырехугольника.С обеих сторон они метались из комнаты в комнату и от бастиона к бастиону в направлении цитадели.
имел ряд дверей, а с другой стороны освещались окнами, которые Кэтрин только успела обнаружить, заглядывала в четырехугольник, прежде чем мисс Тилни вошла в комнату и, едва оставаясь надеяться, что ей будет удобно, оставила ее с тревожной мольбой, чтобы она как можно реже меняла свое платье.Узкий проход привел нас в четырехугольник, вымощенный флагами и обсаженный ужасными жилищами. Дом есть в любую погоду, и дом, как она выражается, «это то, на что она смотрит». Она сидит в своей комнате (в боковом проходе на первом этаже, с арочным окном, возвышающимся над гладким четырехугольником, который через равные промежутки времени украшают гладкие круглые деревья и гладкие круглые блоки камня, как если бы деревья собирались играть в шары с Камни), и весь дом покоится в ее сознании. Замок был их, и ревущее пламя хлынуло из окон и мерцало высоко над башнями по обе стороны четырехугольника.С обеих сторон они метались из комнаты в комнату и от бастиона к бастиону в направлении цитадели.Площадь треугольника (координатная геометрия)
Площадь треугольника (координатная геометрия) — Math Open Reference Зная координаты трех вершин треугольника ABC, площадь можно вычислить по формуле ниже.
Попробуй это Перетащите любую точку A, B, C. Площадь треугольника ABC непрерывно пересчитывается по приведенной выше формуле.Вы также можете перетащить исходную точку на (0,0).
Учитывая координаты трех вершин любого треугольника, площадь треугольника определяется как: где A x и A y — координаты x и y точки A и т. д.Эта формула позволяет вычислить площадь треугольника, зная координаты всех трех вершины. Неважно, какие точки обозначены A, B или C, и он будет работать с любым треугольником, включая те, у которых некоторые или все координаты отрицательны.
Взглянув на формулу выше, вы увидите, что она заключена в две вертикальные полосы, например: Две вертикальные полосы означают «абсолютное значение». Это означает, что он всегда положительный, даже если формула дала отрицательный результат. У полигонов никогда не может быть отрицательной области.
«Ручная работа» точки B
Если вы выполните этот расчет, но пропустите последний шаг, на котором вы берете абсолютное значение, результат может быть отрицательным. Если он отрицательный, это означает, что 2-я точка (B) находится слева от отрезка AC.Здесь мы имеем в виду «левый» в том смысле, что если бы вы стояли в точке A, глядя на C, то B находился бы слева от вас.
Если он отрицательный, это означает, что 2-я точка (B) находится слева от отрезка AC.Здесь мы имеем в виду «левый» в том смысле, что если бы вы стояли в точке A, глядя на C, то B находился бы слева от вас.
Если область нулевая
Если площадь равна нулю, это означает, что три точки коллинеарен. Они лежат прямой линией и не образуют треугольника. Вы можете перетащить точки выше, чтобы создать это условие.
Вы также можете использовать Формулу Герона
Формула Герона позволяет вычислить площадь треугольника, если вам известны длины всех трех сторон.(См. Формулу Герона). В координатной геометрии мы можем найти расстояние между любыми двумя точками если мы знаем их координаты, и поэтому мы можем найти длины трех сторон треугольника, а затем подставить их в формулу Герона найти область.
Если одна сторона вертикальная или горизонтальная
В треугольнике выше сторона AC равна
вертикальный (параллельно оси y).
В этом случае легко использовать традиционный метод «половина основания, умноженная на высоту». См. Площадь треугольника — традиционный метод.
См. Площадь треугольника — традиционный метод.
Здесь AC выбран в качестве базы и имеет длину 8, найденная вычитанием y-координат A и C. Аналогично, высота равна 11, найденная вычитанием x-координат B и A. Таким образом, площадь равна половине 8 умножить на 11 или 44.
Ящик метод
Вы также можете использовать метод коробки, который действительно работает для любого многоугольника. Подробнее об этом см. Площадь треугольника — прямоугольный метод (Координатная геометрия)
Что попробовать
- На схеме вверху страницы перетащите точки A, B или C и обратите внимание, как при вычислении площади используются координаты.Попробуйте точки с отрицательными значениями x и y. Вы можете перетащить исходную точку, чтобы переместить оси.
- Нажмите «скрыть детали». Перетащите треугольник к какой-нибудь новой случайной форме. Вычислите его площадь и нажмите «показать подробности», чтобы узнать, правильно ли вы поняли.
- После вышесказанного оцените площадь, подсчитав квадраты сетки внутри треугольника.
 (Каждый квадрат 5 на 5, поэтому
имеет площадь 25).
(Каждый квадрат 5 на 5, поэтому
имеет площадь 25).
Ограничения
Для большей ясности в приведенном выше апплете координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Это может привести к небольшому отклонению расчетов.
Подробнее см. Учебные заметки
Другие темы о координатной геометрии
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Геометрия. Четырехугольник — форма, имеющая 4 стороны и 4 угла.- Сумма внутренних углов любого четырехугольника равна 360 °.
Презентация на тему: «Геометрия. Четырехугольник — Форма, имеющая 4 стороны и 4 угла. — Сумма внутренних углов любого четырехугольника составляет 360 °». — Стенограмма презентации:
1 Геометрия
2
Четырехугольник — форма, имеющая 4 стороны и 4 угла. — Сумма внутренних углов любого четырехугольника равна 360 °.
— Сумма внутренних углов любого четырехугольника равна 360 °.
3 Thrapezium — Thrapezium имеет как минимум пару параллельных сторон. — Сумма углов лежащих на одном плече трапезия равна 180 °. — Формула для расчета площади: P — площадь a — длина более высокого основания b — длина более низкого основания h — высота — диагонали равнобедренного трапеции пересекаются под прямым углом.
4 Параллелограмм — Параллелограмм — это трапезий.- Имеет 2 пары параллельных сторон. — Его параллельные стороны имеют одинаковую длину. — Его диагонали пересекаются на половину своей длины. — Формула для расчета площади: P — площадь a — длина основания h — высота
5
Ромбовидный — Ромбовидный имеет 2 пары сторон одинаковой длины. — Соприкасаются стороны одинаковой длины. — Углы между сторонами разной длины одинаковы. — Формула для расчета площади: P — площадь e — первая диагональ f — вторая диагональ
— Формула для расчета площади: P — площадь e — первая диагональ f — вторая диагональ
6 Ромб — сумма двух смежных углов равна 180 o.- Диагонали пересекаются под прямым углом и делят ромб на четыре прямоугольных треугольника. — Его стороны такие же. — Формула для расчета площади: P — площадь e — первая диагональ f — вторая диагональ
7 Прямоугольник — у прямоугольника две пары сторон одинаковой длины. — Его диагонали такие же. — Все углы прямоугольника равны 90 o. — Прямоугольник имеет 2 пары параллельных сторон. — Формула для расчета площади: P — площадь a — первая сторона b — вторая сторона
8 Квадрат — Все углы прямые.-Все стороны одинаковые. -Его диагональ пересекается под прямым углом. -Его диагонали такие же. — Формула для расчета площади: Формула для расчета диагонали: P — площадь a — сторона d — диагональ
9
Треугольник — Треугольник имеет 3 стороны. — Сумма его углов равна 180 o. Типы: Классификация по сторонам: — разносторонний треугольник — все его стороны имеют разную длину. — равнобедренный треугольник — обе руки одинаковой длины.- равносторонний треугольник — все его стороны одинаковой длины. Классификация по углам: — остроугольный треугольник — имеет 3 острых угла. — прямоугольный треугольник — имеет 1 прямой угол и 2 острых угла. — тупоугольный треугольник — имеет 1 тупой угол и 2 острых угла. Формула для расчета площади: P — площадь а — основание h — высота
— Сумма его углов равна 180 o. Типы: Классификация по сторонам: — разносторонний треугольник — все его стороны имеют разную длину. — равнобедренный треугольник — обе руки одинаковой длины.- равносторонний треугольник — все его стороны одинаковой длины. Классификация по углам: — остроугольный треугольник — имеет 3 острых угла. — прямоугольный треугольник — имеет 1 прямой угол и 2 острых угла. — тупоугольный треугольник — имеет 1 тупой угол и 2 острых угла. Формула для расчета площади: P — площадь а — основание h — высота
10 Равносторонний треугольник — все стороны имеют одинаковую длину. — Все углы равны 60 o.- Формула для расчета площади: — Формула для расчета высоты: P — площадь a — сторона h — высота
Площадь треугольника
Площадь треугольника , формулы для расчета площади различных типов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади в режиме онлайн и таблица с формулами площадей для треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисление (показано) (скрыто)
— примечания (показаны) (скрыто)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона а
Высота h
Основание треугольника можно выбрать с любой стороны треугольника.
2
Площадь двухстороннего треугольника и угол между ними
Сторона а
Сторона б
Угол α ° между сторонами а и б
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трех сторонам
Сторона а
Сторона б
Сторона c
Радиус r вписанный круг
4
Площадь треугольника по радиусу описанной окружности и трех сторонам
Сторона а
Сторона б
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
Полупериметр:
Сторона а
Сторона б
Сторона c
6
Площадь произвольного треугольника сбоку и двух смежных углов
Сторона а
Угол β °
Угол α °
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по сторонам и основанию
Сторона а (а = б)
Сторона c
8
Площадь равнобедренного треугольника по сторонам и угол между ними
Сторона а (а = б)
Угол α ° между сторонами
9
Площадь равнобедренного треугольника сбоку, в основании и угол между ними
Сторона а (а = б)
Основание треугольника c
Угол β ° между основанием и стороной
10
Площадь равнобедренного треугольника в основании и угол между сторонами
Основание треугольника c
Угол α ° между сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника на стороне
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
Радиус r вписанный круг
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Квадрат прямоугольного треугольника с двумя ножками
Катет а
Катет б
17
Площадь прямоугольного треугольника через гипотенузу и угол
Сторона c
Угол α
18
Площадь прямоугольного треугольника, проходящего через катет и угол
Сторона б
Угол α
19
Площадь прямоугольного треугольника вдоль отрезков, делящих гипотенузу на вписанную окружность
Отрезок d
Сегмент линии и
20
Площадь прямоугольного треугольника, проходящего через гипотенузу и вписанную окружность
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
Полупериметр:
Сторона а
Сторона б
Сторона c
Наш калькулятор для расчета площади поможет вам рассчитать площади разных типов треугольников или проверить уже выполненные расчеты.
В зависимости от известных входных данных для вычисления площади треугольника используются различные формулы. Выше формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные расчеты. Общие формулы даны для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
В зависимости от типа треугольника и известных исходных данных площадь треугольника может быть вычислена с использованием различных формул.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это числовая характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя сегментами (сторонами), соединяющими три точки (вершины), не лежащие на одной прямой.
Треугольник — это геометрическая фигура, образованная тремя сегментами, соединяющими три точки, не лежащие на одной прямой.
