Контрольная работа кинематика точки 10 класс: Контрольная работа по теме «Кинематика точки» (10 класс)

Контрольная работа по теме «Кинематика точки» (10 класс)

Контрольная работа №1 по теме «Кинематика материальной точки»

Вариант 1.

1. Материальная точка движется равномерно прямолинейно из точки с координатой х₀ = 100 м и скоростью 15 м/с. Найдите:
   а) координату точки через 10 с после начала движения,
   б) перемещение за это время
   в) запишите закон движения материальной точки и постройте график движения.

2. Велосипедист движется под уклон с ускорением 0,3 м/с². Какую скорость приобретет велосипедист через 20 с, если его начальная скорость равна 4 м/с.

3. Период вращения молотильного барабана комбайна «Нива» диаметром 600 мм равен 0,05 с. Найдите скорость точек, лежащих на ободе барабана.

4. Автомобиль проехал первую половину пути со скоростью 36 км/ч, а вторую половину пути со скоростью 72 км/ч. Найдите среднюю скорость на всем пути.

Вариант 2.

1.      Уравнение движения тела имеет вид: х = 200 + 20 t. Определите:        
а) координату тела через 15 с после начала движения,
б) постройте график скорости тела , в) за какое время тело совершит путь 1 км?

2.      По графику скорости  материальной точки (см. рис. ) определите: 
а) начальную скорость тела и скорость через 10 с после  начала движения,  
б) ускорение тела,             
в) запишите уравнение скорости тела   

3.Скорость вращения крайних точек платформы карусельного 
станка 3 м/с. Найдите ускорение платформы карусельного станка, если его диаметр 4 м.

4.При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь авто.

Вариант 3.

1. Уравнение скорости  тела имеет вид: v (t) = 10 + 2 t
Найдите:  а) начальную скорость тела и скорость тела через 10 с после начала движения
б) постройте график скорости  этого тела

2.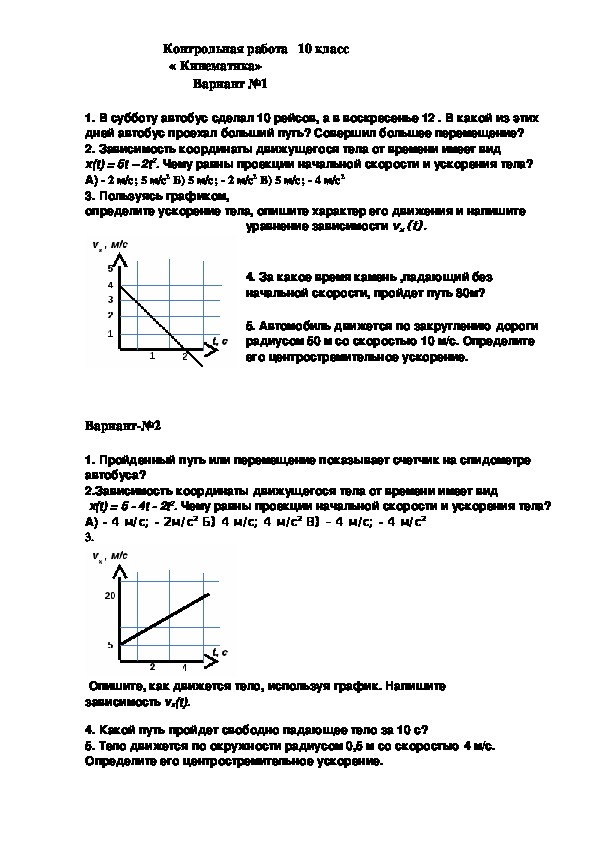 . Материальная точка движется по окружности радиуса 50 см. Найдите:
а) линейную скорость, если частота вращения 0,2 с^-1
б) найдите путь и перемещение тела за 2 с

3.  Тело брошено вертикально вниз с высоты 20 м.  Сколько времени оно будет падать и какой будет скорость в момент удара о землю? 

(g принять равным 10 м/с²)

4. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,5 м/с², пройдет путь 50 м?

Контрольная работа по физике «Кинематика материальной точки» (10 класс)

Методический комментарий: работа проводится в классе с преобладающим количеством сильных учеников. Последняя задача в каждом варианте предусматривает решение с использованием теоремы Виета. Ученики получают тексты работы на листах. Ученики слабые, неуверенные в себе, выполняют работу по другим, тоже дифференцированным, но более легким текстам.

Например:

Вариант 1

1. Шарик начинает скатываться с желоба. Какое расстояние он пройдет за 2 с?

2. С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличилась со 144 до 216 км/ч?

3. Лыжник спускается с горы за 10 с. Начальная скорость его 18 км/ч, а ускорение 0,2 м/с². Найти длину горы.

4. Тело движется по прямой из точки х_о = 2 м с ускорением 0,5 м/с² и начальной скоростью 5 м/с. Написать уравнение движения и формулу зависимости скорости от времени. Построить графики этих зависимостей. Определить время движения и путь, пройденный телом до полной остановки.

С целью подготовки к контрольной работе учащимся было предложено творческое задание: составить задачи по теме с использованием теоремы Виета. Вот некоторые их них.

Задача. По наклонной доске пустили катиться снизу вверх шарик с начальной скоростью v_о. На расстоянии L от начала пути шарик побывал дважды: через t₁ и через t₂ после начала движения. Определите неизвестную величину по данным таблицы. Ускорение считать постоянным.

1

2

3

4

5

6

7

8

9

10

t₁, с

2

1

1

3

1

2

2

2

t₂, с

4

5

3

8

8

3

L

0,5 м

2 м

50 см

4 м

8 м

4 м

V_о, м/с

2

4

6

5

a, м/с²

0,1

0,5

1

0,5

3

0,2

1. Из графика зависимости v(t) найти модуль ускорения а велосипедиста в течение первых 3-х секунд движения

t, с

V, м/с

0 3 4 6 t.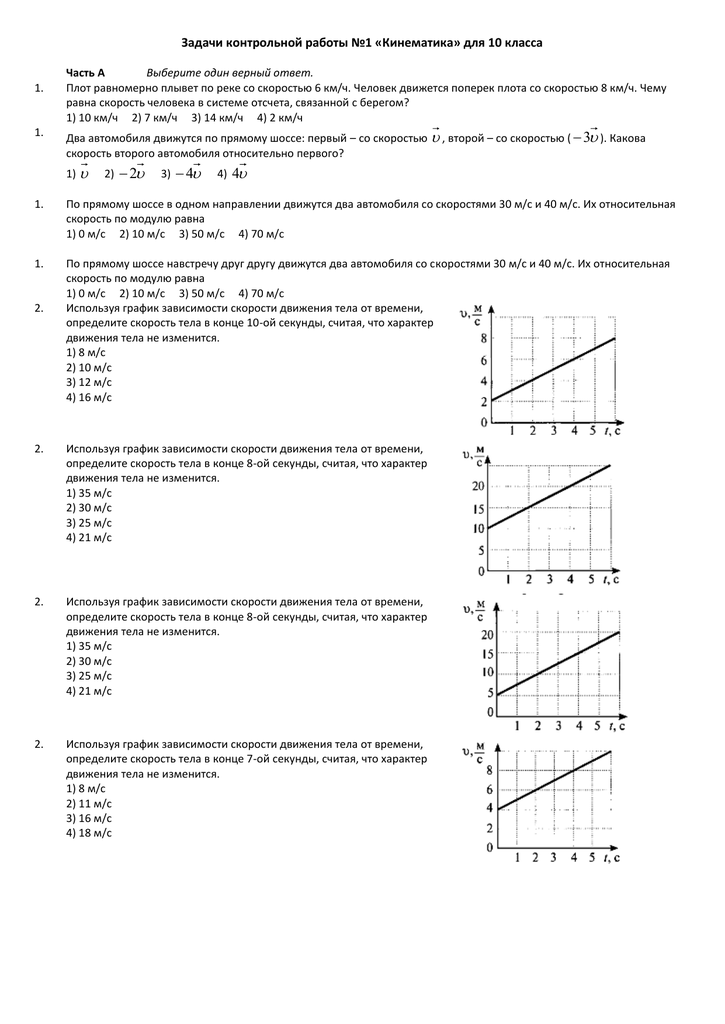

c

2. Теннисный мяч, брошенный горизонтально с высоты 4,9 м, упал на землю на расстоянии 30 м от точки бросания. Какова начальная скорость мяча и время его полета?

3. Тело брошено вертикально вверх с высоты 20 м с начальной скоростью 3 м/с. На какой высоте окажется тело через 2 с после начала движения?

4. Тело брошено под углом 60⁰ к горизонту с начальной скоростью 15м/с. Найти максимальную высоту подъема, дальность полета и время полета.

12

4. Тело брошено под углом 60⁰ к горизонту с начальной скоростью 15м/с. Найти максимальную высоту подъема, дальность полета и время полета.

5. По наклонной плоскости пустили катиться снизу вверх шарик с начальной скоростью 0,6 м/с и ускорением 0,3 м/с². На расстоянии L от начала пути шарик побывал дважды: через t₁ и t₂ после начала движения. Найти t₂ и L, t₁ = 1c.

1 Движение 2-х мотоциклистов заданы уравнениями x₁=15+t² и x₂=8t.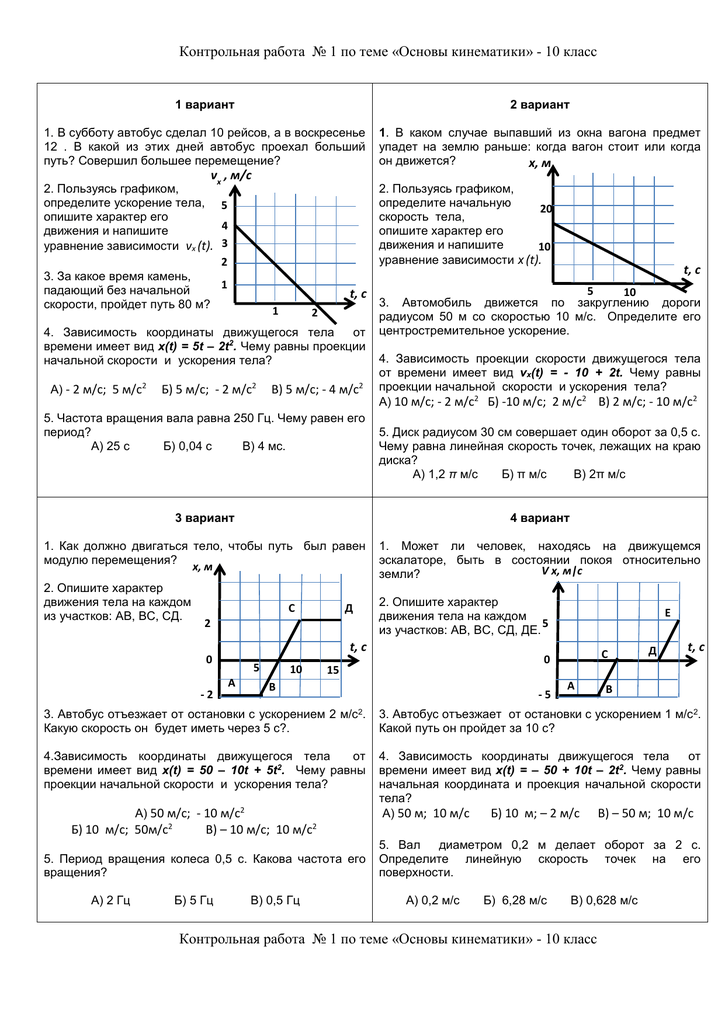 Описать характер движения каждого. Найти время и место встречи.

2. Из окна выбросили мяч в горизонтальном направлении со скоростью 12 м/с. Он упал на землю через 2 с. С какой высоты был выброшен мяч и на каком расстоянии от здания он упал?

3. Камень брошен под углом 30⁰ к горизонту со скоростью 10 м/с. Через какое время камень будет на высоте 1 м?

4. Тело упало с высоты 45 м. Определить время падения.

5. Тело пущено снизу вверх по наклонной плоскости с начальной скоростью 2 м/с и ускорением 0,6 м/с². На расстоянии L от начала пути оно побывало дважды: спустя t₁ и t₂ после начала движения. t₂ = 4 с. Найти t₁ и L.

1. Скорость движения тела задана уравнением v =8 – 2t. Записать уравнение для перемещения.

2. Из пружинного пистолета выстрелили вертикально вверх шариком, который поднялся на высоту 4,9 м. С какой скоростью вылетел шарик из пистолета?

3. Из винтовки, находящейся на высоте 4 м над поверхностью земли, в горизонтальном направлении был произведен выстрел. Определите дальность и время полета пули, если ее горизонтальная скорость при выстреле 1000 м/с.

4. Тело, брошенное под углом 60⁰ к горизонту, достигло максимальной высоты полета. Найти начальную скорость, дальность и время полета тела. Максимальная высота полета равна 40 м.

5. Шарик, пущенный катиться по наклонной плоскости, побывал на расстоянии 10 см от начала пути дважды: спустя 0,1 с и 2 с от начала движения. Считая ускорение постоянным, найти это ускорение и начальную скорость v

   0.

1. По графику, изображенному на рисунке, записать уравнение зависимости скорости и координаты от времени.

V, м/с

1

2

222222

0 1 2 3 t, с

2

2

2. На какую максимальную высоту поднимается тело, брошенное вертикально вверх со скоростью 40 м/с?

3. Мяч был брошен под углом 30⁰ к горизонту с начальной скоростью 20 м/с. Найти максимальную высоту и дальность полета.

4. Тело свободно падает с высоты 80 м. Найти его перемещение за последнюю секунду падения.

5. По наклонной плоскости снизу вверх пустили катиться шарик. На расстоянии 4 м от начала пути шарик побывал дважды: через t₁ и t₂ от начала движения. Ускорение постоянно и равно 0,2 м/с². Найти начальную скорость v₀ и t₂, t₁ = 2 с.

Контрольная работа №1 по теме «Кинематика материальной точки». 10 класс

Контрольная работа №1 по теме «Кинематика материальной точки» 10 класс

Вариант 1

1 Лыжник спускается с горы с начальной скоростью 6 м/с и ускорением 0,5 м/с². Какова длина горы, если спуск с нее продолжался 12 с?

2. Автобус движется со скоростью 54 км/ч. На каком расстоянии от остановки водитель должен начать торможение, если для удобства пассажиров ускорение не должно превышать 1, 2 м/с²?

3. Координата движущегося тела с течением времени меняется по следующему закону: х = -1 + 3t — t². Определите начальную координату тела, проекцию начальной скорости и проекцию ускорения. Укажите характер движения тела.

4. По графику проекции скорости, изображенному

на рисунке, определите ускорение, с которым двигалось тело,

и перемещение, совершенное им за время 8 с.

5. Скорость некоторой точки на грампластинке 0,3 м/с, а центростремительное ускорение 0,9 м/с². Найдите расстояние этой точки от оси вращения.

6. Шарик бросили горизонтально с высоты 20 м, при этом дальность полета составила 6 м. Найдите время полета и начальную скорость шарика.

Контрольная работа №1 по теме «Кинематика материальной точки» 10 класс

Вариант 2

1. При какой скорости самолет может приземлиться на посадочной полосе аэродрома длиной 800 м при торможении с ускорением 5 м/с²?

2. Через сколько секунд после отправления от станции скорость поезда метрополитена достигнет 72 км/ч, если ускорение при разгоне равно 1 м/с²?

3. Координата движущегося тела с течением времени меняется по следующему закону: х=10 -t- 2t². Определите начальную координату тела, проекцию начальной скорости и проекцию ускорения. Укажите характер движения тела.

4.По графику проекции скорости, изображенному на рисунке, определите ускорение, с которым двигалось тело, и перемещение, совершенное им за время 10 с.

5. Самолет при скорости 360 км/ч делает петлю Нестерова радиусом 400 м. Определите центростремительное ускорение, с которым двигался самолет.

6. Мяч бросают горизонтально с высоты 20 м с начальной скоростью 25 м/с.

Найдите дальность полета.

10 класс. Контрольная работа по теме «Кинематика» | Учебно-методический материал по физике (10 класс) на тему:

10 кл

Ответы контрольная работа «Кинематика».

Вариант – последняя цифра.

Разбалловка:     «5» — 13-14 баллов.

«4» — 10-12 баллов.

«3» —  8-9 баллов.

вар	1	2	3	4	5	6	7	8	9	Зад1.	Зад2.	Зад3.
1
2
3
4
5
6

ВАРИАНТ 31.

ОСНОВНАЯ ЧАСТЬ.

1.Материальная точка, это:  

А/Тело, принятое за точку отсчёта.     Б /Тело, относительно которого задаётся положение другого тела.     В/ Тело, размерами которого можно пренебречь.      Г/Тело, массой которого можно пренебречь.

2.Физическая величина, равная отношению изменения координаты ко времени, за которое это изменение произошло, называется:

А/ Пройденный путь.      Б/Перемещение.    В/Ускорение.   Г/ Скорость.  

3.Тело за 4 секунды изменило свою координату с 2 до 18 метров. Какова скорость тела:      А/4 м/с.    Б/12 м/с.   В/7 м/с.   Г/5 м/с.

4.Два автомобиля двигаются навстречу друг другу по параллельным дорогам со скоростями 36 км/ч и 12 м/с.  Чему равна скорость одного автомобиля относительно другого:          А/22 м/с.    Б/48 м/с.   В/24 м/с.   Г/3 м/с.

5.По данному уравнению   U = 5 + 6t   определите, чему равно ускорение  тела:

А/ 12м/с2.       Б/5 м/с2.           В/11 м/с2.            Г/ 6 м/с2.

6.Ускорение, с которым происходит свободное падение тела,:

А/ Одинаково для всех тел.    Б/ Зависит от массы тела.  В/ Зависит от высоты с которой падает тело.   Г/ Зависит от скорости с которой бросили тело.

7.Как направлено ускорение тела при движении по окружности:

А/По касательной к этой окружности.  Б/ Всегда от центра.  В/ Всегда к центру.    Г/При движении по окружности ускорения нет.

8.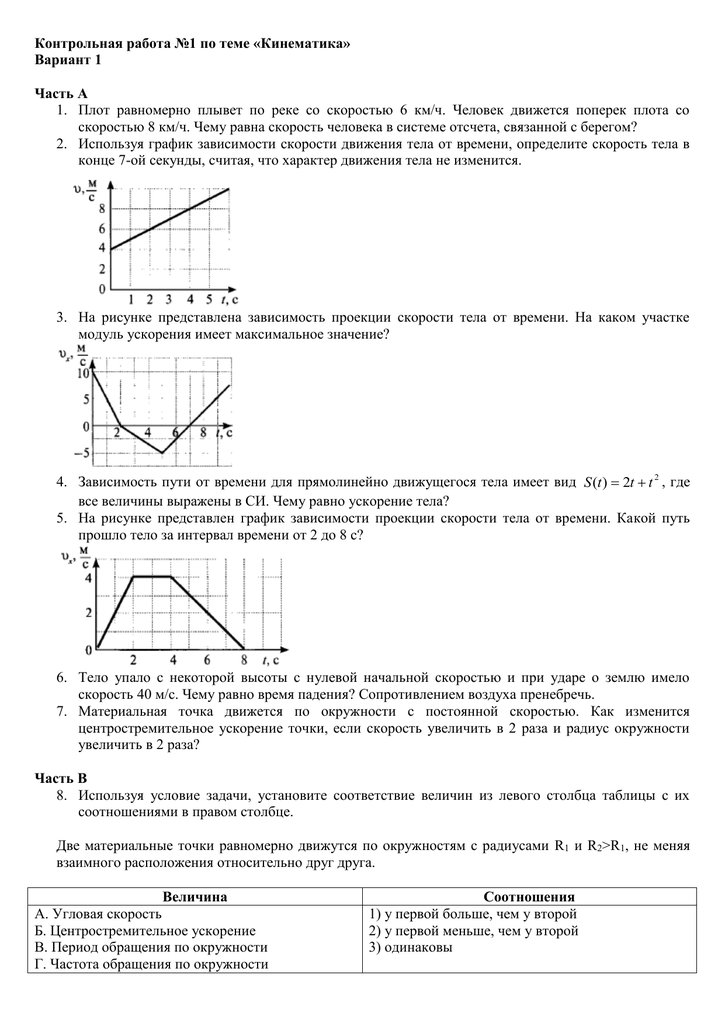 Автомобиль едет со скоростью 20 м/с  по закруглению дороги радиусом 50 метров. Чему равно центростремительное ускорение автомобиля:

А/8м/с2.      Б/0,5 м/с2.          В/ 2,5  м/с2.     Г/5 м/с.2

9. Как направлено ускорение, действующее на тело, брошенное под углом к горизонту:

А/ Вертикально вверх.    Б/ Вертикально вниз.      В/Горизонтально, по направлению движения тела.   Г/ Горизонтально, против движения тела.

ЗАДАЧИ.

1.Тело брошено вертикально вверх со скоростью 60 м/с. Через какое время его скорость будет равна 10м/с? (1 балл)

2.Чему равен радиус окружности, по которой двигается тело совершая 12 оборотов за 3 секунды, если на это тело действует центростремительное ускорение 4 м/с2. (2 балла)

3.Зависимость скорости от времени имеет вид:  U= 80 – 5t.  Постройте график скорости и определите перемещение тела через 8 секунд. (2 балла)

ВАРИАНТ 32.

ОСНОВНАЯ ЧАСТЬ.

1.Что из перечисленного не входит в систему отсчёта:

А/Тело отсчёта.      Б/ Система координат. В/Прибор для измерения времени.  Г/ Материальная точка.    

2.Длина траектории тела называется:

А/ Путь.          Б/ Перемещение.            В/Координата.           Г/Радиус-вектор.

3.Тело, имея координату 3 метра, двигается в течении 4 секунд со скоростью 1,2 м/с. Какова конечная координата тела:

А/10 м.     Б/1 м.    В/13,2 м.     Г/7,8 м.

4.Два автомобиля двигаются равномерно по параллельным дорогам, в одном направлении, со скоростями 72 км/ч и 15 м/с.  Чему равна скорость одного автомобиля относительно другого:

А/35 м/с.    Б/5 м/с.   В/57 м/с.   Г/87 м/с.

5.По данному уравнению  x = 8 – 2t    определите,  чему равна скорость  тела:

А/8 м/с.   Б/ 2 м/с.   В/6 м/с.   Г/ -2 м/с.

6.Свободно падающее тело двигается:

А/ С постоянной скоростью.    Б/ С увеличивающимся ускорением.  В/ С постоянным ускорением.  Г/ Со скорость равной нулю.

7.Как направлено перемещение тела при движении по окружности:

А/По касательной к этой окружности.  Б/.  По хорде.    В/ Всегда к центру Г/При движении по окружности перемещения нет.

8.С какой скоростью двигается тело по окружности радиусом 20 метров, если центростремительное ускорение тела равно  3,2 м/с :

А/8 м/с2     Б/1,6 м/с2       В/64 м/с2    Г/0,8 м/с2

9.Тело, брошенное горизонтально будет двигаться:

А/ По прямой.     Б/ По параболе.   В/ По окружности.   Г/ По любой кривой, это зависит от скорости, с которой бросили тело.

ЗАДАЧИ:

1.Какую скорость будет иметь тело, брошенное вертикально вверх со скоростью 40 м/с, через 2 секунды после начала движения. (1 балл).

2.Определите центростремительное ускорение и радиус окружности, если двигаясь со скоростью 10 м/с тело совершает один оборот за 1 минуту. ( 2 балла)

 3.Зависимость скорости от времени имеет вид:   U = 9 + 3t. Постройте график скорости и определите перемещение тела через 10 секунд. (2 балла)

ВАРИАНТ 33.

ОСНОВНАЯ ЧАСТЬ.

1.Кинематика, это раздел механики, изучающий:

А/ Скалярные и векторные величины.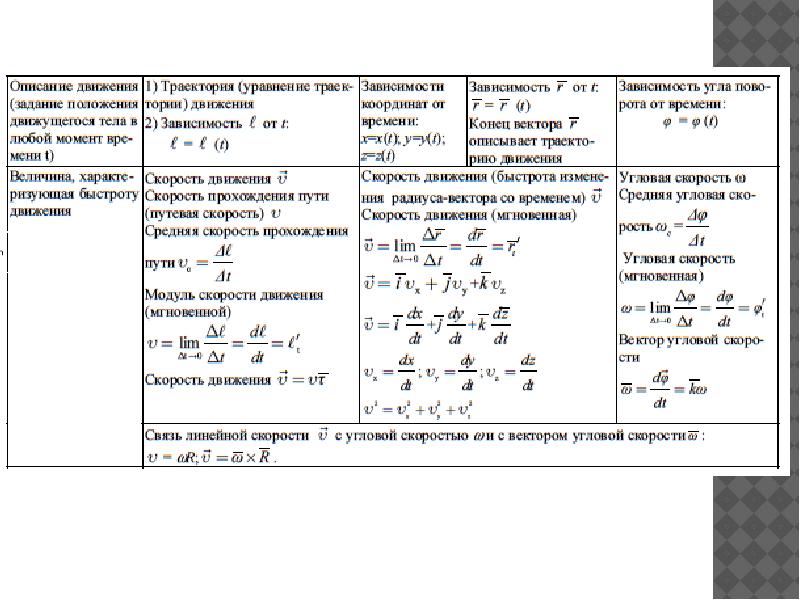   Б/Способы задания положения тела.    В/ Способы описания движения.    Г/Способы определения перемещения тела.

2.Вектор, соединяющий начальное и конечное положение тела, называется:

А/Радиус-вектор.   Б/ Путь.  В/Траектория.    Г/ Перемещение.

3.Тело за 3 секунды изменило свою координату с 7 до 28 метров. Какова скорость тела:

А/ 12 м/с.    Б/32 м/с.   В/ 2.8 м/с.   Г/ 7 м/с.

4.Два поезда двигаются навстречу друг другу по параллельным дорогам со скоростями 108 км/ч и 40 м/с.  Чему равна скорость одного поезда относительно другого:

А/10 м/с.    Б/148 м/с.   В/70 м/с.   Г/68 м/с.

5.По данному уравнению u = — 10 +3t  определите, чему равна начальная скорость тело тела:

А/3 м/с.   Б/-10 м/с.   В/10 м/с.   Г/ 6 м/с.

6.При свободном падении тела, его ускорение:

А/ Равно нулю.  Б/Равномерно уменьшается.   В/ Равномерно увеличивается.             Г/ Не изменяется.   

7.Как направлена  скорость тела при движении по окружности:

А/ Всегда к центру.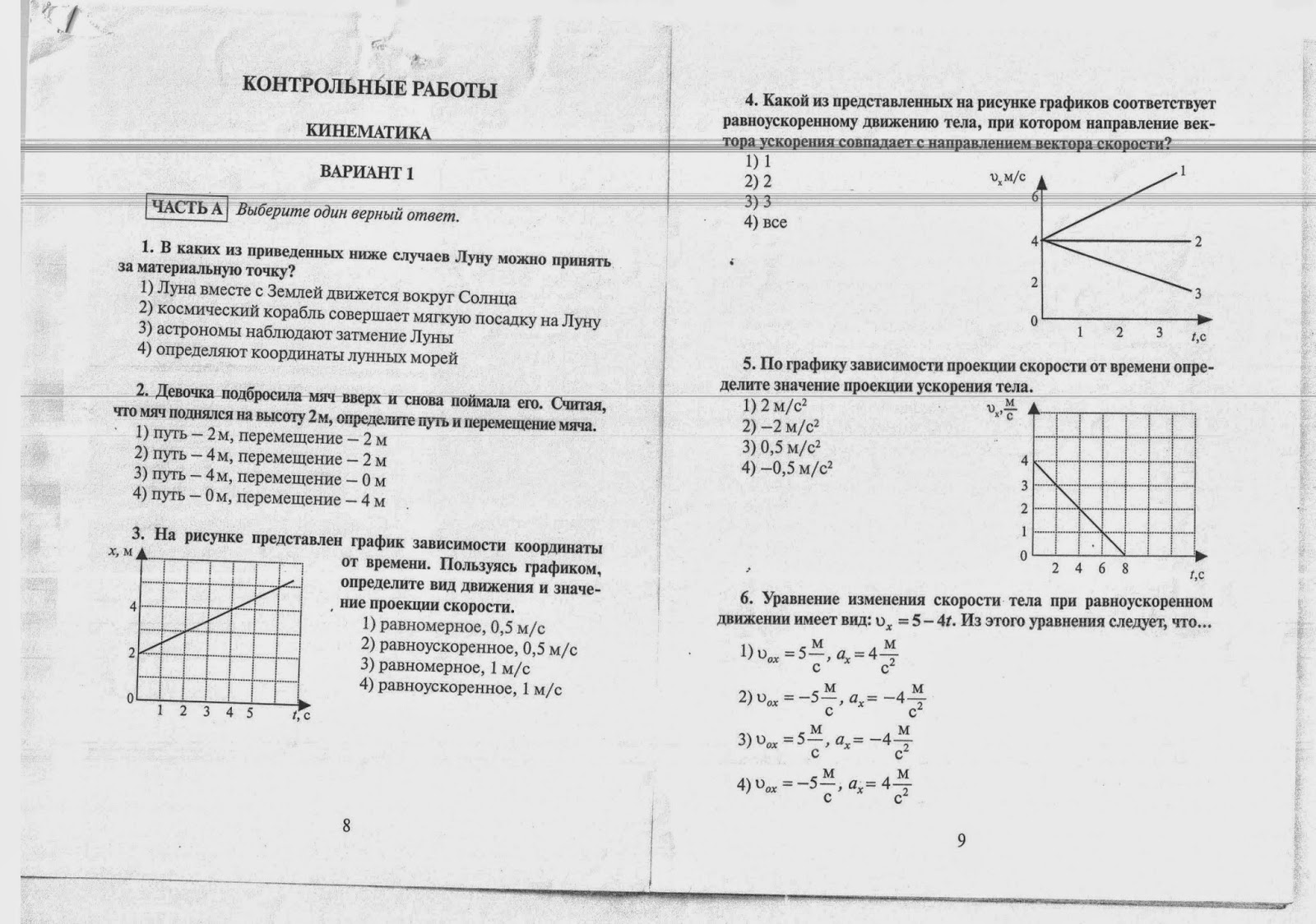  Б/ По касательной к этой окружности.  В/По хорде.    Г/По дуге окружности.

8.Автомобиль едет со скоростью 6 м/с, по закруглению дороги радиусом 12 метров. Чему равно центростремительное ускорение автомобиля:

А/ 3м/с2      Б/ 72  м/с2         В/  0,5 м/с2     Г/2 м/с2 

9.Движение, при котором все точки тела двигаются одинаково, называется:

А/ Поступательное.   Б/Вращение тела.   В/Равноускоренное.  Г/ Равномерное.  

ЗАДАЧИ.

1.Тело свободно падает с высоты 100 метров.   Через какое время оно упадёт на Землю? (1 балл)

2.Определить линейную и угловую скорость движения тела по окружности радиусом 20 см, если период обращения тела 4 секунды. (2 балла)

3.Зависимость скорости от времени имеет вид:   u =  30 — 6t. Постройте график скорости и определите перемещение тела через 6 секунд. (2 балла)

ВАРИАНТ 34.

ОСНОВНАЯ ЧАСТЬ.

1.В систему отсчёта входят:

А/ Тело отсчёта, система координат и часы.     Б/ Точка отсчёта, координаты тела и часы.    В/ Тело отсчёта, часы и радиус-вектор.    Г/Материальная точка, координаты тела и часы.

2.Физическая величина, равная отношению изменения скорости ко времени, за которое это изменение произошло, называется:

А/Скорость.   Б/Перемещение.    В/Ускорение.   Г/Пройденный путь.

3.Тело, имея координату 8 метров, двигается в течении 10 секунд со скоростью    4 м/с. Какова конечная координата тела:

А/ 48м.     Б/84 м.    В/ 20м.     Г/16 м.

4.Два поезда двигаются равномерно по параллельным дорогам, в одном направлении, со скоростями 108 км/ч и 30 м/с.  Чему равна скорость одного поезда относительно другого:

А/60 м/с.    Б/ 78м/с.   В/138 м/с.   Г/0 м/с.

5.По данному уравнению  x = 12 – 4t    определите, чему равна начальная координата  тела:

А /8 м.      Б/ 12 м.      В/ 4 м.        Г/ -4 м.

6.Ускорение, с которым тело двигается под  действием земного притяжения направлено:

А/ Туда, куда двигается тело.   Б/Всегда вниз.   В/ Всегда вверх.  Г/Никуда, так как равно нулю.

7.Какая величина при движении по окружности направлена всегда к центру:

А/ Перемещение.  Б/ Ускорение.   В/Скорость.  Г/Траектория.

8.С какой скорость двигается тело по окружности радиусом 80 метров, если центростремительное ускорение тела равно 20 м/с 2:

А/5 м/с.    Б/4 м/с.       В/40 м/с    Г/100 м/с.

9. Тело совершает один полный оборот по окружность. Какая величина при этом оказывается равной нулю:

А/ Перемещение.          Б / Путь.      В/  Скорость.   Г/ Ускорение.

ЗАДАЧИ:

1.Тело бросили вертикально вверх со скоростью 50 м/с. До какой высоты поднимется тело? (2 балла)

2.Тело двигается по окружности, радиусом 40 см делая один оборот за 10секунд. Определите линейную скорость движения и центростремительное ускорение тела.(1 балл)

3.Зависимость скорости от времени имеет вид:   U =  12 + 4t. Постройте график скорости и определите перемещение тела через 8 секунд. (2 балла)

ВАРИАНТ 35.

ОСНОВНАЯ ЧАСТЬ.

1.Тело отсчёта это:

А/Тело, движение которого описывают.     Б/Тело, размерами которого можно пренебречь.       В/ Тело, массой которого можно пренебречь.     Г/Тело, относительно которого задаётся положение другого тела.   

2.Движение, при котором скорость тела изменяется одинаково за равные промежутки времени, называется:

А/ Равномерное.     Б/ Равноускоренное.    В/Движение по окружности.   Г/Вращение тела.

3.Тело за 6 секунд изменило свою координату с 10 до 34 метров. Какова скорость тела:

А/2,8 м/с.    Б/26 м/с.   В/4 м/с.   Г/17 м/с.

4.Два пешехода двигаются навстречу друг другу по параллельным дорогам со скоростями 7,2 км/ч и 2 м/с.  Чему равна скорость одного пешехода относительно другого:

А/9,2 м/с.    Б/0 м/с.   В/4м/с.   Г/5,2  м/с.

5.По данному уравнению U = 120 – 20t     определите, чему равно ускорение  тела:

А/20 м/с2.   Б/-20 м/с2.   В/120 м/с2.   Г/ 100 м/с2.

6.Как двигается тело под действием притяжения Земли:

А/ Равноускоренно.  Б/ Равномерно.   В/С произвольно меняющейся скоростью.  Г/Это зависит от начальной скорость тела.

7.Какая величина при движении по окружности направлена по касательной:

А/Ускорение.     Б/Перемещение.      В/ Путь.     Г/ Скорость.

8.Автомобиль едет со скоростью 18 м/с. по закруглению дороги радиусом 90 метров. Чему равно центростремительное ускорение автомобиля:

А/ 4500м/с2     Б/ 5 м/с2         В/0,2 м/с2      Г/3,6  м/с2

9.Какая характеристика движения тела остаётся постоянной  при равномерном движении по окружности:

А/Координата.  Б/Скорость.  В/Перемещение.   Г/Период.

ЗАДАЧИ.

1.Тело свободно падает в течении 8 секунд.  С какой скоростью оно упадёт на землю? (1 балл)

2.Колесо велосипеда радиусом 30 см. делает один оборот за 0,4 секунды. Определите скорость движения велосипеда и центростремительное ускорение точек обода колеса. (2 балла)

3.Зависимость скорости от времени имеет вид:   U =  15 +2t. Постройте график скорости и определите перемещение тела через 14 секунд. (2 балла)

ВАРИАНТ 36.

ОСНОВНАЯ ЧАСТЬ.

1.Механическим движением называется:

А/Изменение траектории тела относительно  других тел.  Б/Изменение координаты тела относительно разных тел отсчёта. В/ Изменение скорости тела с течением времени.    Г/ Изменение положения тела относительно других тел с течением времени.

2.Скорость тела в данной точке траектории называется:

А/Средняя.  Б/ Относительная.  В/ Мгновенная.   Г/Ускорение.

3.Тело, имея координату 10 метра, двигается в течении 5 секунд со скоростью 2,5 м/с. Какова конечная координата тела:

А/5 м.     Б/20 м.    В/22,5 м.     Г/12,5 м.

4.Два пешехода двигаются равномерно по параллельным дорогам, в одном направлении, со скоростями 3,6 км/ч и 2 м/с.  Чему равна скорость одного пешехода относительно другого:

А/5,6 м/с.    Б/1,6 м/с.   В/1 м/с.   Г/3 м/с.

5.По данному уравнению скорости  U = — 60+5t    определите, чему равна начальная скорость тела:

А/ -60 м/с.   Б/ -55 м/с.   В/ 5 м/с.   Г/ 60 м/с.

6.Тело брошено вертикально вверх. Как направленно его ускорение:

А/ Вверх.   Б/ Вниз.   В/Тело двигается без ускорения.   Г/Сначала вверх, потом вниз.

7.Какая величина при движении по окружности направлена по хордам окружности:

А/Ускорение.   Б/ Скорость. В/ Перемещение.  Г/ Путь.

8.С какой скоростью двигается тело по окружности, радиусом 100 метров, если центростремительное ускорение тела равно  25 м/с2:

А/ 0,5 м/с.     Б/4 м/с.       В/50 м/с.    Г/6,25 м/с.

9.При каком движении скорость тела остаётся постоянной:

А/ Равномерное движение. Б/Равноускоренное движение.    В/Движение под действием силы тяжести.    Г/ Движение по окружности.  

ЗАДАЧИ:

1.С какой высоты падает тело без начальной скорости, если в момент удара о Землю его скорость равна 80 м/с? (2 балла)

2.Определите частоту и период движения тела по окружности радиусом 40 см, если его скорость равна 20 м/с. (1 балл)

3.Зависимость скорости от времени имеет вид:   U =  50 — 10t. Постройте график скорости и определите перемещение тела через 8 секунд. (2 балла)

Контрольная работа по физике Кинематика периодического движения 10 класс

Контрольная работа по физике Кинематика периодического движения 10 класс с ответами. Контрольная работа включает 4 варианта, в каждом варианте по 6 заданий.

1 вариант

1. Самолет на скорости 360 км/ч делает петлю Несте­рова радиусом 400 м. Определите центростремитель­ное ускорение самолета.

2. Чему равны частота и период колеса ветродвигате­ля, если за 2 мин колесо сделало 50 оборотов?

3. Какова линейная скорость точек шкива мотора, удаленных от оси вращения на 10 см, если шкив совершает 1200 оборотов в минуту?

4. Частица совершает гармонические колебания по закону х = 20 cos ^π/₆t см. Определите координату частицы, модуль ее скорости и ускорения в момент времени t = 2 с.

5. Определите частоту вращения колес поезда, имею­щих диаметр 1,5 м, при скорости поезда 72 км/ч.

6. Каково центростремительное ускорение тела при его равномерном движении по окружности радиусом 10 см, если при этом тело совершает 30 оборотов в ми­нуту?

2 вариант

1. Определите период и частоту вращающегося диска, если он за 10 с делает 40 оборотов.

2. Какова скорость трамвайного вагона, движущегося по закруглению радиусом 50 м с центростремитель­ным ускорением 0,5 м/с²?

3. Частица совершает гармонические колебания по закону х = 10 cos ^π/₂₄t см. Определите координату частицы, модуль ее скорости и ускорения в момент времени t = 8 с.

4. При равномерном движении по окружности тело за 2 с проходит 5 м. Каково центростремительное уско­рение тела, если период обращения равен 5 с?

5. Рассчитайте, во сколько раз скорость конца минут­ной стрелки больше скорости конца часовой стрелки, если минутная стрелка в 1,5 раза длиннее часовой.

6. Тело равномерно движется по окружности ради­усом 1 м. Определите период вращения тела по окружности, если центростремительное ускорение равно 4 м/с².

3 вариант

1. Вычислите центростремительное ускорение искус­ственного спутника Земли, движущегося на высоте 600 км над земной поверхностью по круговой орбите с линейной скоростью 8 км/с. Радиус Земли принять равным 6400 км.

2. Найдите период и частоту вращения минутной стрелки часов.

3. Чему равна скорость велосипедиста, если колесо ве­лосипеда делает 100 оборотов в минуту, а его радиус равен 40 см?

4. Частица совершает гармонические колебания по закону х = 5 cos ^π/₃t см. Определите координату частицы, модуль ее скорости и ускорения в момент времени t = 3 с.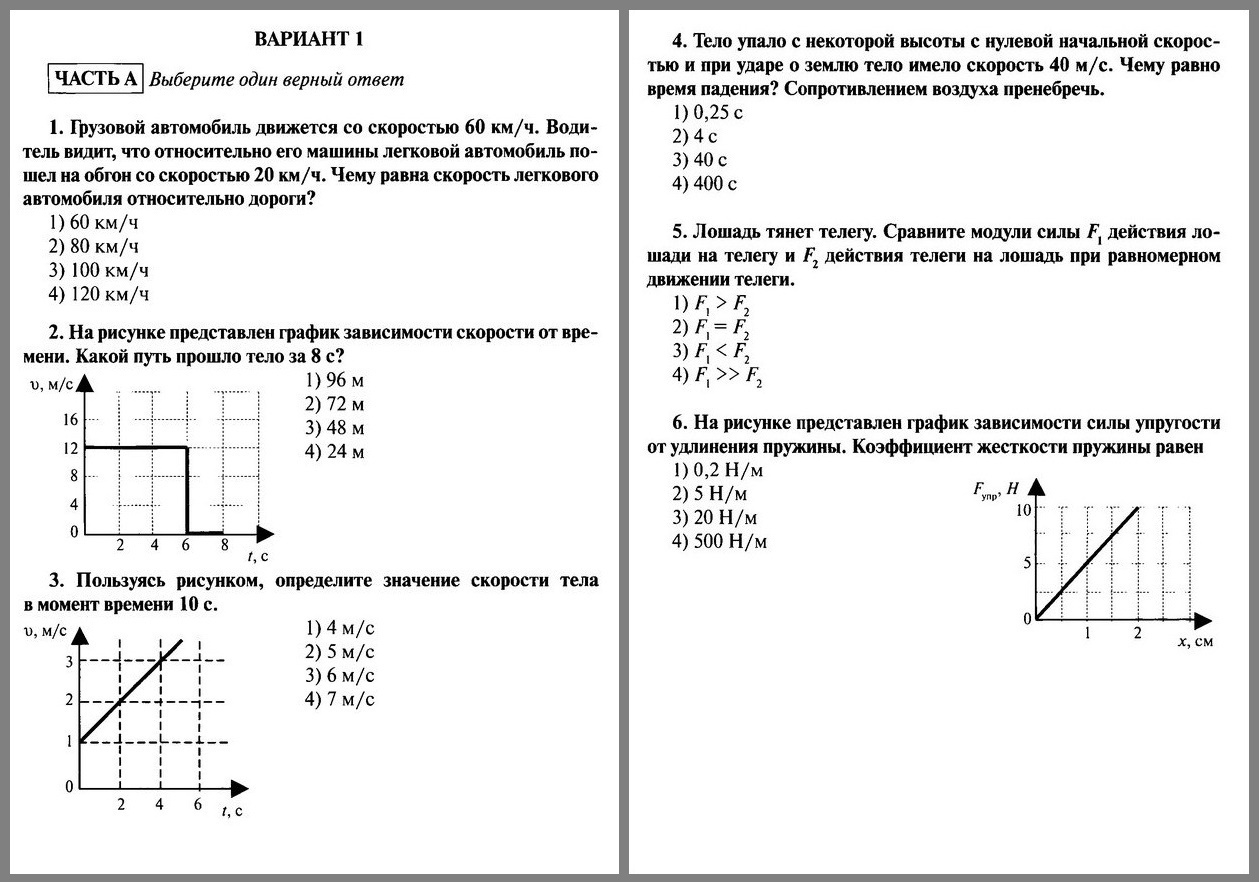

5. Во сколько раз изменяется скорость движения спут­ника на орбите, если при уменьшении в 2 раза радиуса круговой орбиты период его обращения уменьшается в 4 раза?

6. Две материальные точки движутся по окружностям радиусами R₁ и R₂, причем R₁ = R₂. Сравните их центростремительные ускорения, если равны их пери­оды обращения.

4 вариант

1. Каковы период и частота обращения секундной стрелки часов?

2. Конькобежец движется со скоростью 12 м/с по ок­ружности радиусом 50 м. Определите центростремительное ускорение при движении конькобежца.

3. Чему равна скорость поезда, если колеса локомоти­ва, имеющие радиус 1,2 м, делают 160 оборотов в ми­нуту?

4. Частица совершает гармонические колебания по закону х = 4 cos ^π/₁₀t см.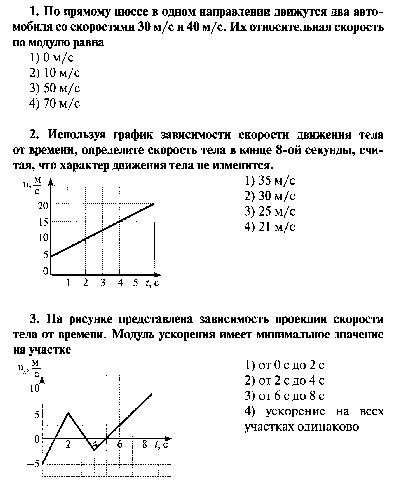 Определите координату частицы, модуль ее скорости и ускорения в момент времени t = 5 с.

5. Найдите частоту вращения барабана лебедки диа­метром 16 см при подъеме груза со скоростью 0,4 м/с.

6. Определите среднюю орбитальную скорость спутни­ка, если средняя высота его орбиты над Землей равна 1200 км, а период обращения равен 105 мин. Радиус Земли равен 6400 км.

ОТВЕТЫ — Контрольная работа по физике Кинематика периодического движения 10 класс
1 вариант
1. 25 м/с²
2. 2,4 Гц; ≈ 0,42 с
3. 12,6 м/с
4. 10 см;
-9 см/с;
-2,74 см/с²
5. ≈ 4,2 Гц
6. 1 м/с²
2 вариант
1. 0,25 с; 4 Гц
2. 5 м/с
3. 5 см;
-1,13 см/с;
-0,086 см/с²
4. 3,14 м/с²
5. в 18 раз
6. 3,14 с
3 вариант
1. 9,1 м/с²
2. 60 мин; 0,0003 Гц
3. ≈ 4,2 м/с
4. -5 см;
0;
5,48 см/с²
5. увеличит­ся в 2 раза
6. 2:1
4 вариант
1. 60 с; ≈ 0,017 Гц
2. 2,9 м/с²
3. ≈ 20 м/с
4. 0;
-1,26 см/с;
0
5. 0,8 Гц
6. ≈ 7,6 км/с

Тест по физике Кинематика точки 10 класс

Тест по физике Кинематика точки 10 класс с ответами. Тест включает два варианта, в каждом по 6 заданий.

Вариант 1

A1. Спортсмен пробежал дистанцию 400 м по круговой дорожке стадиона и возвратился к месту старта. Определите путь L, пройденный спортсменом, и модуль перемещения S.

1) L = S = 0
2) L = S = 400 м
3) S = 0; L = 400 м
4) S = 0; L = 800 м

А2. Тело брошено вертикально вверх со скоростью v₀. Какой из графиков зависимости проекции скорости от времени соответствует этому движению?

1) 1
2) 2
3) 3
4) 4

А3. Координаты движения автомобиля соответствуют уравнению х = 100 + 4t − 3t². Определите ускорение а_х его движения.

1) 4 м/с²
2) 3 м/с²
3) -6 м/с²
4) -3 м/с²

А4. Плот равномерно плывет по реке со скоростью 3 км/ч. Сплавщик движется поперек плота со скоростью 4 км/ч. Какова скорость сплавщика в системе отсчета, связанной с берегом?

1) 3 км/ч
2) 4 км/ч
3) 5 км/ч
4) 7 км/ч

B1. Материальная точка движется в плоскости равномерно и прямолинейно по закону согласно системе координат х = 4 + 3t; y = 3 − 4t. Какова величина скорости точки?

C1. Две моторные лодки движутся навстречу друг другу. Скорости лодок относительно воды равны 3 м/с и 4 м/с. Скорость течения реки 2 м/с. Через какое время после их встречи расстояние между лодками станет равным 84 м?

Вариант 2

A1. Тело, брошенное горизонтально с башни высотой 6 м, упало на расстоянии 8 мот основания башни. Чему равно перемещение тела?

1) 8м
2) 6м
3) 14 м
4) 10 м

А2. Величины скорости течения реки и скорости лодки относительно берега одинаковы и образуют угол 60°. Под каким углом к направлению течения направлена скорость лодки относительно воды?

1) 30°
2) 60°
3) 90°
4) 120°

А3. При равноускоренном прямолинейном движении скорость катера увеличивается за 10 с с 5 м/с до 9 м/с. Какой путь пройдет катер за это время?

1) 140 м
2) 90 м
3) 50 м
4) 70 м

А4. На графике изображена зависимость проекции скорости тела, движущегося вдоль оси 0х, от времени. Чему равен модуль перемещения тела к моменту времени t = 10 с?

1) 1 м
2) 6 м
3) 7 м
4) 13 м

B1. Поезд длиной 200 м въезжает в тоннель длиной 300 м, двигаясь равномерно со скоростью v = 10 м/с.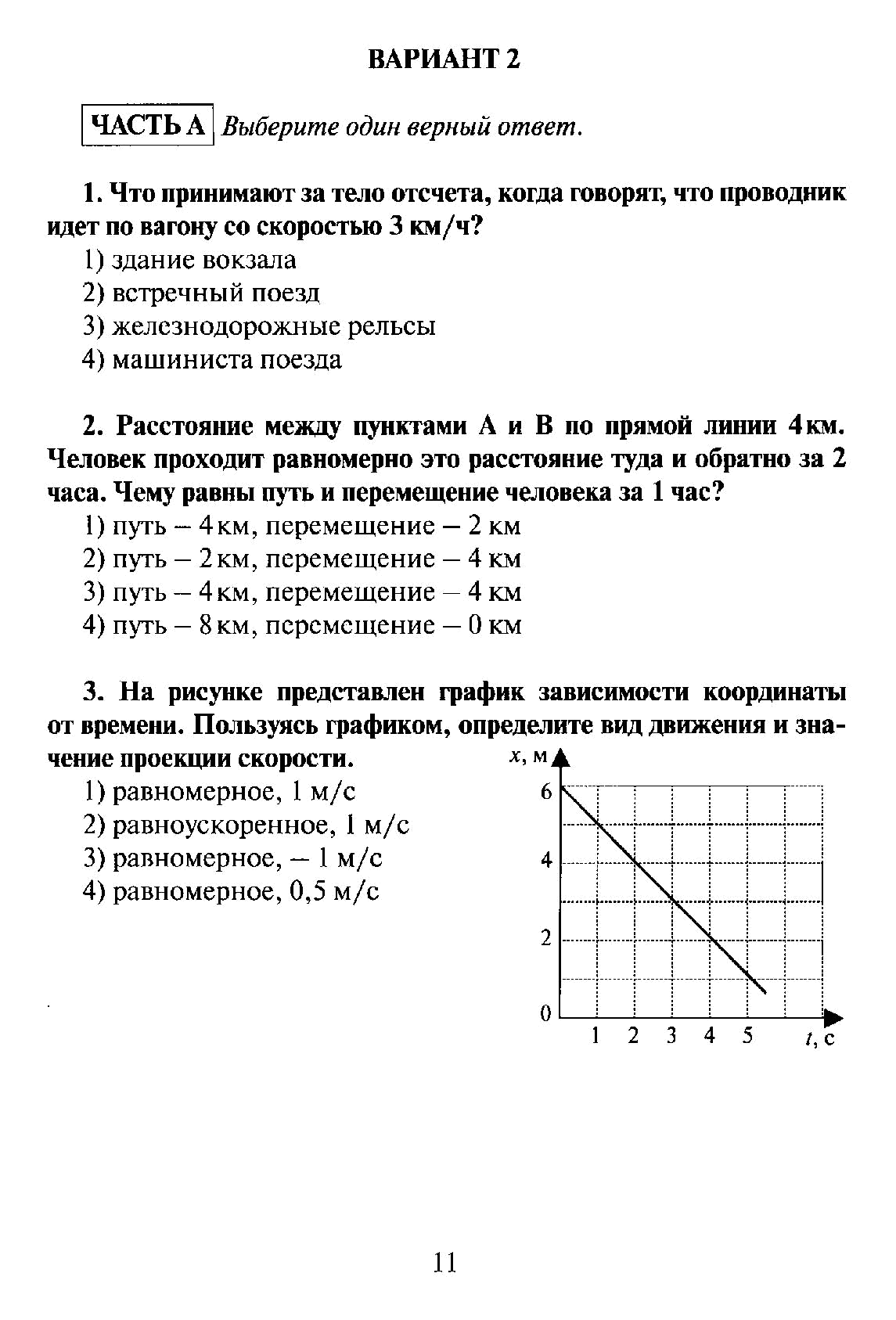 Через какое время он полностью выйдет из тоннеля?

C1. По кольцевой автомобильной дороге длиной L = 5 км в одном направлении едут грузовой автомобиль и мотоциклист со скоростями соответственно v₁ = 40 км/ч и v₂ = 100 км/ч. В начальный момент времени они находились в одном месте. Какое расстояние проедет мотоциклист, когда его догонит автомобиль?

Ответы на тест по физике Кинематика точки 10 класс
Вариант 1
А1-3
А2-2
А3-3
А4-3
В1. 5 м/с
С1. Через 12 с
Вариант 2
А1-4
А2-4
А3-4
А4-1
В1. Через 50 с
С1. 8,3 км

Кинематика 11 класс Физика Численное | Решения

1.

Солнечная,

Водоизмещение y = $ — \ frac {2} {3} $ t ² + 16t + 2

Скорость v = $ \ frac {{{\ rm {dy}}}} {{{\ rm {dt}}}} $ = $ — \ frac {2} {3} $ * 2t + 16 = $ — \ гидроразрыв {4} {3} $ t + 16

Когда тело приходит в состояние покоя v = 0.

Или, $ — \ frac {4} {3} $ t + 16 = 0

Или t = 16 * $ \ frac {3} {4} $ = 12 с

Время, необходимое для того, чтобы тело остановилось, составляет 12 секунд.

2.

Солнечная,

Смещение тела в данном интервале может быть получено по площади, ограниченной графиком скорость — время.

Пусть d ₁ , d ₂ , d ₃ , d ₄ будет смещением в первую секунду, вторую секунду, третью секунду и четвертую секунду.

Или, d = d ₁ + d ₂ + d ₃ + d ₄

= (10 + 20 + 15 + 10) м

= 55 м

3.

Солнечная,

Пусть t ₁ и t ₂ — время, необходимое автобусу для перемещения из Ратна-парка в Калимати и из Калимати в Ратнапарк соответственно.

Расстояние, которое проехал микроавтобус от парка Ратна до Калимати, составляет:

x ₁ = 40 т ₁

Аналогичным образом, расстояние, которое проезжает микроавтобус, чтобы добраться от Калимати до парка Ратна, составляет:

x ₂ = 60 т ₂

Так как, x ₁ = x ₂

Или, 40 т ₁ = 60 т ₂

Или, $ \ frac {{{{\ rm {t}} _ 1}}} {{{{\ rm {t}} _ 2}}} $ = $ \ frac {{40}} {{60}} $ = $ \ frac {2} {3}

долл. США

Средняя скорость = $ \ frac {{{\ rm {total \: distance \: traveled}}}} {{{\ rm {total \: time \: take}}}} $

= $ \ frac {{{{\ rm {x}} _ 1} + {{\ rm {x}} _ 2}}} {{{{{\ rm {t}} _ 1} + {{\ rm {t}) } _2}}}

долл. США

= $ \ frac {{40 {{\ rm {t}} _ 1} + 60 {{\ rm {t}} _ 2}}} {{{{\ rm {t}} _ 1} + {{\ rm { t}} _ 2}}}

долл. США

= $ \ frac {{{{\ rm {t}} _ 2} \ left ({40 \ frac {{{{{\ rm {t}} _ 1}}} {{{{{\ rm {t}}} _ 2}) }} + 60} \ right)}} {{{{\ rm {t}} _ 2} \ left ({\ frac {{{{\ rm {t}} _ 1}}} {{{{{\ rm {t }} _ 2}}} + 1} \ right)}}

долл. США

= $ \ frac {{\ left ({40 {\ rm {*}} \ frac {2} {3} + 60} \ right)}} {{\ frac {2} {3} + 1}} $

Итак, В _ср. = 48км / час.

Так как полное перемещение микроавтобуса составляет 0,

Итак, средняя скорость = $ \ frac {{{\ rm {total \: displacement \: traveled}}}} {{{\ rm {total \: time \: take}}}} $

= $ \ frac {0} {{{{\ rm {t}} _ 1} + {{\ rm {t}} _ 2}}}

долл. США

Итак, В _ср. = 0.

4.

Солнечная,

Пусть A будет положением вершины башни, а B — положением земли. Предположим, они встречаются в точке C.

Для сброшенного объекта, пройденное расстояние,

S = ut + $ \ frac {1} {2} $ gt ²

Или, x = 0 * t + $ \ frac {1} {2} $ gt ²

Или, x = $ \ frac {1} {2} $ gt ² … (i)

Для объекта «Снаряд»,

Или, s = ut — $ \ frac {1} {2} $ gt ²

Или, h — x = 78.4t — $ \ frac {1} {2} $ gt ² .

Или 156,8 = 78,4 т

Итак, t = 2 с.

Положив t = 2s в уравнение (i), получим

Или, x = $ \ frac {1} {2} $ * 9,8 * 2 ² = 19,6 м

Следовательно, они встречаются ниже 19,6 м от вершины башни через 2 секунды.

5.

Солнечная,

Скорость обезьяны V _м = 5 м / с

Скорость собаки V _d = 10 м / с. 2}} $ = $ \ sqrt {100 + 25} $ = $ 5 \ sqrt 5 $ м / с.

Пусть θ — угол между $ {\ rm {\ vec V}} $ _dw с $ {\ rm {\ vec V}} $ _d .

Итак, tanθ = $ \ frac {{{{\ rm {V}} _ {\ rm {m}}}}} {{{{\ rm {V}} _ {\ rm {d}}}}} $.

Или tanθ = $ \ frac {5} {{10}} $.

Итак, θ = tan ^-15 $ \ left ({\ frac {5} {{10}}} \ right) $ = tan ^-1 $ \ left ({\ frac {1} {2}} \ right) $.

6.

Солнечная,

Максимальная дальность R = 16 км = 1600 м.

Или, g = 10 мс ^-1 .2}}} {{\ rm {g}}} $.

Или, u ² = Rg.

= 16000 * 10

= 160000

Итак, u = 400 мс ^-1 .

7.

Солнечная,

Скорость полицейского фургона V _p = 30 км / ч ^-1 .

= $ \ frac {{30 {\ rm {*}} 1000}} {{60 {\ rm {*}} 60}} $ = 8,3 мс ^-1 .

Скорость воровской машины V _т = 192 км / ч ^-1 .

= $ \ frac {{192 {\ rm {*}} 1000}} {{60 {\ rm {*}} 60}} $ = 53.3 мс ^-1 .

Скорость полета пули к полицейскому фургону V _bp = 150 мс ^-1 .

Итак, скорость пули относительно окружающего V _b = (150 + 8,3) мс ^-1 .

= 158,3 мс ^-1 .

Итак, скорость пули, которая попадает в вора

Автомобиль = 158,3 — 53,3

= 105 мс ^-1 .

8.

Солнечная,

Начальная скорость u = 12 м / с в восходящем направлении.2}}} {{2 {\ rm {*}} 10}} $ = $ \ frac {{144}} {{20}} $ = 7,2 м

Пусть v ₁ будет скоростью пакета, с которым он ударяется о землю.

В ₁ ² = u ₁ ² + 2g (h + x)

Или, v ₁ ² = 0 + 2 * 10 * (65 + 7.2)

= 1444,

Итак, v ₁ = 38 м / с.

Время, затрачиваемое пакетом на то, чтобы достичь C от B, чтобы сказать t ₁ = $ \ frac {{{\ rm {Final \: velocity}} — {\ rm {initital \: velocity}}}} {{{ \ rm {ускорение \: due \: to \: gravity}}}} $

= $ \ frac {{0 — \ left ({- 12} \ right)}} {{10}}

долларов США

= 1.2 сек.

Время, необходимое пакету, чтобы достичь земли от B, чтобы сказать t ₂ = $ \ frac {{38 — 0}} {{10}} $ = 3,8 секунды.

Итак, общее время, затраченное на пакет, скажем, t = t ₁ + t ₂

= 1,2 + 3,8

= 5 сек.

9.

Солнечная,

Здесь точки A, B и C представляют положение самолета, положение парашютиста, где он открывает парашют и указывает на землю соответственно, Пусть V ₁ , V ₂ и V ₃ будет скоростью парашютиста в точках A, B и C соответственно,

В ₂ ² = В ₁ ² + 2gS ₁

В ₂ ² = 0 + 2 * 9.2}}} {{2 {\ rm {*}} 2}} $ = 195 млн. Долл. США.

Итак, общее расстояние, пройденное парашютистом, равно = (195 + 40) м = 235м.

Т.е. высота выхода парашютиста от земли 235м.

Период времени для преодоления расстояния S ₁ , скажем, t ₁ = $ \ frac {{{{\ rm {V}} _ 2} — {{\ rm {V}} _ 1}}} {{\ rm {g}}} $ = $ \ frac {{28 — 0}} {{9.8}} $ = 2,9.

Период времени до пройденного расстояния S ₂ sat t ₂ = $ \ frac {{{{\ rm {V}} _ 2} — {{\ rm {V}} _ 1}}} {{\ rm {a }}} $ = $ \ frac {{28 — 0}} {2} $ = 13.

Итак, период пребывания в воздухе = (13 + 2,9) с = 15,9 с.

10.

Солнечная,

Здесь данный случай можно принять таким образом, что бомба выбрасывается горизонтально со скоростью 500 км / ч ^-1 на высоте 1500 м от земли.

Итак, горизонтальный диапазон (R) = $ \ sqrt {\ frac {{2 {\ rm {h}}}} {{\ rm {g}}}} $ u _o

= $ \ sqrt {2 {\ rm {*}} \ frac {{1500}} {{9.8}}} $ * $ \ frac {{500 {\ rm {*}} 1000}} {{36000}} $

= $ \ sqrt {306.2} \ theta}} {{2 {\ rm {g}}}}

долл. США

Или, sin ² θ = 2 * 2sinθ.cosθ

Или $ \ frac {{{\ rm {sin}} \ theta}} {{{\ rm {cos}} \ theta}} $ = 4

Или, tanθ = 4

Или, θ = tan ^-1 (4) = 75,96 °

Следовательно, угол, при котором R и h _max составляет 75,96 °.

12.

Солнечная,

Дан,

u = 10 мс ^-1

v = 15 мс ^-1

а = 1 мс ^-1

(i) затраченное время t = $ \ frac {{{\ rm {v}} — {\ rm {u}}}} {{\ rm {a}}} $ = $ \ frac {{15 — 10} } {1} $ = 5 сек.2} + 2 {\ rm {*}} 1 {\ rm {*}} 100}

долл. США

= $ \ sqrt {100 + 200}

$

= $ \ sqrt {300} $

= 17,3 м / с.

13.

Солнечная,

Начальная скорость, u = 20 м / с

Конечная скорость, v = 0.

Пусть t — время, необходимое для достижения максимальной высоты.

(i) Время, затраченное на возвращение к метателю, 2t =?

(ii) Достигнутая максимальная высота, h =?

Теперь у нас есть

(i) Мы знаем,

v = u + gt

или, 0 = 20 — 10 т

или, 10т = 20

Итак, t = 2сек,

Итак, 2t = 4сек,

(ii) Опять же,

s = ut + $ \ frac {1} {2} $ gt ²

= 20 * 2 + $ \ frac {1} {2} $ (- 10) * 2 ² = 40-20 = 20 м

Итак, h = 20м

14.

Солн:

Начальная скорость, u = 0

Высота h = 20м.

Для нисходящего движения имеем,

Или, v ² = u ² + 2gh

= 0 ² + 2 * 10 * 20 = 400

Итак, V = 20 м / с.

Для движения вверх, пусть u ’будет начальной скоростью, тогда начальная скорость u’ = $ \ frac {3} {4} $ * v

= $ \ frac {3} {4} $ * 20 = 15 м / с.

И конечная скорость, v ’= 0.

Время, необходимое для достижения максимальной высоты, выражается как v ’= u’ — gt ’

Или, 0 = 15–10t ’

Итак, t ’= 1.5сек.

Следовательно, временной интервал между первым и вторым скачками 2t ’= 3сек.

15.

Солнечная,

(i) для вертикального движения вниз, имеем,

Или, h = ut + $ \ frac {1} {2} $ gt ²

Или 45 = 0 * t + $ \ frac {1} {2} $ * 10t ²

Или, 10т ² = 90

Итак, t = 3 сек.

(ii) для горизонтального движения,

В _x = $ \ frac {{\ rm {x}}} {{\ rm {t}}}

долл. США

Или, x = v * t = 10 * 3

Итак, x = 30m

(iii) Для вертикального движения вниз,

В _y = u + gt

= 0 + 10 * 3 = 30 м / с

Из рисунка имеем,

Tanθ = $ \ frac {{{{\ rm {V}} _ {\ rm {y}}}}} {{{{\ rm {V}} _ {\ rm {x}}}}} $ = $ \ frac {{30}} {{10}}

долл. США

Итак, θ = tan ^-1 (3)

Итак, θ = 71.6 °.

Скорость составляет с горизонтом угол 71,6 °.

16.

Солнечная,

Дан,

Скорость снаряда, u = 320 м / с

Угол по горизонтали, θ = 30 °.

(i) Пора достичь максимальной высоты, $ \ frac {{\ rm {T}}} {2} $ =?

(ii) Горизонтальный диапазон, R =?

(iii) Максимальный горизонтальный диапазон, R _max =?

Теперь у нас есть

(i) T = $ \ frac {{2 {\ rm {u}}.2}}} {2} $.

Или, т ² = 2

Итак, t = 1.41 сек

(iii) Когда объект подбрасывается по плоскости,

Начальная скорость, u = 15 м / с

Конечная скорость, v = 0

Ускорение, a = -5м / с ²

Время, необходимое для отдыха, t =?

Мы знаем,

Или, v = u + при

Или, 0 = 15 — 5 * t

Или t = $ \ frac {{15}} {5} $ = 3 сек.

(iv) Здесь, пройденное расстояние,

h = ut + $ \ frac {1} {2} $ при ²

= 15 * 3 + $ \ frac {1} {2} $ (-5) (3) ²

= 45 — $ \ frac {{45}} {2} $ = $ \ frac {{90 — 45}} {2} $ = 22.2}} $ = $ \ sqrt {64 + 36} $ = 10 км / ч ^-1 .

(ii) Опять же, из $ \ Delta $ ABC,

Tanθ = $ \ frac {{{{\ rm {V}} _ {\ rm {B}}}}} {{{{\ rm {V}} _ {\ rm {A}}}}} $ = $ \ frac {6} {8} $.

Или, θ = tan ^-1 $ \ left ({\ frac {6} {8}} \ right) $ = 36,87 °.

А из $ \ Delta $ ABO,

Sinθ = $ \ frac {{{\ rm {BO}}}} {{{\ rm {AB}}}}

долл. США

Или, BO = ABsinθ = 4 * sin36,87 ° = 2,4 км

Итак, БО = 2,4км.

20.

Солнечная,

Дано:

Скорость снаряда, u = 500 мс ^-1 .2} {\ rm {sin}} 2 \ theta}} {{\ rm {g}}}

долл. США

Или, u ² = $ \ frac {{{\ rm {Rg}}}} {{{\ rm {sin}} 2 \ theta}} $

Или u = $ \ sqrt {\ frac {{{\ rm {Rg}}}} {{{\ rm {sin}} 2 \ theta}}} $

Здесь u будет наименьшим, когда sin2θ будет максимальным.

Максимальное значение sin2θ = 1, а наименьшая скорость для получения того же диапазона — u _{минимум} = $ \ sqrt {\ frac {{{\ rm {Rg}}}} {1}} $ = $ \ sqrt {{\ rm {Rg}}} $ = $ \ sqrt {21651 {\ rm {*}} 10} $

Итак, u _{минимум} = 46 м / с.

21.

Солнечная,

Ускорение (а) = 4 м / с.

При t = 0, x _o = 5 м к востоку от указателя,

Начальная скорость u = 15 мс ^-1 .

(i) Время t = 2 с,

Позиция (X) =?
скорость (V) =?

Мы знаем это,

X = X ₀ + ut + $ \ frac {1} {2} $ при ²

= 5 + 15 * 2 + $ \ frac {1} {2} $ * 4 * 2 ²

= 5 + 30 + 8 = 43м

Опять же, v = u + при

= 15 + 4 * 2 = 23 м / с

(ii) Конечная скорость v = 25 мс ^-1 .

Время t = $ \ frac {{{\ rm {v}} — {\ rm {u}}}} {{\ rm {a}}} $

= $ \ frac {{25-15}} {4} $ = $ \ frac {5} {2} $ = 2,5 сек.

А, расстояние X = X ₀ + ut + $ \ frac {1} {2} $ на ²

= 5 + 15 * 2,5 + $ \ frac {1} {2} $ * 4 * 2,5 ²

= 5 + 37,5 + 12,5 = 55м.

Итак, x = 55 м восточнее фонарного столба.

22.

Солнечная,

Предположим, что автомобилист и полицейский участок находятся в 0, и оба движутся вместе.Время t, необходимое для встречи в точке P, одинаково.

(i) Для автомобилиста расстояние перенесено от 0 до p

X _м = u _м + $ \ frac {1} {2} $ в точке ² = $ \ frac {1} {2} $ в точке ²

Так, X _м = X _p

Итак, u _mt = $ \ frac {1} {2} $ на ²

= 15 т = $ \ frac {1} {2} $ * 3 т ²

Итак, t (t — 10) = 0

Либо t = 0, либо t = 10 сек. Офицер ловит автомобилиста через 1 сек.

(ii) Скорость офицера в момент времени t.

В _p = u + at = 0 + 3 * 10 = 30 м / с

23.

Солн:

Начальная скорость, u = 15 м / с

Ускорение свободного падения g = 10 м / с.

(i) Положение и скорость в момент времени t после того, как мяч покидает руку, задаются соответственно как:

y = ut + $ \ frac {1} {2} $ при ²

= 15 * t + $ \ frac {1} {2} $ (- 9,8) t ²

А v = u + at = 15 — 9.8т

Когда t = 1 с.

Или, y = 15 * 1 — $ \ frac {{9.8}} {2} $ = 10,1 м

Мяч находится на высоте 10,1 м над исходным положением и движется вверх со скоростью 5,2 м / с.

Когда t = 4 с, пройденное расстояние y = 18,4 м и скорость v = -24,2 м / с

Мяч находится на 18,4 м ниже исходного положения и движется вниз со скоростью 24,2 м / с.

(ii) Когда мяч находится на высоте 5 м над перилами, скорость задается как:

Или, v ² = u ² + 2as

Или, v ² = 15 ² + 2 * (-9.8) * 5

= 11,3 м / с

(iii) В самой высокой точке v = 0.

Время достижения максимальной высоты, определяемое как v = u + при

.

Или, 0 = 15 — 9,8 * t

Или, t = 1,53 сек.

Если S — расстояние максимальной высоты от крыши здания,

В ² = u ² + 2as.

Или, 0 = 15 ² + 2 * (-9,8) * 5

Или, S = 11,5 м

Время прохождения дистанции (11,5 + 5) м определяется выражением S = ut + $ \ frac {1} {2} $ при ²

Или, $ \ frac {1} {2} $ на ² = 16.5

Или, t ² = $ \ frac {{33}} {{9.8}}

долларов США

Или, t = 1,83 сек.

Следовательно, общее время, затрачиваемое мячом, составляет (1,53 + 1,83) сек = 3,36 сек. После он уйдет из вашей руки.

24.

Солнечная,

Есть,

Или, X (t) = bt ² — ct ³ , поэтому,

Для t = 0, x (0) = 2,4 * 0 ² — 0,12 * 0 ³ = 0

(i) мгновенная скорость, v =?

Мы знаем,

V = $ \ frac {{{\ rm {dx}}}} {{{\ rm {dt}}}} $ = $ \ frac {{{\ rm {d}} \ left ({{\ rm { b}} {{\ rm {t}} ^ 2} — {\ rm {c}} {{\ rm {t}} ^ 3}} \ right)}} {{{\ rm {dt}}}} $ = 2bt — 3ct ²

(а) Для t = 0, v = 0

(b) Для t = 5 с V = 2 * (2.4) (5) — 3 (0,12) (5) ² = 15 м / с

(c) Для t = 10 с, v = 2. (2,4) (10) — 3 (0,12) (10) ² = 12 м / с

(ii) Для V = 0, t = 0.

Есть,

Или, v = 2bt — 3ct ²

Или, 0 = 2bt — 3ct ²

Или, 0 = 2bt — 3ct ²

Или, 3ct ² = 2bt

Или, 3ct = 2b

Или, t = $ \ frac {{2 {\ rm {b}}}} {{3 {\ rm {c}}}} $ = $ \ frac {{2 \ left ({2.4} \ right)} } {{3 \ left ({0.12} \ right)}} $ = 13,3 сек.

Итак, t = 13,3 сек.

25.

Солнечная,

Или, x (t) = 50 + 2t — 0,0625t ²

(i) исходное положение X (0) =?

Начальная скорость V (0) =?

Начальное ускорение a (0) =?

Мы знаем, что V (t) = $ \ frac {{{\ rm {d *}} \ left ({\ rm {t}} \ right)}} {{{\ rm {dt}}}} $ = 2 — 0,0625 * 2т

Или, V (t) = 2 — 0,125 т

И ускорение a (t) = $ \ frac {{{\ rm {dv}} \ left ({\ rm {t}} \ right)}} {{{\ rm {dt}}}} $ = $ \ гидроразрыв {{{{\ rm {d}} ^ 2} \ left ({\ rm {t}} \ right)}} {{{\ rm {d}} {{\ rm {t}} ^ 2}} } $

= -0.125

Итак, x (0) = 50 + 2 * 0 — 0,0625 * 0 ²

= 50 см

Или, V (0) = 2 — 0,125 * 0

= 2 см / с

Или, a (0) = -0,125 см / с ²

(ii) Здесь V (t) = 0

Или, 2 — 0,125t = 0

Или t = $ \ frac {2} {{0,125}} $ = 16 сек.

Следовательно, скорость ползания черепахи становится равной нулю через 16 секунд.

26.

Солн:

Расстояние между двумя точками, s = 70 м

Затраченное время, t = 7 с.

Скорость во второй точке, v = 15 м / с

(i) Скорость в первой точке, u =?

Мы знаем, $ \ frac {{\ rm {s}}} {{\ rm {t}}} $ = $ \ frac {{{\ rm {u}} + {\ rm {v}}}} { 2} $

Или u + v = $ \ frac {{2 {\ rm {s}}}} {{\ rm {t}}} $

Или u = $ \ frac {{2 {\ rm {s}}}} {{\ rm {t}}} $ — v = $ \ frac {{2 {\ rm {*}} 70}} { 7} $ — 15

Или, u = 20-15 = 5 м / с

(ii) Ускорение антилопы, a =?

Мы знаем, a = $ \ frac {{{\ rm {v}} — {\ rm {u}}}} {{\ rm {t}}} $ = $ \ frac {{15 — 5}} { 7} $ = 1.2}}} $ = 8,75 м / с ² .

Опять же, v = u + при

Или, v = 0 + 8,75 * 8

Итак, v = 70 м / с

Следовательно, скорость света самолета при взлете составляет 70 м / с.

28.

Солн:

Для первого случая

Начальная скорость u = 0,

Ускорение a = 1,6 м / с ² .

Период времени t = 14 сек.

Итак, пройденное расстояние S ₁ = ut + $ \ frac {1} {2} $ при ²

= 0 + $ \ frac {1} {2} $ * 1.6 * (14) ²

= 156,8 м

Итак, Конечная скорость v = u + at = 0 + 1,6 * 14 = 22,4 м / с

Для второго случая

Начальная скорость u = 22,4 м / с

Период времени t = 70 сек.

Так как скорость остается постоянной. Итак, расстояние, пройденное поездом метро, ​​составляет

.

S ₂ = 22,4 * 70

= 1568 м

Для третьего случая

Начальная скорость u = 22,4 м / с

замедление = 3,5 м / с ²

Конечная скорость v = 0.

Затраченное время t = $ \ frac {{{\ rm {u}} — {\ rm {v}}}} {{\ rm {a}}} $ = $ \ frac {{22.4}} {{3.5} } $ = 6.4 сек.

Пройденное расстояние S ₃ = ut — $ \ frac {1} {2} $ at ²

= 22,4 * 6,4 — $ \ frac {1} {2} $ * 3,5 * (6,4) ²

= 143,36 — 71,68

= 71,68 м

Итак, общее расстояние, пройденное поездом, составляет:

S = S ₁ + S ₂ + S ₃

= 156,8 + 1568 + 71,68

= 1796.48м

29.

Солн:

h = 0,44 м

Конечная скорость v = 0,

Начальная скорость u = 0,

Если t — период времени для достижения высоты h

Общее время в воздухе, 2t =?

Есть,

Или, v ² = u ² — 2gh

Или, 0 = u ² — 2gh

Ор, u ² = 2gh

Или u = $ \ sqrt {2 {\ rm {gh}}} $ = $ \ sqrt {2 {\ rm {*}} 9.8 {\ rm {*}} 0.44} $ = 2,94 м / с.

Итак, начальная скорость u = 2,94 м / с.

снова,

v = u — gt

или, 0 = u — gt

или, t = $ \ frac {{\ rm {u}}} {{\ rm {g}}} $.

Итак, общее время в воздухе 2t = $ \ frac {{2 {\ rm {u}}}} {{\ rm {g}}} $ = $ \ frac {{2 {\ rm {*}} 2,94 }} {{9.8}} $ = 0,6 сек.
Итак, Общее время, оставшееся в эфире = 0,6 сек

30.

Солнце: Здесь,

u = 6 м / с

(i) Скорость через 2 секунды, v =?

и.2} + 2 {\ rm {*}} 9,8 {\ rm {*}} 10} $ = 15,2 м / с

Итак, V = 15,2 м / с

32.

Солн:

Для g = 9,8 м / с ² .

Пусть u будет начальной скоростью, с которой вы можете прыгать вперед.

Или, v = u — gt.

Или, t = $ \ frac {{\ rm {u}}} {{\ rm {g}}} $ = $ \ frac {{\ rm {u}}} {{9.8}} $

Или, u = 9,8 т

А, h = ut — $ \ frac {1} {2} $ gt ²

For, g ’= 0,98 м / с ² .

Или, t ‘= $ \ frac {{\ rm {u}}} {{{\ rm {g’}}}} $ = $ \ frac {{9.8 {\ rm {t}}}} {{\ rm {g}}} $ = 10т.

И h ’= ut’ — $ \ frac {1} {2} $ g’t ’ ²

= u * 10т — $ \ frac {1} {2} $ * 0,98 * (10т) ²

= 10ut — $ \ frac {1} {2} 98t $ ²

= 10 (ut — $ \ frac {1} {2} 9,8 т $ ² )

= 10 (ut — $ \ frac {1} {2} $ gt ² )

= 10 ч.

= 10 * 0,75

Итак, h ’= 7,5 м

Следовательно, человек может прыгать 7.5 м, когда ускорение свободного падения составляло всего 0,98 м / с ² вместо 9,8 м / с ² .

34.

Солн:

Пусть A, B, C обозначают позицию человека, позицию таракана и позицию счетчика.

Для, таракан,

с = 1,2 м

v = 1,5 м / с, a = 0

Итак, период времени (t) = $ \ frac {{\ rm {s}}} {{\ rm {v}}} $ = $ \ frac {{1.2}} {{1.5}} $ = 0,6 секунды.

на человека,

Или, s = 1.2 + 0,9 = 2,1 м = пройденное расстояние,

Или, v = 0,8 м / с

Итак, период времени такой же, как у таракана

Итак, t = 0,6 сек.

Ускорение a =?

Теперь у нас есть

S = ut + $ \ frac {1} {2} $ при ²

Или 2,1 = 0,8 * 0,8 + $ \ frac {1} {2} $ * a * (0,8) ²

Или 2,1 = 0,64 + 0,32a

Или a = $ \ frac {{2.1 — 0.64}} {{0.32}} $ = 4.56 м / с ²

Следовательно, ускорение, которое вам нужно, чтобы догнать таракана, равно 4.56 м / с ² .

35.

Пусть A, B и C представляют положение земли, положение окна и положение наивысшей точки соответственно,

Пусть u представляет начальную скорость футбола. V ₁ и V ₂ — скорости мяча в точках B и C соответственно,

Или, v ₁ ² = u ² — 2gx.

Or, u ² = v ₁ ² + 2gx

= 5 ² + 2 * 9.2}}} {{2 {\ rm {*}} 9,8}}

долл. США

= 13,3 м

(ii) Время, необходимое для достижения максимальной высоты (t) =?

Или, V ₂ = u — gt.

Итак, t = $ \ frac {{{\ rm {u}} — {{\ rm {v}} _ 2}}} {{\ rm {g}}} $

Итак, t = $ \ frac {{13.3 — 0}} {{9.8}} $ = 1.65 сек.

36.

Мяч, вероятно, застрял на высоте примерно метра над уровнем земли, но мы пренебрегаем этим расстоянием и предполагаем, что он начинается с уровня земли (y _o = 0). Начальная скорость мяча имеет составляющую.

В _x = В _o cosα _o = 37cos 53,1 ° = 22,2 м / с

V _y = V _o sinα _o = 37sin 53,1 ° = 29,6 м / с

Мы хотим найти x, y, V _x1 и V _y1 в момент времени t = 2 секунды, из уравнения.

X = V _x t = (22,2) * 2 = 44,4 м

Y = V _y t — $ \ frac {1} {2} $ a _y t ² = 29,6 — 9,8 * 2 = 10 м / с

Y — компонента скорости положительна, что означает, что мяч все еще движется вверх в это время.2}} $ = 24,3 м / с

Итак, α = tan ^-1 $ \ left ({\ frac {{10}} {{22.2}}} \ right) $ = 24,2 °.

37.

Здесь u = 10 м / с

θ = 20 ° горизонтальный удар, h = 8м.

Мы знаем, что u _x = ucosθ = ucos20 ° = 9,39 м / с

u _y = usinθ = 10sin20 ° = 3,42 м / с

Вертикальная скорость мяча, с которым он ударяется о землю, определяется выражением:

V _y = U _y ² + 2gh

= (3.42) ² + 2 * 9,8 * 8

= 11,69 + 56,8

= 168,49

Итак, V _y = 12.98м / с

Время, необходимое мячу для достижения земли, равно t = $ \ frac {{{{\ rm {V}} _ {\ rm {y}}} — {{\ rm {U}} _ {\ rm {y }}}}} {{\ rm {g}}} $ = $ \ frac {{12.98 — 3.42}} {{9.8}} $ = 0,98

Итак, Горизонтальный диапазон R = U _x * t

= 9,39 * 0,98

= 9,2 м

Таким образом, мяч ударяется о землю на расстоянии 9,2 м по горизонтали от окна. 2}} $ = 260 км / час.

Угол b V _PE с V _P определяется по формуле:

Tanθ = $ \ frac {{{{\ rm {V}} _ {\ rm {w}}}}}} {{{{\ rm {V}} _ {\ rm {p}}}}}

долл. США

Итак, θ = tan ^-1 $ \ left ({\ frac {{{{{\ rm {V}} _ {\ rm {w}}}}}} {{{{{\ rm {V}} _ { \ rm {p}}}}}} \ right) $

= загар ^-1 $ \ left ({\ frac {{100}} {{240}}} \ right)

$

Итак, θ = 23 ° к востоку от севера.

39.

Скорость по оси x, V _x = 1,10 м / с.

Время полета t = 0.35 сек.

(i) Пройденная высота h =?

Для вертикального перемещения,

Или, h = ut + $ \ frac {1} {2} $ gt ²

Или, h = 0 + $ \ frac {1} {2} $ gt ²

= $ \ frac {1} {2} $ * 9,8 * (0,35) ²

= 0,6 м

(ii) Горизонтальный диапазон (R) =?

Для горизонтального перемещения

Или, U _x = $ \ frac {{\ rm {R}}} {{\ rm {T}}} $

Или, R = U _x * T

= 1,10 * 0.{\ circ}}} {{1.6}} $ = 8457m

Эйнштейн. Механика. В 10 классе мы изучали кинематику или движение, описываемое в терминах скорости, ускорения, смещения и так далее.

Эксперимент 6: трение

Эксперимент 6: Трение В предыдущих фунтах мы изучали значения силы тяжести Ньютона в идеальной настройке, то есть такой, при которой трение и сопротивление не учитывались.Однако из нашего повседневного опыта работы с движением мы знаем, что

Подробнее

Операции с многочленами

38 Глава P Предварительные требования P.4 Операции с полиномами Что вы должны уметь: записывать полиномы в стандартной форме и определять коэффициенты передачи и степени полиномов Добавить и вычесть полиномы Умножить

Подробнее

РЕШЕНИЯ ДЛЯ КОНЦЕПЦИЙ ГЛАВА 5

1.m k S 10m Let, ccelertion, Начальная скорость u 0. S ut + 1 / t 10 ½ () 10 ½ () 10 5 м / с orce: m 5 10N (нс) 40000. u 40 км / ч 11,11 м / с. 3600 м 000 к; v 0; s 4m v u ccelertion s РЕШЕНИЯ И КОНЦЕПЦИИ ТЭЦ 5 0 11,11

Подробнее

Тема вертолета с вариациями

Тема и варианты вертолетов Или, некоторые экспериментальные конструкции с использованием конкретных вертолетов Некоторые возможные объяснения относительно: Кто уронит вертолет Длина лопастей несущего винта Высота, с которой

Подробнее

Блок 6: Показатели и радикалы

Eponents nd Rdicls -: Rel Numer Sstem Unit: Eponents nd Rdicls Pure Mth 0 Примечания Nurl Numers (N): — счетные числа.{,,,,,} Целые числа (W): — подсчет чисел с 0. {0 ,,,,,,} Целые числа (I): —

Подробнее

Факторинговые полиномы

Fctoring Polynomils Некоторые определения (не обязательно все для методики средней школы): Многочлен — это сумма одного или нескольких членов, в которых каждый член состоит из произведения const и одного или нескольких vribles

Подробнее

Раздел 5-4 Тригонометрические функции

5- Тригонометрические функции Раздел 5- Тригонометрические функции Определение тригонометрических функций Clcultor Evlution тригонометрических функций Определение тригонометрических функций Альтернативная форма

Подробнее

Неделя 11 — Индуктивность

Неделя — Индуктивность 6 ноября 202 г. Упражнения.: Вопросы для обсуждения) Трансформатор состоит в основном из двух катушек в непосредственной близости, но не в электрическом контакте. Ток в одной катушке магнитно индуцирует n

Подробнее

Сеть малого бизнеса

Почему сеть — это незаменимый инструмент повышения производительности для любого малого бизнеса Эффективные технологии необходимы малым предприятиям, стремящимся повысить производительность своих сотрудников и процессов. Знакомство с технологией

Подробнее

Разминка для дифференциального исчисления

Летнее задание Wrm-up для Differentil Clculus Кто должен заполнить этот пакет? Учащиеся, которые выполнили «Функциональные обязанности» или «Отличники» и будут изучать Differentil Clculus во время заполнения 015.Срок сдачи:

Подробнее

9 НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ

9 НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ Любой случай, чья информация о том, что я знаю, является непрерывным, будет непрерывно распространяться. Непрерывные распределения относительно дискретных

Подробнее

Определенный интеграл

Глава 4 Определенный интеграл 4.Определение расстояния между полученными данными и скоростью Мотивирующие вопросы В этом разделе мы стремимся понять идеи, порожденные следующими важными вопросами: Если мы знаем

Подробнее

Интеграция заменой

Интеграция заменой Доктор Филипп Б. Лвл Университет Кеннеса, 8 августа Краткое содержание В этой статье рассказывается об очень важном методе интеграции, включающем интеграцию путем замены. Замена

Подробнее

Как создать сеть для малого бизнеса

Почему сеть — это незаменимый инструмент повышения производительности для любого малого бизнеса Эффективные технологии необходимы малым предприятиям, стремящимся повысить производительность своих сотрудников и процессов.Знакомство с технологией

Подробнее

Регулярные множества и выражения

Регулярные наборы и выражения Конечное значение имеет важное значение в науке, математике и технике. Такие инженеры, как они, объясняют, что они являются супермоделями для схем (и, поскольку появление систем СБИС иногда ограничено

Подробнее

Вращающиеся двигатели постоянного тока, часть II

Rotting Motors RT II II.1 Эквивалентная схема двигателя Следующим шагом в нашем консьержу двигателей является разработка эквивалентной схемы, которая может использоваться для улучшения работы двигателя. Замечания в двигателях rel

Подробнее

ОБЛАСТЬ ПОВЕРХНОСТИ РЕВОЛЮЦИИ

ОБЛАСТЬ ПОВЕРХНОСТИ ПОВЕРХНОСТИ h cut r πr h Поверхность вращения образуется, когда кривая загибается линией следа. Такая поверхность представляет собой нижнюю границу твердого тела вращения, описанного в разделах 7.

Подробнее

Раздел 7-4 Перевод осей

62 7 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ Раздел 7-4. Вычисление Aes. Equ. Подробнее

Орбиты и законы Кеплера

Obits nd Keple s Lws Этот веб-сайт знакомит с некоторыми основными идеями динмики obitl.Он начинается с описания bsic foce из-за тяжести, затем учитывается ntue и shpe obits. В следующем разделе рассматривается, как

Подробнее

Сеть малого бизнеса

Почему сеть — это незаменимый инструмент повышения производительности для любого малого бизнеса Эффективные технологии необходимы малым предприятиям, стремящимся повысить производительность своих сотрудников и процессов. Знакомство с технологией

Подробнее

Решение проблем BAMO

Решение проблем BAMO Том Двис tomrdvis @ erthlink.net http://www.geometer.org/mthcircles 20 февраля 2000 г. Краткие стратегии решения задач в конкурсе BAMO (The By Are Mthemticl Olympid). Только

Подробнее

Сеть малого бизнеса

Почему сеть — это незаменимый инструмент повышения производительности для любого малого бизнеса Эффективные технологии необходимы для малых предприятий, стремящихся повысить продуктивность своих сотрудников и бизнеса. Знакомство с технологией

Подробнее

Сеть малого бизнеса

Почему сеть — это незаменимый инструмент повышения производительности для любого малого бизнеса Эффективные технологии необходимы для малых предприятий, стремящихся повысить продуктивность своих сотрудников и бизнеса.Знакомство с технологией

Подробнее

КОМПОНЕНТЫ: КОМБИНИРОВАННАЯ НАГРУЗКА

КОМПОНЕНТЫ ЛЕКЦИИ: КОМБИНИРОВАННАЯ НАГРУЗКА Третье издание Школа инженеров А. Дж. Клрка, Отдел гражданской и экологической инженерии 24 Глава 8.4, доктор Ибрихим А. Ассскф ВЕСНА 2003 г. ENES 220 Mechnics of

Подробнее

4.11 Внутренние пространства продукта

314 ГЛАВА 4 Векторные Spces 9.Матрица вида 0 0 b c 0 d 0 0 e 0 f g 0 h 0 не может быть обратимой. 10. Матрица вида bc d e f ghi такая, что bd = 0 cnn не может быть обратимой. 4.11 Внутренние спецификации продукта

Подробнее

УРАВНЕНИЯ ЛИНИЙ И ПЛОСКОСТЕЙ

УРАВНЕНИЯ ЛИНИЙ И ПЛОСКОСТЕЙ MATH 195, РАЗДЕЛ 59 (VIPUL NAIK) Соответствующий метерил в ook: Раздел 12.5. Что студенты обязательно должны получить: Метрическое уравнение линии, заданной в двух точках и точках

Подробнее

Деривативы и курсы изменения

Раздел 2.1 Производные и значения Cnge 2010 Kiryl Tsiscnk Производные и значения Cnge Te Tngent Задача ПРИМЕР: Grp te prbol y = x 2-я кривая линия t te точка P (1,1). Решение: У нас есть: ОПРЕДЕЛЕНИЕ: Te

Подробнее

Векторная дифференциация. Главы 6, 7

Глава 2 Векторы любезно предоставлены NASA / JPL-Cltech Summry (см. Примеры в Hw 1, 2, 3) Около 1900 года нашей эры Дж. Уиллирд Гис изобрел полезную комбинацию величин и векторов направления и их контрпринты более высокой размерности

Подробнее

Векторы 2.1. Резюме векторов

Векторы 2. Набор векторов Векторы являются направленными отрезками прямых — они могут быть представлены в виде компонентов или по направлению и величине. Мы можем использовать тригонометрию и теорему Пифгорса для переключения между формами

Подробнее

Орбитальные маневры с использованием малой тяги

Материалы 8-й Международной конференции WSEAS по обработке сигналов, робототехнике и орбиальным маневрам AUOMAION с использованием LOW-HRUS VIVIAN MARINS GOMES, ANONIO F.Б.А. ПРАДО, HÉLIO KOII KUGA Ntionl Institute

Подробнее

Облачные сервисы для малого бизнеса

Smll Business Cloud Services Summry. Мы находимся в эпицентре исторической смены вычислений. Подобно появлению персональных компьютеров, графических пользовательских интерфейсов и мобильных устройств, облако очень важно. Подробнее

Я рассчитываю уровень безработицы как (В занятой рабочей силе) / В рабочей силе

Введение в правила статистики пятое издание Мур, МакКбе, Раздел 4.5 ответов на домашние задания на 98, 99, 100,102, 103,105, 107, 109,110, 111, 112, 113 рабочих. В луге государственной статистики,

Подробнее

КУБИЧЕСКИЙ ОБЪЕМ ЖУРНАЛА

КУБИЧЕСКИЙ ОБЪЕМ ЖУРНАЛА Позволяет определить объем воды в стопе) ксилометр: введите дерево летнего дерева или войдите в систему и найдите объем вытесненной воды. ) grphic: exmple: длина бревна = 4 фута, каждая секция в футах в

Подробнее

Домашнее задание 3 Решения

CS 341: Основы компьютерных наук II Проф.Mrvin Nkym Домашнее задание 3 Решения 1. Дайте NFA с указанным числом статусов, распознающих каждый из следующих языков. В дальнейшем lphet равен Σ = {, 1}.

Подробнее

Обратная кинематика — Руководство пользователя Spine

Обычный способ анимации называется «прямой кинематикой» или FK. FK — это подход сверху вниз: для позиционирования руки поворачивается верхняя рука, затем нижняя рука. Многие движения могут быть выполнены таким образом, но другие трудны: чтобы удерживать руку на месте, когда скелет встает, кости руки необходимо постоянно регулировать.Чтобы держать руку на месте, нужно много ключей.

Лучшее решение для этой ситуации — «обратная кинематика» или IK. IK — это восходящий подход: задается положение руки, затем Spine автоматически устанавливает вращение для костей верхней и нижней части руки.

IK полезен для многих других задач, таких как предотвращение проникновения ног в пол во время анимации ходьбы, корректировка цели IK во время выполнения, чтобы стоять на неровной поверхности, цыплятах и ​​т. Д. В Spine костями можно управлять с помощью FK, IK или их комбинации.Также можно плавно переключаться между FK и IK во время анимации.

Обратите внимание, что ограничения IK недоступны в Spine Essential.

Для использования IK необходимы три кости: родительская, дочерняя и целевая. Потомок должен быть потомком родителя, но не обязательно должен быть прямым потомком. Цель не должна быть потомком родителя.

Чтобы начать использовать IK:

• Выберите родительскую и дочернюю кости.
• В поле свойств (под деревом) выберите Новый... > Ограничение IK
• Затем выберите существующую кость в качестве цели IK или щелкните в пустом месте, чтобы создать новую кость в качестве цели.

Ограничение IK постоянно регулирует вращение родительской и дочерней костей так, чтобы кончик дочерней кости находился на целевой кости.

Направление изгиба родительской и дочерней костей может быть изменено с помощью ограничения IK.

Когда вращение кости управляется ограничением IK, кость выглядит полой, что указывает на то, что некоторые ручные преобразования невозможны (см. Ниже, как отключить ограничение IK).

Опция Stretch доступна для ограничений IK как для одной, так и для двух костей. Если этот параметр включен, все кости в цепи IK будут растягиваться по мере необходимости, чтобы коснуться целевой кости. Однако кости не будут сжаты, если расстояние до целевой кости меньше исходной длины кости.

Для ограничений IK одной кости параметр Compress вызывает сжатие ограниченной кости, когда расстояние до целевой кости меньше, чем длина ограниченной кости.

И Compress , и Stretch могут иметь ключ.

Как для растяжения, так и для сжатия, присоединения и дочерние элементы ограниченных костей будут масштабироваться по оси X кости. Для ограничений IK одной кости можно дополнительно включить параметр Uniform , поэтому масштабирование выполняется по обеим осям.

Для ограничений IK для двух костей можно включить настройку Softness , которая замедляет кости по мере выпрямления ограниченных костей.Без этого IK кости иногда встают на место, когда цель выходит за пределы диапазона. Мягкость с ключом. Пока Softness включен, параметр Stretch будет проигнорирован.

Ползунок микширования на ограничении IK управляет степенью воздействия ограничения на кость. Когда микс равен 0, используется только FK, а когда 100 используется только IK. Смешивание от 0 до 100 приводит к одновременному воздействию на кость как FK, так и IK.Линии нарисованы, чтобы показать, где находятся кости в позах FK и IK.

Часто смешивание FK и IK необходимо только для перехода от 0 и 100 во время анимации (см. Ключи ниже). Однако в некоторых ситуациях используется смешивание поз FK и IK для достижения движения, которое в противном случае было бы трудно использовать. Например, руки слегка машут вверх / вниз с помощью IK, а также выполняют другую анимацию с помощью FK. В этом случае может быть полезно изменить позу FK, щелкнув точку глаза, чтобы отключить ограничение IK.

Когда ограничение отключено, кости отображаются в позе FK и могут быть преобразованы как обычно. Обратите внимание, что вложения для ограниченных костей нельзя редактировать, пока ограничение отключено.

При изменении направления изгиба или микширования в режиме анимации значок ключа рядом с ограничением становится оранжевым. Щелчок по значку ключа устанавливает ключ для направления изгиба и микширования, которые всегда связаны вместе.

Использование микса часто бывает полезно для включения и отключения IK во время анимации.График можно использовать для применения кривой к клавишам IK, чтобы можно было настроить скорость перехода микширования.

Из-за множества взаимодействий IK с преобразованиями костей применяются несколько незначительных ограничений:

• Целевая кость не может быть дочерним элементом ограниченных костей.
• Для IK с двумя костями дочерняя кость должна быть непосредственным потомком родительской кости.
• Для IK с двумя костями отключение наследования вращения, масштабирования и сдвига невозможно.
• Для IK-кости с двумя костями регулировка местного сдвига родительской IK-кости не допускается.Наследование сдвига или разрезания дочерней кости работает как обычно.
• Для IK с двумя костями, если смесь IK больше нуля и родительская кость IK имеет неоднородный локальный масштаб (то есть шкалы X и Y имеют разные значения), то локальное преобразование Y дочерней кости IK будет привязано к 0. Наследование неоднородного масштаба не запускает эту привязку.

Далее: Ограничения преобразования Предыдущая: Ограничения

Настройка Marlin | Прошивка Marlin

• О Marlin
• Скачать
• Настроить
• Установить
• Инструменты
  • Конвертер битовых карт
  • Калибровочная таблица K-фактора
  • Bugtracker
  • Справка
  Исходный код
  • Конфигурация
    • Все документы
    • Конфигурация Marlin
    • Конфигурация лазера / шпинделя
    • Конфигурация зонда
  Разработка
  • • Все документы
    • Платы
    • Стандарты кодирования
    • Стандарты кодирования Pull
    • Стандарты кодирования
    • Скрипты
    • Участие в Marlin
    • Запросы функций
    • Добавление новых шрифтов
    • Языковая система ЖК-дисплея
  • Функции
    • Все документы
    92 091
    • Автоматическое выравнивание грядки
    • Унифицированное выравнивание грядки
    • Автозапуск
    • EEPROM
    • Отключение микропрограммы
    • Linear Advance
    • Код компенсации температуры датчика
    • Дерево меню
    • G0-G1 : линейное перемещение
    • G2-G3 : перемещение по дуге или окружности
    • G4 : Dwell
    • G5 : кубический шлиц Безье
    • G6175 Прямое перемещение
    • G617 G10 : Убрать
    • G11 : Восстановить
    • G12 : Очистить сопло
    • G17-G19 : Плоскости рабочего пространства ЧПУ
    • G20 : Дюймовые единицы
    • 175
    • единиц измерения Gime G26 : шаблон проверки сетки
    • G27 : Припаркуйте инструментальную головку
    • G28 : Auto Home
    • G29 : Выравнивание станины
    • G29 : Выравнивание станины (3-точечное)
    • G29 : выравнивание станины (линейное)
    • G29 : выравнивание станины (ручное)
    • G29 : Выравнивание станины (билинейное)
    • G29 : Выравнивание станины (унифицированное)
    • G30 : Одиночный Z-зонд
    • G31 : Салазки для стыковки
    • Und
    • Und G33 : Delta Auto Calibration
    • G34 : Z Steppers Auto-Alignment
    • G35 : Assistant Tramming Assistant
    • G38.2-G38.5 : Цель датчика
    • G42 : Перейти к координатам сетки
    • G53 : Переместить в координаты станка
    • G54-G59.3 : Система координат рабочего пространства
    • G60 : Сохранить текущее Положение
    • G61 : возврат в сохраненное положение
    • G76 : калибровка температуры датчика
    • G80 : отмена текущего режима движения
    • G90 : абсолютное позиционирование
    • G91 80 G
    • 0 относительное положение : Установить положение
    • G425 : Калибровка люфта
    • G800-M800 : Отладка анализатора Gcode
    • M0-M1 : Безусловная остановка
    • M3 : Spindle6195 Laser 9199: Вкл. Шпиндель против часовой стрелки / лазер включен
    • M5 : шпиндель / лазер выключен
    • M7-M9 : органы управления охлаждающей жидкостью
    • 9 2175 M16 : Ожидаемая проверка принтера
    • M17 : Включить шаговые двигатели
    • M18, M84 : Отключить степперы
    • M20 : Список SD-карт
    • M21 : Инициализация SD-карты
    • 176: Освободить SD-карту
    • 176 SD-карта
    • M23 : Выбрать SD-файл
    • M24 : Начать или возобновить печать SD
    • M25 : Приостановить печать SD
    • M26 : Установить положение SD
    • M27 : Отчет о состоянии печати SD
    • M28 : Начать запись SD
    • M29 : Остановить запись SD
    • M30 : Удалить файл SD
    • M31 : Время печати
    • M32 : Выбрать и запустить
    M337917 Получить длинный путь
    • M34 : Сортировка SDCard
    • M42 : Установить состояние вывода
    • M43 : Отладочные выводы
    • M43 T : Тумблер
    • M48 : Тест точности датчика
    • M73 : Установить ход печати
    • M75 : Таймер запуска задания печати
    • M76 : Пауза задания печати
    • M77 Таймер печати 9217
    • M78 : Статистика задания печати
    • M80 : Питание включено
    • M81 : Выключено
    • M82 : E Абсолютное
    • M83 : E Относительное отключение
    • M92 : Установить шаги оси на единицу
    • M100 : Свободная память
    • M104 : Установить температуру Hotend
    • M105 : Отчет о температурах
    • M106 910 910 M1979 Скорость вентилятора : Вентилятор выключен
    • M108 : Прервать и продолжить
    • M109 : Дождаться температуры Hotend
    • M110 921 76: Установить номер строки
    • M111 : Уровень отладки
    • M112 : Аварийная остановка
    • M113 : Host Keepalive
    • M114 : Получить текущую позицию
    • M115
    • M117 : Установить сообщение на ЖК-дисплее
    • M118 : Последовательная печать
    • M119 : Конечные состояния
    • M120 : Включить концевые упоры
    • M121 : Отключить концевые упоры
    • M12175 Отладка M12175 : Park Head
    • M126 : Baricuda 1 Open
    • M127 : Baricuda 1 Close
    • M128 : Baricuda 2 Open
    • M129 Температура: Baricuda 2
    • 0
    Установить Установить M141 : установка температуры камеры
    • M145 : установка предварительной установки материала
    • M149 : установка единиц температуры
    • M150 : установка цвета RGB (W)
    • M155 : автоматический отчет температуры
    • M163 : установка коэффициента смешивания
    • M164 : сохранение смеси
    9195 Set Mix
    • M166 : Gradient Mix
    • M190 : Подождите, пока температура слоя

Робототехнический набор инструментов | Peter Corke

Это десятый выпуск Toolbox, представляющий более чем двадцать лет разработки и значительный уровень зрелости.Эта версия содержит большое количество изменений и расширений для поддержки второго издания моей книги «Робототехника, зрение и управление».

Для первого выпуска перейдите на этот сайт, чтобы получить девятый выпуск.

Toolbox всегда предоставлял множество функций, которые полезны для изучения и моделирования классической робототехники типа руки, например, таких как кинематика, динамика и создание траектории.

Набор инструментов содержит функции и классы для представления ориентации и позы в 2D и 3D (SO (2), SE (2), SO (3), SE (3)) в виде матриц, кватернионов, скручиваний, тройных углов и матриц. экспоненты.Toolbox также предоставляет функции для управления и преобразования между типами данных, такими как векторы, однородные преобразования и единичные кватернионы, которые необходимы для представления трехмерного положения и ориентации.

Toolbox использует очень общий метод представления кинематики и динамики манипуляторов с последовательным соединением в виде объектов MATLAB ^® — объекты роботов могут быть созданы пользователем для любого манипулятора с последовательным соединением, и для этого предоставляется ряд примеров известные роботы от Kinova, Universal Robotics, Rethink, а также классические роботы, такие как Puma 560 и Stanford arm.

Набор инструментов также поддерживает мобильных роботов с функциями для моделей движения роботов (одноколесный велосипед, велосипед), алгоритмов планирования пути (ошибка, преобразование расстояния, D *, PRM), кинодинамического планирования (решетка, RRT), локализации (EKF, фильтр частиц) построение карты (EKF) и одновременная локализация и отображение (EKF), а также модель Simulink a неголономного носителя. Toolbox также включает подробную модель Simulink для летающего робота-квадрокоптера.

Преимущества Toolbox заключаются в следующем:

• код является зрелым и обеспечивает точку сравнения для других реализаций тех же алгоритмов;
• процедуры, как правило, пишутся просто, что позволяет их легко понять, возможно, за счет вычислительной эффективности.Если вы серьезно относитесь к вычислительной эффективности, вы всегда можете переписать функцию, чтобы сделать ее более эффективной, скомпилировать M-файл с помощью компилятора Matlab или создать MEX-версию;
• , поскольку доступен исходный код, это полезно для понимания и обучения.

Этот набор инструментов, набор инструментов робототехники для MATLAB, отличается от собственного набора инструментов робототехнических систем MathWorks. Узнайте больше о том, как это произошло, в этом видео.

---

---

Существует две версии Robotics Toolbox:

• RTB9.10, последнее в 9-м выпуске используется в Robotics, Vision & Control (1-е издание) и Robot Academy.
• RTB10.x является текущим выпуском и используется в Robotics, Vision & Control (2-е издание)

оба доступны для установки с использованием одного из трех методов установки :

1. Прямой доступ к общей папке MATLAB Drive (для MATLAB19a и далее)
2. Загрузите установочный файл MATLAB Toolbox (тип .mltbx), это последняя версия из GitHub
3. Клонируйте исходные файлы из GitHub

Установите из общей папки MATLAB Drive

Это будет работать для MATLAB Online или MATLAB Desktop при условии, что у вас есть настройка привода MATLAB.

Обратите внимание, что сюда входит также Machine Vision Toolbox (MVTB).

1. Щелкните соответствующую ссылку ниже, и приглашение поделиться будет отправлено по электронной почте на адрес, связанный с вашей учетной записью MATLAB:
2. Примите приглашение.
3. Папка с именем RVC1 или RVC2 появится на вашем диске MATLAB
4. С помощью обозревателя файлов MATLAB перейдите к папке RVCx / rvctools и дважды щелкните сценарий с именем startup_rvc.m

Обратите внимание, что это комбинированная установка который также включает Machine Vision Toolbox (MVTB).

Установить из файла .mltbx

Эта установка включает набор инструментов Robotics Toolbox для MATLAB и необходимый набор инструментов Spatial Math Toolbox.

1. Загрузите следующий файл, который является последней сборкой на GitHub
2. В браузере файлов MATLAB дважды щелкните каждый файл, он установит и правильно настроит пути
3. Запустите
4. Запустите демонстрацию, чтобы увидеть, что он может сделать

RTB10.4.mltbx

Размер файла: -1.00 B

Создано: 20-02-2020

Обновлено: 23-02-2020

Хиты: 41318

Версия: 10.4

Клонировать исходный код из GitHub

Из командной строки клонировать эти три репозитория:

git clone https://github.com/petercorke/robotics-toolbox-matlab rtb
git clone https://github.com / petercorke / space-math smtb
git clone https://github.com/petercorke/toolbox-common-matlab common

Затем внутри MATLAB добавьте эти папки к своему пути:

>> addpath rtb common smtb

Это будет работать только для текущего сеанса.Вы можете повторять эту команду каждый сеанс, автоматизировать ее, добавляя ее в свой сценарий MATLAB startup.m , или использовать pathtool
, чтобы сохранить текущую конфигурацию пути для следующего раза.

---

• Книга Robotics, Vision & Control, второе издание (Corke, 2017) представляет собой подробное введение в мобильную робототехнику, навигацию, локализацию; кинематика, якобианы и динамика роботов манипулятора, проиллюстрированные с помощью Robotics Toolbox для MATLAB.
• Руководство (ниже) представляет собой PDF-файл для печати (более 400 страниц).Он автоматически генерируется из комментариев в коде MATLAB и полностью: для внешних веб-сайтов, таблица содержания для функций и функции «См. Также» для друг друга.
• Документация Toolbox также появляется в браузере справки MATLAB в разделе «Дополнительное программное обеспечение».

Руководство RTB

Размер файла: 9.00 B

Создано: 20-02-2020

Обновлено: 23-02-2020

Хиты: 17161

Связанные публикации

Если вам нравится Toolbox и хотите процитировать его, укажите его как:

• P.И. Корке, «Робототехника, зрение и управление» , Springer 2017, ISBN 978-3-319-54413-7. [bibtex]

Ниже представлены довольно старые публикации о Toolbox, синтаксис которых значительно изменился со временем:

• P.I. Корке, «Наборы инструментов MATLAB: робототехника и зрение для студентов и преподавателей» , Журнал IEEE Robotics and Automation Magazine, том 14 (4), декабрь 2007 г., стр. 16-17 [PDF]
• P.I. Корке, «Набор инструментов робототехники для MATLAB», журнал IEEE Robotics and Automation Magazine, том 3 (1), март 1996 г., стр.24-32. [PDF]
• P.I. Corke, Компьютерный инструмент для моделирования и анализа: Robotics Toolbox для MATLAB, Proceedings of the 1995 National Conference of the Australian Robot Association, Melbourne, Australia, pp 319-330, July 1995. [PDF]

---

Нет поддержка! Это программное обеспечение предоставляется бесплатно в надежде, что вы сочтете его полезным для решения любых возникающих у вас проблем. Я рад переписываться с людьми, которые обнаружили настоящие ошибки или недостатки, но мой ответ может быть долгим, и я не могу гарантировать, что отвечу на ваше письмо.Я очень рад принять предложения для включения в будущие версии набора инструментов, и вы получите должное признание.

Я могу гарантировать, что не отвечу ни на какие просьбы о помощи с заданиями или домашними заданиями, какими бы срочными или важными они ни были для вас. Это то, за что платят вашим учителям, наставникам, преподавателям и профессорам.

Вместо этого вы можете общаться с другими пользователями через группу Google, которая называется форумом для обсуждения.Вам необходимо зарегистрироваться, чтобы размещать сообщения, и процесс регистрации модерируется мной, поэтому подождите несколько дней, чтобы это произошло. Мне нужно, чтобы вы написали несколько слов о том, почему вы хотите присоединиться к списку, чтобы я мог отличить вас от спамера или веб-бота.

Существует также вики-страница с часто задаваемыми вопросами (FAQ).

---

---

Набор инструментов для робототехники изначально представлял собой набор функций, которые помогали мне во время учебы в аспирантуре. Первый выпуск был в 1995 году вместе с первой опубликованной статьей. После этого был выпущен ряд обновлений для отслеживания изменений в MATLAB, особенно введения объектов.Последняя версия расширяет функциональные возможности и охватывает современную робототехнику, мобильных наземных роботов (управление, локализация, навигация), а также летающих роботов с квадрокоптерами.

Даты выпуска были:

• v4 август 1996
• v5 апрель 1999, сначала с объектами
• v6 апрель 2001
• v7 апрель 2002, файлы MEX, модели Simulink и модифицированная поддержка Denavit-Hartenberg.
• v8 декабря 2008 г., сначала с синтаксисом объекта classdef
• v9 сентября 2011 г., для Robotics, Vision & Control, 1st edition
  • Загрузите его отсюда в формате zip (.zip).
• v10 июня 2017 г., для робототехники, машинного зрения и управления, 2-е издание

02 Кинематика | Космос Эвана

• Высота выхода: 128 100 футов; 39 045 м
• Общая продолжительность прыжка: 9’03 ”
• Время свободного падения: 4’20 ”
• Дальность свободного падения 119 846 футов; 36 529 млн
• Максимальная скорость: 833,9 миль / ч; 1342,8 км / ч; 1,24 Маха

Его представитель первым приветствовал парашютиста на земле.Данные GPS, записанные на микрокарту в сундуке австрийца, будут служить основой для заявлений о высоте и скорости.

Они будут официально представлены на сертификацию через Клуб Аэроспорта Австрии.

В начале погружения были опасения, что у Баумгартнера проблемы. Он должен был принять положение дельты — голова опущена, руки развернуты назад — как можно скорее после выхода из капсулы. Но на видео он снова и снова кувыркался.

В конце концов, однако, он смог использовать свой богатый опыт более чем 2500 профессиональных погружений, чтобы исправить свое падение и получить стабильную конфигурацию.

Еще до этой драмы считалось, что миссию придется отменить. Во время последней проверки внутри капсулы было обнаружено, что обогреватель его козырька не работает. Это означало, что козырек запотел, когда он выдохнул.

«Это очень серьезно, Джо», — сказал он отставному полковнику ВВС США Джо Киттингеру, чьи рекорды он пытался побить, и который действовал как его радиосвязь в центре управления полетами в аэропорту Розуэлла.

Команда взяла на себя просчитанный риск, чтобы продолжить, поняв, почему проблема существует.

Усилия Баумгартнера наконец побили рекорды, которые стояли более 50 лет.

Киттингер поставил отметку самого высокого, самого дальнего и самого длинного свободного падения, когда он прыгнул из гелиевой оболочки в 1960 году. Его высота составляла 102 800 футов (31 км). (Его рекорд по самому продолжительному свободному падению остается неизменным — он упал более четырех с половиной минут, прежде чем развернул парашют; Баумгартнер находился в свободном падении четыре минуты 20 секунд).

Киттингер, теперь восьмидесятилетний, был неотъемлемой частью команды Баумгартнера и давал австрийцу совет и поддержку всякий раз, когда молодой человек сомневался в своей способности завершить такое смелое предприятие.

«Феликс проделал огромную работу, и для меня было большой честью работать с этим храбрым парнем», — сказал старший.

43-летний авантюрист, наиболее известный своими прыжками с небоскребов, впервые всерьез обсудил возможность побить рекорды Киттингера в 2005 году.

С тех пор ему пришлось бороться с техническими и бюджетными проблемами, чтобы это произошло.

То, что он предлагал, было чрезвычайно опасным даже для человека, привыкшего к трюкам с небоскребами.

На высоте прыжка в воскресенье давление воздуха составляет менее 2% от давления на уровне моря, и невозможно дышать без кислорода.

Другие, пытавшиеся побить рекорды, погибли в процессе.

Команда Баумгартнера построила ему специальную герметичную капсулу, чтобы защитить его на пути вверх, и для спуска он был одет в скафандр нового поколения, изготовленный той же компанией, которая изготавливает летные костюмы для космонавтов.

Хотя прыжок выглядел как еще один трюк Баумгартнера, его команда подчеркнула его высокую научную значимость.

Исследователи проекта Red Bull Stratos говорят, что он уже предоставил бесценные данные для разработки высокопроизводительных высотных парашютных систем, и что извлеченные уроки послужат основой для разработки новых идей экстренной эвакуации с транспортных средств, таких как космический корабль, проходящий через стратосферу.

НАСА и ее производители космических аппаратов попросили, чтобы их держали в курсе.

«Часть этой программы заключалась в том, чтобы показать высотный выход, прохождение через Мах и успешный возврат [к дозвуковой скорости], потому что с научной точки зрения мы полагаем, что это принесет пользу будущим частным космическим программам или высотным пилотам; и Феликс доказал это сегодня », — сказал Арт Томпсон, руководитель команды.

Поднявшись на высоту 128 100 футов, Баумгартнер превысил высоту самого высокого пилотируемого полета на воздушном шаре, достигнутого Виктором Пратером и Малькольмом Россом, поднявшимися на высоту 113 720 футов (35 км) в 1961 году.

Однако правила FAI гласят, что для того, чтобы претендовать на официальный рекорд по воздухоплаванию, воздухоплаватель должен также опустить конверт, и поэтому высота австрийца навсегда останется неофициальной отметкой.

Категории: 02 Кинематика, 03 Динамика, 23 вещи вокруг нас | Tags: вещи вокруг нас, тематическая кинематика | Постоянная ссылка.

No related posts.