Контрольная по геометрии 8 класс трапеция: Контрольная работа по геометрии по теме «Трапеция» (8 класс)

Тест по геометрии (8 класс) на тему: Тестовые задания по геометрии 8 кл. Трапеция. Средняя линия треугольника и трапеции

Тестовые задания Трапеция. Средняя линия треугольника и трапеции

Составитель учитель математики КГУ КШДС № 33 Ковалева Ольга Александровна.

Источник материалов: Учебник  Геометрия – 8 класс авторы Ж.Кайдасов, Г.Хабарова, А.Абдиев

Тестовое задание по теме «Трапеция. Средняя линия треугольника и трапеции»

1 вариант

1. Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции.

            А) 130°     В) 50°    С) 155°  Д)  145°

2. Основания трапеции относятся как 4:5, а средняя линия равна 9.  Найдите меньшее основание.

            А) 8     В) 10    С) 2  Д)  18

3. Средняя линия трапеции равна 11, а одно из ее оснований больше другого на 2. Найдите большее основание трапеции

             А) 10     В) 12    С) 22  Д)  18

4. Периметр трапеции равен 112, а сумма непараллельных сторон равна 70. Найдите среднюю линию трапеции.

             А) 42     В) 21    С) 14  Д)  84

5. Сумма двух углов равнобедренной трапеции равна 346° . Найдите меньший угол трапеции

            А) 7°     В) 50°    С) 173°  Д)  14°

6. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 2:3.

             А) 72°     В) 36°    С) 108°  Д)  34°

7. Найти  отрезки, на которые медиана длиной 18 см  делится  центром тяжести

            А) 6 и 12    В) 8 и 10   С) 5 и 13  Д)  7 и 11

8. В каком отношении делится медиана центром тяжести

             А) 1:2    В) 2:3   С) 1:3  Д)  2:1

9. Периметр треугольника, образованного средними линиями данного треугольника., равен 14 см. Найти периметр данного треугольника

             А) 42     В) 7    С) 28  Д) 30

10. Стороны треугольника равны 6,9,13 м. Найдите стороны треугольника, образованного средними линиями данного треугольника.

            А) 2, 3, 3.5     В) 18, 27, 39    С) 12, 18, 26  Д) 3,  4,5,   6.5

11. Периметр треугольника равен 24 см. Найдите периметр треугольника, образованного средними линиями данного треугольника

            А) 48     В) 12    С) 6  Д)  18

12. Основания трапеции равны 6,5 и 8,5 см. Найдите длину ее средней линии.

            А) 14    В) 15    С) 7,5  Д)  30

13. Три медианы  треугольника пересекаются в одной точке. Какую часть, начиная от ее основания, отсекает точка от каждой медианы

            А) ½    В) ¼    С) ⅓  Д) ⅔

14. Разность противолежащих углов равнобедренной трапеции равна 56°. Найдите углы трапеции.

            А) 62°  и 118°   В) 56°  и 124°   С) 60°  и 116 ° Д)  140° и 40°

15. Два угла трапеции равны 112° и 65°. Вычислите ее остальные углы

            А) 68°  и 115°   В) 112° и 65°. С) 78°  и 105 ° Д)  177° и 3°

16. Один из углов равнобедренной трапеции на 70° меньше другого. Вычислите меньший угол  трапеции.

            А) 125°     В) 55°    С) 70°  Д)  40°

17. Один из углов равнобедренной трапеции в 2 раза  меньше другого. Вычислите меньший угол  трапеции.

            А) 30°     В) 90°    С) 120°  Д)  60°

18. Средняя линия трапеции равна 10, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

            А) 8     В) 12    С) 20  Д)  16

19. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 56 и 32. Найдите среднюю линию этой трапеции.

           А) 48     В) 112    С) 56  Д)  24

20. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 46 и 27. Найдите меньшее основание этой трапеции.

           А) 19     В) 46   С) 73  Д) 8

Тестовое задание по теме «Трапеция. Средняя линия треугольника и трапеции.»

2. вариант

1. Сумма двух углов равнобедренной трапеции равна 40°. Найдите больший угол трапеции.

А) 160°     В) 40°    С) 140°  Д)  135°

2. Основания трапеции относятся как  2:3 , а средняя линия равна 10.  Найдите меньшее основание.

А) 12     В) 20    С) 2  Д)  8

3. Средняя линия трапеции равна 10, а одно из ее оснований больше другого на 2. Найдите большее основание трапеции

1. А) 20     В) 11    С) 9  Д)  18

4. Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.

1. А) 30     В) 10    С) 15  Д)  5

5. Сумма двух углов равнобедренной трапеции равна 160° . Найдите меньший угол трапеции

А) 100°     В) 80°    С) 20°  Д)  10°

6. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:3.

1. А) 72°     В) 60°    С) 135°  Д)  45°

7. Найти  отрезки, на которые медиана длиной 36 см  делится  центром тяжести

А) 24 и 12    В) 26 и 10   С) 20 и 16  Д)  9 и 11

8. Стороны треугольника равны 6,8,10 м. Найдите стороны треугольника, образованного средними линиями данного треугольника.

А) 2, 3, 3.5     В) 18, 24, 30    С) 12, 16, 20  Д) 3,  4, 5

9. Основания трапеции равны 6,3 и 8,7 см. Найдите длину ее средней линии.

       А) 7,5     В) 15    С) 30  Д)  14

10. Разность противолежащих углов равнобедренной трапеции равна 50°. Найдите углы трапеции.

А) 50°  и 130°   В)65°  и 115°   С) 65°  и 116 ° Д)  140° и 40°

11. Два угла трапеции равны 100° и 80°. Вычислите ее остальные углы

А) 65°  и 115°   В) 100° и 80°. С) 40°  и 140 ° Д)  50° и 130°

12. Периметр треугольника равен 13 см. Найдите периметр треугольника, образованного средними линиями данного треугольника

1. А) 42     В) 13    С) 6,5  Д)  26

13. Один из углов равнобедренной трапеции на 50° меньше другого. Вычислите меньший угол  трапеции.

А) 120°     В) 50°   С) 70°  Д)  65°    

14. Один из углов равнобедренной трапеции в 3  раза  меньше другого. Вычислите меньший угол  трапеции.

А) 45°     В) 90°    С) 135°  Д)  60°

15. Средняя линия трапеции равна 20, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

А) 8     В) 16   С) 22  Д)  18

16. Три медианы  треугольника пересекаются в одной точке. Какую часть, начиная от ее основания, отсекает точка от каждой медианы

А) ½    В) ¼    С) ⅓  Д) ⅔

17. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 15. Найдите среднюю линию этой трапеции.

А) 12,5     В) 15    С) 25  Д)  60

18. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 40 и 20. Найдите меньшее основание этой трапеции.

А) 10     В) 40   С) 60  Д) 20

19. В каком отношении делится медиана центром тяжести

А) 2:3  В) 1:2   С) 1:3  Д)  2:1

20. Периметр треугольника, образованного средними линиями данного треугольника, равен 10 см. Найти периметр данного треугольника

А) 10     В) 5    С) 30  Д) 20

Ответы.

Вар 2 (№)	Ответ	Вар 1 (№)	Ответ
	А	1.	С
	Д	2.	Д
	В	3.	В
	С	4.	В
	В	5.	А
	Д	6.	В
	А	7.	А
	Д	8.	Д
	А	9.	С
	В	10.	Д
	В	11.	В
	С	12.	С
	Д	13.	С
	А	14.	А
	С	15.	А
	С	16.	В
	В	17.	Д
	Д	18.	В
	Д	19.	С
	Д	20.	А

Трапеция 8 класс | Тест по геометрии (8 класс):

Тест. В-1.А1. В трапеции АВСД основания равны 8 см и 14 см. Чему равна ее средняя линия?

1. 22 см       2) 7 см       3) 11 см       4) 6 см

А2. В трапеции АВСД

1. 163˚      2) 269˚       3) 91˚     4)197˚

А3. В трапеции АВСД из вершины угла В проведена прямая, параллельная стороне СД и пересекающая сторону АД в точке Е так, что

1. 65˚       2) 75˚       3) 40˚       4) 115˚

А4. В равнобедренной трапеции угол при основании равен 60˚, а основания равны 6 см и 10 см. Чему равен периметр трапеции?

1. 28 см    2) 26 см      3) 20 см     4) 24 см

1.В трапеции АВСД ВС-меньшее основание. На отрезке АД взята точка Е так, что ВЕ|| СД,

2. В прямоугольной трапеции острый угол равен 45˚. Меньшая боковая сторона и меньшее основание равны 10 см. Найдите большее основание.

3. В равнобедренной трапеции диагональ составляет с боковой стороной угол 120˚. Боковая сторона равна меньшему основанию. Найдите углы трапеции.

Тест. В-2. А1. В трапеции АВСД основания равны 10 см и 16 см. Чему равна ее средняя линия?

2. 26 см       2) 13 см       3) 8 см       4) 6 см

А2. В трапеции АВСД

2. 117˚      2) 243˚       3) 193˚     4)167˚

А3. В трапеции АВСД из вершины угла В проведена прямая, параллельная стороне СД и пересекающая сторону АД в точке К так, что

2. 65˚       2) 35˚       3) 100˚       4) 115˚

А4. В равнобедренной трапеции высота образует с боковой стороной угол 30˚, а ее основания равны 11 и 5 см. Чему равен периметр трапеции?

2. 28 см    2) 27 см      3) 26 см     4) 32 см

Проверочная работа : Трапеция. Вариант-2

1.В трапеции МНРК МК- большее основание. Прямые МН и РК пересекаются в точке Е,

2. В прямоугольной трапеции острый угол равен 60˚. Большая боковая сторона и Большее основание равны 20 см. Найдите большее основание.

3. В равнобедренной трапеции диагональ составляет с боковой стороной угол 120˚. Боковая сторона равна меньшему основанию. Найдите углы трапеции.

Геометрия 8 Мерзляк Контрольная 2 с ответами

Контрольная работа № 2 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др.  / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 2 + ответы.

Контрольная работа № 2 по геометрии
8 класс УМК Мерзляк и др.

КР-2. Вариант 1 (транскрипт заданий)

1. Найдите периметр треугольника, если его средние линии равны 6 см, 9 см и 10 см.
2. Основания трапеции относятся как 3 : 5, а средняя линия равна 32 см. Найдите основания трапеции.
3. Боковые стороны трапеции равны 7 см и 12 см. Чему равен периметр трапеции, если в неё можно вписать окружность?
4. Основания равнобокой трапеции равны 3 см и 7 см, а диагональ делит тупой угол трапеции пополам. Найдите периметр трапеции.
5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ADB = 43°, ∠ACD = 37°, ∠CAD = 22°.
6. Высота равнобокой трапеции равна 9 см, а её диагонали перпендикулярны. Найдите периметр трапеции, если её боковая сторона равна 12 см.

КР-2. Вариант 2 (транскрипт заданий)

1. Стороны треугольника равны 10 см, 12 см и 14 см. Найдите периметр треугольника, вершины которого — середины сторон данного треугольника.
2. Основания трапеции относятся как 4 : 7, а средняя линия равна 44 см. Найдите основания трапеции.
3. Основания трапеции равны 6 см и 12 см. Чему равен периметр трапеции, если в неё можно вписать окружность?
4. Основания равнобокой трапеции равны 8 см и 10 см, а диагональ делит острый угол трапеции пополам. Найдите периметр трапеции.
5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠CBD = 48°, ∠ACD = 34°, ∠BDC -= 64°.
6. Высота равнобокой трапеции равна 10 см, а её диагонали перпендикулярны. Найдите боковую сторону трапеции, если её периметр равен 48 см.

---

 

ОТВЕТЫ на контрольную работу

КР-02. Вариант 1.

№ 1. Р = 12+18+20 = 50 (см)
№ 2. Ответ: 24 см, 40 см.
№ 3. Р = 38 (см)
№ 4. Р = 3+3+3+7 = 16 (см)
№ 5. Ответ: 121°, 59°, 80°, 100°.
№ 6. Р = 42 (см).

КР-02. Вариант 2.

№ 1. Р = 7+6+5 = 18 (см)
№ 2. Ответ: 32 см, 56 см.

№ 3. Р = 36 (см)
№ 4. Р = 8+8+8+10 = 34 (см)
№ 5. Ответ: 82°, 112°, 68°, 98°.
№ 6. Р = 14 (см).

 

---

Вы смотрели: Контрольная работа № 2 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др.  / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 2 + ответы.

Вернуться к списку контрольных работ по геометрии 8 класс (Мерзляк)

Тест Средняя линия трапеции по теме геометрии (8 класс)

Сложность: новичок. Последний раз тест пройден 23 часа назад.

1. Вопрос 1 из 10

   Основания трапеции относятся как 4:5, а средняя линия равна 9. Найдите меньшее основание.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 84% ответили правильно
   • 84% ответили правильно на этот вопрос

   В вопросе ошибка?

   Следующий вопросОтветить

2. Вопрос 2 из 10

   Средняя линия трапеции равна 11, а одно из ее оснований больше другого на 2. Найдите большее основание трапеции

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 75% ответили правильно
   • 75% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

3. Вопрос 3 из 10

   Периметр трапеции равен 112, а сумма непараллельных сторон равна 70. 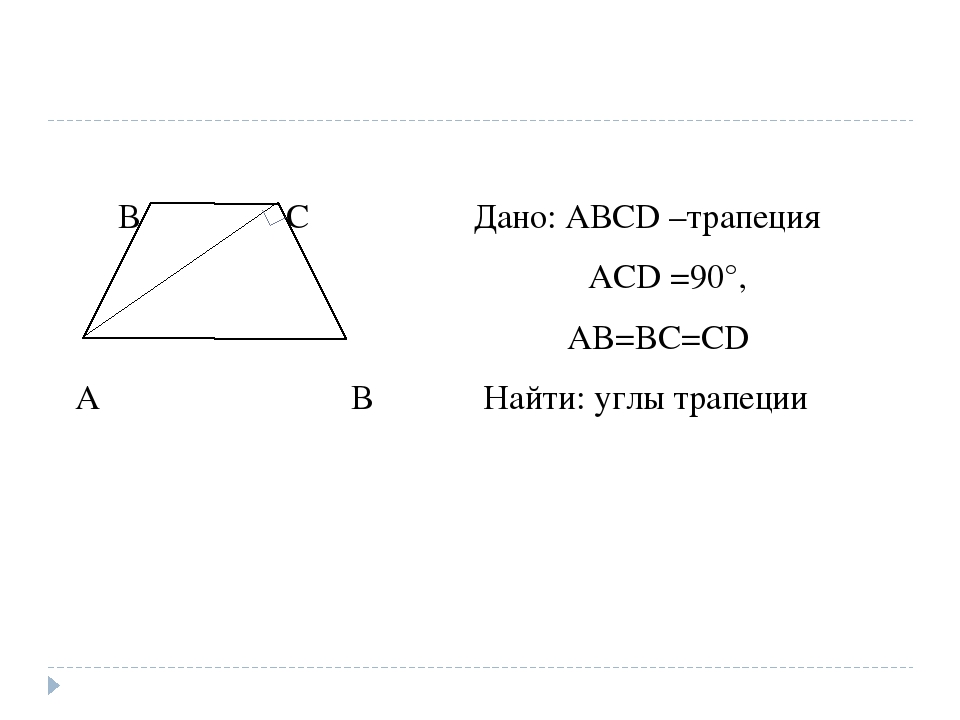Найдите среднюю линию трапеции.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 75% ответили правильно
   • 75% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

4. Вопрос 4 из 10

   Основания трапеции равны 6,5 и 8,5 см. Найдите длину ее средней линии.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 84% ответили правильно
   • 84% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

5. Вопрос 5 из 10

   Средняя линия трапеции равна 10, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 74% ответили правильно
   • 74% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

6. Вопрос 6 из 10

   Основания трапеции относятся как 2:3 , а средняя линия равна 10. 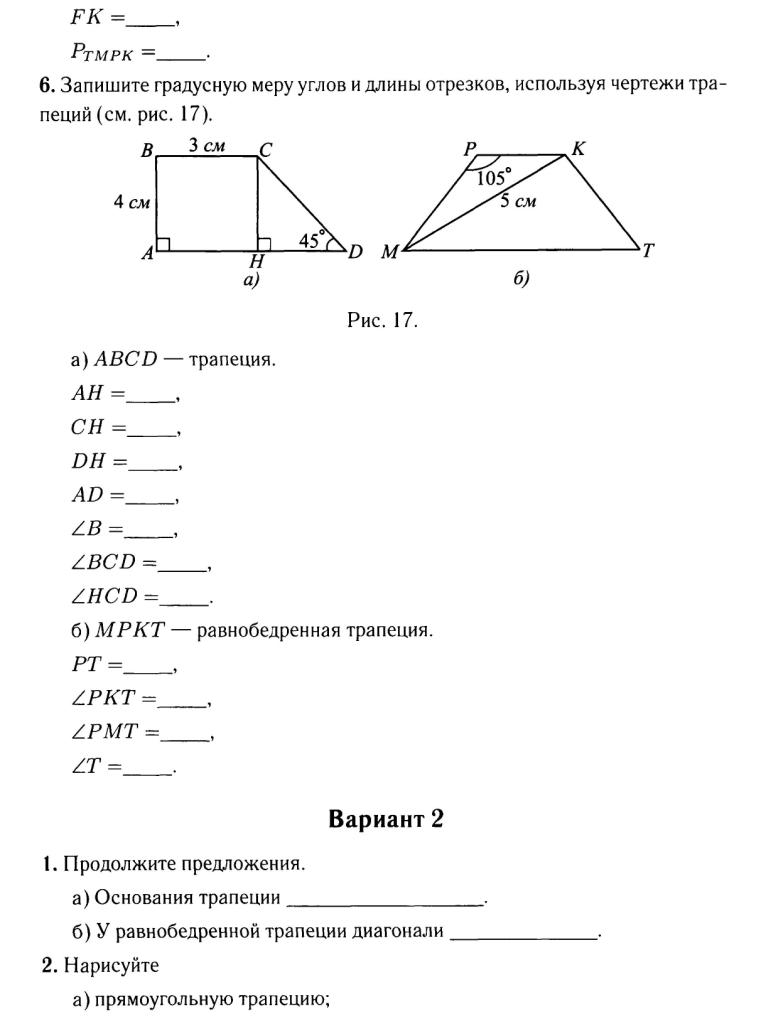Найдите меньшее основание.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 66% ответили правильно
   • 66% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

7. Вопрос 7 из 10

   Средняя линия трапеции равна 10, а одно из ее оснований больше другого на 2. Найдите большее основание трапеции a.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 72% ответили правильно
   • 72% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

8. Вопрос 8 из 10

   Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции. a.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 71% ответили правильно
   • 71% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

9. Вопрос 9 из 10

   Основания трапеции равны 6,3 и 8,7 см. 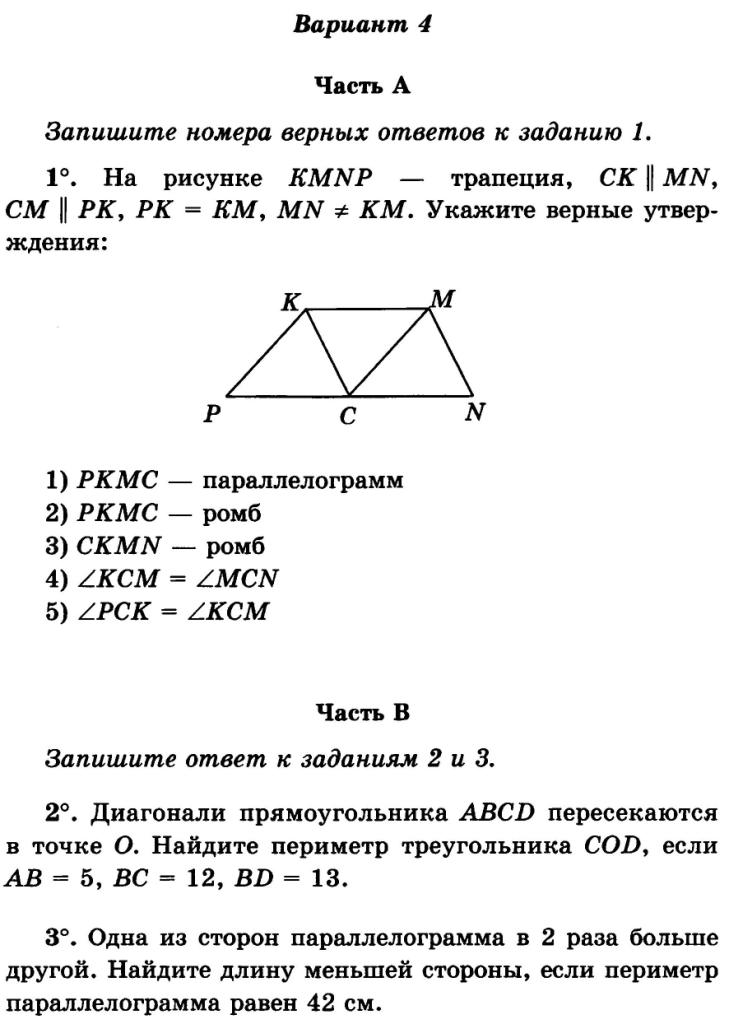Найдите длину ее средней линии.

   • Правильный ответ
   • Неправильный ответ
   • Вы и еще 77% ответили правильно
   • 77% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

10. Вопрос 10 из 10

    Средняя линия трапеции равна 20, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

    • Правильный ответ
    • Неправильный ответ
    • Вы и еще 64% ответили правильно
    • 64% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

ТОП-3 тестакоторые проходят вместе с этим

Рейтинг теста

Средняя оценка: 3. 8. Всего получено оценок: 193.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

областей трапеций | Ресурсы Wyzant

Напомним, что трапеция — это четырехугольник, определяемый одной парой противоположных сторон, идущих параллельно друг другу. Эти стороны называются основаниями , тогда как противоположные стороны, которые пересекающиеся (если они продлены) называются ножками . Давайте узнаем, как измерить площади эти цифры.

Определение площади трапеции зависит от двух основных компонентов этих многоугольников: основания и высоты.Эти характеристики помогли нам найти области параллелограммов. и треугольники в предыдущем разделе, но есть небольшая разница при нахождении площади трапеций: нам нужна мера обоих ее оснований.

Это не было требованием для параллелограммов, и даже если бы это было так, мы бы знали их меры, поскольку основания параллелограмма конгруэнтны.

Приступим к изучению площади трапеции.Площадь трапеции равна половину высоты, умноженную на сумму длин оснований. Выражается как

где A — площадь трапеции, h — высота, и b ₁ и b ₂

— длины из двух баз.

Основания и высота трапеции необходимы для определения ее площади.

Давайте поработаем над двумя упражнениями, которые помогут нам применить эту формулу площади к трапеции.

Упражнение 1

Найдите площадь трапеции ABCD .

Решение:

Эта проблема кажется довольно простой, потому что нам даны длины обоих оснований и высоты трапеции.Неважно, какую базу мы выберем в качестве наша первая или вторая база (потому что сложение коммутативно). Мы просто скажем это

b ₁ равно 10 метров и b ₂ 18 метров .

Высота нашей трапеции — это перпендикулярное расстояние между нашими основаниями. В На рисунке видно, что это расстояние равно 9 метров .Теперь, когда у нас есть размеры обоих оснований и высоты, мы можем вставить их в область формула для трапеций. У нас

Итак, площадь трапеции ABCD составляет 126 квадратных метров .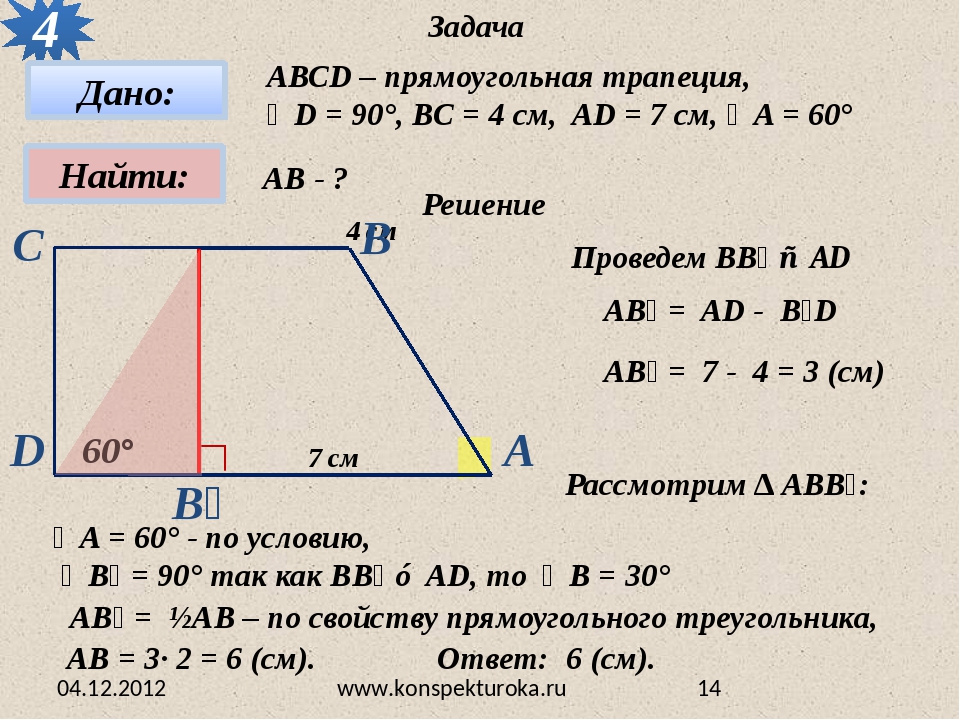

А теперь давайте попробуем упражнение, которое требует немного больше работы, чем первая задача.

Упражнение 2

Найдите площадь трапеции REMN .

Решение:

Для определения площади трапеции REMN потребуется предварительная работа. потому что нам не дается длина обоих оснований или высота фигуры.Давайте использовать известные нам свойства четырехугольников, чтобы помочь нам вывести некоторые важные Информация.

Обратите внимание, что вокруг четырехугольника REAS есть отметки. Это означает что все стороны четырехугольника равны. Итак, мы знаем, что сегменты RS , SA и AE соответствуют RE

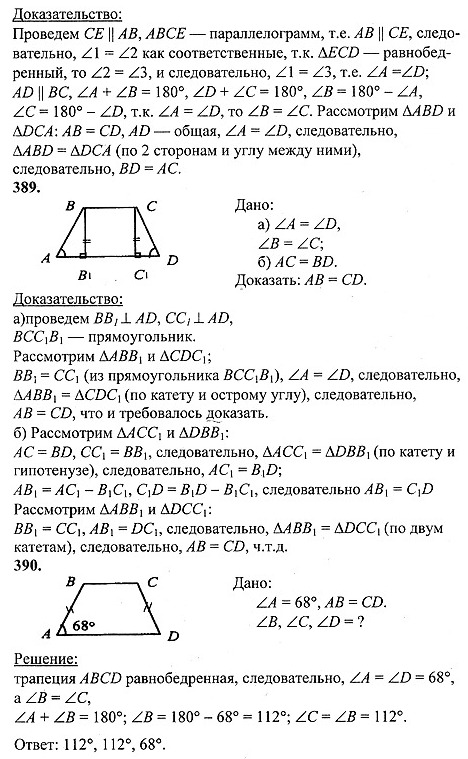; все они имеют длину 5 сантиметров . Перерисуем нашу фигуру так, чтобы она отображает новую информацию, которую мы получили.

Прямые углы на рисунке указывают, что RS и NM бегут перпендикулярно друг другу. Следовательно, мы знаем, что перпендикулярное расстояние, или высота, от RE до NM — 5 сантиметров .

Теперь, когда у нас есть высота трапеции REMN

, нам просто нужно найти длина второго основания этого четырехугольника, NM . Чтобы сделать для этого нам нужно найти сумму сегментов NS , SA и AM :

Мы видим, что наша вторая база имеет длину 12 сантиметров .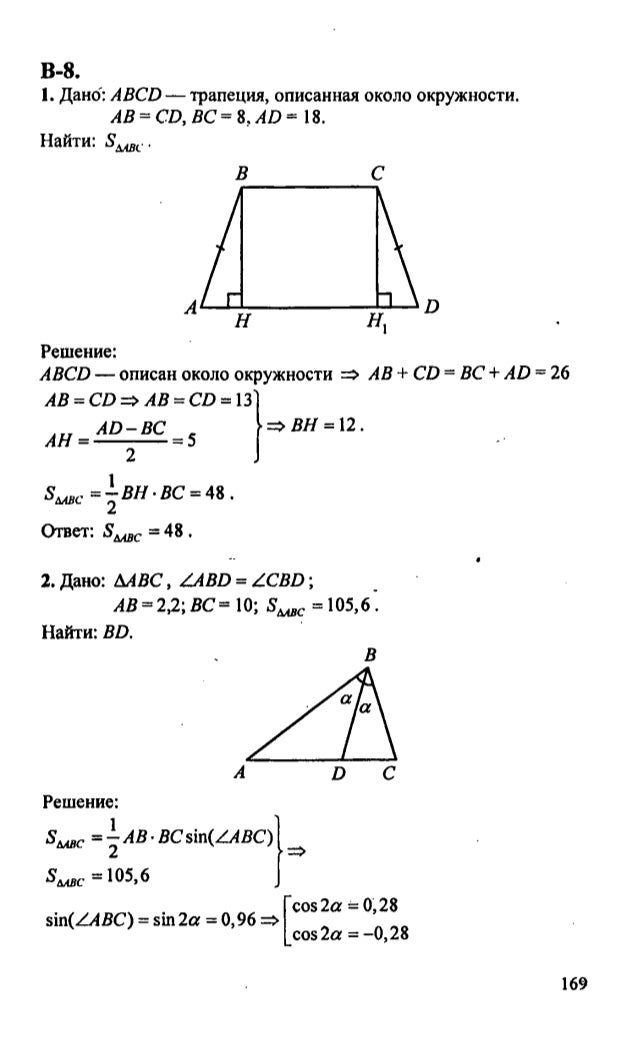 Теперь мы готовы подставить наши значения в формулу площади, чтобы найти площадь трапеции РЭМН . Получаем

Площадь трапеции РЭМН составляет 42,5 квадратных сантиметров .

Альтернативное решение:

Есть ли другой способ решить эту проблему, чтобы убедиться, что наше решение правильно?

Ответ положительный. Обратите внимание, что мы можем разделить трапецию REMN на два треугольника и квадрат. Следовательно, если мы возьмем сумму их площадей, они должны сложить до 42.5 . Посмотрим, работает ли это.

Чтобы найти площадь ? RSN у нас есть

Итак, площадь ? RSN составляет 7,5 квадратных сантиметров . Давайте найдите площадь другой фигуры внутри трапеции.

Мы знаем, что четырехугольник REAS — параллелограмм. На самом деле это квадрат, потому что у него четыре равные стороны и четыре прямых угла. Мы находим это площадь, выполнив следующие действия:

Мы видим, что четырехугольник REAS имеет площадь 25 квадратных сантиметров. Нам просто нужно найти площадь последнего треугольника, прежде чем складывать площади.

Последний треугольник ? EAM определяется следующим образом. шаги:

Итак, ? EAM имеет площадь 10 квадратных сантиметров.

Наконец, мы берем сумму этих трех многоугольников, составляющих трапецию. Мы получите

Действительно, мы правы в отношении трапеции REMN , имеющей площадь 42,5 . квадратных сантиметров .

Геометрия 8-1 Углы многоугольников

1.Сумма измерений внутренних углов. Геометрия 8-1. Внутренние углы. Сумма углов каждого многоугольника может быть найдена сложением углов треугольника. 2. Теорема 8-1 (теорема о сумме внутренних углов). Если у выпуклого многоугольника n сторон и S — сумма мер внутренних углов, то S = 180 (n — 2). onvex Многоугольник Число сторон Число Vs Сумма углов Треугольник 3 1 (1180) или 180 четырехугольник 4 2 (2180) или 360 пятиугольник 5 3 (3180) или 540 шестиугольник 6 4 (4180) или 720 семиугольник 7 5 (5 180) или 900 восьмиугольник 8 6 (6 180) или 1080 Пример 1: Найдите размер каждого внутреннего угла правильного пятиугольника.-Используйте теорему о сумме внутренних углов, чтобы найти сумму угловых мер. S = 180 (n — 2) S = 180 (- 2) S = поэтому каждый угол равен / 5 или. Пример 2: Найдите размер каждого внутреннего угла. R (11x + 4) o S 5x o U 5x o (11x + 4) o T. Сумма измерений внешних углов x x x x x

2 1. Теорема 8-2. Теорема о сумме внешних углов. Если многоугольник выпуклый, то сумма внешних углов, по одному в каждой вершине, равна 360.(внешний угол) (количество сторон) = 360 Пример 3: Найдите размеры внешнего и внутреннего угла правильного шестиугольника. HW: Геометрия 8-1 p нечетное, нечетное 47-48, нечетное, нечетное Hon: 57

3 Геометрия 8-2 Параллелограммы. Стороны и углы параллелограммов 1. Четырехугольник с противоположными сторонами называется параллелограммом. Y. Теоремы 1. Теорема 8-3. Противоположные стороны параллелограмма являются конгруэнтным сокращением: Opp.стороны Y есть. 2. Теорема 8-4. Противоположные углы параллелограмма являются конгруэнтным сокращением: Opp. s из Y есть. 3. Теорема 8-5 о последовательных углах параллелограмма является дополнительной. аббревиатура: ons. s из Y поставляются. 4. Теорема 8-6. Если у параллелограмма один прямой угол, то у него четыре прямых угла. аббревиатура: Если Y имеет 1 рт., он имеет 4 рт. с. Ex. 1: Напишите доказательство теоремы 8-4 в 2 столбца. Дано: Д Докажите :, Утверждения Причины 1. Д 1. Даны 2., и являются дополнительными 3. и являются дополнительными и дополнительными 4., 4.

4 Пр. 2: RSTU — параллелограмм, найдите m URT, m RST и y. R U 3y S 18 o 40o 18 T. Диагонали параллелограммов R S 1. Теорема 8-7. Диагонали параллелограмма делят друг друга пополам. Итак: RQ QT и UQT Пример: 3: Каковы координаты пересечения диагоналей параллелограмма MNPR с вершинами M (-3, 0), N (-1, 3), P (5, 4), R ( 3, 1). 2. Теорема 8-8. Каждая диагональ параллелограмма разделяет параллелограмм на два конгруэнтных треугольника.сокращение: iag. разделяет Y на 2 В с. HW: Геометрия 8-2 стр., 37-39, 50-51, нечетные, 56-57, нечетные Hon: 36, 46 Геометрия 8-3 Тесты для параллелограммов. условия для параллелограмма

5 1. Теорема. Если обе пары противоположных сторон четырехугольника конгруэнтны, то четырехугольник является параллелограммом. аббревиатура: Если обе пары опп. стороны есть, затем четверной. это Y.2. Теорема. Если обе пары противоположных углов четырехугольника конгруэнтны, то четырехугольник является параллелограммом. аббревиатура: Если обе пары опп. е, потом четверной. есть Y. 3. Теорема. Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом. сокращение: Если диаг. разделите друг друга пополам, затем четверть. есть Y. 4. Теорема. Если одна пара противоположных сторон четырехугольника параллельна и конгруэнтна, то четырехугольник является параллелограммом. сокращение: Если одна пара противоположных сторон — и, то четырехугольник.есть Y. Пример 1: определить, является ли четырехугольник параллелограммом. Пример 2: найти x и y так, чтобы каждый четырехугольник был параллелограммом. a.) E 8y 15 F 6x 12 2x + 16 b.) H o (5y + 283) y + 10 (6y + 14 o) G

6. Параллелограммы и координатная плоскость. Вы можете использовать формулу istance (или теорему Пифагора), чтобы определить, является ли четырехугольник параллелограммом в координатной плоскости.Пример 3: Координаты вершин четырехугольника PQRS: P (-5,3), Q (-1,5), R (6,1) и S (2, -1). определить, является ли четырехугольник PQRS параллелограммом. четырехугольник является параллелограммом тогда и только тогда, когда выполняется одно из следующих утверждений: 1. Остальные пары противоположных сторон параллельны. (определение) 2. Другие пары противоположных сторон совпадают. (Теорема 8-9) 3. Ягоны делят друг друга пополам. (Теорема 8-10) 4. Другие пары противоположных углов совпадают (теорема 8-11) 5. Пара противоположных сторон параллельна и конгруэнтна (теорема 8-12) HW: Геометрия 8-3 p, нечетное, 37, 45-50, нечетные Hon: 23-24, 33, 35, 39 Геометрия 8-4 Прямоугольники.Свойства прямоугольников

7 1. Определение — прямоугольник представляет собой четырехугольник с четырьмя прямыми углами. -если обе пары противоположных углов конгруэнтны, то это параллелограмм. — Таким образом, прямоугольник — это параллелограмм. M 2. Теорема 8-13. Если параллелограмм является прямоугольником, то его диагонали конгруэнтны. сокращение: если Y — прямоугольник, диаг. находятся. Пример 1: Четырехугольник РСТУ — прямоугольник.Если RT = 6x + 4 и SU = 7x 4, найдите x. R U S T Пример 2: Найдите x и y, если MNPL — прямоугольник. M 6 y + 2 o N L 5x + 8 o 3x + 2 o P 3. Теорема 8-14. Если диагонали параллелограмма совпадают, то параллелограмм является прямоугольником. Ex. 3: определить, является ли параллелограмм прямоугольником, учитывая (-2, 1), (4, 3), (5, 0) и (-1, -2).

8 HW: Геометрия 8-4 p нечетное, Hon: 42 Геометрия 8-5 Ромби и квадраты M.Свойства ромба 1. Ромб — четырехугольник со всеми 4

9 равных сторон. 2. Теорема. Диагонали ромба перпендикулярны. и 3. Теорема. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом. 4. Теорема. Каждая диагональ ромба делит пополам пару противоположных углов. so и M Ex 1: a.) Найдите y, если 2 m 1 y 10. = L 1 Q N b.) Найдите m PNL, если m MPL = 64. P Пример 2: определите, является ли параллелограмм ромбом, прямоугольником или квадратом для (-4, -2), (-2, 6) (6, 4), (4 , -4). Перечислите все подходящие варианты. (-2, 6) (6, 4) (-4, -2) (4, -4) Пример 3: у квадратного стола четыре ножки на расстоянии 2 фута друг от друга. Стол кладут на подставку для зонтов так, чтобы отверстие в центре стола совпадало с отверстием в подставке. Как далеко от ножки находится центр отверстия?

10 Свойства ромбов и квадратов Ромби-квадраты 1.ромб обладает всеми свойствами 1. квадрата обладает всеми свойствами параллелограмма. параллелограмм 2. Все стороны равны. 2. квадрат обладает всеми свойствами прямоугольника. 3. Ягонали перпендикулярны. 3. Квадрат обладает всеми свойствами ромба. 4. Игонали делят углы ромба пополам. HW: Геометрия 8-5 p, 21-23, 26-31, 32, 46-47, нечетное Hon: 37, 38, 40, 42, 44 Геометрия 8-6 Трапеции. Свойства трапеции 1. Трапеция — это четырехугольник, у которого ровно одна пара параллельных сторон. 2.Параллельные стороны называются основаниями. 3. Базовые углы образованы основанием и одной из ножек. 4. Непараллельные стороны называются ножками. база

11 5. Если ноги конгруэнтны, то трапеция — это равнобедренная трапеция. 6. Теорема о конгруэнтности пар углов основания равнобедренной трапеции. 7. Теорема. Диагонали равнобедренной трапеции конгруэнтны.Пример 1: Завершите потоковое доказательство теоремы. Дано: MNOP — равнобедренная трапеция. Доказательство: MO NP. Доказательство: MNPO. MNOP — равнобедренная форма. V MP NO MPO NOP PO PO. Пример 2: четырехугольник с вершинами (5, 1), (- 3, -1), (-2, 3) и (2, 4). а.) Убедитесь, что это трапеция.

12 b.) Определите, является ли трапеция равнобедренной. Объясните .. Медианы трапеций 1. Отрезок, соединяющий середины сторон трапеции, является средним.(иногда называемый мидсегментом) 2. Теорема Медиана трапеции параллельна основаниям, а ее мера равна половине суммы оснований. 1 Пример: MN = (+) 2 Пример 3: EFG — это равнобедренная трапеция с медианным MN. a.) Найдите G, если EF = 20 и MN = 30. MNE 3 4 MN 1 2 G b.) Найдите m 1, m 2, m 3 и m 4, если m 1 = 3x + 5 и m 3 = 6x 5. HW: Геометрия 8-6 p нечетная, 13-18, 22-28, 42-48, нечетная Hon: 19, 20, 32, 35 Геометрия 8-7 Координатное доказательство с четырехугольниками. Рисунки положения Пример 1. Поместите и отметьте квадрат со сторонами в единицы длины на координатной плоскости.1.) Пусть ,,, и — вершины квадрата. (0,) (,) (0, 0) (, 0)

13 2.) Поместите квадрат с вершиной в начало координат, вдоль положительной оси x и вдоль оси y. Обозначьте вершины ,, и. 3.) Координата Y равна 0, потому что вершина находится на оси x. Поскольку длина стороны равна a, координата x равна. 4.) находится на оси y, поэтому координата x равна 0. Координата y равна 0 + a или.5.) Координата x тоже. Координата Y равна 0 + a, или потому, что сторона имеет длину единицы. Пример 2: Назовите недостающую координату для равнобедренной трапеции. (?,?) (а-2б, в) (0, 0) (а, 0). Доказательство теорем 1. После того, как мы разместили фигуру на координатной плоскости, мы можем использовать формулу наклона, формулу расстояния и формулу средней точки для доказательства теорем. Пример 3: Поместите квадрат на координатную плоскость. Обозначьте середины сторон, M, N, P и Q. Напишите доказательство координат, чтобы показать, что MNPQ представляет собой квадрат. a.) формула средней точки y, координаты точек M, N, O и P следующие: M (,) N (,) P (,) Q (,) (0, 2a) (2a, 2a) b.) Найдите наклоны QP, MN, QM и PN. (0, 0) (2a, 0)

14 Каждая пара противоположных сторон равна, поэтому MNPQ — это a и a c.) Используйте формулу расстояния, чтобы найти QP и QM. MNPQ является квадратом, потому что каждая пара противоположных сторон параллельна, а последовательные стороны образуют и являются. HW: Геометрия 8-7 стр., 24-25, 28-39

Общая математика: практический тест по геометрии (вопросы)

1.Какое из следующих утверждений является определением параллельных прямых?

1. Две отчетливые копланарные линии, пересекающиеся под углом 90 °.
2. Две разные копланарные линии, которые не пересекаются.
3. Два луча с общей конечной точкой, направленные в противоположные стороны.
4. Два луча с общей конечной точкой.

2. К какому из следующих терминов относится определение «функция, которая принимает точки на плоскости в качестве входных данных и дает другие точки в качестве выходных данных»?

1. Совпадение
2. Инвариант
3. Измерение
4. Преобразование

3.Если изображенная ниже трапеция JKLM была повернута на 180 ° по часовой стрелке относительно начала координат, определите, какое обозначение будет представлять новые координаты J ’K’ L’M ’?

1. (x, y) → (-x, -y)
2. (x, y) → (y, -x)
3. (x, y) → (-y, x)
4. ( x, y) → (y, x)

4. На каком из следующих рисунков показан параллелограмм WXYZ, переносимый на его изображение W’X’Y’Z ‘отражением поперек оси x?

5. Если ‾ST отражается через линию y = x, какова новая точка координат T ’?

1. (7,4)
2. (-7, — 4)
3. (4, -7)
4. (-4,7)

6.Какая из следующих фигур была повернута на 90 ° по часовой стрелке относительно начала координат?

7. Какое из следующих правил описывает преобразование JKLM в его изображение J’K’L’M ’?

1. (x, y) → (x-6, y + 8)
2. (x, y) → (x + 6, y-8)
3. (x, y) → (x-8, y) +6)
4. (x, y) → (x + 8, y-6)

8. Какой набор фигур совпадает?

9. Что из следующего верно относительно взаимосвязи между двумя треугольниками, показанными ниже?

1. Треугольники похожи.
2. Треугольники совпадают.
3. Треугольники равносторонние.
4. И ответ A, и ответ B верны.

10. Конгруэнтность треугольников ASA может использоваться, чтобы доказать, какая из следующих пар треугольников конгруэнтна?

Ответы и пояснения

1. B: Параллельные прямые — это две разные прямые в одной плоскости, которые не пересекаются. Ответ A — это определение перпендикулярных прямых. Ответ C — это определение противоположных лучей, образующих линию.Ответ D — это определение угла.

2. D: Преобразование описывается как функция, которая принимает точки на плоскости в качестве входных данных и дает другие точки в качестве выходных данных. В ответе A совпадение означает, что два изображения накладываются друг на друга. В ответе B инвариант означает свойство, которое не может быть изменено данным преобразованием. В ответе C измерение — это измерение геометрических фигур, таких как длина, площадь, угол и объем.

3. A: Поворот на 180 ° по часовой стрелке вокруг начала координат принимает исходные координаты и отменяет их.Следовательно, исходные координаты (x, y) становятся (-x, -y) после поворота. Ответ B — это изменение координат после поворота на 90 ° по часовой стрелке вокруг начала координат. Ответ C — это изменение координат после поворота на 90 ° против часовой стрелки вокруг начала координат. Ответ D — это ответ B — изменение координаты после отражения от линии y = x.

4. C: Отражение — это преобразование, создающее зеркальное отображение. Фигура, отраженная по оси x, будет иметь свои вершины в форме (x, y), преобразованные в (x, -y).Точка W в точке (1, -7) отражает точку W ’в точке (1,7). Только ответ C показывает, что WXYZ переносится на изображение W’X’Y’Z ’за счет отражения по оси x. Ответ A показывает отражение поперек линии y = x. Ответ B показывает поворот на 90 ° против часовой стрелки вокруг начала координат. Ответ D показывает отражение по оси ординат.

5. D: Для отражения поперек линии y = x исходные точки координат (x, y) меняются местами, чтобы стать (y, x) для изображения. Следовательно, поскольку T находится в (7, -4), координаты T ’после отражения от линии y = x становятся (-4,7).Ответ A предназначен для отражения по оси x. Ответ B предназначен для отражения по оси y. Ответ C соответствует повороту на 90 ° по часовой стрелке относительно начала координат.

6. C: Поскольку EFGH изначально расположен в квадранте II, поворот на 90 ° по часовой стрелке повернёт изображение в квадрант I. Поскольку EFGH поворачивается на 90 ° по часовой стрелке, каждая вершина фигуры претерпит изменение координат (x , y) → (y, -x), как в случае с ответом C. Ответ A — это отражение по оси y. Ответ B — это отражение по оси абсцисс.Ответ D — поворот на 90 ° против часовой стрелки.

7. B: Чтобы определить перевод, сравните координаты J (-4,1) и J ‘(2, -7). Чтобы найти изменение в направлении x, вычтите координату x начальной позиции из конечной позиции, которая равна Δx = 2 — (- 4) = 2 + 4 = 6. Точно так же изменение в направлении y составляет -7-1 = -8. Мы можем проверить, что то же самое верно и для других вершин. Следовательно, правило, описывающее преобразование JKLM в его образ J’K’L’M ’: (x, y) → (x + 6, y-8).Ответ A неправильно использовал противоположные знаки. В ответе C неправильно использовались противоположные знаки и были поменяны направления x и y.