Алгебра 7 класс К-2 (угл.) с ответами . Контрольная работа
Контрольная 2 по алгебре 7 класс (угл.)
Алгебра 7 класс К-2 (угл.) с ответами. Контрольная работа по алгебре для 7 класса «Одночлены» с углубленным изучением математики (цитаты) из учебно-методического пособия «Алгебра 7 класс. Дидактические материалы / И.Е. Феоктистов — М.: Мнемозина, 2009». Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных рекомендуем купить указанное пособие.
Для увеличения изображения — нажмите на картинку ! Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»
Контрольная работа по алгебре 7 класс.
К-2. Одночлены
OCR-версия контрольной
Вариант 1
1. Вычислите:
2. Выполните умножение степеней:
3. Выполните деление степеней:
4. Возведите степень в степень:
5. Найдите значение выражения:
6. Упростите выражение:
Упростите выражение:
7. Укажите все натуральные значения переменных тип, при которых степень одночлена … равна 5.
8. При каких значениях х верно равенство:
9. Докажите, что значение выражения … делится на 10.
Вариант 2
1. Вычислите:
2. Выполните умножение степеней:
3. Выполните деление степеней:
4. Возведите степень в степень:
5. Найдите значение выражения:
6. Упростите выражение:
7. Укажите все натуральные значения переменных тип, при которых степень одночлена … равна 5.
8. При каких значениях х верно равенство:
9. Докажите, что значение выражения … делится на 10.
Вариант 1
1. Вычислите:
2. Выполните умножение степеней:
3. Выполните деление степеней:
4. Возведите степень в степень:
5. Найдите значение выражения:
6. Упростите выражение:
7. Укажите все натуральные значения переменных тип, при которых степень одночлена … равна 5.
8. При каких значениях х верно равенство:
9. Докажите, что значение выражения … делится на 10.
Докажите, что значение выражения … делится на 10.
Вариант 2
1. Вычислите:
2. Выполните умножение степеней:
3. Выполните деление степеней:
4. Возведите степень в степень:
5. Найдите значение выражения:
6. Упростите выражение:
7. Укажите все натуральные значения переменных тип, при которых степень одночлена … равна 5.
8. При каких значениях х верно равенство:
9. Докажите, что значение выражения … делится на 10.
ОТВЕТЫ на контрольную работу
Вернуться к Списку контрольных работ по алгебре 7 класс (угл.изуч.)
Алгебра 7 класс К-2 (угл.) с ответами. Цитаты из учебно-методического пособия «Алгебра 7 класс. Дидактические материалы / И.Е. Феоктистов — М.: Мнемозина, 2009». Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных рекомендуем купить указанное пособие.
Контрольная работа №1 М7кл l Вариант 1. 2. Сравните значения выражений: – 0,8х – 1 и 0,8х – 1, при х = 6. 3. Упростите выражение: а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6). 4. Упростите выражение и найдите его значение: – 4(2,5а – 1,5) + 5,5а – 8, при . 5. Из двух городов, расстояние между которыми Sкм, одновременно навстречу друг другу выехали легковой автомобиль и грузовик, и встретились через tч. Скорость легкового автомобиля Ѵкм/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если S = 200, t = 2, Ѵ = 60. 6. Раскройте скобки: 3х – (5х – (3х – 1)). | Контрольная работа №1 М7кл ll Вариант 1. Найдите значение выражения: 16а + 2у, при . 2. Сравните значения выражений: 2 + 0,3а и 2 – 0,3а, при а = – 9. 3. Упростите выражение: а) 5а + 7в – 2а – 8в; б) 3(4х + 2) – 5; в) 20b – (b – 3) + (3b – 10). 4. Упростите выражение и найдите его значение: – 6(0,5х – 1,5) – 4,5х – 8, при . 5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл, и встретились через tч. Найдите расстояние между городами, если скорость автомобиля Ѵ1 км/ч, а скорость мотоцикла Ѵ2 км/ч. Ответьте на вопрос задачи, если t = 3, Ѵ1 = 80, Ѵ2 = 60. 6. Раскройте скобки: 2р – (3р – (2р – с)). | Контрольная работа №1 М7кл l Вариант 1. Найдите значение выражения: 6х – 8у, при . 2. Сравните значения выражений: – 0,8х – 1 и 0,8х – 1, при х = 6. 3. Упростите выражение: а) 2х – 3у – 11х + 8у; б) 5(2а + 1) – 3; в) 14х – (х – 1) + (2х + 6). 4. Упростите выражение и найдите его значение: – 4(2,5а – 1,5) + 5,5а – 8, при . 5. Из двух городов, расстояние между которыми Sкм, одновременно навстречу друг другу выехали легковой автомобиль и грузовик, и встретились через tч. Скорость легкового автомобиля Ѵкм/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, если S = 200, t = 2, Ѵ = 60. 6. Раскройте скобки: 3х – (5х – (3х – 1)). | Контрольная работа №1 М7кл ll Вариант 1. Найдите значение выражения: 16а + 2у, при . 2. Сравните значения выражений: 2 + 0,3а и 2 – 0,3а, при а = – 9. 3. Упростите выражение: а) 5а + 7в – 2а – 8в; б) 3(4х + 2) – 5; в) 20b – (b – 3) + (3b – 10). 4. Упростите выражение и найдите его значение: – 6(0,5х – 1,5) – 4,5х – 8, при . 5. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл, и встретились через tч. Найдите расстояние между городами, если скорость автомобиля Ѵ1 км/ч, а скорость мотоцикла Ѵ2 км/ч. Ответьте на вопрос задачи, если t = 3, Ѵ1 = 80, Ѵ2 = 60. 6. Раскройте скобки: 2р – (3р – (2р – с)). | Контрольная работа №1 М7кл lll Вариант 1. Найдите значение выражения: 4х + 3у, при . 2. Сравните значения выражений: – 0,4а + 2 и – 0,4а – 2, при а = 10. 3. Упростите выражение: а) 5х + 3у – 2х – 9у; б) 2(3а – 4) + 5; в) 15а – (а – 3) + (2а – 1). 4. Упростите выражение и найдите его значение: – 2(3,5у – 2,5) + 4,5у – 1, при . 5. Из двух пунктов, расстояние между которыми Sкм, одновременно навстречу друг другу отправились пешеход и велосипедист, и встретились через tч. Скорость велосипедиста Ѵ км/ч. Найдите скорость пешехода. Ответьте на вопрос задачи, если S =9, t = 0,5, Ѵ = 12. 6. Раскройте скобки: 5а – (3а – (2а – 4)). | Контрольная работа №1 М7кл lV Вариант 1. Найдите значение выражения: 12а – 3b, при . 2. Сравните значения выражений: 1 – 0,6х и 1 + 0,6х , при х = 5. 3. Упростите выражение: а) 12а – 10b – 10а + 6b; б) 4(3х – 2) + 7; в) 8х – (2х + 5) + (х – 1). 4. Упростите выражение и найдите его значение: – 5(0,6с – 1,2) – 1,5с – 3, при . 5. Из двух пунктов одновременно навстречу друг другу вышли два пешехо – да и встретились через tч. Найдите расстояние между пунктами, если скорость одного пешехода Ѵ1 км/ч, а другого Ѵ2 км/ч. Ответьте на вопрос задачи, если Ѵ1 = 5, Ѵ2 = 4, t = 3. 6. Раскройте скобки: 7х – (5х – (3х + у)). | Контрольная работа №1 М7кл lll Вариант 1. Найдите значение выражения: 4х + 3у, при . 2. Сравните значения выражений: – 0,4а + 2 и – 0,4а – 2, при а = 10. 3. Упростите выражение: а) 5х + 3у – 2х – 9у; б) 2(3а – 4) + 5; в) 15а – (а – 3) + (2а – 1). 4. Упростите выражение и найдите его значение: – 2(3,5у – 2,5) + 4,5у – 1, при . 5. Из двух пунктов, расстояние между которыми Sкм, одновременно навстречу друг другу отправились пешеход и велосипедист, и встретились через tч. Скорость велосипедиста Ѵ км/ч. Найдите скорость пешехода. Ответьте на вопрос задачи, если S =9, t = 0,5, Ѵ = 12. 6. Раскройте скобки: 5а – (3а – (2а – 4)). | Контрольная работа №1 М7кл lV Вариант 1. Найдите значение выражения: 12а – 3b, при . 2. Сравните значения выражений: 1 – 0,6х и 1 + 0,6х , при х = 5. 3. Упростите выражение: а) 12а – 10b – 10а + 6b; б) 4(3х – 2) + 7; в) 8х – (2х + 5) + (х – 1). 4. Упростите выражение и найдите его значение: – 5(0,6с – 1,2) – 1,5с – 3, при . 5. Из двух пунктов одновременно навстречу друг другу вышли два пешехо – да и встретились через tч. Найдите расстояние между пунктами, если скорость одного пешехода Ѵ1 км/ч, а другого Ѵ2 км/ч. Ответьте на вопрос задачи, если Ѵ1 = 5, Ѵ2 = 4, t = 3. 6. Раскройте скобки: 7х – (5х – (3х + у)). |
Контрольная работа №2 «Уравнения. Статистические характеристики» | |
I вариант | II вариант |
| |
а) 2х + 1 = 3х — 4 ; б) 1,6(5х – 1) = 1,8х – 4,7 | а) -2х + 1 = — х — 6 ; б) 2(0,6х + 1,85) = 1,3х + 0,7 |
| |
а)Турист проехал в 7 раз большее расстояние, чем прошел пешком. а) Длина прямоугольника на 6 см больше ширины. Найдите площадь прямоугольника, если его периметр равен 48 см. | а) На одной полке на 15 книг большее, чем другой. Всего на двух полках 53 книги. Сколько книг на каждой полке? б) Ширина прямоугольника в 2 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 120 см. |
| |
а) 58, 60, 49, 35, 51, 42, 65, 40; б) 21, 25, 19, 13, 25, 29, 21, 27, 30. | а) 43, 35, 37, 43, 42, 38, 45, 39, 36, 41; б) 88, 75, 91, 88, 85, 83, 80, 78, 74, 92. |
| |
В ряду чисел 15, 4, 11,__, 27, 9, 17, 19 пропущено одно число. | В ряду чисел 18, 5, 12,__, 29, 10, 15, 17 пропущено одно число. Найдите его, если среднее арифметическое равно 14. |
Контрольная работа №2 «Уравнения. Статистические характеристики» | |
I вариант | II вариант |
| |
а) 2х + 1 = 3х — 4 ; б) 1,6(5х – 1) = 1,8х – 4,7 | а) -2х + 1 = — х — 6 ; б) 2(0,6х + 1,85) = 1,3х + 0,7 |
| |
а)Турист проехал в 7 раз большее расстояние, чем прошел пешком. Весь путь туриста составил 24 км. а) Длина прямоугольника на 6 см больше ширины. Найдите площадь прямоугольника, если его периметр равен 48 см. | а) На одной полке на 15 книг большее, чем другой. Всего на двух полках 53 книги. Сколько книг на каждой полке? б) Ширина прямоугольника в 2 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 120 см. |
| |
а) 58, 60, 49, 35, 51, 42, 65, 40; б) 21, 25, 19, 13, 25, 29, 21, 27, 30. | а) 43, 35, 37, 43, 42, 38, 45, 39, 36, 41; б) 88, 75, 91, 88, 85, 83, 80, 78, 74, 92. |
| |
В ряду чисел 15, 4, 11,__, 27, 9, 17, 19 пропущено одно число. | В ряду чисел 18, 5, 12,__, 29, 10, 15, 17 пропущено одно число. Найдите его, если среднее арифметическое равно 14. |
Контрольная работа №2 «Уравнения. Статистические характеристики» | |
I вариант | II вариант |
| |
а) 2х + 1 = 3х — 4 ; б) 1,6(5х – 1) = 1,8х – 4,7 | а) -2х + 1 = — х — 6 ; б) 2(0,6х + 1,85) = 1,3х + 0,7 |
| |
а)Турист проехал в 7 раз большее расстояние, чем прошел пешком. Весь путь туриста составил 24 км. а) Длина прямоугольника на 6 см больше ширины. Найдите площадь прямоугольника, если его периметр равен 48 см. | а) На одной полке на 15 книг большее, чем другой. Всего на двух полках 53 книги. Сколько книг на каждой полке? б) Ширина прямоугольника в 2 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 120 см. |
| |
а) 58, 60, 49, 35, 51, 42, 65, 40; б) 21, 25, 19, 13, 25, 29, 21, 27, 30. | а) 43, 35, 37, 43, 42, 38, 45, 39, 36, 41; б) 88, 75, 91, 88, 85, 83, 80, 78, 74, 92. |
| |
В ряду чисел 15, 4, 11,__, 27, 9, 17, 19 пропущено одно число. | В ряду чисел 18, 5, 12,__, 29, 10, 15, 17 пропущено одно число. Найдите его, если среднее арифметическое равно 14. |
Домашние контрольные работы КР-1 — Вариант 2 гдз по алгебре 7 класс Мордкович задачник Базовый уровень
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 2 Класс
- Математика
Алгебра 7 Макарычев К-2 Уровень 1 Контрольная работа с ответами
Контрольная работа № 2 по алгебре в 7 классе «Уравнения с одной переменной» с ответами по УМК Макарычев (легкий уровень). Глава I. ВЫРАЖЕНИЯ. ТОЖДЕСТВА. УРАВНЕНИЯ. Урок 22 поурочного планирования — Алгебра 7 Макарычев К-2 Уровень 1.
Глава I. ВЫРАЖЕНИЯ. ТОЖДЕСТВА. УРАВНЕНИЯ. Урок 22 поурочного планирования — Алгебра 7 Макарычев К-2 Уровень 1.
Перейти: Список контрольных по алгебре в 7 классе по УМК Макарычев (Оглавление)
Контрольная работа № 2. Уровень 1 (легкий)
«Уравнения с одной переменной»
К-2. Вариант 1 (транскрипт)
- Какие из чисел –3, –2, 2, 3 являются корнями уравнения: а) х2 + 8 = 6х; б) |х – 6| = 3 – 2х?
- Решите уравнение: а) (2х – 1)(х + 3) = 0; б) (3x – 2)/5 = (2x – 3)/4.
- При каком значении переменной разность выражений 6х – 7 и 2х + 3 равна 4?
- При каком значении параметра а уравнение а • х = 3а + х имеет единственный корень? Найдите его.
- На складе хранится 520 т рыбы. При этом трески в 1,5 раза больше, чем наваги. Окуня на 16 т больше, чем трески.

- Найдите три последовательных натуральных числа, если утроенная сумма крайних чисел на 145 больше среднего числа.
К-2. Вариант 2 (транскрипт)
- Какие из чисел –3, –2, 2, 3 являются корнями уравнения: а) х2 + 9 = 6х; б) |х – 4| = –2 – 4х?
- Решите уравнение: а) (1 –3x)(х + 2) = 0; б) (2x – 3)/3 =(4x – 1)/5.
- При каком значении переменной разность выражений 8х – 3 и 3х + 4 равна 5?
- При каком значении параметра а уравнение а • х = 4а + 2х имеет единственный корень? Найдите его.
- На базе хранится 590 т овощей. При этом картофеля в 2,5 раза больше, чем моркови. Лука на 14 т больше, чем картофеля. Сколько тонн моркови, картофеля и лука находится на базе?
- Найдите три последовательных натуральных четных числа, если удвоенная сумма крайних чисел на 84 больше среднего числа.
Ответы на контрольную работу:
ОТВЕТЫ на Вариант 1
- а) 2; б) –3.

- а) х = 1/2 и х = –3; б) х = –3,5.
- х = 3,5.
- При а ≠ 1 х = 3а/(а–1).
- 126 т наваги, 189 т трески, 205 т окуня.
- 28, 29, 30.
ОТВЕТЫ на Вариант 2
- а) х = 3; б) х = –2.
- а) х = 1/3 и х = –2; б) х = –6.
- х = 2,4.
- При а ≠ 2 х = 4а/(а–2).
- 96 т моркови, 240 т картофеля, 254 т лука.
- 26, 28, 30.
Контрольная работа составлена в шести вариантах (варианты 1,2 – самые простые, варианты 3, 4 – средней сложности, варианты 5, 6 – самые сложные). Степень сложности меняется не слишком резко, поэтому можно рекомендовать следующий критерий оценки: при выполнении вариантов 1, 2 оценка «3» ставится за любые три решенные задачи, оценка «4» – за четыре задачи и оценка «5» – за пять задач. Одна задача дает учащимся некоторую свободу выбора. При тех же критериях оценки за решение задач вариантов 3, 4 к набранным баллам добавляются дополнительно 0,5 балла, за решение задач вариантов 5,6 – дополнительно 1 балл (т.
Перед проведением контрольной работы учащихся целесообразно ознакомить с критериями оценки и разной сложностью вариантов. Выбор вариантов может быть осуществлен учителем или предоставлен ученикам (в этом случае предполагается наличие копировальной техники в школе и избыточное количество заданий). При наличии такой техники в классе на стенде (после контрольной) может быть вывешено решение всех задач шести вариантов. Разумеется, разобрать такое количество задач на уроке невозможно (да и не нужно).
К-2 Уровень 2 + Ответы К-2 Уровень 3 + Решения
Вы смотрели: Контрольная работа № 2 по алгебре 7 класс «Уравнения с одной переменной» с ответами по УМК Макарычев (простой уровень). Глава I. ВЫРАЖЕНИЯ. ТОЖДЕСТВА. УРАВНЕНИЯ. Урок № 22 поурочного планирования — Алгебра 7 Макарычев К-2 Уровень 1.
Смотреть Список контрольных по алгебре в 7 классе по УМК Макарычев (Оглавление)
ГДЗ контрольная работа / К-2 / вариант 1 1 алгебра 7 класс дидактические материалы Звавич, Кузнецова
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
|
| Приготовьтесь! | с. 277 277 | ||
| 5-1 | Полиномиальные функции | Упражнения | стр.285 |
| 5-2 | Полиномы, линейные множители и нули | Упражнения | стр.293 |
| 5-3 | Решение полиномиальных уравнений | Упражнения | с.300 |
| 5-4 | Делительные многочлены | Упражнения | п.308 |
| Викторина в середине главы | стр. 311 311 | ||
| 5-5 | Теоремы о корнях полиномиальных уравнений | Упражнения | с.315 |
| 5-6 | Основная теорема алгебры | Упражнения | стр. 322 |
| 5-7 | Биномиальная теорема | Упражнения | п. 328 |
| 5-8 | Полиномиальные модели в реальном мире | Упражнения | с.335 |
| 5-9 | Преобразование полиномиальных функций | Упражнения | стр. 342 342 |
| Обзор главы | п.347 | ||
| Глава Test | стр.353 | ||
| Обзор совокупных стандартов | с.354 |
Алгебра II
- Мои предпочтения
- Мой список чтения
- Литературные заметки
- Подготовка к тесту
- Учебные пособия
- Дом
- Учебные пособия
- Алгебра II
- Бухгалтерский учет
- Принципы бухгалтерского учета I
- Принципы бухгалтерского учета II
- Алгебра
- Алгебра I
- Алгебра II
- Линейная алгебра
- Американское правительство
- Анатомия и психология
- Астрономия
- Основы математики
- Основы математики и предалгебры
- Математические задачи со словами
- Биология
- Биохимия I
- Биохимия II
- Биология
- Микробиология
- Биология растений
- Исчисление
- Исчисление
- Precalculus
- Химия
- Химия
- Органическая химия I
- Органическая химия II
- Уголовное правосудие
- Дифференциальные уравнения
- науки о Земле
- Экономика
- английский
- французкий язык
- Французский I
- Французский II
- Геология
- Геометрия
- Грамматика
- История
- U.
 С. История I
С. История I - История США II
- U.
- Физика
- Принципы Управления
- Психология
- Психология развития
- Психология
- Социология
- испанский
- Испанский I
- Испанский II
- Статистика
- Тригонометрия
- Письмо
- Линейные предложения в одной переменной
- Формулы
- Тест: формулы
- Уравнения абсолютных значений
- Викторина: уравнения абсолютных значений
- Линейные неравенства
- Линейные уравнения
- Викторина: линейные уравнения
- Викторина: линейные неравенства
- Сложные неравенства
- Тест: сложные неравенства
- Абсолютное неравенство
- Викторина: Абсолютное неравенство
- Линии сегментов и неравенства
- Тест: прямоугольная система координат
- Формула расстояния
- Тест: формула расстояния
- Формула средней точки
- Тест: формула средней точки
- Прямоугольная система координат
- Наклон линии
- Тест: наклон линии
- Наклоны параллельных и перпендикулярных линий
- Викторина: уклоны параллельных и перпендикулярных линий
- Уравнения линий
- Викторина: уравнения линий
- Графики линейных неравенств
- Викторина: графики линейных неравенств
- Линейные предложения с двумя переменными
- Линейные уравнения: решения с использованием подстановки с двумя переменными
- Тест: Линейные уравнения: решения с использованием замены с двумя переменными
- Линейные уравнения: решения с использованием исключения с двумя переменными
- Тест: Линейные уравнения: решения с использованием исключения с двумя переменными
- Линейные уравнения: решения с использованием матриц с двумя переменными
- Линейные уравнения: решения с использованием построения графиков с двумя переменными
- Тест: Линейные уравнения: решения с использованием построения графиков с двумя переменными
- Викторина: Линейные уравнения: решения с использованием матриц с двумя переменными
- Линейные уравнения: решения с использованием определителей с двумя переменными
- Викторина: Линейные уравнения: решения с использованием детерминантов с двумя переменными
- Линейные неравенства: решения с использованием графического представления с двумя переменными
- Викторина: Линейные неравенства: решения с использованием построения графиков с двумя переменными
- Линейные уравнения с тремя переменными
- Линейные уравнения: решения с использованием матриц с тремя переменными
- Викторина: Линейные уравнения: решения с использованием матриц с тремя переменными
- Линейные уравнения: решения с использованием определителей с тремя переменными
- Викторина: Линейные уравнения: решения с использованием определителей с тремя переменными
- Линейные уравнения: решения с использованием исключения с тремя переменными
- Тест: Линейные уравнения: решения с использованием исключения с тремя переменными
- Полиномиальная арифметика
- Умножение многочленов
- Тест: умножение многочленов
- Специальные произведения биномов
- Викторина: специальные произведения биномов
- Деление многочленов
- Сложение и вычитание многочленов
- Викторина: деление многочленов
- Викторина: сложение и вычитание многочленов
- Синтетический отдел
- Викторина: синтетический отдел
- Факторинговые полиномы
- Разница квадратов
- Викторина: разница квадратов
- Сумма или разница кубиков
- Викторина: сумма или разница кубиков
- Трехчлены вида x ^ 2 + bx + c
- Наибольший общий делитель
- Викторина: величайший общий фактор
- Викторина: Триномы формы x ^ 2 + bx + c
- Трехчлены вида ax ^ 2 + bx + c
- Тест: триномы формы ax ^ 2 + bx + c
- Квадратные трехчлены
- Викторина: Квадратные трехчлены
- Факторинг путем перегруппировки
- Викторина: Факторинг путем перегруппировки
- Краткое изложение методов факторинга
- Решение уравнений по факторингу
- Викторина: решение уравнений по факторингу
- Рациональные выражения
- Тест: упрощение рациональных выражений
- Умножение рациональных выражений
- Тест: умножение рациональных выражений
- Разделение рациональных выражений
- Викторина: разделение рациональных выражений
- Сложение и вычитание рациональных выражений
Алгебра II
Обзор курса
Алгебра II основывается на алгебраических концепциях, изучаемых в Алгебре I, продолжаясь до функций, выражений и т. Д.и предоставление студентам более глубокого понимания алгебраических концепций. Его преподает Патрик Мара, удостоенный наград главный учитель Acellus. Acellus Algebra II утвержден A-G Калифорнийским университетом.
Д.и предоставление студентам более глубокого понимания алгебраических концепций. Его преподает Патрик Мара, удостоенный наград главный учитель Acellus. Acellus Algebra II утвержден A-G Калифорнийским университетом.Цели курса и результаты обучения студентов
В Acellus Algebra II базовые навыки, полученные в Algebra I, укрепляются и развиваются. После успешного завершения этого курса студенты будут иметь прочную основу в алгебре, необходимую для дальнейшего успеха в более сложных математических курсах.Учащиеся рассмотрят выражения, уравнения, неравенства и системы и расширили свое понимание функций, уравнений и графиков. Они достигли более глубокого понимания линейных, квадратичных, экспоненциальных и рациональных функций и того, как их преобразовывать и использовать для моделирования ситуаций. У них также есть базовое понимание полиномиальных, радикальных и логарифмических функций. Студенты получили представление о комплексных числах и знают, как строить их графики и выполнять с ними различные математические операции. Студенты имеют опыт работы с последовательностями и сериалами. Они знакомы с различными коническими сечениями, их графиками и уравнениями. Студенты знают, как выполнять операции с матрицами и использовать их для решения систем уравнений и выполнения геометрических преобразований. Студенты более уверены в вычислениях, включающих перестановки и комбинации. Они знают, как рассчитать вероятность, связанную с несколькими событиями, а также условную вероятность, и знакомы с вероятностными моделями.Они также работали с функциями биномиального, нормального и вероятностного распределения. Студенты знакомы с единичным кругом и графиками функций синуса, косинуса и тангенса, а также с тем, как их переводить. Они также знают основные триггерные идентификаторы и знают, как их использовать для решения проблем.
Студенты имеют опыт работы с последовательностями и сериалами. Они знакомы с различными коническими сечениями, их графиками и уравнениями. Студенты знают, как выполнять операции с матрицами и использовать их для решения систем уравнений и выполнения геометрических преобразований. Студенты более уверены в вычислениях, включающих перестановки и комбинации. Они знают, как рассчитать вероятность, связанную с несколькими событиями, а также условную вероятность, и знакомы с вероятностными моделями.Они также работали с функциями биномиального, нормального и вероятностного распределения. Студенты знакомы с единичным кругом и графиками функций синуса, косинуса и тангенса, а также с тем, как их переводить. Они также знают основные триггерные идентификаторы и знают, как их использовать для решения проблем.Этот курс разработан Международной академией наук. Учить больше
Объем и последовательность
Блок 1 — Алгебраические выражения В этом модуле студенты изучают алгебраические выражения и наборы чисел. Они изучают решение уравнений и неравенств, упрощение и оценку, а также абсолютные значения. Блок 2 — Функции В этом модуле учащиеся обсуждают определение функции, прямое изменение, наклон-пересечение и точка-наклон. Они исследуют кусочно определенные функции, линейные модели, преобразования функций, функции абсолютного значения и неравенства с двумя переменными. Раздел 3 — Linea
Они изучают решение уравнений и неравенств, упрощение и оценку, а также абсолютные значения. Блок 2 — Функции В этом модуле учащиеся обсуждают определение функции, прямое изменение, наклон-пересечение и точка-наклон. Они исследуют кусочно определенные функции, линейные модели, преобразования функций, функции абсолютного значения и неравенства с двумя переменными. Раздел 3 — Linea Введение в линейную алгебру, 5-е издание
Введение в линейную алгебру, 5-е изданиеНадеюсь, этот сайт станет ценным ресурсом для всех изучение и выполнение линейной алгебры.Вот ключевые ссылки:
** Каждый раздел в Оглавлении содержит ссылки на наборы проблем, решения,
** другие веб-сайты и все материалы, относящиеся к теме этого раздела.
** Читателям предлагается предлагать возможные ссылки.
Содержание для введения в линейную алгебру (5-е издание, 2016 г.)
- 1 Введение в векторы
- 1.1 Векторы и линейные комбинации
- 1.2 Длина и точечные произведения
- 1.3 Матрицы
- 2 Решение линейных уравнений
- 2.1 Векторы и линейные уравнения
- 2.2 Идея исключения
- 2.3 Исключение с использованием матриц
- 2.4 Правила для матричных операций
- 2.5 обратных матриц
- 2,6 Исключение = Факторизация: A = LU
- 2.7 Транспозиции и перестановки
- 3 векторные пространства и подпространства
- 3.1 Пространства векторов
- 3.2 Пустое пространство A : решение Ax = 0 и Rx = 0
- 3.3 Полное решение для Ax = b
- 3.4 Независимость, основа и размер
- 3.5 Размеры четырех подпространств
- 4 Ортогональность
- 4.1 Ортогональность четырех подпространств
- 4.2 Прогнозы
- 4.3 Аппроксимация методом наименьших квадратов
- 4.4 ортонормированных оснований и Грама-Шмидта
- 5 Детерминанты
- 5.1 Свойства детерминантов
- 5.2 Перестановки и кофакторы
- 5.3 Правило Крамера, инверсии и объемы
- 6 собственных значений и собственных векторов
- 7 Разложение по сингулярным значениям (SVD)
- 8 линейных преобразований
- 8.1 Идея линейного преобразования
- 8.2 Матрица линейного преобразования
- 8.3 В поисках хорошей основы
- 9 Комплексных векторов и матриц
- 9.1 Комплексные числа
- 9.2 Эрмитовы и унитарные матрицы
- 9.3 Быстрое преобразование Фурье
- 10 приложений
- 10.1 Графики и сети
- Матрицы 10.2 в машиностроении
- 10.3 Марковские матрицы, население и экономика
- 10.4 Линейное программирование
- 10.5 Ряд Фурье: линейная алгебра функций
- 10.6 Компьютерная графика
- 10.7 Линейная алгебра для криптографии
- 11 Числовая линейная алгебра
- 11.1 Метод исключения Гаусса на практике
- 11.2 Нормы и номера условий
- 11.3 Итерационные методы и предобуславливатели
- 12 Линейная алгебра в теории вероятностей и статистике
- Факторизации матрицы
- Индекс
- Шесть великих теорем / Линейная алгебра в двух словах
[вверху]
Каждый раздел книги имеет набор задач.
Вопросы к практическому экзамену
Ссылки на веб-сайты для каждого семестра в MIT: web.mit.edu/18.06,
Задачи линейной алгебры в лемме
Мой друг Павел Гринфельд из Drexel прислал мне коллекцию интересных задач — в основном элементарных, но с каждой изюминкой. Это часть его большого обучающего сайта под названием LEM.MA, и он создал страницу http: // lem.ma / LAProb / специально для этого веб-сайта, связанного с 5-м изданием.
Стандарт видео H.264 (обещанный в разделе 7.1 книги)
Этот стандарт видео описывает систему кодирования и декодирования («Кодек»), которую инженеры определили для таких приложений, как телевидение высокой четкости. Не ожидается, что вы будете знать значение каждого слова — автор вашей книги тоже не знает. Дело в том, чтобы увидеть важный пример «стандарта», который создается отраслью после многих лет разработки — чтобы все компании знали, какой системе кодирования должны соответствовать их продукты.
Слова «компенсация движения» относятся к способу оценки каждого видеоизображения по сравнению с предыдущим. Проще всего угадать, что последовательные видеоизображения одинаковы. Тогда нам понадобятся только изменения между кадрами — надеюсь, небольшие. Но если камера следит за действием, вся сцена немного сместится и потребует коррекции. Лучше всего посмотреть, в какую сторону движется сцена, и встроить это изменение в следующую сцену. Это КОМПЕНСАЦИЯ ДВИЖЕНИЯ. Фактически, движение может быть разным в разных частях экрана.
Именно такие идеи — о которых легко говорить, но для их совершенствования требуются годы усилий, — делают видеотехнологии и другие технологии возможными и успешными. Инженеры делают свое дело. Я надеюсь, что эти ссылки дают представление о необходимых деталях.
К этой странице обращались как минимум раз с января 2009 года.
Доступность
| 1 | 1.Введение в содержание курса. | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2. Линейные уравнения | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3a. Эквивалентные системы линейных уравнений I: инверсии элементарных операций со строками, эквивалентные по строкам матрицы | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 3b. Эквивалентные системы линейных уравнений II: однородные уравнения, примеры | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 4.Матрицы эшелонов с уменьшенным числом строк | PDF недоступны | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 5. Матрицы эшелонов с сокращенными строками и неоднородные уравнения | PDF недоступны | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 6. Элементарные матрицы, неоднородные уравнения и однородные уравнения Уравнения | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 7. Обратимые матрицы, однородные уравнения Неоднородные уравнения | PDF недоступны | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 8.Векторные пространства | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 9. Элементарные свойства в векторных пространствах. Подпространства | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 10. Подпространства (продолжение), объединяющие множества, линейная независимость, зависимость | PDF недоступен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 11. Основа для векторного пространства04 | 13 | 12. Размерность векторного пространства | PDF недоступен | 14 | 13.Размеры сумм подпространств | PDF недоступен | 15 | 14. Линейные преобразования | PDF недоступен | 16 | 15. Нулевое пространство и пространство диапазонов линейного преобразования04 PDF недоступен | | 17 | 16. Теорема ранговой нулевой размерности. Изоморфизмы между векторными пространствами | PDF недоступен | 18 | 17. Изоморфные векторные пространства, равенство ранга строки и ранга I | PDF недоступен | 19 | 18.Равенство ранга строки и ранга столбца II | PDF недоступен | 20 | 19. Матрица линейного преобразования | PDF недоступен | 21 | 20. Матрица для композиции и Обратный. Преобразование подобия | PDF недоступен | 22 | 21. Линейные функционалы. Двойное пространство. Dual Basis I | PDF недоступен | 23 | 22.Двойная основа II. Subspace Annihilators I | PDF недоступен | 24 | 23. Subspace Annihilators II | PDF недоступен | 25 | 24. Double Dual. Двойной аннигилятор | PDF недоступен | 26 | 25. Транспонирование линейного преобразования. Матрицы линейного преобразования и его транспонирования | PDF недоступен | 27 | 26.Собственные значения и собственные векторы линейных операторов | PDF недоступен | 28 | 27. Диагонализация линейных операторов. Характеристика | PDF недоступен | 29 | 28. Минимальный многочлен | PDF недоступен | 30 | 29. Теорема Кэли-Гамильтона | PDF3 | 32 | 31.Триангулируемость, диагонализация в терминах минимального полинома | PDF недоступен | 33 | 32. Независимые подпространства и операторы проекции | PDF недоступен | 34 | Операторы прямого суммирования | Декомпозиции PDF и | недоступно35 | 34. Операторы прямого суммирования и проекции II | PDF недоступны | 36 | 35.Теорема о первичном разложении и разложение Джордана | PDF недоступен | 37 | 36. Циклические подпространства и аннигиляторы | PDF недоступен | 38 | 37. Циклическая 9000 | 9000 | 9000 | теорема неразложения 9000 39 | 38. Теорема о циклическом разложении II. The Rational Form | PDF недоступен | 40 | 39. Внутренние пространства продукта | PDF недоступен | 41 | 40.Нормы на векторных пространствах. Процедура Грама-Шмидта I | PDF недоступен | 42 | 41. Процедура Грама-Шмидта II. QR-разложение. | PDF недоступен | 43 | 42. Неравенство Бесселя, отступ Парсеваля, наилучшее приближение | PDF недоступен | 44 | 43. Наилучшее приближение: | 44.Ортогональные дополнительные подпространства, ортогональные проекции | PDF недоступен | 46 | 45. Теорема о проекции. Линейные функционалы | PDF недоступен | 47 | 46. Сопряженный оператор | PDF недоступен | 48 | 47. Свойства сопряженной операции. Изоморфизм внутреннего пространства продукта | PDF недоступен | 49 | 48. Leave a Reply
|

 Найдите значение выражения: 6х – 8у, при .
Найдите значение выражения: 6х – 8у, при .






 Весь путь туриста составил 24 км. Какое расстояние турист проехал?
Весь путь туриста составил 24 км. Какое расстояние турист проехал?  Найдите его, если среднее арифметическое равно 15.
Найдите его, если среднее арифметическое равно 15.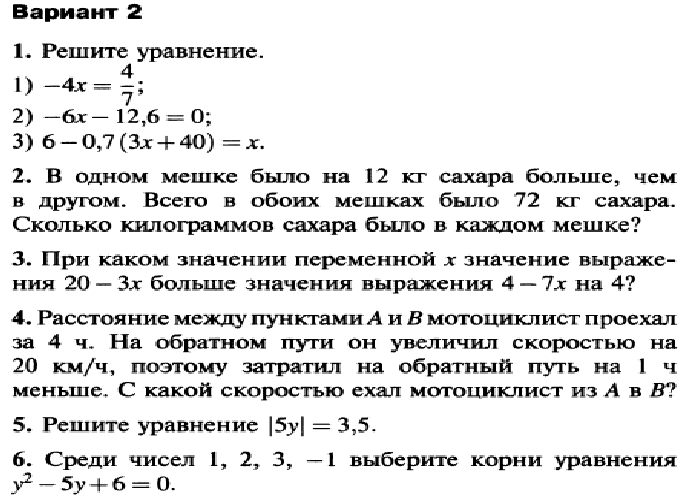 Какое расстояние турист проехал?
Какое расстояние турист проехал?  Найдите его, если среднее арифметическое равно 15.
Найдите его, если среднее арифметическое равно 15. Какое расстояние турист проехал?
Какое расстояние турист проехал?  Найдите его, если среднее арифметическое равно 15.
Найдите его, если среднее арифметическое равно 15. Отчеты округа Хайндс на 2007-2018 гг. Административный календарь округа на 2020-2021 гг. МенюBullyingBid Маршруты автобусовСтаж автобуса 2019-20Местоположения автобусных остановокЦентральный офис / Школа СправочникПроцессы чартерных школГорячая линия по борьбе с жестоким обращением с детьмиПоследствия поведенияУчебная программа для колледжа и диплом о карьереДепартаменты A – ZАварийный случай с сотрудникомСпортал обслуживания сотрудниковРабота несовершеннолетнихПрослушивание по языковой программеПросмотр персонала Политика отбора JBCE School ChoiceLafayetteCheckbook.comLouisiana PASSLPSS платье CodeLPSS Foster Care ProgramMedia RequestLafayette Magnet AcademiesLouisiana Школа FinderMySchoolAppsMySchoolBucksNew ResidentsOrganizational ChartPayrollPublic Информация OfficerPupil Прогрессирование PlanPupil Прогрессирование план поддержки DocumentsPublic отчеты RequestPublic Школа ChoiceRegistrationRisk ManagementSafety Дрель ReportingScholarshipsSchool HoursSpecial диетическими потребностями FormStudent AccidentSchool Библиотеки и СМИ CenterSeclusion & Сдержанность Руководство 2016Student допустимого использования PolicyStudent HandbookStudent счета Meal Возврат FormSupply Списки Билль о правах талантливых учителейКурсы по технологиямTitle IX Процедуры и правилаЗапросы на перевод текстаWisdomwhereWorld Book Online
Отчеты округа Хайндс на 2007-2018 гг. Административный календарь округа на 2020-2021 гг. МенюBullyingBid Маршруты автобусовСтаж автобуса 2019-20Местоположения автобусных остановокЦентральный офис / Школа СправочникПроцессы чартерных школГорячая линия по борьбе с жестоким обращением с детьмиПоследствия поведенияУчебная программа для колледжа и диплом о карьереДепартаменты A – ZАварийный случай с сотрудникомСпортал обслуживания сотрудниковРабота несовершеннолетнихПрослушивание по языковой программеПросмотр персонала Политика отбора JBCE School ChoiceLafayetteCheckbook.comLouisiana PASSLPSS платье CodeLPSS Foster Care ProgramMedia RequestLafayette Magnet AcademiesLouisiana Школа FinderMySchoolAppsMySchoolBucksNew ResidentsOrganizational ChartPayrollPublic Информация OfficerPupil Прогрессирование PlanPupil Прогрессирование план поддержки DocumentsPublic отчеты RequestPublic Школа ChoiceRegistrationRisk ManagementSafety Дрель ReportingScholarshipsSchool HoursSpecial диетическими потребностями FormStudent AccidentSchool Библиотеки и СМИ CenterSeclusion & Сдержанность Руководство 2016Student допустимого использования PolicyStudent HandbookStudent счета Meal Возврат FormSupply Списки Билль о правах талантливых учителейКурсы по технологиямTitle IX Процедуры и правилаЗапросы на перевод текстаWisdomwhereWorld Book Online