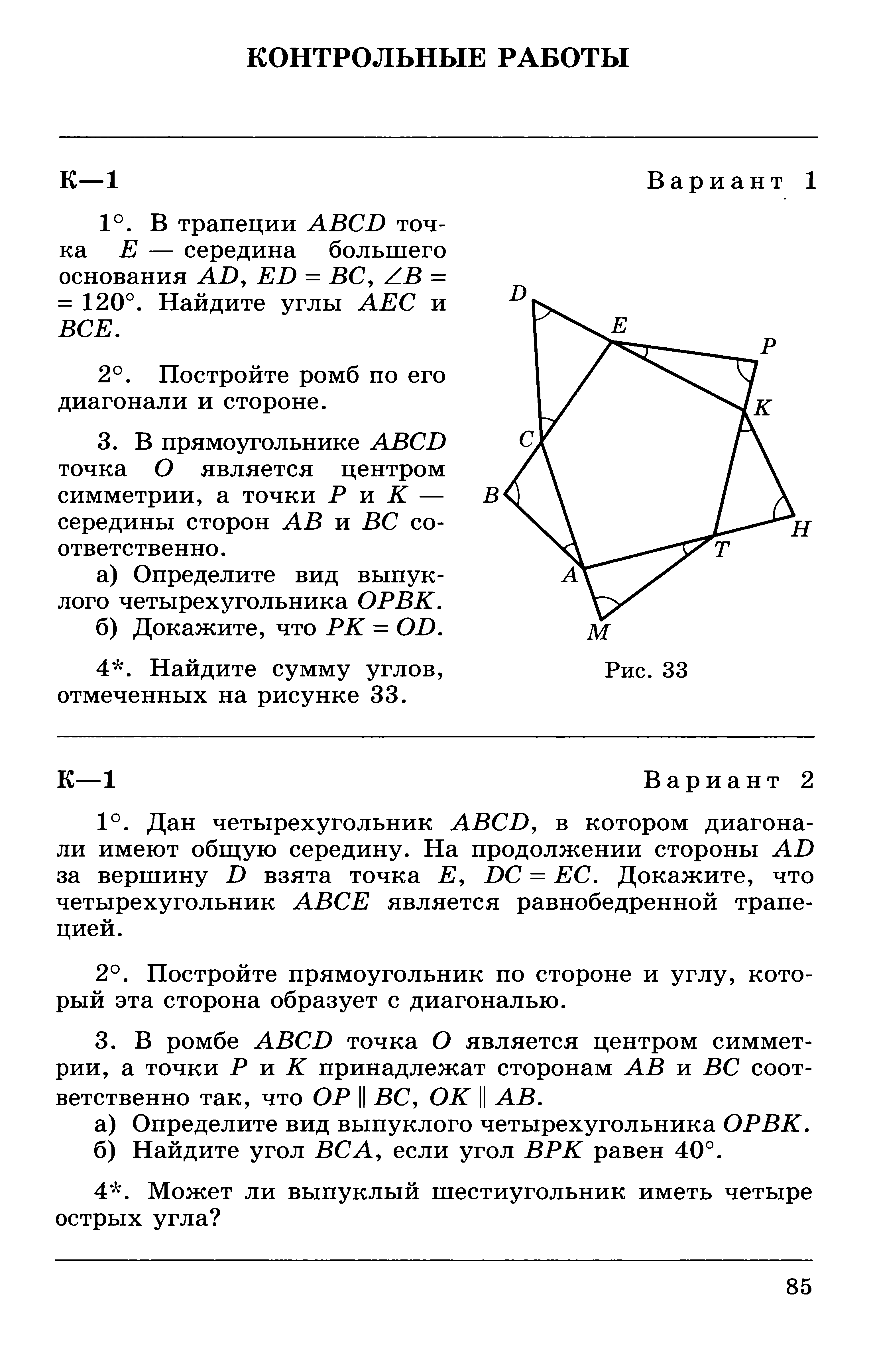
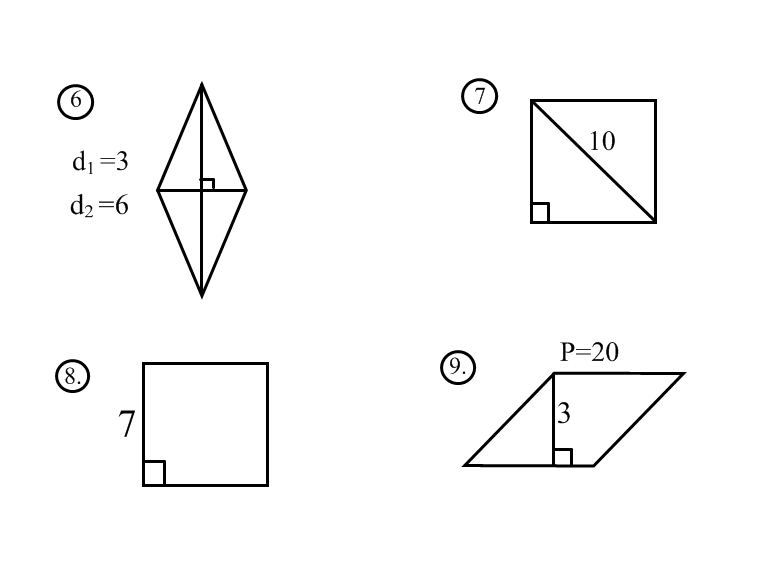
Контрольная работа по геометрии 8 класс «Многоугольники»
Вариант 1
1°. Может ли треугольник иметь углы, равные: а) 45°, 56°, 103°; б) 32°40’, 20°20’, 127°?
2°. Острый угол прямоугольного треугольника равен 59°. Найдите его остальные углы.
3. Определите углы треугольника, если известно, что они относятся как 1:3:5.
4. Найдите сумму углов двенадцатиугольника.
5°. Один из углов параллелограмма равен 54°. Найдите другие его углы.
6°. Периметр параллелограмма равен 92 см. Одна из его сторон на 32 см больше другой. Найдите стороны параллелограмма.
7. Найдите углы параллелограмма, если два его угла относятся как 3:2.
8. Биссектриса тупого угла параллелограмма делит его противоположную сторону в отношении 3:2, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 80 см.
9°.
10°. В ромбе одна из диагоналей равна его стороне. Найдите углы ромба.
11. Углы, образованные стороной ромба с его диагоналями, относятся как 4:5. Найдите углы ромба.
Вариант 2
1°. Может ли треугольник иметь углы, равные: а) 37°, 104°, 49°; б) 57°15’, 27°, 95°45’?
2°. Угол при основании равнобедренного треугольника равен 37°. Найдите его остальные углы.
3. Определите углы прямоугольного треугольника, если известно, что его острые углы относятся
как 3:7.
4. Найдите сумму углов пятнадцатиугольника.
6°. Найдите стороны параллелограмма, если две его стороны относятся как 4:5, а периметр равен 72 см.
7. В параллелограмме ABCD диагональ BD образует со стороной CD угол 34°. Найдите углы, BCD и ADB, если ÐABC=72°.
8. Биссектриса тупого угла параллелограмма делит его противоположную сторону в отношении 2:1, считая от вершины тупого угла. Найдите стороны параллелограмма, если его периметр равен 96 см.
9°. В прямоугольнике диагонали образуют угол 60°. Найдите углы между диагональю прямоугольника и его сторонами.
10°. В ромбе одна из диагоналей равна его стороне. Найдите углы, образованные диагоналями ромба с его сторонами.
11. Углы, образованные стороной ромба с его диагоналями, относятся как 4:5. Найдите углы ромба.
Проверочный тест по геометрии по теме «Многоугольники», (8 класс)
Проверочный тест по теме
«Многоугольники» (8 класс)
I вариант:
Обязательная часть.
А1. Чему равна сумма внутренних углов выпуклого п-угольника?
Варианты ответов:
1) 180∙ (п -2)
2) 180∙ (п +2)
3) 180∙ п
4) 180 : п
Ответ: ___
А2. Чему равна сумма углов( в градусах) выпуклого шестиугольника?
Чему равна сумма углов( в градусах) выпуклого шестиугольника?
Варианты ответов:
1) 360
2) 900
3) 540
4) 720
Ответ: ___
А3. Найдите величину внешнего угла (в градусах) правильного девятиугольника.
Варианты ответов:
1) 40
2) 60
3) 140
4) 90
Ответ: ___
А4. Сумма углов выпуклого многоугольника равна 2520 градусов. Сколько сторон имеет этот многоугольник?
Варианты ответов:
1) 12
2) 16
3) 14
4) 18
Ответ: ___
Дополнительная часть.
В1. Каждый угол выпуклого многоугольника равен 135 градусам. Сколько сторон имеет этот многоугольник?
Каждый угол выпуклого многоугольника равен 135 градусам. Сколько сторон имеет этот многоугольник?
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. В выпуклом четырехугольнике длины сторон относятся как 7:8:9:10, а его периметр равен 68см. Найдите наименьшую сторону четырехугольника.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
II вариант:
Обязательная часть.
А1. Чему равна сумма внешних углов выпуклого п-угольника, взятых по одному при каждой вершине?
Варианты ответов:
1) 180∙ (п -2)
2) 180∙ (п +2)
3) 360
4) 360∙ п
Ответ: ___
А2. Чему равна сумма углов( в градусах) выпуклого пятиугольника?
Варианты ответов:
1) 360
2) 900
3) 540
4) 720
Ответ: ___
А3. Найдите величину внешнего угла (в градусах) правильного восьмиугольника.
Варианты ответов:
1) 45
2) 22,5
3) 135
4) 40
Ответ: ___
А4. Сумма углов выпуклого многоугольника равна 2160 градусов. Сколько сторон имеет этот многоугольник?
Сумма углов выпуклого многоугольника равна 2160 градусов. Сколько сторон имеет этот многоугольник?
Варианты ответов:
1) 12
2) 16
3) 14
4) 18
Ответ: ___
Дополнительная часть.
В1. Каждый угол выпуклого многоугольника равен 140 градусам. Сколько сторон имеет этот многоугольник?
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
В2. В выпуклом пятиугольнике длины сторон относятся как 5:7:8:9:10, а его периметр равен 117см. Найдите наибольшую сторону пятиугольника.
Решение:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:_________
Геометрия 8 класс . Тесты и Тренажеры
Тесты и Тренажеры
ГЕОМЕТРИЯ 8 класс. ТЕСТЫ И ТРЕНАЖЕРЫ
Геометрия 8. Свойства параллелограмма (на чертежах) — 8 заданий …
Геометрия 8. ПАРАЛЛЕЛОГРАММ (на чертежах) — 8 заданий …
Геометрия 8. Многоугольники (теория) — 15 вопросов …
Геометрия 8. Свойства и признаки параллелограмма — 15 вопросов …
Геометрия 8. Виды параллелограммов. Трапеция — 15 вопросов …
Геометрия 8. Средние линии треугольника и трапеции — 15 вопросов …
Геометрия 8. Площади многоугольников — 15 вопросов …
Геометрия 8. ТРАПЕЦИЯ (на чертежах) — 7 заданий …
Геометрия 8. Площадь прямоугольника (на чертежах) — 7 заданий …
Геометрия 8 класс. Площадь трапеции — 10 вопросов …
Геометрия 8 класс. Теорема Пифагора — 10 вопросов …
Геометрия 8 класс. Площади (теория) — 10 вопросов …
Площади (теория) — 10 вопросов …
Геометрия 8. Площадь параллелограмма (на чертежах) — 7 заданий …
Геометрия 8. Площадь треугольника (на чертежах) — 7 заданий …
Геометрия 8. Площадь трапеции (на чертежах) — 7 заданий …
Геометрия 8. Теорема Пифагора (на чертежах) — 7 заданий …
Геометрия 8. Подобные треугольники (на чертежах) — 7 заданий …
Геометрия 8. Определение подобных треугольников — 10 вопросов …
Геометрия 8. Признаки подобия треугольников — 10 вопросов …
Геометрия 8. Применение признаков подобия — 10 вопросов …
Геометрия 8. Соотношения между сторонами и углами — 10 вопросов …
Геометрия 8. Подобные треугольники (теория) — 10 вопросов …
Геометрия 8. Касательная к окружности — 10 вопросов …
Геометрия 8. Центральные и вписанные углы — 10 вопросов …
Центральные и вписанные углы — 10 вопросов …
Геометрия 8. Четыре замечательные точки окружности — 10 вопросов …
Геометрия 8. Вписанные и описанные окружности — 10 вопросов …
Геометрия 8. Окружность (теория) — 10 вопросов …
Геометрия 8. ИТОГОВЫЙ ТЕСТ за год — 16 вопросов …
ГЕОМЕТРИЯ 8 класс. КОНТРОЛЬНЫЕ РАБОТЫ
Рекомендуемые материалы для очного контроля знаний
по предмету «Геометрия 8 класс»:
- Тесты по геометрии. 8 класс. К учебнику Атанасяна Л.С. и др. — Звавич Л.И., Потоскуев Е.В. (2013, 160с.)
- Геометрия. 8 класс. Сборник заданий для тематического и итогового контроля знаний. Ершова А.П. (2013, 128с.)
- Геометрия. 8 класс. Тематические тесты. Мищенко Т.М., Блинков А.Д. (2008, 128с.)
- Геометрия 8 класс. Контрольные измерительные материалы. Рязановский А.Р., Мухин Д.Г. (2014, 96с.)
- Геометрия.
 8 класс. Тематические тесты. Мищенко Т.М. (2011, 176с.)
8 класс. Тематические тесты. Мищенко Т.М. (2011, 176с.) - Геометрия. 8 класс. Итоговая аттестация. Типовые тестовые задания. Глазков Ю.А., Гаиашвили М.Я. (2015, 64с.)
- Дидактические материалы по геометрии. 8 класс. К учебнику Атанасяна Л.С. — Мельникова Н.Б., Захарова Г.А. (2017, 144с.)
- Геометрия. 8 класс. Контрольные работы. Мельникова Н.Б. (2016, 64с.)
- Геометрия. 8 класс. Дидактические материалы. Зив Б.Г., Мейлер В.М. (2016, 159с.)
- Геометрия 8 класс. Тренировочные задания. Дудницын Ю.П., Кронгауз В.А. (2018, 176с.)
- Геометрия. 8 класс. Тематические тесты. Мищенко Т.М. (2010, 96с.)
- Геометрия. Самостоятельные и контрольные работы: 7-9 классы. Иченская М.А. (2017, 144с.)
- Геометрия. 8 класс. Дидактические материалы. Мерзляк А.Г., Полонский В.Б. и др. (2018, 112с.)
Программа обучения по геометрии в 8 классе (основные темы)
Глава I. Четырехугольники
Многоугольники. Параллелограмм и трапеция. Прямоугольник. Ромб. Квадрат. Решение задач
Параллелограмм и трапеция. Прямоугольник. Ромб. Квадрат. Решение задач
Глава II. Площадь
Площадь многоугольника. Площади параллелограмма, треугольника и трапеции. Теорема Пифагора. Решение задач
Глава III. Подобные треугольники
Определение подобных треугольников. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Соотношения между сторонами и углами прямоугольного треугольника.
Глава IV. Окружность
Касательная к окружности. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Решение задач
Вернуться
| 1. |
Ломаная
Сложность: лёгкое | 1 |
2.
|
Вершины и звенья ломаной
Сложность: лёгкое |
1 |
| 3. |
Замкнутая ломаная
Сложность: лёгкое |
|
4.
|
Бесконечная линия
Сложность: лёгкое |
1 |
| 5. |
Линия с самопересечением
Сложность: лёгкое |
1 |
6.
|
Число сторон, вершин и углов многоугольника
Сложность: лёгкое |
2 |
| 7. |
Диагонали многоугольника
Сложность: лёгкое |
2 |
8.
|
Сумма внутренних углов многоугольника
Сложность: лёгкое |
2 |
| 9. |
Сумма углов многоугольника
Сложность: среднее |
3 |
10.
|
Угол правильного n-угольника
Сложность: среднее |
3 |
| 11. |
Количество сторон или вершин многоугольника
Сложность: среднее |
3 |
12.
|
Звенья ломаной
Сложность: среднее |
2 |
| 13. |
Длины звеньев замкнутой ломаной
Сложность: сложное |
3 |
ГЕОМЕТРИЯ
Урок № 1. |
Контрольная работа №1 по теме «Четырехугольники» V-вариант. 1) Периметр параллелограмма ABCD равен 50 см, сторона AB равна 10 см. Найдите стороны параллелограмма. 2) Найдите углы B и D трапеции ABCD с основаниями AD и ВС, если ∠А=360, ∠С=1170.
3) Найдите периметр квадрата АСВД, если сторона АВ=4 см. 4) Найдите периметр ромба АВСД, в котором ∠В=600, АС=10,5 см. 5) Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.
| Контрольная работа №1 по теме «Четырехугольники» VI-вариант. 1) Периметр параллелограмма ABCD равен 70 см, сторона BС равна 15см. Найдите стороны параллелограмма. B 15см C A D 2) Найдите углы B и D трапеции ABCD с основаниями AD и ВС, если ∠А= 460, ∠С=1240. B 6см C 3) Найдите периметр квадрата АСВД, если сторона АВ=6 см. А D 4) Найдите периметр ромба АВСД, в котором ∠А=600, ВD=20,5 см. 5) Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.
|
Полигоны
Многоугольник — это плоская форма с прямыми сторонами.
Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).
| Многоугольник (прямые стороны) | Не Полигон (с изгибом) | Не Полигон (открытый, не закрытый) |
Многоугольник происходит от греческого языка. Poly- означает «много», а -угольник означает «угол».
Poly- означает «много», а -угольник означает «угол».
Типы полигонов
Обычное или нестандартное
Правильный многоугольник имеет все углы и все стороны равны, в противном случае он неправильный
| Обычный | Нерегулярное |
вогнутый или выпуклый
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.
Если какой-либо внутренний угол больше 180 °, то многоугольник будет вогнутым . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклая | вогнутая |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает себя.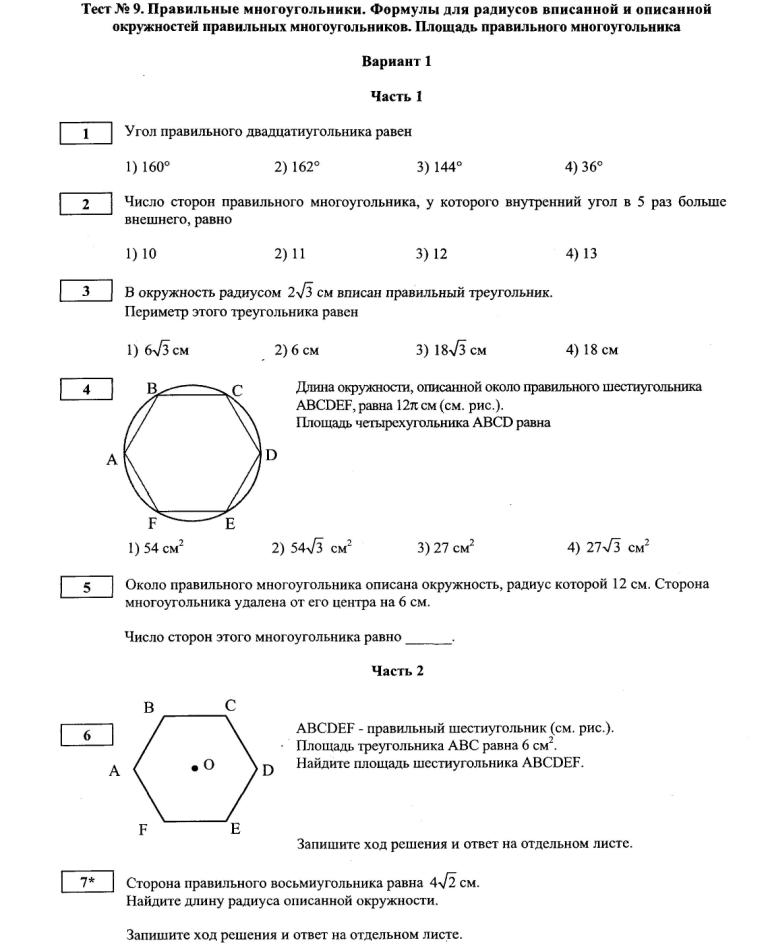 Сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
Сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
| Простой многоугольник (это Пентагон) | Сложный многоугольник (также Пентагон) |
Другие примеры
| Шестигранник неправильной формы | Вогнутый восьмиугольник | Сложный многоугольник («звездообразный многоугольник», в данном случае пентаграмма) |
Играй с ними!
Попробуйте интерактивные многоугольники… сделать их правильными, вогнутыми или сложными.
Имена полигонов
С помощью этого метода можно делать имена:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник — это гексаконтадигон | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
НО, для многоугольников с 13 и более сторонами нормально (и проще) написать « 13-угольник », « 14-угольник » .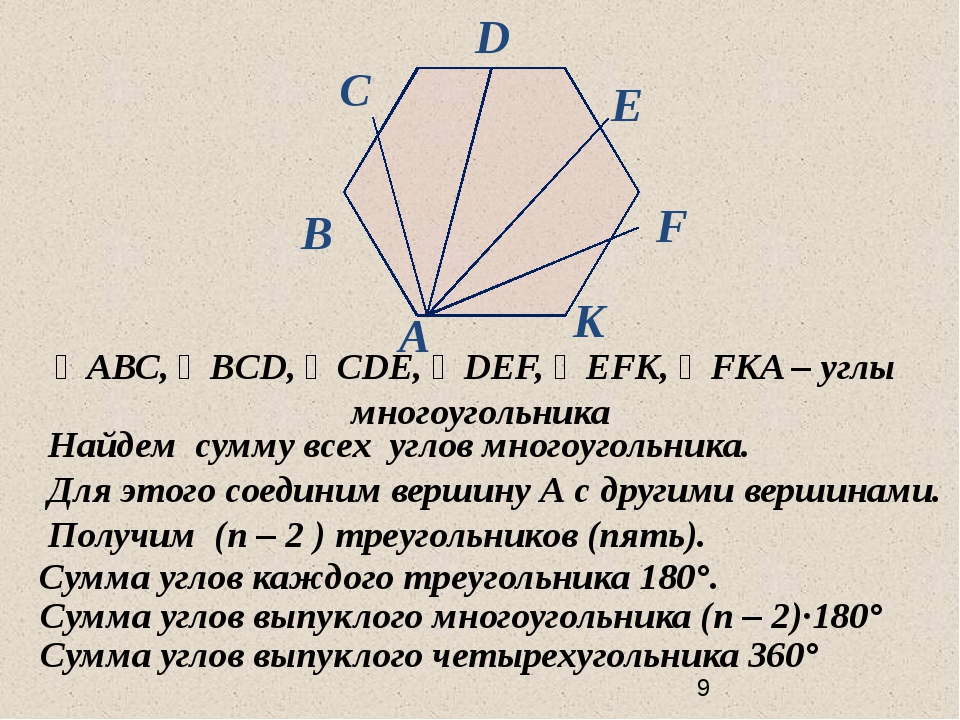 .. « 100-угольник» и т. Д.
.. « 100-угольник» и т. Д.
Вспоминая
Четырехсторонний (4 стороны)
A Quad Велосипед с 4 колесами
Пентагон (5 сторон)
« Пентагон » в Вашингтоне, округ Колумбия, имеет 5 сторон
Шестигранник (6 сторон)
H oneycomb имеет H эксагонов
Септагон (7 сторон)
Think Sept agon — это «Seven- agon»
Восьмиугольник (8 сторон)
Гной Octo имеет 8 щупалец
Nonagon (9 сторон)
Think Non agon is a «Nine- agon»
Десятиугольник (10 сторон)
Think Dec agon имеет 10 сторон,
точно так же, как наша Dec imal система имеет 10 цифр
Полигонов | Ресурсы Wyzant
Прежде чем мы слишком увлечемся волнением
четырехугольники, давайте узнаем названия и основные свойства
разных полигонов . Многоугольники — это двумерные замкнутые плоские формы.
состоит из конечного числа прямых сторон, пересекающихся в точках, называемых вершинами.
Треугольники, которые
мы уже узнали, что это один из типов многоугольника. В этом разделе мы будем
начнем изучать четырехугольники, называемые четырехугольниками . Здесь очень много
однако больше многоугольников, чем просто треугольников и четырехугольников. В этой секции,
мы также узнаем имена и свойства некоторых из наиболее распространенных полигонов, чтобы помочь
Начнем с изучения четырехугольников.
Многоугольники — это двумерные замкнутые плоские формы.
состоит из конечного числа прямых сторон, пересекающихся в точках, называемых вершинами.
Треугольники, которые
мы уже узнали, что это один из типов многоугольника. В этом разделе мы будем
начнем изучать четырехугольники, называемые четырехугольниками . Здесь очень много
однако больше многоугольников, чем просто треугольников и четырехугольников. В этой секции,
мы также узнаем имена и свойства некоторых из наиболее распространенных полигонов, чтобы помочь
Начнем с изучения четырехугольников.
Есть несколько способов классификации полигонов. Один из способов их классифицировать — рассмотреть
их меры углов и длины сторон. Если углы и стороны многоугольника равны
равно, то многоугольник называется правильным многоугольником . Если меры
углы или длина сторон многоугольника различаются, тогда многоугольник называется неправильным многоугольник .
У фигуры слева равные стороны и углы, поэтому она представляет собой правильный многоугольник.поскольку форма справа имеет разные длины сторон и углы, она неправильная.
Именование полигонов
Существует бесчисленное множество полигонов. Потому что все они различаются по количеству их сторон, это приводит к разным угловым размерам в их вершинах. Ниже перечислены названия и количество сторон некоторых многоугольников. «Внутренний угол Мера « столбца таблицы применяется только к правильным многоугольникам, в которых все внутренние углы равны.
Обратите внимание, за исключением треугольника и четырехугольника, все имена многоугольников
заканчиваться на «гон». Что отличает правильные имена многоугольников друг от друга, так это их
префиксы, которые говорят о количестве сторон, которые у них есть. Например, префикс
ведь слово «шестиугольник» — это «гекса», что по сути означает «шесть». Однако, как мы
двигайтесь вниз по нашему списку, и названия полигонов становятся довольно запутанными, нам нужен
более эффективный способ именования полигонов.Один из способов — не вызывать многоугольник по его
настоящее имя, просто указав количество сторон и добавив «-угольник»
в конце. Например, вместо того, чтобы называть 18-сторонний многоугольник восьмиугольником,
мы можем просто назвать это 18-угольником. Таким образом, многоугольник со сторонами n просто
позвонил по номеру n -gon .
Например, префикс
ведь слово «шестиугольник» — это «гекса», что по сути означает «шесть». Однако, как мы
двигайтесь вниз по нашему списку, и названия полигонов становятся довольно запутанными, нам нужен
более эффективный способ именования полигонов.Один из способов — не вызывать многоугольник по его
настоящее имя, просто указав количество сторон и добавив «-угольник»
в конце. Например, вместо того, чтобы называть 18-сторонний многоугольник восьмиугольником,
мы можем просто назвать это 18-угольником. Таким образом, многоугольник со сторонами n просто
позвонил по номеру n -gon .
Мы не будем изучать все полигоны, перечисленные в таблице, но у них есть общие свойства, на которые стоит обратить внимание.Давайте теперь рассмотрим одно из этих свойств.
Теорема о сумме внутренних углов многоугольника
Сумма внутренних углов n-стороннего выпуклого многоугольника составляет
Как видно из приведенного выше утверждения, многоугольник должен быть выпуклым , что не является
термин, который мы еще не изучили. Это означает, что многоугольник не может иметь
углы, которые указывают внутрь.Если многоугольник имеет угол, на который указывает, он называется вогнутый , и эта теорема не применяется. Другими словами, весь интерьер
углы многоугольника должны иметь размер не более 180 ° для
эта теорема работает.
Это означает, что многоугольник не может иметь
углы, которые указывают внутрь.Если многоугольник имеет угол, на который указывает, он называется вогнутый , и эта теорема не применяется. Другими словами, весь интерьер
углы многоугольника должны иметь размер не более 180 ° для
эта теорема работает.
Теорема о сумме внутренних углов многоугольника применима к многоугольнику слева (поскольку это выпуклый многоугольник), но не для того, что справа, потому что выделенный угол указывает в.Этот угол имеет размер больше 180 °.
Теперь давайте убедимся, что эта теорема верна для многоугольника, над которым мы много работали.
с: треугольниками. Напомним, что
Теорема суммы углов треугольника, внутренние углы нашего треугольника должны быть равны
до 180 ° . Давайте проверим это с помощью суммы внутренних углов многоугольника .
Теорема .
Давайте проверим это с помощью суммы внутренних углов многоугольника .
Теорема .
Поскольку у треугольников три стороны, мы знаем, что n = 3 .Итак, давайте подключим это в наше уравнение.
Мы видим, что теорема о сумме внутренних углов многоугольника согласована с треугольником Теорема мы уже изучили.
Теперь давайте выясним, какова сумма внутренних углов четырехугольника.Четырехугольники имеют четыре стороны, что означает, что n = 4 для четырехугольника. Давайте подключим это к нашему уравнению.
По этой теореме мы видим, что все четырехугольники имеют сумму внутренних углов 360 °.
Разрушение теоремы о сумме внутренних углов многоугольника
Вы можете спросить себя, почему работает теорема о сумме внутренних углов многоугольника , или если мы можем использовать его с любым n -угольник .Давайте разберемся, что такое уравнение означает для того, чтобы убедиться, что это работает.
По сути, когда мы используем это уравнение, мы разбиваем многоугольники на треугольники, а затем умножаем на 180 , потому что это сумма углов треугольника. Мы должны следовать двухэтапному процессу, чтобы разделить А вот многоугольник в треугольники. Этот процесс указан ниже:
(1) Выберите вершину, из которой нужно провести прямые линии, а затем
(2) проведите прямую линию от выбранной вершины до других вершин
многоугольник (который еще не соединен с выбранной вершиной отрезком прямой).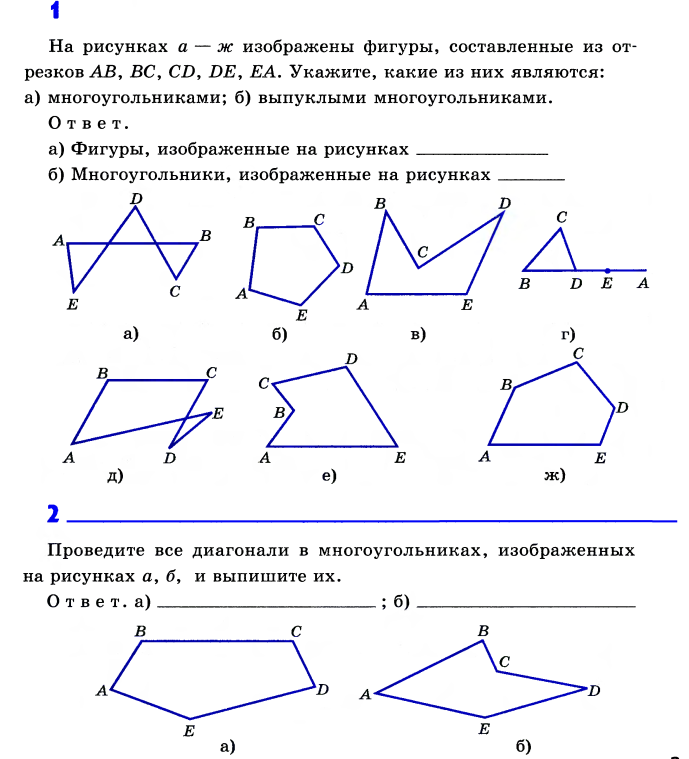
Давайте попробуем это с четырехугольником ниже, поскольку мы уже знаем, что его внутренняя часть углы будут составлять 360 ° .
Выберем точку A , из которой будем рисовать линии. Поскольку уже есть строка сегменты, которые соединяют точку A с точками B и D , нам нужно только провести линию до точки C .
Обратите внимание, что мы создали два треугольника. Сохранение теоремы о сумме углов треугольника помня, мы знаем, что каждый треугольник должен иметь углы, сумма которых равна 180 ° .
Таким образом, умножаем эту меру на два (так как треугольников два), и действительно,
сумма углов четырехугольника составляет 360 ° .
Для любого полигона мы всегда сможем создать на два треугольника меньше. чем количество сторон.Следовательно, для любого n -угольник мы можем создайте из него треугольники (n-2) . Умножаем на 180 на так как это сумма мер треугольника. Обширная таблица различных многоугольники и сумма их внутренних углов показаны ниже.
Свойства четырехугольника
Давайте попробуем несколько упражнений, в которых используется то свойство, что внутренние углы четырехугольников сложить до 360 ° .
Упражнение 1
Определите значение x на рисунке ниже.
Решение:
Мы знаем, что сумма внутренних углов четырехугольника JESK это 360 ° , поэтому мы имеем
Подстановка угловых мер, которые нам дали, дает
.
Теперь мы просто упростим наше уравнение и решим для x .
Итак, получаем x = 9 .
Упражнение 2
Найдите значение z на рисунке ниже.
Решение:
Давайте начнем это упражнение с определения значения решаемых переменных.
с предоставленной информацией.Похоже, что мы не сможем
чтобы определить значение z , пока мы не выясним значения w , x и y .
Мы определяем, что w равно 78 ° , потому что это вертикальный угол к предусмотренному углу 78 ° .
Далее мы можем определить значение x , поскольку оно является дополнительным к угол 64 ° . У нас
Итак, мы выяснили, что x = 116 .
Теперь у нас есть три из четырех углов четырехугольника KLNM .Наш новый Рисунок (с включенными степенями переменных, которые мы решили для) показан ниже.
Мы можем решить относительно y , так как мы знаем, что внутренние углы четырехугольника
должно быть в сумме 360 ° . У нас
У нас
Итак, значение y равно 84 .
Поскольку этот угол является вертикальным по отношению к z , мы заключаем, что размер z также должен быть 84 .
Основная геометрия: многоугольники Учебное пособие
Многоугольники
Многоугольник — это любая замкнутая фигура с тремя или более прямыми сторонами . «Закрыто» означает, что в нем нет зияющих отверстий и все стороны соединяются вместе.
Это многоугольники:
Это не многоугольники:
Первая фигура — это линия, которая определенно не является фигурой с более чем тремя сторонами. Извини, брат, тебя нет. У следующей формы более трех сторон, но не все они соединяются. Плохие новости, чувак, тебя тоже нет. Правильно, круг — это тоже не многоугольник . Хотя это замкнутая фигура, очень сложно подсчитать количество сторон круга, потому что у него их нет. Окончательная форма замкнута, и у нее более трех сторон, но две из них изогнуты.Это не прямые линии, так что еще раз извините, Чарли.
Плохие новости, чувак, тебя тоже нет. Правильно, круг — это тоже не многоугольник . Хотя это замкнутая фигура, очень сложно подсчитать количество сторон круга, потому что у него их нет. Окончательная форма замкнута, и у нее более трех сторон, но две из них изогнуты.Это не прямые линии, так что еще раз извините, Чарли.
Названия некоторых общих многоугольников
| Число сторон | Число углов | Название |
| 3 | 3 | Треугольник |
| 4 | Четырехугольник | |
| 5 | 5 | Пятиугольник |
| 6 | 6 | Шестигранник |
| 7 | 7 | Септагон (или шестиугольник) |
| 8 | 8 | Восьмиугольник |
| 9 | 9 | Nonagon |
| 10 | 10 | Decagon |
| 12 | 12 | Dodecagon |
Важный словарь
Важный словарь многоугольников условия, которые идут с ними. Вам нужно будет их запомнить, но не волнуйтесь, они не так уж и сложны.
Вам нужно будет их запомнить, но не волнуйтесь, они не так уж и сложны.
- Угол : форма, образующаяся, когда два луча встречаются в общей точке. АКА «уголок».
- Вершина : точка, где встречаются два луча; угловая точка многоугольника. Множественное число вершин — это вершины.
- Сторона : прямая кромка многоугольника.
- Выпуклый многоугольник: многоугольник, внутренний угол которого не превышает 180 °.
- Вогнутый многоугольник: многоугольник с хотя бы одним внутренним углом больше 180 °.
- Равноугольный : фигура, на которой все углы равны по размеру.
- Равносторонний : фигура, все стороны которой равны по длине.
- Правильный многоугольник : равносторонний равносторонний многоугольник.
Многоугольники могут быть выпуклыми или вогнутыми. Мы привыкли видеть чаще всего выпуклые многоугольники: квадраты, треугольники, пятиугольники и т.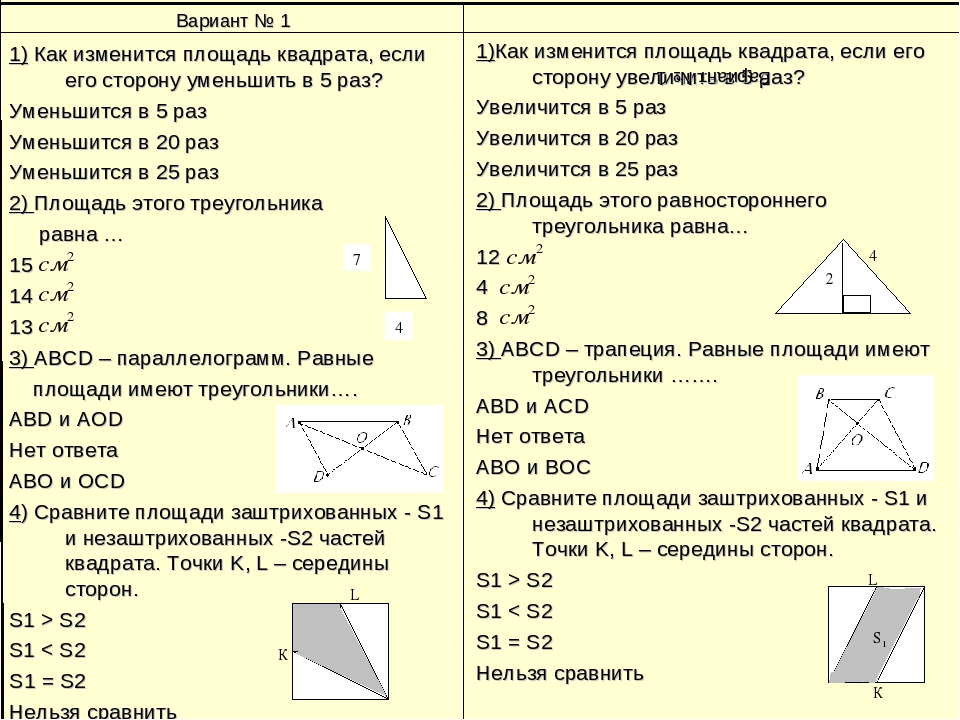 Д.Все вершины выпуклых многоугольников направлены наружу от центра. Официально каждый внутренний угол выпуклого многоугольника меньше 180 °, и это то, что указывает на все вершины. Это примеры выпуклых многоугольников.
Д.Все вершины выпуклых многоугольников направлены наружу от центра. Официально каждый внутренний угол выпуклого многоугольника меньше 180 °, и это то, что указывает на все вершины. Это примеры выпуклых многоугольников.
Если мы проведем линию через любой из этих выпуклых многоугольников, она будет пересекать только двух сторон многоугольника.
Вогнутые многоугольники имеют некоторые углы, которые обращены к центру, как пещера, для мошенников… вогнутая… понятно? Пример вогнутого многоугольника — пятиконечная звезда.Обратите внимание на то, что некоторые углы направлены от центра, как точки звезды, а некоторые — к центру, как углы между точками звезды. Вогнутый многоугольник имеет один или несколько внутренних углов больше 180 °. Вот несколько примеров вогнутых многоугольников.
Если мы проведем линию через любой из этих вогнутых многоугольников, возможно, что линия может пересекать более чем две стороны.
Равносторонние и равносторонние
Некоторые полигоны любят играть честно. Они следят за тем, чтобы все их углы были одинаковыми, чтобы ни один угол не был больше или меньше любого другого. Такие многоугольники называются равноугольными. Прямоугольники равноугольные, потому что все четыре угла равны 90 °. Чтобы многоугольник был равноугольным, стороны не должны быть равной длины.
Они следят за тем, чтобы все их углы были одинаковыми, чтобы ни один угол не был больше или меньше любого другого. Такие многоугольники называются равноугольными. Прямоугольники равноугольные, потому что все четыре угла равны 90 °. Чтобы многоугольник был равноугольным, стороны не должны быть равной длины.
Некоторые многоугольники , например , имеют все стороны одинаковой длины, они называются равносторонними. Ромб — это пример равностороннего многоугольника, потому что у него четыре равные стороны, хотя углы не равны.
А еще есть многоугольники, которые действительно хороши и хотят, чтобы все их стороны были равны и все их углы были равны. Это один супер-красивый, равносторонний и равносторонний многоугольник. Он такой красивый, что получил собственное название: это правильный многоугольник.
Правильные многоугольники
Вы, наверное, знакомы с этими формами. Все их стороны имеют одинаковую длину и все углы одинаковой меры.
Это не регулярные
Основание и высота многоугольника
- Основание : нижняя сторона многоугольника.

 Тема. Четырехугольники
Тема. Четырехугольники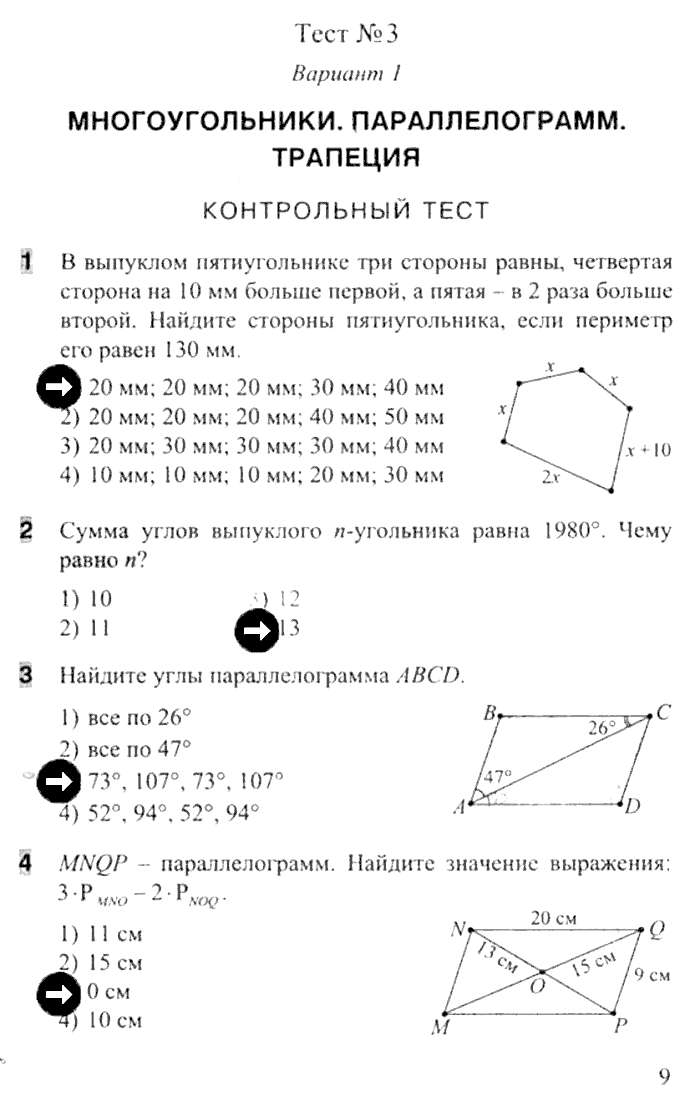 Тема. Градусная мера дуги. Вписанный угол
Тема. Градусная мера дуги. Вписанный угол Тема. Перпендикуляр и наклонная. Решение задач
Тема. Перпендикуляр и наклонная. Решение задач Тема. Синус, косинус и тангенс острого угла прямоугольного треугольника
Тема. Синус, косинус и тангенс острого угла прямоугольного треугольника

 ..
.. Д.
Д.