Геометрия 11 класс контрольная работа векторы: Контрольные работы по геометрии 11 класс Атанасян Л.С.

Контрольные работы по геометрии 10-11 класс к учебнику Л.С.Атанасяна и др.

Учебно-методический комплект

Ю.П, Дудницын ВОЛ, Кронгауз

Контрольные работы по геометрии

К учебнику Лос. Атанасяна,

 В.Ф. Бутузова, с.Б. Кадомцева и др.

 «Геометрия, 10—11»  (М.: Просвещение)

 класс

Рекомендовано

Российской Академией Образования

ИзДание второе, стереотипное

Издательство «ЭКЗАМЕН» москвА 2009

уды-

ББК 74.262.22 я72 дм

Изображение учебного издания «Геометрия, 10—1 1: учеб. для общеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, СБ. Кадомпев и др.]. — М.: Просвещение» приведено на обложке даннот издапИЯ исключительно в качестве иллюстративного материала (ст. 1274

          п.

I части четвертой Гражданского кодекса Российской Федерации).

Дудницын, ЮЛ.

дм Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна, ВО. Бутузова, СБ. Кадомцева и др. «Гес метрия, 10—1 1» / Ю.П. Дудницын, В.Л. Кронгауз. 2-е изд., стереотип. — М.: Издательство «Экзамен», 200. 62, [2] с. (Серия «Учебно-методический комплект»)

(SB.N 978-5-37742207-7

Пособие предназначено учителям математики старших классов. которые ведут преподавание курса геометрии по учебнику Л.С. Атанасяна «Геометрия, 10—1 1» издательства «Просвещение».

В пособии приведены тематичестй план и комплект контрольны.х работ на весь учебный год. Все работы даются в четырех равноценных вариантах, к которым приведены отвеян.

В разделе «К учителю» даны подробные рекомендации по оцениванию качества выполнения контрольных работ и по эффективному использованию материалов раздела «Задания к темамчесшм зачетам», включающего основные теоремы курса и зада^ки к (№новным темам курса.

ББК 74.262.22 „72

Формат 84х108.32. Гарнитура «Таймс». Бумага газетная.

Уч.-изд. л. 1,36. Усл. веч. л. 3,36. Тираж 7 000 экз. Заказ № 6148<2)

ISBN 978-5-37′-0220′-7 С щ•дницын. Ю.П., Кронгауз В.Л., 2009

С Издательство «ЭКЗАМЕН», 2009

 К учителю

1. Материалы к учебнику «Геометрия 10 — 11»

Л.С. Атанасяна и др

Примерное поурочное планирование

Тематика контрольных работ

Контрольная работа № 1

Контрольная работа № 2. Контрольная работа № З

Контрольная работа № 4. Контрольная работа № 5. Контрольная работа № 6.

Ответы к контрольным работам

П. Задания к тематическим зачетам

1.         Вопросы (формулировки определений)…………………..,… З

2.         Теоремы (формулировки и краткие доказательства) З.

Задачи

1. Аксиомы стереометрии ……………………. ..

2. Параллельность прямых в пространстве З. Параллельность прямой и плоскости

4.     Параллельность плоскостей………………….. …е… .

5.     Перпендикуляр и наклонные

6.     Свойства точки, равноудаленной от вершин многоугольника Содержание

7.     Перпендикулярность прямой и плоскости ……………….46

8.     Свойства точки, равноудаленной от сторон многоугольника………….,………… . .

9.     Угол межш прямой и плоскостью…………………………..5О

10. Перпендикулярность плоскостей52

1 1. Угол между плоскостями54

12. Декартовы координаты в пространстве…………………,56 •

      Ответы……………………………… . . .           . . ……………………..57

Уважаемые коллеги!

Предлагаемое пособие содержит материалы, которые, как показывает многолетний опыт, целесообразно иметь учителю, ведущему обучение десятиклассников по учебнику «Геометрия 10 — 1 1» Л. С. Атанасяна и др. Прежде всего — это поурочное планирование изучения материала, соответствующее учебному плану, по которому работает конкретная школа. Вторая проблема, возникающая перед молодыми учителями, — это осуществление контроля за уровнем знаний десятиклассников. Поэтому мы предлагаем в пособии комплект контрольных работ на весь учебный год. Их содержание полностью соответствует требованиям обязательной подготовки десятиклассников, которые предусмотрены в образовательных стандартах по математике. В контрольных работах реализуются научная и методическая концепции указанного выше учебника.

Авторы пособия предлагают два варианта поурочного планирования к учебнику. Первый — «Вариант А». Он рассчитан на 2 учебных часа в неделю. Его использует большинство средних школ с учебным планом, предусматривающим 5 или 6 учебных часов в неделю на изучение курсов крометрии и алгебры и начал анализа. Второй — «Вариант Б». Он предназначен для тех школ, в которых предусматривается изучение курса математики на базовом уровне (при последовательном рассмотрении разделов из .

учебников

«Геометрия 10 — 1» и «Алгебра и начала анализа 10 — I и выделяются 3 или 4 часа в неделю. В пособии мы предлагаем «Вариант Б», рассчитанный на 1,5 часа в неделю.

После поурочного планирования в материалах к каждому учебнику приводится таблица с указанием тематики контрольных работ и временем, выделяемым на проведение каждой из них.

Далее предлагается полный комплект контрольных работ, в котором каждая работа приведена в 4 равноценных по трудности вариантах.

Первая часть каждой работы, отмеченная значком А, содержит материал, соответствующий базовому уровню подготовки десятиклассников по геометрии. Все ученики должны уметь верно выполнять задания этой части. Здесь проверяется усвоение минимального содержания определенной темы, без которого ученик не может успешно усваивать следующие разделы курса геометрии. Например, в первых заданиях контрольных работ № 1 и № 2 проверяется умение десятиклассников правильно изображать простейшие фигуры в пространстве, отражать на чертеже их взаимосвязи, указанные в условии задачи.

Вторым шагом выполнения этих заданий является установление соответствующих свойств элементов построенного чертежа и обоснование (доказательство) их логическим путем, ссылкой на нужные элементы теории.

Вторая часть контрольной работ обозначена значком Она состоит из более сложных заданий, выполнение их проводится; как правило, в 2 — 4 этапа. Подобные задания подробно рассматриваются в учебнике и отрабатываются в классе под руководством учителя. Для их выполнения не требуется дополнительных знаний, выходящих за пределы программы. Этот материал должен быть хорошо знаком десятиклассникам.

6

учителю

Последняя часть контрольной работы выделена значком • . Эти задания позволяют ученикам проявить высокий уровень знаний, логического мышления, интерес к предмету, способность применить знания в нестандартной ситуации.

Однако и эти задания не предполагают знания какихлибо дополнительных разделов геометрии. Они так же, как и все wra. JIbHbre, проверяют уровень владения программным материалом.

Офащаем внимание учителя на большое число заданий во многих контрольных работах. Десятиклассники успешно справляются с ними, если учитель не увлекаися требованиями шасьменного оформления всех рассуждений, т. е. не требует так «сочинений на геоме№ическую тему». Навыки грамотного, последоварльного обоснования соответствующих выводов форирукпся постепенно тишь к началу•или середине обучения геометрии в 1 классе. В первом полугодии обучения в 10 классе основное внимание необходимо уделить формированию умения выполнять грамотно чертеж, который условию задачи и является наглядным изображением соотношений между фигурами. Наприер, в контрольной рботе № 1 при вьшолнении заряия 2 ученик дояжен .№ть ответ (оиосложный) и бтательно изобразить требуемую конфигурацию. Только в этом случае задание считвтся выполненным полностью.

Следует обратить внимание и на то, что требования, связанные с Основаниями (доказательствами) тех или иных фактов, если они выполняются в несколько этапов, вынесены в ряде контрольных работ в самый конец, т.

е. в часть, отмеченную . Этим авторы еще раз подчеркивают, что наличие умения проводить рассуждения дедуктивным методом свидетельствует о высоком уровне развития десятиклассника, о высоком качестве его знатй.

При верном выполнении всех заданий контрольной работы выставляем отметку «5». Если десятиклассники успешно справились со всеми заданиями первой и второй частей работы, а к выполнению последней не приступали или допустили ошибку, которая не привела к принципиально неверному решению, выставляем отметку «4». За безошибочное выполнение всех заданий первой части контрольной работы, даже при наличии ошибок в решениях заданий второй и третьей частей или отсутствии этих решений, выставляем отметку «З» или «зачет», которые свидетельствуют, что обязательное минимальное содержание данной темы курса десятиклассник усвоил. Еще раз подчеркнем, что любая из перечисленных отметок может быть выставлена при условии верного выполнения всех заданий первой части работы.

Десятиклассникам, которые допускают ошибки при выполнении заданий первой части работы и не получают отметку «3» или «зачет», учитель может дать возможность после выполнения работы над допущенными ошибками вторично выполнить задание, аналогичное тому, где допущена ошибка. Для этого удобно использовать соответствующие задания других трех вариантов контрольной работы. При таком подходе ученики более ответственно относятся к выполнению работы над ошибками, и она становится более целенаправленной.

В классах, где изучается предмет «Математика» на базовом уровне и выделено в .неделю З — 4 учебных часа, целесообразно сократить объем большинства контрольных работ, исключив задание, отмеченное знаком • .

Предложенная Вам система выставления отметок за выполнение контрольной работы значительно повышает информативность каждой отметки. Они более точно и определенно характеризуют уровень усвоения основных порций материала по теме каждым учеником. Содержание контрольных работ и

8

учителю

система оценивания их выполнения десятиклассниками обеспечивают благоприятную в психологическом отношении обстаноЁку во время проведения работ.

Заключительная часть пособия «Задания к тематическим зачетам» адресована учителям,. которые в своей практике успешно применяют систему зачетов в дополнение к контрольным работам для поэтапного определения уровня знаний школьников, интенсификации и повышения эффективности их занятий. Эта часть . пособия содержит три раздела: «Вопросы», «Теоремы» и «Задачи». Эти материалы используются для составления индивидуальных карточек к зачетам по основным темам программы. Первые два раздела содержат названия отдельных элементов теоретического материала. Первая группа «Вопросы (формулировки, примеры предлагается ученику, чтобы он только сформулировал соответствующее определение, свойство или привел конкретный пример, их иллюстрирующий. Вторая . группа «Теоремы» содержит перечень основных теорем, содержащихся в курсе Задание из этой группы предлагается десятикласснику для того, чтобы он воспроизвел необходимый чертеж и полное доказательство этого утверждения. Третий раздел содержит 104 задачи, которые сгруппированы по двенадцати основным темам курса.

Используя предложенные материалы, учитель имеет возможность подготовить для проведения зачета по конкретной теме необходимое количество индивищальных карточек, на которых записаны задания для каждого ученика. Форму проведения зачета (устно или письменно) определяет в каждом конкретном случае учитель. Видимо, и место зачетов в учебном процессе может быть различным в зависимости от объема темы, ее значимости во всем курсе геометрии. Многие учите— ля охотно используют зачеты, так как с -их помощью проверя-

ется формальное усвоение теории: знание формулировок определений, теорем и свойств, умение воспроизводить несложные доказательства теорем. Однако напоминаем, что в настоящее время по-прежнему основной формой контроля за уровнем знаний десятиклассников в течение всего учебного года является проведение тематических и итоговых контрольных работ.

Авторы

Геометрия 11 Атанасян Контрольные работы с ответами

Геометрия 11 Атанасян Контрольные работы с ответами. Ориентировано на учебник «Геометрия. 10–11 классы» авторов Л. С. Атанасяна и др., базовый уровень (Просвещение). Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : учеб. пособие для общеобразоват. организаций : базовый уровень / М. А. Иченская» использованы в учебных целях. Ответы адресованы родителям.

При постоянном использовании контрольных работ по геометрии в 10 классе рекомендуем купить книгу: Мира Иченская: Геометрия. 10-11 классы. Контрольные работы. Базовый уровень, в которой кроме контрольных работ есть карточки к итоговым зачётам по курсу геометрии 10–11 классов.

---

 

Геометрия 11 класс (УМК Атанасян)
Контрольные работы с ответами

 

К-1. Проверяемые темы: Цилиндр и его поверхность. Конус и его поверхность. Сфера и шар (пункты учебника 38—51).

Контрольная работа № 1 К-1 + ответы

 

К-2. Темы: Объёмы параллелепипеда, призмы, пирамиды (пункты учебника 52—54, 56—58).

Контрольная работа № 2 К-2 + ответы

 

К-3. Темы: Объёмы цилиндра, конуса, шара (пункты учебника 55, 59—62).

Контрольная работа № 3 К-3 + ответы

 

К-4. Темы: Взаимное расположение многогранников и тел вращения (пункты учебника 38—62).

Контрольная работа № 4 К-4 + ответы

 

К-5. Темы: Векторы в пространстве (пункты учебника 63—70).

Контрольная работа № 5 К-5 + частичные ответы

 

К-6. Темы: Метод координат в пространстве. Скалярное произведение векторов (пункты учебника 71—79).

Контрольная работа № 6 К-6 + ответы

 

---

Вы смотрели: Геометрия 11 Атанасян Контрольные работы с ответами. Ориентировано на учебник «Геометрия. 10–11 классы» авторов Л. С. Атанасяна и др., базовый уровень (Просвещение). Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : учеб. пособие для общеобразоват. организаций : базовый уровень / М. А. Иченская» использованы в учебных целях. Ответы адресованы родителям.

Геометрия 11 Атанасян Контрольная 5 + ответы

Контрольная работа № 5 по геометрии в 11 классе с ответами «Векторы в пространстве» по УМК Атанасян, базовый уровень (Просвещение). Ответы адресованы родителям. Геометрия 11 Атанасян Контрольная 5.

 

Геометрия 11 класс (УМК Атанасян)
Контрольная работа № 5 (авт. Иченская)

К–5. Вариант 1

1. В параллелограмме ABCD диагонали пересекаются в точке О, точка М лежит на стороне BD, причём ВМ = МО, АВ = m, АС = n. Выразите вектор ВМ через векторы m и n.
2. Дан тетраэдр ABCD, в котором точка К – середина ребра АС, точка М – середина отрезка KD, DA = a, DB = b, DC = c. Разложите вектор ВМ по векторам а, b и с.
3. Даны две точки А и В. Докажите, что для любых точек С и D пространства выполняется равенство СВ – СА = DB – DA.

К–5. Вариант 2

1. В треугольнике АВС точка М – середина стороны АВ, точка N – середина стороны АС, отрезки СМ и BN пересекаются в точке О, ВА = а, ВС = b. Выразите вектор ВО через векторы а и b.
2. Дан параллелепипед ABCDA₁B₁C₁D₁, АВ = а, AD = b, AA₁ = c. 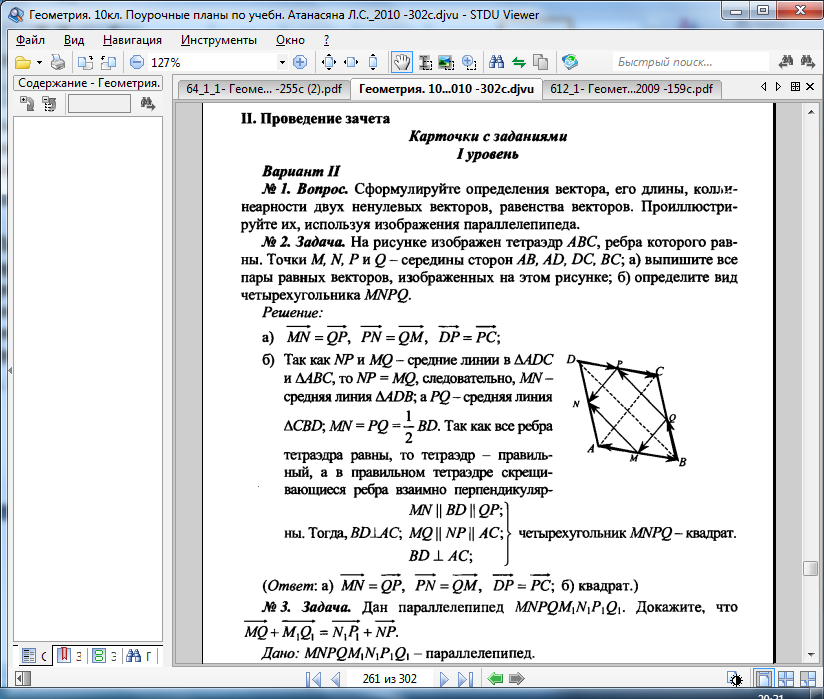Разложите вектор AM по векторам а, b и с, если М – точка пересечения диагоналей DC₁ и D₁C.
3. Дан треугольник АВС, в котором точки К, L и М – середины сторон ВС, АС и АВ. Докажите, что для любой точки D пространства выполняется равенство DK + DL + DM = DA + DB + DC.

Смотреть графический вид контрольной (Варианты 1, 2)

К–5. Вариант 3

1. В треугольнике АВС О – точка пересечения его медиан, АС = а, ВС = b. Выразите вектор АО через векторы а и b.
2. Дан параллелепипед ABCDA₁B₁C₁D₁, B₁A₁ = a, B₁C₁ = b, В₁В = с. Разложите вектор В₁М по векторам а, b и с, если М– точка пересечения диагоналей основания АС и BD.
3. Дан четырёхугольник ABCD, середины противоположных сторон которого пересекаются в точке К. Докажите, что для любой точки L пространства выполняется равенство LK = 1/4 • (LA + LB + LC + LD).

К–5. Вариант 4

1. В параллелограмме ABCD диагонали пересекаются в точке О, точка М лежит на стороне ВС, ВМ = МС, АВ = р, АО = q. Выразите вектор AM через векторы р и q.
2. Дан тетраэдр ABCD, в котором точка Е – середина ребра ВС, точка М – середина отрезка DE, АС = a, AB = b, AD = с. Разложите вектор AM по векторам а, b и с.
3. Дан треугольник АВС и две точки D и E, не лежащие в его плоскости. Докажите, что при выполнении равенства DE = xAB + yAC прямая DE параллельна плоскости АВС.

Смотреть графический вид контрольной (Варианты 3, 4)

 

Ответы на контрольную работу

 

Вернуться к Списку контрольных работ по геометрии в 11 классе (Атанасян)

 

---

Вы смотрели: Контрольная работа по геометрии 11 класс «Векторы в пространстве» с ответами для УМК Атанасян, базовый уровень (Просвещение). Ответы адресованы родителям. Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : базовый уровень / Иченская» использованы в учебных целях. Геометрия 11 Атанасян Контрольная 5 + Ответы.

Геометрия 11 Атанасян Контрольная 6 + ответы

Контрольная работа № 6 по геометрии в 11 классе с ответами «Метод координат в пространстве. Скалярное произведение векторов» по УМК Атанасян, базовый уровень (Просвещение). Ответы адресованы родителям. Геометрия 11 Атанасян Контрольная 6.

 

Геометрия 11 класс (УМК Атанасян)
Контрольная работа № 6 (авт. Иченская)

К-6. Вариант 1

1. Даны векторы а{1; –2; 0}, b{3; –6; 0}, с{0; –3; 4}. Найдите координаты вектора р = 2а – b/3 – с.
2. Найдите угол между прямыми АВ и CD, если А(6; –4; 8), В(8; –2; 4), С(12; –6; 4), D(14; –6; 2).
3. Дан куб ABCDA₁B₁C₁D₁. Найдите угол φ между векторами AD₁ и ВМ, где М – середина ребра DD₁.

К-6. Вариант 2

1. Даны векторы a = 2i – 3j + k и b = 4i – 2k, где i, j, k – единичные взаимно перпендикулярные векторы (орты). Найдите скалярное произведение векторов а и b.
2. Найдите угол между прямыми MN и EF, если М(1; 1; 0), N(3; –1; 0), E(4; –1; 2), F(0; 1; 0).
3. Даны координаты вершин тетраэдра МАВС: М(2; 5; 7), А(1; –3; 2), В(2; 3; 7), С(3; 6; 0). Найдите расстояние от точки К до точки О, где K – середина ребра AM, О – середина ребра ВС.

Смотреть графический вид контрольной (Варианты 1, 2)

 

К-6. Вариант 3

1. Даны векторы а{2; 4; –6}, b{–3; 1; 0}, с{3; 0; –1}. Найдите координаты вектора р = –а/2 + 2b – с.
2. Найдите угол между прямыми АВ и CD, если A(√3; 1; 0), В(0; 0; 2√2), С(0; 2; 0), D(√3; 1; 2√2).
3. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между векторами АС и C₁D.

К-6. Вариант 4

1. Даны векторы a = 5i – 2j + 4k и b = 3j + 2k, где i, j, k – единичные взаимно перпендикулярные векторы (орты). Найдите скалярное произведение векторов а и b.
2. Найдите угол между прямыми MN и КЕ, если М(2; 0; 0), N(0; 2; 0), K(2; 2; 0), E(2; 2; 2).
3. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ точка М – центр грани AA₁D₁D. Найдите угол φ между векторами ВМ и В₁С, если измерения параллелепипеда АВ = 4 м, AD = 3 м, AA₁ = 5 м.

Смотреть графический вид контрольной (Варианты 3, 4)

 

Ответы на контрольную работу

 

Вернуться к Списку контрольных работ по геометрии в 11 классе (Атанасян)

 

---

Вы смотрели: Контрольная работа по геометрии 11 класс «Метод координат в пространстве. Скалярное произведение векторов» с ответами для УМК Атанасян, базовый уровень (Просвещение). Ответы адресованы родителям. Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : базовый уровень / Иченская» использованы в учебных целях. Геометрия 11 Атанасян Контрольная 6 + Ответы.

Контрольная работа по теме «Скалярное произведение. Движения»

Просмотр
содержимого документа

Г-11   К/р № 2 «Скалярное произведение. Движения»

 

 Вариант 1

 

1. Даны векторы , = -5 +  = — -2 + . Найдите :                                                                                   а) ∙ ;           б) ( + ) ∙ 2 ;              в)  .

 

2. Даны точки А(5; -9; 6), В(-3; 4; -7), С(4; 0; -2). Запишите координаты точки, симметричной:                                    а) точке В относительно начала координат;                                                                                                                  б) точке С относительно оси ОХ;                                                                                                                                    в) точке А относительно плоскости ХОZ.
3. Даны точки А(1; 3; 0), В(2; 3; -1), С(1; 2; -1), Е(4; 0; 1) . Найдите угол между прямыми АС и ВЕ .

 

Вариант 2

 

1.  

 

 

 

 

2. Найдите угол между прямыми АВ и CD, если А(1; 1; 0), В(3; -1; 2), С(1; -1; 2) , D(0; 1; 0).
3. Точка А симметрична точке В(6; 3; -2) относительно оси ОУ, точка С симметрична точке А относительно плоскости ХОZ. Найдите расстояние между точками А и С.
4. Дан куб АВСDA₁B₁C₁D₁. Найдите угол между прямыми АС_{и  DС1 используя метод координат.}

 

Вариант 3

 

1.  

 

 

 

 

2. Найдите угол между прямыми АВ и CD, если А(3; -1; 3), В(3; -2; 2), С(2; 2; 3) , D(1; 2; 2).
3. Точка В симметрична точке А(-5; -1; 3) относительно плоскости ХОУ, точка С симметрична точке В относительно оси ОZ. Найдите расстояние между точками В и С.
4. Дан куб АВСDA₁B₁C₁D₁. Найдите угол между прямыми АС₁ и ВМ, где М-середина ребра DD₁.

 

Контрольные работы по геометрии 11 класс Атанасян Л.С.

Контрольные работы по геометрии в 11 классе по учебнику атанасян л.с.

Контрольная работа № 1
(на 20 мин)

Вариант 1

1. Найдите координаты вектора , если А (5; –1; 3), В (2; –2; 4).

2. Даны векторы (3; 1; –2) и (1; 4; –3). Найдите .

3. Изобразите систему координат Oxyz и постройте точку А (1; –2; –4). Найдите расстояния от этой точки до координатных плоскостей.

Вариант 2

1. Найдите координаты вектора , если С (6; 3; – 2), D (2; 4; – 5).

2. Даны вектора (5; – 1; 2) и (3; 2; – 4). Найдите .

3. Изобразите систему координат Oxyz и постройте точку В (– 2; – 3; 4). Найдите расстояние от этой точки до координатных плоскостей.

Контрольная работа № 2

Вариант 1

1. Вычислите скалярное произведение векторов и , если , , = 2, = 3, = 60°, , .

2. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между прямыми AD₁ и BM, где M – середина ребра DD₁.

3. При движении прямая отображается на прямую b₁, а плоскость β – на плоскость β₁ и b || β₁.

Вариант 2

1. Вычислите скалярное произведение векторов и , если , , = 3, = 2, = 60°, , .

2. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между прямыми AC и DC₁.

3. При движении прямая a отображается на прямую a₁, плоскость α – на плоскость α₁, и . Докажите, что .

Контрольная работа № 3

Вариант 1

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см². Найдите площадь поверхности цилиндра.

2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:

а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°;

б) площадь боковой поверхности конуса.

3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.

Вариант 2

1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:

а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;

б) площадь боковой поверхности конуса.

3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.

Контрольная работа № 4

Вариант 1

1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60°. Найдите объем пирамиды.

2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.

Вариант 2

1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60°. Найдите объем пирамиды.

2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45°. Найдите объем конуса.

Контрольная работа № 5

Вариант 1

1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.

2. Объем цилиндра равен 96π см³, площадь его осевого сечения 48 см². Найдите площадь сферы, описанной около цилиндра.

Вариант 2

1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.

2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.

векторов и векторной геометрии 12 класс по математике | Примечания

Векторная и векторная геометрия

Физические величины, характеризующиеся величиной и направлением, называются векторными величинами.

Например, ускорение, импульс и т. Д.

Декартова форма вектора в двух измерениях

Векторы i и j — это векторы длины 1 в направлениях OX и OY соответственно. 2}} $

Типы векторов

Нулевые векторы:

Если величина вектора равна нулю и начальная точка вектора совпадает с конечной точкой.Обозначается он 0⃗. Направление такого вектора неопределенно.

Единичный вектор:

Вектор, имеющий величину единичной длины, называется единичным вектором. Предположим, что если OA⃗ — вектор, имеющий величину OA, то единичный вектор обозначен $ \ widehat {{\ rm {OA}}} $ в направлении вектора OA⃗ и имеет величину, равную 1.

Вектор положения:

Если O берется за начало отсчета, а A — любая произвольная точка в пространстве, то вектор OA⃗ называется вектором положения точки.Вектор положения обозначает положение точки в трехмерной декартовой системе относительно начала координат.

Векторы со-инициализации:

Векторы, имеющие одинаковую начальную точку, называются ко-начальными векторами.

Векторы AB⃗ и AC⃗ называются ко-начальными векторами, поскольку они имеют одну и ту же начальную точку A.

Как и отличия от векторов:

Векторы, имеющие одинаковое направление, называются одинаковыми векторами и векторами, имеющими противоположные направления w.r.t. друг друга называются непохожими векторами.

Копланарные векторы:

Три или более вектора, лежащих в одной плоскости или параллельно одной плоскости, называются копланарными векторами.

Коллинеарные векторы:

Известно, что векторы, лежащие на одних и тех же параллельных прямых, являются коллинеарными векторами.

Равные векторы:

Два или более вектора считаются равными векторами, если их величина и направление одинаковы.

Эти два вектора, как показано, являются равными векторами, поскольку они имеют одинаковое направление и величину.

Вектор смещения :

Если точка смещается из положения A в положение B, то смещение AB представляет собой вектор AB, который известен как вектор смещения.

Негатив вектора :

Если два вектора одинаковы по величине, но точно противоположны по направлению, то оба вектора отрицательны друг относительно друга.

Линейная комбинация векторов

Если r ⃗ — линейные комбинации наборов векторов a ⃗, b⃗, c⃗, то это можно записать как

r⃗ = xa⃗ + yb⃗ + zc⃗ + t⃗v, где x, y, z …… .t — скаляры

Линейно зависимые и независимые векторы

Если существует соотношение xa⃗ + yb⃗ + zc⃗ + t⃗v = 0 такое, что хотя бы один из скаляров не равен нулю, то набор векторов sa ⃗, b⃗, c⃗ называется линейно зависимыми векторами

Если существует соотношение xa⃗ + yb⃗ + zc⃗ + t⃗v = 0 такое, что все скаляры x, y, z …….равны нулю, то набор векторов sa ⃗, b⃗, c⃗ называется линейно независимыми векторами

Пример 1

Найдите $ {\ rm {\ vec a}} $ + $ {\ rm {\ vec b}} $, $ {\ rm {\ vec a}} $ — $ {\ rm {\ vec b}} $, $ — \ frac {1} {3} {\ rm {\ vec b}}

долларов США

Солн:

(я)

$ {\ rm {\ vec a}} $ + $ {\ rm {\ vec b}} $ = (0,0) + (1,2) = (0 + 1,0 + 2) = (1, 2).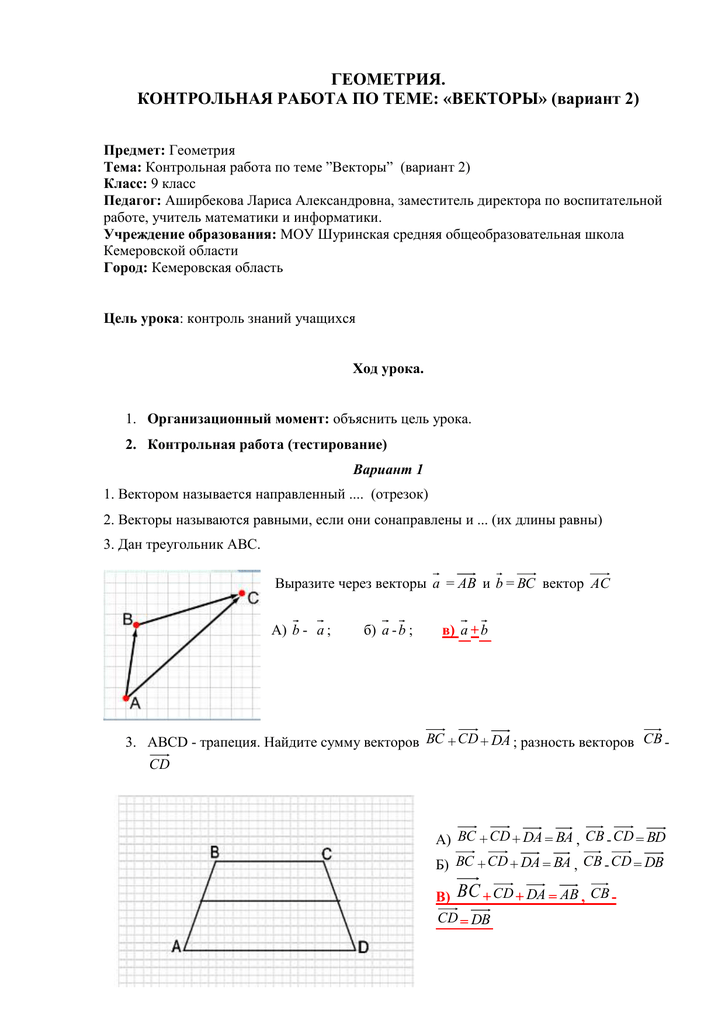

$ {\ rm {\ vec a}} $ — $ {\ rm {\ vec b}} $ = (0,0) — (1,2) = (0 — 1,0 — 2) = (-1 , -2).

2 $ {\ rm {\ vec a}} $ = 2 (0,0) = (0,0).

Или, $ — \ frac {1} {3} {\ rm {\ vec b}} $ = $ — \ frac {1} {3} $ (1,2) = $ \ left ({- \ frac { 1} {3}, — \ frac {2} {3}} \ right) $.

Пример 2

ABCD — это параллелограмм G — точка пересечения диагоналей, и если O — любая точка, покажите, что

$ \ overrightarrow {{\ rm {OA}}} + \ overrightarrow {{\ rm {OB}}} + \ overrightarrow {{\ rm {OC}}} + \ overrightarrow {{\ rm {OD}}} $ = 4. $ {\ Rm {\:}} \ overrightarrow {{\ rm {OG}}} $.

Солн:

G — точка пересечения диагоналей AC и BD.

Итак, GA = GC, GB = GD,

От треугольника OAC,

Или $ \ overrightarrow {{\ rm {OA}}} $ + $ \ overrightarrow {{\ rm {OC}}} $ = 2 $ \ overrightarrow {{\ rm {OG}}} $. (G — это средняя точка AC.)

Опять из треугольника OBD,

Или $ \ overrightarrow {{\ rm {OB}}} $ + $ \ overrightarrow {{\ rm {OD}}} $ = 2 $ \ overrightarrow {{\ rm {OG}}} $.
(G — средняя точка BD).

Добавление, $ \ overrightarrow {{\ rm {OA}}} + \ overrightarrow {{\ rm {OB}}} + \ overrightarrow {{\ rm {OC}}} + \ overrightarrow {{\ rm {OD}} } $ = 4.$ {\ rm {\:}} \ overrightarrow {{\ rm {OG}}} $.

Пример 3

Проверить, являются ли векторы линейно зависимыми или независимыми

$ {\ rm {\ vec i}} $ + $ {\ rm {\ vec k}} $ и $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $

Солн:

Пусть $ {\ rm {\ vec a}} $ = $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec k}} $ = (1,0,1), $ {\ rm {\ vec b}} $ = $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ = (1,1,0)

И $ {\ rm {\ vec c}} $ = — $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec k}} $ = (-1,0, -1).

Пусть $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\: \ vec b}} $ + y. $ {\ Rm {\: \ vec c}} $… .. (i ).

Или (1,0,1) = x (1,1,0) + y (-1,0, -1) = (x — y, x, -y)

Итак, x — y — 1…. (Ii)

Или, x = 0…. (Iii)

А — y = 1…. (Iv)

Из (iii) и (iv) получаем, что

Или, x = 0, y = — 1.

Эти значения x = 0, y = 1 также удовлетворяют,

x — y = 1, т.е. 0 — 1 = — 1, т.е. — 1 = — 1.

Поскольку, y = — 1 ≠ 0, значит, данные векторы линейно зависимы.

г. $ 2 {\ rm {\ vec i}} $ +3 $ {\ rm {\ vec j}} $$ + {\ rm {\:}} 4 {\ rm {\ vec k}} $ и $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec j}} $ + $ {\ rm {\:}} 2 {\ rm {\ vec k}}

долларов

Солн:

Пусть $ {\ rm {\ vec a}} $ = $ 2 {\ rm {\ vec i}} $ +3 $ {\ rm {\ vec j}} $$ + {\ rm {\:}} 4 { \ rm {\ vec k}} $ = (2,3,4), $ {\ rm {\ vec b}} $ = $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec j }} $ + $ {\ rm {\:}} 2 {\ rm {\ vec k}} $ = (1, -1,2)

И $ {\ rm {\ vec c}} $ = 5 $ {\ rm {\ vec i}} $ + 6 $ {\ rm {\ vec j}} $ + $ {\ rm {\:}} 8 {\ rm {\ vec k}} $ = (5,6.8)

Пусть $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\: \ vec b}} $ + y. $ {\ Rm {\: \ vec c}} $… .. (i ).

Или, (2,3,4) = x (1, -1,2) + y (5,6,8)

Итак, (2,3,4) = (x + 5y, — x + 6y, 2x + 8y).

Итак, x + 5y = 2… (ii)

Или, — x + 6y = 3…. (Iii)

Или, 2x + 8y = 4…. (Iv).

Решая (ii) и (iii), имеем y = $ \ frac {5} {{11}} $ и x = $ — \ frac {3} {{11}} $.

Эти значения x и y не удовлетворяют (iv),

Т.е. 2. $ \ left ({- \ frac {3} {{11}}} \ right) + 8 \ left ({\ frac {5} {{11}}} \ right) $ = 4.

, т.е. $ \ frac {{- 5 + 40}} {{11}} $ à 4 à 34 = 44, что неверно,

Следовательно, x и y не удовлетворяют (i), поэтому данные векторы независимы.

Геометрия круга Геометрия (классы 10 или 11)

1 Геометрия круга Геометрия (классы 10 или 11) Пятидневный план занятий с использованием Geometry Sketchpad, графических калькуляторов и различных манипуляторов (веревка, картонные круги, миры и т. ). Деннис Капатос Проект I2T2 01.12.05

2 Обзор модуля Цели модуля: Учащиеся приобретут широкий спектр навыков и знаний. В дополнение ко всем теоремам в каждом разделе студенты смогут делать наблюдения и предположения, а также проверять эти предположения с помощью имеющихся в их распоряжении технологий и манипуляторов. Студенты также смогут работать совместно с другими членами группы, чтобы исследовать свойства геометрических фигур (в частности, кругов) и доказывать теоремы.В дополнение к этому учащиеся смогут распознавать приложения кругов и связанных с ними частей в мире вокруг них. Стандарты NCTM: количество и работа Учащиеся оценивают разумность численных вычислений и их результатов. Алгебра Учащиеся делают разумные выводы о моделируемой ситуации. Геометрия Учащиеся изучают взаимосвязи (включая соответствие и сходство) между классами двух- и трехмерных геометрических объектов, делают и проверяют предположения о них и решают связанные с ними задачи. Студенты устанавливают справедливость геометрических гипотез, используя дедукцию, доказывают теоремы и критикуют аргументы других. Студенты используют декартовы координаты и другие системы координат, такие как навигационная, полярная или сферическая, для анализа геометрических ситуаций. Учащиеся используют геометрические идеи для решения задач и понимания других дисциплин и других областей интересов. Измерение Учащиеся принимают решения относительно единиц и шкал, которые подходят для проблемных ситуаций, связанных с измерением.Решение проблем Студенты получают новые математические знания путем решения задач. Студенты решают задачи, возникающие по математике и в других контекстах. Рассуждения и доказательства Студенты делают и исследуют математические предположения. Студенты разрабатывают и оценивают математические аргументы и доказательства. Студенты выбирают и используют различные типы рассуждений и методы доказательства. Коммуникация Учащиеся организуют и укрепляют свое математическое мышление посредством общения. Связи Учащиеся узнают и применяют математику в контексте, отличном от математики.Стандарты штата Нью-Йорк: G.PS.6 Используйте различные стратегии для расширения методов решения других проблем. G.PS.8 Определение информации, необходимой для решения проблемы, выбор методов получения информации и определение параметров приемлемых решений. G.CM.5 Четко излагайте логические аргументы, показывая, почему результат имеет смысл и почему рассуждения верны.

3 г.CN.7 Распознавать и применять математические идеи к проблемным ситуациям, которые возникают вне математики. G.R.1. Используйте физические объекты, диаграммы, диаграммы, таблицы, графики, символы, уравнения или объекты, созданные с использованием технологий, в качестве представления математических концепций. G.R.3 Используйте представление как инструмент для исследования и понимания математических идей. G.G.27 Напишите доказательство, приводящее от заданной гипотезы к заданному выводу. G.G.29 Определите соответствующие части конгруэнтных треугольников. G.G.49 Исследуйте, обосновывайте и применяйте теоремы, касающиеся хорд окружности.G.G.50 Исследуйте, обосновывайте и применяйте теоремы о касательных прямых к окружности. G.G.51. Исследуйте, обосновывайте и применяйте теоремы о дугах, определяемых лучами углов, образованными двумя прямыми, пересекающими окружность. G.G.52. Исследуйте, обосновывайте и применяйте теоремы о дугах окружности, разрезанных двумя параллельными прямыми. G.G.53 Исследуйте, обосновывайте и применяйте теоремы, касающиеся отрезков, пересекаемых кругом. Материалы и оборудование: Ресурсы: Компьютеры Sketchpad Geometer Проектор Графические калькуляторы Компасы Линейки Mira Транспортиры Струны Картонные круги Пустые банки Учебник: математика Нью-Йорка A / B: комплексный подход Том 2 Бас, Холл, Джонсон и Вуд.New York Math A / B: Комплексный подход Том 2. Издание для учителей. Prentice Hall, Глава 12. Страницы Bennett, Dan. Изучение геометрии с помощью блокнота Geometer. 4-е издание. Key Curriculum Press, Глава 6. Страницы Описание модуля: Этот модуль предназначен для покрытия разделов с первого по пятый в главе 12. Хотя в главе 6 разделов, этот оставшийся раздел можно охватить так же, как и предыдущие пять. Пять уроков предназначены для исследования, хотя некоторые инструкции учителя могут показаться не такими.Учитель должен оказывать ровно столько помощи, сколько необходимо для того, чтобы ученики обдумали ситуацию. Кроме того, GSP используется во всем подразделении; иногда в виде рабочего листа, в котором учащиеся заполняют ответы, глядя на проблемы, иногда как инструмент для экспериментов и предположений, а иногда для моделирования и решения проблем. Кроме того, большинство уроков начинается с проблемы, которая ведет к уроку, чтобы учащиеся увидели, как потребность в более сложных способах мышления возникает из реальных жизненных проблем.(Примечание: хотя теоремы изложены на последней странице

4 этого документа, уроки будут иметь больше смысла, если у вас будет экземпляр учебника, который вы можете посмотреть перед собой. ) Краткое содержание урока: Урок 1 На этом уроке, хотя рабочий лист является интерактивным, учащиеся будут использовать GSP просто для того, чтобы введите ответы на вопросы, которые должны привести их к открытию общего уравнения круга.Выполняя работу над GSP, студенты также лучше знакомятся с ним для будущих занятий. Этот урок не такой исследовательский, как предыдущий, но это потому, что он развивает довольно сложную концепцию. Урок 2 Этот урок начинается с задачи, связанной со спутниками, в которой учащиеся сначала получают представление о ней с помощью манипуляторов и измерений (кругов, ниток, транспортиров и т. Д.). Затем они переходят к GSP, чтобы изучить ситуацию с помощью запросов и открытий. Первоначальные вопросы заставляют студентов тщательно изучить все теоремы, которые они должны изучить, а в конце студенты применяют эти теоремы, чтобы найти точный ответ на исходную проблему.Урок 3 На этом уроке учащиеся снова начинают с манипуляций (Мира, циркуль, линейка и банка (для обводки круга)), чтобы изучить проблему, а затем переходят к GSP, чтобы узнать больше теорем о хордах и дугах. Урок 4 Этот урок начинается с проблемы, которая не так четко связана с реальным миром, как другие. Однако интерес к проблеме развивается из-за удивительных результатов вписывания четырехугольника в круг. Студенты снова переключаются на GSP, чтобы провести больше исследований, и в конечном итоге они смогут понять и доказать результаты вопроса после открытия некоторых новых теорем.Урок 5 Теоремы этого урока показаны таким образом, что они основаны непосредственно на теоремах из предыдущего урока. Но даже в этом случае теорема, которую студенты пытаются формализовать, непроста. На этот раз ученики начинают урок, используя GSP. В конечном итоге студенты используют уникальные графические возможности GSP, чтобы предоставить другую модель для обнаружения взаимосвязи между различными частями проблемы.

5 Урок 1: Введение в круги Открытие уравнения круга Имя: Деннис Капатос Оценка: 11 Тема: Геометрия Материалы и раздаточный материал: Компьютер учителя с проектором GSP Компьютеры учеников с GSP Файл рабочего листа GSP: Проблема с поливом культур Учебники Графические калькуляторы Задачи урока: Студенты смогут написать и применить два общих уравнения круга, одно с центром в начале координат, а второе в любой точке (h, k) (теорема 12. 1). Студенты смогут указать, откуда берутся два общих уравнения, и вывести их, используя эти знания. Учащиеся смогут изобразить круг на своих графических калькуляторах. Предварительный набор: 1. Учитель будет иметь на доске контрольные вопросы, включая формулу расстояния и несколько примеров для ее применения. 2. Учитель обсудит с учениками ответы, на которых основана формула расстояния. Развивающее задание: 3. Учитель расскажет о сельском хозяйстве в этой стране и о том, что нужно больше продуктов питания из меньшего количества земли, используя меньше труда.4. Учащиеся войдут в свои компьютеры, откроют файл рабочего листа GSP: Проблема с поливом сельскохозяйственных культур и начнут работать над этим самостоятельно. 5. Учащиеся будут работать, пока не закончат вопрос. Учитель подойдет к нему и обсудит ответы учащихся. 7. Ученики будут продолжать работать до тех пор, пока не закончат вопрос. Учитель снова подойдет и обсудит ответ, который придумали ученики, уделяя особое внимание вопросу 14 (это может сбивать с толку). 9. Учащиеся заполнят оставшуюся часть рабочего листа.10. Учитель снова подойдет и обсудит ответы учеников. 11. Ученики передадут заполненный рабочий лист учителю с помощью компьютера. 12. Учащиеся заполнят вопросы для размышления, которые будут добавлены в свои тетради. 13. Наконец, учитель покажет ученикам, как использовать графические калькуляторы для построения кругов, и обсудит, почему положительная и отрицательная формы одного и того же уравнения необходимы для получения обеих половин круга. Учитель приведет пример системы уравнений, чтобы показать, насколько это полезно.Домашнее задание: на странице 589 учебника вопросы 1-18, 21-30, 32, 34 и 42

6 Проблемы с поливом культур Имя: Дата: Ответы в коробках в красном Фермер Боб использует новую высокотехнологичную систему полива, которая использует компьютер и множество мощных дождевателей для полива его посевов. Чтобы организовать свою землю, Боб решает разделить все свое поле на 100-метровые квадратные секции.Спринклеры расположены так, чтобы поливать как можно большую часть земли без перекрытий (см. Рисунок). 1) Что вы заметили в таком расположении спринклеров? Некоторые участки не поливают. Линия собственности Bob’s Land выделена красным. 100-метровые квадратные секции выделены синим цветом. Красные точки — это головки дождевателей с зеленой зоной распыления. 2) Оценка. Как вы думаете, примерно какой процент полей Боба не получают воды? Ответы различаются.

7 Обратите внимание, что в некоторых областях поля Боба вообще нет воды.Компьютер использует центральный спринклер в качестве начала координат, то есть присваивает ему координаты (0,0). Все остальные точки в поле Боба, такие как точка (100,0), отсчитываются от этой точки. (0,0) (100,0) Обратите внимание, что в этой точке (90,60) нет воды. 3) Датчик воды, помещенный в землю, сообщает Бобу, что координаты одной из точек, не получающих воду, равны (90,60). К счастью, разбрызгиватели можно запрограммировать на распыление на разное расстояние. На каком расстоянии Боб должен указать оросителю в точке (0,0) распылить, чтобы он достиг этой точки? Очевидно, вы можете настроить спринклер для распыления на гораздо большую площадь, чем необходимо, но он будет тратить воду.Каково точное расстояние от оросителя до точки сушки? (Показать все работы.) D = ((90-0) 2 + (60-0) 2) 108 метров 4) В этой области есть и другие точки. На каком расстоянии Боб должен указать оросителю распылить, чтобы полить любую заданную точку (x, y)? ((x) 2 + (y) 2) Distance = 5) Компьютер Боба называет расстояние буквой r, и он также не любит знаки квадратного корня. Как бы вы могли переписать приведенное выше уравнение, чтобы Боб мог ввести расстояние в компьютер? r 2 = (x) 2 + (y) 2 = Приведенное выше уравнение даст спринклеру новый радиус распыления, который достигнет любой точки (x, y) на координатной сетке.Это общее уравнение круга с центром в точке (0,0) и радиусом r. 6) Каков радиус и центр окружности, образованной уравнением 5 2 = x 2 + y 2? 7) Какие они для круга 36 = x 2 + y 2? r = 6, cntr = (0,0) r = 5, cntr = (0,0) 8) Каково уравнение окружности с центром (0,0) и радиусом 10? С радиусом 4? 100 = х 2 + у 2 16 = х 2 + у 2

8 9) Каково уравнение круга для спринклера в точке (0,0) до того, как его настройки были изменены? = x 2 + y 2 10) Назовите 4 точки, которые лежат на краю этого круга.(100,0), (0,100), (-100,0), (0, -100) Боб решает, что изменение диапазона всех спринклеров приведет к слишком большому перекрытию и, следовательно, к потере слишком большого количества воды (в этом случае вода стоит дорого. часть страны), поэтому он решает установить новый дождеватель в точке (100,58). (0,0) (100,0) 11) Если этот новый спринклер может точно достичь точки (100,43), то каков радиус его распыления? Используйте формулу расстояния и покажите свою работу. r = (() 2 + (58-43) 2) = 15 метров 12) Если этот новый спринклер может точно достичь любой точки (x, y), то каков радиус его распыления? (Примечание: это будет уравнение в терминах r, x и y.) ((100 — x) 2 + (58- y) 2) r = r 2 = (100 — x) 2 + (58- y) 2 Теперь перепишите это без знака квадратного корня: 13) Внутри пары круглых скобок в этом уравнении должны стоять знаки минус. Если x или y идут после знака минус, замените их другим числом. Напишите это уравнение. r 2 = (x — 100) 2 + (y — 58) 2 14) Что это такое, что делать и почему в данном случае это разрешено? То есть, почему это не меняет справедливости уравнения в данном случае? Прежде чем двигаться дальше, убедитесь, что это ничего не меняет.Изменение порядка на обратное аналогично умножению всего, что находится в скобках, на -1, что, поскольку результат возводится в квадрат, не влияет на уравнение. (a — b) 2 = (-1 (a — b)) 2 = (-a + b) 2 = (b a) 2

9 15) Заполните пробел: Уравнение в № 14 — это общее уравнение круга с центром в точке и радиусом r (100,58) 16) Боб хочет установить много таких новых спринклеры во всех других засушливых районах.Какое уравнение представляет собой круг с центром в любой заданной точке (h, k) и который может достигать любой точки (x, y)? (Снова убедитесь, что x и y идут первыми.) R 2 = (x — h) 2 + (y — k) 2 Теперь, используя эту форму уравнения, вы можете написать уравнение любого круга, который вы только можете себе представить. 17) Каков радиус и центр окружности 7 2 = (x-1) 2 + (y-1) 2? 18) Что они для круга 4 = (x + 3) 2 + (y-1) 2? 19) Каково уравнение окружности с центром (4, -5) и радиусом 9? r = 7, cntr = (1,1) r = 2, cntr = (-3,1) 81 = (x — 4) 2 + (y + 5) 2 20) Каково уравнение окружности с центром ( -1,0), который проходит через точку (3,2) 20 = (x + 1) 2 + y 2

10 Обзор основных идей: проблема с поливом культур Поскольку это отражение, оно предназначено только для учащихся.Также ответы будут отличаться _ 1) Опишите, как связаны формула расстояния и уравнение круга с центром в начале координат? Почему это интуитивно понятно? 2) Будет ли фермер Боб когда-нибудь поливать все поле без перекрытия участков? Почему или почему нет? 3) Напишите общие уравнения, которые вы нашли ниже, для использования в будущем. THM 12.1 Общее уравнение окружности с радиусом r, центрированным в начале координат: THM 12.2 Общее уравнение окружности с радиусом r и центром (h, k): 4) Как вы определили первое уравнение? Что ты сделал? 5 Как вы определили второе уравнение? Что ты сделал? 6) При первом использовании этих формул легко ошибиться.Какие ошибки вы допустили в вопросах 6–8 и (например, возведение в квадрат r, отрицательное значение h и т. Д.)? Какие вещи, которые вы можете придумать, помогут вам не делать их снова?

11 Урок 2: Касательные Обнаружение и применение касательных к реальным жизненным ситуациям Материалы и раздаточные материалы: Компьютер учителя с проектором GSP Компьютеры учеников с GSP Учебники Калькуляторы Струнная измерительная лента Линейки Транспортир Предварительно измеренные картонные круги Имя: Деннис Капатос Оценка: 11 Тема: Задачи урока геометрии: студенты смогут написать / описать и доказать теорему 12.Со 2 по 2 Учащиеся смогут моделировать проблемные ситуации, используя окружности, касательные, радиусы и другие линии, проведенные к окружности. Учитывая геометрическую фигуру с отсутствующими измерениями, учащиеся смогут применить свойства окружностей, радиусов и касательных, чтобы найти их. Учащиеся смогут совместно работать над решением данной геометрической задачи. Проверка домашнего задания: 1. Ответы на вопросы домашнего задания будут отображаться с помощью проектора. Студенты сами исправят домашнее задание. 2. Учитель обсудит любые проблемы, с которыми столкнулось большинство учеников.Развивающее задание: 3. Учитель представит на белой доске сегодняшнюю проблемную ситуацию со спутниками. 4. Учитель обсудит с классом, как они могут решить эту проблему. Они решат сначала сделать грубую модель, используя картонные круги и веревку, а позже примут более сложный подход. 5. Учитель разделит класс на группы по 5. Будет 2 человека, которые будут держать концы касательных струн (хотя они пока не назовут это так), 1 человек-спутник, чтобы удерживать две струны вместе на надлежащем расстоянии. , 1 человек для измерения центрального угла и 1 человек для записи данных.6. Каждая группа найдет свое собственное измерение, а затем класс поделится своими результатами. 7. Чтобы найти более точный ответ, Учитель попросит класс разбить группы и подойти к своим компьютерам, чтобы изобразить ситуацию на GSP. 8. Учитель расскажет ученикам, как создать рисунок, используя приведенные ниже инструкции учителя. Учитель задаст вопросы, когда будет указано.

12 9.Учитель посоветует ученикам записывать 3 новые теоремы в свои заметки по ходу дела, они докажут 12,4 для домашнего задания. 10. Поэкспериментировав с GSP, учитель будет работать с учеником, чтобы решить исходный вопрос (им нужно будет определить прямоугольный треугольник и использовать тригонометрию под прямым углом. 11. Учитель попросит учеников обобщить то, что они узнали (три теоремы) и как они использовали теоремы, чтобы получить точный ответ. Домашнее задание: прочитайте доказательство теоремы 12.2 на странице 594, докажите теорему 12.4 и на странице 596 вопросов учебника 1-8, 14-16 и 22

13 Спутников Тысячи спутников вращаются вокруг Земли прямо сейчас в десятках тысяч миль от поверхности.Они используются для чего угодно, от ретрансляции звонков на сотовый телефон и телевизионных программ до отслеживания погодных систем и определения местоположения судов с помощью GPS (глобальные системы позиционирования). Они могут видеть только часть земной поверхности за раз, но чем выше высота спутника, тем больше он видит. Как далеко спутник может видеть вокруг Земли (в градусах) с высоты 22 236 миль? (Примечание: радиус Земли составляет 3960 миль.) Вышеупомянутая высота помещает спутник на геостационарную орбиту, насколько он мог бы видеть, если бы у него была более высокая орбита? Высота спутника Земли = 2.72 см. Видимая область = 5,17 см. Может ли спутник видеть на полпути вокруг Земли, то есть на 180 градусов, если у него достаточно высокая орбита? Зачем?

14 Слова в скобках () — это то, к чему ученикам следует научиться догадываться. Им не следует рассказывать им. Инструкции для учителя Инструкции (произнесите вслух): Постройте круг AB. Проведите линию AC через центр круга AB; удерживайте нажатой клавишу shift, чтобы сделать ее вертикальной. Построить точку D на линии AC. Построить луч DE и луч DF, как показано. Скрыть точки B и C и линию AC. Построить сегмент DA. Построить точку G, пересечение отрезка DA и окружности A. Поверните лучи DE и DF до они точно касаются круга, как вы это сделали со строкой. Постройте радиус AH и AI до точек, где кажется, что лучи касаются круга, убедитесь, что H и я находимся на лучах, а не на круге. Вопросы: Это похоже на очень точный способ построения этого? Что вы заметили по поводу радиусов и лучей? (они выглядят почти перпендикулярно) Проверьте это, измерьте угол AID и угол AHD, что получили люди? Давайте рассмотрим это дальше. Инструкции: Постройте новый круг справа. Построите радиус. Выберите его и его конечную точку и постройте перпендикулярную линию. Вопросы: Что происходит, когда вы перемещаете точку? Эта линия называется касательной, потому что она пересекает окружность ровно в одной точке.Эта точка называется точкой касания. Каким должно быть наше определение касательной? Это теорема 12.2. Сколько разных касательных можно провести к одной окружности из любой точки вне окружности? Инструкции: Постройте линию через центр круга, как вы это делали для другого круга. Дважды щелкните по нему, чтобы отметить его как зеркальную линию. Выберите точку касания, касательную и радиус и отразите их. Скройте зеркальную линию, и она будет point Постройте пересечение этих двух касательных.Скройте 2 касательные линии. Постройте касательные сегменты. Постройте центральный сегмент и точку, в которой он пересекает окружность, как показано. Переместите первую точку касания, которую вы сделали вокруг. Вопросы: Что вы заметили в длинах двух касательных сегментов? (они всегда одинаковой длины) Проверьте это, измерьте их. Теперь переместите их. проверяет это предположение? Это теорема. Возвращаясь к нашему вопросу, мы знаем все, что нам нужно, чтобы решить этот вопрос. E B C D A m! A H D = G m! A ID = E H D A V I W M F F U O

15 Урок 3: Свойства хорд и дуг Использование свойств хорд и дуг для решения задач Материалы и раздаточные материалы: Компьютер учителя с проектором GSP Компьютеры учеников с GSP Файлы рабочего листа GSP Учебники Графические калькуляторы Компасы Линейки Пустые банки Миры Имя: Деннис Капатос Оценка: 11 Предмет: Геометрия Цели урока: Студенты смогут использовать теорему 12.8, чтобы построить центр круга. Студенты смогут писать / описывать и доказывать теоремы 12.6, 12.5, 12.7, а студенты смогут моделировать проблемные ситуации, используя окружности, касательные, радиусы и другие линии, нарисованные на окружности. Учитывая геометрическую фигуру с отсутствующими измерениями, учащиеся смогут применить полученные ранее теоремы, чтобы найти их. Учащиеся смогут вместе строить и проверять гипотезы геометрических фигур. Проверка домашнего задания: 1. Ответы на вопросы домашнего задания 1-8, 14-16 и 22 будут показаны с помощью проектора.Студенты сами исправят домашнее задание. 2. Учитель обсудит любые проблемы, с которыми столкнулось большинство учеников. 3. Учитель попросит одного ученика представить классу доказательство теоремы 12.4 для обсуждения. Предварительный набор: 4. Учитель попросит учащихся построить точку, окружность вокруг этой точки, а затем попросит их построить касательную к окружности, используя только циркуль и линейку. 5. Учитель будет задавать ученикам вопросы, чтобы напомнить им о взаимосвязи между касательной и радиусом до точки касания.Развивающее задание: 6. Учитель спросит учащихся, как бы они построили касательную, не задавая центр круга, а только край. 7. Учитель представит сегодняшнюю проблемную ситуацию со спутниковой тарелкой. 8. В процессе обучения учащиеся будут работать с партнером, каждый из которых будет делать свою работу, но просто поделится мыслями.

16 9. Учитель скажет ученикам построить дугу круга, используя дно банки или что-нибудь еще, что может служить этой цели.Идея в том, что у них нет отверстия в центре, как при использовании компаса. 10. Учитель спросит учеников, как они могли бы найти центр, если бы они использовали Mira. Если ученикам понадобится помощь, учитель посоветует им построить точку около обоих концов дуги. 11. Если учащимся потребуется дополнительная помощь, учитель посоветует им использовать Миру и найти положение, в котором одна из этих точек сопоставляется с другой. 12. Если учащимся по-прежнему нужна дополнительная помощь, попросите их нарисовать линию, на которой находится Мира, когда она сопоставляет две точки друг с другом.13. Учитель задаст ученикам вопросы о том, что это за линия, и приведет их к мысли, что эта линия должна проходить через центр, потому что это линия симметрии круга. 14. Учащиеся должны осознавать необходимость повторения этого, чтобы получить еще одну линию и пересечение. 15. Учитель попросит учеников соединить две пары точек, которые они сопоставили друг с другом, с сегментами, чтобы сказать им, что они называются хордами. 16. Учитель попросит учеников придумать определение аккорда.17. Учитель спросит, что они построили для хорды, которая нашла центр (серединный перпендикуляр к хорде, как определение серединного перпендикуляра). 18. Учитель попросит учащихся сделать предположение об этом (теорема 12.8). 19. Учитель будет разбивать учеников на группы, подходить к их компьютерам и запускать GSP 20. Учитель предлагает ученикам открыть заранее сделанный набросок круга, хорды и серединного перпендикуляра к нему. 21. Студент осмотрит точки, чтобы увидеть, что любой срединный перпендикуляр хорды пересекает центр окружности (см. Первое изображение).22. Учитель обсудит с классом и попросит учащихся формализовать свои предположения и записать теорему 12.8 в свои заметки. 22. Учитель попросит учеников просмотреть другую страницу этого эскиза спутника с самого начала задачи. 23. Учитель попросит учеников найти место для приемника (см. Второй рисунок). 24. Учитель посоветует учащимся просмотреть другие страницы с набросками, которые помогут им открыть для себя теоремы 12.5, 12.6. Они очень очевидны, и поэтому им уделяется не так много времени.(см. третью и четвертую картинки). 25. Студенты внесут эти теоремы в свои заметки. 26. Учащиеся проводят остаток класса, пытаясь решить вопрос 20 на странице 604.? Домашнее задание: длина D’E на m D’E = 4,83 см BC = 5,13 см E перетащите aa = Докажите теорему 12.9, а на странице 603 учебника вопросы 1-13, 18 и завершите 20. G ‘D’ B Длина FG ‘на BC = m G’G = 4,83 см F m AB = 3,27 см GBCA m CD = 3,3 м GE = 3,09 см EFD m EF = 3,06 см

17 Определение центра спутниковой тарелки Спутниковая тарелка в форме дуги (часть круга) принимает информацию, отражая ее от тарелки на приемник.Во время сильного урагана осколок летящего мусора сломал ствольную коробку. Как мы могли найти точное место, где поставить запасной приемник, чтобы снова принять сигнал ??

18 Урок 4: Вписанные углы Изучение свойств вписанных углов и четырехугольников с использованием материалов и раздаточных материалов GSP: Компьютер учителя с проектором GSP Компьютеры учеников с GSP Файлы рабочего листа GSP Учебники Графические калькуляторы Компасы Линейки Транспортеры Миры Имя: Деннис Капатос Оценка: 11 Тема : Цели урока геометрии: Студенты смогут написать / описать и доказать теорему и ее следствия.Студенты смогут доказать теорему 12.11 и объяснить, как ее можно рассматривать как следствие теоремы. Учитывая геометрическую фигуру с отсутствующими измерениями, студенты смогут применить теоремы, изученные до сих пор, чтобы найти их. Учащиеся смогут вместе строить и проверять гипотезы геометрических фигур. Проверка домашнего задания: 1. Ответы на вопросы домашнего задания 1-13 и 18 будут показаны с помощью проектора. Студенты сами исправят домашнее задание. 2. Учитель попросит учащихся обсудить свои ответы на вопрос 20 и любые вопросы, с которыми у большинства учащихся возникли проблемы.3. Учитель попросит одного ученика представить классу доказательство теоремы 12.9 для обсуждения. Предварительный набор: 4. Учитель попросит ученика построить любой четырехугольник с помощью циркуля, линейки и / или Миры. 5. Учитель попросит учеников измерить все углы своего четырехугольника. 6. Учащиеся поделятся своими измерениями углов и сделают вывод, что любой угол может иметь любую меру. Развивающее задание: 6. Учитель попросит учеников построить большой круг с любым четырехугольником внутри него с вершинами на круге (вписанный четырехугольник).7. Опять же, ученики будут измерять свои углы и искать взаимосвязь (противоположные углы являются дополнительными).

19 8. Класс обсудит, почему они думают, что это так. 9. Учитель попросит учеников подойти к своим компьютерам и запустить GSP. 10. Учитель попросит класс начать рисовать четырехугольник, но остановится после создания всего 2 смежных сторон. 12. Учитель попросит учеников построить центральный угол к этой дуге, измерить ее угол дуги, измерить угол дуги вписанного угла и предположить связь между вписанным и центральным углами (это теорема 12.10, надпись должна составлять половину центрального угла. Учитель попросит учащихся дать определения для этих терминов по мере их представления. 13. Учащиеся будут перемещать точки, чтобы проверить эту гипотезу, и записывать теорему в свои заметки (см. Первое изображение). 14. Учитель спросит класс, что если бы был нарисован второй угол AEC или любая точка C (у него был бы такой же угол дуги) (см. Второй рисунок). 15. Студенты будут экспериментировать со своими набросками, обсуждать, что они думают, обнаруживать следствие 1 теоремы 12.10 и внесите это в свои записи. 16. Учитель попросит учеников скрыть угол AEC 17. Учитель спросит учеников, что, если бы A и C находились друг напротив друга на окружности, то есть, если бы они находились на противоположных сторонах диаметра (угол ABC всегда был бы равен 90 ) (см. третью картинку). 18. Студенты будут перемещать точки на своих набросках, обсуждать то, что они думают, обнаруживать следствие 2 теоремы 12.10 и вносить это в свои заметки (см. Третью картинку). 19. Учитель попросит учеников снова сделать угол ADC меньше 180.20. Учитель попросит ученика проверить, выполняется ли теорема 12.10 Hide, поскольку Raypoint B действительно приближается к точке C (в этой точке BC станет касательной к окружности в точке C). 21. Студенты попробуют это, обсудят то, что они видят и думают (см. Рисунок). 22. Студенты обсудят, как прямая BC становится касательной, откроют для себя теорему 12.11, увидят, что это на самом деле просто еще одно следствие теоремы 12.10, а также внесут это в свои заметки. 23. Учитель попросит учеников вернуться к исходному вопросу о вписанных четырехугольниках.24. Студенты должны уметь выполнять эту часть самостоятельно и с m! А Б В = Б Е м! A E C = m! А Б В = Б м! А Б В = Б Д м! А Б В = Г Д В Г А м! A D C = C A m! A D C = C A m! A D C = m! A D C = A B C небольшая трудность (см. Финальную картинку). 25. Учитель попросит их ввести это как в свои заметки, так и официально. Следствие 3 теоремы. В остальном классе ученики будут доказывать теоремы и работать в парах с помощью учителей. Студенты представят свои доказательства, если позволит время.м! A B C = м! A H C = m AHC = m ABC = A Домашнее задание: B D H Вопросы 1-12, 15, 16, 24-27 и 28 на странице 610 учебника. Студентов также попросят придумать, нарисовать и обозначить 1 новое приложение из реальной жизни (не одно из книги или класса) из всего, что они узнали из этого модуля. Они должны включать в себя как можно больше измерений, насколько это возможно или необходимо. C

20 Урок 5: Углы, образованные аккордами и секущими. Построение координат с помощью GSP с использованием графиков для определения геометрических взаимосвязей. Материалы и раздаточные материалы: Компьютер учителя с проектором GSP. Компьютеры учеников с GSP. Файлы рабочего листа GSP Учебники Графические калькуляторы Имя: Деннис Капатос Оценка: 11 Тема : Цели урока по геометрии: Студенты смогут написать / описать и доказать теорему, а студенты смогут распознавать реальные приложения кругов и теоремы, изученные до сих пор.Студенты смогут использовать координатные графики для определения взаимосвязи между частями геометрической фигуры. Студенты смогут совместно работать над доказательством геометрических теорем. Учитывая геометрическую фигуру с отсутствующими измерениями, учащиеся смогут применить полученные ранее теоремы, чтобы найти их. Проверка домашнего задания: 1. Ответы на вопросы домашнего задания 1-12, 15, 16, 24-27 и 28 будут показаны с помощью проектора. Студенты сами исправят домашнее задание. 2. Учитель попросит каждого ученика поделиться реальными приложениями, которые они придумали с помощью проектора, чтобы показать свои рисунки и т. Д.. Предварительный набор: 3. Учащиеся будут смотреть на наброски, сделанные ими на уроке GSP, а учитель будет задавать вопросы, чтобы помочь им вспомнить, какие теоремы они выучили. Развивающая деятельность: 4. Студенты по-прежнему будут получать GSP. 5. Учитель расскажет ученикам, как создать рисунок, используя приведенные ниже инструкции учителя. Учитель задаст вопросы, когда будет указано. Теоремы будут выдвигаться и вноситься в заметки по мере продвижения обсуждения. 6. В конце инструкций учителя ученики будут работать в парах, чтобы попытаться доказать, что Учитель теоремы поможет им, хотя у них не должно быть особых проблем (раньше они уже проводили более сложные доказательства).7. Это доказательство прекрасно приведет к теореме, которую студенты также внесут в свои заметки.

21 8. В оставшееся время студенты будут практиковаться в применении этих новых теорем к некоторым вопросам домашнего задания. Домашнее задание: вопросы 1-9, а также на странице 617 учебника.

22 Слова в скобках () — это то, о чем ученики должны научиться догадываться.Им не следует рассказывать им. Инструкции для учителя Инструкции (произнести вслух): построить круг AB Скрыть точку B Построить сегменты CD и ED, как показано Вопросы: Это новый тип линии, которую мы еще не видели. Их называют секантами. Как мы можем их определить? m CE на AB = Инструкции: Постройте точки пересечения F и G этих секущих. Измерьте углы дуги CE и FG. Измерьте угол D. Переместите точки C и / или E так, чтобы мера угла CE дуги была круглым числом, скажем 60 градусов. Вопросы: Когда вы перемещаете точку D на круг, как эта ситуация выглядит знакомой? (Это теорема о вписанном угле из последнего класса.) А что насчет того, когда D находится внутри круга? За пределами? Давайте исследуем отношения между этими углами. Инструкции: Выберите измерение угла D, а затем угла дуги FG. В меню графика выберите график как (x, y). Поместите ось и измените значения единиц измерения, чтобы график точно соответствовал показанному изображению. Точка, созданная Постройте как (x, y) выше, выберите его и в меню дисплея выберите точку трассировки. Переместите точку D за пределы круга CEA m FG на AB = FGD m! C D E =

23 м CE на AB = m FG на AB = C A F G D m! C D E = J E Вопросы: Что это за график? В чем дело? Какая связь между углом D и двумя углами дуги, которые вы измерили? (Студенты должны работать до тех пор, пока они не придут к выводу, что величина угла A составляет половину разницы между двумя углами дуги.Они могут получить это, задав вопросы о графике, его пересечениях, его наклоне и т. Д.) Инструкции: переместите точки C и / или E так, чтобы они обе были касательными. Переместите D снова за пределы круга Теперь переместите точки C и / или E так, чтобы одна была секущей, а другая — касательной. Переместите D за пределы круга в третий раз. Вопросы: Имеет ли значение погода, DF и DG обе секущие, или касательные, или их комбинации? (Нет, формула верна, это не имеет значения.) Это все три части теоремы 12.13, введите это в свои заметки и докажите, что следующие инструкции: Скройте все измерения, оси и линии сетки. Постройте сегменты CG и FE, как показано. Убедитесь, что линии не касаются. все, что им нужно, из урока 4). Это доказательство также очень хорошо приведет к теореме 12.12, которую студенты внесут в свои записи.) ECAFGD

24 Теоремы для главы 12: 12.1 Стандартная форма уравнения окружности с центром (h, k), а радиус r равен (xh) 2 + (yk) 2 = r Если прямая касается окружности, то она перпендикулярна радиусу, проведенному к точке касания. Если прямая находится в той же плоскости, что и окружность перпендикулярна радиусу в ее конечной точке на окружности, тогда прямая касается окружности Два сегмента, касательных к окружности из точки за пределами круга, совпадают В одной окружности или в конгруэнтных окружностях 1 конгруэнтные центральные углы имеют конгруэнтные дуги и , 2 конгруэнтные дуги имеют конгруэнтные центральные ангелы В одной и той же окружности или в конгруэнтных окружностях 1 конгруэнтные дуги имеют конгруэнтные дуги, а 2 конгруэнтные дуги имеют конгруэнтные хорды Диаметр, перпендикулярный хорде, делит хорду пополам и ее дугу Перпендикуляр биссектрисы хорда содержит центр окружности. В том же круге или в конгруэнтных окружностях 1 хорды, равноудаленные от центра, совпадают, а 2 конгруэнтные хорды равноудалены от центра. Мера вписанного угла составляет половину меры его пересеченной дуги.Следствие 1 Следствие 2 Два вписанных ангела, пересекающих одну и ту же дугу, конгруэнтны. Угол, вписанный в полукруг, — это прямой угол.

25 Следствие 3 Противоположные углы четырехугольника, вписанного в круг, являются дополнительными. Мера угла, образованного хордой, и касательной, которые пересекаются на окружности, составляет половину меры перехваченной дуги. Мера угла, образованного двумя хорды, которые пересекаются внутри круга, составляют половину суммы мер пересеченных дуг.Мера угла, образованного двумя секущими, двумя касательными или секущей и касательной, проведенной из точки за пределами круга, составляет половину разницы измерений перехваченных дуг.

SBAC для 11 классов: практические тесты

Примечание. Практический пакет SBAC НЕ включен в наше премиальное членство.

О программе SBAC для 11 классов

Экзамены SBAC 11-го класса — это единственные экзамены SBAC, которые проводятся в средней школе. Как и все экзамены SBAC, тест состоит из раздела ELA и раздела математики. Однако, в отличие от других экзаменов SBAC, этот экзамен SBAC используется моими колледжами для оценки размещения студентов и аккредитации.Поэтому настоятельно рекомендуется правильно подготовить 11-классника к экзамену.

Заявлений о содержании для 11 класса

Тест SBAC для 11 класса содержит конкретный список заявлений о содержании — навыков, которые, по мнению Совета по образованию SBAC, являются важнейшими компонентами готовности к колледжу. Тест SBAC состоит из теста ELA и теста по математике. Ниже приведены заявления о содержании, предназначенные для каждого раздела теста:

• Английский язык Искусство / Грамотность: Студенты, обучающиеся в колледже на уровне ELA, должны продемонстрировать надлежащие навыки чтения, письма, аудирования и исследования, необходимые для вводных курсов по многочисленным предметным областям.Они также должны продемонстрировать знания предметной области, а также навыки, связанные с подготовкой к начальному уровню, переводным и кредитным курсам английского языка и композиции.
• Математика: Студенты, обучающиеся в колледже по математике, должны быть способны продемонстрировать базовые математические знания, а также навыки количественного мышления, необходимые для вводных курсов по ряду предметных областей. Они также должны продемонстрировать знания предметной области, а также навыки, связанные с подготовкой к начальному уровню, переводным и кредитным курсам математики и статистики.

SBAC ELA

В тесте SBAC ELA для 11 класса используются два метода тестирования: тест на производительность и компьютерный адаптивный тест (CAT). Оба этих метода оценивают готовность к колледжу. Содержание 11-го класса остается таким же, как и на ранних этапах тестирования SBAC. Учащиеся оцениваются на основе их навыков чтения, письма, аудирования и исследования.

Вопросы по чтению требуют от учащихся чтения сложных литературных форм и информационных текстов, чтобы продемонстрировать близкие и критические способности к чтению.

Письменные задания проверяются в разделе экзамена на выполнение заданий. Студентам предоставляется ряд текстов, которые они должны интерпретировать и провести анализ, используя примеры и доказательства из текста. Они также должны оценить силу точек зрения и предположений автора или оратора на основе свидетельств из текста.

Исследовательские навыки также проверяются в задании на выполнение, так как учащихся просят использовать данный текст в качестве основы для своих сочинений и ответов.

Элементы для прослушивания разбросаны по всему разделу CAT. Тексты или отрывки могут быть прочитаны учащимся на разных этапах теста, и они должны продемонстрировать навыки рассуждения, чтобы правильно ответить на следующие вопросы с несколькими вариантами ответов.

Для получения более подробной информации о разделе ELA и о практике SBAC посетите нашу страницу SBAC ELA.

SBAC Math

Основные целевые области, подпадающие под требование о готовности к колледжу для 11 класса, можно разделить на четыре области:

• Концепции и процедуры: студенты должны применять математические концепции и процедуры.
• Решение проблем: учащиеся должны продемонстрировать мастерство решения соответствующих проблем в соответствии с заданиями теста.
• Моделирование / анализ данных: студенты должны использовать соответствующие инструменты и методы для решения реальных и математических задач.
• Коммуникативное обоснование: учащиеся должны уметь продемонстрировать логическое обоснование своего выбора процедур и математических выводов.

Как и тест ELA, математический тест SBAC разделен на раздел задач на производительность и раздел CAT.Для получения дополнительной информации об этих разделах и о том, что они влекут за собой, посетите нашу страницу SBAC Math.

Стандарты оценки SBAC для 11-х классов

Тесты

SBAC оцениваются в зависимости от того, насколько хорошо учащийся придерживается соответствующих требований к содержанию и целей. У каждого элемента теста есть целевой ответ, который студенты должны получить. Полученная общая необработанная оценка объединяет числовые значения, данные каждому элементу теста. Эти баллы называются баллами по шкале, и они варьируются от 2000 до 3000.

Как только учащемуся присваивается балл по шкале, он также получает ранг уровня достижения в диапазоне от 1 до 4.Если учащийся получает оценку уровня достижений 3 или выше, он или она продемонстрировали готовность к колледжу и карьере в соответствии со стандартами SBAC. Для получения подробной информации об уровнях достижений и шкале оценок посетите раздел «Результаты» на нашей странице практики SBAC.

SBAC для практических тестов для 11 класса

SBAC для 11 класса являются наиболее важными из тестов SBAC. Таким образом, практика для них имеет решающее значение. Изучение теста, его содержания и различных методов тестирования — все это ключевые шаги для обеспечения успеха в день тестирования.

OLSAT, NNAT, CogAT, New York City Gifted and Talented Test, ITBS, SBAC и другие товарные знаки являются собственностью соответствующих владельцев товарных знаков. Ни один из владельцев товарных знаков не связан с TestPrep-Online или этим веб-сайтом.

Класс 11 Репетитор по математике, Помощь и практика в Интернете

Не видите то, что вам нужно?

Не волнуйтесь, попробуйте поискать по всем нашим темам

Искать по всему StudyPug

Сложна ли математика в 11 классе?

Математика в 11 классе может быть сложной задачей, и она определенно станет проверкой ваших математических навыков.Из-за этого может показаться, что математика в 11 классе — это сложно и утомительно. Но не бойтесь — мы в StudyPug постарались ответить на все ваши вопросы и проблемы! От таких тем, как квадратичные функции до сигма-нотации, до разгадки формулы вершин (и даже больше!), Мы здесь, чтобы предоставить вам помощь с математикой для 11 класса. Наши тщательно разработанные учебные пособия по математике для 11 класса подходят для всех, поэтому независимо от того, являетесь ли вы учеником, которому требуется переподготовка по основам, или тем, кто хочет опередить игру, у нас есть материалы, охватывающие математику для 11 класса для чайников, а также более продвинутые. , сложное содержание.Независимо от уровня сложности, мы здесь, чтобы помочь вам на каждом этапе пути с помощью пошаговых примеров и множества практических вопросов. Математика в 11 классе не обязательно должна быть трудной! С помощью наших уроков-повторений и систематической практики вы обнаружите, что быстро и уверенно справляетесь с трудными вопросами!

Как подготовиться к 11 классу по математике?

Чувствуете себя неподготовленным к еще одному году математики? Не знаете, как и где начать заниматься математикой в ​​11 классе? В StudyPug есть все инструменты и ресурсы, которые помогут вам подготовиться к 11 классу математики!

Для понимания математики в 11 классе потребуется время, и это может быть сложно, если вы видите своего репетитора только раз в неделю или чувствуете, что вам нужно освежить в памяти темы, ранее затронутые в классе.Здесь, в StudyPug, наши репетиторы по математике для 11 классов и весь наш контент всегда в вашем распоряжении, когда они вам понадобятся. Благодаря круглосуточной поддержке и тысячам уроков, которые у вас под рукой, мы здесь, чтобы помочь вам улучшить свое понимание математических тем 11 класса и подготовиться к предстоящему тесту по математике в 11 классе и / или к экзамену по математике в 11 классе. Все еще чувствуете, что вам нужна дополнительная поддержка и справочная информация по некоторым темам, изучаемым в математике 11 класса? Некоторые из тем, которые вы изучаете в 11 классе по математике (например,грамм. Квадратичные отношения, завершающие квадрат) мы начали вводить в 10 классе по математике. Математика 10-го класса является обязательным курсом для 11-го класса, и мы настоятельно рекомендуем хорошо владеть знаниями и навыками, полученными в 10-м классе, чтобы помочь вам добиться успеха в 11-м классе. Перейдите на нашу страницу математики для 10-го класса, чтобы начать исправление прямо сейчас!

Как использовать StudyPug для изучения математики в 11 классе?

Нашим намерением для StudyPug было создание круглосуточного онлайн-компаньона, способного удовлетворить все ваши потребности в обучении математике в 11 классе.Мы тщательно разработали наш веб-сайт, чтобы он был интуитивно понятным и легким для навигации, но мы также включили этот раздел для тех из вас, кто посещает или пробует нас впервые. Имейте в виду, что если вы студент, который все еще не уверен, подходит ли вам StudyPug, вы все равно можете попробовать наш продукт / услугу, начав с бесплатных уроков, которые доступны сразу и без проблем.

В качестве общего правила, прежде чем переходить к какой-либо из наших тем по математике в 11 классе, мы рекомендуем начать с оценки ваших предварительных знаний.Это просто делается путем проверки вашего знакомства с концепциями, которые, как мы считаем, вы должны относительно хорошо владеть. Почти все наши темы начинаются с описания основных понятий, которые вам следует знать, а также других связанных, актуальных понятий.

Если вы точно знаете, что ищете, мы рекомендуем сразу перейти к использованию нашей поисковой системы. Используйте это, чтобы отточить концепции, темы или вопросы, которые вы считаете наиболее трудными. Помнить; не бойтесь, если вы чувствуете, что вам нужно начать с некоторых элементарных основ, которые вы изучили ранее в 10 классе по математике или где-либо еще.

После того, как вы определили тему, над которой вам требуется дополнительная работа, наши короткие, но информативные видеоуроки проведут вас через примеры (от простых до сложных), чтобы конкретизировать концепции, которые вам необходимо изучить, а также советы и стратегии изучения. Смотрите и пересматривайте эти уроки столько раз, сколько вам нужно! Мы также предоставляем перефразированную расшифровку сути того, о чем говорилось в видео, если вы предпочитаете изучать и исправлять этот способ.

Последний, но, конечно, не последний из этих шагов, мы рекомендуем вам проверить свои знания и навыки! Мы подготовили множество вопросов по каждой теме, чтобы вы усвоили их и довели до совершенства! Посмотрите, насколько хорошо вы научились, и получите больше практики из самых разных и разнообразных (т.е. от простого к сложному) вопросов.

Ищете более увлекательное чтение и метод, чтобы выучить математику в 11 классе? Загляните в наш блог, чтобы узнать о последовательности Фибоначчи и Ким Кардашьян!

Как сдать 11 класс по математике?

Готовитесь к тесту или экзамену по математике в 11 классе? Вы попали в нужное место! На нашей домашней странице https://www.studypug.com/ca/grade11 есть все необходимое для изучения математики в 11 классе. Мы, StudyPug, существуем, чтобы помочь вам в достижении ваших академических целей. Итак, готовитесь ли вы к тесту по главе в единичном круге или вам требуется быстрый обзор нескольких тем для вашего большого выпускного экзамена, мы хотим убедиться, что вы чувствуете себя уверенно при выполнении всех своих оценок.

В StudyPug мы проводим многочисленные уроки математики для 11 классов, охватывающие несколько провинциальных и международных учебных программ. Мы также создаем контент на основе нескольких известных учебников, поэтому мы на пути к тому, чтобы помочь вам сосредоточиться на многочисленных темах и типах вопросов, с которыми вы, возможно, столкнетесь в математике в 11 классе.