Геометрия 10 Контрольные работы Атанасян
Геометрия 10 Контрольные работы Атанасян — контрольные работы по геометрии в 10 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта) В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 10 класс / М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Геометрия 10 класс. Контрольные работы
по учебнику Атанасяна
Глава I. Параллельность прямых и плоскостей (уроки 6-24)
К-1. Контрольная работа с ответами и решениями «Аксиомы стереометрии» (урок 15):
Контрольная работа № 1 + ОтветыК-2. Контрольная работа с ответами и решениями «Параллельные плоскости. Тетраэдр. Параллелепипед» (урок 23):
Контрольная работа № 2 + Ответы
Глава II.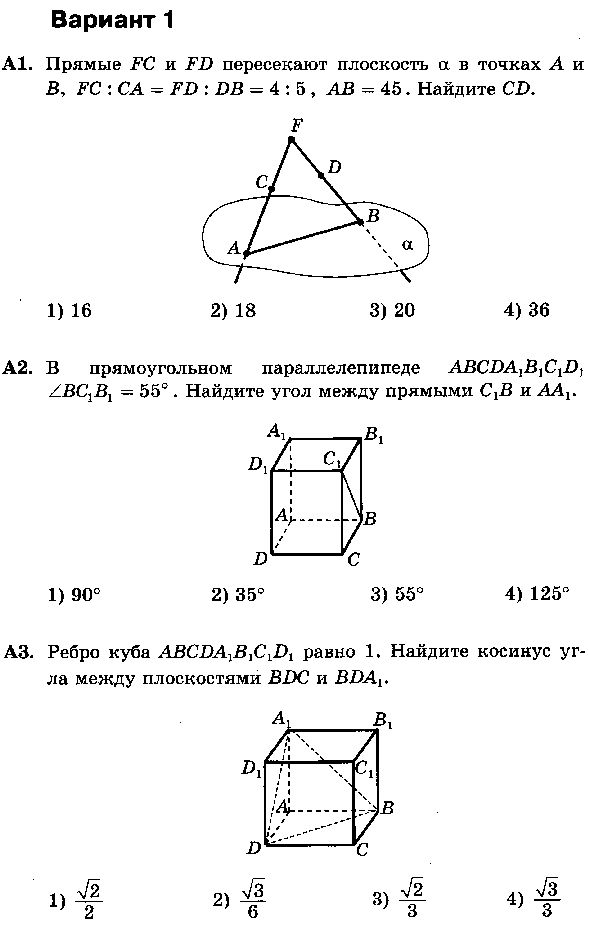
Перпендикулярность прямых и плоскостей (уроки 25-44)
Перпендикулярность прямых и плоскостей (уроки 25-44)К-3. Контрольная работа с ответами и решениями «Перпендикулярность прямых и плоскости» (урок 43):
Глава III. Многогранники (уроки 45-56)
К-4. Контрольная работа с ответами и решениями «Многогранники» (урок 55):
Контрольная работа № 4 + Ответы
Глава IV. Векторы в пространстве (уроки 57-62)
К-5. Зачет по теме «Векторы в пространстве» (урок 62):
Контрольная работа № 5 + Ответы
Итоговое повторение курса геометрии (уроки 63-68)
К-6. Итоговая контрольная работа за курс 10 класса (урок 66):
Контрольная работа № 6 + Ответы
ПОЯСНЕНИЯ
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным).
Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
Смотрите также:
Геометрия 7 класс. Контрольные работы (Атанасян и др.)
Геометрия 8 класс. Контрольные работы (Атанасян и др.)
Геометрия 9 класс. Контрольные работы (Атанасян и др.)
Геометрия 11 класс. Контрольные работы (Атанасян и др.)
Вы смотрели: Геометрия 10 Контрольные работы Атанасян — контрольные работы по геометрии в 10 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта).
В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 10 класс / М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы. Учебник. М.: Просвещение».
Геометрия 10 класс Контрольная № 2 с ответами
Контрольная работа по геометрии в 10 классе «Параллельные плоскости. Тетраэдр. Параллелепипед» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 10 класса (В.А. Яровенко, ВАКО). Урок 23. Геометрия 10 класс Контрольная № 2 «Параллельные плоскости. Тетраэдр. Параллелепипед».
Смотреть Список всех контрольных по геометрии в 10 классе (Атанасян)
Контрольная работа № 2
«Параллельные плоскости.
Тетраэдр. Параллелепипед»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Контрольная работа
I уровень сложности
Вариант 1
- Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1. Найдите А1В1, если АВ = 5 см.
- Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
- Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А
Найдите МА2 и MB2.Вариант 2
- Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см.
- Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?
- Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А1, В1, С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА = m, АА1 = n, АВ = b, ВС = а.
II уровень сложности
Вариант 1
- Построить сечение, проходящее через линии и точки, выделенные на чертеже (рис. 1).
- Ребро куба ABCDA1B1C1D1 равно 2 см. Найдите расстояние между прямыми АВ и B1
- Докажите, что линии пересечения двух пар параллельных плоскостей параллельны.
Вариант 2
- Построить сечение, проходящее через линии и точки, выделенные на чертеже (рис. 2).
- Дан прямой параллелепипед ABCDA1B1C1D1, основанием которого является ромб ABCD, угол BAD = 30°, АВ= 18, BB1 = 12. Найти площадь AB1C1D.
- Непараллельные отрезки АВ и CD лежат соответственно в параллельных плоскостях α и β. Что можно сказать о взаимном расположении прямых АС и ВО?
III уровень сложности
Вариант 1
- Между двумя параллельными плоскостями заключены перпендикуляр длиной 3 м и наклонная, равная 5 м. Расстояние между концами их (в каждой плоскости) равно 4 м. Найдите расстояние между серединами перпендикуляра и наклонной.
Вариант 2
- Построить сечение, проходящее через точки, выделенные на рисунке (рис. 2).
- Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором AD = а, АВ = b, АА1 = с. Найдите длины отрезков D1P и CN, где Р — середина отрезков B1C, N — середина отрезка A
3. Рефлексия учебной деятельности (ОТВЕТЫ)
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.
Решение заданий I уровня сложности
Решение заданий II уровня сложности
Решение заданий III уровня сложности
Вы смотрели: Геометрия 10 класс Контрольная № 2. Поурочное планирование по геометрии для 10 класса. УМК Атанасян (Просвещение). Урок 23. Контрольная работа по геометрии «Параллельные плоскости. Тетраэдр. Параллелепипед» + ОТВЕТЫ.
Смотреть Список всех контрольных по геометрии в 10 классе по УМК Атанасян.
Контрольная работа № 1 Тема: «Параллельность прямых, прямой и плоскости» | |
1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. | 2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. |
Контрольная работа № 2 Тема: «Параллельность плоскостей. Тетраэдр и параллелепипед.» | |
1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. | 2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3. |
Контрольная работа № 3 Тема: «перпендикулярность в пространстве» | |
1 вариант 1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM, в) найдите синус угла между плоскостью ромба и плоскостью α | 2 вариант 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM, в) Найдите синус угла между плоскостью квадрата и плоскостью α. |
Контрольная работа № 4 Тема: «Многогранники» | |
1 вариант 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда | 2 вариант 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. |
КОНТРОЛЬНАЯ РАБОТА № 5 ТЕМА: «ВЕКТОРЫ В ПРОСТРАНСТВЕ» | |
Вариант 1 1. Изобразите параллелепипед ABCDA1B1C1D1. Постройте на рисунке векторы, равные: 1) ; 2) . 2. ABCDA1B1C1D1 – параллелепипед, отрезки АC и BD пересекаются в точке М. Разложите вектор 3. В тетраэдре DABC точка М – точка пересечения медиан грани DBC, Е – середина АС. Разложите вектор 4. DABC – тетраэдр, О – точка пересечения медиан АВС, точка F лежит на AD, причем AF : FD = 3 : 1. Разложите вектор по векторам , , . | Вариант 2 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) ; 2) . 2. В параллелепипеде ABCDA1B1C1D1 диагонали грани АВCD пересекаются в точке О. Разложите вектор 3. DABC – тетраэдр, точка Е – середина ребра АD, а точка М – точка пересечения медиан грани BDC. Разложите вектор по векторам , и . 4. Дан тетраэдр DABC. Медианы грани АВС пересекаются в точке М, , причем DN : NC = 5 : 1. Разложите вектор по векторам , , . |
Тест по геометрии 10 класс (задания и ответы)
Скачать: скачать
Смотреть онлайн:
Интересные задания:
1. Плоскость, притом только одна, проходит через
а) любые три точки;
б) любые три точки лежащие на одной прямой;
в) любые три точки не лежащие на одной прямой.
2. Плоскость, притом только одна, проходит через
а) две пересекающиеся прямые;
б) одну прямую;
в) две скрещивающиеся прямые.
3. Если две точки прямой принадлежат плоскости, то прямая
а) пересекает плоскость;
б) лежит в плоскости;
в) параллельна плоскости.
прямой
а) АВ;
б) АС;
в) ВС
.
8. Точки А, В, С и Д не лежат в одной плоскости, следовательно
а) какие-то три из них лежат на одной прямой;
б) никакие из трех данных точек не лежат на одной прямой;
в) прямые АВ и СД пересекаются.
9. Какое из следующих утверждений верно?
а) любые четыре точки лежат в одной плоскости;
б) любые три точки не лежат в одной плоскости;
в) любые четыре точки не лежат в одной плоскости;
г) через любые три точки проходит плоскость, и притом только одна.
10. Сколько общих точек могут иметь две различные плоскости?
а) 2;
б) 3;
в) несколько;
11. Точки А, В, С лежат на одной прямой, точка D не лежит на ней. Через
каждые три точки проведена одна плоскость. Сколько различных
плоскостей при этом получилось?
а) 2;
б) 3;
в) 1;
г) бесконечно много.
Вам будет интересно:
Диагностическая работа по геометрии для 9 класса (итоговая работа за 8 класс) для школ-участников проекта и школ-кандидатов в проекте «Математическая вертикаль»
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Круг | Примечания, видео, контроль качества и тесты | 10 класс> Обязательная математика> Геометрия
Круг
На приведенных ниже рисунках показаны разные части круга.
Теперь мы изучаем центральный угол, вписанный угол, циклический четырехугольник, касательные и связанные с ними теоремы.
Центральный угол
В окружности PQR радиусы OP и OQ образуют угол в центре O. Итак, острый ∠POQ и рефлекс POQ являются центральными углами.Часть PQ круга представляет собой дугу.
∠POQ соответствует \ (\ widehat {PQ} \), а reflex∠POQ — \ (\ widehat {PRQ} \). По мере увеличения длины дуги величина центрального угла, образованного дугой, также увеличивается. Таким образом, центральный угол можно измерить с помощью соответствующей противоположной дуги. Следовательно, POQ = \ (\ widehat {PQ} \) и reflex∠POQ = \ (\ widehat {PRQ} \)
Угол на окружности (вписанный угол)
Угол, образованный соединением двух поясов на окружности окружности, называется углом на окружности или вписанным углом.На следующем рисунке хорда AB и хорда CB пересекаются в точке B на окружности, и образуется ∠POQ, который представляет собой угол на окружности, лежащий на дуге AC \ ((\ widehat {AC}) \). Вписанный угол также можно измерить (выразить) через соответствующую ему дугу \ ([\ angle ABC = \ frac {1} {2} \ widehat {AC}] \)
Дуга, образованная хордой
В круге ABC хорда AB делит круг на две части. Дуга AB \ ((\ widehat {AB} \) образована хордой AB.Таким образом, при чтении дуги и соответствующей ей хорды мы используем одну и ту же букву, но длина не совсем одинакова. На следующем рисунке \ (\ widehat {AB} \) — это малая дуга, а \ (\ widehat {ACB} \) — большая дуга. Вкратце \ (\ widehat {ADB} \) читается как второстепенный \ (\ widehat {AB} \), а \ (\ widehat {ACB} \) читается как старший \ (\ widehat {AB} \).
Циклический четырехугольник
Если все вершины четырехугольника находятся на окружности окружности, то четырехугольник называется вписанным четырехугольником.На следующем рисунке ABCD — вписанный четырехугольник. Другими словами, вписанный в круг четырехугольник называется вписанным четырехугольником. Точки A, B, C, D параллельны. ABCD — вписанный четырехугольник, но ABCE и ADCE — не вписанные четырехугольники.
| Вопрос | Common Core Standard # | CCSS Math Excerpt |
| 1 | 7.G.1 | … решать задачи, связанные с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей из масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе … |
| 2 | 7.G. 1 | … решать задачи, связанные с масштабными чертежами геометрических фигур, включая вычисление фактической длины и площади на основе масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе … |
| 3 | 7.G.1 | …решать проблемы, связанные с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей из масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе … |
| 4 | 7.G.3 | … описывают двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, например, в плоских сечениях правой прямоугольной призмы и прямоугольных пирамид … / td> |
| 5 | 7.G.4 | … знать формулы площади и окружности круга и использовать их для решения задач; дать неформальный вывод отношения между окружностью и площадью круга… |
| 6 | 7.G.5 | … использовать факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре … |
| 7 | 7.G.6 | … решать реальные и математические задачи, касающиеся площади, объема и площади поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубы и правые призмы … |
| 8 | 7.G.6 | … решать реальные и математические задачи, касающиеся площади, объема и площади поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и правильных призм … |
| 9 | 7.G.6 | … решать реальные и математические задачи, касающиеся площади, объема и площади поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм. |
PPT — Презентация PowerPoint по геометрии 9-го класса, скачать бесплатно
Геометрия 9-го класса Урок 10-5: Касательные
Основная идея • Используйте свойства касательных! • Решение задач, связанных с описанными многоугольниками. Новый словарь • Касательная • Любая линия, которая касается кривой ровно в одном месте • Точка касания • Точка пересечения кривой и линии
Теорема 10.9 • Если прямая касается окружности, то она перпендикулярна радиусу, проведенному до точки касания. • Пример: Если RT является касательной, ИЛИ RT T R O
Пример: Найти длины АЛГЕБРАР является касательной к Q в точке R. Найдите y. S 20 16 Q P R y Поскольку радиус перпендикулярен касательной в точке касания, QRSR. Это делает SRQ прямым углом, а SRQ прямоугольным треугольником. Используйте теорему Пифагора, чтобы найти QR, который составляет половину длины y.
Пример: найти длины (SR) 2 + (QR) 2 = (SQ) 2 Теорема Пифагора 162 + (QR) 2 = 202 SR = 16, SQ = 20 256 + (QR) 2 = 400 Упростить ( QR) 2 = 144 Вычтите 256 из каждой стороны QR = +12 Извлеките квадратный корень из каждой стороны Поскольку y — это длина диаметра, игнорируйте отрицательный результат. Таким образом, y дважды QR или y = 2 (12) = 24 Ответ: y = 24
Пример CD является касательной к B в точке D.Найди. • 15 • 20 • 10 • 5 C a B A D 40 25
Теорема 10.10 • Если прямая перпендикулярна радиусу окружности в ее конечной точке на окружности, то эта прямая касается окружности. • Пример: Если OR RT, RT является касательной. RTO
Пример: Определить касательные Определить, является ли BC касательным к AC 7 9 7 AB 7 Сначала определите, является ли ABC прямоугольным треугольником, используя обратную теорему Пифагора
Пример: Определите касательные ( AB) 2 + (BC) 2 = (AC) 2 Обратное к теореме Пифагора 72 + 92 = 142AB = 7, BC = 9, AC = 14 130 ≠ 196 Упростить Поскольку обратное утверждение теоремы Пифагора не подтвердилось в этом случае, ABC не является прямоугольным треугольником Ответ: Итак, BC не касается A.? ?
Пример: определение касательных Определите, является ли WE касательной к D. E 16 24 10 DW 10 Сначала определите, является ли EWD прямоугольным треугольником, используя обратную теорему Пифагора
Пример: определите касательные (DW) 2 + (EW) 2 = (DE) 2 Обращение к теореме Пифагора 102 +242 = 262DW = 10, EW = 24, DE = 26 676 = 676 Упростим. Поскольку верно обратное теореме Пифагора, EWD — прямоугольный треугольник, а EWD — прямой угол.Ответ: Таким образом, DW WE, делая WE касательной к D.? ?
Quick Review Определите, является ли ED касательной к QA Да B. Нет C. Не может быть определено D √549 18 QE 15
Quick Review Определить, является ли XW касательной к VA Да B. Нет C. Невозможно определить W 10 17 10 VX 10
Теорема 10.11 • Если два сегмента из одной внешней точки касаются окружности, то они совпадают • Пример: AB ≈ AC BCA
Пример: конгруэнтные касательные АЛГЕБРА Найдите x.Предположим, что сегменты, которые кажутся касательными к окружностям, касаются друг друга. ED и FD нарисованы из одной и той же внешней точки и касаются S, поэтому ED ≈ FD. DG и DH проводятся из одной и той же внешней точки и касаются T, поэтому DG ≈ DH H x + 4 F y DG y — 5 E 10
Пример: конгруэнтные касательные ED = FD Определение конгруэнтных сегментов 10 = y Замена Используйте значение y, чтобы найти x. DG = DH Определение конгруэнтных сегментов 10 + (y — 5) = y + (x + 4) Замена 10 + (10-5) = 10 + (x + 4) y = 10 15 = 14 + x Упростить.1 = x Вычтите 14 с каждой стороны Ответ: 1
Быстрый просмотр Найдите. Предположим, что сегменты, которые кажутся касательными к окружностям, касаются друг друга. • 6 • 4 • 30 • -6 30 N b 6 — 4a RA
Пример: треугольники, описанные вокруг круга Треугольник HJK описан около G. Найдите периметр HJK, если NK = JL +29 HN 18 KLM 16 J
Пример: треугольники, описанные вокруг окружности Используйте теорему 10.11, чтобы определить равные меры: JM = JL = 16, JH = HN = 18 и NK = MK Нам дано, что NK = JL + 29, поэтому NK = 16 + 29 или 45 Тогда MK = 45 P = JM + MK + HN + NK + JL + LH Определение периметра = 16 + 45 + 18 + 45 + 16 + 18 или 158 Ответ на замену: Периметр HJK составляет 158 единиц.
Quick Review Треугольник НЕ ограничен около M.