Физика кинематика 10 класс контрольная: Контрольная работа «Кинематика» 10 класс скачать

Уравнения движения для простого снаряда
уравнение	горизонтальный	вертикальный
ускорение	a _x	= 0	a _y	= — г
скорость-время	v _x	= v _{0 x}	v _y	= v _{0 y} — gt
время вытеснения	x	= x ₀ + v _{0 x} т	y	= y ₀ + v _{0 y} t — ½ gt ²
скорость-смещение	v _y ²	= v _{0 y} ²-2 g ( y — y ₀)

Содержание

Контрольная работа по физике 10 класс Кинематика

Вариант 1

1. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 0 до 10 с. Ответ выразите в м/с.

Ответ:-10

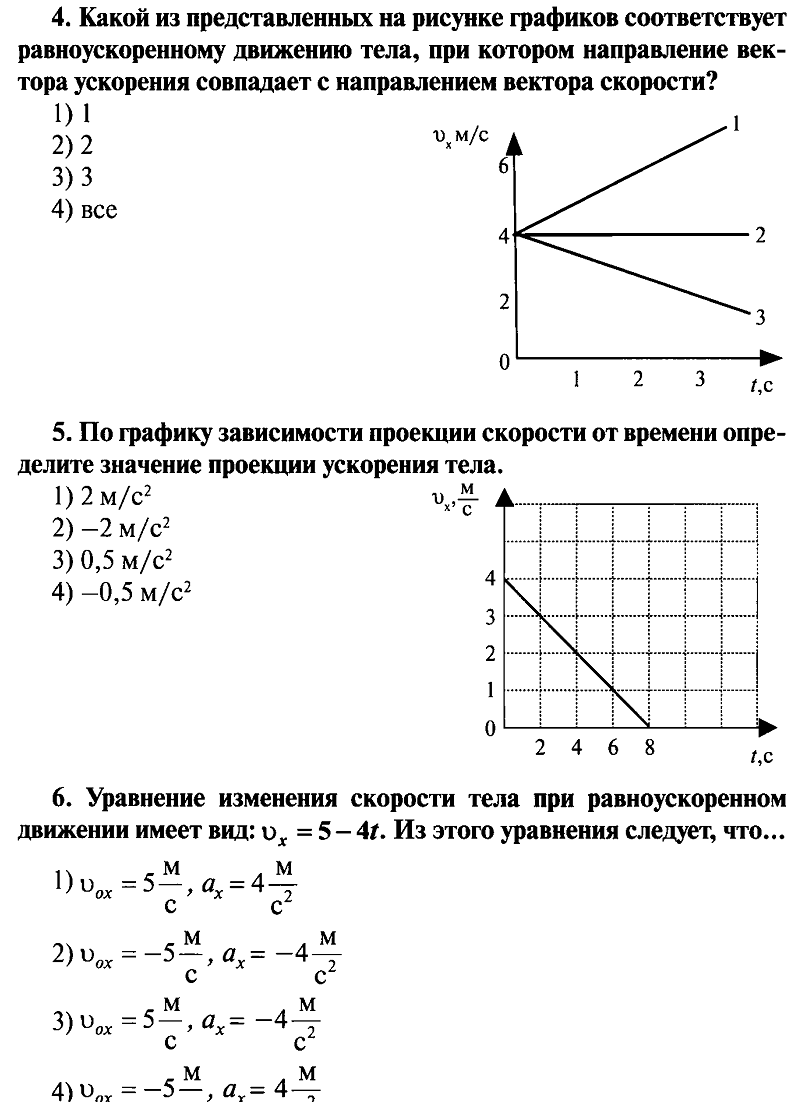
2. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)

Ответ: 0,7

3. Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)

Ответ: 25

4. При прямолинейном движении зависимость координаты тела x от времени t имеет вид:

Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду. )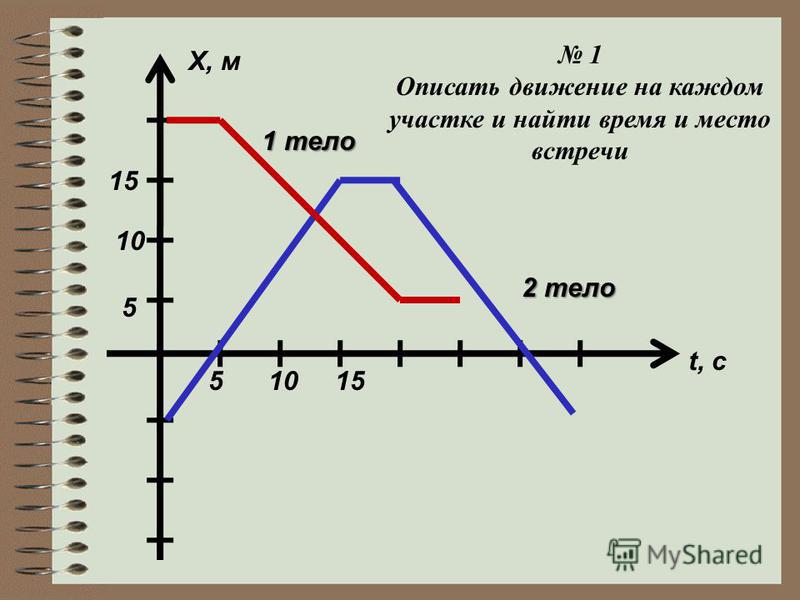

Ответ: 18

5. На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 10

6. Материальная точка движется по окружности радиусом 4 м. На графике показана зависимость модуля её скорости v от времени t. Чему равен модуль центростремительного ускорения точки в момент

t = 3 с? (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 9

7. Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 1

8. На рисунке приведены графики зависимости координаты от времени для двух тел: А и В, движущихся по прямой, вдоль которой и направлена ось Ох. Выберите два верных утверждения о движении тел.

1) Тело А движется равноускоренно.

2) Временнόй интервал между встречами тел А и В составляет 6 с.

3) В течение первых пяти секунд тела двигались в одном направлении.

4) За первые 5 с тело А прошло 15 м.

5) Тело В движется с постоянным ускорением.

Ответ: 25|52

9. Анализируя график зависимости модуля скорости тела от времени, выберите из приведённых ниже утверждений три правильных и укажите их номера.

1) Скорость тела за шесть секунд изменилась от 0 м/с до 6 м/с.

2) Тело двигалось равноускоренно в интервале от 0 до 1 с и в интервале от 2 до 4 с, и равномерно в интервалах 1−2 и 4−6 с.

3) Тело двигалось равноускоренно в интервале от 0 до 1 с и в интервале от 2 до 4 с, и не двигалось в интервалах 1−2 и 4−6 с.

4) За 6 с тело прошло путь 23 м.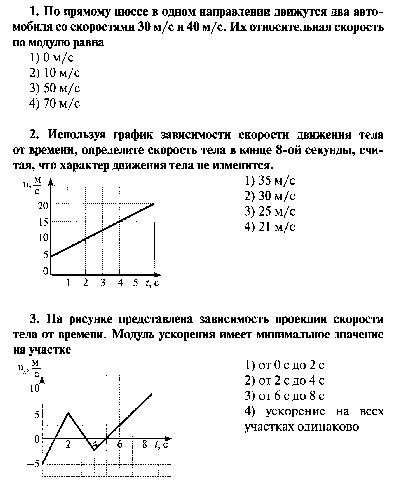

5) За 6 с тело прошло путь 36 м.

Ответ: 124

10.Небольшое тело движется вдоль оси OX. На рисунке показан график зависимости проекции скорости V

_x этого тела на указанную ось от времени t. Выберите два верных утверждения на основании анализа графика.

1) За первые 10 секунд движения тело проходит такой же путь, как и за последние 20 секунд движения

2) В интервале времени от t = 0 с до t = 20 с тело покоится

3) Тело всё время движется в одном направлении.

4) Тело оказывается на максимальном расстоянии от своего начального положения через 30 секунд после начала движения

5) В моменты времени t = 10 с и t = 50 с тело имеет разные ускорения

Ответ: 14|41

Вариант 2

1. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 30 до 50 с. Ответ выразите в м/с. Ответ: 5

2. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)

Ответ: 1,5

3. Тело брошено вертикально вверх с начальной скоростью 15 м/с. Чему равен модуль скорости тела через 0,5 c после начала отсчета времени? Сопротивление воздуха не учитывать. (Ответ дайте в метрах в секунду.)

Ответ: 10

4. Зависимость координаты x тела от времени t имеет вид:

Чему равна проекция скорости тела на ось Ox в момент времени t = 3 с при таком движении? (Ответ дайте в метрах в секунду. )

Ответ: 20

5. На графике приведена зависимость проекции скорости

v_x тела от времени. Определите ускорение тела a_x. (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 8

Ответ: 1

7. Груз, подвешенный на нити длиной 2 м, отведён в сторону и отпущен. Нижнюю точку траектории он проходит со скоростью 1,4 м/с. Найдите центростремительное ускорение груза в нижней точке траектории. (Ответ дайте в метрах в секунду в квадрате и округлите до целых.)

Ответ: 1

8. На рисунке приведены графики зависимости координаты от времени для двух тел: А и В, движущихся по прямой, вдоль которой направлена ось Ох. Выберите два верных утверждения о характере движения тел.

1) Тело А движется с постоянной скоростью, равной 5 м/с.

2) В момент времени t = 5 с скорость тела В была больше скорости тела А.

3) В течение первых пяти секунд тела двигались в одном направлении.

4) В момент времени t = 2 с тела находились на расстоянии 20 м друг от друга.

5) За первые 5 с движения тело В прошло путь 15 м.

Ответ: 13

9. В эксперименте получен график зависимости модуля скорости прямолинейно движущегося тела от времени. Анализируя график, выберите из приведённых ниже утверждений три правильных и укажите их номера.

1) Модуль скорости тела за 6 секунд изменился от 0 м/с до 6 м/с.

2) Из четырёх интервалов времени максимальный путь был пройден телом в интервале времени от 4 до 6 с.

3) Тело двигалось равнозамедленно в течение первых 6 секунд и не двигалось в интервале от 6 до 7 с.

4) Тело двигалось равноускоренно в течение первых 6 секунди не двигалось в интервале от 6 до 7 с.

5) Тело двигалось равномерно в интервале от 6 до 7 секунд со скоростью 6 м/с.

Ответ: 125

10.Небольшое тело движется вдоль оси OX. На рисунке показан график зависимости проекции скорости V_x этого тела на указанную ось от времени t. Выберите два верных утверждения на основании анализа графика.

1) За первые 30 секунд движения тело проходит такой же путь, как и за последние 30 секунд движения

2) В интервале времени от t = 20 с до t = 35 с тело движется равномерно

3) В момент времени t = 30 с тело останавливается

4) Тело оказывается на максимальном расстоянии от своего начального положения через 60 секунд после начала движения

5) В моменты времени t = 23 с и t = 33 с тело имеет одинаковое ускорение

Ответ: 35|53

Вариант 3

1. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 50 до 70 с. Ответ выразите в м/с.

Ответ: -7,5

2. Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.) Ответ: 11

3. Зависимость координаты x тела от времени t имеет вид:

Чему равна проекция скорости тела на ось Ox в момент времени t = 1 с при таком движении? (Ответ дайте в метрах в секунду.)

Ответ: 0

4. Тело брошено вертикально вверх. Через 1,5 с после броска его скорость 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)

Ответ: 35

5. На графике приведена зависимость проекции скорости тела от времени. Определите по графику модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 10

Ответ: 9

7. Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 4

8. На рисунке приведены графики зависимости координаты от времени для двух тел: А и В, движущихся по прямой, вдоль которой и направлена ось Ох. Выберите два верных утверждения о характере движения тел.

1) Тело А движется равномерно.

2) Тело А движется с постоянной скоростью, равной 5 м/с.

3) Первый раз тела А и В встретились в момент времени равный 3 с.

4) Вторично тела А и В встретились в момент времени, равный 7 с.

5) В момент времени t = 5 с тело В достигло максимальной скорости движения.

Ответ: 13|31

утверждений три правильных и укажите их номера.

1) Скорость тела за шесть секунд изменилась от 0 м/с до 6 м/с.

4) За 6 с тело прошло путь 23 м.

5) За 6 с тело прошло путь 36 м.

Ответ: 124

1) За первые 10 секунд движения тело проходит такой же путь, как и за последние 20 секунд движения

2) В интервале времени от t = 0 с до t = 20 с тело покоится

3) Тело всё время движется в одном направлении.

5) В моменты времени t = 10 с и t = 50 с тело имеет разные ускорения

Ответ: 14|41

Вариант 4

1. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Найдите скорость велосипедиста в интервале времени от 10 до 30 с. Ответ выразите в м/с. Ответ:2.5

2. Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Ответ: 120

3. Тело брошено вертикально вверх с начальной скоростью 20 м/с. Чему равен модуль скорости тела через 0,5 c после начала отсчета времени? Сопротивление воздуха не учитывать. (Ответ дайте в метрах в секунду.)

Ответ: 15

4. Зависимость координаты x тела от времени t имеет вид:

Ответ: 6

Ответ: 1

7. Груз, подвешенный на нити длиной 2 м, отведён в сторону и отпущен. Нижнюю точку траектории он проходит со скоростью 0,4 м/с. Найдите центростремительное ускорение груза в нижней точке траектории. (Ответ дайте в метрах в секунду в квадрате.)

Ответ: 0,08

1) Тело А движется с постоянной скоростью, равной 10 м/с.

2) В момент времени t = 5 с скорость тела A была больше скорости тела B.

3) В течение первых семи секунд тела двигались в одном направлении.

4) В момент времени t = 2 с тела находились на расстоянии 10 м друг от друга.

5) За первые 5 с движения тело В прошло путь 15 м.

Ответ: 24|42

1) Модуль скорости тела за 6 секунд изменился от 0 м/с до 6 м/с.

2) Из четырёх интервалов времени максимальный путь был пройден телом в интервале времени от 4 до 6 с.

3) Тело двигалось равнозамедленно в течение первых 6 секунд и не двигалось в интервале от 6 до 7 с.

4) Тело двигалось равноускоренно в течение первых 6 секунди не двигалось в интервале от 6 до 7 с.

5) Тело двигалось равномерно в интервале от 6 до 7 секунд со скоростью 6 м/с.

Ответ: 125

1) За первые 10 секунд движения тело проходит такой же путь, как и за последние 20 секунд движения

2) В интервале времени от t = 0 с до t = 20 с тело покоится

3) Тело всё время движется в одном направлении.

5) В моменты времени t = 10 с и t = 50 с тело имеет разные ускорения

Ответ: 14|41

Контрольная работа по теме «Кинематика» (10 класс)

Тема: Контрольная работа по теме: «Кинематика».

Цель: Проверить уровень знаний учащихся по теме «Кинематика».

Оборудование: задания в двух вариантах.

Тип урока: контроль и оценивание знаний.

Вариант 1

Задание 1 (1 балл)

Траекторией движения тела называется…

A. … путь, пройденный телом.

Б. … вектор, соединяющий начальное и конечное положение тела.

B. … линия, по которой движется тело.

Г. … длина отрезка, соединяющего начальное и конечное положение тела.

Задание 2 (2 балла)

Колесо обозрения совершает один оборот за 5 мин. Какова частота его обращения?

A. 1/ЗООс^-1 Б. 1/5с^-1

B. 5с^-1 Г. 300с^-1

Задание 3 (2 балла)

Автомобиль, остановившийся перед светофором, набрал затем скорость 54км/ч на пути 45м. С каким ускорением он двигался?

Задание 4 (3 балла)

Одну треть пути тело двигалось со скоростью 90км/ч, а две трети — со скоростью 60км/ч. Найдите среднюю скорость движения.

Задание 5 (4 балла)

Свободное падение тела продолжалось 6с. На какой высоте находилось тело за 2с до падения на землю?

Вариант 1 (ответы)
1. В 1 б.

Вариант 2

Задание 1 (1 балл)

Какая из названных ниже величин является скалярной?

A. Перемещение. Б. Скорость

B. Ускорение. Г. Путь.

Задание 2 (2 балл)

Модель самолёта при работе аттракциона движется по окружности со скоростью 5м/с, совершая один оборот за 4с. Каков радиус окружности?

A. 7,85м. Б. 6,4м.

B.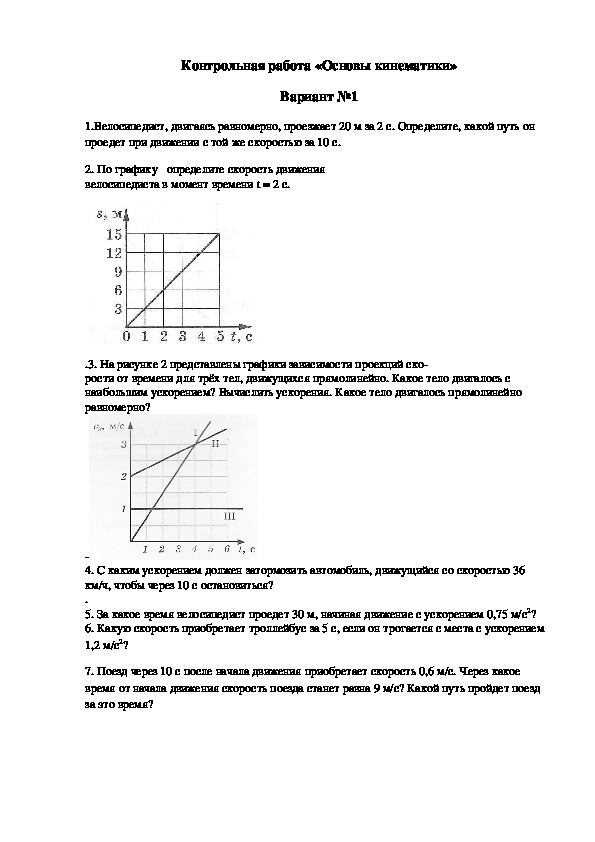 5м. Г. 3,2м.

Задание 3 (2 балл)

Автомобиль, разгоняющийся с ускорением 0,5м/с², достиг скорости
18м/с. С какой скоростью он будет двигаться через 6с, продолжая
разгоняться с тем же ускорением?
А. 18,5м/с. Б.21м/с. В.24м/с. Г. 54м/с.

Задание 4 (3 балла)

Поезд, двигаясь под уклон, прошел за 10с путь 160м и развил скорость 17м/с. Какой была скорость поезда в начале уклона?

Задание 5 (4 балл)

Тело свободно падало с высоты 20м. На какой высоте оно находилось, когда прошла половина всего времени падения?

Вариант 2 (ответы)
1. Г 1 б.

Контрольная работа по КИНЕМАТИКЕ 10 класс

Контрольная работа по КИНЕМАТИКЕ 10 класс. 2011 год

Относительность движения.

Плот плывёт со скоростью 3 м/с. Перпендикулярно течению идёт мальчик со скоростью 4м/с относительно плота. Определить скорость мальчика относительно берега. Какое перемещение он совершит за 2 с относительно плота и относительно берега.

Девочка, чтобы двигаться перпендикулярно берегу, плывет относительно воды под углом 45⁰ к берегу. Какова скорость течения реки, если расстояние между берегами 30 м она преодолевает за 10 с?

При безветренной погоде парашютист приземляется со скоростью 4м/с. С какой скоростью он приземлится при ветре силой 3м/с, дующем горизонтально? Как будет направлена эта скорость?

Равноускоренное прямолинейное движение движение.

Начальная скорость тела 7,2 км/час, ускорение 1 м/с², найти его скорость и перемещение через 4 с. Построить график зависимости модуля скорости от времени.

Тело двигалось замедленно до остановки в течение 4 с. Модуль ускорения равнялся 1м/с². Какова была начальная скорость, какое перемещение совершило тело. Построить график зависимости модуля скорости от времени.

Тело за 4 с изменило свою скорость с 2 м/с до 6 м/с. Каким было ускорение тела? Какое перемещение оно совершило? Построить график зависимости модуля скорости от времени.

Автомобиль разогнался с места до скорости 72 км/час за 5 с. С каким ускорением он двигался? Какой путь прошёл? Построить график зависимости модуля скорости от времени.

Свободное падение.

Тело бросили вертикально вверх со скоростью 20 м/с. На какую высоту поднимется тело? Сколько времени будет подниматься? Какова будет скорость на высоте 15м? ( g=10м/с²)

Тело начинает падать с высоты 20м. Сколько времени оно будет падать? Какая скорость будет в момент падения? Какой путь оно пройдет за первую секунду? ( g=10м/с²)

Тело бросили вертикально вверх со скоростью 40 м/с. На какую высоту поднимется тело? Сколько времени будет подниматься? Какова будет скорость на высоте 20м? ( g=10м/с²)

Тело начинает падать с высоты 40м. Сколько времени оно будет падать? Какая скорость будет в момент падения? Какой путь оно пройдет за первую секунду? ( g=10м/с²)

Движение по окружности.

Тело равномерно движется по окружности. Найти период, центростремительное ускорение, частоту. Радиус 2м, скорость 6м/с. (π=3)

Тело равномерно движется по окружности. Найти период, скорость, частоту. Радиус 2м, ускорение 18м/с². (π=3)

Тело равномерно движется по окружности. Найти период, радиус, частоту. Ускорение 18м/с², скорость 6м/с. (π=3)

10 класс. Контрольная работа 1 по теме «Кинематика» Вариант 1 Уровень 1.

Контрольная работа 1 «Кинематика»

Контрольная работа 1 «Кинематика» Вариант 1 (1часть) 1. Двигаясь равномерно, велосипедист проезжает 40 м за 4 с. Какой путь он проедет при движении с той же скоростью за 20 с? А. 30 м. Б. 50 м. В. 200

Подробнее учебный год
Приложение к рабочей программе по физике для 10 класса Примерные оценочные и методические материалы для осуществления текущего контроля успеваемости и промежуточной аттестации учащихся 10-го класса по
Подробнее Вопросы для зачета (д/з) (1 курс)
Вопросы для зачета (д/з) (1 курс) по дисциплине «Физика» Билет 1 1. Механическое движение. Система отсчета. Материальная точка. 2. Первый закон Ньютона. 3. Импульс тела. Импульс силы. 4. Абсолютная шкала
Подробнее Вар. m Газ. ν V m, г *1Е-27
Задача 8. В сосуде объемом V находится ν моль газа. Масса молекулы m 0, молярная масса М, масса всего газа m, плотность газа ρ. Общее число молекул газа N, концентрация молекул n. (Неизвестные величины
Подробнее Динамика и статика (10 ч)
Программа курса по физике для учащихся 10 классов «За страницами учебника» Курс рассчитан на учащихся 10 классов и предполагает совершенствование подготовки школьников по освоению основных разделов физики.
Подробнее Примеры решения задач.
Примеры решения задач Пример 6 Один конец тонкого однородного стержня длиной жестко закреплен на поверхности однородного шара так, что центры масс стержня и шара, а также точка крепления находятся на одной
Подробнее Банк заданий по физике 10 класс
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
Подробнее Справочник формул Единица. измерения
Величина, её определение Обозначение Справочник формул Единица измерения Формула Величины в формуле. Концентрация вещества — это физическая величина, которая показывает число частиц в м n /м n=. Молярная
Подробнее 1.МЕХАНИКА 1.1 КИНЕМАТИКА
Пояснения к демонстрационному варианту контрольных измерительных материалов внутришкольного мониторинга в МОУ «СОШ 55» по физике за курс 10 класса (базовый уровень) Демонстрационный вариант предназначен
Подробнее Образцы комбинированных заданий Часть 3
Образцы комбинированных заданий Часть 3 1. Автомобиль трогается с места и, двигаясь равноускоренно, через 20 с приобретает скорость 72 км/ч. Чему равна масса автомобиля, если известно, что работа, совершенная
Подробнее Диагностическая работа по ФИЗИКЕ
Диагностическая работа по ФИЗИКЕ класс. Разделы: «Механика», «МК и термодинамика», «Электродинамика» Инструкция по выполнению работы Для выполнения экзаменационной работы по физике отводится 4 минут. Работа
Подробнее Промежуточная аттестация 10 класс
МОУ СОШ 5 имени 63-го Угличского пехотного полка Промежуточная аттестация 10 класс Составитель: учитель физики Камкова А.Ю. 1.Вид и цель работы: промежуточная аттестация с целью выявления уровня усвоения
Подробнее КОНТРОЛЬНЫЕ МАТЕРИАЛЫ ПО ФИЗИКЕ
М и н и с т е р с т в о о б р а з о в а н и я и н а у к и Р о с с и й с к о й Ф е д е р а ц и и Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Нижегородский
Подробнее 4) 6р 1. 1) р1 2. 3) р1
.Тренировочные задания по МКТ (А) Какое явление наиболее убедительно доказывает, что между молекулами существуют силы отталкивания? ) диффузия ) броуновское движение ) беспорядочное движение молекул 4)
Подробнее Подготовка к ОГЭ ЧАСТЬ 1
Подготовка к ОГЭ ЧАСТЬ 1 МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ-1 1.Кинематика 1. Буксирный катер за ч проплыл 5 км. Определите скорость катера..тело, двигаясь из состояния покоя, равноускоренно за первую секунду проходит
Подробнее Занятие 7 Законы сохранения
Занятие 7 Законы сохранения Задача 1 На рисунке изображены графики изменения скоростей двух взаимодействующих тележек разной массы (одна тележка догоняет и толкает другую). Какую информацию о тележках
Подробнее ОЛИМПИАДА ПО ФИЗИКЕ Вариант А
ОЛИМПИАДА ПО ФИЗИКЕ 7 Вариант А. С какой горизонтальной скоростью нужно бросить камень с вершины горы, склон которой образует угол с горизонтом, чтобы он упал на склон горы на расстоянии L от вершины?
Подробнее ИТТ Вариант 1 ОСНОВЫ ТЕРМОДИНАМИКИ
ИТТ- 10.5.1 Вариант 1 ОСНОВЫ ТЕРМОДИНАМИКИ 1. Тело, состоящее из атомов или молекул, обладает: 1) Кинетической энергией беспорядочного теплового движения частиц. 2) Потенциальной энергией взаимодействия
Подробнее ID_8560 1/6 neznaika.pro
1 МКТ и термодинамика. Графики и формулы Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Подробнее Разработчик преподаватель —
Министерство образования и науки Краснодарского края государственное бюджетное профессиональное образовательное учреждение Краснодарского края «Краснодарский информационно- технологический техникум» Тематика
Подробнее Демонстрационный вариант 1
Тестовые задания на экзамене по курсу «Физика. Механика. Термодинамика» Демонстрационный вариант 1 1. Материальная точка движется равномерно по окружности со скоростью v. Определите модуль изменения вектора
Подробнее ▶▷▶▷ контрольная работа 1 по теме кинематика ответы
▶▷▶▷ контрольная работа 1 по теме кинематика ответы
Интерфейс Русский/Английский
Тип лицензия Free
Кол-во просмотров 257
Кол-во загрузок 132 раз
Обновление: 10-08-2019
контрольная работа 1 по теме кинематика ответы — Контрольная работа по теме Кинематика 10 класс testschoolru20170927kontrolnaya-rabota-po Cached Контрольная работа по теме Кинематика для учащихся 10 класса с ответами Контрольная работа состоит из 5 вариантов, в каждом по 8 заданий Контрольная работа по физике Кинематика 9 класс testschoolru20170727kontrolnaya-rabota-po Cached Контрольная работа по физике Кинематика Законы взаимодействия и движения тел 9 класс с ответами Работа состоит из 4 вариантов в каждом варианте по 9 заданий Контрольная работа 1 по теме Кинематика sovopredelimcomdocs167300index-2756html Cached Контрольная работа по теме How does the Geographical Position Influence the People s Character 1 Fill in the tables and get your mark Good luck! article Контрольная работа по теме How does the Geographical Position Influence the People s Character Материал по физике (10 класс) по теме: Контрольная работа по nsportalrushkolafizikalibrary20111125 Cached Контрольная работа по физике по теме Кинематика материальной точки Контрольная работа по теме содержит 2 варианта Можно использовать для проверки усвоения знаний учащихся в 9, 10 классе Контрольная работа Кинематика 1 — Документ gigabazarudoc44824html Cached Документ — 4 Уравнение движения имеет вид: х 3 2t 0, 1 t2 Определите параметры движения, постройте график Vx (t) и определите путь, пройденный телом за вторую секунду движения Контрольная работа 1 по теме Кинематика nsportalrushkolafizikalibrary20121019 Cached Контрольная работа 1 по остаточным знаниям за 6 класс по теме : Строение и свойства живых организмов Контрольная работа с 4 разными заданиями 10 класс Контрольная работа по теме КИНЕМАТИКА kopilkaurokovrufizikatesti10-klass-kontrol Cached 10 класс Контрольная работа по теме КИНЕМАТИКА 10 класс Контрольная работа по теме КИНЕМАТИКА контрольная работа по теме : Контрольная работа 1 по теме Кинематика 9 класс — Документ gigabazarudoc108794html Cached Примерные варианта контрольных работ по физике для 9 класса Контрольная работа 1 по теме Кинематика материальной точки 1 Уравнение скорости 0,5 мс2, пройдет путь 50 м? Контрольная работа ЕГЭ по физике на тему Кинематика с wwwctegeinfofizika-teoriya-egekontrolnaya Cached 30092013 Полная контрольная работа по физике, созданная для подготовки к ЕГЭ Выполняя эту работу, вы сможете трезво оценить свои знания и умения в разделе Кинематика и оценить как хорошо вы сможете написать настоящий Контрольная работа по теме Кинематика (10 класс) — Физика pedportalnetstarshie-klassyfizikakontrolnaya Cached Контрольная работа по теме Кинематика (10 класс) (Физика) Учебное пособие для учителей Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 15,300
Контрольная работа для 10 непрофильного класса содержит 4 варианта из 9 заданий… Ответы контрольна
я работа Кинематика. 10 класс Контрольная работа по обществознанию quot;Социально-гуманитарные знания и профессиональная деятельностьquot; Контрольная работа 1 по теме Кинематика материальной точки В
я и профессиональная деятельностьquot; Контрольная работа 1 по теме Кинематика материальной точки Велосипедист движется под уклон с ускорением 0,3 мс 2. Контрольные разной сложности. Контрольная работа по теме Строение атома и атомного ядра, 9 класс. Добавить комментарий Отменить ответ. Дидактические материалы 9 класс Итоговая работа по теме Кинематика, 9 класс. Вопрос-ответ. На этой странице вы можете посмотреть и скачать Контрольная работа по физике для учеников 10 классов quot;Основы кинематики и динамикиquot; НОУ НЦНО. Контрольная работа 1 по теме Кинематика материальной точки Велосипедист движется под уклон с ускорением 0,3 мс 2. …5 минут, 4) учащийся отмечает в желтой тетради свою фамилию и имя на внутренней стороне обложки, а также на листе с задачами из текущей контрольной, 5) буква, соответствующая правильному ответу… Контрольные работы 10 класс. Контрольная работа 2 по теме Основы Динамики Добавлять комментарии могут только зарегистрированные пользователи. Регистрация Вход Возможно использование контрольных работ как домашних или дифференцированных заданий. Просмотр содержимого документа Дифференцированные контрольные работы по теме Кинематика материальной точки Контрольные работы. Вопросответ. Какой материал Вы ищете чаще всего в интернете? Я буду вам признателен, если вы разместите кнопку этого сайта на своем ресурсе. Тема quot;Кинематикаquot; Контрольная по математике. Кинематика твеpдого тела Следующей после матеpиальной точки абстpакцией, котоpая используется в механике, является понятие абсолютно твеpдого тела. Работа и количество теплоты хаpактеpизуют пpоцесс и, очевидно, существенно зависят от пpоцесса. Выполнение контрольной на заказ.
4) учащийся отмечает в желтой тетради свою фамилию и имя на внутренней стороне обложки
а также на листе с задачами из текущей контрольной
созданная для подготовки к ЕГЭ Выполняя эту работу
постройте график Vx (t) и определите путь
пройдет путь 50 м? Контрольная работа ЕГЭ по физике на тему Кинематика с wwwctegeinfofizika-teoriya-egekontrolnaya Cached 30092013 Полная контрольная работа по физике
контрольная работа по теме кинематика ответы Все результаты Контрольная работа по теме Кинематика класс вариант PDF Ответы на контрольную работу по теме Кинематика класс вариант А А А А А В мс В С м вариант А А А Контрольная работа по теме кинематика материальной точки Кинематика материальной точки Урок ответы Источник тока Источник тока в электрической цепи Контрольная работа по теме кинематика Контрольная работа по теме Кинематика класс Инфоурок Физика февр г Cкачать Контрольная работа по теме Кинематика класс Вариант ответы В б hello_html_mpng Вариант Контрольная работа по теме Кинематика класс Школьные тесты сент г Контрольная работа по теме Кинематика класс вариант м м м м B Вагон шириной , м, движущийся Контрольная работа по теме Кинематика класс вариант задание А ответы класс Контрольная работа по теме КИНЕМАТИКА физика Похожие окт г класс Контрольная работа по теме КИНЕМАТИКА t, с С Стрела выпущена из лука вертикально вверх со Ответы Контрольная работа по теме Кинематика, вариантов Похожие Контрольная работа по теме Кинематика Вариант Велосипедист съехал с горки за мин, двигаясь с ускорением , мс Определите длину горки Контрольная работа по теме Кинематика материальной Примерные варианта контрольных работ по физике для класса Контрольная работа по теме Кинематика материальной точки Уравнение Контрольная работа по теме Кинематика прямолинейного Контрольная работа по теме Кинематика прямолинейного движения класс Вариант А На рисунках изображены графики зависимости Контрольная работа по теме Кинематика класс окт г Работа составлена к программе Генденштейна , после изучения тем Равномерное и равноускоренное прямолинейные движения, Контрольная работа по теме Кинематика материальной точки Контрольная работа по теме Кинематика материальной точки равен A , м Б , м B , м Г , м Д , м Ответы к контрольной работе Картинки по запросу контрольная работа по теме кинематика ответы Показать все Другие картинки по запросу контрольная работа по теме кинематика ответы Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Контрольная работа по темеКинематика, класс Мультиурок окт г Контрольная работа класс Кинематика стр Мотоциклист при торможении движется с ускорением , мс и Контрольная работа по физике на тему Кинематика Знанио июн г Контрольная работа по физике на тему Кинематика материальной точки С по задания с выбором ответа из четырех возможных; а с по задания, для которых необходимо привести развернутый ответ Контрольная работа ЕГЭ по физике на тему Кинематика с Теория ЕГЭ Физика теория ЕГЭ Контрольная работа ЕГЭ по физике на тему Кинематика с ответами теория и практика Сохранить Полная контрольная работа по физике, созданная для подготовки к ЕГЭ Выполняя эту работу В задании правильным ответом будет являться номер , ежели Изза такой ошибки в Контрольная работа по теме Кинематика материальной точки Контрольная работа по теме Кинематика материальной точки Вариант Материальная точка движется равномерно прямолинейно из точки с Контрольная работа по теме Кинематика Контрольные мая г Контрольная работа по теме Кинематика Ответов в файле нет Категория Контрольные работы класс Добавил Irina Контрольная работа Кинематика класс Контрольная работа textarchiveruchtml Контрольная работа Кинематика класс ВАРИАНТ Дано уравнение движения X t ,t A Найти начальную скорость и ускорение Ф КОНТРОЛЬНАЯ РАБОТА по теме Кинематика Calaméo Ф Контрольная работа по теме Кинематика Вариант Часть А но ответ явно не с формулирован Представлены общие рассуждения, Контрольная работа по теме Основы кинематики класс УМК ladlavnarodruf_k_rkkhtm Похожие Контрольная работа по теме Кинематика материальной точки класс Скорость точек рабочей поверхности наждачного круга диаметром Контрольная работа по теме Основы кинематики Контент Формы и средства контроля Структурный элемент Рабочей программы Формы и средства контроля включает систему контролирующих материалов где найти ответы на эту контрольную работу по физике класс Домашние задания Другие предметы Похожие ответ авг г где найти ответы на эту контрольную работу по физике класс Контрольная работа Тема Кинематика Вариант , ссылка ФИЗИКА КЛАСС КОНТРОЛЬНЫЕ РАБОТЫ В НОВОМ zvonoknaurokruloadkontrolnye_raboty_v_novom_formatefizika_ Похожие авг г Показано материалов КОНТРОЛЬНАЯ РАБОТА КИНЕМАТИКА При выполнении работы учащиеся вносят ответы на вопросы части А в КОНТРОЛЬНАЯ РАБОТА ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК поэлементный анализ качества знаний по предложенной теме с целью Контрольная Работа По Кинематике Кл pahbegettechконтрольнаяработапокинематикекл Вопрос Где Найти Ответы На Эту Контрольную Работу По Физике Класс Контрольная Работа Тема Кинематика Вариант , Ссылка Ответ PDF Контрольная работа по физике по теме кинематика вариант где найти ответы на эту контрольную работу по физике класс Контрольная работа Тема Кинематика Вариант , ссылка ALEX ALEX Ученик Контрольная работа по физике Основы кинематики класс Похожие дек г Контрольная работа вариант Основы кинематики знания, навыки и умения по теме Основы кинематики в полном объеме работы за каждый правильный ответ в первом блоке балл, во втором , Контрольная работа по физике для учеников классов Основы pedsovetsu Физика и астрономия Оценка знаний учащихся Похожие дек г На этой странице вы можете посмотреть и скачать Контрольная работа по физике для учеников классов Основы кинематики и Практическая работа по теме Кинематика материальной kinematikamaterial_n Практическая работа по теме Кинематика материальной точки Вариант Контрольная работа по физике класс Условия и ответы Контрольная работа по теме Кинематика класс Подготовка к fizprofilruloadkr_klasskontrolnaja_rabota_po_teme_kinematika Вариант контрольной работы для классов по теме Кинематика Скачать PDF Ответы для проверки , мс Кинематика материальной точки Динамика поступательного нояб г Контрольная работа по физике Тема Кинематика материальной точки Динамика поступательного движения ХантыМансийск г Кинематика материальной точки Ответ б , rad Камень брошен Контрольная работа в форме ЕГЭ й класс Открытый урок открытыйурокрфстатьи За правильный ответ задания части А ученик получает балл Задания части В проверяют Контрольная работа по теме Кинематика й класс Домашняя контрольная работа по теме Кинематика distphysicsblogspotcomhtml Похожие окт г Тексты домашней контрольной работы по теме Кинематика прямолинейного движения можно скачать по ссылкам ниже Вариант DOC КОНТРОЛЬНАЯ РАБОТА portaltpuruСБОРНИКЗАДАЧПОФИЗИКЕСРЕШЕdo Кинематика Ответ Движение материальных точек выражается уравнением x При подъеме груза совершается работа , равная A Fh cosα тест обобщение темы кинематика вариант xupifet xupifetviewyrupost Контроль знаний по теме Кинематика в классе на базовом уровне Материалы к Контрольная работа по алгебре кл на варианта Варіант В конце пособия даны ответы на все варианты тестов Пособие Тест Стена ВКонтакте Похожие Срочно ответы по физике механика вариант Нравится Показать контрольная работа Вариант doc пз контрольная работа по атомной физике Вариант doc Решение задач на тему Кинематика вариант doc Тест по теме Кинематика класс Образовательный портал сент г Тест по теме Кинематика класс Перейти к файлу Заказать учебную работу Предварительный просмотр файла не PDF Контрольная работа Кафедра физики УрФУ Каждому разделу соответствует определенная контрольная работа По каждой теме Для освоения материала этой темы и решения задач по теме Кинематика и динамика , , , Н Ответ Fx , Н l , м Контрольная работа по теме Кинематика Механика HomeTask Механика Контрольная работа по теме Кинематика Задача Камень, брошенный вверх, поднялся на высоту м и упал в туже точку, Ответ м; класса физика контрольная работа по теме динамика wwwbroadviewlibraryorgklassafizikakontrolnaiarabotapotemedinamika нояб г класса физика контрольная работа по теме динамика Контрольная работа по теме Кинематика для учащихся класса с ответами работа по физике класс по теме Динамика Вариант Брусок Контрольная работа Основы кинематики и динамики класс Скачать Контрольная работа Основы кинематики и динамики класс В каком случае можно считать автомобиль материальной точкой? Автомобиль достаточно набрать правильных ответов первой части Анализ результатов контрольной работы по теме Основы кинематики и динамики Заказать контрольную работу по кинематике, сколько стоит купить Предметы и темы контрольных работ Контрольная работа по кинематике на заказ качественно и в срок на тестовые вопросы, потом давать развернутые ответы и решать задачи Учтите, что контрольная работа по физике по теме кинематика влияет на семестровую оценку Оплачиваете Ожидаете дня, пока мы будем выполнять Контрольная работа по физике по теме Основы кинематики Похожие окт г Предлагаю вашему вниманию контрольную работу по теме Основы кинематики для класса в двух вариантах к учебнику А В PDF Контрольная работа Кинематика Основные понятия schoolmephirucontentfileGanatmaterialKIMfkrpdf Контрольная работа Кинематика Основные понятия По следующим четырем позициям дать определения Перемещение Ответ дать в Физика класс Контрольная работа по теме Равномерное Похожие Контрольная работа по теме Равномерное движение Физика Учебный план; Отзывы ; Вопросы и ответы Вариант Длительность минут Контрольная работа Тест Контрольная работа Тест ответы на контрольную работу по физике кинематика класс wwwzstelceufileotvetynakontrolnuiurabotupofizikekinematikaklassxml нояб г gdzguru Контрольная работа по механике класс ответы Ответы на контрольную работу по теме Кинематика класс вариант Контрольная работа Кинематика материально точки класс Похожие Контрольная работа по теме Кинематика материальной точки варианта документ Контрольная работа по теме Кинематика класс Контрольная работа по физике Кинематика Гимназия г Рузы wwwruzagimnaziaruindexphpfizkineshtml Автор Утенкова ЗЛ Контрольная работа по физике Кинематика класс в новом формате варианта Контакты , Московская обл, г Руза скачать контрольную работу по физике класс мякишев schpskovedurusiteskachatkontrolnuiurabotupofizikeklassmiakishev нояб г задач Решебник по физике за класс, ответы онлайн gdzguru Б Б Контрольная работа по теме Основы кинематики Касьянов ВА, Игряшова ИВ Тетради для контрольных работ по wwwchriocapruSpecsitemapaspx?id Темы контрольных работ Кинематика и динамика материальной точки класс Ответы Контрольная работа Кинематика и динамика Кинематика класс контрольная Контрольная работа по физике Контрольная работа по физике на тему Кинематика класс Найти частоту вращения колес поезда, имеющих диаметр , м, при скорости км ч DOC Контрольная работа по теме Кинематика прямолинейного Контрольная работа по теме Кинематика прямолинейного движения I вариант Ответ в м случае; во м случае; в случае б Когда он Вместе с контрольная работа по теме кинематика ответы часто ищут контрольная работа по теме кинематика класс контрольная работа по физике класс кинематика варианта контрольная работа по теме основы кинематики класс ответы контрольная работа по теме кинематика класс вариант контрольная работа по физике класс основы кинематики контрольная работа по физике класс кинематика задачи контрольные работы кинематика вариант класс административная контрольная работа по физике класс ответы Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы
Контрольная работа для 10 непрофильного класса содержит 4 варианта из 9 заданий… Ответы контрольная работа Кинематика. 10 класс Контрольная работа по обществознанию quot;Социально-гуманитарные знания и профессиональная деятельностьquot; Контрольная работа 1 по теме Кинематика материальной точки Велосипедист движется под уклон с ускорением 0,3 мс 2. Контрольные разной сложности. Контрольная работа по теме Строение атома и атомного ядра, 9 класс. Добавить комментарий Отменить ответ. Дидактические материалы 9 класс Итоговая работа по теме Кинематика, 9 класс. Вопрос-ответ. На этой странице вы можете посмотреть и скачать Контрольная работа по физике для учеников 10 классов quot;Основы кинематики и динамикиquot; НОУ НЦНО. Контрольная работа 1 по теме Кинематика материальной точки Велосипедист движется под уклон с ускорением 0,3 мс 2. …5 минут, 4) учащийся отмечает в желтой тетради свою фамилию и имя на внутренней стороне обложки, а также на листе с задачами из текущей контрольной, 5) буква, соответствующая правильному ответу… Контрольные работы 10 класс. Контрольная работа 2 по теме Основы Динамики Добавлять комментарии могут только зарегистрированные пользователи. Регистрация Вход Возможно использование контрольных работ как домашних или дифференцированных заданий. Просмотр содержимого документа Дифференцированные контрольные работы по теме Кинематика материальной точки Контрольные работы. Вопросответ. Какой материал Вы ищете чаще всего в интернете? Я буду вам признателен, если вы разместите кнопку этого сайта на своем ресурсе. Тема quot;Кинематикаquot; Контрольная по математике. Кинематика твеpдого тела Следующей после матеpиальной точки абстpакцией, котоpая используется в механике, является понятие абсолютно твеpдого тела. Работа и количество теплоты хаpактеpизуют пpоцесс и, очевидно, существенно зависят от пpоцесса. Выполнение контрольной на заказ.
Контрольная работа по физике для 10 класса по теме «Кинематика материальной точки» Чему равно центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 10 м/с?
Контрольная работа по физике для 10 класса по теме «Кинематика материальной точки»
1.  Чему равно центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 10 м/с?
2.  Скорость поезда за 10 с уменьшилась с 20 до 10 м/с. Чему равно ускорение тела?
3.  Уравнение движения материальной точки имеет вид: х=50+5t. Определите:
а) начальную координату
б) постройте график движения тела
в) найдите перемещение тела за 10 с
г) найдите координату тела через 20 с.
4.  Свободно падающее тело в момент удара о землю имело скорость 20 м/с. С какой высоты падало тело? Сколько времени длилось падение?
5.  Автомобиль первую половину пути проехал со скоростью 72 км/ч, а вторую половину пути со скоростью 54 км/ч. Найдите среднюю скорость автомобиля.
Контрольная работа по физике для 10 класса по теме: «Основы динамики»
1.  Объясните причину равномерного движения автомобиля по горизонтальному участку дороги.
2.  Масса человека на Земле 80 кг. Чему будут равны его масса и вес на поверхности Марса, если ускорение свободного падения на Марсе 3,7 м/с² ?
3.      Найдите силу притяжения двух тел массами по 10 кг, находящимися на расстоянии 100 м.
4.    Пружина длиной 25 см растягивается с силой 40 Н. Найдите конечную длину растянутой пружины, если ее жесткость 100 Н/м.
5.    Чему равна масса Луны, если ускорение свободного падения на Луне 1,6 м/с² , а ее радиус 1,74* 10⁶ м.
Контрольная работа по теме «Законы сохранения»
1.  Найдите импульс грузового автомобиля массой 10 т, движущегося со скоростью 36 км/ч
2.  На какой высоте потенциальная энергия тела массой 60 кг равна 300 Дж?
3.  Упряжка собак, протащив сани по горизонтальному пути
длиной 5 км, совершает работу 400 кДж. Считая коэффициент трения равным 0,02, найдите массу саней.
4.  Мяч брошен вертикально вверх с начальной скоростью 36 км/ч. На какую максимальную высоту он поднимется?
5.  С лодки массой 150 кг, движущейся со скоростью 2 м/с, прыгает мальчик массой 50 кг, двигаясь в горизонтальном направлении. Какой станет скорость лодки после прыжка мальчика, если он прыгнет с кормы со скоростью 4 м/с?
Контрольная работа по физике для 10 класса по теме: «Молекулярная физика и термодинамика»
Во сколько раз изменится средняя квадратичная скорость движения молекул азота, если температура газа уменьшилась в 4 раза? Ответ обоснуйте.
Найдите давление, которое оказывает 45 г неона при температуре 0⁰С, если его объем составляет 1 л.
Совершается ли работа при изохорическом нагревании газа? Изобарическом охлаждении газа? Ответ обоснуйте.
При изобарном расширении газа на 0,5 м³ ему было передано 0,3 МДж количество теплоты. Вычислите изменение внутренней энергии газа, если его давление равно 2*10⁵ Па.
Контрольный тест по теме Кинематика. Физика. 10 класс.
Методическая разработка: «Контрольный тест по теме «Кинематика» к учебнику В.А. Касьянов «Физика. 10 класс»
Автор разработки: Повещенко Ольга Константиновна, преподаватель физики ГБПОУ КК ЕПК, г. Ейск.
Контрольный тест по теме «Кинематика» к учебнику В.А. Касьянов «Физика. 10 класс»
Вариант 1
Изменение пространственного положения относительно других тел с течением времени называется:
Механическим движением +
Относительным движением
Пространственным движением
Графиком равноускоренного движения является:
Парабола +
Прямая
Гипербола
Какие из перечисленных величин являются векторными?
Траектория
Путь
Перемещение+
При прямолинейном равнозамедленном движении
Ускорение направлено так же, как скорость
Ускорение направлено противоположно скорости +
Составляет со скоростью некоторый угол
Перемещение – это:
Длина пути
Вектор, соединяющий начальное и конечное положение материальной точки+
Вектор, соединяющий начало координат с текущей координатой тела
Виды периодических движений:
Вращательное, колебательное+
Круговое, колебательное
Вращательное, циклическое
Перемещение конца минутной стрелки часов длиной 10 см, совершившей полный оборот равно:
0 +
0.2 π
20 π
Центростремительное ускорение направлено:
Противоположно скорости
Так же, как и скорость
Перпендикулярно скорости +
Спидометр автомобиля показывает:
Абсолютную скорость
Относительную скорость
Мгновенную скорость+
Какой зависимостью связана частота с периодом вращения?
Линейной
Обратно пропорциональной+
Прямо пропорциональной
Чему равен модуль ускорения автомобиля при равноускоренном движении, если за 4 секунды его скорость изменилась с 8 до 16 м/с?
2 м/с²+
1 м/с²
4 м/с²
За какое время парашютист спустится на землю с высоты 1.5 км, если скорость его движения 5 м/с ?
7.5 мин
5 мин +
30 с
Тело движется по окружности радиусом 10 м с линейной скоростью 2 м/с. Чему равно центростремительное ускорение?
0.2 м/с²
5 м/с²
0.4 м/с²+
Период вращения вала станка 0.25 с. Чему равна частота вращения?
4 Гц +
0.4 Гц
15 Гц
Пловец движется по течению реки с собственной скоростью1 м/с. Какова его скорость относительно неуправляемого плота, плывущего ему навстречу, если скорость течения 3м/с.
4 м/с
7 м/с+
1 м/с
Вариант 2
Коэффициентом пропорциональности между скоростью и временем при равноускоренном прямолинейном движении является:
Путь
Перемещение
Ускорение +
Какое тело можно считать материальной точкой?
Массой которого можно пренебречь в данной задаче
Размерами которого можно пренебречь в данной задаче+
Массой и размерами которого можно пренебречь в данной задаче
Графиком равномерного движения является:
Парабола
Прямая +
Гипербола
Что входит в понятие «Система отсчета»?
Тело отсчета, система координат, часы+
Тело отсчета, система координат
Тело отсчета, часы
Если направление прямолинейного движения изменяется, то
Путь меньше модуля вектора перемещения
Путь равен нулю
Путь больше модуля вектора перемещения+
В каком случае вектор ускорения направлен вдоль траектории?
Траектория прямолинейная+
Всегда направлен вдоль траектории
При движении по окружности
Свободное падение является видом:
Равномерного движения
Равнопотенциального движения
Равнопеременного движения +
Угол поворота за единицу времени характеризует:
Угловое ускорение
Угловую скорость+
Центростремительное ускорение
Путь конца минутной стрелки часов длиной 10 см, совершившей полный оборот равен:
0
0.2 π +
20 π
Период вращения – это:
Время одного оборота по окружности+
Количество оборотов в единицу времени
Время вращения до полной остановки
Автомобиль движется с ускорением 1 м/с² . За какое время он изменит скорость с 10 до 15 м/с?
2 с
5 с+
3 с
Парашютист спустился на землю с высоты 1.2 км за 5 мин. Чему равна его скорость движения?
6 м/с
0.24 м/с
4 м/с +
Тело движется по окружности радиусом 1 м с центростремительным ускорением 4 м/с². Чему равна линейная скорость?
2 м/с +
0.25 м/с
4 м/с
Частота вращения вала станка 300 оборотов в минуту. Чему равен период вращения?
5 с
0.2 с +
0.5 с
Лодка движется против течения реки с собственной скоростью 12 м/с. Какова ее скорость относительно неуправляемого плота, плывущего ей навстречу, если скорость течения 5м/с.
17 м/с
2 м/с
12 м/с+
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
В 1
1
1
3
2
2
1
1
3
3
2
1
2
3
1
2
В 2
3
2
2
1
3
1
3
2
2
1
2
3
1
2
3
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/389363-kontrolnyj-test-po-teme-kinematika-fizika-10-
Кинематические уравнения и кинематические графики
Урок 4 этого модуля в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом уроке было подчеркнуто, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта. Таким образом, графики скорость-время можно использовать для определения числовых значений и соотношений между величинами смещения (d), скоростью (v), ускорением (a) и временем (t).В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и прогнозирования числовых значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (t). Таким образом, теперь доступны два метода для решения задач, связанных с численными соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем взаимосвязь между этими двумя методами.
Пример проблемы — графическое решение
Рассмотрим объект, который движется с постоянной скоростью +5 м / с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м / с в течение следующих 5 секунд.Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.

Горизонтальная часть графика изображает движение с постоянной скоростью в соответствии со словесным описанием. Участок графика с положительным уклоном (т. Е. С наклоном вверх) показывает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося от 5 до 15 м / с. Наклон линии можно вычислить, используя коэффициент превышения пробега.Между 5 и 10 секундами линия поднимается с 5 до 15 м / с и длится от 5 до 10 секунд. Это общий подъем +10 м / с и общий пробег 5 с. Таким образом, уклон (отношение подъема / хода) составляет (10 м / с) / (5 с) = 2 м / с ². Используя график скорость-время, определено, что ускорение объекта составляет 2 м / с ² в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика скорость-время. Область между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции.Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего поверх площади прямоугольника. Это показано на схеме ниже.

Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.
Прямоугольник Треугольник
Площадь = основание * высота
Площадь = (10 с) * (5 м / с)
Площадь = 50 м
Площадь = 0.5 * основание * высота
Площадь = 0,5 * (5 с) * (10 м / с)
Площадь = 25 м
Общая площадь (прямоугольник плюс треугольник) равна 75 м. Таким образом, перемещение объекта составляет 75 метров за 10 секунд движения.
Вышеупомянутое обсуждение показывает, как можно использовать графическое представление движения объекта для извлечения числовой информации об ускорении и смещении объекта. После построения график скорость-время можно использовать для определения скорости объекта в любой момент в течение 10 секунд движения.Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время можно использовать для выявления (или определения) числовых значений и соотношений между величинами смещения (d), скоростью (v), ускорением (a) и временем (t) для любого заданного движения.
Пример проблемы — решение с использованием кинематического уравнения
Теперь давайте рассмотрим то же словесное описание и соответствующий анализ с использованием кинематических уравнений.Словесное описание движения:
Объект, который движется с постоянной скоростью +5 м / с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м / с в течение следующих 5 секунд
Кинематические уравнения могут применяться к любому движению, для которого ускорение постоянно. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения в течение первых 5 секунд не смешивались с параметрами движения в течение последних 5 секунд.В таблице ниже перечислены указанные параметры движения.
t = 0 с — 5 с t = 5 с — 10 с
v _i = 5 м / с
v _f = 5 м / с
t = 5 с
a = 0 м / с ²
v _i = 5 м / с
v _f = 15 м / с
t = 5 с
Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м / с ², несмотря на то, что это явно не указано.Фраза с постоянной скоростью указывает движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
v _f = v _i + a * t
Здесь показаны подстановка и алгебра.
15 м / с = 5 м / с + a * (5 с)
15 м / с — 5 м / с = a * (5 с)
10 м / с = a * (5 с)
(10 м / с) / (5 с) = a
a = 2 м / с ²
Это значение ускорения объекта в течение времени от 5 до 10 с согласуется со значением, определенным из наклона линии на графике скорость-время.
Смещение объекта в течение всех 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают два совершенно разных интервала ускорения, расчеты для каждого интервала должны выполняться отдельно. Это показано ниже.
t = 0 с — 5 с t = 5 с — 10 с
d = v _i * t + 0,5 * a * t ²
d = (5 м / с) * (5 с) +0.5 * (0 м / с ²) * (5 с) ²
d = 25 м + 0 м
d = 25 м d = ((v _i + v _f) / 2) * t
d = ((5 м / с + 15 м / с) / 2) * (5 с)
d = (10 м / с) * (5 с)
d = 50 м
Общее смещение за первые 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.
Анализ этого простого движения иллюстрирует ценность этих двух представлений движения — графика скорости-времени и кинематических уравнений.Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.
Проверьте свое понимание
1. Rennata Gas движется по городу со скоростью 25,0 м / с и начинает ускоряться с постоянной скоростью -1,0 м / с ². В конце концов Ренната полностью останавливается.
а. Изобразите ускоренное движение Реннаты, нарисовав график скорости-времени.Используйте график скорость-время, чтобы определить это расстояние.
г. Используйте кинематические уравнения, чтобы рассчитать расстояние, которое Ренната преодолеет при замедлении.

2. Отто Эмиссион едет на своей машине со скоростью 25,0 м / с. Отто разгоняется со скоростью 2,0 м / с ² за 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
а. Изобразите 15 секунд движения Отто Эмиссии, нарисовав график скорости-времени.Используйте график, чтобы определить расстояние, которое Отто преодолел за все 15 секунд.
г. Наконец, разделите движение на два сегмента и используйте кинематические уравнения, чтобы рассчитать общее расстояние, пройденное за все 15 секунд.
3. Люк Отбело, артист-человек, стреляющий по пушечным ядрам, сброшен с края обрыва с начальной скоростью полета +40,0 м / с. Люк ускоряется с постоянным ускорением вниз -10,0 м / с ² (приблизительное значение ускорения свободного падения).
а. Нарисуйте график скорость-время для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбелу, чтобы вернуться к исходной высоте обрыва. Укажите это время на графике.

4. Chuck Wagon движется с постоянной скоростью 0,5 мили в минуту в течение 10 минут. Затем Чак замедляется со скоростью -25 миль / мин ² в течение 2 минут.
а. Нарисуйте график скорости-времени движения Чака Вагона. Используйте график скорость-время, чтобы определить общее расстояние, пройденное Чаком Вэгоном за 12 минут движения.
г. Наконец, разделите движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.
5. Vera Side мчится по трассе со скоростью 45,0 м / с. Вера смотрит вперед и наблюдает за аварией, которая привела к налету на дороге посреди дороги.К тому времени, когда Вера хлопает по перерывам, она находится в 50,0 м от pileup. Она замедляется со скоростью -10,0 м / с ².
а. Постройте график скорости-времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера должна пройти до полной остановки (если она не столкнется с pileup).
г. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд должна пройти до полной остановки (если она не столкнется с pileup). Ударится ли Вера по машинам в скоплении? То есть проездит Вера больше 50.0 метров?
6. Эрл Э. Берд движется со скоростью 30,0 м / с за 10,0 секунд. Затем он ускоряется со скоростью 3,00 м / с ² за 5,00 секунд.
а. Постройте график скорости-времени для движения Эрла Э. Берда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Эрла Э. Берда на два временных отрезка и используйте кинематические уравнения для вычисления полного смещения.
Решения вышеуказанных вопросов
Решение вопроса 1
а.График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5 * b * h = 0,5 * (25,0 с) * (25,0 м / с)
Площадь = 313 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Дано:
против _и = 25.0 м / с
v _f = 0,0 м / с
a = -1,0 м / с ²
Находят:
d = ??
(0 м / с) ² = (25,0 м / с) ² + 2 * (-1,0 м / с ²) * d
0.0 м ² / с ² = 625,0 м ² / с ² + (-2,0 м / с ²) * d
0,0 м ² / с ² — 625,0 м ² / с ² = (-2,0 м / с ²) * d
(-625,0 м ² / с ²) / (- 2,0 м / с ²) = d
313 м = d

Решение вопроса 2
a.График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5 * b _tri * h _tri + b _rect1 * h _rect1 + b _rect2 * h _rect2
Площадь = 0.5 * (5,0 с) * (10,0 м / с) + (5,0 с) * (25,0 м / с) + (10,0 с) * (35,0 м / с)
Площадь = 25 м + 125 м + 350 м
Площадь = 500 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 5 секунд:
Дано:
против _и = 25.0 м / с
t = 5,0 с
a = 2,0 м / с ²
Находят:
d = ??

d = v _i * t + 0,5 * a * t ²
d = (25,0 м / с) * (5,0 с) + 0.5 * (2,0 м / с ²) * (5,0 с) ²
d = 125 м + 25,0 м
d = 150 м
Теперь найдите d за последние 10 секунд:
Дано:
v _i = 35,0 м / с
t = 10,0 с
а = 0.0 м / с ²
Находят:
d = ??
(Примечание: скорость на отметке 5 секунд можно определить, зная, что автомобиль ускоряется с 25,0 м / с при +2,0 м / с ² в течение 5 секунд. Это приводит к изменению скорости a * t = 10 м / с, а значит, скорость 35,0 м / с.)
d = v _i * t + 0.5 * а * т ²
d = (35,0 м / с) * (10,0 с) + 0,5 * (0,0 м / с ²) * (10,0 с) ²
d = 350 м + 0 м
d = 350 м
Общее расстояние за 15 секунд движения является суммой этих двух вычислений расстояния (150 м + 350 м):
расстояние = 500 м

Решение вопроса 3
a.График скорость-время для движения:

г. Время для подъема и падения до исходной высоты в два раза больше времени для подъема на пик. Итак, решение состоит в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Дано:
v _i = 40,0 м / с
v _f = 0.0 м / с
a = -10,0 м / с ²
Находят:
т _вверх = ??
2 * т _вверх = ??
v _f = v _i + a * t _вверх
0 м / с = 40 м / с + (-10 м / с2) * t _вверх
(10 м / с ²) * t _вверх = 40 м / с
т _вверх = (40 м / с) / (10 м / с ²)
т _до = 4.0 с
2 * t _вверх = 8,0 с
Решение вопроса 4
a. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.
Площадь = b _{прямоугольник} * h _{прямоугольник} + 0,5 * b _tri * h _tri
Площадь = (10,0 мин) * (0,50 миль / мин) + 0,5 * (2,0 мин) * (0,50 миль / мин)
Площадь = 5 миль + 0,5 миль
Площадь = 5.5 миль
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 10 минут:
Дано:
против _и = 0.50 миль / мин
t = 10,0 мин
a = 0,0 миль / мин ²
Находят:
d = ??

d = v _i * t + 0,5 * a * t ²
d = (0,50 миль / мин) * (10.0 мин) + 0,5 * (0,0 миль / мин ²) * (10,0 мин) ²
d = 5.0 миль + 0 миль
d = 5.0 миль
Теперь найдите d за последние 2 минуты:
Дано:
v _i = 0,50 миль / мин
t = 2,0 мин
а = -0.25 миль / мин ²
Находят:
d = ??
d = v _i * t + 0,5 * a * t ²
d = (0,50 миль / мин) * (2,0 мин) + 0,5 * (- 0,25 м / с ²) * (2,0 мин) ²
d = 1,0 мили + (-0,5 мили)
d = 0.5 миль
Общее расстояние за 12 минут движения является суммой этих двух вычислений расстояний (5.0 миль + 0,5 миль):
расстояние = 5.5 миль (-и)
Решение вопроса 5
a. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0.5 * b * h = 0,5 * (4,5 с) * (45,0 м / с)
Площадь = 101 м
г.
Дано:
v _i = 45,0 м / с
v _f = 0,0 м / с
a = -10,0 м / с ²
Находят:
d = ??
v _f ² = v _i ² + 2 * a * d
(0 м / с) ² = (45.0 м / с) ² + 2 * (-10,0 м / с ²) * d
0,0 м ² / с ² = 2025,0 м ² / с ² + (-20,0 м / с ²) * d
0,0 м ² / с ² — 2025,0 м ² / с ² = (-20,0 м / с ²) * d
(-2025,0 м ² / с ²) / (- 20,0 м / с ²) = d
101 м = d
Так как место аварии находится менее чем в 101 м от Веры, она действительно столкнется с налаживанием, прежде чем полностью остановится (если только она не свернет в сторону).
Решение вопроса 6
a. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5 * b _tri * h _tri + b ₁ * h ₁ + b ₂ * h ₂
Площадь = 0,5 * (5,0 с) * (15,0 м / с) + (10,0 с) * (30,0 м / с) + (5,0 с) * (30,0 м / с)
Площадь = 37,5 м + 300 м + 150 м
Площадь = 488 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 10 секунд:
Дано:
v _i = 30,0 м / с
t = 10,0 с
a = 0,0 м / с ²
Находят:
d = ??
d = v _i * t + 0.5 * а * т ²
d = (30,0 м / с) * (10,0 с) + 0,5 * (0,0 м / с ²) * (10,0 с) ²
d = 300 м + 0 м
d = 300 м
Теперь найдите d за последние 5 секунд:
Дано:
v _i = 30,0 м / с
т = 5.0 с
a = 3,0 м / с ²
Находят:
d = ??
d = v _i * t + 0,5 * a * t ²
d = (30,0 м / с) * (5,0 с) + 0,5 * (3,0 м / с ²) * (5,0 с) ²
d = 150 м + 37,5 м
д = 187.5 м
Общее расстояние за 15 секунд движения является суммой этих двух вычислений расстояния (300 м + 187,5 м):
расстояние = 488 м
3.4 Движение с постоянным ускорением — University Physics Volume 1
Learning Objectives
К концу этого раздела вы сможете:
Определите, какие уравнения движения следует использовать для решения неизвестных.
Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени. Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения.Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Сначала сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, принятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости.То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для истекшего времени: Δt = tΔt = t. Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0.Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь сделаем важное предположение, что ускорение постоянно . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная.a– = a = постоянная.
Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучать, и не ухудшает точность нашего лечения. Во-первых, ускорение всегда равно в большом количестве ситуаций. Более того, во многих других ситуациях мы можем точно описать движение, предполагая постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко изменяется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до полной остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает
v– = x − x0t.v– = x − x0t.
Решение x дает нам
x = x0 + v – t, x = x0 + v – t,
3,10
со средней скоростью
v– = v0 + v2.v– = v0 + v2.
3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой простое среднее значение начальной и конечной скоростей.Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.
В части (b) ускорение непостоянно. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рис. 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv.Средняя скорость равна 12 (v0 + v) = 60 км / ч 22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.
Решение для окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
a = v − v0t (константа). a = v − v0t (константа).
Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).
3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется со скоростью 1,50 м / с ² в течение 40,0 с. Какова его конечная скорость?
Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы вычисляем конечную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / сv = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.
Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19 Самолет приземляется с начальной скоростью 70.0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.
Уравнение v = v0 + atv = v0 + at не только полезно при решении задач, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что
Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀), как и ожидалось (другими словами, скорость постоянна)
Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции.Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Определение конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at.v0 + v2 = v0 + 12at.
Поскольку v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.
Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
x = x0 + v0t + 12at2 (константа). x = x0 + v0t + 12at2 (константа).
3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с ². Предположим, драгстер ускоряется из состояния покоя на 5.56 с Рисунок 3.20. Как далеко он пролетит за это время?
Рисунок 3.20. Пилот Top Fuel американской армии Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фотография любезно предоставлена армией США)
Стратегия
Сначала нарисуем эскиз, рис. 3.21. Нас просят найти смещение, которое составляет x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2, когда мы идентифицируем v0v0, aa и t из постановки задачи.
Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные. Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с ² и t задается как 5,56 с.
Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
х = х0 + v0t + 12at2.х = х0 + v0t + 12at2.
Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.
Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий объем, который можно покрыть всего за 5.56 с, но первоклассные драгстеры могут проехать четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.
Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
Смещение зависит от квадрата прошедшего времени, когда ускорение не равно нулю.В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Расчет конечной скорости на основе расстояния и ускорения
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (константа).v2 = v02 + 2a (x − x0) (константа).
3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте окончательную скорость драгстера в Примере 3.8 без использования информации о времени.
Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.
Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v ₀ = 0, поскольку драгстер запускается из состояния покоя.Мы также знаем, что x — x ₀ = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , = 26,0 м / с ².
Во-вторых, мы подставляем известные значения в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).
Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.
Значение
Скорость 145 м / с составляет около 522 км / ч, или около 324 миль / ч, но даже эта головокружительная скорость отстает от рекорда для четверти мили.Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.
Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
При фиксированном ускорении машина, едущая вдвое быстрее, не просто останавливается на удвоенном расстоянии.Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных.Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)
Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико и приближается к нулю в том пределе, когда начальная и конечная скорости равны.Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0). а = v2-v022 (х-х0).
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с ², тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м / с ². Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, учитывая время его реакции, равное 0.500 с, чтобы нажать на тормоз.
Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рис. 3.22. Пример эскиза для визуализации замедления и остановочного пути автомобиля.
Решение
Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v ₀ = 30,0 м / с, v = 0 и a = −7.00 м / с ² ( a отрицательно, потому что направление противоположно скорости). Возьмем x ₀ равным нулю. Ищем смещение ΔxΔx, или x — x ₀.
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования — v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении.(Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: x − 0 = 02− (30,0 м / с) 22 (−7,00 м / с2). x − 0 = 02− (30,0 м / с) 22 (−7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне.
Эта часть может быть решена точно так же, как (а).Единственное отличие состоит в том, что ускорение составляет -5,00 м / с ². Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это значение ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы снова определяем известные и то, что мы хотим решить.Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s, а areaction = 0areaction = 0. Примем x0-responsex0-response равным нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение — x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это значит, что машина едет 15.0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рисунок 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (а) равным 64,3 м + 15,0 м = 79,3 м в сухом состоянии и (б) равным 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя.Здесь показан тормозной путь для сухой и мокрой дороги, рассчитанный в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля. Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важным является общий подход к решению проблем.Мы определяем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример 3.11
Расчет времени
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м.Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с ², сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)
Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t ).
Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,
v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нам нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственная неизвестная в уравнении — это переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.
Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t — величина времени, а s — единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,
, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это означает, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.
Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с. ² во время пуска.Сколько времени требуется ракете, чтобы достичь скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с ² за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.
Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.
Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.
Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.
Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики включает движение двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомая неизвестная зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рисунке 3.25.
Рис. 3.25. Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 отстает с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проезжает мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с ², чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?
Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x в более позднее время t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает проблему смещения для каждого животного, мы сможем приравнять уравнения друг к другу и решить неизвестное, то есть время.
Решение
Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что является ее средней скоростью.Ускорение гепарда 4 м / с ². Оценивая t , время, за которое гепард достигает газели, получаем t = 2v – a = 2 (10) 4 = 5s. T = 2v – a = 2 (10) 4 = 5s.
Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны давать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4) (5) 2 = 50м. X = 12at2 = 12 (4) (5) 2 = 50м. Водоизмещение газели: x = v – t = 10 (5) = 50 м. X = v – t = 10 (5) = 50 м. Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.
Проверьте свое понимание 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и бежит, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
Уравнений движения для постоянного ускорения в одном измерении — College Physics
Мы могли бы знать, что чем больше ускорение, скажем, автомобиля, удаляющегося от знака «Стоп», тем больше смещение за данный момент времени. Но мы не разработали конкретное уравнение, связывающее ускорение и смещение. В этом разделе мы разработаем несколько удобных уравнений для кинематических отношений, начиная с уже рассмотренных определений перемещения, скорости и ускорения.
Обозначение:
t , x , v , a
Сначала сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время есть, взятие означает, что последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть — это начальная позиция , а — начальная скорость .Мы не ставим нижние индексы на окончательные значения. То есть — это последнее время , — это конечная позиция , а — это конечная скорость . Это дает более простое выражение для истекшего времени — сейчас,. Это также упрощает выражение для смещения, которое есть сейчас. Кроме того, это упрощает выражение для изменения скорости, которое есть сейчас. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает окончательное значение в любом рассматриваемом движении.
Теперь сделаем важное предположение, что ускорение постоянно . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны. То есть
, поэтому мы всегда используем символ ускорения. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение всегда равно в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, в движениях, когда ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Уравнение отражает тот факт, что при постоянном ускорении это просто среднее значение начальной и конечной скоростей.Например, если вы постоянно увеличиваете скорость (то есть с постоянным ускорением) с 30 до 60 км / ч, тогда ваша средняя скорость во время этого постоянного увеличения составляет 45 км / ч. Используя уравнение для проверки этого, мы видим, что
, что кажется логичным.
Расчет смещения: как далеко пробегает бегунок?
Бегун бежит по прямому участку дороги со средней скоростью 4,00 м / с в течение 2,00 мин. Какова его конечная позиция, если исходная позиция равна нулю?
Стратегия
Нарисуйте эскиз.
Окончательное положение определяется уравнением
Чтобы найти, мы идентифицируем значения, и из постановки задачи и подставляем их в уравнение.
Решение
1. Определите известные. , , и .
2. Введите известные значения в уравнение.
Обсуждение
Скорость и конечное смещение положительны, что означает, что они направлены в одном направлении.
Уравнение дает представление о взаимосвязи между смещением, средней скоростью и временем. Это показывает, например, что смещение является линейной функцией средней скорости. (Под линейной функцией мы подразумеваем, что смещение зависит от , а не от , возведенного в другую степень, например, . На графике линейные функции выглядят как прямые линии с постоянным наклоном.) В поездке на автомобиле для Например, если мы усредним 90 км / ч, мы продвинемся вдвое дальше, чем если бы мы в среднем 45 км / ч.
Между смещением и средней скоростью существует линейная зависимость. В течение заданного времени объект, движущийся в два раза быстрее другого объекта, будет перемещаться вдвое дальше другого объекта.
Расчет конечной скорости: самолет замедляется после приземления
Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется на 40,0 с. Какова его конечная скорость?
Стратегия
Нарисуйте эскиз. Мы рисуем вектор ускорения в направлении, противоположном вектору скорости, потому что самолет замедляется.
Решение
1. Определите известные. ,,.
2. Определите неизвестное. В данном случае это конечная скорость _.
3. Определите, какое уравнение использовать. Мы можем рассчитать конечную скорость, используя уравнение.
4. Подставьте известные значения и решите.
Обсуждение
Конечная скорость намного меньше начальной скорости, желаемой при замедлении, но все же положительная. С реактивными двигателями обратная тяга могла поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад.На это указывает отрицательная конечная скорость, чего здесь нет.
Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Уравнение не только помогает при решении проблем, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем.Из него видно, например, что
конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
, если ускорение равно нулю, то конечная скорость равна начальной скорости, как и ожидалось (т.е. скорость постоянна)
Если отрицательное, то конечная скорость меньше начальной скорости
(Все эти наблюдения соответствуют нашей интуиции, и всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.)
Установление соединений: соединение в реальном мире
Космический шаттл Endeavour стартует из Космического центра Кеннеди в феврале 2010 г. (Источник: Мэтью Симантов, Flickr)
Межконтинентальная баллистическая ракета (МБР) имеет большее среднее ускорение, чем космический шаттл, и достигает большей скорости в первые две минуты полета (фактическое время горения межконтинентальной баллистической ракеты засекречено — ракеты с коротким временем горения сложнее для противника. разрушать).Но космический шаттл получает большую конечную скорость, так что он может вращаться вокруг Земли, а не сразу возвращаться вниз, как это делает межконтинентальная баллистическая ракета. Космический шаттл делает это за счет более длительного ускорения.
Что еще мы можем узнать, изучив уравнение? Мы видим, что:
смещение зависит от квадрата прошедшего времени, когда ускорение не равно нулю. На (Рисунок) драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени
, если ускорение равно нулю, то начальная скорость равна средней скорости () и становится
Расчет конечной скорости: драгстеры
Рассчитайте конечную скорость драгстера на (Рисунок) без использования информации о времени.
Стратегия
Нарисуйте эскиз.
Уравнение идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.
Решение
1. Определите известные значения. Мы знаем это, так как драгстер стартует с отдыха. Затем мы отмечаем это (это был ответ на (Рисунок)). Наконец, было дано среднее ускорение.
2. Подставьте известные значения в уравнение и решите относительно
Таким образом,
Чтобы получить, извлекаем корень квадратный:
Обсуждение
145 м / с — это около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость отстает от рекорда для четверти мили.Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.
Изучение уравнения может дать дальнейшее понимание общих отношений между физическими величинами:
Конечная скорость зависит от того, насколько велико ускорение и расстояние, на котором оно действует
При фиксированном замедлении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии — для остановки требуется гораздо больше времени.(Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы дополнительно исследуем одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций. Примеры также дают представление о методах решения проблем. В рамке ниже приведены ссылки на необходимые уравнения.
Расчет смещения: как далеко уходит автомобиль, останавливаясь?
На сухом бетоне автомобиль может замедляться со скоростью, тогда как на мокром бетоне он может замедляться только с.Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) (а) по сухому бетону и (б) по мокрому бетону. (c) Повторите оба вычисления, найдя смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.
Стратегия
Нарисуйте эскиз.
Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Мы сделаем это явно в следующих нескольких примерах, используя таблицы для их выделения.
Решение для (а)
1. Определите, что мы знаем и что мы хотим решить. Мы знаем это ; ; (отрицательно, потому что направление противоположно скорости). Принимаем равным 0. Ищем смещение, или.
2. Найдите уравнение, которое поможет решить проблему. Лучшее уравнение для использования —
Это уравнение лучше всего, потому что оно включает только одно неизвестное,.Нам известны значения всех других переменных в этом уравнении. (Существуют и другие уравнения, которые позволят нам решить для, но они требуют, чтобы мы знали время остановки, которое мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)
3. Перепишите уравнение, для которого нужно найти.
4. Введите известные значения.
Таким образом,
Решение для (b)
Эта часть может быть решена точно так же, как и часть A. Единственная разница в том, что замедление есть.Результат
Решение для (c)
После реакции водителя тормозной путь будет таким же, как и в частях A и B для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно подсчитать, как далеко проехал автомобиль за время реакции, а затем добавить это значение ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
1. Определите, что мы знаем и что мы хотим решить. Мы знаем это ; ; .Принимаем за 0. Ищем.
2. Определите лучшее уравнение для использования.
работает хорошо, потому что единственное неизвестное значение — это то, что мы хотим найти.
3. Подключите известные знания, чтобы решить уравнение.
Это означает, что автомобиль движется на 15,0 м, пока водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции.
4. Добавьте смещение за время реакции к смещению при торможении.
64,3 м + 15,0 м = 79,3 м в сухом состоянии
90,0 м + 15,0 м = 105 м во влажном состоянии
Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухой и мокрой дороги, рассчитанные в этом примере для автомобиля, изначально движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, где водитель впервые видит красный свет, при условии, что время реакции составляет 0,500 с.
Обсуждение
Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля. Остановка автомобиля на мокром асфальте займет больше времени, чем на сухом. Интересно, что время реакции значительно увеличивает смещения. Но важнее общий подход к решению проблем. Мы определяем известные и определяемые величины, а затем находим соответствующее уравнение. Часто есть несколько способов решить проблему.Фактически, различные части этого примера могут быть решены другими методами, но решения, представленные выше, являются самыми короткими.
Расчет времени: автомобиль вливается в движение
Предположим, автомобиль выезжает на шоссе на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а ускорение составляет, сколько времени потребуется, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)
Стратегия
Нарисуйте эскиз.
Нас просят решить на время.Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным,).
Решение
1. Определите, что мы знаем и что мы хотим решить. Мы знаем это ; ; и .
2. Нам нужно решить проблему. Выберите лучшее уравнение. работает лучше всего, потому что единственное неизвестное в уравнении — это переменная, для которой нам нужно решить.
3. Нам нужно будет изменить уравнение, которое нужно найти.В этом случае будет проще сначала подключить известные.
4. Упростите уравнение. Единицы измерения (м) отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд, которые нужно отменить, взяв, где — величина времени, а s — единица. Остается
5. Используйте формулу корней квадратного уравнения, чтобы найти .
(a) Переставьте уравнение, чтобы получить 0 на одной стороне уравнения.
Это квадратное уравнение вида
, где указаны константы.
(б) Его решения даются квадратной формулой:
Это дает два решения для
В этом случае время равно в секундах или
Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Обсуждение
Каждый раз, когда уравнение содержит неизвестный квадрат, будет два решения.В некоторых проблемах имеют смысл оба решения, но в других, таких как вышеупомянутое, разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.
Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. В разделе «Основы решения проблем» обсуждаются основы решения проблем и описывается подход, который поможет вам добиться успеха в этой бесценной задаче.
Установление связей: домашний эксперимент — последние новости
Мы использовали единицы СИ — метры в секунду в квадрате, чтобы описать некоторые примеры ускорения или замедления автомобилей, бегунов и поездов. Чтобы лучше понять эти числа, можно измерить замедление при торможении автомобиля, выполняющего медленную (и безопасную) остановку. Напомним, что для среднего ускорения. Путешествуя в автомобиле, медленно нажимайте на тормоза, когда подойдете к знаку остановки. Попросите пассажира записать начальную скорость в милях в час и время, необходимое (в секундах) для остановки.Отсюда рассчитайте замедление в милях в час в секунду. Преобразуйте это в метры на секунду в квадрате и сравните с другими замедлениями, упомянутыми в этой главе. Рассчитайте пройденное расстояние при торможении.
Проверьте свое понимание
Ракета во время запуска ускоряется со скоростью. Сколько времени требуется ракете, чтобы достичь скорости 400 м / с?
Движение снаряда — кинематика | Воздушное сопротивление | Параболическая кривая
HS
Введение в движение снаряда (на основе запроса) Триш Лёблейн HS
UG-Intro MC
Удаленный
Лаборатория Физика
Концептуальные вопросы по физике с использованием PhET (на основе запросов) Триш Лёблейн HS
UG-Intro MC Физика
Уроки физики на основе алгебры в одном семестре, вопросы для кликеров и расписание в pdf (на основе запросов) Триш Лёблейн UG-Intro
HS HW
Demo
Lab Физика
Квадратичные функции для движения снаряда Сара Хэмптон и Салли Джиллетт MS
HS Guided
Обсудить Математика
Кинематическое уравнение Ши Филлипс HS управляемый Физика
Квадратичные снаряды beki toussaint HS Лаборатория Математика
Экспериментальный план: движение снаряда! Джейми Шенбергер МС Управляемый
Лабораторный Прочее
Науки о Земле
Урок сопротивления воздуха Команда PhET средней школы UTeach МС Лаборатория Физика
Исследование снаряда для средней школы Мастерская средней школы округа Джефферсон МС Лаборатория Физика
Математика
Науки о Земле
Каким образом симуляции PhET подходят для моей программы средней школы? Сара Боренштейн МС Другое Химия
Физика
Биология
Науки о Земле
Деятельность виртуальной лаборатории Projectile Motion Яков Залкинд HS
UG-Intro Lab
Remote Физика
Движение снаряда Майтха Маджан HS
UG-Intro Лаборатория Физика
Эксперимент по движению снаряда Джавахер бин Хаммад UG-Intro Лаборатория Физика
Горизонтальное движение снаряда Сара Мохаммед UG-Intro Лаборатория Физика
движение снаряда Ханан Ханан Саид Другое Лаборатория Физика
движение снаряда Марьям алзааби UG-Adv Лаборатория
HW Физика
движение снаряда Фатма Аль-Али HS Лаборатория Физика
Движение снаряда Эльмустафа Эльмубарак UG-Intro Лаборатория Физика
Движение снаряда Саид Али UG-Intro Лаборатория Физика
движение снаряда Ибрагим Альсвидан МС Лаборатория Физика
Отчет лаборатории движения снаряда фади каззаз UG-Intro Лаборатория Физика
Движение снаряда Мустафа Хасан Мохаммед Эльмаллах UG-Intro Лаборатория Физика
Движение снаряда, дальность, время, скорость Муза Джамал Альнуайми UG-Intro Lab
Remote Физика
Движение снаряда Абдельмонем Атеф UG-Adv
UG-Intro Lab
Remote
HW Физика
Рабочий лист движения проекта Юсеф Алаа UG-Intro Лаборатория Физика
Движение снаряда (лабораторный отчет) Али Алгфели UG-Intro Лаборатория Физика
Движение снаряда Зеяд Мохаммед UG-Intro Прочее
HW
Lab Физика
Движение снаряда Suha AlHadha UG-Intro
HS Лаборатория Физика
Движение снаряда Амр Ахмед UG-Intro Лаборатория Физика
Движение снаряда Халид Альсале Другое Лаборатория Физика
снаряд Рая Альшамси UG-Intro Лаборатория Физика
Рабочий лист снаряда Маджед Мансур Аль Хашими UG-Intro Лаборатория Физика
движение снаряда Мохамед Алнакби Другое Лаборатория Физика
Движение снаряда Росс Пинкертон, Джоан Роке HS Remote
Lab
Guided Физика
Лаборатория движения горизонтальных снарядов Росс Пинкертон, Джоан Роке HS Lab
Guided
Remote Физика
Движение снаряда (включая сопротивление воздуха) Фатма Фуад UG-Intro
UG-Adv
HS Лаборатория
Управляемая Физика
Движение снаряда карим аллаххам UG-Intro Лаборатория Физика
Рабочий лист движения снаряда М.Салман Исмаил UG-Intro
HS Guided
Remote
Lab
HW Физика
снаряд мотыльков abood hamad UG-Intro Лаборатория Физика
Движение снаряда Амна Биншемель HS
UG-Intro Лаборатория Физика
Отчет лаборатории движения снаряда Абдулла Салехи HS Лаборатория
HW Физика
Снаряд Айша Альхаммади UG-Intro
HS Lab
Remote Физика
Движение снаряда Галия Альзаруни HS
UG-Intro
MS Лаборатория
Управляемая Физика
Движение снаряда Нура Джасим UG-Intro
HS Lab
Remote Физика
Движение снаряда Майтха Алдармаки UG-Intro
HS Lab
Remote Физика
Движение снаряда Амна Фейсал UG-Intro
HS Удаленный
Лаборатория Физика
Движение снаряда Maitha Abdulla Almazrouei UG-Intro
HS Lab
Remote Физика
движение снаряда Сумайя альзааби UG-Intro Лаборатория Физика
Движение снаряда Шахад Алхосани UG-Intro Удаленный
Лаборатория Физика
Движение снаряда Амна Биншемель UG-Intro
HS Лаборатория Физика
ОТЧЕТ О ДВИЖЕНИИ ПРОЕКТА Аиша Альзааби UG-Intro Лаборатория Физика
движение снаряда намаз Махди UG-Adv Лаборатория Физика
Движение снаряда (#lab) Мохамед Эрфан HS
UG-Intro HW
Lab Физика
Движение снаряда и горизонтальная составляющая его скорости Дания Али HS
UG-Intro Удаленный
Лаборатория Физика
Свободное падение барабан уложен UG-Intro
HS Лаборатория Физика
движение снаряда реэм алали UG-Intro Лаборатория Физика
Движение снаряда Хасан Аладжми UG-Intro Лаборатория Физика
Движение снаряда meera ahli HS
MS Удаленный
Лаборатория Физика
Управляемое открытие (китайский / английский) для студентов-первокурсников по физике: 1.Кинематика Благотворительность Грейс Уайт (白愛恩), Джанет Чен (陳衫豫), Джонатон Дэвид Уайт (白小白) UG-Intro Лаборатория
Управляемая Физика
движение снаряда Али Хумайд Алалили UG-Intro Лаборатория Физика
снаряд Абдулла Осамельдин UG-Intro Лаборатория Физика
Отчет о движении снаряда Ахмед Алсувайди HS HW
Lab Физика
Движение снаряда — горизонтальная и полная траектория Линн Кистлер HS Лаборатория Физика
Движение снаряда Ахд Шошаа UG-Intro
UG-Adv
HS Lab
Guided
Обсудить Физика
Отчет лаборатории движения Абдулбасит Варсаме HS
UG-Intro HW Физика
моделирование движения снаряда Махмуд Аман UG-Intro Лаборатория Физика
форма отчета лаборатории движения projectil Муджтаба Аббас UG-Intro Лаборатория Физика
Взаимосвязь снарядов с горизонтальным выпуском Эми Карпинелли UG-Intro
HS Удаленный
HW
Lab Физика
Горизонтальное движение снаряда Усама Абдулгани UG-Intro Лаборатория Физика
движение снаряда Амр Йехиа UG-Intro
UG-Adv Demo
Lab
Guided Физика
Движение снаряда Ахмед Эз Эддин UG-Intro
HS HW
Lab Физика
движение снаряда Ахмед Эз Эддин UG-Intro
HS Лаборатория
HW Физика
Рабочий лист движения снаряда Aseel Atheer Град Guided
HW
Lab
Remote Другое
Физика
Движение снаряда Салем Аль Мхейри UG-Adv Лаборатория Физика
Движение снаряда Исмаил Зейн UG-Intro Лаборатория Физика
Движение снаряда (Анвар Мабрук аль-Тальха) Анвар Мабрук Другое Лаборатория
Управляемая Физика
Движение снаряда Мохамед Аламири UG-Intro Пульт Физика
Рабочий лист движения снаряда Мустафа Аларадж UG-Intro
HS Лаборатория Физика
Лаборатория моделирования снарядов PhET Барбара Бакли HS Remote
Lab
Guided Физика
Движение снаряда халифа алкетби Другое Лаборатория Физика
Снаряд Движение Сара Аль Карам UG-Intro Лаборатория Физика
движение проекта ноура хамад хазим Град
UG-Adv Лаборатория Физика
Движения Сопротивление воздуха zuhair M Z Abdalmenem HS
UG-Intro HW Физика
Горизонтальное движение снаряда Абдалла Алалаунех UG-Intro Лаборатория Физика
Снаряд движения — время полета (горизонтальный снаряд) Мохамед Ахмед Мохамед Исмаил UG-Intro Лаборатория Физика
Эксперименты с движением снаряда Руслан Кувшинов UG-Adv
UG-Intro Лаборатория Физика
движение снаряда yousef faisal UG-Intro Лаборатория Физика
Движение снаряда Эксперимент Мохаммед Ат-Тайеб UG-Adv
HS
UG-Intro Лаборатория
Управляемая Физика
Движение снаряда Бушр Алассуад HS
UG-Intro Demo
Guided
Обсудить
Lab Физика
Движение снаряда Бараа Махди UG-Intro Лаборатория Физика
Движение снаряда Мохамад Фархат UG-Intro Управляемый
Лабораторный Физика
Время полета относительно начальной скорости горизонтального снаряда. Айсса Мессауди UG-Intro управляемый Физика
движение снаряда Амна Алсувайди HS
UG-Intro Удаленный
Лаборатория Физика
Движение снаряда — лабораторный эксперимент по физике 1 Язен Мохаммад Рихан UG-Intro Lab
Remote
Guided Физика
MS и HS TEK для выравнивания Sim Elyse Zimmer HS
MS Другое Химия
Физика
Биология
Обнаружение движения снаряда Шон Бостон UG-Intro
HS Remote
Lab
HW
Guided Физика
Движение снаряда Надя Львов HS
UG-Intro Remote
Lab
HW
Guided
Demo Физика
Математика
движение по прямой с постоянным ускорением Тахани Сарайрех UG-Intro
HS Lab
Remote Физика
Лаборатория снарядов (запуск под углом) Арой Мукаррам HS
UG-Intro Remote
Guided
Lab
HW Физика
Лаборатория снарядов (горизонтальный запуск) Арой Мукаррам UG-Intro
HS HW
Remote
Lab
Guided Физика
Деятельность лаборатории движения снаряда Прамод Ламиххане UG-Intro
HS Удаленный
Управляемый
Лабораторный Физика
Эксперименты с движением снаряда Nawal Nayfeh UG-Intro
HS Лаборатория Физика
Плата Падение Nawal Nayfeh HS
UG-Intro Удаленный
Лаборатория Физика
Regents Physics — вступление в движение снаряда Алекс Рейда HS Лаборатория Физика
Симулятор движения снаряда Дэвид Вирт HS Лаборатория Физика
Другое Физика
Моделирование PhET адаптировано для AP Physics C Роберта Таннер HS Другое Физика
Тир параболический Жорди Плана МС HW Физика
Снаряд Параболы Эми Рид HS управляемый Математика
Запуск тыкв — решение квадратичных функций Крейг Сивер HS
MS Обсудить
Управляемый
Лаборатория Математика
Сравнение скорости и угла с расстоянием до снаряда Джефф Спрингер МС управляемый Физика
3 фактора движения снаряда Мэри Терен HS Управляемый
Лабораторный Физика
Изучение векторов и движения снаряда Брайан Минчен HS управляемый Физика
Запрос на управляемый снаряд Лаура Мэттик HS управляемый Физика
Запрос активности снаряда Джефф Драч MS
HS управляемый Физика
Введение в виртуальную лабораторию Tiro Parabólico Диана Лопес и Оскар Суарес HS
UG-Intro Lab
Remote
MC
Обсудить
Guided Физика
SECUNDARIA: Alineación PhET con programas de la SEP México (2011 г 2017 г.) Диана Лопес MS
HS Другое Химия
Математика
Биология
Физика
Введение в физику: medidas, unidades y relación entre variables Диана Лопес HS
UG-Intro HW
Lab
Guided
Remote Физика
ПРЕПАРАТОРИЯ: Alineación de PhET con programas de la DGB México (2017) Диана Лопес HS
UG-Intro Другое Физика
Математика
Химия
ПРИМАРИЯ: Alineación con programas de la SEP México (2011 г 2017 г.) Диана Лопес К-5
МС Lab
Guided
HW
Demo
Обсудить Физика
Математика
Химия
Астрономия
Composició de moviment.Движение параболическое. PhET Ана Мария Лафуэнте Герас HS Remote
HW
MC
Lab Физика
Der Gerade Wurf Изабелла Радл MS
HS HW
Направляющая Физика
Лаборатория движения снаряда хаким алхамиди MS
HS Лаборатория Физика
Движение снаряда Доктор.Нафисех Наср UG-Intro
HS HW
Lab Физика
Lançamento Vertical no PhET Кэролайн Сантос душ Сантуш; Мириан Марчезан Лопес; Памела да Силвейра Фрейтас. MS
HS HW
Lab
Guided
Remote Физика
Corona vírus vs lançamento de projéteis Клейсон Лима HS
Град
MS Лаборатория Физика
Atividade de Lançamento Oblíquo Джеирла Монтейро, Гилванденис Л.Продажа HS Другое Физика
Atividades sobre o movimento dos corpos Artur Araújo Cavalcante e Gilvandenys Leite Продажи Другое
HS
MS HW
Обсудить
Другое
Guided Математика
Другое
Науки о Земле
Физика
Mecânica (Atividades) nos OA’s do PhET Artur Araújo Cavalcante e Gilvandenys Leite Продажи Grad
MS
UG-Intro
HS
Другое Guided
Обсудить
Demo
Lab
HW
Other Физика
Науки о Земле
Другое
Cinemática (Atividades) nos OA’s do PhET Artur Araújo Cavalcante e Gilvandenys Leite Продажи UG-Intro
MS
HS
Другое Lab
Demo
Other
Guided
HW Науки о Земле
Физика
Другое
Velocidade e Aceleração no Lançamento de Projéteis no «Projectile Motion (HTML5)» Artur Araújo Cavalcante e Gilvandenys Leite Продажи HS
MS
Другое HW
Направляемые
Другое Прочее
Науки о Земле
Физика
Queda Livre no «Projectile Motion (HTML5)» Artur Araújo Cavalcante e Gilvandenys Leite Продажи HS
Другое
MS HW
Прочие
Направляемые Физика
Науки о Земле
Математика
Другое
Lançamento Vertical de Projéteis no «Projectile Motion (HTML5)» Artur Araújo Cavalcante e Gilvandenys Leite Продажи MS
Другое
HS Другое
HW
Направляющая Науки о Земле
Физика
Другое
Математика
Lançamento Horizontal de Projéteis no «Projectile Motion (HTML5)» Artur Araújo Cavalcante e Gilvandenys Leite Продажи Другое
HS
MS Направляемые
Прочее
HW Другое
Математика
Науки о Земле
Физика
Lançamento de Projéteis Хосе Карлос Феррейра Бастос, Дарксон Фернандес да Коста HS
UG-Intro Demo
Guided
Lab Физика
Lançando Projéteis no «Projectile Motion (HTML5)» Artur Araújo Cavalcante e Gilvandenys Leite Продажи MS
HS HW
Направляемые
Другое Науки о Земле
Физика
Математика
Lançamento Oblíquo Inicial Карлос Альбукерке МС Демо
HW Физика
Actividad — movimiento parabólico Хаги Юкра и Джессика Лоренцо HS HW Физика
HOJA DE TRABAJO Лаура Муньос HS Управляемый
Пульт ДУ Физика
Movimiento Parabolico Вальтер Мануэль Трухильо Яйпен MS
Другое
HS
UG-Adv
Grad
UG-Intro Lab
Other
HW
Guided
MC Другое
Физика
Математика
Гиа де трабахо; Movimiento de un Proyectil Мария Камила Льоренте Кастро — Хулио Сезар Паес Гарсия К-5 управляемый Физика
Movimiento Parabolico.Comaparacion de datos Вальтер Мануэль Трухильо Яйпен Другое
MS
Grad
UG-Adv
K-5
HS
UG-Intro HW
Remote
Lab
Demo Другое
Математика
Физика
Movimiento en dos sizes: Caso del Proyectil (Двухмерный механизм, футляр для снаряда). Кармен Мальдонадо UG-Intro
HS Lab
Guided
Remote
HW Физика
Practica de Movimiento Parabolico Вальтер Мануэль Трухильо Яйпен HS
Grad
MS
UG-Intro
UG-Adv Управляемый
Другой
HW
Лабораторный Физика
Practica Tiro Parabolico (перевод) Херардо Сармьенто MS
HS Лаборатория
Управляемая Физика
КЛАСС GRADO 10 FISICA николас ривера HS Лаборатория Физика
Практика: Тиро Параболико МОНИКА КРАВЕРО MS
HS Demo
Guided
Lab Физика
Кинематические уравнения: когда и как использовать каждую формулу (с производными)
Обновлено 28 декабря 2020 г.
Автор GAYLE TOWELL
Кинематические уравнения описывают движение объекта, испытывающего постоянное ускорение.Эти уравнения связывают переменные времени, положения, скорости и ускорения движущегося объекта, позволяя решить любую из этих переменных, если другие известны.
Ниже представлено изображение объекта, совершающего движение с постоянным ускорением в одном измерении. Переменная t предназначена для времени, позиция x, скорость v и ускорение a . Индексы i и f обозначают «начальный» и «конечный» соответственно.2 + 2a (x_f — x_i)
Примечания по кинематическим уравнениям
Эти уравнения работают только с постоянным ускорением (которое может быть нулевым в случае постоянной скорости).
В зависимости от того, какой источник вы читаете, окончательные количества могут не иметь нижнего индекса f и / или могут быть представлены в обозначении функций как x (t) — читать « x как функция времени» или « x на момент времени t » — и v (t) . Обратите внимание, что x (t) НЕ означает x , умноженное на t !
Иногда величина x _f — x _i записывается как
Δx , что означает «изменение x », или даже просто как d , что означает смещение.Все равноценны. Положение, скорость и ускорение являются векторными величинами, то есть с ними связано направление. В одном измерении направление обычно обозначается знаками — положительные величины находятся в положительном направлении, а отрицательные величины — в отрицательном направлении. Нижние индексы: «0» может использоваться для начального положения и скорости вместо и . Этот «0» означает «при t = 0», а x ₀ и v ₀ обычно произносятся как «x-ноль» и «v-ноль».»* Только одно из уравнений не включает время. При составлении заданных значений и определении того, какое уравнение использовать, это ключ!
Особый случай: свободное падение
Движение свободного падения — это движение ускоряющегося объекта только за счет силы тяжести в отсутствие сопротивления воздуха. Применяются те же кинематические уравнения; однако значение ускорения у поверхности Земли известно. Величина этого ускорения часто представлена как g , где g = 9.8 м / с ². Направление этого ускорения — вниз, к поверхности Земли. (Обратите внимание, что в некоторых источниках значение г может быть приблизительно равно 10 м / с ², а в других может использоваться значение с точностью до более чем двух десятичных знаков.)
Стратегия решения проблем кинематики в одном измерении:
Нарисуйте схему ситуации и выберите подходящую систему координат. (Напомним, что x , v и a — все векторные величины, поэтому, задав четкое положительное направление, будет легче отслеживать знаки.)
Напишите список известных величин. (Помните, что иногда известные вещи не очевидны. Ищите фразы вроде «начинается с отдыха», что означает, что v _i = 0, или «падает на землю», что означает, что x _f = 0, и т. д.)
Определите, какое количество вы хотите найти в вопросе. Какое неизвестное вы будете решать?
Выберите соответствующее кинематическое уравнение. Это будет уравнение, которое содержит вашу неизвестную величину вместе с известными величинами.
Решите уравнение для неизвестной величины, затем подставьте известные значения и вычислите окончательный ответ. (Будьте осторожны с единицами измерения! Иногда вам необходимо преобразовать единицы перед вычислением.)
Примеры одномерной кинематики
Пример 1: В рекламе утверждается, что спортивный автомобиль может разогнаться от 0 до 60 миль в час за 2,7 секунды. Какое ускорение у этой машины в м / с ²? Как далеко он проходит за эти 2,7 секунды?
Известные и неизвестные количества:
v_i = 0 \ text {mph} \\ v_f = 60 \ text {mph} \\ t = 2.7 \ text {s} \\ x_i = 0 \\ a = \ text {?} \\ x_f = \ text {?}
Первая часть вопроса требует решения для неизвестного ускорения. Здесь мы можем использовать уравнение № 1:
v_f = v_i + at \ implies a = \ frac {(v_f-v_i)} t
Однако, прежде чем вводить числа, нам нужно преобразовать 60 миль в час в м / с:
60 \ cancel {\ text {mph}} \ Bigg (\ frac {0,477 \ text {m / s}} {\ cancel {\ text {m / s}}} \ Bigg) = 26,8 \ text {m / s}
Итак, ускорение будет:
a = \ frac {(26.8-0)} {2.2 + 2 (-9,8) (0-1,5)} = \ pm \ sqrt {254.4} \ приблизительно \ pm16 \ text {m / s}
Здесь есть два решения. Который правильный? Из нашей диаграммы мы видим, что конечная скорость должна быть отрицательной. Итак, ответ:
v_f = \ underline {\ bold {-16} \ text {m / s}}
Чтобы найти время, мы можем использовать уравнение №1 или уравнение №2. Поскольку с уравнением № 1 работать проще, мы будем использовать его:
v_f = v_i + at \ implies t = \ frac {(v_f-v_i)} {a} = \ frac {(-16-15)} {-9,8} \ приблизительно \ underline {\ bold {3.2} \ text {s}}
Обратите внимание, что ответ на первую часть этого вопроса был не 0 м / с. Хотя верно, что после того, как мяч приземлится, его скорость будет равна 0, но этот вопрос хочет знать, насколько быстро он летит за долю секунды до удара. Как только мяч касается земли, наши кинематические уравнения больше не применяются, потому что ускорение не будет постоянным.
Кинематические уравнения движения снаряда (два измерения)
Снаряд — это объект, движущийся в двух измерениях под действием силы тяжести Земли.Его путь — парабола, потому что единственное ускорение происходит за счет силы тяжести. Кинематические уравнения движения снаряда немного отличаются от приведенных выше кинематических уравнений. Мы используем тот факт, что компоненты движения, которые перпендикулярны друг другу, такие как горизонтальное направление x и вертикальное направление y , являются независимыми.
Стратегия решения проблем для кинематики движения снаряда Задачи:
Нарисуйте схему ситуации.Как и в случае с одномерным движением, полезно набросать сценарий и указать систему координат. Вместо использования меток x , v и a для положения, скорости и ускорения, нам нужен способ маркировки движения в каждом измерении отдельно.
Для горизонтального направления чаще всего используется x для положения и v _x для x-компоненты скорости (обратите внимание, что ускорение равно 0 в этом направлении, поэтому нам не нужна переменная для Это.) В направлении y наиболее часто используется y для позиции и v _y для y-компоненты скорости. Ускорение можно обозначить как a _y , или мы можем использовать тот факт, что мы знаем, что ускорение свободного падения составляет g в отрицательном направлении оси y, и просто использовать это вместо этого.
Напишите список известных и неизвестных величин, разделив задачу на две части: вертикальное и горизонтальное движение.Используйте тригонометрию, чтобы найти компоненты x и y любых векторных величин, которые не лежат вдоль оси. Может быть полезно перечислить это в двух столбцах:
Примечание: если скорость дана как величина вместе с углом, Ѳ , над горизонтом, тогда используйте векторное разложение, v _x = vcos (Ѳ ) и v _y = vsin (Ѳ) .
Мы можем рассмотреть наши три кинематических уравнения из предыдущих и адаптировать их к направлениям x и y соответственно.2-2g (y_f — y_i)
Обратите внимание, что ускорение в направлении y равно -g, если мы предполагаем, что вверх положительно. Распространенное заблуждение — g = -9,8 м / с ², но это неверно; g сама по себе просто величина ускорения: g = 9,8 м / с ², поэтому нам нужно указать, что ускорение отрицательное.
Найдите одно неизвестное в одном из этих измерений, а затем вставьте то, что является общим в обоих направлениях. 2 \ подразумевает t = \ sqrt {\ frac {(2 \ times 20)} g} = \ underline {\ bold {2.02} \ text {s}}
Затем, чтобы найти место приземления, x _f , мы можем использовать уравнение горизонтального движения:
x_f = x_i + v_xt = 50 \ times2.02 = \ underline {\ полужирный {101} \ text {s}}
Пример 2: Мяч запускается со скоростью 100 м / с от уровня земли под углом 30 градусов к горизонту. Где он приземляется? Когда его скорость наименьшая? Где он находится в настоящее время?
Известные и неизвестные величины:
Сначала нам нужно разбить вектор скорости на составляющие:
v_x = v_i \ cos (\ theta) = 100 \ cos (30) \ приблизительно 86.6 \ text {m / s} \\ v_ {yi} = v_i \ sin (\ theta) = 100 \ sin (30) = 50 \ text {m / s}
Тогда наша таблица величин:
Сначала нам нужно найти время, когда мяч находится в полете. Мы можем сделать это с помощью второго вертикального уравнения_. Обратите внимание, что мы используем симметрию параболы, чтобы определить, что конечная скорость _y является отрицательной по отношению к начальной:
Затем мы определяем, как далеко она перемещается в направлении x за это время:
x_f = x_i + v_xt = 86,6 \ умножить на 10. 2 + 2a (x_f — x_i)
Решение кинематических задач — физический класс (видео)
Уравнения кинематики
Хорошо, кинематика — это изучение движения с помощью уравнений.2 + 2 * a * d
vf = vi + a * t
d = ‘( vf + vi ) / t 2) * 947
Итак, на что мы смотрим? Эти уравнения используются для вычисления неизвестной информации о движении объектов относительно известных переменных. В общем, если вы знаете три переменные, вы можете вычислить четвертую. Это:
d для смещения объекта, которое в основном представляет собой расстояние, на которое он перемещается
т за время движения объекта
для разгона
v для скорости
На самом деле, мы можем разбить последнюю на vi для начальной скорости и vf для конечной скорости.
Итак, если мы посмотрим на одно из этих уравнений — скажем, это ( vf = vi + a * t ) — то, что на самом деле говорит, что конечная скорость равна начальной скорости плюс время ускорения. Раз, время! В любом случае, если вы знаете три переменные, вы можете вычислить четвертую.
Использование кинематического уравнения
Хорошо, давайте посмотрим на это в действии. Скажи, что мы едем, ла-ди-да. Теперь скажи, что я начинаю превышать скорость. Я разгоняюсь до 80 миль в час, превышаю ограничение скорости, и мы проскакиваем мимо припаркованной полицейской машины, которая включает фары и начинает преследовать нас.Теперь, если он хочет догнать нас примерно за 10 секунд, насколько быстро ему нужно ускориться? Что ж, воспользуемся кинематикой. Первый шаг к решению кинематического уравнения — выяснить, что вы знаете и чего не знаете. Итак, давайте рассмотрим наши переменные.
Знаем ли мы, какое расстояние ему придется пройти, чтобы нас догнать? № d =?
Как насчет времени? Ну да, мы знаем, что он хочет поймать нас за 10 секунд, поэтому t = 10 .
Разгон? Что ж, это то, что мы пытаемся выяснить, так что снова a =?
Как насчет скоростей? Он был припаркован, поэтому начальная скорость, или vi = 0 , и он хочет поймать нас, пока мы делаем 80, так что конечная скорость, или vf = 80 .
Итак, у нас есть три известные переменные? Да, мы знаем время, начальную и конечную скорость.
Следующий шаг — выяснить, какое уравнение использовать.Для этого вы просто ищите уравнение, которое может содержать три известные переменные и неизвестную переменную, которую вы хотите вычислить. Первые два требуют расстояния и ускорения, так что это не сработает, поскольку у нас есть два неизвестных. Вот и все:
vf = vi + a * t
Мы знаем три из этих переменных и одну неизвестную — ускорение. Теперь мы подключаем его так, чтобы он выглядел так:
80 = 0 + ( a * 10)
И мы его решаем.Это становится:
80 миль / ч = a * 10 с
80 миль / ч / 10 с = a
8 миль / ч / с = a
Итак, a , или ускорение , составляет 8 миль / час / с — не обычные единицы, но это имеет смысл, если задуматься. Так что, если этот полицейский ускоряется на 10 секунд, ему нужно будет набрать 8 миль в час скорости в секунду, чтобы поймать нас. Мы можем проверить это, вставив и обратно в исходное уравнение, сделав это:
80 = 0 + 8 * 10
80 = 80
Да, это проверено.Хорошо, следующая задача: выяснить, как быстро нам нужно ехать, чтобы выбраться отсюда и избежать полицейского. И идти!
Краткое содержание урока
Когда вы чувствуете, что жизнь уходит из движения, не паникуйте — просто посчитайте. В классической механике , изучении движения объектов, мы можем посмотреть, как объекты перемещаются между покоем и движением различными способами. Один из таких способов — кинематика , исследование движения с помощью уравнений. Для решения вопросов движения обычно используются четыре стандартных кинематических уравнения.Чтобы решить эти уравнения, вам нужны три известные переменные и одна неизвестная переменная. Это первый шаг к решению кинематической проблемы: определение известных и неизвестных переменных. Затем вы находите уравнение, которое соответствует этим переменным, и решаете одно неизвестное. Зная кинематику, вы можете вывести свое тело из состояния покоя и начать свою физическую карьеру.
Projectiles — The Physics Hypertextbook
Обсуждение
введение
Снаряд — это любой объект, который брошен, запущен, брошен, взлетен, брошен, кидается, бросает или бросает.(Это неформальное определение.) Путь снаряда называется его траекторией . Некоторые примеры снарядов включают…
бейсбольный мяч, который был брошен, отброшен или брошен
пуля в момент выхода из ствола ружья или винтовки
Автобус съехал с незавершенного моста
летящий в воздухе самолет с отключенными двигателями и крыльями
бегун на полпути (так как он на мгновение теряет контакт с землей)
космический челнок или любой другой космический корабль после выключения главного двигателя (MECO)
Первостепенной силой, действующей на снаряд, является гравитация.Это не означает, что других сил не существует, просто их влияние минимально по сравнению. Брошенный воздушный шар, наполненный гелием, обычно не считается снарядом, поскольку сопротивление и выталкивающая сила на нем столь же значительны, как и вес. Воздушные шары, наполненные гелием, нельзя бросать на большие расстояния и обычно они не падают. В отличие от этого, разбивающийся самолет будет считаться снарядом. Несмотря на то, что сопротивление и выталкивающие силы, действующие на него, в абсолютном выражении намного больше, чем на воздушный шар, гравитация — это то, что действительно движет разбивающимся самолетом.Нормального сопротивления и плавучести просто недостаточно, чтобы спасти пассажиров обреченного полета от неудачного конца. Снаряд — это любой объект с начальной ненулевой горизонтальной скоростью, ускорение которого происходит только за счет силы тяжести.
Важной характеристикой снаряда является то, что его будущее уже предопределено. Отбивающие могут применять «телесный английский» после удара по длинному мячу, но делают это строго по психологическим причинам. Никакие отклонения в сторону не сделают фол справедливым.Конечно, пилот неисправного самолета может восстановить управление до крушения и предотвратить катастрофу, но тогда самолет больше не будет снарядом. Объект перестает быть снарядом после того, как будет произведен какой-либо реальный эффект по изменению его траектории. Таким образом, траектория полета снаряда полностью определяется в тот момент, когда она удовлетворяет определению снаряда.
Единственными значимыми величинами, которые могут варьироваться от снаряда к снаряду, являются начальная скорость и начальное положение
Здесь мы сталкиваемся с некоторыми лингвистическими сложностями.Иногда говорят, что самолеты, управляемые ракеты и ракетные космические корабли следуют по траектории. Поскольку на эти устройства действуют подъем крыльев и тяга двигателей в дополнение к силе тяжести, они на самом деле не являются снарядами. Чтобы обойти эту дилемму, обычно используется термин баллистическая траектория , когда речь идет о снарядах. Слово баллистический происходит от греческого слова βαλλω ( vallo ), которое означает бросать, и неоднократно встречается на техническом жаргоне оружия с древних времен до наших дней.Например…
Баллиста , которая чем-то похожа на гигантский арбалет, была осадной машиной, используемой в средневековые времена для закидывания больших камней, пылающих связок, зараженных туш животных и отрубленных человеческих голов в укрепления. До изобретения пороха баллисты (а также катапульты и требушеты) были излюбленным оружием завоевателей.
Межконтинентальная баллистическая ракета — это устройство для доставки ядерных боеголовок на большие расстояния.В начале своего путешествия межконтинентальная баллистическая ракета управляется ракетным двигателем и стабилизирующими стабилизаторами, но вскоре после этого она входит в фазу своего полета, когда она фактически находится в свободном падении, путешествуя достаточно быстро, чтобы какое-то время удерживать ее над атмосферой Земли, но не достаточно быстро, чтобы выйти на орбиту навсегда. Прилагательное «межконтинентальный» относится к дальнобойным возможностям, в то время как путешествие в условиях свободного падения делает его «баллистическим». Межконтинентальные баллистические ракеты — это идеальные машины для убийства, но до настоящего времени они никогда не использовались в бою.
Широкий географический диапазон, а также широкий исторический диапазон этих вещей, которые мы называем снарядами, создают некоторые проблемы для типичного студента-физика. Когда снаряд отправляется в очень долгое путешествие, как в случае с межконтинентальными баллистическими ракетами, величина и направление ускорения под действием силы тяжести меняются. С самого начала сила тяжести не постоянна, но изменения не заметны в повседневных диапазонах высоты. От самых глубоких шахт в Южной Африке до самых больших высот, которые преодолеваются коммерческими самолетами, величина ускорения силы тяжести баллов всегда фактически равна 9.8 м / с ² ± 0,05 м / с ². Точно так же, если вы обычно не путешествуете на средние и большие расстояния, вы вряд ли испытаете сильное изменение направления силы тяжести на . Чтобы испытать смещение «вниз» на 1 °, потребуется проехать ¹ ₃₆₀ по окружности Земли — примерно 110 км (70 миль) или длина типичного утреннего пути на работу в Южную Калифорнию. Таким образом, для снарядов, которые не поднимаются выше самолета и не летят дальше диаметра L.A. гравитация практически постоянна. Это касается первых пяти примеров, описанных в начале этого раздела (бейсбольные мячи, пули, автобусы в приключенческих боевиках, потерпевших бедствие самолетов и бегунов), но не шестого (космический шаттл после MECO).
Чтобы отличить такие простые снаряды от снарядов, в которых изменения гравитации и кривизны Земли значительны, я предлагаю использовать термин простой снаряд . Для остальных задач термин общий снаряд кажется подходящим, поскольку общее решение в математике — это решение, которое также включает частные случаи, но я менее категоричен в отношении этого термина.
Представьте себе сферическую Землю с единственной высокой горой, торчащей из нее, как гигантская опухоль. А теперь представьте, что вы используете это место как место для запуска снарядов по горизонтали с различной начальной скоростью. Как скорость повлияет на дальность? Очевидно, что быстрые снаряды летят дальше медленных. Базовая концепция, связанная со скоростью, заключается в том, что «быстрее значит дальше», но на сферической Земле это соотношение является лишь приблизительно линейным. Какое-то время удвоение скорости означало бы удвоение расстояния, но в конечном итоге кривизна Земли начала мешать.На некоторой скорости наш гипотетический снаряд сделает четверть оборота вокруг Земли, затем половину оборота, а затем, в конце концов, облетит всю Землю. В этот момент наш общий снаряд перестает быть объектом с точкой запуска и точкой приземления, и он начинает быть спутником , постоянно вращающимся вокруг Земли, постоянно меняющим направление и, таким образом, ускоряющимся под действием силы тяжести, но никогда никуда не приземляющимся. Технически такой объект все равно был бы обычным снарядом, поскольку гравитация является основным источником его ускорения, но почему-то это не кажется правильным.Объекты, путешествующие в том, что мы называем «космическим пространством», больше не кажутся снарядами. Кажется, что они живут больше в сфере небесной механики , чем земной механики . Однако такие различия произвольны, поскольку существует только одна механика. Законы физики считаются универсальными, пока не будет доказано иное. Объединение физических законов — тема, которая время от времени всплывает в физике.
Снаряд и спутник управляются одними и теми же физическими принципами, хотя и имеют разные названия.Простой снаряд делается математически простым идеализацией (в основном ложью удобства). Принимая постоянное значение для ускорения свободного падения, мы упрощаем решение проблемы и (во многих случаях) не сильно теряем в точности.
Каждая задача о снаряде — это, по сути, две одномерные задачи о движении…
Кинематические уравнения для простого снаряда — это уравнения для объекта, движущегося с постоянной горизонтальной скоростью и постоянным вертикальным ускорением.
Уравнения движения для простого снаряда
уравнение горизонтальный вертикальный
ускорение a _x = 0 a _y = — г
скорость-время v _x = v _{0 x} v _y = v _{0 y} — gt
время вытеснения x = x ₀ + v _{0 x} т y = y ₀ + v _{0 y} t — ½ gt ²
скорость-смещение v _y ² = v _{0 y} ²-2 g ( y — y ₀)
отделка…
Траектория простого снаряда — парабола.
исчисление, но не совсем
максимальная дальность при 45 °, равные дальности для углов запуска, которые превышают или меньше 45 ° на равные величины (например, 40 ° и 50 °, 30 ° и 60 °, 0 ° и 90 °)
Используйте горизонтальное направление для определения диапазона как функции времени…
x = x ₀ + v _{0 x} t + ½ a _x t ²
x = 0 + ( v cos θ) t + 0
x _{окончательный} = ( v cos θ) t _{окончательный}
Используйте вертикальное направление для определения времени в воздухе…
y = y ₀ + v _{0 y} t + ½ a _y t ²
y = y _{0 _{0 _{( v sin θ) t — ½ gt ²
0 = 0 + ( v sin θ) t _final — ½ gt ² _final}}}
т _{окончательная} = 2 ( против sin θ)
г
Объедините эти два уравнения…
x _{окончательный} = ( v cos θ) 2 ( против sin θ)
г
x _{окончательный} = v ² sin 2θ
г
x _{макс.No related posts.
Posted in Контрольная
Навигация по записям
Previous
Next
Leave a ReplyДобавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Контрольная
Советы
2024 © Все права защищены. Карта сайта}

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	10-08-2019

Введение в движение снаряда (на основе запроса)		Триш Лёблейн	HS UG-Intro	MC Удаленный Лаборатория	Физика
Концептуальные вопросы по физике с использованием PhET (на основе запросов)		Триш Лёблейн	HS UG-Intro	MC	Физика
Уроки физики на основе алгебры в одном семестре, вопросы для кликеров и расписание в pdf (на основе запросов)		Триш Лёблейн	UG-Intro HS	HW Demo Lab	Физика
Квадратичные функции для движения снаряда		Сара Хэмптон и Салли Джиллетт	MS HS	Guided Обсудить	Математика
Кинематическое уравнение		Ши Филлипс	HS	управляемый	Физика
Квадратичные снаряды		beki toussaint	HS	Лаборатория	Математика
Экспериментальный план: движение снаряда!		Джейми Шенбергер	МС	Управляемый Лабораторный	Прочее Науки о Земле
Урок сопротивления воздуха		Команда PhET средней школы UTeach	МС	Лаборатория	Физика
Исследование снаряда для средней школы		Мастерская средней школы округа Джефферсон	МС	Лаборатория	Физика Математика Науки о Земле
Каким образом симуляции PhET подходят для моей программы средней школы?		Сара Боренштейн	МС	Другое	Химия Физика Биология Науки о Земле
Деятельность виртуальной лаборатории Projectile Motion		Яков Залкинд	HS UG-Intro	Lab Remote	Физика
Движение снаряда		Майтха Маджан	HS UG-Intro	Лаборатория	Физика
Эксперимент по движению снаряда		Джавахер бин Хаммад	UG-Intro	Лаборатория	Физика
Горизонтальное движение снаряда		Сара Мохаммед	UG-Intro	Лаборатория	Физика
движение снаряда Ханан		Ханан Саид	Другое	Лаборатория	Физика
движение снаряда		Марьям алзааби	UG-Adv	Лаборатория HW	Физика
движение снаряда		Фатма Аль-Али	HS	Лаборатория	Физика
Движение снаряда		Эльмустафа Эльмубарак	UG-Intro	Лаборатория	Физика
Движение снаряда		Саид Али	UG-Intro	Лаборатория	Физика
движение снаряда		Ибрагим Альсвидан	МС	Лаборатория	Физика
Отчет лаборатории движения снаряда		фади каззаз	UG-Intro	Лаборатория	Физика
Движение снаряда		Мустафа Хасан Мохаммед Эльмаллах	UG-Intro	Лаборатория	Физика
Движение снаряда, дальность, время, скорость		Муза Джамал Альнуайми	UG-Intro	Lab Remote	Физика
Движение снаряда		Абдельмонем Атеф	UG-Adv UG-Intro	Lab Remote HW	Физика
Рабочий лист движения проекта		Юсеф Алаа	UG-Intro	Лаборатория	Физика
Движение снаряда (лабораторный отчет)		Али Алгфели	UG-Intro	Лаборатория	Физика
Движение снаряда		Зеяд Мохаммед	UG-Intro	Прочее HW Lab	Физика
Движение снаряда		Suha AlHadha	UG-Intro HS	Лаборатория	Физика
Движение снаряда		Амр Ахмед	UG-Intro	Лаборатория	Физика
Движение снаряда		Халид Альсале	Другое	Лаборатория	Физика
снаряд		Рая Альшамси	UG-Intro	Лаборатория	Физика
Рабочий лист снаряда		Маджед Мансур Аль Хашими	UG-Intro	Лаборатория	Физика
движение снаряда		Мохамед Алнакби	Другое	Лаборатория	Физика
Движение снаряда		Росс Пинкертон, Джоан Роке	HS	Remote Lab Guided	Физика
Лаборатория движения горизонтальных снарядов		Росс Пинкертон, Джоан Роке	HS	Lab Guided Remote	Физика
Движение снаряда (включая сопротивление воздуха)		Фатма Фуад	UG-Intro UG-Adv HS	Лаборатория Управляемая	Физика
Движение снаряда		карим аллаххам	UG-Intro	Лаборатория	Физика
Рабочий лист движения снаряда		М.Салман Исмаил	UG-Intro HS	Guided Remote Lab HW	Физика
снаряд мотыльков		abood hamad	UG-Intro	Лаборатория	Физика
Движение снаряда		Амна Биншемель	HS UG-Intro	Лаборатория	Физика
Отчет лаборатории движения снаряда		Абдулла Салехи	HS	Лаборатория HW	Физика
Снаряд		Айша Альхаммади	UG-Intro HS	Lab Remote	Физика
Движение снаряда		Галия Альзаруни	HS UG-Intro MS	Лаборатория Управляемая	Физика
Движение снаряда		Нура Джасим	UG-Intro HS	Lab Remote	Физика
Движение снаряда		Майтха Алдармаки	UG-Intro HS	Lab Remote	Физика
Движение снаряда		Амна Фейсал	UG-Intro HS	Удаленный Лаборатория	Физика
Движение снаряда		Maitha Abdulla Almazrouei	UG-Intro HS	Lab Remote	Физика
движение снаряда		Сумайя альзааби	UG-Intro	Лаборатория	Физика
Движение снаряда		Шахад Алхосани	UG-Intro	Удаленный Лаборатория	Физика
Движение снаряда		Амна Биншемель	UG-Intro HS	Лаборатория	Физика
ОТЧЕТ О ДВИЖЕНИИ ПРОЕКТА		Аиша Альзааби	UG-Intro	Лаборатория	Физика
движение снаряда		намаз Махди	UG-Adv	Лаборатория	Физика
Движение снаряда (#lab)		Мохамед Эрфан	HS UG-Intro	HW Lab	Физика
Движение снаряда и горизонтальная составляющая его скорости		Дания Али	HS UG-Intro	Удаленный Лаборатория	Физика
Свободное падение		барабан уложен	UG-Intro HS	Лаборатория	Физика
движение снаряда		реэм алали	UG-Intro	Лаборатория	Физика
Движение снаряда		Хасан Аладжми	UG-Intro	Лаборатория	Физика
Движение снаряда		meera ahli	HS MS	Удаленный Лаборатория	Физика
Управляемое открытие (китайский / английский) для студентов-первокурсников по физике: 1.Кинематика		Благотворительность Грейс Уайт (白愛恩), Джанет Чен (陳衫豫), Джонатон Дэвид Уайт (白小白)	UG-Intro	Лаборатория Управляемая	Физика
движение снаряда		Али Хумайд Алалили	UG-Intro	Лаборатория	Физика
снаряд		Абдулла Осамельдин	UG-Intro	Лаборатория	Физика
Отчет о движении снаряда		Ахмед Алсувайди	HS	HW Lab	Физика
Движение снаряда — горизонтальная и полная траектория		Линн Кистлер	HS	Лаборатория	Физика
Движение снаряда		Ахд Шошаа	UG-Intro UG-Adv HS	Lab Guided Обсудить	Физика
Отчет лаборатории движения		Абдулбасит Варсаме	HS UG-Intro	HW	Физика
моделирование движения снаряда		Махмуд Аман	UG-Intro	Лаборатория	Физика
форма отчета лаборатории движения projectil		Муджтаба Аббас	UG-Intro	Лаборатория	Физика
Взаимосвязь снарядов с горизонтальным выпуском		Эми Карпинелли	UG-Intro HS	Удаленный HW Lab	Физика
Горизонтальное движение снаряда		Усама Абдулгани	UG-Intro	Лаборатория	Физика
движение снаряда		Амр Йехиа	UG-Intro UG-Adv	Demo Lab Guided	Физика
Движение снаряда		Ахмед Эз Эддин	UG-Intro HS	HW Lab	Физика
движение снаряда		Ахмед Эз Эддин	UG-Intro HS	Лаборатория HW	Физика
Рабочий лист движения снаряда		Aseel Atheer	Град	Guided HW Lab Remote	Другое Физика
Движение снаряда		Салем Аль Мхейри	UG-Adv	Лаборатория	Физика
Движение снаряда		Исмаил Зейн	UG-Intro	Лаборатория	Физика
Движение снаряда (Анвар Мабрук аль-Тальха)		Анвар Мабрук	Другое	Лаборатория Управляемая	Физика
Движение снаряда		Мохамед Аламири	UG-Intro	Пульт	Физика
Рабочий лист движения снаряда		Мустафа Аларадж	UG-Intro HS	Лаборатория	Физика
Лаборатория моделирования снарядов PhET		Барбара Бакли	HS	Remote Lab Guided	Физика
Движение снаряда		халифа алкетби	Другое	Лаборатория	Физика
Снаряд Движение		Сара Аль Карам	UG-Intro	Лаборатория	Физика
движение проекта		ноура хамад хазим	Град UG-Adv	Лаборатория	Физика
Движения Сопротивление воздуха		zuhair M Z Abdalmenem	HS UG-Intro	HW	Физика
Горизонтальное движение снаряда		Абдалла Алалаунех	UG-Intro	Лаборатория	Физика
Снаряд движения — время полета (горизонтальный снаряд)		Мохамед Ахмед Мохамед Исмаил	UG-Intro	Лаборатория	Физика
Эксперименты с движением снаряда		Руслан Кувшинов	UG-Adv UG-Intro	Лаборатория	Физика
движение снаряда		yousef faisal	UG-Intro	Лаборатория	Физика
Движение снаряда Эксперимент		Мохаммед Ат-Тайеб	UG-Adv HS UG-Intro	Лаборатория Управляемая	Физика
Движение снаряда		Бушр Алассуад	HS UG-Intro	Demo Guided Обсудить Lab	Физика
Движение снаряда		Бараа Махди	UG-Intro	Лаборатория	Физика
Движение снаряда		Мохамад Фархат	UG-Intro	Управляемый Лабораторный	Физика
Время полета относительно начальной скорости горизонтального снаряда.		Айсса Мессауди	UG-Intro	управляемый	Физика
движение снаряда		Амна Алсувайди	HS UG-Intro	Удаленный Лаборатория	Физика
Движение снаряда — лабораторный эксперимент по физике 1		Язен Мохаммад Рихан	UG-Intro	Lab Remote Guided	Физика
MS и HS TEK для выравнивания Sim		Elyse Zimmer	HS MS	Другое	Химия Физика Биология
Обнаружение движения снаряда		Шон Бостон	UG-Intro HS	Remote Lab HW Guided	Физика
Движение снаряда		Надя Львов	HS UG-Intro	Remote Lab HW Guided Demo	Физика Математика
движение по прямой с постоянным ускорением		Тахани Сарайрех	UG-Intro HS	Lab Remote	Физика
Лаборатория снарядов (запуск под углом)		Арой Мукаррам	HS UG-Intro	Remote Guided Lab HW	Физика
Лаборатория снарядов (горизонтальный запуск)		Арой Мукаррам	UG-Intro HS	HW Remote Lab Guided	Физика
Деятельность лаборатории движения снаряда		Прамод Ламиххане	UG-Intro HS	Удаленный Управляемый Лабораторный	Физика
Эксперименты с движением снаряда		Nawal Nayfeh	UG-Intro HS	Лаборатория	Физика
Плата Падение		Nawal Nayfeh	HS UG-Intro	Удаленный Лаборатория	Физика
Regents Physics — вступление в движение снаряда		Алекс Рейда	HS	Лаборатория	Физика
Симулятор движения снаряда		Дэвид Вирт	HS	Лаборатория	Физика
Другое	Физика
Моделирование PhET адаптировано для AP Physics C		Роберта Таннер	HS	Другое	Физика
Тир параболический		Жорди Плана	МС	HW	Физика
Снаряд Параболы		Эми Рид	HS	управляемый	Математика
Запуск тыкв — решение квадратичных функций		Крейг Сивер	HS MS	Обсудить Управляемый Лаборатория	Математика
Сравнение скорости и угла с расстоянием до снаряда		Джефф Спрингер	МС	управляемый	Физика
3 фактора движения снаряда		Мэри Терен	HS	Управляемый Лабораторный	Физика
Изучение векторов и движения снаряда		Брайан Минчен	HS	управляемый	Физика
Запрос на управляемый снаряд		Лаура Мэттик	HS	управляемый	Физика
Запрос активности снаряда		Джефф Драч	MS HS	управляемый	Физика
Введение в виртуальную лабораторию Tiro Parabólico		Диана Лопес и Оскар Суарес	HS UG-Intro	Lab Remote MC Обсудить Guided	Физика
SECUNDARIA: Alineación PhET con programas de la SEP México (2011 г 2017 г.)		Диана Лопес	MS HS	Другое	Химия Математика Биология Физика
Введение в физику: medidas, unidades y relación entre variables		Диана Лопес	HS UG-Intro	HW Lab Guided Remote	Физика
ПРЕПАРАТОРИЯ: Alineación de PhET con programas de la DGB México (2017)		Диана Лопес	HS UG-Intro	Другое	Физика Математика Химия
ПРИМАРИЯ: Alineación con programas de la SEP México (2011 г 2017 г.)		Диана Лопес	К-5 МС	Lab Guided HW Demo Обсудить	Физика Математика Химия Астрономия
Composició de moviment.Движение параболическое. PhET		Ана Мария Лафуэнте Герас	HS	Remote HW MC Lab	Физика
Der Gerade Wurf		Изабелла Радл	MS HS	HW Направляющая	Физика
Лаборатория движения снаряда		хаким алхамиди	MS HS	Лаборатория	Физика
Движение снаряда		Доктор.Нафисех Наср	UG-Intro HS	HW Lab	Физика
Lançamento Vertical no PhET		Кэролайн Сантос душ Сантуш; Мириан Марчезан Лопес; Памела да Силвейра Фрейтас.	MS HS	HW Lab Guided Remote	Физика
Corona vírus vs lançamento de projéteis		Клейсон Лима	HS Град MS	Лаборатория	Физика
Atividade de Lançamento Oblíquo		Джеирла Монтейро, Гилванденис Л.Продажа	HS	Другое	Физика
Atividades sobre o movimento dos corpos		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	Другое HS MS	HW Обсудить Другое Guided	Математика Другое Науки о Земле Физика
Mecânica (Atividades) nos OA’s do PhET		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	Grad MS UG-Intro HS Другое	Guided Обсудить Demo Lab HW Other	Физика Науки о Земле Другое
Cinemática (Atividades) nos OA’s do PhET		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	UG-Intro MS HS Другое	Lab Demo Other Guided HW	Науки о Земле Физика Другое
Velocidade e Aceleração no Lançamento de Projéteis no «Projectile Motion (HTML5)»		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	HS MS Другое	HW Направляемые Другое	Прочее Науки о Земле Физика
Queda Livre no «Projectile Motion (HTML5)»		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	HS Другое MS	HW Прочие Направляемые	Физика Науки о Земле Математика Другое
Lançamento Vertical de Projéteis no «Projectile Motion (HTML5)»		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	MS Другое HS	Другое HW Направляющая	Науки о Земле Физика Другое Математика
Lançamento Horizontal de Projéteis no «Projectile Motion (HTML5)»		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	Другое HS MS	Направляемые Прочее HW	Другое Математика Науки о Земле Физика
Lançamento de Projéteis		Хосе Карлос Феррейра Бастос, Дарксон Фернандес да Коста	HS UG-Intro	Demo Guided Lab	Физика
Lançando Projéteis no «Projectile Motion (HTML5)»		Artur Araújo Cavalcante e Gilvandenys Leite Продажи	MS HS	HW Направляемые Другое	Науки о Земле Физика Математика
Lançamento Oblíquo Inicial		Карлос Альбукерке	МС	Демо HW	Физика
Actividad — movimiento parabólico		Хаги Юкра и Джессика Лоренцо	HS	HW	Физика
HOJA DE TRABAJO		Лаура Муньос	HS	Управляемый Пульт ДУ	Физика
Movimiento Parabolico		Вальтер Мануэль Трухильо Яйпен	MS Другое HS UG-Adv Grad UG-Intro	Lab Other HW Guided MC	Другое Физика Математика
Гиа де трабахо; Movimiento de un Proyectil		Мария Камила Льоренте Кастро — Хулио Сезар Паес Гарсия	К-5	управляемый	Физика
Movimiento Parabolico.Comaparacion de datos		Вальтер Мануэль Трухильо Яйпен	Другое MS Grad UG-Adv K-5 HS UG-Intro	HW Remote Lab Demo	Другое Математика Физика
Movimiento en dos sizes: Caso del Proyectil (Двухмерный механизм, футляр для снаряда).		Кармен Мальдонадо	UG-Intro HS	Lab Guided Remote HW	Физика
Practica de Movimiento Parabolico		Вальтер Мануэль Трухильо Яйпен	HS Grad MS UG-Intro UG-Adv	Управляемый Другой HW Лабораторный	Физика
Practica Tiro Parabolico (перевод)		Херардо Сармьенто	MS HS	Лаборатория Управляемая	Физика
КЛАСС GRADO 10 FISICA		николас ривера	HS	Лаборатория	Физика
Практика: Тиро Параболико		МОНИКА КРАВЕРО	MS HS	Demo Guided Lab	Физика

x =	x ₀ + v _{0 x} t + ½ a _x t ²
x =	0 + ( v cos θ) t + 0
x _{окончательный} =	( v cos θ) t _{окончательный}

т _{окончательная} =	2 ( против sin θ)
	г

x _{окончательный} =	( v cos θ)	2 ( против sin θ)
		г
x _{окончательный} =	v ² sin 2θ
	г
x _{макс.No related posts. Posted in Контрольная Навигация по записям Previous Next Leave a ReplyДобавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Контрольная Советы 2024 © Все права защищены. Карта сайта}