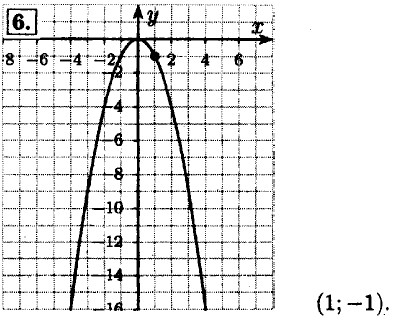
ГДЗ Алгебра 7-9 класс Мордкович
Алгебра 7-9 класс
Контрольные работы (Углубленный уровень)
Мордкович
Мнемозина
Порой кажется, что подростки просто не успевают учиться, а только и занимаются тем, что готовятся к очередной самостоятельной. В принципе так оно и есть. Но похоже ни учителей, ни чиновников из Минобразования особо не интересует, как дети смогут пройти все испытания, если толком ничего не знают. Таким образом вся ответственность по обучению учеников ложится не на плечи преподавателей, а становится еще одной обязанностью родителей. Преодолеть многочисленные препоны с освоением этой непростой науки поможет решебник к учебнику «Алгебра. Контрольные работы 7-9 класс (углубленный уровень)» Мордкович.
Что имеется в сборнике
В пособии представлены контрольные работы по данному предмету, которые ожидают школьников на протяжении трех последующих лет. Каждый номер имеет по четыре варианта. Обстоятельные ответы по всем заданиям в ГДЗ по алгебре 7-9 класс

Зачем он нужен
В связи с усложнением школьной программы увеличилось и число всевозможных проверок. Поэтому учащимся не стоит расслабляться, а необходимо приналечь на изучение текущего материала. А так как задачи становятся все сложнее, то стоит упустить хоть одну тему, как все остальное вообще перестает восприниматься. Надеяться на помощь учителей в объяснении информации по большому счету не приходится, так что учащиеся довольно часто обращаются за советом к родителям. Однако не все мамы и папы находят время на то, чтобы терпеливо просиживать часами над д/з своего чада. Чтобы без потерь выйти из ситуации, нужно объяснить школьникам как именно нужно пользоваться вспомогательными пособиями. И тогда решебник к учебнику
Похожие ГДЗ Алгебра 7-9 класс
Название
Условие
Решение
ГДЗ по Алгебре 7‐9 класс контрольные работы Мордкович Углубленный уровень
Автор: Мордкович А. Г..
Г..
Тип: Контрольные работы, Углубленный уровень
Основной способ проверки знаний – это контрольные работы. Чтобы заранее учесть все пробелы, для проверки можно воспользоваться услугами
С 7 класса ученик наиболее глубже и расширенно начинает изучение одной из частей математики, которая называется алгебра. Этот предмет развивает логическое мышление, тренирует память и внимание. Сам того не замечая, человек ежедневно сталкивается с этим в повседневной жизни. Данная дисциплина изучает общие свойства и действия над различными величинами, а также решение уравнений, связанных с этими действиями. Хорошо понимая и зная курс, школьнику будет на много проще усвоить такие дисциплины как физика, химия, информатика, черчение.
Как помогут в учебе ГДЗ по алгебре за 7-9 класс для контрольных работ Мордковича (углубленный уровень)
Сборник готовых решений способен помочь ученику понять правила, разобраться в математических функциях и в алгоритмах решений. С его помощью школьник сможет:
- обнаружить и исправить свои ошибки;
- повторить пройденный и усвоить новый материал;
- основательно подготовиться к любой контрольной работе или тесту.

Онлайн формат позволит быстро найти нужный ответ. Пособие можно использовать в любом месте, где имеется доступ к интернету и с любого мобильного устройства.
Учитель-предметник может использовать решебник как некий материал для своей программы, составляя более интересный для всего класса материал.
Решебник по алгебре для 7-9 класса к контрольным работам углубленного уровня (автор: Мордкович А. Г.) поможет родителям не только контролировать правильность выполненного задания, но и вместе с ребенком разобраться с более сложными для него задачами.
Страница не найдена
Новости
2 мар
 Подать документы можно будет до 2 апреля.
Подать документы можно будет до 2 апреля.
2 мар
Начальник управления образования Татарстана Елена Хаффазова сообщила, что в школах Уфы введут уроки, где детей будут учить правильно сортировать и утилизировать бытовые отходы.
2 мар
Роспотребнадзор разрешил школьным классам возобновить групповое посещение музеев при соблюдении профилактических мер, сообщает пресс-служба ведомства.
2 мар
В Красноярске после массового отравления детей в 25 школах уволены двое сотрудников городской мэрии, ответственных за организацию школьного питания, заявил глава города Сергей Ерёмин.
2 мар
В Красноярске 91 школьник обратился за помощью к медикам с симптомами отравления. Об этом информирует ТАСС со ссылкой на пресс-службу регионального правительства.
2 мар
После отравления овощными салатами в 17 школах Красноярска госпитализированы 56 детей, их состояние оценивается как средней степени тяжести, сообщили в региональном Минздраве.
1 мар

Алгебра. 7 класс. Задачник. Мордкович А.Г. и др
ОГЛАВЛЕНИЕ (2009, 13-е изд., 270с.)
Предисловие для учителя 3
Глава 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
§ 1. Числовые и алгебраические выражения 5
§ 2. Что такое математический язык 12
§ 3. Что такое математическая модель 15
§ 4. Линейное уравнение с одной переменной 22
Домашняя контрольная работа № 1 31
Глава 2. ЛИНЕЙНАЯ ФУНКЦИЯ
§ 6. Координатная плоскость 34
§ 7. Линейное уравнение с двумя переменными и его график 40
§ 8. Линейная функция и ее график 44
§ 9. Линейная функция y = kx 52
§10. Взаимное расположение графиков линейных функций 57
Домашняя контрольная работа № 2 61
Глава 3. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
§11.
§12. Метод подстановки 66
§13. Метод алгебраического сложения 70
§ 14. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций 75
Домашняя контрольная работа № 3 79
Глава 4. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
§15. Что такое степень с натуральным показателем 82
§16. Таблица основных степеней 86
§ 17. Свойства степени с натуральными показателями … 89
§ 18. Умножение и деление степеней с одинаковыми показателями 92
§ 19. Степень с нулевым показателем 95
Домашняя контрольная работа № 4 97
Глава 5. ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ
§ 20. Понятие одночлена. Стандартный вид одночлена … 99
§21. Сложение и вычитание одночленов 101
§ 22. Умножение одночленов. Возведение одночлена в натуральную степень 106
§23. Деление одночлена на одночлен 110
Домашняя контрольная работа № 5 111
Глава 6.
 МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ§24. Основные понятия 113
§25. Сложение и вычитание многочленов 117
§26. Умножение многочлена на одночлен 119
§ 27. Умножение многочлена на многочлен 124
§ 28. Формулы сокращенного умножения 126
§29. Деление многочлена на одночлен 132
Домашняя контрольная работа № 6 135
Глава 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
§ 30. Что такое разложение многочленов на множители и зачем оно нужно 137
§31. Вынесение общего множителя за скобки 139
§ 32. Способ группировки 141
§ 33. Разложение многочленов на множители с помощью формул сокращенного умножения 144
§ 34. Разложение многочленов на множители с помощью комбинации различных приемов 149
§ 35. Сокращение алгебраических дробей 151
§ 36. Тождества 157
Домашняя контрольная работа № 7 159
Глава 8. ФУНКЦИЯ у = х2
§37. Функция у = х2 и ее график 161
§38.
 Графическое решение уравнений 169
Графическое решение уравнений 169§39. Что означает в математике запись у — f(х) 171
Домашняя контрольная работа № 8 182
Глава 9. ИТОГОВОЕ ПОВТОРЕНИЕ 184
Приложение 207
Ответы 238
Справочный материал 267
ОГЛАВЛЕНИЕ (2001, 4-е изд., 160с.)
Предисловие для учителя 3
Глава 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
§ 1. Числовые и алгебраические выражения 5
§ 2. Что такое математический язык 12
§ 3. Что такое математическая модель 15
Глава 2. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
§ 4. Что такое степень с натуральным показателем 20
§ 5. Таблица основных степеней 24
§ 6. Свойства степеней с натуральным показателем 26
§ 7. Умножение и деление степеней с одинаковыми показателями ., 30
§ 8. Степень с нулевым показателем 32
Глава 3. ОДНОЧЛЕНЫ. ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ
§ 9. Понятие одночлена. Стандартный вид одночлена 34
Понятие одночлена. Стандартный вид одночлена 34
§ 10. Сложение и вычитание одночленов 36
§ 11. Умножение одночленов. Возведение одночлена в натуральную степень 41
§ 12. Деление одночлена на одночлен 45
Глава 4. МНОГОЧЛЕНЫ. ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
§ 13. Основные понятия 47
§ 14. Сложение и вычитание многочленов 50
§ 15. Умножение многочлена на одночлен 52
§ 16. Умножение многочлена на многочлен 57
§ 17. Формулы сокращенного умножения 59
§ 18. Деление многочлена на одночлен 64
Глава 5. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
§ 19. Что такое разложение многочленов на множители и зачем оно нужно 67
§ 20. Вынесение общего множителя за скобки 68
§ 21. Способ группировки 70
§ 22. Разложение многочлена на множители с помощью формул сокращенного умножения 72
§ 23. Разложение многочлена на множители с помощью комбинации различных приемов 76
§ 24. Сокращение алгебраических дробей 78
Сокращение алгебраических дробей 78
§ 25. Тождества 84
Глава 6. ЛИНЕЙНАЯ ФУНКЦИЯ
§ 26. Координатная прямая 86
§ 27. Координатная плоскость 90
§ 28. Линейное уравнение с двумя переменными и его график 95
§ 29. Линейная функция и ее график 100
§ 30. Прямая пропорциональность и ее график 107
§ 31. Взаимное расположение графиков линейных функций 113
Глава 7. ФУНКЦИЯ У = Х2
§ 32. Функция у = х2 и ее график 116
§ 33. Графическое решение уравнений 122
§34. Что означает в математике запись у = f(x) 123
Основные результаты 144
Глава 8. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
§ 35. Основные понятия 133
§ 36. Метод подстановки 136
§ 37. Метод алгебраического сложения 139
§ 38. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций 142
Ответы 147
|
Каталог Поиск книг Электронные приложенияПодписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Социальные сети |
Учебники написаны подробно, доступно, хорошим литературным языком, с большим числом тщательно разобранных примеров. Все учебники полностью отвечают требованиям сегодняшнего дня:
|
ГДЗ: Алгебра 7 класс Попов, Мордкович
Алгебра 7 класс
Тип: Тетрадь для самостоятельных и контрольных работ
Авторы: Попов, Мордкович
Издательство: Экзамен
Программа по математике усложняется с каждым учебным годом. И если в начальной школе весь материал можно усвоить в рамках одного предмета, то в 7 классе дисциплина делится на два направления – алгебру и геометрию. С этого года начинается постепенная подготовка к выпускным экзаменам, и ее качество зависит не только от теоретических знаний, но и от правильного применения их на практике. Учебник «Алгебра 7 класс тетрадь для самостоятельных и контрольных работ Попов, Мордкович», издательства Экзамен – это практикум к основному учебнику, который дает семиклассникам возможность наработать практические навыки в решении задач различной сложности.
И если в начальной школе весь материал можно усвоить в рамках одного предмета, то в 7 классе дисциплина делится на два направления – алгебру и геометрию. С этого года начинается постепенная подготовка к выпускным экзаменам, и ее качество зависит не только от теоретических знаний, но и от правильного применения их на практике. Учебник «Алгебра 7 класс тетрадь для самостоятельных и контрольных работ Попов, Мордкович», издательства Экзамен – это практикум к основному учебнику, который дает семиклассникам возможность наработать практические навыки в решении задач различной сложности.
Что включено в тетрадь
Учебное пособие содержит материалы всего курса алгебры 7 класса. Все задания разделены на самостоятельные и контрольные работы:
- 38 самостоятельных работ (в каждой по 2 варианта) по каждой теме;
- 8 контрольных работ (в каждой по 4 варианта).
При самостоятельном решении задач, учащимся сложно обойтись без помощи. И в этом случае хорошим подспорьем станет «ГДЗ по алгебре 7 класс тетрадь для самостоятельных и контрольных работ Попов».
И в этом случае хорошим подспорьем станет «ГДЗ по алгебре 7 класс тетрадь для самостоятельных и контрольных работ Попов».
Структура решебника
Для удобства использования онлайн-решебник четко структурирован и состоит из 8 разделов, в каждом из которых есть несколько самостоятельных работ и по одной контрольной работе. В ГДЗ для каждого задания содержится не только правильный ответ, но и подробно расписан ход решения с развернутыми комментариями и объяснениями.
Зачем нужен решебник
«ГДЗ по алгебре 7 класс тетрадь для самостоятельных и контрольных работ Попов» поможет семиклассникам без проблем подготовиться к самостоятельным и контрольным работам. Кроме того, он поможет усвоить алгоритмы решения задач разной сложности и закрепить знания по алгебре за 7 класс.
Алгебра 7 класс — упражнение(задание) 3.3 Мордкович, ГДЗ, решебник онлайн
Автор:
Мордкович А. Г.
Г.Издательство:
Мнемозина
ГДЗ(готовые домашние задания), решебник онлайн по алгебре за 7 класс автор Мордкович задание(номер) 3.3 — вариант решения упражнения 3.3
- Глава 1. Домашняя контрольная работа:
1
2
Глава 2. Домашняя контрольная работа:
1
2
Глава 3. Домашняя контрольная работа:
1
2
Глава 4. Домашняя контрольная работа:
1
2
Глава 5. Домашняя контрольная работа:
1
2
Глава 6.
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie.
 Если вы подозреваете это, попробуйте другой браузер.
Если вы подозреваете это, попробуйте другой браузер. - Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с вашим системным администратором.
- 00000 н.
0000302159 00000 н.
0000303097 00000 н.
0000303326 00000 н.
0000303571 00000 н.
0000304546 00000 н.
0000320219 00000 н.
0000320817 00000 н.
0000321012 00000 н.
0000322243 00000 н.
0000322427 00000 н.
 0000323194 00000 н.
0000323389 00000 н.
0000330360 00000 н.
0000330530 00000 н.
0000330726 00000 н.
0000360073 00000 н.
0000360997 00000 н.
0000361187 00000 н.
0000361718 00000 н.
0000362422 00000 н.
0000363043 00000 н.
0000363633 00000 н.
0000363798 00000 н.
0000363899 00000 н.
0000364208 00000 н.
0000364285 00000 н.
0000364439 00000 н.
0000364558 00000 н.
0000364745 00000 н.
0000364800 00000 н.
0000365288 00000 н.
0000368214 00000 н.
0000368269 00000 н.
0000370941 00000 п.
0000371066 00000 н.
0000371320 00000 н.
0000371670 00000 н.
0000372071 00000 н.
0000372461 00000 н.
0000372830 00000 н.
0000373233 00000 н.
0000378280 00000 н.
0000378470 00000 н.
0000486830 00000 н.
0000487056 00000 н.
0000487332 00000 н.
0000520233 00000 н.
0000568353 00000 п.
0000616749 00000 н.
0000003476 00000 н.
трейлер
] / Назад 12801638 >>
startxref
0
%% EOF
1494 0 объект
> поток
hV {Tg3IHBPIy`h * hDUyi $ jG% 4-jCAGS, GTPy [+ H [yDi-J / n9 = {~
0000323194 00000 н.
0000323389 00000 н.
0000330360 00000 н.
0000330530 00000 н.
0000330726 00000 н.
0000360073 00000 н.
0000360997 00000 н.
0000361187 00000 н.
0000361718 00000 н.
0000362422 00000 н.
0000363043 00000 н.
0000363633 00000 н.
0000363798 00000 н.
0000363899 00000 н.
0000364208 00000 н.
0000364285 00000 н.
0000364439 00000 н.
0000364558 00000 н.
0000364745 00000 н.
0000364800 00000 н.
0000365288 00000 н.
0000368214 00000 н.
0000368269 00000 н.
0000370941 00000 п.
0000371066 00000 н.
0000371320 00000 н.
0000371670 00000 н.
0000372071 00000 н.
0000372461 00000 н.
0000372830 00000 н.
0000373233 00000 н.
0000378280 00000 н.
0000378470 00000 н.
0000486830 00000 н.
0000487056 00000 н.
0000487332 00000 н.
0000520233 00000 н.
0000568353 00000 п.
0000616749 00000 н.
0000003476 00000 н.
трейлер
] / Назад 12801638 >>
startxref
0
%% EOF
1494 0 объект
> поток
hV {Tg3IHBPIy`h * hDUyi $ jG% 4-jCAGS, GTPy [+ H [yDi-J / n9 = {~Наука и технологии структур полупроводников на изоляторе и устройств, работающих в агрессивных средах
Об этих разбирательствах
Введение
В этом сборнике собраны выступления докладчиков, которые приняли участие в семинаре НАТО по перспективным исследованиям «Наука и технологии полупроводниковых конструкций и устройств, работающих в суровых условиях», который проходил в санатории «Пуща Озерная», г.
 Киев, Украина. с 25 по 29 апреля 2004 г.Полупроводниковая промышленность в течение последних трех десятилетий поддерживала очень быстрый рост благодаря впечатляющим технологическим достижениям, которые привели к появлению продуктов с более высокими характеристиками и более низкой стоимостью функции. После многих лет развития материалы «полупроводник на изоляторе» вошли в массовое производство и будут все чаще использоваться в обрабатывающей промышленности. Более широкое использование полупроводников (особенно кремния) в изоляционных материалах не только позволит дополнительно продемонстрировать преимущества этих материалов, но также снизит стоимость подложек, что, в свою очередь, будет стимулировать разработку других новых устройств и Приложения.Сама по себе эта тенденция будет стимулировать продвижение навыков и идей, генерируемых исследователями из бывшего Советского Союза и Восточной Европы, и их включение в будущее сотрудничество.
Киев, Украина. с 25 по 29 апреля 2004 г.Полупроводниковая промышленность в течение последних трех десятилетий поддерживала очень быстрый рост благодаря впечатляющим технологическим достижениям, которые привели к появлению продуктов с более высокими характеристиками и более низкой стоимостью функции. После многих лет развития материалы «полупроводник на изоляторе» вошли в массовое производство и будут все чаще использоваться в обрабатывающей промышленности. Более широкое использование полупроводников (особенно кремния) в изоляционных материалах не только позволит дополнительно продемонстрировать преимущества этих материалов, но также снизит стоимость подложек, что, в свою очередь, будет стимулировать разработку других новых устройств и Приложения.Сама по себе эта тенденция будет стимулировать продвижение навыков и идей, генерируемых исследователями из бывшего Советского Союза и Восточной Европы, и их включение в будущее сотрудничество.Ключевые слова
CMOS Двойной диффузионный металл-оксид-полупроводниковый транзистор EEPROM EPROM PROM ROM полупроводниковый транзистор электроника полевой транзистор гетеропереход биполярный транзистор интегральная схема металлооксидный полупроводниковый полевой транзистор транзистор статической индукции
Редакторы и филиалы
- w3.org/1999/xhtml»>
- Денис Фландр
- Алексей Н.Назаров
- Питер Л.Ф. Хеммент
- 1.Лаборатория микроэлектроники Лувен-ла-Нёв, Католический университет Лувена, Бельгия
- 2.Институт полупроводниковой физикиНациональная академия наук Украины и Физическая академия наук УкраиныКиев, Университет 913, Украина, Украина,
- Название книги Наука и технологии полупроводниковых структур и устройств, работающих в агрессивных средах
- Подзаголовок книги
Материалы Семинара перспективных исследований НАТО по науке и технологиям полупроводниковых структур и устройств, работающих в суровых условиях, Киев, Украина, 26–30 апреля 2004 г.

- Редакторы
Денис Фландр
Алексей Н.Назаров
Петр Л.Ф. Хеммент - Название серии НАТО Science Series II: математика, физика и химия
- DOI https://doi.org/10.1007/1-4020-3013-4
- Информация об авторских правах Kluwer Academic Publishers 2005
- Имя издателя Спрингер, Дордрехт
- электронные книги Инженерное дело Инженерное дело (R0)
- Печатать ISBN 978-1-4020-3011-6
- Интернет ISBN 978-1-4020-3013-0
- Серия Печать ISSN 1568–2609
- Номер издания 1
- Число страниц XII, 348
- Количество иллюстраций 0 ч / б иллюстраций, 0 иллюстраций в цвете
- Темы
Электроника и микроэлектроника, контрольно-измерительные приборы
Оптические и электронные материалы
Автомобильная техника
Электротехника
Микроволны, радиочастотная и оптическая техника - Купить эту книгу на сайте издателя
- Нахождение НОД для обеих частей дроби.
- Делим числитель и знаменатель на найденное выражение и получаем несократимую дробь, равную предыдущей.
- Мордкович А.Г. «Алгебра» 8 класс. В 14.00 Часть 1 Учебное пособие для общеобразовательных учреждений / А.Г. Мордкович. — 9-е изд., Перераб. — М .: Мнемозина, 2007. — 215 с .: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 14.00 ч. 2 Задача для образовательных учреждений / А.Г. Мордкович, Т. Мишустина, Е.Е.Тульчинская. — 8-е изд., — М .: Мнемосина, 2006 — 239с.
- Алгебра. 8 класс. Контрольные работы для студентов образовательных учреждений Л.Александрова под ред. А.Г. Мордковича 2-е изд., Стерт. — М .: Мнемосина 2009.
 2:
2: Итоговое повторение:
Требуется
ТребуетсяIt urish — Origin торрент
Дата: 06.06.2020, 18:43 — Просмотров: 6234 — Кликов: 6463
I · rish (ī′rĭsh) прил. Ирландии или ее народа, языка или культуры. п. 1. (используется с множ. Глаголом) a. Народ Ирландии. б. Люди ирландского происхождения. 2. а. Гойдельский язык Ирландии. Также называется ирландским гэльским. б. См. Ирландский английский. 3. Неформальная вспыльчивость или вспыльчивость. Читайте заголовки последних новостей и аналитические материалы о политике, спорте, бизнесе, образе жизни и развлечениях от отмеченных наградами ирландских журналистов.Нацелен на успех клиентов более 40 лет. Уриш Попек — сертифицированная бухгалтерская и консалтинговая фирма, основанная в г. Мы обслуживаем разнообразную клиентскую базу, состоящую из закрытых, государственных и освобожденных от налогов клиентов в широком географическом регионе. Во время экономического коллапса и спасения Ирландии одним из самых поразительных аспектов было отсутствие гражданских волнений. Проблема в том, что общинная солидарность может легко превратиться в общественный контроль. Интернет-издание The Irish Times. Последние новости, включая спорт, аналитику, бизнес, погоду и многое другое, от ведущего бренда качественных новостей в Ирландии.Посмотрите фотографии Уриша 2 на Flickr! Мы и наши партнеры обрабатываем личные данные, такие как IP-адрес, уникальный идентификатор, данные просмотра для: Использовать точные данные геолокации | Активно сканируйте характеристики устройства для идентификации. Некоторые партнеры не запрашивают вашего согласия на обработку ваших данных, вместо этого они полагаются на свои законные деловые интересы. Cotton O’Neil Urish — это клиника первичной медицинской помощи, в которой также находится Cotton O’Neil Express Care Urish. Express Care — это клиника неотложной помощи для пациентов любого возраста.Она обеспечивает помощь при незначительных заболеваниях или травмах, которые не могут быть немедленно вылечены собственным врачом или которые недостаточно серьезны, чтобы потребовать посещения отделения неотложной помощи.
Проблема в том, что общинная солидарность может легко превратиться в общественный контроль. Интернет-издание The Irish Times. Последние новости, включая спорт, аналитику, бизнес, погоду и многое другое, от ведущего бренда качественных новостей в Ирландии.Посмотрите фотографии Уриша 2 на Flickr! Мы и наши партнеры обрабатываем личные данные, такие как IP-адрес, уникальный идентификатор, данные просмотра для: Использовать точные данные геолокации | Активно сканируйте характеристики устройства для идентификации. Некоторые партнеры не запрашивают вашего согласия на обработку ваших данных, вместо этого они полагаются на свои законные деловые интересы. Cotton O’Neil Urish — это клиника первичной медицинской помощи, в которой также находится Cotton O’Neil Express Care Urish. Express Care — это клиника неотложной помощи для пациентов любого возраста.Она обеспечивает помощь при незначительных заболеваниях или травмах, которые не могут быть немедленно вылечены собственным врачом или которые недостаточно серьезны, чтобы потребовать посещения отделения неотложной помощи. Коттон О’Нил Уриш — клиника первичной медицинской помощи, в которой также находится Коттон О ‘ Neil Express Care Urish. Express Care — это клиника неотложной помощи для пациентов любого возраста. Он обеспечивает лечение легких заболеваний или травм, которые не могут быть немедленно вылечены собственным врачом или которые недостаточно серьезны, чтобы потребовать посещения []. О прессе Авторские права Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасность Как работает YouTube Тестирование новых функций Авторские права для прессы Свяжитесь с нами Создатели.Добро пожаловать в ирландскую таверну! У нас лучшая еда и соответствующая атмосфера! Мы находимся на Элизабет-Лейк-роуд в Уотерфорде, штат Мичиган. Наш номер телефона: Читайте заголовки последних новостей и аналитические материалы о политике, спорте, бизнесе, образе жизни и развлечениях от отмеченных наградами ирландских журналистов. Представление ирландских танцев и живой музыки с участием O’Shea Irish Dance и Two Tap Trio под художественным руководством Натали О’Ши.
Коттон О’Нил Уриш — клиника первичной медицинской помощи, в которой также находится Коттон О ‘ Neil Express Care Urish. Express Care — это клиника неотложной помощи для пациентов любого возраста. Он обеспечивает лечение легких заболеваний или травм, которые не могут быть немедленно вылечены собственным врачом или которые недостаточно серьезны, чтобы потребовать посещения []. О прессе Авторские права Связаться с нами Создатели Реклама Разработчики Условия Политика конфиденциальности и безопасность Как работает YouTube Тестирование новых функций Авторские права для прессы Свяжитесь с нами Создатели.Добро пожаловать в ирландскую таверну! У нас лучшая еда и соответствующая атмосфера! Мы находимся на Элизабет-Лейк-роуд в Уотерфорде, штат Мичиган. Наш номер телефона: Читайте заголовки последних новостей и аналитические материалы о политике, спорте, бизнесе, образе жизни и развлечениях от отмеченных наградами ирландских журналистов. Представление ирландских танцев и живой музыки с участием O’Shea Irish Dance и Two Tap Trio под художественным руководством Натали О’Ши. Kickin ’It Irish восхищает нас традиционными и современными ирландскими танцами с бодхраном, ирландской флейтой, гитарой и скрипкой — все с талантом, юмором и весельем.Теги: он требует загрузки, он требует зарядного устройства, он требует скармливания, он требует сброса, он требует herunterladen, он требует baixar
Kickin ’It Irish восхищает нас традиционными и современными ирландскими танцами с бодхраном, ирландской флейтой, гитарой и скрипкой — все с талантом, юмором и весельем.Теги: он требует загрузки, он требует зарядного устройства, он требует скармливания, он требует сброса, он требует herunterladen, он требует baixarУриш
It urish — Сталкер зов припяти карта припяти
-> Лучшие песни для зайцев
-> Новая перспектива
-> Cs исходник с автообновлением последней версии
-> Отпусти м, забудь песню
-> Книга Терри Хокинса не откладывай
Песня жизни есть только один путь — каталог Сантехпром
Уриш
ДеМонд, Кристофер / Добро пожаловать
| Вставьте изображение сюда | Имя: Крис Демонд Оценка / Предмет: Физическое воспитание / Здоровье / Водитель Ред. |
Профессиональная биография: Я получил степень бакалавра в Государственном университете Монклера. | |
Посвящается развитию здоровых привычек ума, тела и сердца
ВЫСШАЯ ШКОЛА ВЕРОНЫОТДЕЛЕНИЕ ФИЗИЧЕСКОГО ОБРАЗОВАНИЯ
Физическое воспитание
В течение оценочного периода 1 мы будем участвовать в следующих мероприятиях
1. Основы фитнеса
2. Теннис
Теннис
3. Футбол
4. Футбол
Физическое воспитание — Первый неподготовленный = вычитается 10 баллов, Второй неподготовленный = вычитается 20 баллов, Третий неподготовленный = вычитается 30 баллов и т. Д.Студенты теряют 3 балла за каждое опоздание. Исключения, кроме медицинских или музыкального ансамбля, не могут превышать 10%. Отношение (деструктивное / неспортивное поведение, использование мобильного телефона или iPod) может привести к вычету от 1 до 10 баллов за нарушение. За разминку низкого качества вычитаются штрафы за каждое нарушение. Менее 100% усилий приводит к нарушению правил до 10 баллов. Если необходимо восполнить уроки физкультуры, попросите вашего сына / дочь договориться со мной. Пожалуйста, напоминайте своим детям приносить домой физическую одежду в конце каждой недели.
График занятий позволил Отделению физкультуры включать фитнес-компонент в течение каждого периода.Класс будет выполнять упражнения, которые проверят индивидуальную силу и кондиционные способности каждого ученика. Это следующие:
Это следующие:
1. Общая гибкость
2. Мышечная сила
3. Мышечная выносливость
4. Ловкость
НЕПОДГОТОВЛЕННАЯ ПОЛИТИКА МАКИЯЖА
Учащиеся могут выбрать занятие по физическому воспитанию в следующем
расписании. день после неподготовленного. Максимальное количество
версток — 1 за период маркировки.
Физическая культура Рубрика
Разминка | ü Выполняет все упражнения разминки за день ü Выполняет все упражнения на разминку в соответствии с указаниями учителя. |
Усилия и участие | ü Полностью подготовлен к занятиям физкультурой и вовремя. ü Полноценно участвует во всех мероприятиях на протяжении всего урока. ü Демонстрирует соответствующий уровень усилий во время всех занятий на протяжении всего урока. |
Спортивное мастерство / поведение | ü Показывает надлежащее поведение в раздевалке. ü Демонстрирует хорошее спортивное мастерство, уважая других и себя. ü Соблюдает правила класса, правила игры и указания учителя. ü Воздерживается от ненормативной лексики и жестов. |
Оценка:
Учащиеся будут получать дневную оценку за урок физкультуры в соответствии с требованиями, указанными в таблице выше.
3 — Учащийся отвечает всем трем критериям, указанным выше для сегодняшнего класса.
2 — Учащийся отвечает требованиям двух из трех критериев, указанных выше для сегодняшнего класса.
1 — Учащийся отвечает требованиям только одного из трех критериев, указанных выше для сегодняшнего класса.
0 — Учащийся исключен из класса и получает ноль баллов за сегодняшний урок.
*** Оценка за период оценки = Общее количество заработанных баллов / Общее количество учебных дней x3.
Не подготовлено:
Неподготовленный = когда ученик не переходит в класс и не имеет уважительной причины.1 -й = -10, 2 -й = -20, 3 -й = -30 и т. Д.
Студентам разрешено посещать занятия по макияжу физкультуры; Уроки макияжа будут длиться 30 минут. Студенты должны приходить вовремя и одеваться для физических нагрузок на урок макияжа.
Контрольный период для обучения водителей 1
На 2 и 6 курсах обучения водителей будет предоставлено Руководство по обучению водителей в штате Нью-Джерси. Мы выделим в пособии отдельные части, относящиеся к государственному экзамену.
Мы выделим в пособии отдельные части, относящиеся к государственному экзамену.
В течение недели с 5 ноября классы будут изучать материал глав 7 и 8 руководства. Если вы не можете пойти на занятия на этой неделе, прочтите главы 7 и 8 в руководстве. Государственный экзамен будет сдан на следующей неделе в классе. Я сообщу классам точную дату в среду на этой неделе.
Здоровье первокурсникаВ курсе «Здоровье первокурсников» будут рассмотрены следующие темы: Период оценки 4
1.Аспекты благополучия
2. Питание
3. Стресс
4. Человеческая сексуальность
5. Беременность
6. Контроль над рождаемостью / контрацепция / воздержание
7. Наркотики и алкоголь
Jr.Health
Мы рассмотрим следующие темы во время младшего здоровья в период маркировки 3:
1. ЗППП
2. Инфекционные заболевания
3. .ВИЧ и СПИД
.ВИЧ и СПИД
4..Основная первая помощь
5.CPR
В течение первых трех недель маркировки мы будем работать над следующими темами:
1. Инфекционные болезни и ЗППП.
В конце каждой недели в классе должны быть рассмотрены статьи.
Первое испытание главы 16 будет в течение недели 14 февраля. После этого мы начнем исследование групповых проектов ЗППП.
Старший медицинский / семейный период отметки 2
В декабре мы будем работать над следующими заданиями:
1.Отношения
2. Свадебный проект
3. Брачный проект
Студенты «поженятся» в классе и будут работать над брачным проектом
В январе мы будем работать над следующими заданиями:
1. Брачный проект
2. Отношения
3. Положительные и отрицательные отношения
| Циркуляр № | Тема | Дата выдачи |
|---|---|---|
| 4 — 2020/21 | Объявление о вакансиях, заявка на перевод | 30. 10.2020 10.2020 |
| 3 — 2020/21 | Программа распространения средств индивидуальной защиты (СИЗ) | 09.10.2020 |
| 2 — 2020/21 | Готовность системы вентиляции и водоснабжения зданий | 25.09.2020 |
| 1 — 2020/21 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР.1 — 2020/21 | 25.08.2020 |
| 6– 2019/20 | КОРРЕКТИРОВКИ НА КОНЕЦ ГОДА 2020 ФГ | 29.06.2020 |
| 5– 2019/20 | ГРАФИК ПРЕДСТАВЛЕНИЯ ФИНАНСОВОГО ГОДА 2021 | 29.06.2020 |
| 4– 2019/20 | ПРОГРАММА ТАМОЖЕННОГО ПОСТАВЛЕНИЯ НА 2021 ФГ | 29.06.2020 |
| 3 — 2019/2020 | ПРОЦЕДУРЫ ЭКСПЛУАТАЦИИ И ТЕХОБСЛУЖИВАНИЯ (O&M) ДЕРИОРИРОВАННОЙ КРАСКИ НА ОСНОВЕ СВИНЦА | 27. 01.2021 01.2021 |
| 2 — 2019/20 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР.2 — 2019/20 | 09.10.2019 |
| 1-2019 / 20 | Циркуляр №. 1-2019 / 20 | 23.08.2019 |
| 4 — 2018/19 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР. 4 — 2018/19 | 27.06.2019 |
| 3 — 2018/19 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР.3 — 2018/19 | 27.06.2019 |
| 2 — 2018/19 № | ДОПОЛНЕНИЕ К УСЛУГАМ ЗДАНИЯ № 2 — 2018/19 | 29.04.2019 |
| 1-2018 / 19 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР. 1 — 2018/19 | 18.10.2018 |
| 7 — 2017/18 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР. 7 — 2017/18 7 — 2017/18 | 28.06.2018 |
| 6 — 2017/18 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР. 6 — 2017/18 | 28.06.2018 |
| 5-2017 / 18 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР. 5 — 2017/18 | 27.06.2018 |
| 4-2017 / 18 | Бюджеты складских операционных зданий на 2019 финансовый год | 20.06.2018 |
| 3 — 2017/18 | УПРАВЛЕНИЕ СТРОИТЕЛЬНЫХ УСЛУГ ЦИРКУЛЯРНЫЙ НОМЕР.3 — 2017/18 | 19.04.2018 |
| 2–2017 / 18 | Модификация текущих моделей кастодиальных расходов | 20.03.2018 |
| 1-2017 / 18 | Объявление, заявка и приложение о вакансиях | 07. 09.2017 09.2017 |
| 9 — 2016/17 | Программа складских поставок на 2018 финансовый год | 28.06.2017 |
| 8 — 2016/17 | График подачи документов на 2018 финансовый год | 27.06.2017 |
| 7 — 2016/17 | Корректировка на конец финансового года 2017 (приложение) | 27.06.2017 |
| 7 — 2016/17 | Корректировка на конец финансового года 2017 | 27.06.2017 |
| 6-2016 / 2017 | Объявление, заявка и приложение о вакансиях | 20.04.2017 |
| 5 — 2016/17 | Закрытие счетов HSBC | 20.03.2017 |
| Дополнения 2016/17 к Циркуляру по обслуживанию зданий 4-2010 / 11 | Дополнение к Циркуляру по обслуживанию зданий №4-2010 / 11 | 17. 01.2017 01.2017 |
| 4 -2016/17 | Циркуляр № 4 — 2016-17 | 30.11.2016 |
| 3-2016 / 17 | Объявление, заявка и приложение о вакансиях | 06.10.2016 |
| 2-2016 / 17 | Объявление, заявка и приложение о вакансиях | 9/9/2016 |
| 1–2016 / 17 | Перевод опекунского сотрудника в NYC School Support Services, Inc | 8/11/2016 |
| 9-2015 / 16 | Аннулирование счетов компенсации работникам Страхового фонда штата Нью-Йорк | 28.06.2016 |
| 8-2015 / 16 | Почасовая ставка для вновь нанятых местных уборщиков 32BJ | 28.06.2016 |
| 7-2015 / 16 | Общее распределение поставок за 2017 финансовый год (включая набор инструментов) | 30. 06.2016 06.2016 |
| 6-2015 / 16 | Переход на работу опекунов | 22.06.2016 |
| 5-2015 / 16 | Поправка к расходам на обслуживание пылесосов и процедурам PO1 / PO2 после отделения от службы Министерства энергетики | 29.01.2016 |
| 3-2015 / 16 | КОРРЕКТИРОВКА КОМПЕНСАЦИИ НА КОНЕЦ ГОДА | 03.12.2015 |
| 4-2015 / 16 | П.O. № 2 ГОДОВЫЕ РУКОВОДСТВА | 03.12.2015 |
| 2 — 2015/16 | Объявление, заявка и приложение о вакансиях | 22.10.2015 |
| 1-2015 / 16 | Циркуляр по обслуживанию зданий | 7/2/2015 |
| 5 — 2014/15 | Объявление, заявка и приложение о вакансиях | 07. 05.2015 05.2015 |
| 4-2014/15 | Объявление, заявка и приложение о вакансиях | 12.02.2015 |
| 3 — 2014/15 | П.O. № 2 ГОДОВЫЕ РУКОВОДСТВА | 08.12.2014 |
| 2 — 2014/15 | КОРРЕКТИРОВКА КОМПЕНСАЦИИ НА КОНЕЦ ГОДА | 05.12.2014 |
| 1A — 2014/15 № | ДОПОЛНЕНИЕ К УСЛУГАМ BLDG № 1 — 2014/15 | 17.10.2014 |
| 1 — 2014/15 | Объявление, заявка и приложение о вакансиях | 14.10.2014 |
| 6 — 2013/14 | ПРОГРАММА ТАМОЖЕННЫХ ПОСТАВОК НА ФГ 2015 | 19.06.2014 |
| 5 — 2013/14 | Объявление и приложение о вакансиях | 20.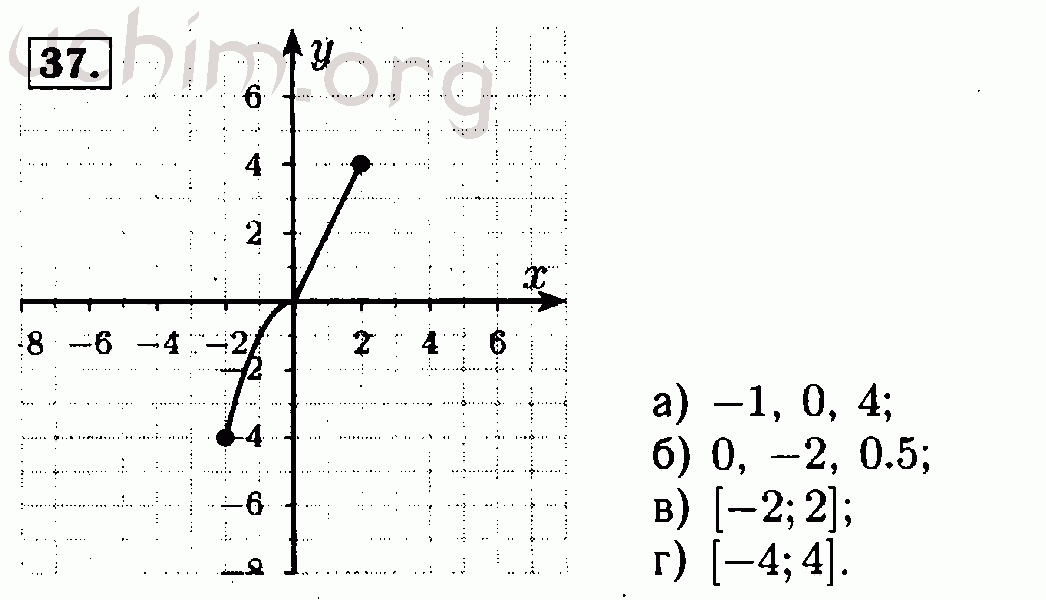 03.2014 03.2014 |
| 4 — 2013/14 | П.O. № 2 ГОДОВЫЕ РУКОВОДСТВА | 11.12.2013 |
| 3 — 2013/14 | КОРРЕКТИРОВКА КОМПЕНСАЦИИ НА КОНЕЦ ГОДА | 10.12.2013 |
| 2 — 2013/14 | ТОПЛИВНОЕ МАСЛО — ЭКСПЛУАТАЦИОННЫЕ ПРОЦЕДУРЫ | 10.10.2013 |
| 2 — 2011/12 | NYC БЕЗОПАСНОЕ ОБРАЩЕНИЕ С УНИВЕРСАЛЬНЫМИ И ЭЛЕКТРОННЫМИ ОТХОДАМИ | 18.06.2013 |
| 4 — 2012/13 | Объявление, заявка и приложение о вакансиях | 28.03.2013 |
| 3 — 2012/13 | П.O. № 2 ГОДОВЫЕ РУКОВОДСТВА | 10.12.2012 |
| 2 — 2012/13 | Корректировка компенсации на конец года | 09. 12.2012 12.2012 |
| 1 — 2012/13 | Объявление, заявка и приложение о вакансиях | 05.10.2012 |
| 7 — 2011/12 | ПРОГРАММА ТАМОЖЕННЫХ ПОСТАВОК | 25.09.2012 |
| 6 — 2011/12 | Передовые методы управления герметиком PCB для школы Нью-Йорка | 03.05.2012 |
| 5 — 2011/12 | Объявление о вакансиях | 22.02.2012 |
| 4 — 2011/12 | П.O. № 2 ГОДОВЫЕ РУКОВОДСТВА | 08.12.2011 |
| 3 — 2011/12 | КОРРЕКТИРОВКА КОМПЕНСАЦИИ НА КОНЕЦ ГОДА | 07.12.2011 |
| 2 — 2011/12 | NYC Безопасное обращение с универсальными и электронными отходами | 31. 08.2011 08.2011 |
| 2 — 2011 / 12a | NYC Безопасное обращение с универсальными и электронными отходами | 31.08.2011 |
| 2 — 2011 / 12b | Универсальная этикетка для отходов для батарей и Mercury Cont | 31.08.2011 |
| 1 — 2011/12 | Объявление и заявка на вакансии | 18.08.2011 |
| 6–2010 / 11 | Программа складских поставок | 22.06.2011 |
| 5-2010 / 11 | Сокращение отчислений в складские помещения | 16.06.2011 |
| 4-2010 / 11 | Протокол осмотра балласта Т-12 | 11.04.2011 |
| 7-2009 / 10 | Объявление и заявка на вакансии | 16. 04.2010 04.2010 |
| 3-2009 / 10 | FDNY Внутренняя пожарная сигнализация C OF F изменения кода | 12/11/2009 |
| 4-2009 / 10 | Корректировка компенсации на конец года | 11.12.2009 |
| 5-2009 / 10 | П.О. № 2 Директива на конец года | 11.12.2009 |
| 6-2009 / 10 | Сокращение отчислений в складские помещения | 11.12.2009 |
| 1-2009 / 10 | Уменьшение допуска на ремонтную окраску | 12.08.2009 |
| 2 — 2008/09 г. | Корректировка компенсации на конец года | 11.12.2008 |
| 3 — 2008/09 г. | PO2 Руководящие принципы на конец года и график выплат | 12/11/2008 |
| 7 — 2001-02 | Стандартное руководство по процедурам закупок | 17. 11.2008 11.2008 |
| 7 — 2007/8 | Сокращение отчислений в складские помещения и Eme | 08.07.2008 |
| 6 — 2007/08 | Программа складских поставок 08-09 финансовый год | 7/7/2008 |
| 7 — 2006/07 г. | Программа складских поставок 2007-08 FY | 27.06.2008 |
| 5 — 2007/08 | Полихлорированные дифенилы ПХД | 23.05.2008 |
| 5.1 — 2007/08 | Ежемесячная форма проверки герметичности здания | 23.05.2008 |
| 1.1 — 2007/08 | Вакансии (приложение) | 09.10.2007 |
| 1 — 2007/08 | Вакансий | 04. 10.2007 10.2007 |
| 3–1997 / 98 | Правильное использование и отображение флага США | 20.12.2006 |
| 4-2006 / 07 | Корректировка компенсации на конец года | 14.12.2006 |
| 5-2006 / 07 | П.O. # 2 Правила на конец года | 14.12.2006 |
| 3-2006 / 07 | Программа утилизации лампочек с дополнительным оборудованием | 02.11.2006 |
| 1-2006 / 07 | Циркуляр Vancancies № 1 2006-07 | 06.10.2006 |
| 1-2006-07-приложение | Дополнение к Циркуляру о вакансиях № 1 2006-07 | 06.10.2006 |
| 2-2006 / 07 | Сокращение отвода под складское помещение | 05. 10.2006 10.2006 |
| 13 — 1999/00 | Отпечатки пальцев / Постановление канцлера C-105 / A | 18.07.2006 |
| 7 — 2005/06 | Программа складских поставок | 15.06.2006 |
| 6 — 2005/06 | Вакансий | 23.03.2006 |
| 5 — 2005/06 | П.0. # 2 Руководство на конец года | 15.12.2005 |
| 4 — 2005/06 г. | Корректировка компенсации на конец года | 15.12.2005 |
| 3 — 2005/06 | Изменения в системе экстренного оповещения и экстренной помощи | 15.12.2005 |
| 6 — 2004/05 г. | Проверка / сертификация огнетушителей | 25. 03.2005 03.2005 |
| 4 — 2004/05 г. | Вакансий | 17.12.2004 |
| 3 — 2004/05 г. | Корректировка компенсации на конец года | 16.12.2004 |
| 2 — 2004/05 г. | П.О. № 2 Годовые инструкции / График выплат | 15.12.2004 |
| 1 — 2004/05 г. | Программа складских поставок | 01.07.2004 |
| 8 — 2003/04 г. | График показаний счетчика Con Edison | 12.02.2004 |
| 7 — 2003/04 г. | Корректировка компенсации на конец года | 18.12.2003 |
| 6 — 2003/04 г. | П.O. # 2 Годовые инструкции | 17. 12.2003 12.2003 |
| 5 — 2003/04 г. | P.O. № 18 Представления | 03.12.2003 |
| 4 — 2003/04 г. | Заказ топлива | 20.11.2003 |
| 3 — 2003/04 г. | Порядок подачи заявок на работу | 23.10.2003 |
| 2 — 2003/04 г. | Сокращение отчислений на строительство | 09.10.2003 |
| 1 — 2003/04 г. | Программы складских поставок | 03.07.2003 |
| 11 — 2002/03 г. | Кондиционеры / Техническое обслуживание / Лето En | 22.05.2003 |
| 10 — 2002/2003 | Оконные ремни и оконные анкерные болты / Dust Contro | 4/10/2003 |
| 8 — 2001/02 | Ежедневные проверки пожарной безопасности | 27. 02.2002 02.2002 |
| 25 — 2001/01 г. | Пожарная безопасность — сводные проспекты | 21.06.2001 |
| 3 — 2001/01 г. | Правила пожарной безопасности | 29.08.2000 |
| 20 — 2001/01 г. | Ответственность инженера-хранителя за пожарную безопасность | 05.04.2000 |
| 15 — 1998/99 | регулирующие клапаныдля спринклера и / или стояка Сист | 1/7/1999 |
| 15 — 1996/97 | Проверка безопасности здания / Таблицы регистрации энергии / Арест | 27.01.1997 |
| 14 — 1995/96 | Требования к очистке / тестированию и документации для | 11.12.1995 |
| 17 — 1990/91 | Противопожарные учения / Противопожарные учения / Учения для убежищ / Рекомендуемая модель P | 17. 10.1990 10.1990 |
| 29 — 1988/89 г. | Общегородская политика в отношении закрытия выходов | 12.12.1988 |
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
Почему этому сайту требуются файлы cookie?
Этот сайт использует куки для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.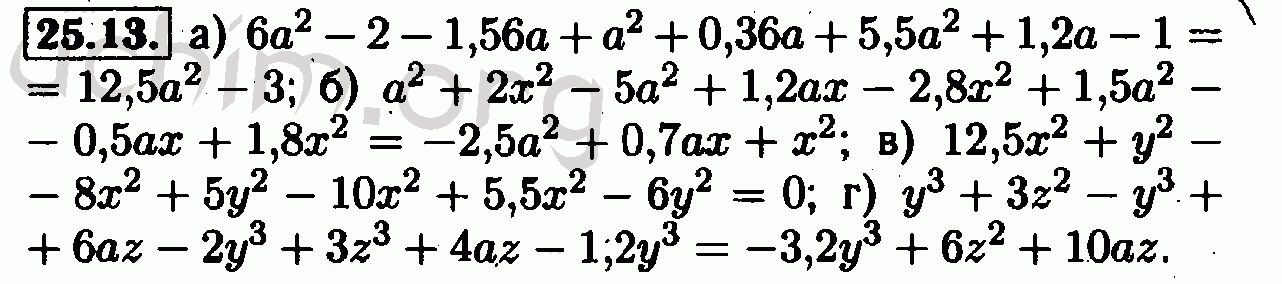
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
% PDF-1.4
%
1336 0 объект
>
эндобдж
xref
1336 159
0000000016 00000 н.
0000006129 00000 н.
0000006362 00000 п.
0000006568 00000 н.
0000008089 00000 н.
0000008181 00000 п.
0000008583 00000 н.
0000009324 00000 п.
0000009961 00000 н.
0000012509 00000 п.
0000012841 00000 п.
0000013052 00000 п.
0000016282 00000 п.
0000016620 00000 п.
0000016996 00000 н.
0000017104 00000 п.
0000017154 00000 п.
0000017210 00000 п.
0000017261 00000 п.
0000017312 00000 п.
0000017363 00000 п.
0000017414 00000 п.
0000017464 00000 п. 0000017514 00000 п.
0000017565 00000 п.
0000017614 00000 п.
0000017664 00000 п.
0000017713 00000 п.
0000017763 00000 п.
0000017813 00000 п.
0000017863 00000 п.
0000017913 00000 п.
0000017952 00000 п.
0000018001 00000 п.
0000018052 00000 п.
0000020021 00000 н.
0000020249 00000 п.
0000020316 00000 п.
0000020382 00000 п.
0000020606 00000 п.
0000058601 00000 п.
0000079935 00000 н.
0000102439 00000 н.
0000123847 00000 н.
0000145074 00000 н.
0000166971 00000 н.
0000167505 00000 н.
0000168043 00000 н.
0000168139 00000 н.
0000168233 00000 н.
0000168326 00000 н.
0000168630 00000 н.
0000171646 00000 н.
0000171951 00000 н.
0000172151 00000 н.
0000172305 00000 н.
0000175493 00000 н.
0000175783 00000 н.
0000175967 00000 н.
0000197966 00000 н.
0000198180 00000 н.
0000200990 00000 н.
0000204942 00000 н.
0000215054 00000 н.
0000215934 00000 н.
0000216997 00000 н.
0000218773 00000 н.
0000219002 00000 н.
0000219939 00000 н.
0000220390 00000 н.
0000225675 00000 н.
0000017514 00000 п.
0000017565 00000 п.
0000017614 00000 п.
0000017664 00000 п.
0000017713 00000 п.
0000017763 00000 п.
0000017813 00000 п.
0000017863 00000 п.
0000017913 00000 п.
0000017952 00000 п.
0000018001 00000 п.
0000018052 00000 п.
0000020021 00000 н.
0000020249 00000 п.
0000020316 00000 п.
0000020382 00000 п.
0000020606 00000 п.
0000058601 00000 п.
0000079935 00000 н.
0000102439 00000 н.
0000123847 00000 н.
0000145074 00000 н.
0000166971 00000 н.
0000167505 00000 н.
0000168043 00000 н.
0000168139 00000 н.
0000168233 00000 н.
0000168326 00000 н.
0000168630 00000 н.
0000171646 00000 н.
0000171951 00000 н.
0000172151 00000 н.
0000172305 00000 н.
0000175493 00000 н.
0000175783 00000 н.
0000175967 00000 н.
0000197966 00000 н.
0000198180 00000 н.
0000200990 00000 н.
0000204942 00000 н.
0000215054 00000 н.
0000215934 00000 н.
0000216997 00000 н.
0000218773 00000 н.
0000219002 00000 н.
0000219939 00000 н.
0000220390 00000 н.
0000225675 00000 н.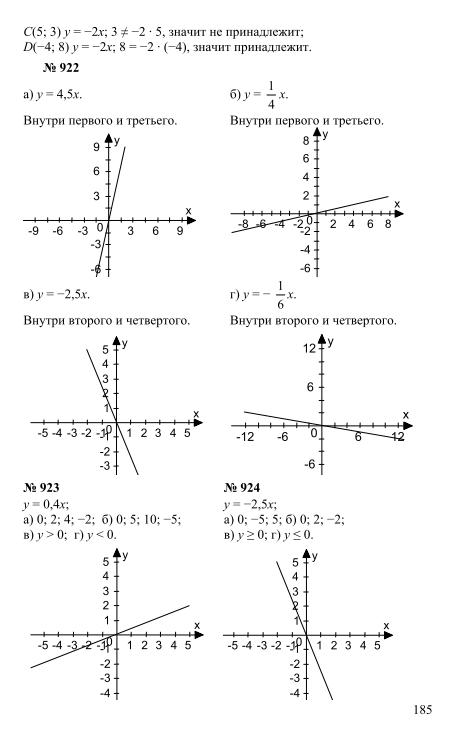 0000225851 00000 п.
0000227062 00000 н.
0000228131 00000 н.
0000232256 00000 н.
0000232840 00000 н.
0000237263 00000 н.
0000238097 00000 н.
0000238447 00000 н.
0000239414 00000 н.
0000240466 00000 н.
0000241245 00000 н.
0000242749 00000 н.
0000243430 00000 н.
0000244880 00000 н.
0000246826 00000 н.
0000249014 00000 н.
0000250773 00000 н.
0000252235 00000 н.
0000253781 00000 н.
0000255233 00000 н.
0000256245 00000 н.
0000257320 00000 н.
0000258494 00000 н.
0000259768 00000 н.
0000259996 00000 н.
0000261149 00000 н.
0000263255 00000 н.
0000264462 00000 н.
0000265101 00000 п.
0000266055 00000 н.
0000268670 00000 н.
0000283046 00000 н.
0000284191 00000 н.
0000286388 00000 п.
0000286784 00000 н.
0000288382 00000 н.
00002 00000 н.
00002
0000225851 00000 п.
0000227062 00000 н.
0000228131 00000 н.
0000232256 00000 н.
0000232840 00000 н.
0000237263 00000 н.
0000238097 00000 н.
0000238447 00000 н.
0000239414 00000 н.
0000240466 00000 н.
0000241245 00000 н.
0000242749 00000 н.
0000243430 00000 н.
0000244880 00000 н.
0000246826 00000 н.
0000249014 00000 н.
0000250773 00000 н.
0000252235 00000 н.
0000253781 00000 н.
0000255233 00000 н.
0000256245 00000 н.
0000257320 00000 н.
0000258494 00000 н.
0000259768 00000 н.
0000259996 00000 н.
0000261149 00000 н.
0000263255 00000 н.
0000264462 00000 н.
0000265101 00000 п.
0000266055 00000 н.
0000268670 00000 н.
0000283046 00000 н.
0000284191 00000 н.
0000286388 00000 п.
0000286784 00000 н.
0000288382 00000 н.
00002 00000 н.
00002
Библиографическая справка
Значение алгебраической дроби.
 Как решать алгебраические дроби? Теория и практика
Как решать алгебраические дроби? Теория и практикаЭтот урок знакомит с концепцией алгебраической дроби. Человек встречает дроби в простейших жизненных ситуациях: когда необходимо разделить предмет на несколько частей, например, торт разрезать поровну на десять человек. Очевидно, каждому достанется кусок пирога. В данном случае мы сталкиваемся с понятием числовой дроби, но возможна ситуация, когда объект делится на неизвестное количество частей, например, по x.В этом случае возникает понятие дробного выражения. Вы уже встречались с целочисленными выражениями (не содержащими разделения на выражения с переменными) и их свойствами в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные понятия
1.Определение и примеры алгебраических дробей Рациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений: — дробные выражения; — целые выражения. Например, в первом выражении он действует как числитель и знаменатель.
Значение алгебраической дроби , как и любое алгебраическое выражение , зависит от числового значения тех переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
2. Вычисление значения алгебраической дроби и две основные задачи на дробьРассмотрим первую типичную задачу: вычисление значения рациональной дроби для разных значений входящих в нее переменных.
Пример 1. Вычислить значение дроби в пунктах а), б), в)
Решение. Подставьте значения переменных в указанную дробь: а), б), в) — не существует (так как на ноль делить нельзя).
Ответ: 3; 1; не существует.
Как видите, для любой дроби возникают две типичные задачи: 1) вычисление дроби, 2) поиск действительных и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — значения переменных, для которых выражение имеет смысл.Набор всех допустимых значений переменных называется ODZ или домен .
3. Допустимые (ODZ) и недопустимые значения переменных в долях с одной переменнойЗначение буквальных переменных может быть недопустимым, если знаменатель дроби для этих значений равен нулю. Во всех остальных случаях значения переменных действительны, так как дробь может быть вычислена.
Пример 2.Определить, при каких значениях переменной дробь не имеет смысла.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недействительными будут только те значения переменной, у которых знаменатель равен нулю. Знаменатель дроби, поэтому решим линейное уравнение:
Знаменатель дроби, поэтому решим линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Решение примера подразумевает правило поиска недопустимых значений переменных — знаменатель дроби равен нулю и находятся корни соответствующего уравнения.
Давайте рассмотрим несколько похожих примеров.
Пример 3. Определить, при каких значениях переменной дробь не имеет смысла.
Решение. …
Ответ. …
Пример 4. Определить, при каких значениях переменной дробь не имеет смысла.
Решение ..
Есть и другие постановки этой задачи — найти домен или диапазон допустимых значений выражения (ODZ) … Это означает — найти все допустимые значения переменных. В нашем примере это все значения кроме. На числовой оси удобно нанести область определения.
Для этого проткнем на нем точку, как указано на рисунке:
Таким образом, домен дроби будет состоять из всех чисел, кроме 3.
Ответ ..
Пример 5. Определить, при каких значениях переменной дробь не имеет смысла.
Решение ..
Нарисуем получившееся решение на числовой оси:
Ответ ..
4. Графическое представление области допустимых (ODV) и недопустимых значений переменных в дробяхПример 6. Определить, при каких значениях переменных дробь не имеет смысла.
Решение .. Получили равенство двух переменных, приводим числовые примеры: или и т. Д.
Постройте это решение в декартовой системе координат:
Рисунок: 3. Функциональный график.
Координаты любой точки на этом графике не входят в диапазон допустимых значений дроби.
Ответ. …
5. Дело «деление на ноль»В рассмотренных примерах мы столкнулись с ситуацией, когда происходило деление на ноль.Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типов.
Пример 7. Определить, при каких значениях переменных дробь не имеет смысла.
Решение ..
Оказывается, дробь не имеет смысла. Но кто-то может возразить, что это не так, потому что:.
Может показаться, что если итоговое выражение равно 8 at, то исходное также может быть вычислено и, следовательно, имеет смысл при. Однако если подставить его в исходное выражение, мы получим — смысла нет.
Ответ ..
Чтобы разобраться в этом примере более подробно, решим следующую задачу: при каких значениях указанная дробь равна нулю?
(дробь равна нулю, когда ее числитель равен нулю) … Но необходимо решать исходное уравнение с дробью, и это не имеет смысла при, потому что при этом значении переменной знаменатель равен нулю. Следовательно, это уравнение имеет только один корень.
6. Правило поиска DLD Таким образом, можно сформулировать точное правило нахождения диапазона допустимых значений дроби: для нахождения ODZ дробей необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения .
Мы рассмотрели две основные задачи: вычисление значения дроби для заданных значений переменных и нахождение диапазона допустимых значений дроби .
Давайте теперь рассмотрим еще несколько проблем, которые могут возникнуть при работе с дробями.
7. Различные цели и выводыПример 8. Докажите, что для любых значений переменной дробь.
Доказательства.В числителе положительное число. … В результате и числитель, и знаменатель являются положительными числами, следовательно, дробь также является положительным числом.
Проверено.
Пример 9. Как известно, find.
Решение. Разделите дробь на член. Мы вправе уменьшить на, учитывая, какое недопустимое значение переменной для этой дроби.
Ответ ..
В этом уроке мы рассмотрели основные понятия, связанные с дробями.В следующем уроке мы рассмотрим основное свойство дроби .
Список литературы
1. Башмаков М. И. Алгебра 8 класс. — М .: Просвещение, 2004.
И. Алгебра 8 класс. — М .: Просвещение, 2004.
2. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. — 5-е изд. — М .: Просвещение, 2010.
.3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. — М .: Просвещение, 2006.
.1. Фестиваль педагогических идей.
2. Старая школа.
3. Интернет-портал lib2.podelise. RU.
Домашнее задание
1. №4, 7, 9, 12, 13, 14. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. — 5-е изд. — М .: Просвещение, 2010.
.2. Запишите рациональную дробь, область определения которой: а) множество, б) множество, в) вся числовая ось.
3. Докажите, что для всех допустимых значений переменной значение дроби неотрицательно.
4.Найдите объем выражения. Подсказка: рассмотрите отдельно два случая: когда знаменатель младшей дроби равен нулю, и когда знаменатель исходной дроби равен нулю.
Когда ученик поступает в среднюю школу, математика делится на 2 предмета: алгебру и геометрию. Понятий становится все больше, задачи усложняются. Некоторым людям трудно понимать дроби. Пропустил первый урок по этой теме, и вуаля. фракции? Вопрос, который будет мучить вас на протяжении всей школьной жизни.
Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимается выражение P / Q, где P — числитель, а Q — знаменатель. Буквенный ввод может скрывать число, числовое выражение, числово-буквенное выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала вам нужно понять, что такое выражение является частью целого.
Как правило, все равно 1.Число в знаменателе показывает, на сколько частей разделена единица измерения. Числитель нужен, чтобы знать, сколько элементов берется. Дробная черта соответствует знаку деления. Допускается записывать дробное выражение в виде математической операции «Деление». В этом случае числитель — делимое, знаменатель — делитель.
В этом случае числитель — делимое, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда ученики изучают эту тему в школе, им дают примеры для подкрепления. Чтобы их правильно решать и находить различные пути выхода из сложных ситуаций, нужно применить основное свойство дробей.
Это звучит так: если умножить числитель и знаменатель на одно и то же число или выражение (ненулевое), то значение обыкновенной дроби не изменится. Частным случаем этого правила является деление обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.
Ниже мы рассмотрим, как решать сложение и вычитание алгебраических дробей, умножение, деление и сокращение дробей.
Математические операции с дробями
Давайте рассмотрим, как решить основное свойство алгебраической дроби, как применить его на практике.Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, вы всегда должны следовать правилам.
Итак, для операций сложения и вычитания необходимо найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби указаны с одинаковыми Q-выражениями, то этот пункт следует опустить. Когда общий знаменатель найден, как решить алгебраические дроби? Сложите или вычтите числители. Но! Следует помнить, что если перед дробью стоит знак «-», все знаки в числителе меняются местами.Иногда не следует делать никаких замен и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как сокращение дробей … Это означает следующее: если числитель и знаменатель делятся выражением, отличным от единицы (одинаковым для обеих частей), то получается новая дробь. Дивиденд и делитель меньше, чем предыдущие, но из-за основного правила дробей они остаются равными исходному примеру.
Цель этой операции — получить новое неприводимое выражение. Эту проблему можно решить, уменьшив числитель и знаменатель на наибольший общий множитель. Алгоритм работы состоит из двух точек:
Алгоритм работы состоит из двух точек:
Ниже приведена таблица со списком формул.Для удобства его можно распечатать и носить с собой в записной книжке. Однако, чтобы в дальнейшем при решении контрольного или экзамена не возникало затруднений в вопросе, как решать алгебраические дроби, эти формулы нужно заучивать наизусть.
Несколько примеров с решениями
С теоретической точки зрения рассматривается вопрос о том, как решать алгебраические дроби. Приведенные в статье примеры помогут лучше усвоить материал.
1. Переведите дроби и приведите их к общему знаменателю.
2. Переведите дроби и приведите их к общему знаменателю.
После изучения теоретической части и рассмотрения практических вопросов больше возникнуть не должно.
В § 42 было сказано, что если деление многочленов не может быть выполнено полностью, то частное записывается в форме дробного выражения, в котором делимое является числителем, а делитель — знаменателем.
Примеры дробных выражений:
Числитель и знаменатель дробного выражения могут сами быть дробными выражениями, например:
Из дробных алгебраических выражений чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются многочленами (в частности, и одночленами). Каждое такое выражение называется алгебраической дробью.
Определение. Алгебраическое выражение, представляющее собой дробь, числитель и знаменатель которой являются полиномами, называется алгебраической дробью.
Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.
В будущем, изучив действия над алгебраическими дробями, мы сможем преобразовать любое дробное выражение в алгебраическую дробь, используя идентичные преобразования.
Примеры алгебраических дробей:
Обратите внимание, что все выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно записать это выражение в числителе, а в знаменателе — 1. Например:
Например:
2. Допустимые значения букв.
Буквы, входящие только в числитель, могут принимать любые значения (если по условию задачи не вводятся дополнительные ограничения).
Для букв, включенных в знаменатель, допускаются только те значения, которые не обращаются в нуль знаменатель. Поэтому в дальнейшем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.
Этот урок знакомит с концепцией алгебраической дроби.Человек встречает дроби в простейших жизненных ситуациях: когда необходимо разделить предмет на несколько частей, например, торт разрезать поровну на десять человек. Очевидно, каждому достанется кусок пирога. В данном случае мы сталкиваемся с понятием числовой дроби, но возможна ситуация, когда объект делится на неизвестное количество частей, например, по x. В этом случае возникает понятие дробного выражения. Вы уже встречались с целочисленными выражениями (не содержащими разделения на выражения с переменными) и их свойствами в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Далее мы рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Рациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений : — дробные выражения; — целые выражения.Например, в первом выражении он действует как числитель и знаменатель.
Значение алгебраической дроби , как и любое алгебраическое выражение , зависит от числового значения тех переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
Рассмотрим первую типичную задачу: вычисление значения рациональной дроби для разных значений входящих в нее переменных.
Пример 1. Рассчитайте значение дроби в пунктах а), б), в)
Решение. Подставьте значения переменных в указанную дробь: а), б), в) — не существует (так как на ноль делить нельзя).
Подставьте значения переменных в указанную дробь: а), б), в) — не существует (так как на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видите, для любой дроби возникают две типичные задачи: 1) вычисление дроби, 2) поиск действительных и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — значения переменных, для которых выражение имеет смысл. Набор всех допустимых значений переменных называется ODZ или домен .
Значение буквальных переменных может быть недопустимым, если знаменатель дроби для этих значений равен нулю. Во всех остальных случаях значения переменных действительны, так как дробь может быть вычислена.
Пример 2.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недействительными будут только те значения переменной, у которых знаменатель равен нулю. Знаменатель дроби, поэтому решим линейное уравнение:
Знаменатель дроби, поэтому решим линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Решение примера подразумевает правило поиска недопустимых значений переменных — знаменатель дроби равен нулю и находятся корни соответствующего уравнения.
Давайте рассмотрим несколько похожих примеров.
Пример 3. Установить, при каких значениях переменной дробь не имеет смысла .
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной дробь не имеет смысла.
Решение. .
Есть и другие постановки этой задачи — найти домен или диапазон допустимых значений выражения (ODZ) … Это означает — найти все допустимые значения переменных. В нашем примере это все значения кроме. На числовой оси удобно нанести область определения.
Для этого проткнем на нем точку, как указано на рисунке:
Рисунок: 1
Таким образом, домен дроби будет состоять из всех чисел, кроме 3.
Ответ. .
Пример 5. Установить, при каких значениях переменной дробь не имеет смысла.
Решение. .
Нарисуем получившееся решение на числовой оси:
Рисунок: 2
Ответ. .
Пример 6.
Решение. … Мы получили равенство двух переменных, приведем числовые примеры: или и т. Д.
Постройте это решение в декартовой системе координат:
Рисунок: 3. График функций
Координаты любой точки на этом графике не входят в диапазон допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы столкнулись с ситуацией, когда происходило деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типов.
Пример 7. Установить, при каких значениях переменных дробь не имеет смысла.
Решение. .
Оказывается, дробь не имеет смысла.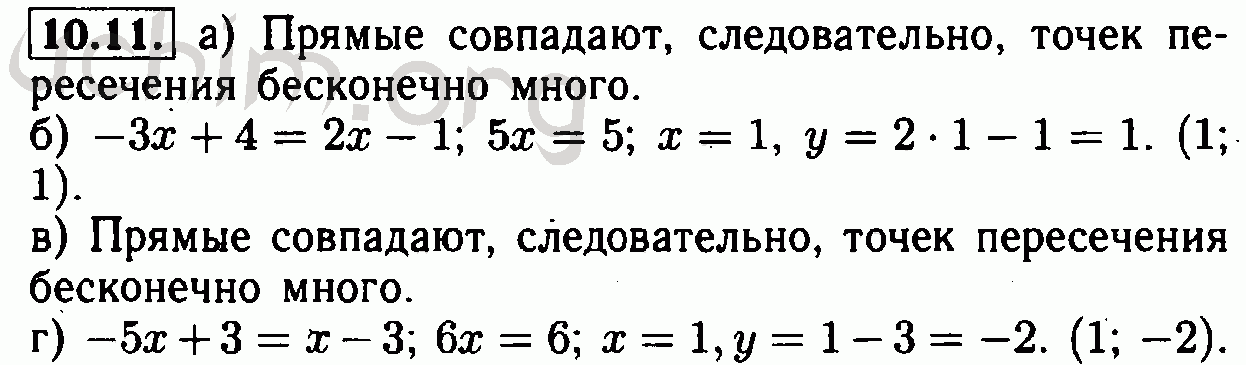 Но кто-то может возразить, что это не так, потому что: .
Но кто-то может возразить, что это не так, потому что: .
Может показаться, что если итоговое выражение равно 8 at, то исходное также может быть вычислено и, следовательно, имеет смысл при. Однако если подставить его в исходное выражение, мы получим — смысла нет.
Ответ. .
Чтобы разобраться в этом примере более подробно, решим следующую задачу: при каких значениях указанная дробь равна нулю?
§ 1 Понятие алгебраической дроби
Алгебраическая дробь — это выражение
, где P и Q — многочлены; P — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Вот несколько примеров алгебраических дробей:
Любой многочлен — это частный случай алгебраической дроби, потому что любой многочлен можно записать как
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, рассчитаем значение дроби
1)
2)
В первом случае получаем:
Обратите внимание, что эта дробь может быть уменьшена:
Таким образом, вычисление значения алгебраической дроби упрощается. Воспользуемся этим.
Воспользуемся этим.
Во втором случае получаем:
Как видите, значение алгебраической дроби изменилось с изменением значений переменных.
§ 2 Допустимые значения переменных алгебраической дроби
Рассмотрим алгебраическую дробь
Значение x = -1 недопустимо для этой дроби, потому что знаменатель дроби при этом значении x обращается в нуль. При таком значении переменной алгебраическая дробь не имеет смысла.
Таким образом, допустимые значения переменных алгебраической дроби — это те значения переменных, для которых знаменатель дроби не обращается в нуль.
Давайте решим несколько примеров.
При каких значениях переменной алгебраическая дробь не имеет смысла:
Для поиска недопустимых значений переменных знаменатель дроби приравнивается к нулю, и находятся корни соответствующего уравнения.
При каких значениях переменной алгебраическая дробь равна нулю:
Дробь равна нулю, если числитель равен нулю.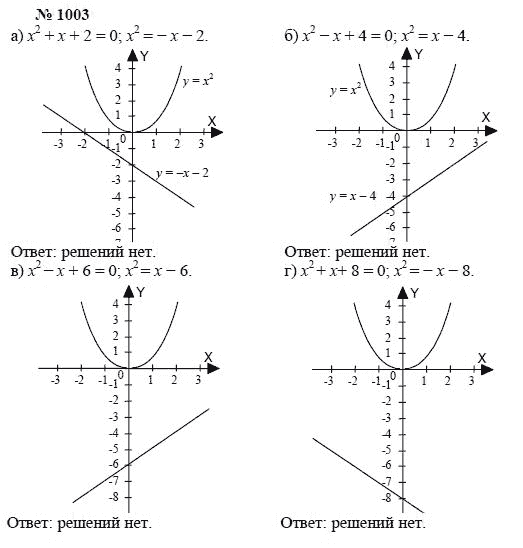 Приравняем числитель нашей дроби к нулю и найдем корни получившегося уравнения:
Приравняем числитель нашей дроби к нулю и найдем корни получившегося уравнения:
Таким образом, при x = 0 и x = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Итак, на этом уроке вы узнали основные понятия алгебраической дроби: числитель и знаменатель дроби, а также допустимые значения переменных алгебраической дроби.
Список использованной литературы:

 Г. Мордковича». Алгебра. 7– 9 классы
Г. Мордковича». Алгебра. 7– 9 классы Приоритетной содержательно-методической линией остаётся функционально-графическая, лучше отвечающая возрастным особенностям учащихся, чем традиционные установки на приоритет алгебраических формул.
Приоритетной содержательно-методической линией остаётся функционально-графическая, лучше отвечающая возрастным особенностям учащихся, чем традиционные установки на приоритет алгебраических формул.

 Г. / Семенов П.В. / Александрова Л.А. / Мардахаева Е.Л.
Г. / Семенов П.В. / Александрова Л.А. / Мардахаева Е.Л. Материал пособия выстроен в соответствии с главами и параграфами учебника «Алгебра. 8 класс», созданного авторским коллективом под руководством А. Г. Мордковича, но пособие может быть использовано при работе по другим учебникам и самостоятельном изучении курса.
Материал пособия выстроен в соответствии с главами и параграфами учебника «Алгебра. 8 класс», созданного авторским коллективом под руководством А. Г. Мордковича, но пособие может быть использовано при работе по другим учебникам и самостоятельном изучении курса. Г. / Семенов П.В. / Александрова Л.А. / Мардахаева Е.Л.
Г. / Семенов П.В. / Александрова Л.А. / Мардахаева Е.Л. Материал пособия выстроен в соответствии с главами и параграфами учебника «Алгебра. 9 класс», созданного авторским коллективом под руководством А.Г. Мордковича, но пособие может быть использовано при работе по другим учебникам и самостоятельном изучении курса.
Материал пособия выстроен в соответствии с главами и параграфами учебника «Алгебра. 9 класс», созданного авторским коллективом под руководством А.Г. Мордковича, но пособие может быть использовано при работе по другим учебникам и самостоятельном изучении курса. В настоящее время я работаю помощником футбольного тренера в Вероне и руковожу тренажерными залами зимой, весной и летом. .Я также специалист по силовой и физической подготовке для спортсменов средней школы и колледжей.
В настоящее время я работаю помощником футбольного тренера в Вероне и руковожу тренажерными залами зимой, весной и летом. .Я также специалист по силовой и физической подготовке для спортсменов средней школы и колледжей.