Главная »
Реферат »
Законы распределения случайных погрешностей реферат
Предмет и задачи метрологии. Структура метрологии. Законы распределения случайных погрешностей реферат
3Акон распределения случайных погрешностей
Полностью избежать или исключить совершенно случайные погрешности невозможно, так как факторы, их вызывающие, не поддаются учёту и носят случайный характер. Возникает вопрос: как уменьшить влияние случайных погрешностей на окончательный результат измерения и как оценить точность и достоверность последнего? Ответ на этот вопрос даёт теория вероятностей. Теория вероятностей — это математическая наука, выясняющая закономерности случайных событий (явлений), которые проявляются при действии большого числа случайных факторов.
Случайные погрешности измерений относятся к группе непрерывных величин. Непрерывные величины характеризуются бесчисленным множеством возможных значений. Вероятность любого значения непрерывной случайной величины бесконечно мала. Поэтому, чтобы выявить распределение вероятностей для какой-то непрерывной случайной величины, например, величины  , рассматривают ряд интервалов
, рассматривают ряд интервалов  значений этой величины и подсчитывают частоты
значений этой величины и подсчитывают частоты  попадания значений величины
попадания значений величины  в каждый интервал
в каждый интервал  . Таблица, в которой приведены интервалы в порядке их распределения вдоль оси абсцисс и соответствующие им частоты, называется статистическим рядом (табл.1).
. Таблица, в которой приведены интервалы в порядке их распределения вдоль оси абсцисс и соответствующие им частоты, называется статистическим рядом (табл.1).
Таблица 1
| Интервалы I | 
| 
| . . . . . . . | 
| . . . . . . . | 
|
| Частоты Р* | 
| 
| . . . . . . . | 
| . . . . . . . | 
|
Статистический ряд графически представляется в виде ступенчатой кривой, которую называют гистограммой. При построении гистограммы по оси абсцисс откладываются интервалы возможных значений случайной величины, а по оси ординат — частоты или число случаев, когда значение случайной величины попадает в данный интервал. Для большинства интересующих нас случайных погрешностей гистограмма имеет вид, показанный на рис. 1. На этом рисунке высота, а следовательно, и площадь прямоугольника для каждого интервала ошибок пропорциональны числу опытов, в которых данная ошибка наблюдалась.
П ри увеличении числа опытов (измерений) и уменьшении интервала разбиения оси абсцисс гистограмма теряет свой ступенчатый характер и стремится (переходит) к плавной кривой (рис. 2). Такую кривую называют кривой плотности распределения для данной случайной величины, а уравнение, описывающее эту кривую, называется законом распределения случайной величины.
ри увеличении числа опытов (измерений) и уменьшении интервала разбиения оси абсцисс гистограмма теряет свой ступенчатый характер и стремится (переходит) к плавной кривой (рис. 2). Такую кривую называют кривой плотности распределения для данной случайной величины, а уравнение, описывающее эту кривую, называется законом распределения случайной величины.
С читается, что случайная величина полностью определена, если известен закон её распределения. Этот закон может быть представлен (задан) в интегральной или дифференциальной форме. Интегральный закон распределения случайной величины обозначается символом
читается, что случайная величина полностью определена, если известен закон её распределения. Этот закон может быть представлен (задан) в интегральной или дифференциальной форме. Интегральный закон распределения случайной величины обозначается символом  и называется функцией распределения. Производная функция от
и называется функцией распределения. Производная функция от  называется плотностью вероятности случайной величины X или дифференциальным законом распределения:
называется плотностью вероятности случайной величины X или дифференциальным законом распределения:
 .
.
При решении многих практических задач нет необходимости характеризовать случайную величину исчерпывающим образом. Достаточно бывает указать только её некоторые числовые характеристики, например, её математическое ожидание  (можно писать
(можно писать  ) и дисперсию
) и дисперсию  (можно писать
(можно писать ).
).
Для непрерывной случайной величины X с плотностью вероятности  математическое ожидание вычисляется по формуле
математическое ожидание вычисляется по формуле
 . (3)
. (3)
Для непрерывной случайной величины X дисперсия определяется по формуле:
 . (4)
. (4)
Положительный квадратный корень из дисперсии обозначается символом  и называется средним квадратическим отклонением (сокращенно с. к. о.):
и называется средним квадратическим отклонением (сокращенно с. к. о.):
 . (5)
. (5)
При конечном числе опытов  в качестве оценки
в качестве оценки  принимают среднее арифметическое наблюденных (измеренных) значений
принимают среднее арифметическое наблюденных (измеренных) значений  , т. е.
, т. е.
 . (6)
. (6)
Для оценки дисперсии (с. к. о.) используют формулу
 . (7)
. (7)
Следует иметь в виду, что среднее арифметическое случайной величины  само является случайной величиной, так как вычисляется на основании ограниченного числа опытов. Разброс значений величины характеризуют средним квадратическим отклонением , которое связало с упомянутым выше
само является случайной величиной, так как вычисляется на основании ограниченного числа опытов. Разброс значений величины характеризуют средним квадратическим отклонением , которое связало с упомянутым выше  соотношением:
соотношением:
 . (8)
. (8)
При ограниченном числе опытов в качестве оценки принимают отношение
 . (9)
. (9)
Согласно закону больших чисел все три оценки при увеличении числа опытов приближаются (сходятся по вероятности) соответственно к  и
и 
Практика обработки статистических данных показывает, что числовые характеристики случайной величины ( и
и  ) существенно зависят от вида предполагаемого закона распределения рассматриваемой случайной величины.
) существенно зависят от вида предполагаемого закона распределения рассматриваемой случайной величины.
Предельная кривая, к которой в большинстве случаев стремятся гистограммы случайных погрешностей измерений физических величин при неограниченном увеличении числа опытов, имеет колоколообразный вид и называется кривой Гаусса (рис. 2). Аналитическое выражение этой кривой называется законом распределения Гаусса или законом нормального распределения. Для случайной величины  этот закон можно записать в виде:
этот закон можно записать в виде:
 . (10)
. (10)
где  — плотность вероятности;
— плотность вероятности;  и
и  — математическое ожидание и среднее квадратическое отклонение — параметры нормального распределения, физический смысл и способ вычисления которых были пояснены выше.
— математическое ожидание и среднее квадратическое отклонение — параметры нормального распределения, физический смысл и способ вычисления которых были пояснены выше.
При рассмотрении свойств и характеристик распределения случайных погрешностей мы ограничимся только нормальным законом, так как случайные погрешности измерений чаще всего распределяются нормально (по закону Гаусса). Это означает:
1) случайная погрешность измерения может принимать любые значения в интервале 
2) случайные погрешности, равные по абсолютной величине, но противоположные по знаку, равновероятны, то есть встречаются одинаково часто;
3) чем больше по абсолютной величине случайные погрешности, тем они менее вероятны, то есть встречаются реже.
studfiles.net
Законы распределения случайных погрешностей
(на примере математического маятника).
Цель работы: изучить основные законы распределения случайных погрешностей.
Введение.
Измерить физическую величину абсолютно точно принципиально невозможно по следующим причинам:
а) несовершенство приборов;
б) влияние внешних условий на характеристики приборов;
в) влияние внешних факторов на параметры изучаемого объекта;
г) субъективные человеческие факторы.
Учитывая все выше изложенное, на практике возможно указать лишь диапазон значений, в который попадает истинное значение искомой величины с определенной вероятностью:
хх,
где х– абсолютная ошибка измерений.
Этот диапазон называют доверительным интервалом с соответствующей надежностью . Абсолютную ошибку измерений определяют как разницу между истинным и измеренным значением определяемой величины. Но, так как, истинное значение не известно, то существуют разные способы оценки абсолютной погрешности. Для бесконечно большого числа измерений применяют следующие способы (на практике они применяются при условииn30):
1) в качестве абсолютно погрешности х принимают среднеарифметическую погрешность:
 с надежностью=0,57, (1)
с надежностью=0,57, (1)
где:  – средняя величинаnизмеренных значений искомой величины,
– средняя величинаnизмеренных значений искомой величины,
xi– величина каждого измерения;
2) в качестве абсолютной погрешности хпринимают среднеквадратичную погрешность:
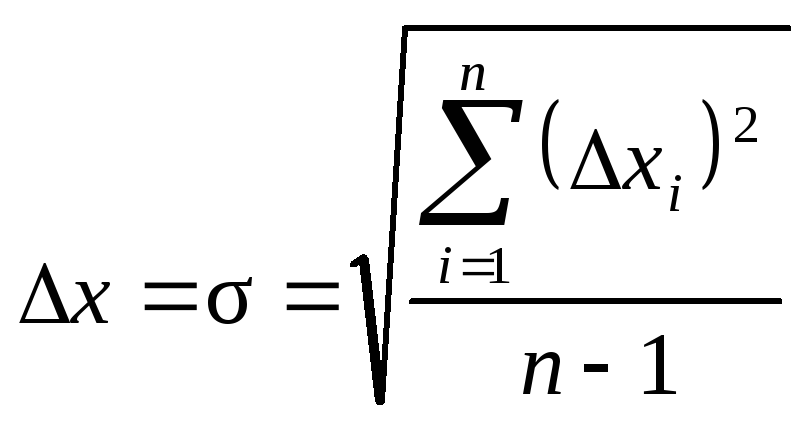 , с надежностью=0,68; (2)
, с надежностью=0,68; (2)
3) в качестве абсолютной погрешности х принимают вероятную погрешность:
х=, с надежностью=0,5.
Для нахождения вероятной погрешности все экспериментально определенные погрешностихi, взятые по модулю, записывают в ряд по мере их возрастания и в качестве вероятной погрешности берут ошибку, приходящуюся на средину ряда.
Для ,исуществуют теоретические соотношения:
 ;
; ;
; (3)
(3)
Все абсолютные погрешности разделяют на две большие группы:
1. Систематические погрешности. Систематическими называют погрешности, величина и знак которых не изменяются при повторении измерений.
2. Случайные погрешности. Случайными называются погрешности, величина и знак которых изменяются при повторении измерений.
Несмотря на хаотичность случайных погрешностей, их значения подчиняются определенным закономерностям. Изучить эти закономерности можно на примере математического маятника. Делается это следующим образом. По значениям периодов колебаний вычисляются абсолютные погрешности отдельно взятых измерений i. В качестве примера в данной работе предлагается таблица значений абсолютных погрешностей (таблица 1). Для удобства анализа они систематизированы по порядку возрастания, а не так как они получались на опыте. Для изучения закономерностей распределения случайных погрешностей на основании экспериментальных данных строится гистограмма.
Таблица 1
| 1 | -0,047 | 7 | -0,024 | 13 | -0,009 | 19 | 0 | 25 | 0,013 | 31 | 0,027 |
| 2 | -0,041 | 8 | -0,021 | 14 | -0,007 | 20 | 0,002 | 26 | 0,014 | 32 | 0,032 |
| 3 | -0,039 | 9 | -0,018 | 15 | -0,006 | 21 | 0,004 | 27 | 0,017 | 33 | 0,034 |
| 4 | -0,034 | 10 | -0,016 | 16 | -0,004 | 22 | 0,006 | 28 | 0,019 | 34 | 0,039 |
| 5 | -0,032 | 11 | -0,014 | 17 | -0,003 | 23 | 0,009 | 29 | 0,021 | 35 | 0,041 |
| 6 | -0,026 | 12 | -0,013 | 18 | -0,001 | 24 | 0,011 | 30 | 0,023 | 36 | 0,048 |
| =0,025 |
Выбирается система координат 0,причем осьстроится как в положительном, так и в отрицательном направлении. Осьразбивается на отрезки равной длины, т.е. с одинаковым шагом. В качестве размера шага, как правило, выбирается половина разряда первой значащей цифры границы доверительного интервала рассчитанного по формуле (2). Таким образом, для данного примера шаг осиравен 0,005с (в данном примере первая значащая цифраравна 2, ее разряд равен 0,01). Осьимеет единичный отрезок равный 1. По этой оси откладывается количество значений погрешностей, которые попадают в каждый выбранный интервал на оси.
Интервалы значений по оси выбираются равными величине разряда первой значащей цифры границы доверительного интервала рассчитанного по формуле (2). Для рассматриваемого примера величина интервала будет равна 0,01. Первый интервал выбирается симметрично относительно оси. Таким образом, для данного случая первый интервал будет от –0,005 до 0,005. Из таблицы 1 следует, что в этот интервал попадает 6 значений погрешностей. Поэтому на этом шаге строится прямоугольник шириной равной выбранному интервалу и высотой в шесть единиц. В следующий интервал от 0,005 до 0,015 попадает 5 значения погрешностей, т.е. на этом интервале строится прямоугольник высотой в 5 единиц и т.д. Аналогично, строятся прямоугольники для отрицательных значений абсолютных погрешностей. Пример построенной гистограммы приведен на рис.1.

Рис.1. Гистограмма
Если шаг по оси устремить к нулю, все прямоугольники превратятся в вертикальные линии, а верхние концы этих линий сформируют плавную колоколообразную линию. После построения гистограммы на ней проводится плавная кривая, огибающая вершины прямоугольников, как показано на рисунке.
Аналитически появление случайных ошибок описывается законом нормального распределения Гаусса:
 , (4)
, (4)
где f(xi) – плотность вероятности появления ошибкихi, рассчитываемая по формуле:
 (5)
(5)
Если по оси Yоткладывать не значения, а выражение , то получим кривую, которая называется графиком распределения Гаусса. На рисунке 2 показаны графики распределения Гаусса с разной дисперсией.
, то получим кривую, которая называется графиком распределения Гаусса. На рисунке 2 показаны графики распределения Гаусса с разной дисперсией.

Рис.2
Анализируя функцию распределения Гаусса и гистограмму на рисунках 1,2 можно установить основные закономерности распределения случайных погрешностей в зависимости от их величины:
1. При большом числе измерений случайные ошибки принимают непрерывный ряд значений. Это подтверждает сплошная линия на рис.1.
2. Ошибки одинаковые по величине, но разного знака встречаются одинаково часто. Из гистограммы рис.1 видно, количество ошибок в интервале от 0,005 до 0,015 на положительной ветви оси Травно количеству ошибок в таком же интервале на отрицательной ветви осиТ.
3. Частота появления ошибок уменьшается с увеличением их величины. Из гистограммы рис.1 видно, высота прямоугольников убывает вдоль оси Ткак в положительную, так и в отрицательную сторону.
Функция распределения случайных погрешностей Гаусса (6) позволяет установить физический смысл понятия «доверительная вероятность» или «надежность».
Если в соответствии с данными рис.1 доверительный интервал выберем от –0,02 до 0,02, то доверительная вероятность вычисляется путем интегрирования функции (4) в пределах выбранного интервала погрешностей:
 . (6)
. (6)
Тогда ответ можно будет представить в виде:
Тист= 0,02 с надежностью=Р.
0,02 с надежностью=Р.
Если интервал взять «шире» от –0,05 до 0,05, то доверительная вероятность, посчитанная по формуле (6), возрастет. Это и понятно: чем шире доверительный интервал, тем вероятнее истинное значение периода колебаний попадет в этот интервал. Если интеграл (6) посчитать в пределах от –до +, то получим цифру 1. Это означает, истинное значение периода колебаний абсолютно достоверно попадет в интервал от –до +. Равенство интеграла (6) единице называется условием нормировки вероятностей.
Функция распределения Гаусса в виде, представленном формулой (4) применима на бесконечно малом интервале . В этой работе интервалынельзя считать бесконечно малыми, поэтому следует вести речь о дискретных значениях функции распределения Гаусса определенных для границ рассматриваемых интервалов.
Приравняем выражения (4) и (5):
 .
.
Выразим и перейдем к дискретным значениям:
 , (7)
, (7)
где х– величина интервала,– граница интервала.
Систематические погрешности смещают гистограмму вправо или влево по оси Т,не искажая характер распределения случайных погрешностей.
studfiles.net
4. Систематические погрешности. Случайные погрешности. Законы распределения случайных погрешностей. Определение доверительных границ погрешностей для нормального закона распределения.
Систематические погрешности - постоянные или закономерно изменяющиеся погрешности.
Их основной отличительный признак: они могут быть предсказаны или устранены введением поправок.
Постоянные погрешности определяют при поверке по образцовым мерам или сигналам.
Закономерно изменяющиеся погрешности – большинство дополнительных погрешностей. Дополнительные погрешности устраняют схемной коррекцией.
Прогрессирующие погрешности – непредсказуемые погрешности медленно изменяющиеся во времени. Они вызываются старением деталей и их можно скорректировать только на данный момент времени, т.е. они требуют непрерывного повторения коррекции.
Случайные погрешности – вызываются несколькими причинами неподдающимися анализу. Их обнаруживают при повторных измерениях в виде разброса результатов.
Случайные погрешности проявляются при повторных измерениях одной и той же величины в виде разброса показаний. Оценку СП проводят с помощью теории вероятности.
Полным описанием случайной величины является ее закон распределения. Он может быть задан в интегральной или дифференциальной форме.
Часто СП подчиняются закону Гауса (нормальный закон распределения).

 - плотность распределения вероятности СП.
- плотность распределения вероятности СП.
средне квадратичное отклонение.
При увеличении кривая становится более плоской.

дифференциальный закон
распределения
интегральный закон
распределения
Основные характеристики законов распределения – математическое ожидание m и дисперсия D.
Математическое ожидание ряда измерений будет истинное значение измеряемой величины. Систематическая погрешность смещает математическое ожидание.
Дисперсия ряда измерений характеризует степень рассеяния результатов отдельных измерений вокруг математического ожидания. Чем меньше дисперсия, тем точнее измерения. Т.к. D измеряется в квадрате измеряемой величины, то применяют:  .
.
m и D можно определить, если произведено большое число измерений ( ).
).
Если число измерений n<20, то определяют оценку m и D.
Допустим провели ряд измерений и получили a1, a2, a3, …, an, где ai – результаты отдельных измерений, n – число измерений.
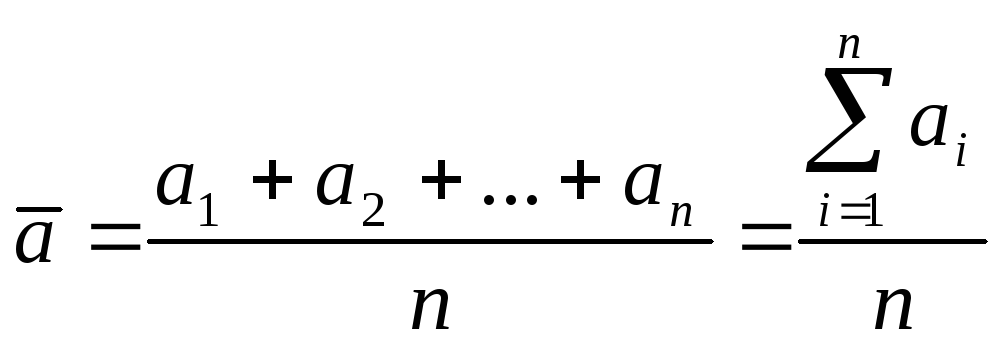 ,
,  - средне арифметическое.
- средне арифметическое.
При 

Рассчитаем остаточные погрешности : 

…

Оценка дисперсии ряда наблюдений подсчитывается:

Если  , то
, то и
и
 - если отсутствует систематическая погрешность.
- если отсутствует систематическая погрешность.
Если  , то из ряда измерений вычитают систематическую погрешность и ряд называетсяисправным.
, то из ряда измерений вычитают систематическую погрешность и ряд называетсяисправным.
Из теории вероятности известно, что  - дисперсия средне арифметического вn-раз меньше дисперсии ряда измерений или
- дисперсия средне арифметического вn-раз меньше дисперсии ряда измерений или 
 - средне квадратичное отклонение в
- средне квадратичное отклонение в меньше средне квадратичного отклонения ряда измерений.
меньше средне квадратичного отклонения ряда измерений.
Погрешность дискретности подчиняется равномерному закону распределения.
В качестве дифференциальных законов распределения берут кривые, площадь под которыми равна 1. Она отображает вероятность всех возможных событий.


интегральный закон
распределения
дифференциальный закон
распределения
Если известен закон распределения, то можно определить вероятность появления погрешности не выходящей за пределы некоторой границы. Этот интервал называется доверительным, а его вероятность доверительной.
В метрологии доверительная вероятность: Рд=0.9; 0.95
В теории надежности: Рд=0.8.

Рд числено = площади ограничения кривой осью абсцисс и вертикальными линиями соответствующих доверительному интервалу. Результат измерения может быть представлен в виде:
осью абсцисс и вертикальными линиями соответствующих доверительному интервалу. Результат измерения может быть представлен в виде:
Для нормального закона распределения можно записать:
 , где
, где  - функция Лапласса.
- функция Лапласса.
Ф(0)=0, Ф(-х)=-Ф(х) - свойства функции Лапласса.
Часто нужно найти вероятность того, что СП по абсолютному величине меньше заданного положительного числа :

Найдем вероятность того, что 
Правило трех .
Считают невозможным выход случайной ошибки за пределы трех , т.е. в 997 из 1000 случаев погрешность не превосходит трех
Если погрешность больше трех , то результат этого измерения называется промахом, и его отбрасывают.
Если случайная ошибка распределена по нормальному закону и n<20, то истинное значение измеряемой величины находят с использованием закона Стьюдента.
 .
.
Коэффициент t берут из таблицы распределения Стьюдента.
В результат измерения входит не исключаемая систематическая погрешность и случайная погрешность.
Если  , то пренебрегают и считают, что погрешность только случайная.
, то пренебрегают и считают, что погрешность только случайная.
Если  , то пренебрегают СП, т.е. остается только систематическая погрешность.
, то пренебрегают СП, т.е. остается только систематическая погрешность.
Если  , то границы погрешности находят по формуле из справочника.
, то границы погрешности находят по формуле из справочника.
7
studfiles.net
Лекция №4
Лекция №4
Случайные погрешности.
Вероятностное описание случайных погрешностей
 Присутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения.
Присутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения.
 Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения.
Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения.
Интегральной функцией распределенияF(x) называют функцию, каждое значение которой для каждогохявляется вероятностью события, заключающегося в том, что случайная величинахi; вi-м опыте принимает значение, меньшеех:
F(x)=P{xi<x}=P{- <xi≤x}
<xi≤x}
 График интегральной функции распределения показан на рис. 1. Она имеет следующие свойства:
График интегральной функции распределения показан на рис. 1. Она имеет следующие свойства:
неотрицательная, т.е. F(x) ≥0;
неубывающая, т.е. F(x2)≥ F(x1), если х2≥х1;
диапазон ее изменения простирается от 0 до 1, т.е. F(- ) = 0; F(+
) = 0; F(+ ) = 1;
) = 1;
вероятность нахождения случайной величины хв диапазоне от x1дох2Р{х1< х < х2} = F(x2) - F(x1).
Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемойплотностью распределения вероятностейр(х)=dF(x)/dx. Она всегда неотрицательна и подчиняется условию нормирования в виде:

 Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2)
Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2)

 Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величиныхв интервал [-
Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величиныхв интервал [- ; +
; + ] равна единице, т.е. представляет собой достоверное событие.
] равна единице, т.е. представляет собой достоверное событие. Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (x1;х2) равна площади, заключенной под кривой р(х) между абсциссами х1и х2(рис. 1).
Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (x1;х2) равна площади, заключенной под кривой р(х) между абсциссами х1и х2(рис. 1).

Рис. 1.
Поэтому по форме кривой плотности вероятности p(x)можно судить о том, какие значения случайной величины хнаиболее вероятны, а какие наименее.
Числовые параметры законов распределения
 Общие сведения.Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются:
Общие сведения.Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются: - центр распределения;
- центр распределения; - начальные и центральные моменты и производные от них коэффициенты - математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии;
- начальные и центральные моменты и производные от них коэффициенты - математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии; - энтропийный коэффициент.
- энтропийный коэффициент. Понятие центра распределения.Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:
Понятие центра распределения.Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:

 Точку ХMназываютмедианойили 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент.
Точку ХMназываютмедианойили 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент. Можно определить центр распределения как центр тяжести распределения, т.е. такой точки
Можно определить центр распределения как центр тяжести распределения, т.е. такой точки , относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:
, относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:

 Эта точка называетсяматематическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.
Эта точка называетсяматематическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.
При симметричной кривой р(х) в качестве центра может использоваться абсцисса моды, т.е. максимума распределения XM.
Моменты распределений.Все моменты представляют собой некоторые средние значения, причем если усредняются величины, отсчитываемые от начала координат, то моменты называютначальными, а если от центра распределения, тоцентральными. Начальные и центральные моменты r-го порядка определяются соответственно по формулам

Нулевой начальный момент равен единице. Он используется для задания условия нормирования плотности распределения:

Также с помощью начального момента нулевого порядка вводится понятие медианы распределения.
Первый начальный момент - МО случайной величины:

Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины.
Начальные и центральные моменты случайной погрешности  совпадают между собой и с центральными моментами результатов измерений:
совпадают между собой и с центральными моментами результатов измерений: , поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю.Важное значение имеет второй центральный момент
, поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю.Важное значение имеет второй центральный момент

называемый дисперсиейи являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания используетсясреднее квадратическое отклонение

имеющее такую же размерность, как и МО. Для примера на (рис)показан вид нормального распределения при различных значениях СКО

 Отдельные значения случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняется определенным закономерностям, которые являются вероятностными. Они описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину.
Отдельные значения случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняется определенным закономерностям, которые являются вероятностными. Они описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину.
Математическое описание непрерывных случайных величин осуществляется обычно с помощью дифференциальных законов распределения случайной величины. Эти законы определяют связь между возможными значениями случайной величины и соответствующими им плотностями вероятностей.
Наиболее распространенным при измерениях является нормальный закон распределения. Для некоторой измеряемой величины Xкривая распределения плотности вероятностиP(x) для закона нормального распределения имеет вид, показанный на рис. 6.
П ри этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения случайной погрешности в данной точке. Плотность вероятности для закона распределения описывается уравнением:
ри этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения случайной погрешности в данной точке. Плотность вероятности для закона распределения описывается уравнением:

 (9)
(9)
где М[x]иσ– характеристики нормального распределения.
Кривую 1 можно рассматривать как кривую распределения случайной погрешности, перенеся начало координат в точку X=M[x](рис.7).
В этом случае плотность вероятности:
 (10)
(10)
где  - случайная погрешность.
- случайная погрешность.
Характеристики M[x]иσ называют соответственноматематическим ожиданиемисреднеквадратическим отклонением. Они являются важными числовыми характеристиками случайной величины.
Математическое ожидание является тем значение величины, вокруг которого группируются результаты отдельных наблюдений, а среднеквадратическое отклонение характеризует рассеяние результатов отдельных наблюдений относительно математического ожидания. На рисунках 6 и 7 показаны кривые закона нормального распределения (кривые Гаусса) случайной величины Xи ее случайной погрешностиψпри различных значениях среднеквадратического отклонения; рассеяние для кривой 3, больше, чем рассеяние для кривой 2, а рассеяние для кривой 2 – больше , чем кривой 1.
Г еометрическиσопределяется как расстояние от оси симметрии нормального распределения до точкиАперегиба кривой распределения (Рис.6,7).
еометрическиσопределяется как расстояние от оси симметрии нормального распределения до точкиАперегиба кривой распределения (Рис.6,7).
Чтобы определить вероятность P попадания результата измерения или случайной погрешности в некоторой наперед заданной интервал от-ддо+д(рис. 8), необходимо найти площадь под кривой распределения, ограниченную вертикалями на границе интервала.
Для нормального распределения:
 (11)
(11)
Решить интеграл (11) аналитически невозможно. Обычно он приводится в виде таблиц, позволяющих определить его значение приближенно в долях единицы.
Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для более подробного описания распределения используются моменты более высоких порядков.  Третий центральный момент
Третий центральный момент

служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии . Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на(рис. а)
. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на(рис. а)

 Четвертый центральный момент
Четвертый центральный момент

служит для характеристики плоско- или островершинности распределения. Эти свойства описываются с помощью эксцесса

 Значения коэффициента
Значения коэффициента лежат в диапазоне от -2 до
лежат в диапазоне от -2 до . Для нормального распределения он равен 0. Чаще эксцесс задается формулой
. Для нормального распределения он равен 0. Чаще эксцесс задается формулой

 Его значения лежат в диапазоне от 1 до
Его значения лежат в диапазоне от 1 до . Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на(рис. б).
. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на(рис. б).

 Для удобства часто используютконтрэксцесс
Для удобства часто используютконтрэксцесс

 Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
Основные законы распределения
 Общие сведения.Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего, предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом:
Общие сведения.Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего, предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом: - трапецеидальные (плосковершинные) распределения;
- трапецеидальные (плосковершинные) распределения; - уплощеные (приблизительно плосковершинные) распределения;
- уплощеные (приблизительно плосковершинные) распределения; - экспоненциальные распределения;
- экспоненциальные распределения; - семейство распределений Стьюдента;
- семейство распределений Стьюдента; - двухмодальные распределения.
- двухмодальные распределения. Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение(рис. а)описывается уравнением
Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение(рис. а)описывается уравнением


 Трапецеидальное распределение(рис. б)
Трапецеидальное распределение(рис. б)

 Треугольное (Симпсона) распределение(рис. в)
Треугольное (Симпсона) распределение(рис. в)

где Хц, a, b - параметры распределения.  Математическое ожидание всех трапецеидальных распределений Хц=(х1+х2)/2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а.
Математическое ожидание всех трапецеидальных распределений Хц=(х1+х2)/2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а. Среднее квадратическое отклонение в зависимости от распределения определяется по формуле:
Среднее квадратическое отклонение в зависимости от распределения определяется по формуле: - равномерное
- равномерное
 - трапецеидальное
- трапецеидальное
 - треугольное
- треугольное .
. Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл.
Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл.

 Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон.
Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон. Экспоненциальные распределенияЭкспоненциальные распределения описываютсяформулой 1
Экспоненциальные распределенияЭкспоненциальные распределения описываютсяформулой 1

 где
где ;
; - СКО;
- СКО; - некоторая характерная для данного распределения константа; Хц - координата центра; Г(х) - гамма-функция. В нормированном виде, т.е. при Хц = О и
- некоторая характерная для данного распределения константа; Хц - координата центра; Г(х) - гамма-функция. В нормированном виде, т.е. при Хц = О и = 1,
= 1,

 где А(
где А( ) - нормирующий множитель распределения.
) - нормирующий множитель распределения. Интегральная функция нормированного экспоненциального распределения описывается выражением
Интегральная функция нормированного экспоненциального распределения описывается выражением

 Интеграл, входящий в эту формулу, выражается через элементарные функции только при
Интеграл, входящий в эту формулу, выражается через элементарные функции только при = 1/n, n = 1; 2; 3; ... При
= 1/n, n = 1; 2; 3; ... При = n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам.
= n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам. Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам:
Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам:

 Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При
Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При < 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При
< 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При = 1 получается распределение Лапласа
= 1 получается распределение Лапласа , при
, при = 2 - нормальное распределение или распределение Гаусса. При
= 2 - нормальное распределение или распределение Гаусса. При > 2 распределения, описываемые формулой 1, близки по свойствам к трапецеидальным. При очень больших значениях а формула (1) описывает практически равномерное распределение. В табл. приведены параметры некоторых из экспоненциальных распределений.
> 2 распределения, описываемые формулой 1, близки по свойствам к трапецеидальным. При очень больших значениях а формула (1) описывает практически равномерное распределение. В табл. приведены параметры некоторых из экспоненциальных распределений.

 Вид экспоненциальных распределений при различных значениях показателя
Вид экспоненциальных распределений при различных значениях показателя приведен на(рис).
приведен на(рис).

studfiles.net
1.2.2. Случайные погрешности
Случайные погрешности вызываются большой совокупностью причин, остающихся при проведении измерений неизвестными. Случайные погрешности неизбежны и неустранимы. Случайная погрешность, как и всякая случайная величина, наиболее полно характеризуется законом распределения. В практике встречаются различные законы распределения случайных погрешностей. Наиболее часто приходиться иметь дело с нормальным законом распределения, но встречаются также: равномерный закон распределения; треугольный закон (закон Симпсона) и др. [6, 8].
Таким образом, погрешность результата измерений в общем случае включает систематическую и случайную составляющие
 (1.5)
(1.5)
(грубая погрешность  входит в состав случайной погрешности).
входит в состав случайной погрешности).
В выражении (1.5) перед составляющими погрешности оставлен только знак “+”, но и здесь, и далее следует иметь ввиду что  может иметь как знак “+”, так и знак “-“, а если систематическая погрешность задана в виде границ (как чаще всего и бывает для неисключенных остатков систематической погрешности), то перед значением
может иметь как знак “+”, так и знак “-“, а если систематическая погрешность задана в виде границ (как чаще всего и бывает для неисключенных остатков систематической погрешности), то перед значением 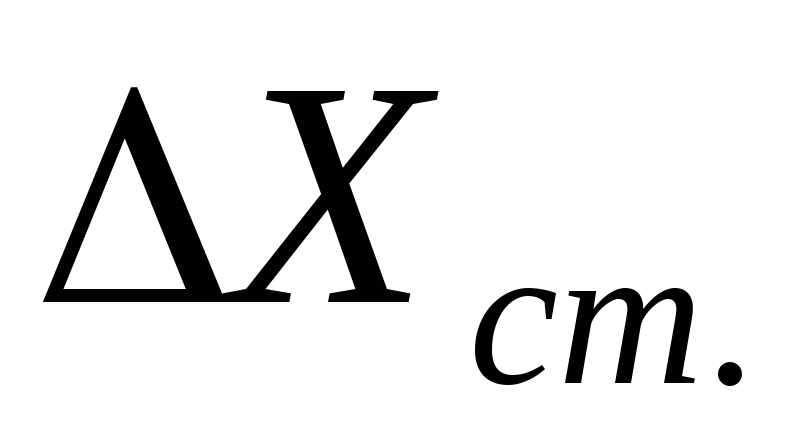 подразумевается знак “” (т.е.
подразумевается знак “” (т.е.  ). Значение случайной погрешности всегда указывается в виде границ (т.е.
). Значение случайной погрешности всегда указывается в виде границ (т.е.  ).
).
В соответствии с законами теории вероятностей погрешность  , записанная в форме (1.5), также становиться случайной величиной, имеющей тот же закон распределения, что и
, записанная в форме (1.5), также становиться случайной величиной, имеющей тот же закон распределения, что и  . Все сказанное в равной мере относится и к результату измерения, если на основании (1.2) и (1.5) его записать в виде
. Все сказанное в равной мере относится и к результату измерения, если на основании (1.2) и (1.5) его записать в виде
 (1.6)
(1.6)
Из теории вероятностей известно, что закон распределения можно охарактеризовать числовыми характеристиками, которые являются уже неслучайными величинами. Эти характеристики и используются для количественной оценки случайной погрешности.
Основными числовыми характеристиками законов распределения погрешности  , записанной в виде (1.5), являются
, записанной в виде (1.5), являются
Математическое ожидание - 
 , (1.7)
, (1.7)
где  - плотность вероятности погрешности
- плотность вероятности погрешности  ;
;
и дисперсия - 
 . (1.8)
. (1.8)
Математическое ожидание погрешности измерений, вычисляемое в соответствии с (1.7) есть неслучайная величина, она характеризует систематическую составляющую погрешности измерения. Т.е.  , для чисто случайной погрешности (когда
, для чисто случайной погрешности (когда  )
)  .
.
Дисперсия характеризует степень разброса отдельных значений погрешности относительно  и может служить характеристикой точности проведенных измерений, но имеет размерность в единицах измеряемой величины в квадрате. Поэтому в качестве числовой характеристики случайной погрешности чаще используют средне квадратическое отклонение
и может служить характеристикой точности проведенных измерений, но имеет размерность в единицах измеряемой величины в квадрате. Поэтому в качестве числовой характеристики случайной погрешности чаще используют средне квадратическое отклонение 
 (1.9)
(1.9)
Положительное значение  , вычисленное в соответствии с (1.9), называется средним квадратическим отклонением (СКО) случайной величины
, вычисленное в соответствии с (1.9), называется средним квадратическим отклонением (СКО) случайной величины  , а применительно к погрешностям измерений ее следует называть средней квадратической погрешностью (СКП) результата измерений.
, а применительно к погрешностям измерений ее следует называть средней квадратической погрешностью (СКП) результата измерений.
Графическое представление нормального закона распределения случайных погрешностей (дифференциальная функция распределения  или плотность вероятностей) приведена на рисунке 1.5, а аналитическое выражение этого закона имеет вид:
или плотность вероятностей) приведена на рисунке 1.5, а аналитическое выражение этого закона имеет вид:
 (1.10)
(1.10)
В такой форме записи вид кривой распределения будет изменяться в зависимости от величины  (см. рис. 1.5), но если характеризовать случайную погрешность безразмерным нормированным числом
(см. рис. 1.5), но если характеризовать случайную погрешность безразмерным нормированным числом  (нормировка относительно СКП), то получим кривую нормированного нормального распределения
(нормировка относительно СКП), то получим кривую нормированного нормального распределения
 , (1.11)
, (1.11)
с аргументом
 . (1.12)
. (1.12)
Вид кривой нормированного нормального распределения чисто случайной погрешности ( ) приведен на рисунке 1.6.
) приведен на рисунке 1.6.
Графическое представление дифференциальной функции равномерного и треугольного законов распределения приведены на рисунке 1.7 и рисунке 1.8. Аналитическая запись этих законов распределения представлена выражениями (1.13) и (1.14) соответственно.
Часто по условиям измерительной задачи требуется найти максимальную (предельную) случайную погрешность, которая может иметь место. Максимальная случайная погрешность ( ) связана с
) связана с  и зависит от закона распределения. Так, например, для нормального закона максимальная случайная погрешность часто принимается равной (см. рис. 1.6):
и зависит от закона распределения. Так, например, для нормального закона максимальная случайная погрешность часто принимается равной (см. рис. 1.6):
 . (1.15)
. (1.15)
Для других законов распределения соотношения между  и
и  отличаются от (1.15). Так для равномерного закона распределения
отличаются от (1.15). Так для равномерного закона распределения  ; для треугольного
; для треугольного  соответственно и т.д. [8].
соответственно и т.д. [8].
Определить числовые характеристики случайной погрешности воспользовавшись (1.7) и (1.8) можно только в том случае, если известно аналитическое описание закона распределения  .
.

Рисунок 1.5

Рисунок 1.6

 (1.13)
(1.13)
Рисунок 1.7

 (1.14)
(1.14)
Рисунок 1.8
На практике числовые характеристики случайной погрешности приходится находить путем соответствующей математической обработки результатов измерений. Для нахождения числовых характеристик случайной погрешности измерения должны быть многократными (статистическими), т.е. необходимо n раз провести измерение одного и того же значения измеряемой ФВ и получить ряд результатов измерений в виде:  .
.
Если все результаты полученного ряда исправлены (т.е. не содержат систематических погрешностей), то пользуясь правилами теории вероятностей можно найти действительное значение измеряемой ФВ и числовые характеристики случайной погрешности. При этом следует учитывать тот факт, что числовые характеристики  и
и  находятся всегда на основании ограниченного ряда результатов измерений (на практике n всегда конечное число, т.е.
находятся всегда на основании ограниченного ряда результатов измерений (на практике n всегда конечное число, т.е.  ). Поэтому в результате вычислений при обработке результатов измерений находим не теоретические значения
). Поэтому в результате вычислений при обработке результатов измерений находим не теоретические значения  и
и 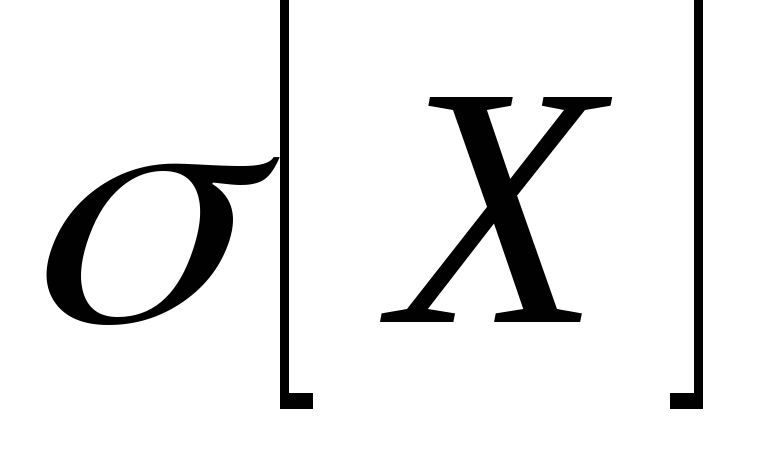 , а их оценки. Для того, чтобы подчеркнуть этот факт, оценки, в отличии от теоретических значений числовых характеристик, обозначаются другими символами. Для вычисления оценок в соответствии с ГОСТ 8.207-76 используются следующие формулы:
, а их оценки. Для того, чтобы подчеркнуть этот факт, оценки, в отличии от теоретических значений числовых характеристик, обозначаются другими символами. Для вычисления оценок в соответствии с ГОСТ 8.207-76 используются следующие формулы:
 ; (1.16)
; (1.16)
 . (1.17)
. (1.17)
где  - среднее арифметическое значение результатов серии из n измерений (оценка математического ожидания результата измерений), оценка действительного значения измеряемой ФВ;
- среднее арифметическое значение результатов серии из n измерений (оценка математического ожидания результата измерений), оценка действительного значения измеряемой ФВ;
 - оценка средней квадратической погрешности единичного измерения в ряду равноточных измерений.
- оценка средней квадратической погрешности единичного измерения в ряду равноточных измерений.
Средняя квадратическая погрешность  и ее оценка
и ее оценка  , полученная путем обработки опытных данных, является основным показателем точности применительно к случайным погрешностям измерений. Но кроме этого показателя иногда (например, в экспериментальной физике) применяются и другие показатели точности: средняя абсолютная погрешность (САП), мера точности. Соотношения между этими показателями для нормального распределения следующие:
, полученная путем обработки опытных данных, является основным показателем точности применительно к случайным погрешностям измерений. Но кроме этого показателя иногда (например, в экспериментальной физике) применяются и другие показатели точности: средняя абсолютная погрешность (САП), мера точности. Соотношения между этими показателями для нормального распределения следующие:
Вероятная погрешность -  ,
,
 ,
,
погрешность, соответствующая доверительному интервалу при  ;
;
Средняя арифметическая погрешность (САП) -  ,
,
 (теоретическое значение),
(теоретическое значение),
 оценка САП по экспериментальным данным для большого количества наблюдений, или
оценка САП по экспериментальным данным для большого количества наблюдений, или
 оценка САП при малом количестве экспериментальных данных;
оценка САП при малом количестве экспериментальных данных;
Мера точности -  ,
,
 .
.
Точность оценок, полученных по формулам (1.16) и (1.17) растет с увеличением n и в пределе (при  ) они стремятся к теоретическим значениям числовых характеристик.
) они стремятся к теоретическим значениям числовых характеристик.
Поскольку при вычислении по формуле (1.16) получаем оценку математического ожидания  и эту оценку принимаем за результат измерения, необходимо знать степень разброса величины
и эту оценку принимаем за результат измерения, необходимо знать степень разброса величины  относительно
относительно  . Характеристикой меры разброса служит оценка средней квадратической погрешности среднего арифметического -
. Характеристикой меры разброса служит оценка средней квадратической погрешности среднего арифметического -  , вычисляемая по формуле:
, вычисляемая по формуле:
 . (1.18)
. (1.18)
Как следует из (1.18) средняя квадратическая погрешность среднего арифметического  в
в  раз меньше средней квадратической погрешности единичного измерения
раз меньше средней квадратической погрешности единичного измерения  .
.
Полученные в соответствии с (1.17) и (1.18) оценки СКП имеют размерность измеряемой ФВ, т.е. выражены в абсолютной форме. Для выражения этих оценок в относительной форме следует поступать по общему правилу (см.(1.3)), т.е.:
 ;
;  .
.
 и
и  могут быть выражены как безразмерным числом, так и в процентах, что чаще всего и бывает.
могут быть выражены как безразмерным числом, так и в процентах, что чаще всего и бывает.
Полученные по формулам (1.16 - 1.18) числовые характеристики выражаются определенным числом и называются точечными оценками.
С использование точечных оценок результат измерения с учетом случайной погрешности может быть представлен в виде :
 . (1.19)
. (1.19)
Такая запись говорит о том, что действительное значение измеряемой ФВ может находиться в интервале значений  до
до  . Вероятность этого события пока не определена. Более того, результат измерения может находиться и вне интервала ограниченного значения
. Вероятность этого события пока не определена. Более того, результат измерения может находиться и вне интервала ограниченного значения  и
и  . Вероятность этого события также пока не определена. Более полную информацию о действительном значении измеряемой величины дает представление результата измерения в виде доверительного интервала при заданной доверительной вероятности
. Вероятность этого события также пока не определена. Более полную информацию о действительном значении измеряемой величины дает представление результата измерения в виде доверительного интервала при заданной доверительной вероятности  .
.
Для результата измерения доверительным называется интервал, который с заданной вероятностью, называемой доверительной вероятностью ( ), включает действительное значение измеряемой ФВ, т.е. это интервал значений (
), включает действительное значение измеряемой ФВ, т.е. это интервал значений ( ,
,  ), для которого
), для которого
 (1.20)
(1.20)
Для случайной погрешности доверительным интервалом называется интервал значений случайной погрешности, внутри которого с заданной вероятностью находится искомое значение погрешности  , т.е.
, т.е.
 . (1.21)
. (1.21)
При определении доверительных интервалов доверительной вероятностью задаются (если она не задана условиями измерительной задачи). В зависимости от условий измерений и конкретных требований  принимают, например, равной от 0.9 до 0.999. Чем больше принятое значение
принимают, например, равной от 0.9 до 0.999. Чем больше принятое значение  , тем более надежно будет оценен интервал, но тем шире будут его границы, т.е. надежность оценок (
, тем более надежно будет оценен интервал, но тем шире будут его границы, т.е. надежность оценок ( ,
,  ) будет выше. Для технических измерений при нормальном законе распределения в большинстве случаев достаточной считается величина
) будет выше. Для технических измерений при нормальном законе распределения в большинстве случаев достаточной считается величина  .
.
Следует заметить, что точечная оценка  , полученная на основании экспериментальных данных при ограниченном числе измерений n остается случайной величиной (так, например, если обработать другую выборку результатов измерения той же ФВ с другим числом измерений
, полученная на основании экспериментальных данных при ограниченном числе измерений n остается случайной величиной (так, например, если обработать другую выборку результатов измерения той же ФВ с другим числом измерений  , то получим новую оценку
, то получим новую оценку  , немного отличающуюся от
, немного отличающуюся от  ). Следовательно может быть рассмотрена задача о определении доверительного интервала для оценки средней квадратической погрешности среднего арифметического
). Следовательно может быть рассмотрена задача о определении доверительного интервала для оценки средней квадратической погрешности среднего арифметического  при некоторой доверительной вероятности. Методику определения доверительного интервала для
при некоторой доверительной вероятности. Методику определения доверительного интервала для  , при необходимости, можно найти в [5, 6].
, при необходимости, можно найти в [5, 6].
При определении характеристик случайной погрешности приходиться решать как задачи определения доверительных границ СКП при заданной доверительной вероятности, так и обратную задачу, определения доверительной вероятности  с которой СКП не выйдет за границы заданного (симметричного или несимметричного) интервала при заданном законе распределения случайной погрешности.
с которой СКП не выйдет за границы заданного (симметричного или несимметричного) интервала при заданном законе распределения случайной погрешности.
Границы симметричного доверительного интервала ( ), за пределы которого с заданной доверительной вероятностью не выходят случайные погрешности результата статистических измерений, определяют в соответствии с выражением:
), за пределы которого с заданной доверительной вероятностью не выходят случайные погрешности результата статистических измерений, определяют в соответствии с выражением:
 , (1.22)
, (1.22)
где  - безразмерный коэффициент, определяемый задаваемой доверительной вероятностью (
- безразмерный коэффициент, определяемый задаваемой доверительной вероятностью ( ) и видом закона распределения случайных погрешностей.
) и видом закона распределения случайных погрешностей.
При несимметричном задании доверительного интервала говорят о нижней -  и верхней -
и верхней -  границах интервала для случайной погрешности результата измерений. Выражение (1.21) в этом случае следует записать в виде:
границах интервала для случайной погрешности результата измерений. Выражение (1.21) в этом случае следует записать в виде:
 ,
,
а вероятность того, что случайная погрешность окажется внутри указанного интервала определяется в общем случае в соответствии с выражением
 (1.23)
(1.23)
Для случайной погрешности, распределенной по нормальному закону, выражение (1.23), с использованием нормированной функции нормального распределения (1.11), можно записать в виде:
 , (1.24)
, (1.24)
где  - значение безразмерного коэффициента для нижней границы доверительного интервала;
- значение безразмерного коэффициента для нижней границы доверительного интервала;
 - значение того же коэффициента для верхней границы доверительного интервала. Для симметричного интервала (
- значение того же коэффициента для верхней границы доверительного интервала. Для симметричного интервала ( ) (1.24) можно переписать в виде:
) (1.24) можно переписать в виде:
 . (1.25)
. (1.25)
Интеграл вида:
 (1.26)
(1.26)
называется нормированной функцией Лапласа или интегралом вероятностей. Значения этого интеграла или интеграла вида (1.25) для различных значений аргумента приводятся в справочных таблицах (см. таблицу 1 приложения в методических указаниях), с использованием которых можно решить прямую и обратную задачи определения характеристик случайной погрешности, распределенной по нормальному закону. При этом не следует забывать, что пользуясь табличными значениями интеграла вида (1.25) находим полную вероятность попадания в симметричный интервал с границами 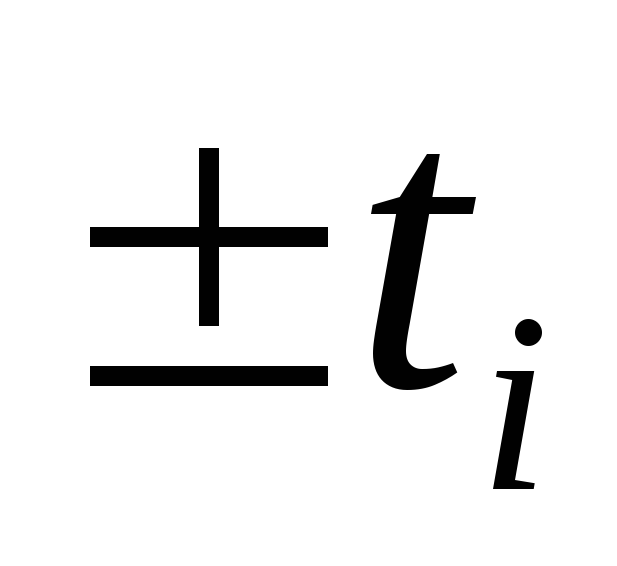 , а пользуясь табличными значениями интеграла вида (1.26) - только половину полной вероятности для одной части симметричного доверительного интервала. При решении этих задач можно использовать также таблицы значений нормированной интегральной функции нормального распределения вида:
, а пользуясь табличными значениями интеграла вида (1.26) - только половину полной вероятности для одной части симметричного доверительного интервала. При решении этих задач можно использовать также таблицы значений нормированной интегральной функции нормального распределения вида:
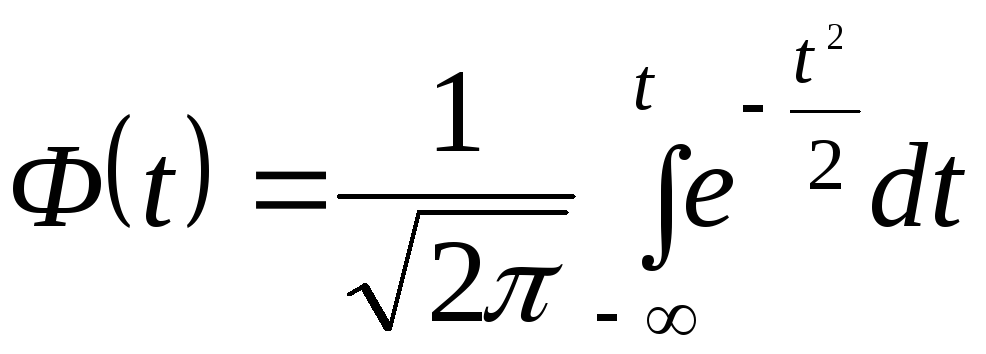 (1.27)
(1.27)
С использованием табличных значений функции  (см. таблицу 2 приложения в методических указаниях) выражение (1.24) для доверительной вероятности нахождения случайной погрешности внутри несимметричного интервала от
(см. таблицу 2 приложения в методических указаниях) выражение (1.24) для доверительной вероятности нахождения случайной погрешности внутри несимметричного интервала от  до
до  записывается следующим образом:
записывается следующим образом:
 (1.28)
(1.28)
Табличными значениями нормированной функции Лапласа удобно пользоваться для решения задач при симметричном задании доверительного интервала, а табличными значениями нормированной интегральной функции - при несимметричном.
При определении числовых характеристик случайной погрешности по результатам эксперимента табличные значения интегралов вида (1.25) и (1.28) следует использовать в том случае, если количество наблюдений в выборке достаточно велико ( ). При малом n точечные оценки случайной погрешности сами становятся случайными величинами. Учитывая это, выражение (1.12) для нормированного отклонения результата измерений от действительного значения при
). При малом n точечные оценки случайной погрешности сами становятся случайными величинами. Учитывая это, выражение (1.12) для нормированного отклонения результата измерений от действительного значения при  следует записать в виде:
следует записать в виде:
 . (1.29)
. (1.29)
Использование символа  в (1.29) подчеркивает тот факт, что нормированное отклонение определено с использованием оценок (
в (1.29) подчеркивает тот факт, что нормированное отклонение определено с использованием оценок ( и
и  ) полученных при обработке выборки малого объема.
) полученных при обработке выборки малого объема.
Величина  , таким образом, является некоторой функцией числа наблюдений в выборке n. Следовательно и границы доверительного интервала определяемые в соответствии с (1.22) будут зависеть не только от доверительной вероятности, но и от числа наблюдений n. Закон распределения случайной величины
, таким образом, является некоторой функцией числа наблюдений в выборке n. Следовательно и границы доверительного интервала определяемые в соответствии с (1.22) будут зависеть не только от доверительной вероятности, но и от числа наблюдений n. Закон распределения случайной величины  отличается от нормального и называется распределением Стьюдента. Это различие существенно при малых n, а при
отличается от нормального и называется распределением Стьюдента. Это различие существенно при малых n, а при  распределение Стьюдента полностью совпадает с нормальным. Таким образом, при обработке результатов статистических измерений при малом количестве наблюдений (
распределение Стьюдента полностью совпадает с нормальным. Таким образом, при обработке результатов статистических измерений при малом количестве наблюдений ( ) доверительный интервал следует определять с использованием распределения Стьюдента. Чтобы подчеркнуть, что в этом случае коэффициент t в (1.22) зависит не только от доверительной вероятности
) доверительный интервал следует определять с использованием распределения Стьюдента. Чтобы подчеркнуть, что в этом случае коэффициент t в (1.22) зависит не только от доверительной вероятности  , но и от числа наблюдений n, выражение (1.22) записывается в виде:
, но и от числа наблюдений n, выражение (1.22) записывается в виде:
 (1.30)
(1.30)
где  - коэффициент, определяемый по таблицам распределения Стьюдента при выбранной доверительной вероятности для конкретного количества наблюдений n.
- коэффициент, определяемый по таблицам распределения Стьюдента при выбранной доверительной вероятности для конкретного количества наблюдений n.
Распределение Стьюдента также табулировано и значения коэффициента  при выбранной доверительной вероятности для каждого конкретного значения n можно определить по таблице 4 (см. приложение в методических указаниях).
при выбранной доверительной вероятности для каждого конкретного значения n можно определить по таблице 4 (см. приложение в методических указаниях).
Формулой (1.22) для определения границ симметричного доверительного интервала можно пользоваться при любом законе распределения случайной погрешности, если имеются таблицы соответствующего закона распределения аналогичные таблицам 1 и 2 (см. приложение в методических указаниях). К сожалению, для других законов распределения (кроме нормального) такие таблицы не получили широкого применения. Но анализ интегральных кривых различных законов распределения обнаружил уникальное свойство доверительного интервала, соответствующего доверительной вероятности  . Оказалось, что для широкого класса симметричных распределений (нормального, равномерного, треугольного, трапецеидального, экспоненциального и даже ряда двухмодальных законов) с погрешностью не более 10% границы симметричного доверительного интервала при
. Оказалось, что для широкого класса симметричных распределений (нормального, равномерного, треугольного, трапецеидального, экспоненциального и даже ряда двухмодальных законов) с погрешностью не более 10% границы симметричного доверительного интервала при  равны
равны  [8]. Поэтому ГОСТ 11.001-73 предписывает при отсутствии данных о виде закона распределения определять симметричный доверительный интервал только при
[8]. Поэтому ГОСТ 11.001-73 предписывает при отсутствии данных о виде закона распределения определять симметричный доверительный интервал только при  пользуясь соотношением:
пользуясь соотношением:
 .
.
Таким же образом следует определять доверительный интервал для перечисленных выше законов распределение при отсутствии таблиц соответствующего распределения.
Результат измерений с многократными наблюдениями, при указании случайной погрешности в виде симметричного доверительного интервала должен быть представлен в виде:
 (1.31)
(1.31)
Как уже отмечалось, ряд экспериментальных данных, полученных при многократном измерении одного и того же значения измеряемой ФВ, может содержать результаты, имеющие в своем составе грубые погрешности. Для того, чтобы эти данные не искажали результат измерений, их следует исключить до того, как будет определяться оценка  и доверительный интервал
и доверительный интервал  (или
(или  ). Эта процедура называется исключением грубых погрешностей. Статистический критерий обнаружения грубых погрешностей разработан для случая, когда группа обрабатываемых данных подчиняется нормальному закону распределения. В этом случае теория вероятностей позволяет при выбранной доверительной вероятности
). Эта процедура называется исключением грубых погрешностей. Статистический критерий обнаружения грубых погрешностей разработан для случая, когда группа обрабатываемых данных подчиняется нормальному закону распределения. В этом случае теория вероятностей позволяет при выбранной доверительной вероятности  рассчитать теоретически допустимые границы максимальных (по модулю) нормированных отклонений для выборки из n наблюдений
рассчитать теоретически допустимые границы максимальных (по модулю) нормированных отклонений для выборки из n наблюдений
 (1.32)
(1.32)
Теоретически допустимые границы  табулированы для различных значений n при разных уровнях доверительной вероятности
табулированы для различных значений n при разных уровнях доверительной вероятности  (или разных уровнях значимости g, где
(или разных уровнях значимости g, где  ). Табличные значения
). Табличные значения  приведены в таблице 3 приложения в методических указаниях.
приведены в таблице 3 приложения в методических указаниях.
Применение статистического критерия обнаружения грубых погрешностей регламентировано ГОСТ 11.002-73 и состоит в следующем. После определения  и
и  для некоторого
для некоторого  , который резко выделяется из общей совокупности обрабатываемых результатов, определяют величину нормированного отклонения
, который резко выделяется из общей совокупности обрабатываемых результатов, определяют величину нормированного отклонения
 . (1.33)
. (1.33)
Задав уровень доверительной вероятности  по таблице 3 (см. приложение в методических указаниях) для числа n, соответствующего обрабатываемой выборке, находят допустимое нормированное отклонение
по таблице 3 (см. приложение в методических указаниях) для числа n, соответствующего обрабатываемой выборке, находят допустимое нормированное отклонение  .
.
Если  , то результат
, то результат  можно отбросить. В противном случае результат должен быть оставлен.
можно отбросить. В противном случае результат должен быть оставлен.
Если после исключения  вызывает сомнение какое-либо другое данное, то указанный порядок действий(определение
вызывает сомнение какое-либо другое данное, то указанный порядок действий(определение  ;
;  и
и  ) повторяют, но уже не учитывая исключенное данное
) повторяют, но уже не учитывая исключенное данное  .
.
Следует подчеркнуть, что если нет достаточных оснований считать обрабатываемую совокупность результатов нормально распределенной, описанный критерий обнаружения грубых погрешностей применять нельзя.
Если о виде распределения опытных данных заранее ничего определенного сказать нельзя, то прежде чем исключать грубые погрешности, определять  и
и 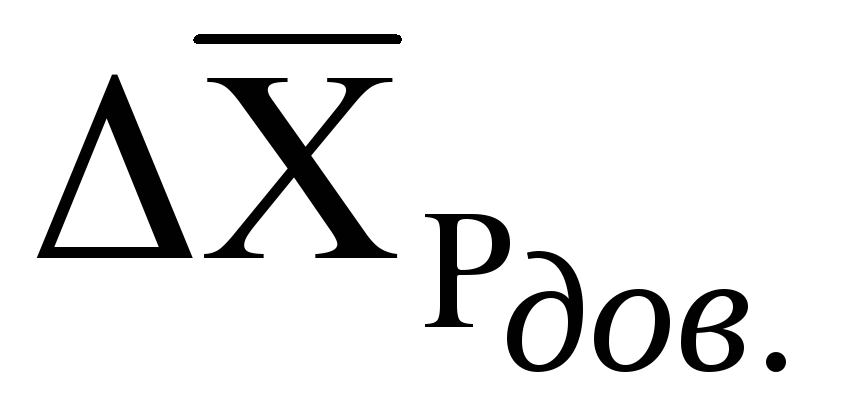 необходимо проверить гипотезу о принадлежности группы экспериментальных данных нормальному распределению. Проверить гипотезу о том, что распределение опытных данных не противоречит теоретическому, можно по ряду критериев. Но следует иметь ввиду, что при n<10 проверить гипотезу о виде распределения экспериментальных данных невозможно. При
необходимо проверить гипотезу о принадлежности группы экспериментальных данных нормальному распределению. Проверить гипотезу о том, что распределение опытных данных не противоречит теоретическому, можно по ряду критериев. Но следует иметь ввиду, что при n<10 проверить гипотезу о виде распределения экспериментальных данных невозможно. При  проверка гипотезы затруднена, в этом случае пользуются, как правило, составным критерием [5]. При достаточно большом числе данных (
проверка гипотезы затруднена, в этом случае пользуются, как правило, составным критерием [5]. При достаточно большом числе данных ( ) лучшим критерием проверки гипотезы о виде распределения является критерий
) лучшим критерием проверки гипотезы о виде распределения является критерий  (или критерий согласия К. Пирсона) [5, 6].
(или критерий согласия К. Пирсона) [5, 6].
Критерий Пирсона используется для проверки согласия распределения предварительно сгруппированных по интервалам опытных данных теоретическому распределению. Идея метода состоит в контроле отклонения гистограммы опытных данных от гистограммы с таким же числом интервалов, построенной на основе теоретического распределения. Мерой расхождения служит сумма квадратов разностей экспериментального количества результатов, попавших в соответствующий интервал, и количества результатов, которые теоретически должны попадать в этот интервал. Сумма квадратов разностей ( ) не должна выходить за границы (
) не должна выходить за границы ( ),определенные по таблицам
),определенные по таблицам  -распределения (таблица 5 см. приложение в методических указаниях) при заданном уровне доверительной вероятности (или уровне значимости
-распределения (таблица 5 см. приложение в методических указаниях) при заданном уровне доверительной вероятности (или уровне значимости  ). Положительный ответ, полученный при использовании критерия согласия
). Положительный ответ, полученный при использовании критерия согласия  , следует трактовать так, что распределение опытных данных не противоречит теоретическому (на соответствие которому проверялось). Но это не означает что оно полностью соответствует теоретическому. При определенной доверительной вероятности критерий
, следует трактовать так, что распределение опытных данных не противоречит теоретическому (на соответствие которому проверялось). Но это не означает что оно полностью соответствует теоретическому. При определенной доверительной вероятности критерий может дать положительный результат и для некоторого другого теоретического закона распределения. Однозначным ответом является лишь отрицательный результат применения критерия
может дать положительный результат и для некоторого другого теоретического закона распределения. Однозначным ответом является лишь отрицательный результат применения критерия  , который трактуется так: распределение опытных данных не соответствует теоретическому, на соответствие которому проверялось. Таким образом при использовании критерия согласия Пирсона следует помнить следующее.
, который трактуется так: распределение опытных данных не соответствует теоретическому, на соответствие которому проверялось. Таким образом при использовании критерия согласия Пирсона следует помнить следующее.
Критерий  позволяет проверить соответствие опытных данных любому (выбранному заранее по каким либо признакам) теоретическому распределению, а не только нормальному. Однако этот критерий (как, впрочем, и другие критерии согласия) не позволяет однозначно установить вид распределения этих данных.
позволяет проверить соответствие опытных данных любому (выбранному заранее по каким либо признакам) теоретическому распределению, а не только нормальному. Однако этот критерий (как, впрочем, и другие критерии согласия) не позволяет однозначно установить вид распределения этих данных.
Методика использования критерия  с необходимыми пояснениями приводится на примере в п.1.3.4.
с необходимыми пояснениями приводится на примере в п.1.3.4.
studfiles.net
14) описание случайных погрешностей с помощью функции распределения
14) Описание случайных погрешностей с помощью функции распределения
Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат наблюдения многих случайных возмущений и сама является случайной величиной
Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.
Рассмотрим формирование дифференциального закона на примере измерений с многократными наблюдениями. Пусть произведено п последовательных наблюдений одной и той же величины х и получена группа наблюдений х1?х2, х3,..., х„. Каждое из значений х,- содержит ту или иную случайную погрешность. Расположим результаты наблюдений в порядке их возрастания, от Xmin до Хmах и найдем размах ряда L = Хmах - Xmin. Разделив размах ряда на к равных интервалов Al = L/k, подсчитаем количество наблюдений пк, попадающих в каждый интервал. Изобразим полученные результаты графически, нанеся на оси абсцисс значения физической величины и обозначив границы интервалов, а по оси ординат — относительную частоту попаданий пк/п . Построив на диаграмме прямоугольники, основанием которых является ширина интервалов, а высотой пк /п, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте. На рис. 2.4 показана полученная в од-
ном из опытов гистограмма, построенная на основании результатов 50 наблюдений, сгруппированных в табл. 2.1.


В данном опыте в первый и последующие интервалы попадает соответственно 0,1; 0,2; 0,36; 0,22 и 0,12 от общего количества наблюдений; при этом очевидно, что сумма этих чисел равна единице.
Если распределение случайной величины х статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает, что единожды построив гистограмму, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам. Приняв общую площадь, ограниченную контуром гистограммы и осью абсцисс, за единицу, S0 = 1, относительную частоту попаданий результатов наблюдений в тот или иной интервал можно определить как отношение площади соответствующего прямоугольника шириной А/ к общей площади.
При бесконечном увеличении числа наблюдений п -> со и бесконечном уменьшении ширины интервалов Д/ -> 0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую

Дх) (рис. 2.5), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее, — дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде -
 Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х{ до х2
Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х{ до х2 
Графически эта вероятность выражается отношением площади, лежащей под кривой fix) в интервале от х{ до х2 к общей площади, ограниченной кривой распределения.
Кроме непрерывных случайных величин в метрологической практике встречаются и дискретные случайные величины. Пример распределения дискретной случайной величины приведен на рис. 2.6.
Для описания частных свойств случайной величины используют числовые характеристики распределений. В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные. Все они представляют собой некоторые средние значения; причем, если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра закона распределения — то центральными.
Начальный момент Ус-го порядка определяется формулами  где Pi—вероятность появления дискретной величины.
где Pi—вероятность появления дискретной величины.
Здесь и ниже первая формула относится к непрерывным, а вторая к дискретным случайным величинам. Из начальных моментов наибольший интерес представляет математическое ожидание случайной величины {к - 1),  Центральные моменты к-ro порядка рассчитываются по формулам
Центральные моменты к-ro порядка рассчитываются по формулам  ...
...  Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.
Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.
15) Числовые параметры законов распределения. Центр распределения вероятности.
Числовые параметры законов распределения
Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются: 1) центр распределения; 2) начальные и центральные моменты и производные от них коэффициенты — математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии; 3) энтропийный коэффициент.
Понятие центра распределения
Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа | от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5: 
Точку Хм называют медианой или 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент.
Можно определить центр распределения как центр тяжести распределения, т.е. такой точки X , относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю: 
Эта точка называется математическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.
При симметричной кривой р(х) в качестве центра может использоваться абсцисса моды, т.е. максимума распределения Хм. Однако существуют распределения, у которых нет моды, например равномерное. Распределения с одним максимумом называются одно модальными, с двумя — двух модальными и т.д. Те из них, у которых в средней части расположен не максимум, а минимум, называются антимодальными. Для двухмодальных распределений применяется оценка центра в виде центра сгибов: где хс1, хс2 — сгибы, т.е. абсциссы точек, в которых распределение достигает своих максимумов. Для ограниченных распределений (равномерного, трапецеидального, арксинусоидального и др.) применяется оценка в виде центра размаха:
где хс1, хс2 — сгибы, т.е. абсциссы точек, в которых распределение достигает своих максимумов. Для ограниченных распределений (равномерного, трапецеидального, арксинусоидального и др.) применяется оценка в виде центра размаха:  где х,, х2 — первый и последний члены вариационного ряда, соответствующего распределению.
где х,, х2 — первый и последний члены вариационного ряда, соответствующего распределению.
Разные оценки центра имеют различную эффективность. При статистической обработке экспериментальных данных важно использовать наиболее эффективную из них, т.е. оценку, имеющую минимальную дисперсию. Это связано с тем, что погрешность в определении Хц влечет за собой неправильную оценку СКО, границ доверительного интервала, эксцесса, контрэксцесса, вида распределения и др., т.е. всех последующих оценок, кроме энтропийных.
16) Моменты распределения вероятности. Математическое ожидание и дисперсия. Коэффициент асимметрии. Эксцесс и контрэксцесс.
Моменты распределений
Все моменты представляют собой некоторые средние значения, причем если усредняются величины, отсчитываемые от начала координат, то моменты называют начальными, а если от центра распределения, то центральными. Начальные и центральные моменты г-го порядка определяются соответственно по формулам 
Нулевой начальный момент равен единице. Он используется  Также с помощью начального момента нулевого порядка вводится понятие медианы распределения. Первый начальный момент — МО случайной величины:
Также с помощью начального момента нулевого порядка вводится понятие медианы распределения. Первый начальный момент — МО случайной величины:  Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины. Начальные и центральные моменты случайной погрешности Л совпадают между собой и с центральными моментами результатов измерений: аг [Л] = цг [А] = Цг [х], поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю. Важное значение имеет второй центральный момент
Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины. Начальные и центральные моменты случайной погрешности Л совпадают между собой и с центральными моментами результатов измерений: аг [Л] = цг [А] = Цг [х], поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю. Важное значение имеет второй центральный момент  называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение
называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение  имеющее такую же размерность, как и МО. Для примера на рис. 6.3 показан вид нормального распределения при различных значениях СКО. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для"более подробного описания распределения используются моменты более высоких порядков.
имеющее такую же размерность, как и МО. Для примера на рис. 6.3 показан вид нормального распределения при различных значениях СКО. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для"более подробного описания распределения используются моменты более высоких порядков.

 служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на рис. 6.4,а.
служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на рис. 6.4,а.
Третий центральный момент

Рис. 6.4. Вид дифференциальной функции распределения при различных значениях коэффициента асимметрии (а) и эксцесса (б)
Четвертый центральный момент  служит для характеристики плоско- или островершинности распределения. Эти свойства описываются с помощью эксцесса
служит для характеристики плоско- или островершинности распределения. Эти свойства описываются с помощью эксцесса 
Значения коэффициента е' лежат в диапазоне от -2 до °°. Для нормального распределения он равен 0. Чаще эксцесс задается формулой  Его значения лежат в диапазоне от 1 до w. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на рис. 6.4,6. Для удобства часто используют контрэксцесс
Его значения лежат в диапазоне от 1 до w. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на рис. 6.4,6. Для удобства часто используют контрэксцесс  Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
17) Законы распределения случайных погрешностей.
Энтропийное значение погрешности Развитие теории вероятностей применительно к процессам получения измерительной информации привело к созданию вероятностной теории информации. С точки зрения этой теории смысл измерения состоит в сужении интервала неопределенности от значения, известного до его проведения, до величины d, называемой энтропийным интервалом неопределенности, ставшей известной после измерения. Энтропийный интервал определяется, по формуле  , где Дэльта Э – энтропийное значение погрешности.
, где Дэльта Э – энтропийное значение погрешности.  — энтропия действительного значения х измеряемой величины вокруг полученного после измерения значения хд, т.е. энтропия погрешности измерений; р(х) — плотность распределения вероятности измеряемой величины.
— энтропия действительного значения х измеряемой величины вокруг полученного после измерения значения хд, т.е. энтропия погрешности измерений; р(х) — плотность распределения вероятности измеряемой величины.
Основное достоинство информационного подхода к описанию измерений состоит в том, что размер энтропийного интервала неопределенности может быть найден строго математически для любого закона распределения. Это устраняет исторически сложившийся произвол, неизбежный при волевом назначении различных значений доверительной вероятности.
Основные законы распределения
Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом: 1) Трапецеидальные (плосковершинные) распределения; 2) уплощеные (приблизительно плосковершинные) распределения; 3) экспоненциальные распределения; 4) семейство распределений Стьюдента; 5) двухмодальные распределения.
Трапецеидальные распределения
К трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение (рис. 6.5,а) описывается уравнением  Трапецеидальное распределение (рис 6.5,6) образуется как композиция двух равномерных распределений шириной а, и а2.
Трапецеидальное распределение (рис 6.5,6) образуется как композиция двух равномерных распределений шириной а, и а2. 
 Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона)
Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона)
Треугольное (Симпсона) распределение (рис. 6.5,в) — это частный случай трапецеидального, для которого размеры исходных равномерных распределений одинаковы.

где Хц> a, b — параметры распределения.
Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон.
Экспоненциальные распределения Экспоненциальные распределения описываются формулой 
где - некоторая характерная для данного распределения константа; Хц — координата центра; Г(х) — гамма-функция. В нормированном виде, т.е. при Хц =0 и оХ= 1,
- некоторая характерная для данного распределения константа; Хц — координата центра; Г(х) — гамма-функция. В нормированном виде, т.е. при Хц =0 и оХ= 1,
 где А(а) — нормирующий множитель распределения.
где А(а) — нормирующий множитель распределения.
Интегральная функция нормированного экспоненциального распределения описывается выражением  Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.
Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.

Рис. 6.6. Экспоненциальные распределения
Нормальное распределение (распределение Гаусса)
Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гауссах  где о — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.
где о — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.
При введении новой переменной t = (х-Хц)/а из (6.6) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:
 Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49]. Определенный интеграл с переменным верхним пределом
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49]. Определенный интеграл с переменным верхним пределом  называют функцией Лапласа. Для нее справедливы следующие равенства:
называют функцией Лапласа. Для нее справедливы следующие равенства:
Ф(-оо) = -0,5; Ф(0) = 0; Ф(+оо) = 0,5; O(t) = -O(t). Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция F(t) связана с функцией Лапласа формулой F(t) = 0,5+Ф(1>). Поскольку интеграл не выражается через элементарные функции, то значения функции Лапласа для различных значений t сведены в таблицу.
Уплощенные распределения
Данные распределения представляют собой композицию равномерного и какого-либо экспоненциального распределения. Уплощенные распределения отличаются от экспоненциальных тем, что при почти плоской вершине имеют длинные, медленно спадающие "хвосты", в то время как экспоненциальные распределения обрываются тем круче, чем более плоской является их вершина
18) Цели и задачи стандартизации. Виды стандартов. Принципы и методы стандартизации.
Понятие стандартизация охватывает широкую область общественной деятельности, включающую в себя научные, технические, хозяйственные, экономические, юридические, эстетические, политические аспекты. В нашей стране действует государственная система стандартизации (ГСС), объединяющая и упорядочивающая работы по стандартизации в масштабе всей страны, на всех уровнях производства и управления на основе комплекса государственных стандартов. Стандартизация – установление и применение правил с целью упорядочения деятельности при участии всех заинтересованных сторон. Стандартизация должна обеспечить возможно полное удовлетворение интересов производителя и потребителя, повышение производительности труда, экономное расходование материалов, энергии, рабочего времени и гарантировать безопасность при производстве и эксплуатации.
Объекты стандартизации: изделия, нормы, правила, требования, методы, термины, обозначения и т.п., имеющие перспективу многократного применения в науке, технике, и т.п.
В зависимости от формы руководства стандартизацией и сферы действия стандартов различают государственную, национальную и международную стандартизацию.
Государственная стандартизация – форма развития и проведения стандартизации, осуществляемая под руководством государственных органов по единым государственным планам стандартизации.
Национальная стандартизация проводится в масштабе государства без государственной формы руководства. Международная стандартизация проводится специальными международными организациями или группой государств с целью облегчения взаимной торговли, научных, технических и культурных связей.
Устанавливаемые при стандартизации нормы оформляются в виде нормативно-технической документации по стандартизации – стандартов и технических условий.
Стандарт – нормативно-технический документ, устанавливающий комплекс норм, правил, требований к объекту стандартизации и утвержденный компетентным органом. Стандарт может быть разработан как на предметы (продукцию, сырье, образцы веществ), так и на нормы, правила, требования к объектам организационно-методического и общетехнического характера труда, порядок разработки документов, нормы безопасности, системы управления качеством и др.
Технические условия (ТУ) – нормативно-технический документ по стандартизации, устанавливающий комплекс требований к конкретным типам, маркам, артикулам продукции. Технические условия являются неотъемлемой частью комплекта технической документации на продукцию, на которую они распространяются.
Цели и задачи стандартизации: 1)установление требований к качеству готовой продукции на основе стандартизации ее качественных характеристик, а также характеристик сырья, материалов, полуфабрикатов и комплектующих изделий; 2) разработка и установление единой системы показателей качества продукции, методов и средств контроля и испытаний, а также необходимого уровня надежности изделий с учетом их назначения и условий эксплуатации; 3) установление норм, требований и методов в области проектирования и производства с целью обеспечения оптимального качества и исключения нерационального многообразия видов, марок и типоразмеров продукции;4) развитие унификации промышленной продукции, повышения уровня взаимозаменяемости, эффективности эксплуатации и ремонта изделий; 5) обеспечение единства и достоверности измерений, создание государственных эталонов единиц физических величин; и т.д.
Виды и методы стандартизации:
Наряду со стандартизацией, осуществляемой в масштабах государства, широко используются:
отраслевая стандартизация, осуществляемая в отдельных отраслях промышленности с целью обеспечения единства технических требований и норм к продукции отрасли и создания условий для кооперации и специализации в этой отрасли. Под отраслью понимается совокупность предприятий и организаций независимо от их территориального расположения и ведомственной принадлежности, разрабатывающих и изготавливающих определенные виды продукции;
республиканская стандартизация, проводимая в союзной республике в целях установления требований и норм на продукцию, не охваченную государственной или отраслевой стандартизацией;
местная стандартизация, проводимая на предприятиях (в объединениях) и устанавливающая требования, нормы и правила, применяемые только на данном предприятии.
В зависимости от последующего влияния на развитие народного хозяйства можно выделить три вида стандартизации, принципиально отличающиеся подходом к установлению в стандартах соответствующих норм: 1) стандартизация по достигнутому уровню, устанавливающая показатели, отражающие свойства существующей и освоенной в производстве продукции, и таким образом фиксирующая достигнутый уровень производства; 2) опережающая стандартизация, заключающаяся в установлении повышенных по отношению к уже достигнутому на практике уровню норм; 3) комплексная стандартизация, при которой для оптимального решения конкретной проблемы осуществляется целенаправленное и планомерное установление и применение системы взаимосвязанных требований как к самому объекту комплексной стандартизации в целом, так и к его основным элементам.
В зависимости от метода решения основной задачи различают несколько форм стандартизации.
Симплификация – форма стандартизации, заключающаяся в простом сокращении числа применяемых при разработке изделия или при его производстве марок полуфабрикатов, комплектующих изделий и т.п. до количества, технически и экономически целесообразного, достаточного для выпуска изделий с требуемыми показателями качества. Унификация – рациональное уменьшение числа типов, видов и размеров объектов одинакового функционального назначения. Типизация – это разновидность стандартизации, заключающаяся в разработке и установлении типовых решений (конструктивных, технологических, организационных и т. п.) на основе наиболее прогрессивных методов и режимов работы. Агрегатирование – метод создания новых машин, приборов и другого оборудования путем компоновки конечного изделия из ограниченного набора стандартных и унифицированных узлов и агрегатов, обладающих геометрической и функциональной взаимозаменяемостью.
refdb.ru
Случайные погрешности, Распределения случайных величин - Метрология, стандартизация и сертификация
5. Случайные погрешности
Случайные погрешности представляют собой погрешности, в появлении каждой из которых не наблюдается какой-либо закономерности. Случайные погрешности неизбежны и неустранимы и всегда присутствуют в результате измерения. Они вызывают рассеяние результатов при многократном и достаточно точном измерении одной и той же величины при неизменных условиях, вызывая различие их в последних значащих цифрах (результаты многократных измерений одной и той же постоянной величины в одних и тех же условиях с помощью одного и того же измерительного устройства одним и тем же оператором могут отличаться друг от друга).
Каждая случайная погрешность возникает в результате воздействия многих факторов, каждый из которых сам по себе не оказывает значительного влияния на результат.
Так как случайные погрешности не поддаются исключению из результатов измерений, то при рассмотрении их влияния на результат измерений задача сводится к изучению свойств совокупностей результатов отдельных наблюдений.
Природа и физическая сущность случайных и систематических составляющих погрешности измерений различна. Однако оценки неисключенных остатков систематических погрешностей и случайных погрешностей осуществляются на основе обработки статистического материала, представляющего собой совокупность результатов измерений.
Для изучения случайных погрешностей используются методы теории вероятностей и математической статистики. Эти методы применимы и для неисключенных систематических составляющих.
5.1. Распределения случайных величин
Дискретные и непрерывные случайные величины. По своей физической природе измеряемые величины могут быть детерминированными и случайными.
Дискретной (прерывной) называют случайную величину, отдельные значения которой можно перенумеровать.
Примерами дискретных случайных величин являются число изделий, отказавших в процессе испытаний, количество бракованных деталей в партии и т. д.
Непрерывной называют случайную величину, возможные значения которой непрерывно заполняют некоторый промежуток. Примеры непрерывных случайных величин: отклонение размера изготовленной детали от номинала, погрешность измерения, величина отклонения формы детали, высота микронеровностей в данной точке поверхности и т. д.
Случайная величина не может характеризоваться каким-то одним значением. Для нее необходимо обязательно указать множество возможных значений и вероятностные характеристики, заданные на этом множестве.
Дискретные случайные величины полностью характеризуются вероятностями своих отдельных значений

Равенство X = хк является случайным событием.
Так как равенства X = хк образуют полную группу событий, то

Вероятностным описанием случайной величины является закон ее распределения.
Законом распределения случайной величины называют соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может быть задан в различной форме. Простейшей формой задания закона распределения является таблица, в которой перечислены в порядке возрастания все возможные значения дискретной случайной величины и соответствующие им вероятности, например:

Такую таблицу называют рядом распределения. Графическое изображение ряда распределения называют полигоном распределения случайной величины (рис. 5.1).
Задание функции распределения является обшей формой закона распределения как для дискретных, так и для непрерывных случайных величин. Функцию распределения можно задать в виде интегрального закона распределения (функция распределения) и в виде дифференциального закона распределения (плотность вероятности).
Функцией распределения случайной величины X называют вероятность выполнения неравенства X< х

где х - неслучайный аргумент.

Рис. 5.1. График распределения вероятностей дискретной случайной величины
Функция распределения F(x) должна быть неубывающей функцией своего аргумента, т. е. F(-
На рис. 5.2 приведены графики функции распределения F(x) для дискретной (5.2, а) и непрерывной (5.2, б) случайных величин.

Рис. 5.2. Функции распределения дискретной: а) и непрерывной б) случайных величин
Плотностью вероятности непрерывной случайной величины называют производную функцию распределения

Плотность вероятности со(х) обладает следующими свойствами: ср(х) > 0 - неотрицательна;

Функция распределения F(x) выражается через плотность вероятности (р (х)

Функция распределения Я", как и вероятность, есть величина безразмерная, а плотность вероятности имеет размерность, обратную размерности случайной величины.
Вероятность попадания непрерывной случайной величины на заданный интервал (а, Ь) определяется выражением

Геометрически эта вероятность равна площади криволинейной трапеции, ограниченной кривой распределения, осью абсцисс и прямыми х = а и х = Ь (рис. 5.3).

Рис. 5.3. Одно- (а) и двухмодальное (б) распределение вероятности случайной величины х
geum.ru
 , рассматривают ряд интервалов
, рассматривают ряд интервалов  значений этой величины и подсчитывают частоты
значений этой величины и подсчитывают частоты  попадания значений величины
попадания значений величины  в каждый интервал
в каждый интервал  . Таблица, в которой приведены интервалы в порядке их распределения вдоль оси абсцисс и соответствующие им частоты, называется статистическим рядом (табл.1).
. Таблица, в которой приведены интервалы в порядке их распределения вдоль оси абсцисс и соответствующие им частоты, называется статистическим рядом (табл.1).







 ри увеличении числа опытов (измерений) и уменьшении интервала разбиения оси абсцисс гистограмма теряет свой ступенчатый характер и стремится (переходит) к плавной кривой (рис. 2). Такую кривую называют кривой плотности распределения для данной случайной величины, а уравнение, описывающее эту кривую, называется законом распределения случайной величины.
ри увеличении числа опытов (измерений) и уменьшении интервала разбиения оси абсцисс гистограмма теряет свой ступенчатый характер и стремится (переходит) к плавной кривой (рис. 2). Такую кривую называют кривой плотности распределения для данной случайной величины, а уравнение, описывающее эту кривую, называется законом распределения случайной величины. читается, что случайная величина полностью определена, если известен закон её распределения. Этот закон может быть представлен (задан) в интегральной или дифференциальной форме. Интегральный закон распределения случайной величины обозначается символом
читается, что случайная величина полностью определена, если известен закон её распределения. Этот закон может быть представлен (задан) в интегральной или дифференциальной форме. Интегральный закон распределения случайной величины обозначается символом  и называется функцией распределения. Производная функция от
и называется функцией распределения. Производная функция от  называется плотностью вероятности случайной величины X или дифференциальным законом распределения:
называется плотностью вероятности случайной величины X или дифференциальным законом распределения: .
. (можно писать
(можно писать  ) и дисперсию
) и дисперсию  (можно писать
(можно писать ).
). математическое ожидание вычисляется по формуле
математическое ожидание вычисляется по формуле . (3)
. (3) . (4)
. (4) и называется средним квадратическим отклонением (сокращенно с. к. о.):
и называется средним квадратическим отклонением (сокращенно с. к. о.): . (5)
. (5) в качестве оценки
в качестве оценки  принимают среднее арифметическое наблюденных (измеренных) значений
принимают среднее арифметическое наблюденных (измеренных) значений  , т. е.
, т. е. . (6)
. (6) . (7)
. (7) само является случайной величиной, так как вычисляется на основании ограниченного числа опытов. Разброс значений величины характеризуют средним квадратическим отклонением , которое связало с упомянутым выше
само является случайной величиной, так как вычисляется на основании ограниченного числа опытов. Разброс значений величины характеризуют средним квадратическим отклонением , которое связало с упомянутым выше  соотношением:
соотношением: . (8)
. (8) . (9)
. (9) и
и 
 и
и  ) существенно зависят от вида предполагаемого закона распределения рассматриваемой случайной величины.
) существенно зависят от вида предполагаемого закона распределения рассматриваемой случайной величины. этот закон можно записать в виде:
этот закон можно записать в виде: . (10)
. (10) — плотность вероятности;
— плотность вероятности;  и
и  — математическое ожидание и среднее квадратическое отклонение — параметры нормального распределения, физический смысл и способ вычисления которых были пояснены выше.
— математическое ожидание и среднее квадратическое отклонение — параметры нормального распределения, физический смысл и способ вычисления которых были пояснены выше.
 с надежностью=0,57, (1)
с надежностью=0,57, (1) – средняя величинаnизмеренных значений искомой величины,
– средняя величинаnизмеренных значений искомой величины,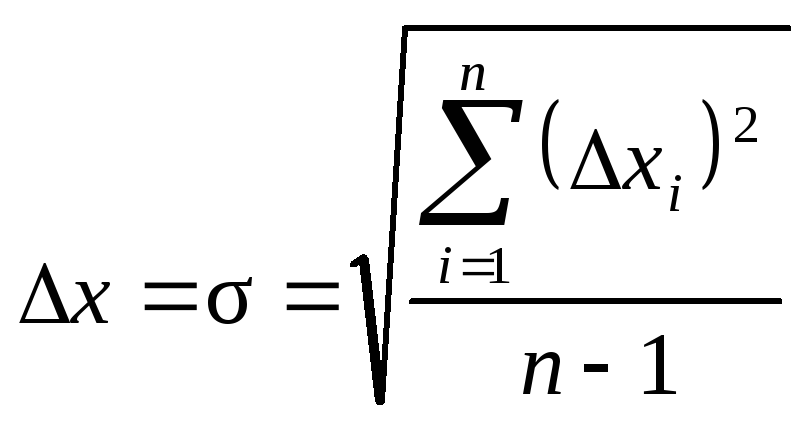 , с надежностью=0,68; (2)
, с надежностью=0,68; (2) ;
; ;
; (3)
(3)
 , (4)
, (4) (5)
(5) , то получим кривую, которая называется графиком распределения Гаусса. На рисунке 2 показаны графики распределения Гаусса с разной дисперсией.
, то получим кривую, которая называется графиком распределения Гаусса. На рисунке 2 показаны графики распределения Гаусса с разной дисперсией.
 . (6)
. (6) 0,02 с надежностью=Р.
0,02 с надежностью=Р. .
. , (7)
, (7)
 - плотность распределения вероятности СП.
- плотность распределения вероятности СП.
 .
. ).
).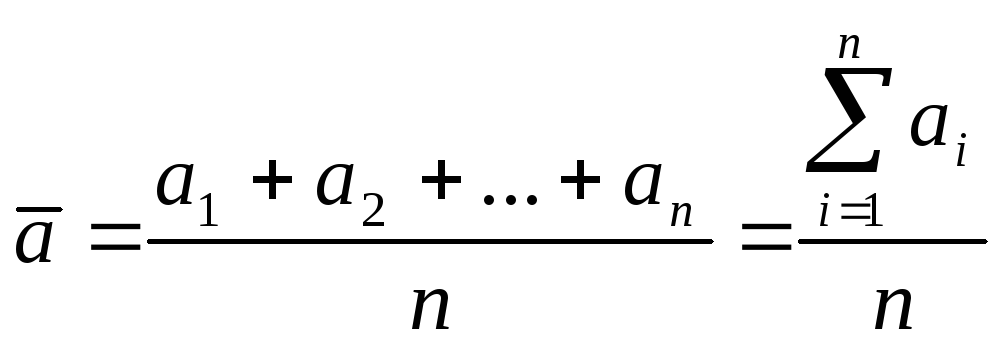 ,
,  - средне арифметическое.
- средне арифметическое.





 , то
, то и
и
 - если отсутствует систематическая погрешность.
- если отсутствует систематическая погрешность. , то из ряда измерений вычитают систематическую погрешность и ряд называетсяисправным.
, то из ряда измерений вычитают систематическую погрешность и ряд называетсяисправным. - дисперсия средне арифметического вn-раз меньше дисперсии ряда измерений или
- дисперсия средне арифметического вn-раз меньше дисперсии ряда измерений или 
 - средне квадратичное отклонение в
- средне квадратичное отклонение в меньше средне квадратичного отклонения ряда измерений.
меньше средне квадратичного отклонения ряда измерений.


 осью абсцисс и вертикальными линиями соответствующих доверительному интервалу. Результат измерения может быть представлен в виде:
осью абсцисс и вертикальными линиями соответствующих доверительному интервалу. Результат измерения может быть представлен в виде:
 , где
, где  - функция Лапласса.
- функция Лапласса.

 .
. , то пренебрегают и считают, что погрешность только случайная.
, то пренебрегают и считают, что погрешность только случайная. , то пренебрегают СП, т.е. остается только систематическая погрешность.
, то пренебрегают СП, т.е. остается только систематическая погрешность. , то границы погрешности находят по формуле из справочника.
, то границы погрешности находят по формуле из справочника. Присутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения.
Присутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения. Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения.
Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения. <xi≤x}
<xi≤x} График интегральной функции распределения показан на рис. 1. Она имеет следующие свойства:
График интегральной функции распределения показан на рис. 1. Она имеет следующие свойства: ) = 0; F(+
) = 0; F(+ ) = 1;
) = 1;
 Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2)
Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х1; х2)
 Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величиныхв интервал [-
Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величиныхв интервал [- ; +
; + ] равна единице, т.е. представляет собой достоверное событие.
] равна единице, т.е. представляет собой достоверное событие. Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (x1;х2) равна площади, заключенной под кривой р(х) между абсциссами х1и х2(рис. 1).
Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (x1;х2) равна площади, заключенной под кривой р(х) между абсциссами х1и х2(рис. 1).
 Общие сведения.Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются:
Общие сведения.Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются: - центр распределения;
- центр распределения; - начальные и центральные моменты и производные от них коэффициенты - математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии;
- начальные и центральные моменты и производные от них коэффициенты - математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии; - энтропийный коэффициент.
- энтропийный коэффициент. Понятие центра распределения.Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:
Понятие центра распределения.Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:
 Точку ХMназываютмедианойили 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент.
Точку ХMназываютмедианойили 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент. Можно определить центр распределения как центр тяжести распределения, т.е. такой точки
Можно определить центр распределения как центр тяжести распределения, т.е. такой точки , относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:
, относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:
 Эта точка называетсяматематическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.
Эта точка называетсяматематическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.


 совпадают между собой и с центральными моментами результатов измерений:
совпадают между собой и с центральными моментами результатов измерений: , поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю.Важное значение имеет второй центральный момент
, поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю.Важное значение имеет второй центральный момент


 Отдельные значения случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняется определенным закономерностям, которые являются вероятностными. Они описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину.
Отдельные значения случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняется определенным закономерностям, которые являются вероятностными. Они описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину.
 ри этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения случайной погрешности в данной точке. Плотность вероятности для закона распределения описывается уравнением:
ри этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения случайной погрешности в данной точке. Плотность вероятности для закона распределения описывается уравнением:
 (9)
(9) (10)
(10) - случайная погрешность.
- случайная погрешность. еометрическиσопределяется как расстояние от оси симметрии нормального распределения до точкиАперегиба кривой распределения (Рис.6,7).
еометрическиσопределяется как расстояние от оси симметрии нормального распределения до точкиАперегиба кривой распределения (Рис.6,7). (11)
(11) Третий центральный момент
Третий центральный момент
 . Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на(рис. а)
. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на(рис. а)
 Четвертый центральный момент
Четвертый центральный момент

 Значения коэффициента
Значения коэффициента лежат в диапазоне от -2 до
лежат в диапазоне от -2 до . Для нормального распределения он равен 0. Чаще эксцесс задается формулой
. Для нормального распределения он равен 0. Чаще эксцесс задается формулой
 Его значения лежат в диапазоне от 1 до
Его значения лежат в диапазоне от 1 до . Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на(рис. б).
. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на(рис. б).
 Для удобства часто используютконтрэксцесс
Для удобства часто используютконтрэксцесс
 Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577. Общие сведения.Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего, предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом:
Общие сведения.Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего, предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом: - трапецеидальные (плосковершинные) распределения;
- трапецеидальные (плосковершинные) распределения; - уплощеные (приблизительно плосковершинные) распределения;
- уплощеные (приблизительно плосковершинные) распределения; - экспоненциальные распределения;
- экспоненциальные распределения; - семейство распределений Стьюдента;
- семейство распределений Стьюдента; - двухмодальные распределения.
- двухмодальные распределения. Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение(рис. а)описывается уравнением
Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение(рис. а)описывается уравнением

 Трапецеидальное распределение(рис. б)
Трапецеидальное распределение(рис. б)
 Треугольное (Симпсона) распределение(рис. в)
Треугольное (Симпсона) распределение(рис. в)
 Математическое ожидание всех трапецеидальных распределений Хц=(х1+х2)/2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а.
Математическое ожидание всех трапецеидальных распределений Хц=(х1+х2)/2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а. Среднее квадратическое отклонение в зависимости от распределения определяется по формуле:
Среднее квадратическое отклонение в зависимости от распределения определяется по формуле: - равномерное
- равномерное
 - трапецеидальное
- трапецеидальное
 - треугольное
- треугольное .
. Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл.
Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл.
 Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон.
Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон. Экспоненциальные распределенияЭкспоненциальные распределения описываютсяформулой 1
Экспоненциальные распределенияЭкспоненциальные распределения описываютсяформулой 1
 где
где ;
; - СКО;
- СКО; - некоторая характерная для данного распределения константа; Хц - координата центра; Г(х) - гамма-функция. В нормированном виде, т.е. при Хц = О и
- некоторая характерная для данного распределения константа; Хц - координата центра; Г(х) - гамма-функция. В нормированном виде, т.е. при Хц = О и = 1,
= 1,
 где А(
где А( ) - нормирующий множитель распределения.
) - нормирующий множитель распределения. Интегральная функция нормированного экспоненциального распределения описывается выражением
Интегральная функция нормированного экспоненциального распределения описывается выражением
 Интеграл, входящий в эту формулу, выражается через элементарные функции только при
Интеграл, входящий в эту формулу, выражается через элементарные функции только при = 1/n, n = 1; 2; 3; ... При
= 1/n, n = 1; 2; 3; ... При = n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам.
= n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам. Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам:
Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам:
 Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При
Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При < 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При
< 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При = 1 получается распределение Лапласа
= 1 получается распределение Лапласа , при
, при = 2 - нормальное распределение или распределение Гаусса. При
= 2 - нормальное распределение или распределение Гаусса. При > 2 распределения, описываемые формулой 1, близки по свойствам к трапецеидальным. При очень больших значениях а формула (1) описывает практически равномерное распределение. В табл. приведены параметры некоторых из экспоненциальных распределений.
> 2 распределения, описываемые формулой 1, близки по свойствам к трапецеидальным. При очень больших значениях а формула (1) описывает практически равномерное распределение. В табл. приведены параметры некоторых из экспоненциальных распределений.
 Вид экспоненциальных распределений при различных значениях показателя
Вид экспоненциальных распределений при различных значениях показателя приведен на(рис).
приведен на(рис).
 (1.5)
(1.5) входит в состав случайной погрешности).
входит в состав случайной погрешности). может иметь как знак “+”, так и знак “-“, а если систематическая погрешность задана в виде границ (как чаще всего и бывает для неисключенных остатков систематической погрешности), то перед значением
может иметь как знак “+”, так и знак “-“, а если систематическая погрешность задана в виде границ (как чаще всего и бывает для неисключенных остатков систематической погрешности), то перед значением 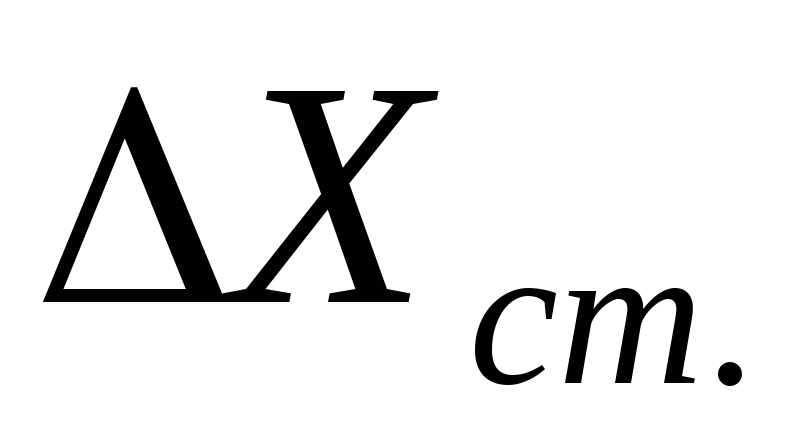 подразумевается знак “” (т.е.
подразумевается знак “” (т.е.  ). Значение случайной погрешности всегда указывается в виде границ (т.е.
). Значение случайной погрешности всегда указывается в виде границ (т.е.  ).
). , записанная в форме (1.5), также становиться случайной величиной, имеющей тот же закон распределения, что и
, записанная в форме (1.5), также становиться случайной величиной, имеющей тот же закон распределения, что и  . Все сказанное в равной мере относится и к результату измерения, если на основании (1.2) и (1.5) его записать в виде
. Все сказанное в равной мере относится и к результату измерения, если на основании (1.2) и (1.5) его записать в виде (1.6)
(1.6) , записанной в виде (1.5), являются
, записанной в виде (1.5), являются
 , (1.7)
, (1.7) - плотность вероятности погрешности
- плотность вероятности погрешности  ;
;
 . (1.8)
. (1.8) , для чисто случайной погрешности (когда
, для чисто случайной погрешности (когда  )
)  .
. и может служить характеристикой точности проведенных измерений, но имеет размерность в единицах измеряемой величины в квадрате. Поэтому в качестве числовой характеристики случайной погрешности чаще используют средне квадратическое отклонение
и может служить характеристикой точности проведенных измерений, но имеет размерность в единицах измеряемой величины в квадрате. Поэтому в качестве числовой характеристики случайной погрешности чаще используют средне квадратическое отклонение 
 (1.9)
(1.9) , вычисленное в соответствии с (1.9), называется средним квадратическим отклонением (СКО) случайной величины
, вычисленное в соответствии с (1.9), называется средним квадратическим отклонением (СКО) случайной величины  , а применительно к погрешностям измерений ее следует называть средней квадратической погрешностью (СКП) результата измерений.
, а применительно к погрешностям измерений ее следует называть средней квадратической погрешностью (СКП) результата измерений. или плотность вероятностей) приведена на рисунке 1.5, а аналитическое выражение этого закона имеет вид:
или плотность вероятностей) приведена на рисунке 1.5, а аналитическое выражение этого закона имеет вид: (1.10)
(1.10) (см. рис. 1.5), но если характеризовать случайную погрешность безразмерным нормированным числом
(см. рис. 1.5), но если характеризовать случайную погрешность безразмерным нормированным числом  (нормировка относительно СКП), то получим кривую нормированного нормального распределения
(нормировка относительно СКП), то получим кривую нормированного нормального распределения  , (1.11)
, (1.11) . (1.12)
. (1.12) ) приведен на рисунке 1.6.
) приведен на рисунке 1.6. ) связана с
) связана с  и зависит от закона распределения. Так, например, для нормального закона максимальная случайная погрешность часто принимается равной (см. рис. 1.6):
и зависит от закона распределения. Так, например, для нормального закона максимальная случайная погрешность часто принимается равной (см. рис. 1.6): . (1.15)
. (1.15) и
и  отличаются от (1.15). Так для равномерного закона распределения
отличаются от (1.15). Так для равномерного закона распределения  ; для треугольного
; для треугольного  соответственно и т.д. [8].
соответственно и т.д. [8]. .
.


 (1.13)
(1.13)
 (1.14)
(1.14) .
. и
и  находятся всегда на основании ограниченного ряда результатов измерений (на практике n всегда конечное число, т.е.
находятся всегда на основании ограниченного ряда результатов измерений (на практике n всегда конечное число, т.е.  ). Поэтому в результате вычислений при обработке результатов измерений находим не теоретические значения
). Поэтому в результате вычислений при обработке результатов измерений находим не теоретические значения  и
и 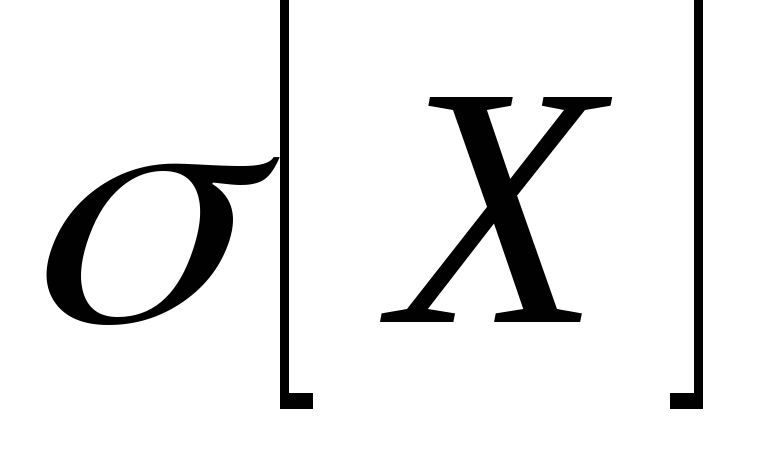 , а их оценки. Для того, чтобы подчеркнуть этот факт, оценки, в отличии от теоретических значений числовых характеристик, обозначаются другими символами. Для вычисления оценок в соответствии с ГОСТ 8.207-76 используются следующие формулы:
, а их оценки. Для того, чтобы подчеркнуть этот факт, оценки, в отличии от теоретических значений числовых характеристик, обозначаются другими символами. Для вычисления оценок в соответствии с ГОСТ 8.207-76 используются следующие формулы: ; (1.16)
; (1.16) . (1.17)
. (1.17) - среднее арифметическое значение результатов серии из n измерений (оценка математического ожидания результата измерений), оценка действительного значения измеряемой ФВ;
- среднее арифметическое значение результатов серии из n измерений (оценка математического ожидания результата измерений), оценка действительного значения измеряемой ФВ; - оценка средней квадратической погрешности единичного измерения в ряду равноточных измерений.
- оценка средней квадратической погрешности единичного измерения в ряду равноточных измерений. и ее оценка
и ее оценка  , полученная путем обработки опытных данных, является основным показателем точности применительно к случайным погрешностям измерений. Но кроме этого показателя иногда (например, в экспериментальной физике) применяются и другие показатели точности: средняя абсолютная погрешность (САП), мера точности. Соотношения между этими показателями для нормального распределения следующие:
, полученная путем обработки опытных данных, является основным показателем точности применительно к случайным погрешностям измерений. Но кроме этого показателя иногда (например, в экспериментальной физике) применяются и другие показатели точности: средняя абсолютная погрешность (САП), мера точности. Соотношения между этими показателями для нормального распределения следующие: ,
, ,
, ;
; ,
, (теоретическое значение),
(теоретическое значение), оценка САП по экспериментальным данным для большого количества наблюдений, или
оценка САП по экспериментальным данным для большого количества наблюдений, или оценка САП при малом количестве экспериментальных данных;
оценка САП при малом количестве экспериментальных данных; ,
, .
. ) они стремятся к теоретическим значениям числовых характеристик.
) они стремятся к теоретическим значениям числовых характеристик. и эту оценку принимаем за результат измерения, необходимо знать степень разброса величины
и эту оценку принимаем за результат измерения, необходимо знать степень разброса величины  относительно
относительно  . Характеристикой меры разброса служит оценка средней квадратической погрешности среднего арифметического -
. Характеристикой меры разброса служит оценка средней квадратической погрешности среднего арифметического -  , вычисляемая по формуле:
, вычисляемая по формуле: . (1.18)
. (1.18) в
в  раз меньше средней квадратической погрешности единичного измерения
раз меньше средней квадратической погрешности единичного измерения  .
. ;
;  .
. и
и  могут быть выражены как безразмерным числом, так и в процентах, что чаще всего и бывает.
могут быть выражены как безразмерным числом, так и в процентах, что чаще всего и бывает. . (1.19)
. (1.19) до
до  . Вероятность этого события пока не определена. Более того, результат измерения может находиться и вне интервала ограниченного значения
. Вероятность этого события пока не определена. Более того, результат измерения может находиться и вне интервала ограниченного значения  и
и  . Вероятность этого события также пока не определена. Более полную информацию о действительном значении измеряемой величины дает представление результата измерения в виде доверительного интервала при заданной доверительной вероятности
. Вероятность этого события также пока не определена. Более полную информацию о действительном значении измеряемой величины дает представление результата измерения в виде доверительного интервала при заданной доверительной вероятности  .
. ), включает действительное значение измеряемой ФВ, т.е. это интервал значений (
), включает действительное значение измеряемой ФВ, т.е. это интервал значений ( ,
,  ), для которого
), для которого (1.20)
(1.20) , т.е.
, т.е. . (1.21)
. (1.21) принимают, например, равной от 0.9 до 0.999. Чем больше принятое значение
принимают, например, равной от 0.9 до 0.999. Чем больше принятое значение  , тем более надежно будет оценен интервал, но тем шире будут его границы, т.е. надежность оценок (
, тем более надежно будет оценен интервал, но тем шире будут его границы, т.е. надежность оценок ( ,
,  ) будет выше. Для технических измерений при нормальном законе распределения в большинстве случаев достаточной считается величина
) будет выше. Для технических измерений при нормальном законе распределения в большинстве случаев достаточной считается величина  .
.  , полученная на основании экспериментальных данных при ограниченном числе измерений n остается случайной величиной (так, например, если обработать другую выборку результатов измерения той же ФВ с другим числом измерений
, полученная на основании экспериментальных данных при ограниченном числе измерений n остается случайной величиной (так, например, если обработать другую выборку результатов измерения той же ФВ с другим числом измерений  , то получим новую оценку
, то получим новую оценку  , немного отличающуюся от
, немного отличающуюся от  ). Следовательно может быть рассмотрена задача о определении доверительного интервала для оценки средней квадратической погрешности среднего арифметического
). Следовательно может быть рассмотрена задача о определении доверительного интервала для оценки средней квадратической погрешности среднего арифметического  при некоторой доверительной вероятности. Методику определения доверительного интервала для
при некоторой доверительной вероятности. Методику определения доверительного интервала для  , при необходимости, можно найти в [5, 6].
, при необходимости, можно найти в [5, 6]. с которой СКП не выйдет за границы заданного (симметричного или несимметричного) интервала при заданном законе распределения случайной погрешности.
с которой СКП не выйдет за границы заданного (симметричного или несимметричного) интервала при заданном законе распределения случайной погрешности. ), за пределы которого с заданной доверительной вероятностью не выходят случайные погрешности результата статистических измерений, определяют в соответствии с выражением:
), за пределы которого с заданной доверительной вероятностью не выходят случайные погрешности результата статистических измерений, определяют в соответствии с выражением: , (1.22)
, (1.22) - безразмерный коэффициент, определяемый задаваемой доверительной вероятностью (
- безразмерный коэффициент, определяемый задаваемой доверительной вероятностью ( ) и видом закона распределения случайных погрешностей.
) и видом закона распределения случайных погрешностей. и верхней -
и верхней -  границах интервала для случайной погрешности результата измерений. Выражение (1.21) в этом случае следует записать в виде:
границах интервала для случайной погрешности результата измерений. Выражение (1.21) в этом случае следует записать в виде: ,
, (1.23)
(1.23) , (1.24)
, (1.24) - значение безразмерного коэффициента для нижней границы доверительного интервала;
- значение безразмерного коэффициента для нижней границы доверительного интервала; - значение того же коэффициента для верхней границы доверительного интервала. Для симметричного интервала (
- значение того же коэффициента для верхней границы доверительного интервала. Для симметричного интервала ( ) (1.24) можно переписать в виде:
) (1.24) можно переписать в виде: . (1.25)
. (1.25) (1.26)
(1.26)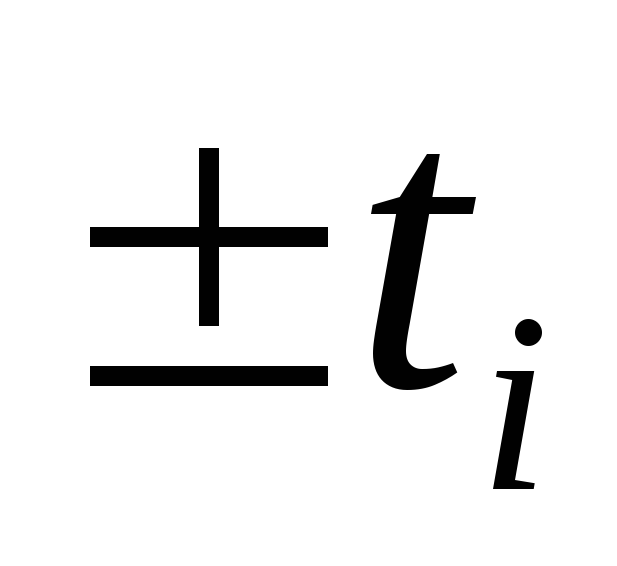 , а пользуясь табличными значениями интеграла вида (1.26) - только половину полной вероятности для одной части симметричного доверительного интервала. При решении этих задач можно использовать также таблицы значений нормированной интегральной функции нормального распределения вида:
, а пользуясь табличными значениями интеграла вида (1.26) - только половину полной вероятности для одной части симметричного доверительного интервала. При решении этих задач можно использовать также таблицы значений нормированной интегральной функции нормального распределения вида: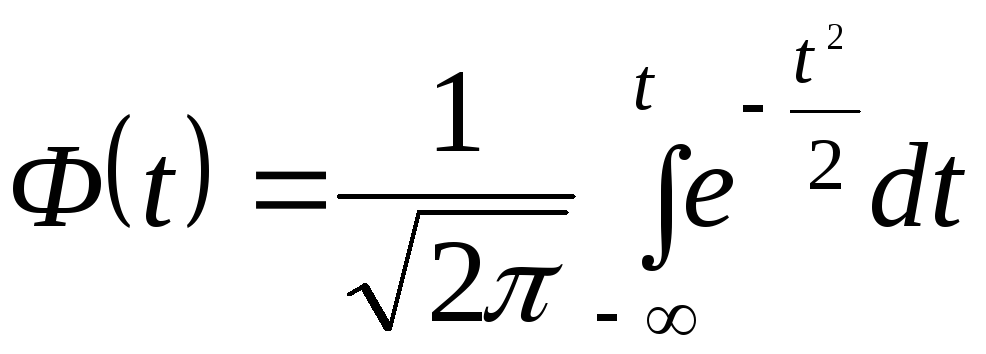 (1.27)
(1.27) (см. таблицу 2 приложения в методических указаниях) выражение (1.24) для доверительной вероятности нахождения случайной погрешности внутри несимметричного интервала от
(см. таблицу 2 приложения в методических указаниях) выражение (1.24) для доверительной вероятности нахождения случайной погрешности внутри несимметричного интервала от  до
до  записывается следующим образом:
записывается следующим образом: (1.28)
(1.28) ). При малом n точечные оценки случайной погрешности сами становятся случайными величинами. Учитывая это, выражение (1.12) для нормированного отклонения результата измерений от действительного значения при
). При малом n точечные оценки случайной погрешности сами становятся случайными величинами. Учитывая это, выражение (1.12) для нормированного отклонения результата измерений от действительного значения при  следует записать в виде:
следует записать в виде: . (1.29)
. (1.29) в (1.29) подчеркивает тот факт, что нормированное отклонение определено с использованием оценок (
в (1.29) подчеркивает тот факт, что нормированное отклонение определено с использованием оценок ( и
и  ) полученных при обработке выборки малого объема.
) полученных при обработке выборки малого объема. , таким образом, является некоторой функцией числа наблюдений в выборке n. Следовательно и границы доверительного интервала определяемые в соответствии с (1.22) будут зависеть не только от доверительной вероятности, но и от числа наблюдений n. Закон распределения случайной величины
, таким образом, является некоторой функцией числа наблюдений в выборке n. Следовательно и границы доверительного интервала определяемые в соответствии с (1.22) будут зависеть не только от доверительной вероятности, но и от числа наблюдений n. Закон распределения случайной величины  отличается от нормального и называется распределением Стьюдента. Это различие существенно при малых n, а при
отличается от нормального и называется распределением Стьюдента. Это различие существенно при малых n, а при  распределение Стьюдента полностью совпадает с нормальным. Таким образом, при обработке результатов статистических измерений при малом количестве наблюдений (
распределение Стьюдента полностью совпадает с нормальным. Таким образом, при обработке результатов статистических измерений при малом количестве наблюдений ( ) доверительный интервал следует определять с использованием распределения Стьюдента. Чтобы подчеркнуть, что в этом случае коэффициент t в (1.22) зависит не только от доверительной вероятности
) доверительный интервал следует определять с использованием распределения Стьюдента. Чтобы подчеркнуть, что в этом случае коэффициент t в (1.22) зависит не только от доверительной вероятности  , но и от числа наблюдений n, выражение (1.22) записывается в виде:
, но и от числа наблюдений n, выражение (1.22) записывается в виде: (1.30)
(1.30) - коэффициент, определяемый по таблицам распределения Стьюдента при выбранной доверительной вероятности для конкретного количества наблюдений n.
- коэффициент, определяемый по таблицам распределения Стьюдента при выбранной доверительной вероятности для конкретного количества наблюдений n. при выбранной доверительной вероятности для каждого конкретного значения n можно определить по таблице 4 (см. приложение в методических указаниях).
при выбранной доверительной вероятности для каждого конкретного значения n можно определить по таблице 4 (см. приложение в методических указаниях). . Оказалось, что для широкого класса симметричных распределений (нормального, равномерного, треугольного, трапецеидального, экспоненциального и даже ряда двухмодальных законов) с погрешностью не более 10% границы симметричного доверительного интервала при
. Оказалось, что для широкого класса симметричных распределений (нормального, равномерного, треугольного, трапецеидального, экспоненциального и даже ряда двухмодальных законов) с погрешностью не более 10% границы симметричного доверительного интервала при  равны
равны  [8]. Поэтому ГОСТ 11.001-73 предписывает при отсутствии данных о виде закона распределения определять симметричный доверительный интервал только при
[8]. Поэтому ГОСТ 11.001-73 предписывает при отсутствии данных о виде закона распределения определять симметричный доверительный интервал только при  пользуясь соотношением:
пользуясь соотношением: .
. (1.31)
(1.31) и доверительный интервал
и доверительный интервал  (или
(или  ). Эта процедура называется исключением грубых погрешностей. Статистический критерий обнаружения грубых погрешностей разработан для случая, когда группа обрабатываемых данных подчиняется нормальному закону распределения. В этом случае теория вероятностей позволяет при выбранной доверительной вероятности
). Эта процедура называется исключением грубых погрешностей. Статистический критерий обнаружения грубых погрешностей разработан для случая, когда группа обрабатываемых данных подчиняется нормальному закону распределения. В этом случае теория вероятностей позволяет при выбранной доверительной вероятности  рассчитать теоретически допустимые границы максимальных (по модулю) нормированных отклонений для выборки из n наблюдений
рассчитать теоретически допустимые границы максимальных (по модулю) нормированных отклонений для выборки из n наблюдений (1.32)
(1.32) табулированы для различных значений n при разных уровнях доверительной вероятности
табулированы для различных значений n при разных уровнях доверительной вероятности  (или разных уровнях значимости g, где
(или разных уровнях значимости g, где  ). Табличные значения
). Табличные значения  приведены в таблице 3 приложения в методических указаниях.
приведены в таблице 3 приложения в методических указаниях. и
и  для некоторого
для некоторого  , который резко выделяется из общей совокупности обрабатываемых результатов, определяют величину нормированного отклонения
, который резко выделяется из общей совокупности обрабатываемых результатов, определяют величину нормированного отклонения . (1.33)
. (1.33) по таблице 3 (см. приложение в методических указаниях) для числа n, соответствующего обрабатываемой выборке, находят допустимое нормированное отклонение
по таблице 3 (см. приложение в методических указаниях) для числа n, соответствующего обрабатываемой выборке, находят допустимое нормированное отклонение  .
. , то результат
, то результат  можно отбросить. В противном случае результат должен быть оставлен.
можно отбросить. В противном случае результат должен быть оставлен. вызывает сомнение какое-либо другое данное, то указанный порядок действий(определение
вызывает сомнение какое-либо другое данное, то указанный порядок действий(определение  ;
;  и
и  ) повторяют, но уже не учитывая исключенное данное
) повторяют, но уже не учитывая исключенное данное  .
. и
и 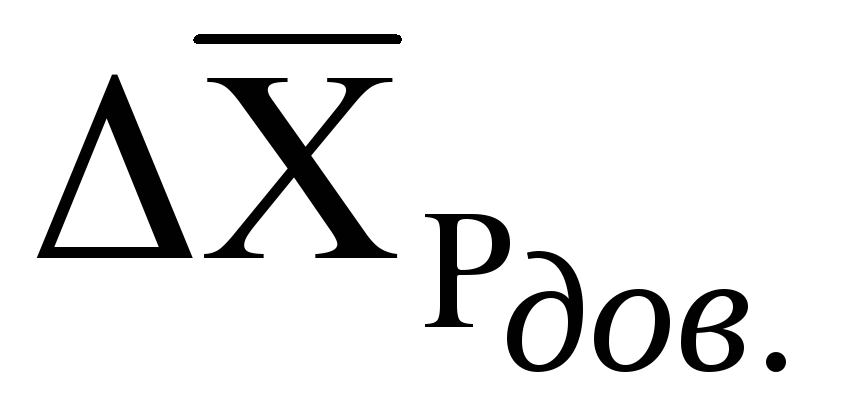 необходимо проверить гипотезу о принадлежности группы экспериментальных данных нормальному распределению. Проверить гипотезу о том, что распределение опытных данных не противоречит теоретическому, можно по ряду критериев. Но следует иметь ввиду, что при n<10 проверить гипотезу о виде распределения экспериментальных данных невозможно. При
необходимо проверить гипотезу о принадлежности группы экспериментальных данных нормальному распределению. Проверить гипотезу о том, что распределение опытных данных не противоречит теоретическому, можно по ряду критериев. Но следует иметь ввиду, что при n<10 проверить гипотезу о виде распределения экспериментальных данных невозможно. При  проверка гипотезы затруднена, в этом случае пользуются, как правило, составным критерием [5]. При достаточно большом числе данных (
проверка гипотезы затруднена, в этом случае пользуются, как правило, составным критерием [5]. При достаточно большом числе данных ( ) лучшим критерием проверки гипотезы о виде распределения является критерий
) лучшим критерием проверки гипотезы о виде распределения является критерий  (или критерий согласия К. Пирсона) [5, 6].
(или критерий согласия К. Пирсона) [5, 6]. ) не должна выходить за границы (
) не должна выходить за границы ( ),определенные по таблицам
),определенные по таблицам  -распределения (таблица 5 см. приложение в методических указаниях) при заданном уровне доверительной вероятности (или уровне значимости
-распределения (таблица 5 см. приложение в методических указаниях) при заданном уровне доверительной вероятности (или уровне значимости  ). Положительный ответ, полученный при использовании критерия согласия
). Положительный ответ, полученный при использовании критерия согласия  , следует трактовать так, что распределение опытных данных не противоречит теоретическому (на соответствие которому проверялось). Но это не означает что оно полностью соответствует теоретическому. При определенной доверительной вероятности критерий
, следует трактовать так, что распределение опытных данных не противоречит теоретическому (на соответствие которому проверялось). Но это не означает что оно полностью соответствует теоретическому. При определенной доверительной вероятности критерий может дать положительный результат и для некоторого другого теоретического закона распределения. Однозначным ответом является лишь отрицательный результат применения критерия
может дать положительный результат и для некоторого другого теоретического закона распределения. Однозначным ответом является лишь отрицательный результат применения критерия  , который трактуется так: распределение опытных данных не соответствует теоретическому, на соответствие которому проверялось. Таким образом при использовании критерия согласия Пирсона следует помнить следующее.
, который трактуется так: распределение опытных данных не соответствует теоретическому, на соответствие которому проверялось. Таким образом при использовании критерия согласия Пирсона следует помнить следующее. позволяет проверить соответствие опытных данных любому (выбранному заранее по каким либо признакам) теоретическому распределению, а не только нормальному. Однако этот критерий (как, впрочем, и другие критерии согласия) не позволяет однозначно установить вид распределения этих данных.
позволяет проверить соответствие опытных данных любому (выбранному заранее по каким либо признакам) теоретическому распределению, а не только нормальному. Однако этот критерий (как, впрочем, и другие критерии согласия) не позволяет однозначно установить вид распределения этих данных. с необходимыми пояснениями приводится на примере в п.1.3.4.
с необходимыми пояснениями приводится на примере в п.1.3.4.



 Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х{ до х2
Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х{ до х2 
 где Pi—вероятность появления дискретной величины.
где Pi—вероятность появления дискретной величины. Центральные моменты к-ro порядка рассчитываются по формулам
Центральные моменты к-ro порядка рассчитываются по формулам  ...
...  Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.
Дисперсия случайной величины характеризует рассеяние отдельных ее значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.

 где хс1, хс2 — сгибы, т.е. абсциссы точек, в которых распределение достигает своих максимумов. Для ограниченных распределений (равномерного, трапецеидального, арксинусоидального и др.) применяется оценка в виде центра размаха:
где хс1, хс2 — сгибы, т.е. абсциссы точек, в которых распределение достигает своих максимумов. Для ограниченных распределений (равномерного, трапецеидального, арксинусоидального и др.) применяется оценка в виде центра размаха:  где х,, х2 — первый и последний члены вариационного ряда, соответствующего распределению.
где х,, х2 — первый и последний члены вариационного ряда, соответствующего распределению.
 Также с помощью начального момента нулевого порядка вводится понятие медианы распределения. Первый начальный момент — МО случайной величины:
Также с помощью начального момента нулевого порядка вводится понятие медианы распределения. Первый начальный момент — МО случайной величины:  Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины. Начальные и центральные моменты случайной погрешности Л совпадают между собой и с центральными моментами результатов измерений: аг [Л] = цг [А] = Цг [х], поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю. Важное значение имеет второй центральный момент
Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины. Начальные и центральные моменты случайной погрешности Л совпадают между собой и с центральными моментами результатов измерений: аг [Л] = цг [А] = Цг [х], поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю. Важное значение имеет второй центральный момент  называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение
называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение  имеющее такую же размерность, как и МО. Для примера на рис. 6.3 показан вид нормального распределения при различных значениях СКО. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для"более подробного описания распределения используются моменты более высоких порядков.
имеющее такую же размерность, как и МО. Для примера на рис. 6.3 показан вид нормального распределения при различных значениях СКО. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для"более подробного описания распределения используются моменты более высоких порядков.
 служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на рис. 6.4,а.
служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на рис. 6.4,а. 
 служит для характеристики плоско- или островершинности распределения. Эти свойства описываются с помощью эксцесса
служит для характеристики плоско- или островершинности распределения. Эти свойства описываются с помощью эксцесса 
 Его значения лежат в диапазоне от 1 до w. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на рис. 6.4,6. Для удобства часто используют контрэксцесс
Его значения лежат в диапазоне от 1 до w. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на рис. 6.4,6. Для удобства часто используют контрэксцесс  Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577. , где Дэльта Э – энтропийное значение погрешности.
, где Дэльта Э – энтропийное значение погрешности.  — энтропия действительного значения х измеряемой величины вокруг полученного после измерения значения хд, т.е. энтропия погрешности измерений; р(х) — плотность распределения вероятности измеряемой величины.
— энтропия действительного значения х измеряемой величины вокруг полученного после измерения значения хд, т.е. энтропия погрешности измерений; р(х) — плотность распределения вероятности измеряемой величины. Трапецеидальное распределение (рис 6.5,6) образуется как композиция двух равномерных распределений шириной а, и а2.
Трапецеидальное распределение (рис 6.5,6) образуется как композиция двух равномерных распределений шириной а, и а2. 
 Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона)
Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное; в — треугольное (Симпсона) 

 - некоторая характерная для данного распределения константа; Хц — координата центра; Г(х) — гамма-функция. В нормированном виде, т.е. при Хц =0 и оХ= 1,
- некоторая характерная для данного распределения константа; Хц — координата центра; Г(х) — гамма-функция. В нормированном виде, т.е. при Хц =0 и оХ= 1, где А(а) — нормирующий множитель распределения.
где А(а) — нормирующий множитель распределения. Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.
Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.
 где о — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.
где о — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.  Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49]. Определенный интеграл с переменным верхним пределом
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49]. Определенный интеграл с переменным верхним пределом  называют функцией Лапласа. Для нее справедливы следующие равенства:
называют функцией Лапласа. Для нее справедливы следующие равенства: 










