19. Внутренняя энергия идеального газа. Работа. Внутренняя энергия идеального газа реферат
Внутренняя энергия идеального газа | Бесплатные курсовые, рефераты и дипломные работы
Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии может обладать запасом внутренней энергии, которая связана с механическим движением атомов или молекул, составляющих тело, а также с их взаимодействием. Для идеального газа его внутренняя энергия является энергией молекулярно-кинетического движения атомов или молекул этого газа. Средняя кинетическая энергия поступательного движения молекулы согласно равенству (10.10) зависит только от температуры и равна E = 3kT/2 . Скорость молекул связана со своими составляющими по осям x , y и z соотношением 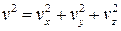 . Умножая это равенство на m/2 , получим
. Умножая это равенство на m/2 , получим  . Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, … связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
. Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, … связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы. Для одноатомного газа, например гелия, каждый атом однозначно определяется заданием трех координат. Поэтому для одноатомного газа число степеней свободы i = 3 . Энергией вращательного движения одноатомная молекула практически не обладает, так как ее масса сосредоточена в ядре. В силу хаотичности движения атомов средние значения энергии, приходящиеся на каждую степень свободы движения, будут одинаковыми и равными третьей части от энергии поступательного движения, т.е. равными kT/2 . Полная средняя энергия поступательного движения молекулы может быть представлена в виде eпост = i kT/2 .
Если молекула газа состоит из трех или более атомов, то при хаотических соударениях молекул энергия поступательного движения молекул будет переходить в энергию вращательного движения молекул и наоборот. В результате этого получается, что средние энергии поступательного и вращательного движения многоатомных молекул одинаковы. Вращение многоатомной молекулы может происходить относительно трех независимых осей и его можно описать с помощью трех угловых величин. Поэтому вращательное движение имеет также три степени свободы движения. Полное число степеней свободы движения молекул многоатомного газа i = iпост + iвр = 3 + 3 = 6 . Причем полную кинетическую энергию многоатомной молекулы можно записать в виде
e = i kT/2. (10.1)
Полученный результат Максвелл обобщил в принципе равного распределения энергии: в системе, состоящей из большого числа частиц, механическая энергия распределяется поровну между их степенями свободы движения.
 Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Для киломоля идеального газа, содержащего NA число молекул, внутренняя энергия в соответствии с выражением (10.1) определяется соотношением Um = NA i kT/2 или
Um = i RT/2, (10.2)
где R — универсальная газовая постоянная. Выражение (10.2) показывает, что внутренняя энергия киломоля является функцией лишь от температуры газа. Для произвольной массы газа m получим U = i(m/m)RT/2 , где m — моль газа.
В реальном газе между молекулами действуют силы притяжения, которые при расширении газа будут совершать работу. Поэтому его внутренняя энергия будет зависеть не только от температуры, но и от объема. Для реального газа внутренняя энергия будет являться функцией только от температуры и объема: U = f(T,V) . Если реальный газ вернется в некоторое прежнее состояние, то его внутренняя энергия будет иметь прежнее значение.
refac.ru
Внутренняя энергия идеального газа, реферат — allRefers.ru
Внутренняя энергия идеального газа - Лекция, раздел Философия, Часть 1. МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии может обладать запасом внутренней энергии, которая связана с механическим движением атомов или молекул, составляющих тело, а также с их взаимодействием. Для идеального газа его внутренняя энергия является энергией молекулярно-кинетического движения атомов или молекул этого газа. Средняя кинетическая энергия поступательного движения молекулы согласно равенству (10.10) зависит только от температуры и равна E = 3kT/2 . Скорость молекул связана со своими составляющими по осям x , y и z соотношением 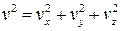 . Умножая это равенство на m/2 , получим
. Умножая это равенство на m/2 , получим  . Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
. Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы. Для одноатомного газа, например гелия, каждый атом однозначно определяется заданием трех координат. Поэтому для одноатомного газа число степеней свободы i = 3 . Энергией вращательного движения одноатомная молекула практически не обладает, так как ее масса сосредоточена в ядре. В силу хаотичности движения атомов средние значения энергии, приходящиеся на каждую степень свободы движения, будут одинаковыми и равными третьей части от энергии поступательного движения, т.е. равными kT/2 . Полная средняя энергия поступательного движения молекулы может быть представлена в виде eпост = i kT/2 .
Если молекула газа состоит из трех или более атомов, то при хаотических соударениях молекул энергия поступательного движения молекул будет переходить в энергию вращательного движения молекул и наоборот. В результате этого получается, что средние энергии поступательного и вращательного движения многоатомных молекул одинаковы. Вращение многоатомной молекулы может происходить относительно трех независимых осей и его можно описать с помощью трех угловых величин. Поэтому вращательное движение имеет также три степени свободы движения. Полное число степеней свободы движения молекул многоатомного газа i = iпост + iвр = 3 + 3 = 6 . Причем полную кинетическую энергию многоатомной молекулы можно записать в виде
e = i kT/2. (10.1)
Полученный результат Максвелл обобщил в принципе равного распределения энергии: в системе, состоящей из большого числа частиц, механическая энергия распределяется поровну между их степенями свободы движения.
 Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост + iвр = 3 + 2 = 5.
Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост + iвр = 3 + 2 = 5.
Для киломоля идеального газа, содержащего NA число молекул, внутренняя энергия в соответствии с выражением (10.1) определяется соотношением Um = NA i kT/2 или
Um = i RT/2, (10.2)
где R - универсальная газовая постоянная. Выражение (10.2) показывает, что внутренняя энергия киломоля является функцией лишь от температуры газа. Для произвольной массы газа m получим U = i(m/m)RT/2 , где m - моль газа.
В реальном газе между молекулами действуют силы притяжения, которые при расширении газа будут совершать работу. Поэтому его внутренняя энергия будет зависеть не только от температуры, но и от объема. Для реального газа внутренняя энергия будет являться функцией только от температуры и объема: U = f(T,V) . Если реальный газ вернется в некоторое прежнее состояние, то его внутренняя энергия будет иметь прежнее значение.
Все темы данного раздела:
Несколько вводных замечаний о предмете физики. Мир, окружающий нас материален: он состоит из вечно существующей и непрерывно движущейся материи.
Мате
Механика Простейшим видом движения материи является механическое движение.
ОПРЕДЕЛЕНИЕ: механическое движени
Кинематика движения материальной точки. Характеристики движения. Положение материальной точки M в пространстве в данный момент времени может быть задано радиус-вектором
Вектор скорости. Средняя и мгновенная скорость. Движения различных тел различаются тем, что тела за одинаков
Путь при неравномерном движении. За малый промежуток времени Dt перемещение графически изобра
Ускорение при криволинейном движении (тангенциальное и нормальное ускорение). Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем на
Угловая скорость. ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно тве
Угловое ускорение. Вектор угловой скорости может изменяться как за счет изменен
Связь между линейной и угловой скоростью. Пусть за малый промежуток времени Dt тело повернулось на угол Dj (рис. 2.17). Точка, находящаяся на рассто
Динамика Раздел механики, исследующий законы и причины, вызывающие движение тел, т.е. изучает движение материальных
II закон Ньютона. ОПРЕДЕЛЕНИЕ: Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционал
III закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия: если тело M1 действует на тело M2
Импульс. Закон сохранения импульса. В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами систе
Работа и энергия. Пусть тело, на которое действует сила , проходит, двигаясь по
Мощность. На практике имеет значение не только величина совершенной работы, но и время, в течение которого она соверш
Энергия. Из опыта известно, что тела часто оказываются в состоянии совершать работу над другими телами.
ОПРЕДЕЛ
Кинетическая энергия тела. Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки).
Напишем уравнение дви
Потенциальное поле сил. Силы консервативные и неконсервативные. Если частица (тело) в каждой точке пространства подвержена воздействию других тел, то говорят, что эта части
Потенциальная энергия тела в поле сил тяжести (в поле тяготения Земли). Поле тяготения Земли есть силовое поле, поэтому любое движение тела в силовом поле сопровождается совершен
Потенциальная энергия в гравитационном поле (в поле всемирного тяготения). Установленный Ньютоном закон всемирного тяготения гласит:
ОПРЕДЕЛЕНИЕ: Гравитационная сила или
Потенциальная энергия упруго деформированного тела. Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруг
Закон сохранения энергии. Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частиц
Поступательное движение твердого тела. ОПРЕДЕЛЕНИЕ: Абсолютно твердым телом будем называть такое тело, деформациями которого в условиях рассм
Вращательное движение твердого тела. ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки
Момент импульса тела. Для описания вращательного движения потребуется ещё одна величина
Основное уравнение динамики вращательного движения. Рассмотрим систему материальных точек, каждая из которых может перемещаться, оставаясь в одной из плоскост
Кинетическая энергия вращающегося твердого тела. 1. Рассмотрим вращение тела вокруг неподвижной оси Z. Разо
Работа внешних сил при вращательном движении твердого тела. Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z.
Пусть на массу
Линии и трубки тока. Гидродинамика изучает движение жидкостей, однако ее законы п
Уравнение Бернулли. Будем рассматривать идеальную несжимаемую жидкость, в котор
Силы внутреннего трения. Реальной жидкости присуща вязкость, которая проявляется в то
Ламинарное и турбулентное течения. При достаточно малой скорости движения жидкости наблюдается слоистое или ламинарное течение, ког
Течение жидкости в круглой трубе. При движении жидкости в круглой трубе ее скорость равна нулю
Движение тел в жидкостях и газах. При движении симметричных тел в жидкостях и газах возникает сила лобового сопротивления, направл
Законы Кеплера. К началу 17 столетия большинство ученых окончательно убедилось в справедливости гелиоцентрической системы
Опыт Кавендиша. Первой успешной попыткой определения «g» были измерения, осу
Напряженность гравитационного поля. Потенциал гравитационного поля. Гравитационное взаимодействие осуществляется через гравитационное поле. Это поле проявляет себя в том, по
Принцип относительности. В разд. 2.1. для механических систем был сформулирован следующий принцип относительности: во всех
Постулаты специальной (частной) теории относительности. Преобразования Лоренца Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности:
1. Физиче
Следствия из преобразований Лоренца. Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.
Интервал между событиями. В теории относительности вводят понятие события, которое определяется местом, где оно произошло, и врем
Уравнение гармонического колебательного движения. Пусть на некоторое тело массы “m” действует квазиупругая сила
Графическое изображение гармонических колебаний. Векторная диаграмма. Сложение нескольких колебаний одинакового направления (или, что то же самое, сложение нескольких гармониче
Скорость, ускорение и энергия колеблющегося тела. Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного проце
Гармонический осциллятор. Систему, описываемую уравнением , где
Физический маятник. ОПРЕДЕЛЕНИЕ: Физическим маятником будем называть твердо
Затухающие колебания. При выводе уравнения гармонических колебаний считалось, что колеблющаяся точка находится под действием то
Вынужденные колебания. Резонанс. Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колеб
Предмет и методы молекулярной физики. Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя и так
Термодинамическая система. Параметры состояния системы. Равновесное и неравновесное состояние. ОПРЕДЕЛЕНИЕ: Термодинамической системой называется совокупность тел, обменивающихся энергией, как дру
Идеальный газ. Параметры состояния идеального газа. ОПРЕДЕЛЕНИЕ: Идеальным газом называется газ, при рассмотрении свойств которого соблюдаются следующие усло
Газовые законы. Если разрешить уравнение состояния идеального газа
Физический смысл универсальной газовой постоянной. Универсальная газовая постоянная имеет размерность работы,
Основное уравнение кинетической теории газов Если в предыдущем разделе применялся термодинамический метод исследования, то в этом разделе будет исполь
Барометрическая формула. Распределение Больцмана Давно известно, что давление газа над поверхностью Земли уме
Максвелловское распределение молекул по скоростям В результате столкновений молекулы обмениваются скоростями, а в случае тройных и более сложных столкновен
Явления переноса. Длина свободного пробега молекул В предыдущих разделах мы рассматривали свойства тел, находящихся в тепловом равновесии. Данный раздел посв
Явление диффузии Диффузией называют процесс взаимного проникновения молекул соприкасающихся веществ, обусловле
Явление теплопроводности и вязкости Явление теплопроводности вещества определяет многие очень важные технические процессы и широко применяет
Работа и теплота. Первое начало термодинамики Внутренняя энергия газа (и другой термодинамической системы) может изменяться в основном за счет двух проц
Работа газовых изопроцессов Пусть газ заключен в цилиндрический сосуд, закрытый плотно п
Молекулярно-кинетическая теория теплоемкостей Теплоемкостью тела C называют физическую величину, численно равную количеству тепла, которое
Адиабатический процесс Наряду с изопроцессами существует адиабатический процесс, широко распространенный в природе. Адиабат
Круговые обратимые процессы. Цикл Карно Механические процессы обладают замечательным свойством обратимости. Например, брошенный камень, описав не
Понятие об энтропии. Энтропия идеального газа Для цикла Карно из формул (10.17) и (10.21) легко получить соотношение
Q1 /T1 - Q2 /T2 = 0.
Второе начало термодинамики Понятие энтропии помогло строго математически сформулировать закономерности, позволяющие определить нап
Статистическое толкование второго начала термодинамики Состояние макроскопического тела (т.е. тела, образованного огромным числом молекул) может быть задано с пом
Уравнение Ван-дер-Ваальса Поведение реальных газов при их малых плотностях хорошо описывается уравнением Клапейрона:
Критическое состояние вещества
Важное значение уравнения Ван-дер-Ваальса заклю
Эффект Джоуля-Томсона В реальном газе между молекулами действуют силы притяжения и отталкивания. Силы притяжения обусловлены ди
allrefers.ru
Внутренняя энергия идеального газа
Количество просмотров публикации Внутренняя энергия идеального газа - 41
Внутренняя энергия идеального газа - ϶ᴛᴏ сумма кинетических энергий всех его молекул:
U=∑Wк=N ,
,
где N – число молекул в газе. А так как  , где i – число степеней свободы молекулы, то
, где i – число степеней свободы молекулы, то
 .
.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, внутренняя энергия идеального газа зависит только от его температуры и не зависит от давления: U=U(T)≠f(p).
3.5. Теплоёмкость термодинамической системы
В случае если ТД системе сообщить некоторую теплоту dQ, то, вообще говоря, температура системы повысится на некоторую величину dT, причём dQ пропорционально dT. Эту линейную зависимость для малых количеств теплоты можно записать в виде
dQ=C0dT. (5)
Коэффициент пропорциональности С0 в формуле (5) принято называть теплоёмкостью системы (тела).
Определение 1. Теплоёмкость, отнесённая к единице массы,
 , (6)
, (6)
принято называть удельной теплоёмкостью тела.
Определение 2. Теплоёмкость, отнесённая к молю тела,
 , (7)
, (7)
принято называть молярной теплоёмкостью тела.
Из сравнения (6) и (7), а также с учётом, что ν=m/M, получаем, что
С=сМ.
Далее везде под термином ʼʼтеплоёмкостьʼʼ будем понимать именно молярную теплоёмкость.
3.6. Теплоёмкости идеального газа
Так как теплота Q не является функцией состояния системы, а зависит от условий нагрева, то и молярная теплоёмкость С тоже зависит от условий нагрева: нагрев при V=const, нагрев при р=const или при других условиях. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, ʼʼтеплоёмкость вообщеʼʼ определённого значения для газа не имеет: исходя из условий нагрева, теплоёмкость С может принимать любое значение от 0 до ∞, и даже должна быть отрицательной.
Рассмотрим два варианта нагрева идеального газа: при постоянном объёме и при постоянном давлении. Соответствующие этим условиям молярные теплоёмкости будем обозначать СV и Ср:
 ,
,  .
.
Вариант 1: V=const (газ нагревают в жёстком баллоне (рис. 1)).
 Так как dQ=pdV+dU|V=const=dU=
Так как dQ=pdV+dU|V=const=dU= ,
,
то СV=
(здесь берётся полная производная, так как U имеет единственный аргумент Т). Таким образом,
dU=νCVdT, (8)
где ν=m/M – число молей газа, СV = – молярная теплоёмкость при посто-янном объёме. И тогда первый закон ТД для элементарных процессов можно записать в виде:
– молярная теплоёмкость при посто-янном объёме. И тогда первый закон ТД для элементарных процессов можно записать в виде:
dQ=pdV+νCVdT. (9)
Замечание.Уравнение (8) легко интегрируется:
U=νCVT+U0,
где U0 – константа интегрирования, которая представляет собою внутреннюю энергию газа при Т=0. Её можно положить равной нулю, так как при Т=0 хаотического движения молекул нет (υ=0). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, U0=0, и внутренняя энергия идеального газа U=νCVT (Дж).
Вариант 2: р=const (газ нагревают в цилиндре под тяжёлым поршнем (рис. 2)).
 Так как dQ=pdV+νCVdT,
Так как dQ=pdV+νCVdT,
то Ср= .
.
Но из уравнения состояния (3) при р=const следует, что
pdV=νRdT,
и тогда Ср=СV+ .
.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, Ср всегда больше СV. Это объясняется тем, что при V=const тепло Q идёт только на нагрев газа, а при р=const – ещё и на совершение газом работы А при увеличении его объёма.
Так как СV= , то Ср=СV+R=
, то Ср=СV+R= .
.
Поскольку pdV=νRdT, то первый закон ТД теперь должна быть записан не только в виде (9), но и в виде
dQ=νCрdT.
referatwork.ru
19. Внутренняя энергия идеального газа. Работа.
Внутренняя энергия U— энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Внутренняя энергия — однозначная функция термодинамического состояния системы, т. е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергийNa молекул:
Внутренняя энергия для произвольной массы т газа. гдеМ —молярная масса,— количество вещества.
гдеМ —молярная масса,— количество вещества.
19. Работа.Если газ, расширяясь, передвигает поршень на бесконечно малое расстояниеdl, то производит над ним работу гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом,
гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом, Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы
Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы

20. Теплоемкость. Уравнение Майера.
Удельная теплоемкость вещества— величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)).
Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)).
Молярная теплоемкость—величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).
где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).
Удельная теплоемкость ссвязана с молярнойСm, соотношением
где М —молярная масса вещества.
Молярная теплоемкость газа при постоянном объеме СVравна
 Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде
Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение СpкСV :
21. Применение первого начала термодинамики к изопроцессам.
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
Изохорный процесс(V=const). Изохорный процесс(V=const). Диаграмма этого процесса (изохора) в координатахр,Vизображается прямой, параллельной оси ординат где процесс1—2есть изохорное нагревание, а1—3 —изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
Теплота, сообщаемая газу, идет на увеличение его внутренней энергии:

Тогда для произвольной массы газа получим

Изобарный процесс(p=const). при увеличения объема отV1доV2равна
 или
или и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты
и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты
его внутренняя энергия возрастает на величину 
Изотермический процесс(T=const). изотермический процесс описывается законом Бойля—Мариотта: Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
работу изотермического расширения газа:

Так как при Т=const внутренняя энергия идеального газа не изменяется:
 то
то
studfiles.net
19. Внутренняя энергия идеального газа. Работа.
Внутренняя энергия U— энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Внутренняя энергия — однозначная функция термодинамического состояния системы, т. е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергийNa молекул:
Внутренняя энергия для произвольной массы т газа. гдеМ —молярная масса,— количество вещества.
гдеМ —молярная масса,— количество вещества.
19. Работа.Если газ, расширяясь, передвигает поршень на бесконечно малое расстояниеdl, то производит над ним работу гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом,
гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом, Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы
Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы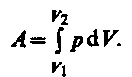

20. Теплоемкость. Уравнение Майера.
Удельная теплоемкость вещества— величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)).
Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)).
Молярная теплоемкость—величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).
где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).
Удельная теплоемкость ссвязана с молярнойСm, соотношением
где М —молярная масса вещества.
Молярная теплоемкость газа при постоянном объеме СVравна
 Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде
Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение СpкСV :
21. Применение первого начала термодинамики к изопроцессам.
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
Изохорный процесс(V=const). Изохорный процесс(V=const). Диаграмма этого процесса (изохора) в координатахр,Vизображается прямой, параллельной оси ординат где процесс1—2есть изохорное нагревание, а1—3 —изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
Теплота, сообщаемая газу, идет на увеличение его внутренней энергии:

Тогда для произвольной массы газа получим

Изобарный процесс(p=const). при увеличения объема отV1доV2равна
 или
или и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты
и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты
его внутренняя энергия возрастает на величину 
Изотермический процесс(T=const). изотермический процесс описывается законом Бойля—Мариотта: Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
работу изотермического расширения газа:

Так как при Т=const внутренняя энергия идеального газа не изменяется:
 то
то
studfiles.net
Внутренняя энергия идеального газа
Количество просмотров публикации Внутренняя энергия идеального газа - 123
Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии может обладать запасом внутренней энергии, которая связана с механическим движением атомов или молекул, составляющих тело, а также с их взаимодействием. Для идеального газа его внутренняя энергия является энергией молекулярно-кинетического движения атомов или молекул этого газа. Средняя кинетическая энергия поступательного движения молекулы согласно равенству (10.10) зависит только от температуры и равна E = 3kT/2 . Скорость молекул связана со своими составляющими по осям x , y и z соотношением  . Умножая это равенство на m/2 , получим
. Умножая это равенство на m/2 , получим  . Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. По этой причине говорят, что молекула имеет три степени свободы движения.
. Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. По этой причине говорят, что молекула имеет три степени свободы движения.
Числом степеней свободы механической системы принято называть количество независимых величин, с помощью которых должна быть задано положение системы. Для одноатомного газа, к примеру гелия, каждый атом однозначно определяется заданием трех координат. По этой причине для одноатомного газа число степеней свободы i = 3 . Энергией вращательного движения одноатомная молекула практически не обладает, так как ее масса сосредоточена в ядре. В силу хаотичности движения атомов средние значения энергии, приходящиеся на каждую степень свободы движения, будут одинаковыми и равными третьей части от энергии поступательного движения, ᴛ.ᴇ. равными kT/2 . Полная средняя энергия поступательного движения молекулы должна быть представлена в виде eпост = i kT/2 .
В случае если молекула газа состоит из трех или более атомов, то при хаотических соударениях молекул энергия поступательного движения молекул будет переходить в энергию вращательного движения молекул и наоборот. В результате этого получается, что средние энергии поступательного и вращательного движения многоатомных молекул одинаковы. Вращение многоатомной молекулы может происходить относительно трех независимых осей и его можно описать с помощью трех угловых величин. По этой причине вращательное движение имеет также три степени свободы движения. Полное число степеней свободы движения молекул многоатомного газа i = iпост + iвр = 3 + 3 = 6 . Причем полную кинетическую энергию многоатомной молекулы можно записать в виде
e = i kT/2. (10.1)
Полученный результат Максвелл обобщил в принципе равного распределения энергии: в системе, состоящей из большого числа частиц, механическая энергия распределяется поровну между их степенями свободы движения.
 Эксперимент подтверждает данный принцип. К примеру, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и в связи с этим обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Эксперимент подтверждает данный принцип. К примеру, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и в связи с этим обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Для киломоля идеального газа, содержащего NA число молекул, внутренняя энергия в соответствии с выражением (10.1) определяется соотношением Um = NA i kT/2 или
Um = i RT/2, (10.2)
где R - универсальная газовая постоянная. Выражение (10.2) показывает, что внутренняя энергия киломоля является функцией лишь от температуры газа. Для произвольной массы газа m получим U = i(m/m)RT/2 , где m - моль газа.
В реальном газе между молекулами действуют силы притяжения, которые при расширении газа будут совершать работу. По этой причине его внутренняя энергия будет зависеть не только от температуры, но и от объёма. Для реального газа внутренняя энергия будет являться функцией только от температуры и объёма: U = f(T,V) . В случае если реальный газ вернется в неĸᴏᴛᴏᴩᴏᴇ прежнее состояние, то его внутренняя энергия будет иметь прежнее значение.
Читайте также
- Термодинамическая система. Внутренняя энергия идеального газа Лекция 9
ГЛАВА 7. ОСНОВЫ ТЕРМОДИНАМИКИ
Термодинамическая система (ТС) - это совокупность макроскопических тел обменивающихся энергией в форме работы и тепла как друг с другом, так и внешней средой.
Внутренняя энергия системы U складывается из внутренних... [читать подробнее].
- Внутренняя энергия идеального газа Внутренняя энергия идеального газа – это сумма кинетических энергий всех его молекул:
U=&... [читать подробнее].
- Первое начало термодинамики. Внутренняя энергия идеального газа. Количество теплоты. Работа. 2) Внутренняя энергия
Внутренняя энергия тела(U) складывается с кинетической энергией поступательного и вращательного движения молекул относительно центра масс, энергией взаимодействия, внутренней молекулярной энергией.
Внутренняя энергия – полная энергия за вычетом... [читать подробнее].
- Внутренняя энергия идеального газа. Количество теплоты. Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно-кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств... [читать подробнее].
- Средняя кинетическая энергия молекул. Внутренняя энергия идеального газа. Число степеней свободы молекулы.
Средняя, средняя квадратичная, наивероятнейшая скорости молекулы газа.
Распределение Максвелла
Распределение молекул по скоростям
Основные понятия теории вероятности. Дискретная случайная... [читать подробнее].
- Число степеней свободы. Внутренняя энергия идеального газа
Рис. 9.4
Числом степеней свободы называется число независимых координат, которыми описывается движение тела в пространстве. Материальная точка имеет три степени свободы, поскольку при ее движении в пространстве изменяются три координаты x, y, z. Система из двух... [читать подробнее].
referatwork.ru
/ Реферат / 26. Внутренняя энергия идеального газа. работа и теплота. Закон сохранения энергии. Первое начало термодинамики
26. Внутренняя энергия идеального газа.
Сумма всех видов энергий движения и взаимодействия частиц тела или системы тел называется внутренней энергией тела или системы. В состав внутренней энергии тела входит энергия всех видов движения, а именно: энергия поступательного и вращательного движения молекул, энергия колебательного движения атомов в молекулах, а также энергия взаимодействия входящих в тело молекул. Внутренняя энергия не включает в себя кинетическую и потенциальную энергию тела, как целого.
Если известен закон взаимодействия между частицами в том или ином теле, то молекулярно-кинетическая теория позволяет рассчитать внутреннюю энергию этого тела. Проще всего определить внутреннюю энергию идеального газа. Так как в идеальном газе взаимодействие между молекулами отсутствует (взаимная потенциальная энергия молекул равна нулю), то его внутренняя энергия складывается только из энергии теплового движения отдельных молекул. Тогда внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергий NА молекул:
U0 = (i/2)kTNA = (i/2)RT.
Внутренняя энергия для произвольной массы М газа
U = (M/)i RT/2 = Z i RT/2.
Из полученной формулы видно, что внутренняя энергия данной массы идеального газа зависит только от температуры и совершенно не зависит от объема, занимаемого газом при данной температуре. Для реального газа это не так.
РАБОТА И ТЕПЛОТА. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ. ПЕРВОЕНАЧАЛО ТЕРМОДИНАМИКИ.
Известно, что газ, как и всякое другое тело, можно нагреть или охладить (т.е. изменить его внутреннюю энергию) и другим способом, при котором никакая механическая работа не совершается. Для этого тело приводится в контакт с другим телом, имеющим более высокую или более низкую температуру, чем данное тело. При таком контакте происходит обмен энергией между телами, причем одно тело передает внутреннюю энергию другому без совершения работы. Такой процесс изменения внутренней энергии тела без совершения механической работы называется теплопередачей.
Теплопередача осуществляется не только при непосредственном контакте, но и в том случае, когда тела различной температуры разделены какой-либо средой или даже пустотой. В первом случае говорят, что передача осуществляется путем теплопроводности, а в другом – теплоизлучением. Количество энергии, передаваемой одним телом другому при их контакте (непосредственно или через третье тело) или путем излучения называется количеством теплоты. Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Количество теплоты, также как и механическая работа, является мерой изменения энергии тела или системы тел. Энергия механического движения может превращаться в энергию теплового движения, и наоборот.
Работу можно охарактеризовать как макроскопическую форму передачи энергии, связанную с макроскопическим перемещением в системе (например, перемещение поршня в цилиндре с газом), а теплоту – как микроскопическую форму изменения энергии, связанную с микроскопическими процессами, происходящими в системе.
При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных.
Если система подвергается одновременно и механическому и тепловому воздействию, то
Q=dU+A (1)
т.е., бесконечно малое количество тепла, передаваемого системе, идет на бесконечно малое изменение ее внутренней энергии и на элементарную работу, совершаемую системой против внешних сил. Уравнение (1) выражает первое начало термодинамики в дифференциальной форме, т.е. для бесконечно малого изменения состояния системы.
В интегральном виде, т.е для конечного изменения состояния системы первое начало термодинамики имеет вид
Q = U2 – U1 + A,
где U2 – U1 -изменение внутренней энергии тела или системы при переходе ее из состояния 1 в состояние 2, Q – количество теплоты, полученное при этом системой, и А – полная работа, производимая системой при переходе из 1 состояния во 2-ое.
Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии U = 0. Тогда, согласно первому началу термодинамики,
А = Q,
т.е. вечный двигатель первого рода - периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, - невозможен (одна из формулировок первого начала термодинамики).
studfiles.net
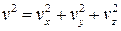 . Умножая это равенство на m/2 , получим
. Умножая это равенство на m/2 , получим  . Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, … связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
. Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, … связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения. Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.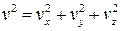 . Умножая это равенство на m/2 , получим
. Умножая это равенство на m/2 , получим  . Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
. Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения. Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост + iвр = 3 + 2 = 5.
Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост + iвр = 3 + 2 = 5.
 гдеМ —молярная масса,— количество вещества.
гдеМ —молярная масса,— количество вещества. гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом,
гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом, Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы
Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы

 Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)).
Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)). где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).
где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).

 Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде
Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде






 или
или и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты
и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты

 Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
 то
то

 гдеМ —молярная масса,— количество вещества.
гдеМ —молярная масса,— количество вещества. гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом,
гдеS —площадь поршня,Sdl=dV—изменение объема системы. Таким образом, Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы
Полную работуА,совершаемую газом при изменении его объема отV1доV2,найдем интегрированием формулы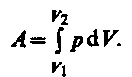

 Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)).
Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кгК)). где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).
где=m/М—количество вещества.Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(мольК)).

 Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде
Выражение называется уравнением Майера;оно показывает, чтоСрвсегда большеСVна величину молярной газовой постоянной. Это объясняется тем, что при нагревании газапри постоянном давлениитребуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Можно записать в виде






 или
или и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты
и определяется площадью заштрихованного прямоугольника. В изобарном процессе при сообщении газу массойтколичества теплоты

 Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Диаграмма этого процесса (изотерма) в координатахр, Vпредставляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
 то
то
