|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Реферат: Показатели вариации:. Вариации реферат
Реферат: Показатели вариации
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Размах вариации (R)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
В нашем примере: лет;
Ответ: 2, 4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1, 25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия
Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
В нашем примере:
Дисперсия взвешенная:
Более удобно вычислять дисперсию по формуле:
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:
Для сгруппированных данных:
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком — через . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
,
средний квадрат отклонений
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий , а среднее квадратическое отклонение или 17, 1%.
Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.
Относительные показатели вариации
Относительные показатели вариации включают:
Коэффициент осцилляции
Относительное линейное отклонение (линейный коэффициент варианции)
Коэффициент вариации (относительное отклонение)
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
|
Коэффициент осцилляции |
|
|
Относительное линейное отклонение |
|
|
Коэффициент вариации |
Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан
,
так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.
В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение , где — средний квартиль полусуммы разности третьего (или верхнего) квартиля () и первого (или нижнего) квартиля ().
.
На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).
Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологии при , а по другой — при. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (. Относительная мера вариации (позволяет сделать противоположный вывод
Пример расчета показателей вариации
На этапе отбора кандидатов для участия в осуществлении сложного проекта фирма объявлила конкурс профессионалов. Распределение претендентов по опыту работы показало средующие результаты:
Вычислим средний производственный опыт работы, лет
Рассчитаем дисперсию по продолжительности опыта работы
Такой же результат получается, если использовать для расчета другую формулу расчета дисперсии
Вычислим среднее квадратическое отклонение, лет:
Определим коэффициент вариации, %:
Правило сложения дисперсий
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).
Общая дисперсия характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
— групповые средние,
— численность единиц i-й группы
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— дисперсия i-ой группы.
Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()
Эмпирический коэффициент детерминации () характеризует долю межгрупоовой дисперсии в общей дисперсии:
и показывает насколько вариация признака в совокупности обусловлена фактором группировки.
Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }
оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениями являются нуль и единица. Чем ближе к единице, тем теснее связь.
Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:
При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.
Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади: Общую дисперсию определим по формуле:
.
Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:
а) для домов, построенных вблизи центра:
б) для домов, построенных далеко от центра:
Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии:
Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии
Найденные дисперссии в сумме дают величину общей дисперсии
Эмпирический коэффициент детерминации:
показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81, 8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18, 2% — другими факторами.
Эмприческое корреляционное отношение свидетельствует о существенном влиянии на стоимость жилья месторасположения домов.
Правило сложения дисперсий для доли признака записывается так:
а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:
общая дисперсия:
Формулы межгрупповой и внутригрупповой дисперсий:
Характеристики формы распределения
Для получения представления о форме распределения используются показатели среднего уровня (средняя арифметическая, мода, медиана), показатели вариации, ассиметрии и эксцесса.
В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность , которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Ассиметричное распределение
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
В качестве обобщающих характеристик вариации используются центральные моменты распределения -го порядка , соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:
Для сгруппированных данных:
Момент первого порядка согласно свойству средней арифметической равен нулю .
Момент второго порядка является дисперсией .
Моменты третьего и четвертого порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях , как все центральные моменты нечетного порядка.Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если , то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если , то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (). Для нормального распределения , поэтому эксцесс находят по формуле:
Для нормального распределения обращается в нуль. Для островершинных распределений , для плосковершинных .
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения.
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение, полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределах от величины средней. При этом в границах находится около 70% всех единиц, а в пределах — 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.
www.referatmix.ru
Реферат: Показатели вариации
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Размах вариации (R)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность.
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю, либо возводить значения отклонений в квадрат
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение— это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
В нашем примере:лет;
Ответ: 2, 4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение:~ 1, 25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия
Дисперсия- представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
В нашем примере:
Дисперсия взвешенная:
Более удобно вычислять дисперсию по формуле:
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:
Для сгруппированных данных:
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой, а долю единиц, не обладающих этим признаком — через. Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
,
средний квадрат отклонений
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когдат.е.. Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий, а среднее квадратическое отклонениеили 17, 1%.
Среднее квадратическое отклонениеравно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.
Относительные показатели вариации
Относительные показатели вариации включают:
Коэффициент осцилляции
Относительное линейное отклонение (линейный коэффициент варианции)
Коэффициент вариации (относительное отклонение)
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
Коэффициент осцилляции | |
Относительное линейное отклонение | |
Коэффициент вариации |
Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан
,
так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.
В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение, где— средний квартиль полусуммы разности третьего (или верхнего) квартиля () и первого (или нижнего) квартиля ().
.
На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).
Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологиипри, а по другой —при. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (. Относительная мера вариации (позволяет сделать противоположный вывод
Пример расчета показателей вариации
На этапе отбора кандидатов для участия в осуществлении сложного проекта фирма объявлила конкурс профессионалов. Распределение претендентов по опыту работы показало средующие результаты:
Вычислим средний производственный опыт работы, лет
Рассчитаем дисперсию по продолжительности опыта работы
Такой же результат получается, если использовать для расчета другую формулу расчета дисперсии
Вычислим среднее квадратическое отклонение, лет:
Определим коэффициент вариации, %:
Правило сложения дисперсий
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).
Общая дисперсияхарактеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
Межгрупповая дисперсияизмеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
— групповые средние,
— численность единиц i-й группы
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— дисперсия i-ой группы.
Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()
Эмпирический коэффициент детерминации () характеризует долю межгрупоовой дисперсии в общей дисперсии:
и показывает насколько вариация признака в совокупности обусловлена фактором группировки.
Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }
оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениямиявляются нуль и единица. Чем ближек единице, тем теснее связь.
Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:
При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.
Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади:Общую дисперсию определим по формуле:
.
Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:
а) для домов, построенных вблизи центра:
б) для домов, построенных далеко от центра:
Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии:
Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии
Найденные дисперссии в сумме дают величину общей дисперсии
Эмпирический коэффициент детерминации:
показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81, 8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18, 2% — другими факторами.
Эмприческое корреляционное отношениесвидетельствует о существенном влиянии на стоимость жилья месторасположения домов.
Правило сложения дисперсий для доли признака записывается так:
а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:
общая дисперсия:
Формулы межгрупповой и внутригрупповой дисперсий:
Характеристики формы распределения
Для получения представления о форме распределения используются показатели среднего уровня (средняя арифметическая, мода, медиана), показатели вариации, ассиметрии и эксцесса.
В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность, которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Ассиметричное распределение
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
В качестве обобщающих характеристик вариации используются центральные моменты распределения-го порядка, соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:
Для сгруппированных данных:
Момент первого порядкасогласно свойству средней арифметической равен нулю.
Момент второго порядкаявляется дисперсией.
Моменты третьегои четвертогопорядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях, как все центральные моменты нечетного порядка.Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если, то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если, то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (). Для нормального распределения, поэтому эксцесс находят по формуле:
Для нормального распределенияобращается в нуль. Для островершинных распределений, для плосковершинных.
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения.
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение, полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределахот величины средней. При этом в границахнаходится около 70% всех единиц, а в пределах— 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.
superbotanik.net
Реферат - Показатели вариации - Математика
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Размах вариации (R)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
В нашем примере: лет;
Ответ: 2, 4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1, 25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия
Дисперсия — представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
В нашем примере:
Дисперсия взвешенная:
Более удобно вычислять дисперсию по формуле:
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:
Для сгруппированных данных:
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком — через . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
,
средний квадрат отклонений
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий , а среднее квадратическое отклонение или 17, 1%.
Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.
Относительные показатели вариации
Относительные показатели вариации включают:
Коэффициент осцилляции
Относительное линейное отклонение (линейный коэффициент варианции)
Коэффициент вариации (относительное отклонение)
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
Коэффициент осцилляции | |
Относительное линейное отклонение | |
Коэффициент вариации |
Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан
,
так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.
В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение , где — средний квартиль полусуммы разности третьего (или верхнего) квартиля () и первого (или нижнего) квартиля ().
.
На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).
Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологии при , а по другой — при. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (. Относительная мера вариации (позволяет сделать противоположный вывод
Пример расчета показателей вариации
На этапе отбора кандидатов для участия в осуществлении сложного проекта фирма объявлила конкурс профессионалов. Распределение претендентов по опыту работы показало средующие результаты:
Вычислим средний производственный опыт работы, лет
Рассчитаем дисперсию по продолжительности опыта работы
Такой же результат получается, если использовать для расчета другую формулу расчета дисперсии
Вычислим среднее квадратическое отклонение, лет:
Определим коэффициент вариации, %:
Правило сложения дисперсий
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).
Общая дисперсия характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
— групповые средние,
— численность единиц i-й группы
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— дисперсия i-ой группы.
Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()
Эмпирический коэффициент детерминации () характеризует долю межгрупоовой дисперсии в общей дисперсии:
и показывает насколько вариация признака в совокупности обусловлена фактором группировки.
Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }
оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениями являются нуль и единица. Чем ближе к единице, тем теснее связь.
Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:
При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.
Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади: Общую дисперсию определим по формуле:
.
Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:
а) для домов, построенных вблизи центра:
б) для домов, построенных далеко от центра:
Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии:
Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии
Найденные дисперссии в сумме дают величину общей дисперсии
Эмпирический коэффициент детерминации:
показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81, 8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18, 2% — другими факторами.
Эмприческое корреляционное отношение свидетельствует о существенном влиянии на стоимость жилья месторасположения домов.
Правило сложения дисперсий для доли признака записывается так:
а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:
общая дисперсия:
Формулы межгрупповой и внутригрупповой дисперсий:
Характеристики формы распределения
Для получения представления о форме распределения используются показатели среднего уровня (средняя арифметическая, мода, медиана), показатели вариации, ассиметрии и эксцесса.
В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность , которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Ассиметричное распределение
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
В качестве обобщающих характеристик вариации используются центральные моменты распределения -го порядка , соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:
Для сгруппированных данных:
Момент первого порядка согласно свойству средней арифметической равен нулю .
Момент второго порядка является дисперсией .
Моменты третьего и четвертого порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях , как все центральные моменты нечетного порядка.Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если , то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если , то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (). Для нормального распределения , поэтому эксцесс находят по формуле:
Для нормального распределения обращается в нуль. Для островершинных распределений , для плосковершинных .
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения.
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение, полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределах от величины средней. При этом в границах находится около 70% всех единиц, а в пределах — 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.
www.ronl.ru
Реферат Вариации
скачатьРеферат на тему:
План:
- Введение
- 1 Классификация
- 2 Организация формы
- 3 Вариации на выдержанную мелодию
- 3.1 Тема
- 3.2 Варьирование
- 4 Вариации на basso ostinato
- 4.1 Тема
- 4.2 Варьирование
- 5 Фигурационные вариации
- 5.1 Тема
- 5.2 Варьирование
- 6 Жанрово-характерные вариации
- 6.1 Тема
- 6.2 Варьирование
- 7 Вариации на несколько тем
- 8 Вариации с темой в конце ПримечанияЛитература
Введение
Вариацио́нная фо́рма, или вариации, тема с вариациями, вариационный цикл, — музыкальная форма, состоящая из темы и её нескольких (не менее двух) изменённых воспроизведений (вариаций). Это одна из старейших музыкальных форм (известна с XIII века).
Следует различать вариационную форму и вариационность как принцип. Последний имеет неограниченный спектр применения (варьироваться могут мотив, фраза, предложение в периоде и т. д., вплоть до варьированной репризы в сонатной форме). Однако однократное применение принципа варьирования не создаёт на его основе форму. Вариационная форма возникает только при систематическом применении этого принципа, поэтому для её создания необходимо не менее 2 вариаций.
Тема вариаций может быть оригинальной (написанной самим композитором) или заимствованной.
Вариации могут наполняться совершенно разным содержанием: от очень простого до глубокого и философского (Бетховен. Ариетта из Сонаты № 32 для фортепиано).
1. Классификация
Вариации принято классифицировать по четырём параметрам:
- По тому, затрагивает ли процесс варьирования тему или только сопровождающие голоса выделяют:
- Прямые вариации
- Косвенные вариации
- По степени изменения:
- Строгие (в вариациях сохраняются тональность, гармонический план и форма темы)
- Свободные (широкий диапазон изменений, в том числе гармонии, формы, жанрового облика и т. д.; связи с темой порой условны: каждая вариация может достигать самостоятельности как пьеса с индивидуальным содержанием)
- По тому, какой метод варьирования преобладает:
- Полифонические
- Гармонические
- Фактурные
- Тембровые
- Фигурационные
- Жанрово-характерные
- По количеству тем в вариациях:
- Однотемные
- Двойные (двухтемные)
- Тройные (трехтемные)
В процессе развития этой формы укрепились несколько основных типов вариаций с относительно стабильной комбинацией указанных признаков. Это: вариации на выдержанную мелодию, вариации на basso ostinato, фигурационные вариации и жанрово-характерные вариации. Эти типы существовали параллельно (по крайней мере с XVII века), но в разные эпохи какие-то из них были более востребованы. Так, композиторы эпохи барокко чаще обращались к вариациям на basso ostinato, венские классики — к фигурационным, композиторы-романтики — к жанрово-характерным. В музыке XX века все эти типы сочетаются, появляются новые, когда в качестве темы может выступать отдельный аккорд, интервал и даже отдельный звук.
Кроме того, существуют несколько специфических типов вариаций, которые встречаются реже: это вариационная кантата (см. Кантата) эпохи барокко и вариации с темой в конце (появившиеся на исходе XIX века).
Определенным родством с вариационной формой обладают куплетно-вариационная и куплетно-вариантная форма (см. Куплетные формы). Близка вариациям также хоральная обработка XVIII века.
Важно отметить, что во многих произведениях применяются разные типы варьирования. Например, начальная группа вариаций может быть вариациями на выдержанную мелодию, далее — цепь фигурационных вариаций.
2. Организация формы
Любой вариационный цикл — разомкнутая форма (то есть новые вариации можно в принципе прибавлять бесконечно). Поэтому перед композитором встает задача создать форму второго порядка. Это может быть «волна» с нарастанием и кульминацией, либо любая типовая форма: наиболее часто это трёхчастная форма или рондо. Трёхчастность возникает в результате введения контрастной вариации (или группы вариаций) в середине формы. Рондообразность возникает вследствие неоднократного возвращения контрастного материала.
Часто вариации объединяются в группы, создавая локальные нарастания и локальные кульминации. Это достигается за счёт единой фактуры или за счёт ритмического нарастания (диминуирование). Ради придания форме рельефности и чтобы как-то разбить непрерывный поток сходных вариаций, уже в классическую эпоху в развёрнутых циклах одна или несколько вариаций проводились в другом ладу. В вариациях XIX века это явление усилилось. Теперь уже отдельные вариации могут проводиться в других тональностях («Симфонические этюды» Шумана — при исходном cis-moll, есть вариации в E-dur и gis-moll, финальная вариация — Des-dur).
Возможны различные окончания вариационного цикла. Завершение может быть сходным с началом либо, наоборот, максимально контрастным. В первом случае в конце произведения проводится тема в близком к первоначальному варианте (Прокофьев. Концерт для фортепиано с оркестром № 3, 2-я часть). Во втором окончание представляет собой максимум продвижения в данном направлении (например, самые мелкие во всем цикле длительности). Ради контраста финальной вариации может меняться метр и жанр (частое явление у Моцарта). Как наибольший контраст гомофонной теме в конце цикла может звучать фуга (в классическую и послеклассическую эпоху).
3. Вариации на выдержанную мелодию
В вариациях этого типа сохраняется мелодия, а варьирование происходит за счёт сопровождающих голосов[1]. В силу этого они принадлежат к косвенным вариациям.
Вариации на выдержанную мелодию применяются в основном в вокальной музыке, неизменность мелодии сближает их с куплетными формами (отличие в том, что в этих формах меняется не сопровождение темы, а текст). Их любили русские композиторы — этот тип варьирования особенно соответствовал духу русской песни, соответственно и применялся в операх в хорах и песнях народного характера. В западноевропейской музыке в качестве самостоятельного произведения вариации на выдержанную мелодию — редкость (Гайдн. Квартет ор. 76 № 3, 2-я часть), но в фигурационнных циклах венских классиков могут применяться в качестве начальных вариаций.
Иногда в куплетной форме варьируется не только текст, но и сопровождение (тогда она называется куплетно-вариационной или куплетно-вариантной). Тогда отличия от вариационной формы переходят в количественную категорию. Если изменения сравнительно невелики и не меняют общий характер, то форма ещё остается куплетной, при более масштабных изменениях она переходит в разряд вариационных.
Применительно к этому типу вариаций несколько меняется понятие строгости и свободы. Строгими называются те вариации, где мелодия остаётся на исходной высоте. Обычная для строгих вариаций неизменность гармонизации здесь неактуальна.
3.1. Тема
Тема может быть оригинальной или заимствованной, обычно из народной музыки. Форма темы не регламентирована. Это могут быть одна-две фразы, период, большое предложение, вплоть до простой трехчастной формы (Григ. «В пещере горного короля» из музыки к драме «Пер Гюнт»). Возможны оригинальные формы в случае народного происхождения темы (хор раскольников из III действия «Хованщины» М. Мусоргского).
3.2. Варьирование
Поскольку тема (строго говоря, мелодия) практически неизменна, варьирование может быть фактурным, тембровым, полифоническим, гармоническим и жанровым.
Фактурно-тембровое варьирование предполагает изменение фактуры, введение нового рисунка, переоркестровку, в хоре — передачи мелодии другим голосам. При полифоническом варьировании композитор вводит новые подголоски или достаточно самостоятельные мелодические линии. Возможно полифоническое оформление самой темы в виде канона и т. п. Гармоническое варьирование выражается в перегармонизации мелодии. Масштабы изменений могут быть разными, вплоть до изменения лада (Глинка. «Персидский хор» из «Руслана и Людмилы», 3-я вариация) или даже переноса мелодии в другую тональность (Римский-Корсаков. Хор «Высота» из оперы «Садко»). Жанровое варьирование возникает тогда, когда все перечисленные типы варьирования приводят к образованию нового жанрового облика темы. Этот тип варьирования в вариациях на выдержанную мелодию редок.
4. Вариации на basso ostinato
Вариациями на basso ostinato называется такая форма, которая основана на неизменном проведении темы в басу и постоянном обновлении верхних голосов.
В XVII — начале XVIII века это самый распространенный тип вариаций. В классическую эпоху он исчезает, так как не имеет процессуальности, необходимой в классической эстетике, а способствует скорее углублению одного состояния. Хотя иногда встречается на локальных участках формы (Бетховен. Симфония № 9, кода 1-й части). Отчасти вариациями на basso ostinato являются знаменитые 32 вариации до минор Бетховена. Неактуален этот тип и для романтиков, применялся он ими редко (Брамс. Финал Симфонии № 4). Интерес к вариациям на basso ostinato снова возникает в XX веке. Их используют все крупные композиторы. У Шостаковича пример таких вариаций есть даже в опере (антракт между 4-й и 5-й картинами оперы «Катерина Измайлова»).
Два основных инструментальных жанра таких вариаций в эпоху барокко — пассакалия и чакона. В английской музыке эта форма вариаций называется «граунд» (англ. ground). В вокальной музыке применяется в хорах (И. С. Бах. Crucifixus из Мессы си минор) или в ариях (Пёрселл. Ария Дидоны из оперы «Дидона и Эней»).
4.1. Тема
Тема — небольшая (2-8 тактов, обычно — 4) одноголосная последовательность в разной степени мелодизированная. Обычно ее характер очень обобщённый. Множество тем представляют собой нисходящее движение от I к V ступени, часто хроматическое. Бывают темы менее обобщенные и более мелодически оформленные (Бах. Пассакалия до минор для органа).
4.2. Варьирование
В процессе варьирования тема может переходить в верхние голоса (Бах. Пассакалия до минор для органа), фигурированно изменяться и даже транспонироваться в другую тональность (Букстехуде. Пассакалия ре минор для органа).
В силу краткости темы часто имеет место объединение вариаций попарно (по принципу сходной фактуры верхних голосов). Границы вариаций не всегда четко совпадают во всех голосах. У Баха часто несколько вариаций в одной фактуре образуют единое мощное развитие, их границы пропадают. Если этот принцип проводится на протяжении всего произведения, целое трудно назвать вариациями, так как нельзя признать вариациями проведения баса в нижнем голосе без учёта верхних. Возникает своеобразный контрапункт формы.
Завершение цикла может выходить за пределы вариаций. Так, органная Пассакалия Баха заканчивается большой фугой.
5. Фигурационные вариации
В таком типе вариаций преобладающий метод варьирования — гармоническая или мелодическая фигурация. В силу этого область применения таких вариаций — почти исключительно инструментальная музыка. Особенно часто встречаются в музыке венских классиков[2]. У них это может быть самостоятельная пьеса (множество вариационных циклов Моцарта, Бетховена) или часть цикла (финал, медленная часть, реже — первая). В романтическую эпоху преобладают самостоятельные пьесы в форме фигурационных вариаций, причем они могут иметь другое жанровое название (например, «Колыбельная» Шопена).
5.1. Тема
Важное слагаемое темы — гармония (в отличие от предыдущего типа). В подавляющем большинстве случаев тема написана в гомофонной фактуре. Фактура экономная, что даёт свободу дальнейшего её изменения и накопления движения в фактуре (за счёт уменьшения длительностей).
Поскольку большинство примеров принадлежит композиторам венской школы и их последователям, в большинстве случаев классична и форма темы. Чаще всего — простая двухчастная (обычно репризная), иногда трёхчастная, намного реже — период. В в музыке композиторов барокко возможна тема в форме бар.
5.2. Варьирование
В фигурационных вариациях осуществляется прямое варьирование, так как преобразуется сама тема.
При этом применяются типовые фигуры — фигурации. Они могут быть арпеджированными, гаммообразными и т. п. Сохраняются опорные точки мелодии, которые заполняются фигурированным материалом. Мелодическая фигурация часто возникает в результате появления неаккордовых звуков вокруг этих опорных точек. Гармоническая фигурация — то или иное движение по звукам аккорда (часто — арпеджио). При этом опорные точки мелодии становятся основанием или вершиной этих фигураций. В результате эти опорные точки могут смещаться на другие доли такта.
Большинство циклов фигурационных вариаций — строгие, так как обновление фактуры почти не затрагивает гармонию, никогда не меняя ее кардинально. Однако есть примеры свободных фигурационных вариаций («Вариации на тему Корелли» Рахманинова).
6. Жанрово-характерные вариации
К этому типу принадлежат вариационные циклы, в которых вариации приобретают новый жанр, либо где каждая вариация обладает своим индивидуальным типом выразительности.
Как и фигурационные вариации, жанрово-характерные главным образом применяются в инструментальной музыке. Они могут быть частью цикла, нередко — самостоятельной пьесой, в том числе с другим жанровым названием (Лист. Этюд «Мазепа»). Иногда отдельные жанровые вариации появляются в вариационных циклах уже у венских классиков. Циклы, целиком состоящие из таких вариаций, распространяются в послеклассическую эпоху.
6.1. Тема
Тема во многом аналогична теме фигурационных вариаций. Отличие в том, что тема жанровых вариаций может быть изложена менее скромно, чем вариационных, так как варьирование здесь идет в меньшей мере за счёт обогащения фактуры.
6.2. Варьирование
Понятие характерности предполагает индивидуальный тип выразительности для каждой вариации. Понятие жанровости — новый жанр для каждой вариации. Наиболее часто встречающиеся жанры: марш, скерцо, ноктюрн, мазурка, романс и др. (причем эти жанры могут быть выражены очень обобщенно). Иногда среди вариаций возникает фуга, которая понимается как жанр. (Чайковский. Трио «Памяти великого артиста», 2-я часть).
7. Вариации на несколько тем
Кроме вариаций на одну тему, встречаются вариации на две темы (двойные) и на три (тройные). Двойные вариации редки, тройные — исключительны (Балакирев. Увертюра на темы трех русских песен).
Темы двойных вариаций могут быть близки друг другу или, наоборот, контрастны («Камаринская» Глинки).
Расположены вариации могут быть по-разному: либо регулярное чередование вариаций на одну и вторую тему, либо — группа вариаций на первую тему, затем группа — на вторую и т. д.
Двойные и тройные вариации могут быть любого типа.
8. Вариации с темой в конце
Возникновение этого типа вариаций связано с отходом от классического мышления в области формы, которое требовало темы в начале и ее дальнейшего развития. Появляются они в самом конце XIX века (прецеденты были в эпоху барокко в некоторых вариационных кантатах).
Наиболее значительные сочинения такого рода: симфонические вариации «Иштар» Венсана д’Энди (1896), Третий фортепианный концерт Р. Щедрина (1973), фортепианный концерт Шнитке (1979).
Какая-либо регламентация формы отсутствует. В концерте Щедрина вариации соединяются очень сложно, вплоть до их асинхронного начала в оркестре и в партии солиста. Элементы темы разбросаны по всему концерту, целиком она возникает в заключительной каденции. В концерте Шнитке тема — комплекс, включающий додекафонную серию, трезвучия и речитацию на одном звуке.
Примечания
- В советской музыкальной теории этот тип вариаций называют «глинкинскими», так как М. И. Глинка часто использовал его в своих операх. Это название не корректно, потому что «глинкинские» вариации применяли ещё композиторы эпохи барокко. Другое иногда встречающееся название — «вариации на soprano ostinato». Оно тоже не совсем корректно, так как мелодия в процессе варьирования не всегда проводится в верхнем голосе (soprano).
- Поэтому часто называются «классическими». Этот термин не совсем верен, так как фигурационный тип вариаций применялся и до венской школы, и после.
Литература
- Кюрегян Т. Форма в музыке XVII—XX веков. М., 1998. ISBN 5-89144-068-7
- Фраёнов В. Музыкальная форма. Курс лекций. М., 2003. ISBN 5-89598-137-2
- Холопова В. Формы музыкальных произведений. Санкт-Петербург, «Лань», 1999. ISBN 5-8114-0032-2
wreferat.baza-referat.ru
Показатели вариации | Рефераты KM.RU
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Размах вариации (R)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2, 3, 4, 7 и 9 лет.
В нашем примере: лет;
Ответ: 2, 4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1, 25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия
Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
В нашем примере:
Дисперсия взвешенная:
Более удобно вычислять дисперсию по формуле:
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:
Для сгруппированных данных:
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком — через . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
,
средний квадрат отклонений
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий , а среднее квадратическое отклонение или 17, 1%.
Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.
Относительные показатели вариации
Относительные показатели вариации включают:
Коэффициент осцилляции
Относительное линейное отклонение (линейный коэффициент варианции)
Коэффициент вариации (относительное отклонение)
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
| Коэффициент осцилляции |
|
| Относительное линейное отклонение |
|
| Коэффициент вариации |
|
Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан
,
так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.
В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение , где — средний квартиль полусуммы разности третьего (или верхнего) квартиля () и первого (или нижнего) квартиля ().
.
На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).
Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологии при , а по другой — при. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (. Относительная мера вариации (позволяет сделать противоположный вывод
Пример расчета показателей вариации
На этапе отбора кандидатов для участия в осуществлении сложного проекта фирма объявлила конкурс профессионалов. Распределение претендентов по опыту работы показало средующие результаты:
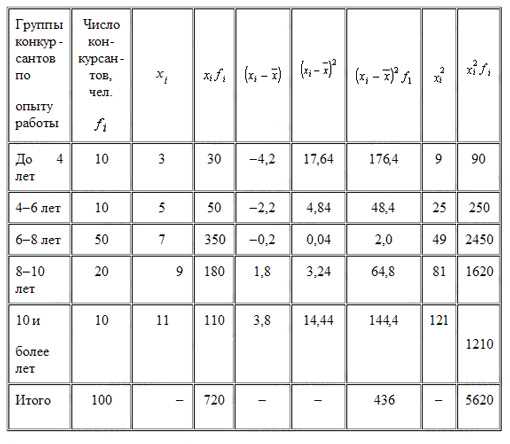
Вычислим средний производственный опыт работы, лет
Рассчитаем дисперсию по продолжительности опыта работы
Такой же результат получается, если использовать для расчета другую формулу расчета дисперсии
Вычислим среднее квадратическое отклонение, лет:
Определим коэффициент вариации, %:
Правило сложения дисперсий
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).
Общая дисперсия характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
— групповые средние,
— численность единиц i-й группы
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— дисперсия i-ой группы.
Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()
Эмпирический коэффициент детерминации () характеризует долю межгрупоовой дисперсии в общей дисперсии:
и показывает насколько вариация признака в совокупности обусловлена фактором группировки.
Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }
оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениями являются нуль и единица. Чем ближе к единице, тем теснее связь.
Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:
При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.
Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади: Общую дисперсию определим по формуле:
.
Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:
а) для домов, построенных вблизи центра:
б) для домов, построенных далеко от центра:
Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии:
Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии
Найденные дисперссии в сумме дают величину общей дисперсии
Эмпирический коэффициент детерминации:
показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81, 8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18, 2% — другими факторами.
Эмприческое корреляционное отношение свидетельствует о существенном влиянии на стоимость жилья месторасположения домов.
Правило сложения дисперсий для доли признака записывается так:
а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:
общая дисперсия:
Формулы межгрупповой и внутригрупповой дисперсий:
Характеристики формы распределения
Для получения представления о форме распределения используются показатели среднего уровня (средняя арифметическая, мода, медиана), показатели вариации, ассиметрии и эксцесса.
В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность , которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Ассиметричное распределение
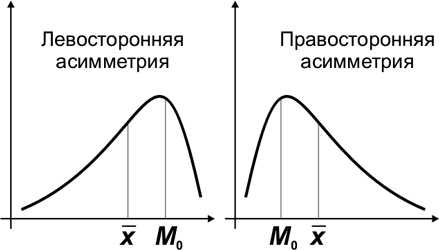
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
В качестве обобщающих характеристик вариации используются центральные моменты распределения -го порядка , соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:
Для сгруппированных данных:
Момент первого порядка согласно свойству средней арифметической равен нулю .
Момент второго порядка является дисперсией .
Моменты третьего и четвертого порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях , как все центральные моменты нечетного порядка.Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если , то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если , то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (). Для нормального распределения , поэтому эксцесс находят по формуле:
Для нормального распределения обращается в нуль. Для островершинных распределений , для плосковершинных .
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения.
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение, полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределах от величины средней. При этом в границах находится около 70% всех единиц, а в пределах — 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.grandars.ru
Дата добавления: 02.03.2013
www.km.ru
Средние величины и показатели вариации
14
Реферат
Средние величины и показатели вариации
Содержание
1.Сущность средних в статистике
2.Виды средних величин и способы их расчёта
3.Основные показатели вариации и их значение в статистике
1. Сущность средних величин в статистике
В процессе изучения массовых социально-экономических явлений возникает необходимость выявления их общих свойств, типичных размеров и характерных признаков. Необходимость в обобщающем среднем показателе возникает в том случае, когда признаки, характеризующие единицы изучаемой совокупности, количественно варьируют. Например, размер дневной выработки ткачей на текстильной фабрике зависит от общих условий производства, ткачи используют одинаковое сырьё, работают на одинаковых станках и т.д. В то же время часовая выработка отдельных ткачей колеблется, т.е. варьирует, так как зависит от индивидуальных особенностей каждого ткача (его квалификации, профессионального опыта и т.д.). Чтобы характеризовать дневную выработку всех ткачей предприятия, необходимо исчислить среднюю величину дневной выработки, так, как, только, в, этом, показателе найдут отражение общие для ткачей условия производства.
Таким образом, исчисление средних обобщающих показателей означает отвлечение (абстрагирование) от особенностей, отражающихся в величине признака у отдельных единиц, и выявление общих для данной совокупности типичных черт и свойств.
Таким образом, средней величиной в статистике является обобщённая, количественна характеристика признака и статистической совокупности. Она выражает характерную, типичную величину признака у единиц совокупности, образующихся в данных условиях места и времени под влиянием всей совокупности факторов. Действие разнообразных факторов порождает колебание, вариацию усредняемого признака. Средняя величина является общей мерой их действия, равнодействующей всех этих факторов. Средняя величина характеризует совокупность по усредняемому признаку, но относится к единице совокупности. Например, средняя выработка продукции на одного рабочего данного предприятия представляет собой отношение всей выработки (за любой период времени) к общей (средней за тот же период) численности его рабочих. Она характеризует производительность труда данной совокупности, но относится к одному рабочему. В средней величине массового явления погашаются индивидуальные различия единиц статистической совокупности в значениях усредняемого признака, обусловленные случайными обстоятельствами. Вследствие этого взаимопогашения в средней проявлявляется общее, закономерное свойство данной статистической совокупности явлений. Между средней и индивидуальными значениями осреднённого признака существует диалектическая связь как между общим и отдельным. Средняя является важнейшей категорией статистической науки и важнейшей формой обобщающих показателей. Многие явления общественной жизни становятся ясными, определёнными, лишь, будучи обобщенными, в форме средних величин. Таковы, например, упомянутая выше производительность труда, совокупность рабочих, урожайность сельскохозяйственных культур и т.д. Средняя выступает в статистике важнейшим методом научного обобщения. В этом смысле говорят о методе средних величин, который широко применяется в экономической науке. Многие категории экономической науки определяются с использованием понятия средней.
Основным условием правильного применения средней величины является однородность статистической совокупности по усредняемому признаку. Однородной статистической совокупностью называется такая совокупность, в которой её составные элементы (единицы) сходны между собой по существенным для данного исследования признакам и относятся к одному и тому же типу явлений. Однородная совокупность, будучи однородна по одним признакам, может быть разнородной по другим. Только в средних для таких совокупностей проявляются специфические особенности, закономерности развития анализируемого явления. Средняя вычисленная для неоднородной статистической совокупности, т.е. такой в которой объединены качественно различные явления, теряет своё научное значений. Такие средние являются фиктивными, не только не дающими представления о действительности, но и искажающими её. Для формирования однородных статистических совокупностей производится соответствующая группировка. С помощью группировок и в качественно однородной совокупности могут быть выделены характерные в количественном отношении группы. Для каждой из них может быть вычислена своя средняя, называемая средней групповой (частной) в отличие от общей средней (для совокупности в целом).
2. Виды средних величин
Большое значение в методологии средних величин имеют вопросы выбора формы средней, т.е. формулы по которой можно правильно вычислить среднюю величину, и выбора весов средней. Наиболее часто в статистике применяются средняя агрегатная, средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратичная, мода и медиана. Применение той или иной формулы зависит от содержания усредняемого признака и конкретных данных, по которым её необходимо рассчитать. Для выбора формы средней можно воспользоваться так называемым средним исходным соотношением.
2.1 Средняя арифметическая
Средняя арифметическая - одна из наиболее распространенных форм средней величины. Средняя арифметическая рассчитывается как частное от деления суммы индивидуальных значений (вариантов) варьирующего признака на их число. Средняя арифметическая применяется в тех случаях, когда объём варьирующего признака явлений однородной статистической совокупности, образуется путём суммирования значений признака всех единиц явлений статистической совокупности. Различают следующие средне арифметические величины:
1) Простая средняя арифметическая, которая определяется путём простого суммирования количественных значений варьирующего признака и деления этой сумы на их варианты и рассчитывается по следующей формуле:
где:
Х - средняя величина статистической совокупности,
xi- сумма отдельных варьирующих вариантов явлений статистической совокупности,
ni - количество варьирующих вариантов явлений статистической совокупности.
2) Среднеарифметическая взвешенная - средняя величина признака явления, вычисленная с учётом весов. Веса средних величин - частоты, с которыми отдельные значения признака осредняемого принимаются в расчёт при исчислении его средней величины. Выбор весов средней величины зависит от сущности усредняемого признака и характера данных, которыми располагают для вычисления средних величин. В качестве весов средних величин могут быть показатели численности единиц или размеры частей статистической совокупности (в форме абсолютных или относительных величин), обладающих данным вариантом (значением) усредняемого признака явления статистической совокупности, а также величины показателя связанного с усредняемым признаком. Среднеарифметическая взвешенная рассчитывается по следующей формуле:
где:
X- средняя арифметическая взвешенная,
х - величина отдельных варьирующих вариантов явлений статистической совокупности,
f - веса.
Назначение простой, и взвешенной средней арифметической является определение среднего значения варьирующего признака. Если в изучаемой статистической совокупности варианты значений признака встречаются по одному разу или имеют одинаковый вес, то применяется простая средняя арифметическая, если же варианты значений данного признака встречаются в изучаемой совокупности по несколько раз или имеют различные веса, для определения среднего значения варьирующего признака применяется средняя арифметическая взвешенная.
2.2 Средняя гармоническая
Средняя гармоническая применяется для расчёта средней величины тогда, когда непосредственные данные о весах отсутствуют, а известны варианты усредняемого признака (х) и произведения значений вариантов на количество единиц, обладающих данным его значением w (w = xf).
Данная средняя рассчитывается по следующим формулам:
1.) Среднегармоническая простая:
где:
Х - средняя гармоническая простая,
х - сумма отдельных варьирующих вариантов явлений статистической совокупности,
n - количество варьирующих вариантов явлений статистической совокупности.
2) Среднегармоническая взвешенная:
где:
Х - средняя гармоническая взвешенная,
х - сумма отдельных варьирующих вариантов явлений статистической совокупности,
w - x f,
f - веса.
При использовании гармонической взвешенной выявляют веса и таким образом получают тот же результат, который дал бы расчёт по средней арифметической взвешенной, если бы были известны все необходимые для этого данные.
2.3 Средняя агрегатная
Средняя агрегатная рассчитывается по формуле:
где:
X - средняя агрегатная,
w - x f,
х - сумма отдельных варьирующих вариантов явлений статистической совокупности,
f - веса.
Средняя агрегатная вычисляется в тех случаях, когда известны (имеются) значения числителя и значения знаменателя исходного соотношения средней.
2.4 Средняя геометрическая
Средняя геометрическая является одной из форм средней величины и вычисляется как корень n-й степени из произведения отдельных значений - вариантов признака (х) и определяется по следующей формуле:
Или
Средняя геометрическая применяется в основном при расчётах средних темпов роста.
2.5 Мода и медиана
Наряду с рассмотренными выше средними в качестве статистических характеристик вариационных рядов рассчитываются так называемые структурные средние - мода и медиана.
Модой (Мо) называется наиболее часто встречающееся значение признака у единиц совокупности. Для дискретных рядов - этот вариант, имеющий наибольшую частоту.
В интервальных вариационных рядах можно определить, прежде всего, интервал, в котором находится мода, т.е. так называемый модальный интервал. В вариационном ряду с равными интервалами модальный интервал определяется по наибольшей частоте, в рядах с неравными интервалами по наибольшей плотности распределения.
Для определения моды в рядах с равными интервалами пользуются формулой следующего вида:
где:
Хн - нижняя граница модального интервала,
h - величина интервала,
f1, f2, f3 - частоты (или частности) соответственно предмодального, модального и послемодального интервалов.
В интервальном ряду моду можно найти графически. Для этого в самом высоком столбце гистограммы от границ двух смежных столбцов проводят две линии. Затем из точки их пересечения опускают перпендикуляр на ось абсцисс. Значение признака на оси абсцисс, соответствующее перпендикуляру, и будет модой.
Во многих случаях при характеристике совокупности в качестве обобщённого показателя отдаётся предпочтение моде, а не средней арифметической.
Так, при изучении цен на рынке фиксируется и изучается в динамике не средняя цена на определённую продукцию, а модальная; при изучении спроса населения на определённый размер обуви или одежды представляет интерес определение модального размера обуви, а средний размер как таковой здесь вообще не имеет значения. Мода представляет не только самостоятельный интерес, но и исполняет роль вспомогательного показателя при средней, характеризуя её типичность. Если средняя арифметическая близка по значению к моде, значит она типична.
Медианой (Ме) называется значение признака у средней единицы ранжированного ряда. (Ранжированным называют ряд, у которого значения признака записаны в порядке возрастания или убывания.)
Чтобы найти медиану, сначала определяется её порядковый номер. Для этого при нечётном числе единиц к сумме всех частот прибавляется единица, и всё делится на два. При чётном числе единиц в ряду будет две средних единицы, и по всем правилам медиана должна определяться как средняя из значений этих двух единиц. При этом практически при чётном числе единиц медиана отыскивается как значение признака у единицы, порядковый номер которой определяется по общей сумме частот, делённой на два. Зная порядковый номер медианы, легко по накопленным частотам найти её значение.
В интервальных рядах после определения порядкового номера медианы по накопительным частотам (частностям) отыскивается медиальный интервал, а затем при помощи простейшего интерполяционного приёма определяется значение самой медианы. Этот расчёт выражает следующая формула:
где:
Xn- нижняя граница медианного интервала,
h - величина медианного интервала,
- порядковый номер медианы,
SMe- 1 частота (частотность), накопленная до медианного интервала,
FMe- частота (частность) медианного интервала.
Согласно записанной формуле к нижней границе медианного интервала прибавляется такая часть величины интервала, которая приходится на долю единиц этой группы, недостающих до порядкового номера медианы. Другими словами, расчёт медианы построен на предположении, что нарастание признака среди единиц каждой группы происходит равномерно. На основе сказанного можно рассчитать медиану и по иному. Определив медианный интервал, можно из верхней границы медианного интервала (Хв) вычесть ту часть интервала, которая приходится на долю единиц, превышающих порядковый номер медианы, т.е. по следующей формуле:
Медиану можно также определить и графически. Для этого строиться кумулята и из точки на шкале накопленных частот (частностей), соответствующей порядковому номеру медианы, проводится прямая, параллельная оси х до пересечения с кумулятой. Затем из точки пересечения указанной прямой с куммулятой опускается перпендикуляр на ось абсцисс. Значение признака на оси абсцисс, соответствующее проведённой ординате (перпендикуляру), и будет медианой.
По такому же принципу легко найти значение признака у любой единицы ранжированного ряда.
Таким образом, для расчёта средней величины вариационного ряда можно использовать целую совокупность показателей.
3. Основные показатели вариации и их значение в статистике
При изучении варьирующего признака у единиц совокупности нельзя ограничиваться лишь расчётом средней величины из отдельных вариантов, так как одна и та же средняя может относиться далеко не к одинаковым по составу совокупностям. Это можно проиллюстрировать следующим условным примером, отражающим данные о числе дворов в агрохозяйствах двух районов:
Среднее число дворов в агрохозяйствах двух районов одинаково - 160. При этом состав этих агрохозяйств в двух районах далеко не одинаков. Поэтому возникает необходимость измерить вариацию признака в совокупности.
Для этой цели в статистике рассчитывают ряд характеристик, т.е. показателей. Самым элементарным показателем вариации признака является размах вариации R, представляющий собой разность между максимальными и минимальными значениями признака в данном вариационном ряду, т.е. R = Xmax - Xmin. В нашем примере в 1 районе R = 300 - 80 - 220, а во втором районе R = 180 - 145 = 35.
Показатель размаха вариации не всегда применим, так как он учитывает только крайние значения признака, которые могут сильно отличаться от всех других единиц. Иногда находят отношение размаха вариации к средней арифметической и пользуются этой величиной, именуя её показателем осцилляции.
Более точно можно определить вариацию в ряду при помощи показателей, учитывающих отклонения всех вариантов от средней арифметической. Таких показателей в статистике два - среднее линейное и среднее квадратическое отклонение.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных величин отклонений вариантов от средней. Знаки отклонений в данном случае игнорируются, в противном случае сумма всех отклонений будет равна нулю. Данный показатель рассчитывается по формуле:
а) для несгрупированных данных:
б) для вариационного ряда:
Следует иметь в виду, что среднее линейное отклонение будет минимальным, если отклонения рассчитаны от медианы, т.е. по формуле:
Среднее квадратическое отклонение () исчисляется следующим образом - каждое отклонение от средней возводится в квадрат, все квадраты суммируются (с учётом весов), после чего сумма квадратов делиться на число членов ряда и из частного извлекается корень квадратный.
Все данные действия выражаются следующими формулами:
а) для несгрупированных данных:
б) для вариационного ряда:
f, т.е. среднее квадратическое отклонение предятавляет собой корень квадратный из средней арифметической квадратов отклонений средней. Выражение под корнем носит название дисперсии. Дисперсия имеет самостоятельное выражение в статистике и относится к числу важнейших показателей вариации.
referatwork.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|





