2. Подходы в теории удара С физической точки зрения ударные силы – отклик на деформации, возникающие вблизи площадки контакта и волнообразно распространяющиеся в данных телах. Математические модели отражают этот процесс с большей или меньшей полнотой. В классической теории удара деформации не учитываются и проблема сводится к определению интегральных характеристик ударных сил – их импульсов. В основе этой теории лежат законы механики и некоторые дополнительные гипотезы. Рассмотрим для примера простейшую задачу о прямом ударе двух шаров с массами m1 и m2.
На рисунке шары массой m1 и m2. до соударения имеют скорости v1- и v2- требуется найти их скорости после удара.
Закон сохранения импульса выражается формулой:
m1 v1i + m2 v2i = m1 v1 + m2 v2
где v1i и v2i ; v1 и v2 соответствуют до – и послеударным значениям скоростей. Этого единственного уравнения недостаточно для определения двух неизвестных v1 и v2. Чтобы построить единственное решение, можно принять одну из следующих гипотез: суммарная кинетическая энергия при ударе сохраняется (абсолютно упругий удар), шары после удара не разделяются, т.е. v1 = v2 (абсолютно неупругий удар). Можно выбрать более общую гипотезу Ньютона, согласно которой
v2 - v1 = e ( v1i - v2i )
Коэффициент восстановления e, как экспериментально установил Ньютон, зависит от материала шаров и лежит в пределах от нуля до единицы. Волновая теория удара, восходящая к Б. Сен – Венану, наиболее полно описывает напряженное состояние соударяемых тел. В ее основе лежит довольно сложные уравнения математической физики, допускающие точное решение лишь в исключительных случаях. В общем случае использование волновой теории нецелесообразно, в частности, с ее помощью не удается решить рассмотренную задачу об ударе шаров. Компромиссом между этими двумя крайними подходами служат модели, частично учитывающие деформации. Идею таких методов предложил Даламбер, который мысленно помещал маленькую пружинку (деформируемый элемент) в точку ударного контакта. С математической точки зрения проблема удара сводится к решению обыкновенных дифференциальных уравнений, что не представляет принципиальных трудностей. В вышеприведенном примере идеальная пружинка не рассеивает энергию, поэтому удар будет абсолютно упругим.
3. Упругое соударение тел При упругом соударении тел тела претерпевают упругую деформацию. При этом кинетическая энергия движущихся тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Взаимодействующие тела представляют собой замкнутую систему, если на них не действуют силы со стороны других тел. В замкнутых системах выполняются законы сохранения энергии и импульса. Зная движение тел до столкновения и применяя законы сохранения, можно определить движение тел после столкновения. Но при этом мы ничего не узнаем о том, как происходит само столкновение. Для решения же ряда задач о столкновении микрочастиц, как правило, достаточно знать об их движении после взаимодействия. "Моделью" для задач подобного рода служит задача о столкновении шаров. Если шары катаются по гладкой горизонтальной поверхности, и если силой трения качения можно пренебречь, то систему из двух шаров можно считать замкнутой. Существует два предельных вида удара: абсолютно неупругий и абсолютно упругий. Столкновение (соударение) - это кратковременное взаимодействие, при котором тела непосредственно касаются друг друга. Анализ явлений, имеющий место при ударе упругих сплошных тел, довольно сложен, поэтому рассмотрим самый простой случай - центральное соударение двух однородных шаров. Соударение называется центральным, если векторы скорости шаров до удара направлены по прямой, проходящей через их центры. Абсолютно упругие и неупругие столкновения - это идеальные случаи. На практике они могут быть реализованы лишь с определенной степенью приближения. В произвольном случае соударения шаров справедливы законы сохранения импульса и энергии: Абсолютно упругим называется такой удар, после которого во взаимодействующих телах не остается никаких деформаций и суммарная кинетическая энергия, которой обладали тела до удара, равна кинетической энергии тел после удара. Чтобы удар был абсолютно упругим, взаимодействующие тела должны обладать определенными свойствами. А именно, силы, возникающие при ударе, должны зависеть от величины деформации и не зависеть от ее скорости. Наиболее близкими к этим свойствами обладают хорошие сорта стали, слоновая кость. Соударение таких тел происходит следующим образом. При ударе возникают деформации соударяющихся тел, а значит и силы, сообщающие ускорения обоим телам, в противоположных направлениях. В какой то момент времени скорости шаров становятся равными, деформации достигают максимального значения, силы продолжают действовать, изменяя скорости в тех же направлениях, что и раньше. Поэтому шары будут "отодвигаться" друг от друга, а деформации уменьшаться пока совсем не исчезнут. К этому моменту времени упругие силы, возникающие в телах, совершат такую же работу, какая была затрачена на деформацию. В результате вся кинетическая энергия, которой обладали тела до удара, снова перейдет в кинетическую энергию тела после удара. Для определения скорости тел после упругого взаимодействия рассмотрим удар двух шаров (материальных точек), образующих замкнутую систему.
3.1. Центральное упругое столкновение тел Имеются два сферических объекта (шарика) с массами m1 и m2. Предположим, что эти шарики движутся без вращения по одной оси и испытывают центральное упругое соударение. В этом случае закон сохранения импульса запишется в виде:
m1v1i + m2v2i = m1v1 + m2v2
где v1i и v2i - начальные скорости каждого объекта, а v1 и v2 - их конечные скорости. Закон сохранения энергии записывается в виде:
m1v1i2 / 2 + m2v2i2 / 2 = m1v12 / 2 + m2v22 / 2
Векторы скоростей шаров после упругого удара будут лежать на линии центров шаров, потому что силы взаимодействия во время удара вследствие симметрии будут направлены по этой же прямой. Закон сохранения импульса может быть преобразован следующим образом:
m1 (v1i - v1) = m2 (v2 - v2i)
Также преобразуем выражение для закона сохранения энергии
m1 (v1i2 - v12) = m2 (v22 - v2i2)
Если разница между начальной и конечной скоростями не равна нулю (то есть столкновение действительно произошло), мы можем разделить второе из двух последних уравнений на первое, что дает:
v1i + v1 = v2 + v2i
или
v1i - v2i = v2 - v1
Другими словами, в одномерном случае упругих столкновений относительная скорость движения объектов после столкновения равняется относительной скорости движения до столкновения. Чтобы получить конечные скорости движения объектов через их начальные скорости и массы, нужно выразить v2 из последнего уравнения и подставить его в уравнение для закона сохранения импульса. Окончательно получаем:
v1 = v1i (m1 - m2) / (m1 + m2) + v2i (2 m2) / (m1 + m2)
Таким же способом находим выражение для v2
v2 = v1i (2 m1) / (m1 + m2) + v2i (m2 - m1) / (m2 + m1)
Далее предположим, что сталкиваются объекты с одинаковой массой, т.е. m1= m2 = m. В этом случае:
v1 = v1i (m - m) / (m + m) + v2i (2 m) / (m + m) v2 = v1i (2 m) / (m + m) + v2i (m - m) / (m + m)
Окончательно получаем, что
v1 = v2i и v2 = v1i
Это означает, что в случае центрального упругого соударения объектов с равными массами, они будут просто обмениваться скоростями. Если один из объектов до столкновения покоился, то после столкновения он остановится, а второй объект начнёт движение. При этом скорость движения второго объекта будет равна скорости первого объекта до столкновения. В общем случае центрального и абсолютно упругого столкновения объектов с разными массами, один из которых до столкновения покоился (v2i =0), можно записать следующие выражения для скоростей после удара:
v1 = v1i (m1 - m2) / (m1 + m2)
v2 = v1i (2 m1) / (m1 + m2)
Если масса налетающего шара m1 больше массы покоящегося шара m2, то v1 и v2 будут положительными и оба шара после столкновения будут двигаться в одном направлении, совпадающем с направлением начального движения налетающего шара. Если же масса налетающего шара m1 меньше массы покоящегося шара m2, то v1 будет отрицательной, а v2 - положительной, и шары после столкновения будут разлетаться в противоположных направлениях. При этом, т.к. 2 m1 > m1 - m2, то маленький шарик отразиться с большей скоростью. Такова картина удара двух любых тел, если начальная скорость направлена вдоль линии, соединяющей центры масс этих тел, и если силы взаимодействия направлены вдоль этой же линии центров. В противном случае удар будет представлять сложное явление. При нецентральном ударе шаров картина соударения будет иная.
3.2. Нецентральное упругое столкновение тел Здесь во время удара имеет место как приближение центров шаров друг к другу вследствие их деформации, так и скольжение поверхности одного шара по поверхности другого. Очевидно, что вследствие скольжения поверхностей возникнут силы трения, которые вместе с упругими силами взаимодействия определят изменение скорости шаров после удара. Кроме того, силы трения вызовут вращение шаров относительно их центров масс. Для того чтобы представить механизм удара, разложим векторы скоростей обоих шаров до удара на направление линии центров шаров и на направление перпендикулярное к этой линии. V1ц
V1i F'Т
V1п F'y Fy
V2i v2п
FT
V2ц
В следствии "скольжения" поверхности шаров возникнут силы трения F'T и FT, которые вместе с упругими силами взаимодействия F'y и Fy определят изменение скорости шаров после удара. Кроме того, силы трения вызовут вращение шаров вокруг центра. Только в том случае, когда силы трения FT очень малы по сравнению с упругими силами Fy, т.е. FT В этом случае задача о нецентральном столкновении шаров решается достаточно просто. Действительно, соединяя центры масс сталкивающихся шаров прямой и разложив скорость каждого шара на нормальную составляющую, направленную вдоль линии центров, и тангенциальную составляющую, перпендикулярную к ней. Так как согласно нашему предположению силы трения отсутствуют, то тангенциальные силы во время столкновения не возникают и, следовательно, тангенциальные скорости шаров изменяться не будут. Нормальные же составляющие скорости после удара можно определить на основании закона сохранения количества движения и закона сохранения энергии таким же путем, как и при центральном ударе. Запишем уравнения:
m1 v1ц + m2 v2ц = m1ц v' 1ц + m2 v'2ц
m1 ( v21п + v21ц ) + m2 (v22п + v22ц) = m1 ( v'21п + v21ц ) + m2 (v'22п + v22ц
здесь неизвестны только две величины: v'1ц и v'2ц. Общие закономерности нецентрального удара шаров в этом случае можно найти следующим путем. Предположим, что до удара шар 2 покоится, а шар 1 движется. Сила взаимодействия в момент удара проходит через центры шаров (нет трения), и ее направление зависит от "прицельного" расстояния ?, равного расстоянию центра покоящегося шара от линии полета центра другого шара (до удара). Плоскость чертежа совпадает с плоскостью, проходящей через центры шаров и вектор скорости шара 1.
F
2
r2
?
r1
Р 1
F'
Удар произойдет при условии ? По закону постоянства количества движения:
P = P1 + P2
где P – количество движения шара 1 до удара, P1 и P2 – количества движения шаров 1 и 2 после удара соответственно.
P2 P1
?
P
Закон сохранения энергии можно записать так:
P2/m1 = P21/m1 + P22/m2 Так как P = m v и mv2 = P2 / m для любого тела. Вектор P2 составляет угол ? с вектором P, покоившийся шар отскочит под углом ? к начальной скорости первого шара, тогда из треугольника векторов следует:
P21 = P22 + P2 - 2 P P2 cos ?
Учитывая постоянство энергии, исключаем P1 и получаем
P2 = 2 m2 P cos ? / (m1 + m2) = ? P cos ?
? = 2 m2 / (m1 + m2)
Отсюда видно, что общее соотношение между Р2 и Р зависит от угла ? и соотношения масс m1/m2. Следует различать два случая: m1 > m2 и m1
? Р2 Р1
А В Р ?
?Р
Точка В представляет центральный удар, оба шара летят после удара по одному направлению. Точка А представляет промах (шары не задели друг друга). Во втором случае, при m1 1 и шар 1 после удара может лететь назад. Угол отклонения налетающего шара ? изменяется от 0 до ?.
А В
?Р
Точка В представляет центральный удар. Каждому значению ? соответствует только одно значение ?. При одинаковых массах шаров m1 = m2 картина возможных количеств движения показана на рисунке.
Р2
А В ?
Угол ? изменяется от 0 до ?/2. При центральном ударе шар 1 останавливается, а шар 2 с той же скоростью движется далее (точка В). Угол разлета шаров ? + ? всегда равен ?/2. Угол ? нетрудно связать с прицельным расстоянием ? и показать, что
(r1 + r2)sin ? = ?
Зная ?, диаметры шаров и их массы, найдем ? и ?, по данным Р определим Р2 и Р1, которые в свою очередь определяют скорости и направления шаров после удара.
4. Неупругое соударение тел Абсолютно неупругим называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми. Чтобы это стало возможным, соударяющиеся тела должны обладать такими свойствами, что силы, возникающие при их деформации, зависят не от величины деформации, а от скорости изменения деформации. Такие свойства присущи, например, мягкой глине, пластилину. При неупругом соударении происходит следующее. В начальный момент удара скорость деформации велика (шары сжимаются), поэтому возникают значительные силы, сообщающие обоим шарам ускорения, направленные в противоположные стороны. По мере развития удара скорости деформации шаров уменьшаются, а сами деформации увеличиваются до тех пор, пока скорости шаров не окажутся равными. В этот момент деформации шаров перестанут изменяться, исчезнут силы, и оба шара будут двигаться с одинаковой скоростью. При абсолютно неупругом ударе выполняются законы сохранения импульса и полной энергии. Механическая же энергия тел до удара больше механической энергии после удара, так как она частично (или полностью) переходит во внутреннюю энергию тел и расходуется на работу по деформации тел. Для определения скорости тел после взаимодействия рассмотрим удар двух шаров (материальных точек), образующих замкнутую систему. Массы шаров m1 и m2, скорости до удара V1i и V2i. Согласно закону сохранения суммарный импульс шаров до удара должен быть таким же, как после удара:
m1 V1i + m2 V2i = (m1 + m2) U
где U - скорость после удара, одинаковая для обоих шаров. Из уравнения следует, что:
U = ( m1 V1i + m2 V2i ) / (m1 + m2)
Закон сохранения энергии для неупругого удара рассматриваемых шаров имеет следующий вид:
m1 V1i2 / 2 + m2 V2i2 / 2 = (m1 + m2 ) U2 + W
где W - изменение внутренней энергии системы. Кинетическая энергия тел до удара имеет следующую величину:
W1 = m1 V1i2 / 2 + m2 V2i2 / 2
А кинетическая энергия после удара:
W2 = (m1 + m2 ) U2/2 = ( m1 V1i + m2 V2i )2 /2 (m1 + m2)
Потери механической энергии, или часть энергии, которая перешла в тепловую форму составляет:
W = W1 - W2 = m1 m2 (V1i – V2i)2 / 2 (m1 + m2 )
Величина V1i – V2i представляет относительную скорость движения тел до удара. Поэтому энергия, перешедшая в тепло, зависит от соотношения масс соударяющихся тел m1 m2 /(m1 + m2 ) и относительной скорости движения их до удара. Энергию потерь можно рассматривать как кинетическую энергию некоторой эффективной массы:
m0 = m1 m2 / (m1 + m2)
движущихся с относительной скоростью V'i =V1i – V2i. Для конкретных расчетов скорости нужно спроектировать соотношение импульсов на выбранные направления. Если до удара скорости шаров направлены вдоль прямой, проходящей через их центры, удар называют центральным. Скорость шаров после такого удара будет направлена по той же прямой. Поэтому уравнение сохранения импульсов можно рассматривать как скалярное. Но скорости при этом надо считать совпадающими по знаку, когда они направлены в одну сторону и противоположными по знаку, когда они направлены в противоположные стороны. Рассмотрим некоторые частные случаи. 1. Шары движутся в одном направлении. Удар возможен, если скорости V1i и V2i различны. Например, V2i > V1i, т.е. второй шар догоняет первый. После удара шары будут двигаться в ту же сторону со скоростью большей, чем скорость первого шара и меньшей, чем скорость второго. Если при этом массы шаров одинаковы, то U =( V1i + V2i ) / 2
2. Шары движутся навстречу друг другу. После удара шары будут двигаться вместе в ту сторону, в которую двигался шар, обладающий большим импульсом. Если импульсы обоих шаров равны по величине, то после удара оба шара остановятся. 3. В случае нецентрального удара (рис.3.6.2а) скорости V1i и V2i можно разложить на составляющие V1X и V2X в направлении линии, соединяющей центры шаров (ось Х), и состaвляющие V1Y и V2Y в перпендикулярном направлении (ось У). Для составляющих V1X, V2X и V1Y,V2Y записать закон сохранения импульса в том же виде, как и при центральном ударе и определить составляющую результирующей скорости. Рассмотрим неупругий удар более подробно. При неупругом ударе часть кинетической энергии налетающего шара теряется с выделением тепла. В предельном случае абсолютно неупругого удара налетающее тело слепляется с покоящимся телом, кинетическая энергия их относительного движения обращается в ноль и они продолжают движение, как единое тело. В большинстве практических случаев мы имеем дело с частично упругим ударом, когда в теле после столкновения возбуждаются деформационные колебания, затухающие со временем. Возбуждение таких колебаний можно смоделировать при помощи двух одинаковых шариков, соединённых пружиной. Предположим, что абсолютно упругий шар сталкивается с пружинным осциллятором. Массы шаров одинаковы и равны m. Так как в момент удара пружина ещё не действует, налетающий шар останавливается, а левый шар осциллятора приводится в движение со скоростью налетающего шара v. При этом центр масс осциллятора движется со скоростью v/2. Со временем колебания осциллятора затухнут и он будет продолжать поступательное движение со скоростью v/2, а суммарная энергия всей системы составит лишь половину от энергии налетающего шара. Другая половина выделится в виде тепла в осцилляторе. Удар обычных неупругих тел соответствует промежуточному случаю между идеально упругим и полностью неупругим ударами. Ему аналогичен удар аналогичен удар двух шаров через неупругую пружину, которая сжимаясь за первую половину времени удара до некоторой величины, не примет своих первоначальных размеров после удара; или расталкивающая сила во время сжатия будет больше, чем во вторую половину времени удара при расширении пружины. Часть потенциальной энергии сжатия пружины перейдет в тепло и не будет обращена в кинетическую энергию движения. Следовательно, закон сохранения механической энергии в этом случае нельзя применять. Условие равенства скоростей после удара также не будет иметь места, как это было при полностью неупругом ударе, так как после удара оба тела движутся с различными скоростями. Неупругий удар можно характеризовать той долей энергии деформации, которая обращается в тепло за время удара. Но еще Ньютоном было найдено, что при неупругом ударе шаров из определенного материала величины относительных скоростей до и после удара находятся в постоянном отношении, и такой удар характеризуется коэффициентом восстановления относительной скорости после удара:
е = |V2 – V1| / |V2i – V1i|
где V2i – V1i – относительная скорость до удара, а V2 – V1 – после удара. Опыт показывает, что с некоторой степенью точности можно считать величину е постоянной и зависящей только от материала соударяющихся шаров. При идеально упругом ударе относительная скорость остается той же самой по величине, но меняет свой знак:
V1i – V2i = - (V1 – V2)
Коэффициент восстановления всегда меньше единицы, ибо при упругом ударе он равен единице, при полностью неупругом ударе равен нулю, так как в этом случае
V2 – V1 = 0 Зная коэффициент е, можно подсчитать скорости движения шаров после удара и потери энергии.
Используемая литература: 1. Д.В.Сивухин, "Общий курс физики. Механика", Наука, 1979 2. О.Д.Шебалин, "Физические основы механики и акустики", Высш. школа, 1981 3. С.П.Стрелков, "Механика", Наука, 1975 4. К.Шварц, Т.Гольдфарб, "Поиски закономерностей в физическом мире", пер. с англ., Москва, Мир, 1977 5. Лабораторные занятия по физике, под ред. Л.Л.Гольдина, Москва, Наука, 1983 6. А.И. Иванов, "Закономерности удара в механических системах", Природа, 1999, №10
9
www.ronl.ru
Реферат на тему:
Уда́р — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.
При ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии. Предполагается, что за время удара действием внешних сил можно пренебречь, тогда полный импульс тел при ударе сохраняется, в противном случае нужно учитывать импульс внешних сил. Часть энергии обычно уходит на нагрев тел.
Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара. Обычно рассматривают либо абсолютно упругий удар, либо вводят коэффициент сохранения энергии k, как отношение кинетической энергии после удара к кинетической энергии до удара при ударе одного тела о неподвижную стенку, сделанную из материала другого тела. Таким образом, k является характеристикой материала, из которого изготовлены тела, и (предположительно) не зависит от остальных параметров тел (формы, скорости и т. п.).
Если не известны потери энергии, происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначно движение тел после удара невозможно. В этом случае рассматривается зависимость возможных углов рассеяния и скоростей тел после удара от начальных условий. Например, при столкновении двух элементарных частиц рассеяние может произойти лишь в некотором диапазоне углов, определяющемся предельным углом рассеяния.
В общем случае решение задачи о столкновении кроме знания начальных скоростей требует дополнительных параметров.
Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.
Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Энергия, конечно же, никуда не исчезает, а переходит в тепловую.
Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.
При реальном ударе макроскопических тел происходит деформация соударяющихся тел и распространение по ним упругих волн, передающих взаимодействие от сталкивающихся границ по всему телу. Пусть сталкиваются одинаковые тела. Если c — скорость звука в теле, L — характерный размер каждого тела, то время удара будет порядка t = 2L / c. Множитель 2 соответствует распространению волны в прямом и обратном направлении. Соответственно, систему сталкивающихся тел можно считать замкнутой, если импульс внешних сил за время t мал по сравнению с импульсами тел. Кроме того, само время t должно быть достаточно мало, в противном случае становится проблематично оценить потери энергии на деформации за время удара (часть энергии всегда расходуется на внутреннее трение), а само описание сталкивающихся тел становится неполным из-за существенного вклада внутренних степеней свободы. Необходимо, чтобы все деформации при ударе были существенно меньше, чем размеры тел.
wreferat.baza-referat.ru
59
Лекция 5
Удар абсолютно упругих и неупругих ТЕЛ
Удар – столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Например: столкновение бильярдных шаров. Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Поэтому систему тел в процессе их соударения приближенно можно рассматривать как замкнутую систему и применять к ней законы сохранения.
Сущность удара: кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара происходит перераспределение энергии между соударяющимися телами. Опыт показывает, что относительная скорость тел после удара не достигает прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.
5.1. Центральный абсолютно упругий удар
Центральный удар – удар, при котором тела до удара движутся вдоль прямой, проходящей через их центр масс.
Абсолютно упругий удар – это столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Абсолютно упругий удар – это идеализация. При абсолютно упругом ударе выполняются законы сохранения импульса и механической энергии.
;
.
Скорости тел после упругого удара:
.
Получаем систему уравнений:
.
Подставим в первое уравнение:
;
;
;
.
;
;
.
Итак, скорости тел после абсолютно упругого удара:
;
.
Проанализируем эти выражения.
1. 
;
. Вывод: шары равной массы «обмениваются» энергией.
2. 
;
;
.
3. 
;
;
.
Вывод: если второй шар висел неподвижно (
), то после удара остановится первый шар (
), а второй будет двигаться с той же скоростью в том же направлении, в котором двигался первый шар до удара (
).
5.2. Центральный абсолютно неупругий удар
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое (общей массой). Например: шары из пластилина или свинца, движущиеся навстречу друг другу.
Пусть сталкиваются шары массами 
и
. Скорости шаров до удара 
и
,
общая скорость шаров после удара.
В случае абсолютно неупругого удара выполняется закон сохранения импульса:
,
следовательно, общая скорость шаров после удара:
.
Вывод: движение шаров навстречу друг другу. Шары будут продолжаться вместе в ту сторону, в которую движется шар, обладающий большим импульсом.
Если 
, то
.
В процессе центрального абсолютно неупругого удара шаров вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии. Следовательно, закон сохранения механической энергии не соблюдается.
«Потерю» можно определить по разности кинетической энергии тел до и после удара:
.
Учтем что 
.
Разность кинетических энергий до и после удара:
.
В случае, когда ударяемое тело неподвижно: 
;
.
Если 
(масса неподвижного тела очень большая), то
и почти вся кинетическая энергия при ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молота.
Абсолютно неупругий удар – пример того, как происходит «потеря» механической энергии под действием диссипативных сил.
Контрольные вопросы
Чем отличается абсолютно упругий удар от абсолютно неупругого? Дайте определения удара, центрального удара, абсолютно упругого удара, абсолютно неупругого удара.
Как определить скорости тел после центрального абсолютно упругого удара? Следствием каких законов являются эти выражения?
Выполняется ли закон сохранения механической энергии при абсолютно неупругом ударе? Получите выражение для «потери» кинетической энергии в случае абсолютно неупругого удара. Почему масса молотка должна быть больше массы забиваемого гвоздя?
Задачи
Из орудия массой 5 тонн вылетает снаряд массой 100 кг. Кинетическая энергия снаряда при вылете 7,5 МДж. Какую кинетическую энергию приобретает орудие вследствие отдачи. [150 кДж].
При центральном абсолютно упругом ударе движущееся тело массой 
ударяется о покоящееся тело массой
, в результате чего скорость первого тела уменьшается в
раза. Определите: 1) отношение
; 2) кинетическую энергию
второго тела после удара, если первоначальная кинетическая энергия первого тела
Дж. [1) 5; 2) 550 Дж].
Тело массой 
кг движется со скоростью
м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определите количество теплоты, выделившееся при ударе.[9 Дж].
ЛЕКЦИЯ 6
ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (СТО)
Релятивистская механика изучает законы движения макроскопических тел, движущихся со скоростями, сравнимыми со скоростью распространения света в вакууме ( = с).
Релятивистская механика основана на специальной теории относительности, сформулированной Эйнштейном в начале ХХ века. Это совершенная физическая теория пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно.
6.1. Преобразования Галилея. Принцип относительности Галилея
Любое механическое движение является относительным. Поэтому о движении тела можно говорить, лишь указав систему отсчета. Известно, что законы механики выполняются только в инерциальных системах отсчета и при этом форма записи этих законов сохраняется. Это положение называют принципом относительности Галилея: во всех инерциальных системах отсчета механические процессы протекают одинаково. Например, движение корабля с точки зрения пассажира и наблюдателя на берегу.
studfiles.net
Упругий и неупругий удар двух однородных шаров
1. Введение
Столкновения движущихся тел присущи всем уровням Мироздания – от микроскопического до космического, поэтому ударные явления весьма многообразны. В динамике изучают влияние соударений на движение механических систем. Эта задача привлекала внимание многих известных ученых, включая Х. Гюйгенса, И. Ньютона, Ж. Даламбера, С. Пуансона, Г. Дарбу, Э. Дж. Рауса, А.М. Ляпунова, Н.Е. Жуковского, С.П. Тимошенко и многих других. Специфика ударов состоит в их интенсивности и скоротечности. Данное свойство может оказаться и полезным, как при забивке свай, добыче руды или игре в мяч, и опасным, как при транспортных происшествиях. Следовательно, проблема удара важна не только для теоретиков, но и для конструкторов, автолюбителей, спортсменов и др.
2. Подходы в теории удара
С физической точки зрения ударные силы – отклик на деформации, возникающие вблизи площадки контакта и волнообразно распространяющиеся в данных телах. Математические модели отражают этот процесс с большей или меньшей полнотой. В классической теории удара деформации не учитываются и проблема сводится к определению интегральных характеристик ударных сил – их импульсов. В основе этой теории лежат законы механики и некоторые дополнительные гипотезы.
Рассмотрим для примера простейшую задачу о прямом ударе двух шаров с массами m1и m2.
|
На рисунке шары массой m1и m2. до соударения имеют
скорости v1- и v2- требуется найти их скорости после удара.
Закон сохранения импульса выражается формулой:
m1 v1i + m2 v2i = m1 v1 + m2 v2
где v1i и v2i; v1 и v2 соответствуют до – и послеударным значениям скоростей. Этого единственного уравнения недостаточно для определения двух неизвестных v1 и v2. Чтобы построить единственное решение, можно принять одну из следующих гипотез: суммарная кинетическая энергия при ударе сохраняется (абсолютно упругий удар), шары после удара не разделяются, т.е. v1 = v2 (абсолютно неупругий удар). Можно выбрать более общую гипотезу Ньютона, согласно которой
v2 - v1 = e ( v1i - v2i)
Коэффициент восстановления e, как экспериментально установил Ньютон, зависит от материала шаров и лежит в пределах от нуля до единицы.
Волновая теория удара, восходящая к Б. Сен – Венану, наиболее полно описывает напряженное состояние соударяемых тел. В ее основе лежит довольно сложные уравнения математической физики, допускающие точное решение лишь в исключительных случаях. В общем случае использование волновой теории нецелесообразно, в частности, с ее помощью не удается решить рассмотренную задачу об ударе шаров.
Компромиссом между этими двумя крайними подходами служат модели, частично учитывающие деформации. Идею таких методов предложил Даламбер, который мысленно помещал маленькую пружинку (деформируемый элемент) в точку ударного контакта. С математической точки зрения проблема удара сводится к решению обыкновенных дифференциальных уравнений, что не представляет принципиальных трудностей. В вышеприведенном примере идеальная пружинка не рассеивает энергию, поэтому удар будет абсолютно упругим.
3. Упругое соударение тел
Столкновение (соударение) - это кратковременное взаимодействие, при котором тела непосредственно касаются друг друга.
Анализ явлений, имеющий место при ударе упругих сплошных тел, довольно сложен, поэтому рассмотрим самый простой случай - центральное соударение двух однородных шаров. Соударение называется центральным, если векторы скорости шаров до удара направлены по прямой, проходящей через их центры.
Абсолютно упругие и неупругие столкновения - это идеальные случаи. На практике они могут быть реализованы лишь с определенной степенью приближения. В произвольном случае соударения шаров справедливы законы сохранения импульса и энергии:
Абсолютно упругим называется такой удар, после которого во взаимодействующих телах не остается никаких деформаций и суммарная кинетическая энергия, которой обладали тела до удара, равна кинетической энергии тел после удара. Чтобы удар был абсолютно упругим, взаимодействующие тела должны обладать определенными свойствами. А именно, силы, возникающие при ударе, должны зависеть от величины деформации и не зависеть от ее скорости. Наиболее близкими к этим свойствами обладают хорошие сорта стали, слоновая кость. Соударение таких тел происходит следующим образом. При ударе возникают деформации соударяющихся тел, а значит и силы, сообщающие ускорения обоим телам, в противоположных направлениях. В какой то момент времени скорости шаров становятся равными, деформации достигают максимального значения, силы продолжают действовать, изменяя скорости в тех же направлениях, что и раньше. Поэтому шары будут "отодвигаться" друг от друга, а деформации уменьшаться пока совсем не исчезнут. К этому моменту времени упругие силы, возникающие в телах, совершат такую же работу, какая была затрачена на деформацию. В результате вся кинетическая энергия, которой обладали тела до удара, снова перейдет в кинетическую энергию тела после удара. Для определения скорости тел после упругого взаимодействия рассмотрим удар двух шаров (материальных точек), образующих замкнутую систему.
3.1. Центральное упругое столкновение тел
Имеются два сферических объекта (шарика) с массами m1 и m2. Предположим, что эти шарики движутся без вращения по одной оси и испытывают центральное упругое соударение. В этом случае закон сохранения импульса запишется в виде:
m1v1i + m2v2i = m1v1 + m2v2
где v1i и v2i - начальные скорости каждого объекта, а v1 и v2 - их конечные скорости. Закон сохранения энергии записывается в виде:
m1v1i2 / 2 + m2v2i2 / 2 = m1v12 / 2 + m2v22 / 2
Векторы скоростей шаров после упругого удара будут лежать на линии центров шаров, потому что силы взаимодействия во время удара вследствие симметрии будут направлены по этой же прямой.
Закон сохранения импульса может быть преобразован следующим образом:
m1 (v1i - v1) = m2 (v2 - v2i)
Также преобразуем выражение для закона сохранения энергии
m1 (v1i2 - v12) = m2 (v22 - v2i2)
Если разница между начальной и конечной скоростями не равна нулю (то есть столкновение действительно произошло), мы можем разделить второе из двух последних уравнений на первое, что дает:
v1i + v1 = v2 + v2i
или
v1i - v2i = v2 - v1
Другими словами, в одномерном случае упругих столкновений относительная скорость движения объектов после столкновения равняется относительной скорости движения до столкновения.
Чтобы получить конечные скорости движения объектов через их начальные скорости и массы, нужно выразить v2 из последнего уравнения и подставить его в уравнение для закона сохранения импульса. Окончательно получаем:
v1 = v1i (m1 - m2) / (m1 + m2) + v2i (2 m2) / (m1 + m2)
Таким же способом находим выражение для v2
v2 = v1i (2 m1) / (m1 + m2) + v2i (m2 - m1) / (m2 + m1)
Далее предположим, что сталкиваются объекты с одинаковой массой, т.е. m1= m2 = m. В этом случае:
v1 = v1i (m - m) / (m + m) + v2i (2 m) / (m + m)
v2 = v1i (2 m) / (m + m) + v2i (m - m) / (m + m)
Окончательно получаем, что
v1 = v2i и v2 = v1i
Это означает, что в случае центрального упругого соударения объектов с равными массами, они будут просто обмениваться скоростями. Если один из объектов до столкновения покоился, то после столкновения он остановится, а второй объект начнёт движение. При этом скорость движения второго объекта будет равна скорости первого объекта до столкновения.
В общем случае центрального и абсолютно упругого столкновения объектов с разными массами, один из которых до столкновения покоился (v2i =0), можно записать следующие выражения для скоростей после удара:
v1 = v1i (m1 - m2) / (m1 + m2)
v2 = v1i (2 m1) / (m1 + m2)
Если масса налетающего шара m1больше массы покоящегося шара m2 , то v1 и v2будут положительными и оба шара после столкновения будут двигаться в одном направлении, совпадающем с направлением начального движения налетающего шара.
Если же масса налетающего шара m1меньше массы покоящегося шара m2 , то v1будет отрицательной, а v2 - положительной, и шары после столкновения будут разлетаться в противоположных направлениях. При этом, т.к. 2 m1 > m1 - m2 , то маленький шарик отразиться с большей скоростью.
Такова картина удара двух любых тел, если начальная скорость направлена вдоль линии, соединяющей центры масс этих тел, и если силы взаимодействия направлены вдоль этой же линии центров. В противном случае удар будет представлять сложное явление.
При нецентральном ударе шаров картина соударения будет иная.
3.2. Нецентральное упругое столкновение тел
Здесь во время удара имеет место как приближение центров шаров друг к другу вследствие их деформации, так и скольжение поверхности одного шара по поверхности другого. Очевидно, что вследствие скольжения поверхностей возникнут силы трения, которые вместе с упругими силами взаимодействия определят изменение скорости шаров после удара. Кроме того, силы трения вызовут вращение шаров относительно их центров масс.
Для того чтобы представить механизм удара, разложим векторы скоростей обоих шаров до удара на направление линии центров шаров и на направление перпендикулярное к этой линии.
V1ц
 |
V1i
F'Т
V1п
F'y Fy
V2i v2п
FT
 |
V2ц
В следствии "скольжения" поверхности шаров возникнут силы трения F'T и FT , которые вместе с упругими силами взаимодействия F'y и Fy определят изменение скорости шаров после удара. Кроме того, силы трения вызовут вращение шаров вокруг центра. Только в том случае, когда силы трения FT очень малы по сравнению с упругими силами Fy, т.е. FT << Fy, можно пренебречь действием сил трения.
В этом случае задача о нецентральном столкновении шаров решается достаточно просто. Действительно, соединяя центры масс сталкивающихся шаров прямой и разложив скорость каждого шара на нормальную составляющую, направленную вдоль линии центров, и тангенциальную составляющую, перпендикулярную к ней. Так как согласно нашему предположению силы трения отсутствуют, то тангенциальные силы во время столкновения не возникают и, следовательно, тангенциальные скорости шаров изменяться не будут. Нормальные же составляющие скорости после удара можно определить на основании закона сохранения количества движения и закона сохранения энергии таким же путем, как и при центральном ударе.
Запишем уравнения:
m1 v1ц + m2 v2ц = m1ц v' 1ц + m2 v'2ц
m1 ( v21п + v21ц ) + m2 (v22п + v22ц) = m1 ( v'21п + v21ц ) + m2 (v'22п + v22ц
здесь неизвестны только две величины: v'1ц и v'2ц.
Общие закономерности нецентрального удара шаров в этом случае можно найти следующим путем. Предположим, что до удара шар 2 покоится, а шар 1 движется. Сила взаимодействия в момент удара проходит через центры шаров (нет трения), и ее направление зависит от "прицельного" расстояния δ, равного расстоянию центра покоящегося шара от линии полета центра другого шара (до удара). Плоскость чертежа совпадает с плоскостью, проходящей через центры шаров и вектор скорости шара 1.
F
2
r2
 |
δ
r1
 |
|||
 |
|||
Р
1
 |
F'
Удар произойдет при условии δ < r1 + r2, где r1 и r2 – радиусы шаров. Угол θ зависит от δ и r1 + r2. Составляющая количества движения шара 1 (ударяющего), нормальная к F (сила взаимодействия), остается неизменной. Составляющие количеств движения шаров по направлению силы F изменяются в соответствии с законами центрального удара.
По закону постоянства количества движения:
P = P1 + P2
где P – количество движения шара 1 до удара, P1и P2 – количества движения шаров 1 и 2 после удара соответственно.
P2
P1
θ
P
Закон сохранения энергии можно записать так:
P2/m1 = P21/m1 + P22/m2
Так как P = m v и mv2 = P2 / m для любого тела.
Вектор P2 составляет угол θ с вектором P , покоившийся шар отскочит под углом θ к начальной скорости первого шара, тогда из треугольника векторов следует:
P21 = P22 + P2 - 2 P P2 cos θ
Учитывая постоянство энергии, исключаем P1 и получаем
P2 = 2 m2 P cos θ / (m1 + m2) = β P cos θ
β = 2 m2 / (m1 + m2)
Отсюда видно, что общее соотношение между Р2и Р зависит от угла θ и соотношения масс m1/m2.
Следует различать два случая: m1 > m2 и m1 < m2. В первом случае β < 1, тяжелый шар ударяет легкий. Конец вектора Р2 описывает окружность диаметром βР. Оба шара после удара летят в сторону начального движения первого шара. Величина угла θ изменяется от 0 до π/2. Угол отклонения первого шара может изменяться от 0 до некоторого φмакс.. Одному значению φ соответствуют два значения θ.
β < 1
Р2
Р1
А
В Р
φ
βР
 |
Точка В представляет центральный удар, оба шара летят после удара по одному направлению. Точка А представляет промах (шары не задели друг друга).
Во втором случае, при m1 < m2, легкий шар ударяет тяжелый. Здесь β > 1 и шар 1 после удара может лететь назад. Угол отклонения налетающего шара φ изменяется от 0 до π.
 |
А
В
βР
 |
Точка В представляет центральный удар. Каждому значению φ соответствует только одно значение θ.
При одинаковых массах шаров m1 = m2 картина возможных количеств движения показана на рисунке.
 |
Р2
 |
А
В
φ
Угол φ изменяется от 0 до π/2. При центральном ударе шар 1 останавливается, а шар 2 с той же скоростью движется далее (точка В). Угол разлета шаров θ + φ всегда равен π/2.
Угол θ нетрудно связать с прицельным расстоянием δ и показать, что
(r1 + r2)sin θ = δ
Зная δ, диаметры шаров и их массы, найдем θ и β, по данным Р определим Р2 и Р1, которые в свою очередь определяют скорости и направления шаров после удара.
Абсолютно неупругим называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми. Чтобы это стало возможным, соударяющиеся тела должны обладать такими свойствами, что силы, возникающие при их деформации, зависят не от величины деформации, а от скорости изменения деформации. Такие свойства присущи, например, мягкой глине, пластилину. При неупругом соударении происходит следующее. В начальный момент удара скорость деформации велика (шары сжимаются), поэтому возникают значительные силы, сообщающие обоим шарам ускорения, направленные в противоположные стороны. По мере развития удара скорости деформации шаров уменьшаются, а сами деформации увеличиваются до тех пор, пока скорости шаров не окажутся равными. В этот момент деформации шаров перестанут изменяться, исчезнут силы, и оба шара будут двигаться с одинаковой скоростью. При абсолютно неупругом ударе выполняются законы сохранения импульса и полной энергии. Механическая же энергия тел до удара больше механической энергии после удара, так как она частично (или полностью) переходит во внутреннюю энергию тел и расходуется на работу по деформации тел. Для определения скорости тел после взаимодействия рассмотрим удар двух шаров (материальных точек), образующих замкнутую систему. Массы шаров m1 и m2, скорости до удара V1i и V2i. Согласно закону сохранения суммарный импульс шаров до удара должен быть таким же, как после удара:
m1 V1i + m2 V2i = (m1 + m2) U
где U - скорость после удара, одинаковая для обоих шаров. Из уравнения следует, что:
U = ( m1 V1i + m2 V2i ) / (m1 + m2)
Закон сохранения энергии для неупругого удара рассматриваемых шаров имеет следующий вид:
m1 V1i2 / 2 + m2 V2i2 / 2 = (m1 + m2 ) U2 + W
где W - изменение внутренней энергии системы.
Кинетическая энергия тел до удара имеет следующую величину:
W1 = m1 V1i2 / 2 + m2 V2i2 / 2
А кинетическая энергия после удара:
W2 = (m1 + m2 ) U2/2 = ( m1 V1i + m2 V2i )2 /2 (m1 + m2)
Потери механической энергии, или часть энергии, которая перешла в тепловую форму составляет:
W = W1 - W2 = m1 m2 (V1i – V2i)2 / 2 (m1 + m2 )
Величина V1i – V2i представляет относительную скорость движения тел до удара. Поэтому энергия, перешедшая в тепло, зависит от соотношения масс соударяющихся тел m1 m2 /(m1 + m2 ) и относительной скорости движения их до удара.
Энергию потерь можно рассматривать как кинетическую энергию некоторой эффективной массы:
m0 = m1 m2 / (m1 + m2)
движущихся с относительной скоростью V'i =V1i – V2i.
Для конкретных расчетов скорости нужно спроектировать соотношение импульсов на выбранные направления. Если до удара скорости шаров направлены вдоль прямой, проходящей через их центры, удар называют центральным. Скорость шаров после такого удара будет направлена по той же прямой. Поэтому уравнение сохранения импульсов можно рассматривать как скалярное. Но скорости при этом надо считать совпадающими по знаку, когда они направлены в одну сторону и противоположными по знаку, когда они направлены в противоположные стороны. Рассмотрим некоторые частные случаи.
1. Шары движутся в одном направлении. Удар возможен, если скорости V1i и V2i различны. Например, V2i > V1i, т.е. второй шар догоняет первый. После удара шары будут двигаться в ту же сторону со скоростью большей, чем скорость первого шара и меньшей, чем скорость второго. Если при этом массы шаров одинаковы, то
U =( V1i + V2i ) / 2
2. Шары движутся навстречу друг другу. После удара шары будут двигаться вместе в ту сторону, в которую двигался шар, обладающий большим импульсом. Если импульсы обоих шаров равны по величине, то после удара оба шара остановятся.
3. В случае нецентрального удара (рис.3.6.2а) скорости V1i и V2i можно разложить на составляющие V1X и V2X в направлении линии, соединяющей центры шаров (ось Х), и состaвляющие V1Y и V2Y в перпендикулярном направлении (ось У). Для составляющих V1X , V2X и V1Y ,V2Y записать закон сохранения импульса в том же виде, как и при центральном ударе и определить составляющую результирующей скорости.
Рассмотрим неупругий удар более подробно. При неупругом ударе часть кинетической энергии налетающего шара теряется с выделением тепла. В предельном случае абсолютно неупругого удара налетающее тело слепляется с покоящимся телом, кинетическая энергия их относительного движения обращается в ноль и они продолжают движение, как единое тело. В большинстве практических случаев мы имеем дело с частично упругим ударом, когда в теле после столкновения возбуждаются деформационные колебания, затухающие со временем. Возбуждение таких колебаний можно смоделировать при помощи двух одинаковых шариков, соединённых пружиной. Предположим, что абсолютно упругий шар сталкивается с пружинным осциллятором. Массы шаров одинаковы и равны m. Так как в момент удара пружина ещё не действует, налетающий шар останавливается, а левый шар осциллятора приводится в движение со скоростью налетающего шара v. При этом центр масс осциллятора движется со скоростью v/2. Со временем колебания осциллятора затухнут и он будет продолжать поступательное движение со скоростью v/2, а суммарная энергия всей системы составит лишь половину от энергии налетающего шара. Другая половина выделится в виде тепла в осцилляторе.
Удар обычных неупругих тел соответствует промежуточному случаю между идеально упругим и полностью неупругим ударами. Ему аналогичен удар аналогичен удар двух шаров через неупругую пружину, которая сжимаясь за первую половину времени удара до некоторой величины, не примет своих первоначальных размеров после удара; или расталкивающая сила во время сжатия будет больше, чем во вторую половину времени удара при расширении пружины. Часть потенциальной энергии сжатия пружины перейдет в тепло и не будет обращена в кинетическую энергию движения. Следовательно, закон сохранения механической энергии в этом случае нельзя применять. Условие равенства скоростей после удара также не будет иметь места, как это было при полностью неупругом ударе, так как после удара оба тела движутся с различными скоростями.
Неупругий удар можно характеризовать той долей энергии деформации, которая обращается в тепло за время удара. Но еще Ньютоном было найдено, что при неупругом ударе шаров из определенного материала величины относительных скоростей до и после удара находятся в постоянном отношении, и такой удар характеризуется коэффициентом восстановления относительной скорости после удара:
е = |V2 – V1| / |V2i – V1i|
где V2i – V1i – относительная скорость до удара, а V2 – V1 – после удара. Опыт показывает, что с некоторой степенью точности можно считать величину е постоянной и зависящей только от материала соударяющихся шаров.
При идеально упругом ударе относительная скорость остается той же самой по величине, но меняет свой знак:
V1i – V2i = - (V1 – V2)
Коэффициент восстановления всегда меньше единицы, ибо при упругом ударе он равен единице, при полностью неупругом ударе равен нулю, так как в этом случае
V2 – V1 = 0
Зная коэффициент е, можно подсчитать скорости движения шаров после удара и потери энергии.
Используемая литература: 1. Д.В.Сивухин, "Общий курс физики. Механика", Наука, 1979 2. О.Д.Шебалин, "Физические основы механики и акустики", Высш. школа, 1981 3. С.П.Стрелков, "Механика", Наука, 1975 4. К.Шварц, Т.Гольдфарб, "Поиски закономерностей в физическом мире", пер. с англ., Москва, Мир, 1977 5. Лабораторные занятия по физике, под ред. Л.Л.Гольдина, Москва, Наука, 1983
6. А.И. Иванов, "Закономерности удара в механических системах", Природа, 1999, №10
www.referatmix.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО Уральский государственный экономический университет
Центр дистанционного образования
РЕФЕРАТ
По курсу: Физика
на тему: Соударение тел. Удар абсолютно упругих и неупругих тел.
Исполнитель: Н.П. Владимирович
Студент группы: УНу-12 Сб
Научный руководитель: С.А.Упоров
Дата сдачи: 01.06.2013
Оценка:________________________
Екатеринбург 2013
СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………………………………………………….3
1 ПОДХОДЫ В ТЕОРИИ УДАРА……………………………………………..5
2 УПРУГОЕ СОУДАРЕНИЕ ТЕЛ………………………………………………7
2.1 ЦЕНТРАЛЬНОЕ УПРУГОЕ СТОЛКНОВЕНИЕ ТЕЛ………………….8
2.2 НЕЦЕНТРАЛЬНОЕ УПРУГОЕ СТОЛКНОВЕНИЕ ТЕЛ……………..10
3 НЕУПРУГОЕ СОУДАРЕНИЕ ТЕЛ………………………………………….16
ЗАКЛЮЧЕНИЕ………………………………………………………………….22
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ…………………………….23
ВВЕДЕНИЕ
Столкновения движущихся тел присущи всем уровням Мироздания: от
микроскопического - до космического, поэтому ударные явления весьма многообразны.
С явлением удара каждый человек знакомится с первых своих шагов, что свидетельствует о важности этого явления. На определенном уровне развития человечества появилась необходимость в изучении теории удара. У истоков научной теории ударов стояли Гютгенс, Валлис, Рене и другие.
Правильный учет явления удара невозможен без задания физических свойств соударяемых тел. Этим объясняется многообразие теорий удара – от простейших, основанных на ньютоновском восстановлении и кулоновской теории, до более реалистических моделей динамической теории упругости. Выбор модели для решения конкретных задач связан с компромиссом между простотой и реалистичностью, достигнуть которого трудно.
В задачах динамики важно исследование поведения системы в течение значительных промежутков времени, за которые может произойти большое число соударений. При этом безударное движение описывается дифференциальными уравнениями, а удар – разностными, что делает невозможным применять метод анализа. Традиционный метод «припасовывания» граничных условий может применяться при решении простых задач, но не позволяет получить результаты общего характера, описывающие качественные свойства движения в системах с односторонними связями.
Движение материальных тел под действием тех или иных тел происходит в соответствии с законами Ньютона. Ударные силы характеризуются кратковременностью действия и значительной величиной. В результате координаты рассматриваемой механической системы за время удара не изменяются, а скорости получают конечные приращения.
Под действием ударной силы происходит лишь изменение скоростей без заметных перемещений. Если ударные импульсы заданы или каким-то образом определены, то расчет новых значений скорости производится чисто алгебраически.
Существует два типа задач на явление удара: одни из них сводятся к определению приращения скоростей по заданным ударным импульсам, в других ударные импульсы подлежат определению в зависимости от заданных приращений скоростей. В обоих случаях решения описываются одними и теми же алгебраическими соотношениями.
С механической точки зрения явление удара характеризуется тем, что скорости точек механической системы (количество движения системы) за весьма малый промежуток времени, в течение которого происходит соприкосновение тел, изменяются на конечную величину. Поскольку при этом ускорения тел оказываются очень большими, то и силы, возникающие при ударе, оказываются большими. Хотя эти силы действуют на соударяющиеся тела в течение весьма малого промежутка времени, но их импульсы за этот промежуток являются конечными величинами.1
Силы, возникающие при ударе и действующие на соударяющиеся тела в течение времени соударения, называются ударными силами. Главной особенностью ударной силы является именно кратковременностью действия. За время действия ударных сил действием обычных сил, как правило, можно пренебречь. Импульсы ударных сила за время удара называются ударными импульсами . Ударные импульсы зависят не только от масс и скоростей соударяющихся тел, но и от их упругих свойств. Поэтому полностью описать явление удара можно, лишь применяя теорию упругости. Однако задача теории удара в теоретической механике не облегчается тем, что здесь не исследуется характер деформации, а определяются изменения скоростей точек системы, обусловленное уже совершившимся ударом.
В данной работе изучены подходы в теории удара, рассмотрены понятия ударов – упругого и неупругого.
С физической точки зрения ударные силы – отклик на деформации, возникающие вблизи площадки контакта и волнообразно распространяющиеся в данных телах. Математические модели отражают этот процесс с большей или меньшей полнотой. В классической теории удара деформации не учитываются и проблема сводится к определению интегральных характеристик ударных сил – их импульсов. В основе этой теории лежат законы механики и некоторые дополнительные гипотезы.
Рассмотрим для примера простейшую задачу о прямом ударе двух шаров с
массами m1 и m2.
На рисунке шары массой m1 и m2. до соударения имеют скорости v1- и v2- требуется найти их скорости после удара.
Закон сохранения импульса выражается формулой:
m1 v1i + m2 v2i = m1 v1 + m2 v2
где v1i и v2i ; v1 и v2 соответствуют до – и послеударным значениям скоростей. Этого единственного уравнения недостаточно для определения двух неизвестных v1 и v2.
Чтобы построить единственное решение, можно принять одну из следующих гипотез: суммарная кинетическая энергия при ударе сохраняется (абсолютно упругий удар), шары после удара не разделяются, т.е. v1 = v2 (абсолютно неупругий удар). Можно выбрать более общую гипотезу Ньютона, согласно которой
v2 - v1 = e ( v1i - v2i )
Коэффициент восстановления e, как экспериментально установил Ньютон, зависит от материала шаров и лежит в пределах от нуля до единицы.
Волновая теория удара, восходящая к Б. Сен – Венану, наиболее полно описывает напряженное состояние соударяемых тел. В ее основе лежит довольно сложные уравнения математической физики, допускающие точное решение лишь в исключительных случаях. В общем случае использование волновой теории нецелесообразно, в частности, с ее помощью не удается решить рассмотренную задачу об ударе шаров.
Компромиссом между этими двумя крайними подходами служат модели, частично учитывающие деформации. Идею таких методов предложил Даламбер, который мысленно помещал маленькую пружинку (деформируемый элемент) в точку ударного контакта. С математической точки зрения проблема удара сводится к решению обыкновенных дифференциальных уравнений, что не представляет принципиальных трудностей. В вышеприведенном примере идеальная пружинка не рассеивает энергию, поэтому удар будет абсолютно упругим.2
2 УПРУГОЕ СОУДАРЕНИЕ ТЕЛ
При упругом соударении тел тела претерпевают упругую деформацию. При этом кинетическая энергия движущихся тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел.
Взаимодействующие тела представляют собой замкнутую систему, если на них не действуют силы со стороны других тел. В замкнутых системах выполняются законы сохранения энергии и импульса. Зная движение тел до столкновения, и применяя законы сохранения, можно определить движение тел после столкновения. Но при этом мы ничего не узнаем о том, как происходит само столкновение. Для решения же ряда задач о столкновении микрочастиц, как правило, достаточно знать об их движении после взаимодействия. "Моделью" для задач подобного рода служит задача о столкновении шаров. Если шары катаются по гладкой горизонтальной поверхности, и если силой трения качения можно пренебречь, то систему из двух шаров можно считать замкнутой. Существует два предельных вида удара: абсолютно неупругий и абсолютно упругий.
Столкновение (соударение) - это кратковременное взаимодействие, при котором тела непосредственно касаются друг друга. Анализ явлений, имеющий место при ударе упругих сплошных тел, довольно сложен, поэтому рассмотрим самый простой случай - центральное соударение двух однородных шаров. Соударение называется центральным, если векторы скорости шаров до удара направлены по прямой, проходящей через их центры.
Абсолютно упругие и неупругие столкновения - это идеальные случаи. На практике они могут быть реализованы лишь с определенной степенью приближения.
В произвольном случае соударения шаров справедливы законы сохранения импульса и энергии.
Абсолютно упругим называется такой удар, после которого во взаимодействующих телах не остается никаких деформаций и суммарная кинетическая энергия, которой обладали тела до удара, равна кинетической энергии тел после удара.
Чтобы удар был абсолютно упругим, взаимодействующие тела должны обладать определенными свойствами. А именно, силы, возникающие при ударе, должны зависеть от величины деформации и не зависеть от ее скорости. Наиболее близкими к этим свойствами обладают хорошие сорта стали, слоновая кость.
Соударение таких тел происходит следующим образом. При ударе возникают деформации соударяющихся тел, а значит и силы, сообщающие ускорения обоим телам, в противоположных направлениях. В какой-то момент времени скорости шаров становятся равными, деформации достигают максимального значения, силы продолжают действовать, изменяя скорости в тех же направлениях, что и раньше.
Поэтому шары будут "отодвигаться" друг от друга, а деформации уменьшаться, пока совсем не исчезнут. К этому моменту времени упругие силы, возникающие в телах, совершат такую же работу, какая была затрачена на деформацию. В результате вся кинетическая энергия, которой обладали тела до удара, снова перейдет в кинетическую энергию тела после удара. Для определения скорости тел после упругого взаимодействия рассмотрим удар двух шаров (материальных точек), образующих замкнутую систему.3
2.1 Центральное упругое столкновение тел
Имеются два сферических объекта (шарика) с массами m1 и m2. Предположим, что эти шарики движутся без вращения по одной оси и испытывают центральное упругое соударение. В этом случае закон сохранения импульса запишется в виде:
m1v1i + m2v2i = m1v1 + m2v2
где v1i и v2i - начальные скорости каждого объекта, а v1 и v2 – их конечные скорости. Закон сохранения энергии записывается в виде:
m1v1i2 / 2 + m2v2i2 / 2 = m1v12 / 2 + m2v22 / 2
Векторы скоростей шаров после упругого удара будут лежать на линии центров шаров, потому что силы взаимодействия во время удара вследствие симметрии будут направлены по этой же прямой.
Закон сохранения импульса может быть преобразован следующим образом:
m1 (v1i - v1) = m2 (v2 - v2i)
Также преобразуем выражение для закона сохранения энергии
m1 (v1i2 - v12) = m2 (v22 - v2i2)
Если разница между начальной и конечной скоростями не равна нулю (то есть столкновение действительно произошло), мы можем разделить второе из двух последних уравнений на первое, что дает:
v1i + v1 = v2 + v2i
или
v1i - v2i = v2 - v1
Другими словами, в одномерном случае упругих столкновений относительная скорость движения объектов после столкновения равняется относительной скорости движения до столкновения.
Чтобы получить конечные скорости движения объектов через их начальные скорости и массы, нужно выразить v2 из последнего уравнения и подставить его в уравнение для закона сохранения импульса. Окончательно получаем:
yaneuch.ru
Реферат на тему:
Уда́р — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.
При ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии. Предполагается, что за время удара действием внешних сил можно пренебречь, тогда полный импульс тел при ударе сохраняется, в противном случае нужно учитывать импульс внешних сил. Часть энергии обычно уходит на нагрев тел.
Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара. Обычно рассматривают либо абсолютно упругий удар, либо вводят коэффициент сохранения энергии k, как отношение кинетической энергии после удара к кинетической энергии до удара при ударе одного тела о неподвижную стенку, сделанную из материала другого тела. Таким образом, k является характеристикой материала, из которого изготовлены тела, и (предположительно) не зависит от остальных параметров тел (формы, скорости и т. п.).
Если не известны потери энергии, происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначно движение тел после удара невозможно. В этом случае рассматривается зависимость возможных углов рассеяния и скоростей тел после удара от начальных условий. Например, при столкновении двух элементарных частиц рассеяние может произойти лишь в некотором диапазоне углов, определяющемся предельным углом рассеяния.
В общем случае решение задачи о столкновении кроме знания начальных скоростей требует дополнительных параметров.
Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.
Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Энергия, конечно же, никуда не исчезает, а переходит в тепловую.
Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.
При реальном ударе макроскопических тел происходит деформация соударяющихся тел и распространение по ним упругих волн, передающих взаимодействие от сталкивающихся границ по всему телу. Пусть сталкиваются одинаковые тела. Если c — скорость звука в теле, L — характерный размер каждого тела, то время удара будет порядка t = 2L / c. Множитель 2 соответствует распространению волны в прямом и обратном направлении. Соответственно, систему сталкивающихся тел можно считать замкнутой, если импульс внешних сил за время t мал по сравнению с импульсами тел. Кроме того, само время t должно быть достаточно мало, в противном случае становится проблематично оценить потери энергии на деформации за время удара (часть энергии всегда расходуется на внутреннее трение), а само описание сталкивающихся тел становится неполным из-за существенного вклада внутренних степеней свободы. Необходимо, чтобы все деформации при ударе были существенно меньше, чем размеры тел.
wreferat.baza-referat.ru
Общие понятия_______________
Удар (соударение)_____
Примеры: столкновение бильярдных шаров, удар человека о землю при прыжке с поезда и т.д.
. Столкновение двух или более тел, при котором взаимодействие длится очень короткое время.
Система тел в процессе соударения — замкнутая система
Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процессе их соударения приближенно рассматривать как замкнутую систему и применять к ней законы сохранения.
Сущность удара__
Кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.
Коэффициент восстановления___
О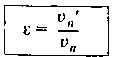
тношениенормальных составляющих относительной скорости тел после (
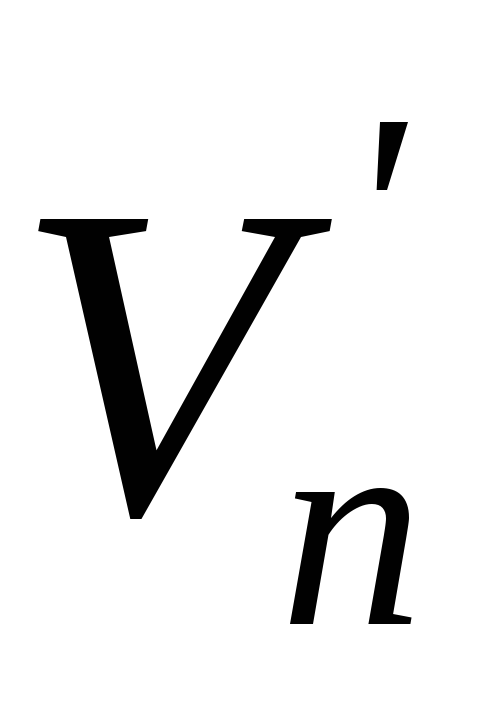)и до (Vn) удара.
Такие тела — абсолютно неупругие.
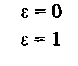Такие тела — абсолютно упругие .
Примеры: для стальных шаров ε ≈ 0,56; для слоновой кости ε ≈ 0,89; для свинца ε ≈ 0.
Линия удара_
Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.
Центральный удар__
Удар, при котором тела до удара движутся вдоль прямой, проходящей через их центры масс.
Центральный абсолютно упругий удар
Абсолютно упругий удар_
Столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
Следует отметить, что это идеализация.
Исходные данные_
Сталкиваются шары массами т1 и т2; скорости шаров до удара — v1 и v2, после удара — v{ и v'2. В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учитываются знаками: положительное значение приписывается движению вправо, отрицательное — движению влево. Выполняются законы сохранения импульса и энергии.
Законы сохранения импульса и механической энергии______
Э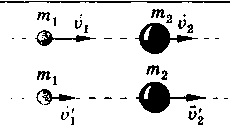
ти законы записаны при сделанных выше допущениях.
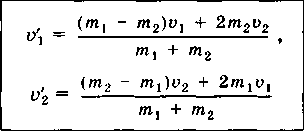
Скорости тел после абсолютно упругого удара
После преобразования законов сохранения
; (*)
; (**)
.
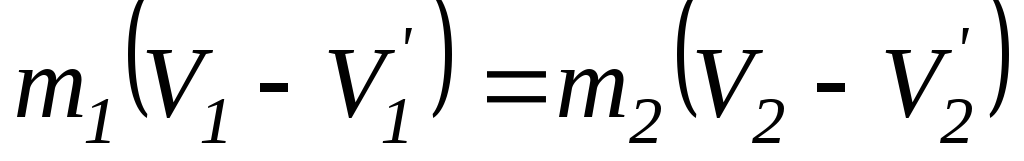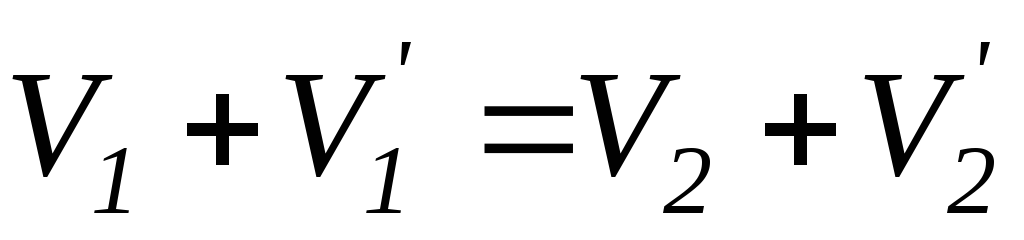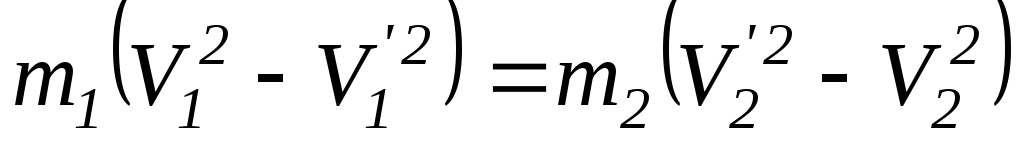Решая (*) и (**), получим записанные выражения.
Частные случаи
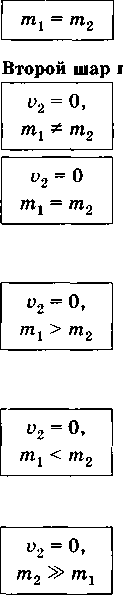
и\ = v2 ;
V2 = Uj.
Шары равной массы «обмениваются» энергией. окоится
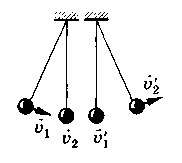г ..
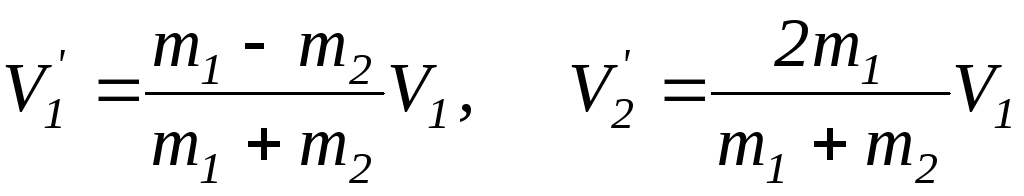
Если второй шар до удара висел неподвижно (v2 = 0), то после удара остановится первый шар ( v\ = 0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара ( v'2 = i^).
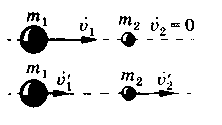Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (v\ < i>j). Скорость второго шара после удара больше, чем скорость первого после удара ( V2 > v\).
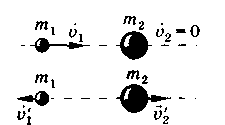Направление движения первого шара при ударе изменяется — шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью,
т. е. и о < v
Пример: столкновение шара со стеной:
Центральный абсолютно неупругий удар
Абсолютно неупругий удар___________
С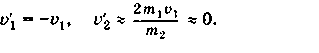
толкновение двух тел, в результате которого тела объединяются, двигаясь дальше какединое целое.
Пример: шары из пластилина, движущиеся навстречу друг другу.
Исходные данные___
Сталкиваются шары массами m1, и m2; скорости шаров до удара —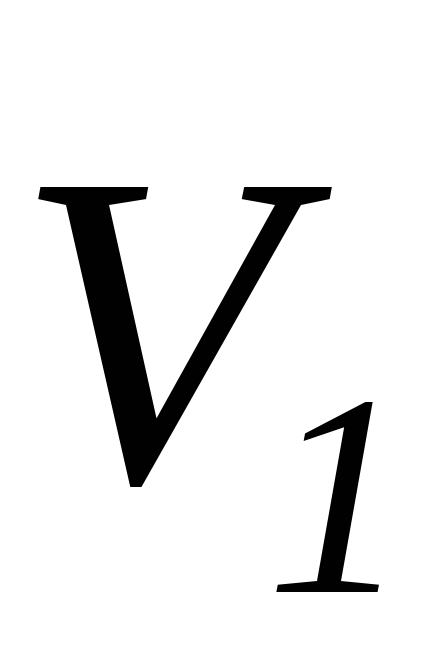 
и 
; 
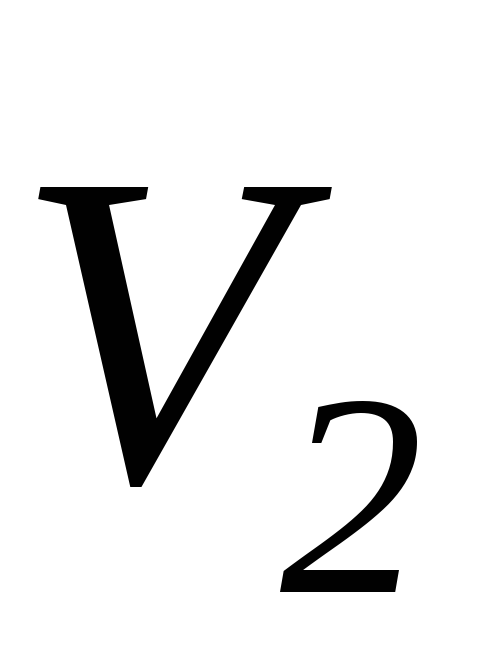— общая скорость шаров после удара.
Общая скорость шаров после удар
Вычисляется, согласно закону сохранения импульса:
.
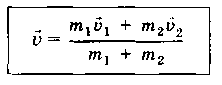
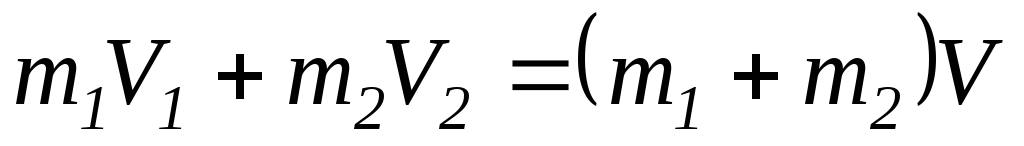Движение шаров навстречу друг другу__
Ш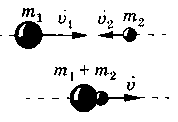
ары будут продолжать двигаться вместе в ту сторону, в которую двигался шар, обладающий большим импульсом.
О законе сохранения механической энергии_
В процессе центрального абсолютно неупругого удара шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, поэтому эти силы подобны силам трения и закон сохранения механической энергии не соблюдается. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии.
Разность кинетических энергий тел до и после абсолютно неупругого удара_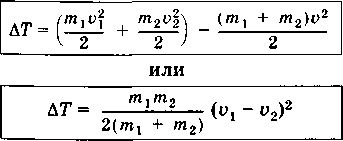
Учли выражение для V.
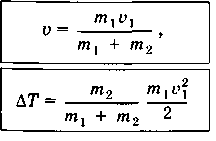Случай V2 = 0 (ударяемое тело первоначально неподвижно)
Если т2 >> т1 (масса неподвижного тела очень большая), то V << V1 и почти вся кинетическая энергия при ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молота.
studfiles.net
