Вводный урок геометрии в 7 классе с использованием средств мультимедиа.
Тип урока:. комбинированный, с применением компьютерных технологий.
Цели урока:
•Образовательные - ознакомление с геометрией, с первыми основными геометрическими понятиями: точка и прямая, «лежать между» («лежать на») для точек прямой, с их условными обозначениями; с простейшими геометрическими фигурами на плоскости.
•Развивающие – развивать творческую и мыслительную деятельность учащихся на уроке с помощью решения задач исследовательского характера, развитие умений сравнивать, выявлять закономерности, обобщать; формирование наглядно-образного мышления.
•Воспитательные – прививать учащимся интерес к предмету с помощью изучения истории и развития науки, применения информационных технологий.
Ход урока:
I.Постановка цели урока.
Приходилось ли вам когда-нибудь слышать слово «геометрия»? Знаете ли вы, что оно означает? Что изучает? Работа на уроке позволит ответить на эти вопросы.
II.Подготовка к изучению нового материала.
Разберем слово «Геометрия» по частям:
«гео»-«метрия».
Какие еще слова начинаются с «Гео»? (География, геология, геодезия…) Следовательно, «Гео» (от греческого «ge») означает «Земля».
А что означает «Метрия»? «Метрия» - (с греческого «metrio») - мерить.
Вспомним, для чего нужен метр и где мы пользуемся метром. (Для измерения).
Значит слово «Геометрия» переводится как «Землемерие». (Слайд 2).
Что изучает геометрия?
III.Ознакомление с новым материалом.
С геометрическими понятиями вы уже знакомы с самого детства: круг, квадрат, угол, куб, измерение отрезков, площадь, объем, и т.д.
(Слайд 3,4). Внимательно посмотрим на эти рисунки. На них изображены разные предметы и объекты, сгруппированные по какому-то определенному принципу.
1.Определите, по какому принципу они объединены.
Что вам сразу бросилось в глаза? (Все они имеют одну форму).
Итак, мы рассмотрели самые разные предметы и объекты. Не будем обращать внимание на то, какого они цвета, из чего сделаны и т.д. Ведь в каждом из них есть то, что объединяет его со многими другими предметами и объектами. Это – форма. Все рассмотренные предметы и объекты каждой группы имеют одинаковую форму.
2. Ответим на вопрос: какую именно форму?
И ствол дерева, и ствол пушки, и башня имеют цилиндрическую форму.
Шишки, шляпки грибов, горы – коническую форму.
Земля, яблоко, мыльные пузыри – форму шара.
Аквариум, кубик, беседка – форму куба.
Геометрия, прежде всего, рассматривает форму предметов, поэтому предметы называют фигурами, что означает в переводе с латинского языка «внешний вид», «образ». Многое из того, чем занимается геометрия, можно увидеть в жизни. Чтобы представить себе геометрические фигуры, нужно внимательно посмотреть на окружающие нас предметы и объекты.
Расположением геометрических фигур занимаются различные разделы геометрии: (Слайд 5)
- Планиметрия - (от латинского «Planum») равнина, плоскость.
- Стереометрия – (от латинского «Sterio») телесный, пространственный.
Геометрические фигуры, точки которых лежат в одной плоскости, изучает планиметрия.
Геометрические фигуры, точки которых не лежат в одной плоскости, изучает стереометрия.
Но, прежде чем начать изучение фигур в одной плоскости, заглянем в историю возникновения геометрии.
Геометрические познания древних египтян.
Если не учитывать весьма скромный вклад древних обитателей долины между Тигром и Евфратом и Малой Азии, то геометрия зародилась в Древнем Египте до 1700 до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянами стали такие виды их деятельности, как возведение пирамид и изобразительное искусство. (Слайд 6).
Об уровне геометрических познаний можно судить из древних рукописей, которые специально посвящены математике и являются чем-то вроде учебников, или, вернее, за¬дачников, где даны решения разных практических задач.
Древнейшая математическая рукопись египтян переписана неким учеником между 1800 – 1600 г.г. до н.э. с более древнего текста. Папирус разыскал русский египтолог Владимир Семенович Голенищев. Он хранится в Москве - в Музее изобразительных искусств имени А.С. Пушкина, и называется Московским папирусом.
Другой математический папирус, написанный лет на двести-триста позднее Московского, хранится в Лондоне. Он называется: „Наставление, как достигнуть знания всех тёмных вещей, всех тайн, которые скрывают в себе вещи… По старым памятникам писец Ахмес написал это". Рукопись так и называют „папирусом Ахмеса", или папирусом Райнда — по имени англичанина, который разыскал и купил этот папирус в Египте. В папирусе Ахмеса даётся решение 84 задач на различные вычисления, которые могут понадобиться на практике. (Слайд 7).
Меры длины древних египтян.
Главной мерой длины у египтян служил локоть. Локоть делился на семь «ладоней», «ладонь» — на четыре «пальца». Как и многие другие народы, в качестве мерок длины египтяне использовали части человеческого тела. Но люди бывают разного роста, и локти у них не одинаковые. Египтяне это, конечно, понимали. Для того чтобы измерения получались точными и не происходило никакой путаницы, они придумали образцовые меры: локоть, ладонь и палец, общие для всего Египта. Теперь было уже неважно, какой длины руки у человека, который хотел что-нибудь измерить. Он мерил не своим, а «общим» локтем. (Слайд 8)
Измерение площадей.
После каждого разлива Нила египтянам заново приходилось разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площади различных фигур: ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараонов, которые собирали с земледельцев налоги.
Землемеры использовали в качестве измерительного инструмента туго натянутую веревку, разделенную метками на локти, ладони и пальцы.
Если участок земли квадратный или прямоугольный, то это дело несложное. Надо измерить длину и ширину поля, а потом их перемножить. Например, длина десять локтей, а ширина восемь. Значит, на этом участке можно уложить 80 квадратов со стороной в локоть. Его площадь — восемьдесят квадратных локтей.
Но участки могут иметь разную форму. Не всякий участок можно разделить на прямоугольники. А вот на треугольники можно разбить любой участок,— если только он ограничен прямыми линиями. (Слайд 9).
Египтяне рассуждали примерно так. Если в прямоугольнике провести прямую линию через два противоположных угла, то получится два одинаковых треугольника с прямыми углами. Площадь каждого из них вдвое меньше площади прямоугольника, из которого они получились. Значит, для того чтобы узнать площадь прямоугольного треугольника, надо измерить те его стороны, которые образуют прямой угол, перемножить длину их и от того, что получится, взять половину. (Слайд 10).
Если получается такой треугольник, у которого нет прямого угла, надо провести линию под прямым углом к одной из сторон треугольника так, чтобы она проходила через вершину противоположного этой стороне угла и образовала со стороною прямой угол.
В геометрии такую линию называют высотой, а ту сторону, с которой она пересекается, - основанием треугольника. Видно, что высота делит треугольник опять же на два, но уже прямоугольных треугольника, вычислить площадь которых просто. Площадь любого треугольника равна половине произведения основания на высоту. (Слайд 11).
Египетский треугольник.
Египтяне знали, что у треугольника со сторонами в 3, 4 и 5 локтей один угол прямой. Такой треугольник до сих пор называется «египетским». (Слайд 12).
Почему так получается они не объясняли. Как и многие народы, египтяне просто пользовались готовыми правилами, которые «ощупью» находили на опыте и запоминали.
Скорее всего, египтяне нашли треугольник с прямым углом следующим образом: Представим себе, что мы египетские мастера и собираемся построить пирамиду. Сделать это надо так, чтобы пирамида не получилась кособокой и чтобы стороны её смотрели на север, юг, восток и запад. Поступим так, как это делали все египетские строители. Воткнём в землю отвесный шест. В полдень, когда тень от шеста будет короче всего, она покажет нам направление север - юг. Наметим на земле линию север - юг. Теперь проведём линию восток - запад. Для этого нужно взять верёвку с двумя колышками и провести на земле дуги так, как это показано на нашем рисунке. Через точки пересечения дуг натянем верёвку. Это и будет направление с востока на запад.
Линии север - юг и запад - восток пересекаются под прямым углом. (Слайд 13).
Самые важные достижения египтян.
Египтяне наиболее точно определили число П (ПИ – греческая буква). Важность этого открытия нам с вами еще предстоит понять. Число П - это величина постоянная и равна отношению длины окружности к ее диаметру. В папирусе Райнда приводится значение (16/9)2 , в десятичном приближении 3,16. (Для справки - П=3,14).
С помощью этого числа можно вычислить площадь круга (S=ПR2), а следовательно и объем пространственных тел, в основании которых лежит окружность (цилиндр).
В папирусах также есть формулы для нахождения объема усеченной пирамиды, призмы, куба, параллелепипеда. Зная объем пирамиды, можно подсчитать, сколько камня необходимо подготовить для строительства, сколько рабов привлечь и определить сроки строительства. (Слайд 14)
Подведём итоги:
Египтяне знали геометрию - они строили удивительные постройки, мерили землю разных форм (треугольную, круглую, прямоугольную), придумали «египетский» треугольник.
Но, это были правила для решения конкретных задач, имевших практическое значение. И лишь постепенно, задачи начали обобщаться и приобретать более абстрактные черты.
И все же математические знания египтян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.
Если в Древнем Египте геометрия была сугубо прикладной наукой, то в древней Греции она стала математической теорией. И имена знаменитых греков будут постоянно встречаться вам в курсе геометрии. Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз Академии Платона гласил: "Да не войдёт сюда не знающий геометрии". (Слайд 15).
Настает время привести все разрозненные знания в систему.
(Пифагор VI век до н.э., основал свою школу).
Пифагор известен как великий ученый – философ, математик, выдающийся оратор и тонкий психолог.
Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя. Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он "запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы". В связи с этим более правдоподобной можно считать следующую запись: "… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста".
Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
Евклид жил в Александрии около 300 года до нашей эры, был современником царя Птоломея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.
Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.
В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах.
Ученый гордо ответил: "В геометрии нет царской дороги".
В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида. (Слайд 17).
Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией».
IV. Основные понятия планиметрии
Конечно, геометрия дает не только представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.
Мы начинаем изучать планиметрию.
Даже самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших фигур.
Конечно, самая главная - это точка.
Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык непосредственно не с греческого, а через латинский язык.
Точка – результат мгновенного касания, укол
Отсюда же произошел медицинский термин пункция-прокол. Пунктир.
Линия – льняная нить.
Линолеум – первоначально означал промасленное льняное полотно.
Как уже было сказано ранее, все названия геометрических фигур первоначально были названиями конкретных предметов, имеющих форму, более или менее близкую к форме данной фигуры.
V. Повторение известного материала о точках и прямых и их расположении относительно друг друга.
Давайте вспомним, как обозначают на чертеже прямые и точки.
- Прямая безгранична, поэтому на чертеже изображают часть.
- Прямые обозначают двумя заглавными латинскими буквами, соответствующим двум точкам на прямой или одной малой буквой.
- Точки обозначают заглавными латинскими буквами. (Слайд 18).
- Знак Є означает принадлежание, т.е. А Є n означает, что точка А принадлежит прямой n или лежит на ней. И C Є n соответственно, не принадлежит или не лежит. (Слайд 19).
Выполнить задание
Опишите этот рисунок, используя условные обозначения.
VI. Проверка усвоения изученного материала.
1.Практические задания № 1, 2, 3, 7.
2.Учитель выдает кроссворд каждому ученику.
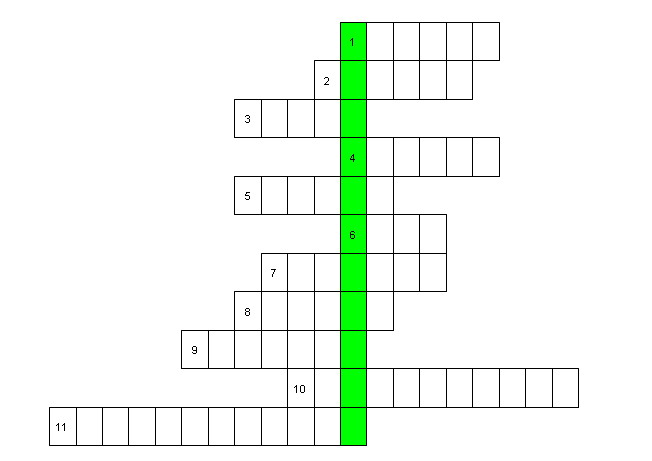
Кроссворд (Слайд 20, 21).

Вопросы: (Слайд 22).
1. Едет ручка вдоль листа. По линеечке, по краю. Получается черта, называется …
2. Древнегреческий ученый.
3. Результат мгновенного касания.
4.Учебная книга, состоящая из 13 томов, которая в течение многих веков являлась основным руководством по геометрии.
5. Древнегреческий ученый, автор собирательного труда «Начала».
6. Единица измерения длины.
7. Часть прямой, ограниченная двумя точками.
8. Единица измерения длины в Древнем Египте.
9. Древнегреческий математик, доказавший теорему, которая носит его имя.
10. Є математический знак.
11. Раздел геометрии.
VII. Домашнее задание № 4, 5, 6.
VIII. Подведение итогов урока.
На все ли вопросы вы получили сегодня ответы?
(Учитель обращает внимание учащихся на вопросы, поставленные в начале урока, и просит кратко еще раз на них ответить.)
Выставление отметок за практические задания и кроссворд.
Презентация к уроку: Медиа:Геометрия_вокруг_нас._Дашкина_М.Н..ppt
Дашкина Мариям Николаевна
wiki.tgl.net.ru
Выполнил ученик 9 класса «А»
Сироткин Илья
Древний Египет
- Древний Египет считается первым государством, оставившим самые ранние математические тексты. Древние греки, достижения которых лежат в основе современной науки, считали себя учениками египтян. Геродот писал: «Египетские жрецы говорили, что царь разделил землю между всеми египтянами, дав каждому по равному прямоугольному участку; из этого он создал себе доходы, приказав ежегодно вносить налог. Если же река отнимала что-нибудь, то царь посылал людей, которые должны. Измерить участок и уменьшить налог». Первой книгой, содержащей геометрические задачи, считается папирус Райнда (в некоторых источниках Г.Ринла), который датируется ХХ веком до нашей эры.
- Геометрия , по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.
Древняя Греция
Фалес решил следующие задачи.
- Предложил способ определения расстояния до корабля на море.
- Вычислил высоту египетской пирамиды Хеопса по длине отбрасываемой тени.
- Доказал равенство углов при основании равнобедренного треугольника.
- Ввел понятие движения, в частности поворота.
- Доказал второй признак равенства треугольников и впервые применял его в задаче.
- Теорема Фалеса о равных отрезках, отсекаемых параллельнымипрямыми на сторонах угла.
Задача об измерении высоты пирамиды.
Однажды, отправившись по торговым делам в Египет, он задержался там на несколько лет. Случилось так, что фараон пожелал узнать высоту пирамиды, но никто не мог ее определить. Фалес смог легко справиться с задачей.
Выбрав день и час, когда его собственная тень стала равной его росту, он измерил тень, отбрасываемую пирамидой, и установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его приближенные изумились такому достаточно простому решению.
Древняя Греция
- Центральное место среди античных трудов по геометрии занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом.
Средние века
- Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.
Геометрия Лобачевского
В 1826 году великий русский математик Николай Иванович Лобачевский поставил точку в проблеме пятого постулата. Вместо него он принял допущение, согласно которому в плоскости можно построить, по крайней мере, две прямые, не пересекающиеся. Дальнейшие его рассуждения привели его к новой безупречной геометрической системе, называемой сейчас геометрией Лобачевского. В его геометрии сумма углов треугольника меньше 180°, в ней нет подобных фигур. В ней существуют треугольники с попарно параллельными сторонами.
Геометрия Лобачевского
- Независимо от Лобачевского в 1832 ту же геометрию построил Я. Больяй (те же идеи развивал К. Гаусс, но он не опубликовал их). Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений; однако она оставалась гипотетической, пока не был выяснен (в 1868) её реальный смысл и тем самым было дано её полное обоснование. Переворот в геометрии, произведённый Лобачевским, по своему значению не уступает ни одному из переворотов в естествознании, и недаром Лобачевский был назван "Коперником геометрии". В его идеях были намечены три принципа, определившие новое развитие геометрии. Первый принцип заключается в том, что логически мыслима не одна евклидова геометрия , но и другие "геометрии". Второй принцип - это принцип самого построения новых геометрических теорий путём видоизменения и обобщения основных положений евклидовой геометрии. Третий принцип состоит в том, что истинность геометрической теории, в смысле соответствия реальным свойствам пространства, может быть проверена лишь физическим исследованием и не исключено, что такие исследования установят, в этом смысле, неточность евклидовой геометрии. Современная физика подтвердила это. Однако от этого не теряется математическая точность евклидовой геометрии, т.к. она определяется логической состоятельностью (непротиворечивостью) этой геометрии. Точно так же в отношении любой геометрической теории нужно различать их физическую и математическую истинность; первая состоит в проверяемом опытом соответствии действительности, вторая - в логической непротиворечивости. Лобачевский дал, т. о., материалистическую установку философии математики
- Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря) 1792, Нижний Новгород — 12 (24) февраля 1856, Казань), великий русский математик, создатель геометрии Лобачевского, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии».















www.yurii.ru
Выполнил ученик 9 класса «А»
Сироткин Илья
Древний Египет
— Древний Египет считается первым государством, оставившим самые ранние математические тексты. Древние греки, достижения которых лежат в основе современной науки, считали себя учениками египтян. Геродот писал: «Египетские жрецы говорили, что царь разделил землю между всеми египтянами, дав каждому по равному прямоугольному участку; из этого он создал себе доходы, приказав ежегодно вносить налог. Если же река отнимала что-нибудь, то царь посылал людей, которые должны. Измерить участок и уменьшить налог». Первой книгой, содержащей геометрические задачи, считается папирус Райнда (в некоторых источниках Г.Ринла), который датируется ХХ веком до нашей эры.
— Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.
Древняя Греция
Фалес решил следующие задачи.
— Предложил способ определения расстояния до корабля на море.
— Вычислил высоту египетской пирамиды Хеопса по длине отбрасываемой тени.
— Доказал равенство углов при основании равнобедренного треугольника.
— Ввел понятие движения, в частности поворота.
— Доказал второй признак равенства треугольников и впервые применял его в задаче.
— Теорема Фалеса о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.
Задача об измерении высоты пирамиды.
Однажды, отправившись по торговым делам в Египет, он задержался там на несколько лет. Случилось так, что фараон пожелал узнать высоту пирамиды, но никто не мог ее определить. Фалес смог легко справиться с задачей.
Выбрав день и час, когда его собственная тень стала равной его росту, он измерил тень, отбрасываемую пирамидой, и установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его приближенные изумились такому достаточно простому решению.
Древняя Греция
— Центральное место среди античных трудов по геометрии занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом.
Средние века
— Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.
Геометрия Лобачевского
В 1826 году великий русский математик Николай Иванович Лобачевский поставил точку в проблеме пятого постулата. Вместо него он принял допущение, согласно которому в плоскости можно построить, по крайней мере, две прямые, не пересекающиеся. Дальнейшие его рассуждения привели его к новой безупречной геометрической системе, называемой сейчас геометрией Лобачевского. В его геометрии сумма углов треугольника меньше 180°, в ней нет подобных фигур. В ней существуют треугольники с попарно параллельными сторонами.
Геометрия Лобачевского
— Независимо от Лобачевского в 1832 ту же геометрию построил Я. Больяй (те же идеи развивал К. Гаусс, но он не опубликовал их). Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений; однако она оставалась гипотетической, пока не был выяснен (в 1868) её реальный смысл и тем самым было дано её полное обоснование. Переворот в геометрии, произведённый Лобачевским, по своему значению не уступает ни одному из переворотов в естествознании, и недаром Лобачевский был назван «Коперником геометрии». В его идеях были намечены три принципа, определившие новое развитие геометрии. Первый принцип заключается в том, что логически мыслима не одна евклидова геометрия, но и другие «геометрии». Второй принцип — это принцип самого построения новых геометрических теорий путём видоизменения и обобщения основных положений евклидовой геометрии. Третий принцип состоит в том, что истинность геометрической теории, в смысле соответствия реальным свойствам пространства, может быть проверена лишь физическим исследованием и не исключено, что такие исследования установят, в этом смысле, неточность евклидовой геометрии. Современная физика подтвердила это. Однако от этого не теряется математическая точность евклидовой геометрии, т.к. она определяется логической состоятельностью (непротиворечивостью) этой геометрии. Точно так же в отношении любой геометрической теории нужно различать их физическую и математическую истинность; первая состоит в проверяемом опытом соответствии действительности, вторая — в логической непротиворечивости. Лобачевский дал, т. о., материалистическую установку философии математики
— Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря) 1792, Нижний Новгород — 12 (24) февраля 1856, Казань), великий русский математик, создатель геометрии Лобачевского, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии».
www.ronl.ru