Равноускоренное движение. Реферат равноускоренное движение

Равноускоренное движение — реферат

Реферат

по физике                

Ученика 10-11 класса э3

Школы № 179 МИОО

Чинь  Бач    

Октябрь 2011

Содержание

1) Ускорение

2) Скорость при движении с постоянным ускорением.

3) Уравнения движения с постоянным ускорением.

4) Свободное  падение тел.                         

Ускорение – это величина, которая характеризует быстроту изменения скорости.

 Рассмотрим криволинейное и неравномерное  движение точки. ЕЕ скорость с течением времени изменится как по модулю, так и по направлению. Пусть в  некоторый момент времени t точка занимает положение М и имеет скорость . По прошествии промежутка времени Δt1  от этого момента точка займет положение М1 и будет иметь скорость 1. Чтобы найти изменение скорости за время Δt1, надо из вектора 1 вычесть вектор

: = 1-

Поделив вектор Δ на промежуток времени Δt, получим вектор направленный так же, как и вектор изменения скорости  Δ 1. Этот вектор называется средним ускорением точки за промежуток времени Δt1. Обозначив его через , запишем: .

Ускорение точки - предел отношения изменения скорости Δ к промежутку времени Δt, в течение которого это изменение произошло, при стремлении промежутка Δt к нулю.

Пусть 0 – скорость точки в начальный момент времени t0, в - ее скорость в любой момент времени t. Тогда Δt = t-t0, = - 0, и формула для ускорения примет вид .

Если  начальный момент времени t0 принять равным нулю, то получим . Отсюда .

Зависимость проекции скорости от времени можно  изобразить наглядно с помощью графиков. Если начальная скорость равно нулю, то график зависимости проекции скорости на ось Ох от времени имеет вид прямой, выходящей из начала координат. Этот график для случая ах>0.

Движение  с постоянным ускорением совершается  в одной плоскости; пусть это будет плоскость хОу. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе ее координаты х и у. Обозначим через х0 и у0 координаты в начальный момент времени t0=0, а через х и у – координаты в момент времени t. Тогда за время Δt = t-t0 изменения координат будут равны Δx = x-x0 и Δy = y-y0.

Отсюда  x = x0+Δx, y = y0+Δy.

Для нахождения положения точки в любой момент времени надо знать ее начальные  координаты и уметь находить изменения координат Δx и Δy за время движения. В случае движения с постоянным ускорением изменения координат можно найти с помощью графиков зависимости проекций скорости от времени.

Покажем, что в этом случае значение Δx численно равно площади соответствующей трапеции OABC. Длина отрезка OC численно равна времени t  движения точки. Разделим его на n малых одинаковых интервалов Δt. Значения проекции скоростей в серединах этих промежутков времени обозначим через v1x, v2x и т.д. Построим на каждом из отрезков, равных промежуткам времени Δt, прямоугольники, высоты которых численно равны проекциям скоростей v1x, v2x и т.д. Площади этих прямоугольников равны изменениям координат Δx1, Δx2 и т.д. за промежутки времени Δt, если считать что движение в течение каждого интервала является равномерным. Нетрудно увидеть, что сумма площадей всех прямоугольников равна площади трапеции OABC, так как площадь малого прямоугольника abcd равна площади элементарной трапеции ab’c’d. Все прямоугольники образуют ступенчатую фигуру. Переход от одного прямоугольника к другому происходит скачкообразно, так как мы заменяли истинное движение суммой равномерных движений на интервалах времени Δt. Чтобы это движение совпало с истинным, необходимо уменьшить промежутки времени Δt. Тогда различие между проекциями ab’ и dc’ скорости в начале и в конце отрезка времени Δt будет все меньше и меньше, и в пределе, т.е. когда интервалы времени будут становиться бесконечно малыми (Δt à 0), равномерные движения не будут отличаться от истинного. Таким образом, и площадь трапеции OABC численно станет равной Δx за все время движения t. Длины оснований OA и BC этой трапеции численно равны проекциям начальной и конечной скоростей, а длины высоты OC – времени движения. По формуле площади трапеции имеем . Учитывая, что , получаем . Мы рассмотрели случай, когда v0x>0 и a0x>0. Но полученная формула справедлива и тогда, когда одна из этих величин отрицательна или когда обе они отрицательны. Свободное падение- это не обязательно движение вниз если начальная скорость направлена вверх, то тело при свободном падении некоторое время будет лететь вверх,  уменьшая свою скорость и лишь за тем начнет падать. Ускорение свободного падения изменяется в зависимости географической широты место на поверхности земли и от высоты тело над землей, точнее, от расстояния до центра земли. На широте Москвы измерения дают следующее значение ускорения свободного падения : g = 9.82 м/ .

turboreferat.ru

Равноускоренное прямолинейное движение

Рис. 5

Это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т.е. ускорение постоянно.

Примерами такого движения является свободное падение тел вблизи поверхности Земли и движение под действием постоянной силы.

При равноускоренном прямолинейном движении координата тела меняется с течением времени в соответствии с законом движения:

где x0– начальная координата материальной точки,0x– проекция начальной скорости иax– проекция ускорения точки на ось 0X.

Проекция скорости материальной точки на ось 0Xв этом случае меняется по следующему закону:

При этом проекции скорости и ускорения могут принимать различные значения, в том числе и отрицательные.

Графики зависимости x(t) иx(t) представляют собой соответственно прямую и параболу, причем, как и в алгебре, по коэффициентам в уравнениях прямой и параболы можно судить о расположении графика функции относительно координатных осей.

Рис. 6

На рисунке 6 приведены графики для x(t),x(t),s(t) в случаеx0> 0,0x> 0,ax< 0. Соответственно прямая(t) имеет отрицательный наклон (tg=ax< 0).

3. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.

Равномерное движение по окружностипроисходит с постоянной по модулю скоростью, т.е.= const (рис. 7). Однако направление скорости при таком движении непрерывно изменяется, поэтому равномерное движение тела по окружности является движением с ускорением.

Рис. 7

Для описания равномерного движения тела по окружности вводят следующие физические величины: период,частота обращения,линейная скорость,угловая скоростьицентростремительное ускорение.

Период обращенияT– время, за которое совершается один полный оборот.

Частота обращения– это число оборотов, совершаемых телом за 1 с. Единицей частоты обращения в СИ является с–1.

Частота и период обращения связаны между собой соотношением .

Вектор скорости при движении точки по окружности постоянно изменяет свое направление (рис. 8).

При равномерном движении тела по окружности отрезок пути s, пройденный за промежуток времениt, является длиной дуги окружности. Отношениепостоянно во времени и называетсямодулем линейной скорости.За время, равное периоду обращенияТ, точка проходит расстояние, равное длине окружности 2R, поэтому

Рис. 8

Скорость вращения твердых тел принято характеризовать физической величиной, называемой угловой скоростью , модуль которой равен отношению угла поворота телак промежутку времени, за которое этот поворот совершен (рис. 8):

Единицей угловой скорости в СИ является с–1.

Так как ориентация твердого тела одинакова во всех системах отсчета, движущихся друг относительно друга поступательно, то и угловая скорость обращения твердого тела будет одинакова во всех системах отсчета, движущихся друг относительно друга поступательно.

При равномерном вращении твердого тела относительно некоторой оси любая точка этого тела движется вокруг этой же оси по окружности радиусом Rс линейной скоростью, которая равна

= R.

Если начальные координаты точки равны (R; 0), то ее координаты меняются по законуx(t) =Rcostиy(t) =Rsint.

studfiles.net

Равноускоренное движение

Количество просмотров публикации Равноускоренное движение - 582

Рассмотрим еще один простой вид поступательного движения – равноускоренного.

Равноускоренным принято называть движение с постоянным ускорением. Часто дается другое определœение: равноускоренным принято называть движение, при котором за любые одинаковые промежутки времени скорость тела изменяется на одинаковую величину. В случае если под постоянством ускорения подразумевать его постоянство как по модулю так и по направлению, то эти два определœения эквивалентны. В отличие от равномерного движения, равноускоренное движение не обязательно является прямолинœейным.

Для равноускоренного движения понятия среднего и мгновенного ускорений совпадают. Значит ускорение, определяемое выражением , одновременно является и средним и мгновенным ускорением.

Пусть в начальный момент времени t0 скорость тела была равна v0, а в некоторый последующий момент t скорость тела стала равна v. Тогда можно написать: , а . Значит

или

Это выражение определяет зависимость скорости от времени для равноускоренного движения и является одним из базовых уравнений. В случае если принять t0 = 0, то . В проекции на ось Х эта зависимость записывается в виде:

(*)

Здесь v0x – проекция вектора начальной скорости на ось Х; vx(t) – проекция вектора скорости в момент времени t; ах – проекция вектора ускорения на ось Х. Аналогично записываются зависимости скорости от времени в проекциях на оси Y и Z. Здесь принято t0 = 0. Для того, чтобы записать еще одно основное соотношение для равноускоренного движения, воспользуемся так называемым графическим методом. Так как зависимость скорости от времени для равноускоренного движения является линœейной, то график зависимости проекции скорости от времени представляет собой прямую линию. Нарисуем примерный график зависимости vx от t. Как известно, на графике зависимости скорости от времени пройденное расстояние численно равно площади под графиком. Значит площадь заштрихованной трапеции на нашем графике равна изменению координаты:

Но . Значит, получается:

Обычно считают, что t0 = 0 и записывают эту формулу в следующем виде:

Эта формула представляет собой зависимость координаты х от времени для равноускоренного движения и является другой основной формулой. х0 – начальная координата. Аналогично записываются зависимости координат y и z от времени. В векторном виде эта зависимость имеет такой вид:

Запишем еще одну формулу. Она не является основным соотношением для равноускоренного движения, но оказывается очень полезной при решении задач. Выразим время из (*): и подставим его в зависимость x(t). После преобразований получается формула:

Аналогичные зависимости можно записать в проекциях на другие оси координат. В общем виде эта зависимость записывается так:

referatwork.ru

Равноускоренное движение

При рассмотрении движения тела с ускорением особого внимания заслуживает движение тела с ускорением, постоянным по величине и направлению. Такое движение по определению является поступательным - поскольку вектор скорости, как и вектор ускорения, имеет постоянное направление, и траектория тела является прямой линией.

При равноускоренном движении мгновенное ускорение равно среднему ускорению: $\overrightarrow{\ a}=\left\langle \overrightarrow{а}\right\rangle =\frac{\triangle v}{\triangle t}=const$, где $\triangle \overrightarrow{v}=\overrightarrow{v}-{\overrightarrow{v}}_0$ -- приращение скорости за время $\triangle t=t-t_0$, ${\overrightarrow{v}}_0=\overrightarrow{v}\left(t_0\right)$ -- начальная скорость, $t_0$ -- начальный момент времени.

Рисунок 1. График скорости при равноускоренном движении

Скорость равноускоренного движения $\overrightarrow{v}\left(t\right)$ в момент времени t определяется из соотношения

где $a_x,\ a_y,a_z$ --- проекции вектора $\overrightarrow{a}$ на оси координат.

Уравнение для траектории движения $\overrightarrow{r}\left(t\right)$ имеет вид:

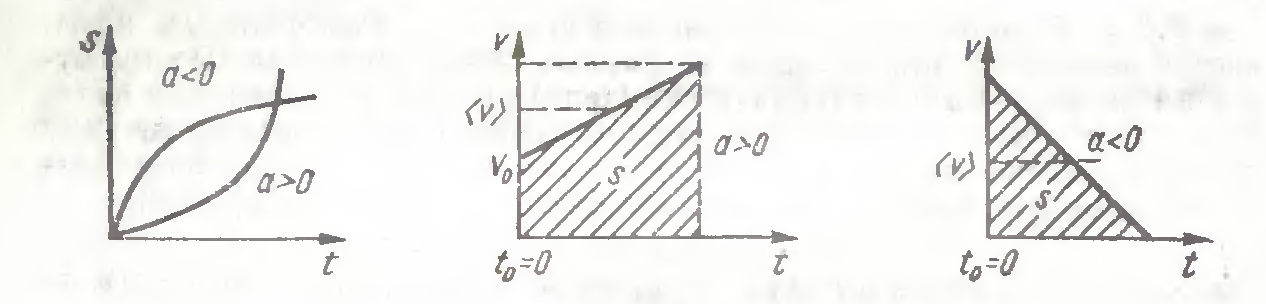
Рисунок 2. Связь между параметрами равноускоренного движения

Учитывая, что равноускоренное движение есть движение поступательное, описывающие его уравнения в векторной и скалярной форме идентичны.

Считая, что t0 = 0, получаем следующие формулы для вычисления пути, пройденного телом при равноускоренном движении за время $t$:

Скорость при равноускоренном движении:

Средняя скорость равноускоренного движения за время t:

Время движения при равноускоренном движении:

Ускорение при равноускоренном движении:

Задача 1

Построить графики зависимости скорости от времени при следующих начальных условиях.

Показать на этом графике перемещение вычислить его при заданном значении времени $t$

Решение

Рисунок 3. \[s_1=S_{\triangle ABC}=\frac{1}{2}\left(v-v_0\right)t=\frac{0-\left(-2\right)}{2}\times 4=4\ м;;\ \ \ \ \]\[\ s_2=S_{ODEF}=v_0t+\frac{at^2}{2}=3\times 5,5-\frac{{5.5}^2}{3\times 2}=11,46\ м\]

author24.ru

Смотрите также

• 
  Нефтегазовое дело реферат
• 
  Реферат история освоения
• 
  Реферат распределительные устройства
• 
  Реферат современный этикет
• 
  Реферат культура франции
• 
  Профессиональная адаптация реферат
• 
  Культура франции реферат
• 
  Реферат древняя япония
• 
  Реферат древний казахстан
• 
  Древний казахстан реферат
• 
  Температура воздуха реферат