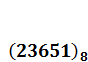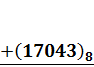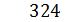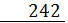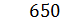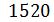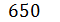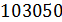Курсовая работа: Другие системы счисления и их происхождение. Реферат пятеричная система счисления
История возникновения систем счисления.
 Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной 
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.  Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Лекция 1. Системы счисления
1. История возникновения систем счисления.
2. Позиционные и непозиционные системы счисления.
3. Десятичная система счисления, запись чисел в ней.
4. Разряды
Человеку постоянно приходится иметь дело с числами, поэтому нужно уметь правильно называть и записывать любое число, производить действия над числами. Как правило, все с этим успешно справляются. Помогает здесь способ записи чисел, который в настоящее время используется повсеместно и носит название десятичной системы счисления.
Изучение этой системы начинается в начальных классах, и , конечно, учителю нужны определенные знания в этой области. Он должен знать различные способы записи чисел, алгоритмы арифметических действий и их обоснование. Материал данной лекции дает тот минимум, без которого невозможно разобраться с различными методическими подходами к обучению младших школьников способам записи чисел и выполнению над ними действий.
История возникновения систем счисления.
Понятие числа возникло в глубокой древности. Тогда же появилась необходимость в названии и записи чисел. Язык для наименования, записи чисел и выполнения действий над ними называют системой счисления.
Простейшая система записи натуральных чисел требует лишь одной цифры, например «палочки» (или зарубки на дереве, как у первобытного человека, или узелка на веревке, как у индейцев Америки), которая изображает единицу. Повторяя этот знак, можно записать любое число: каждое число n записывается просто n «палочками». В такой системе счисления удобно выполнять арифметические действия. Но подобный способ записи очень не экономичен и для больших чисел неизбежно приводит к ошибкам в счете.
Поэтому со временем возникли иные, более экономичные и удобные способы записи чисел. Рассмотрим некоторые из них.
В Древней Греции была распространена так называемая аттическая нумерация. Числа 1, 2, 3, 4 обозначались черточками:
 . .
Число 5 записывалось знаком Г (древнее начертание буквы «пи», с которой начинается слово «пенте» - пять). Числа 6, 7, 8, 9 обозначались так:

Число 10 обозначалось Δ (начальной буквой слова «дека» - десять). Числа 100, 1000 и 10 000 обозначались Н, Х, М – начальными буквами соответствующих слов.

Другие числа записывались различными комбинациями этих знаков.
В третьем веке до нашей эры аттическая нумерация была вытеснена так называемой ионийской системой. В ней числа 1 – 9 обозначаются первыми девятью буквами алфавита: α (альфа), β (бэта), γ (гамма), δ (дельта), ε (эпсилон), ς (фау), ζ (дзета), η (эта),  (тэта). (тэта).

Числа 10, 20, 30, 40, 50, 60, 70, 80, 90 – следующими девятью буквами: i (йота),κ (каппа), λ (ламбда), μ (мю), ν (ню), ξ (кси), ο (омикрон), π (пи), с (копа).

Числа 100, 200, 300, 400, 500, 600, 700, 800, 900 – последними девятью буквами греческого алфавита.
Алфавитную нумерацию, подобную древнегреческой, имели в древности евреи, арабы и многие другие народы Ближнего Востока. У какого народа она возникла впервые неизвестно.
В Древнем Риме в качестве «ключевых» использовались числа 1, 5, 10, 50, 100, 500 и 1000. Они обозначались соответственно буквами I, V, X, L, C, D и М.
Все целые числа (до 5000) записывались с помощью повторения выше приведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей: VI = 6, т.е. 5 + 1; IV = 4, т.е. 5 – 1;XL = 40, т.е. 50 – 10; LX = 60, т.е. 50 + 10. Подряд одна и та же цифра ставится не более трех раз: LXX = 70, LXXX = 80, число 90 записывается XC (а не LXXXX).
Например: XXVIII = 28, XXXIX = 39, CCCXCVII = 397, MDCCCXVIII = 1818.
Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Однако римская нумерация сохранилась до настоящего времени. Ее используют для обозначения юбилейных дат, наименования конференций, глав в книгах и т.д.
На Руси в старину цифры обозначались буквами. Для указания того, что знак является не буквой, а цифрой, сверху над ними ставился специальный знак, называемый «титло». Первые девять цифр записывались так:

Десятки обозначались так:
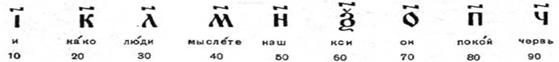
Сотни обозначались так:

Тысячи обозначались теми же буквами с «титлами», что и первые девять цифр, но у них слева ставился знак «≠»: ≠А = 1000, ≠В = 2000, ≠Е = 5000.
   Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками: Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками:
= 10 000, = 20 000, = 80 000.
Отсюда произошло выражение «Тьма народу», т.е. очень много народу.
Сотни тысяч назывались «легионами», их обозначали, обводя знаки единиц кружками из точек:
  
= 100 000, = 200 000, = 800 000.
Миллионы назывались «леодрами». Их обозначали, обводя знаки единиц кружками из лучей или запятых:
= 1 000 000, = 2 000 000.
Десятки миллионов назывались «воронами» или «вранами» и их обозначали, обводя знаки единиц кружками из крестиков или ставя по обе стороны букву К:
Сотни миллионов назывались «колодами». «Колода» имела специальное обозначение – над буквой и под буквой ставились квадратные скобки:
 = 100 000 000. = 100 000 000.
Иероглифы жителей Древнего Вавилона составлялись из узких вертикальных и горизонтальных клинышков, эти два значка использовались и для записи чисел. Один вертикальный клинышек обозначал единицу, горизонтальный – десяток. В Древнем Вавилоне считали группами по 60 единиц. Например, число 185 представлялось как 3 раза по 60 и еще 5. Записывалось такое число с помощью всего двух знаков, один из которых обозначал, сколько раз взято по 60, а другой - сколько взято единиц.
О том, когда и как возникла у вавилонян шестидесятеричная система, существует много гипотез, но ни одна пока не доказана. Одна из гипотез, состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывают с числом 60.
Шестидесятеричная система, в некоторой степени, сохранилась до наших дней, например, в делении часа на 60 минут, а минуты - на 60 секунд и в аналогичной системе измерение углов: 1 градус равен 60 минутам, 1 минута – 60 секундам.
Двоичной системой счисления пользовались при счете некоторые первобытные племена, она была известна еще древнекитайским математикам, но по настоящему развил и построил двоичную систему великий немецкий математик Лейбниц, видевший в ней олицетворение глубокой метафизической истины.
Двоичной системой счисления пользуются некоторые (местные) культуры в Африке, Австралии и Южной Америке.
Для изображения чисел в двоичной системе счисления требуется лишь две цифры: 0 и 1. По этой причине двоичную запись числа легко представить, пользуясь физическими элементами, которые имеют два различных устойчивых состояния. Именно это и послужило одной из важных причин широкого использования двоичной системы в современных электронных вычислительных машинах.
Самой экономичной из всех систем счисления является троичная. Двоичная и равносильная ей, в смысле экономичности, четверичная системы, несколько уступают в этом отношении троичной, но превосходят все основные возможные системы. Если для записи чисел от 1 до 10 в десятичной системе требуется 90 различных состояний, а в двоичной – 60, то в троичной системе достаточно 57 состояний.
Наиболее привычная ситуация, в которой проявляется необходимость троичного анализа, - это, пожалуй, взвешивание на чашечных весах. Здесь могут возникнуть три разных случая: либо одна из чашек перевесит другую, либо наоборот, либо же чашки уравновесят друг друга.
Четверичной системой счисления пользуются, главным образом, индейские племена Южной Америки и индейцы юкки в Калифорнии, считающих на промежутках между пальцами.
Пятеричная система счислениябыла распространена гораздо шире, чем все остальные. Индейцы племени таманакос в Южной Америке употребляют для обозначения числа 5 то же слово, что и для обозначения «всей руки». Слово «шесть» по-таманакски означает «один палец на другой руке», семь – «два пальца на другой руке» и т.д. для восьми и девяти. Десять называется «двумя руками». Желая назвать число от 11 до 14, таманакос протягивают вперед обе руки и считают: «один на ноге, два на ноге» и т.д. до тех пор, пока не доходят до 15 – «всей ноги». Затем следует «один на другой ноге» (число 16) и т.д. до 19. Число 20 по-таманакски означает «один индеец», 21 – «один на руке другого индейца». «Два индейца» означают 40, «три индейца» - 60.
У жителей древней Явы и у ацтеков продолжительность недели составляла 5 дней.
Некоторые историки считают, что римское число X (десять) составлено из двух римских пятерок V (одна из них перевернута), а число V в свою очередь возникло из стилизованного изображения человеческой руки.
Широкое распространение имела в древности двенадцатеричная система счисления. Происхождение ее тоже связано со счетом на пальцах. А именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимают за единицу следующего разряда.
Основное преимущество двенадцатеричной системы состоит в том, что ее основание делится без остатка на 2, 3 и 4. Сторонники двенадцатеричной системы появились еще в XVI веке. В более позднее время к их числу принадлежали столь выдающиеся люди, как Герберт Спенсер, Джон Квинси Адамс и Джордж Бернард Шоу. Существует даже американское двенадцатеричное общество, выпускающее два периодических издания: «Двенадцатеричный бюллетень» и «Руководство по двенадцатеричной системе». Всей «двенадцатеричников» общество снабжает специальной счетной линейкой, в которой в качестве основания используется 12.
В устной речи остатки двенадцатеричной системы сохранились и до наших дней: вместо того, чтобы сказать «двенадцать», часть говорят «дюжина». Сохранился обычай считать многие предметы не десятками, а именно дюжинами, например, столовые приборы в сервизе (сервиз на 12 персон) или стулья в мебельном гарнитуре.
Название единицы третьего разряда в двенадцатеричной системе счисления – гросс – встречается теперь редко, но в торговой практике начала XX столетия оно бытовало и, еще сто лет назад, его можно было легко встретить. Например, в написанном в 1928 году стихотворении «Плюшкин» В.В. Маяковский, высмеивая мещан, скупающих подряд все нужное и ненужное, писал:
..Оглядев
товаров россыпь,
в жадности
и в алчи
укупил | megapredmet.ru
Реферат - Другие системы счисления и их происхождение
Десятичная система счисления далеко не сразу заняла то господствующее положение, которое она имеет сейчас. В разные исторические периоды многие народы пользовались системами счисления, отличными от десятичной.
Так, например, довольно широкое распространение имела двенадцатеричная система. Ее происхождение связано, несомненно, тоже со счетом на пальцах, а именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимается за единицу следующего разряда и т. д. В устной речи остатки двенадцатеричной системы сохранились и до наших дней: вместо того чтобы сказать «двенадцать», мы часто говорим «дюжина». Многие предметы (ножи, вилки, тарелки, носовые платки и т. п.) очень часто считают именно дюжинами, а не десятками, (Вспомните, например, что сервиз бывает, как правило, на 12 или на 6 человек и значительно реже на 10 или на 5.) Сейчас уже крайне редко встречается слово «гросс», означающее «дюжину дюжин» (т. е. единицу третьего разряда в двенадцатеричной системе), но еще несколько десятков лет тому назад оно было довольно широко распространено, особенно в торговом мире. Дюжина гроссов называлась «масса», однако сейчас такое значение слова «масса» мало кому известно. (Хотя, возможно, именно в нем лежит корень таких употребительных выражений, как «масса дел», «масса людей» и т. п. (ср. с выражениями «тысяча дел» и т.д.).
Несомненные остатки двенадцатеричной системы счисления имеются у англичан – в системе мер (например, 1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
Заметим, что с математической точки зрения двенадцатеричная система имела бы, пожалуй, некоторые преимущества перед десятичной, поскольку число 12 делится на 2, 3, 4 и 6, а число 10 только на 2 и 5, а больший запас делителей у числа, служащего основанием системы счисления, создает известные удобства в ее использовании.
В древнем Вавилоне, культура которого, в том числе и математическая, была довольно высока, существовала весьма сложная шестидесятеричная система. Мнения историков по поводу того, как именно возникла такая система, расходятся. Одна из гипотез, впрочем не особенно достоверная, состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывалось с числом 60. Однако это предположение тоже нельзя считать достаточно обоснованным: астрономические познания древних вавилонян были довольно значительны, поэтому следует думать, что погрешность, с которой они определяли продолжительность года, была значительно меньше, чем 5 суток. Несмотря на то, что происхождение шестидесятеричной системы остается неясным, самый факт ее существования и широкого распространения в Вавилонском государстве достаточно хорошо установлен. Эта система, как и двенадцатеричная, в какой-то степени сохранилась и до наших дней (например, в делении часа на 60 минут, а минуты – на 60 секунд и в аналогичной системе измерения углов: градус = 60 минутам, 1 минута = 60 секундам). В целом, однако, эта система, требующая шестидесяти различных «цифр», довольно громоздка и менее удобна, чем десятичная.
По свидетельству известного исследователя Африки Стенли, у ряда африканских племен была распространена пятеричная система счисления. Связь этой системы со строением человеческой руки – первоначальной «счетной машины» – достаточно очевидна.
У ацтеков и майя – народов, населявших в течение многих столетий обширные области американского континента и создавших там высокую культуру, почти полностью уничтоженную испанскими завоевателями в 16–17 вв.,– была принята двадцатеричная система. Та же двадцатеричная система была принята и у кельтов, населявших Западную Европу, начиная со второго тысячелетия до нашей эры. Некоторые следы двадцатеричной системы кельтов сохранились в современном французском языке: например, «восемьдесят» по-французски будет quatre-vingts, т.е. буквально «четырежды двадцать». Число 20 встречается и во французской денежной системе: основная денежная единица – франк – делится на 20 су.
Из четырех перечисленных выше систем счисления (двенадцатеричной, пятеричной, шестидесятеричной и двадцатеричной), сыгравших наряду с десятичной заметную роль в развитии человеческой культуры, все, кроме шестидесятеричной, источники которой неясны, связаны с тем или иным способом счета по пальцам рук (или и рук, и ног), т. е. имеют, подобно десятичной системе, несомненное «анатомическое» происхождение.
Как показывают приведенные выше примеры (иx число можно было бы значительно увеличить), многочисленные следы этих систем счисления сохранились до наших дней и в языках многих народов, и в принятых денежных системах, и в системах мер. Однако для записи чисел и для выполнения тех или иных вычислений мы всегда пользуемся десятичной системой.
www.ronl.ru
Реферат Десятеричная система счисления
скачатьРеферат на тему:
План:
Введение- 1 История
- 2 Основные сведения
- 2.1 Двоично-десятичное кодирование
- 2.2 Таблица сложения в десятичной системе счисления
- 2.3 Таблица умножения в десятичной системе
Введение
Десяти́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 (ноль), называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.
1. История
Десятичная непозиционная система счисления с единичным кодированием десятичных цифр возникла во второй половине третьего тысячелетия до н. э. в древнем Египте. В другой великой цивилизации — вавилонской — за две тысячи лет до н. э. внутри шестидесятеричных разрядов использовалась позиционная десятичная система счисления с единичным кодированием десятичных цифр.[1]
Древнейшая известная запись позиционной десятичной системы обнаружена в Индии в 595 г. Нуль в то время применялся не только в Индии, но и в Китае. В этих старинных системах для записи одинакового числа использовались символы, рядом с которыми дополнительно помечали, в каком разряде они стоят. Потом перестали помечать разряды, но число всё равно можно прочитать, так как у каждого разряда есть своя позиция. А если позиция пустая, её нужно пометить нулём. В поздних вавилонских текстах такой знак стал появляться, но в конце числа его не ставили. Лишь в Индии нуль окончательно занял своё место, эта запись распространилась затем по всему миру.
Индийская нумерация пришла сначала в арабские страны, затем и в Западную Европу. О ней рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания чисел, записанных в позиционной системе, сделали её особенно популярной. А поскольку труд аль-Хорезми был написан на арабском, то за индийской нумерацией в Европе закрепилось неправильное название — «арабская» (арабские цифры).
1.1. Кипу инков
Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[2], так и не числовых записей в двоичной системе кодирования[3]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[4]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[5].
2. Основные сведения
Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:
 , где
, где  — это целые числа, называемые цифрами, удовлетворяющие неравенству
— это целые числа, называемые цифрами, удовлетворяющие неравенству 
Обычно для ненулевого числа x требуют, чтобы старшая цифра an − 1 в десятичном представлении x была также ненулевой.
Например, число сто три представляется в десятичной системе счисления в виде:

С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до 10n − 1, то есть, всего 10n различных чисел.
Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:

где n — число разрядов целой части числа, m — число разрядов дробной части числа.
2.1. Двоично-десятичное кодирование
В двоичных компьютерах применяют двоично-десятичное кодирование десятичных цифр (Binary-Coded Decimal), при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Двоично-десятичные числа требуют большего количества бит для своего хранения.[6] Так, четыре двоичных разряда имеют 16 состояний, и при двоично-десятичном кодировании 6 из 16 состояний двоичной тетрады не используются.[7]
2.2. Таблица сложения в десятичной системе счисления
+ 0 1 2 3 4 5 6 7 8 9 10
0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
10 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
2.3. Таблица умножения в десятичной системе
× 0 1 2 3 4 5 6 7 8 9 10
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
wreferat.baza-referat.ru
Реферат по математике на тему: " Системы счисления"
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 90»
Реферат
Системы счисления
Выполнил
Ученица 5 класса Д
Кириллова Анна
Руководитель
Учитель математики
Штадельман Елена Викторовна
Северск 2012
Содержание
-
-
-
«Из подъезда вышел человек лет около 49; пройдя по улице метров 196, он зашел в магазин, купил там две семерки яиц и пошел дальше...». Не правда ли, такое описание звучит несколько странно? Когда мы оцениваем какую-то величину - возраст человека, расстояние и т.п. - приблизительно, то мы всегда пользуемся круглыми числами и говорим обычно «метров 200», человек лет 50» и т.п.
Вообще с круглыми числами легче оперировать, чем с некруглыми, их легче запомнить, с ними удобнее производить арифметические действия. Например, ни для кого не составит труда умножить в уме 100 на 200, если же нужно перемножить два некруглых трехзначных числа, скажем 147 и 343, то далеко не всякий сделает это без карандаша и бумаги.
Говоря о круглых числах, мы обычно не отдаем себе отчета в том, что деление чисел на круглые и некруглые, по существу условно. Одно и то же число может быть круглым или некруглым в зависимости от того, какой системой записи числа или, как обычно говорят, какой системой счисления мы пользуемся.
Чтобы разобраться в этом вопросе, посмотрим, прежде всего, что представляет собой наша обычная десятичная система счисления, которой мы все пользуемся. В этой системе каждое целое положительное число представляется в виде суммы различных степеней числа 10 с коэффициентами, могут принимать значения от 0 до 9 включительно.
Например, запись 2548 означает, что рассматриваемое число содержит 8 единиц, 4 десятка, 5 сотен и 2 тысячи, т.е. 2548 - это сокращенное обозначение выражения
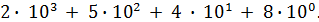
Однако можно было бы с таким же успехом представить каждое число в виде комбинации степеней не числа 10, а какого - либо другого целого числа (кроме 1), например, числа 8. В этой системе, называемой «восьмеричной системой счисления» или «системой счисления с основанием 8», мы вели бы счет от 0 до 7 обычным образом, а число 8 приняли бы за единицу следующего разряда. Его естественно обозначить в нашей новой восьмеричной системе символом 10 (единица второго разряда). Чтобы не путать это обозначение с десятичным числом 10, припишем к нему значок 8, т.е. окончательно вместо 8 будем писать 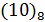 .
.
Единицами следующих разрядов должны служить числа 8 , 8 и т.д. Их естественно обозначить 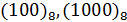 и т.д.
и т.д.
Восьмеричная система не имеет сколько-нибудь широкого распространения и никак не может конкурировать с повсеместно распространенной десятичной системой.
-
Почему именно числу 10 отведена такая привилегированная роль? Человек, далекий от этих вопросов, ответил бы, вероятно, не задумываясь, так: дело просто в том, что число 10 - круглое, на него удобно умножать любое число, поэтому удобно считать десятками, сотнями и т.д. Мы, однако, уже выяснили, что дело обстоит как раз наоборот: число 10 потому и круглое, что оно принято за основание системы счисления. При переходе к какой-либо иной системе счисления, скажем семеричной (где оно записывается в виде 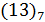 ), его «круглость» немедленно исчезнет.
), его «круглость» немедленно исчезнет.
Причины, по которым именно десятичная система оказалась общепринятой, совсем не математического характера. Десять пальцев рук - вот тот первоначальный аппарат для счета, которым человек пользовался, начиная с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т.е. использовав до конца возможности нашего природного «счетного аппарата», естественно принять само число 10 за новую, более крупную единицу ( единицу следующего разряда), и т.д. Таким образом, именно счет по пальцам рук положил начало той системе, которая кажется нам сейчас чем-то само собой разумеющимся.
-

Десятичная система счисления далеко не сразу заняла то господствующее положение, которое она имеет сейчас. В разные исторические периоды многие народы пользовались системами счисления, отличными от десятичной
Двенадцатеричная система.
Так, например, довольно широкое распространение имела двенадцатеричная система. Ее происхождение связано, несомненно, тоже со счетом на пальцах. А, именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг (рис.1), то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимается за единицу следующего разряда и т.д.
В устной речи остатки двенадцатеричной системы сохранились и до наших дней: вместо того чтобы сказать «двенадцать», мы часто говорим «дюжина». Многие предметы (ножи, вилки, тарелки, носовые платки и т.п.) очень часто считают именно дюжинами, а не десятками. Вспомните, например, что сервиз бывает, как правило, на 12 или на 6 человек и значительно реже на 10 или на 5. Сейчас уже крайне редко встречается слово «гросс», означающее «дюжину дюжин» (т.е. единицу третьего разряда в двенадцатеричной системе), но еще несколько десятков лет тому назад оно было довольно широко распространено, особенно в торговом мире. Дюжина гроссов называлась «масса», однако сейчас такое значение слова «масс» мало кому известно. Хотя, возможно, именно в нем лежит корень таких употребительных выражений, как «масса дел», «масса людей» и т.п. (можно сравнивать с выражением «тысяча дел»).
Несомненно, остатки двенадцатеричной системы счисления имеются у англичан - в системе мер (например. 1 фут =12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
С математической точки зрения, двенадцатеричная система имела бы, пожалуй, некоторые преимущества перед десятичной, поскольку число 12 делится на 2, 3, 4, и 6, а число 10 только на 2 и 5. А больший запас делителей и у числа, служащего основанием системы счисления, создает известные удобства в ее использовании.
Шестидесятеричная система
В древнем Вавилоне, культура которого, в том числе и математическая, была довольно высока, существовала весьма сложная шестидесятеричная система. Мнения историков по поводу того, как именно возникла такая система, расходятся. Одна из гипотез, впрочем, не особенно достоверная, состоит в том, что произошло смешение двух племён, одно из которых пользовалось шестеричной системой, а другое - десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывалось с числом 60. Однако это предположение тоже нельзя считать достаточно обоснованным: астрономические познания древних вавилонян были довольно значительны, поэтому следует думать, что погрешность, с которой они определяли продолжительность года, была значительно меньше, чем 5 суток. Несмотря на то, что происхождение шестидесятеричной системы остаётся неясным, самый факт её существования и широкого распространения в Вавилонском государстве достаточно хорошо установлен. Эта система, как и двенадцатеричная, в какой-то степени сохранилась и до наших дней (например, в делении часа на 60 минут, а минуты - на 60 секунд и в аналогичной системе измерения углов: градус = 60 минутам, 1 минута = 60 секундам). В целом, однако, эта система, требующая шестидесяти различных «цифр», довольно громоздка и менее удобна, чем десятеричная.
По свидетельству известного исследователя Африки Стенли, у ряда африканских племён была распространена пятеричная система счисления. Связь этой системы со строением человеческой руки - первоначальной «счётной машины» - достаточно очевидна.
Двадцатеричная система.
У ацтеков и майя - народов, населявших в течении многих столетий обширные области американского континента и создавших там высокую культуру, почти полностью уничтоженную испанскими завоевателями в 16 - 17 вв., - была принята двадцатеричная система. Та же двадцатеричная система была принята и у кельтов, населявших Западную Европу, начиная со второго тысячелетия до нашей эры. Некоторые следы двадцатеричной системы кельтов сохранились в современном французском языке: например, «восемьдесят» по-французски будет как «четырежды двадцать». Число 20 встречается и во французской денежной системе: основная денежная единица - франк - делится на 20 су.
Из четырех перечисленных выше систем счисления (двенадцатеричной, пятеричной, шестидесятеричной и двадцатеричной), сыгравших наряду с десятичной заметную роль в развитии человеческой культуры, все, кроме шестидесятеричной, источники которой неясны, связаны с тем или иным способом счета по пальцам рук (или и рук, и ног), т.е. имеют, подобно десятичной системе, несомненное «анатомическое» происхождение.
Как показывают приведенные выше примеры (их число можно было бы значительно увеличить), многочисленные следы этих систем счисления сохранились до наших дней и в языках многих народов, и в принятых денежных системах, и в системах мер. Однако для записи чисел и для выполнения тех или иных вычислений мы всегда пользуемся десятичной системой.
-
Для чисел, записанных в десятичной системе пользуются правилами сложения и умножения чисел «столбиком», деления - «углом». Рассмотрим сложение. Как в десятичной, так и в любой другой системе складывают сначала единицы, затем переходят к следующему разряду и т.д. до тех пор, пока не доходят до самого старшего из имеющихся разрядов. При этом необходимо помнить, что всякий раз, когда при сложении в предыдущем разряде получается сумма, большая, чем основание той системы счисления, в которой ведется запись, или равная ему, надо сделать перенос в следующий разряд. Например,
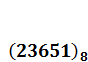
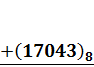

Перейдем теперь к умножению. Основой для перемножения любых чисел служит таблица умножения, определяющая произведение чисел, меньших, чем основание счисления. Нетрудно убедиться в том, что для восьмеричной системы таблица умножения выглядит так:
18
28
38
48
58
68
78
18
28
28
38
48
58
68
78
28
28
48
68
108
128
148
168
38
з8
68
118
148
178
228
258
48
48
108
148
208
248
зо8
348
58
58
128
178
248
318
368
438
68
68
148
228
зо8
368
448
528
78
78
168
25 8
348
438
528
618
Здесь в каждой клетке стоит произведение чисел, представляющих собой номера строки и столбца, на пересечении которых стоит эта клетка, причем все числа записаны здесь в восьмеричной системе.
Пользуясь этой таблицей, легко перемножить «столбиком» числа, содержащие любое количество разрядов. Например,
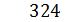
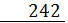
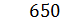
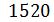
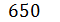
Используемая литература
С. В. ФОМИН Системы счисления — М.: Наука, Гл. ред. физ.-мат. лит., 1987. — 48 с.
«Натуральные числа и десятичные дроби»: Учебное пособие для 5 класса. – Томск: Изд. Томского университета, 2001.
http://ru.wikipedia.org
infourok.ru
Курсовая работа - Другие системы счисления и их происхождение
Десятичная система счисления далеко не сразу заняла то господствующее положение, которое она имеет сейчас. В разные исторические периоды многие народы пользовались системами счисления, отличными от десятичной.
Так, например, довольно широкое распространение имела двенадцатеричная система. Ее происхождение связано, несомненно, тоже со счетом на пальцах, а именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимается за единицу следующего разряда и т. д. В устной речи остатки двенадцатеричной системы сохранились и до наших дней: вместо того чтобы сказать «двенадцать», мы часто говорим «дюжина». Многие предметы (ножи, вилки, тарелки, носовые платки и т. п.) очень часто считают именно дюжинами, а не десятками, (Вспомните, например, что сервиз бывает, как правило, на 12 или на 6 человек и значительно реже на 10 или на 5.) Сейчас уже крайне редко встречается слово «гросс», означающее «дюжину дюжин» (т. е. единицу третьего разряда в двенадцатеричной системе), но еще несколько десятков лет тому назад оно было довольно широко распространено, особенно в торговом мире. Дюжина гроссов называлась «масса», однако сейчас такое значение слова «масса» мало кому известно. (Хотя, возможно, именно в нем лежит корень таких употребительных выражений, как «масса дел», «масса людей» и т. п. (ср. с выражениями «тысяча дел» и т.д.).
Несомненные остатки двенадцатеричной системы счисления имеются у англичан – в системе мер (например, 1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
Заметим, что с математической точки зрения двенадцатеричная система имела бы, пожалуй, некоторые преимущества перед десятичной, поскольку число 12 делится на 2, 3, 4 и 6, а число 10 только на 2 и 5, а больший запас делителей у числа, служащего основанием системы счисления, создает известные удобства в ее использовании.
В древнем Вавилоне, культура которого, в том числе и математическая, была довольно высока, существовала весьма сложная шестидесятеричная система. Мнения историков по поводу того, как именно возникла такая система, расходятся. Одна из гипотез, впрочем не особенно достоверная, состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывалось с числом 60. Однако это предположение тоже нельзя считать достаточно обоснованным: астрономические познания древних вавилонян были довольно значительны, поэтому следует думать, что погрешность, с которой они определяли продолжительность года, была значительно меньше, чем 5 суток. Несмотря на то, что происхождение шестидесятеричной системы остается неясным, самый факт ее существования и широкого распространения в Вавилонском государстве достаточно хорошо установлен. Эта система, как и двенадцатеричная, в какой-то степени сохранилась и до наших дней (например, в делении часа на 60 минут, а минуты – на 60 секунд и в аналогичной системе измерения углов: градус = 60 минутам, 1 минута = 60 секундам). В целом, однако, эта система, требующая шестидесяти различных «цифр», довольно громоздка и менее удобна, чем десятичная.
По свидетельству известного исследователя Африки Стенли, у ряда африканских племен была распространена пятеричная система счисления. Связь этой системы со строением человеческой руки – первоначальной «счетной машины» – достаточно очевидна.
У ацтеков и майя – народов, населявших в течение многих столетий обширные области американского континента и создавших там высокую культуру, почти полностью уничтоженную испанскими завоевателями в 16–17 вв.,– была принята двадцатеричная система. Та же двадцатеричная система была принята и у кельтов, населявших Западную Европу, начиная со второго тысячелетия до нашей эры. Некоторые следы двадцатеричной системы кельтов сохранились в современном французском языке: например, «восемьдесят» по-французски будет quatre-vingts, т.е. буквально «четырежды двадцать». Число 20 встречается и во французской денежной системе: основная денежная единица – франк – делится на 20 су.
Из четырех перечисленных выше систем счисления (двенадцатеричной, пятеричной, шестидесятеричной и двадцатеричной), сыгравших наряду с десятичной заметную роль в развитии человеческой культуры, все, кроме шестидесятеричной, источники которой неясны, связаны с тем или иным способом счета по пальцам рук (или и рук, и ног), т. е. имеют, подобно десятичной системе, несомненное «анатомическое» происхождение.
Как показывают приведенные выше примеры (иx число можно было бы значительно увеличить), многочисленные следы этих систем счисления сохранились до наших дней и в языках многих народов, и в принятых денежных системах, и в системах мер. Однако для записи чисел и для выполнения тех или иных вычислений мы всегда пользуемся десятичной системой.
www.ronl.ru
"История возникновения и развития систем счисления"

Разделы: Информатика
Продолжительность: 1 урок (45 минут)
ЦЕЛЬ УРОКА:
- Обучающая: Познакомить с возникновением и
развитием систем счисления. Привести
исторические факты.
- Развивающая: Развивать внимание, умение
анализировать.
- Воспитательная: воспитывать интерес к
информатике через исторические факты.
Тип урока: урок-лекция.
Оборудование: компьютер, проектор.
Программное обеспечение: презентация в PowerPoint
по теме урока “История возникновения и развития
систем счисления”.
При подготовке урока использовалась
литература: Приложение к газете “Первое
сентября”, ноябрь 1995 г.
1. Объяснение нового материала.
Урок-лекция.
Презентация
Таблица (слайд №2)
Системы счисления.
Десятичная система счисления.
(слайд №3)
Язык чисел, как и любой другой, имеет свой
алфавит. В том языке чисел, в котором мы обычно
пользуемся, алфавитом служат десять цифр – от 0
до 9. Это десятичная система счисления. Системой
счисления мы будем называть способ
представления числа символами некоторого
алфавита, которые называют цифрами.
Причина, по которой десятичная система
счисления стала общепринятой, вовсе не
математическая. Десять пальцев рук – вот аппарат
для счета, которым человек пользуется с
доисторических времен. Древнее изображение
десятичных цифр не случайно: каждая цифра
обозначает число по количеству углов в ней.
Например, 0 – углов нет, 1 – один угол, и т. д.
Написание десятичных цифр претерпело
существенные изменения. Форма, которой мы
пользуемся, установилась в XVI веке.
Исторически десятичная система счисления
сложилась и развивалась в Индии. Европейцы
заимствовали индийскую систему счисления у
арабов, назвав ее арабской. Это исторически
неправильное название удерживается и сейчас.
Возникновение и развитие десятичной системы
счисления явилось одним из важнейших достижений
человеческой мысли (наряду с появлением
письменности).
Однако десятичной системой счисления люди
пользовались не всегда. В разные исторические
периоды многие народы использовали другие
системы счисления
Двенадцатеричная система счисления.
(слайд №4)
Довольно широкое распространение имела
двенадцатеричная система счисления.
Происхождение ее тоже анатомическое. Подумайте,
где у человека удобно считать до 12? Считали
фаланги пальцев на руке кроме большого. 4 пальца
по три фаланги всего 12. Элементы
двенадцатеричной системы счисления сохранились
в Англии в системе мер (1 фут = 12 дюймов) и в
денежной системе (1 шиллинг = 12 пенсам). Где вы еще
встречали счет по 12? Нередко и мы сталкиваемся в
быту с двенадцатеричной системой счисления:
чайные и столовые сервизы на 12 персон, комплект
носовых платков – 12 штук.
Пятеричная система счисления.
По свидетельству известного исследователя
Африки Стэнли, у ряда африканских племен была
распространена пятеричная система счисления,
Долгое время пользовались пятеричной системой
счисления и в Китае. Очевидна связь этой системы
со строением человеческой руки.
Двадцатеричная система счисления.
У ацтеков и майя – народов, населявших в
течение многих столетий обширные области
Американского континента и создавших там
высочайшую культуру, в том числе и
математическую, была принята двадцатеричная
система счисления. Также двадцатеричная система
счисления бала принята и у кельтов, населявших
Западную Европу начиная со второго тысячелетия
да нашей эры. Основу для счета в этой системе
счисления составляли пальцы рук и ног. Некоторые
следы двадцатеричной системы счисления кельтов
сохранились во французской денежной системе:
основная денежная единица, франк, делится на 20 (1
франк = 20 су)
Алфавитные системы счисления.
(слайд №5)
Алфавитные системы счисления представляют
особую группу. В них для записи чисел
использовался буквенный алфавит. Примером
алфавитной системы счисления является
славянская. У одних славянских народов числовые
значения букв устанавливались в порядке
следования букв славянского алфавита, у других, в
частности у русских, роль цифр играли не все
буквы, а только те, которые имеются в греческом
алфавите. Над буквой, обозначающей цифру,
ставился специальный знак – “титло”.
Славянская система счисления сохранилась в
богослужебных книгах.
Алфавитная система счисления бала
распространена у древних армян, грузин, греков
(ионическая система счисления), арабов, евреев, и
других народов Ближнего востока.
Но в древнеармянском и древнегрузинском
алфавитах было гораздо больше букв, чем в
древнегреческом. Это позволило ввести особые
обозначения для чисел 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000,
9000.
Числовые значения следовали порядку букв в
армянском и грузинском алфавитах.
Алфавитная нумерация преобладала до XVIII в., хотя
арабская нумерация употреблялась в отдельных
случаях гораздо раньше (в грузинской литературе
такие случаи восходят к X- XI вв.; в памятниках
армянской математической литературы они
установлены пока только для XV в.). В Армении
алфавитная нумерация употребляется и сейчас для
обозначения глав в книгах, строф в
стихотворениях и т. п. В Грузии алфавитная
нумерация вышла из употребления.
Шестидесятеричная система счисления
(слайд№ 6)
Особый интерес представляет так называемая
“вавилонская”, или шестидесятеричная система
счисления, существовавшая в Древнем Вавилоне.
Мнение историков по поводу того, как именно
возникла эта система счисления, расходятся.
Существуют две гипотезы. Первая исходит из того,
что произошло слияние двух племен, одно из
которых пользовалось шестеричной, другое –
десятичной. Шестидесятеричная система счисления
в данном случае могла возникнуть в результате
своеобразного политического компромисса. Суть
второй гипотезы в том, что древние вавилоняне
считали продолжительность года равной 360 суткам,
что связано с числом 60. Отголоски использования
этой системы счисления дошли до наших дней.
Например, 1 час = 60 минутам. В целом
шестидесятеричная система счисления громоздка и
неудобна.
В Древнем Вавилоне примерно за сорок веков до
нашего времени создалась поместная (позиционная)
нумерация, т.е. такой способ изображения чисел,
при которой одна и та же цифра может обозначать
разные числа в зависимости от места занимаемого
этой цифрой. Наша современная нумерация тоже
поместная: в числе 52 цифра 5 обозначает пятьдесят,
т.е. 5*10, а в числе 576 эта же цифра обозначает
пятьсот, т.е. 5*10*10. В вавилонской поместной
нумерации ту роль, которую у нас играет число 10,
играло число 60. Числа, меньшие 60 обозначались с
помощью: для единицы и для десятка.

Они имели клинообразный вид, так как вавилоняне
писали на глиняных дощечках палочками
треугольной формы. Эти знаки повторялись нужное
число раз например:
Шестидесятеричная запись не получила
распространения за пределами
ассиро-вавилонского царства.
Римская система счисления.
(слайд №7)
Эта система счисления появилась в Древнем Риме.
Первые двенадцать натуральных чисел в римской
системе записываются так: I, II, III, IV, V, VI, VII, VIII, IX, X,
XI, XII.
Примеры записи чисел XXVIII – 28, MCMXXXV – 1935. С этими
числами очень трудно производить арифметические
действия. По этой причине в настоящее время
римская система счисления используется там, где
это действительно удобно: в литературе
(нумерация глав), в оформлении документов (серия
паспорта, ценных бумаг и др.), в декоративных
целях – на циферблате часов, в ряде других
случаев.
“Машинные” системы счисления.
Перед математиками и конструкторами в 50-х
встала проблема отыскания таких систем
счисления, которые отвечали бы требованиям, как
разработчиков ЭВМ, так и создателей программного
обеспечения. Одним из итогов этих исследований
стало значительное изменение представлений о
системах счисления и о методах вычислений.
Оказалось, что арифметический счет, которым
человечество пользуется с древнейших времен,
может совершенствоваться, подчас весьма
неожиданно и на удивление эффективно.
Специалисты выделили так называемую
“машинную” группу систем счисления и
разработали способы преобразования чисел этой
группы.
К “машинным” системам счисления относятся:
- Двоичная
- Восьмеричная
- Шестнадцатеричная
Официальное рождение двоичной арифметики
связано с именем Г.В. Лейбница, опубликовавшего в
1703 г. статью, в которой он рассмотрел правила
выполнения арифметических действий над
двоичными числами.
Подведение итогов. На этом уроке вы узнали о
истории развития систем счисления, а на
следующих уроках мы более подробно поговорим о
двоичной, восьмеричной и шестнадцатеричной
системах счисления.
2. Задание на дом: Системы счисления
xn--i1abbnckbmcl9fb.xn--p1ai


 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. .
.

 (тэта).
(тэта).


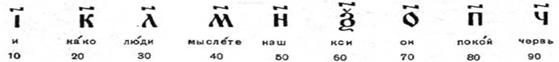



 Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками:
Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками:




 = 100 000 000.
= 100 000 000.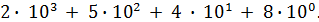
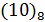 .
.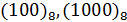 и т.д.
и т.д.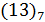 ), его «круглость» немедленно исчезнет.
), его «круглость» немедленно исчезнет.