.1) Систематизировать приемы построения графиков.
2) Показать их применение при построении:
а) графиков сложных функций;
б) при решении заданий ЕГЭ из части C.
График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.
Замечание. Точки пересечения графика с осью x остаются неиз мен ными.
График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.
Замечание. Точка пересечения графика с осью y остается неизменной.
График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.
График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.
>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в раз.
k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.
Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).
Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).
Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.
Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).
График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.
Замечание. Описанное построение производить только для функции, имеющей обратную.
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
В одной системе координат, построим графики функций: а)
Решение : Преобразуем функцию f(x).
Так как, то
Тогда g(f(x))=20.
Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;
f(g(x))=12
Пусть g(x)=t, тогда f(t)=12 или
а)
График данной функции получается построением графика
В системе x’o’y’, где o’(1;0).
б)
В системе x”o”y”, где o”(6;4), построим график функции
Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.
Помогают найти нетрадиционное решение сложных задач.
www.ronl.ru
Преобразование графиков. Приемы построения графиков функций с помощью преобразования графиков основных элементарных функций являются весьма актуальными.
Пусть задан график функции .
Справедливы следующие утверждения (правила):
1. График функции 
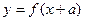есть график , сдвинутый (при 
влево, при 
вправо) на 
единиц параллельно оси Ох (рис. 4.28).
2. График функции 
есть график , сдвинутый (при 
вверх, при 
вниз) на 
единиц в направлении оси Оу (см. рис. 4.28).
3. График функции 
есть график , растянутый (при 
) в … m раз или сжатый (при 
) вдоль оси Оу (рис. 4.29). При 
график функции есть зеркальное отображение графика 
от оси Ох.
4. График функции 
есть график , сжатый (при 
) в k раз или растянутый (при 
) вдоль оси Ох (рис. 4.30). При 
график функции есть зеркальное отображение графика 
от оси Оу.
Пример. Построить график функции 
.
Решение. Проводим построение графика следующим образом (рис. 4.31).
1) строим график 
;
2) 
сжатие графика в два раза вдоль оси Ох 
;
3) 
зеркальное отражение графика от оси Ох 
;
4) 
растяжение графика в три раза вдоль оси Оу
.
4.4. Уравнение линии на плоскости. Различные
уравнения прямой.
Определение.Под линией L на плоскости понимается множество точек этой плоскости, обладающих некоторым общим для этих точек геометрическим свойством, которым не обладает ни одна точка, не принадлежащая этой линии.
Если это геометрическое свойство выразить через координаты любой точки 
, получим уравнение 
.
Если точка 
перемещается по линии L, она называется текущей точкой. Координаты текущей (произвольной) точки линии удовлетворяют уравнению линии.
Определение.называется уравнением линии L, если ему удовлетворяют координаты (х,у) любой точки данной линии и не удовлетворяют координаты ни одной точки, не лежащей на данной линии.
Рассмотрим обратную задачу: дано уравнение .
Определение.Множество пар чисел (х,у), удовлетворяющих уравнению , и геометрически представляющих множество точек , расположенных на плоскости хОу, образуют линию, которая называется графиком данного уравнения.
Если от уравнения перейти к виду , то линия является графиком функции .
Таким образом, между уравнениями и их графиками существует взаимное соответствие: L
F(x,y)=0 (y=f(x)).
Если две линии заданы уравнениями 
и 
, то точка их пересечения находится из решения системы:
refac.ru
1) Систематизировать приемы построения графиков.
2) Показать их применение при построении:
а) графиков сложных функций;
б) при решении заданий ЕГЭ из части C.
График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.
Замечание. Точки пересечения графика с осью x остаются неиз мен ными.
График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.
Замечание. Точка пересечения графика с осью y остается неизменной.
График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.
График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.
>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в раз.
k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.
Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).
Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).
Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.
Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).
График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.
Замечание. Описанное построение производить только для функции, имеющей обратную.
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
В одной системе координат, построим графики функций: а)
Решение : Преобразуем функцию f(x).
Так как, то
Тогда g(f(x))=20.
Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;
f(g(x))=12
Пусть g(x)=t, тогда f(t)=12 или
а)
График данной функции получается построением графика
В системе x’o’y’, где o’(1;0).
б)
В системе x”o”y”, где o”(6;4), построим график функции
Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.
Помогают найти нетрадиционное решение сложных задач.
www.ronl.ru
1) Систематизировать приемы построения графиков.
2) Показать их применение при построении:
а) графиков сложных функций;
б) при решении заданий ЕГЭ из части C.
График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.
Замечание. Точки пересечения графика с осью x остаются неиз мен ными.
График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.
Замечание. Точка пересечения графика с осью y остается неизменной.
График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.
График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.
>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в раз.
k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.
Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).
Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).
Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.
Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).
График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.
Замечание. Описанное построение производить только для функции, имеющей обратную.
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)
В одной системе координат, построим графики функций: а)
Решение : Преобразуем функцию f(x).
Так как, то
Тогда g(f(x))=20.
Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;
f(g(x))=12
Пусть g(x)=t, тогда f(t)=12 или
а)
График данной функции получается построением графика
В системе x’o’y’, где o’(1;0).
б)
В системе x”o”y”, где o”(6;4), построим график функции
Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.
Помогают найти нетрадиционное решение сложных задач.
www.ronl.ru
