Курсовая работа: Преобразование графиков функции. Преобразование графиков реферат

Реферат: Преобразование графиков функции

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

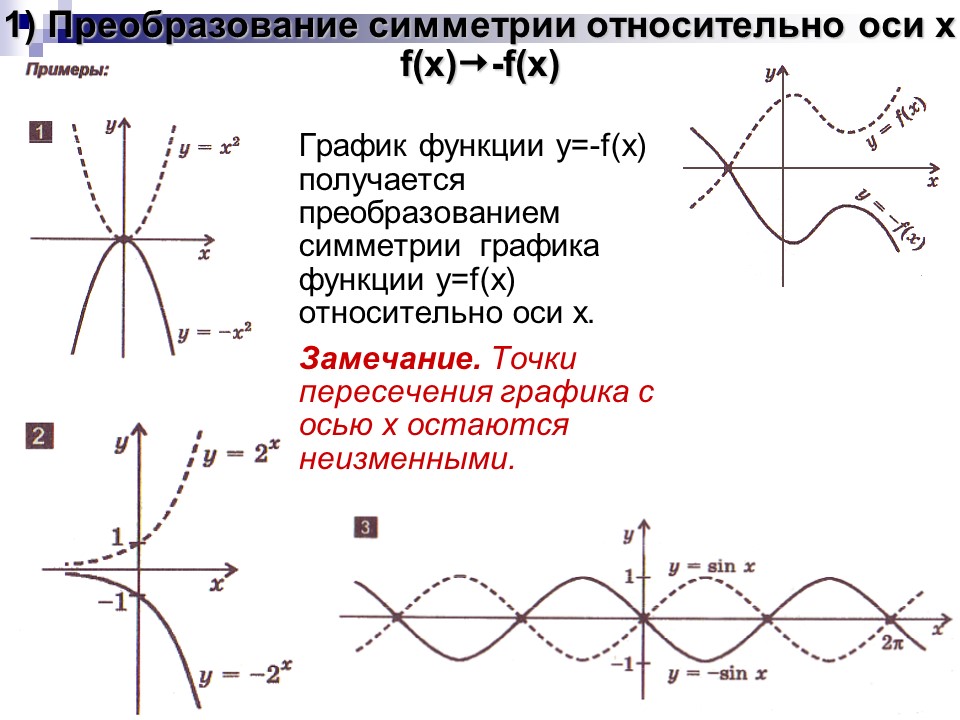
График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание.Точки пересеченияграфика с осью x остаются неизменными.

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание.Точка пересечения графика с осью y остается неизменной.

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.

График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.

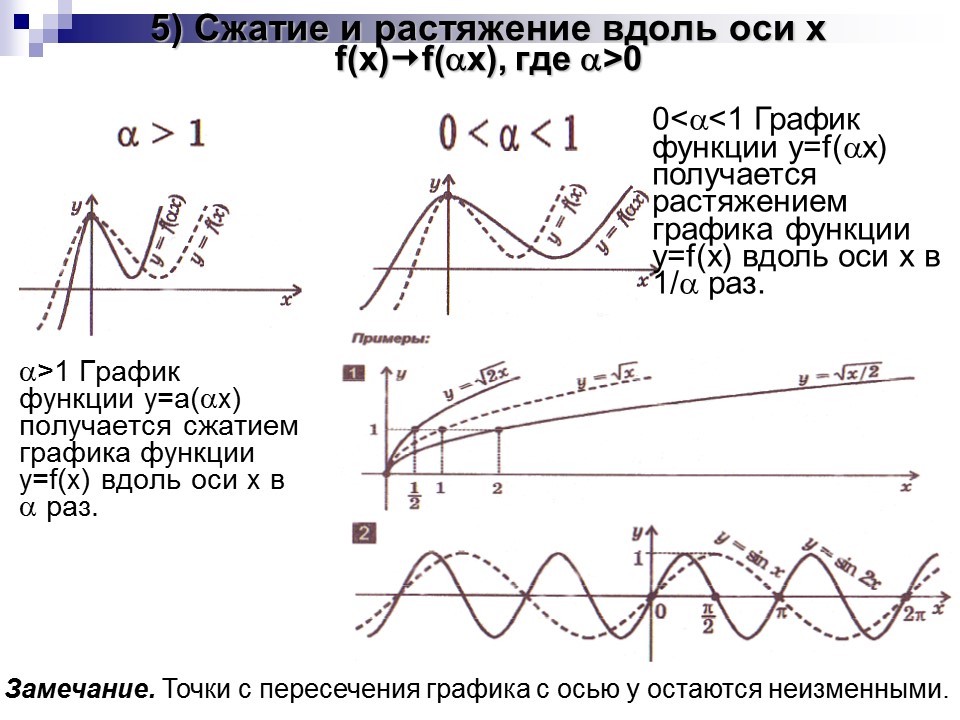
>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание.Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание.Функция y=f(|x|) четная (ее график симметричен относительно оси y).

График функции y=g(x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание.Описанное построение производить только для функции, имеющей обратную.

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

В одной системе координат, построим графики функций: а)

Решение:Преобразуем функцию f(x).

Так как , то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

superbotanik.net

Реферат - Преобразование графиков функции

Тема: « Преобразование графиков функции »

Цели:

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

Рассмотрим основные правила преобразования графиков на примерах элементарных функций

1) Преобразование симметрии относительно оси x f(x)  -f(x)

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неиз мен ными.

2) Преобразование симметрии относительно оси y f(x)  f( - x)

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание. Точка пересечения графика с осью y остается неизменной.

3) Параллельный перенос вдоль оси x f(x) f(x-a)

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.

4) Параллельный перенос вдоль оси y f(x)  f(x)+b

График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.

5) Сжатие и растяжение вдоль оси x f(x)  f(  x), где  >0

>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

6) Сжатие и растяжение вдоль оси y f(x) kf(x), где k>0

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

7) Построение графика функции y=|f(x)|

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

8) Построение графика функции y=f(|x|)

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

9) Построение графика обратной функции

График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание. Описанное построение производить только для функции, имеющей обратную.

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Применение правил преобразования графиков при решении заданий ЕГЭ (части C).

Решить систему уравнений:

В одной системе координат, построим графики функций: а)

Решить уравнение: f(g(x))+g(f(x))=32 , если известно, что и

Решение : Преобразуем функцию f(x).

Так как, то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Вывод:

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

Тема: « Преобразование графиков функции »

www.ronl.ru

Реферат на тему «Преобразование графиков функции»

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неиз мен ными.

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание. Точка пересечения графика с осью y остается неизменной.

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a0 и вниз при b0

>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание. Описанное построение производить только для функции, имеющей обратную.

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

В одной системе координат, построим графики функций: а)

Решение : Преобразуем функцию f(x).

Так как , то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

botanim.ru

Курсовая работа - Преобразование графиков функции

Тема: « Преобразование графиков функции »

Цели:

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

Рассмотрим основные правила преобразования графиков на примерах элементарных функций

1) Преобразование симметрии относительно оси x f(x)  -f(x)

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неиз мен ными.

2) Преобразование симметрии относительно оси y f(x)  f( - x)

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание. Точка пересечения графика с осью y остается неизменной.

3) Параллельный перенос вдоль оси x f(x) f(x-a)

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.

4) Параллельный перенос вдоль оси y f(x)  f(x)+b

График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.

5) Сжатие и растяжение вдоль оси x f(x)  f(  x), где  >0

>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

6) Сжатие и растяжение вдоль оси y f(x) kf(x), где k>0

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

7) Построение графика функции y=|f(x)|

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

8) Построение графика функции y=f(|x|)

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

9) Построение графика обратной функции

График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание. Описанное построение производить только для функции, имеющей обратную.

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Применение правил преобразования графиков при решении заданий ЕГЭ (части C).

Решить систему уравнений:

В одной системе координат, построим графики функций: а)

Решить уравнение: f(g(x))+g(f(x))=32 , если известно, что и

Решение : Преобразуем функцию f(x).

Так как, то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Вывод:

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

Тема: « Преобразование графиков функции »

www.ronl.ru

Преобразование графиков функций | Социальная сеть работников образования

Аннотация

Автор: Ковалевский Александр  Александрович,

«Преобразование графиков функций», исследовательский реферат.

С.Тасеево, МБОУ «Тасеевская СОШ №2», 8 класс

Руководитель: Сазыкина   Людмила Ивановна,                                                                                          

МБОУ «Тасеевская СОШ №2», учитель математики и информатики

Цель: получить навык построения графиков функций, работа с которыми не подразумевается в рамках программы по математике 8 класса.

Задачи, поставленные для реализации цели работы:

1. Изучить методы построения графиков на примере квадратичной функции;
2. Изучить метод выделения полного квадрата из квадратного трехчлена;
3. Освоить методы построения графиков функций, содержащих модуль.

В работе применялись следующие методы исследования:

1.Изучение литературы по данной теме;

2.Анализ методов преобразования графиков функций;

3.Математическое моделирование.

После проделаной работы я пришел к выводу: в целях экономии времени при построении графиков функций необходимо знать и применять методы преобразований графиков.

Результатом данной работы, является получение новых знаний, не изучаемых в курсе 8 класса по изучению преобразований графиков функций с модулем.  В приложении 1 приводятся упражнения по теме «Построение графика квадратичной функции», к которым даны ответы. Упражнения можно использовать на уроках и во внеурочной деятельности.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ        

1 КВАДРАТИЧНАЯ ФУНКЦИЯ        

2 ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ        

2.1 РАСТЯЖЕНИЕ (СЖАТИЕ) ВДОЛЬ ОСИ ОУ        

2.2 ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОХ        

2.3 ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОУ        

2.4 ПОСТРОЕНИЕ ГРАФИКА у =f(│x│)        

2.5 ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = │f (│x│)│.        

2.6 ПРИМЕР ПРЕОБРАЗОВАНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ С МОДУЛЕМ        

ЗАКЛЮЧЕНИЕ        

СПИСОК ЛИТЕРАТУРЫ        

ПРИЛОЖЕНИЕ 1        

ВВЕДЕНИЕ

Первоначально тема преобразования графиков функций рассматривается на примере графика квадратичной функции в курсе 8 класса предмета «Алгебра». Кроме этого, столь интересный и важный вопрос входит в ГИА и ЕГЭ в более сложном варианте. В тестах можно встретить задания на построение и чтение графиков функции с модулем, а также примеры на преобразование функций. Однако, в школьном курсе математики 8 класса мы не встречаемся с построением графиков функций с модулем. Именно поэтому меня заинтересовала данная тема, так как навыки, полученные при выполнении работы, будут необходимы для прохождения Государственной Итоговой Аттестации и сдачи Единого Государственного Экзамена.

По этой причине передо мной возникла проблема построения графиков функций с модулем.

Предполагаю, что если освоить методы преобразований функций, то на построение графиков будет уходить меньшее количество времени.

Целью работы является получение навыков построения графиков функций, работа с которыми не подразумевается в рамках программы по математике 8 класса.

Для достижения цели, необходимо решить следующие задачи:

1.        Изучить методы преобразований графиков функций на примере квадратичной функции;

2.       Изучить метод выделения полного квадрата из квадратного трехчлена;

3.     Освоить методы построения графиков функций с модулем.

Для проведения исследования использованы методы:

1.Изучение литературы по данной теме;

2.Анализ методов преобразования графиков функций;

3. Математическое моделирование .

1. КВАДРАТИЧНАЯ ФУНКЦИЯ

Функция вида y = ax2 + bx + с (a, b, с - постоянные величины; а ≠ 0) называется квадратичной. График функции y = ax2 называется параболой. Ось симметрии параболы есть ось ординат, именуемая осью параболы. График функции y = ax2 + bx + с также является параболой.

2. ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

 График квадратичной функции у = а(х – m)2 + n можно построить в несколько этапов. Рассмотрим их.

1. РАСТЯЖЕНИЕ (СЖАТИЕ) ВДОЛЬ ОСИ ОУ

Растяжение графика y =x2 вдоль оси ОУ в  а  раз. Если  │ а │2.

2. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОХ

Параллельный перенос графика функции  y = ax2 вдоль оси абсцисс на m единиц вправо при m > 0 и влево при m 2

3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ ОУ

Параллельный перенос графика функции  y = ax2   выполняется путем смещения вдоль оси абсцисс на m единиц вправо при m > 0 и влево при m 2

4. ПОСТРОЕНИЕ ГРАФИКА у =f(│x│)

Часть графика функции у = f(x), лежащую в первой и четвертой координатных четвертях, а также на оси ординат не изменяем, а вместо части во второй и третьей координатных четвертях строим график, симметричный правой части относительно оси ординат.

5. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = │f (│x│)│.

 Часть графика функции у = f(x), лежащую в третьей и четвертой координатных четвертях, отображаем симметрично относительно оси абсцисс, а затем отображаем симметрично эту часть относительно оси ординат.

6. ПРИМЕР ПРЕОБРАЗОВАНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ С МОДУЛЕМ

y = │x2 – 4│x│-2│

Выделим полный квадрат из трехчлена  x2 – 4x -2 = (x – 2)2 -6.

Построим график функции у=│ (│x│- 2)2 -6│, применяя этапы преобразования:

ЗАКЛЮЧЕНИЕ

В ходе проведенного исследования решены задачи:

1.        Изучены методы построения графиков;

2.       Изучен метод выделения полного квадрата из квадратного трехчлена;

3.     Освоены методы построения графиков функций с модулем.

После проделаной работы я пришел к выводу:действительно, зная основные методы преобразования графиков функций можно съэкономить время на их построение.  

Результатом данной работы, является получение новых знаний, не изучаемых в курсе 8 класса по изучению преобразований графиков функций с модулем.  В приложении 1 приводятся упражнения по теме «Построение графика квадратичной функции», к которым даны ответы. Этот задачник может быть использован на уроке и во внеурочной деятельности.

СПИСОК ЛИТЕРАТУРЫ

1. Аверьянов Д.И., Алтынов П.И., Баврин И.И. и др. «Математика: большой справочник для школьников и поступающих в вузы» -  М.: Дрофа, 1999 г. – 863с.
2. Виленкин Н.Я. Учебное пособие для школ и классов с углубленным изучением математики/ Н.Я. Виленкин, Г.С. Сурвилло, Новосибирск: ВО «Наука», 1992г
3. Лаппо Л.Д., Попов М.А. ГИА 9. Практикум. Реальные тесты, М.: Экзамен, 2013г
4. Лысенко Ф.Ф. Математика. Тренажер по новому плану ГИА, Ростов- на -Дону, Легион, 2013г
5. Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.2: Задачник для общеобразоват. учреждений/А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская, М.: Мнемозина, 2010г
6. Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.2: Учебник для общеобразоват. учреждений, М.: Мнемозина, 2010г
7. Мордкович А.Г., Суходский А. М. «Справочник школьника по математике» 5- 11 классы – М.: ОНИКС·АЛЬЯНС – В,1999г.- 288с.
8. Семенов А.Л., Ященко И.В. «Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2012», М.: Экзамен, 2011 г.
9. http:/ www.match.ru/web/prog31_1.php

ПРИЛОЖЕНИЕ 1

ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

Построить графики функций:

1)

2)

3)

4)

Ответы:

1)

2)

3) Выделим полный квадрат трехчлена и построим график квадратичной функции:

4)

nsportal.ru

Реферат: Преобразование графиков функции

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неиз мен ными.

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание. Точка пересечения графика с осью y остается неизменной.

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.

График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.

>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание. Описанное построение производить только для функции, имеющей обратную.

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

В одной системе координат, построим графики функций: а)

Решение : Преобразуем функцию f(x).

Так как , то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

www.yurii.ru

Презентация: Преобразование графиков функции

Презентация: Преобразование графиков функции

Тема: «Преобразование графиков функции»

Цели:

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

Рассмотрим основные правила преобразования графиков на примерах элементарных функций

1) Преобразование симметрии относительно оси xf(x)-f(x)

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неизменными.

2) Преобразование симметрии относительно оси yf(x)f(-x)

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание. Точка пересечения графика с осью y остается неизменной.

3) Параллельный перенос вдоль оси x f(x)f(x-a)

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.

4) Параллельный перенос вдоль оси y f(x)f(x)+b

График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.

5) Сжатие и растяжение вдоль оси xf(x)f(x), где >0

>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

6) Сжатие и растяжение вдоль оси yf(x)kf(x), где k>0

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

7) Построение графика функции y=|f(x)|

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

8) Построение графика функции y=f(|x|)

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

9) Построение графика обратной функции

График функции y=g(x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание. Описанное построение производить только для функции, имеющей обратную.

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Применение правил преобразования графиков при решении заданий ЕГЭ(части C).

Решить систему уравнений:

В одной системе координат, построим графики функций: а)

Решить уравнение: f(g(x))+g(f(x))=32, если известно, что и

Решение: Преобразуем функцию f(x).

Так как , то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Вывод:

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

Тема: «Преобразование графиков функции»

www.referatmix.ru

Смотрите также

• 
  Реферат стеноз гортани
• 
  Реферат древнегреческая цивилизация
• 
  Древнегреческая цивилизация реферат
• 
  Информационный терроризм реферат
• 
  Профилактика инсульта реферат
• 
  Реферат язык математики
• 
  Реферат социология предпринимательства
• 
  Туберкулез глаз реферат
• 
  Падение метеоритов реферат
• 
  Джузеппе верди реферат
• 
  Верди джузеппе реферат