Исследовательская работа Теоремы Чевы и Менелая. Реферат на тему теорема чевы
Доклад на тему "Теорема Менелая"
Менелай Александрийский (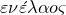 , I в.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.
, I в.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.
Теорема Менелая. Пусть прямая пересекает треугольник 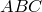 , причем
, причем 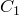 – точка ее пересечения со стороной
– точка ее пересечения со стороной  ,
, 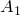 – точка ее пересечения со стороной
– точка ее пересечения со стороной 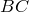 , и
, и 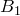 – точка ее пересечения с продолжением стороны
– точка ее пересечения с продолжением стороны  . Тогда
. Тогда

Доказательство. Проведем через точку 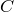 прямую, параллельную
прямую, параллельную  . Обозначим через
. Обозначим через 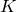 ее точку пересечения с прямой
ее точку пересечения с прямой  .
.
Треугольники  и
и  подобны (
подобны (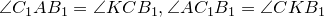 ). Следовательно,
). Следовательно,
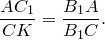
Треугольники  и
и 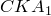 также подобны (
также подобны (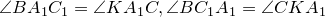 ). Значит,
). Значит,
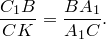
Из каждого равенства выразим 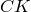 :
:
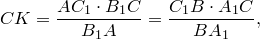
откуда

что и требовалось доказать.
Теорема (обратная теорема Менелая). Пусть дан треугольник 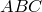 . Пусть точка
. Пусть точка 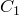 лежит на стороне
лежит на стороне  , точка
, точка 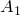 – на стороне
– на стороне 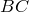 , а точка
, а точка 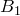 – на продолжении стороны
– на продолжении стороны  , причем выполняется соотношение
, причем выполняется соотношение

Тогда точки 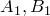 и
и 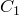 лежат на одной прямой.
лежат на одной прямой.
Доказательство. Заметим для начала, что 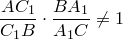 , поскольку, по условию, это выражение равно
, поскольку, по условию, это выражение равно 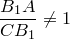 . Следовательно, прямые
. Следовательно, прямые 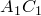 и
и  не параллельны.
не параллельны.
Проведем прямую через точки 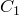 и
и 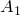 . Она пересечет прямую
. Она пересечет прямую  в некоторой точке
в некоторой точке 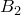 . Для точек
. Для точек 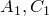 и
и 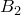 справедлива теорема Менелая, так что
справедлива теорема Менелая, так что
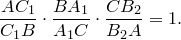
Отсюда следует, что

Из этого равенства следует, что обе точки 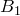 и
и 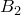 лежат на продолжении отрезка
лежат на продолжении отрезка  за одну и ту же точку, ибо правее
за одну и ту же точку, ибо правее 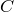 данное отношение меньше
данное отношение меньше 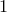 , а левее
, а левее 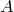 оно строго больше
оно строго больше  . Пусть
. Пусть 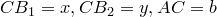 . Тогда, учитывая, что
. Тогда, учитывая, что 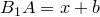 и
и 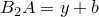 , перепишем полученное равенство в виде
, перепишем полученное равенство в виде
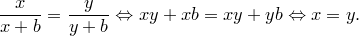
Из равенства 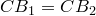 следует, что
следует, что 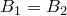 , и доказано, что точка
, и доказано, что точка 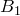 , совпадающая с
, совпадающая с 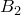 , лежит на прямой
, лежит на прямой 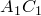 .
.
Замечание. Теоремы Менелая (прямая и обратная) верны также и в том случае, когда все три точки 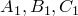 лежат на продолжениях сторон треугольника
лежат на продолжениях сторон треугольника 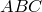 . То есть справедлива следующая
. То есть справедлива следующая
Теорема. Пусть дан треугольник 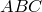 . Точки
. Точки 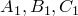 лежат на продолжениях сторон
лежат на продолжениях сторон 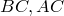 и
и  соответственно. Три точки
соответственно. Три точки 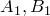 и
и 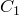 лежат на одной прямой тогда и только тогда, когда выполняется равенство
лежат на одной прямой тогда и только тогда, когда выполняется равенство

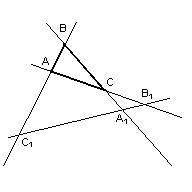 Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше.
Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше.
Источники: В.В. Ткачук, “Математика абитуриенту”, М.: Изд-во МЦНМО, 2004.
Мой реферат посвящен применению подобия к доказательству теорем и решению задач, а именно глубоко изучить обобщение теоремы Фалеса, теоремы Чевы и Менелая, которые не изучаются в школьной программе. Теме подобия, которая проходится в восьмом классе, отведено всего лишь 19 часов, что недостаточно для изучения этой темы более углубленно. В тему подобия входят: определение подобных треугольников, признаки подобия, отношение площадей подобных треугольников, средняя линия треугольника, пропорциональные отрезки и т.д.
Источники информации:
Дополнительные главы по геометрии 8 класса (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, С. А. Шестаков, И. И. Юдина) - настоящее пособие является дополнением к учебнику `Геометрия, 7-9` авторов Л.С.Атанасяна, В.Ф.Бутузова и др. (М.: Просвещение, 1990 и последующие издания). Оно полностью соответствует программе углубленного изучения математики.
Сайты:
http://festival.1september.ru
http://www.problems.ru
Вывод.
С помощью обобщения теоремы Фалеса, теорем Чевы и Менелая, не изучаемых в школьной программе, можно быстрее и легче доказывать определенные теоремы и решать более широкий круг задач. Я смогла доказать такие теоремы: теорема о пропорциональных отрезках (с помощью обобщения теоремы Фалеса), теоремы о пересечении медиан, высот и биссектрис треугольника в одной точке (воспользовалась теоремами Чевы и Менелая).
Историческая справка
Теорема Менелая - это классическая теорема аффинной геометрии. Эта теорема доказывается в третьей книге "Сферики" древнегреческого математика и астронома Менелая Александрийского (ок. 100 г. н.э.). Менелай сначала доказывает теорему для плоского случая, а потом центральным проектированием переносит её на сферу. Возможно, что плоский случай теоремы рассматривался ранее в несохранившихся "Поризмах" Евклида.
Сферическая теорема Менелая была основным средством, с помощью которого решались разнообразные прикладные задачи позднеантичной и средневековой астрономии и геодезии. Ей посвящён ряд сочинений под названием "Книга о фигуре секущих", составленных такими математиками средневекового Востока, как Сабит ибн Кора (836 - 901, астроном, математик, механик и врач), ан-Насави (1010 - 1075, газневидский математик и астроном), ал-Магриби (1220 - 1283, математик и астроном государства Хулагу), Абу Саид ибн Мухаммад ибн Абд-ал-Джалил ас-Сиджизи (951 - 1024, газневидский математик и астроном), Хусам ад-Дин Али ибн Фадлаллах ас-Салар аш-Шами (ум. 1262, среднеазиатский математик и астроном Хорезшахов), Абу Мухаммад Джабир ибн Афлах ал-Ишбили (первая половина 12 в., западноарабский математик и астроном), Абу Джафар Мухаммад ибн Мухаммад Насир ад-Дин ат-Туси (1201 - 1274, персидский математик, механик и астроном).
В начале нашей исследовательской работы мы поставили проблему – Зачем нужна математика? В ходе изучения литературы и материалов сети интернет мы выяснили, что изначально математика возникла из повседневных нужд человека (подсчеты, измерения) и многие годы служила мощным инструментом познания окружающего мира. Значит, если бы математические знания не передавались из поколения в поколение люди бы надолго застряли на уровне пещерного человека. В ходе проведения экспериментов мы выяснили, что полученные в школе знания очень помогают при решении практических задач с которыми мы сталкиваемся постоянно. Проведенные нами статистические исследования помогли убедиться в правильности выдвинутой гипотезы: математические знания полученные в школе применимы в жизни. Теоретическая значимость нашей работы заключается в том, что познакомившись с нашим исследованием, многие ученики, на вопрос о необходимости изучать математику, ответят положительно. Практическая значимость ее в том, что она может быть использована школьниками для повышения своего образовательного уровня, а также научить применять полученные в школе знания на практике, что сегодня очень актуально.
Введение
Я хочу изучить треугольник Рёло , потому что мне стала интересна его история. Если в древние времена наиболее широко применялся прямоугольный треугольник Пифагора, то в настоящий момент людей больше интересуют необычные свойства треугольника Рёло.
Цель моей работы – выяснить, что такое треугольник Рёло, узнать его историю и где он применяется.
Для этого поставлены задачи:
1.Узнать что такое треугольник Рёло
2.Узнать историю Треугольника Рёло
3.Построить треугольник Рёло самостоятельно
4.Узнать где используется треугольник Рёло
Гипотеза
Мне кажется, что Треугольник Рёло является ненужным механизмом в истории человечества. В конце работы я узнаю, прав я или нет. Заключение.
Я рассмотрел применение треугольника Рело в некоторых архитектурных строениях, механических устройствах, в автомобильных двигателях.
Я считаю, что изобретенная крышка люка для рекуперированной воды в Сан-Франциско, является очень интересной для человечества. За счет своей формы, такая крышка никогда не перевернется. Если бы архитекторы пересмотрели наши канализационные люки, и взяли бы для примера такую крышку, то можно было бы избежать множество трагических ситуаций, когда люди падали в канализационные люки.
Поиски альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. По прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. Сколько из этого количества придется на традиционные ДВС и как будет меняться пропорция по мере удешевления себестоимости производства компонентов привода на топливных элементах? Увидим в ближайшие годы.
Я опровергнул свою гипотезу, так как Треугольник Рёло используется во многих механизмах. Я думаю, что он будет использоваться и в будущем.
.
infourok.ru
Доклад на тему Теорема Менелая
Менелай Александрийский ( , I в.) - древнегреческий
математик</ и астроном. Автор работ по сферической
тригонометрии: написал 6 книг о вычислении хорд и 3 книги
"Сферики'', сохранившиеся в арабском переводе. Для получения формул
сферической тригонометрии использовал теорему, известную сегодня
как теорема Менелая.
, I в.) - древнегреческий
математик</ и астроном. Автор работ по сферической
тригонометрии: написал 6 книг о вычислении хорд и 3 книги
"Сферики'', сохранившиеся в арабском переводе. Для получения формул
сферической тригонометрии использовал теорему, известную сегодня
как теорема Менелая.
Теорема Менелая. Пусть прямая пересекает треугольник  , причем
, причем  - точка ее пересечения со
стороной
- точка ее пересечения со
стороной  ,
,
 - точка ее
пересечения со стороной
- точка ее
пересечения со стороной  , и
, и  - точка ее пересечения с
продолжением стороны
- точка ее пересечения с
продолжением стороны  . Тогда
. Тогда

Доказательство. Проведем через точку  прямую, параллельную
прямую, параллельную
 . Обозначим
через
. Обозначим
через  ее
точку пересечения с прямой
ее
точку пересечения с прямой  .
.

Треугольники  и
и  подобны (
подобны ( ). Следовательно,
). Следовательно,

Треугольники  и
и  также подобны (
также подобны ( ). Значит,
). Значит,

Из каждого равенства выразим  :
:

откуда

что и требовалось доказать.
Теорема (обратная теорема Менелая). Пусть дан треугольник
 . Пусть точка
. Пусть точка
 лежит на
стороне
лежит на
стороне  , точка
, точка
 - на стороне
- на стороне
 , а точка
, а точка
 - на
продолжении стороны
- на
продолжении стороны  , причем выполняется соотношение
, причем выполняется соотношение

Тогда точки  и
и
 лежат на одной
прямой.
лежат на одной
прямой.
Доказательство. Заметим для начала, что  , поскольку, по
условию, это выражение равно
, поскольку, по
условию, это выражение равно  . Следовательно, прямые
. Следовательно, прямые  и
и  не параллельны.
не параллельны.
Проведем прямую через точки  и
и  . Она пересечет прямую
. Она пересечет прямую  в некоторой точке
в некоторой точке
 . Для точек
. Для точек
 и
и  справедлива теорема
Менелая, так что
справедлива теорема
Менелая, так что

Отсюда следует, что

Из этого равенства следует, что обе точки  и
и  лежат на продолжении
отрезка
лежат на продолжении
отрезка  за одну
и ту же точку, ибо правее
за одну
и ту же точку, ибо правее  данное отношение меньше
данное отношение меньше  , а левее
, а левее  оно строго больше
оно строго больше
 . Пусть
. Пусть  . Тогда, учитывая,
что
. Тогда, учитывая,
что  и
и
 , перепишем
полученное равенство в виде
, перепишем
полученное равенство в виде

Из равенства  следует, что
следует, что  , и доказано, что точка
, и доказано, что точка
 , совпадающая
с
, совпадающая
с  , лежит на
прямой
, лежит на
прямой  .
.
Замечание. Теоремы Менелая (прямая и обратная) верны также и в
том случае, когда все три точки  лежат на продолжениях сторон
треугольника
лежат на продолжениях сторон
треугольника  .
То есть справедлива следующая
.
То есть справедлива следующая
Теорема. Пусть дан треугольник  . Точки
. Точки  лежат на продолжениях
сторон
лежат на продолжениях
сторон  и
и
 соответственно. Три точки
соответственно. Три точки
 и
и  лежат на одной прямой
тогда и только тогда, когда выполняется равенство
лежат на одной прямой
тогда и только тогда, когда выполняется равенство

 Доказательство этой теоремы точно
такое же, как и доказательство, приведенное выше.
Доказательство этой теоремы точно
такое же, как и доказательство, приведенное выше.
Источники: В.В. Ткачук, "Математика абитуриенту", М.: Изд-во
МЦНМО, 2004.
Мой реферат посвящен применению подобия к доказательству теорем
и решению задач, а именно глубоко изучить обобщение теоремы Фалеса,
теоремы Чевы и Менелая, которые не изучаются в школьной программе.
Теме подобия, которая проходится в восьмом классе, отведено всего
лишь 19 часов, что недостаточно для изучения этой темы более
углубленно. В тему подобия входят: определение подобных
треугольников, признаки подобия, отношение площадей подобных
треугольников, средняя линия треугольника, пропорциональные отрезки
и т.д.
Источники информации:
Дополнительные главы по геометрии 8 класса (Л. С. Атанасян, В.
Ф. Бутузов, С. Б. Кадомцев, С. А. Шестаков, И. И. Юдина) -
настоящее пособие является дополнением к учебнику `Геометрия, 7-9`
авторов Л.С.Атанасяна, В.Ф.Бутузова и др. (М.: Просвещение, 1990 и
последующие издания). Оно полностью соответствует программе
углубленного изучения математики.
Сайты:
festival.1september.ru
www.problems.ru
Вывод.
С помощью обобщения теоремы Фалеса, теорем Чевы и Менелая, не
изучаемых в школьной программе, можно быстрее и легче доказывать
определенные теоремы и решать более широкий круг задач. Я смогла
доказать такие теоремы: теорема о пропорциональных отрезках (с
помощью обобщения теоремы Фалеса), теоремы о пересечении медиан,
высот и биссектрис треугольника в одной точке (воспользовалась
теоремами Чевы и Менелая).
Историческая справка
Теорема Менелая - это классическая теорема аффинной геометрии.
Эта теорема доказывается в третьей книге "Сферики" древнегреческого
математика и астронома Менелая Александрийского (ок. 100 г. н.э.).
Менелай сначала доказывает теорему для плоского случая, а потом
центральным проектированием переносит её на сферу. Возможно, что
плоский случай теоремы рассматривался ранее в несохранившихся
"Поризмах" Евклида.
Сферическая теорема Менелая была основным средством, с помощью
которого решались разнообразные прикладные задачи позднеантичной и
средневековой астрономии и геодезии. Ей посвящён ряд сочинений под
названием "Книга о фигуре секущих", составленных такими
математиками средневекового Востока, как Сабит ибн Кора (836 - 901,
астроном, математик, механик и врач), ан-Насави (1010 - 1075,
газневидский математик и астроном), ал-Магриби (1220 - 1283,
математик и астроном государства Хулагу), Абу Саид ибн Мухаммад ибн
Абд-ал-Джалил ас-Сиджизи (951 - 1024, газневидский математик и
астроном), Хусам ад-Дин Али ибн Фадлаллах ас-Салар аш-Шами (ум.
1262, среднеазиатский математик и астроном Хорезшахов), Абу
Мухаммад Джабир ибн Афлах ал-Ишбили (первая половина 12 в.,
западноарабский математик и астроном), Абу Джафар Мухаммад ибн
Мухаммад Насир ад-Дин ат-Туси (1201 - 1274, персидский математик,
механик и астроном).
В начале нашей исследовательской работы мы поставили проблему -
Зачем нужна математика? В ходе изучения литературы и материалов
сети интернет мы выяснили, что изначально математика возникла из
повседневных нужд человека (подсчеты, измерения) и многие годы
служила мощным инструментом познания окружающего мира. Значит, если
бы математические знания не передавались из поколения в поколение
люди бы надолго застряли на уровне пещерного человека. В ходе
проведения экспериментов мы выяснили, что полученные в школе знания
очень помогают при решении практических задач с которыми мы
сталкиваемся постоянно. Проведенные нами статистические
исследования помогли убедиться в правильности выдвинутой гипотезы:
математические знания полученные в школе применимы в жизни.
Теоретическая значимость нашей работы заключается в том, что
познакомившись с нашим исследованием, многие ученики, на вопрос о
необходимости изучать математику, ответят положительно.
Практическая значимость ее в том, что она может быть использована
школьниками для повышения своего образовательного уровня, а также
научить применять полученные в школе знания на практике, что
сегодня очень актуально.
Введение
Я хочу изучить треугольник Рёло , потому что мне
стала интересна его история. Если в древние времена наиболее широко
применялся прямоугольный треугольник Пифагора, то в настоящий
момент людей больше интересуют необычные свойства треугольника
Рёло.
Цель моей работы - выяснить, что такое
треугольник Рёло, узнать его историю и где он применяется.
Для этого поставлены задачи:
1.Узнать что такое треугольник Рёло
2.Узнать историю Треугольника Рёло
3.Построить треугольник Рёло самостоятельно
4.Узнать где используется треугольник Рёло
Гипотеза
Мне кажется, что Треугольник Рёло является
ненужным механизмом в истории человечества. В конце работы я узнаю,
прав я или нет. Заключение.
Я рассмотрел применение треугольника Рело в
некоторых архитектурных строениях, механических устройствах, в
автомобильных двигателях.
Я считаю, что изобретенная крышка люка для
рекуперированной воды в Сан-Франциско, является очень интересной
для человечества. За счет своей формы, такая крышка никогда не
перевернется. Если бы архитекторы пересмотрели наши канализационные
люки, и взяли бы для примера такую крышку, то можно было бы
избежать множество трагических ситуаций, когда люди падали в
канализационные люки.
Поиски альтернативных видов топлива для
автомобилей заставил вновь обратить внимание на роторно-поршневой
двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей
роторно-поршневой агрегат гораздо лучше приспособлен для работы на
водороде, нежели традиционные моторы. По прогнозам специалистов,
уже к 2025 году более четверти мирового автопарка будет
использовать в качестве топлива водород. Сколько из этого
количества придется на традиционные ДВС и как будет меняться
пропорция по мере удешевления себестоимости производства
компонентов привода на топливных элементах? Увидим в ближайшие
годы.
Я опровергнул свою гипотезу, так как Треугольник
Рёло используется во многих механизмах. Я думаю, что он будет
использоваться и в будущем.
.
botana.cc
Исследовательская работа Теоремы Чевы и Менелая















 Городская научно-практическая конференция
Городская научно-практическая конференция«В науку шаг за шагом»
Исследовательская работа
Теоремы Чевы и Менелая
Выполнена: учеником 9-А класса МОУ «Гимназия №20»
Храмеевым Максимом
Александровичем
Руководитель: учитель математики,
Бондаренко Ольга Валентиновна.
Донской,2011год
Оглавление
- Введение. 3-5
- Основная часть.
- Теорема Менелая 6-7
- Теорема Чевы. 7-8
- Задачи на применение доказанных теорем. 9-18
- Заключение. 19
- Задачи для самостоятельного решения 20
- Список литературы. 21
- Приложение. 22-37
Введение
«Обладая литературой более обширной, чем алгебра и арифметика вместе взятые, и, по крайней мере, столь же обширной, как анализ, геометрия в большей степени, чем любой другой раздел математики, является богатейшей сокровищницей интереснейших, но полузабытых вещей, которыми спешащее поколение не имеет времени насладиться». Е. Т. Белл.
Геометрия - одна из наиболее древних математических наук.
Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах.
Возникновение геометрических знаний связано с практической деятельностью людей. И уже в древности геометрия превратилась в дедуктивную, строго логическую науку, построенную на основе системы аксиом. Постепенно развиваясь, она обогащалась новыми теоремами, идеями, методами. Интересы геометров и направление их научных исследований порою менялись в процессе исторического развития этой науки, поэтому, нелегко дать точное и исчерпывающее определение, что такое геометрия сегодня, каков её предмет, содержание и методы.
В III в. до н. э. древнегреческий учёный Евклид написал книгу под названием «Начала». В этой книге Евклид подытожил накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки. Написана она была настолько хорошо, что в течение 2000 лет всюду преподавание геометрии велось либо по переводам, либо по незначительным переработкам книги Евклида.
Например, таким пособием был учебник А. Д. Александрова, затем А.П. Киселёва, по которым советская школа работала до середины 20 столетия.
Но жизнь идёт своим чередом, издаются новые учебники, под редакцией А.В. Погорелова; Л. С. Атанасяна, И.М. Смирнова и др.
В результате различных преобразований со страниц этих учебников как – то незаметно исчезли многие замечательные утверждения, свойства, которые просто необходимо знать при решении многих планиметрических задач.
Обучаясь в Научном Обществе Гимназии и работая с различной дополнительной литературой по геометрии, я столкнулся с тем, что в действительности многие удивительные соотношения и изящные геометрические факты не входят в основной курс геометрии. Многие из них сейчас выглядят малоинтересными, несовершенными и встречаются только в энциклопедиях. Однако некоторые из них продолжают жить, и по сей день. Одни из них теоремы Менелая и Чевы. Это теорема, которая была доказана древнегреческим математиком и астрономом Менелаем Александрийским, жившим в I веке до нашей эры и теорема, опубликованная в 1678 году итальянским математиком и инженером Джованни Чевой. В честь этих учёных теоремы названы их именами.
Эти теоремы просты, интересны и находят применение при решении как простых, так и весьма сложных задач. Несмотря на это Теоремы Менелая и Чевы не изучаются в школе на уроках геометрии и встречаются только в школьном учебнике геометрии под редакцией Атанасяна Л.С. в приложении. Доказательства, предложенные автором сложны. Задачи, помещённые в учебнике на применение обратной теоремы Менелая трудны, а задачи на применение прямой теоремы вовсе не рассматриваются. Актуальность темы:
- Данная тема является дополнением и углублением изученных в курсе геометрии свойств.
- Применение опыта решения планиметрических задач с использованием теоремы Чевы и Менелая помогает повысить уровень пространственного воображения и уровень логической культуры.
- Изучение данной темы поможет более глубоко подготовиться к вступительным экзаменам и олимпиадам.
- Хорошо известно, что выводы школьной геометрии находят широкое применение при решении самых разнообразных практических задач. Знание геометрии необходимо всем кому приходиться исследовать свойства различных фигур и тел. Геометрия изучает наш реальный мир.
Цель работы:
- ознакомление с теоремами Чевы и Менелая ;
- исследование способов доказательства теорем;
- овладение приемами решений планиметрических задач с использованием теоремы Чевы и Менелая;
- систематизация и обобщение теоретического и практического материалов.
Задачи исследования:
- изучить состояние проблемы в научной литературе и школьной программе;
- выявить теоретические положения для доказательства теорем;
- систематизировать теоретический материал доказательств:
а) Теоремы Чевы,б) Теоремы Менелая;
- проверить эффективность и целесообразность применения теорем при решении задач;
- научиться применять теоремы Чевы и Менелая в задачах разной сложности;
- сравнить задачи, решенные с использованием теорем Менелая и Чевы с задачами, решенными традиционным способом;
Теоремы Чевы и Менелая можно назвать «двойственными» они, похоже, формулируются и доказываются. В своей работе я предлагаю доказательства теоремы Менелая (прямая и обратная), используя подобия треугольников, а теорему Чевы доказываю с помощью теоремы Менелая.Однако при решении целого класса задач эти теоремы позволяют легко и изящно получить решение, в то время когда традиционные подходы приводят к громоздким и утомительным преобразованиям.Научная новизна исследования
состоит в том, что в нем проблема доказательства теоремы Чевы и Менелая решается разными способами.
Теоремы Чевы и Менелая позволили нам обнаружить глубоко скрытое общее содержание в таких важнейших теоремах элементарной геометрии, как теорема о трех высотах, медианах и биссектрисах треугольника.
2.Основная часть
Переходя к основной части работы, я начну с замечательных точек треугольника. К числу таких точек, изучаемых в школьном курсе геометрии, относятся:
а) точка пересечения биссектрис (центр вписанной окружности), которая
находится внутри треугольника;
б) точка пересечения серединных перпендикуляров (центр описанной
окружности), которая может находится внутри (остроугольный треугольник),
вне треугольника (тупоугольный треугольник) или в вершине прямого угла
прямоугольного треугольника;
в) точка пересечения высот (ортоцентр). Для остроугольного треугольника
ортоцентр находится внутри треугольника, а в тупоугольном – вне.
г) точка пересечения медиан (центроид), которая находится внутри треугольника.
Тот факт, что, каждая из троек данных отрезков пересекаются в одной точке, я докажу позже.
2.1.Теорема Менелая.
Теорема названа в честь древнегреческого учёного Менелая ( I в. н.э.), которая была им доказана и опубликована в третей книге «Сферики». Долгое время её называли «теоремой о секущих».
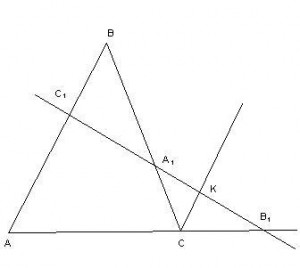
Теорема Менелая. Если прямая пересекает стороны или продолжения сторон BC, CA и AB треугольника ABC соответственно в точках A1 , B1 и C1 , не совпадающие с вершинами треугольника, то имеет место равенство

C
A1
C1
B
A
B1
D
Доказательство
Пусть прямая пересекает стороны BC и CA треугольника АВС в точках А1 иВ1 ,а продолжение стороны АВ в точке С1.
- Через вершину С треугольника АВС проведем прямую CD
 АВ; которая пересечет прямую А1В1 в точке D.
АВ; которая пересечет прямую А1В1 в точке D.  А1ВС1
А1ВС1 
 А1CD по двум углам
А1CD по двум углам В1АС1
В1АС1 
 В1CD по двум углам
В1CD по двум углам- из пунктов 2 и 3 следует, что
 и
и  .
.
5. Перемножим эти равенства, получим доказываемое соотношение.Доказательство остается в силе и в том случае, когда все три точки A1 , B1 и C1 лежат на продолжениях сторон  АВС.
АВС.
Для пояснения приведённого доказательства сделаем одно уточнение. Пусть  – ненулевые коллинеарные векторы. Если
– ненулевые коллинеарные векторы. Если  , то будем писать:
, то будем писать:  Значит, число k равно отношению длин векторов
Значит, число k равно отношению длин векторов  , взятому со знаком «плюс», если векторы сонаправленны, и со знаком «минус», если они направлены противоположно.
, взятому со знаком «плюс», если векторы сонаправленны, и со знаком «минус», если они направлены противоположно.
Легко проверить, что при таком соглашении полученное выше равенство принимает вид:

Обратная теорема. Если выполняется равенство , то точки A1 , B1 и C1 лежат на одной прямой.
, то точки A1 , B1 и C1 лежат на одной прямой.
Для доказательства обратной теоремы используем вышеуказанное уточнение
Доказательство.
Допустим, что выполнено равенство  , и пусть прямая А1В1 пересекает прямую АВ в точке С2. Согласно прямой теореме,
, и пусть прямая А1В1 пересекает прямую АВ в точке С2. Согласно прямой теореме,
Сравнивая это соотношение с данным, заключаем, что 
Прибавив к обеим частям равенства 1, получим:  откуда
откуда  , т. е. точки C1 и C2 совпадают.
, т. е. точки C1 и C2 совпадают.
Объединяя прямую и обратную теоремы, получаем следующий результат.
Если на сторонах ВС, СА, АВ треугольника АВС или на их продолжениях взяты точки A1 , B1 и C1, то эти точки лежат на одной прямой тогда и только тогда,когда
ЗАМЕЧАНИЕ. При решении задач, когда расположение точек A1 , B1 и C1 известно равенство используют в скалярном виде, т. е. рассматривают длины отрезков, а правую часть равенства берут равной 1.

2.2. Теорема Чевы.
Джовани Чева (1648-1734) – итальянский инженер-гидравлик и экономист. Носящая его имя теорема содержится в опубликованной им в 1678г. работе « О прямых линиях».
Теорема Чевы. Пусть на сторонах ВС, СА, АВ треугольника АВС или их продолжениях взяты соответственно точки А1, В1, С1, не совпадающие с вершинами треугольника. Тогда если прямые АА1, ВВ1, СС1 пересекаются или попарно параллельны, то

Доказательство.
I) Пусть прямые АА1, ВВ1, СС1 пересекаются в точке О, лежащей внутри или вне треугольника АВС. В том и другом случае, применив теорему Менелая к треугольнику ВСС1 и секущей АА1, Получим:

А
С
В
 А1
А1
С1
В1
О
О
В
А
С
 А1
А1
В1
С1
а)
б)
Аналогично из треугольника АСС1, пересеченного прямой ВВ1, находим:

Перемножим последние два равенства
почленно и получим:

С1
В1
A
С
В
А
II) Рассмотрим случай, когда прямые АА1, ВВ1, СС1 параллельны. Пусть точка В1 лежит на продолжении стороны АС, точка А1 лежит на стороне ВС, точка С1 лежит на стороне АВ. Тогда достаточно доказать, что

Используя теорему об отрезках, отсекаемых на сторонах угла параллельными прямыми, имеем:

Подставим эти равенства в левую часть формулы (*) имеем:

Что и требовалось доказать.
Обратная теорема. Если выполняется равенство  , то прямые AA1 , BB1 и CC1 либо пересекаются в одной точке, либо попарно параллельны.
, то прямые AA1 , BB1 и CC1 либо пересекаются в одной точке, либо попарно параллельны.
Доказательство.
Предположим теперь, что выполняется равенство (*), и докажем, что тогда прямые АА1, ВВ1, СС1 пересекаются в одной точке. Пусть С2 – Точка пересечения прямой АВ с прямой проходящей через точку С и точку пересечения прямых АА1, ВВ1. Для точки С2 выполняется отношение , как и для точки С1.

Поэтому,  =
=  . Следовательно, C2 совпадает C1 , т. е. прямые AA1 , BB1 и CC1 пересекаются в одной точке.
. Следовательно, C2 совпадает C1 , т. е. прямые AA1 , BB1 и CC1 пересекаются в одной точке.
Замечание. Записывая отношение отрезков, следует двигаться по контуру треугольника от вершины до точки пересечения с прямой и от точки пересечения до следующей вершины.
ist.na5bal.ru
Доклад на тему Теорема Менелая
Менелай Александрийский (, I в.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая. Теорема Менелая. Пусть прямая пересекает треугольник , причем – точка ее пересечения со стороной , – точка ее пересечения со стороной , и – точка ее пересечения с продолжением стороны . ТогдаДоказательство. Проведем через точку прямую, параллельную . Обозначим через ее точку пересечения с прямой .
Треугольники и подобны (). Следовательно,
Треугольники и также подобны (). Значит,
Из каждого равенства выразим :
откуда
что и требовалось доказать.
Теорема (обратная теорема Менелая). Пусть дан треугольник . Пусть точка лежит на стороне , точка – на стороне , а точка – на продолжении стороны , причем выполняется соотношение
Тогда точки и лежат на одной прямой.
Доказательство. Заметим для начала, что , поскольку, по условию, это выражение равно . Следовательно, прямые и не параллельны.Проведем прямую через точки и . Она пересечет прямую в некоторой точке . Для точек и справедлива теорема Менелая, так что
Отсюда следует, что
Из этого равенства следует, что обе точки и лежат на продолжении отрезка за одну и ту же точку, ибо правее данное отношение меньше , а левее оно строго больше . Пусть . Тогда, учитывая, что и , перепишем полученное равенство в виде
Из равенства следует, что , и доказано, что точка , совпадающая с , лежит на прямой .
Замечание. Теоремы Менелая (прямая и обратная) верны также и в том случае, когда все три точки лежат на продолжениях сторон треугольника . То есть справедлива следующая
Теорема. Пусть дан треугольник . Точки лежат на продолжениях сторон и соответственно. Три точки и лежат на одной прямой тогда и только тогда, когда выполняется равенство
Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше.
Источники: В.В. Ткачук, “Математика абитуриенту”, М.: Изд-во МЦНМО, 2004.
Я.П. Понарин, “Элементарная геометрия. Т.1. Планиметрия, преобразования плоскости”, М.: Изд-во МЦНМО, 2004.
Введение.
Мой реферат посвящен применению подобия к доказательству теорем и решению задач, а именно глубоко изучить обобщение теоремы Фалеса, теоремы Чевы и Менелая, которые не изучаются в школьной программе. Теме подобия, которая проходится в восьмом классе, отведено всего лишь 19 часов, что недостаточно для изучения этой темы более углубленно. В тему подобия входят: определение подобных треугольников, признаки подобия, отношение площадей подобных треугольников, средняя линия треугольника, пропорциональные отрезки и т.д.
Источники информации:
Дополнительные главы по геометрии 8 класса (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, С. А. Шестаков, И. И. Юдина) - настоящее пособие является дополнением к учебнику `Геометрия, 7-9` авторов Л.С.Атанасяна, В.Ф.Бутузова и др. (М.: Просвещение, 1990 и последующие издания). Оно полностью соответствует программе углубленного изучения математики.
Сайты:
http://festival.1september.ru
http://www.problems.ru
Вывод.
С помощью обобщения теоремы Фалеса, теорем Чевы и Менелая, не изучаемых в школьной программе, можно быстрее и легче доказывать определенные теоремы и решать более широкий круг задач. Я смогла доказать такие теоремы: теорема о пропорциональных отрезках (с помощью обобщения теоремы Фалеса), теоремы о пересечении медиан, высот и биссектрис треугольника в одной точке (воспользовалась теоремами Чевы и Менелая).
Историческая справка
Теорема Менелая - это классическая теорема аффинной геометрии. Эта теорема доказывается в третьей книге "Сферики" древнегреческого математика и астронома Менелая Александрийского (ок. 100 г. н.э.). Менелай сначала доказывает теорему для плоского случая, а потом центральным проектированием переносит её на сферу. Возможно, что плоский случай теоремы рассматривался ранее в несохранившихся "Поризмах" Евклида.
Сферическая теорема Менелая была основным средством, с помощью которого решались разнообразные прикладные задачи позднеантичной и средневековой астрономии и геодезии. Ей посвящён ряд сочинений под названием "Книга о фигуре секущих", составленных такими математиками средневекового Востока, как Сабит ибн Кора (836 - 901, астроном, математик, механик и врач), ан-Насави (1010 - 1075, газневидский математик и астроном), ал-Магриби (1220 - 1283, математик и астроном государства Хулагу), Абу Саид ибн Мухаммад ибн Абд-ал-Джалил ас-Сиджизи (951 - 1024, газневидский математик и астроном), Хусам ад-Дин Али ибн Фадлаллах ас-Салар аш-Шами (ум. 1262, среднеазиатский математик и астроном Хорезшахов), Абу Мухаммад Джабир ибн Афлах ал-Ишбили (первая половина 12 в., западноарабский математик и астроном), Абу Джафар Мухаммад ибн Мухаммад Насир ад-Дин ат-Туси (1201 - 1274, персидский математик, механик и астроном).
В начале нашей исследовательской работы мы поставили проблему – Зачем нужна математика? В ходе изучения литературы и материалов сети интернет мы выяснили, что изначально математика возникла из повседневных нужд человека (подсчеты, измерения) и многие годы служила мощным инструментом познания окружающего мира. Значит, если бы математические знания не передавались из поколения в поколение люди бы надолго застряли на уровне пещерного человека. В ходе проведения экспериментов мы выяснили, что полученные в школе знания очень помогают при решении практических задач с которыми мы сталкиваемся постоянно. Проведенные нами статистические исследования помогли убедиться в правильности выдвинутой гипотезы: математические знания полученные в школе применимы в жизни. Теоретическая значимость нашей работы заключается в том, что познакомившись с нашим исследованием, многие ученики, на вопрос о необходимости изучать математику, ответят положительно. Практическая значимость ее в том, что она может быть использована школьниками для повышения своего образовательного уровня, а также научить применять полученные в школе знания на практике, что сегодня очень актуально.
Введение
Я хочу изучить треугольник Рёло , потому что мне стала интересна его история. Если в древние времена наиболее широко применялся прямоугольный треугольник Пифагора, то в настоящий момент людей больше интересуют необычные свойства треугольника Рёло.
Цель моей работы – выяснить, что такое треугольник Рёло, узнать его историю и где он применяется.
Для этого поставлены задачи:
1.Узнать что такое треугольник Рёло2.Узнать историю Треугольника Рёло3.Построить треугольник Рёло самостоятельно
4.Узнать где используется треугольник РёлоГипотеза
Мне кажется, что Треугольник Рёло является ненужным механизмом в истории человечества. В конце работы я узнаю, прав я или нет. Заключение.
Я рассмотрел применение треугольника Рело в некоторых архитектурных строениях, механических устройствах, в автомобильных двигателях.
Я считаю, что изобретенная крышка люка для рекуперированной воды в Сан-Франциско, является очень интересной для человечества. За счет своей формы, такая крышка никогда не перевернется. Если бы архитекторы пересмотрели наши канализационные люки, и взяли бы для примера такую крышку, то можно было бы избежать множество трагических ситуаций, когда люди падали в канализационные люки.
Поиски альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. По прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. Сколько из этого количества придется на традиционные ДВС и как будет меняться пропорция по мере удешевления себестоимости производства компонентов привода на топливных элементах? Увидим в ближайшие годы.
Я опровергнул свою гипотезу, так как Треугольник Рёло используется во многих механизмах. Я думаю, что он будет использоваться и в будущем.
.
weburok.com
Применение подобия к доказательству теорем и решению задач (Обобщение теоремы Фалеса. Теоремы Чевы и Менелая.)
Применение подобия к доказательству теорем и решению задач (Обобщение теоремы Фалеса. Теоремы Чевы и Менелая.)
Содержание:
Введение;
Обобщение теоремы Фалеса;
Формулировка;
Доказательство;
Теорема о пропорциональных отрезках;
Теорема Чевы;
Формулировка;
Доказательство;
Теорема Менелая;
Формулировка;
Доказательство;
Задачи и их решения;
Источники информации;
Вывод.
Введение.
Мой реферат посвящен , которые не изучаются в школьной программе. Теме подобия, которая проходится в восьмом классе, отведено всего лишь 19 часов, что недостаточно для изучения этой темы более углубленно. В тему подобия входят: определение подобных треугольников, признаки подобия, отношение площадей подобных треугольников, средняя линия треугольника, пропорциональные отрезки и т.д.
Напомню определение подобных треугольников:
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Оказывается, что у подобных треугольников не только отношение сходственных сторон, но и отношение любых других сходственных отрезков равно коэффициенту подобия. Например, отношение сходственных биссектрис AD и A1D1, т.е. биссектрис равных углов A и A1в подобных треугольниках ABC и A1B1C1, равно коэффициенту подобия k, отношение сходственных медиан AM и A1M1 равно k и точно так же отношение сходственных высот AH и A1h2 равно k.
С помощью данного материала, который изучается в школьной программе, мы можем решать довольно узкий круг задач. При создании своего реферата я собираюсь углубить свои знания по данной теме, что позволит решать более широкий круг задач на пропорциональные отрезки. В этом и заключается актуальность моего реферата.
Одна из теорем – это обобщение теоремы Фалеса. Сама теорема Фалеса проходится в восьмом классе. Но главными теоремами являются теоремы Чевы и Менелая.
Обобщение теоремы Фалеса.
Формулировка:
Параллельные прямые, пересекающие две данные прямые, отсекают на этих прямых пропорциональные отрезки.
Доказать:
 =…=
=…= .
.
Доказательство:
Докажем, например, что

Рассмотрим два случая:
1 случай
Прямые a и b параллельны. Тогда четырехугольники А1А2В2В1 и А2А3В3В2 – параллелограммы. Поэтому А1А2=В1В2 и А2А3=В2В3, откуда следует, что

2 случай
Прямые a и b не параллельны. Через точку А1 проведем прямую с, параллельную прямой b. Она пересечет прямые А2В2 и А3В3 в некоторых точках С2 и С3. Треугольники А1А2С2 и А1А3С3подобны по двум углам (угол А1 – общий, углы А1А2С2 и А1А3С3 равны как соответственные при параллельных прямых А2В2 и А3В3 секущей А2А3), поэтому

Отсюда по свойству пропорций получаем:


 (1)
(1)
С другой стороны, по доказанному в первом случае имеем А1С2=В1В2, С2С3=В2В3. Заменяя в пропорции (1) А1С2 на В1В2 и С2С3 на В2В3, приходим к равенству
 (2)
(2)
что и требовалось доказать.
Теорема о пропорциональных отрезках в треугольнике.
На сторонах АС и ВС треугольника АВС отмечены точки К и М так, что АК:КС=m:n, BM:MC=p:q. Отрезки АМ и ВК пересекаются в точке О.
Доказать:


Доказательство:
Через точку М проведем прямую, параллельную ВК. Она пересекает сторону АС в точке D, и согласно обобщению теоремы Фалеса

Пусть АК=mx. Тогда в соответствии с условием задачи КС=nx, а так как KD:DC=p:q, то  Снова воспользуемся обобщением теоремы Фалеса:
Снова воспользуемся обобщением теоремы Фалеса:

Аналогично доказывается, что  .
.
Теорема Чевы.
Теорема названа в честь итальянского математика Джованни Чевы, который доказал её в 1678 году.
Формулировка:
Если на сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки С1, А1 и В1, то отрезки АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда
 (3)
(3)
Доказать:
1.  (3)
(3)
2.отрезки АА1, ВВ1 и СС1 пересекаются в одной точке
Доказательство:
1. Пусть отрезки АА1, ВВ1 и СС1 пересекаются в одной точке О. Докажем, что выполнено равенство (3). По теореме о пропорциональных отрезках в треугольнике имеем:
 и
и  .
.
Левые части этих равенств одинаковы, значит, равны и правые части. Приравнивая их, получаем
 .
.
Разделив обе части на правую часть, приходим к равенству (3).
2. Докажем обратное утверждение. Пусть точки С1, А1 и В1 взяты на сторонах АВ, ВС и СА так, что выполнено равенство (3). Докажем, что отрезки АА1, ВВ1 и СС1 пересекаются в одной точке. Обозначим буквой О точку пересечения отрезков АА1 и ВВ1 и проведем прямую СО. Она пересекает сторону АВ в некоторой точке, которую обозначим С2. Так как отрезки АА1, ВВ1 и СС1 пересекаются в одной точке, то по доказанному в первом пункте
 . (4)
. (4)
Итак, имеют место равенства (3) и (4).
Сопоставляя их, приходим к равенству  =
= , которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки C1 и C2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке O. Теорема доказана.
, которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки C1 и C2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке O. Теорема доказана.
Теорема Менелая.
Формулировка:
Если на сторонах АВ и ВС и продолжении стороны АС (либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С1, А1, В1, то эти точки лежат на одной прямой тогда и только тогда, когда
 (5)
(5)
Доказать:
1.  (5)
(5)
2. точки А1,С1,В1 лежат на одной прямой
Доказательство:
1. Пусть точки А1,В1 и С1 лежат на одной прямой. Докажем, что выполнено равенство (5). Проведем AD,BE и CF параллельно прямой В1А1 (точка D лежит на прямой ВС). Согласно обобщению теоремы Фалеса имеем:
 и
и 
Перемножая левые и правые части этих равенств, получаем
 , откуда
, откуда  ,
,
т.е. выполнено равенство (5).
2. Докажем обратное утверждение. Пусть точка В1 взята на продолжении стороны АС, а точки С1 и А1 – на сторонах АВ и ВС, причем так, что выполнено равенство (5). Докажем, что точки А1,В1 и С1 лежат на одной прямой, то по доказанному а первом пункте
 (6)
(6)
Сопоставляя (5) и (6), приходим к равенству  =
= , которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении. Следовательно, точки А1 и А2 совпадают, и, значит, точки А1,В1 и С1 лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А1,В1 и С1 лежат на продолжениях соответствующих сторон. Теорема доказана.
, которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении. Следовательно, точки А1 и А2 совпадают, и, значит, точки А1,В1 и С1 лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А1,В1 и С1 лежат на продолжениях соответствующих сторон. Теорема доказана.
Решение задач.
Задача №1.

Условие:
В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.
Найти:
АК:КС=?:?
Решение: Пусть ВD = DС = а, АО = ОD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника АDС. По теореме Менелая получаем

Задача №2.

Условие:
Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два.
Найти:

Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти
отношение  . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то
. Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то
По теореме Менелая для треугольника ADC и секущей РВ имеем

Итак,  .
.
Доказательства теорем.
Задача №3.
Формулировка: Медианы треугольника пересекаются в одной точке. Точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины.

Условие:
Медианы треугольника пересекаются в одной точке.
Доказать:
Точка пересечения делит каждую медиану в отношении 2 : 1, считая от вершины.
Доказательство: Пусть АМ1, ВМ2, СМ3 – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что  Тогда по теореме Чевы (обратной) отрезки АМ1, ВМ2 и СМ3 пересекаются в одной точке. Имеем:
Тогда по теореме Чевы (обратной) отрезки АМ1, ВМ2 и СМ3 пересекаются в одной точке. Имеем:

Итак, доказано, что медианы треугольника пересекаются в одной точке.
Пусть О – точка пересечения медиан. Прямая М3С пересекает две стороны треугольника АВМ2 и продолжение третьей стороны этого треугольника. По теореме Менелая

Рассматривая теорему Менелая для треугольников АМ1С и АМ2С, мы получаем, что

Теорема доказана.
Задача №4.
Формулировка:
Биссектрисы треугольника пересекаются в одной точке.
Доказать:
Биссектрисы треугольника пересекаются в одной точке.

Доказательство: Достаточно показать, что  . Тогда по теореме Чевы (обратной) AL1, BL2, CL3 пересекаются в одной точке. По свойству биссектрис треугольника:
. Тогда по теореме Чевы (обратной) AL1, BL2, CL3 пересекаются в одной точке. По свойству биссектрис треугольника:
 . Перемножая почленно полученные равенства, получаем:
. Перемножая почленно полученные равенства, получаем:  . Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.
. Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.
Задача №5.
Формулировка:
Высоты остроугольного треугольника пересекаются в одной точке.
Доказать:
Высоты остроугольного треугольника пересекаются в одной точке.

Доказательство: Пусть АН1, АН2, АН3 – высоты треугольника АВС со сторонами a, b, c. Из прямоугольных треугольников АВН2 и ВСН2 по теореме Пифагора выразим, соответственно, квадрат общего катета ВН2, обозначив АН2 = х, СН2 = b – х.
(ВН2)2 = с2 – х2 и (ВН2)2 = а2 – (b – х)2. приравнивая правые части полученных равенств, получаем с2 – х2 = а2 – (b – х)2, откуда х =  .
.
Тогда b –x = b -  =
=  .
.
Итак, АН2 =  , СН2 =
, СН2 =  .
.
Аналогично рассуждая для прямоугольных треугольников АСН2 и ВСН3, ВАН1 и САН1, получим АН3 =  , ВН3 =
, ВН3 =  и ВН1 =
и ВН1 =  ,
,
СН1 =  .
.
Для доказательства теоремы достаточно показать, что  . Тогда по теореме Чевы (обратной) отрезки АН1, ВН2 и СН3 пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН3, ВН3, ВН1, СН1, СН2 и АН2 через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.
. Тогда по теореме Чевы (обратной) отрезки АН1, ВН2 и СН3 пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН3, ВН3, ВН1, СН1, СН2 и АН2 через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.
Источники информации:
- настоящее пособие является дополнением к учебнику `Геометрия, 7-9` авторов Л.С.Атанасяна, В.Ф.Бутузова и др. (М.: Просвещение, 1990 и последующие издания). Оно полностью соответствует программе углубленного изучения математики.
Сайты:
Вывод.
С помощью обобщения теоремы Фалеса, теорем Чевы и Менелая, не изучаемых в школьной программе, можно быстрее и легче доказывать определенные теоремы и решать более широкий круг задач. Я смогла доказать такие теоремы: теорема о пропорциональных отрезках (с помощью обобщения теоремы Фалеса), теоремы о пересечении медиан, высот и биссектрис треугольника в одной точке (воспользовалась теоремами Чевы и Менелая).
uchebana5.ru
 , I в.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.
, I в.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.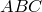 , причем
, причем 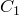 – точка ее пересечения со стороной
– точка ее пересечения со стороной  ,
, 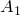 – точка ее пересечения со стороной
– точка ее пересечения со стороной 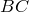 , и
, и 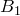 – точка ее пересечения с продолжением стороны
– точка ее пересечения с продолжением стороны  . Тогда
. Тогда
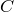 прямую, параллельную
прямую, параллельную 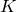 ее точку пересечения с прямой
ее точку пересечения с прямой 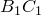 .
.
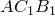 и
и 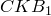 подобны (
подобны (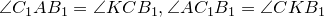 ). Следовательно,
). Следовательно,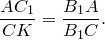
 и
и 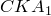 также подобны (
также подобны (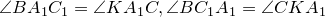 ). Значит,
). Значит,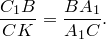
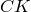 :
: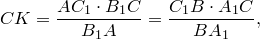

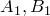 и
и 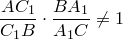 , поскольку, по условию, это выражение равно
, поскольку, по условию, это выражение равно 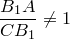 . Следовательно, прямые
. Следовательно, прямые 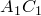 и
и 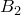 . Для точек
. Для точек 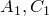 и
и 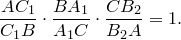

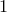 , а левее
, а левее 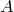 оно строго больше
оно строго больше 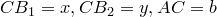 . Тогда, учитывая, что
. Тогда, учитывая, что 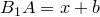 и
и 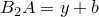 , перепишем полученное равенство в виде
, перепишем полученное равенство в виде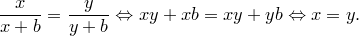
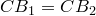 следует, что
следует, что 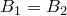 , и доказано, что точка
, и доказано, что точка 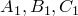 лежат на продолжениях сторон треугольника
лежат на продолжениях сторон треугольника 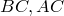 и
и  Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше.
Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше. , I в.) - древнегреческий
математик</ и астроном. Автор работ по сферической
тригонометрии: написал 6 книг о вычислении хорд и 3 книги
"Сферики'', сохранившиеся в арабском переводе. Для получения формул
сферической тригонометрии использовал теорему, известную сегодня
как теорема Менелая.
, I в.) - древнегреческий
математик</ и астроном. Автор работ по сферической
тригонометрии: написал 6 книг о вычислении хорд и 3 книги
"Сферики'', сохранившиеся в арабском переводе. Для получения формул
сферической тригонометрии использовал теорему, известную сегодня
как теорема Менелая.
 , причем
, причем  - точка ее пересечения со
стороной
- точка ее пересечения со
стороной  ,
,
 - точка ее
пересечения со стороной
- точка ее
пересечения со стороной  , и
, и  - точка ее пересечения с
продолжением стороны
- точка ее пересечения с
продолжением стороны  . Тогда
. Тогда

 прямую, параллельную
прямую, параллельную
 ее
точку пересечения с прямой
ее
точку пересечения с прямой  .
.

 и
и  подобны (
подобны ( ). Следовательно,
). Следовательно,

 и
и  также подобны (
также подобны ( ). Значит,
). Значит,

 :
:


 и
и
 , поскольку, по
условию, это выражение равно
, поскольку, по
условию, это выражение равно  . Следовательно, прямые
. Следовательно, прямые  и
и  . Для точек
. Для точек
 и
и 

 , а левее
, а левее  оно строго больше
оно строго больше
 . Тогда, учитывая,
что
. Тогда, учитывая,
что  и
и
 , перепишем
полученное равенство в виде
, перепишем
полученное равенство в виде

 следует, что
следует, что  , и доказано, что точка
, и доказано, что точка
 лежат на продолжениях сторон
треугольника
лежат на продолжениях сторон
треугольника  и
и
 Доказательство этой теоремы точно
такое же, как и доказательство, приведенное выше.
Доказательство этой теоремы точно
такое же, как и доказательство, приведенное выше.


 Городская научно-практическая конференция
Городская научно-практическая конференция
 АВ; которая пересечет прямую А1В1 в точке D.
АВ; которая пересечет прямую А1В1 в точке D. А1ВС1
А1ВС1 
 и
и  .
.  – ненулевые коллинеарные векторы. Если
– ненулевые коллинеарные векторы. Если  , то будем писать:
, то будем писать:  Значит, число k равно отношению длин векторов
Значит, число k равно отношению длин векторов 
 , то точки A1 , B1 и C1 лежат на одной прямой.
, то точки A1 , B1 и C1 лежат на одной прямой. 

 откуда
откуда  , т. е. точки C1 и C2 совпадают.
, т. е. точки C1 и C2 совпадают.


 А1
А1




 , то прямые AA1 , BB1 и CC1 либо пересекаются в одной точке, либо попарно параллельны.
, то прямые AA1 , BB1 и CC1 либо пересекаются в одной точке, либо попарно параллельны.
 =
=  . Следовательно, C2 совпадает C1 , т. е. прямые AA1 , BB1 и CC1 пересекаются в одной точке.
. Следовательно, C2 совпадает C1 , т. е. прямые AA1 , BB1 и CC1 пересекаются в одной точке. =…=
=…= .
.



 (1)
(1) (2)
(2)


 Снова воспользуемся обобщением теоремы Фалеса:
Снова воспользуемся обобщением теоремы Фалеса:
 .
. (3)
(3) и
и  .
. .
. . (4)
. (4) =
= , которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки C1 и C2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке O. Теорема доказана.
, которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки C1 и C2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке O. Теорема доказана. и
и 
 , откуда
, откуда  ,
, (6)
(6) =
= , которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении. Следовательно, точки А1 и А2 совпадают, и, значит, точки А1,В1 и С1 лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А1,В1 и С1 лежат на продолжениях соответствующих сторон. Теорема доказана.
, которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении. Следовательно, точки А1 и А2 совпадают, и, значит, точки А1,В1 и С1 лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А1,В1 и С1 лежат на продолжениях соответствующих сторон. Теорема доказана.



 . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то
. Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то

 .
.
 Тогда по теореме Чевы (обратной) отрезки АМ1, ВМ2 и СМ3 пересекаются в одной точке. Имеем:
Тогда по теореме Чевы (обратной) отрезки АМ1, ВМ2 и СМ3 пересекаются в одной точке. Имеем:



 . Тогда по теореме Чевы (обратной) AL1, BL2, CL3 пересекаются в одной точке. По свойству биссектрис треугольника:
. Тогда по теореме Чевы (обратной) AL1, BL2, CL3 пересекаются в одной точке. По свойству биссектрис треугольника: . Перемножая почленно полученные равенства, получаем:
. Перемножая почленно полученные равенства, получаем:  . Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.
. Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана. 
 .
.  .
.  , ВН3 =
, ВН3 =  и ВН1 =
и ВН1 =  ,
, .
. . Тогда по теореме Чевы (обратной) отрезки АН1, ВН2 и СН3 пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН3, ВН3, ВН1, СН1, СН2 и АН2 через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.
. Тогда по теореме Чевы (обратной) отрезки АН1, ВН2 и СН3 пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН3, ВН3, ВН1, СН1, СН2 и АН2 через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана. 