Реферат на тему:
При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
В XIX веке классическая механика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе осчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда , преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
wreferat.baza-referat.ru
Реферат на тему:
При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
В XIX веке классическая механика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе осчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда , преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
www.wreferat.baza-referat.ru
«Физика - 10 класс»
Изменится ли движение, если мы будем его описывать в разных системах координат?В любой ли системе координат удобно описывать движение?
Пусть по реке плывёт моторная лодка и нам известна её скорость 
1 относительно воды, точнее, относительно системы координат K1, движущейся вместе с водой (рис. 1.19).
Такую систему координат можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна ещё и скорость течения реки относительно системы координат К2, связанной с берегом, т. е. скорость системы координат Кх относительно системы координат К2, то можно определить скорость лодки 2 относительно берега.
За промежуток времени Δt перемещения лодки и мяча относительно берега равны Δ
2 и Δ (рис. 1.20), а перемещение лодки относительно мяча равно Δ1. Из рисунка 1.20 видно, что
Δ2 = Δ1 + Δ. (1.7)
Разделив левую и правую части уравнения (1.7) на Δt, получим
Учтём также, что отношения перемещений к интервалу времени равны скоростям. Поэтому
2 = 1 + .
Скорости складываются геометрически, как и все другие векторы. Уравнение (1.8) называют законом сложения скоростей.
Закон сложения скоростей
Если тело движется относительно некоторой системы координат К1 со скоростью и сама система К1 движется относительно другой системы координат К2 со скоростью 1, то скорость тела относительно второй системы равна геометрической сумме скоростей 1 и .
Как запишется классический закон сложения скоростей, если (1.9) неподвижной считать систему, связанную с мячом, а подвижной — с берегом?
Как и любое векторное уравнение, уравнение (1.8) представляет собой компактную запись скалярных уравнений, в данном случае — для сложения проекций скоростей движения на плоскости:
υ2x = υ1x + υx, υ2y = υ1y + υy. (1.9)
Проекции скоростей складываются алгебраически.
Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчёта, движущихся относительно друг друга.
Классический закон сложения скоростей справедлив для тел, движущихся со скоростями, много меньшими скорости света.
Часто скорость тела относительно неподвижной системы координат называют абсолютной скоростью, относительно подвижной системы координат — относительной, а скорость тела отсчёта, связанного с подвижной системой, относительно неподвижной — переносной скоростью.
Тогда закон сложения скоростей имеет вид a = отн + пер.
Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика - Физика, учебник для 10 класса - Класс!ная физика
Физика и познание мира --- Что такое механика --- Механическое движение. Система отсчёта --- Способы описания движения --- Траектория. Путь. Перемещение --- Равномерное прямолинейное движение. Скорость. Уравнение движения --- Примеры решения задач по теме «Равномерное прямолинейное движение» --- Сложение скоростей --- Примеры решения задач по теме «Сложение скоростей» --- Мгновенная и средняя скорости --- Ускорение --- Движение с постоянным ускорением --- Определение кинематических характеристик движения с помощью графиков --- Примеры решения задач по теме «Движение с постоянным ускорением» --- Движение с постоянным ускорением свободного падения --- Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» --- Равномерное движение точки по окружности --- Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение --- Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями --- Примеры решения задач по теме «Кинематика твёрдого тела»
Вверх
class-fizika.ru
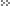СЛОЖЕНИЕ СКОРОСТЕЙ Количество просмотров публикации СЛОЖЕНИЕ СКОРОСТЕЙ - 165
| Наименование параметра | Значение |
| Тема статьи: | СЛОЖЕНИЕ СКОРОСТЕЙ |
| Рубрика (тематическая категория) | Математика |
Пусть точка М движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведём векторы
и
, характеризующие положение точки М относительно неподвижной и подвижной систем осей координат, и вектор
точки О. Для любого момента времени
Продифференцируем по времени это векторное тождество, учитывая изменения векторов относительно неподвижных осей координат, т. е. вычислим полные производные. Получим
(1)
По определению, является абсолютной скоростью точки М,
- абсолютной скоростью точки О. Для вычисления
применим формулу Бура. Имеем
Относительная производная является относительной скоростью точки М по отношению к подвижной системе отсчета͵ а
- угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора
, если бы он в рассматриваемый момент времени был скреплен с подвижной
системой осей координат. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, из (1) получаем
(2)
Скорость
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка М в движении тела относительно неподвижной системы осей координат. Это есть переносная
скорость точки М. Получаем следующую теорему сложения
(3) скоростей для точки:
т. е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
СЛОЖЕНИЕ СКОРОСТЕЙ - понятие и виды. Классификация и особенности категории "СЛОЖЕНИЕ СКОРОСТЕЙ" 2014, 2015.
Определим скорость абсолютного движения точки М, если известны скорости абсолютного и переносного движений этой точки. За малый промежуток времени вдоль траектории точка М совершит относительное перемещение, определяемое вектором . Сама кривая , двигаясь вместе с... [читать подробнее].
Пусть система отсчета O1x1y1z1 - неподвижная, а система отсчета Oxyz - подвижная. Движение точки относительно основной неподвижной системы отсчета O1x1y1z1 называется абсолютным. Движение точки относительно подвижной системы отсчета Oxyz называется относительным.Переносным... [читать подробнее].
referatwork.ru
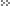Сложение скоростей Количество просмотров публикации Сложение скоростей - 123
| Наименование параметра | Значение |
| Тема статьи: | Сложение скоростей |
| Рубрика (тематическая категория) | Механика |
Пусть система отсчета O1x1y1z1 - неподвижная, а система отсчета Oxyz - подвижная. Движение точки относительно основной неподвижной системы отсчета O1x1y1z1 принято называть абсолютным. Движение точки относительно подвижной системы отсчета Oxyz принято называть относительным.Переносным движением точки принято называть движение, ĸᴏᴛᴏᴩᴏᴇ она совершает вместе с подвижной системой отсчета͵ как точка, жестко скрепленная с этой системой в рассматриваемый момент времени. Относительные скорость и ускорение обозначают
и
, переносные -
и
, а абсолютные -
и
.
Рис. 9-2
Движение подвижной системы отсчета относительно неподвижной можно охарактеризовать скоростью ее поступательного движения , к примеру вместе с точкой О, и вектором угловой скорости
ее вращения вокруг О.
Теорема. Скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
Доказательство. Рассмотрим движение точки . Положение точки
относительно неподвижной системы отсчета определяется вектором
, а относительно подвижной вектором
. Положение точки
относительно неподвижной системы отсчета определяется вектором
. Для любого момента времени выполняется тождество
.
Продифференцируем его по времени (вычислим производные в неподвижной системе отсчета) и получим
(9-5)
По определению, - абсолютная скорость точки
,
- абсолютная скорость точки
. Для вычисления
применим формулу Бура. Имеем
. Относительная производная
- является относительной скоростью точки
по отношению к неподвижной системе отсчета͵ а
- угловая скорость вращения подвижной системы отсчета.
Таким образом из (9-5) получаем
(9-6)
Скорость
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка в движении тела относительно неподвижной системы отсчета. Это есть переносная скорость точки
.
Окончательно получаем
, (9-7)
что и требовалось доказать.
Сложение скоростей - понятие и виды. Классификация и особенности категории "Сложение скоростей" 2014, 2015.
Пусть точка М движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведём векторы и , характеризующие положение точки М относительно неподвижной и подвижной систем осей координат, и вектор точки О. Для любого момента... [читать подробнее].
Определим скорость абсолютного движения точки М, если известны скорости абсолютного и переносного движений этой точки. За малый промежуток времени вдоль траектории точка М совершит относительное перемещение, определяемое вектором . Сама кривая , двигаясь вместе с... [читать подробнее].
referatwork.ru
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
В XIX веке классическая механика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложения скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда , преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся эти две теории — первая является обобщением второй.
Сложение скоростей Информация Видео
Сложение скоростей Просмотр темы.Сложение скоростей что, Сложение скоростей кто, Сложение скоростей объяснение
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Ещё в младших классах вы сталкивались с тем, что иногда необходимо складывать скорости. Например, если две машины едут навстречу друг другу, то скорость их сближения — это сумма скоростей первой и второй машины.
Если же они двигаются в одном направлении, то скорость их сближения (или удаления) будет определяться разностью скоростей. Как мы уже говорили, решающее значение имеет выбор системы отсчёта.
Закон сложения скоростей:
если тело двигается со скоростью 
в системе отсчёта 
а система отсчёта 
двигается со
скоростью 
в
системе отсчёта 
,
то скорость движения тела, относительно системы 
равна:
Напомним, что скорость — это векторная величина, поэтому, скорости складываются геометрически.
Пример решения задач.
Лодка двигается по реке с собственной скоростью 8 м/с, так, как показано на рисунке. Скорость течения реки составляет 1 м/с. Определите скорость лодки относительно берега.
Расположим оси координат
так, чтобы направление оси х совпадало с направлением течения реки.
Тогда проекция скорости на ось х будет равна 
, т.к. на рисунке нам
указан угол между направлением течения и скоростью лодки. Обратите внимание,
что эта проекция будет отрицательной. В этом можно убедиться при построении
проекции, да и чисто логически ясно, что лодка плывет против течения, а значит,
одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения
на ось х, конечно же, будет равна 1 м/с, поскольку направление течение
совпадает с направлением оси х. Тогда скорость движения лодки по оси х
относительно берега равна: 
Проекция вектора
скорости лодки на ось у равна 
Разумеется, проекция скорости течения на ось у будет равна нулю, потому что вектор скорости течения перпендикулярен этой оси. С помощью геометрической суммы проекций мы можем найти модуль скорости лодки, относительно берега:
Давайте рассмотрим теперь пример, который научит вас складывать какие угодно скорости.
Найдём скорость машины,
относительно самолёта в заданной системе координат. Сначала найдем проекции
скорости машины на оси х и у. Точно так же, как и в предыдущем
примере, проекция на ось х равна: 
, а проекция на ось у
равна 
.
Точно так же находим проекции скорости самолёта на координатные оси:
Напомним, что проекции являются скалярными величинами, поэтому их мы складываем алгебраически:
Теперь, когда мы нашли проекции скорости машины относительно самолёта на оси х и у, мы можем найти модуль скорости с помощью геометрической суммы:
Таким образом, мы получили расчётную формулу для вычисления модуля скорости одного движущегося тела, относительно другого движущегося тела. Эта формула справедлива для тех случаев, когда оба тела двигаются в одной плоскости.
Заметим, что закон сложения скоростей справедлив и для неравномерного движения. В этом случае нужно складывать мгновенные скорости.
Пример решения задачи.
Задача. Мяч катится с постоянной скоростью 10 м/с. Ему наперерез бежит футболист со скоростью 7 м/с, так, как показано на рисунке. Через какое время футболист поймает мяч, если изначально между футболистом и мячом было 40 метров?
Начнём с того, что когда футболист поймает мяч, они будут находиться в одной точке. Расположим систему координат так, чтобы направление движения футболиста совпадало с направлением оси х. Тогда, скорость мяча будет направлена под углом 45о градусов к оси х. Сделаем проекции скорости мяча на оси х и у.
videouroki.net
