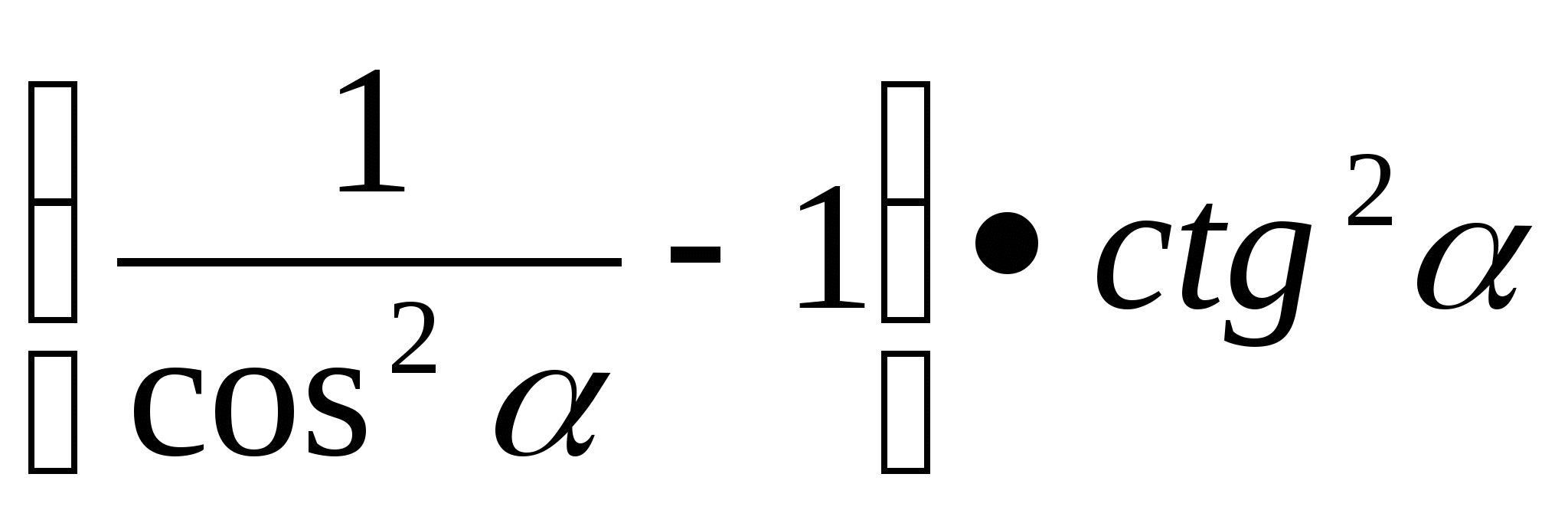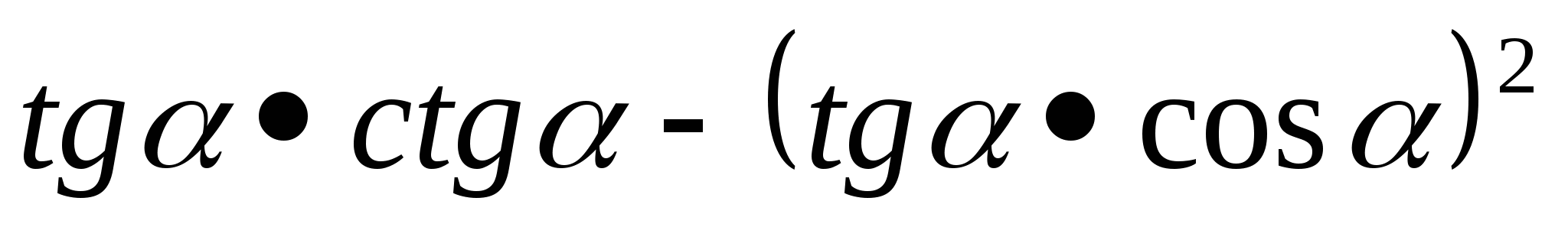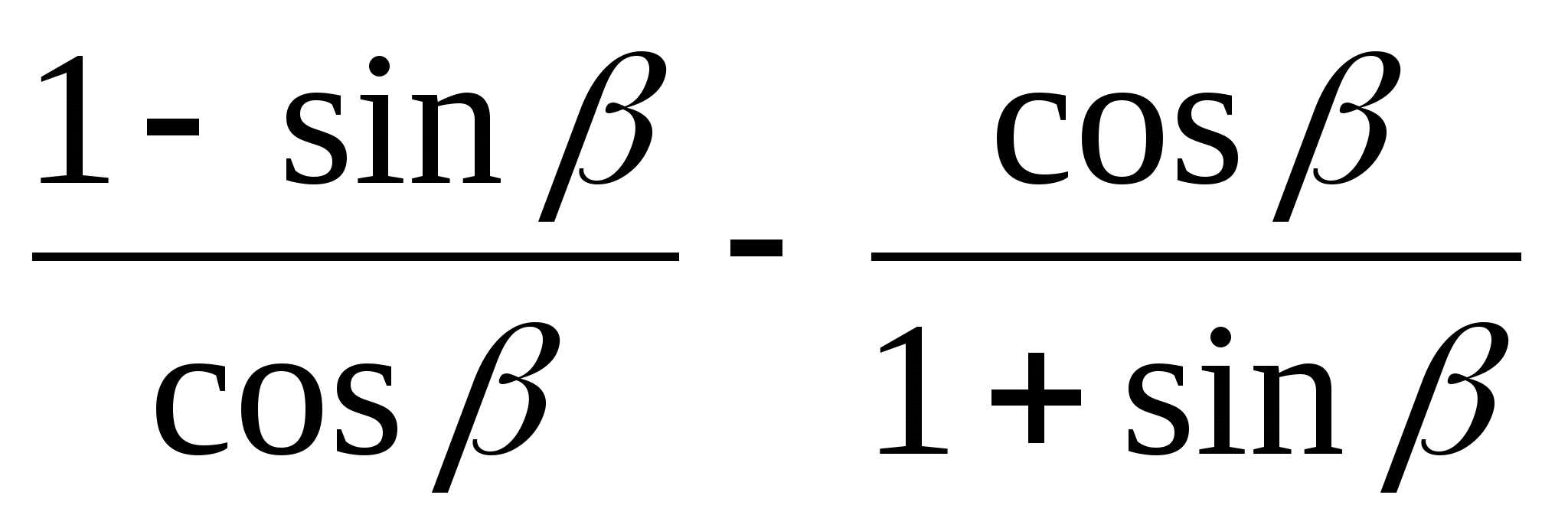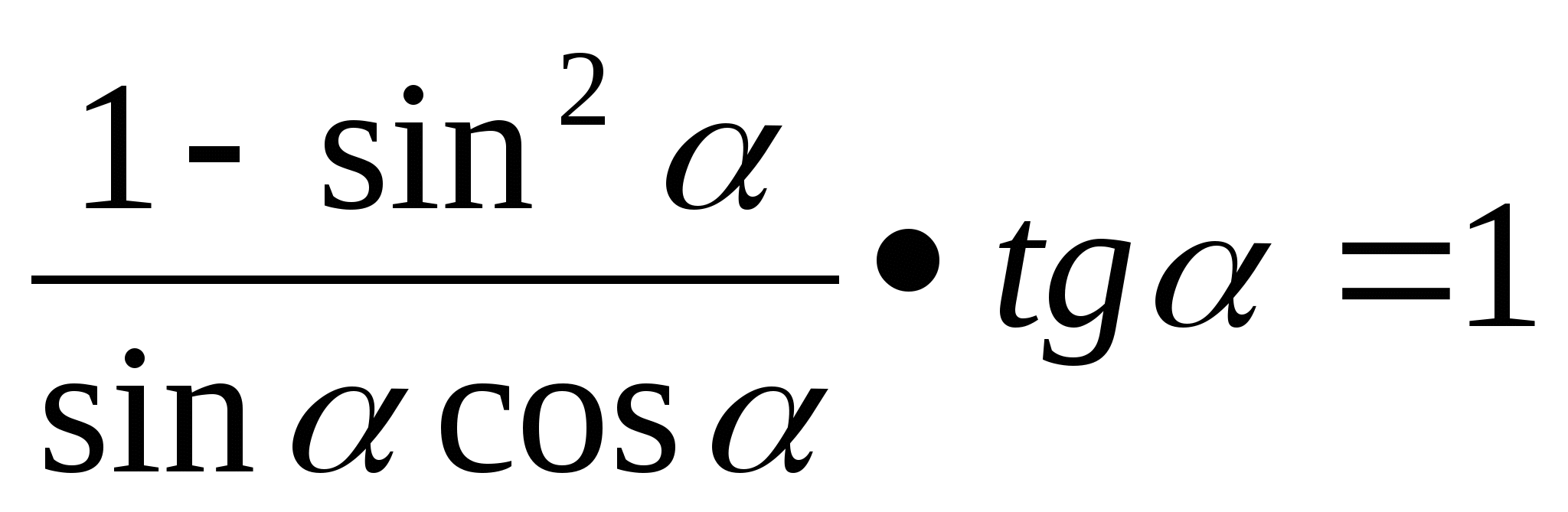|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Урок. "Преобразование тригонометрических выражений.". Реферат на тему преобразование тригонометрических выражений
Преобразование тригонометрических выражений.
Количество просмотров публикации Преобразование тригонометрических выражений. - 397
1º. На плоскости xOy рассмотрим окружность с центром в начале координат и радиусом, равным 1. На единичной окружности отметим точку A(1;0). Радиус OA называют начальным радиусом. При повороте начального радиуса на угол α около центра О точка А(1;0) перейдет в некоторую точку М(x;y). Заметим, что поворот можно осуществить по часовой стрелки (угол поворота положителен) или против часовой стрелки (угол поворота отрицателен).
Косинусом угла α принято называть абсцисса точки М:
.
Синусом угла α принято называть ордината точки М: .
Тангенсом угла α принято называть отношение ординаты точки М к ее абсциссе: .
Котангенсом угла α принято называть отношение абсциссы точки М к ее ординате: .
являются тригонометрическими функциями аргумента α.
2º. Единицами измерения величины угла являются градус и радиан.
В случае если начальный радиус окружности совершит один полный оборот, то получится угол, равный 360˚ или 2π радиан.
Связь между градусной и радианной мерами измерения угла: рад.
Из этой формулы следует:
а) ; б)
; в)
; г)
; д)
и т.д.
3º. Свойства тригонометрических функций:
Функции - нечетные функции:
.
Функция - четная:
.
Функции - периодические с наименьшим периодом 2π:
.
Функции - периодические с наименьшим периодом π:
.
4º. Основное тригонометрическое тождество.
Согласно теореме Пифагора (“в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы”) координаты любой точки М(x;y) единичной окружности удовлетворяют уравнению: . Отсюда:
где
(10.1)
Из этой формулы следует:
а) ; б)
.
5º. Основные соотношения между тригонометрическими функциями:
, (10.2)
, (10.3)
, (10.4)
, (10.5)
. (10.6)
6º. Формулы сложения аргументов:
, (10.7)
, (10.8)
. (10.9)
7º. Формулы двойного аргумента:
, (10.10)
, (10.11)
. (10.12)
8º. Формулы понижения степени синуса и косинуса:
. (10.13)(10.14)
9º. Преобразование суммы и разности одноименных тригонометрических функций в произведение:
, (10.15)
, (10.16)
, (10.17)
. (10.18)
10º. Преобразование произведения тригонометрических функций в сумму:
, (10.19)
, (10.20)
. (10.21)
11º. Выражение тригонометрических функций через тангенс половинного аргумента.
При доказательстве тождеств, решении тригонометрических уравнений и т.п. часто возникает крайне важно сть выразить все 4 тригонометрические функции через какую-нибудь одну функцию f(x). Для этого пользуются следующими формулами:
а) , (10.22)
б) , (10.23)
в) . (10.24)
12º. Формулы приведения. Это соотношения, при помощи которых значения тригонометрических функций аргументов выражают через тригонометрические функции угла α. Все формулы приведения можно свести в следующую таблицу:
Пример 34. Найдите , в случае если
.
Решение: . По формуле (10.6)
. Так как α находится в 3-ей четверти, то
и, следовательно,
. Ответ:
.
Пример 35. Вычислить значение выражения , в случае если
.
Решение: Используем формулу (10.10), а затем числитель и знаменатель дроби разделим на . Тогда:
Ответ: 9,25.
Пример 36. Доказать тождество: .
Решение: Используя формулы (10.15), (10.16), получим:
.
Пример 37. Вычислить , в случае если
.
Решение: Выразив и
через
по формулам (10.22), (10.23), получим:
.
Ответ: ¼.
Пример 38. Упростить выражение: .
Решение: Воспользуемся свойствами четности и нечетности тригонометрических функций, а также выделим период в аргументе функций и исключим его, опираясь на свойство периодичности функций:
,
,
,
,
.
Получаем:
Далее используем формулы приведения:
.
Ответ: -1.
Пример 39. Найти .
Решение: Воспользуемся формулой приведения и определением котангенса:
.
Поскольку угол находится в 4-ой четверти
, то
. Получаем:
.
referatwork.ru
Математика. Тождественные преобразования тригонометрических выражений: Тождественные преобразования тригонометрических выражений
Тождественные преобразования тригонометрических выражений
Комментарий. Цель данного раздела — проработать выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а так же комбинированных заданий. Для решения задач на упрощение тригонометрических выражений требуется достаточно хорошо знать правила преобразования алгебраических выражений и тригонометрические формулы (уметь применять их как по одной, так и в комплексе).
Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно.
Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы:
 |
 |
Формулы зависимости между функциями одного и того же аргумента:
Формулы сложения.
Формулы двойных и половинных углов.
Формулы преобразования суммы в произведение:
Формулы преобразования произведения в сумму:
Формулы приведения:
|
|
|
|
|
|
|
|
|
|
| sin φ | - sin α |
cos α |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos φ |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos α |
cos α |
tg φ |
- tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg φ |
- ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
Рассмотрим сначала достаточно простые задания на применение формул тригонометрии.
Пример 2.1.
Вычислить значение sin α, если cos α = 0,3, α — угол в первой четверти.
Решение
Применим основное тригонометрическое тождество, связывающее тригонометрические функции  .
.
Так как по условию задачи cos α = 0,3, то cos2α
= 0,09. Значит, sin2α
+ 0,09 = 1, sin2α
= 1 – 0,09 = 0,91. Решая уравнение sin2α
= 0,91, получаем два случая ( ), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно,
), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно,  .
.
Ответ: 
 .
.
Пример 2.2.
Вычислите значение tg α, если ctg α = 0,2.
Решение
Воспользуемся формулой, связывающей тригонометрические функции y = tg α, y = ctg α : tg α ∙ ctg α = 1. Подставляя заданное в условии значение 0,2, получаем, что tg α ∙ 0,2 = 1, откуда tg α = 5.
Ответ:  5.
5.
Пример 2.3.
Упростите выражения;
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
Решение
Данные задания — на применение формул сложения.
Ответ: 

Пример 2.4.
Вычислите:
Решение
Ответ: 

Отдельную группу заданий этого типа составляют задания на вычисление одних тригонометрических функций по известным другим.
Пример 2.5.
Известно, что sin α – cos α = 0,3. Найти:
1) sin2α ;
2) sin4α + cos4α ;
3) sin6α + cos6α .
Решение
1) Возведем в квадрат обе части заданного в условии примера равенства и используем формулу «квадрат разности», получаем, что:
sin2α - 2sinα cosα + cos2α = 0,09.
Вспомним основное тригонометрическое тождество и применим формулу синуса двойного угла:
1 - sin2α = 0,09, откуда:
sin2α = 1 - 0,09 = 0,91.
2) Воспользуемся полученным результатом для ответа на вопрос 2.
Для этого сумму sin4α + cos4α представим в специальном виде:
sin4α + cos4α = (sin4α + 2sin2α cos2α + cos4α ) — 2sin2α cos2α = (sin2α + cos2α )2 - 1/2 ∙ sin22α = 1 - 1/2 ∙ 0,91 = 0,545.
Комментарий. Специальный вид, использованный при решении данного примера, позволяет применить формулу «квадрат суммы» и использовать результат, полученный в пункте 1. При последующих преобразованиях использована формула синуса двойного угла.
3) Обратим внимание, что для вычисления значения выражение sin6α + cos6α можно представить в виде суммы кубов.
sin6α + cos6α = (sin2α )3 + (cos2α )3 = (sin2α + cos2α )(sin4α - sin2α cos2α + cos4α ) = 1 ∙ (0,545 – 1/4 ∙ 0,91) = 0,3175.
Ответ:

1) 0,91;
2) 0,545;
3) 0,3175.
Пример 2.6.
Найти tgα, если 
Решение
Проверкой можно убедиться, что при cos α = 0 приведенное равенство неверно. Поэтому следует разделить числитель и знаменатель дроби на cos α (на основании основного свойства дроби):
 , следовательно,
, следовательно,  тогда:
тогда:

раскрывая скобки, приведем далее подобные слагаемые:
3tgα + 4 = 5tgα - 10, 2tgα = 14, получаем, что tgα = 7.
Ответ:  7.
7.
Пример 2.7.
Вычислить cos α, если cos2α = 3/4 и 
Решение
Как известно,  . Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим:
. Выясним, в каких пределах лежит угол α и какой знак при этом имеет его косинус. Преобразуем заданное в условии задачи двойное неравенство. Разделив одновременно все три части двойного неравенства на 2, получим:
 , то есть угол α располагается во второй четверти и, следовательно, cos α < 0.
, то есть угол α располагается во второй четверти и, следовательно, cos α < 0.
В приведенной выше формуле выберем знак «минус»:

Ответ: 

Комментарий. Следующая группа заданий — вычисление значений различных тригонометрических выражений с использованием тригонометрических формул.
Пример 2.8.
Найти значение выражения:  .
.
Выполним упрощение каждой дроби по отдельности.
С целью сокращения дроби  воспользуемся формулой «разность кубов» и получим:
воспользуемся формулой «разность кубов» и получим:
 .
.
Рассмотрим далее выражение  . Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом:
. Нужно заметить, что первое третье слагаемые в сумме дают единицу в силу основного тригонометрического тождества. Таким образом:
 .
.
Обратимся далее к преобразованию второй дроби. Применим одну из формул приведения:  . Поэтому:
. Поэтому:

Тогда  .
.
Окончательно получаем: 
Ответ:  1.
1.
Пример 2.9.
Вычислить sin10° sin30° sin50° sin70°.
Используем формулу преобразования произведения тригонометрических функций в сумму: sin10° sin50° = 1/2 (cos40° - cos60°) = 1/2 cos 40° - 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30° = 1/2, получаем:

Ответ: 

Комментарий. Для выполнения аналогичных заданий необходимо знание не только тригонометрических формул, но и табличных значений тригонометрических функций.
Рассмотрим далее примеры упрощения тригонометрических выражений с произвольным аргументом.
Пример 2.10.
Упростить выражение:  .
.
Так как числитель заданной дроби имеем достаточно простой вид, начнем с упрощения знаменателя. Для этого применим представление  :
:
 .
.
Приведем полученную разность дробей к общему знаменателю:
 .
.
Следовательно, 
Ответ: 

Пример 2.11.
Доказать тождество при 
Комментарий. Задания на доказательство тождеств вполне можно воспринимать как задания на упрощение выражений, причем с готовым ответом в виде более простой и компактной части равенства.
Решение
В частности, в данном примере попробуем упростить левую часть, чтобы получить такое же выражение, как справа. Для этого помножим числитель и знаменатель подкоренного выражения на 1 + sin α:
 .
.
Вспомнив, что  , получаем
, получаем 
Исследуем далее знак числителя и знаменателя подмодульного выражения:
sin α ≥ -1, тогда 1 + sin α ≥ 0 поэтому  ;
;
при  следовательно,
следовательно, 
Таким образом:

Аналогичным образом преобразуем второе слагаемое левой части:

Тогда , 
что и требовалось доказать.
Пример 2.12.
Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если  .
.
Решение
Выпишем формулы для вычисления искомых функций:
 .
.
Из основного тригонометрического тождества вычислим:

Далее найдем значения искомых выражений:

Ответ: 

Пример 2.13.
Доказать тождество  .
.
Решение
Приведем левую часть к 1:
 .
.
Тождество доказано.
Пример 2.14.
Вычислить значение выражения:
 .
.
Решение
Обратим вниманием, что 
Далее, используя формулы приведения, получим:

Воспользуемся табличными значениями и свойствами тригонометрических функций:

Итак, значение выражения равно 0.
Ответ:  0.
0.
Комментарий. Для выполнения заданий, связанных с обратными тригонометрическими функциями, нужно, во-первых, четко помнить определения этих понятий:

Удобно при решении таких задач сделать замену (например, α = arcsin x) и работать с более привычным объектом — углом α, лежащем в первой или четвертой четверти тригонометрического круга, синус которого равен х. При этом выясняется, что задача намного проще, чем казалось вначале.
Пример 2.15.
Вычислить cos(4arctg 5).
Решение
Пусть α = arctg5, тогда tg α = 5. Требуется найти cos4α. Вычислим вначале cos2α, используя универсальную подстановку:

Тогда получаем, что:

Ответ: 

Пример 2.16.
Выразить через все обратные функции 
Решение
Пусть  . Угол α лежит в четвертой четверти, следовательно, cos α > 0.
. Угол α лежит в четвертой четверти, следовательно, cos α > 0.
Найдем все тригонометрические функции угла:

В четвертой четверти находятся арктангенсы отрицательных чисел, поэтому можно утверждать, что  .
.
Но  , так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом
, так как арккосинусы положительных чисел принадлежат первой четверти. В силу четности косинуса cos (-α) = cos α, при этом  , то есть
, то есть  , тогда
, тогда  .
.
Арккотангенсы отрицательных чисел расположены во второй четверти. Например,  , следовательно,
, следовательно,  . Таким образом, угол α выражен через все обратные функции.
. Таким образом, угол α выражен через все обратные функции.
Ответ: 

Пример 2.17.
Найти arcsin (sin 12).
Решение
По условию задачи требуется найти угол, синус которого равен синусу угла в 12 радиан и который принадлежит промежутку  . Заметим, что
. Заметим, что  , поэтому
, поэтому  .
.
Поскольку  , угол 12 - 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
, угол 12 - 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
Ответ:  arcsin (sin12) = 12 - 4π.
arcsin (sin12) = 12 - 4π.
Пример 2.18.
Вычислить 
Решение
Введем два угла:  Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что
Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны. Мы знаем, что  . Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
. Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
Во-первых, 
Во-вторых,  .
.
Следовательно, 
Ответ: 

www.e-biblio.ru
Преобразование тригонометрических выражений
скачатьТема: Преобразование тригонометрических выраженийЦель: научить учащихся применять нестандартные приемы при преобразовании тригоно
метрических выражений.
I.Организационный момент.
Сообщить учащимся цель занятия, его ход.
II.Повторение пройденного материала
Задание: вынесите за скобки общий множитель
1. 3ах - 2ау =
2. 7а - 49в =
3. 6х2 + 9х3 =
- 2y2 + 2y + y + 1 =
- sin4a + cos2asin2a =
5. (ключевое) ас + bd =
{Здесь у учащихся возникают трудности в определении общего множителя. В этот момент необходимо вспомнить правило:
вынести - значит разделить
Таким образом в данном примере за скобки можно вынести любой из сомножителей обоих слагаемых. Демонстрируем это.}
Это правило часто помогает значительно упростить преобразования тригонометрических выражений. Но прежде, чем мы приступим к их решению, проведем небольшую подготовительную работу. Выразим из формулы
 косинус,
косинус,  , а из формулы
, а из формулы синус,
синус, 
III.Объяснение нового материала. (1 часть)
Правило 1. Если в тригонометрическом выражении есть сумма тангенса и синуса, то выноси за скобки тангенс.
Задание 1. Докажите, что разность квадратов тангенса и синуса равна их произведению.
Решение:
Будем использовать только что сообщенное правило. Вынесем за скобки тангенс.
tg2a - sin2a = tg2a (1 - cos2a) = tg2a sin2a
Правило 1 можно дополнить: если в тригонометрическом выражении есть сумма косинуса и котангенса, то выноси за скобки котангенс.
^ .Закрепление нового материала
Задание 2. № 3048 [1]. Докажите, что
(sin2a + tg2a +1) (cos2a - ctg2a +1)
---------------------------------------- = 1
(cos2a + ctg2a +1) (sin2a + tg2a -1)
Решение:
tg2a (cos2a + 1 + ctg2a) ctg2a (sin2a - 1 + tg2a)
--------------------------------------------------- = 1 используя формулу tg a ctg a = 1
(cos2a + ctg2a + 1) (sin2a + tg2a -1)
На уроках мы неоднократно убеждались в пользе формул, выражающих тангенс через котангенс и наоборот.
 ,
, 
При использовании правила вынести - разделить они также позволяют значительно упростить решение заданий.
Задание 3. № 3.004 [1]. Упростите выражение:
tg 2a + ctg 3b tg 2a
----------------- = ----------
ctg 2a + tg 3b tg 3b
Решение:
ctg 3b
tg 2a (1 + --------)
tg 2a tg 2a (1 + ctg 3b ctg 2a) tg 2a
---------------------- = ---------------------------- = --------
ctg 2a tg 3b (1 + ctg 2a ctg 3b) tg 3b
tg 3b (-------- + 1)
tg 3b
^ .Объяснение нового материала (2 часть)
Рассмотрим выражения:
(а + b)2 = а2 + b2 + 2аb , отсюда a2 + b2 = (a + b)2 - 2ab
(а + b)3 = а3 + b3 + 3а2b + 3аb2 = a3 + b3 + 3ab (a +b) , a3 +b3 = (a + b)3 - 3ab (a + b)
(а + b)4 = а4 + b4 + 4a3b + 8a2b2 + 4ab3 = a4 + b4 + 4ab (a + b)2 , a4 +b4 = (a + b)4 - 4ab (a + b)2
-----------------------------------------------------------------------------------------------------------
(а + b)n = an + bn + nab (a +b)n-2 , an + bn = (a + b)n -nab (a + b)n-2
Заметим, что в скобках при этом всегда будет выражение a + b. Если положить a = sin2a, b = cos2a будем иметь, то значения выражения в скобках будут равны 1.
Правило 2. Если в тригонометрическом выражении есть сумма синуса и косинуса четных степеней, то применяй формулу
sinna + cosna = (sin2a + cos2a)k - ksin2a cos2a (sin2a + cos 2a)k-2 , где k = n/2
VI.Закрепление нового материал (2 часть)
Пример 4. № 3.051 [1]. Докажите, что значение выражения sin6a + cos6a + 3sin2a cos2a не зависит от а. (Условие задания изменено)
Решение:
sin6a + cos6a + 3sin2a cos2a = (sin2a + cos2a)3 - 3sin2a cos2a (sin2a + cos2a) + 3sin2a cos2a = 1
Пример 5. № 3.186 Докажите тождество
sin4a + cos4a -1 2
-------------------- = ---
sin6a + cos6a -1 3
Решение:
Пользуясь правилом 2 преобразуем отдельно числитель и знаменатель. Имеем
sin4a + cos4a - 1 = (sin2a + cos2a)2 - 2sin2acos2a - 1 = -2sin2acos2a
sin6a + cos6a - 1 = (sin2a + cos2a)3 - 3sin2a cos2a (sin2a + cos2a) -1 = -3sin2acos2a
sin4a + cos4a -1 -2sin2a cos2a 2
------------------ = ---------------- = ---
cos6a + sin6a -1 -3sin2a cos2a 3
{Подводим итог работы на уроке}
^ .Домашнее задание
Теоретический материал
выучить:
- правила
Практический материал
решить:
Докажите тождество:
2(sin6a + cos6a) - 3(sin4a + cos4a) + 1 = 0
Литература:
- Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И. Сканави),
- Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И. Сканави),
- Пинский А.И., Цыпкин А.Г. «Справочное пособие по методам решения задач по мате
База данных защищена авторским правом © kursovaya-referat.ru 2017При копировании материала укажите ссылку
kursovaya-referat.ru
Преобразование тригонометрических выражений

Разделы: Математика
Цели:
- Образовательные:
- обобщить теоретический материал по теме тригонометрические тождества;
- формировать умения применять основные тригонометрические тождества для преобразования тригонометрических выражений.
- Развивающие:
- развивать зрительную память, познавательную активность, творческие способности.
- Воспитательные:
- воспитывать интерес к предмету.
Делу обучиться – всегда пригодиться.
(Русская пословица)
ХОД УРОКА
I. Организационный момент
II. Актуализация опорных знаний (записать на доске)
А) – формулы для  ;
– основное тригонометрическое тождество;
– формулу, выражающую зависимость
;
– основное тригонометрическое тождество;
– формулу, выражающую зависимость  и
и  ;
– формулу, выражающую зависимость
;
– формулу, выражающую зависимость  и
и  .
.
Б) упростить выражения (устно)


Мудрым никто не родился, а научился
(Русская пословица)
III. Работа в тетрадях
А) упростить выражение:
1. 
Решение:

2. 
Решение:

3. 
Решение:

? Какие знания мы применяли для решения данных выражений?
Выполняя упрощение выражений использовали тригонометрические тождества и формулы сокращенного умножения.
Б) Доказать тождество:
? В чем отличие тождества от формулы?
Тождество – равенство двух аналитических выражений, справедливых для любых допустимых значений входящих в него букв.
Формула – комбинация математических знаков и букв, выражающая какое-либо предложение
1. 

2. 

3. 


? Что необходимо для успешного выполнения преобразований тригонометрических выражений?
Свободное владение тригонометрическими тождествами и формулами сокращенного умножения.
IV. Работа с учебником
Дано: 
Найти: 
Решение:

V. Итог урока
Учащиеся под руководством учителя анализируют работу на уроке, делают выводы, оценивают работу товарищей.
VI. Постановка домашнего задания.
Пока мы размышляли над проблемой О тождествах, возможностях его. Истек лимит наш, и прощаться с темой грядет минута. Жаль. Звенит звонок.
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Тема урока: "Преобразование тригонометрических выражений"

Разделы: Математика
Цели урока:
- Систематизировать и обобщить знания о тригонометрических выражениях, опираясь на числовые окружности;
- Развивать вычислительные навыки, творческое мышление, оригинальность мышления;развивать умения критически анализировать ситуации, навыки самоконтроля;создавать для учащихся ситуации критической самооценки.
- подготовка к ЕГЭ.
Оборудование:1) набор перфокарт для индивидуальной работы.
Ход урока
Тема нашего урока: “Преобразование тригонометрических выражений”. Задача:обобщить и систематизировать материал по данной теме и выявить основные недочеты и трудности, над которыми надо еще поработать.
План урока:
- Опрос по индивидуальным перфокартам.
- Тест.
- Развивающие задания.
- Работа в группах.
- Индивидуально-дифференцированная работа.
- Диагностика учащихся по данной теме.
- Рефлексия.
Девиз урока: ”Не берись за новое, не усвоив предыдущего”.
Обращаю ваше внимание, ребята на то, что все факты, связанные с тригонометрией не нужно запоминать наизусть, а достаточно понимать, где искать их на числовой окружности. Это и основное тригонометрическое тождество: sin? a +cos?a=1. (и все производные формулы), это и знаки тригонометрических функций по четвертям, все основные значения тригонометрических функций, это и решения всех простых уравнений.
I. Блиц-опрос по индивидуальным перфокартам.
Цель: проверка умений работать устно по единичной окружности.
Анализ работы. Результаты блиц – опроса ребята отмечают в листе учёта.
II. Вводный тест. (индивидуальный)
Цель: проверка вычислительных навыков.
Двое учащихся решают с обратной стороны доски для дальнейшей быстрой проверки.
| I вариант | II вариант |
| А1. Вычислите:
1) 1 2) -1 3) -2 4) 2 |
А1. Вычислите: sin 2 450 + cos 600 + ctg 2 300 1) 3 2) 4 3) – 4 4) 2 |
| A2. Вычислите:
1) 4 2) 3 3) 2 4) 1 |
А2. Вычислите:
1) 1 2) 3 3) 2 4) -2 |
| А3. Найдите значение выражения: 14sin 2 x – 3, если cos 2 x= 0, 7 1) 2, 2 2) -1, 2 3) 1, 2 4) -2, 2 |
А3. Вычислите cosx, если sinx = 1) -0, 6 2) -0, 5 3) 0, 6 4) 1, 5 |
| А4. Вычислите: sin 75 0 1) v2 2) |
А4. Вычислите:  1) 6 2) 8 3) 4 4) 5 |
В1. Вычислите:  |
В1. Вычислите:
|
Анализ работы по тестам. Результаты ребята отмечают в листах учёта. Задаю вопросы: какие задания вызвали особые трудности, какой материал необходим для того , чтобы хорошо научиться решать эти задания, что особенно понравилось.
На 20 мин. – развивающие задания.
3) Развивающий канон – это элемент интеллектуальной игры, составленный из шести элементов, связанных между собой логическими связями. Например,
 |
- сos ( |
2) Проанализируйте следующие последовательности, выявите закономерность и продолжите запись:
 .
.
3) Известно, что  Найдите
Найдите  . Проанализируйте задание.
Хватает ли данных в условии задачи?
. Проанализируйте задание.
Хватает ли данных в условии задачи?
| 4) Развивающий канон: |  |
- - arcsin x |
Arcsin a = x - x Є [  |
|
Arccos a = x - x Є [ 0; ] ] |
|
| Arcctg a = x - ? | Ответ: (0; ) ) |
5) Работа в группах. Учащимся предлагаются карточки. Свободный выбор.
- карточка “консультант” -ребята решают по образцу;
- карточки для самостоятельного решения (часть “А”) ;
- карточки для самостоятельного решения (часть “В” и часть “С”)
А5. Вычислите  |
А6. Вычислите  |
А7. Найдите  |
В2. Найдите 50 sin 2x, если cos x = -  |
Анализ работы в группах. Результаты отмечают ребята в листах учёта.
Индивидуально- дифференцированная работа.
На “3”:
1) Упростите выражение: 
1) 1+ сos 2) 2 3) -12 4) 12.
2) 2 3) -12 4) 12.
2) Вычислите 2 – tg ?x
1) 1, 2 2) 1, 96 3) 1, 04 4) 1, 6
3) Вычислите cos x, если 
1) – 0, 6 2) 0, 6 3) 1, 6 4) – 1, 6.
На “4”:
4) Вычислите  ;
;
5) Найдите значение выражения: 6
На “5”:
6) Вычислите: 
7) Дополнительные задания:
а) Какое общее название у объектов, входящих в эту группу?
у = sinx, y = cosx, y = tgx, y = ctgx. (Это тригонометрические функции).
б) Найдите лишнее: tgx, arcsinx, cosx, sinx. (arcsin x т. к – это обратная тригонометрическая функция)
в) Придумайте задание по тригонометрии для своего соседа по парте.
г) Вычислите 50sin2 , если cos
, если cos =
=  ,
, 
 . Посмотрите нет ли лишних данных в
условии задачи?
. Посмотрите нет ли лишних данных в
условии задачи?
8) В конце урока каждый учащийся проводит самодиагностику с использованием кодификатора Нужно отметить в таблице своё отношение:
* -в повторении не нуждаюсь, знаю хорошо;
** - нужно напомнить на следующем уроке способ деятельности(алгоритм), еще раз обсудить;
*** - трудно, хочу решить подобную задачу в классе.
| Задания | * | ** | *** |
| 1) Нахождение значений
тригонометрических выражений:
|
|||
| 2) Преобразование тригонометричеcких
выражений: 5sin
|
|||
| 3) Для преобразования выражений
использую формулы: а) основное тригонометрическое тождество:
б) произведение тангенса и котангенса одного и того же аргумента: tgx в) зависимость между тангенсом и косинусом одного и того же аргумента:
г) зависимость между ctgx и sinx:
|
|||
| 4) Использую формулы сложения: а) синус суммы: sin(x+y) =sinx б) синус разности:
в) косинус суммы:
г) косинус разности:
|
|||
| 5) Использую следствия из формул
сложения: а) sin 2 б) cos2 1-2sin2 в) |
|||
Подводим итоги по листам учёта.
Учащиеся сами оценивают.
“Сегодня на уроке математики…”, “Мне понравилось…”, “Хочу предложить …”.
Ваши ассоциации при изучении темы “Преобразование тригонометрических выражений ”.
ТерпениеРадостьИнтересноГ ОкружностьНравитсяО М ЕГЭТрудолюбиеРеальноИ Ясно
Лист учёта
Фамилия, имя _____________________________________________________________
| Этапы | Кто оценивает | наибольшее кол-во баллов |
| 1. Блиц опрос. | Взаимопроверка в парах. | 11 |
| 2. Вводный тест. | самооценка | 5 |
| 3. Работа в группах: а) часть “А” б) часть “В” в) часть “С” |
консультант | 1 2 3 |
| 4. Индивидуально-дифференцированная
работа: а) на “3” б) на “4” в) на “5” |
учитель | 3 4 5 |
| 5. Дополнительные задания. | учитель | 1 |
| 6. Работа в классе по развивающим заданиям. | учитель | 1 |
| 7. Итого | ||
| 8. Оценка. | ||
| Критерии оценок: На “5”- 33-36 баллов; На “4”- 20- 32 баллов; На “3”- 12-19 баллов. |
xn--i1abbnckbmcl9fb.xn--p1ai
Урок. "Преобразование тригонометрических выражений."
Тема урока: Преобразование тригонометрических выражений.
- обобщить теоретический материал по теме тригонометрические тождества, формировать умения применять основные тригонометрические тождества для преобразования тригонометрических выражений.
- развитие зрительной памяти, познавательной активности, творческих способностей.
- воспитывать интерес к предмету.
Делу обучиться – всегда пригодиться.
Русская пословица.
Ход урока:
Организационный момент.
Актуализация опорных знаний (записать на доске)
А) - формулы для  ;
;
- основное тригонометрическое тождество;
- формулу, выражающую зависимость  и
и 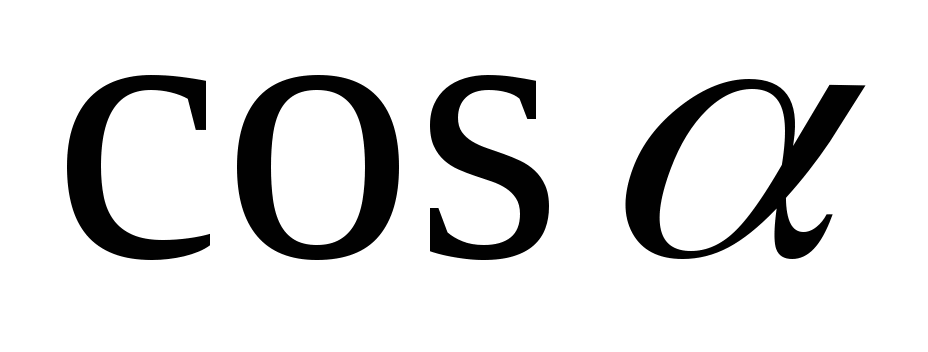 ;
;
- формулу, выражающую зависимость  и
и  .
.
Б) упростить выражения (устно)
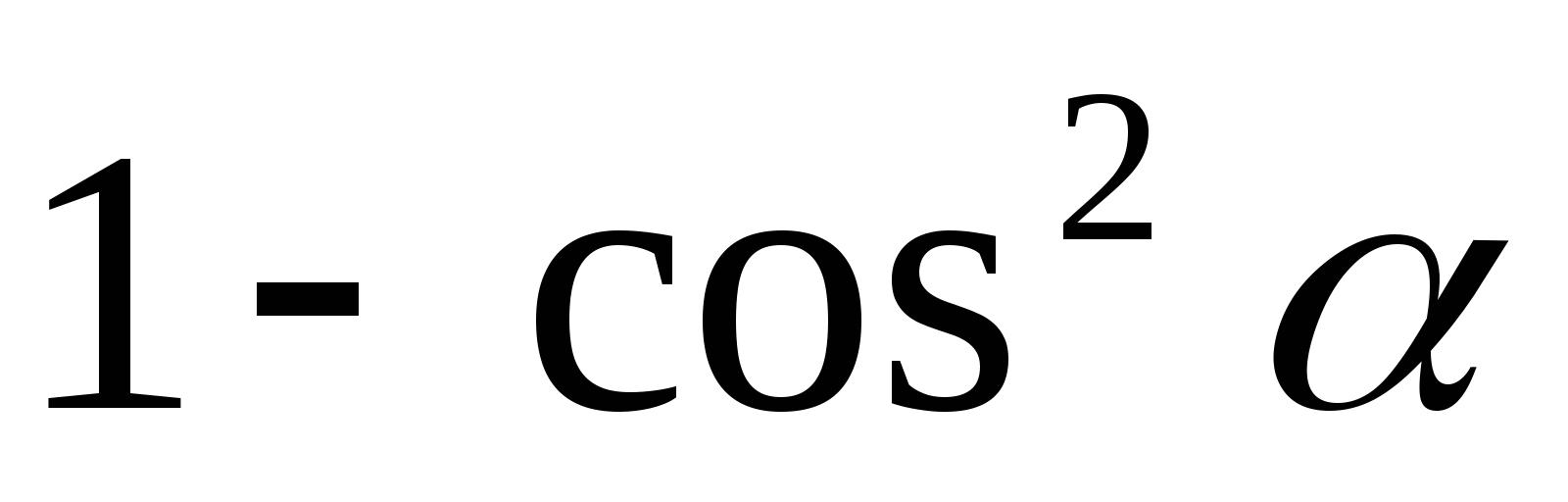

Мудрым никто не родился, а научился
Русская пословица
Работа в тетрадях:
А) упростить выражение:
Решение:

Решение:
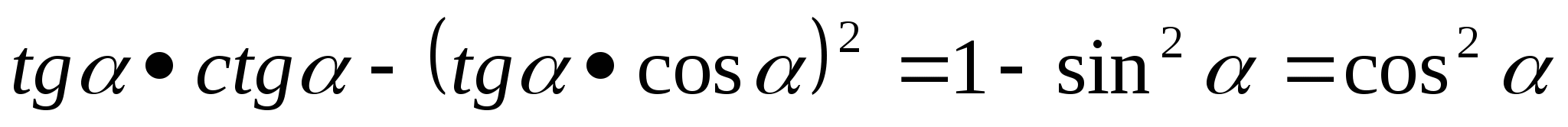
Решение:
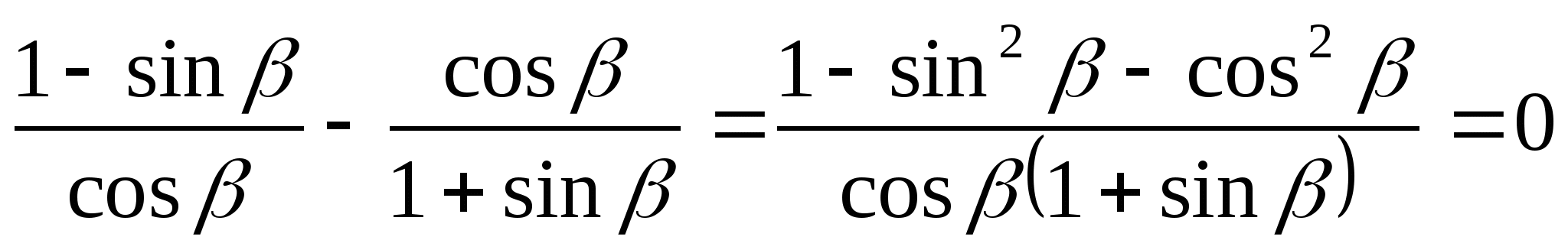
? Какие знания мы применяли для решения данных выражений?
Выполняя упрощение выражений использовали тригонометрические тождества и формулы сокращенного умножения.
Б) Доказать тождество:
? В чем отличие тождества от формулы?
Тождество – равенство двух аналитических выражений, справедливых для любых допустимых значений входящих в него букв.
Формула – комбинация математических знаков и букв, выражающая какое-либо предложение.
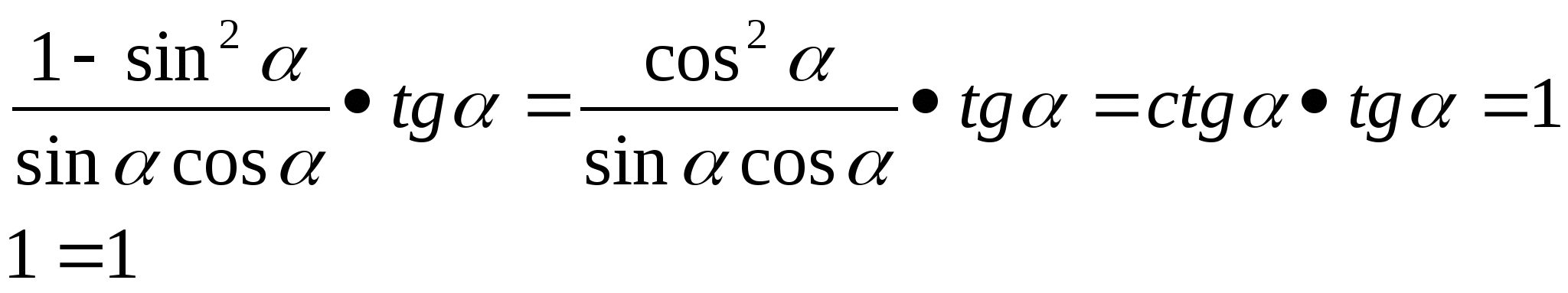
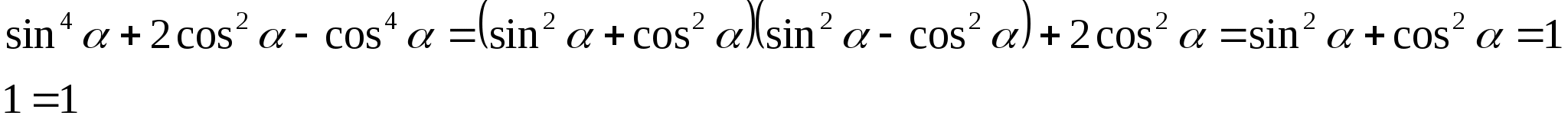
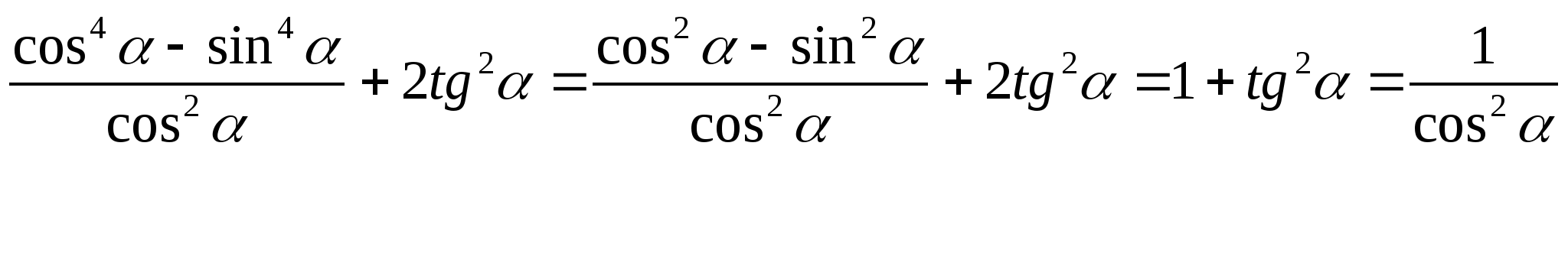
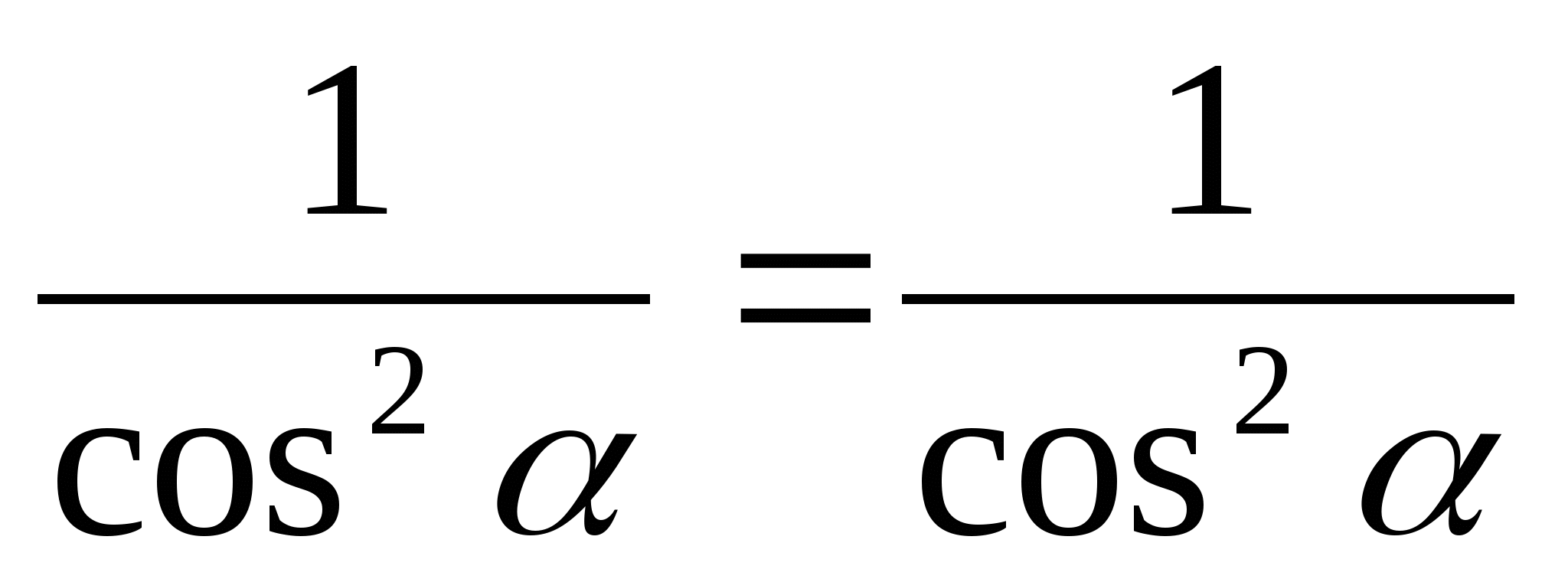
? Что необходимо для успешного выполнения преобразований тригонометрических выражений?
Свободное владение тригонометрическими тождествами и формулами сокращенного умножения.
Работа с учебником.
Дано: 
Найти: 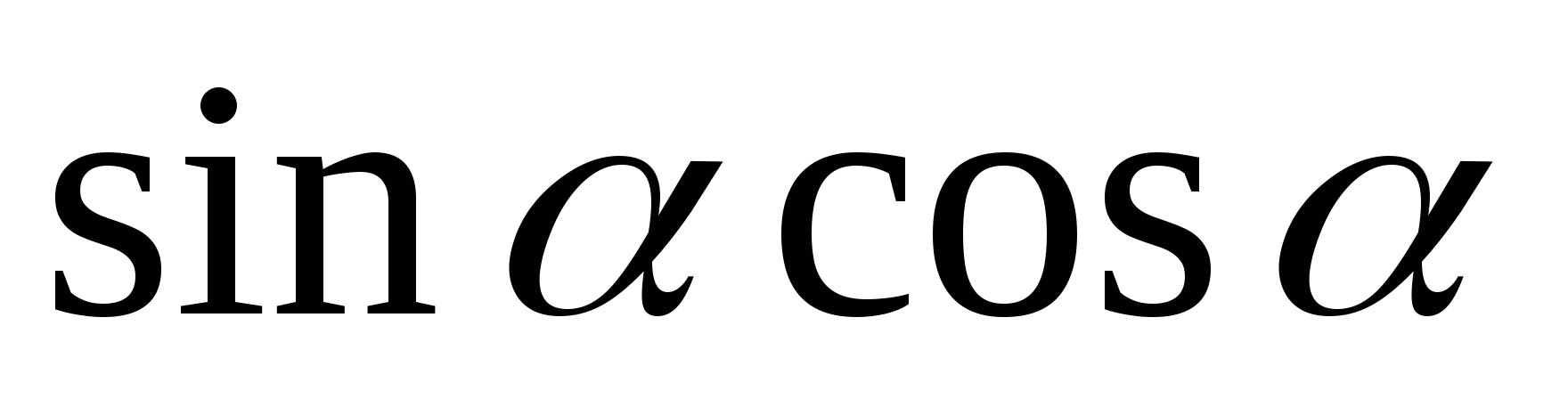
Решение:
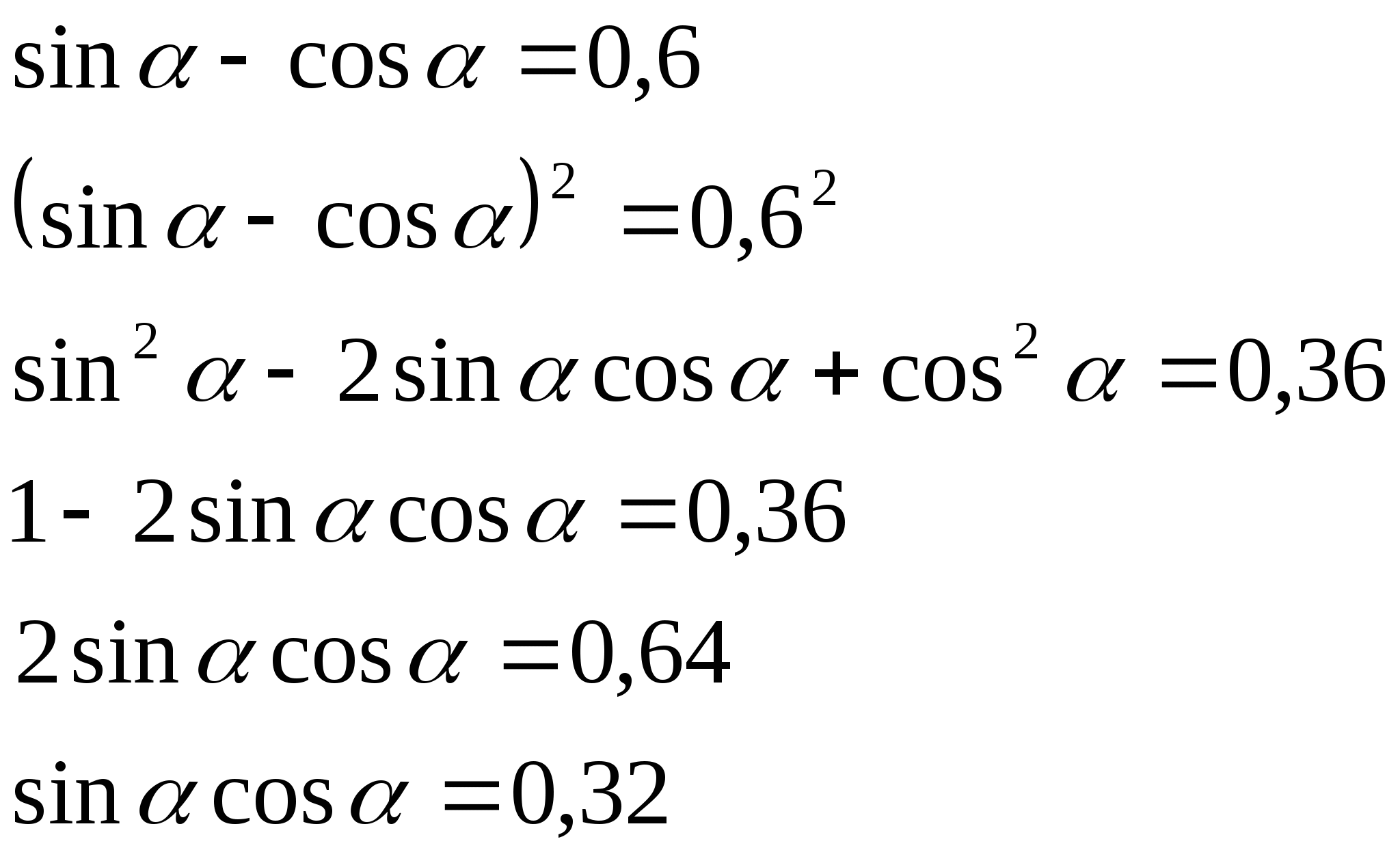
Итог урока: Учащиеся под руководством учителя анализируют работу на уроке, делают выводы, оценивают работу товарищей.
Постановка домашнего задания.
Пока мы размышляли над проблемой
О тождествах, возможностях его.
Истек лимит наш, и прощаться с темой
грядет минута.
Жаль. Звенит звонок.
infourok.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|












 0+2sin300
+
0+2sin300
+  tg 2
600-ctg 450
tg 2
600-ctg 450


 3) v3 4)
3) v3 4) 


 ;
; и
т. д.
и
т. д. 
 ;
; ;
; .
.  ;
;


 ;
;