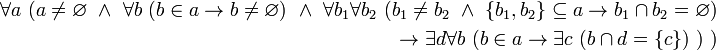|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Аксиоматика теории множеств. Реферат на тему парадокс теории множеств бар
Реферат Парадокс брадобрея
 Опубликовать
ОпубликоватьРеферат на тему:
План:
- Введение
- 1 Варианты формулировок ЛитератураПримечания
Введение
Парадокс Рассела — открытый в 1903 году Бертраном Расселом и позднее независимо переоткрытый Э. Цермело теоретико-множественный парадокс, демонстрирующий противоречивость логической системы Фреге, являвшейся ранней попыткой формализации наивной теории множеств Г. Кантора.
Парадокс Рассела формулируется следующим образом:
Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли K само себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие. Если нет — то, по определению K, оно должно быть элементом K — вновь противоречие.
Противоречие в парадоксе Рассела возникает из-за использования в рассуждении внутренне противоречивого[1] понятия множества всех множеств и представления о возможности неограниченного применения законов классической логики при работе с множествами. Для преодоления этого парадокса было предложено несколько путей. Наиболее известный состоит в предъявлении для теории множеств непротиворечивой формализации , по отношению к которой являлись бы допустимыми все «действительно нужные» (в некотором смысле) способы оперирования с множествами. В рамках такой формализации утверждение о существовании множества всех множеств было бы невыводимым.
Действительно, допустим, что множество U всех множеств существует. Тогда, согласно аксиоме выделения, должно существовать и множество K, элементами которого являются те и только те множества, которые не содержат себя в качестве элемента. Однако предположение о существовании множества K приводит к парадоксу Рассела. Следовательно, ввиду непротиворечивости теории , утверждение о существовании множества U невыводимо в этой теории, что и требовалось доказать.
В ходе реализации описанной программы «спасения» теории множеств было предложено несколько возможных её аксиоматизаций (теория Цермело — Френкеля ZF, теория Неймана — Бернайса — Гёделя NBG и т. д.), однако ни для одной из этих теорий до настоящего момента не найдено доказательства непротиворечивости. Более того, как показал Гёдель, разработав ряд теорем о неполноте, такого доказательства не может существовать (в некотором смысле).
Другой реакцией на открытие парадокса Рассела явился интуиционизм Л. Э. Я. Брауэра.
1. Варианты формулировок
Существует много популярных формулировок этого парадокса. Одна из них традиционно называется парадоксом брадобрея и звучит так:
Одному деревенскому брадобрею приказали «брить всякого, кто сам не бреется, и не брить того, кто сам бреется», как он должен поступить с собой?Еще один вариант:
В одной стране вышел указ: «Мэры всех городов должны жить не в своем городе, а в специальном Городе мэров», где должен жить мэр Города мэров?И ещё один:
Некая библиотека решила составить библиографический каталог, в который входили бы все те и только те библиографические каталоги, которые не содержат ссылок на самих себя. Должен ли такой каталог включать ссылку на себя?Литература
- Курант Р., Роббинс Г. Что такое математика? — гл. II, § 4.5
- Мирошниченко П. Н. Что же разрушал парадокс Рассела в системе Фреге? // Современная логика: проблемы теории, истории и применения в науке. — СПб., 2000. — С. 512—514.
- Катречко С. Л. Расселовский парадокс брадобрея и диалектика Платона — Аристотеля // Современная логика: проблемы теории, истории и применения в науке. — СПб., 2002. — С. 239—242.
- Мартин Гарднер А ну-ка, догадайся! = Aha! Gotcha. Paradoxes to puzzle and delight. — М.: Мир, 1984. — С. 22-23. — 213 с.
Примечания
- Френкель А.А, Бар-Хиллел И. Основания теории множеств / А.А. Френкель, И. Бар-Хиллел. – М.: Мир, 1966. – C. 17-18
Категории: Теоремы, Теория множеств, Математические парадоксы.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
Реферат Аксиоматика теории множеств
скачатьРеферат на тему:
План:
- Введение
- 1 Аксиомы ZFC
- 2 Пояснение к аксиомам ZFC
- 3 Примечания
- 4 Историческая справка Литература
Введение
Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, — из которых выводятся все теоремы и утверждения теории множеств.
Система аксиом Цермело—Френкеля (ZF) является стандартной системой аксиом для теории множеств. Эта и подобные ей системы аксиом любопытны потому, что любая математическая теория может быть «переведена» на язык теории множеств таким образом, что теоремы этой теории станут теоремами о множествах, доказуемыми из аксиом ZF (любой объект можно считать множеством, соответственно и переформулировать утверждение не представляет собой проблему).
К этой системе аксиом часто добавляют аксиому выбора, и называют системой Цермело — Френкеля с аксиомой выбора (ZFC).
Эта система аксиом записана на языке логики первого порядка, и содержит бесконечное количество аксиом. Существуют и другие, конечные системы. Например, система NBG (von Neumann — Bernays — Godel) наряду с множествами рассматривает так называемые классы объектов. NBG равносильна ZF в том смысле, что любая теорема о множествах (то есть не упоминающая о классах), доказуемая в одной системе, также доказуема и в другой.
1. Аксиомы ZFC
Аксиомами ZFC называется следующая совокупность высказываний теории множеств:
2. Пояснение к аксиомам ZFC
Аксиомы ZFC включают в себя:
0) группу высказываний о равенстве множеств (1 аксиома),
1) группу высказываний о существовании множеств (2 аксиомы),
2) группу высказываний об образовании множеств из уже имеющихся множеств (3 аксиомы и 2 схемы), в которой можно выделить три подгруппы,
3) группу высказываний об упорядоченности образованных множеств (2 аксиомы).
0. Критерий равенства множеств в ZFC
Следующее высказывание выражает необходимое условие идентичности двух множеств.
Аксиома экстенсиональности (Аксиома объёмности)
Примечание
«Аксиому объёмности» можно сформулировать следующим образом: «Если каждый элемент первого множества принадлежит второму множеству, а каждый элемент второго множества принадлежит первому множеству, тогда первое множество идентично второму [множеству].»
Достаточное условие идентичности двух множеств имеет вид и выводится из аксиом предиката
, а именно:
Соединение указанного достаточного условия [идентичности множеств] с аксиомой объёмности даёт следующий критерий равенства множеств:
1. Аксиомы ZFC о существовании множеств
«Аксиома объёмности» была бы бесполезным высказыванием, если бы не существовало ни одного множества или существовало только одно множество.
Следующие два высказывания гарантируют существование по меньшей мере двух разных множеств, а именно: а) множества, в котором нет ничего, и б) множества, содержащего бесконечное количество элементов.
1.0 Аксиома пустого множества
Примечание
«Аксиому [существования] пустого множества» можно сформулировать следующим образом: «Существует [по меньшей мере одно] множество без единого элемента.»
Доказывается, что «аксиома пустого множества» равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя. Употребительны два имени:
и
. Используя указанные имена, «аксиому пустого множества» записывают так:
1.1 Аксиома бесконечности
Примечание
«Аксиому бесконечности» можно сформулировать следующим образом: «Существует [по меньшей мере одно] „бесконечное множество“, которое состоит из .»
Высказывание о существовании бесконечного множества отличается от (ложного в данной аксиоматике) высказывания о существовании «множества всех множеств» ().
2. Аксиомы ZFC об образовании множеств
Следующие пять высказываний можно назвать аксиомами образования множеств [из имеющихся множеств, включая и по меньшей мере одну
].
Каждое из этих пяти высказываний создано на основе высказывания , которое выводится из аксиом предиката
.
Эти пять высказываний можно объединить в следующие подгруппы:
2.0) группу постулатов об образовании множеств путём перечисления их элементов,
2.1) группу деклараций об учреждении и об упразднении семейств множеств,
2.2) группу схем образования множеств с помощью математически корректных суждений.
2.0. Постулаты об образовании множеств путём перечисления их элементов
Простейший способ образовать новое множество [из уже имеющихся множеств] состоит в том, чтобы «ткнуть пальцем» в каждое множество, которое должно стать элементом [образуемого множества]. В ZFC указанный способ образования множеств представлен одной аксиомой, в которой «тыканье пальцем» моделируется с помощью предиката .
2.0 Аксиома пары
Примечание
«Аксиому [неупорядоченной] пары» можно сформулировать следующим образом: «Из любых двух множеств можно образовать „неупорядоченную пару“, то есть такое множество , каждый элемент
которого идентичен данному множеству
или данному множеству
».
Доказывается, что «аксиома пары» равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя
. Используя указанное имя, «аксиому пары» записывают так:
2.1. Декларации об учреждении и об упразднении семейств множеств
Следующие две аксиомы, именуемые «аксиомой множества подмножеств» и «аксиомой объединения», можно рассматривать как естественное дополнение к «аксиоме пары». Чтобы убедиться в этом, заметим следующее.
Известно, что каждое множество имеет подмножества, включая [копию пустого множества]
и [копию самого множества]
. Иначе говоря,
Руководствуясь «аксиомой пары», из названных подмножеств можно образовать неупорядоченную пару . Назовём эту пару семейством
.
Если можно образовать семейство из двух подмножеств множества
, тогда можно объявить об образовании семейства
из всех подмножеств множества
.
Если можно объявить об учреждении семейства , тогда можно объявить об упразднении названного семейства.
Из изложенного следует, что высказывания и
можно считать независимыми условно.
2.1.0 Аксиома множества подмножеств (Аксиома булеана)
Примечание
«Аксиому множества подмножеств» можно сформулировать следующим образом: «Из любого множества можно образовать „суперкучу“, то есть такое множество , каждый элемент
которого является [собственным либо несобственным] подмножеством
данного множества
.»
Доказывается, что «аксиома множества подмножеств» равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя
, которое произносится: «множество всех подмножеств [множества]
» или «булеан [множества]
». Используя указанное имя, «аксиому множества подмножеств» записывают так:
2.1.1 Аксиома объединения
Примечание
Аксиому объединения [множеств] можно сформулировать следующим образом: «Из любого семейства множеств можно образовать „кучу-малу“, то есть такое множество , каждый элемент
которого принадлежит по меньшей мере одному множеству
данного семейства
».
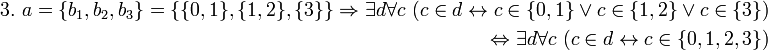
Доказывается, что аксиома объединения равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя
, которое произносится: «объединение множеств семейства
». Используя указанное имя, аксиому объединения записывают так:
Объединение множеств семейства (
) не следует путать с пересечением множеств семейства
(
), о котором известно:
2.2. Схемы образования множеств с помощью математически корректных суждений
Среди математических высказываний встречаются аксиомы связи, включая:
а) аксиому связи между алгебраической операцией (сложить) и алгебраической операцией
(умножить)
б) аксиому связи между отношением порядка (меньше или равно) и алгебраической операцией
(сложить)
Следующие два высказывания, именуемые «схемой выделения» и «схемой преобразования», являются аксиомами связи между множествами (например, множеством ) и математически корректными суждениями (например, суждением
).
«Схема выделения» и «схема преобразования» выражают следующую простую мысль: «Каждое математически корректное суждение об элементах любого множества приводит к образованию [того же самого или другого] множества.»
Математически корректные суждения, фигурирующие в «схеме выделения», позволяют «довести [до товарного вида]» множества, которые образованы, например, с помощью аксиомы булеана. Поэтому указанные математические суждения аналогичны штихелям, надфелям, часовым отвёрткам и иным доводочным инструментам.
Математически корректные суждения, фигурирующие в «схеме преобразования», позволяют создавать «[математические] изделия» из ["неотёсанных"] множеств, образованных, например, с помощью аксиомы булеана. Поэтому указанные математические суждения аналогичны прецизионным станкам.
2.2.0 Схема выделения
Примечание
Схему выделения [подмножеств] можно сформулировать следующим образом: «Из каждого множества можно выделить [по меньшей мере одно] подмножество , высказав суждение
о каждом элементе
данного множества
.»
![\begin{align} 6. \
(\Phi[x] \leftrightarrow \exist k \ (k \in \mathbb{N} \land x = 2k)) \land a = \mathbb{N} \Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathbb{N} \land \exist k \ (k \in \mathbb{N} \land b = 2k))
\\ \
\Leftrightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \{0,2,4,6,...\})
\end{align}](/800/600/http/upload.wikimedia.org//math/b/0/7/b0727116ef47508606afb1be6ff1f495.png)
![\begin{align} 7. \
(\Phi[x] \ \leftrightarrow \ \exist u \exist v \ (u \in U \ \land \ v \in V \ \land \ x = (u,v) \ ) \ ) \quad \land \quad a = \mathcal{P}(\mathcal{P}(U \cup V))
\\ \
\Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathcal{P}(\mathcal{P}(U \cup V)) \ \land \ \exist u \exist v \ (u \in U \land v \in V \land b = (u,v)))
\end{align}](/800/600/http/upload.wikimedia.org//math/4/1/c/41c0a6d82a7a120016a40d2ccbd327d4.png)
Доказывается, что схема выделения равносильна высказыванию . Поэтому единственному подмножеству
можно присвоить имя
. Используя указанное имя, схему выделения записывют так:
Схема выделения равносильна счётному множеству аксиом.
2.2.1 Схема преобразования
Примечание
Схему преобразования [множеств] можно сформулировать следующим образом: «Любое множество можно преобразовать в [то же самое или другое] множество , высказав любое истинное математически корректное функциональное суждение
обо всех элементах
данного множества
.»
![\begin{align} 2. \
(\phi[x,y] \leftrightarrow y = x^2) \ \land \ a = \{1,2,3\} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \{1,2,3\} \ \land \ c = b^2))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{1,4,9\})
\end{align}](/800/600/http/upload.wikimedia.org//math/2/4/2/2425aa016eef88362a816f214f6f0705.png)
![\begin{align} 4. \
(\phi[x,y] \leftrightarrow (x = \varnothing \to y = a_1) \land (x \ne \varnothing \to y = a_2) \ ) \quad \land \quad a = \mathcal{P}(\mathcal{P}(\varnothing)) = \{\varnothing, \{\varnothing\}\}
\\ \
\Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \{\varnothing, \{\varnothing\}\} \land (b = \varnothing \to c = a_1) \land (b \ne \varnothing \to c = a_2)\ ))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c = a_1 \ \lor \ c = a_2)
\end{align}](/800/600/http/upload.wikimedia.org//math/c/5/b/c5bb14b0c297a15d1137ccc22ec6826f.png)
![\begin{align} 5. \
(\phi[x,y] \leftrightarrow y = 2x) \ \land \ a = \mathbb{N} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \mathbb{N} \land c = 2b))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{0,2,4,6,...\})
\end{align}](/800/600/http/upload.wikimedia.org//math/3/0/f/30f0f864a1e171c485838d5c6059450e.png)
![\begin{align} 6. \
(\phi[x,y] \leftrightarrow y = 2x + 1) \ \land \ a = \mathbb{N} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \mathbb{N} \land c = 2b + 1))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{1,3,5,7,...\})
\end{align}](/800/600/http/upload.wikimedia.org//math/6/3/1/6316623a316fcedfb05a300077fb3cf8.png)
![\begin{align} 7. \
(\phi[x,y] \leftrightarrow (x \in \mathbb{N} \ \land \ x < 2 \to y = x) \ \land \ (x \in \mathbb{N} \ \land \ \neg (x < 2) \to y = 1)) \quad \land \quad a = \mathbb{N}
\\ \
\Rightarrow \exist d \forall c (c \in d \leftrightarrow \exist b (b \in \mathbb{N} \ \land \ (b \in \mathbb{N} \land b < 2 \to c = b) \ \land \ (b \in \mathbb{N} \land \neg (b < 2) \to c = 1)))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \mathbb{N} \ \land \ c < 2) \Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{0,1\})
\end{align}](/800/600/http/upload.wikimedia.org//math/8/9/6/8965999f79908556c163beba8eb3c331.png)
Доказывается, что в схеме преобразования множество единственно. Поэтому указанному множеству можно присвоить имя
. Используя указанное имя, схему преобразования записывают так:
Схема преобразования равносильна счётному множеству аксиом.
3. Аксиомы ZFC об упорядоченности множеств
Следующие два высказывания определяют упорядоченность множеств, которые образованы из и каждой
с помощью аксиом образования множеств. Образно говоря, высказывания об упорядоченности множеств образуют «сортировочный цех» теории ZFC, тогда как высказывания об образовании множеств образуют «производственный цех» этой теории.
3.0 Аксиома регулярности
Примечание
«Аксиому регулярности» можно сформулировать следующим образом: «В любом семействе множеств есть [по меньшей мере одно] множество , каждый элемент
которого не принадлежит данному семейству
.»
 Сравните с высказываниями
Сравните с высказываниями  Сравните с высказываниями
Сравните с высказываниями 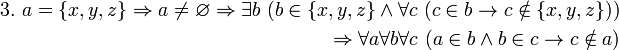 Сравните с высказываниями
Сравните с высказываниями 3.1 Аксиома выбора
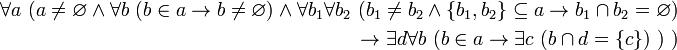
Примечание
«Аксиому выбора» можно сформулировать следующим образом: «Из любого семейства непустых попарно непересекающихся множеств можно выбрать „делегацию“, то есть такое множество , в котором есть по одному элементу
от каждого множества
данного семейства
.»
3. Примечания
1. Непротиворечивость аксиоматики ZFC не установлена.
4. Историческая справка
По-видимому, первоначальный вариант теории множеств, умышленно названный немецким математиком Георгом Кантором учением о множествах, состоял из двух аксиом, а именно:
1) аксиомы объёмности«Аксиома математической свободы» имеет рациональные следствия, включая следующие:
В 1903 году английский философ Бертран Рассел обратил внимание на следующее:
1) руководствуясь «аксиомой математической свободы», невозможно отличить «свободу» от «вседозволенности», 2) выбрав в качествеЭти критические высказывания о «немецком учении [о множествах]» побудили немецкого математика Эрнста Цермело заменить «аксиому математической свободы» такими её следствиями, которые не вызывали бы протеста ни у математиков, ни у философов.
В 1908 году в журнале Mathematische Annalen Эрнст Цермело опубликовал следующие семь аксиом:
1) Axiom der Bestimmtheit, то есть аксиому объёмности, 2) Axiom der Elementarmengen, то есть аксиому о существовании «элементарных множеств»Так «учение о множествах» превратилось в теорию множеств, а именно в теорию ZC [Zermelo set theory with the Axiom of Choice].
Последняя аксиома теории ZC (аксиома бесконечности) сблизила сторонников Георга Кантора со сторонниками Леопольда Кронекера, которые рассматривали множество натуральных чисел как священный грааль математики.
Предпоследняя аксиома теории ZC (аксиома выбора) стала предметом оживлённых математических дискуссий. Действительно, эта аксиома не является следствием «аксиомы математической свободы».
В 1922 году немецкий математик Абрахам Френкель и норвежский математик Торальф Сколем (Thoralf Skolem) дополнили теорию ZC схемой преобразования. В результате теория ZC превратилась в теорию ZFC [Zermelo-Fraenkel set theory with the Axiom of Choice].
В 1925 году венгерский математик Джон фон Нейман дополнил теорию ZFC аксиомой регулярности. Одно из следствий этой аксиомы () «похоронило» и «множество всех множеств», и «парадокс Рассела».
Литература
- Колмогоров А. Н., Драгалин А. Г. Математическая логика. — М.: УРСС, 2005. — 240 с.
- Френкель А. А., Бар-Хиллел И. Основания теории множеств. — М.: Мир, 1966. — 556 с.
- Аксиоматика теории множеств - planetmath.org/encyclopedia/ZermeloFraenkelAxioms.html (англ.) на сайте PlanetMath.
wreferat.baza-referat.ru
Парадоксы теории множеств | Мировая экономика
Основано на информация википедии, в частности статьи Кризис оснований математики, Парадокс Рассела, Парадокс Кантора, Парадокс Бурали-ФортиТеоретико-множественный подход, получивший широкое развитие в конце XIX века, позволил возвести математику на прочном, и, казалось, надежном фундаменте — канторовой теории множеств. Развитие канторовой теории множеств привело к возможности выразить в терминах этой теории все основные математические понятия. Возможность построения математики на теоретико-множественном фундаменте Гильберт охарактеризовал как «рай для математиков», а уже построенную на этой основе часть математики называл «симфонией бесконечного». Однако восторги сменились шоковым состоянием, когда была обнаружена противоречивость данного подхода.
Ниже есть продолжение.На рубеже XIX—XX веков были открыты так называемые парадоксы теории множеств. Сущность парадокса заключается в том, что с помощью логически правильных рассуждений удаётся обосновать (доказать средствами данной теории) одновременно некоторое утверждение и его отрицание, то есть противоречие.
С целью избежания некоторых парадоксов было предложено ограничить принцип свёртывания — широко распространённой математической конструкции, позволяющей образовывать множества с помощью тех или иных свойств объектов.
Принцип свёртывания заключается в том, что для любого свойства P считается существующим множество, состоящее из тех и только тех объектов, которые обладают свойством P.
В ограниченном принципе свёртывания, к условию P(x) добавляется условие, согласно которому элементы M берутся из некоторого заданного множества E, существование которого выведено из некоторого («надёжного») списка аксиом.
Однако даже полное избавление от обнаруженных парадоксов не спасает и не страхует теорию множеств от новых парадоксов. Поэтому по-прежнему оставалась актуальной задача «спасения» математики. Фактически перед математиками стояла задача переосмысления логических средств, используемых в математических рассуждениях, надежности этих средств и соответствия их существу математики. Гарантировать невозможность противоречий в математической теории могло лишь доказательство непротиворечивости этой теории.
Приведём в качестве примеров три парадокса.
Парадокс Рассела. Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли K само себя в качестве элемента? Если предположить, что содержит, то мы получаем противоречие с "Не содержат себя в качестве своего элемента". Если предположить, что K не содержит себя как элемент, то вновь возникает противоречие, ведь K — множество всех множеств, которые не содержат себя в качестве своего элемента, а значит должно содержать все возможные элементы, включая и себя.
Противоречие в парадоксе Рассела возникает из-за использования в рассуждении внутренне противоречивого понятия множества всех множеств и представления о возможности неограниченного применения законов классической логики при работе с множествами. Для преодоления этого парадокса было предложено несколько путей. Наиболее известный состоит в предъявлении для теории множеств непротиворечивой формализации M, по отношению к которой являлись бы допустимыми все «действительно нужные» (в некотором смысле) способы оперирования с множествами. В рамках такой формализации утверждение о существовании множества всех множеств было бы невыводимым.
Парадокс Кантора — парадокс теории множеств, который демонстрирует, что предположение о существовании множества всех множеств ведёт к противоречиям и, следовательно, противоречивой является теория, в которой построение такого множества возможно.
Предположим, что множество всех множеств V существует. В этом случае справедливо, что всякое множество t является подмножеством V. Но из этого следует, что мощность любого множества t не превосходит мощности V, т.е. $|P (V)|<=|V|$
С другой стороны для V, как и любого множества, существует множество всех подмножеств P(V), и по теореме Кантора $|P (V)| = 2^{|V|} > |V|$, что противоречит предыдущему утверждению. Следовательно, V не может существовать, что вступает в противоречие с «наивной» гипотезой о том, что любое синтаксически корректное логическое условие определяет множество.
Другая формулировка парадокса Кантора: Не существует максимального кардинального числа. В самом деле: пусть оно существует и равно $\mu$. Тогда по теореме Кантора $2^\mu > \mu$, т.е. мы построили кардинальное число больше, чем $\mu$, в противоречии с тем, что это максимум.
Этот парадокс, открытый Кантором около 1899 года, обнаружил необходимость пересмотра «наивной теории множеств» (парадокс Рассела был открыт несколько позднее, около 1901 года).
Парадокс Бурали-Форти демонстрирует, что предположение о существовании множества всех порядковых чисел ведёт к противоречиям и, следовательно, противоречивой является теория множеств, в которой построение такого множества возможно.
Можно доказать, что если x — произвольное множество порядковых чисел, то множество-сумма $\cup x$ есть порядковое число, большее или равное каждому из элементов x. Предположим теперь, что $\Omega$ — множество всех порядковых чисел. Тогда $\cup \Omega$ — порядковое число, большее или равное любому из чисел в $\Omega$. Но тогда и $\cup \Omega \cup \{\cup \Omega\} = \cup \Omega + 1$ — порядковое число, причём уже строго большее, а значит, и не равное любому из чисел в $\Omega$. Но это противоречит условию, по которому $\Omega$ — множество всех порядковых чисел.
Парадокс был обнаружен Чезаре Бурали-Форти в 1897 году и оказался одним из первых парадоксов, показавших, что наивная теория множеств противоречива, а следовательно, непригодна для нужд математики. Несуществование множества всех порядковых чисел противоречит концепции наивной теории множеств, разрешающей построение множеств с произвольным свойством элементов, то есть термов вида "множество всех x таких, что P".
Тем не менее сущность кризиса не исчерпывалась только парадоксами, а заключалась также и в следующем.
* Во-первых, к концу XIX века среди математиков наметились существенные расхождения во взглядах на основные математические понятия и принципы, а также на логические принципы, используемые в математике.
* Во-вторых, возникли расхождения во взглядах на выбор путей избавления от парадоксов.
* Наконец, и по-видимому это самое главное, существовали принципиальные трудности обоснования непротиворечивости математики, её «спасения», многие из которых не преодолены до сих пор.
В результате различных взглядов на использование логических и теоретико-множественных принципов, а также различных взглядов на пути выхода из кризиса сформировались разные математические школы, яростно противостоявших друг другу.
Лидирующей школой являлась формалистская, самым ярким последователем которой был Давид Гильберт. Свои идеи он собрал в так называемой Гильбертовой программе, в которой предполагалось обосновать математику на небольшом логическом базисе, содержащемся в финитизме.
Основным противником данной школы была школа интуиционистов, отрицавшая возможность использования двойного отрицания и считающая недопустимым принятие принципа абстракции актуальной бесконечности. Возглавлял школу Лёйтзен Брауэр. Он безбоязненно отвергал формализм как бессмыссленную игру с символами. В 1920 году Гильберт добился исключения Брауэра, которого он считал угрозой математике, из группы редакторов Mathematische Annalen, главного математического журнала того времени.
Однако теоремы Гёделя о неполноте, доказанные в 1931 году, показали, что ключевые аспекты программы Гильберта не могут быть достигнуты.
Гёдель показал, как сконструировать для любой достаточно сильной и непротиворечивой рекурсивно аксиоматизируемой системы (такой, которая необходима, чтобы аксиоматизировать элементарную теорию арифметики на множестве натуральных чисел) утверждение, для которого может быть показана его правдивость, но не доказуемое системой. Таким образом, стало ясно, что математические основы не могут быть сведены к чисто формальной системе, как предполагалось в Гильбертовой программе. Тем самым был нанесен сокрушительный удар в сердце Гильбертовой программы, — программы, которая предполагала, что непротиворечивость может быть установлена финитическими средствами.В то же время, интуиционистская школа не привлекла к себе каких-либо постоянных последователей среди активных математиков из-за проблем в конструктивной математике.
Кризис всё ещё не пройден, но он затух. Большинство математиков или не работают с уровня аксиоматических систем, или, если работают, то не сомневаются в корректности системы ZFC, наиболее популярной аксиоматической системы. В большинстве разделов практической математики математические парадоксы и так не играли никакой роли, а в тех разделах, которые напрямую связаны с основами математики — в частности, математическая логика и теория категорий, — их можно обойти.
www.toalexsmail.com
Реферат Парадокс Сколема
скачатьРеферат на тему:
Парадокс Сколема представляет собой рассуждение, связанное с использованием теоремы Лёвенгейма — Сколема для аксиоматической теории множеств.
В отличие от парадокса Рассела, парадокса Кантора, парадокса Бурали-Форти, где при помощи логически верных выводов обнаруживается противоречие, «замаскированное» в исходных посылках, «противоречие» парадокса Сколема возникает от ошибки в рассуждениях, и аккуратное рассмотрение вопроса показывает, что это лишь мнимый парадокс. Тем не менее, рассмотрение парадокса Сколема имеет большую дидактическую ценность.
Формулировка
Если система аксиом любой аксиоматической теории множеств непротиворечива, то она в силу теорем Гёделя и Лёвенгейма — Сколема имеет модель и, более того, эта модель может быть построена на натуральных числах. То есть всего лишь счётное множество объектов M (каждый из которых будет соответствовать уникальному множеству) требуется для того, чтобы подобрать значение предиката для каждой пары объектов, полностью удовлетворяющее системам аксиом теории множеств (например, ZF или ZFC, см. Аксиоматика теории множеств). В такой ситуации для каждого объекта модели y лишь конечное или счётное количество объектов (больше просто нет в предметной области) могут входить в отношение
. Фиксируем такую модель
со счётным M в качестве предметной области.
В силу теорем ZF, вне зависимости от принятой модели в ZF выводимо, например, существование терма , мощность которого несчётна. Но в счётной модели любое множество вынужденно не более чем счётно — противоречие?
Разрешение
Проведём рассуждение аккуратно. Факт означает, что существует такой объект
, что формула первого порядка, соответствующая выражению
, истинна в модели
на оценке, при которой индивидной переменной x поставлен в соответствие объект c. Теорема Кантора утверждает, что x — несчётно, что по определению значит
(f</math> — биекция между
и ω) \and \exists f(f</math> - биекция между ω и
), где "f - биекция между A и B" означает
, где < x,y > - любое кодирование пар, например, < x,y > = x,y,x.
Но это значит лишь то, что среди элементов M нет такого f, что в модели оно удовлетворяло бы свойствам биекции между
и ω. При этом не важно, что в отношение принадлежности с объектом из M, соответствующим терму
может входить не более чем счётное число объектов из M — важно то, что среди объектов M не существует f, осуществляющего необходимую биекцию.
Рассуждение «если модель счётна, то в отношение с любым объектом может входить не более чем счётное число объектов» есть рассуждение внешнее по отношению к изучаемой аксиоматической теории и никакой формуле в этой теории не соответствует. С внешней точки зрения на теорию ZF «множество всех множеств» (второй раз слово «множество» здесь обозначает лишь некоторый объект предметной области ZF) может существовать и даже быть счётным, что никак не связано (и потому не может противоречить) с выводимыми в ZF формулами.
Литература
- Колмогоров А. Н., Драгалин А. Г. Математическая логика. — М.: УРСС, 2005. — 240 с.
- Френкель А. А., Бар-Хиллел И. Основания теории множеств. — М.: Мир, 1966. — 556 с.
wreferat.baza-referat.ru
Реферат Аксиоматика теории множеств
скачатьРеферат на тему:
План:
- Введение
- 1 Аксиомы ZFC
- 2 Пояснение к аксиомам ZFC
- 3 Примечания
- 4 Историческая справка Литература
Введение
Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, — из которых выводятся все теоремы и утверждения теории множеств.
Система аксиом Цермело—Френкеля (ZF) является стандартной системой аксиом для теории множеств. Эта и подобные ей системы аксиом любопытны потому, что любая математическая теория может быть «переведена» на язык теории множеств таким образом, что теоремы этой теории станут теоремами о множествах, доказуемыми из аксиом ZF (любой объект можно считать множеством, соответственно и переформулировать утверждение не представляет собой проблему).
К этой системе аксиом часто добавляют аксиому выбора, и называют системой Цермело — Френкеля с аксиомой выбора (ZFC).
Эта система аксиом записана на языке логики первого порядка, и содержит бесконечное количество аксиом. Существуют и другие, конечные системы. Например, система NBG (von Neumann — Bernays — Godel) наряду с множествами рассматривает так называемые классы объектов. NBG равносильна ZF в том смысле, что любая теорема о множествах (то есть не упоминающая о классах), доказуемая в одной системе, также доказуема и в другой.
1. Аксиомы ZFC
Аксиомами ZFC называется следующая совокупность высказываний теории множеств:
2. Пояснение к аксиомам ZFC
Аксиомы ZFC включают в себя:
0) группу высказываний о равенстве множеств (1 аксиома),
1) группу высказываний о существовании множеств (2 аксиомы),
2) группу высказываний об образовании множеств из уже имеющихся множеств (3 аксиомы и 2 схемы), в которой можно выделить три подгруппы,
3) группу высказываний об упорядоченности образованных множеств (2 аксиомы).
0. Критерий равенства множеств в ZFC
Следующее высказывание выражает необходимое условие идентичности двух множеств.
Аксиома экстенсиональности (Аксиома объёмности)
Примечание
«Аксиому объёмности» можно сформулировать следующим образом: «Если каждый элемент первого множества принадлежит второму множеству, а каждый элемент второго множества принадлежит первому множеству, тогда первое множество идентично второму [множеству].»
Достаточное условие идентичности двух множеств имеет вид и выводится из аксиом предиката
, а именно:
Соединение указанного достаточного условия [идентичности множеств] с аксиомой объёмности даёт следующий критерий равенства множеств:
1. Аксиомы ZFC о существовании множеств
«Аксиома объёмности» была бы бесполезным высказыванием, если бы не существовало ни одного множества или существовало только одно множество.
Следующие два высказывания гарантируют существование по меньшей мере двух разных множеств, а именно: а) множества, в котором нет ничего, и б) множества, содержащего бесконечное количество элементов.
1.0 Аксиома пустого множества
Примечание
«Аксиому [существования] пустого множества» можно сформулировать следующим образом: «Существует [по меньшей мере одно] множество без единого элемента.»
Доказывается, что «аксиома пустого множества» равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя. Употребительны два имени:
и
. Используя указанные имена, «аксиому пустого множества» записывают так:
1.1 Аксиома бесконечности
Примечание
«Аксиому бесконечности» можно сформулировать следующим образом: «Существует [по меньшей мере одно] „бесконечное множество“, которое состоит из .»
Высказывание о существовании бесконечного множества отличается от (ложного в данной аксиоматике) высказывания о существовании «множества всех множеств» ().
2. Аксиомы ZFC об образовании множеств
Следующие пять высказываний можно назвать аксиомами образования множеств [из имеющихся множеств, включая и по меньшей мере одну
].
Каждое из этих пяти высказываний создано на основе высказывания , которое выводится из аксиом предиката
.
Эти пять высказываний можно объединить в следующие подгруппы:
2.0) группу постулатов об образовании множеств путём перечисления их элементов,
2.1) группу деклараций об учреждении и об упразднении семейств множеств,
2.2) группу схем образования множеств с помощью математически корректных суждений.
2.0. Постулаты об образовании множеств путём перечисления их элементов
Простейший способ образовать новое множество [из уже имеющихся множеств] состоит в том, чтобы «ткнуть пальцем» в каждое множество, которое должно стать элементом [образуемого множества]. В ZFC указанный способ образования множеств представлен одной аксиомой, в которой «тыканье пальцем» моделируется с помощью предиката .
2.0 Аксиома пары
Примечание
«Аксиому [неупорядоченной] пары» можно сформулировать следующим образом: «Из любых двух множеств можно образовать „неупорядоченную пару“, то есть такое множество , каждый элемент
которого идентичен данному множеству
или данному множеству
».
Доказывается, что «аксиома пары» равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя
. Используя указанное имя, «аксиому пары» записывают так:
2.1. Декларации об учреждении и об упразднении семейств множеств
Следующие две аксиомы, именуемые «аксиомой множества подмножеств» и «аксиомой объединения», можно рассматривать как естественное дополнение к «аксиоме пары». Чтобы убедиться в этом, заметим следующее.
Известно, что каждое множество имеет подмножества, включая [копию пустого множества]
и [копию самого множества]
. Иначе говоря,
Руководствуясь «аксиомой пары», из названных подмножеств можно образовать неупорядоченную пару . Назовём эту пару семейством
.
Если можно образовать семейство из двух подмножеств множества
, тогда можно объявить об образовании семейства
из всех подмножеств множества
.
Если можно объявить об учреждении семейства , тогда можно объявить об упразднении названного семейства.
Из изложенного следует, что высказывания и
можно считать независимыми условно.
2.1.0 Аксиома множества подмножеств (Аксиома булеана)
Примечание
«Аксиому множества подмножеств» можно сформулировать следующим образом: «Из любого множества можно образовать „суперкучу“, то есть такое множество , каждый элемент
которого является [собственным либо несобственным] подмножеством
данного множества
.»
Доказывается, что «аксиома множества подмножеств» равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя
, которое произносится: «множество всех подмножеств [множества]
» или «булеан [множества]
». Используя указанное имя, «аксиому множества подмножеств» записывают так:
2.1.1 Аксиома объединения
Примечание
Аксиому объединения [множеств] можно сформулировать следующим образом: «Из любого семейства множеств можно образовать „кучу-малу“, то есть такое множество , каждый элемент
которого принадлежит по меньшей мере одному множеству
данного семейства
».
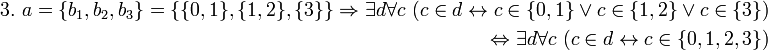
Доказывается, что аксиома объединения равносильна высказыванию . Поэтому единственному множеству
можно присвоить имя
, которое произносится: «объединение множеств семейства
». Используя указанное имя, аксиому объединения записывают так:
Объединение множеств семейства (
) не следует путать с пересечением множеств семейства
(
), о котором известно:
2.2. Схемы образования множеств с помощью математически корректных суждений
Среди математических высказываний встречаются аксиомы связи, включая:
а) аксиому связи между алгебраической операцией (сложить) и алгебраической операцией
(умножить)
б) аксиому связи между отношением порядка (меньше или равно) и алгебраической операцией
(сложить)
Следующие два высказывания, именуемые «схемой выделения» и «схемой преобразования», являются аксиомами связи между множествами (например, множеством ) и математически корректными суждениями (например, суждением
).
«Схема выделения» и «схема преобразования» выражают следующую простую мысль: «Каждое математически корректное суждение об элементах любого множества приводит к образованию [того же самого или другого] множества.»
Математически корректные суждения, фигурирующие в «схеме выделения», позволяют «довести [до товарного вида]» множества, которые образованы, например, с помощью аксиомы булеана. Поэтому указанные математические суждения аналогичны штихелям, надфелям, часовым отвёрткам и иным доводочным инструментам.
Математически корректные суждения, фигурирующие в «схеме преобразования», позволяют создавать «[математические] изделия» из ["неотёсанных"] множеств, образованных, например, с помощью аксиомы булеана. Поэтому указанные математические суждения аналогичны прецизионным станкам.
2.2.0 Схема выделения
Примечание
Схему выделения [подмножеств] можно сформулировать следующим образом: «Из каждого множества можно выделить [по меньшей мере одно] подмножество , высказав суждение
о каждом элементе
данного множества
.»
![\begin{align} 6. \
(\Phi[x] \leftrightarrow \exist k \ (k \in \mathbb{N} \land x = 2k)) \land a = \mathbb{N} \Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathbb{N} \land \exist k \ (k \in \mathbb{N} \land b = 2k))
\\ \
\Leftrightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \{0,2,4,6,...\})
\end{align}](/800/600/http/upload.wikimedia.org//math/b/0/7/b0727116ef47508606afb1be6ff1f495.png)
![\begin{align} 7. \
(\Phi[x] \ \leftrightarrow \ \exist u \exist v \ (u \in U \ \land \ v \in V \ \land \ x = (u,v) \ ) \ ) \quad \land \quad a = \mathcal{P}(\mathcal{P}(U \cup V))
\\ \
\Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathcal{P}(\mathcal{P}(U \cup V)) \ \land \ \exist u \exist v \ (u \in U \land v \in V \land b = (u,v)))
\end{align}](/800/600/http/upload.wikimedia.org//math/4/1/c/41c0a6d82a7a120016a40d2ccbd327d4.png)
Доказывается, что схема выделения равносильна высказыванию . Поэтому единственному подмножеству
можно присвоить имя
. Используя указанное имя, схему выделения записывют так:
Схема выделения равносильна счётному множеству аксиом.
2.2.1 Схема преобразования
Примечание
Схему преобразования [множеств] можно сформулировать следующим образом: «Любое множество можно преобразовать в [то же самое или другое] множество , высказав любое истинное математически корректное функциональное суждение
обо всех элементах
данного множества
.»
![\begin{align} 2. \
(\phi[x,y] \leftrightarrow y = x^2) \ \land \ a = \{1,2,3\} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \{1,2,3\} \ \land \ c = b^2))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{1,4,9\})
\end{align}](/800/600/http/upload.wikimedia.org//math/2/4/2/2425aa016eef88362a816f214f6f0705.png)
![\begin{align} 4. \
(\phi[x,y] \leftrightarrow (x = \varnothing \to y = a_1) \land (x \ne \varnothing \to y = a_2) \ ) \quad \land \quad a = \mathcal{P}(\mathcal{P}(\varnothing)) = \{\varnothing, \{\varnothing\}\}
\\ \
\Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \{\varnothing, \{\varnothing\}\} \land (b = \varnothing \to c = a_1) \land (b \ne \varnothing \to c = a_2)\ ))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c = a_1 \ \lor \ c = a_2)
\end{align}](/800/600/http/upload.wikimedia.org//math/c/5/b/c5bb14b0c297a15d1137ccc22ec6826f.png)
![\begin{align} 5. \
(\phi[x,y] \leftrightarrow y = 2x) \ \land \ a = \mathbb{N} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \mathbb{N} \land c = 2b))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{0,2,4,6,...\})
\end{align}](/800/600/http/upload.wikimedia.org//math/3/0/f/30f0f864a1e171c485838d5c6059450e.png)
![\begin{align} 6. \
(\phi[x,y] \leftrightarrow y = 2x + 1) \ \land \ a = \mathbb{N} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \mathbb{N} \land c = 2b + 1))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{1,3,5,7,...\})
\end{align}](/800/600/http/upload.wikimedia.org//math/6/3/1/6316623a316fcedfb05a300077fb3cf8.png)
![\begin{align} 7. \
(\phi[x,y] \leftrightarrow (x \in \mathbb{N} \ \land \ x < 2 \to y = x) \ \land \ (x \in \mathbb{N} \ \land \ \neg (x < 2) \to y = 1)) \quad \land \quad a = \mathbb{N}
\\ \
\Rightarrow \exist d \forall c (c \in d \leftrightarrow \exist b (b \in \mathbb{N} \ \land \ (b \in \mathbb{N} \land b < 2 \to c = b) \ \land \ (b \in \mathbb{N} \land \neg (b < 2) \to c = 1)))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \mathbb{N} \ \land \ c < 2) \Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{0,1\})
\end{align}](/800/600/http/upload.wikimedia.org//math/8/9/6/8965999f79908556c163beba8eb3c331.png)
Доказывается, что в схеме преобразования множество единственно. Поэтому указанному множеству можно присвоить имя
. Используя указанное имя, схему преобразования записывают так:
Схема преобразования равносильна счётному множеству аксиом.
3. Аксиомы ZFC об упорядоченности множеств
Следующие два высказывания определяют упорядоченность множеств, которые образованы из и каждой
с помощью аксиом образования множеств. Образно говоря, высказывания об упорядоченности множеств образуют «сортировочный цех» теории ZFC, тогда как высказывания об образовании множеств образуют «производственный цех» этой теории.
3.0 Аксиома регулярности
Примечание
«Аксиому регулярности» можно сформулировать следующим образом: «В любом семействе множеств есть [по меньшей мере одно] множество , каждый элемент
которого не принадлежит данному семейству
.»
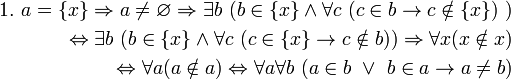 Сравните с высказываниями
Сравните с высказываниями 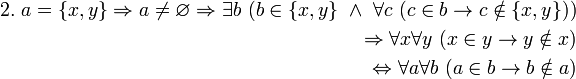 Сравните с высказываниями
Сравните с высказываниями 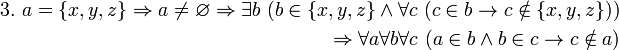 Сравните с высказываниями
Сравните с высказываниями 3.1 Аксиома выбора
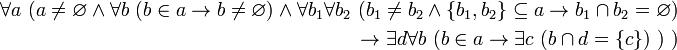
Примечание
«Аксиому выбора» можно сформулировать следующим образом: «Из любого семейства непустых попарно непересекающихся множеств можно выбрать „делегацию“, то есть такое множество , в котором есть по одному элементу
от каждого множества
данного семейства
.»
3. Примечания
1. Непротиворечивость аксиоматики ZFC не установлена.
4. Историческая справка
По-видимому, первоначальный вариант теории множеств, умышленно названный немецким математиком Георгом Кантором учением о множествах, состоял из двух аксиом, а именно:
1) аксиомы объёмности«Аксиома математической свободы» имеет рациональные следствия, включая следующие:
В 1903 году английский философ Бертран Рассел обратил внимание на следующее:
1) руководствуясь «аксиомой математической свободы», невозможно отличить «свободу» от «вседозволенности», 2) выбрав в качествеЭти критические высказывания о «немецком учении [о множествах]» побудили немецкого математика Эрнста Цермело заменить «аксиому математической свободы» такими её следствиями, которые не вызывали бы протеста ни у математиков, ни у философов.
В 1908 году в журнале Mathematische Annalen Эрнст Цермело опубликовал следующие семь аксиом:
1) Axiom der Bestimmtheit, то есть аксиому объёмности, 2) Axiom der Elementarmengen, то есть аксиому о существовании «элементарных множеств»Так «учение о множествах» превратилось в теорию множеств, а именно в теорию ZC [Zermelo set theory with the Axiom of Choice].
Последняя аксиома теории ZC (аксиома бесконечности) сблизила сторонников Георга Кантора со сторонниками Леопольда Кронекера, которые рассматривали множество натуральных чисел как священный грааль математики.
Предпоследняя аксиома теории ZC (аксиома выбора) стала предметом оживлённых математических дискуссий. Действительно, эта аксиома не является следствием «аксиомы математической свободы».
В 1922 году немецкий математик Абрахам Френкель и норвежский математик Торальф Сколем (Thoralf Skolem) дополнили теорию ZC схемой преобразования. В результате теория ZC превратилась в теорию ZFC [Zermelo-Fraenkel set theory with the Axiom of Choice].
В 1925 году венгерский математик Джон фон Нейман дополнил теорию ZFC аксиомой регулярности. Одно из следствий этой аксиомы () «похоронило» и «множество всех множеств», и «парадокс Рассела».
Литература
- Колмогоров А. Н., Драгалин А. Г. Математическая логика. — М.: УРСС, 2005. — 240 с.
- Френкель А. А., Бар-Хиллел И. Основания теории множеств. — М.: Мир, 1966. — 556 с.
- Аксиоматика теории множеств - planetmath.org/encyclopedia/ZermeloFraenkelAxioms.html (англ.) на сайте PlanetMath.
www.wreferat.baza-referat.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|